Effect of the Degree of Hybridization and Energy Management Strategy on the Performance of a Fuel Cell/Battery Vehicle in Real-World Driving Cycles
Abstract
1. Introduction
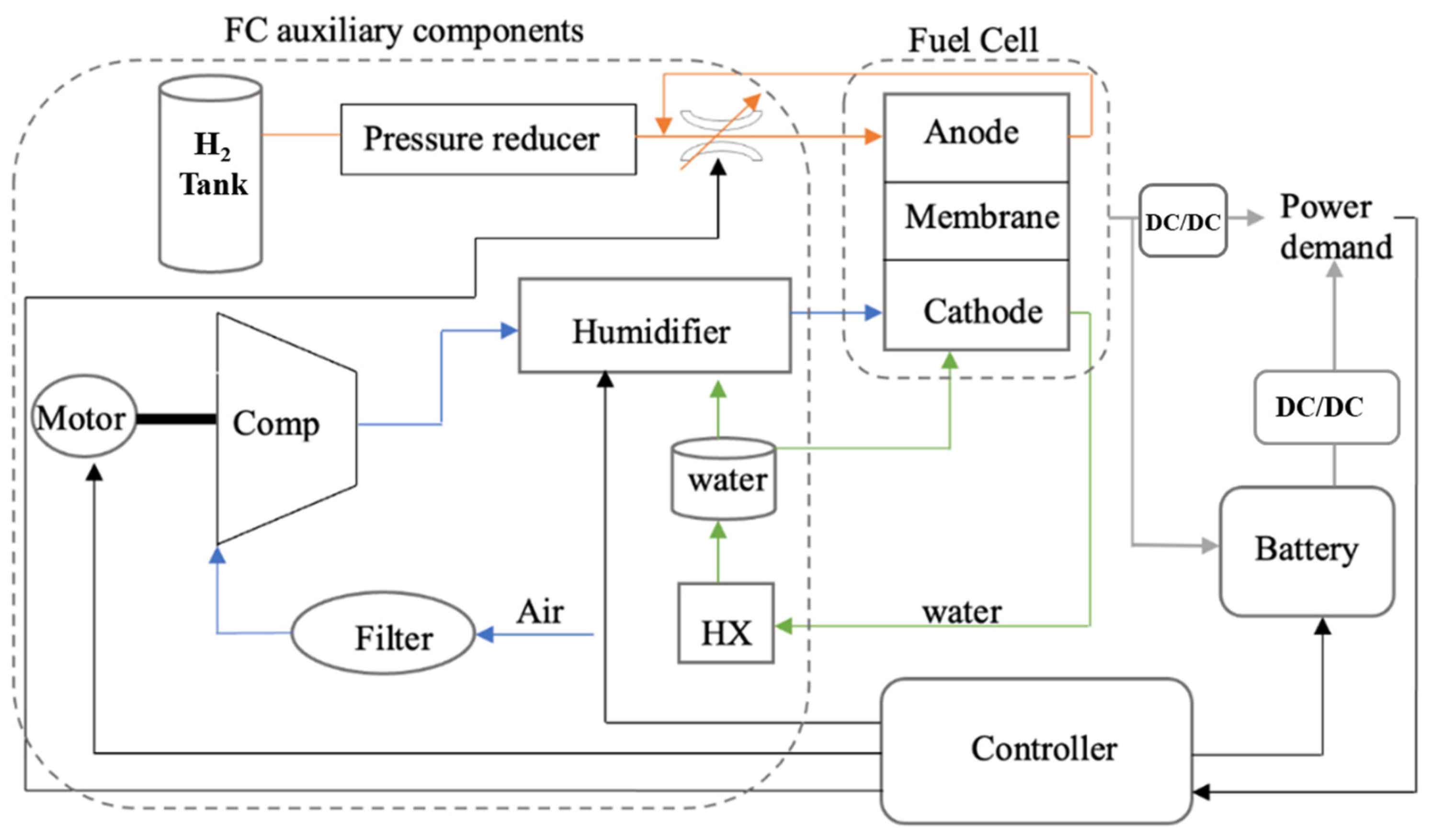
2. Methodology and Adopted Models
2.1. Energy Management System (EMS)
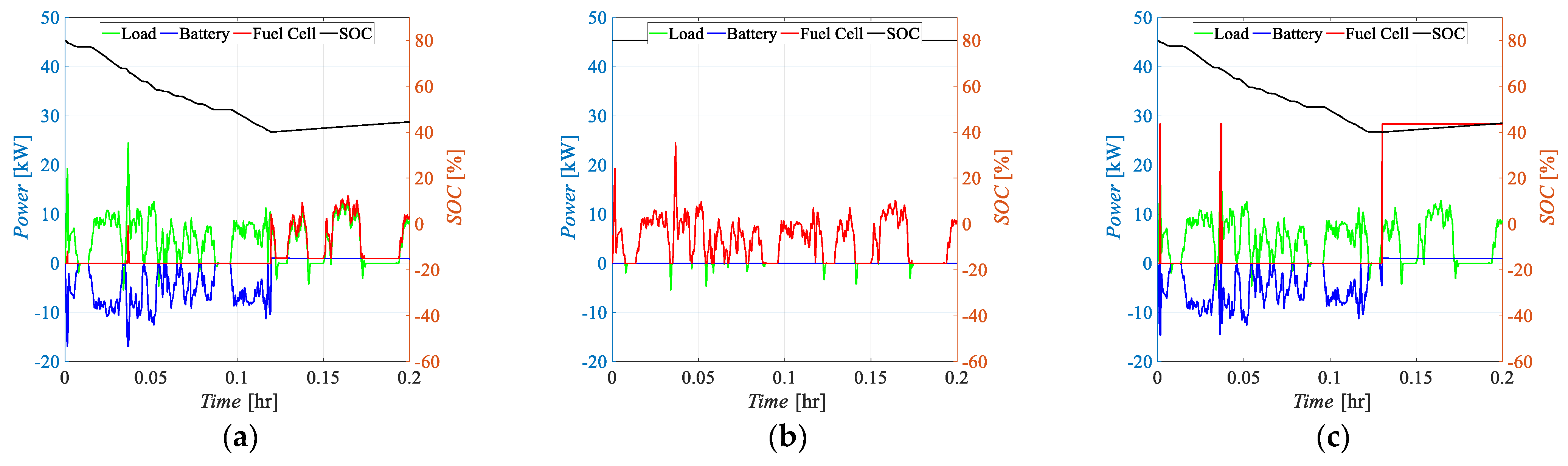
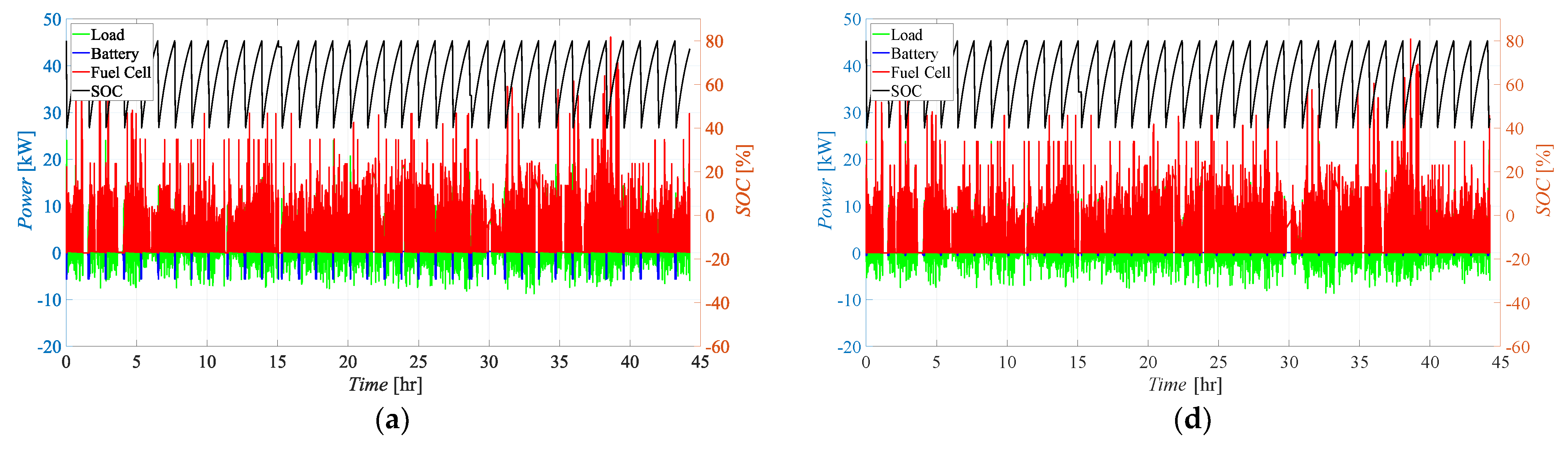
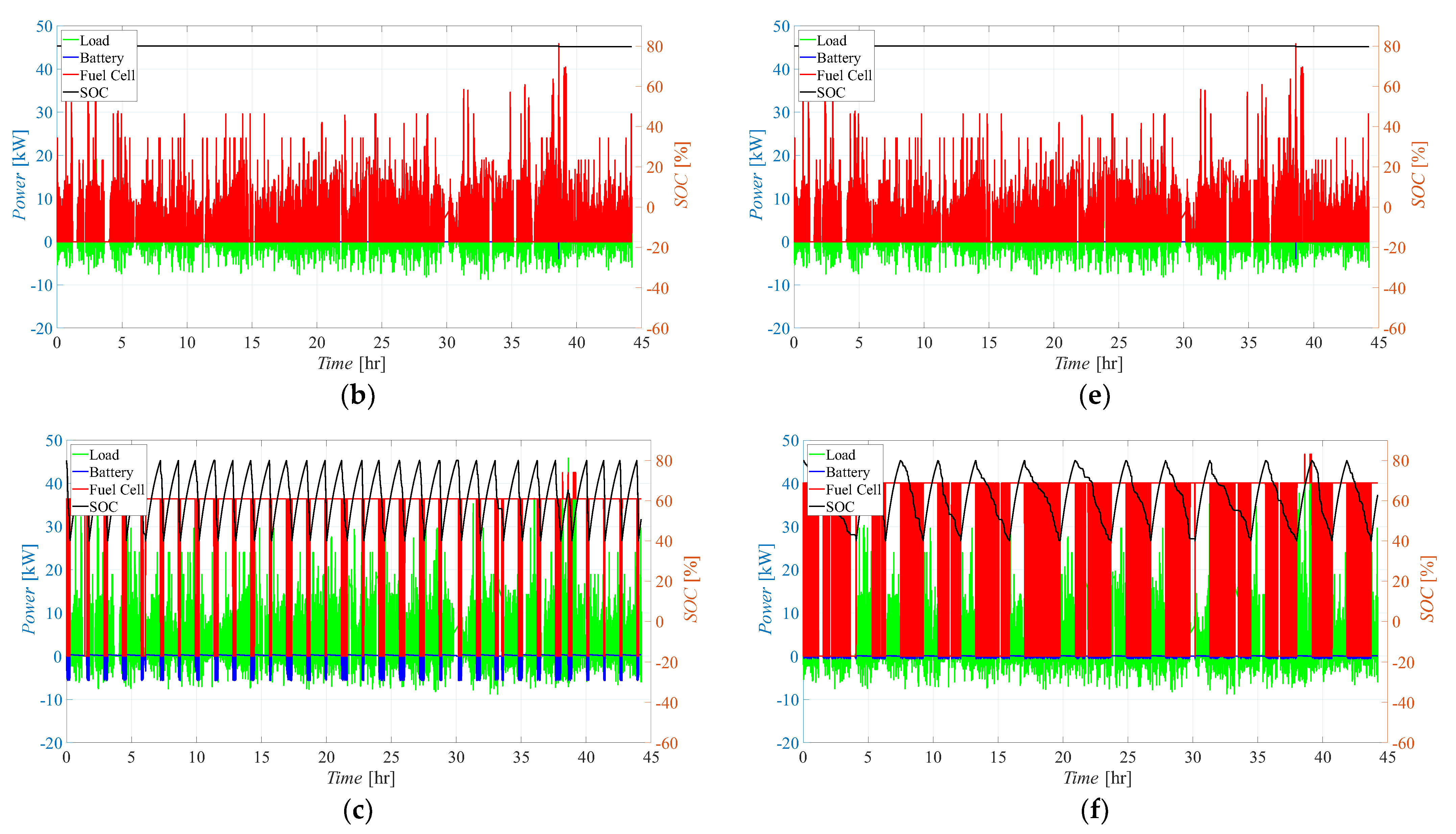
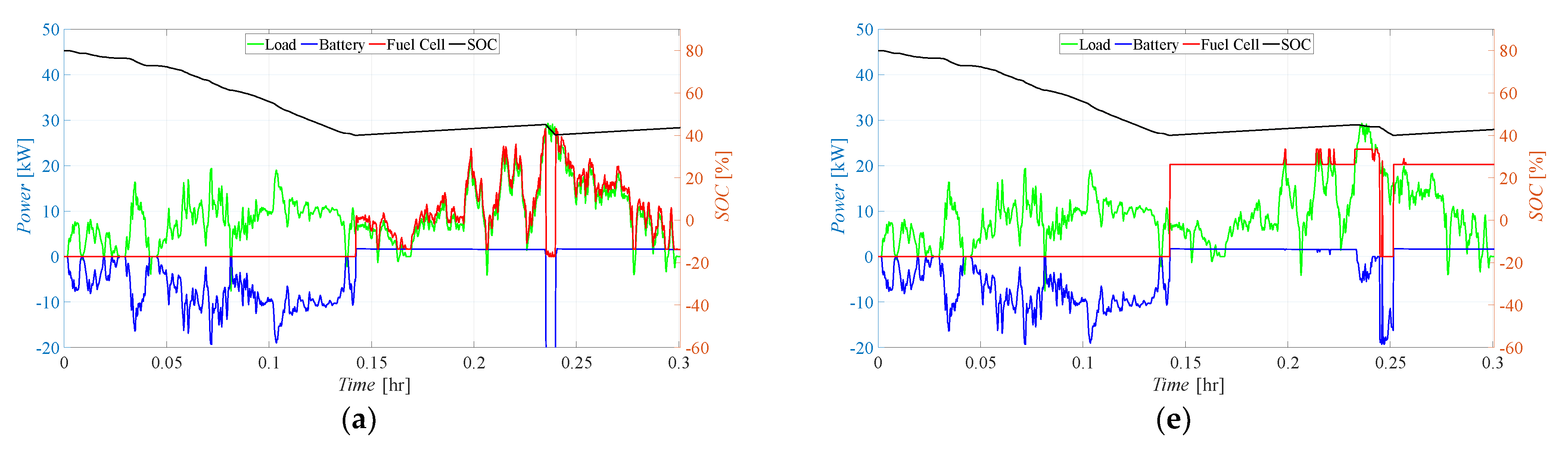
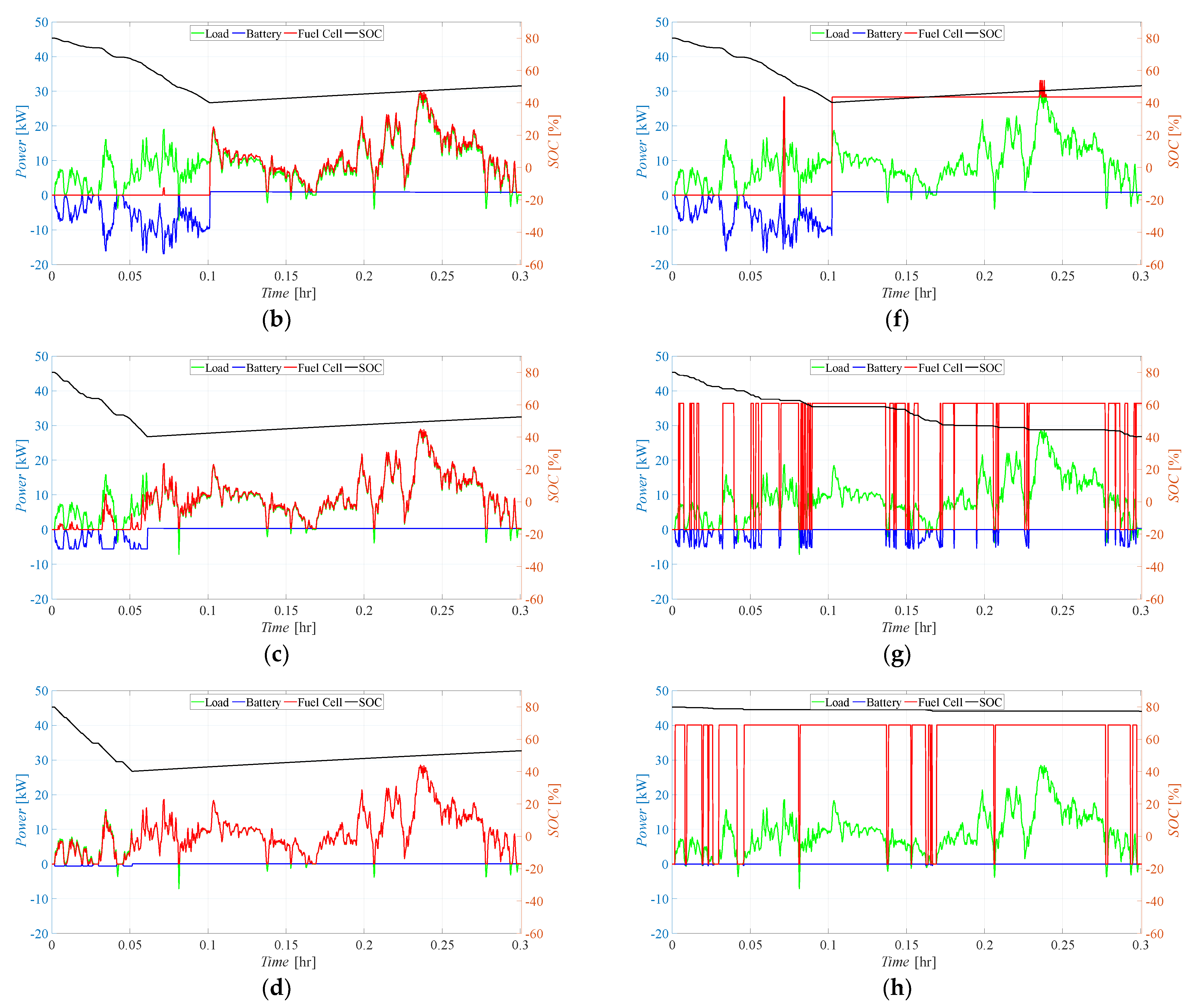
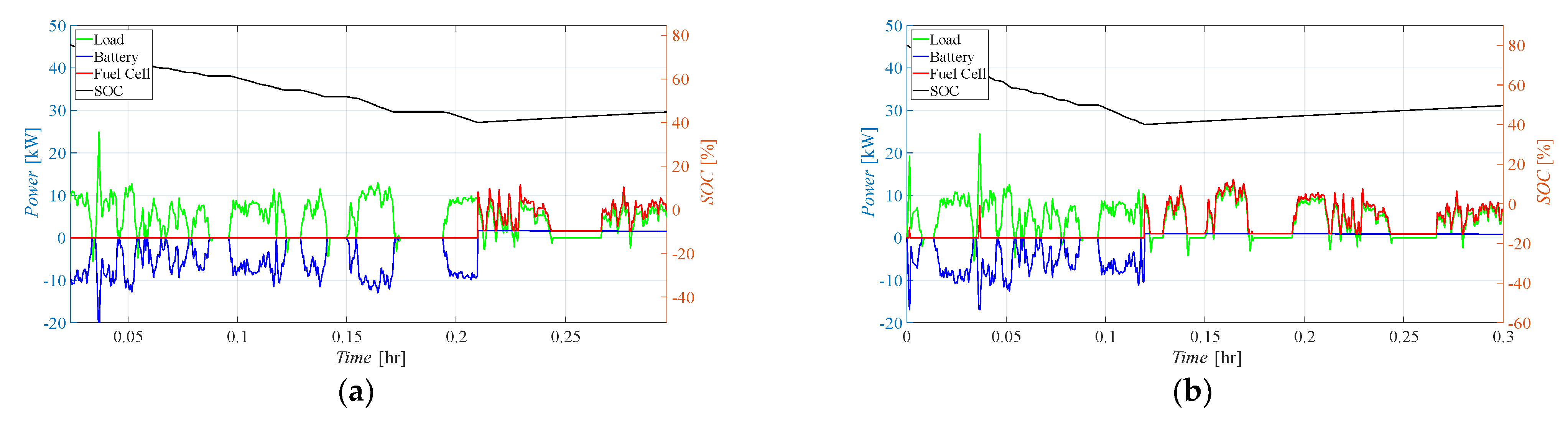
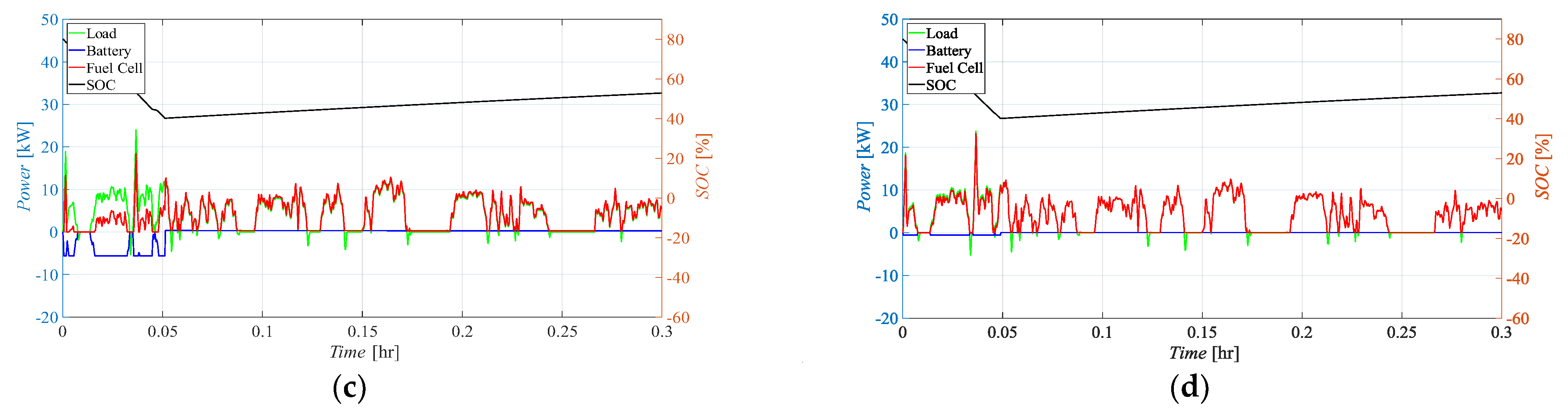
- Battery Main (BTM): In this case, the power is provided mainly by the batteries, with the FC activating only to cover the peaks or to recharge the batteries when their state of charge falls below (in this case also covering the load);
- Fuel Cell Main (FCM): In the second control logic, the FC operates continuously in response to the load, with additional support from batteries during demand peaks. The batteries are charged when the load is smaller than the FC maximum power and SOC is smaller than ;
- Fuel Cell Fixed (FCF): In the third scenario, the FC operates only in the range between 90 and 105% of its nominal power (Pfc,nom = 0.8·Pfc,max) to protect its lifespan. The batteries cover the peaks and follow the load when it is smaller than the FC operating range. In the case that the batteries’ SOC becomes smaller than , and the load is smaller than the FC’s working power range, the FC covers the load and recharges the batteries. Since the FC always works between 90 and 105% of its nominal power, during battery recharge it may result in fuel waste when the load is very small. If the load is larger than 1.05·Pfc,nom, batteries should cover the gap, even if the SOC is smaller than , until needed or until they can.
2.2. Fuel Cell Degradation Prediction
3. Simulation Details
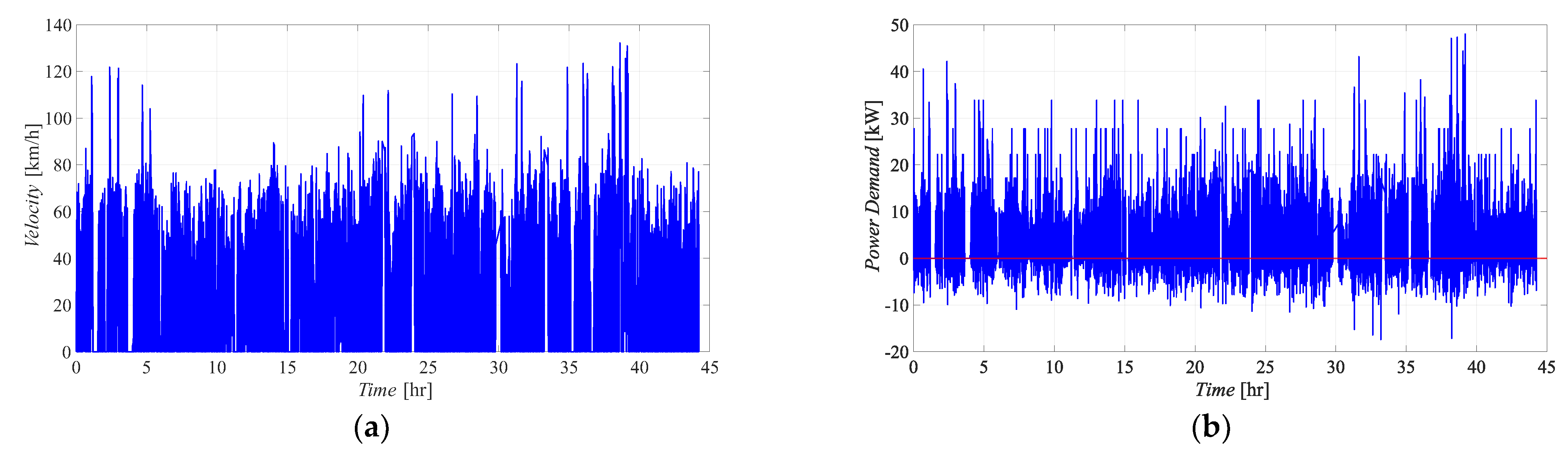
3.1. Case of Study and Generation of Power Demand Curve
3.2. Vehicle Powertrain Sizing
4. Results
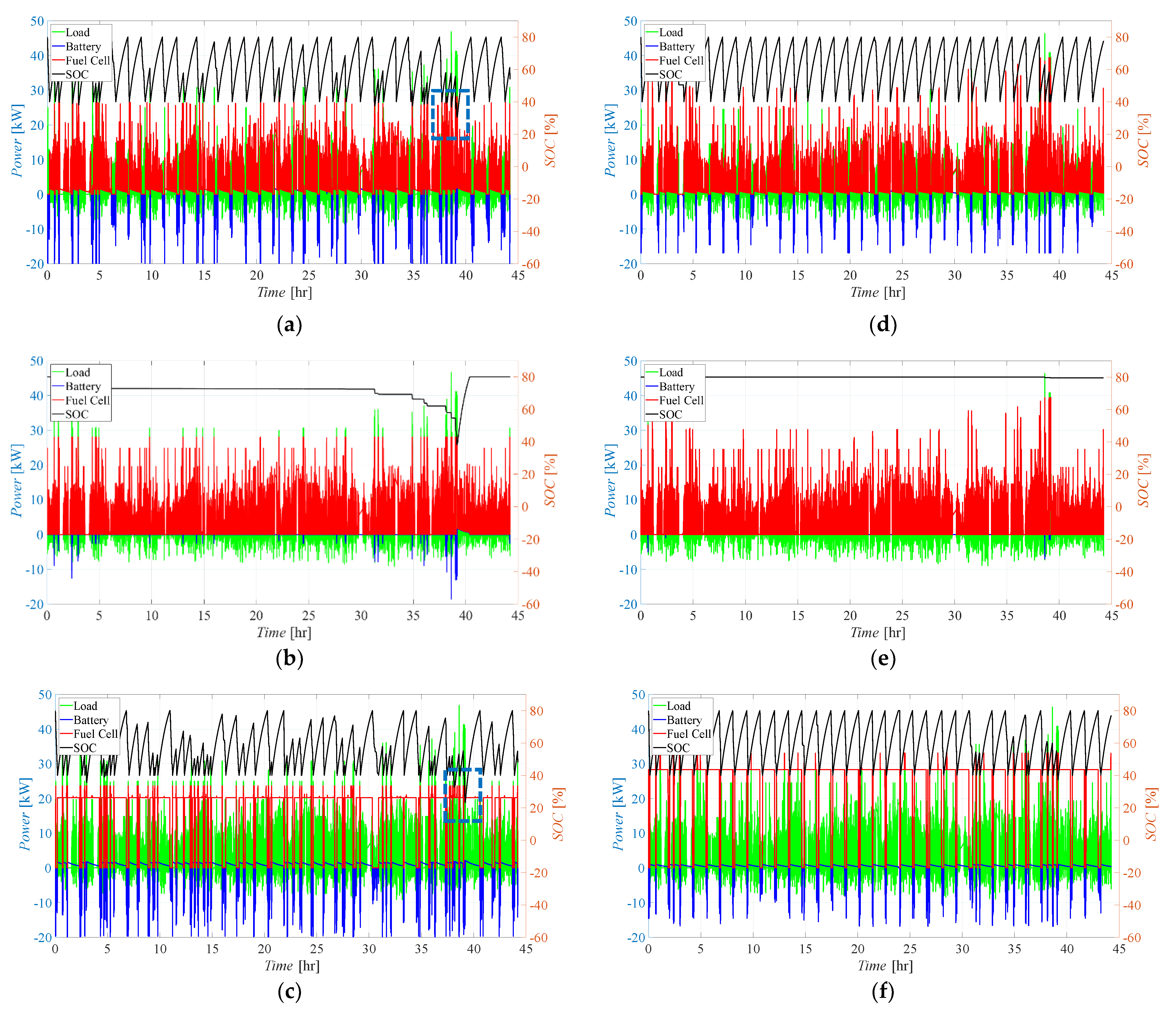
4.1. Effects of the Control Logic
4.2. Effects of the Degree of Hybridization
4.3. Effect of the Driving Cycles
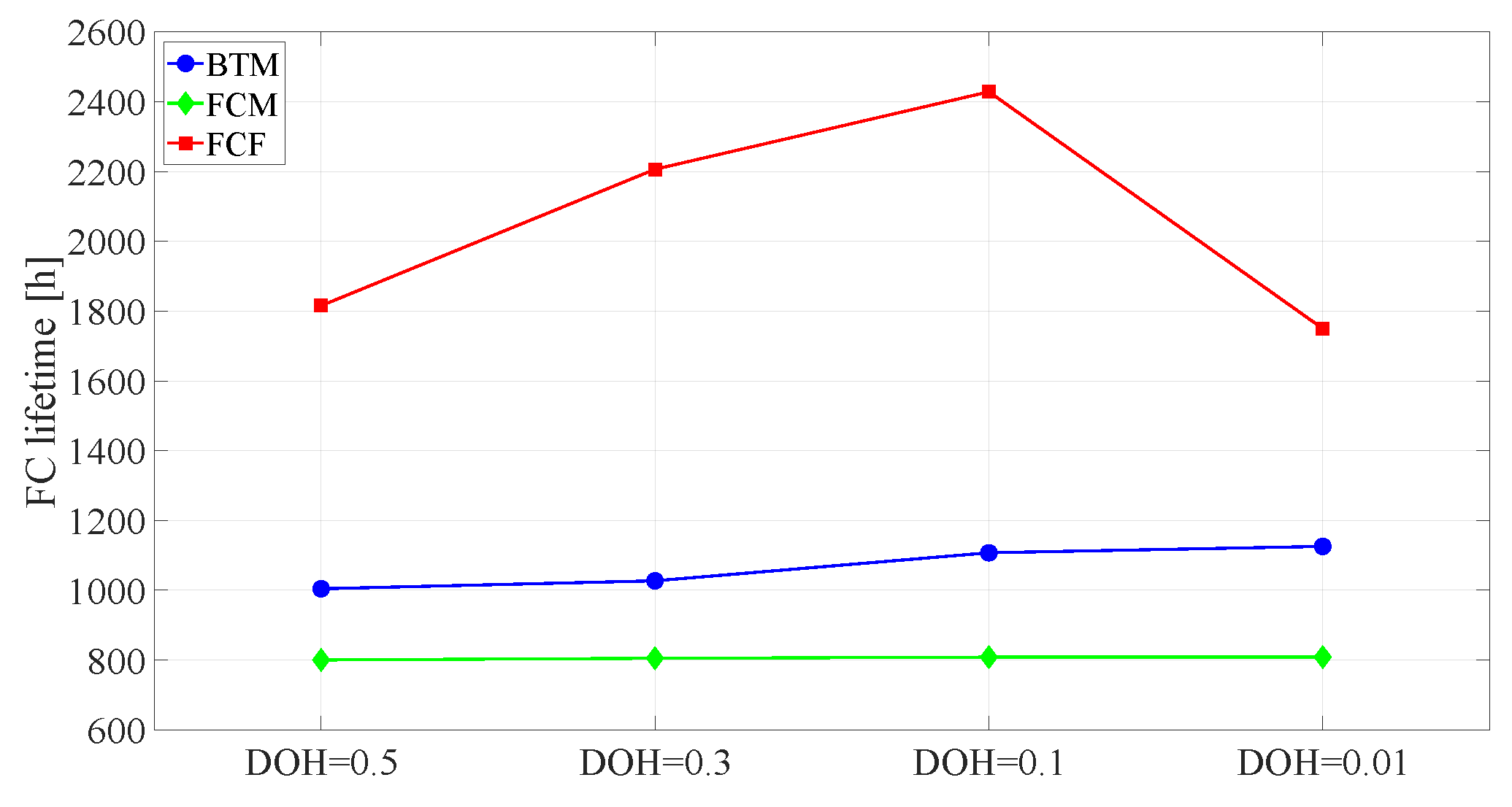
4.4. Fuel Cell Lifetime Prediction and Aging Effect on Vehicle Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eriksson, E.L.V.; Gray, E.M. Optimization and integration of hybrid renewable energy hydrogen fuel cell energy systems—A critical review. Appl. Energy 2017, 202, 348–364. [Google Scholar] [CrossRef]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef]
- IEA. Renewables 2022, Analysis and Forecast to 2027; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Bang, Y.H.; Di Noto, V. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- IEA. The Future of Hydrogen; IEA: Paris, France, 2019; Available online: https://www.iea.org/reports/the-future-of-hydrogen (accessed on 18 January 2024).
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzhahrani, H.; Senior, B.T.F.; Ashuri, T.; Krohn, J. Hydrogen Fuel Cell Vehicles; Current Status and Future Prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- Yue, M.; LambertM, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Krithika, V.; Subramani, C. A comprehensive review on choice of hybrid vehicles and power converters, control strategies for hybrid electric vehicles. Int. J. Energy Res. 2018, 42, 1789–1812. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Control strategies for high-power electric vehicles powered by hydrogen fuel cell, battery and supercapacitor. Expert Syst. Appl. 2013, 40, 4791–4804. [Google Scholar] [CrossRef]
- Niu, L.; Yang, H.; Zhang, Y. Intelligent HEV Fuzzy Logic Control Strategy Based on Identification and Prediction of Drive Cycle and Driving Trend. World J. Eng. Technol. 2015, 3, 215–226. [Google Scholar] [CrossRef]
- Ettihir, K.H.; Cano, M.H.; Boulon, L.; Agbossou, K. Design of an adaptive EMS for fuel cell vehicles. Int. J. Hydrogen Energy 2017, 42, 1481–1489. [Google Scholar] [CrossRef]
- Fu, Z.; Zhu, L.; Tao, F.; Si, P.; Sun, L. Optimization based energy management strategy for fuel cell/battery/ultracapacitor hybrid vehicle considering fuel economy and fuel cell lifespan. Int. J. Hydrogen Energy 2020, 45, 8875–8886. [Google Scholar] [CrossRef]
- Wu, D.; Guan, Y.; Xia, X.; Du, C.; Yan, F.; Li, Y.; Hua, M.; Liu, W. Coordinated control of path tracking and yaw stability for distributed drive electric vehicle based on AMPC and DYC. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Meng, Z.; Xia, X.; Xu, R.; Liu, W.; Ma, J. HYDRO-3D: Hybrid object detection and tracking for cooperative perception using 3D LiDAR. IEEE Trans. Intell. Veh. 2023, 8, 4069–4080. [Google Scholar] [CrossRef]
- Marx, N.; Hissel, D.; Gustin, F.; Boulon, L.; Agbossou, K. On the sizing and energy management of an hybrid multistack fuel cell—Battery system for automotive applications. Int. J. Hydrogen Energy 2017, 42, 1518–1526. [Google Scholar] [CrossRef]
- Alpaslan, E.; Karaoğlanm, U.M.; Colpan, C.O. Investigation of drive cycle simulation performance for electric, hybrid, and fuel cell powertrains of a small-sized vehicle. Int. J. Hydrogen Energy 2017, 48, 39497–39513. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Wang, S. Multi-objective energy management strategy for fuel cell hybrid electric vehicle based on stochastic model predictive control. ISA Trans. 2022, 131, 178–196. [Google Scholar] [CrossRef]
- Fontaras, G.; Zacharof, N.G.; Ciuffo, B. Fuel consumption and CO2 emissions from passenger cars in Europe—Laboratory versus real-world emissions. Prog. Energy Combust. Sci. 2017, 60, 97–131. [Google Scholar] [CrossRef]
- Oh, G.; Leblanc, D.J.; Peng, H. Vehicle Energy Dataset (VED), A Large-Scale Dataset for Vehicle Energy Consumption Research. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3302–3312. [Google Scholar] [CrossRef]
- Andrè, M. The ARTEMIS European driving cycles for measuring car pollutant emissions. Sci. Total Environ. 2004, 334–335, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Sagaria, S.; Neto, R.C.; Baptista, P. Assessing the performance of vehicles powered by battery, fuel cell and ultra-capacitor: Application to light-duty vehicles and buses. Energy Convers. Manag. 2021, 229, 113767. [Google Scholar] [CrossRef]
- Wang, Y.; Moura, S.J.; Advani, S.G.; Prasad, A.K. Power management system for a fuel cell/battery hybrid vehicle incorporating fuel cell and battery degradation. Int. J. Hydrogen Energy 2019, 44, 8479–8492. [Google Scholar] [CrossRef]
- Hahn, S.; Braun, J.; Kemmer, H.; Reuss, H.C. Optimization of the efficiency and degradation rate of an automotive fuel cell system. Int. J. Hydrogen Energy 2021, 46, 29459–29477. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Ni, Y.; Lyu, C.; Wu, C.; Zhang, H.; Yang, Q.; Feng, F. Fast Identification of Micro-Health Parameters for Retired Batteries Based on a Simplified P2D Model by Using Padé Approximation. Batteries 2023, 9, 64. [Google Scholar] [CrossRef]
- TRNSYS 18: A Transient System Simulation Program; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2017. Available online: https://sel.me.wisc.edu/trnsys (accessed on 18 January 2024).
- Amin; Bambang, R.T.; Rohman, A.S.; Dronkers, C.J.; Ortega, R.; Sasongko, A. Energy Management of Fuel Cell/Battery/Supercapacitor Hybrid Power Sources Using Model Predictive Control. IEEE Trans. Ind. Inform. 2014, 10, 1992–2002. [Google Scholar] [CrossRef]
- Ziaeinejad, S.; Sangsefidi, Y.; Mehrizi-Sani, A. Fuel Cell-Based Auxiliary Power Unit: EMS, Sizing, and Current Estimator-Based Controller. IEEE Trans. Veh. Technol. 2016, 65, 4826–4835. [Google Scholar] [CrossRef]
- Kim, M.; Sohn, Y.S.; Lee, W.L.; Kim, C.S. Fuzzy control based engine sizing optimization for a fuel cell/battery hybrid mini-bus. J. Power Sources 2008, 178, 706–710. [Google Scholar] [CrossRef]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. A user-friendly advanced powertrain simulation using a combined backward/forward approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Borup, R.; Meyers, R.; Pivovar, B.; Kim, Y.S.; Mukundan, R. Scientific Aspects of Polymer Electrolyte Fuel Cell Durability and Degradation. Chem. Rev. 2007, 107, 3904–3951. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Chu, Y.; Xie, Z.; Eggen, K.; Girard, F.; Shi, Z. Effects of Fuel Cell Operating Conditions on Proton Exchange Membrane Durability at Open-Circuit Voltage. Fuel Cells 2020, 20, 176–184. [Google Scholar] [CrossRef]
- Bai, X.; Luo, L.; Huang, B.; Jian, Q.; Cheng, Z. Performance improvement of proton exchange membrane fuel cell stack by dual-path hydrogen supply. Energy 2022, 246, 123297. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Han, J.; Nguyen, X.L.; Goo, Y.-M.; Le, D.D. Review of the Durability of Polymer Electrolyte Membrane Fuel Cell in Long-Term Operation: Main Influencing Parameters and Testing Protocols. Energies 2021, 14, 4048. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Li, W.; Wang, Z.; Wang, S.; Xie, X.; Ramani, V. A high-performance membrane electrode assembly for polymer electrolyte membrane fuel cell with poly(arylene ether sulfone) nanofibers as effective membrane reinforcements. J. Power Sources 2019, 444, 227250. [Google Scholar] [CrossRef]
- Pivac, I.; Bezmalinović, D.; Barbir, F. Catalyst degradation diagnostics of proton exchange membrane fuel cells using electrochemical impedance spectroscopy. Int. J. Hydrogen Energy 2018, 43, 13512–13520. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.; Xu, L.; Hu, Z.; Jia, X.; Qin, Z.; Li, J.; Ouyang, M. Characteristic Analysis of Fuel Cell Decay Based on Actual Vehicle Operating Conditions. In Proceedings of the IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021. [Google Scholar]
- Chen, H.; Pei, P.; Song, M. Lifetime prediction and the economic lifetime of Proton Exchange Membrane fuel cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Fragiacomo, P.; Piraino, F.; Genovese, M.; Flaccomio, L.; Dei, N.; Donati, D.; Migliarese Caputi, M.V.; Borello, D. Sizing and Performance Analysis of Hydrogen- and Performance Analysis of Hydrogen- and Battery-Based Powertrains, Integrated into a Passenger Train for a Regional Track, Located in Calabria (Italy). Energies 2022, 15, 6004. [Google Scholar] [CrossRef]
- DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles. Available online: https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles (accessed on 18 January 2024).


| Operating Conditions | Voltage Degradation Rate |
|---|---|
| Start–Stop | |
| Idling | |
| Load Change | |
| High Power Load |
| DOH | Pfc,max [kW] | Pbat,max [kW] | Cbat [Wh] | Wbat [kg] | Wfc [kg] | Wfc,sys [kg] | Wkerb [kg] | |
|---|---|---|---|---|---|---|---|---|
| Pmot | 0.5 | 28.13 | 28.13 | 2812.50 | 100.9 | 11.43 | 103.18 | 1550 |
| 50 | 0.3 | 39.38 | 16.88 | 1687.50 | 60.5 | 16.00 | 107.75 | 1514 |
| Ptot | 0.1 | 50.63 | 5.63 | 562.50 | 20.2 | 20.57 | 112.32 | 1478 |
| 56 | 0.01 | 55.69 | 0.56 | 56.25 | 2.02 | 22.62 | 114.38 | 1462 |
| Hydrogen Consumption (kg) | FC Efficiency | System Efficiency | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DOH | BTM | FCM | FCF | BTM | FCM | FCF | BTM | FCM | FCF |
| 0.50 | 12.06 | 11.96 | 44.88 | 0.61 | 0.59 | 0.5 | 0.54 | 0.54 | 0.15 |
| 0.30 | 11.42 | 11.33 | 66.38 | 0.64 | 0.61 | 0.5 | 0.56 | 0.56 | 0.10 |
| 0.10 | 10.88 | 10.87 | 86.83 | 0.67 | 0.63 | 0.5 | 0.58 | 0.58 | 0.07 |
| 0.01 | 10.69 | 10.87 | 82.13 | 0.66 | 0.63 | 0.5 | 0.59 | 0.59 | 0.08 |
| Hydrogen Consumption (kg) | FC Efficiency | System Efficiency | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DOH | BTM | FCM | FCF | BTM | FCM | FCF | BTM | FCM | FCF |
| 0.50 | 0.105 | 0.156 | 0.191 | 0.557 | 0.569 | 0.503 | 0.605 | 0.530 | 0.370 |
| 0.30 | 0.125 | 0.148 | 0.344 | 0.580 | 0.590 | 0.504 | 0.581 | 0.553 | 0.227 |
| 0.10 | 0.135 | 0.141 | 0.482 | 0.607 | 0.605 | 0.504 | 0.576 | 0.568 | 0.164 |
| 0.01 | 0.139 | 0.139 | 0.668 | 0.620 | 0.610 | 0.504 | 0.575 | 0.574 | 0.120 |
| Hydrogen Consumption (kg) | FC Efficiency | System Efficiency | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DOH | BTM | FCM | FCF | BTM | FCM | FCF | BTM | FCM | FCF |
| 0.50 | 0.025 | 0.075 | 0.109 | 0.610 | 0.595 | 0.504 | 0.748 | 0.561 | 0.299 |
| 0.30 | 0.046 | 0.071 | 0.295 | 0.638 | 0.613 | 0.504 | 0.660 | 0.581 | 0.132 |
| 0.10 | 0.060 | 0.068 | 0.330 | 0.672 | 0.628 | 0.504 | 0.620 | 0.595 | 0.120 |
| 0.01 | 0.066 | 0.067 | 0.515 | 0.656 | 0.632 | 0.504 | 0.604 | 0.600 | 0.079 |
| n1: Start–Stop Cycles (1/h) | t1: Idle Time (min/h) | n2: Load Change Cycles (1/h) | t2: Average High-Power Operation Time (min/h) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DOH | BTM | FCM | FCF | BTM | FCM | FCF | BTM | FCM | FCF | BTM | FCM | FCF |
| 0.50 | 5.79 | 8.91 | 14.67 | 10.04 | 379.66 | 454.05 | 4.27 | 0.84 | 1.01 | 1.08 | ||
| 0.30 | 7.66 | 15.07 | 7.32 | 404.53 | 460.22 | 4.09 | 0.16 | 0.17 | 0.27 | |||
| 0.10 | 3.00 | 15.07 | 6.09 | 449.76 | 460.13 | 3.05 | 0.00 | 0.00 | 0.02 | |||
| 0.01 | 2.01 | 15.07 | 12.02 | 458.91 | 460.13 | 5.02 | 0.00 | 0.00 | 0.00 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agati, G.; Borello, D.; Migliarese Caputi, M.V.; Cedola, L.; Gagliardi, G.G.; Pozzessere, A.; Venturini, P. Effect of the Degree of Hybridization and Energy Management Strategy on the Performance of a Fuel Cell/Battery Vehicle in Real-World Driving Cycles. Energies 2024, 17, 729. https://doi.org/10.3390/en17030729
Agati G, Borello D, Migliarese Caputi MV, Cedola L, Gagliardi GG, Pozzessere A, Venturini P. Effect of the Degree of Hybridization and Energy Management Strategy on the Performance of a Fuel Cell/Battery Vehicle in Real-World Driving Cycles. Energies. 2024; 17(3):729. https://doi.org/10.3390/en17030729
Chicago/Turabian StyleAgati, Giuliano, Domenico Borello, Michele Vincenzo Migliarese Caputi, Luca Cedola, Gabriele Guglielmo Gagliardi, Adriano Pozzessere, and Paolo Venturini. 2024. "Effect of the Degree of Hybridization and Energy Management Strategy on the Performance of a Fuel Cell/Battery Vehicle in Real-World Driving Cycles" Energies 17, no. 3: 729. https://doi.org/10.3390/en17030729
APA StyleAgati, G., Borello, D., Migliarese Caputi, M. V., Cedola, L., Gagliardi, G. G., Pozzessere, A., & Venturini, P. (2024). Effect of the Degree of Hybridization and Energy Management Strategy on the Performance of a Fuel Cell/Battery Vehicle in Real-World Driving Cycles. Energies, 17(3), 729. https://doi.org/10.3390/en17030729
















