Planning of Reserve Storage to Compensate for Forecast Errors
Abstract
1. Introduction
- Formal definition of the approach to reserve a storage share for short-term operation;
- Model-based evaluation with a simple sector-coupled energy system and systematically generated load profiles;
- Quantification of the potential of the proposed method and the corresponding necessary reserve share with a real case study.
2. General Approach, Methods, and Model
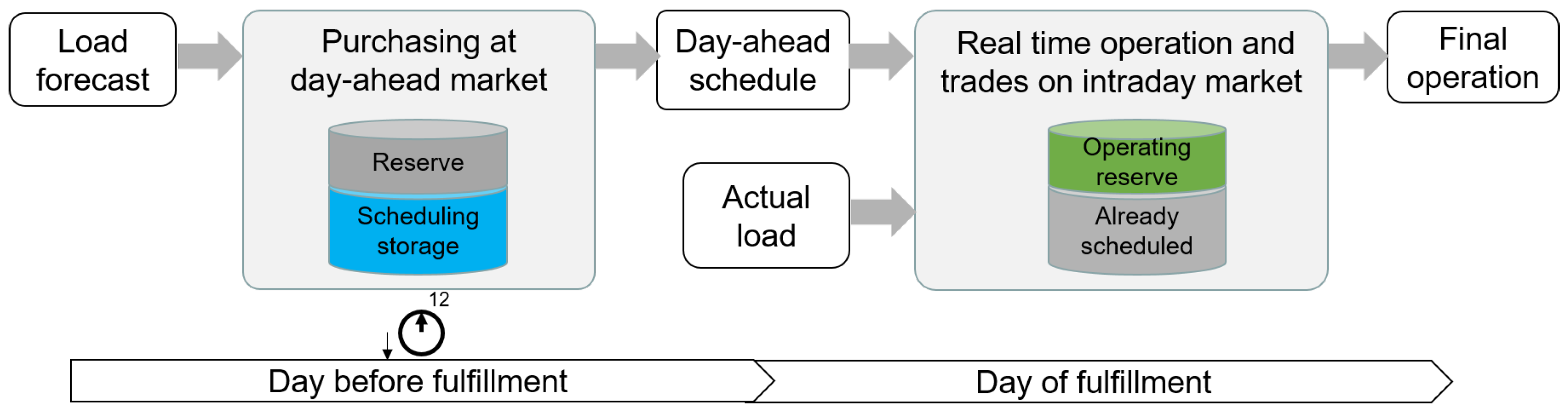
2.1. General Approach
2.1.1. Electricity Purchasing on Day-Ahead Market
2.1.2. Operation and Trades at Intraday Market
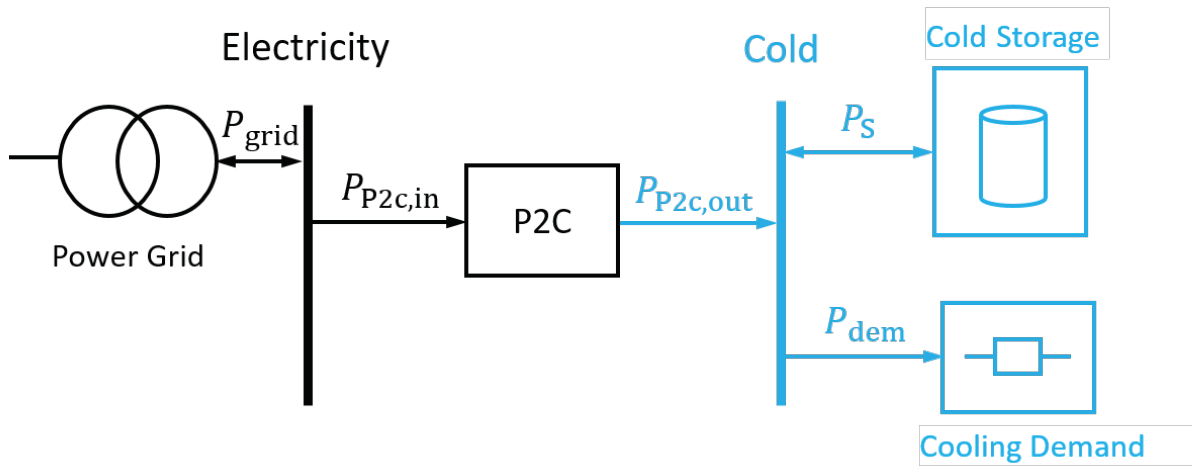
2.1.3. Investigated System and Model Equations
2.1.4. Power-to-Cold Plant
2.1.5. Energy Storage System
2.1.6. Power Balances
2.2. Scheduling and Trading
2.2.1. Day-Ahead Market
2.2.2. Intraday Market
2.3. Evaluation
2.4. Definition of Forecast Quality
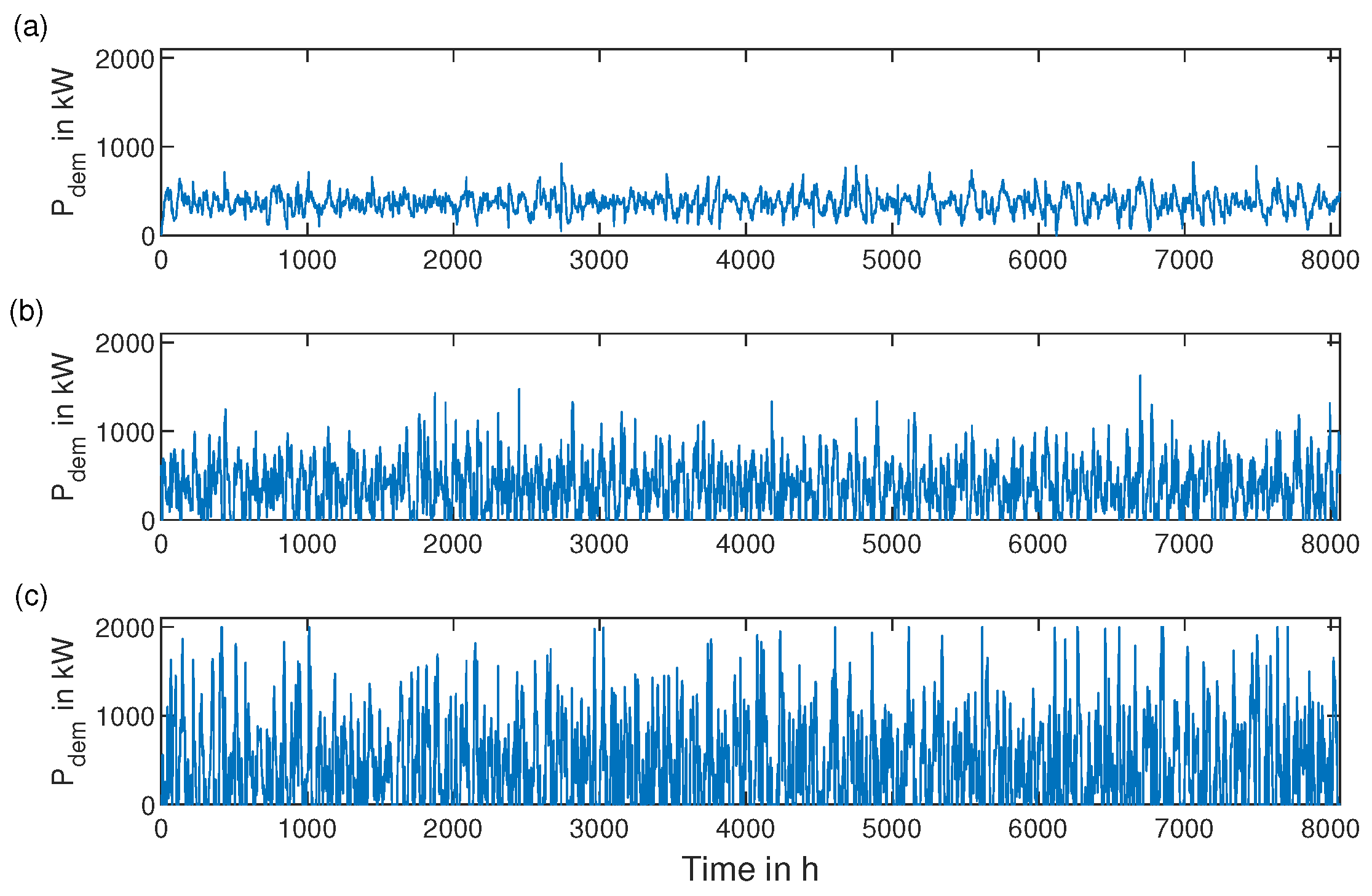
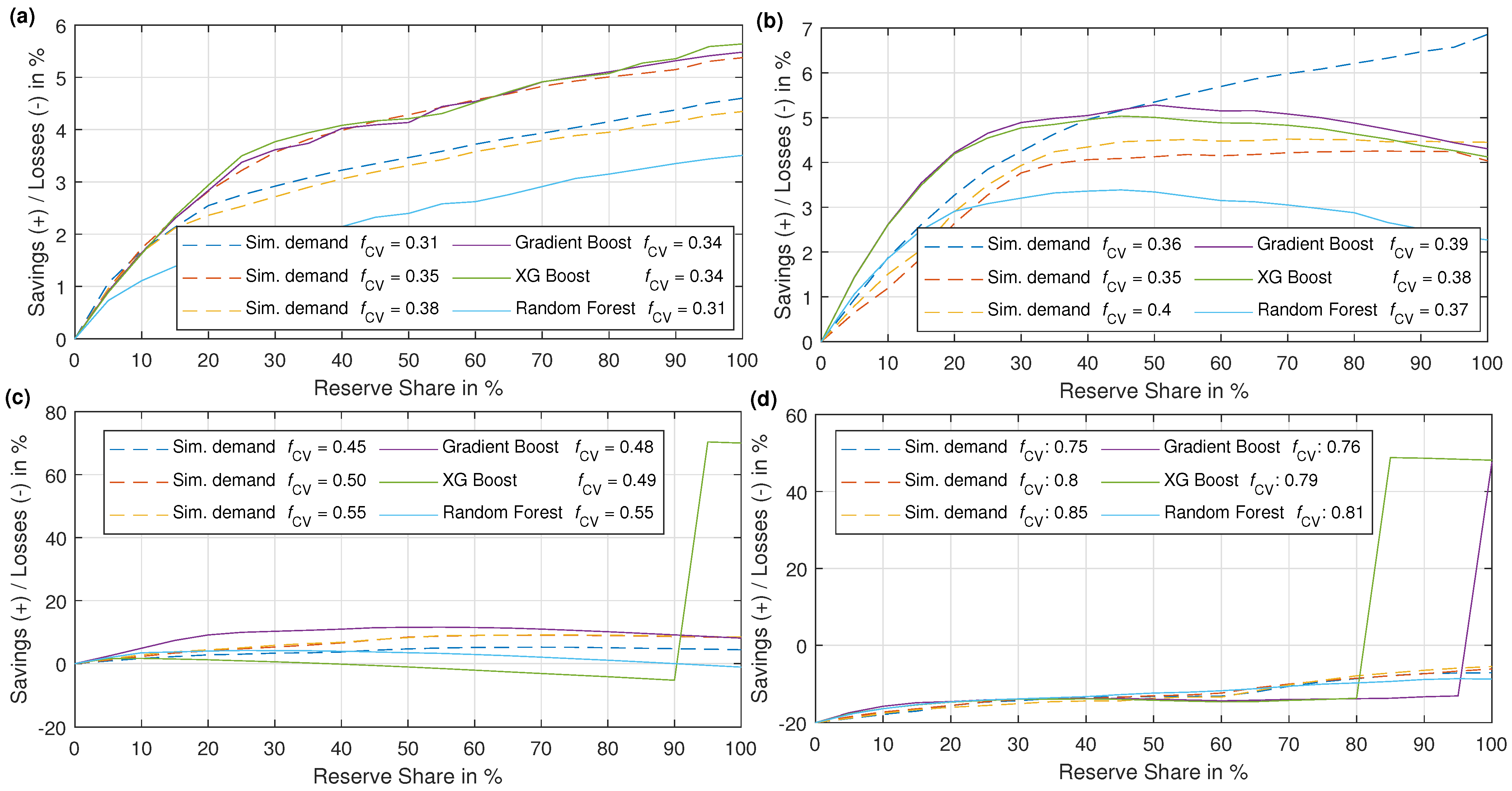
3. Results for Generated Case Study
3.1. Definition of Case Study
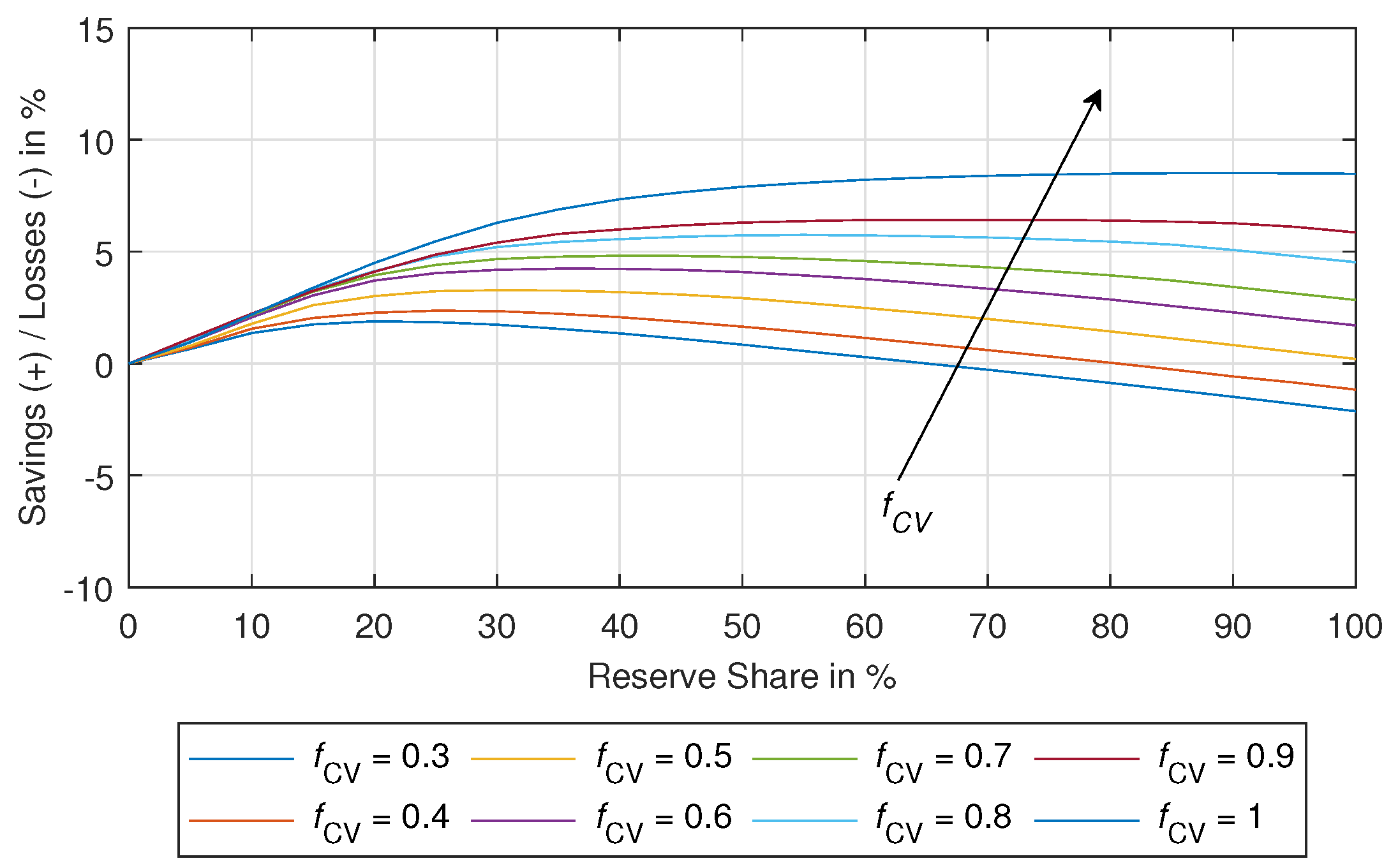
3.2. Results for Base Case
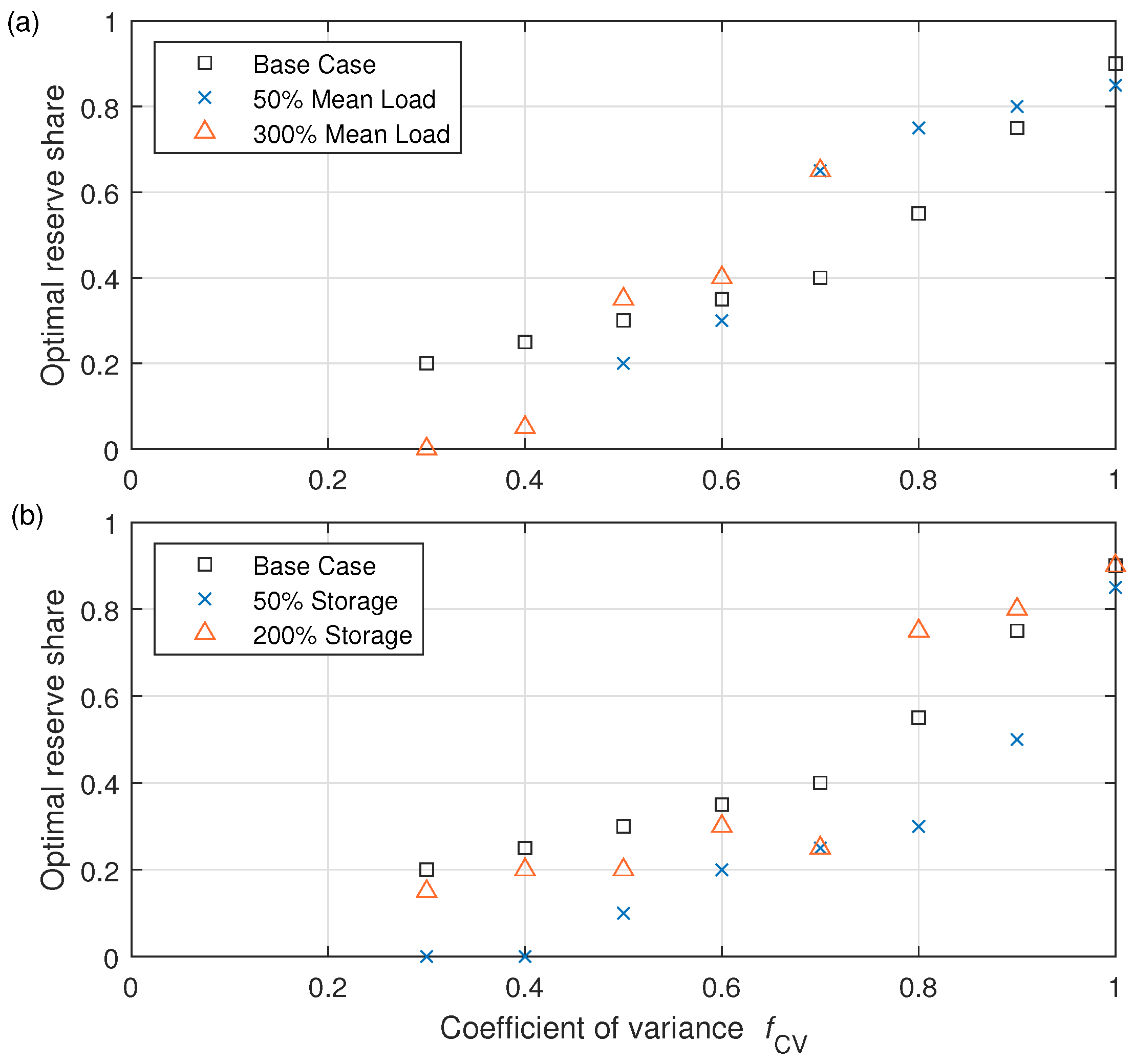
3.3. Variation of Technical Parameters
4. Results with Measured Data
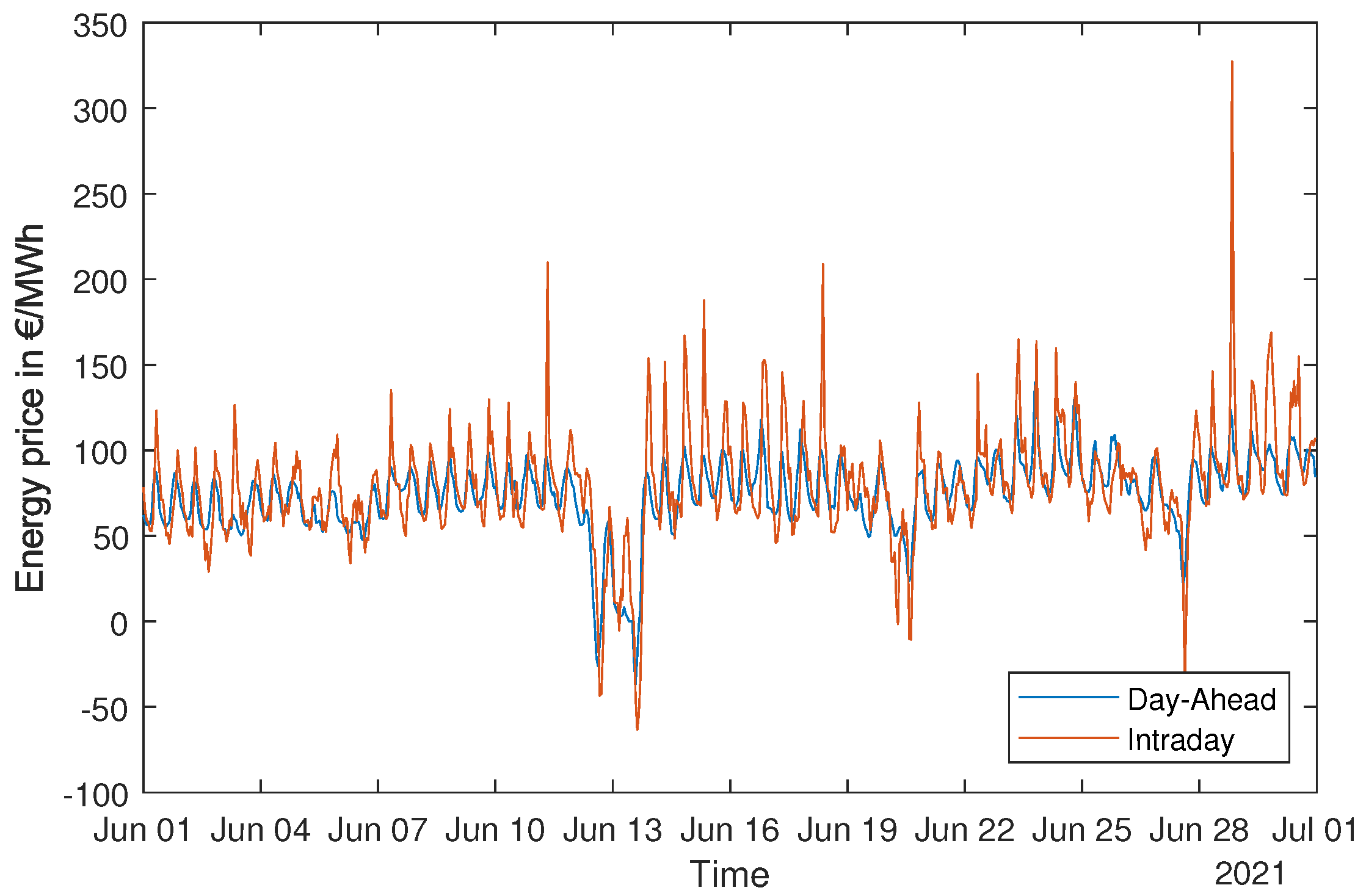
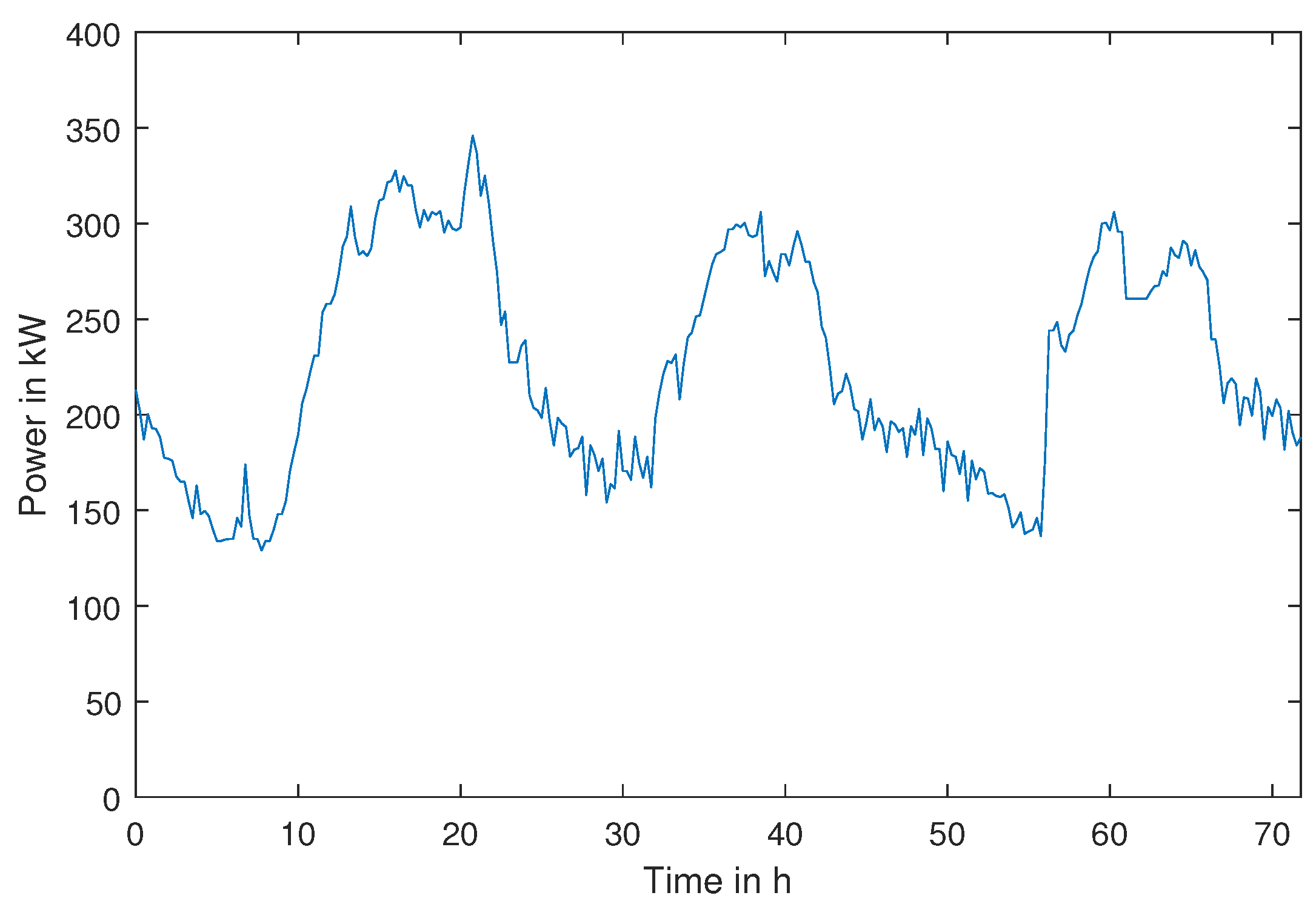
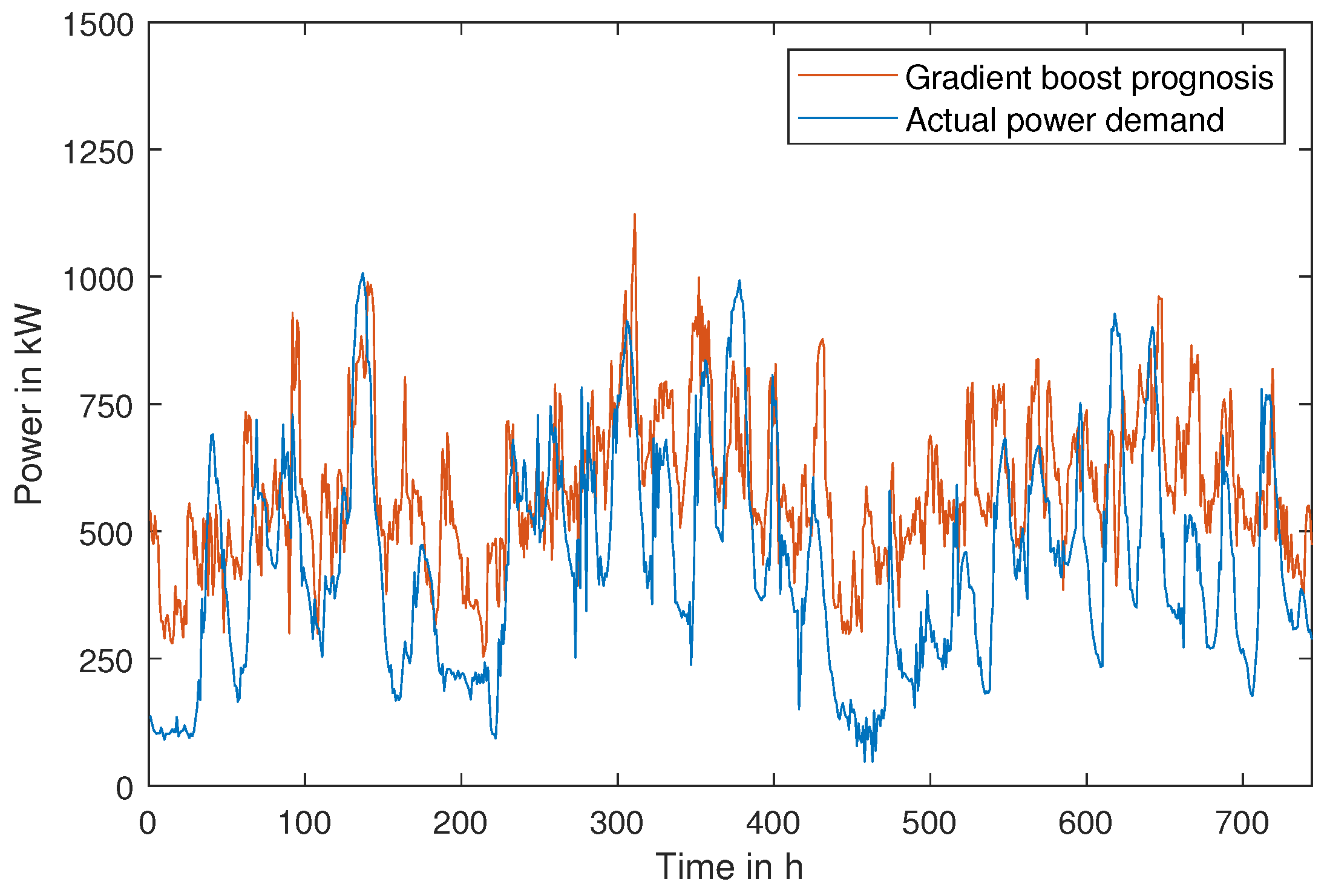
4.1. Input Signals
4.2. Results
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- García Vera, Y.E.; Dufo-López, R.; Bernal-Agustín, J.L. Energy Management in Microgrids with Renewable Energy Sources: A Literature Review. Appl. Sci. 2019, 9, 3854. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Nemati, M.; Braun, M.; Tenbohlen, S. Optimization of unit commitment and economic dispatch in microgrids based on genetic algorithm and mixed integer linear programming. Appl. Energy 2018, 210, 944–963. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Feng, X.; Wu, Q. Optimal Stochastic Deployment of Heterogeneous Energy Storage in a Residential Multienergy Microgrid With Demand-Side Management. IEEE Trans. Ind. Inform. 2021, 17, 991–1004. [Google Scholar] [CrossRef]
- Kaya, O.; van der Roest, E.; Vries, D.; Keviczky, T. Hierarchical Model Predictive Control for Energy Management of Power-to-X Systems. In Proceedings of the Smart Grids: Key Enablers of a Green Power System, Piscataway, NJ, USA, 26–28 October 2020; pp. 1094–1098. [Google Scholar] [CrossRef]
- Vasilj, J.; Jakus, D.; Sarajcev, P. Robust Nonlinear Economic MPC Based Management of a Multi Energy Microgrid. IEEE Trans. Energy Convers. 2021, 36, 1528–1536. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, J.; Luo, X.; Lai, C.S.; Yang, P.; Lai, L.L.; Li, P.; Guerrero, J.M.; Shahidehpour, M. Distributed Robust Model Predictive Control-Based Energy Management Strategy for Islanded Multi-Microgrids Considering Uncertainty. IEEE Trans. Smart Grid 2022, 13, 2107–2120. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Pippia, T.; de Schutter, B.; Dotoli, M. A Robust MPC Energy Scheduling Strategy for Multi-Carrier Microgrids. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), IEEE, Hong Kong, China, 20–21 August 2020; pp. 152–158. [Google Scholar] [CrossRef]
- Kneiske, T.M. Reducing CO2 Emissions for PV-CHP Hybrid Systems by Using a Hierarchical Control Algorithm. Energies 2023, 16, 6176. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, W.; Yang, Q. Multi-stage optimal energy management of multi-energy microgrid in deregulated electricity markets. Appl. Energy 2022, 310, 118528. [Google Scholar] [CrossRef]
- Scattolini, R. Architectures for distributed and hierarchical Model Predictive Control—A review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Ejeh, J.O.; Roberts, D.; Brown, S.F. A flexible energy storage dispatch strategy for day-ahead market trading. Comput. Aided Chem. Eng. 2022, 49, 1957–1962. [Google Scholar] [CrossRef]
- Beucker, S.; Doderer, H.; Funke, A.; Koch, C.; Kondziella, H.; Hartung, J.; Maeding, S.; Medert, H.; Meyer-Braune, G.; Rath, M.; et al. Flexibility, Markets and Regulation: Insights from the WindNODE Reality Lab. Available online: https://www.windnode.de/fileadmin/Daten/Downloads/FMR_eng.pdf (accessed on 31 January 2024).
- Zhuang, H.; Tang, Z.; Zhang, J. Two-Stage Energy Management for Energy Storage System by Using Stochastic Model Predictive Control Approach. Front. Energy Res. 2021, 9, 803615. [Google Scholar] [CrossRef]
- Tanja, M. Kneiske and Martin Braun Flexibility potentials of a combined use of heat storages and batteries in PV-CHP hybrid systems. Energy Procedia 2017, 135, 482–495. [Google Scholar] [CrossRef]
- Bischi, A.; Taccari, L.; Martelli, E.; Amaldi, E.; Manzolini, G.; Silva, P.; Campanari, S.; Macchi, E. A detailed MILP optimization model for combined cooling, heat and power system operation planning. Energy 2014, 74, 12–26. [Google Scholar] [CrossRef]
- Molina, D.; Lu, C.; Sherman, V.; Harley, R.G. Model Predictive and Genetic Algorithm-Based Optimization of Residential Temperature Control in the Presence of Time-Varying Electricity Prices. IEEE Trans. Ind. Appl. 2013, 49, 1137–1145. [Google Scholar] [CrossRef]
- Rath, M.; Ray, H.; van Treek, M.; Meeder, A. Untersuchung verschiedener Lastprognoseverfahren für die prognosebasierte Steuerung dezentraler Energieanlagen. BauSim Conf. 2022, 9. [Google Scholar] [CrossRef]
- Zhang, Q.; Grossmann, I.E.; Heuberger, C.F.; Sundaramoorthy, A.; Pinto, J.M. Air separation with cryogenic energy storage: Optimal scheduling considering electric energy and reserve markets. AIChE J. 2015, 61, 1547–1558. [Google Scholar] [CrossRef]
- Schäfer, P.; Caspari, A.; Mhamdi, A.; Mitsos, A. Economic nonlinear model predictive control using hybrid mechanistic data-driven models for optimal operation in real-time electricity markets: In-silico application to air separation processes. J. Process Control 2019, 84, 171–181. [Google Scholar] [CrossRef]
- Chen, J.; Garcia, H.E. Economic optimization of operations for hybrid energy systems under variable markets. Appl. Energy 2016, 177, 11–24. [Google Scholar] [CrossRef]
- Yin, W.; Liu, H.; Ni, X.; Zhou, H.; Hou, Y. A Two-stage Rolling Scheduling Strategy for Battery Energy Storage in Multi-periods Electricity Market. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Z.; Hao, T.; Zhu, S.; Tang, Y.; Liu, H. Optimal Intraday Rolling Operation Strategy of Integrated Energy System with Multi-Storage. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, Q.; Zhao, J.; Yang, Y.; Sun, L. Day-ahead and intra-day optimization for energy and reserve scheduling under wind uncertainty and generation outages. Electr. Power Syst. Res. 2021, 195, 107133. [Google Scholar] [CrossRef]
- Abdeltawab, H.; Mohamed, Y.A.-R.I. Energy Storage Planning for Profitability Maximization by Power Trading and Ancillary Services Participation. IEEE Syst. J. 2022, 16, 1909–1920. [Google Scholar] [CrossRef]
- Nguyen Duc, H.; Nguyen Hong, N. Optimal Reserve and Energy Scheduling for a Virtual Power Plant Considering Reserve Activation Probability. Appl. Sci. 2021, 11, 9717. [Google Scholar] [CrossRef]
- Bundesnetzagentur. SMARD|Marktdaten. Available online: https://www.smard.de/en/downloadcenter/download-market-data/ (accessed on 1 October 2021).
- Shinozuka, M.; Deodatis, G. Simulation of Stochastic Processes by Spectral Representation. Appl. Mech. Rev. 1991, 44, 191–204. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Krishnapuram, B., Shah, M., Smola, A., Aggarwal, C., Shen, D., Rastogi, R., Eds.; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]

| Demand Lower than Forecast | Demand Equal to Forecast | Demand Lower than Forecast | |
|---|---|---|---|
| Price lower than maximum buy price | Storage empty OR storage (partially) charged: | Storage empty OR storage (partially) charged: | Storage empty OR storage (partially) charged: |
| Charge storage as much as possible using excess energy and energy bought at the intraday market. If excess energy cannot be stored completely, sell as much excess energy as possible at the intraday market. | Charge storage as much as possible using energy bought at the intraday market. | Buy as much energy as possible at the intraday market to meet the demand and charge the storage. | |
| The equations that result from this are
| The equations that result from this are
| The equations that result from this are
| |
| Price in range | Storage empty: Sell as much excess energy as possible at the intraday market. | Storage empty OR storage (partially) charged: Run the original operation plan as scheduled, no intervention. | Storage empty OR storage (partially) charged: Buy energy at the intraday market to meet demand. |
| Storage (partially) charged: Use as much energy as possible from the storage to meet the demand and sell excess energy at the intraday market. | |||
| The equations that result from this are
| The equations that result from this are
| The equations that result from this are
| |
| Price higher than minimum sell price | Storage empty: Sell as much excess energy as possible at the intraday market. | Storage empty: Run the original schedule, no intervention. | Storage empty: Buy energy at the intraday market to meet the demand. |
| Storage (partially) charged: Use as much energy as possible from the storage to meet the demand and sell excess energy at the intraday market. | Storage (partially) charged: Use as much energy as possible from the storage to meet the demand and sell excess energy at the intraday market. | Storage (partially) charged: Use as much energy as possible from the storage to meet the demand. If the demand can be fulfilled with storage energy, sell excess energy at the intraday market. If the demand exceeds stored energy, buy energy at the intraday market. | |
| The equations that result from this are
| The equations that result from this are
| The equations that result from this are
| |
| Parameter | Variable | Value |
|---|---|---|
| Coefficient of performance | 3.67 | |
| Rated power of power-to-cold plant | 2000 kW | |
| Energy capacity of storage system | 5000 kWh | |
| Rated power of storage system (charge and discharge) | 500 kW | |
| Storage system efficiency for charge resp. discharge process | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, J.; Bensmann, A.; Eckert, C.; Rath, M.; Hanke-Rauschenbach, R. Planning of Reserve Storage to Compensate for Forecast Errors. Energies 2024, 17, 720. https://doi.org/10.3390/en17030720
Koch J, Bensmann A, Eckert C, Rath M, Hanke-Rauschenbach R. Planning of Reserve Storage to Compensate for Forecast Errors. Energies. 2024; 17(3):720. https://doi.org/10.3390/en17030720
Chicago/Turabian StyleKoch, Julian, Astrid Bensmann, Christoph Eckert, Michael Rath, and Richard Hanke-Rauschenbach. 2024. "Planning of Reserve Storage to Compensate for Forecast Errors" Energies 17, no. 3: 720. https://doi.org/10.3390/en17030720
APA StyleKoch, J., Bensmann, A., Eckert, C., Rath, M., & Hanke-Rauschenbach, R. (2024). Planning of Reserve Storage to Compensate for Forecast Errors. Energies, 17(3), 720. https://doi.org/10.3390/en17030720





