A Novel Dual-Channel Temporal Convolutional Network for Photovoltaic Power Forecasting
Abstract
1. Introduction
- (1)
- A novel model DC_TCN for day-ahead PV power forecasting is proposed. its dual-channel modeling structure is able to learn the spatio-temporal correlation between multiple features, as well as the temporal correlation between historical power and current power.
- (2)
- A Multihead Attention (MHA) and TCN cascade channel that takes multivariate features as inputs, and extracts temporally and spatially constrained relationships between elements within the historical power series and between historical power and other meteorological series, while paying attention to important features.
- (3)
- A single TCN channel with univariate features (historical power) as inputs is targeted to extract long-term temporal dependencies between target sequence elements. Dual-channel feature fusion thus obtain better forecasting performance.
- (4)
- In this paper, the effect of different input window widths on model performance is also investigated. Optimal forecasting performance is achieved for shorter input window widths.
2. Methodology
- (1)
- Raw data was imported and data pre-processing was performed: the input photovoltaic data was preprocessed, including filling missing values and outliers with the adjacent values, and normalizing the data.
- (2)
- Converting data format: a sliding window was used to change the form of the data to achieve dynamic forecasting, and satisfy the shape (sample, time step, and feature) required for the data input of the deep learning model. Then, the obtained data were filtered to ensure that the target feature data corresponding to different samples do not overlap, which facilitated the evaluation of the forecasting model.
- (3)
- Training the models: the proposed DC_TCN model was compared with the benchmark model (which currently has superior forecasting performance in the domain), and then ablation experiments were performed. The optimal weights for each model were obtained by training and tuning the hyperparameters.
- (4)
- Experiment and analysis: the experimental results were visualized, and the forecasting results of each model were evaluated by MAE, RMSE and R2.
2.1. MultiHead Attention
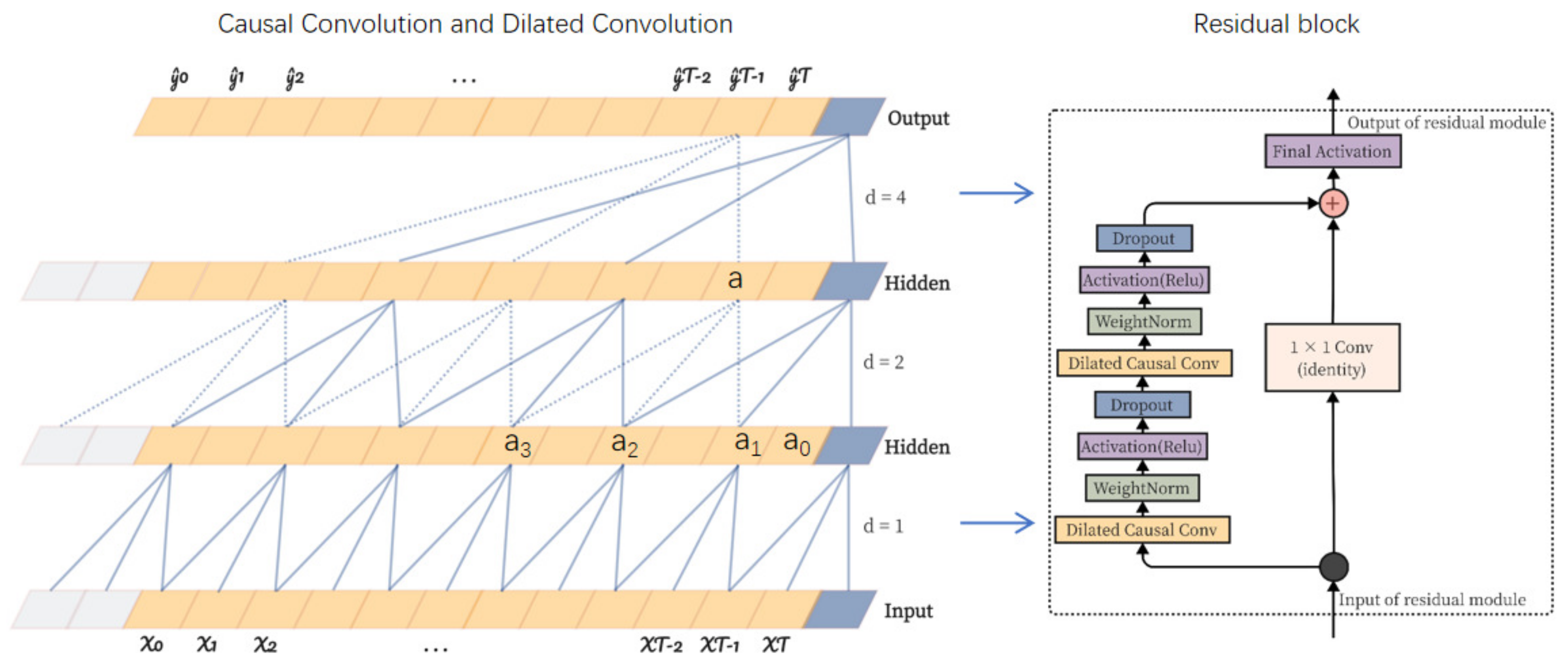
2.2. TCN
2.3. DC_TCN Model
3. Performance Evaluation Index
4. Case Study
4.1. Experimental Input Data
4.2. Data Processing
4.3. Experiments and Analysis
5. Conclusions
- (1)
- In order to verify the effect of input window width on model performance, all the experiments in this paper were conducted under seven input window widths, and all the experimental results showed that all the models obtain the best performance under a window width of 1 day (96 time steps). The performance of all models showed a decreasing trend with increasing input window width, with the proposed model being the most sensitive to the width of the input window.
- (2)
- Ablation experiments were carried out in order to verify the feature extraction capability of the proposed model’s dual-channel structure. The experimental results showed that the proposed model obtained better forecasting results compared to the two-branch models, single TCN, and multihead attention combined with the TCN, which also indicates that the design of the dual-channel results can provide more useful feature information for the model and increase the interpretability of the model.
- (3)
- In order to verify the forecasting performance of the proposed model, comparison experiments were carried out. The experimental results showed that the proposed model achieved better forecasting performance than CNN and CNN_LSTM, which had better performance in PV power forecasting, with a maximum improvement of 5.3% in MAE, and 2.9% in RMSE.
- (4)
- In addition, it was found that none of the models can forecast fast ramps well on the 15 min resolution data used in the study. While it can be applied to specific application scenarios that do not require high day-ahead ramp forecasting, such as day-ahead generation planning; unit deployment; and day-ahead power market trading, the forecasting value is still insufficient for those day-ahead application scenarios that are sensitive to power ramp changes. In the follow-up study, we will continue to investigate the forecasting performance of the proposed model in terms of both reducing the data resolution, and improving the upper limit of the model’s learning capability, with a view to being able to apply the model to a wider range of application scenarios and improve its applicability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Net Zero by 2050–Analysis-IEA. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 16 December 2023).
- Ren, X.; Zhang, F.; Zhu, H.; Liu, Y. Quad-kernel deep convolutional neural network for intra-hour photovoltaic power forecasting. Appl. Energy 2022, 323, 119682. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of different physical models for PV power output forecasting. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Celikel, R.; Yilmaz, M.; Gundogdu, A. A voltage scanning-based MPPT method for PV power systems under complex partial shading conditions. Renew. Energy 2022, 184, 361–373. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Yilmaz, M.; Celikel, R.; Gundogdu, A. Enhanced Photovoltaic Systems Performance: Anti-Windup PI Controller in ANN-Based ARV MPPT Method. IEEE Access 2023, 11, 90498–90509. [Google Scholar] [CrossRef]
- Srivastava, S.; Lessmann, S. A Comparative Study of Lstm Neural Networks in Forecasting Day-Ahead Global Horizontal Irradiance with Satellite Data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Zhou, B.; Li, C.; Cao, G.; Voropai, N.; Barakhtenko, E. Taxonomy research of artificial intelligence for deterministic solar power forecasting. Energy Convers. Manag. 2020, 214, 112909. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Qu, X. Deep learning approaches on pedestrian detection in hazy weather. IEEE Trans. Ind. Electron. 2019, 67, 8889–8899. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, K.; Zhang, X.; Yang, S. A deep learning model for short-term power load and probability density forecasting. Energy 2018, 160, 1186–1200. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2017, 31, 2727–2740. [Google Scholar] [CrossRef]
- Yao, G.; Lei, T.; Zhong, J. A Review of Convolutional-Neural-Network-Based Action Recognition. Pattern Recogn. Lett. 2019, 118, 14–22. [Google Scholar] [CrossRef]
- Zhang, J.; Ling, C.; Li, S. EMG Signals based Human Action Recognition via Deep Belief Networks. IFAC Pap. Online 2019, 52, 271–276. [Google Scholar] [CrossRef]
- Chen, S.; Yu, J.; Wang, S. One-dimensional convolutional auto-encoder-based feature learning for fault diagnosis of multivariate processes. J. Process Control 2020, 87, 54–67. [Google Scholar] [CrossRef]
- Yang, X.; Cao, M.; Li, C.; Zhao, H.; Yang, D. Learning Implicit Neural Representation for Satellite Object Mesh Reconstruction. Remote Sens. 2023, 15, 4163. [Google Scholar] [CrossRef]
- Liu, L.M.; Ren, X.Y.; Zhang, F.; Gao, L.; Hao, B. Dual-dimension Time-GGAN data augmentation method for improving the performance of deep learning models for PV power forecasting. Energy Rep. 2023, 9, 6419–6433. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Wang, H.; Zhao, F.; Yan, F.; Wang, M. A Convolutional Neural Network for Regional Photovoltaic Generation Point Forecast. E3S Web Conf. 2020, 185, 01079. [Google Scholar] [CrossRef]
- Suresh, V.; Janik, P.; Rezmer, J.; Leonowicz, Z. Forecasting solar PV output using convolutional neural networks with a sliding window algorithm. Energies 2020, 13, 723. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J. Temporal convolutional networks applied to energy-related time series forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Luo, H.; Dou, X.; Sun, R.; Wu, S. A Multi-Step forecasting Method for Wind Power Based on Improved TCN to Correct Cumulative Error. Front. Energy Res. 2021, 9, 723319. [Google Scholar] [CrossRef]
- Lin, Y.; Koprinska, I.; Rana, M. Temporal Convolutional Neural Networks for Solar Power Forecasting. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Limouni, T.; Yaagoubi, R.; Khalid, B.; Khalid, G.; El Houssain, B. Accurate one step and multistep forecasting of very short-term PV power using LSTM-TCN model. Renew. Energy 2023, 205, 1010–1024. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Abd Rahim, N. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Qu, J.; Zheng, Q.; Pei, Y. Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables forecasting pattern. Energy 2021, 232, 120996. [Google Scholar] [CrossRef]
- Li, P.; Zhou, K.; Lu, X.; Yang, S. A hybrid deep learning model for short-term PV power forecasting. Appl. Energy 2020, 259, 114216. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Luo, X.; Cao, X.; Du, S.; Sun, H. Short-term photovoltaic power forecasting based on modal reconstruction and hybrid deep learning model. Energy Rep. 2022, 8, 9919–9932. [Google Scholar] [CrossRef]
- Tovar, M.; Robles, M.; Rashid, F. PV Power forecasting, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México. Energies 2020, 13, 6512. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- de Jesús, D.A.R.; Mandal, P.; Chakraborty, S.; Senjyu, T. Solar PV Power forecasting Using a New Approach Based on Hybrid Deep Neural Network. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- de Jesús, D.A.R.; Mandal, P.; Velez-Reyes, M.; Chakraborty, S.; Senjyu, T. Data Fusion Based Hybrid Deep Neural Network Method for Solar PV Power Forecasting. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Ali, I.H. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, K.; Zhang, S.; Zhang, Z. Photovoltaic power forecasting: A hybrid deep learning model incorporating transfer learning strategy. Renew. Sustain. Energy Rev. 2022, 162, 112473. [Google Scholar] [CrossRef]
- Li, F.; Zheng, H.; Li, X. A novel hybrid model for multi-step ahead photovoltaic power forecasting based on conditional time series generative adversarial networks. Renew. Energy 2022, 199, 560–586. [Google Scholar] [CrossRef]
- Hu, Y.; Xiao, F. Network self attention for forecasting time series. Appl. Soft Comput. 2022, 124, 109092. [Google Scholar] [CrossRef]
- DKA Solar Center’s Online Hub for Sharing Solar-Related Knowledge and Data from the Northern Territory, Australia. Available online: http://dkasolarcentre.com.au/download (accessed on 16 October 2022).


















| Samples | Time | |
|---|---|---|
| Group 1 Sample Data | Start and end time of multi-feature data: | 1/1/2014 0:00–3/1/2014 23:45 (288) |
| Start and end time of target feature data: | 4/1/2014 0:00–4/1/2014 23:45 (96) | |
| Group 2 Sample Data | Start and end time of multi-feature data: | 2/1/2014 0:00–4/1/2014 23:45 (288) |
| Start and end time of target feature data: | 5/1/2014 0:00–5/1/2014 23:45 (96) | |
| … | Start and end time of multi-feature data: | … |
| Start and end time of target feature data: | … | |
| Group 653 Sample Data | Start and end time of multi-feature data: | 15/10/2015 0:00–17/10/2015 23:45 (288) |
| Start and end time of target feature data: | 18/10/2015 0:00–18/10/2015 23:45 (96) |
| Models | Evaluation Indicators | Timesteps | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | ||
| TCN | MAE | 0.985 | 1.004 | 1.005 | 0.986 | 1.019 | 1.025 | 1.034 |
| RMSE | 1.870 | 1.871 | 1.861 | 1.881 | 1.923 | 1.917 | 1.950 | |
| R2 | 0.854 | 0.848 | 0.851 | 0.852 | 0.843 | 0.845 | 0.838 | |
| MHA_TCN | MAE | 0.956 | 1.017 | 1.050 | 1.001 | 1.030 | 0.973 | 0.981 |
| RMSE | 1.919 | 1.914 | 1.987 | 1.969 | 1.900 | 2.206 | 2.073 | |
| R2 | 0.861 | 0.846 | 0.844 | 0.849 | 0.839 | 0.847 | 0.843 | |
| DC_TCN | MAE | 0.906 | 0.987 | 0.996 | 0.977 | 0.999 | 1.026 | 1.029 |
| RMSE | 1.776 | 1.864 | 1.907 | 1.881 | 1.961 | 1.915 | 1.882 | |
| R2 | 0.868 | 0.856 | 0.852 | 0.857 | 0.842 | 0.847 | 0.848 | |
| Models | Evaluation Indexes | Timesteps | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | ||
| CNN | MAE | 0.957 | 0.981 | 0.957 | 1.010 | 0.955 | 1.034 | 1.036 |
| RMSE | 1.824 | 1.849 | 1.836 | 1.917 | 1.888 | 1.932 | 1.932 | |
| R2 | 0.859 | 0.852 | 0.858 | 0.848 | 0.843 | 0.838 | 0.836 | |
| CNN_LSTM | MAE | 0.947 | 0.970 | 0.972 | 0.941 | 0.950 | 0.944 | 0.991 |
| RMSE | 1.829 | 1.844 | 1.847 | 2.016 | 2.022 | 2.004 | 1.869 | |
| R2 | 0.859 | 0.857 | 0.854 | 0.857 | 0.854 | 0.853 | 0.849 | |
| DC_TCN | MAE | 0.906 | 0.987 | 0.996 | 0.977 | 0.999 | 1.026 | 1.029 |
| RMSE | 1.776 | 1.864 | 1.907 | 1.881 | 1.961 | 1.915 | 1.882 | |
| R2 | 0.868 | 0.856 | 0.852 | 0.857 | 0.842 | 0.847 | 0.848 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Zhang, F.; Sun, Y.; Liu, Y. A Novel Dual-Channel Temporal Convolutional Network for Photovoltaic Power Forecasting. Energies 2024, 17, 698. https://doi.org/10.3390/en17030698
Ren X, Zhang F, Sun Y, Liu Y. A Novel Dual-Channel Temporal Convolutional Network for Photovoltaic Power Forecasting. Energies. 2024; 17(3):698. https://doi.org/10.3390/en17030698
Chicago/Turabian StyleRen, Xiaoying, Fei Zhang, Yongrui Sun, and Yongqian Liu. 2024. "A Novel Dual-Channel Temporal Convolutional Network for Photovoltaic Power Forecasting" Energies 17, no. 3: 698. https://doi.org/10.3390/en17030698
APA StyleRen, X., Zhang, F., Sun, Y., & Liu, Y. (2024). A Novel Dual-Channel Temporal Convolutional Network for Photovoltaic Power Forecasting. Energies, 17(3), 698. https://doi.org/10.3390/en17030698






