Assessing the Reliability and Optimizing Input Parameters of the NWP-CFD Downscaling Method for Generating Onshore Wind Energy Resource Maps of South Korea
Abstract
1. Introduction
2. NWP-CFD Coupled Method
2.1. NWP-CFD Downscaling Procedure
2.2. WRF-Based Mesoscale Meteorological Data
2.3. Computaional Domain and Pre-Processing Procedure of CFD
2.4. Computational Fluid Dynamics
2.5. NWP-CFD Synthesis and Annual Energy Production
3. Results of the Convergence Test
3.1. Grid Resolution (Δzmin) Convergence Test
3.2. Convergence Test of the Wind Direction Resolution (Δdir)
3.3. Influence of l0 Regularization on Computational Result
4. Quantitative Evaluation Using the NWP-MCP-CFD Method
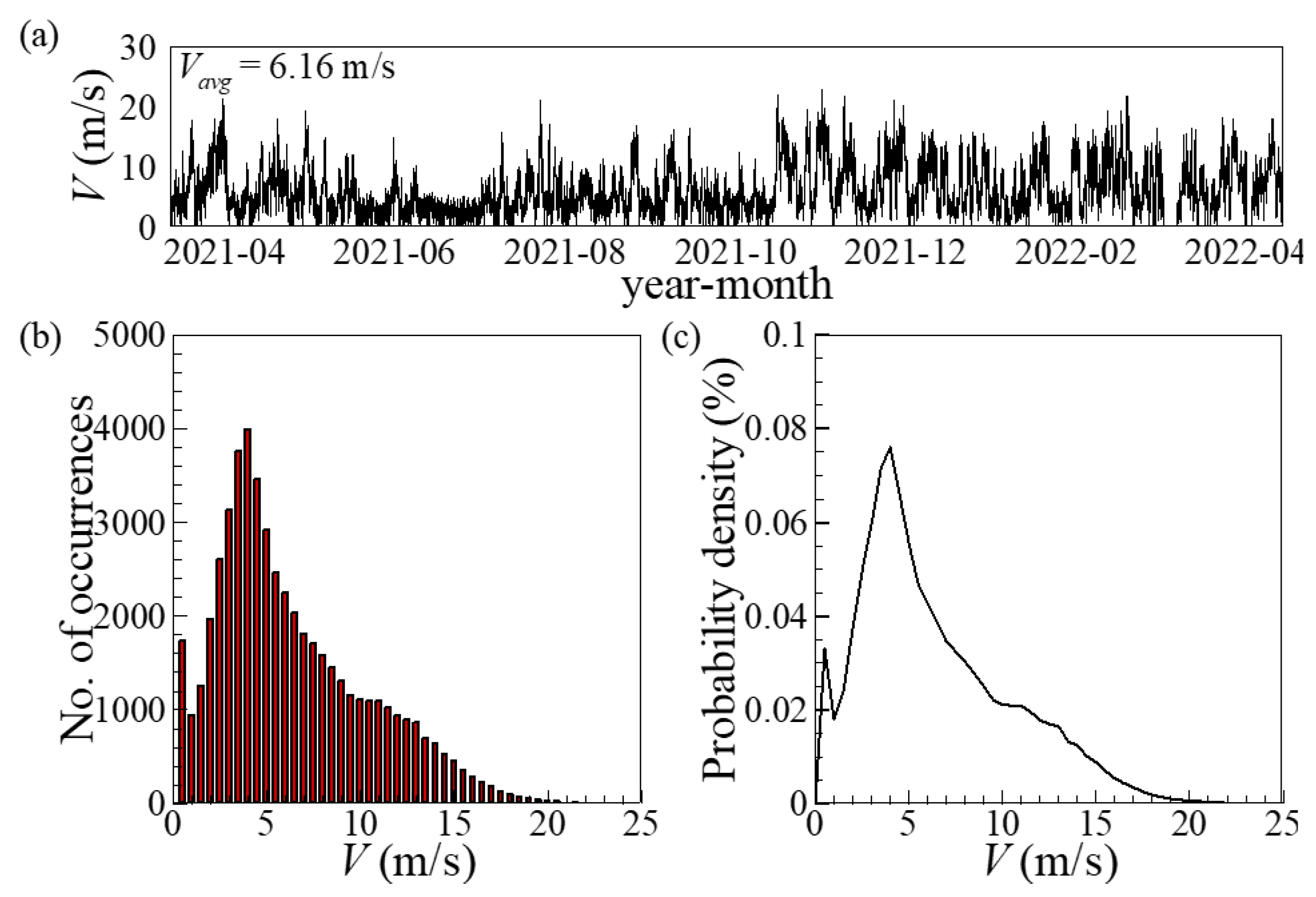
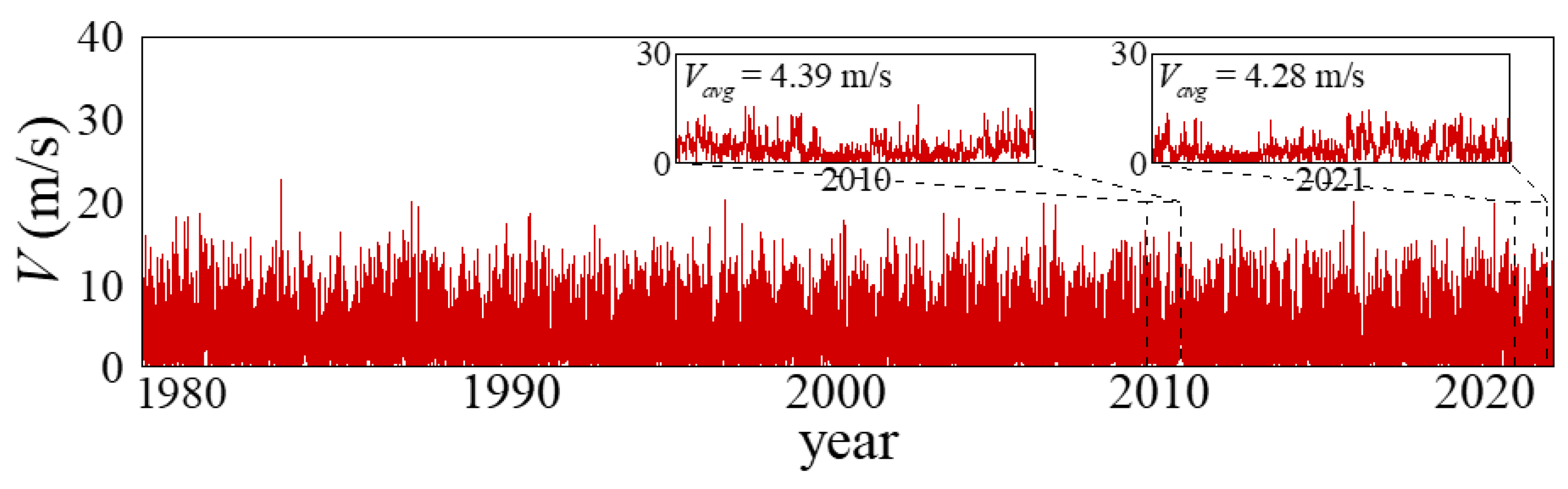
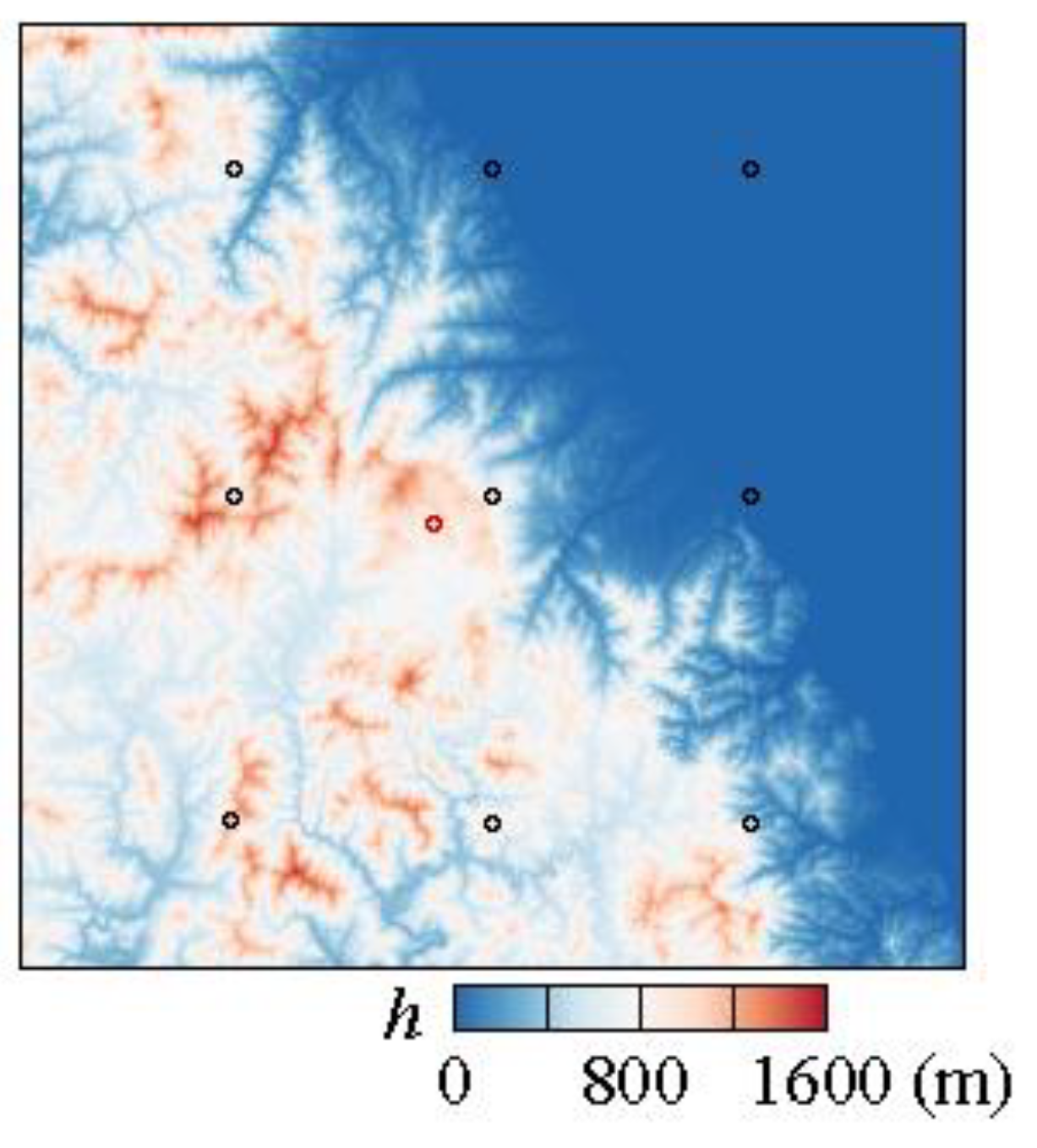
4.1. Measured Meteorological Data
4.2. ERA5 Meteorological Data
4.3. Measure Correlate Predict (MCP) Method
4.4. Quantitative Evaluation of NWP-MCP-CFD Coupled Method
5. Conclusions
- Our simulations, informed by parameters obtained from previous studies, show an approximate 8.5% deviation from the corrected measurement data. This suggests that although the NWP-CFD approach is more reliable for wind resource predictions in complex terrains like Korea compared to the standalone NWP method, further parameter optimization is necessary to enhance prediction accuracy.
- In the NWP-CFD downscaling method, Δzmin, Δdir, and l0 emerge as three key influencing factors. Our analysis suggests that the effects of Δzmin and Δdir on the simulation outcomes are relatively minimal once their values reach a stabilized region. Thus, within this optimal range, changes in Δzmin and Δdir do not significantly impact the simulation results.
- On the other hand, the l0 factor exerts a significant influence on the forest model activation area and the ensuing simulation results. Adjusting l0 according to the specific land characteristics is found to be essential for more accurate wind resource prediction, emphasizing the importance of fine-tuning model parameters based on local conditions. The sensitivity of the wind distribution to the activation length decreases when the activation length exceeds 0.3.
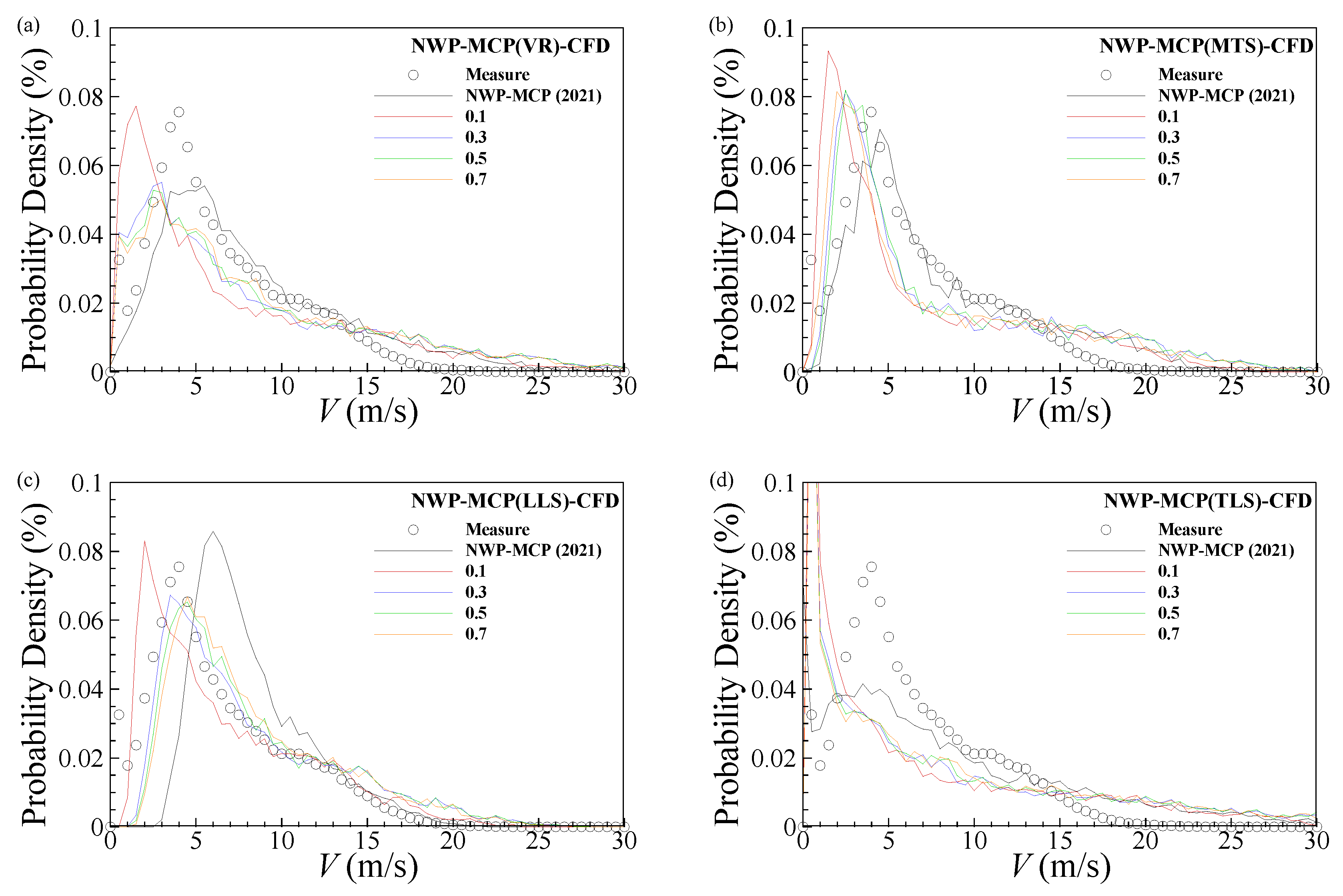
- The meteorological data, derived from applying the NWP-MCP using the MST method, demonstrate good estimation performance compared to the measured data before considering geographical characteristics. Upon incorporating these data into the CFD simulation, the highest R2 value, approximately 0.87, is observed in the NWP-MCP (LLS)-NWP method. This suggests that the LLS method could be an effective option for projecting short-term NWP data onto long-term meteorological data prior to employing the NWP-MCP-CFD coupled method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Zhao, Q.; Zhang, G.; Xiong, B. Energy revolution: From a fossil energy era to a new energy era. Nat. Gas Ind. B 2016, 3, 1–11. [Google Scholar] [CrossRef]
- BP. BP Statistical Review of World Energy; BP: London, UK, 2015; Available online: http://large.stanford.edu/courses/2015/ph240/zerkalov2/docs/bp2015.pdf (accessed on 1 June 2023).
- Sadorsky, P. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- BP. BP Statistical Review of World Energy; BP: London, UK, 2019; Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2019-full-report.pdf (accessed on 1 June 2023).
- Kim, C.S. New & Renewable Energy Statistics 2020, 2021st ed.; Korea Energy Agency: Ulsan, Republic of Korea, 2021. [Google Scholar]
- Shikha, S.; Bhatti, T.; Kothari, D. A review of wind-resource-assessment technology. J. Energy Eng. 2006, 132, 8–14. [Google Scholar]
- Gharaati, M.; Xiao, S.; Wei, N.; Martinez-Tossas, L.A.; Dabiri, J.O.; Yang, D. Large-eddy simulation of helical- and straight-bladed vertical-axis wind turbines in boundary layer turbulence. J. Renew. Sustain. Energy 2022, 14, 053301. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Gastli, A. Review of the use of numerical weather prediction (NWP) models for wind energy assessment. Renew. Sustain. Energy Rev. 2010, 14, 3192–3198. [Google Scholar] [CrossRef]
- Done, J.; Davis, C.A.; Weisman, M. The next generation of NWP: Explicit forecasts of convection using the Weather Research and Forecasting (WRF) model. Atmos. Sci. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
- Bang, C.H.; Lee, J.W.; Hong, S.Y. Predictability experiments of fog and visibility in local airports over Korea using the WRF model. J. Korean Soc. Atmos. Environ. 2008, 24, 92–101. [Google Scholar]
- Byun, U.Y.; Hong, S.Y.; Shin, H.; Lee, J.W.; Song, J.I.; Hahm, S.J.; Kim, J.K.; Kim, H.W.; Kim, J.S. WRF-based short-range forecast system of the Korea Air Force: Verification of prediction skill in 2009 summer. Atmosphere 2011, 21, 197–208. [Google Scholar]
- Kim, H.G.; Lee, H.W. Wind Resource Assessment of Baekado by NWP-CFD Downscaling. Korean Soc. New Renew. Energy 2019, 15, 117. [Google Scholar]
- Che, Y.; Salazar, A.A.; Peng, S.; Zheng, J.; Chen, Y.; Yuan, L. A multi-scale model for day-ahead wind speed forecasting: A case study of the Houhoku wind farm, Japan. Sustain. Energy Technol. Assess. 2022, 52, 101995. [Google Scholar] [CrossRef]
- Durán, P.; Cathérine, M.; Pau, C. A new meso-microscale coupled modelling framework for wind resource assessment: A validation study. Renew. Energy 2020, 160, 538–554. [Google Scholar] [CrossRef]
- Kim, J.; Hwang, S.J.; Kim, J.Y.; Park, S.G.; Kim, H.G. High-Resolution Mapping of Onshore Wind Resource Using NWP-CFD Downscaling. J. Wind Eng. Inst. Korea 2022, 26, 3–8. [Google Scholar] [CrossRef]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Paulo, A.C.R.; Ricardo, C.S.; Carla, F.A.; Maria, E.V.S. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Appl. Energy 2012, 89, 395–400. [Google Scholar]
- Kim, M.J.; Song, Y.; Peak, I. Development of an In-house Code to Predict Annual Energy Production and Economic Analysis of Wind Farms Using CFD Results. J. Wind Energy 2020, 11, 23–30. [Google Scholar]
- Polo, J.; Wilbert, S.; Ruiz-Arias, J.A.; Meyer, R.; Gueymard, C.; Suri, M.; Martin, L.; Mieslinger, T.; Blanc, P.; Grant, I.; et al. Preliminary survey on site-adaptation techniques for satellite-derived and reanalysis solar radiation datasets. Sol. Energy 2016, 132, 25–37. [Google Scholar] [CrossRef]
- Carta, J.A.; Velázquez, S.; Cabrera, P. A review of measure-correlate-predict (MCP) methods used to estimate long-term wind characteristics at a target site. Renew. Sustain. Energy Rev. 2013, 27, 362–400. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kim, J.Y.; Hwang, S.J.; Kim, H.G.; Park, C.Y.; Jeong, J.Y. Site Adaptation of the Reanalysis Data ERA5 on the Power Prediction of Wind Farms. J. Korean Sol. Energy Soc. 2022, 42, 79–91. [Google Scholar] [CrossRef]
- Gualtieri, G. Reliability of era5 reanalysis data for wind resource assessment: A comparison against tall towers. Energies 2021, 14, 4169. [Google Scholar] [CrossRef]
- Rogers, A.L.; Rogers, J.W.; Manwell, J.F. Comparison of the performance of four measure–correlate–predict algorithms. J. Wind Eng. Ind. Aerodyn. 2005, 93, 243–264. [Google Scholar] [CrossRef]
- Lambert, T.; Grue, A. The matrix time series method for MCP. In Proceedings of the WINDPOWER 2012 Conference, Atlanta, GA, USA, 3–6 June 2012. [Google Scholar]
- Hyun, S.G.; Jang, M.S.; Ko, S.H. Variability Characteristics Analysis of the Long-term Wind and Wind Energy Using the MCP Method. J. Korean Sol. Energy Soc. 2013, 33, 1–8. [Google Scholar] [CrossRef][Green Version]



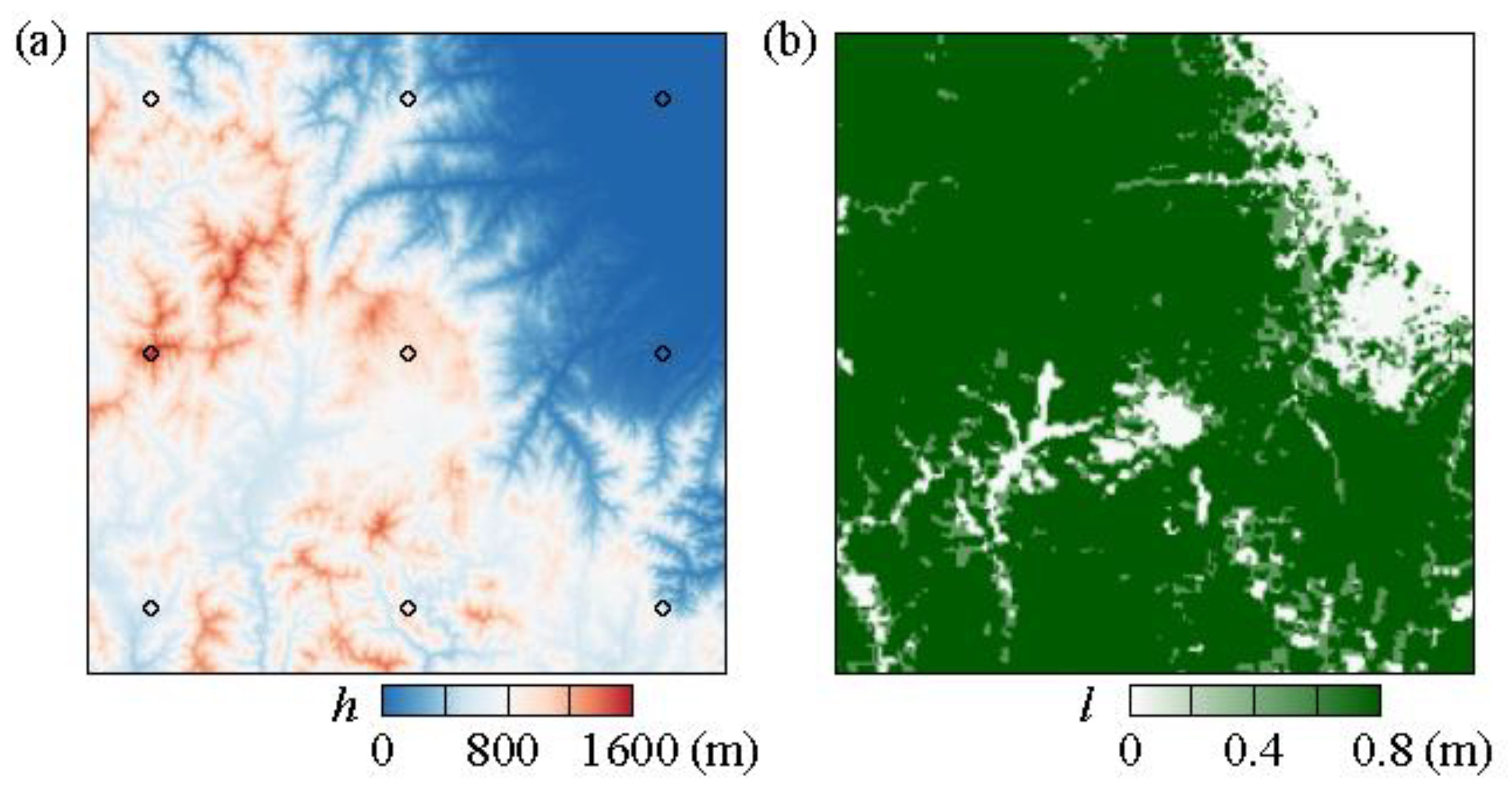
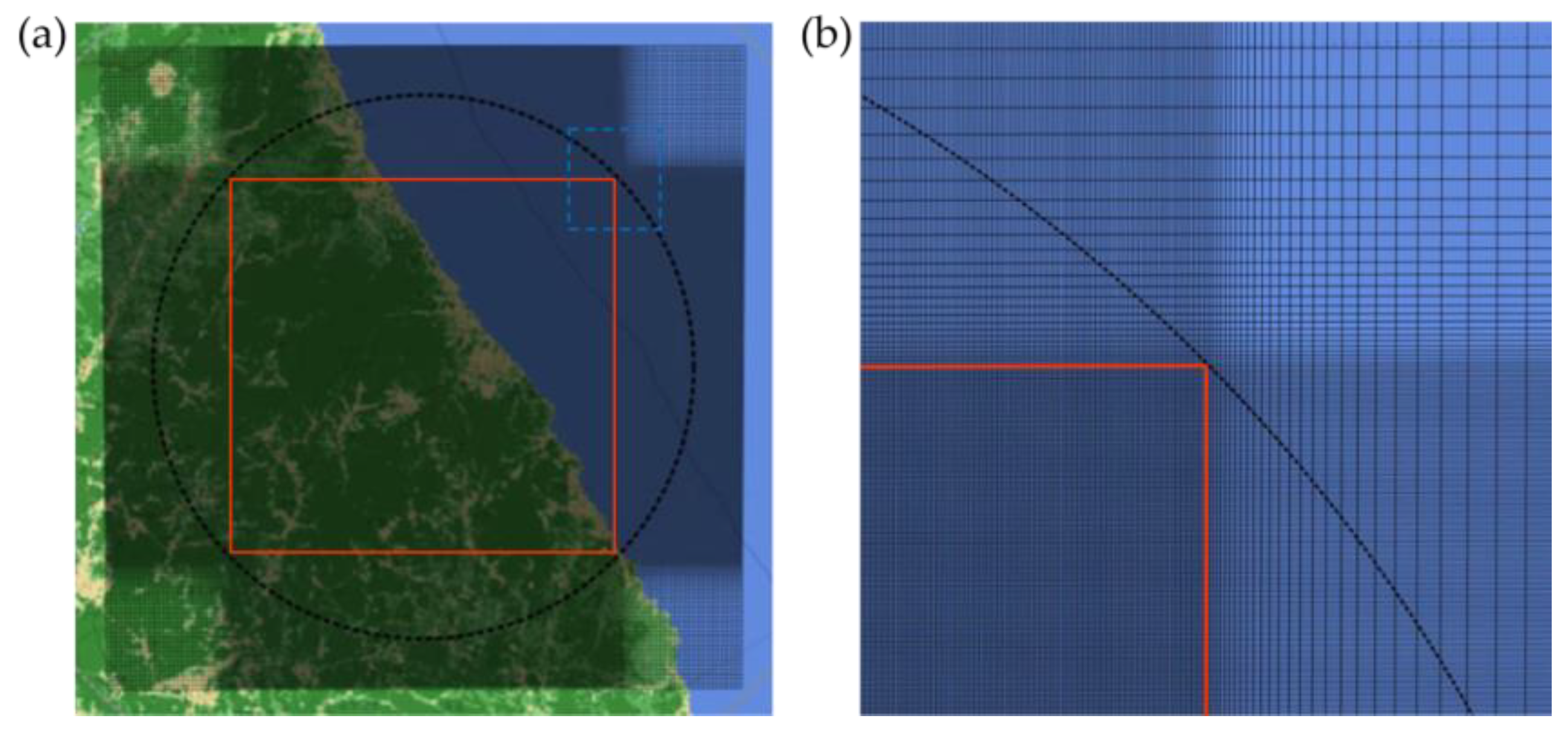
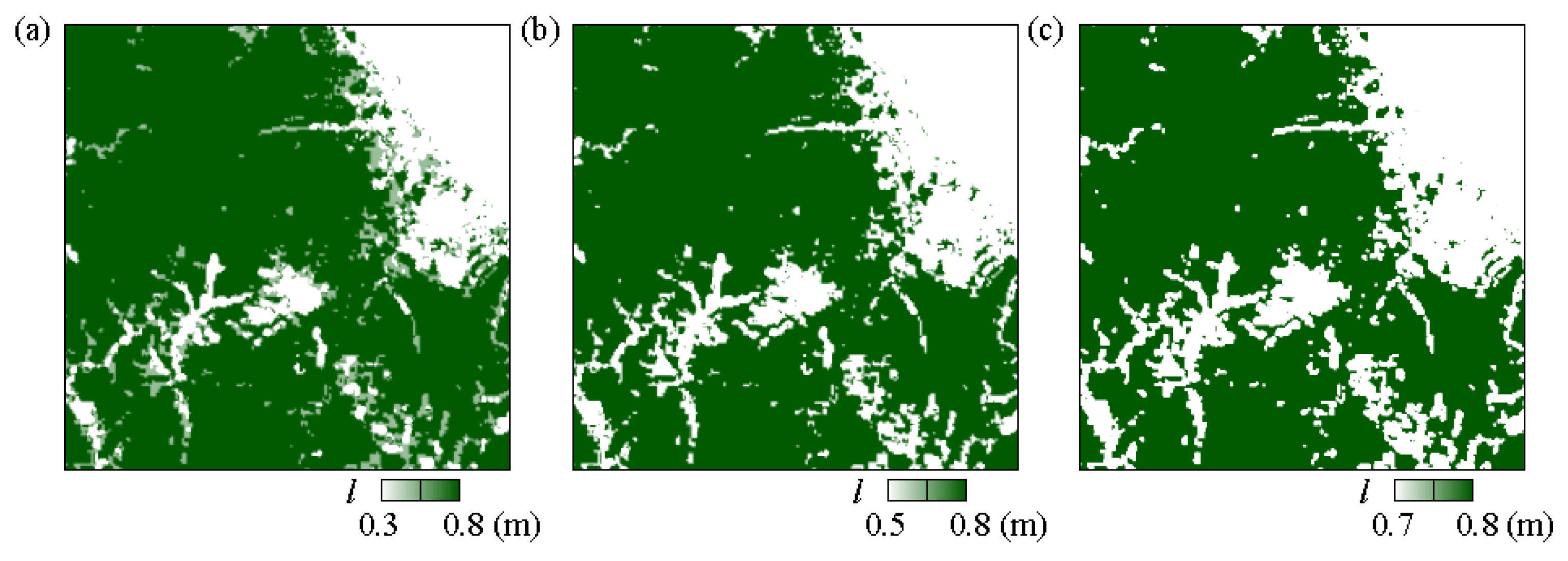



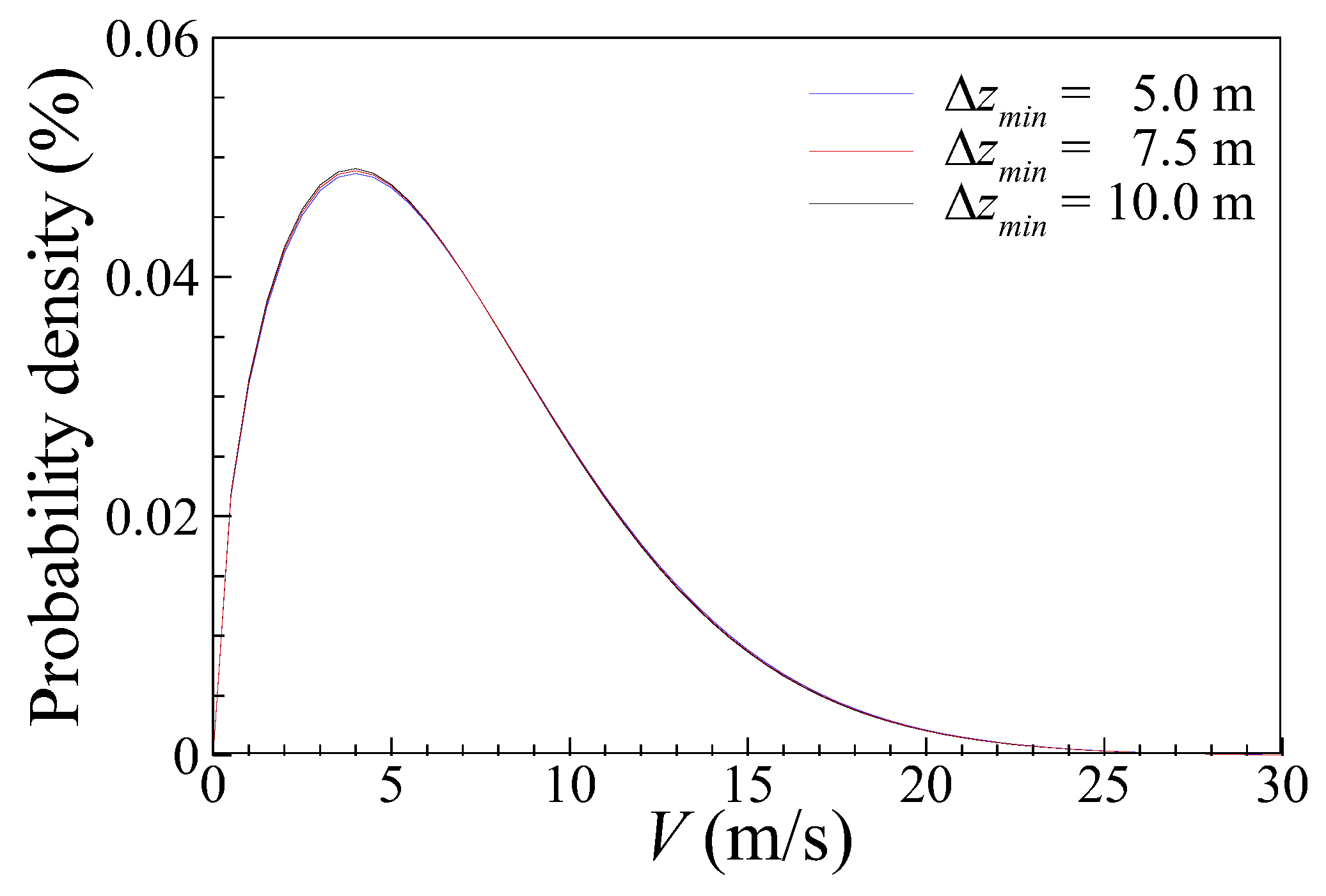


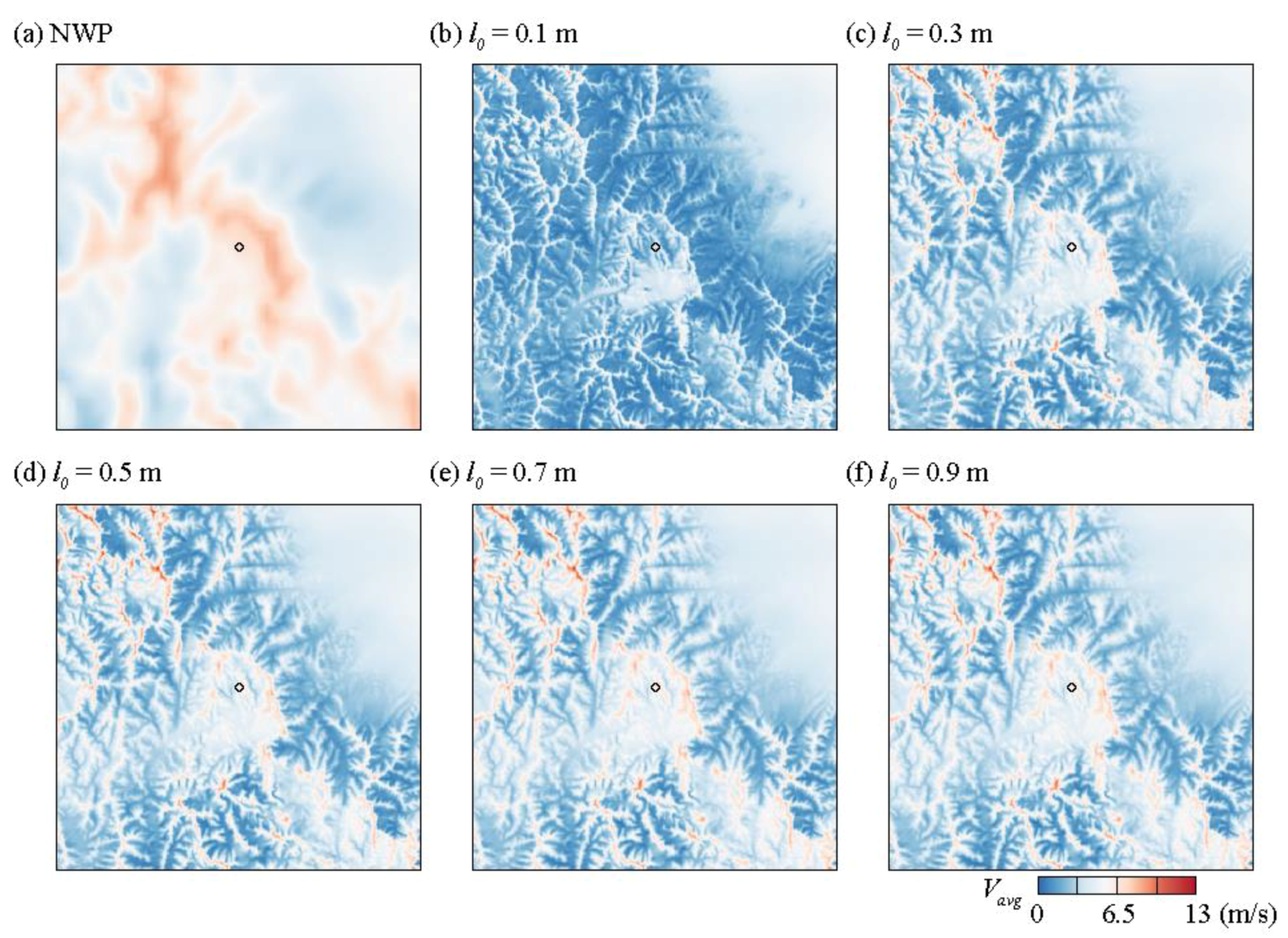
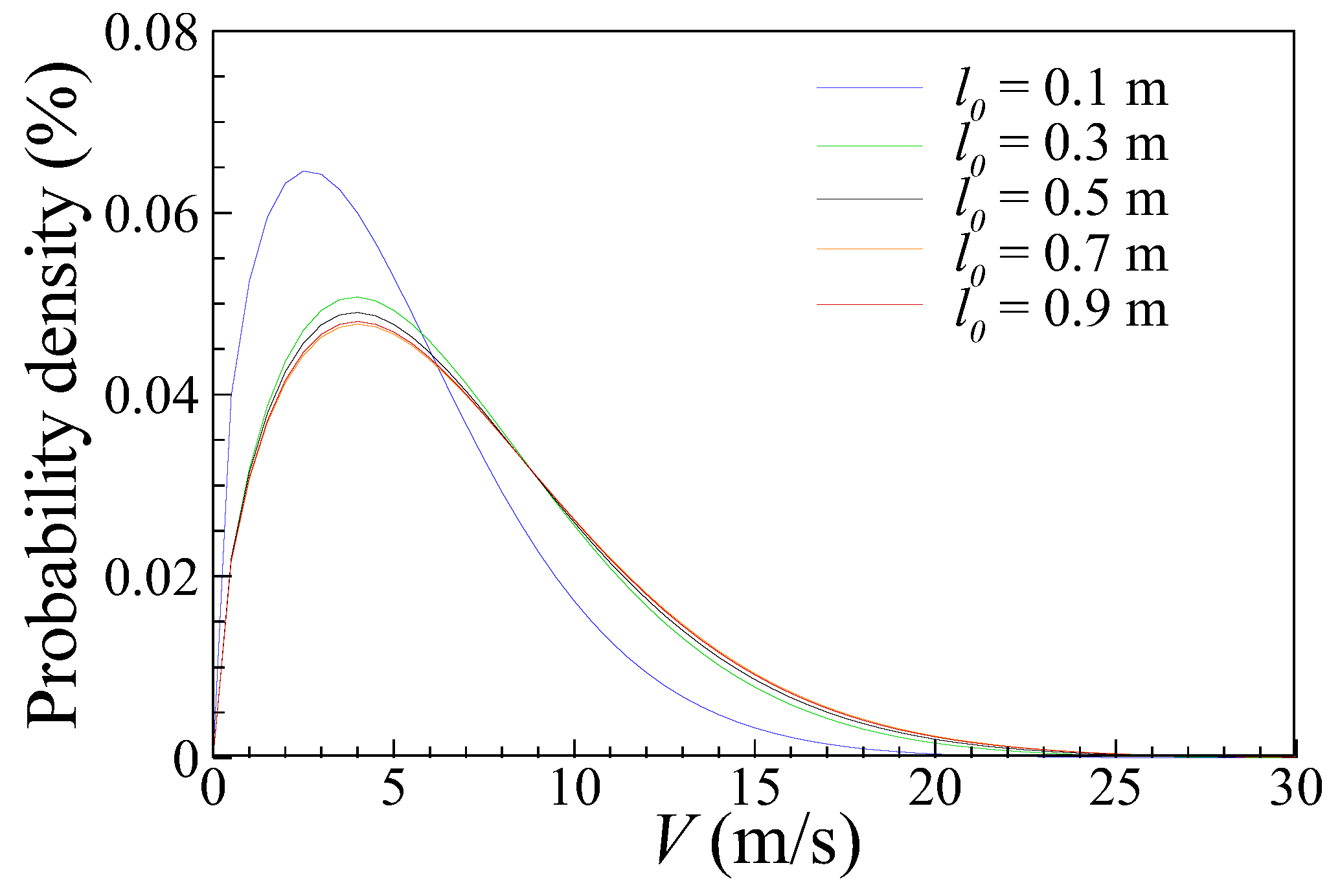


| Δzmin (m) | Vavg (m/s) | AEP (MW) |
|---|---|---|
| 5 | 6.959 | 10,572.829 |
| 7.5 | 6.928 | 10,504.428 |
| 10 | 6.902 | 10,446.890 |
| Δdir (o) | Vavg (m/s) | AEP (MW) |
|---|---|---|
| 15 | 6.889 | 10,423.650 |
| 30 | 6.902 | 10,446.890 |
| 45 | 6.976 | 10,597.309 |
| l0 (m) | Vavg (m/s) | AEP (MW) |
|---|---|---|
| 0.1 | 5.188 | 6041.079 |
| 0.2 | 6.302 | 9056.832 |
| 0.3 | 6.696 | 10,000.072 |
| 0.4 | 6.833 | 10,298.702 |
| 0.5 | 6.902 | 10,446.890 |
| 0.6 | 6.988 | 10,630.660 |
| 0.7 | 7.082 | 10,826.366 |
| 0.8 | 7.063 | 10,787.763 |
| 0.9 | 7.039 | 10,738.914 |
| MCP Method | VR | MTS | LLS | TLS | |
|---|---|---|---|---|---|
| R2 (NWP-MCP-CFD) | 0.1 | 0.512012191 | 0.478613892 | 0.764439075 | 0.172561868 |
| 0.3 | 0.807865206 | 0.700670966 | 0.872962351 | 0.215983043 | |
| 0.5 | 0.848751756 | 0.734510185 | 0.818943799 | 0.220863726 | |
| 0.7 | 0.869351275 | 0.632518286 | 0.771429777 | 0.219811708 |
| Simulation | CFD | Synthesis | |
|---|---|---|---|
| Computational Time | 0.1 | 181 h 30 min | 89 h 30 min |
| 0.3 | 154 h 57 min | 91 h 24 min | |
| 0.5 | 181 h 5 min | 89 h 24 min | |
| 0.7 | 188 h 57 min | 97 h 21 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Moon, H.; Kim, J.-Y.; Kim, K.H.; Kim, H.-G.; Park, S.G. Assessing the Reliability and Optimizing Input Parameters of the NWP-CFD Downscaling Method for Generating Onshore Wind Energy Resource Maps of South Korea. Energies 2024, 17, 648. https://doi.org/10.3390/en17030648
Kim J, Moon H, Kim J-Y, Kim KH, Kim H-G, Park SG. Assessing the Reliability and Optimizing Input Parameters of the NWP-CFD Downscaling Method for Generating Onshore Wind Energy Resource Maps of South Korea. Energies. 2024; 17(3):648. https://doi.org/10.3390/en17030648
Chicago/Turabian StyleKim, Jeonghyeon, Hyungoo Moon, Jin-Yong Kim, Keon Hoon Kim, Hyun-Goo Kim, and Sung Goon Park. 2024. "Assessing the Reliability and Optimizing Input Parameters of the NWP-CFD Downscaling Method for Generating Onshore Wind Energy Resource Maps of South Korea" Energies 17, no. 3: 648. https://doi.org/10.3390/en17030648
APA StyleKim, J., Moon, H., Kim, J.-Y., Kim, K. H., Kim, H.-G., & Park, S. G. (2024). Assessing the Reliability and Optimizing Input Parameters of the NWP-CFD Downscaling Method for Generating Onshore Wind Energy Resource Maps of South Korea. Energies, 17(3), 648. https://doi.org/10.3390/en17030648








