Abstract
Achieving the UN Sustainable Development Goals is impossible without sustainable oil and gas production, both in terms of ensuring equal access to cheap energy and preserving the environment, as well as caring for non-renewable fossil energy sources. This actualizes the need for the digital 3D modeling of wells, which allows one to assess their current condition and predict their future condition as well as determine the feasibility of investing in their reconstruction and the expansion of the well network. This is possible due to the fact that the visualization of a well, reflecting its physical and technical parameters, gives engineers, designers and ecologists the opportunity to recognize the defects of the well (cracks, cavities, behind casing and interlayer leaks, etc.) and predict their appearance and proliferation on which the service life, hydrocarbon flow rate, pollution, operating and capital costs directly depend. The software required for this must be versatile enough to cover different types of logging and fit different operating systems. The goal of the study is to develop a software for creating visual 3D models of wells based on acoustic and various types of radioactive logging data, capable of integrating drilling rig parameters and geophysical survey data with modern 3D modeling and programming methods. The developed software meets the requirements of various operating systems and the specifics of different types of logging, which is designed to help in increasing the productivity of oil and gas wells, save energy consumption and reduce groundwater pollution from chemicals used in hydrocarbon production. This is achievable by ensuring trouble-free execution and the operation of well systems, minimizing the risks of collapses and the destruction of well walls through accurate monitoring and forecasting their dynamic condition in real time using 3D models, which is not available for static 2D models.
1. Introduction
The role of the oil and gas sector as a source of fossil energy sources in achieving sustainable development goals is constantly increasing, which is true both nationally and globally. Natural gas cannot be considered only as a transitional fossil energy source from coal to renewables, since by 2040, its share in primary energy production is expected to increase from 22 to 26% [1]. At the same time, today the share of the countries of Southeast Asia in global gas consumption has reached 24% and whilst the countries of the Middle East constituted 15% in 2022, collectively equaling the USA and the EU [2].
As for the production and consumption of oil, its high share in fossil sources of primary energy (about 30%) is due to the provision of energy for transport (up to 90%) and industry (up to 40%). Natural gas, in turn, provides up to 40% of the demand for primary energy from industry, 20% of the demand for the electric power industry and 76% of the demand for households [3]. This serves to forecast an increase in global oil demand from 97 in 2021 to 110 million barrels per day by 2045 (mainly due to the increased production in OPEC countries) [1].
The predominance of oil and gas in the structure of fossil energy sources makes their production an important component in the process of achieving the UN Sustainable Development Goals [4], in particular, Goal 1—No Property (by expanding access to cheap energy for developing countries and promoting their financial stability). Furthermore, Goal 7—Affordable and Clean Energy—implies the development of the production of cheap, environmentally and technologically safe fossil energy resources that ensure an uninterrupted energy supply, primarily to developing countries, which corresponds to natural gas [5]. Goal 9—Industry, Innovation and Infrastructure—means the requirement for constant upstream, midstream and downstream technologies modernization [6].
The important role of oil production and, above all, natural gas as fossil energy sources, determines high requirements for the technical condition of upstream, midstream and downstream systems, the elements of which throughout the world show significant signs of aging and operate at maximum or close to maximum power [7]. At the same time, global investments in the production of oil and gas (about USD 720 billion per year) correspond to investments in the production of electricity (about USD 780 billion); at the same time, investments in fossil fuel power directly do not exceed USD 120 billion [8].
An important requirement for the sustainable production of oil and gas as fossil energy sources is the maintenance of a large number of wells around the world, which requires the timely receipt of the geological documentation of well sections, the industrial assessment of mineral resources and control over the development of the fields. This requires the development of geophysical research methods, one of which is logging, including the development of software for 3D modeling of wells, which form the basis of a sustainable upstream.
The problem with developing such software is that existing programs are focused on solving specific application problems—in our case, they cover one type of logging, and universal multifunctional geoinformation platforms, such as ArcInfo by ESRI [9], are at different technological levels in terms of software engineering perspective. In turn, supporting a variety of software and hardware platforms, localized for different machine languages, various standards, including passing the official certification procedure for compliance with these standards—all these significantly increase the development costs to an unacceptable level. Most existing products in the field of 3D well modeling have their own formats for storing spatial data, which increases the likelihood of their partial loss during import/export. This is also typical for advanced software ArcGIS for Desktop [10], GeoMedia by Hexagon [11] and MapInfo Professional 11.0 by Precisely [12].
The development of a universal software tool for the operational visualization of the well walls for different types of logging is especially in demand for horizontal drilling, since it is key to the development of deep reserves of liquid hydrocarbons today [13], and a condition for maintaining production in the future. The development of complex offshore fields is unacceptably expensive for traditional drilling technologies [14]. Along with this, modeling the results of geophysical surveys of wells during horizontal drilling will help reduce greenhouse gas emissions, as it allows hydrocarbons to be extracted from deeper layers, where they are under higher pressure, which allows decreasing energy to be consumed for production and transportation [15].
The versatility of software for 3D well modeling is also determined by its applicability for all types of logging: induction and lateral logging, based on the study of electromagnetic fields of various natures in rocks [15], gamma ray logging, designed to study the natural radiation of rocks [16]; density gamma–gamma logging [17] and neutron logging [18] based on the effect of the interaction with the rock of radiation sources and neutrons, as well as acoustic logging, based on the study of the characteristics of elastic waves of the ultrasonic and sound range in rocks [19].
Three-dimensional well modeling research can be divided into two groups: modeling the geology of oil and gas fields, as well as constructing volumetric models of wells by combining data from various logging methods.
The first group includes an analysis of the possibilities for integrating logging data from various sources [20], including for the 3D modeling of hydrogeological objects [21], using neural networks for these purposes [22], the application of the finite element method [23], integration of logging and seismic monitoring data in reservoir structure modeling [24].
The second group of studies is related to the 3D modeling of horizontal drilling [25], modeling pore pressure in a well [26,27] and the oil–water zones [28], advanced 3D modeling using the spectral-element method [29] as well as the 3D visualization of the bottom of wells during the analysis of productive zones [30].
It should be noted that these studies discuss 3D modeling approaches and tools that do not provide a complete picture of the reservoir, which is critical for oil and gas production engineers, so it is important to make the transition to the models which allow the observation of the reservoir in volume, determining its shape, dimensions, as well as the presence of various structures, such as cracks, cavities, etc. That is everything that determines the sustainability of oil and gas production and the impact of this process on the environment. All these require a special software that allows one to visualize the influence of neighboring reservoirs and structures on the studied reservoir, suitable for the wells at any depth and in any rock intervals, while changing the view in real time as the new logging data of different types is obtained. The solution to this problem is the development of the software presented in this article.
2. Materials and Methods
2.1. Obtaining Oil and Gas Well Logging Data Necessary for the Development of Software for 3D Well Modeling
In this study, acoustic and radioactive logging was used to obtain data on the condition of wells for their 3D modeling. Acoustic logging is based on measuring the parameters of the radial resonance signals of the irradiated segment of the casing pipe, which arise during the normal incidence of an acoustic pulse on the inner wall of the pipe (reverberation signals).
Radioactive logging is a research based on measuring the parameters of the fields of ionizing particles (neutrons and gamma rays) in order to determine the nuclear physical properties and elemental composition of rocks. During radioactive logging, signals from ionizing radiation detectors are directly measured in the form of a count rate—the number of pulses recorded per unit time. The principle of gamma ray logging is based on the registration by downhole instruments of the natural radioactivity of rocks that make up the well in its section. The neutron logging method is based on irradiating a borehole and rocks with neutrons from a stationary ampoule source and measuring the flux densities of epithermal and thermal neutrons and gamma rays produced as a result of nuclear reactions of neutrons scattering and capture.
Geophysical equipment for well logging includes a variety of devices that allow one to obtain all the necessary initial data for 3D modeling using radioactive and acoustic logging methods. Examples of such devices include: a core retrieving barrel with a removable sliding crown SRK-76 (for compensated neutron logging using thermal neutrons, with a Pu–Be source with an average neutron energy of about 4.5 MeV, with a removable sliding drill bit with a diameter of 76 mm) [31]; downhole devices AST-K-80 for acoustic logging [32] (with a measurement range of the internal radius of the well of 55–120 mm and two transducers with radiation frequencies of 400 and 1000 kHz); ASPG measuring probe. The latter contains eight electroacoustic transducers evenly spaced at 45° along a spiral enclosing the probe, and with a measurement range of the inner radius of the well of 60–120 mm, and eight transducers with radiation frequencies of 500 kHz [33]. Their designs are presented in Figure 1.
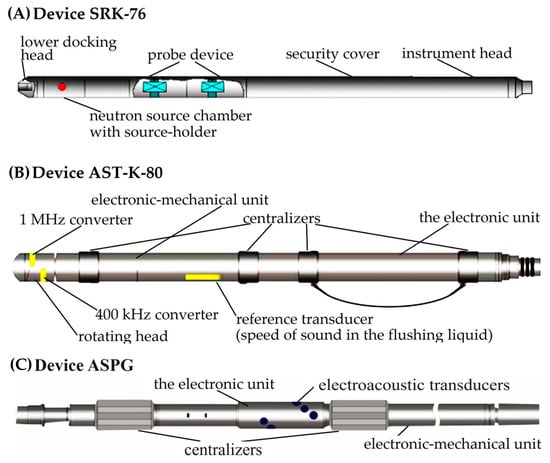
Figure 1.
Designs of SRK-76 for neutron logging (A), AST-K-80 (B) and ASPG for acoustic logging (C) (made by Authors).
In our research, we rely on the experience of using a family of devices for acoustic and radioactive logging. In particular, the ASPG scanner was used for a number of sonic logging studies. The main measurement parameters are the propagation times and amplitudes. The recording was made in an open well without a whipstock on a downhole device; the logging speed was 700 ÷ 750 m/hour. In reservoirs with a known rock lithotype and a thickness of more than 3 ÷ 5 m, the porosity values calculated from the readings of short, long and ratio probes corrected for this lithotype should be reproduced with an absolute error of no more than ±1.5%.
We note that for future acoustic and radioactive logging measurements, it is possible to use other azimuthal devices (receiving data from four sensors), such as CrossWave azimuthal sonic tool by Weatherford International plc (Houston, TX, USA), Sonic Scanner tool by Schlumberger plc (Houston, TX, USA), UBI (ultrasonic acoustic borehole imager) by Schlumberger Limited (Houston, TX, USA), ZoneTrak G near-bit gamma service by Baker Hughes plc (Houston, TX, USA), etc.
The development of a 3D well model used to create the well visualization software is initially based on an analytical and numerical solution to the single-phase filtration problem to ensure that the well pressure is calculated exactly with the analytical expression. Accordingly, the calculation of the pressure in the wellbore in a certain calculation cell was carried out in comparison with the reservoir pressure in this cell, and taking into account the assumption that the flow near the well is single-phase:
where:
- p(r)—average reservoir pressure;
- —drilling fluid viscosity;
- k—relative phase permeability;
- U—bottom hole pressure;
- Q—well flow rate under standard conditions;
- rw—maximum wellbore radius;
- r—minimum wellbore radius.
The basis of well modeling is the determination of its radii in each specific cell (Peaceman radius) at which the calculated pressure in the cell is equal to pressure p0 on the supply circuit of the modeled well [34].
All expressions for the Peaceman radius r0 were obtained for a separate well (or group of wells), i.e., under the assumption that other wells and reservoir boundaries are sufficiently distant and do not affect the flow pattern near this well. In our case, this means that there must be at least 10 calculation cells between neighboring wells, and at least 5 cells between the well and the nearest boundary of the modeled area.
The model of a horizontal well parallel to one of the coordinate axes xi (i = 1, 2, 3) of the system x1, x2, x3 is similar to the model of a vertical well (2):
where:
- r0—the equivalent radius of the cell;
- Δxi—the size of the calculation cell in the direction of the xi axis.
Expressions for productivity can also be adjusted due to the incomplete opening of the calculation cell. In the future, as we develop the method of the 3D modeling of wells, expression (2) will become more complicated, since the well may be inclined or have a more complex trajectory, and the dimensions of the calculation cells in the vertical direction are usually much smaller than in the horizontal direction (due to features of the reservoir structure).
To build a future visual 3D model of a well, it is necessary to obtain the radii of the wellbore. In relation to acoustic logging, the radii are calculated for eight channels (radiation frequency 500 kHz), the speed of sound in the drilling fluid and the known distance from the axis of the device to the radiating surface of the electroacoustic transducer. On the right side in the column in Figure 2, an image of the well wall is constructed. The results of using the logging devices include the values of the radioactive logging data (along with the average, minimum and maximum diameters of the well), presented in the left part of Figure 2. The results of acoustic logging (well profile) are presented in the right part of Figure 2.
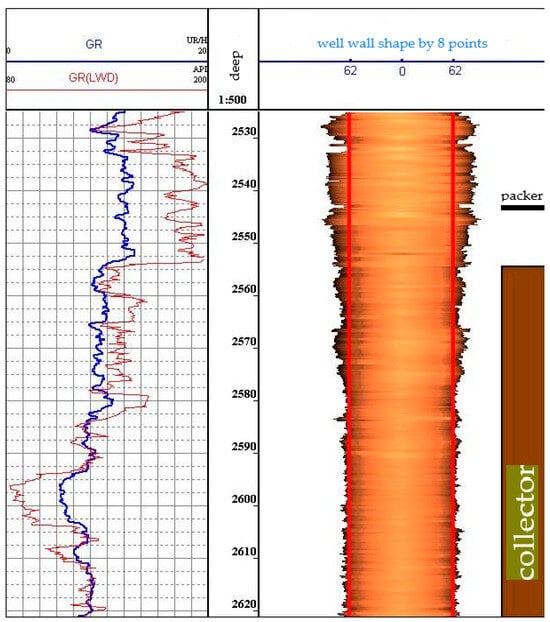
Figure 2.
Gamma ray data and results of processing data from an acoustic profiler with a sensor radiation frequency of 500 kHz.
Figure 2 shows the results of using two types of logging to construct a well profile (gamma ray logging is used to link sonic logging data by depth).
For clarity, Figure 3 presents the data from the types of logging described above at eight points of a circle in a plane.
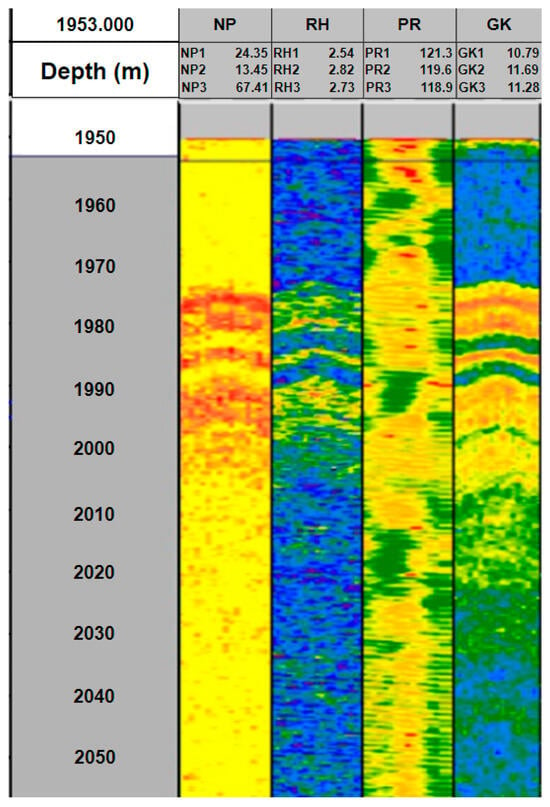
Figure 3.
An example of a volumetric model for the types of logging described above (from left to right: column NP presents azimuthal data of neutron gamma ray logging; RH—azimuthal data of density gamma–gamma ray logging; PR—azimuthal data of acoustic logging; GK—azimuthal data of gamma ray logging).
The pictures obtained in Figure 3 represent data without taking into account the volume and dimensions of the well.
2.2. Review of Existing 3D Solutions in Well Modeling
To date, there are several projects based on the use of spatial data warehouses Oracle Locator/Spatial and PostGIS. There are also many companies that offer complete solutions or the development of custom Geo Information Systems (GIS), which are based on the platforms of the giants ArcInfo and MapInfo, or on open source software. The solutions they offer are focused on solving applied problems in specific areas, while not being an independent GIS platform. The problem is that when purchasing such a system, focused on solving problems in a specific subject area, you will most likely be able to obtain a result that is only suitable for one type of logging [35]. If you purchase a universal GIS like ArcInfo or MapInfo, then you need to be prepared for the fact that, without purchasing additional modules or involving experienced developers who can adapt this GIS to the required requirements, you most likely will not be able to obtain a satisfactory result [36]. The most common platforms for building the 3D models of wells and other underground structures include the following:
- -
- ArcGIS for Desktop (Environmental Systems Research Institute, Inc., Redlands, CA, USA);
- -
- desktop applications (regular PC programs) for working with GIS, supported platforms from Windows XP to Windows 11 in 32 and 64 bit editions. There are several versions of the program, differing in the range of functions and cost;
- -
- GeoMedia (Intergraph, Madison, AL, USA) is a modern GIS platform with an open architecture that allows building GIS systems using the first, third, or fourth technological schemes for working with spatial data. It uses a unique technology of built-in data servers (data servers), which allows one to directly work with the spatial data of many formats and coordinate systems, without prior conversion.
- -
- MapInfo Professional 11.0 (Precisely Holdings, LLC, Englewood Cliffs, NJ, USA) is a desktop application for the end user that has a rich set of functions for displaying, creating and editing spatial and semantic data. The software includes Crystal Reports—a report generator, which allows the generation of complex multi-page reports containing spatial data. This software is available only for Microsoft Windows 32 bit platform.
A comparison of these platforms is presented in Table 1.

Table 1.
Comparison of GIS analogues.
In general, the software packages listed in Table 1 have a number of advantages:
- -
- Ability to create detailed well models that can be used for drilling planning and risk assessment;
- -
- Integration with other programs and data, which allow the creation of more accurate models;
- -
- Capable of performing real-time data analysis that can support decision making at the drilling site.
However, there are also some disadvantages:
- -
- The high cost of programs and the necessity to train personnel to use them;
- -
- Need for a large amount of data to create an accurate model, which may not be available in some regions;
- -
- Limitations in the modeling accuracy due to incomplete data or errors in the source data.
Different comparisons between 3D well modelling software and the currently used software listed above include the following.
In the ArcGIS 10.8.2 software, the calculation of the productivity index of a horizontal well extended along the coordinate axis was used as a control solution. We combined this solution with an analytical expression for calculating the pressure field in a profile problem on a Cartesian grid with a large ratio of the cell width to its height. This made it possible to calculate the well productivity index from the sections in a three-dimensional problem, which is impossible in ArcGIS.
GeoMedia 16.7.0.210 software allows one to model an individual single-hole inclined well in a laterally infinite layered system. The corresponding semi-analytical solution, based on the reflection method and the analytical solution of the slender body theory, was combined by us in the software presented in the article with a finite-difference solution for pressure, with boundary conditions for lateral pressure. To do this, in our software, we solved the Laplace equation in the elliptic coordinates using a geometric transformation to take into account the inclination of a well in an infinite formation. This result was used in conjunction with a numerical solution to determine the suitable well conductivity factors.
MapInfo Pro 21.1.25 software uses more complex well geometries based on the methods of the numerical integration of differential equations. A number of its modules shows the relationship between wellbore hydraulics (i.e., the final conductivity of wells) and the flow movement in the reservoir. All semi-analytic methods used in MapInfo have the advantage of a limited dataset and high computational efficiency compared to finite-difference modeling. This makes MapInfo well suited for the purpose of the preliminary estimation of primary production during reservoir energy depletion. At the same time, the software presented in the article allows us to visually evaluate a well throughout its operation.
The analysis of the above-listed GIS software shows the need for a program tool, which significantly differs from existing solutions and must be based on open source; the shader kits should be collected from free solutions and provide good performance and acceptable accuracy. The interface also need to be quite simple. That is why the software tool we developed and presented below reflects these features and is on par with the most popular geophysical modeling programs.
The accuracy of the simulations in the software listed above depends on many factors, including the input data, the algorithms used and the model settings. Each of these software programs has its own characteristics and modeling capabilities, so a direct comparison of their accuracy may not entirely be correct. Therefore, we compared the reference radii of wells with the radii determined using our program, as well as ArcGIS, GeoMedia and MapInfo (Figure 4, Figure 5, Figure 6 and Figure 7).
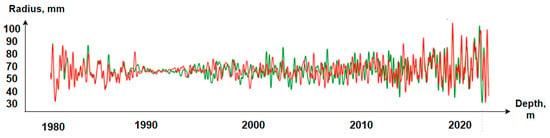
Figure 4.
Graphs of the well walls of the reference (green) and those constructed by the software presented in this article (red).
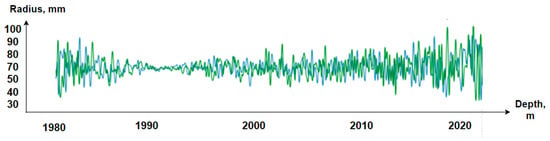
Figure 5.
Graphs of the well walls of the reference (green) and those constructed by ArcGIS software (blue).
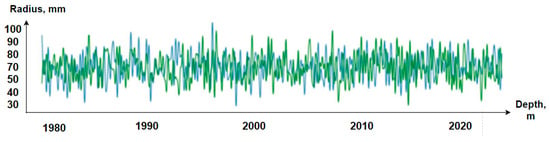
Figure 6.
Graphs of the well walls of the reference (green) and those constructed by GeoMedia software (blue).
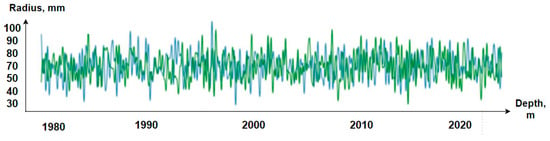
Figure 7.
Graphs of the well walls of the reference (green) and those constructed by MapInfo software (blue).
From the graphs, we can conclude that the 3D model presented in this article is quite accurate on par with ArcGIS. The analysis showed that GeoMedia and MapInfo models are inaccurate due to the fact that they lack the TkrPlot shader package built into the C++ programming language. Our use of TkrPlot has become the next higher level of graphics for displaying geophysical parameters.
3. Results
This paper proposes an approach to creating a software for the 3D visualization of a wellbore for different types of logging, within which a set of algorithms has been developed that allows one to construct the grid model of a medium of complex geometry and perform the necessary calculations [37]. Depending on the current goal and available resources, it is proposed to carry out 3D modeling in the entire area of interest, or modeling in sections of the original area containing the most interesting characteristic features of the wellbore, or a combination of these approaches. Thus, the proposed software includes a tool for modeling the data obtained from acoustic, gamma ray, neutron and density logging, as well as a color palette for each 3D model.
The development of software was carried out taking into account the architecture of the Windows 10 operating system; an NVIDIA 1650Ti was used as a video card, so peak performance did not exceed the norm. To effectively use shaders, it was necessary to adapt and optimize the algorithms used during modeling based on the knowledge of the architecture of the framework, its components and the necessary software [38].
The developed software package includes a medium model builder, which allows one to construct complex models of elastic media at the grid level based on the idea of the Z-order. In parallel execution, the data are immediately constructed on those computing nodes on which the calculation will subsequently be carried out. A parallel program has also been created for drawing the walls of the well, implementing the previously mentioned methods, adapted to the volume of incoming data. To parallelize this problem, the decomposition of the region into layers along the direction of one of the coordinate axes is used. Each layer is calculated on a separate node, where, in turn, it is further divided into sublayers along a different coordinate axis to the number of graphics accelerators on the node. With this implementation, each graphics card calculates its mesh region within a sublayer at each time step, independently of the others, with the exception of points located on the boundary between two adjacent regions. These points are common to each of the areas, and to continue counting, it is necessary to exchange information about the desired values between graphic cards on the node and between the neighboring nodes in the direction of different coordinate axes. Exchanges are made using MPI (message passing interface) technology; and work with graphics accelerators is carried out using CUDA (Compute Unified Device Architecture) technology.
3.1. Construction of a 3D Model of a Well Using Data Obtained Using Acoustic Logging
For the construction of a 3D model of the well using data obtained using acoustic logging, two methods were used to determine the times of the first reflection from the well wall: threshold or spectral ones. Both methods allow one to obtain the arrival times of the first reflection for each channel. Based on these time values, radii along the entire circumference of the well are subsequently calculated.
3.1.1. Determination of Times Using a Threshold Method
The original data—the wave pictures—include its own signal and noise interference. To increase the signal-to-noise ratio, the data should be filtered with a band-pass filter. The frequency filtering of data is performed during processing, while the original data contained in the file remain in the same form. The threshold method implements the principle of determining the time of the first extremum of a given sign, the amplitude of which exceeds the discrimination level, and the entry time is the value of the blocking time. The discrimination level must exceed the noise level on all channels. The advantage of this method is the visibility of the actions performed, which makes it easier to adjust processing parameters during failure intervals.
The threshold method is used when processing qualitative data. The disadvantage of this method is the need to change the discrimination level at different intervals throughout the well section, which increases the data processing time. At faulty intervals, the processing is carried out again, changing the discrimination level and blocking the position to cut off noise.
3.1.2. Determination of Times by Spectral Method
Considering the fact that the frequency of the emitted signal (~500 kHz) practically does not change when reflected from the wall of the well, and the first reflection has the maximum amplitude in the wave pattern, it is convenient to use the spectral representation of the signal to determine its arrival time. The arrival time is determined by a sliding time window, in which the amplitude spectra are calculated and the maximum of their maximum values is found in the frequency range corresponding to the filter passband. The search starts from the blocking time. The countdown of the arrival time of the reflected signal corresponds to the beginning of the window in which the maximum of the spectra maxima is found.
The threshold method is preferable when the quality of the primary data is good; the spectral method is preferable when the quality of the data is low due to the large deviation of the instrument from the well axis or the acoustic inhomogeneity of the drilling fluid. It should be borne in mind that the correct calculation of data is not possible in gas-producing wells.
To build a future visual 3D model of a well, its radii are calculated using the arrival times from eight electroacoustic transducers (channels), the speed of sound in the flushing fluid and the known distance from the axis of the device to the radiating surface of the electroacoustic transducer. The result of the device’s operation, in addition to determining the size of the radii, is to determine the values of the average, minimum and maximum diameters of the well.
An example of isolating the wave pattern of the first reflection signal from the wall of the well using a spectral method is shown in Figure 8.

Figure 8.
Results of data processing (times of first reflection of signals from the borehole wall and diameters).
Figure 8 shows the data after noise subtraction. Almost throughout the entire interval, the amplitudes of the reflection signals significantly exceed the amplitudes of the noise. The arrival times of reflected signals, after subtracting noise, can be measured by the simplest threshold method. However, the use of this method is inconvenient due to the large amount of data.
3.2. Building a Well Model Based on Data Obtained from Density Logging
Density gamma–gamma logging is based on recording scattered gamma radiation created by a pulsed source of gamma rays. The main types of interaction of gamma radiation with matter are Compton scattering, photoelectric absorption (photoelectric effect) and the formation of electron–positron pairs with subsequent positron annihilation. Thus, the flux and energy spectrum of the recorded gamma radiation are determined by the density and atomic number of the rock. This circumstance is used in density and lithological-density gamma–gamma logging devices to determine the specified rock parameters—density and effective atomic number.
3.3. Construction of a 3D Well Model Based on Data Obtained Using Gamma Ray Logging
To build a 3D model, the values of natural radioactivity of rocks were used, calculated from the initial data of a gamma ray logging device—natural radioactivity (or gamma activity) of rocks in a well, formed due to radioactive isotopes of clay minerals (feldspar, mica, illite and minerals phosphate group).
The shape of the gamma ray logging curve against the reservoirs of finite thickness and increased gamma activity for a device pressed against the wall of the well weakly depends on the technical measurement conditions and is determined by the density of the reservoir. The boundaries of the reservoir are determined by the position of points with a value of 1/2 of the anomaly amplitude for an arbitrary thickness. In the reservoirs of limited thickness, the amplitude of the anomaly is underestimated by the amount (3):
where:
- —recorded anomaly amplitude;
- —the magnitude of the anomaly for a layer of the same activity, but of infinite thickness.
The dependence of the anomaly amplitude () on the thickness of the layer H is expressed in Figure 9 in the form of a correction factor H*:
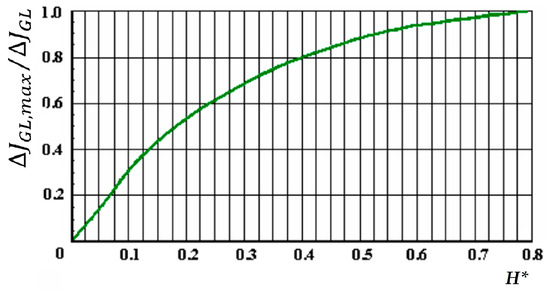
Figure 9.
Correction factor for the influence of the final thickness of the reservoir.
Corrected for the influence of the final thickness of the reservoirs, gamma ray logging readings are brought to standard conditions by making the necessary corrections (4):
where:
- —instrument readings, reduced to standard specifications of measurements;
- —instrument readings against the studied reservoir, corrected for the influence of the host;
- P1—correction factor taking into account the attenuation of reservoir radiation by drilling fluid (well design);
- P2—a multiplier that converts gamma ray logging readings to volumetric activity in accordance with the volumetric model adopted for radioactive logging methods;
- P2 = σ/2.71, where σ is the density of the studied reservoir;
- P3—correction factor taking into account the activity of the flushing liquid.
The value of determines the contribution of well radiation to the readings of the gamma ray logging probe and is determined in one of the following ways:
- -
- According to the minimum sectional readings of the device (5):
- -
- According to the known ratio m of the radioactivity of mud powder AMP and clays AGEL, reliably released in the section , which can be determined from laboratory research data (6):
- JGEL denotes the instrument readings under standard conditions against the supporting gel layer; denotes the ratio of reservoir radiation and drilling fluid with equal radioactivity under standard conditions; σdf, σMP denotes the density of the washing liquid and mineralogical density of mud powder (usually σMP = 2.50); and the value of P3 is determined for the conditions for measuring the value of JGEL.
An example of calculating in the software presented in this article is shown in Appendix A.
The software module for the transition from 2D to 3D when modeling a well uses vertex shaders. They operate with data associated with the vertices of polyhedra, for example, with the coordinates of a vertex (point) in the space, texture coordinates, the color of a vertex, a tangent vector, a binormal vector and a normal vector. According to Yuchi Huo [39], the vertex shader is used for the view and perspective transformation of vertices, for generating texture coordinates and is responsible for data convolution. An example of the implementation of the algorithm is given in Appendix B.
3.4. Visual 3D Models of Wells Created Using Developed Software Tool
For a three-dimensional representation of the input data, it is necessary to obtain a three-dimensional geometry while preserving attribute data. To facilitate and accelerate the process of converting data from a plane to 3D, we need to create an additional software module that allows the convolution of plane data into a cylinder for a given center and radius. It should be noted that the resulting 3D geometry is stored in a true coordinate system, which makes it possible to combine the results obtained with other data at any time.
The visual result of well modeling using the acoustic logging method is presented in Figure 10.
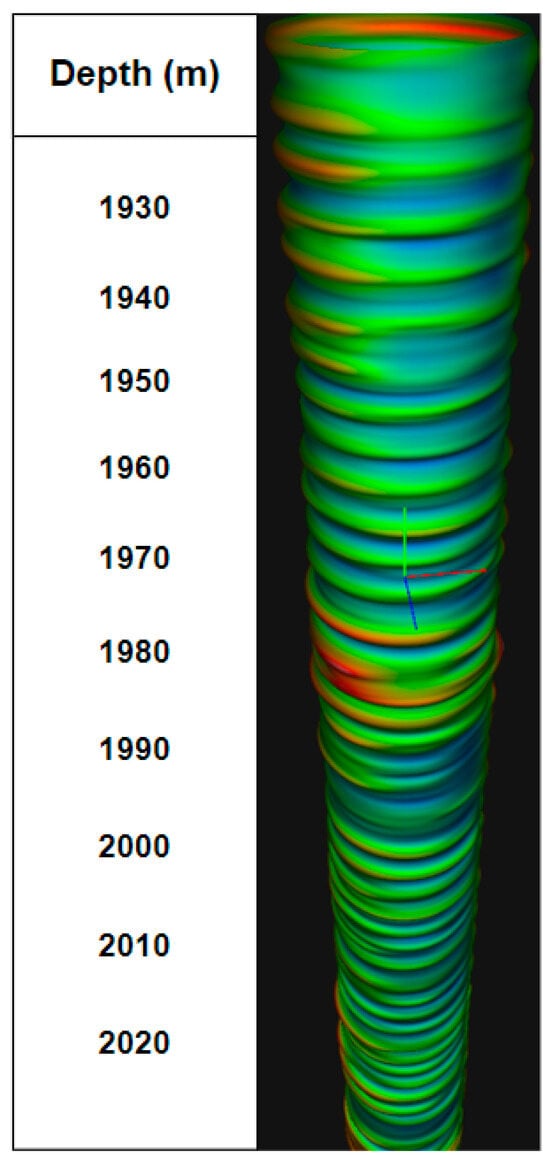
Figure 10.
Three-dimensional model of a well created using the results of acoustic logging.
From Figure 10, we see a 3D model built from acoustic logging data. The text document (Figure 11) contains data for visualization when constructing a profile and other geophysical parameters of the well. The palette presented in Figure 12 was selected for the model of well and built using acoustic logging.
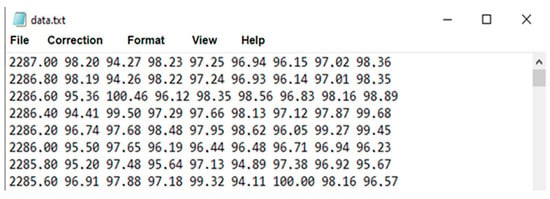
Figure 11.
Example of data for visualizing a well profile shown in Figure 10.

Figure 12.
Distribution of colors on the acoustic logging model.
In each line in Figure 11, the first number indicates the logging depth, and the remaining eight numbers are the radii from the center of the tool to the borehole wall at that depth. For other types of logging, the data are presented in the same way, and they only differ in size.
It can be seen that, in the red interval, the geophysical parameters have changed, and in the blue interval, a reservoir is possible, since the radius has not increased.
The three-dimensional model of a well, built using the gamma ray logging method, is presented in Figure 13, and the palette is presented in Figure 14.
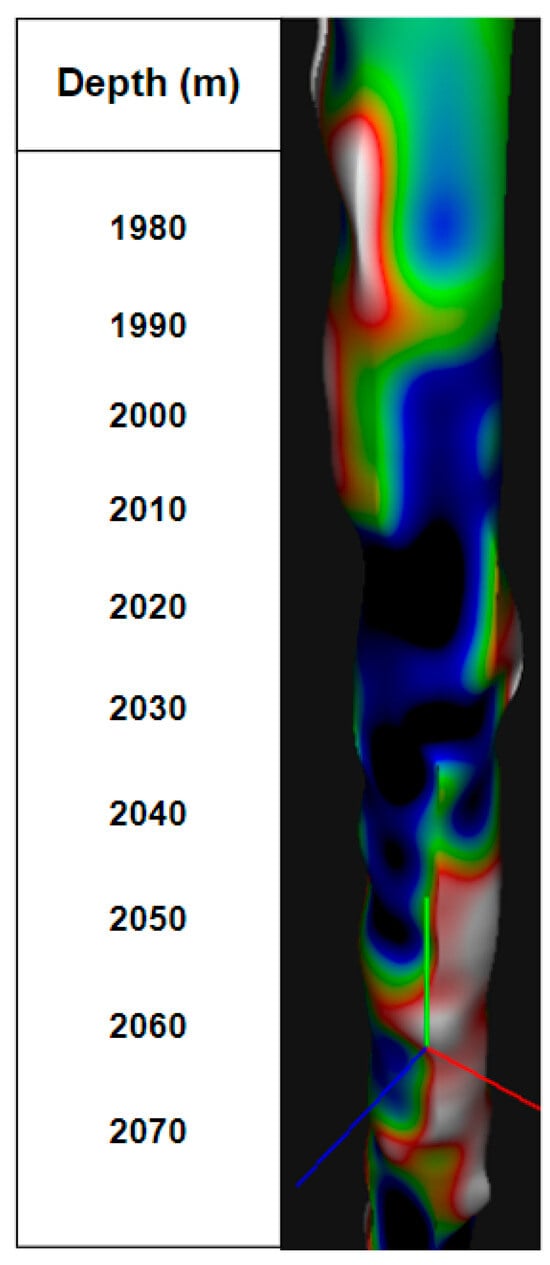
Figure 13.
Three-dimensional model of a well based on the gamma ray logging data.

Figure 14.
Distribution of colors on the gamma ray logging model.
It can be seen that, in the red interval, there is limestone, which indicates the presence of a reservoir.
The model based on the results of density logging is presented in Figure 15.
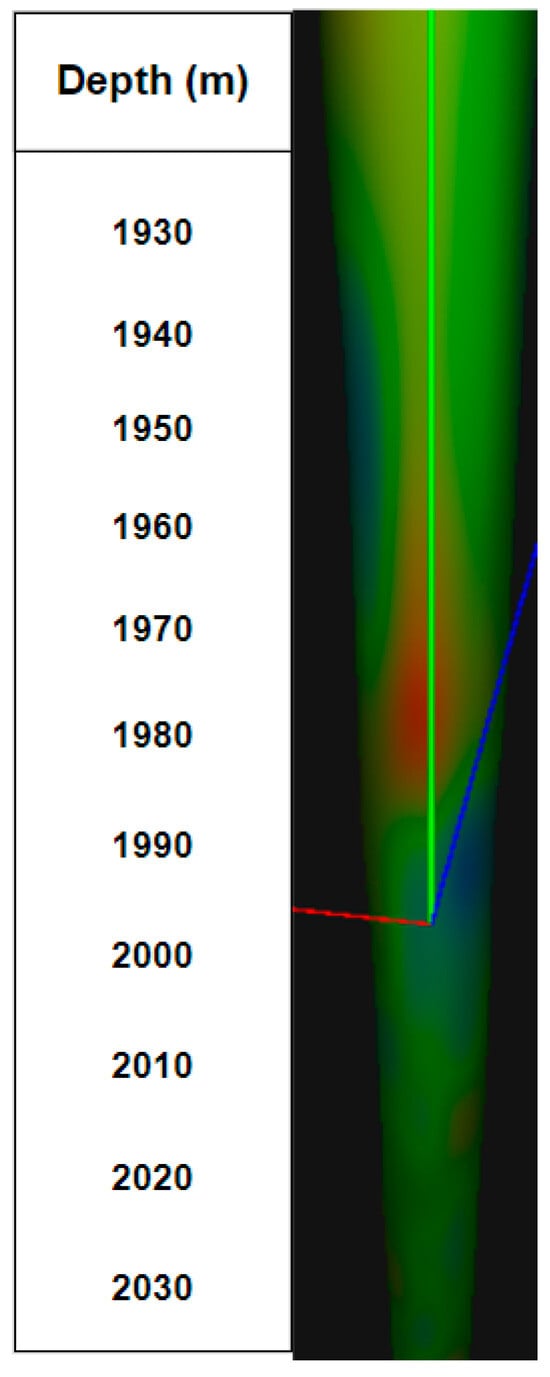
Figure 15.
Three-dimensional model of the well created using density gamma ray logging.
In Figure 15, we see a 3D model built using density gamma ray logging data, which features a more uniform color distribution due to a more accurate display of the rock density of the walls of the well. The palette presented in Figure 16 was chosen for this model.
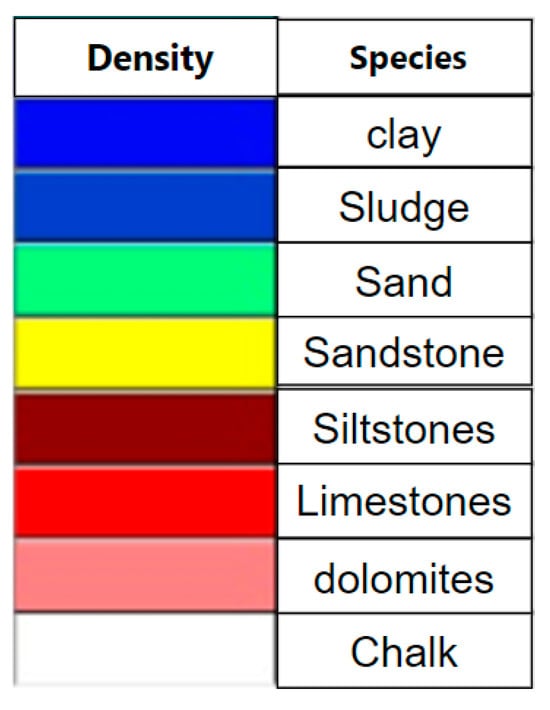
Figure 16.
Distribution of colors on the well model for density gamma ray logging.
It can be seen that the interval has red limestone, so there is a possible reservoir in this interval.
The well 3D model based on the results of neutron gamma ray logging is shown in Figure 17. The palette of this model is presented in Figure 18.
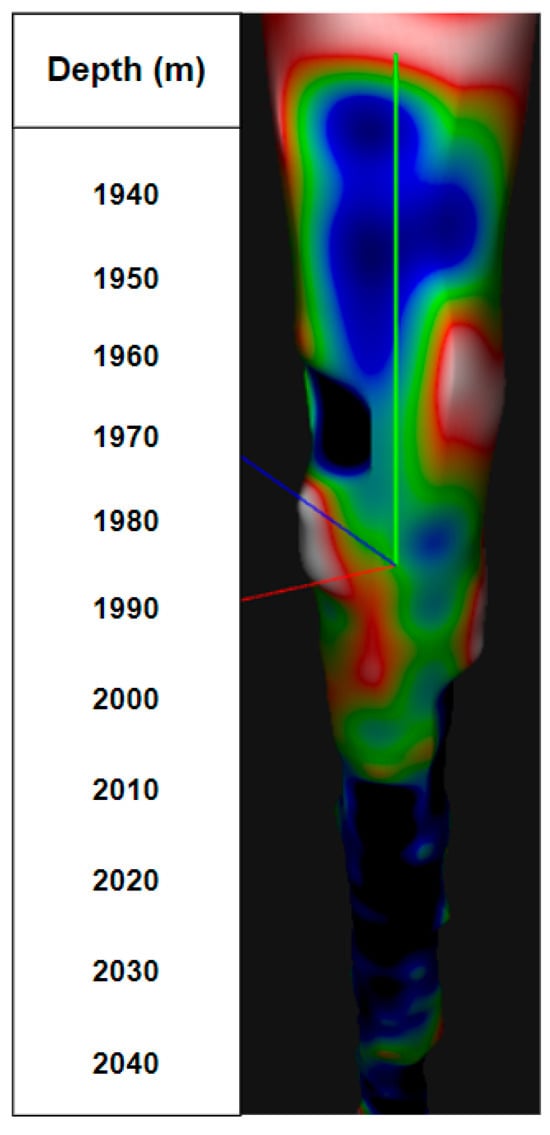
Figure 17.
Three-dimensional model of a well created using neutron gamma ray logging.

Figure 18.
Color distribution on the model for neutron gamma ray logging.
It can be seen that, in the interval of red limestone, there is a high porosity in the rocks, and oil may be found there.
The color palette of the resulting model is set manually and depends on the type of logging. However, for uniformity, the colors are uniform and the values are arranged from smallest to largest. For sonic logging, the color indicates increasing borehole diameters. For density logging, color reflects the density of the rock wall of the borehole; for neutron logging, color reflects the porosity of the rock wall of the borehole. For gamma ray logging, color plays the role of different rocks. When analyzing the pictures, it can be noticed that, at a depth of 1980 m in Figure 3, the color change appears. By analyzing the 3D models, the assumptions are confirmed, which indicates the correctness of the models.
All three models (Figure 9, Figure 11 and Figure 13) represent different geophysical parameters: radii, natural radioactivity of rocks, porosity and density. All data for construction were obtained in one well interval.
The developed technical solutions in the future will provide more efficient processing, synthesis and visualization of data at a fundamentally new qualitative level in the universal software tool. Such an analytical system will provide not only engineers but also specialists from the technical services for reliable and timely information at all stages of a well life cycle.
The accuracy of 3D well modeling depends on the accuracy of the selected calculation method. In our case, to calculate the spatial position of the wellbore axis points, we use the minimum curvature method, which is recognized as the most accurate among other calculation methods. In the minimum curvature method, the calculation is an effective replacement by the portion of the actual wellbore curve between two measurement points with a spherical arc. Thus, the task is to find a space vector, which is determined by the inclination angles and directions at each of the two measurement points, and which smoothly connects the arc to these points using the ratio factor determined by the curvature of the wellbore section.
To assess the accuracy of the modeling, several datasets for one 3000 m deep one well, were selected. The first set consisted of 4 radii, the second of 8 radii, the third of 16 and the last of 20 radii. All sets had the following identical parameters: effective reservoir thickness; drainage funnel radius; initial reservoir pressure; reservoir development with one production well; oil volumetric expansion rate; viscosity; water cut; oil density; rock permeability; porosity; skin factor; and bottomhole pressure.
The modeling accuracy error in percentage was determined by expression (7):
Here, the values and are the distances between the well diameters for different depths, and the variable i determines the step for the next plotting point, as specified by values in a combination of three variables (k, S, N). For permeability values k = 1.1 µm2 × 10−3, the skin factor values S is 0.1 and the number of construction radii is N.
The calculation using expression (5) gives a value of 0.67% for the used set of eight points. It can be assumed that, for a model built from a set consisting of less than four points, the error will exceed 2%, which is already critical.
The evaluation of the performance of the developed software for the 3D modeling of wells follows field studies that were carried out on oil wells in the northern Russia, using SRK-76 (neutron logging), AST-K-80, and ASPG (acoustic logging) devices.
Within one month, 3 wells were examined, in which sandstone, clay and limestone intervals predominated, and an array of necessary data was obtained and processed. Three-dimensional models were built (Figure 10, Figure 13, Figure 15 and Figure 17) and the performance of the software presented in this article was determined for a different number of points and deviations in the diameter of wells when their depth changes (Figure 19).
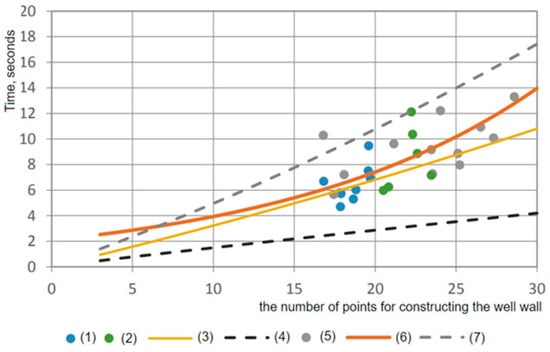
Figure 19.
Plot of software performance for different number of points and well diameter deviation as the various well depths: (1) well diameter deviation for limestone interval; (2) well diameter deviation for sandstone interval; (3) averaged curve based on Peng and Zhang [40], and Morales and Marcinew [41] dependences; (4) curve drawn according to Morales and Marcinew dependence; (5) well diameter deviation for the clay interval; (6) expected software performance schedule; and (7) curve drawn according to Peng and Zhang dependence.
From Figure 19, it can be seen that, in clay intervals (5), we observe an increase in the time of constructing a wellbore, since in this area, there is a strong deviation of the model diameter from the nominal value of the well. In the sandstone interval (2), the deviation is smaller, since the diameter deviation is average. At the limestone interval, the diameter deviation (1) tends towards a minimum.
Using the data obtained as a result of logging, a set of points was determined for constructing the 3D models of wells. The software performance evaluation was carried out using the Peng and Zhang dependence (7) as well as the Morales and Marcinew dependence (4).
To determine the optimal number of construction points, an averaged curve drawn between these dependencies (3) was used (Figure 19). The expected performance graph (6) should be between the lines (7) and (4).
From Figure 19, it follows that the well model is resistant to increasing the number of points for construction. You can see that having 15–20 points to plot guarantees a better performance. Thus, the methodology for 3D well modelling, proposed in this article, is resistant to changes in data and its increase.
4. Discussion
To analyze the performance of the developed software, its strong and weak scalability was studied, the program execution was simulated on a large amount of data, and the program operating time was compared for different types of logging. By strong scalability, we mean a reduction in the computation time of one step of the same task when using a larger number of shaders within one graphics card. Its study allows us to understand how effectively the applied algorithms use system resources (Figure 20). By weak scalability, we mean saving the computation time of one step of the same task size while simultaneously increasing the data array (Figure 21).
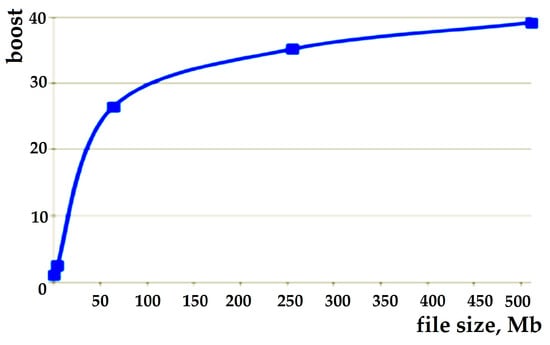
Figure 20.
Graph of strong scalability study.
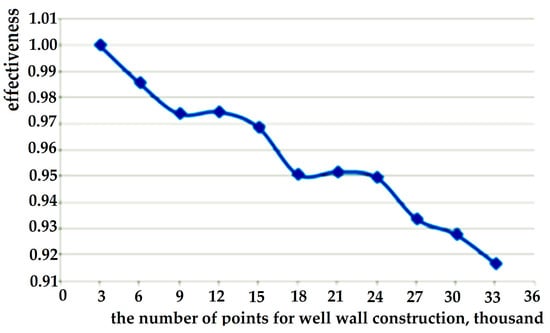
Figure 21.
Graph of weak scalability study.
The graph in Figure 21 shows that the task fits well with the graphics card architecture (a 40-fold greater acceleration was obtained when using all GPU cores of the framework compared to when using a single GPU core). The graph in Figure 16 shows that an efficiency of about 92% was achieved when the number of graphics cards was increased to 30 pieces of data volume.
Thus, we can summarize the advantages and disadvantages of the proposed software for the 3D modeling of wells using logging data. The advantages include:
- -
- High performance and scalability for different operation systems;
- -
- Implementation of unique algorithms and techniques for processing and storing data;
- -
- Support for most popular vector and raster spatial data formats;
- -
- Support for working with three-dimensional representation of spatial data.
In turn, we consider the following disadvantages:
- -
- The presence of restrictions on the use of the data format makes it difficult to develop additional modules for working with spatial data and integration with other information systems;
- -
- The ability of the common use of spatial data in a computer network is limited at the level of sharing data files and those data access control functions that the network operating system provides at the file system level.
Overcoming these shortcomings is the next stage of this study; this involves developing a digital twin similar to a real well. This is in demand for assessing the survivability of a well, and the feasibility of capital expenditures for its reconstruction and continued further operation, as well as for predicting the condition of neighboring wells for the purpose of carrying out new well systems in the oil and gas fields.
5. Conclusions
The important role played by the oil and gas sector in ensuring that sustainable development is determined by its participation important UN Sustainable Development Goals. This is inextricably linked with the global task of maintaining a large number of oil and gas wells in working condition, ensuring both stable production and environmental protection. Today, there is a demand for universal software tools that allow one to solve modeling problems for different types of logging (acoustic and radioactive—neutron, density gamma–gamma logging, gamma ray logging), on different platforms and for different operating systems.
The result of the work performed herein is a program that provides the visualization of data coming from different logging devices, which allows one to obtain a visual and informative view of the well walls. The main difference between the presented software and existing ones is the ability to visually monitor the condition of wells in real time on a 3D model, dynamically updated as different types of logging data become available. This allows engineers to ensure the trouble-free making and operating of a large number of wells, to minimize the risks of the well walls collapsing and being destroyed (due to the timely detection of their defects), which cannot be ensured when using static 2D models. Additionally, the simplicity and completeness of 3D visualization makes the visual model accessible not only to engineers, but also to ecologists, which cannot only extend the life of well systems and reduce the capital costs for their maintenance, but also reduce environmental pollution.
The article describes the software for constructing a 3D model of a well for various types of logging, taking into account the numerical methods for studying heterogeneous data and focused on the hybrid architecture of a computer equipped with graphics accelerators. A set of parallel programs has been developed that takes into account the selected architecture, which implements the construction of 3D models in complex environments that are characteristic of geodetic structures. A study of the operating time of the software was carried out, including the simulation of program execution on a large amount of data, which shows that the created software has a high performance and can effectively use computer resources.
A project of creating a software tool consists of a folder with shaders necessary for the program to work. This folder is needed for detailing, accurate and correct representation of the well model. In addition, there is a text file containing the necessary data for modeling, as shown in Figure 11. The final component is a program for drawing the walls of the well, the results of which are presented in Figure 10, Figure 13, Figure 15 and Figure 17. The final software product can be used by drilling engineers for the more efficient and safe drilling and casing of the wellbore, as well as identifying intervals for installing packers.
Author Contributions
Conceptualization, F.A.-A. and S.Z.; methodology, F.A.-A. and S.Z.; software, F.A.-A. and K.P.; validation, K.P. and S.Z.; formal analysis, F.A.-A. and S.Z.; investigation, F.A.-A. and S.Z.; resources, F.A.-A. and K.P.; data curation, K.P.; writing—original draft preparation, F.A.-A., K.P. and S.Z.; writing—review and editing, F.A.-A., K.P. and S.Z.; visualization, K.P.; supervision, F.A.-A. and S.Z.; project administration, F.A.-A. and S.Z.; funding acquisition, F.A.-A. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Example of Calculating Contribution of Well Radiation to the Readings of the Gamma Ray Logging Probe ()
- HDROP hDrop = (HDROP)wParam;
- UINT file_count = DragQueryFileW(hDrop, 0xFFFFFFFF, 0, 0);
- for (s64 i = file_count - 1; (file_count > 0) && (i < file_count); i++)// last only
- {
- UINT file_name_length = DragQueryFileW(hDrop, i, 0, 0);
- LPWSTR buffer = Allocate<WCHAR>(file_name_length + 1);
- UINT dqfw_result = DragQueryFileW(hDrop, i, buffer, file_name_length + 1);
- FAIL_IF(!dqfw_result);
- LoadData(buffer);
- Free(buffer);
- }
- DragFinish(hDrop);
- return 0;
- } break;
- case WM_DESTROY: { PostQuitMessage(0); } break;
- case WM_SIZE:
- {
- s32 new_width_ = LOWORD(lParam);
- s32 new_height = HIWORD(lParam);
- if ((client_width_ != new_width_) ||
- (client_height != new_height))
- {
- client_width_ = new_width_;
- client_height = new_height;
- NeedResize = 1;
- }
- } break;
- }
- return DefWindowProcW(hWnd, uMsg, wParam, lParam);
Appendix B. Example of Implementation of the Algorithm of the Software Module for Transition from 2D to 3D
- Array<u8> LoadFile(LPCWSTR lpFileName)
- {
- Array<u8> result;
- HANDLE hFile = CreateFileW(
- /* LPCSTR lpFileName */ lpFileName,
- /* DWORD dwDesiredAccess */ GENERIC_READ,
- /* DWORD dwShareMode */ 0,
- /* LPSECURITY_ATTRIBUTES lpSecurityAttributes */ 0,
- /* DWORD dwCreationDisposition */ OPEN_EXISTING,
- /* DWORD dwFlagsAndAttributes */ 0,
- /* HANDLE hTemplateFile */ 0);
- if (hFile == INVALID_HANDLE_VALUE)
- {
- DWORD e = GetLastError();
- WCHAR buffer [1024];
- swprintf(buffer, 1024, L”Failed to load:\n%s\nLast error: 0x%08X\n”,
- lpFileName, e);
- MessageBoxW(0, buffer, L”“, 0);
- }
References
- IEA. Oil Market Report—August 2023. Available online: https://www.iea.org/reports/oil-market-report-august-2023 (accessed on 13 December 2023).
- Venier, S.; Li, Y.; Opdal, M. Global Gas Report 2023. Rystad Energy—International Gas Union—Snam. Available online: https://www.snam.it/content/dam/snam/pages-attachments/it/investor-relations/documents/scenari/global-gas-report/global_gas_report_2023.pdf (accessed on 13 December 2023).
- The Future of Natural Gas; Massachusetts Institute of Technology: Cambridge, UK, 2011; 308p.
- Kinstler, A. How Suppliers in the Oil and Gas Industry Can Contribute to the Implementation of the Sustainable Development Goals. 8 June 2022. Available online: https://as-schneider.blog/2022/06/08/sustainable-development-goals-and-how-suppliers-in-the-oil-and-gas-industry-can-contribute-to-their-implementation/ (accessed on 13 December 2023).
- Hu, T. Technological core and economic aspects of modernization on the Industry 4.0 platform. Econ. Innov. Manag. 2022, 3, 5–18. [Google Scholar] [CrossRef]
- Lukyanenok, P.P.; Zhironkina, O.V. Factors of innovative development of oil and gas industry in transition to Industry 4.0. Econ. Innov. Manag. 2023, 4, 77–85. [Google Scholar] [CrossRef]
- Mahmood, Y.; Afrin, T.; Huang, Y.; Yodo, N. Sustainable Development for Oil and Gas Infrastructure from Risk, Reliability, and Resilience Perspectives. Sustainability 2023, 15, 4953. [Google Scholar] [CrossRef]
- Dadd, E.; Kirou, V.; Velasquez, J.; Kalhori, S.K.; Galatro, D. Sustainability and future of the oil and gas industry: A mini-review. DYNA 2023, 90, 130–138. [Google Scholar] [CrossRef]
- ESRI. ArcInfo, The Professional Geographic Information System. Available online: https://support.esri.com/en-us/technical-paper/arcinfo-the-professional-geographic-information-system-260 (accessed on 13 December 2023).
- ESRI. ArcGIS Desktop. Available online: https://www.esri.com/ru-ru/arcgis/products/arcgis-desktop/overview (accessed on 13 December 2023).
- HEXAGON. Leverage Your Geospatial Data with GeoMedia for GIS and Mapping. Available online: https://hexagon.com/products/geomedia (accessed on 13 December 2023).
- Precisely. MapInfo Professional 11.0. Available online: https://mapinfo-professional.software.informer.com/11.0/ (accessed on 13 December 2023).
- Mikhailov, V.G.; Zhironkin, V.S. Development of recycling economy technologies in the context of transition to Industry 4.0. Econ. Innov. Manag. 2022, 4, 57–69. [Google Scholar] [CrossRef]
- Han, M.; Ayirala, S.; Al-Yousef, A. Review of Offshore Chemical Flooding Field Applications and Key Lessons Learned. SPE Reserv. Eval. Eng. 2023, 26, 1439–1453. [Google Scholar] [CrossRef]
- Nan, Z.; Tan, M.; Li, J. Numerical Simulation, Response Analysis, and Physical Experiment of Induction Logging in an Inclined Fractured Formation. IEEE Trans. Geosci. Remote Sens. 2021, 99, 5901511. [Google Scholar] [CrossRef]
- Zong, C.; Liu, J.; Liu, Z.; Liu, Y. A fast forward algorithm of azimuthal gamma imaging logging while drilling. Appl. Radiat. Isot. 2023, 194, 110659. [Google Scholar] [CrossRef] [PubMed]
- Vogt, A.; Haeussler, A.; Banzarov, B.V.; Ritzmann, N. Characterization of a New Litho-Density Logging-While-Drilling Tool to Ensure High-Confidence Reservoir Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 18 October 2023; p. SPE-214893-MS. [Google Scholar] [CrossRef]
- Zhou, C.; Zhao, H.; Zhang, J.; Meng, K. Study on Neutron Lifetime Logging Technology in Horizontal Well. In Proceedings of the International Field Exploration and Development Conference 2019, Xi’an, China, 16–18 October 2019; pp. 1900–1913. [Google Scholar] [CrossRef]
- Liu, H.; Wang, B.; Tao, G.; Zhang, K. Study on the simulation of acoustic logging measurements in horizontal and deviated wells. Appl. Geophys. 2017, 14, 337–350. [Google Scholar] [CrossRef]
- Liu, X.; Qiang, Z.; Huang, Y.; Zhang, Z. Application of 3D Geological Modeling Technology for Horizontal Well Based on Data Fusion of Multiple Sources. In Proceedings of the International Field Exploration and Development Conference, Qingdao, China, 20–22 October 2021; pp. 236–247. [Google Scholar]
- El-Meselhy, A.; Mitrofanov, G.; Nayef, A. 3D hydrogeological modeling and visualization of the aquifer system based on borehole data for selecting the optimal well site: A case study in El-Oweinat, Egypt. Model. Earth Syst. Environ. 2023, 9, 783–799. [Google Scholar] [CrossRef]
- Liu, L.; Li, T.; Ma, C. Research on 3D Geological Modeling Method Based on Deep Neural Networks for Drilling Data. Appl. Sci. 2024, 14, 423. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H.; YeJiaying, H.; Li, J. Generation of 3D finite element mesh of layered geological bodies in intersecting fault zones. PLoS ONE 2024, 19, e0293193. [Google Scholar] [CrossRef]
- Ovelavo, J.A.; Huwa, D.; Akinyemi, S. Reservoir and Structural Analysis through Modeling using Well Logs and 3D Seismic Data in OY-1 Field, Onshore Niger Delta, Nigeria. Int. J. Innov. Sci. Res. Technol. 2023, 8, 2705–2723. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, G.; Wang, G.; Luo, Y.; Zou, X. Shale Reservoir 3D Structural Modeling Using Horizontal Well Data: Main Issues and an Improved Method. Front. Earth Sci. 2021, 9, 695502. [Google Scholar] [CrossRef]
- Cruz, N.V.V. 3D Pore Pressure Modeling from Well Data. Master’s Thesis, Departamento de Engenharia Civil, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil, 2009; 82p. [Google Scholar]
- Behaki, W.A.; Sukapradja, A.; Siregar, R.C.; Wisnu, R.; Djaelani, S.; Sjafwan, B.A. 3D Pore Pressure Prediction Model in Bentu Block—Central Sumatra Basin. In Proceedings of the AAPG International Convention and Exhibition, Singapore, 16–19 September 2012; p. 41105. Available online: https://www.searchanddiscovery.com/pdfz/documents/2012/41105behaki/ndx_behaki.pdf.html (accessed on 13 December 2023).
- Potekhin, D.V.; Shiryaev, E.O.; Galkin, S.V. 3D-modeling technology of initial oil saturation in transitional oil-water zone by complex of capillarimetry and electric logging methods. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2023, 334, 98–107. [Google Scholar] [CrossRef]
- Huang, X.; Huang, L.; Yan, L.; Wang, X.; Xie, X.; Zhou, L.; Cao, X. Grounded source transient electro-magnetic 3D forward modeling with the spectral-element method and its application in hydraulic fracturing monitoring. Front. Earth Sci. 2023, 11, 1279966. [Google Scholar] [CrossRef]
- Hasanov, A.; Abbasov, E.Y.; Mammadova, D.N. Graphical 3D Detailing of the Bottomhole Part of the Well with the Identification of Drainage Zones within of Productive Interval. In Proceedings of the SPE Caspian Technical Conference and Exhibition, Baku, Azerbaijan, 21–23 November 2023; p. SPE-217648-MS. [Google Scholar] [CrossRef]
- Alkhashman, W.K.; Lobankov, V.M. Effect of sodium chloride concentration in sand bed and well on the indication of neutron logging instruments. Pet. Eng. 2020, 1, 6–14. [Google Scholar] [CrossRef]
- Mari, J.L.; Vergniault, C. Well Seismic Surveying and Acoustic Logging; EDP Sciences: Paris, France, 2018; 137p. [Google Scholar] [CrossRef]
- Gilmanova, A.M. Centralizing devices to complement acoustic logging tools. J. Phys. Conf. Ser. 2021, 1753, 012072. [Google Scholar] [CrossRef]
- Peaceman, D.W. Representation of a Horizontal Well in Numerical Reservoir Simulation. Adv. Technol. Ser. 1993, 1, 7–16. [Google Scholar] [CrossRef]
- Abu-Abed, F.; Ivanov, A. Application of computer modeling software for mining vehicle fleet telemetry monitoring. Acta Montan. Slovaca 2021, 26, 593–602. [Google Scholar] [CrossRef]
- Abu-Abed, F. Development of three-dimensional models of mining industry objects. E3S Web Conf. 2021, 278, 01002. [Google Scholar] [CrossRef]
- Abu-Abed, F.; Pivovarov, K.; Zhironkin, V.; Zhironkin, S. Development of a Software Tool for Visualizing a Mine (Wellbore) in the Industrial Drilling of Oil Wells. Processes 2023, 11, 624. [Google Scholar] [CrossRef]
- Abu-Abed, F.; Zhironkin, S. New Game Artificial Intelligence Tools for Virtual Mine on Unreal Engine. Appl. Sci. 2023, 13, 6339. [Google Scholar] [CrossRef]
- Huo, Y.; Li, S.; Yuan, Y.; Chen, X.; Wang, R.; Zheng, W.; Lin, H.; Bao, H. Shader Trans-former: Predicting Shader Quality via One-shot Embedding for Fast Simplification. In Proceedings of the ACM SIGGRAPH 2022 Conference, Vancouver, BC, Canada, 8–11 August 2022; p. 44. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, J. Engineering Geology for Underground Rocks; Springer: Berlin, Germany, 2007; 331p. [Google Scholar]
- Morales, R.H.; Marcinew, R.P. Fracturing of High-Permeability Formations: Mechanical Properties Correlations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993; p. SPE-26561-MS. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).