Abstract
The development of space exploration technologies puts higher demand on space power systems. The space reactor gas turbine cycle (SRGTC) has the advantages of compact configuration and small mass and volume and is one of the optimal options for future high-power space power systems. The SRGTC operates in an isolated island state and the radiator is fragile if it is hit by asteroids and space debris. The transient characteristics of the SRGTC are fundamental for safe operation in radiator loss accidents. In this paper, a dynamic model for the SRGTC is established, and the performance of the SRGTC with dual power conversion unit (PCU) modules (SRGTC-DPCU) after radiator loss was investigated. The results indicated that the waste heat of the system was accumulated in the radiator after radiator loss, which increased the consumed power of the compressor and further led to speed fluctuations. The bypass valve control and the temperature negative feedback effect can ensure the safe operation of the shaft and the reactor. More radiator loss decreased the speed far below the rated speed and exceeded the safety margin of the bypass valve control, which further led to system shutdown. There is a safety boundary of radiator loss accidents. Furthermore, the coupling effects of multiple PCUs after radiator loss were analyzed. The working fluid inventory was redistributed among the PCU modules. The reduction of working fluid inventory in the accident PCU module promoted the safety boundary. This study provides a reference for the operation of the SRGTC.
1. Introduction
With the continuous improvement of science and technology, humans have gradually seen the mysteries of the universe through planetary and satellite detection devices. The development of space exploration technologies such as planetary bases and orbital propulsion has higher requirements for space power systems. Therefore, studying safe, efficient, and compact space power systems is of great significance [1,2].
The reactor coolant of the space reactor coupled gas turbine cycle (SRGTC) is also the cycle working fluid, which has the advantages of compact structure and small mass and volume. The SRGTC can also meet the requirements of long life and high efficiency and power required for spacecraft and is one of the best options for future high-power space power systems [3,4].
The SRGTC operates in an isolated island with frequent changes in load, and it is prone to being hit by meteors and space debris. Therefore, it often encounters accidents such as load loss, reactivity insertion, mechanical failures, and radiator area loss. The transient characteristics of the SRGTC under accident conditions are the focus of off-design conditions.
Some researchers investigated the safety characteristics of the space gas-cooled reactor coupled with gas turbine cycle under accident conditions. Bettis et al. [5] established the dynamic model of the SRGTC with dual power conversion units (PCUs) and studied the transient safety characteristics under accident conditions, such as load loss, reactivity insertion, mechanical failure, and working fluid leakage accidents. It was found that the accident caused fluctuations of system parameters, but the negative feedback effect of the reactor can ensure the safe operation of the system. Zhang et al. [6] established the dynamic model of the SRGTC and investigated the safety characteristics of the system under mechanical failures and reactivity insertion accidents, and the results indicated that the SRGTC had good self-stability for the negative reactivity feedback of the reactor. Qin et al. [7] established the dynamic model, developed the simulation program of the SRGTC, and studied the transient characteristics of the system under coolant loss and reactivity insertion accidents. It was found that the SRGTC had good safety characteristics for the negative reactivity feedback of the reactor. Li et al. [8] established the off-design model of the SRGTC, studied the safety characteristics of the system under load loss accidents, and proposed a new control method of bleeding control. Wang et al. [9] studied safety characteristics of the SRGTC under reactivity insertion and emergency shutdown accidents and found that insertion reactor waste heat of the reactor can be discharged into the environment through heat conduction and radiation heat dissipation. The negative reactivity feedback and passive decay heat discharge of the reactor make it inherently safe. Meng et al. [10] studied the dynamic characteristics of the SRGTC under reactivity insertion, reactor coolant loss, and coolant leakage accidents and found that the negative reactivity temperature coefficient improved the safety of the reactor. Ma et al. [11] analyzed safety characteristics of the SRGTC under load loss accidents and found that the speed of the shaft exceeded the upper limit after load loss and timely countermeasures should be taken.
Some studies researched accident characteristics of the space lithium-cooled reactor coupled with indirect gas turbine cycle. Wright et al. [12,13,14] investigated the safety characteristics of the space lithium-cooled fast reactor indirect gas turbine cycle during turbocompressor coast down. The results showed that there is no fuel temperature or shaft speed overshoot under the control of the reactor controller. Zhao et al. [15,16] analyzed the characteristics of the lithium-cooled space reactor combined with the Stirling engine under an unprotected reactivity insertion accident and an unprotected loss of heat sink accident, which verified the inherent safety of the system.
The existing studies analyzed the safety characteristics of the SRGTC under accident conditions, including reactivity insertion, mechanical failures, and load loss accidents. However, these studies focus on the safety features of the SRGTC with a single PCU under accident conditions. To promote redundancy and eliminate the gyrostatic effect, the high-power SRGTC has multiple PCUs sharing a common gas inventory and reactor. The research of Ma et al. [11,17] indicates that the multiple PCUs of the SRGTC operating asynchronously during start-up and in load loss conditions shows an interaction mechanism between PCUs. Therefore, the safety characteristics and coupling effect of the SRGTC with multiple PCUs under radiator loss accident conditions should be investigated.
Radiator loss is a serious accident of the SRGTC. Therefore, this paper establishes the dynamic model for the SRGTC and studies the safety characteristics of the SRGTC and the coupling effect between multiple PCUs after radiator loss.
2. Mathematical Models
2.1. System Description
The space reactor gas turbine cycle uses helium and xenon mixtures as the working fluid. To promote redundancy and eliminate the gyrostatic effect, the high-power SRGTC has multiple PCUs sharing a common gas inventory and reactor, as shown in Figure 1a [18]. The noble gas binary mixtures separate at the reactor outlet, enter each PCU, and gather at the reactor inlet and absorb heat from the reactor [19]. Each PCU adopts the recuperative Brayton cycle with centrifugal turbomachines, as shown in Figure 1b. The working fluid separates at the reactor outlet (node 4) and expands at each PCU turbine (process 4-5), then flows through the low-pressure side of the recuperator to recover the heat (process 5-6) and dump the waste heat in the radiator at the gas cooler (process 6-1), then it is compressed by the compressor (process 1-2) and preheated at the high-pressure side of the recuperator (process 2-3). The working fluid finally gathers at the reactor inlet and enters the reactor to absorb heat (process 7-4). To ensure that the bearing and the generator do not exceed the temperature limit, part of the working fluid separates at the compressor outlet and mixes with the mainstream working fluids at the outlet on the high-pressure side of the recuperator (process 8-7 and process 3-7) after cooling the bearing and the generator (process 2-8) [20]. There is a bypass structure (process 2-5) between the compressor and turbine outlet, which bypasses reactor and turbine. The high-pressure gas at the compressor outlet and the low-pressure gas at the turbine outlet quickly mix through the bypass, which further changes the performance of the components and system. The heat rejection system adopts liquid metal as the coolant. The coolant absorbs heat through the heat-absorbing side of the gas cooler (process 11-9), enters the radiator to eject heat to the space environment (process 9-10), and returns to the gas cooler through the pump (process 10-11).

Figure 1.
Schematic diagram for the SRGTC with multiple PCUs.
2.2. Dynamic Model of the SRGTC
The SRGTC consists of the reactor, recuperator, gas cooler, radiator, turbomachines, and so on. According to the mass, momentum, and energy conservation equations of components, the dynamic model of the SRGTC is established based on the following assumptions:
- (1)
- The SRGTC is a closed adiabatic system, therefore, there is no working fluid leakage and component heat dissipation.
- (2)
- The proportion of accelerated pressure drop to the total pressure drop is small, therefore, the accelerated pressure drop in the momentum conservation equation is ignored.
- (3)
- To simplify the model and program and save computational costs, the one-dimensional lumped parameter model is adopted.
2.2.1. Recuperator
The working fluids on both sides of the recuperator undergo convective heat transfer to recover the waste heat from the turbine exhaust. Considering the constraints of volume and mass, the recuperator adopts an offset strip fin heat exchanger, as shown in Figure 2.

Figure 2.
Schematic diagram of the recuperator.
The conservation equations of the mass and momentum on both sides of the recuperator are similar. Therefore, the conservation equations of mass and momentum on both sides of the recuperator can be simplified as follows:
where , and , are the mass flow rate and pressure at the inlet and outlet of the high-pressure side of the recuperator, respectively; , , , , , are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate. , and , are the mass flow rate and pressure at the inlet and outlet of the low-pressure side of the recuperator, respectively; , , , , , are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate. The pressure loss rate is the ratio of pressure loss to average pressure of the recuperator and can be expressed as:
The pressure loss includes friction loss and local loss, which can be expressed as:
where and are the friction loss coefficient and local loss coefficient; is the channel characteristic diameter.
The energy conservation equation of the working fluid on both sides of the recuperator can be simplified as:
where , , , , , and , , , , , are average temperature, working fluid mass, specific heat capacity, mass flow rate, heat transfer coefficient, and heat transfer area on both sides of the recuperator, respectively; , and , are the inlet and outlet temperature on both sides of the recuperator, respectively; is the temperature of the recuperator, which can be calculated as:
where and are the mass and specific heat capacity of recuperator, respectively.
A 40 helium and xenon mixture is a low Prandtl number working fluid (approximately 0.2) [21]. The resistance factor and heat transfer factor follow the modified Reynolds analogy. Therefore, the heat transfer coefficient is expressed as [22]:
where is the Prandtl number; is the resistance factor, which can be expressed as [17]:
where is the Reynolds number.
2.2.2. Gas Cooler
The gas cooler transfers waste heat to the radiator through convective heat transfer of working fluids on both sides, as shown in Figure 3.

Figure 3.
Schematic diagram of the gas cooler.
The equations on both sides of the gas cooler are similar, and the mass and momentum conservation equations on both sides of the gas cooler can be simplified as follows:
where , and , are mass flow rate and pressure on the heat-releasing side of gas cooler, respectively; , , , , , and are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate; , and , are mass flow rate and pressure on the heat-absorbing side of gas cooler, respectively; , , , , , and are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate.
The energy conservation equation of the working fluid on both sides of the gas cooler can be expressed as:
where , , , , , and , , , , , are average temperature, working fluid mass, specific heat capacity, mass flow rate, heat transfer coefficient, and heat transfer area on both sides of the gas cooler, respectively; , and , are the inlet and outlet temperature on both sides of the gas cooler, respectively; is the temperature of the gas cooler, which can be calculated as:
where and are the mass and specific heat capacity of the gas cooler, respectively.
2.2.3. Radiator
One side of the radiator is connected to the heat-absorbing side of the gas cooler using liquid sodium as the working fluid. The other side of the radiator ejects waste heat of the system to the space environment through radiation, as shown in Figure 4.

Figure 4.
Schematic diagram of the radiator.
The outlet flow rate and pressure of the radiator are calculated through the mass and momentum conservation equations, which can be expressed as:
where , and , are inlet and outlet mass flow rate and pressure of radiator, respectively; , , , , , and are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate.
The convection heat transfer of liquid sodium working fluid inside the radiator can be expressed as:
where , , , , , and are average temperature, working fluid mass, specific heat capacity, mass flow rate, heat transfer coefficient, and heat transfer area of the radiator, respectively; and are the inlet and outlet temperatures of the radiator, respectively; is the temperature of the radiator, which can be calculated as:
where , , and are the mass, specific heat capacity and radiation heat dissipation area of the radiator, respectively; is the emissivity; is the Stefan–Boltzmann constant; is the environment temperature.
The Nusselt number calculating the convective heat transfer coefficient is calculated according to the Seban–Shimazaki correlation [23]:
2.2.4. Turbomachine
Helium xenon working fluid enters the turbine to expand and output work, which drives the compressor and generator to rotate and generate electricity. The flow field of centrifugal turbomachines under off-design conditions is complex [24]. The mass and momentum conservation equations can be expressed as:
where , and , are the inlet and outlet mass flow rate and pressure of the compressor, respectively; , and , are the inlet and outlet mass flow rate and pressure of the turbine, respectively.
The outlet temperature of the turbomachine can be calculated according to energy conservation equations, which can be expressed as:
where and are the average adiabatic coefficient of the turbine and compressor, respectively; , and , are the pressure ratio and isentropic efficiency of the turbine and compressor, which can be obtained from characteristic curves as shown in Figure 5 [25,26,27,28]:
where , , and are the inlet mass flow rate, temperature, and pressure of the turbomachines; is the rotating speed of the shaft, which can be expressed as [29]:
where is the moment of inertia; is the load of the generator; and are the power of the compressor and turbine, respectively, which can be expressed as:
where and are the average specific heat capacity of the turbine and compressor, respectively.
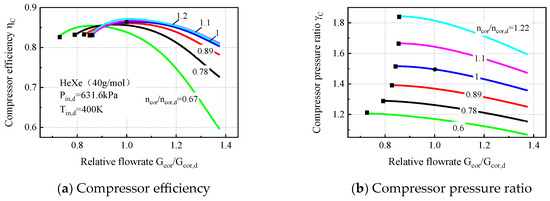
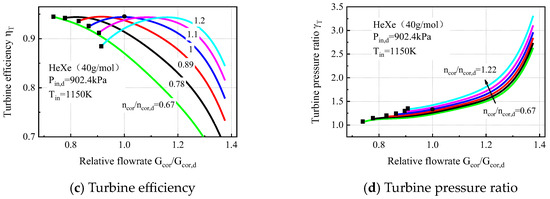
Figure 5.
Performance curves of centrifugal turbomachines.
2.2.5. Bypass Value
The high-pressure gas at the compressor outlet mixes with the low-pressure gas at the turbine outlet through the bypass valve, which bypasses the reactor and turbine. Local flow rate changes in the system result in components deviating from rated operating conditions. The bypass flow rate can be expressed as:
where and are the flow rate coefficient and density of the working fluid; is the opening of the bypass valve. According to the deviation between the set speed and the actual speed of the shaft, the opening of the bypass valve is controlled by a proportional integral differential controller [30], which can be expressed as:
where is the full opening of the bypass valve. , , and are the proportional gain, integral, and differential constant.
2.2.6. Reactor
Helium xenon working fluid absorbs heat through the reactor. This section simplifies the reactor as a control body with working fluid flowing in, out, and absorbing heat, as shown in Figure 6.
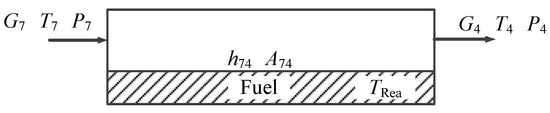
Figure 6.
Schematic diagram of the reactor.
The mass and momentum conservation equations of the reactor can be simplified as follows:
where , and , are inlet and outlet mass flow rate and pressure of the reactor, respectively; , , , , , and are average pressure, volume, length of flow channel, velocity, density, and pressure loss rate.
The energy conservation equation of the working fluid in the reactor can be simplified as:
where , , , and are working fluid mass, specific heat capacity, mass flow rate, and heat transfer area of the reactor, respectively; and are the inlet and outlet temperature of the reactor, respectively; is the average temperature of working fluid, ; is the temperature of the fuel; is the heat transfer coefficient between fuel and working fluid, which can be calculated according to the Kays formula of the Nusselt number [31,32]:
The fuel transfers heat to the working fluid, and the energy conservation equation of the fuel can be simplified as:
where and are the mass and specific heat capacity of the fuel, respectively; is the rated thermal power of the reactor; is the relative neutron density, which can be calculated according to the reactor point dynamics equations, which can be expressed as:
where , , , , and are fraction of the delayed neutron, decay constant, density of the precursors, neutron lifetime, and total reactivity of the reactor, respectively. The fractions of the six groups of delayed neutrons are 0.000222, 0.00116, 0.00113, 0.00321, 0.000958, and 0.000334. The corresponding decay constants are 0.01249, 0.03179, 0.10953, 0.31769, 1.35224, and 8.68655 [10]. The total reactivity of the reactor is equal to external inserted reactivity plus reactivity feedback effects. The total reactivity is given as:
where , , and are external inserted reactivity, reference temperature, and equivalent feedback coefficient considering the reactivity feedback mechanisms of the fuel, core block, and pressure vessel, respectively.
2.2.7. Overall Parameters
The inventory of a closed system is constant. The total inventory of the system is the sum of the inventories of the reactor and components, which can be expressed as:
where , , and are average pressure, temperature, and volume of components, respectively; and are compression factor and gas constant; is the number of components and pipes in a single PCU; is the number of PCUs.
The PCU power generation of the generator is the difference between turbine and compressor power, which can be expressed as:
The power generation of the system is the sum of the PCU power generation, which can be expressed as:
Power generation efficiency of the system is the ratio of the total power generation to the thermal power of the reactor, which can be expressed as:
2.3. Model Validation
Based on a modular modeling approach, this paper describes a Simulink program for system solving. The component model of the system is solved independently. The mass, momentum, and energy transfer between components are achieved through data input and output.
Due to the lack of dynamic test data, the calculation results of the model in this paper are compared with the simulation results of Wang et al. [9]. The comparison adopts the same performance curves of turbomachines [25,26,27,28] and physical property model of the helium and xenon mixture working fluid [33,34], and the model is solved using the same initial and boundary conditions. The system operates stably and inserts 0.4 $ external reactivity at time 0. The promoted external reactivity leads to a step increase in reactor reactivity as shown in Figure 7a. The fuel temperature and reactor power increase to maximum values as shown in Figure 7b,c. Subsequently, the negative feedback effect of the fuel decreases the reactor reactivity, which reduces the average fuel temperature and reactor power to stable values. The calculation results of the model in this article have some deviation compared to the literature data over time. For example, the maximum relative error of the average fuel temperature is 14% and the maximum error of the reactor reactivity is 0.05 $, which is due to the uncertainty in the design parameters of the reactor and heat exchanger in the literature. However, the transient response trends of these parameters calculated in this paper are generally consistent with the data in the literature shown in Figure 7, which verifies the accuracy of the thermal inertia and transient response time of the dynamic model proposed in this study. The steady simulation results are further compared and well matched with the rated design parameters of the SRGTC shown in Table 1 and Table 2, which further verifies the accuracy of the model in this study.

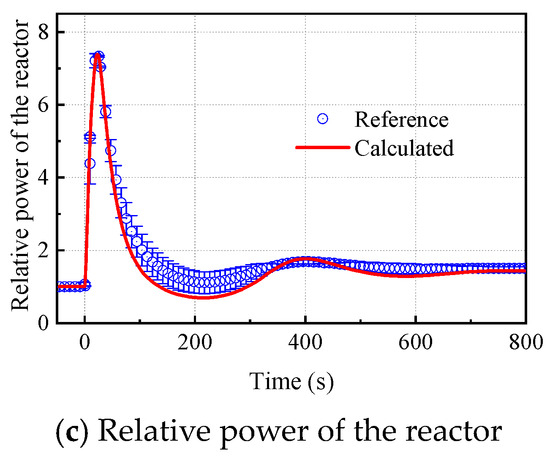
Figure 7.
Model and program validation.

Table 1.
Comparative validation of node parameters.

Table 2.
Comparative validation of the system parameters.
3. Results and Discussion
According to the dynamic model, this section analyzes the safety characteristics of the SRGTC with dual PCUs under radiator loss as shown in Figure 8. The parameters, including node temperature, pressure, and so on of the SRGTC under rated working conditions, are shown in Figure 8.

Figure 8.
Schematic diagram of SRGTC with dual PCUs.
3.1. Influence of Radiator Loss on the SRGTC
This section investigates the effect of the two-PCU radiator synchronous loss on the safety characteristics of the SRGTC-DPCU. When the SRGTC-DPCU operates at an initial relative power generation (the ratio of initial power generation to rated power generation) of 80% for 200 s, the heat dissipation area of the two-PCU radiators loses 20%. Parameters of the two PCUs change consistently as shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.
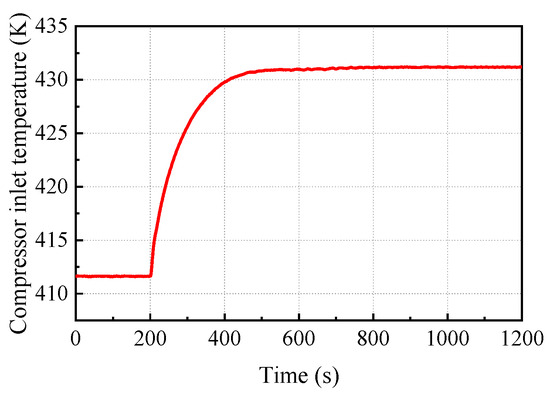
Figure 9.
The variation of compressor inlet temperature with time.
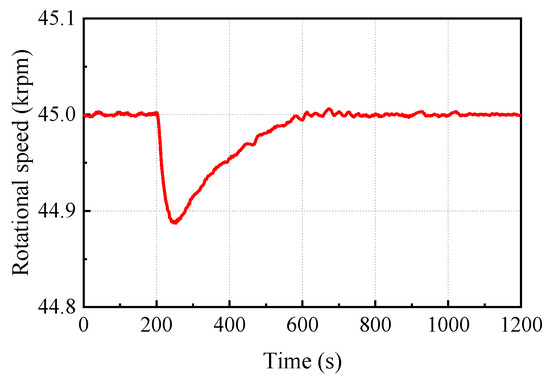
Figure 10.
The variation of rotational speed with time.

Figure 11.
The variation of bypass valve flow rate with time.

Figure 12.
The variation of node temperatures with time.

Figure 13.
The variation of power with time. (a) Relative power of compressor; (b) Relative power of turbine; (c) Relative power generation of PCU; (d) Relative power generation of system.
The reduction of radiator heat dissipation area means that the waste heat of the system cannot be timely discharged, which further increases the temperature of the radiator and inlet temperature of the compressor to 431 K, as shown in Figure 9. The elevated inlet temperature of the compressor increases the consumed power of the compressor, and the remaining power of the shaft is negative. The negative torque decreases the speed of the shaft, as shown in Figure 10. When the speed deviates from the rated value of 45 krpm, the bypass valve receives the speed change signal, the valve opening decreases, and the relative bypass flow rate (ratio of the bypass flow rate to the rated flow rate of the PCU) decreases, as shown in Figure 11. The flow rate and power of the compressor decrease, and the positive torque of the shaft promotes the speed to the rated value, thereby ensuring stable operation of the shaft.
The increase in the compressor inlet temperature changes node temperatures of the system, as shown in Figure 12. The outlet temperatures of the compressor and the recuperator’s high-pressure side increase. The decrease in the bypass flow rate reduces the low-temperature working fluid passing through the bypass to the inlet of the low-pressure side of the recuperator, which increases the inlet temperature of the low-pressure side of the recuperator and the outlet temperature of the high-pressure side of the recuperator. The increase in the flow rate in the high-pressure side of the recuperator decreases the outlet temperature of the high-pressure side. Taking into account the above influencing factors, the outlet temperature of the recuperator’s high-pressure side and inlet temperature of the reactor increase 7 K. The transient negative reactivity of the reactor decreases thermal power of the reactor. The outlet temperature of the reactor increases 0.36 K according to changes in the reactor inlet temperature and reactor power. Therefore, the temperature negative feedback effect can ensure the safe operation of the reactor.
The decrease in bypass flow rate promotes turbine flow rate and decreases the compressor flow rate, which further reduces pressure ratios and relative power of the compressor and turbine (ratio of compressor and turbine powers to rated values), as shown in Figure 13a,b. Under the control of the bypass valve, the relative powers of the turbine and compressor change synchronously. The relative power generation of the two PCU modules (ratio of the power generations to rated values) fluctuates briefly and balances with the load to ensure safe operation of the system, as shown in Figure 13c,d.
The radiator loss leads to the accumulation of the system waste heat in the radiator. The increase in the consumed power of the compressor further leads to speed fluctuations. The bypass valve control and the temperature negative feedback effect can ensure the safe operation of the SRGTC under partial radiator loss.
3.2. Safety Boundary of the SRGTC for Radiator Loss Accidents
Based on Section 3.1, this section investigates the effect of the large radiator loss on the safety characteristics of the SRGTC-DPCU.
When the SRGTC-DPCU operates at an initial relative power generation of 80% for 200 s, the heat dissipation area of the two-PCU radiators loses 25%. Compared to the radiator loss of 20% working condition in Section 3.1, more heat sink loss increases the inlet temperature and consumed power of the compressor, and the negative torque of the turbomachines on the shaft decreases the speed to a lower value, as shown in Figure 14. The deviation of the actual speed from the rated speed causes the bypass valve to close and the relative bypass flow rate to decrease to 0, as shown in Figure 15. Afterwards, the positive torque of the turbomachines increases the speed of the shaft to the rated value, which ensures the safe operation of the system.
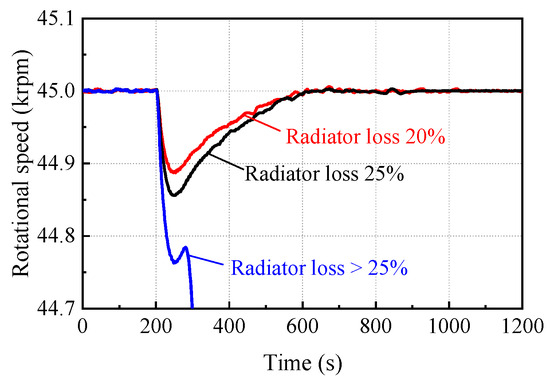
Figure 14.
The variation of rotational speed with time.

Figure 15.
The variation of bypass valve flow rate with time.
When the radiator loss exceeds 25%, the shaft speed drops too much and the bypass valve control is lost. The SRGTC cannot operate stably and is forced to shut down. Therefore, the SRGTC has a safety boundary for radiator loss accidents. This section further studies the accident safety boundary of the system operating at different initial relative power generation levels. The results show that the lower the system operating power, the greater the bypass valve opening and, therefore, the higher the safety margin for radiator loss, as shown in Figure 16. For example, the radiator loss limitation of the SRGTC is 45% when the initial relative power generation is at 60%. Below the safety boundary is the safe operating area after radiator loss, and above the safety boundary is the forced shutdown area, as shown in Figure 16.
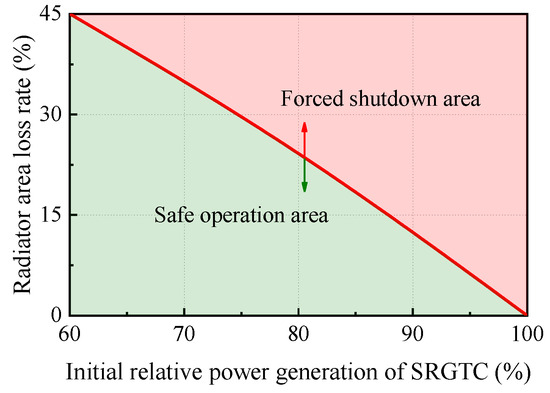
Figure 16.
Safety boundary for radiator loss accident.
3.3. Coupling Influence of One-PCU Radiator Loss on Other PCUs
This section investigates the coupling characteristics between the two PCU modules of the SRGTC in case of one-PCU radiator loss. It is assumed that the radiator area of the PCU2 step decreases 20% at 200 s when the initial relative power generation of the SRGTC is at 80%, and parameters of the two PCUs are shown in Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24.

Figure 17.
The variation of compressor inlet temperature with time.
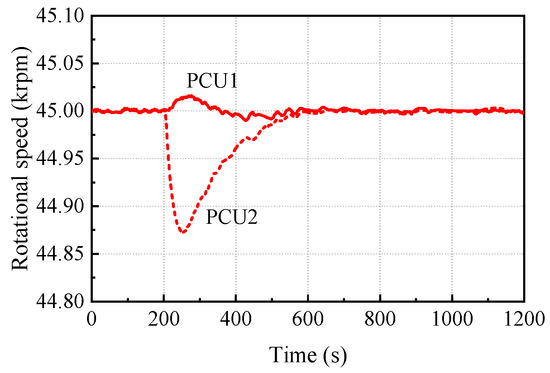
Figure 18.
The variation of rotational speed with time.

Figure 19.
The variation of bypass valve flow rate with time.

Figure 20.
The variation of pressure ratios with time.

Figure 21.
The variation of node temperatures with time.

Figure 22.
The variation of node pressures with time.

Figure 23.
The variation of relative inventory with time.
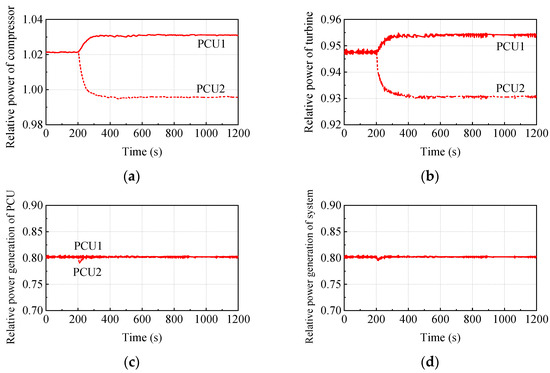
Figure 24.
The variation of power with time; (a) Relative power of compressor; (b) Relative power of turbine; (c) Relative power generation of PCU; (d) Relative power generation of system.
The decrease in the PCU2 radiator area leads to the accumulation of system waste heat in the radiator, which further raises the inlet temperature of the compressor to 429 K, as the dashed line shows in Figure 17. The increase in compressor power decreases the speed of the PCU2, as the dashed line shows in Figure 18. The decrease in the speed reduces the bypass valve opening and the relative bypass flow rate of the PCU2, as the dashed line shows in Figure 19. The increase in the turbine flow rate and the decrease in the compressor flow rate cause turbomachines to deviate from the rated conditions. Therefore, pressure ratios of the compressor and turbine decrease, as the dashed line shows in Figure 20.
The changes in turbomachine pressure ratios and the radiator temperature change node temperatures and pressures of the PCU2, as the dashed lines show in Figure 21 and Figure 22. The increase in the compressor inlet temperature increases the outlet temperature of the compressor and the outlet temperature of the recuperator’s high-pressure side and further promotes the inlet temperature of the reactor, which reduces the reactivity and the reactor power. The increase in the reactor inlet temperature and the decrease in the reactor power keep the reactor outlet temperature basically unchanged. It can be seen that the radiator loss increases node temperatures of the PCU2 as the dashed lines show in Figure 21. Node temperatures of the PCU1 remain basically unchanged, as the solid line shows in Figure 21. Therefore, the average temperature of the system increases, and the inventory of the system is constant. According to the gas state equation, the node pressures of the system increase, as shown in Figure 22.
The change in average temperature and pressure redistributes working fluid inventory in the two PCUs. The elevated average temperature of the PCU2 decreases the inventory of the PCU2, as the dashed line shows in Figure 23. The total inventory of the system is constant. Therefore, the inventory of the PCU1 increases, as the solid line shows in Figure 23. It can be seen that the radiator loss of the PCU2 leads to asynchronous operation of two PCUs, and the coupling effect between two PCUs redistributes the inventory of the working fluid.
The operation of the PCU1 is similar to increasing inventory control. The flow rate and node pressures of the PCU1 increase proportionately as the solid line shows in Figure 22. The turbomachines operate near the rated operating conditions, and the pressure ratios and node temperatures are basically unchanged, as the solid lines show in Figure 20 and Figure 21.
Figure 24 is the variation of turbomachine relative power (ratio of compressor and turbine powers to rated values) and the system relative power generation (ratio of power generation to rated values) with time. The operation of the PCU1 is similar to increasing inventory control. The promoted flow rate increases relative power of the turbine and compressor in the PCU1, as the solid line shows in Figure 24. The decreased pressure ratios reduce relative power of the turbine and compressor in the PCU2, as the dashed line shows in Figure 24. The control of the bypass valve keeps the balance between the load and the power generation of the system, as shown in Figure 24c,d, which ensures safe operation of the system.
When the radiation loss of the PCU2 exceeds the safety boundary, the shaft speed drops too much and the bypass valve control of the PCU2 is lost. The PCU2 cannot operate stably and is forced to shut down. Therefore, the SRGTC has a safety boundary in case of one-PCU radiator loss. The accident safety boundary of the SRGTC-DPCU operating at different initial relative power generation levels in case of PCU2 radiator loss is shown in Figure 25. The results show that the single-PCU radiator loss limitation of the SRGTC-DPCU is 45.5% when the initial relative power generation is at 60%. Below the safety boundary is the safe operating area after single-PCU radiator loss, and above the safety boundary is the forced shutdown area of the PCU2, as shown in Figure 25. The coupling influence between PCUs of the SRGTC after one-PCU radiator loss decreases the working fluid inventory of the accident PCU, which further increases the safety boundary of the accident PCU compared to that after the two-PCU radiator synchronous loss in Section 3.2.

Figure 25.
Safety boundary for single-PCU radiator loss accident.
4. Conclusions
Radiator loss is a serious accident of the SRGTC. This paper established the dynamic model for the SRGTC, studied the safety characteristics of the SRGTC and safety boundary of the SRGTC for radiator loss accidents, and further analyzed the coupling effect between multiple PCUs after radiator loss. The following conclusions can be drawn.
- (1)
- The bypass valve control can ensure the safe and stable operation of the SRGTC. The waste heat of the system is accumulated in the radiator for the radiator loss, which increases the consumed power of the compressor and further leads to speed fluctuations. The bypass valve control and the temperature negative feedback effect can ensure the safe operation of the shaft and the reactor under partial radiator loss.
- (2)
- It is found that the SRGTC has a safety boundary for radiator loss accidents. More heat sink loss increases the power consumption of the compressor. The speed decreases far below the rated speed and exceeds the safety margin of the bypass valve control. The continuous decrease in speed leads to system shutdown, and there is a safety boundary of the radiator area loss.
- (3)
- There is a coupling effect between PCUs of the SRGTC after one-PCU radiator loss. It redistributes the working fluid inventory between the PCU modules. The accumulation of the waste heat in the accident PCU module increases the average temperature and decreases working fluid inventory of the accident PCU, which further increases safety boundary of the accident PCU.
Author Contributions
Conceptualization, X.Y.; Data curation, W.M. and P.Y.; Formal analysis, P.Y.; Funding acquisition, X.Y.; Investigation, W.M.; Methodology, W.M. and X.Y.; Resources, X.Y.; Software, P.Y., Y.G., Y.H. and Y.Y.; Supervision, X.Y.; Validation, Y.G., Y.H. and Y.Y.; Writing—original draft, W.M.; Writing—review and editing, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National S&T Major Project (grant number 2011ZX069); the National Hi-tech R&D Program of China (Program 863) (grant number 2005AA511010); the Nuclear Energy Development Program of China Atomic Energy Authority (CAEA), LingChuang Research Project of China National Nuclear Corporation, National Funding Postdoctoral Researcher Program (GZC20231242), and China Postdoctoral Science Foundation (2023M741914).
Data Availability Statement
Due to confidentiality requirements of the partner enterprise, the data used in this study are not publicly available. For access to the data related to this research, please contact the corresponding author.
Conflicts of Interest
No conflicts of interest exist in the submission of this manuscript, and the manuscript is approved by all authors for publication. I declare on behalf of my co-authors that the work described herein is original research that has not been published previously, and is not under consideration for publication elsewhere, in whole or in part.
Nomenclature
| area for heat transfer, [] | |
| specific heat of constant pressure, [] | |
| specific heat of component, [] | |
| density of the precursors | |
| diameter, [] | |
| friction loss coefficient | |
| local loss coefficient | |
| mass flow rate, [] | |
| heat transfer coefficient | |
| moment of inertia, [kg] | |
| proportional gain | |
| length of the flow channel, [] | |
| mass of the working fluid or component, [] | |
| inventory of helium and xenon, [] | |
| number of single PCU components | |
| number of power conversion units | |
| load of generator | |
| rotational speed of the shaft, [] | |
| relative neutron density | |
| pressure, [] | |
| power generation of the PCU, [] | |
| power generation of the system, [] | |
| thermal power of the reactor, [] | |
| power of the turbomachine, [] | |
| gas constant, [] | |
| temperature, [K] | |
| time, [s] | |
| velocity of the working fluid, [] | |
| volume of the component, [] | |
| gas compressibility factor |
Greek Letters
| feedback coefficient | |
| density, [] | |
| fraction of the delayed neutron | |
| pressure loss rate of the component | |
| pressure ratio of the turbomachine | |
| efficiency of components or system | |
| emissivity | |
| Stefan–Boltzmann constant | |
| integral and differential constant | |
| opening of the bypass valve |
Subscripts
| Byp | bypass |
| Com | compressor |
| Coo | cooler |
| Env | environment |
| Fue | fuel |
| Gen | generator |
| Loa | load |
| Rad | radiator |
| Rea | reactor |
| Rec | recuperator |
| Sys | system |
| Tur | turbine |
Abbreviations
| PCU | power conversion unit |
| SRGTC | space reactor gas turbine cycle |
| SRGTC-DPCU | SRGTC with dual PCUs |
References
- Ayodele, O.L.; Luta, D.N.; Kahn, M.T. A Micro-Nuclear Power Generator for Space Missions. Energies 2023, 16, 4422. [Google Scholar] [CrossRef]
- Ge, L.; Li, H.; Tian, X.; Ouyang, Z.; Kang, X.; Li, D.; Shan, J.; Jiang, X. Improvement and validation of the system analysis model and code for heat-pipe-cooled microreactor. Energies 2022, 15, 2586. [Google Scholar] [CrossRef]
- Cheng, K.; Li, J.; Yu, J.; Qin, J.; Jing, W. Dynamic Characteristics Analysis for a Novel Double-Rotor He-Xe Closed-Brayton-Cycle Space Nuclear Power Generation System. Energies 2023, 16, 6620. [Google Scholar] [CrossRef]
- Zhou, B.; Sun, J.; Sun, Y. Investigation on Laminar Flow and Heat Transfer of Helium–Xenon Gas Mixtures with Variable Properties. Energies 2023, 16, 1899. [Google Scholar] [CrossRef]
- Levine, B. Space Nuclear Power Plant Pre-Conceptual Design Report, for Information; Knolls Atomic Power Laboratory: Niskayuna, NY, USA, 2006. [Google Scholar]
- Zhang, R.; Guo, K.; Wang, C.; Zhang, D.; Tian, W.; Qiu, S.; Su, G.H.; Deng, J. Thermal-hydraulic analysis of gas-cooled space nuclear reactor power system with closed Brayton cycle. Int. J. Energy Res. 2020, 45, 11851–11867. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, R.; Guo, K.; Wang, C.; Tian, W.; Su, G.; Qiu, S. Thermal-hydraulic analysis of an open-grid megawatt gas-cooled space nuclear reactor core. Int. J. Energy Res. 2021, 45, 11616–11628. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X.; Wang, J.; Zhang, Z. Off-design performance and control characteristics of space reactor closed Brayton cycle system. Ann. Nucl. Energy 2019, 128, 318–329. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, R.; Guo, K.; Zhang, D.; Tian, W.; Qiu, S.; Su, G. Dynamic simulation of a space gas-cooled reactor power system with a closed Brayton cycle. Front. Energy 2021, 15, 916–929. [Google Scholar] [CrossRef]
- Meng, T.; Cheng, K.; Zhao, F.; Xia, C.; Tan, S. Dynamic simulation of the gas-cooled space nuclear reactor system using SIMCODE. Ann. Nucl. Energy 2021, 159, 108293. [Google Scholar] [CrossRef]
- Ma, W.; Ye, P.; Gao, Y.; Yang, X. Study on the load loss characteristics of a space nuclear power system with multi Brayton loops. Ann. Nucl. Energy 2023, 185, 109702. [Google Scholar] [CrossRef]
- Wright, S. Preliminary Results of a Dynamic Systems Model for a Closed-Loop Brayton Cycle System Coupled to a Nuclear Reactor. In Proceedings of the International Energy Conversion Engineering Conference, Portsmouth, VA, USA, 17–21 August 2003. [Google Scholar]
- Wright, S.A.; Sanchez, T. Dynamic modeling and control of nuclear reactors coupled to closed-loop Brayton cycle systems using SIMULINK™. AIP Conf. Proc. Am. Inst. Phys. 2005, 746, 991–1004. [Google Scholar]
- Wright, S.A.; Lipinski, R.J.; Vernon, M.E.; Sanchez, T. Closed Brayton Cycle Power Conversion Systems for Nuclear Reactors; Sandia National Laboratory: Albuquerque, NM, USA, 2006. [Google Scholar]
- Jin, Z.; Wang, C.; Liu, X.; Dai, Z.; Tian, W.; Su, G.; Qiu, S. Operation and safety analysis of space lithium-cooled fast nuclear reactor. Ann. Nucl. Energy 2022, 166, 108729. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, C.; Liu, X.; Dai, Z.; Tian, W.; Qiu, H.; Su, G. Thermal-hydraulic and Safety Analysis of Space Hundred-kilowatt Lithium-cooled Fast Reactor. At. Energy Sci. Technol. 2022, 56, 443. [Google Scholar]
- Ma, W.; Ye, P.; Gao, Y.; Yang, X. Comparative study on sequential and simultaneous startup performance of space nuclear power system with multi brayton loops. Acta Astronaut. 2022, 199, 142–152. [Google Scholar] [CrossRef]
- Johnson, P.; Mason, L. Performance and Operational Characteristics for a Dual Brayton Space Power System with Common Gas Inventory. In Proceedings of the 4th International Energy Conversion Engineering Conference and Exhibit (IECEC), San Diego, CA, USA, 26–29 June 2006. [Google Scholar] [CrossRef]
- Ashcroft, J.; Belanger, S.; Burdge, W.; Clementoni, E.; Jensen, K.; Proctor, N.B.; Zemo-Fulkerson, A. Key Factors Influencing the Decision on the Number of Brayton Units for the Prometheus Space Reactor. AIP Conf. Proc. 2007, 880, 522–540. [Google Scholar]
- Ma, W.; Ye, P.; Zhao, G.; Yang, X.; Wang, J. Effect of cooling schemes on performance of MW-class space nuclear closed Brayton cycle. Ann. Nucl. Energy 2021, 162, 108485. [Google Scholar] [CrossRef]
- Taylor, M.; Bauer, K.; McEligot, D. Internal forced convection to low-Prandtl-number gas mixtures. Int. J. Heat Mass Transf. 1988, 31, 13–25. [Google Scholar] [CrossRef]
- von Arx, A.V.; Ceyhan, I. Laminar heat transfer for low Prandtl number gases. AIP Conf. Proc. Am. Inst. Phys. 1991, 217, 719–722. [Google Scholar]
- Hong, J.; Lee, J.; Eoh, J. Study on convective heat transfer correlations for sodium-to-sodium heat exchanger based on STELLA-1 experimental results. Nucl. Eng. Des. 2020, 371, 110963. [Google Scholar] [CrossRef]
- Yuan, Z.; Zheng, Q.; Yue, G.; Jiang, Y. Performance evaluation on radial turbines with potential working fluids for space closed Brayton cycle. Energy Convers. Manag. 2021, 243, 114368. [Google Scholar] [CrossRef]
- Gallo, B.M.; El-Genk, M.S. Brayton rotating units for space reactor power systems. Energy Convers. Manag. 2009, 50, 2210–2232. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Gallo, B.M. High-Power Brayton Rotating Unit for Reactor and Solar Dynamic Power Systems. J. Propuls. Power 2010, 26, 167–176. [Google Scholar] [CrossRef]
- Gallo, B.M.; El-Genk, M.S.; Tournier, J.M. Compressor and turbine models of Brayton units for space nuclear power systems. AIP Conf. Proc. 2007, 880, 472–482. [Google Scholar]
- El-Genk, M.; Gallo, B. High Performance Brayton Rotating Unit (UNM-BRU-3) for Space Reactor Power Systems. In Proceedings of the International Energy Conversion Engineering Conference, Denver, CO, USA, 2–5 August 2009. [Google Scholar]
- Ming, Y.; Liu, K.; Zhao, F.; Fang, H.; Tan, S.; Tian, R. Dynamic modeling and validation of the 5 MW small modular supercritical CO2 Brayton-Cycle reactor system. Energy Convers. Manag. 2022, 253, 115184. [Google Scholar] [CrossRef]
- Kim, J.H.; NO, H.C.; Kim, H.M.; Lim, H.S. A system analysis tool with a 2D gas turbine modeling for the load transients of HTGRS. Nucl. Eng. Des. 2009, 239, 2459–2467. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Vitovsky, O.V. Study of heat transfer of a helium–xenon mixture in heated channels with different cross-sectional shapes. J. Appl. Mech. Tech. Phys. 2017, 58, 664–669. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Elistratov, S.L.; Vitovsky, O.V.; Slesareva, E.Y. Experimental investigation of heat transfer in helium-xenon mixtures in triangle channels. J. Eng. Thermophys. 2015, 24, 139–142. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Tournier, J.-M. Noble gas binary mixtures for gas-cooled reactor power plants. Nucl. Eng. Des. 2008, 238, 1353–1372. [Google Scholar] [CrossRef]
- Xu, C.; Kong, F.; Yu, D.; Yu, J.; Khan, M.S. Influence of non-ideal gas characteristics on working fluid properties and thermal cycle of space nuclear power generation system. Energy 2021, 222, 119881. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).