Abstract
Combined concentrated solar power with photovoltaics can provide electricity and heat at the same system while maximizing the power output with reduced losses. Spectral splitting is required in such systems to separate the infrared part of the solar spectrum towards the thermal system, while the visible and near-infrared radiation can be converted by the photovoltaic solar cell. The performance of concentrated solar power plants comprising reflective beam splitters for combined generation of electricity and heat is presented in this work. A 50 MW power plant is considered in this work as a case of study in Southern Crete, Greece. The solar power plant consists of parabolic trough collectors and utilizes beam splitters with varying reflectivity. The dynamic performance of the power plant is modeled, and the annual energy yield can be calculated. Up to 350 MWt of thermal power can be delivered to the photovoltaic system utilizing a 50% reflecting splitter. The penalty to the high-reflectivity system is limited to 16.9% and the annual energy yield is calculated as 53.32 GWh. During summer months, a higher energy yield by up to 84.8 MWh/month is produced at 80% reflectivity compared to 90% as a result of the number of parabolic troughs. The reported energy yields with reflectivity by dynamic modeling can highlight discrete points for improvement of the performance in concentrated solar power photovoltaics.
1. Introduction
The energy transition from conventional energy sources to clean and renewable energy sources is one of the main objectives of the European Commission, formulated through a series of Community Directives, such as the Directive on the energy upgrade of the building stock (Energy Performance of Buildings Directive: 2018/844/EU) [1] and the Renewable Energy Directive (2018/2001/EU) [2], including the establishment of energy communities [3]. Through these directives, the member states of the European Union are invited to draw up national action plans to approach the objectives of the European Commission. Regarding the production of electricity or thermal energy, Greece still relies on thermal power plants in more than 80% of total energy supply [4]. In recent decades, however, with the country’s compliance with the European Directives, the annual penetration of Renewable Energy Sources (RES) in the energy balance of the non-interconnected islands is increasing.
Important research has been reported in the field of guaranteed electric power production in autonomous island systems [5] based on the implementation of hybrid plants with power generation technologies from RES and storage technologies [6]. While international efforts are being made to make these systems technically and economically competitive with wind farm-reversible hydroelectric systems, the total energy transition towards clean forms of energy, especially in island systems with strong seasonal variation in power demand, requires the utilization of all possible technologies of available RES and the experience already developed.
Four types of concentrated solar power (CSP) systems have been developed so far, which, respectively, use the following technologies: (a) linear parabolic mirrors, (b) Fresnel collectors with a central heat collector, (c) solar towers with heliostats, and (d) solar energy dish with Stirling engines. These solar systems have potential for electricity and heat co-generation systems.
However, each technology poses different environmental, and especially visual, impacts. For example, concentrated solar power systems, due to the high concentrated intensity of solar radiation, which can be from 10 up to 5000 suns [7,8], may have a significant impact on the man-made and natural environment [9]. Moreover, access to solar field area can be a significant challenge; it can reach more than 17 ha/MWe [10] for power plants of separate CSP and photovoltaic technologies [11].
One way to address these impacts, while simultaneously maximizing electricity and heat generation, is by integration of low-cost photovoltaics on CSP systems. Spectral splitting devices are required in these systems, which separate the infrared solar radiation, invisible to the human eye, and concentrate it towards the solar thermal unit. Dielectric coatings of selective transmission are implemented and can be therefore directly applicable to solar power devices.
There can be several configurations for spectrally splitting the solar photovoltaic and thermal fraction of the solar spectrum. Vossier et al. reported on the bounds in performance by examining distinct configurations [12]. In spectral splitting configurations, the PV fraction is higher than 55% considering a 0.01 Ω cm2 series resistance, while for the radiative limit it can reach 75.7%. One of these configurations where the photovoltaic cell is integrated on the parabolic concentrator is displayed in Figure 1.
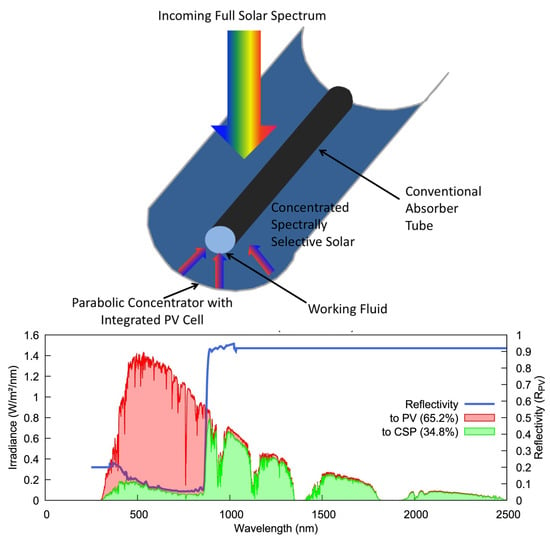
Figure 1.
CSP-PV spectral splitting configuration, adopted by reference [13]. Spectral irradiance and reflectivity of solar cell (cell reflectivity in blue [14], power absorbed by PV in red, power sent to CSP in green) [15].
The long wavelength infrared radiation, best converted by the CSP system, is reflected towards the receiver, while the visible and near-infrared radiation is transmitted towards the solar cell. In this configuration, the solar cell operates at a lower temperature and a higher efficiency, limiting the possibility of damage in concentrating systems [16,17]. The high reflectivity of an exemplary solar cell can be seen in Figure 1, with a cut-off wavelength at approximately 750 nm. This cut-off wavelength corresponds to the band-gap of GaAs or perovskite solar cells, while for Si with the highest share of installed solar power systems, this is at approximately 1200 nm. Spectral filters, however, may have appropriate cut-on wavelength to further direct ultraviolet (UV) radiation to a thermal receiver. A discrepancy in regard to the optimal wavelengths for Si solar cells exists which varies between 751 and 1126 nm [18] 732 and 1067 nm [19], 640 and 1127 nm [20], 600 and 1150 nm [21], 400 and 1100 nm [22], 300 and 1100 nm [23], while when the second-law efficiency of the thermal converter and the solar concentration are taken under consideration, the optimum window spans from 290 nm to 1110 nm [24].
A comprehensive comparison of selective transmitters was reported in [25], concluding that ZnS/Ag/Zns and ITO perform best at low cost for the latter. ITO was also reported as an antireflection coating for silicon solar cells [26], while filters with appropriate cut-off at 1200 nm, suitable for silicon solar cells, were reported in [27]. The filters exhibited high reflectivity above 80% at an angle of incidence of 45°. The filter consisted of 96 alternating layers of Nb2O5 as high and SiO2 as low refractive index layer. For reduced costs, double TiO2 [28] or TiO2/MgF layered coatings [29] have been reported as suitable alternatives.
For a beam splitting configuration that separates the spectral splitter from the solar cell, the spectral splitter should be highly reflective in the visible and near-infrared part of the spectrum. Nb:TiO2 [30] and TiO2/SiO2 [22] can be suitable solutions to this end, and reported higher than 80% and 95% reflectivity, respectively. The overall optical efficiency of a parabolic system with a Nb2O5/SiO2 filter was reported to be 76.4% while reducing the heat load of the solar cells by 20.7% [31]. The spectral splitter can further be thermochromic as inspired by its application in building windows [32], that is, at elevated temperatures, reflectivity increases as reported in VO2 receivers for parabolic troughs [33]. A 50x concentrated parabolic trough with interference filters was modeled in [34] with reported efficiencies of 27% and 50% for the PV and thermal receiver, respectively. The spectral splitter consisted of Si, AlGaAs and Ge solar cells [35] that reduced the power output of the PV by 25% to increase the thermal output by 51.4 MJ/m2 [22]. The conversion efficiency of the CPV/CSP system with c-Si with a spectral window of 541–1117 nm was also enhanced by 25%, while the efficiency was enhanced by 50% with GaAs and a spectral window of 431–877 nm [36]. A two-stage concentrator was utilized in the latter system with the spectral filter deposited on the secondary concentrator. This configuration demands the high durability of the coating to solar irradiance in the range of 10,000 W/m2. For a detailed review on spectral splitting for decoupled photovoltaic/thermal systems, the reader is directed towards reference [37]. The performance of the most representative spectral splitters for concentrating solar photovoltaic systems can be seen in Table 1.

Table 1.
Characteristics of the spectral filters for concentrating solar power photovoltaic systems.
The application of spectral filters in CSP systems may follow techniques already applied in the application of coatings in reflector technology. Silver or aluminum coatings are commonly applied in concentrating thermal collectors. Due to the sensitivity of silver to oxidation, it is usually deposited at the back of the glass structure of the collector. Aluminum coatings are protected from oxidation by application of a layer of alumina overcoat [42]. A spectral splitting system could utilize multi-layer coatings in addition to the reflective layer. Such multi-layer coatings are commonly deposited by chemical vapor deposition or physical vapor deposition methods, producing high-quality coatings. For lower cost, wet chemical processing such as sol–gel processing with spray or dipping can be utilized as applied in the fabrication of solar thermal coatings for thermal receivers [42]. The high durability of the coating at high temperatures should also be ensured in this case, since common wet chemical processing is applied at room temperature [43,44,45,46].
Despite the breadth of spectral splitting configurations with high performance in the literature, the energy yield of the system is rarely reported. In this work, the performance of the CSP power plant with a parabolic trough collector is reported. The system is modeled for varying reflectivity of the spectral splitter available from the literature to obtain the power output, annual energy yield and evaluate the flow rate in the receiver and overall system for the assessment of the system’s performance.
2. Materials and Methods
CSP plants primarily collect sunlight’s direct irradiance Ib. For clear skies, the direct irradiance Perez–Ineichen model was utilized [47]. Heat input Qi impinging on the solar collectors was calculated as [48]
where θi is the incidence angle and ηopt is the optical efficiency of the receiver. The dimensionless geometrical solar concentration Cgeo could be calculated as the ratio of the area of collectors Ac and receivers Ar as
The collection efficiency of parabolic troughs varies with incidence angle θi. For several parabolic trough technologies, incidence angle modifier Kθi has been widely reported. In this treatment, we apply the expression in terms of
Consequently, the net heat input available to produce work W was calculated as
where
is the radiative flux and Qconv is the convective flux to the environment, while α and ε are the absorptivity and emissivity of the receiver, respectively. For parabolic troughs, the convective loss is considered negligible here. Work W produced by the turbine of the power block operating was finally calculated from the net heat input and the isentropic efficiency of the Rankine cycle and the efficiency of the generator ηG as
The heat losses of the storage system and the pipes connecting the system all together were considered based on empirical relation
where
All equations were developed in a publicly available code [49] that follows the flowchart presented in Figure 2. The code, in addition to the dynamic modeling of parabolic troughs, features the modeling of solar power tower plants based on heliostats. Consequently, the modeling of combined CSP power plants with solar power towers and parabolic troughs can be dynamically modeled. By dynamically modeling the performance of a CSP power plant, the annual energy yield as well as the financial characteristics of the plant can be computed for a complete feasibility assessment. Moreover, detailed dynamic simulations with hourly resolution can highlight methods for improvement of existing technologies. In the case of combined CSP power plants, an increased day-to-day performance and higher-capacity factors compared to standalone plants were recently reported [48].
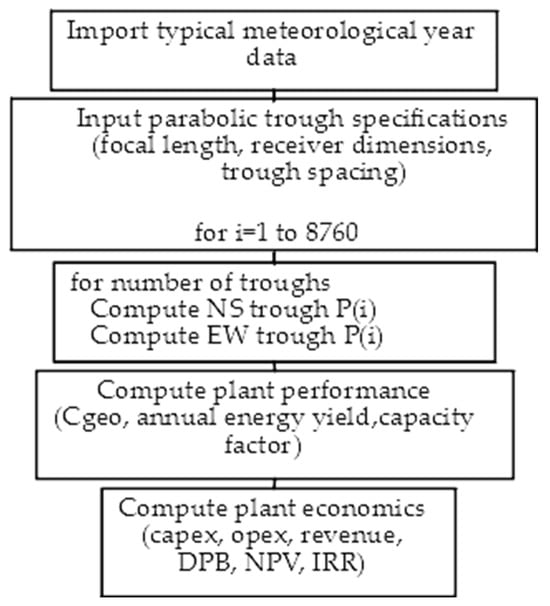
Figure 2.
Flow chart of the algorithm for concentrating solar power plant with parabolic trough collectors.
The meteorological data were sourced from the location of the site from the Photovoltaic Geographical Information System (PVGIS). The meteorological data of the Mediterranean basin are important for site selection of a CSP power plant. The annual average DNI is calculated at 250 W/m2, while the maximum at 1002 W/m2 reveals suitable solar potential in the area under consideration. A solar thermal station has already been proposed for Crete and licensed by the Energy Regulatory Authority, with a nominal guaranteed power of 50 MW for the Atherinolakkos area of Sitia. Consequently, the designed power output of the CSP power plant was considered in this work as 50 Mwe, and the solar field consisted of 472.320 m2 of parabolic trough collectors with dimensions 6 × 115 m and a total reflective area of 656 m2. The heat transfer fluid was considered to operate at temperatures between 290 °C and 390 °C, in agreement with commercial synthetic oils enjoying high thermal conductivity [8]. For the purposes of this work, the system operates with direct steam generation (DSG) in the receiver without energy storage. This commonly reduces the system’s set-up cost and the increase in the overall efficiency due to the elimination of the heat transfer losses in the oil–steam heat exchanger.
3. Results and Discussion
Figure 3a displays the mass flow delivered by the power plant. The flow rate fluctuates between 1 and 12 kg/s in relative agreement with medium concentration photovoltaic-thermal systems [50]. It can be seen that reduction in reflectivity reduces the mass flow at the receiver. This is especially pronounced during summer months, when the highest irradiance occurs. Between the months of January and April and September and December, there is no apparent change in the mass flow. Below 60% reflectivity, fluctuations in the mass flow can be seen due to insufficient flux delivered to the receiver. Nevertheless, these fluctuations do not significantly reduce the performance of the overall mass flow at the end of the solar field, as can be seen in Figure 3b. The mass flow of the entire solar field presents no apparent reduction upon the change in reflectivity of the filter throughout the year.
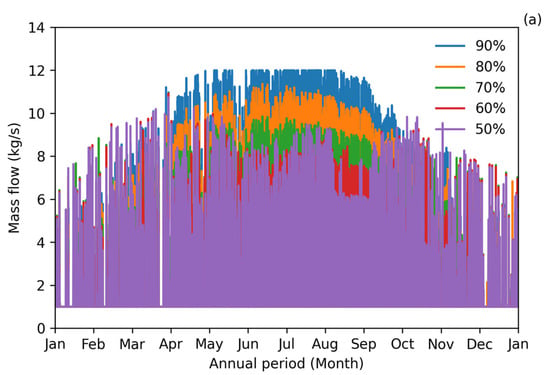

Figure 3.
Mass flow at the (a) receiver and (b) end of the solar array for different spectral filter reflectivity.
The change in reflectivity induces a direct increase in the thermal power incident on the receiver. The incident thermal power as a function of reflectivity of the spectral filter can be seen in Figure 4. The incident thermal power is reduced proportionally in each month for the entire simulated year. While an average of 150 MWt is incident at 90% reflectivity, the power increases to 250 MWt at 70% and can reach 350 MWt at 50% reflectivity.
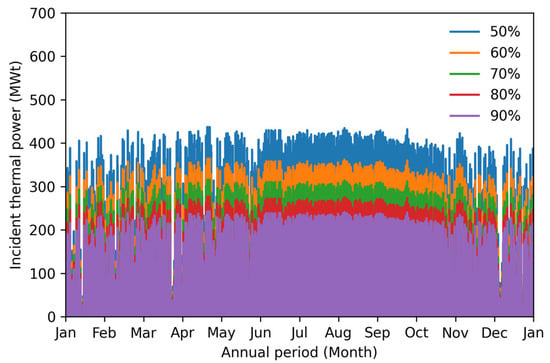
Figure 4.
Incident thermal power as a function of spectral filter reflectivity.
This power is transmitted to the solar cell unless an appropriate selective coating is applied. Despite the significant reduction in reflected power to the receiver, the monthly produced energy is not significantly reduced; see Figure 5. From 1.15 GWh at 90%, the delivered energy drops to 1.05 GWh at 50% reflectivity during July. For the winter months, the reduction in power is less pronounced due to the lower power production with lower irradiance. The reduction is proportional for all months. Below 60% reflectivity, the delivered energy during the winter months of December and January cannot meet the target levels and require supplementary sources.
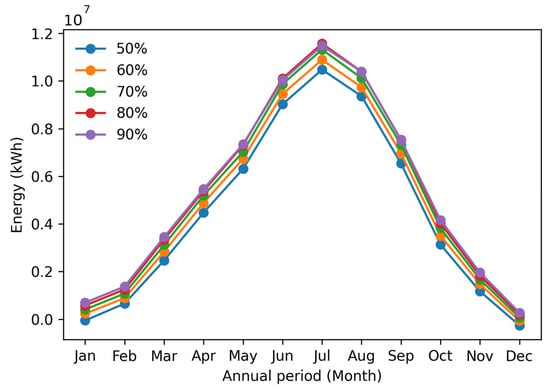
Figure 5.
Produced energy by the CSP power plant as a function of spectral filter reflectivity.
Focusing on the summer months, Figure 5 indicates that the energy yield of the plant drops with reduced reflectivity during months January to April and September to December. However, the opposite trend is observed for collectors with 90% reflectivity during the months of June to August. As shown in Figure 6, at 80% reflectivity, the CSP power plant produces 68,700 kWh, 84,800 kWh and 2600 kWh more energy than a plant with 90% reflectivity in June, July, and August, respectively. This difference is caused by an increased number of collector loops in the CSP model. To produce a nominal guaranteed power output of 50 MW, a specific number of loops x collectors are required for each variation in reflectivity, that is, at 90% reflectivity, 50 loops × 8 collectors are required. On the contrary, at 80% reflectivity, the required loops increase to 57 loops × 8 collectors and at 70%, 65 loops × 8 collectors are utilized. Consequently, at the same nominal power output of 50 Mwe, a reduction in the reflectivity of the spectral splitter by 10% requires 7 more loops of 8 parabolic collectors, that is, 56 more parabolic troughs. The additional parabolic troughs with 80% reflectivity produce more power than the 90% reflective troughs during the months of June, July, and August in agreement with the summer solstice in the location of the CSP plant.
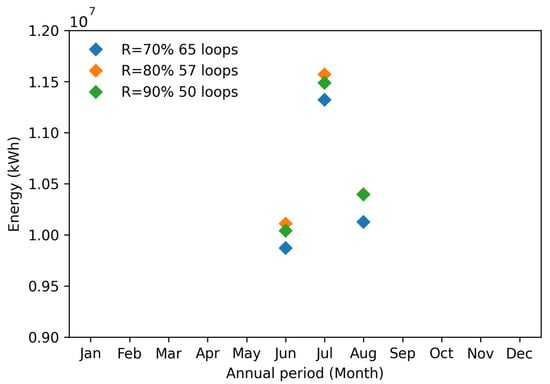
Figure 6.
Produced energy by the CSP power plant as a function of spectral filter reflectivity during the summer months.
The minimal reduction caused by changing the reflectivity is further confirmed by the power output, shown in the maps of Figure 7. A more detailed day-by-day picture of the power output can be seen. Very limited drops in power output can be seen during the early morning hours throughout the year. The difference in power output is in the range of 5 to 10 MW. Although this reduction merely reduces the produced power during peak summer months, this is more detrimental during the winter months where the power output is limited to 20 MW. To increase the chances for better performance during these months, the solar multiple of the power plant can be increased. Alternatively, an auxiliary source of power is required to support steady production during these months. It can be seen that operating hours appear shorter when 50% reflectivity is used, which can be explained by the reflected light to the photovoltaic converter. The calculated annual energy yield of the 50% reflectivity system was 53.32 GWh, while that of the 90% one was 64.16 GWh.
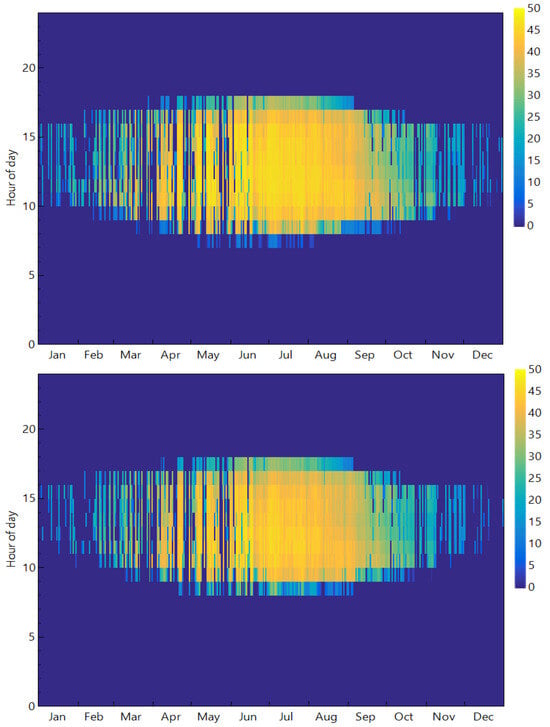
Figure 7.
Power output in MWe of the power plant with 90% (above) and 50% reflectivity (below).
The economic evaluation of a retrofit parabolic trough collector system with crystalline Si solar cells and dichroic filters produced a specific cost of USD 0.9/W and an increase in overall efficiency of 1.4% to the CSP plant [51]. It was noted that under the current maturity of GaAs solar cells, c-Si concentrator cells were proven more economically viable. The annual energy output increased by 10.7% with potential for even higher power output assuming more stable production of the PV with reduced requirements for maintenance and downtime. The internal revenue rate of 18% with a 30-year agreement is maintained with an electricity price of USD 0.14/kWh.
4. Conclusions
The annual energy performance of a spectral splitting CSP power plant with PV was presented in this paper. The reflectivity of the collector was varied according to a range of possible values commensurate with state-of-the-art filters. While reduction in the flow rate was obtained especially below 50% reflectivity, the total flow rate at the end of the solar field was not reduced by more than 1% of the high-reflectivity system. The thermal power to the PV system varied from 150 MWt to 350 MWt for 90% and 50% reflectivity, respectively. The energy delivered to the thermal receiver was not reduced significantly, that is, a reduction of 16.9% from a 90% to a 50% reflectivity. The results of this work present an alternative configuration that utilizes, on the one hand, low-cost photovoltaics, and CSP on the other to convert thermal radiation. Future research could further focus on the spectral selectors with appropriate cut-off wavelengths, as well as the utility of thermal storage in the same configuration. In this way, on the one hand, the visual impact by concentrated sunlight can be reduced, while on the other hand, new degrees of freedom can be introduced in hybrid solar thermal photovoltaic systems.
Author Contributions
Methodology, G.E.A.; Software, G.E.A.; Formal analysis, G.E.A.; Investigation, G.E.A.; Data curation, G.E.A.; Writing—original draft, G.E.A. and D.A.K.; Writing—review & editing, G.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors are thankful to the academic fellowship of the postdoctoral program provided by HMU during which the presented concepts were developed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Parliament. Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018 amending Directive 2010/31/EU on the energy performance of buildings and Directive 2012/27/EU on energy efficiency (Text with EEA relevance). OJL 2018, 156, 75–91. [Google Scholar]
- European Parliament. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the promotion of the use of energy from renewable sources (Text with EEA relevance). OJL 2018, 328, 82–209. [Google Scholar]
- Katsaprakakis, D.A.; Proka, A.; Zafirakis, D.; Damasiotis, M.; Kotsampopoulos, P.; Hatziargyriou, N.; Dakanali, E.; Arnaoutakis, G.; Xevgenos, D. Greek Islands’ Energy Transition: From Lighthouse Projects to the Emergence of Energy Communities. Energies 2022, 15, 5996. [Google Scholar] [CrossRef]
- World Energy Balances Total Energy Supply (TES) by Source, Greece 1990–2022. Available online: https://www.iea.org/countries/greece (accessed on 9 January 2024).
- Katsaprakakis, D.A.; Dakanali, I.; Condaxakis, C.; Christakis, D.G. Comparing Electricity Storage Technologies for Small Insular Grids. Appl. Energy 2019, 251, 113332. [Google Scholar] [CrossRef]
- Katsaprakakis, D.A.; Christakis, D.G. Seawater Pumped Storage Systems and Offshore Wind Parks in Islands with Low Onshore Wind Potential. A Fundamental Case Study. Energy 2014, 66, 470–486. [Google Scholar] [CrossRef]
- Li, L.; Coventry, J.; Bader, R.; Pye, J.; Lipiński, W. Optics of Solar Central Receiver Systems: A Review. Opt. Express 2016, 24, A985–A1007. [Google Scholar] [CrossRef] [PubMed]
- Arnaoutakis, G.E.; Katsaprakakis, D.A. Concentrating Solar Power Advances in Geometric Optics, Materials and System Integration. Energies 2021, 14, 6229. [Google Scholar] [CrossRef]
- Hernandez, R.R.; Easter, S.B.; Murphy-Mariscal, M.L.; Maestre, F.T.; Tavassoli, M.; Allen, E.B.; Barrows, C.W.; Belnap, J.; Ochoa-Hueso, R.; Ravi, S.; et al. Environmental Impacts of Utility-Scale Solar Energy. Renew. Sustain. Energy Rev. 2014, 29, 766–779. [Google Scholar] [CrossRef]
- Desideri, U.; Campana, P.E. Analysis and Comparison between a Concentrating Solar and a Photovoltaic Power Plant. Appl. Energy 2014, 113, 422–433. [Google Scholar] [CrossRef]
- Zurita, A.; Mata-Torres, C.; Cardemil, J.M.; Escobar, R.A. Assessment of Time Resolution Impact on the Modeling of a Hybrid CSP-PV Plant: A Case of Study in Chile. Sol. Energy 2020, 202, 553–570. [Google Scholar] [CrossRef]
- Vossier, A.; Zeitouny, J.; Katz, E.A.; Dollet, A.; Flamant, G.; Gordon, J.M. Performance Bounds and Perspective for Hybrid Solar Photovoltaic/Thermal Electricity-Generation Strategies. Sustain. Energy Fuels 2018, 2, 2060–2067. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Theisen, S.; Norman, T.; Tyagi, H.; Taylor, R.A. Envisioning Advanced Solar Electricity Generation: Parametric Studies of CPV/T Systems with Spectral Filtering and High Temperature PV. Appl. Energy 2015, 140, 224–233. [Google Scholar] [CrossRef]
- Ganapati, V.; Xiao, T.P.; Yablonovitch, E. Ultra-Efficient Thermophotovoltaics Exploiting Spectral Filtering by the Photovoltaic Band-Edge. arXiv 2018, arXiv:1611.03544. [Google Scholar]
- Ziyati, D.; Dollet, A.; Flamant, G.; Volut, Y.; Guillot, E.; Vossier, A. A Multiphysics Model of Large-Scale Compact PV–CSP Hybrid Plants. Appl. Energy 2021, 288, 116644. [Google Scholar] [CrossRef]
- Ahmed, A.; Alzahrani, M.; Shanks, K.; Sundaram, S.; Mallick, T.K. Effect of Using an Infrared Filter on the Performance of a Silicon Solar Cell for an Ultra-High Concentrator Photovoltaic System. Mater. Lett. 2020, 277, 128332. [Google Scholar] [CrossRef]
- Alzahrani, M.M.; Roy, A.; Sundaram, S.; Mallick, T.K. Investigation of Thermal Stress Arising in a Graphene Neutral Density Filter for Concentrated Photovoltaic System. Energies 2021, 14, 3515. [Google Scholar] [CrossRef]
- Taylor, R.A.; Otanicar, T.; Rosengarten, G. Nanofluid-Based Optical Filter Optimization for PV/T Systems. Light Sci. Appl. 2012, 1, e34. [Google Scholar] [CrossRef]
- Crisostomo, F.; Taylor, R.A.; Surjadi, D.; Mojiri, A.; Rosengarten, G.; Hawkes, E.R. Spectral Splitting Strategy and Optical Model for the Development of a Concentrating Hybrid PV/T Collector. Appl. Energy 2015, 141, 238–246. [Google Scholar] [CrossRef]
- Bierman, D.M.; Lenert, A.; Wang, E.N. Spectral Splitting Optimization for High-Efficiency Solar Photovoltaic and Thermal Power Generation. Appl. Phys. Lett. 2016, 109, 243904. [Google Scholar] [CrossRef]
- Otanicar, T.; Dale, J.; Orosz, M.; Brekke, N.; DeJarnette, D.; Tunkara, E.; Roberts, K.; Harikumar, P. Experimental Evaluation of a Prototype Hybrid CPV/T System Utilizing a Nanoparticle Fluid Absorber at Elevated Temperatures. Appl. Energy 2018, 228, 1531–1539. [Google Scholar] [CrossRef]
- Shou, C.; Luo, Z.; Wang, T.; Shen, W.; Rosengarten, G.; Wei, W.; Wang, C.; Ni, M.; Cen, K. Investigation of a Broadband TiO2/SiO2 Optical Thin-Film Filter for Hybrid Solar Power Systems. Appl. Energy 2012, 92, 298–306. [Google Scholar] [CrossRef]
- Soule, D.E.; Rechel, E.F.; Smith, D.W.; Willis, F.A. Efficient Hybrid Photovoltaic-Photothermal Solar Conversion System with Cogeneration. In Proceedings of the Optical Materials Technology for Energy Efficiency and Solar Energy Conversion IV, San Diego, CA, USA, 20–22 August 1985; SPIE: Bellingham, WA, USA, 1985; Volume 562, pp. 166–175. [Google Scholar]
- Huang, G.; Wang, K.; Markides, C.N. Efficiency Limits of Concentrating Spectral-Splitting Hybrid Photovoltaic-Thermal (PV-T) Solar Collectors and Systems. Light Sci. Appl. 2021, 10, 28. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.A.; Hewakuruppu, Y.; DeJarnette, D.; Otanicar, T.P. Comparison of Selective Transmitters for Solar Thermal Applications. Appl. Opt. 2016, 55, 3829–3839. [Google Scholar] [CrossRef] [PubMed]
- Law, A.M.; Jones, L.O.; Walls, J.M. The Performance and Durability of Anti-Reflection Coatings for Solar Module Cover Glass—A Review. Sol. Energy 2023, 261, 85–95. [Google Scholar] [CrossRef]
- Amotchkina, T.; Fattahi, H.; Pervak, Y.A.; Trubetskov, M.; Pervak, V. Broadband Beamsplitter for High Intensity Laser Applications in the Infra-Red Spectral Range. Opt. Express 2016, 24, 16752. [Google Scholar] [CrossRef] [PubMed]
- Richards, B.S.; Rowlands, S.F.; Honsberg, C.B.; Cotter, J.E. TiO2 DLAR Coatings for Planar Silicon Solar Cells. Prog. Photovolt. Res. Appl. 2003, 11, 27–32. [Google Scholar] [CrossRef]
- Rüdiger, M.; Fischer, S.; Frank, J.; Ivaturi, A.; Richards, B.S.; Krämer, K.W.; Hermle, M.; Goldschmidt, J.C. Bifacial N-Type Silicon Solar Cells for Upconversion Applications. Sol. Energy Mater. Sol. Cells 2014, 128, 57–68. [Google Scholar] [CrossRef]
- Maghanga, C.M.; Niklasson, G.A.; Granqvist, C.G.; Mwamburi, M. Spectrally Selective Reflector Surfaces for Heat Reduction in Concentrator Solar Cells: Modeling and Applications of TiO2:Nb-Based Thin Films. Appl. Opt. 2011, 50, 3296–3302. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, P.; Mo, S.; Chen, Z. Optical Modeling for a Two-Stage Parabolic Trough Concentrating Photovoltaic/Thermal System Using Spectral Beam Splitting Technology. Sol. Energy Mater. Sol. Cells 2010, 94, 1686–1696. [Google Scholar] [CrossRef]
- Arnaoutakis, G.E.; Katsaprakakis, D.A. Energy Performance of Buildings with Thermochromic Windows in Mediterranean Climates. Energies 2021, 14, 6977. [Google Scholar] [CrossRef]
- Wang, Q.; Shen, B.; Huang, J.; Yang, H.; Pei, G.; Yang, H. A Spectral Self-Regulating Parabolic Trough Solar Receiver Integrated with Vanadium Dioxide-Based Thermochromic Coating. Appl. Energy 2021, 285, 116453. [Google Scholar] [CrossRef]
- Mitchell, B.; Peharz, G.; Siefer, G.; Peters, M.; Gandy, T.; Goldschmidt, J.C.; Benick, J.; Glunz, S.W.; Bett, A.W.; Dimroth, F. Four-Junction Spectral Beam-Splitting Photovoltaic Receiver with High Optical Efficiency. Prog. Photovolt. Res. Appl. 2011, 19, 61–72. [Google Scholar] [CrossRef]
- Liew, N.J.Y.; Yu, Z.J.; Holman, Z.; Lee, H.-J. Application of Spectral Beam Splitting Using Wavelength-Selective Filters for Photovoltaic/Concentrated Solar Power Hybrid Plants. Appl. Therm. Eng. 2022, 201, 117823. [Google Scholar] [CrossRef]
- Liang, H.; Han, H.; Wang, F.; Cheng, Z.; Lin, B.; Pan, Y.; Tan, J. Experimental Investigation on Spectral Splitting of Photovoltaic/Thermal Hybrid System with Two-Axis Sun Tracking Based on SiO2/TiO2 Interference Thin Film. Energy Convers. Manag. 2019, 188, 230–240. [Google Scholar] [CrossRef]
- Hong, W.; Li, B.; Li, H.; Niu, X.; Li, Y.; Lan, J. Recent progress in thermal energy recovery from the decoupled photovolta-ic/thermal system equipped with spectral splitters. Renew. Sustain. Energy Rev. 2022, 167, 112824. [Google Scholar] [CrossRef]
- Kandilli, C.; Külahlı, G. Performance Analysis of a Concentrated Solar Energy for Lighting-Power Generation Combined System Based on Spectral Beam Splitting. Renew. Energy 2017, 101, 713–727. [Google Scholar] [CrossRef]
- Zhang, X.; Lei, D.; Zhang, B.; Yao, P.; Wang, Z. SiNx/Cu Spectral Beam Splitting Films for Hybrid Photovoltaic and Concentrating Solar Thermal Systems. ACS Omega 2021, 6, 21709–21718. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, H.; Hu, M.; Huang, X.; Li, J.; Pei, G. Preliminary Performance Study of a High-Temperature Parabolic Trough Solar Evacuated Receiver with an Inner Transparent Radiation Shield. Sol. Energy 2018, 173, 640–650. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, M.; Yang, H.; Cao, J.; Li, J.; Su, Y.; Pei, G. Performance Evaluation and Analyses of Novel Parabolic Trough Evacuated Collector Tubes with Spectrum-Selective Glass Envelope. Renew. Energy 2019, 138, 793–804. [Google Scholar] [CrossRef]
- Atkinson, C.; Sansom, C.L.; Almond, H.J.; Shaw, C.P. Coatings for Concentrating Solar Systems—A Review. Renew. Sustain. Energy Rev. 2015, 45, 113–122. [Google Scholar] [CrossRef]
- Hamdy, M.A.; Osborn, D.E. The Potential for Increasing the Efficiency of Solar Cells in Hybrid Photovoltaic/Thermal Concentrating Systems by Using Beam Splitting. Sol. Wind Technol. 1990, 7, 147–153. [Google Scholar] [CrossRef]
- Osborn, D.E.; Chendo, M.A.C.; Hamdy, M.A.; Luttmann, F.; Jacobson, M.R.; Macleod, H.A.; Swenson, R. Spectral Selectivity Applied to Hybrid Concentration Systems. Sol. Energy Mater. 1986, 14, 299–325. [Google Scholar] [CrossRef]
- Ju, X.; Xu, C.; Han, X.; Du, X.; Wei, G.; Yang, Y. A Review of the Concentrated Photovoltaic/Thermal (CPVT) Hybrid Solar Systems Based on the Spectral Beam Splitting Technology. Appl. Energy 2017, 187, 534–563. [Google Scholar] [CrossRef]
- Widyolar, B.; Jiang, L.; Winston, R. Spectral Beam Splitting in Hybrid PV/T Parabolic Trough Systems for Power Generation. Appl. Energy 2018, 209, 236–250. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A New Operational Model for Satellite-Derived Irradiances: Description and Validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- Arnaoutakis, G.E.; Katsaprakakis, D.A.; Christakis, D.G. Dynamic Modeling of Combined Concentrating Solar Tower and Parabolic Trough for Increased Day-to-Day Performance. Appl. Energy 2022, 323, 119450. [Google Scholar] [CrossRef]
- Arnaoutakis, G.E.; Papadakis, N.; Katsaprakakis, D. CombiCSP: A Python Routine for Dynamic Modeling of Concentrating Solar Power Plants. Softw. Impacts 2022, 13, 100367. [Google Scholar] [CrossRef]
- Lamnatou, C.; Vaillon, R.; Parola, S.; Chemisana, D. Photovoltaic/Thermal Systems Based on Concentrating and Non-Concentrating Technologies: Working Fluids at Low, Medium and High Temperatures. Renew. Sustain. Energy Rev. 2021, 137, 110625. [Google Scholar] [CrossRef]
- Orosz, M.; Zweibaum, N.; Lance, T.; Ruiz, M.; Morad, R. Spectrum-Splitting Hybrid CSP-CPV Solar Energy System with Standalone and Parabolic Trough Plant Retrofit Applications. AIP Conf. Proc. 2016, 1734, 070023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).