2.1. Description and Characteristics of the Object
The analyzed object is a hybrid generation system consisting of a photovoltaic section with a rated power of , a wind section with a rated power of turbines , and a lithium-ion energy storage EES with a rated energy capacity of intended to support the power supply of a housing estate of 20 single-family houses. The generation system and the storage are located in the area of the provided housing estate, and all houses are connected to the low-voltage distribution network.
The choice of the facility is primarily due to the increasing role of distributed RESs in national power systems. The issues of their positive impact on local balancing of electricity, the possibility of controlling the production profile by using opposing sources (PV and wind turbines) and energy storage facilities, as well as the diversification of energy supplies, which is so important for the country’s energy security, are increasingly raised. Another reason for choosing the facility analyzed is the previous research that the authors conducted on hybrid systems intended to power single-family housing estates, taking into account the impact of the development of electromobility on the economic profitability of the indicated installations. It was shown there that even in the absence of electric vehicles, the use of optimized structures of a hybrid system with RES and an energy storage facility in the scope of supporting the power supply of these types of recipients is economically justified—it pays off within a period of several to 10 years (depending on the configuration of the system, mainly on the energy capacity of the energy storage facility) [
38]. The indicated aspects and the pro-ecological nature of this type of solution indicate the future dissemination of such systems, provided, however, that collective prosumers (prosumer cooperatives) are taken into account in the legal provisions of distribution companies.
The total electrical load
of the housing estate is the sum of the loads of individual houses. This article analyzes two cases covering the load of houses in accordance with the single-zone tariff G11 (variant I) and the two-zone tariff G12 (variant II) of the Polish electricity distributor—ENEA Operator. A random disturbance was introduced into the load profile of each house according to the normal distribution, with a mean value of 0 and a variance of 0.33. The annual electricity consumed by individual homes ranges between 3500 kWh and 4500 kWh (
Table 1). The hourly load profiles of the estate, from a one-year period, for tariffs G11 and G12 determined for the average value of energy consumed by the estate buildings during the year of 4036.8 kWh are presented in
Figure 1.
The tariffs indicated above and used in the rest of the article include averaged loads of individual recipients (data from thousands of households from the distribution network operator) of single-zone (G11) and dual-zone (G12). According to
Figure 1, the differences between the tariffs include the time shifts of the peak loads. Tariffs are, therefore, one of the elements that determine the optimal structure of the RESs generation system with an energy storage (PV section power, wind section power, energy storage capacity) obtained as part of the optimization. However, the article does not conduct research on the impact of changes in the receiving tariff on the operation of the generation system. In the case of the G12 tariff, a significant part of the peak loads are transferred to late evening and night hours, when the photovoltaic system is not operating. This may result in the need to significantly oversize the wind section or increase the energy storage capacity, depending on the type and power of the stacked wind turbines. Both actions result in an increase in investment expenditures and a shift in the payback period.
2.2. Model of the Generation System and Energy Storage
The power of the wind section and the photovoltaic and the power to charge/discharge the energy storage are determined for synchronized elements of the time series of wind speed (data from height 10 (meters above ground level), irradiation and ambient temperature collected as part of the NASA Prediction Of Worldwide Energy Resources project for locations in Poland. These data were obtained from the NASA Langley Research Center (LaRC) POWER project funded through the NASA Earth Science/Applied Science Program. The time step for the series is . The calculations of the average powers generated in both sections in periods t are carried out using the mathematical models of the components of the generating system and the energy storage described in the following.
The wind turbine is modeled using the power characteristic
that relates the output electrical power
to the wind speed
at the height of the rotor center
. The characteristic given in discrete form describes the turbine output powers given for total wind speed values most often in the range of 0 to 25 m/s. The power of the wind turbine
for the wind speed
corresponding to the element
t of the wind speed time series is determined by linear interpolation. The interpolation nodes are two successive points of the discrete power characteristic
and
, between which lies the considered speed
. The characteristic is then presented by the following relationship [
39]:
where
and
—wind turbine power values corresponding to wind speeds
and
;
—wind speed enabling the achievement of the rated power of the wind turbine
.
Wind speed values (time series elements (
t,
):
) obtained for a height of 10 (meters above ground level) are converted to the actual height of the turbine rotor center
according to the following exponential relationship [
38]:
where:
—wind speed converted (for the time series element
t) to the rotor center height (
;
—the wind speed (for the time series element
t) at the measurement height (
;
—the wind speed measurement height (
;
—coefficient related to the roughness (type) of the ground.
To determine the power of the PV section, a two-diode model of photovoltaic cells described by the relationships in [
40] was used:
where
—current and voltage on the PV cell terminals;
—solar current generated at the actual irradiance
and at the PV module surface temperature T;
—solar current generated at irradiance
;
—actual irradiance on the PV cell surface;
,
—saturation currents of the first and second diode;
,
—coefficients of quality of the first and second diode;
—series resistance;
—parallel resistance; k—Boltzmann constant; T—PV cell temperature; q—elementary charge.
Cell temperature
T—dependencies (
3) and (
4) depend on ambient temperature
, incident irradiation on its surface
, and wind speed
. These values, together with the method of module assembly, are related by the empirical formula presented in [
41] in the following form:
where
—ambient temperature (synchronized with irradiance and wind speed data) for element
t;
—irradiance on the surface of PV modules for element
t of the
;
series—wind speed at the height of the photovoltaic installation for element
t of the
;
series—coefficient of the PV system mounting method (
= 1—standalone system (
= 1.2—on a flat roof,
= 1.8—on a sloped roof).
The solution of the system of non-linear Equations (3)–(5) using the Newton–Raphson matrix method can be used to store the total maximum power generated by a single PV module for subsequent irradiances in the range of 50 W/m2 to 1500 W/m2 with a step of 50 W/m2 and subsequent module temperatures T in the range from −30 °C to 70 °C with step 5 °C. Based on the values of the matrix , using a two-dimensional approximation, the values are determined for the elements t of the time series of irradiance and module temperature.
The applied energy storage model includes energy dependencies, and its basic parameters are the energy capacity
, the maximum values of the currents of charging (
) and discharging (
) powers, the efficiency of energy conversion in the charge and discharge cycle
, the self-discharge process described by the power of non-load losses (
), and the allowed range of values
. The determination of the energy stored in storage takes place in periods
t, which are subsequent elements of the time series of synchronized input data
,
, and
. The energy at the moment
t is described by the following relationship:
where
—average power of the storage drawn from or returned to the network (in the output of the power electronics systems) for element
t of the time series;
—charging efficiency and discharge of the storage.
Additionally, for the elements of the generating system that require cooperation with inverters/rectifiers (storage, PV system, wind turbines), the models of the converter systems were reduced to their efficiency depending on the ratio of the system’s output power to their rated power.
2.3. Multi-Criteria Optimization
Most optimization problems that occur in real life have a multi-criteria nature. This means that the goal of the optimization is to satisfy more than one optimization criterion:
where
—a set of decision variables;
—a set of optimization criteria;
—a set of inequality constraints;
—a set of equality constraints.
In the case where these criteria are mutually contradictory, i.e., improving the value of one of the criteria is connected with worsening the conditions of another, obtaining an absolute best solution is not possible. On the other hand, it is right to say that the solution
is better than the solution
, then
where
—is an operator that generally means that the value of the criterion
for
is better than for
(lower in the case of minimization, and higher in the case of maximization of this criterion). Similarly, the operator ⊵ means that the value of the criterion considered on the left is not worse than on the right. In multi-criteria optimization, it is determined that the solution
dominates the solution
.
The goal of multi-criteria optimization is to find a single solution or a whole set of solutions that are not dominated by any other solutions in the feasible region. The set of all non-dominated solutions is the so-called Pareto front.
Two approaches are used to solve a multi-criteria problem: a priori and a posteriori. In the first approach, certain external factors (metadata) are assumed to be known, which determine the priority or weight of individual criteria. In this way, it is possible to obtain a single solution from the entire Pareto front. This solution is the best for the assumed external conditions. Methods in this group include methods such as linear scalarization [
42],
-constraint [
42], or Chebyshev scalarization [
43].
The a posteriori approach assumes that we first try to obtain a set of all possible solutions from the Pareto front, and from among them we select one based on an analysis of external factors, which can be determined after the initial selection of solutions. The second approach requires the use of optimization methods that allow the processing of many solutions simultaneously. Such methods include evolutionary algorithms such as non-dominated sorting genetic algorithm (NSGA-II) [
44], multi-objective particle swarm optimization (MPSO) [
45], and Strength Pareto Evolutionary Algorithm 2 (SPEA-2) [
46].
An additional advantage of using methods based on evolutionary algorithms is coping with the case when the optimization problem is non-linear and non-convex, and then there may be difficulties such as local Pareto fronts and the problem of finding solutions along non-convex fragments of the Pareto front [
2].
The NSGA-II method, which belongs to the group of evolutionary algorithms, was used to solve the problem presented. It is a multi-objective version of the genetic algorithm. During the selection process
N of individuals (solutions) that will be the basis for creating a new generation, a two-stage sorting is used [
44]:
Stage I: Solutions are sorted based on their non-dominance. For this purpose, individuals are grouped based on their non-dominance. Each group consists of individuals that are not dominated by each other, simultaneously dominated by an individual located in groups for and dominant over individuals located in groups for . Such a group of individuals is called the i-th front.
Stage II: Individuals located on the same front are sorted based on the distance to their nearest neighbor. This is the so-called crowding distance, determined on the basis of the Manhattan distance measure between neighboring individuals in the criteria space. First, individuals are selected on the basis of their affiliation with individual fronts. An individual from a lower front has priority over an individual from a higher front. In the case of individuals from the same front, the crowding distance is decisive. Individuals with a greater distance (more distant from neighbors) have priority over those who are more crowded together. Thanks to this, solutions are found along the entire length of the actual Pareto front.
The remaining genetic operators (crossover and mutation) are used in a similar way to the classic single-criterion genetic algorithm [
47].
2.4. AHP Method
The AHP (analytic hierarchy process) decision-making support method consists of breaking down complex problems into smaller ones and comparing them with each other, using preference comparison scales. As a result of such actions, a ranking is finally created for a finite set of known variants. The operation of the AHP algorithm is based on the implementation of the following steps [
10]:
- 1.
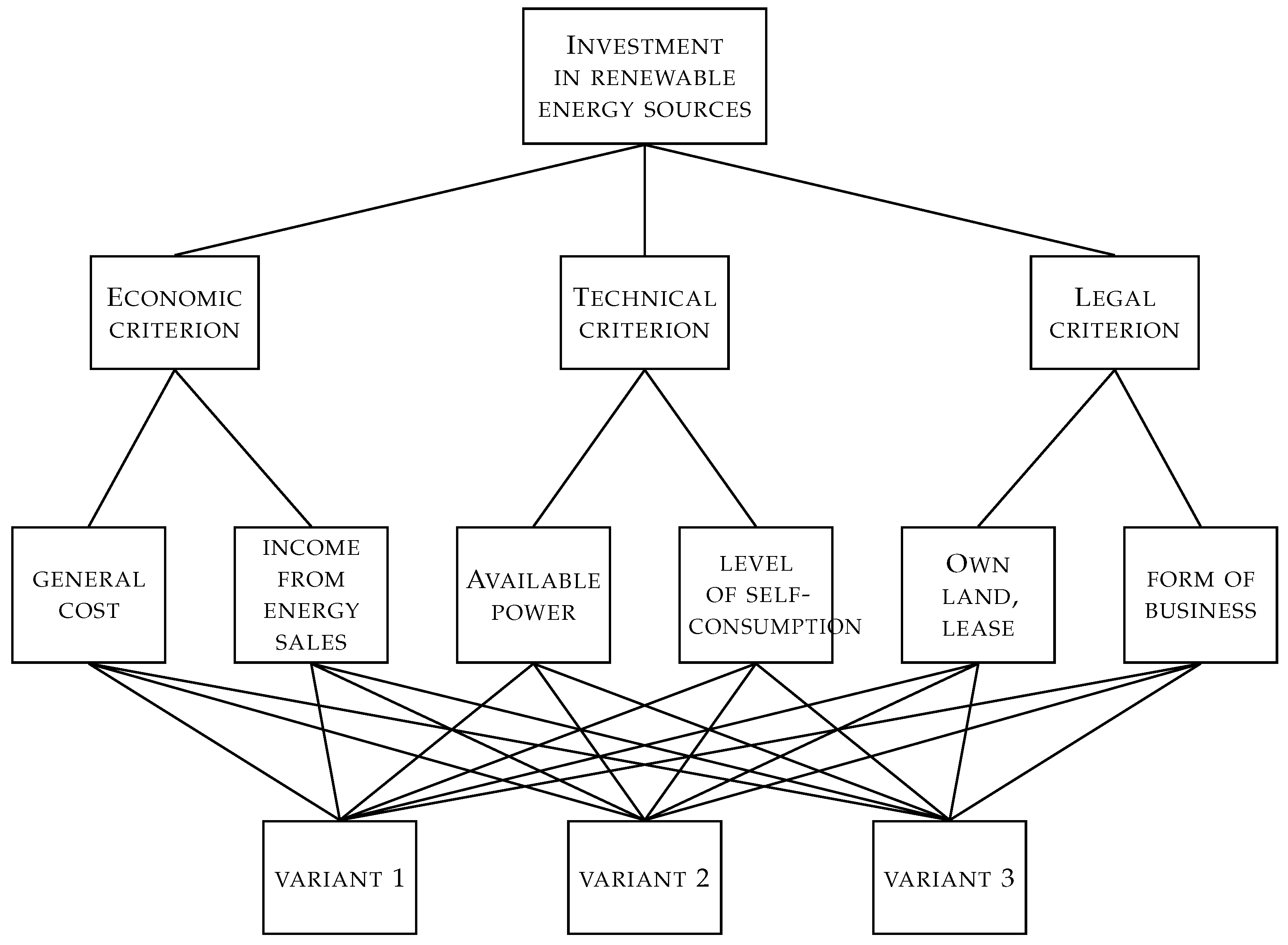
Creating a multi-level (at least three levels) hierarchical structure of the decision-making process (
Figure 2):
- (a)
Goal level, e.g., assessment of the investment location or type of investment for a given location.
- (b)
Criteria level (it is also possible to introduce lower-level criteria, but this is not mandatory), e.g., economic, technical, social, quantitative, and qualitative.
- (c)
Alternatives (variants) level, e.g., color, surface, and type of pavement.
- 2.
When creating a comparison matrix, where comparisons of preferences are made between elements in the hierarchy, using comparison scales, e.g., the Saaty scale (after making an assessment for individual pairs, the matrix should be transformed into a normalized synthetic form (the elements of the synthetic matrix are quotients of values from a given position of the matrix and the sum of values from a given column) and the elements of the importance vector should be determined), which contains ratings from 1 to 9.
- 3.
The consistency of the preference matrix is tested, where the ratings made in the comparison matrices are checked for logic and consistency. If the ratings are inconsistent, this may require correction of the ratings.
- 4.
Creating the final ranking.
- 5.
Sensitivity analysis (additional element that allows a detailed analysis of the impact of changes in the criteria values on the final ranking).
In practice, due to limited human perception, it is recommended that hierarchical structures do not exceed nine levels and that the number of variants is less than nine. An example of a four-level structure is shown in
Figure 2. In the AHP method, the criteria are independent of each other and constitute a separate evaluation path for individual variants [
10].
Table 2 includes the Saaty comparison scale, in which integer values from the set {1, 3, 5, 7, 9} are assigned a verbal interpretation regarding the evaluation of element A relative to B in terms of the preferences of the decision-makers.
The input data required to implement the algorithm are the values defined in the comparison matrix and they have a direct impact on the results of the analysis conducted. They are selected by decision-makers based on their substantive premises and\or subjective assessment. The comparison matrix is an inversely symmetrical matrix, and the elements lying on its diagonal are always the same. The general notation of the comparison matrix
is presented in Equation (
9):
After assessing the individual pairs, the matrix is transformed into a normalized synthetic form (the elements of the synthetic matrix are the quotients of the values from a given position of the matrix and the sum of the values from a given column), and then the elements of the importance vector are determined, which are the arithmetic means of the values from a given row and the number of rows:
An important stage of the analysis is to check the consistency of the comparison matrix, which allows us to check whether the decision-maker made any logical errors at the stage of its creation. Checking this condition requires determination of the maximum eigenvalue of the matrix
—
. If the value is close to the number of variants considered, it means that the consistency coefficient is appropriate. Its precise determination consists of first estimating the consistency index
(consistency index) described by the following relationship [
10]:
In the next step, the consistency index
(consistency ratio) is determined for the given criterion [
10]:
where
—random index dependent on the degree of the matrix. These values (
Table 3) were determined experimentally by T. Saaty [
10].
The value of the coefficient
is assumed to mean that the matrix is not coherent, which may indicate an illogical structure of the data estimated by the decision-maker, and the comparison results obtained may not be correct. Finally, the calculation of the final assessment for the
j-th variant, in order to develop the final ranking, is presented by the following relationship [
10]:
An additional stage introduced to the algorithm is the sensitivity analysis, which consists of determining the impact of changing individual elements in the hierarchy on the final result. The most commonly used approach consists of searching for the minimum values by which the weight of a given criterion should be changed to change the order of variants in the final ranking. We denote by
(for
and
) the smallest change of the current weight
of criterion
such that the order of variants
and
will change in the final ranking and
defines this value expressed as a percentage of weight
. The value of
can be determined from the following formulas:
or
where
—total score of
j-th variant;
—total score of
i-th variant;
—score of
j-th variant in the context of
k-th criterion;
—score of
i-th variant in the context of
k-th criterion;
—weight of
k-th criterion. The swap of variants is possible when the following condition is met: