Abstract
This paper concerns the application of the AHP (analytic hierarchy process) multi-criteria decision support method for the final selection of the structure of a hybrid power system with RESs (renewable energy sources) and EES (electrical energy storage) from a set of solutions obtained through multi-criteria optimization. These solutions, depending on their position within the Pareto front, may differ significantly in terms of the values of the criteria functions, or may be located very close to each other in the solution space. The role of the expert is to select the final solution, taking into account many additional criteria, often of a subjective nature. The article optimizes the structure of the proposed system using the multi-criteria NSGA-II (Non-dominated Sorting Genetic Algorithm) method, taking into account three technical criteria. The AHP method was used to select the final solution, which allows determination of the ranking of solution variants, taking into account selected additional criteria. In the analyzed case, these are primarily economic indicators, technical conditions, and preferences of the system recipients. In addition to determining the ranking of solutions, a sensitivity analysis was performed, which gives the expert extensive knowledge on the impact of individual criteria on the order of variants in the ranking. It was shown that in the case of selecting hybrid structures of generating systems with EES for a specific type of receiver, the use of the AHP method significantly facilitates making the final decision.
1. Introduction
Multi-criteria optimization tasks lead, for a certain group of applied methods, to a set of solutions equivalent to the so-called Pareto front [1,2]. Elements of such a set may lie very close to each other, and then it is problematic to make a decision on the selection of one final solution. Selecting the aforementioned solution is a particularly difficult task when, in addition to analytical criterion functions, a number of other parameters must be taken into account, which may be contradictory, cannot be described analytically, or are subjective in nature. Tasks defined in this way can be solved using a wide group of multi-criteria decision support methods, MCDA (Multi-Criteria Decision Aid), which includes the following methods [3,4,5]: analytical hierarchy, e.g., AHP (analytic hierarchy process), FAHP (fuzzy AHP), ANP (analytic network process); verbal, for example, ZAPROS (which means locked procedures close to reference situations) [6]; ELECTRE (ÉLimination Et Choix Traduisant la REalité, which means Elimination and Choice Translating Reality); and using reference points, e.g., TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) [7,8,9].
Among the listed methods, one of the frequently used ones, due to its low computational effort, transparent decision-making structure, and the quality of the obtained results, is the AHP method. Decision-making problems are presented in the form of a hierarchical structure. The highest layer is the decision goal, below that are the criteria, and the lowest structure is the decision variants. Based on pairwise comparisons of elements located at each level of the hierarchy, a weight matrix structure is created, which, after transformations, allows determination of the result in the form of a ranking of the variants considered [10,11].
The AHP method is widely used in decision making in the areas of politics, social affairs, and industry. In [12], they describe the application of AHP during the selection of the best subassembly contractor. For this purpose, a hierarchical structure of prequalified criteria was created for a group of five potential contractors, such as experience, quality of workmanship, financial stability, and human and physical resources. In the articles [13,14,15], the AHP method was used to select appropriate ICT solutions. In each case, a structure of criteria was used that was a response to the specific needs of the company (decision-maker) and the role (type) of the selected tools in the production process. The literature review conducted indicates that the AHP method is often used in issues related to renewable energy sources. One of them is supporting the selection of the location of RESs (renewable energy sources) (photovoltaic and wind farms of various sizes), taking into account various criteria of technical, economic, and social nature and information from GIS (Geographic Information Systems) [16,17,18,19,20,21,22].
It is also possible to use the AHP method to assess investments in RES generation systems in terms of jointly considered social and economic criteria. In one of the works [23], the value of the economic criterion is determined using the LCOE method (levelized cost of energy). Another work [24] indicates that the AHP method can be used to determine the management of the sustainable development of the supply chain in the renewable energy sector, taking into account the triple bottom line (TBL) principle: the management not only of traditional financial and economic indicators, but also social and environmental factors.
In the case of particularly complex multi-criteria decision-making tasks, it is advisable to combine the AHP method with other methods, e.g., those using reference points or using methods that are modifications of AHP. Hybrid methods, for example, AHP + TOPSIS [25], AHP + VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje, meaning Multicriteria Optimization and Compromise Solution) [26], or extended AHP methods (FAHP, ANP) [27,28] are particularly interesting from this perspective.
The first of the extended AHP methods is based on the theory of fuzzy sets [29,30]. In many cases, obtaining point values is impractical and often impossible. The use of fuzzy sets allows decision-makers to express interval decisions, which is much easier than making judgments with fixed-point values. Fuzzy techniques can be seen here as a generalized form of interval analysis for handling uncertain information, resulting in greater flexibility in dealing with differences in decision-makers’ assessments. An example of the application of this approach is the work [31], covering the assessment of risk (based on expert judgments, often characterized by indecisiveness and cognitive bias) of investing in renewable energy sources.
The ANP method, unlike the AHP, does not make assumptions related to the independence of higher-level elements from lower-level elements and the independence of elements within one level. The method does not impose the definition of levels, which allows taking into account both interactions and feedback within the analyzed elements [10,32]. An example of the use of the ANP method together with information from the GIS system is the work [33], which seeks a suitable map of wind farm locations, taking into account the minimization of negative environmental, economic, and social effects of their construction. For the task of selecting the structure of a hybrid generation system with RESs and EES (electrical energy storage), solved in this paper, the geographical location is explicitly indicated and characterized by sets of input data of wind speed, irradiance, and ambient temperature. Therefore, to solve it, it is not necessary to combine the AHP method with data from GIS systems. The use of hybrid methods or FAHP and ANP is not necessary, because the multi-criteria decision-making algorithm uses a set of solutions resulting from the multi-criteria optimization procedure. Therefore, in the later part of this paper, the AHP method is used to make the final decision regarding the selection of the structure of the hybrid power supply system with RESs and energy storage.
An analysis of the available literature shows that there are studies related to the use of combined multi-criteria optimization methods and AHP [34,35,36,37], but they do not directly concern issues related to RES. This approach is a novelty in relation to the research currently conducted on the selection of hybrid RES installations. The proposed approach can significantly facilitate the final decision within the framework of ongoing RES investments, while taking into account the opinion of the local community, which is the largest beneficiary of the construction of such facilities while having to accept the negative effects of their existence.
The manuscript is organized in the following way. First, the justification for the selection of the object for analysis is presented and the methods used for calculations within the multi-criteria optimization and the AHP algorithm are characterized. The next section presents the results of calculations based on both methods, along with a detailed discussion of the results of the sensitivity analysis (AHP). The manuscript ends with a summary that contains the most important conclusions regarding the proposed hybrid method of RES installation selection.
2. Materials and Methods
2.1. Description and Characteristics of the Object
The analyzed object is a hybrid generation system consisting of a photovoltaic section with a rated power of , a wind section with a rated power of turbines , and a lithium-ion energy storage EES with a rated energy capacity of intended to support the power supply of a housing estate of 20 single-family houses. The generation system and the storage are located in the area of the provided housing estate, and all houses are connected to the low-voltage distribution network.
The choice of the facility is primarily due to the increasing role of distributed RESs in national power systems. The issues of their positive impact on local balancing of electricity, the possibility of controlling the production profile by using opposing sources (PV and wind turbines) and energy storage facilities, as well as the diversification of energy supplies, which is so important for the country’s energy security, are increasingly raised. Another reason for choosing the facility analyzed is the previous research that the authors conducted on hybrid systems intended to power single-family housing estates, taking into account the impact of the development of electromobility on the economic profitability of the indicated installations. It was shown there that even in the absence of electric vehicles, the use of optimized structures of a hybrid system with RES and an energy storage facility in the scope of supporting the power supply of these types of recipients is economically justified—it pays off within a period of several to 10 years (depending on the configuration of the system, mainly on the energy capacity of the energy storage facility) [38]. The indicated aspects and the pro-ecological nature of this type of solution indicate the future dissemination of such systems, provided, however, that collective prosumers (prosumer cooperatives) are taken into account in the legal provisions of distribution companies.
The total electrical load of the housing estate is the sum of the loads of individual houses. This article analyzes two cases covering the load of houses in accordance with the single-zone tariff G11 (variant I) and the two-zone tariff G12 (variant II) of the Polish electricity distributor—ENEA Operator. A random disturbance was introduced into the load profile of each house according to the normal distribution, with a mean value of 0 and a variance of 0.33. The annual electricity consumed by individual homes ranges between 3500 kWh and 4500 kWh (Table 1). The hourly load profiles of the estate, from a one-year period, for tariffs G11 and G12 determined for the average value of energy consumed by the estate buildings during the year of 4036.8 kWh are presented in Figure 1.

Table 1.
Energy consumption data for estate of 20 single-family houses: —consumer annual energy.
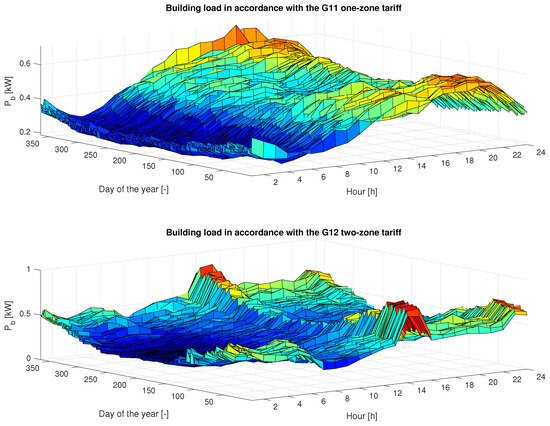
Figure 1.
Daily power distribution for the house according to the tariff: G11 (top), G12 (bottom).
The tariffs indicated above and used in the rest of the article include averaged loads of individual recipients (data from thousands of households from the distribution network operator) of single-zone (G11) and dual-zone (G12). According to Figure 1, the differences between the tariffs include the time shifts of the peak loads. Tariffs are, therefore, one of the elements that determine the optimal structure of the RESs generation system with an energy storage (PV section power, wind section power, energy storage capacity) obtained as part of the optimization. However, the article does not conduct research on the impact of changes in the receiving tariff on the operation of the generation system. In the case of the G12 tariff, a significant part of the peak loads are transferred to late evening and night hours, when the photovoltaic system is not operating. This may result in the need to significantly oversize the wind section or increase the energy storage capacity, depending on the type and power of the stacked wind turbines. Both actions result in an increase in investment expenditures and a shift in the payback period.
2.2. Model of the Generation System and Energy Storage
The power of the wind section and the photovoltaic and the power to charge/discharge the energy storage are determined for synchronized elements of the time series of wind speed (data from height 10 (meters above ground level), irradiation and ambient temperature collected as part of the NASA Prediction Of Worldwide Energy Resources project for locations in Poland. These data were obtained from the NASA Langley Research Center (LaRC) POWER project funded through the NASA Earth Science/Applied Science Program. The time step for the series is . The calculations of the average powers generated in both sections in periods t are carried out using the mathematical models of the components of the generating system and the energy storage described in the following.
The wind turbine is modeled using the power characteristic that relates the output electrical power to the wind speed at the height of the rotor center . The characteristic given in discrete form describes the turbine output powers given for total wind speed values most often in the range of 0 to 25 m/s. The power of the wind turbine for the wind speed corresponding to the element t of the wind speed time series is determined by linear interpolation. The interpolation nodes are two successive points of the discrete power characteristic and , between which lies the considered speed . The characteristic is then presented by the following relationship [39]:
where and —wind turbine power values corresponding to wind speeds and ; —wind speed enabling the achievement of the rated power of the wind turbine .
Wind speed values (time series elements (t, ): ) obtained for a height of 10 (meters above ground level) are converted to the actual height of the turbine rotor center according to the following exponential relationship [38]:
where: —wind speed converted (for the time series element t) to the rotor center height (; —the wind speed (for the time series element t) at the measurement height (; —the wind speed measurement height (; —coefficient related to the roughness (type) of the ground.
To determine the power of the PV section, a two-diode model of photovoltaic cells described by the relationships in [40] was used:
where —current and voltage on the PV cell terminals; —solar current generated at the actual irradiance and at the PV module surface temperature T; —solar current generated at irradiance ; —actual irradiance on the PV cell surface; , —saturation currents of the first and second diode; , —coefficients of quality of the first and second diode; —series resistance; —parallel resistance; k—Boltzmann constant; T—PV cell temperature; q—elementary charge.
Cell temperature T—dependencies (3) and (4) depend on ambient temperature , incident irradiation on its surface , and wind speed . These values, together with the method of module assembly, are related by the empirical formula presented in [41] in the following form:
where —ambient temperature (synchronized with irradiance and wind speed data) for element t; —irradiance on the surface of PV modules for element t of the ; series—wind speed at the height of the photovoltaic installation for element t of the ; series—coefficient of the PV system mounting method ( = 1—standalone system ( = 1.2—on a flat roof, = 1.8—on a sloped roof).
The solution of the system of non-linear Equations (3)–(5) using the Newton–Raphson matrix method can be used to store the total maximum power generated by a single PV module for subsequent irradiances in the range of 50 W/m2 to 1500 W/m2 with a step of 50 W/m2 and subsequent module temperatures T in the range from −30 °C to 70 °C with step 5 °C. Based on the values of the matrix , using a two-dimensional approximation, the values are determined for the elements t of the time series of irradiance and module temperature.
The applied energy storage model includes energy dependencies, and its basic parameters are the energy capacity , the maximum values of the currents of charging () and discharging () powers, the efficiency of energy conversion in the charge and discharge cycle , the self-discharge process described by the power of non-load losses (), and the allowed range of values . The determination of the energy stored in storage takes place in periods t, which are subsequent elements of the time series of synchronized input data , , and . The energy at the moment t is described by the following relationship:
where —average power of the storage drawn from or returned to the network (in the output of the power electronics systems) for element t of the time series; —charging efficiency and discharge of the storage.
Additionally, for the elements of the generating system that require cooperation with inverters/rectifiers (storage, PV system, wind turbines), the models of the converter systems were reduced to their efficiency depending on the ratio of the system’s output power to their rated power.
2.3. Multi-Criteria Optimization
Most optimization problems that occur in real life have a multi-criteria nature. This means that the goal of the optimization is to satisfy more than one optimization criterion:
where —a set of decision variables; —a set of optimization criteria; —a set of inequality constraints; —a set of equality constraints.
In the case where these criteria are mutually contradictory, i.e., improving the value of one of the criteria is connected with worsening the conditions of another, obtaining an absolute best solution is not possible. On the other hand, it is right to say that the solution is better than the solution , then
where —is an operator that generally means that the value of the criterion for is better than for (lower in the case of minimization, and higher in the case of maximization of this criterion). Similarly, the operator ⊵ means that the value of the criterion considered on the left is not worse than on the right. In multi-criteria optimization, it is determined that the solution dominates the solution .
The goal of multi-criteria optimization is to find a single solution or a whole set of solutions that are not dominated by any other solutions in the feasible region. The set of all non-dominated solutions is the so-called Pareto front.
Two approaches are used to solve a multi-criteria problem: a priori and a posteriori. In the first approach, certain external factors (metadata) are assumed to be known, which determine the priority or weight of individual criteria. In this way, it is possible to obtain a single solution from the entire Pareto front. This solution is the best for the assumed external conditions. Methods in this group include methods such as linear scalarization [42], -constraint [42], or Chebyshev scalarization [43].
The a posteriori approach assumes that we first try to obtain a set of all possible solutions from the Pareto front, and from among them we select one based on an analysis of external factors, which can be determined after the initial selection of solutions. The second approach requires the use of optimization methods that allow the processing of many solutions simultaneously. Such methods include evolutionary algorithms such as non-dominated sorting genetic algorithm (NSGA-II) [44], multi-objective particle swarm optimization (MPSO) [45], and Strength Pareto Evolutionary Algorithm 2 (SPEA-2) [46].
An additional advantage of using methods based on evolutionary algorithms is coping with the case when the optimization problem is non-linear and non-convex, and then there may be difficulties such as local Pareto fronts and the problem of finding solutions along non-convex fragments of the Pareto front [2].
The NSGA-II method, which belongs to the group of evolutionary algorithms, was used to solve the problem presented. It is a multi-objective version of the genetic algorithm. During the selection process N of individuals (solutions) that will be the basis for creating a new generation, a two-stage sorting is used [44]:
- Stage I: Solutions are sorted based on their non-dominance. For this purpose, individuals are grouped based on their non-dominance. Each group consists of individuals that are not dominated by each other, simultaneously dominated by an individual located in groups for and dominant over individuals located in groups for . Such a group of individuals is called the i-th front.
- Stage II: Individuals located on the same front are sorted based on the distance to their nearest neighbor. This is the so-called crowding distance, determined on the basis of the Manhattan distance measure between neighboring individuals in the criteria space. First, individuals are selected on the basis of their affiliation with individual fronts. An individual from a lower front has priority over an individual from a higher front. In the case of individuals from the same front, the crowding distance is decisive. Individuals with a greater distance (more distant from neighbors) have priority over those who are more crowded together. Thanks to this, solutions are found along the entire length of the actual Pareto front.
The remaining genetic operators (crossover and mutation) are used in a similar way to the classic single-criterion genetic algorithm [47].
2.4. AHP Method
The AHP (analytic hierarchy process) decision-making support method consists of breaking down complex problems into smaller ones and comparing them with each other, using preference comparison scales. As a result of such actions, a ranking is finally created for a finite set of known variants. The operation of the AHP algorithm is based on the implementation of the following steps [10]:
- 1.
- Creating a multi-level (at least three levels) hierarchical structure of the decision-making process (Figure 2):
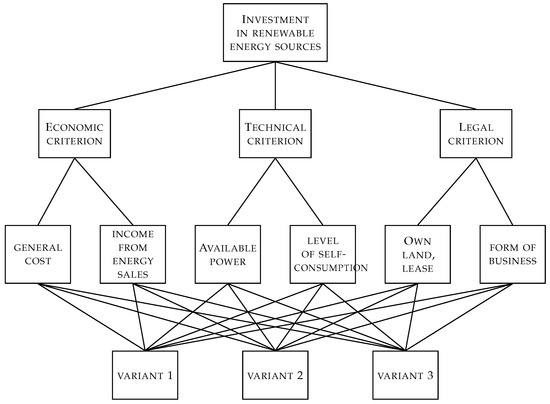 Figure 2. Example of a four-level hierarchical structure of the decision-making process for the problem of assessing the location for RES installations, consisting of ranking three variants assessed against three main criteria and two subcriteria.
Figure 2. Example of a four-level hierarchical structure of the decision-making process for the problem of assessing the location for RES installations, consisting of ranking three variants assessed against three main criteria and two subcriteria.- (a)
- Goal level, e.g., assessment of the investment location or type of investment for a given location.
- (b)
- Criteria level (it is also possible to introduce lower-level criteria, but this is not mandatory), e.g., economic, technical, social, quantitative, and qualitative.
- (c)
- Alternatives (variants) level, e.g., color, surface, and type of pavement.
- 2.
- When creating a comparison matrix, where comparisons of preferences are made between elements in the hierarchy, using comparison scales, e.g., the Saaty scale (after making an assessment for individual pairs, the matrix should be transformed into a normalized synthetic form (the elements of the synthetic matrix are quotients of values from a given position of the matrix and the sum of values from a given column) and the elements of the importance vector should be determined), which contains ratings from 1 to 9.
- 3.
- The consistency of the preference matrix is tested, where the ratings made in the comparison matrices are checked for logic and consistency. If the ratings are inconsistent, this may require correction of the ratings.
- 4.
- Creating the final ranking.
- 5.
- Sensitivity analysis (additional element that allows a detailed analysis of the impact of changes in the criteria values on the final ranking).
In practice, due to limited human perception, it is recommended that hierarchical structures do not exceed nine levels and that the number of variants is less than nine. An example of a four-level structure is shown in Figure 2. In the AHP method, the criteria are independent of each other and constitute a separate evaluation path for individual variants [10].
Table 2 includes the Saaty comparison scale, in which integer values from the set {1, 3, 5, 7, 9} are assigned a verbal interpretation regarding the evaluation of element A relative to B in terms of the preferences of the decision-makers.

Table 2.
T. Saaty’s scale of comparisons [10].
The input data required to implement the algorithm are the values defined in the comparison matrix and they have a direct impact on the results of the analysis conducted. They are selected by decision-makers based on their substantive premises and\or subjective assessment. The comparison matrix is an inversely symmetrical matrix, and the elements lying on its diagonal are always the same. The general notation of the comparison matrix is presented in Equation (9):
After assessing the individual pairs, the matrix is transformed into a normalized synthetic form (the elements of the synthetic matrix are the quotients of the values from a given position of the matrix and the sum of the values from a given column), and then the elements of the importance vector are determined, which are the arithmetic means of the values from a given row and the number of rows:
An important stage of the analysis is to check the consistency of the comparison matrix, which allows us to check whether the decision-maker made any logical errors at the stage of its creation. Checking this condition requires determination of the maximum eigenvalue of the matrix —. If the value is close to the number of variants considered, it means that the consistency coefficient is appropriate. Its precise determination consists of first estimating the consistency index (consistency index) described by the following relationship [10]:
In the next step, the consistency index (consistency ratio) is determined for the given criterion [10]:
where —random index dependent on the degree of the matrix. These values (Table 3) were determined experimentally by T. Saaty [10].

Table 3.
Saaty’s random indices as a function of the number of considered variants .
The value of the coefficient is assumed to mean that the matrix is not coherent, which may indicate an illogical structure of the data estimated by the decision-maker, and the comparison results obtained may not be correct. Finally, the calculation of the final assessment for the j-th variant, in order to develop the final ranking, is presented by the following relationship [10]:
An additional stage introduced to the algorithm is the sensitivity analysis, which consists of determining the impact of changing individual elements in the hierarchy on the final result. The most commonly used approach consists of searching for the minimum values by which the weight of a given criterion should be changed to change the order of variants in the final ranking. We denote by (for and ) the smallest change of the current weight of criterion such that the order of variants and will change in the final ranking and defines this value expressed as a percentage of weight . The value of can be determined from the following formulas:
or
where —total score of j-th variant; —total score of i-th variant; —score of j-th variant in the context of k-th criterion; —score of i-th variant in the context of k-th criterion; —weight of k-th criterion. The swap of variants is possible when the following condition is met:
3. Results
3.1. Multi-Criteria Optimization of the Structure of a Hybrid Power Supply System
The selection of the structure of a hybrid power supply system with RESs and energy storage that functions as an element that supports the maintenance of power continuity in a single-family housing estate is a complex and ambiguous task (synthesis task). Determining the basic parameters of such a system (total power, shares of PV and wind section power, energy storage capacity) is often dependent not on one, but on several mutually exclusive criteria of a technical and economic nature (e.g., investment cost, NPV value in the last year of operation, self-consumption coefficient, course of the electrical load of receivers). Taking the above into account, one of the methods of synthesizing hybrid power supply systems is the use of multi-criteria optimization. In the case of the analyzed problem, one of the heuristic methods was used to solve this task—NSGA-II (Section 2.3).
The vector of decision variables includes the following parameters: the ratio of the photovoltaic section power to the total power of the system, the total power of the generation system, and the energy capacity of the energy storage. Based on the determined annual energy demand for the analyzed housing estate, the ranges of individual variables were determined: , kW, kWh.
The multi-criteria objective function was used for the investigation, taking into account the following criteria resulting from the pragmatic premises of the operation and construction of a hybrid power supply system with RES and energy storage:
- Maximization of the self-consumption coefficient (minimization of the transmission of energy generated in RESs to the grid) .
- Minimization of the energy capacity of the energy storage (reduction of the investment cost) .
- Minimization of the annual deviation of the power of the generating system’s production profile and the receiver’s load profile (matching the generation and load profiles) () .
The self-consumption coefficient is defined as the quotient of energy consumed in the receivers of the analyzed object and produced in its own generation system to the total energy produced in the aforementioned system. High values of the indicator mean direct consumption of a significant part of the energy produced in the hybrid system, without discharging it to the power system. The improvement of the indicator is guaranteed by the energy storage used in the system, which, however, significantly increases the investment and operating costs of the system. Additionally, the indicator cannot be the only criterion for optimizing generation systems, because the value of 100% can be obtained by installing an RES system with very low power in relation to the power required to cover demand. For actual values, that is, below 100%, discharging part of the energy to the power system and its subsequent collection is associated with a financial loss resulting from the negative difference between the energy sales price and its purchase price.
The annual deviation of the power of the generating system profile and the load profile of the receiver is determined based on the following relationship:
where —load power; —power generated by RESs and obtained from energy storage.
The value of the indicator determines the level of matching of the power generated in the RES system and the demand (load) over a period of one year. The value of 0 means that the generation and load curves are covered. Differences between the load and generated power (both positive and negative) increase the value of the indicator. In the case of a shortage of generated power, the value of the indicator can be reduced by using energy storage. The indicator cannot be used as the only criterion for optimizing the structure of hybrid generation systems with RESs, because it can lead to very high RES system capacities and large energy storage capacities, and, consequently, to the economic unprofitability of the system.
For the defined objective function , using the NSGA-II method, the structure of the hybrid power supply system was optimized that supports the supply of energy to the analyzed housing estate. Calculations were performed separately for the electric load according to the single-zone tariff G11 (variant I) and the two-zone tariff G12 (variant II)—Figure 1. Figure 3 and Figure 4 present solutions found by the NSGA-II method as points described in the criteria space (respectively, , , and ). Each point represents a single solution (installation of hybrid RES and energy storage), which, through the analysis presented in the section, gives specific values of the criteria considered (position in the criteria space). Each of the solutions belonging to the Pareto front is a proportion of individual elements of the system, that is, resources (production sources and storage capacity), which provide an optimal mix of the values of the criteria considered with different weights. The size of the front and the location of the solutions on the Pareto front (slight differences in the values of individual criteria) cause the decision-maker to have objective problems in choosing the final solution. For this reason, this choice, taking into account additional criteria (often subjective) that are difficult to include in the optimization parameters, should be supported by multi-criteria decision-making methods, and not only by experience. In the next chapter, based on selected Pareto-optimal solutions (commonly for variants I and II, i.e., load G11 and G12), a detailed analysis of the selected solutions is performed using the AHP method.
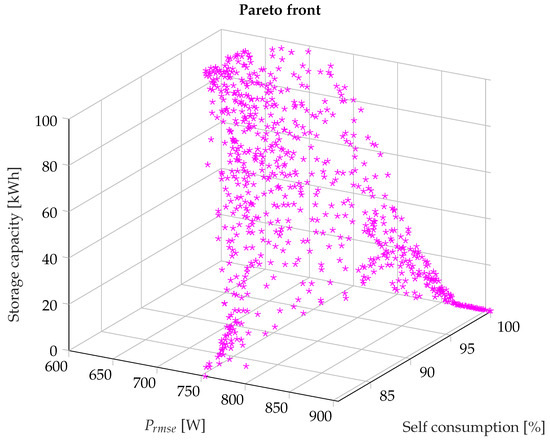
Figure 3.
Optimization results (Pareto front) of the structure of the hybrid RES system with energy storage for the G11 tariff.
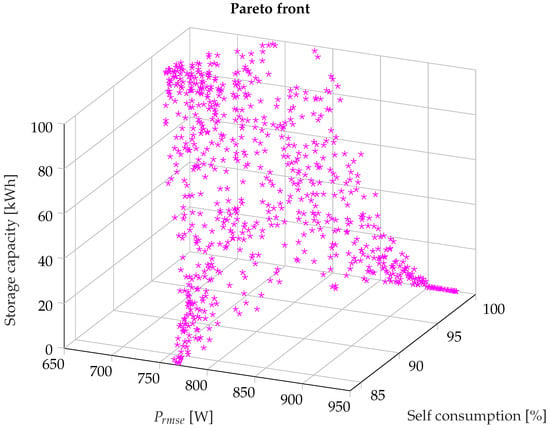
Figure 4.
Optimization results (Pareto front) of the structure of the hybrid RES system with energy storage for the G12 tariff.
3.2. Hierarchical Structure of the Decision-Making Process
The use of the AHP method requires defininition of the hierarchical structure of the decision-making process. In the analyzed task, a three-layer structure is adopted. The first layer consists of solution variants, including selected solutions obtained through multi-criteria optimization of the structure of the hybrid power supply system with RESs and energy storage for the analyzed housing estate.
Among many solutions obtained through optimization, four were selected for analysis purposes using the AHP method, characterized by the best results in terms of profit and annual electricity coverage (AEB) from both calculation variants, that is, for tariffs G11 and G12 (Table 4). Each of them is described by a set of data that includes characteristic parameters identifying the system in subsequent columns: power of photovoltaic modules (), power of wind turbines (), energy capacity of energy storage (kWh), self-consumption coefficient (%), annual average deviation of the generation profile of the generation system and the load profile of the receiver (W), annual energy balance (kWh), investment cost (PLN), and profit after 25 years (PLN). These parameters were selected for two reasons: they sufficiently describe a specific installation (its characteristics, technical capabilities, and economic parameters) and are understandable from the point of view of potential investors who will make decisions (prepare weights for individual criteria, e.g., based on surveys).

Table 4.
Table of optimization problem solutions selected for comparison.
In order to determine the final ranking of selected solutions obtained in the multi-criteria optimization process, five criteria were distinguished for the AHP method:
- The value of the annual coverage of the demand for electricity of the AEB estate (annual energy balance) determined as the difference between the energy demand and the energy generated in the RES system—a positive value means energy deficit, and a negative value means overproduction).
- The investment cost of the RES installation with an energy storage.
- The discounted profit achieved after 25 years of use of the installation (calculations using the NPV method).
- The power of photovoltaic modules.
- The power of wind turbines.
The last two criteria are related to social and environmental preferences.
Calculations of the profit achieved after 25 years from individual generation systems (Table 4) were determined using the NPV method for a discount rate of 5% adopted on the basis of the analysis of rates for countries in the European Union provided on the websites of the European Commission [48].
3.3. Basic Analysis of AHP Results
The ranking of variants (Table 5) for the established criteria was determined using the Super Decisions (ver 3.2.0 rev. 3197) software [49]. The research was carried out for three different comparison matrices (Table 6, Table 7 and Table 8) that reflect three cases of decision-maker preferences:

Table 5.
Final ranking of variants.

Table 6.
Comparison matrix for Case 1 (cost priority).

Table 7.
Comparison matrix for Case 2 (AEB priority).

Table 8.
Comparison matrix for Case 3 (AEB, profit, and solar power priority).
- The most important is the cost related to the investment (Case 1);
- The most important is the level of coverage of the annual demand for electricity (AEB) (Case 2);
- The most important are AEB, profit, and the advantage of the power of photovoltaic panels over the power of wind turbines (Case 3).
The results of the final ranking (Table 5) are values normalized to 1, which allows a clear presentation of the distribution of individual places in the ranking. The best results for individual cases are marked in green.
The analysis carried out showed that as the preferences of decision-makers changed, the final ranking also changed. Each time, a different variant achieved the highest score. This made it possible to select an installation consistent with the preferences of the people deciding on the implementation of the investment. For cases 1 and 2 in Table 5, the most clear advantage of the winning variants was achieved. Case 3 is characterized by the smallest differences in the assessment of all installations. This is directly related to the weights assigned to the parameters for individual cases. Cases 1 and 2 have a strong preference for one parameter, while the weights in Case 3 are distributed more evenly. Despite this, it was possible to indicate the variant with the best fit. Direct achievement of a similar result within multi-criteria optimization methods is difficult due to the large number of potential “equivalent” results. The use of a ranking based on the AHP method also provides the possibility of influencing the decision by conducting surveys among residents. A huge advantage of using a ranking based on the AHP method is the speed of decision-making. In the case of a large amount of data, it is not necessary to create additional algorithms or perform additional analysis of individual cases. The most important stage of the entire process is the selection of appropriate criteria and assigning them weights based on the opinion of decision-makers.
3.4. Sensitivity Analysis of Solutions
The AHP method (implemented in the Super Decisions (ver 3.2.0 rev. 3197) software) allows sensitivity analysis to be performed. The impact of changes in the priority of a given criterion on the final ranking of the variants analyzed is presented graphically and numerically. Figure 5, Figure 6 and Figure 7 present a sensitivity analysis for changes in the AEB criteria, the power of the photovoltaic module section , and the power of the wind turbine section for Case 1. It was shown that in this case, in addition to variant 4, which has the lowest investment cost, it is also possible to achieve the first position by the other installations analyzed. The lowest probability of obtaining the highest position concerns variant 2.
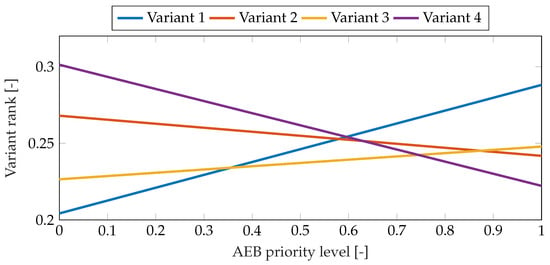
Figure 5.
Results of sensitivity analysis for AEB priority level change for Case 1.
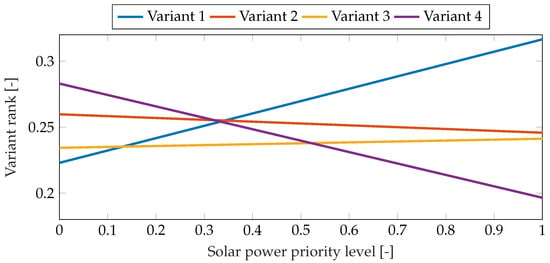
Figure 6.
Results of sensitivity analysis for solar power priority level change for Case 1.
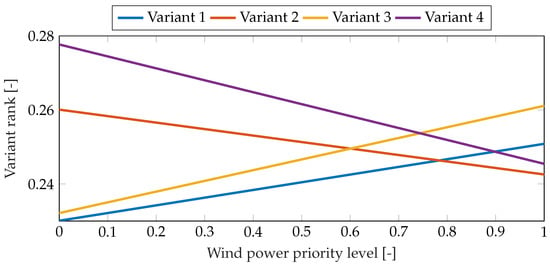
Figure 7.
Results of sensitivity analysis for wind power priority level change for Case 1.
For Case 2, the results of the sensitivity analysis are presented in Figure 8, Figure 9 and Figure 10. Three criteria were selected for the sensitivity assessment: analysis of changes in the weight of the investment cost, profit, and the power of the photovoltaic module section . They clearly indicate that due to the significant preference related to the largest possible coverage of electricity demand (AEB), variant 1 remains in first place in the ranking throughout the entire range of priority changes of this criterion. However, in the case of modification of the values of other criteria, it is possible to achieve the best result using other variants. A particularly interesting case concerns variant 4, whose AEB value is the highest, but its low initial cost and the related profit mean that small changes in favor of these two criteria will clearly increase the position of variant 4 in the final ranking. This variant is also interesting because it has the lowest power of the photovoltaic module section, and in this case it will be clearly preferred in the case where the decision-maker increases the weight assigned to the power of the wind turbine section.
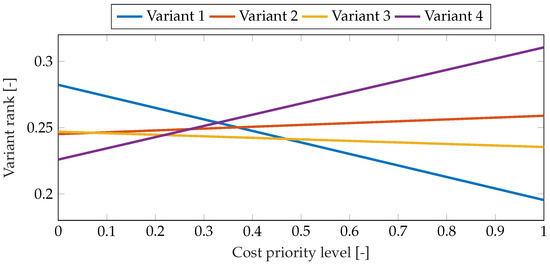
Figure 8.
Results of sensitivity analysis for cost priority level change for Case 2.
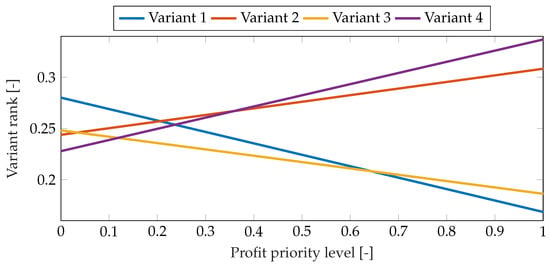
Figure 9.
Results of sensitivity analysis for profit priority level change for Case 2.
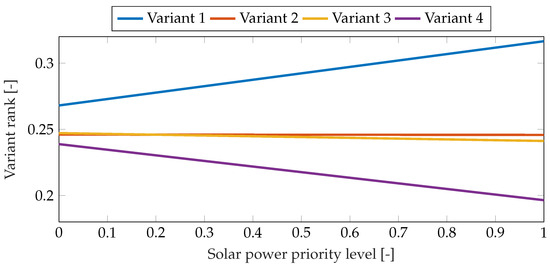
Figure 10.
Results of sensitivity analysis for solar power priority level change for Case 2.
The results of the sensitivity analysis for Case 3 are presented in Figure 11, Figure 12 and Figure 13. The impact of changes in the weights of three criteria was assessed: AEB, profit, and power of the wind turbine section . The final results for the individual variants are much closer to each other than in the other cases. Each variant has a chance to win, and even small changes in individual criteria can lead to a significant reshuffling of the final ranking. This is mainly due to a more proportional distribution of the weights in the comparison matrix (Table 8) between the individual criteria. In this case, the final ranking is not unambiguous and, as has been shown, is susceptible to small changes in the decision-makers’ approach.
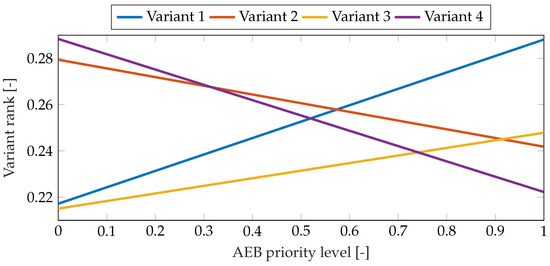
Figure 11.
Results of sensitivity analysis for AEB priority level change for Case 3.
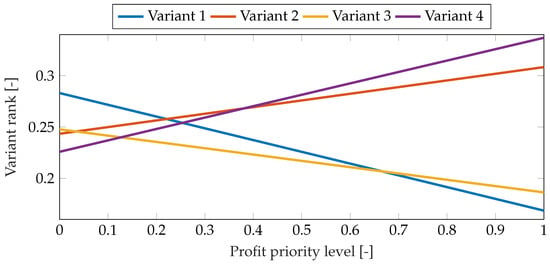
Figure 12.
Results of sensitivity analysis for profit priority level change for Case 3.
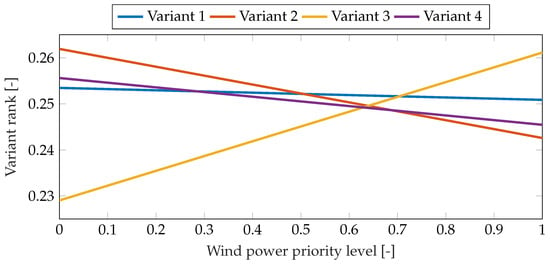
Figure 13.
Results of sensitivity analysis for wind power priority level change for Case 3.
4. Conclusions
The method of staged search (stage I—multi-criteria optimization, stage II—selection of the final solution using the AHP multi-criteria decision support method) for the optimal structure of a hybrid RES generation system with an energy storage designed to support the power supply of a single-family housing estate, used in the article allowed for the following:
- Inclusion in the decision-making process of criteria, the inclusion of which in the multi-criteria optimization task makes it difficult to interpret the results (too many criteria cause a significant expansion of the Pareto front).
- Inclusion in the analysis of subjective criteria and criteria of a socio-legal nature (e.g., issues of preferences for the selection of types of RESs by the residents of the estate, areas covered by bans on the use of wind turbines, local development plan).
- Analysis of a initially limited set of solutions characterized by correct technical structure of the hybrid generation system.
- Increase in the universality of the calculation tool, due to the lack of necessity to modify the optimization algorithm each time.
From among many (often hundreds) solutions of the multi-criteria optimization task of the structure of a hybrid generation system with RESs and energy storage, the decision-maker can select a set of system configurations with features that are particularly interesting from a technical point of view. In the indicated set, the differences between the values of the adopted criteria are often small (Figure 3 and Figure 4), but the structures of the systems (power, storage capacity) may differ significantly. In such cases, the use of the AHP method is the most effective and allows the inclusion of additional conditions in the decision-making process which is an important advantage of this approach. This is often achieved by using the concept of the triple bottom line (TBL) related to the joint management of social, environmental (or ecological), and economic indicators—people, planet, and profit. In the current socio-economic situation of the world, the TBL concept is one of the most important directions of action in the areas of designing and implementing technical systems that achieve a balance between the development of civilization (including increased electricity generation) and care for the future of humanity, including ecology, while taking into account the requirements of the quality of human life.
The main goal of installing generation systems is not always to achieve maximum profit. This approach is particularly visible in countries of the European Union, where the main goal is currently to reduce carbon dioxide emissions into the atmosphere. This forces maximization of energy demand coverage from RES systems, which, as has been shown, does not exist hand in hand with the profit achieved.
Local communities are increasingly influencing the preferences for the construction of RES installations. Wind turbines are often associated with increased burden for residents due to noise generation and greater impact on the landscape surrounding residential buildings. In other areas, photovoltaic modules, which require larger areas for installation, may be a worse solution for the local community. In this case, the AHP method works very well and allows the selection of a solution that best suits the preferences of decision-makers. The development of results in the form of a final ranking of variants significantly facilitates the decision-maker’s final decision; in addition, the structure of the RES generation system supports the power supply of the group of individual recipients.
In the analyzed example, the variants compared using the AHP method (Table 4) in terms of two optimization criteria (indicators and ) are characterized by similar values. The differences range from 0.5% to 3% and from 4% to 11%, respectively. Making a final decision on the selection of a specific variant on this basis, taking into account other criteria, is risky. The results of the AHP analysis in the form of a variant ranking (Table 5) indicate, in some cases, a stronger differentiation of solutions, resulting in an easier final choice.
The conducted research shows that in undersized generation systems, where it is important to limit investment costs or maximize profit, increasing the capacity of the energy storage leads to large losses in terms of profit achieved after 25 years of system operation with a relatively small improvement (increase in value) of the self-consumption coefficient (only a few percent). The sensitivity analysis performed showed that in certain ranges of changes in priority value, the final ranking may be significantly changed. This applies especially to cases where there are significant differences between the parameters of individual variants. In the analyzed case, it was primarily the profit obtained after 25 years of operation, the investment cost, and the AEB parameter.
The biggest challenge when using the proposed method, which may be its drawback, is the need to implement two calculation methods within one task. However, currently available ready-made specialized software modules significantly improve the possibilities of quick use of the proposed methodology in practice.
Due to its great universality, this method can be used in many cases, and its limitations are related to the well-known limitations of multi-criteria methods and the AHP method.
A great advantage of the method proposed in the manuscript, for selecting the final solution from a set of hybrid manufacturing systems that are a solution of multi-criteria optimization, is its potential application as an indicator for selecting economically justified systems in other types of facilities, e.g., schools, universities, shopping centers, passenger service areas along expressways and motorways (parking lots, rest areas with restaurants), or the surroundings of roads. The last example, due to the very large number of facilities and thousands of kilometers of expressways and motorways, should be one of the cases considered by the authors in the future.
Author Contributions
Conceptualization, A.T.; investigation, A.T., S.M. and J.S.; methodology, A.T., S.M. and J.S.; software S.M. and J.S.; writing—original draft preparation, A.T., S.M. and J.S.; formal analysis, A.T.; supervision, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Centre for Research and Development (Narodowe Centrum Badań i Rozwoju) and the General Directorate for National Roads and Motorways (Generalna Dyrekcja Dróg Krajowych i Autostrad), grant number RID2/0004/2022, entitled “A comprehensive system for acquiring, storing and distributing electricity from renewable sources with the use of infrastructure located in the road lane”.
Data Availability Statement
The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jones, D.F.; Florentino, H.O. Multi-Objective Optimization: Methods and Applications. In The Palgrave Handbook of Operations Research; Salhi, S., Boylan, J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 181–207. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms, 1st ed.; Wiley-Interscience Series in Systems and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Trzaskalik, T. Wielokryterialne wspomaganie decyzji. Przegląd metod i zastosowań. Zesz. Nauk. Organ. Zarządzanie/Politechnika Śląska 2014, 74, 239–263. [Google Scholar]
- Xu, D.; Dong, L. Strategic diagnosis of China’s modern coal-to-chemical industry using an integrated SWOT-MCDM framework. Clean Technol. Environ. Policy 2019, 21, 517–532. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Zhu, Y.; Xiao, M.; Yang, H.; Huang, H.; Li, L. Assessing the sustainability of urban community renewal projects in southern China based on a hybrid MADM approach. Sustainability 2023, 15, 3023. [Google Scholar] [CrossRef]
- Larichev, O.; Moshkovich, H. ZAPROS-LM—A method and system for ordering multiattribute alternatives. Eur. J. Oper. Res. 1995, 82, 503–521. [Google Scholar] [CrossRef]
- Agustiansyah, R.; Ambarsari, N. Implementation of analytic network process (ANP) and analytic hierarchy process (AHP) method to determine priorities of roads to be repaired at Bogor City Department of Public Works. In Proceedings of the 2013 International Conference of Information and Communication Technology (ICoICT), Bandung, Indonesia, 20–22 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 61–66. [Google Scholar]
- Łuczak, A. Assessing the Strategic Factors and Choosing the Development Scenarios for Local Administrative Units Using AHP. Mult. Criteria Decis. Mak. 2017, 12, 119–133. [Google Scholar] [CrossRef]
- Bedessi, S.; Lisi, S. AHP, ANP and ANN: Technical differences, conceptual connections, hybrid models. In Proceedings of the International Symposium on the Analytic Hierarchy Process, Naples, Italy, 15–18 June 2011. [Google Scholar]
- Saaty, T.; Vargas, L.; St, C. The Analytic Hierarchy Process; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Gonzalez-Urango, H.; Mu, E.; García-Melón, M. Stakeholder engagement and ANP best research practices in sustainable territorial and urban strategic planning. In Multiple Criteria Decision Making for Sustainable Development: Pursuing Economic Growth, Environmental Protection and Social Cohesion; Springer: Berlin/Heidelberg, Germany, 2022; pp. 93–130. [Google Scholar]
- Al-Harbi, K.M.A.S. Application of the AHP in project management. Int. J. Proj. Manag. 2001, 19, 19–27. [Google Scholar] [CrossRef]
- Lai, V.S.; Wong, B.K.; Cheung, W. Group decision making in a multiple criteria environment: A case using the AHP in software selection. Eur. J. Oper. Res. 2002, 137, 134–144. [Google Scholar] [CrossRef]
- Lai, V.S.; Trueblood, R.P.; Wong, B.K. Software selection: A case study of the application of the analytical hierarchical process to the selection of a multimedia authoring system. Inf. Manag. 1999, 36, 221–232. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, S.H. Using analytic network process and goal programming for interdependent information system project selection. Comput. Oper. Res. 2000, 27, 367–382. [Google Scholar] [CrossRef]
- Potić, I.; Joksimović, T.; Milinčić, U.; Kićović, D.; Milinčić, M. Wind energy potential for the electricity production-Knjaževac Municipality case study (Serbia). Energy Strategy Rev. 2021, 33, 100589. [Google Scholar] [CrossRef]
- Ali, S.; Stewart, R.A.; Sahin, O.; Vieira, A.S. Integrated GIS-AHP-based approach for off-river pumped hydro energy storage site selection. Appl. Energy 2023, 337, 120914. [Google Scholar] [CrossRef]
- Saraswat, S.; Digalwar, A.K.; Yadav, S.; Kumar, G. MCDM and GIS based modelling technique for assessment of solar and wind farm locations in India. Renew. Energy 2021, 169, 865–884. [Google Scholar] [CrossRef]
- Waewsak, J.; Ali, S.; Natee, W.; Kongruang, C.; Chancham, C.; Gagnon, Y. Assessment of hybrid, firm renewable energy-based power plants: Application in the southernmost region of Thailand. Renew. Sustain. Energy Rev. 2020, 130, 109953. [Google Scholar] [CrossRef]
- Demir, A.; Dinçer, A.E.; Yılmaz, K. A novel method for the site selection of large-scale PV farms by using AHP and GIS: A case study in İzmir, Türkiye. Solar Energy 2023, 259, 235–245. [Google Scholar] [CrossRef]
- Albraheem, L.; AlAwlaqi, L. Geospatial analysis of wind energy plant in Saudi Arabia using a GIS-AHP technique. Energy Rep. 2023, 9, 5878–5898. [Google Scholar] [CrossRef]
- Lenarczyk, A. Zastosowanie metody ahp do porównania kryteriów wyboru lokalizacji budowy farmy wiatrowej. Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej; Wydział Elektrotechniki i Automatyki Politechniki Gdańskiej: Gdańsk, Poland, 2015; pp. 187–190. [Google Scholar]
- Cho, S.; Kim, J.; Lim, D. Optimal design of renewable energy certificate multipliers using an LCOE-Integrated AHP model: A case study of South Korea. Renew. Energy 2024, 226, 120386. [Google Scholar] [CrossRef]
- Mastrocinque, E.; Ramírez, F.J.; Honrubia-Escribano, A.; Pham, D.T. An AHP-based multi-criteria model for sustainable supply chain development in the renewable energy sector. Expert Syst. Appl. 2020, 150, 113321. [Google Scholar] [CrossRef]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of feasibility study of solar farms deployment using hybrid AHP-TOPSIS analysis: Case study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]
- Abdul, D.; Wenqi, J.; Tanveer, A. Prioritization of renewable energy source for electricity generation through AHP-VIKOR integrated methodology. Renew. Energy 2022, 184, 1018–1032. [Google Scholar] [CrossRef]
- Lyu, H.; Zhou, W.; Shen, S.; Zhou, A. Inundation risk assessment of metro system using AHP and TFN-AHP in Shenzhen. Sustain. Cities Soc. 2020, 56, 102103. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Shah, S.A.A.; Zameer, H.; Ikram, M.; Saracoglu, B.O. Assessing the solar PV power project site selection in Pakistan: Based on AHP-fuzzy VIKOR approach. Environ. Sci. Pollut. Res. 2019, 26, 30286–30302. [Google Scholar] [CrossRef] [PubMed]
- Yayla, A.Y.; Yildiz, A. Fuzzy Analitic Network Process based Multi Criteria Decision Making methodology for a family automobile purchasing decision. S. Afr. J. Ind. Eng. 2013, 24, 167–180. [Google Scholar]
- Bozanic, D.; Tešić, D.; Marinković, D.; Milić, A. Modeling of neuro-fuzzy system as a support in decision-making processes. Rep. Mech. Eng. 2021, 2, 222–234. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar] [CrossRef]
- Fei, L. D-ANP: A multiple criteria decision making method for supplier selection. Appl. Intell. 2020, 50, 2537–2554. [Google Scholar] [CrossRef]
- Uyan, M.; Dogmus, O.L. An integrated GIS-based ANP analysis for selecting solar farm installation locations: Case study in Cumra region, Turkey. Environ. Model. Assess. 2023, 28, 105–119. [Google Scholar] [CrossRef]
- Sharma, K.; Trivedi, M.K. AHP and NSGA-II-Based Time–Cost–Quality Trade-Off Optimization Model for Construction Projects. In Proceedings of the Artificial Intelligence and Sustainable Computing; Dubey, H.M., Pandit, M., Srivastava, L., Panigrahi, B.K., Eds.; Springer: Singapore, 2022; pp. 45–63. [Google Scholar]
- Soni, S.; Chauhan, M.; Singh, P.; Agarwal, A.K.; Sharma, K. Optimizing construction time, cost, and quality: A hybrid AHP-NSGA-II optimization model. Asian J. Civ. Eng. 2024, 25, 4053–4067. [Google Scholar] [CrossRef]
- Lu, H.; Niu, R.; Liu, J.; Zhu, Z. Multicriteria Decision Mechanism CNSGA-AHP for the Automatic Test Task Scheduling Problem. Inf. Technol. J. 2012, 11, 1449. [Google Scholar] [CrossRef][Green Version]
- Zhang, M.; Liu, L. Evolutionary algorithm with AHP decision-making method for cloud workflow service composition. In Proceedings of the 2015 IEEE 7th International Conference on Cloud Computing Technology and Science (CloudCom), Vancouver, BC, Canada, 30 November–5 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 339–346. [Google Scholar]
- Tomczewski, A.; Mikulski, S.; Piotrowski, A.; Sowa, S.; Wróbel, K. Multicriteria Optimisation of the Structure of a Hybrid Power Supply System for a Single-Family Housing Estate in Poland, Taking into Account Different Electromobility Development Scenarios. Energies 2023, 16, 4132. [Google Scholar] [CrossRef]
- Tomczewski, A.; Kasprzyk, L. Optimisation of the structure of a wind farm—Kinetic energy storage for improving the reliability of electricity supplies. Appl. Sci. 2018, 8, 1439. [Google Scholar] [CrossRef]
- Kasprzyk, L.; Tomczewski, A.; Pietracho, R.; Mielcarek, A.; Nadolny, Z.; Tomczewski, K.; Trzmiel, G.; Alemany, J. Optimization of a PV-Wind hybrid power supply structure with electrochemical storage intended for supplying a load with known characteristics. Energies 2020, 13, 6143. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovoltaics Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Miettinen, K. A Priori Methods. In Nonlinear Multiobjective Optimization; Miettinen, K., Ed.; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Golovin, D.; Zhang, Q. Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization. arXiv 2020, arXiv:2006.04655. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mohd Zain, M.Z.B.; Kanesan, J.; Chuah, J.H.; Dhanapal, S.; Kendall, G. A multi-objective particle swarm optimization algorithm based on dynamic boundary search for constrained optimization. Appl. Soft Comput. 2018, 70, 680–700. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH Zurich: Zurich, Switzerland, 2001; 21p. [Google Scholar] [CrossRef]
- Deep, K.; Singh, K.P.; Kansal, M.L.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]
- Reference and Discount Rates (in %) Since 1 August 1997. Available online: https://competition-policy.ec.europa.eu/state-aid/legislation/reference-discount-rates-and-recovery-interest-rates/reference-and-discount-rates_en (accessed on 9 December 2024).
- Super Decisions. Available online: https://www.superdecisions.com/ (accessed on 8 November 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).