Substation Abnormal Scene Recognition Based on Two-Stage Contrastive Learning
Abstract
1. Introduction
- A novel few-shot learning method, which utilizes two-stage contrastive learning (2-SCL) to construct the learning objective, is proposed. In the first stage, a pre-trained model is constructed through self-supervised learning, thereby enhancing the model’s inter-class discrimination ability.
- Supervised contrastive learning is introduced in the second stage of the model, further fine-tuning the pre-trained model within a supervised framework to improve sample identification capability and model generalization ability.
- In the self-supervised phase, multiple data augmentation methods are proposed to enhance sample diversity, thereby obtaining more generalized feature representations.
- A large-scale dataset of substation abnormal scenarios has been constructed, which can provide better data support for subsequent research.
2. Related Work
2.1. Few-Shot Learning
2.2. Self-Supervised Learning
3. Materials and Methods
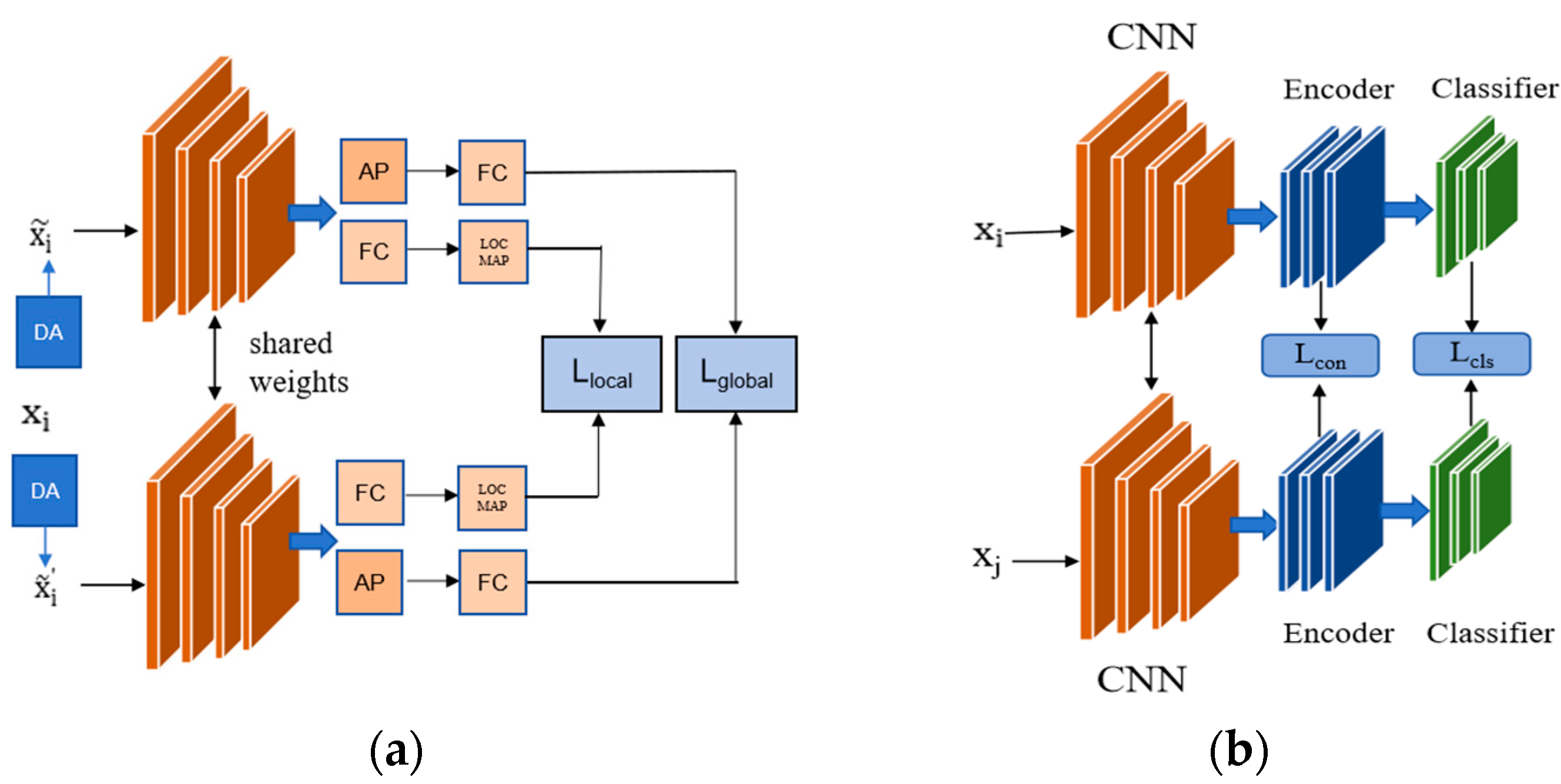
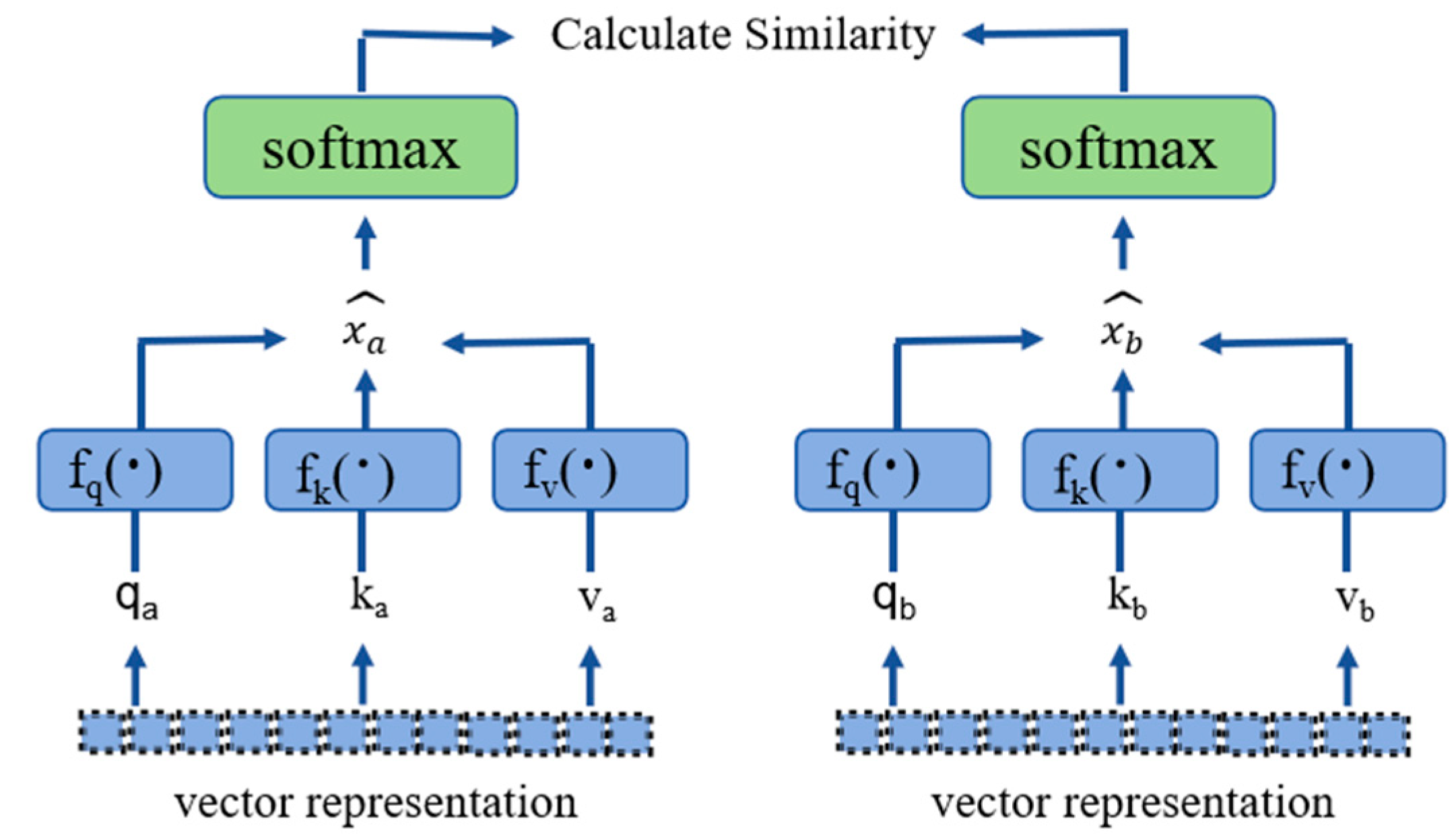
3.1. Global Self-Supervised Contrastive Loss
3.2. Local Self-Supervised Contrastive Loss
3.3. Supervised Fine-Tune
4. Experimental Results and Discussion
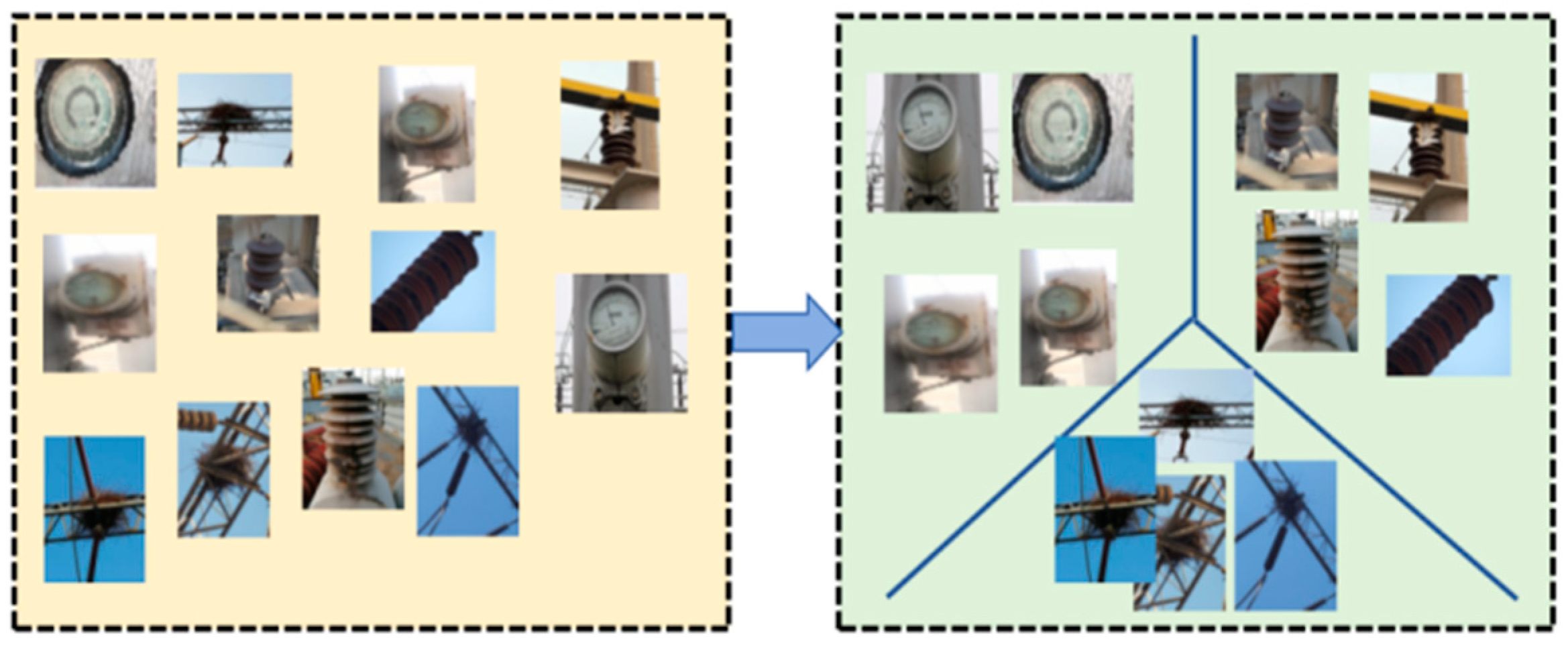
4.1. Dataset of Abnormal Scenes in Substation
4.2. Experimental Setup
4.3. Evaluation Metrics
4.4. Experimental Results
4.5. Ablation Experiments
4.6. Parameter Sensitivity Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ge, L.; Li, Y.; Li, Y.; Yan, J.; Sun, Y. Smart distribution network situation awareness for high-quality operation and maintenance: A brief review. Energies 2022, 15, 828. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Xu, Y.; Jia, M. Multichannel fault diagnosis of wind turbine driving system using multivariate singular spectrum decomposition and improved Kolmogorov complexity. Renew. Energy 2021, 170, 724–748. [Google Scholar] [CrossRef]
- Kong, Y.; Jing, M. An Identification Method of Abnormal Patterns for Video Surveillance in Unmanned Substation; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Wu, Y.; Xiao, F.; Liu, F.; Sun, Y.; Deng, X.; Lin, L.; Zhu, C. A Visual Fault Detection Algorithm of Substation Equipment Based on Improved YOLOv5. Appl. Sci. 2023, 13, 11785. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, X. Investigation into recognition technology of helmet wearing based on HBSYOLOX-s. Appl. Sci. 2022, 12, 12997. [Google Scholar] [CrossRef]
- Xu, C.; Ni, D.; Wang, B.; Wu, M.; Gan, H. Two-stage anomaly detection for positive samples and small samples based on generative adversarial networks. Multimed. Tools Appl. 2023, 82, 20197–20214. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, Y.; Chua, T.S.; Schiele, B. Meta-transfer learning for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Oreshkin, B.; Rodríguez López, P.; Lacoste, A. Tadam: Task dependent adaptive metric for improved few-shot learning. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Sohn, K. Improved deep metric learning with multi-class N-pair loss objective. Adv. Neural Inf. Process. Syst. 2016, 29, 1–9. [Google Scholar]
- Su, J.C.; Maji, S.; Hariharan, B. When Does Self-supervision Improve Few-shot Learning. In European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the 32nd International Conference on Machine, Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching Networks for One Shot Learning. Adv. Neural Inf. Process. Syst. 2016, 29, 1–9. [Google Scholar]
- Hou, R.; Chang, H.; Ma, B.; Shan, S.; Chen, X. Cross attention network for few-shot classification. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Ye, H.J.; Hu, H.; Zhan, D.C.; Sha, F. Few-shot learning via embedding adaptation with set-to-set functions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Lim, J.Y.; Lim, K.M.; Ooi, S.Y.; Lee, C.P. Efficient-prototypicalnet with self knowledge distillation for few-shot learning. Neurocomputing 2021, 459, 327–337. [Google Scholar] [CrossRef]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhang, X.; Qiang, Y.; Sung, F.; Yang, Y.; Hospedales, T.M. RelationNet2: Deep comparison columns for few-shot learning. arXiv 2018, arXiv:1811.07100. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Bertinetto, L.; Henriques, J.F.; Torr, P.H.; Vedaldi, A. Meta-learning with differentiable closed-form solvers. arXiv 2018, arXiv:1805.08136. [Google Scholar]
- Alexey, D.; Fischer, P.; Tobias, J.; Springenberg, M.R.; Brox, T. Discriminative unsupervised feature learning with exemplar convolutional neural networks. IEEE TPAMI 2016, 38, 1734–1747. [Google Scholar]
- Gidaris, S.; Singh, P.; Komodakis, N. Unsupervised representation learning by predicting image rotations. arXiv 2018, arXiv:1803.07728. [Google Scholar]
- Doersch, C.; Gupta, A.; Efros, A.A. Unsupervised visual representation learning by context prediction. In Proceedings of the IEEE International Conference on Computer Vision, Nashville, TN, USA, 11–15 June 2015. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A. Split-brain autoencoders: Unsupervised learning by cross-channel prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Lee, H.; Hwang, S.J.; Shin, J. Self-supervised label augmentation via input transformations. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020. [Google Scholar]
- Chen, D.; Chen, Y.; Li, Y.; Mao, F.; He, Y.; Xue, H. Self-supervised learning for few-shot image classification. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021. [Google Scholar]
- Yang, Z.; Wang, J.; Zhu, Y. Few-shot classification with contrastive learning. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]

| Backbone | Methods | 5-Way 1-Shot | 5-Way 5-Shot | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | F1-Score | Recall | Accuracy | Precision | F1-Score | Recall | ||
| Conv-4 | RelationNets [16] | 61.76 ± 0.48 | 58.32 ± 0.81 | 57.5 ± 0.43 | 56.71 ± 0.54 | 77.59 ± 0.73 | 68.27 ± 0.78 | 70.52 ± 0.81 | 72.93 ± 0.76 |
| MatchingNets [12] | 64.52 ± 0.67 | 56.14 ± 0.63 | 59.13 ± 0.52 | 62.45 ± 0.7 | 80.63 ± 0.53 | 73.37 ± 0.54 | 72.55 ± 0.65 | 71.76 ± 0.64 | |
| PrototypicalNets [18] | 67.67 ± 0.58 | 56.21 ± 0.59 | 60.84 ± 0.59 | 66.31 ± 0.63 | 82.39 ± 0.42 | 74.15 ± 0.61 | 73.32 ± 0.73 | 72.5 ± 0.75 | |
| R2D2 [19] | 69.56 ± 0.42 | 62.6 ± 0.53 | 64.94 ± 0.72 | 67.47 ± 051 | 87.65 ± 0.63 | 64.86 ± 0.65 | 73.9 ± 0.72 | 85.89 ± 0.76 | |
| RelationNets2 [17] | 72.12 ± 0.82 | 64.9 ± 1.21 | 67.66 ± 0.93 | 70.67 ± 0.36 | 85.49 ± 0.59 | 79.5 ± 0.63 | 76.39 ± 0.58 | 73.52 ± 0.65 | |
| 2-SCL (ours) | 73.76 ± 0.56 | 67.85 ± 0.48 | 69.64 ± 0.51 | 71.54 ± 0.46 | 88.76 ± 0.56 | 82.54 ± 0.55 | 84.29 ± 0.54 | 86.13 ± 0.51 | |
| Backbone | Methods | 5-Way 1-Shot | 5-Way 5-Shot | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | F1-Score | Recall | Accuracy | Precision | F1-Score | Recall | ||
| ResNet-12 | RelationNets [16] | 72.56 ± 0.63 | 61.67 ± 0.75 | 65.23 ± 0.67 | 69.23 ± 0.59 | 85.93 ± 0.49 | 74.75 ± 0.77 | 70.67 ± 0.72 | 67.02 ± 0.74 |
| MatchingNets [12] | 75.91 ± 0.49 | 72.18 ± 0.47 | 71.87 ± 0.46 | 71.58 ± 0.53 | 88.37 ± 0.69 | 82.18 ± 0.61 | 80.37 ± 0.63 | 78.64 ± 0.64 | |
| PrototypicalNets [18] | 76.43 ± 0.52 | 77.12 ± 0.43 | 75.08 ± 0.48 | 73.15 ± 0.51 | 89.61 ± 0.83 | 85.12 ± 0.72 | 82.82 ± 0.76 | 80.64 ± 0.81 | |
| TADAM [8] | 81.72 ± 0.67 | 74.32 ± 0.68 | 77.19 ± 0.59 | 80.3 ± 0.57 | 90.72 ± 0.72 | 77.11 ± 0.67 | 80.62 ± 0.63 | 84.46 ± 0.66 | |
| R2D2 [19] | 82.61 ± 0.73 | 81.23 ± 0.78 | 79.5 ± 0.72 | 77.85 ± 0.71 | 91.59 ± 0.51 | 85.18 ± 0.58 | 82.83 ± 0.56 | 80.6 ± 0.54 | |
| 2-SCL (ours) | 83.13 ± 0.49 | 84.35 ± 0.48 | 82.77 ± 0.46 | 81.25 ± 0.42 | 93.12 ± 0.64 | 86.6 ± 0.52 | 87.97 ± 0.5 | 89.39 ± 0.48 | |
| Model | 5-Way 1-Shot | 5-Way 5-Shot |
|---|---|---|
| (ours) | 83.83 ± 0.57 | 93.12 ± 0.43 |
| w/o Contrastive pre-training | −8.15 | −6.13 |
| w/o Supervised contrastive learning | −4.56 | −3.32 |
| w/o Contrastive pre-training + w/o Supervised contrastive learning | −9.35 | −7.69 |
| Backbone | Contrastive Loss | Classification Loss | 5-Way 1-Shot | 5-Way 5-Shot |
|---|---|---|---|---|
| Conv-4 | × | √ | 62.43 ± 0.96 | 75.32 ± 0.87 |
| √ | × | 71.29 ± 0.42 | 85.91 ± 0.62 | |
| √ | √ | 73.76 ± 0.56 | 88.76 ± 0.56 | |
| ResNet-12 | × | √ | 73.89 ± 0.45 | 82.19 ± 0.61 |
| √ | × | 79.47 ± 0.68 | 88.40 ± 0.55 | |
| √ | √ | 83.83 ± 0.57 | 93.12 ± 0.43 |
| Backbone | 5-Way 1-Shot | 5-Way 5-Shot | |
|---|---|---|---|
| Conv-4 | 0.2 | 72.53 ± 0.82 | 86.37 ± 0.63 |
| 0.4 | 73.76 ± 0.56 | 88.76 ± 0.56 | |
| 0.6 | 71.61 ± 0.42 | 84.30 ± 0.67 | |
| 0.8 | 72.66 ± 0.15 | 85.81 ± 0.72 | |
| ResNet-12 | 0.2 | 80.18 ± 0.49 | 89.29 ± 0.54 |
| 0.4 | 83.83 ± 0.57 | 93.12 ± 0.43 | |
| 0.6 | 83.44 ± 0.58 | 92.89 ± 0.50 | |
| 0.8 | 83.01 ± 0.60 | 91.94 ± 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Su, H.; Mao, W.; Li, M.; Zhang, J.; Bao, H. Substation Abnormal Scene Recognition Based on Two-Stage Contrastive Learning. Energies 2024, 17, 6282. https://doi.org/10.3390/en17246282
Liu S, Su H, Mao W, Li M, Zhang J, Bao H. Substation Abnormal Scene Recognition Based on Two-Stage Contrastive Learning. Energies. 2024; 17(24):6282. https://doi.org/10.3390/en17246282
Chicago/Turabian StyleLiu, Shanfeng, Haitao Su, Wandeng Mao, Miaomiao Li, Jun Zhang, and Hua Bao. 2024. "Substation Abnormal Scene Recognition Based on Two-Stage Contrastive Learning" Energies 17, no. 24: 6282. https://doi.org/10.3390/en17246282
APA StyleLiu, S., Su, H., Mao, W., Li, M., Zhang, J., & Bao, H. (2024). Substation Abnormal Scene Recognition Based on Two-Stage Contrastive Learning. Energies, 17(24), 6282. https://doi.org/10.3390/en17246282





