Lithium-Ion Battery Health Management and State of Charge (SOC) Estimation Using Adaptive Modelling Techniques

Abstract

Effective health management and accurate state of charge (SOC) estimation are crucial for the safety and longevity of lithium-ion batteries (LIBs), particularly in electric vehicles. This paper presents a health management system (HMS) that continuously monitors a 4s2p LIB pack’s parameters—current, voltage, and temperature—to mitigate risks such as overcurrent and thermal runaway while ensuring balanced charge distribution between cells. An improved online battery model (IOBM) is developed to enhance SOC estimation accuracy. The system utilises forgetting factor recursive least squares (FFRLS) for real-time parameter updates, an adaptive nonlinear sliding mode observer (ANSMO) for SOC estimation, and a long short-term memory (LSTM) network to dynamically adjust capacity based on operating conditions. Validation using the urban dynamometer driving schedule (UDDS) test demonstrated high accuracy, with the proposed battery model achieving a root mean square error (RMSE) of 12.13 mV and the LSTM achieving an RMSE of 0.0118 Ah. Regular updates to the battery’s current capacity, along with the proposed IOBM, significantly improved SOC estimation performance, maintaining estimation errors within 1.08%.

1. Introduction

Lithium-ion batteries (LIBs) are prevalent energy providers thanks to their high energy density, low associated costs, high-temperature stability, and long cycle life [1,2,3]. However, like any other regular system, LIBs degrade with time and usage. Their capacity to store energy and supply power decreases over charging and discharging cycles [4]. Studies show that LIBs’ performance strictly depends on the operating conditions [5,6]. Cycling outside the permitted range of temperature, voltage, and current can accelerate the ageing process, leading to self-ignition or even explosion in critical cases [7]. Therefore, it is crucial to establish an intelligent health management system (HMS) to monitor the battery’s working conditions and improve the powered system’s safety level.

Lithium nickel manganese cobalt oxide (NMC) batteries, widely used in electric vehicles and energy storage systems, present additional challenges for health management. These challenges include their susceptibility to thermal runaway under high loads, especially in fast-charging scenarios and the complexities of accurately estimating their state of health (SOH) due to non-linear degradation patterns. Effective HMS design for NMC batteries requires advanced approaches that can adapt to these unique characteristics to ensure safety, longevity, and performance. Traditional methods for battery management may not be sufficient for NMC batteries, as they do not account for the specific degradation and thermal management needs of this chemistry. This highlights the need for more sophisticated solutions that can provide real-time adaptation to changing operational conditions.

The battery HMS is a smart system that combines hardware and software to oversee a battery pack, which is an assembly of battery cells linked in series/parallel to fulfil the system’s capacity and power requirement. The main goal of the HMS is to keep the battery pack within its safe operation area (SOA) in terms of voltage, current, and temperature during the charge and discharge cycle [8]. In addition to internal state estimation, which includes the assessment of the battery state of charge (SOC) and SOH, the HMS has to ensure even charge distribution between the pack cells. In the case where the voltage difference between the cells exceeds the permitted limit, it will bring down the voltage of that cell so that all cells have the same voltage [9,10]. This function is known in the literature as cell balancing. When manageing NMC batteries, maintaining this safe operation area is particularly important due to their sensitivity to temperature fluctuations and high current loads. Effective cell balancing and accurate SOH tracking can help mitigate risks associated with thermal runaway and extend the battery’s operational life. There are two types of cell balancing: passive cell balancing and active cell balancing. This classification is based on how the excess charge is removed from the battery. For passive cell balancing, the energy of the cell with the highest voltage is dissipated through a resistor in the form of heat [11]. This equalising approach is widely implemented because it is simple and cost-effective. On the other hand, active cell balancing equalises the charge between the cells by transferring the energy from the cell with high voltage to the cell with low voltage [12]. Therefore, the energy is not wasted; however, it requires more components than the passive approach, which means higher cost and more occupied surface.

SOC estimation is a vital function of the HMS that helps improve the system’s overall performance and reliability. It represents the ratio of the battery’s remaining capacity to its nominal capacity. To the best of the authors’ knowledge, there is no physical sensor that can directly assess the SOC. Various indirect methods with ranging accuracy and complexity levels have been proposed in the literature to assess the battery SOC. The most straightforward method is known as coulomb counting (CC). It identifies the battery SOC by integrating the current drawn from and supplied to the battery over time. However, The CC method is susceptible to sensor noise and the initial SOC settings [13]. The open circuit voltage (OCV) method is commonly combined with the CC method to improve the accuracy of SOC estimation. The SOC-OCV look-up table is experimentally established first to scale the initial SOC for the CC method. In recent years, model-based estimation methods have gained attention. This category of methods begins by setting the battery state-space model equations and then developing the state observer to assess SOC using control theory and observer design methods. Among these, Kalman filters, especially the extended Kalman filter (EKF) [14,15,16] and unscented Kalman filter (UKF) [17,18], have been widely applied for SOC estimation due to their ability to handle non-linear systems and measurement noise. These methods continuously adjust the SOC estimation by comparing the predicted and measured battery voltages, allowing for more accurate SOC tracking, especially under varying load conditions [19].

Battery internal state estimation requires establishing a model that describes the battery behaviour and internal states based on external parameters. The accuracy of the developed model reflects the battery’s performance and safety. The literature presents numerous battery models with varying accuracy and complexity levels. These models can be grouped into electrochemical battery models (EMs) [20,21,22], equivalent circuit models (ECMs) [23,24,25] and data-driven battery models [26,27,28]. Among these three battery model categories, ECM offers a good compromise between model accuracy and complexity. The model has been widely used in various applications to simulate real-time battery behaviour. The ECM is made of circuit components such as resistors, capacitors and voltage sources to reflect the static and dynamic characteristics of the battery. The number of RC networks n depends on the application. However, considering model accuracy and complexity, studies have shown that 2RC-ECM can provide reliable results at a reduced cost [29,30,31]. One primary concern about ECM is that the model parameters depend on the batteries’ working conditions, such as SOC, SOH and temperature [32]. An offline identification of the model parameters requires running extensive experiments to capture the battery response over the entire range of operating conditions. Besides, cyclic ageing will impact the battery’s performance. Thus, an online parameter identification approach is preferred to conquer these limitations. The online recursive estimation of the ECM parameters has been the focus of recent studies. In [33], Chen et al. conducted an evaluation study of the offline mechanism-based and least square methods and online recursive least-squares with forget factor (FFRLS) and EKF under three different conditions. Under noisy conditions, the online approaches showed better results, for which the recorded SOC errors were −1.1% for FFRLS and 0.51% for the EKF-based method. Trung et al. [34] used FFRLS to identify the parameters of the 1-RC ECM model. The developed model has good accuracy with an error margin of less than 1%. Joint estimation of the battery model parameters and SOC was investigated in [35]. The authors applied FFRLS and an adaptive nonlinear sliding mode observer (AN-SMO) to jointly estimate the ECM parameters and SOC. The dual filter method is used in [36] to simulate the battery’s dynamic behaviour and estimate its SOC.

The battery SOH is used to evaluate the ageing level of the LIBs. It represents the ratio of the current maximum available capacity to the initial maximum capacity. Since no physical sensor can gauge the battery capacity, researchers have developed indirect methods that use the battery’s measured quantities, such as voltage, current, and temperature to estimate the LIB’s SOH. In [37], Li et al. proposed a battery capacity and SOC co-estimation scheme. The parameters of the first-order ECM and the battery SOC were identified simultaneously using the RLS method and adaptive extended Kalman filter, and the battery’s actual capacity was leveraged using the Elman neural network. Taichun Qin et al. [38] used particle swarm optimisation (PSO) and support vector regression (SVR) to estimate the battery SOH. In [39] an online capacity estimation of the Li-ion battery was achieved using the long short-term memory (LSTM) method. The study shows that the proposed method performs well despite sensor noise and incomplete data with reduced computation times. Additionally, a new SOH estimation method based on model-data fusion [40] was introduced, providing a hybrid approach that combines model-based and data-driven techniques to improve accuracy and robustness in varying conditions.

When designing an HMS, accuracy, complexity, and cost are essential factors. The HMS has to ensure that each cell of the battery pack operates within its SOA, estimate the battery SOC, track its ageing process, and balance the charge distribution between cells. In the literature, several HMS designs and testing platforms have been proposed. In [41], Chen et al. developed a 6s1p Li-ion battery pack testing platform based on the STM32 controller. The BQ76930 communicates each cell’s voltage, current, and temperature measurements to the STM32 and ensures that each cell operates within its safe operating area (SOA). The STM32 receives the collected data through IIC and estimates the battery SOC using a combination of the CC method and the OCV method. Angela et al. [42] designed a modular BMS with point-to-point SOC estimation using machine learning. A modular battery cell monitoring system was developed in [43]. The system can accurately assess the battery voltage, temperature, charge current and discharge, which are transmitted to a mixed signal processor for protection, monitoring and balancing. Although the proposed detection platforms proposed in the literature were successfully tested, they miss some essential functions, such as cell balancing and health management, that significantly affect the battery performance and life cycle.

Hence, this paper proposes an intelligent HMS with SOC estimation and balancing for a 4s2p NMC battery pack. This paper’s novelty evolves from using an improved online battery model (IOBM) representing battery behaviour, which continuously adjusts model parameters to reflect changes caused by battery ageing and varying load conditions. This adaptive approach improves the accuracy and performance of the HMS. Additionally, using a seventh-order polynomial to model the nonlinear OCV–SOC relationship contributes to more accurate SOC predictions and minimises system modelling errors. Furthermore, an LSTM network continuously estimates battery capacity, providing real-time capacity updates into the SOC algorithm. The AN-SMO uses the provided battery capacity and estimates the SOC based on the proposed IOBM, reducing the errors caused by capacity degradation under the influence of ageing.

The proposed system has a master–slave topology, which improves the system’s reliability and scalability. The STM32 communicates with the master unit to provide battery data, including the voltage of individual cells, the current that flows in and out of the battery pack, and the temperature at the hot spot within the battery pack. The master control unit module, the Raspberry pi3, uses this information to estimate the battery states, ensure that the battery operates within its SOA, and balance the charge between the cells.

The rest of the paper is organised as follows. Section 2 details the experimental setup and algorithm development of the HMS. Section 3 describes the circuit design of the proposed system. Section 4 discusses the results and validates the HMS, while Section 5 concludes the work.

2. Algorithm Development

2.1. Experimental Setup

Experimental data for the commercial 3 Ah LG-HG2 18650 (LG Chem, Seoul, South Korea) cylindrical cell with a graphite anode and a Li[NiMnCo]O₂ cathode were collected under various operating conditions, providing a robust foundation for battery modelling. The battery was characterised using the Enhanced Hybrid Power Pulse Characterisation (EHPPC) test, covering a wide temperature range and SOC intervals. The specifications of the cell are given in

Table 1. LG-HG2 18650 cell specification.

Category	Specification
Manufacturer	LG Chemical (LG Chem, Seoul, South Korea)
Type	Cylindrical
Chemistry	Li[NiMnCo]O2 (H-NMC)/Graphite + SiO
Nominal Voltage	3.6 V
Nominal Capacity	3.0 Ah
Energy Density	240 (Wh/Kg)
Charge	1.5 A, 4.2, 50 mA End-Current (CC-CV) Normal
	4 A, 4.2 V, 100 mA End-Current (CC-CV) Fast
Discharge	2 V End Voltage, 20 A MAX Continuous Current

.

The tests for the characterisation and modelling of this battery were performed by Dr. Phillip Kollmeyer at McMaster University in Hamilton, Ontario, Canada [44]. It includes the EHPPC test along with cycle tests conducted at six different ambient temperatures (40 °C, 25 °C, 10 °C, 0 °C, −10 °C, and −20 °C) organised by temperature, test type, and drive cycle.

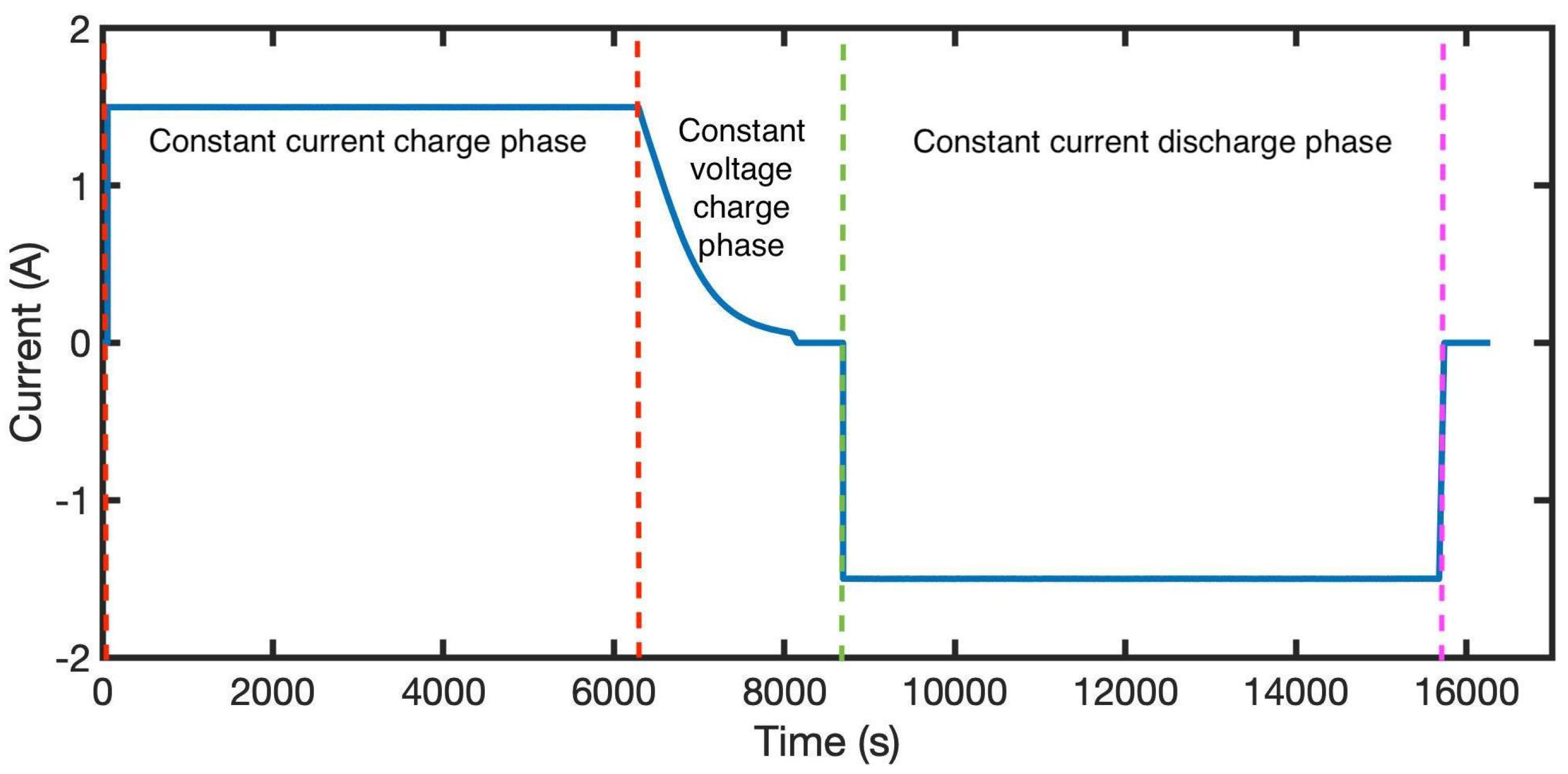
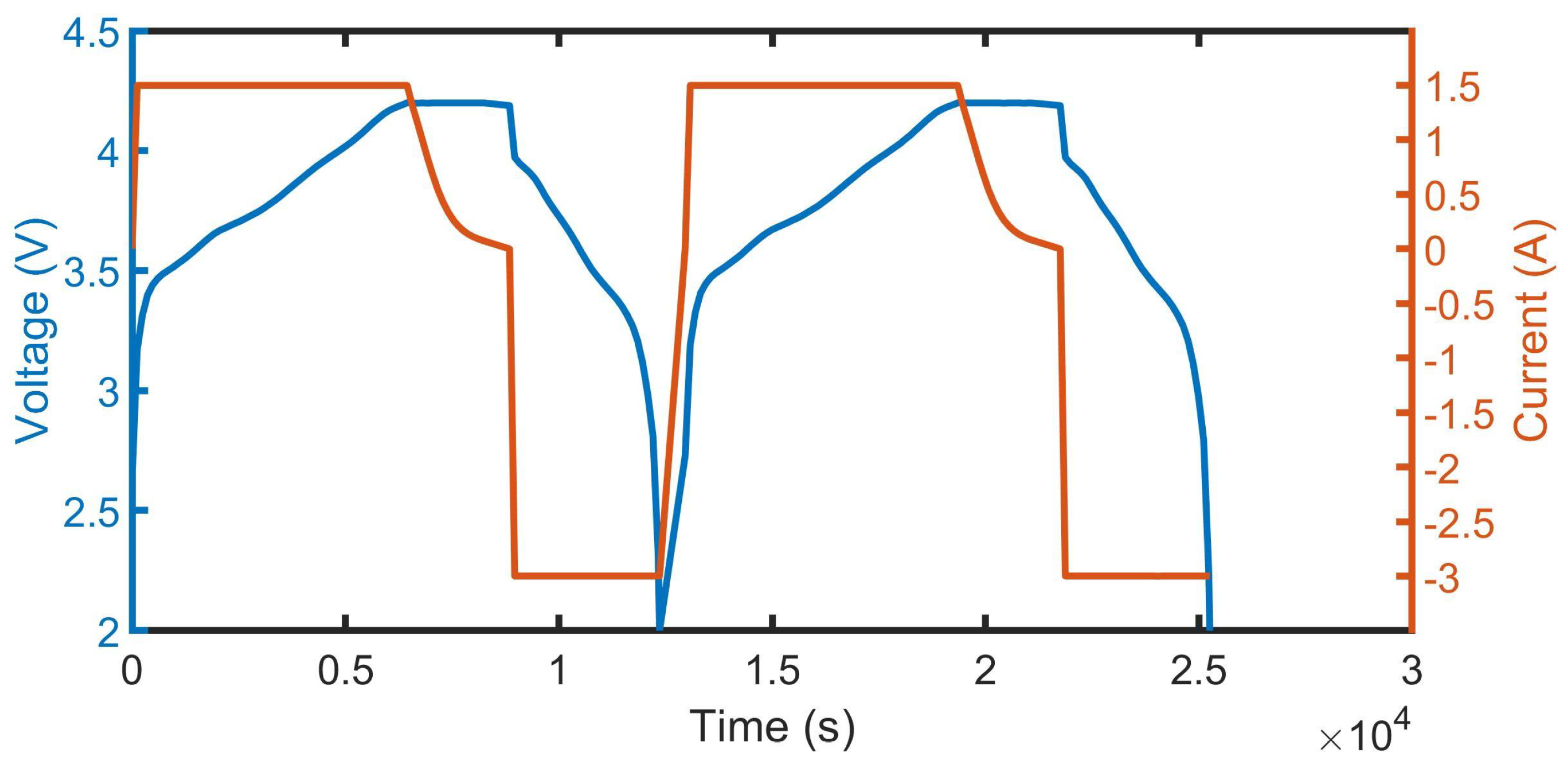
The EHPPC test is a combination of four sets of HPPC tests. The sequence of each combination includes a discharging pulse, a resting period, and a charging pulse. The current amplitudes are 1 C, 2 C, 4 C and 6 C for discharge and 0.5 C, 1 C, 1.5 C and 2 C for charge. The C unit is the battery current rate (C-rate), which represents the rate at which a battery is discharged relative to its maximum capacity. The EHPPC is performed at different SOC intervals until the battery is fully discharged (100%, 95%, 90%, 80%, 70–20%, 15%, 10%, 5%, 2.5%, 0% ). Figure 1 illustrates the EHPPC current load and the voltage response.

To understand the degradation process of LIBs, Y. Perger et al. released a multi-year cycling study of three chemistries of 18,650 form cells, including the NMC from LG Chem [45]. The data are available on the Battery Archive website and are shared under a double attribution license [46]. Hereinto, the cycling ageing test was performed at different ambient temperatures (5 °C, 15 °C, 25 °C, 35 °C, 45 °C), discharge currents and depths of discharge (1 C, 5 A 10 A and 20 A).

The ageing test procedure is shown in Figure 2 and the degradation results at different temperatures are illustrated in Figure 3.

The test was repeated until the battery reached its end-of-life (EOL), equivalent to a loss of 20% of its initial capacity. The dataset includes per-cycle and in-cycle measurements of the battery voltage, current, temperature, capacity, and energy.

2.2. Online Battery Parameter Identification

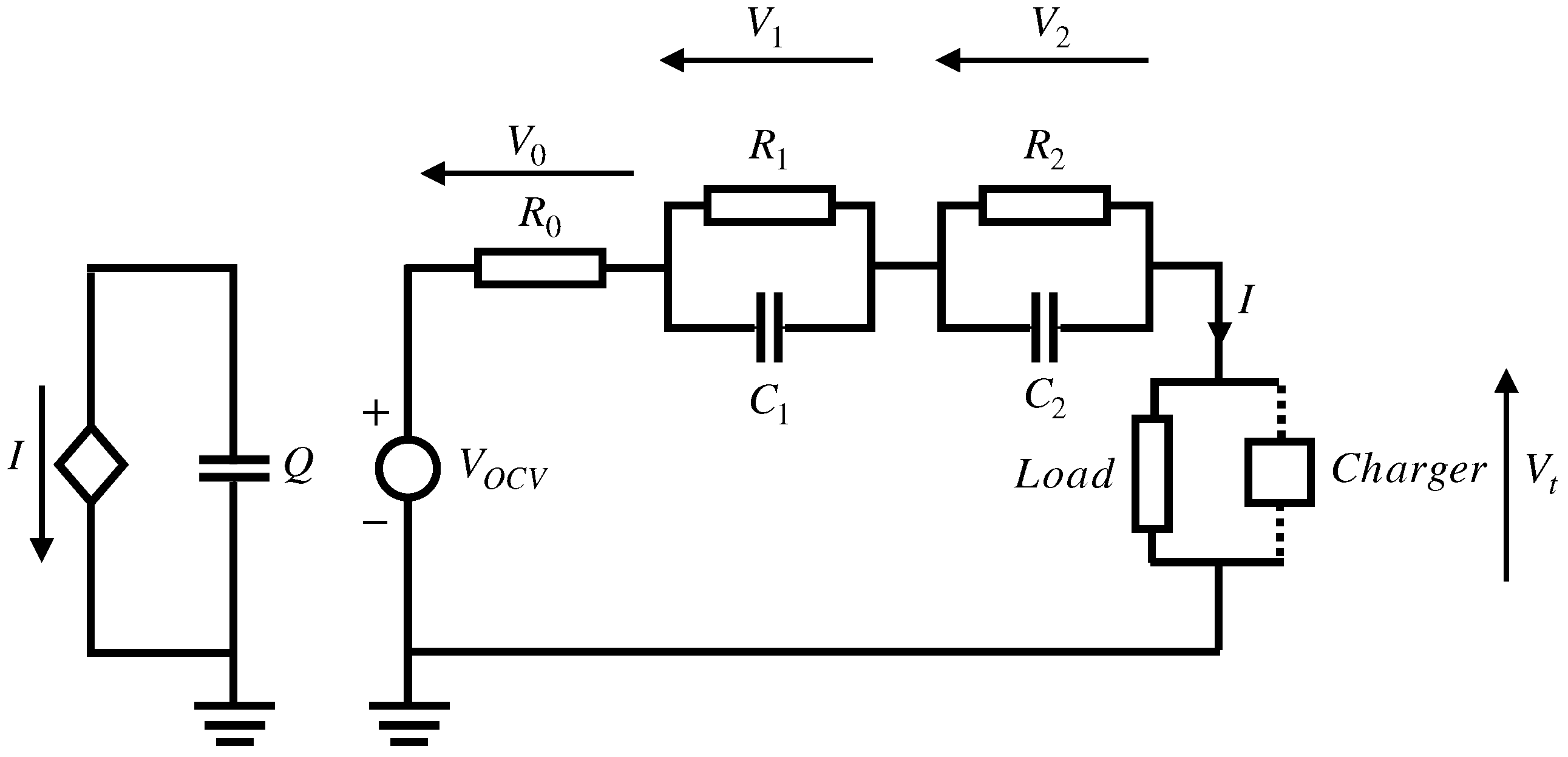
The 2RC-ECM model is adopted in this study to represent the battery dynamics. The model includes an ideal voltage source representing the battery OCV, a series resistor used to capture the internal resistance, and two capacitor–resistor networks reflecting the battery’s fast dynamic response (FDR) (i.e., the $R_1{C}_1$ branch) and slow dynamic response (SDR) (i.e., the $R_2{C}_2$ branch). The circuit topology is illustrated in Figure 4, where $V_{OCV}$, $R_0$, $R_1$, $R_2$, $C_1$, and $C_2$ are the battery parameters to be identified.

According to the Kirchoff’s Voltage Law (KVL), the state-space equation of the 2RC-ECM model is given as

$$\left\{\begin{array}{cc}{\displaystyle \frac{d{V}_1}{dt}}\hfill & =-{\displaystyle \frac{V_1}{R_1{C}_1}}+{\displaystyle \frac{I}{C_1}}\hfill \\ {\displaystyle \frac{d{V}_2}{dt}}\hfill & =-{\displaystyle \frac{V_2}{R_2{C}_2}}+{\displaystyle \frac{I}{C_2}}\hfill \\ V_t\hfill & =V_{OCV}-V_1-V_2-I{R}_0\hfill \end{array}\right.$$

(1)

Let ${\tau }_1=R_1{C}_1$ and ${\tau }_2=R_2{C}_2$ be the time constant of the two RC networks; by taking the Laplace transform of Equation (1) we obtain

$$\left\{\begin{array}{cc}{V}_1\left(s\right)\hfill & ={\displaystyle \frac{R_1}{{\tau }_{1}s+1}}I\left(s\right)\hfill \\ V_2\left(s\right)\hfill & ={\displaystyle \frac{R_2}{{\tau }_{2}s+1}}I\left(s\right)\hfill \\ V_t\left(s\right)\hfill & =V_{ocv}\left(s\right)-\left({\displaystyle \frac{R_1}{{\tau }_{1}s+1}}+{\displaystyle \frac{R_2}{{\tau }_{2}s+1}}+R_0\right)I\left(s\right)\hfill \end{array}\right.$$

(2)

where s represents the Laplace transform operator.

Let y be the sum of the potentials across the ohmic resistor and the RC network; one has $y\left(s\right)=V_0\left(s\right)+V_1\left(s\right)+V_2\left(s\right)$.

$$y\left(s\right)=V_{OCV}\left(s\right)-V_t\left(s\right)=\left({\displaystyle \frac{R_1}{{\tau }_{1}s+1}}+{\displaystyle \frac{R_2}{{\tau }_{2}s+1}}+R_0\right)I_t\left(s\right)$$

(3)

By taking $y\left(s\right)$ as the system output and I as the system input, the transfer function of Equation (3) can be described as

$$G\left(s\right)={\displaystyle \frac{y\left(s\right)}{I\left(s\right)}}={\displaystyle \frac{R_1}{{\tau }_{1}s+1}}+{\displaystyle \frac{R_2}{{\tau }_{2}s+1}}+R_0$$

(4)

Let a = ${\tau }_1{\tau }_2$, $b={\tau }_1+{\tau }_2$, $c=R_0+R_1+R_2$, $d=R_1{\tau }_2+R_2{\tau }_1+R_0({\tau }_1+{\tau }_2)$ and $e=a{R}_0$; Equation (4) then becomes

$$G\left(s\right)={\displaystyle \frac{c+ds+e{s}^2}{1+bs+a{s}^2}}$$

(5)

Using the bi-linear transformation $\left(s\to {\displaystyle \frac{2}{T}}{\displaystyle \frac{1-z^{-1}}{1+z^{-1}}}\right)$, Equation (5) is discretised regarding the sampling time T into

$$G\left(z^{-1}\right)={\displaystyle \frac{{\theta }_3+{\theta }_4{z}^{-1}+{\theta }_5{z}^{-2}}{1-{\theta }_1{z}^{-1}-{\theta }_2{z}^{-2}}}$$

(6)

By discretising the transfer function (Equation (6)) using bilinear transformation, the system is modelled in a way that enables real-time parameter adaptation. The coefficients ${\theta }_i$, identified using FFRLS, represent the battery’s internal dynamics and are continuously updated to reflect changes in operating conditions.

The coefficients ${\theta }_i$ are as follows

$$\left\{\begin{array}{cc}{\theta }_1\hfill & ={\displaystyle \frac{8a-2T^2}{4a+2bT+T^2}},\hfill \\ {\theta }_2\hfill & ={\displaystyle \frac{2bT-4a-T^2}{4a+2bT+T^2}},\hfill \\ {\theta }_3\hfill & ={\displaystyle \frac{4a{R}_0+2dT+c{T}^2}{4a+2bT+T^2}},\hfill \\ {\theta }_4\hfill & ={\displaystyle \frac{2c{T}^2-8a{R}_0}{4a+2bT+T^2}},\hfill \\ {\theta }_5\hfill & ={\displaystyle \frac{4a{R}_0-2dT+c{T}^2}{4a+2bT+T^2}}\hfill \end{array}\right.$$

(7)

The discrete recurrence formula of Equation (3) can be expressed as

$$y\left(k\right)={\theta }_{1}y(k-1)+{\theta }_{2}y(k-2)+{\theta }_{3}I\left(k\right)+{\theta }_{4}I(k-1)+{\theta }_{5}I(k-2)$$

(8)

where $y\left(k\right)$, $y(k-1)$, $y(k-2)$ define the difference between the battery terminal and open circuit voltage at the $k\mathrm{th}$, $(k-1)\mathrm{th}$, $(k-2)\mathrm{th}$ sampling instances, respectively.

Similarly, $I\left(k\right)$, $I(k-1)$, $I(k-2)$ define the battery current at the $k\mathrm{th}$, $(k-1)\mathrm{th}$, $(k-2)\mathrm{th}$ sampling instances, respectively.

Let $\theta ={[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5]}^T$ and ${\varphi }_k={[y(k-1),y(k-2),I\left(k\right),I(k-1),I(k-2)]}^T$, the discrete-time transfer function model can be further rewritten into the ARX form as

$$y\left(k\right)={\theta }^T{\varphi }_k+ϵ\left(k\right)$$

(9)

where ${\varphi }_k$ is the information vector, $\theta$ is the parameter vector to be identified and $ϵ\left(k\right)$ represents the measurement noises.

The coefficients ${\theta }_i$ in Equation (5) are identified using forgetting factor recursive least squares (FF-RLS).

In contrast to traditional static parameter estimation techniques, the Forgetting Factor Recursive Least Squares (FFRLS) was employed to dynamically track time-varying parameters of the 2RC-ECM model. This method continuously updates the model to reflect changes in internal resistance and capacitance as the battery ages, ensuring accurate and real-time parameter estimation. As a result, the model adapts to varying conditions, significantly improving prediction accuracy over static models. The detailed definition steps of the FFRLS are summarised in Algorithm 1.

Algorithm 1: Steps of the FFRLS algorithm.

Definition ${\displaystyle y_k={\varphi }_k^T{\theta }_k+{ϵ}_k}$ Initialisation ${\displaystyle {\widehat{\varphi }}_k=[y_{k-1},y_{k-2},I_k,I_{k-1},I_{k-2}]}$ ${\displaystyle {\widehat{\theta }}_k=[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5]}$ Algorithm gain $K_k$ and covariance matrix $P_k$ ${\displaystyle K_k=\frac{P_{k-1}{\varphi }_k^T}{{\varphi }_k{P}_{k-1}{\varphi }_k^T+\lambda }}$ ${\displaystyle P_k=\frac{1}{\lambda }\left[I-K_k{\varphi }_k^T\right]P_{k-1}}$ Prediction error and update model parameter ${\displaystyle e_k=y_{t,k}---{\varphi }_k{\theta }_{k-1}}$ ${\displaystyle {\theta }_k={\theta }_{k-1}+K_k{e}_k}$ Measurement update ${\displaystyle y_{t,k}={\varphi }_k{\theta }_k}$

Once the parameter vector is identified, we can deduce the calculation expression of the battery parameter $R_i$ and $C_i$ by applying the inverse bilinear transform rule $\left(z^{-1}=1-{\displaystyle \frac{T}{2}}s/1+{\displaystyle \frac{T}{2}}s\right)$ and comparing the corresponding coefficient in Equations (5) and (10)

$$G\left(s\right)={\displaystyle \frac{\frac{{\theta }_3+{\theta }_4+{\theta }_5}{1-{\theta }_1-{\theta }_2}+\frac{{\theta }_3-{\theta }_5}{1-{\theta }_1-{\theta }_2}Ts+\frac{{\theta }_3-{\theta }_4+{\theta }_5}{1-{\theta }_1-{\theta }_2}\frac{T^2}{4}{s}^2}{1+\frac{1+{\theta }_2}{1-{\theta }_1-{\theta }_2}Ts+\frac{1+{\theta }_1-{\theta }_2}{1-{\theta }_1-{\theta }_2}\frac{T^2}{4}{s}^2}}$$

(10)

$$\left\{\begin{array}{c}{k}_1={\displaystyle \frac{1+{\theta }_1-{\theta }_2}{1-{\theta }_1-{\theta }_2}}{\displaystyle \frac{T^2}{4}}\hfill \\ k_2={\displaystyle \frac{1+{\theta }_2}{1-{\theta }_1-{\theta }_2}}T\hfill \\ k_3={\displaystyle \frac{{\theta }_3+{\theta }_4+{\theta }_5}{1-{\theta }_1-{\theta }_2}}\hfill \\ k_4={\displaystyle \frac{{\theta }_3-{\theta }_5}{1-{\theta }_1-{\theta }_2}}T\hfill \\ k_5={\displaystyle \frac{{\theta }_3-{\theta }_4+{\theta }_5}{1-{\theta }_1-{\theta }_2}}{\displaystyle \frac{T^2}{4}}\hfill \end{array}\right.$$

(11)

The FFRLS continuously calculates the parameters ${\theta }_i$ based on the measurable inputs and outputs by minimising the cost function as

$$J\left({\theta }_k\right)=\sum _{k=1}^L{\lambda }^{L-k}{[\tilde{y}\left(k\right)-{\varphi }^T\left(k\right)\widehat{\theta }]}^2,0<\lambda <1$$

(12)

where $\lambda$ is the forgetting factor, $\widehat{\theta }$ is the estimate of $\theta$, and $\tilde{y}$ is the noisy output.

Finally, we obtain the 2RC-ECM parameters as follows

$$\left\{\begin{array}{c}{R}_0={\displaystyle \frac{k_5}{k_1}}={\displaystyle \frac{{\theta }_3-{\theta }_4+{\theta }_5}{1+{\theta }_1-{\theta }_2}}\hfill \\ R_2={\displaystyle \frac{k_4-k_3{\tau }_2-R_0{\tau }_1}{{\tau }_1-{\tau }_2}}\hfill \\ R_1=k_3-R_0-R_2={\displaystyle \frac{k_3{\tau }_1+R_0{\tau }_2-k_4}{{\tau }_1-{\tau }_2}}\hfill \\ {\tau }_1=min\left({\displaystyle \frac{k_2-\sqrt{k_2^2-4k_1}}{2}},{\displaystyle \frac{k_2+\sqrt{k_2^2-4k_1}}{2}}\right)\hfill \\ {\tau }_2=max\left({\displaystyle \frac{k_2-\sqrt{k_2^2-4k_1}}{2}},{\displaystyle \frac{k_2+\sqrt{k_2^2-4k_1}}{2}}\right)\hfill \\ C_1={\displaystyle \frac{{\tau }_1}{R_1}}\hfill \\ C_2={\displaystyle \frac{{\tau }_2}{R_2}}\hfill \end{array}\right.$$

(13)

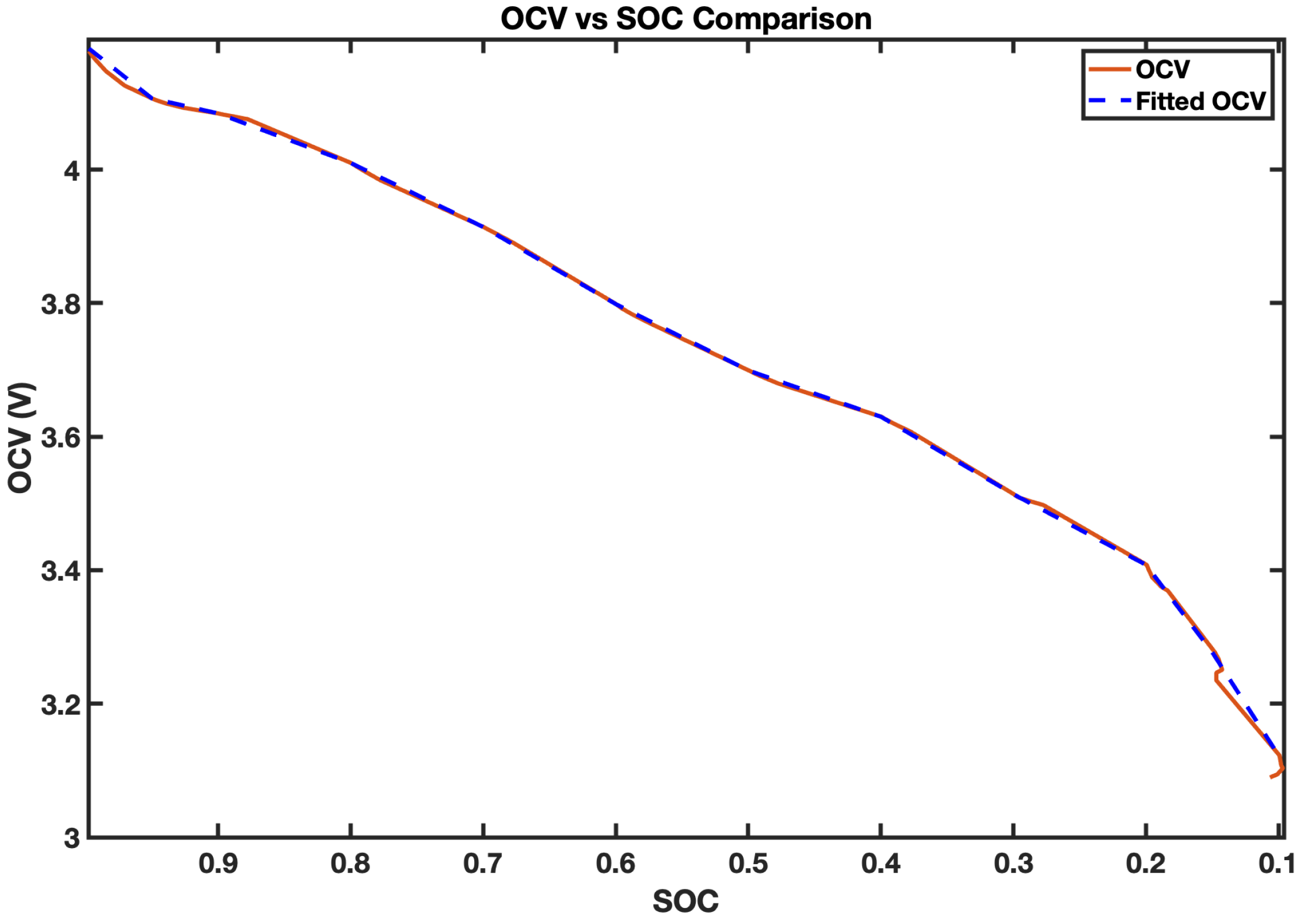
The battery OCV is extracted for each discharge pulse equivalent to the SOC point at the corresponding sampling points (1, 0.95, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.15, 0.1, 0.05, 0.025, 0) and the corresponding voltage points in the EHPPC data (Figure 5). The SOC is initially calculated under the laboratory test using the CC method. The intermediate points between the pre-determined OCV values are calculated using linear interpolation.

2.3. SOC Estimation

The SOC is a crucial state that assesses the system’s reliability by providing critical information like remaining energy and the remaining time before it is entirely discharged. It indicates the remaining electrical capacity relative to its nominal capacity $Q_N$ as follows

$$SOC\left(t_2\right)={\displaystyle \frac{Q_r\left(t\right)}{Q\left(t\right)}}=SOC\left(t_1\right)-{\displaystyle \frac{1}{Q}}{\int }_{t_1}^{t_2}\eta \left(t\right)i\left(t\right)dt$$

(14)

where $SOC\left(t_1\right)$, $SOC\left(t_2\right)$ are the SOC value at time instants $t_1$ and $t_2$, respectively; I is the load current; and $\eta$ denotes the Coulomb efficiency, expressed as:

$$\eta ={\displaystyle \frac{\mathrm{total}\mathrm{capacity}\mathrm{measured}\mathrm{while}\mathrm{discharging}}{\mathrm{total}\mathrm{capacity}\mathrm{measured}\mathrm{while}\mathrm{charging}}}$$

(15)

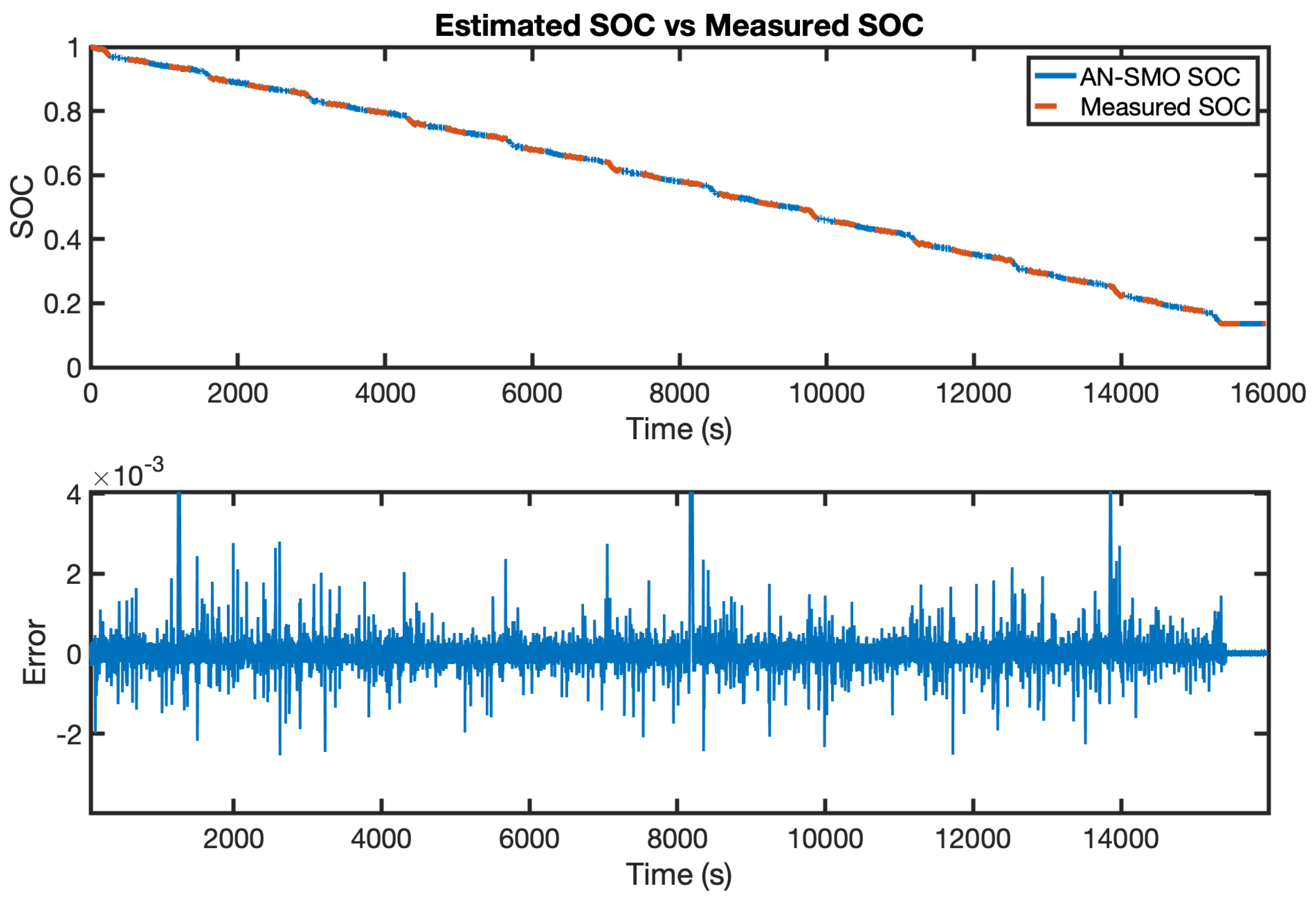
Traditional methods like Coulomb counting (CC) are prone to errors due to noise, inaccurate initial conditions, and battery ageing. To address these limitations, we propose an Adaptive Nonlinear Sliding Mode Observer (AN-SMO), designed to improve accuracy and robustness in SOC estimation under dynamic conditions.

The 2RC-ECM is employed to describe the discrete state-space model of the SOC estimation system, expressed as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{V}_{1,k}\\ V_{2,k}\\ SO{C}_k\end{array}\right]& =\left[\begin{array}{ccc}{e}^{-{\displaystyle \frac{\Delta T}{R_1{C}_1}}}& 0& 0\\ 0& e^{-{\displaystyle \frac{\Delta T}{R_2{C}_2}}}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{V}_{1,k-1}\\ V_{2,k-1}\\ SO{C}_{k-1}\end{array}\right]+\hfill \\ & \left[\begin{array}{c}\left(1-e^{-{\displaystyle \frac{\Delta T}{R_1{C}_1}}}\right)R_1\\ \left(1-e^{-{\displaystyle \frac{\Delta T}{R_2{C}_2}}}\right)R_2\\ -{\displaystyle \frac{\Delta T}{3600Q}}\end{array}\right]I_{k-1}+w_{k-1}\hfill \end{array}$$

(16)

where $\Delta T$ is the sampling time, $w_{k-1}$ represents the process noise, and Q is the battery capacity. The output voltage is calculated by

$$V_{t,k}=V_{ocv,k}-V_{1,k}-V_{2,k}-I_k{R}_0$$

(17)

where $V_{ocv}$ is the open-circuit voltage, $V_1$ and $V_2$ are the voltages across the RC networks, and $R_0$ is the internal resistance.

An accurate SOC estimation will guide the cell-balancing unit, energy, and power calculations. Hence, an adaptive nonlinear sliding mode observer (AN-SMO) is developed in this study to estimate the average SOC of the 4s2p battery pack.

This paper designed a novel (AN-SMO) that aims to improve the accuracy and robustness of the battery’s SOC. It provides an adaptive, nonlinear control strategy combined with a dynamic sliding surface.

The AN-SMO compensates for estimation errors in SOC and voltage by employing an adaptive sliding mode surface that dynamically adjusts to real-time battery conditions. These errors, $e_{soc}\left(t\right)$ (18) and $e_v\left(t\right)$ (19), defined as the difference between the true value $SO{C}_{true}\left(t\right)$, $V_{true}\left(t\right)$ and the estimated value $SO{C}_{est}\left(t\right)$, $V_{est}\left(t\right)$, are minimised through an adaptive control law that ensures robustness against model uncertainties, noise, and capacity degradation.

SOC estimation error

$$e_{soc}\left(t\right)=SO{C}_{true}\left(t\right)-SO{C}_{est}\left(t\right)$$

(18)

Voltage estimation error

$$e_v\left(t\right)=V_{true}\left(t\right)-V_{est}\left(t\right)$$

(19)

To ensure system stability and guarantee observer convergence to the true SOC and voltage values, a Lyapunov-based approach is used. For the observer stability analysis, a scalar positive definite function $V\left(e\right)$, representing the system’s energy, is chosen as the Lyapunov candidate function:

$$V\left(e\right)={\displaystyle \frac{1}{2}}·e^{T}e={\displaystyle \frac{1}{2}}·(e_{soc}^2+e_v^2)$$

(20)

where $e_{\mathrm{soc}}$ and $e_v$ denote the errors in SOC and voltage, respectively. The sliding mode control law further enhances stability by dynamically adapting to error dynamics and mitigating the effects of perturbations, avoiding discontinuities and ensuring robust system performance.

Since $V\left(e\right)>0$ for $e\ne 0$ and $V\left(e\right)=0$ if and only if $e=0$, $V\left(e\right)$ is a positive definite function.

According to the Lyapunov theory, for the system to be stable, the time derivative of the defined Lyapunov function, $\dot{V}\left(e\right)$ must be negative semi-definite.

$$\dot{V}\left(e\right)=e_{soc}{\dot{e}}_{soc}+e_v{\dot{e}}_v$$

(21)

Using a hyperbolic tangent function, dynamic sliding surfaces are defined to enhance the system stability by avoiding sharp discontinuities and smoothing transitions.

$$s_{soc}=e_{soc}+{\lambda }_{soc}·tanh(k_{soc}·e_{soc})$$

(22)

$$s_v=e_v+{\lambda }_v·tanh(k_v·e_v)$$

(23)

where ${\lambda }_{soc}$, ${\lambda }_v$, $k_{soc}$ and $k_v$ are adaptive observer gains that vary based on the error dynamics.

The sliding mode control law is chosen to ensure that the system reaches the switching surface and stays on this surface when perturbations occur, as follows:

$$u_{soc}=-{\lambda }_{soc}·{\left|s_{soc}\right|}^{\alpha }sign\left(s_{soc}\right)$$

(24)

$$u_v=-{\lambda }_v·{\left|s_v\right|}^{\alpha }sign\left(s_v\right)$$

(25)

Using these control laws, the derivative Lyapunov function can be expressed as

$$\dot{V}\left(e\right)=-{\lambda }_{soc}·{\left|s_{soc}\right|}^{\alpha +1}-{\lambda }_v·{\left|s_v\right|}^{\alpha +1}$$

(26)

Since $\dot{V}\left(e\right)\le 0$, the system is Lyapunov-stable. As $e_{soc}$ and $e_v$ approach zero, the developed observer converges to the true SOC and voltage values, ensuring accurate and robust SOC estimation.

2.4. Ageing Estimation

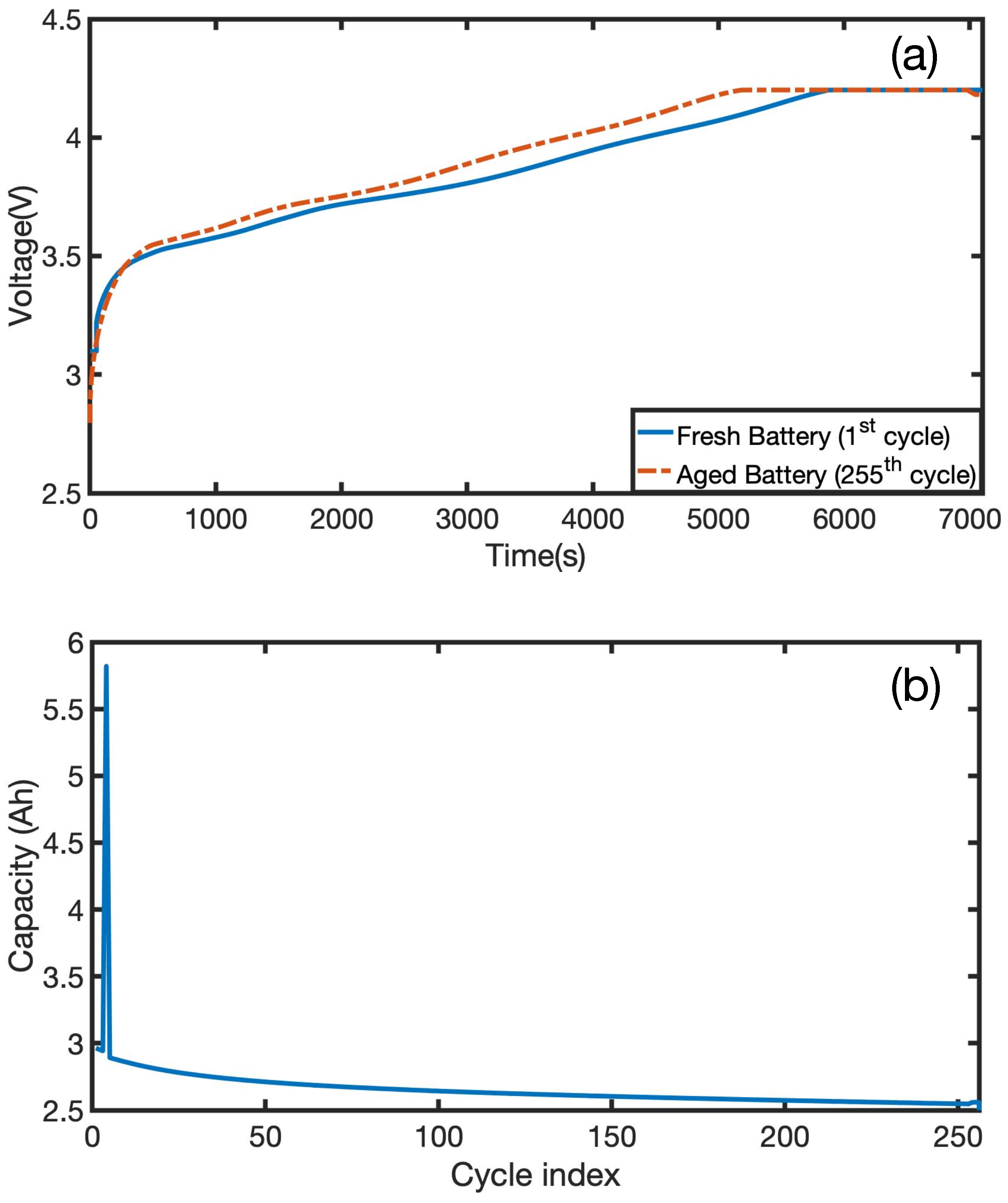
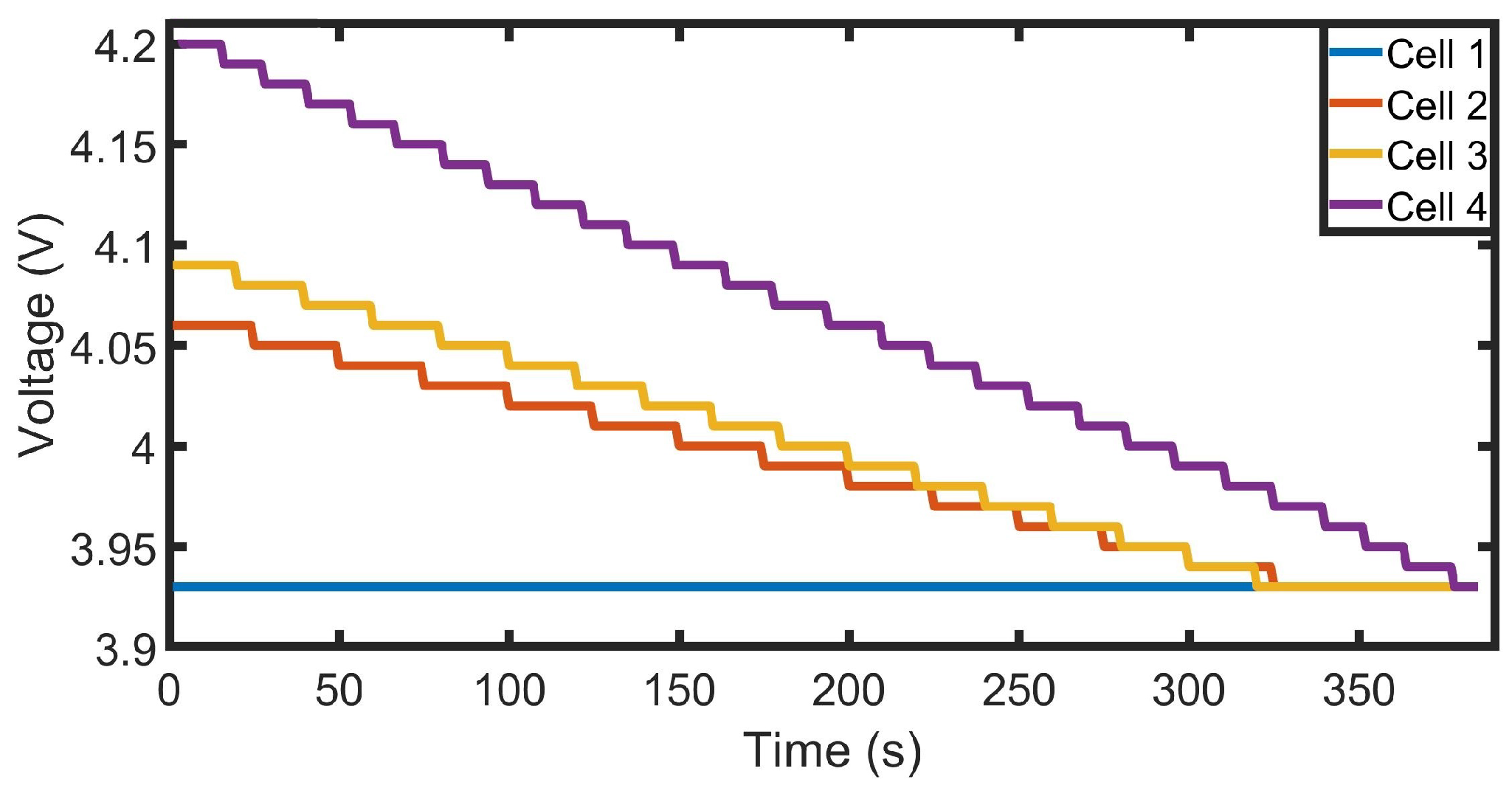
LIBs are subject to ongoing performance decay throughout their lifetime due to side reactions and unfavourable working conditions. As the number of charge–discharge cycles increases, the battery performance declines, reflecting a decrease in the battery capacity. Figure 6 shows a notable difference between the voltage response of a fresh battery during its first charging profile compared to the same battery response after 255 cycles. The aged battery reaches the upper voltage limit of 4.2 V before the fresh cell. Moreover, the battery capacity gradually decays with increased charge–discharge cycles. Hence, the precise metering of the battery’s actual capacity can be used to reflect the current health and thus the remaining cycles before the EOL event. Real-time updates of the present capacity will enhance the system’s overall performance and the SOC algorithm’s accuracy.

Herein, the LSTM-RNN approach is leveraged to estimate the remaining battery capacity using the data gathered from ageing experiments. The proposed framework follows three consecutive steps: data preprocessing, training, and prediction, each detailed below.

2.4.1. Step 1:Data Preprocessing

Effective data preprocessing is crucial step of the LSTM-based methods. It enssures clean, structured, and normalised data, essential for accurate estimation of the battery capacity. The primary preprocessing steps include:

• Normalisation: The min-max normalisation is used to remove deviant features and outliers. This step enhances the model’s convergence and stability. Every feature is transformed into a decimal between 0 and 1 using the following formula:

  $$v_i^k={\displaystyle \frac{x_i^k-min\left(x\right)}{max\left(x\right)-min\left(x\right)}},i\in \{1,...,n\}$$

  (27)

  where $x_i^k$ is the data to be scaled and n is the number of samples per cycle.
• Data segmentation: Subsequently, the normalised data set is sliced into training data that will be used to teach the model and testing data set to validate the prediction.

2.4.2. Step 2: Model Architecture and Training

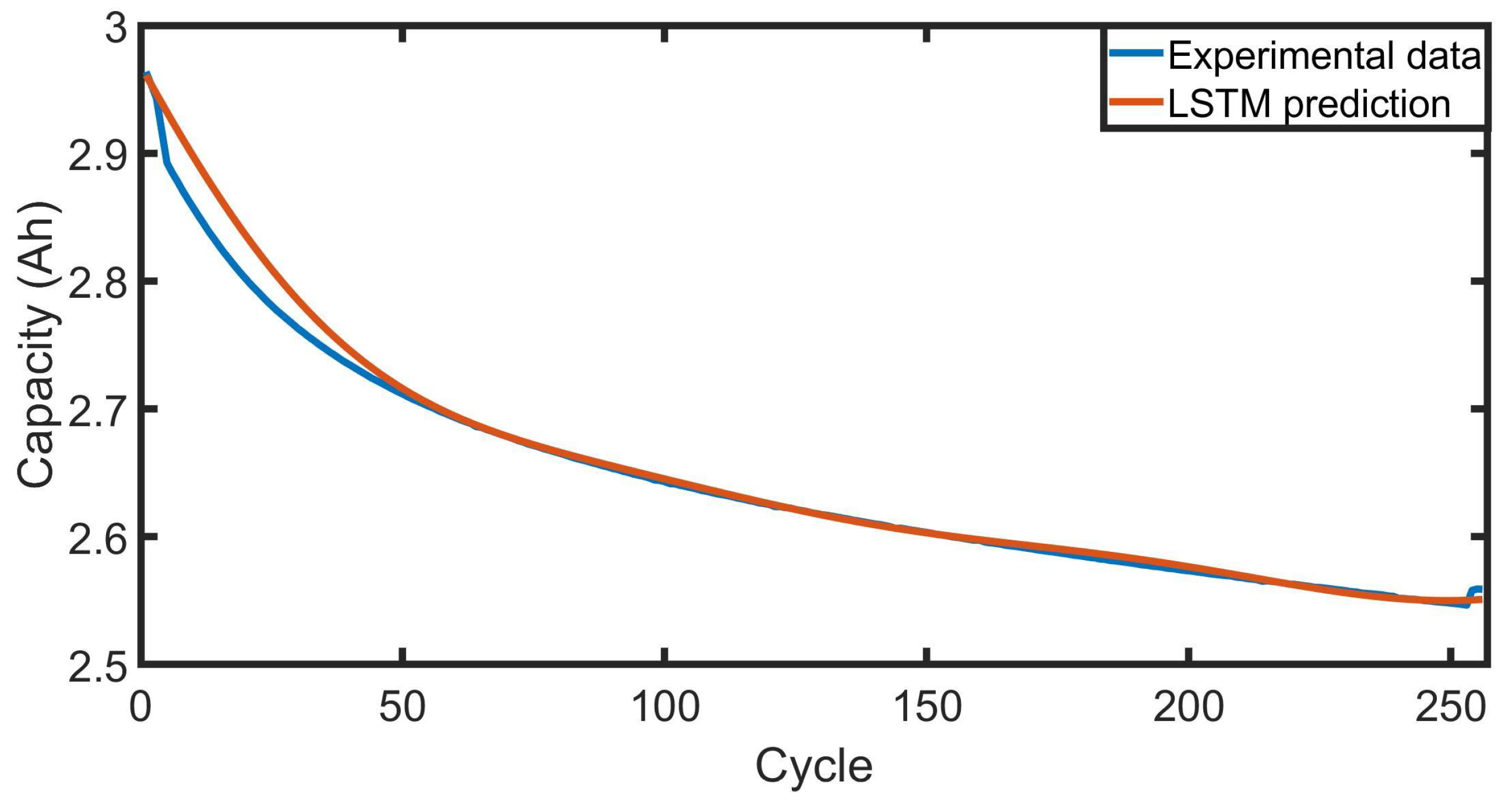
The LSTM model includes three main layers, each playing a unique role in estimating the battery capacity. At its core, the model has an LSTM layer with 50 units, chosen to model the long-term dependencies within sequential battery ageing data. Next, a dropout layer with a rate of 0.2 is included to prevent overfitting, which randomly deactivates 20% of the neurons during each training cycle. This regularisation ensures better performance by minimising dependence on individual neurons. Finally, a dense layer with a single neuron and a linear activation function generates a continuous estimate of capacity.

2.4.3. Step 3: Prediction Process

LSTMs are designed to mitigate the long-term dependency problem. As shown in Figure 7, the general structure of the LSTM includes an input gate, a cell, a forget gate, and an output gate. The network unrolls the inputs ($x_t$) over arbitrary time intervals learning new information from each time step. The three gates regulate data flow into and out of the memory blocks. First, the forget gate optimises the performance of the LSTM by filtering the information acquired from the previous time step to keep the information relevant for the system and discard the less critical ones. The forget gate takes as input the hidden state of the prior cell ($h_{t-1}$), the current input ($x_t$), the weight associated with the input ($W_{x,f}$) and the weight associated with the hidden state ($W_{h,f}$). Then, the sigmoid function $\sigma$ is applied to adjust the forget gate to output a number between 0 and 1 for each data point in the cell state $C_{t-1}$. The equation for the forget gate as

$$f_t=\sigma \left(W_{x,f}{x}_t+W_{h,f}{h}_{t-1}+b_f\right)$$

(28)

The input gate evaluates the importance of the input to decide which information to update using the following equation:

$$i_t=\sigma \left(W_{x,i}{x}_t+W_{h,i}{h}_{t-1}+b_i\right)$$

(29)

Next, the Rectified Linear Unit (ReLu) activation function is applied to create the new candidate values that could be used to update the cell state. The new information will have a value between −1 and 1 to remove the new data from the cell state if its value is negative or add the new data to the cell state if it is negative.

$${\tilde{C}}_t=ReLU\left(W_{x,c}{x}_t+W_{h,c}{h}_{t-1}+b_c\right)$$

(30)

The old cell state is updated as follows

$$C_t=f_t·C_{t-1}+i_t·{\tilde{C}}_t$$

(31)

This data manipulation is achieved using a sigmoid neural net layer and a pointwise multiplication operation. The sigmoid function outputs a vector of numbers between 0 and 1, representing the weight of each component in the cell state.

The output gate equation is expressed as

$$o_t=\sigma \left(W_{xo}{x}_i+W_{ho}{h}_{t-1}+b_o\right)$$

(32)

Finally, using the $o_t$ and $ReLu$ of the updated cell state $C_t$, the current hidden state is calculated as follows:

$$h_t=o_t·ReLu\left(C_t\right)$$

(33)

3. Hardware Description

This section encompasses the hardware design of the HMS for SOC estimation, fault detection, and health management of a Li-ion battery pack. The battery pack is constructed by connecting the LG-HG2 18650 lithium nickel cobalt manganese (NMC) battery in four parallel strings and two units in series (4S2P). The specification of the battery cell is listed in Table 1.

The schematic diagram of the proposed HMS is illustrated in Figure 8. The protection and measurement unit reads the current that flows in and out of the battery pack, the voltage across each cell, and the temperature variation within the battery pack at six different spots. The STM32F429 (STMicroelectronics, Geneva, Switzerland) sends the collected data to the Raspberry Pi3 (Raspberry Pi Foundation, Cambridge, United Kingdom) and waits for its orders. The Raspberry Pi3 evaluates the data report of each cell, checks if the operating conditions are respected, marks the cells with a critical state and carries out the HMS functionalities.

For the Li-ion battery to perform safely for a long period, the proposed HMS has a master–slave topology in which the slave unit (STM32F4) communicates with the battery and collects the data readings from the sensors’ platform with a 12-bit resolution. The master (Raspberry Pi3) receives the measured voltage, current, and temperature and handles computation and communication (see Figure 9).

Figure 10 summarises the functions of the HMS measurement and protection sub-unit. It is responsible for data gathering, typically voltage acquisition of the pack and the voltage of each battery, pack current collection and temperature measurement. The collected data are transmitted to the STM32F4 for analog-to-digital conversion. The cell balancing block controls the charge distribution of the cells by bringing all cells to the same SOC, while the overcharging protection block ensures that the battery functions within its SOA during the charge and discharge cycle. The slave unit communicates the converted data to the Raspberry Pi 3 through SPI communication. The Raspberry Pi uses the collected information to estimate the battery states and control the protection and management units.

3.1. Voltage Acquisition

The real-time measurement of individual cell voltage is a crucial task that is directly related to the performance of the HMS. It helps to keep the battery within its safe operating zone, spot cell voltage differences, and estimate its remaining capacity. For a pack of series-connected cells, the reference point remains constant, which hinders the individual cell voltage measurement. This problem does not appear for the first cell directly connected to the ground. Nevertheless, the voltage of other cells must be calculated based on the voltage of the previous cell. A simple way to assess this will be the usage of a voltage divider to map down the potential levels before measuring them. However, this will reduce the resolution of the voltage read to more than 0.1 V. In this study, two OPA4197s (Texas Instruments, Dallas, USA) are used to measure the voltage of each battery in the pack. The first Quad Op-Amp acts as a buffer circuit to prevent the cells from getting loaded individually, while the second forms a differential amplifier circuit. Figure 11 illustrates the circuit diagram for measuring the voltage across each battery of the pack.

Pins PA1-PA4 are connected to the ADC pins of the STM32F429 discovery board.

3.2. Current Measurement

In addition to voltage measurement, the HMS requires readings of the battery current which is essential for estimating the battery SOC and remaining useful life (RUL) and to perform security and safety functions. The accuracy of the current measurement will directly influence the performance of the HMS. Here, we propose using the Hall-effect-based current sensor ACS712-30A (Allegro Microsystems, Worcester, MA, USA) with a sensitivity of 66 mV/A to measure the current that flows from the pack to the load, as shown in Figure 12. The slave board receives the measured current through the PA0 ADC pin.

3.3. Temperature Measurement

LIBs are sensitive to temperature. High and low temperatures outside the optimal range of operation will accelerate the ageing process, leading to battery failure and even explosion. Thus, tracking temperature evaluation inside the pack is essential to ensure the pack cells operate within their SOA. The proposed HMS uses six 10 KΩ negative temperature coefficient (NTC) thermistors placed between the adjacent cells in the battery pack to measure the temperature. Figure 13 shows the temperature acquisition circuit. The thermistor is connected to a 10 KΩ fixed resistor, which is used as a reference to probe the decrease and increase in the NTC resistance. The STM32 (STMicroelectronics, Geneva, Switzerland) reads the resistance value and converts it to temperature using the Steinhart and Hart equation.

3.4. Cell Balancing

One major problem that the control system must tackle is voltage imbalance. This problem arises because of cell-to-cell variation and different charging histories, specifically when cells are connected in series. During operation, the uneven temperature distribution inside the pack and the varying internal resistance cause the cells to charge/discharge at various rates; some cells could drain before others, and thus, the pack is considered fully discharged while it still has available energy and vice versa.

Given the above, cell balancing is fundamental for the safety and longevity of the battery. It refers to the process of bringing the SOC levels of the pack cells closer to each other to maximise the battery’s capacity. In this study, we adopt passive cell balancing, a widely used technique by commercial BMS, to even out charge distribution. The method offers the best compromise between system performance and cost.

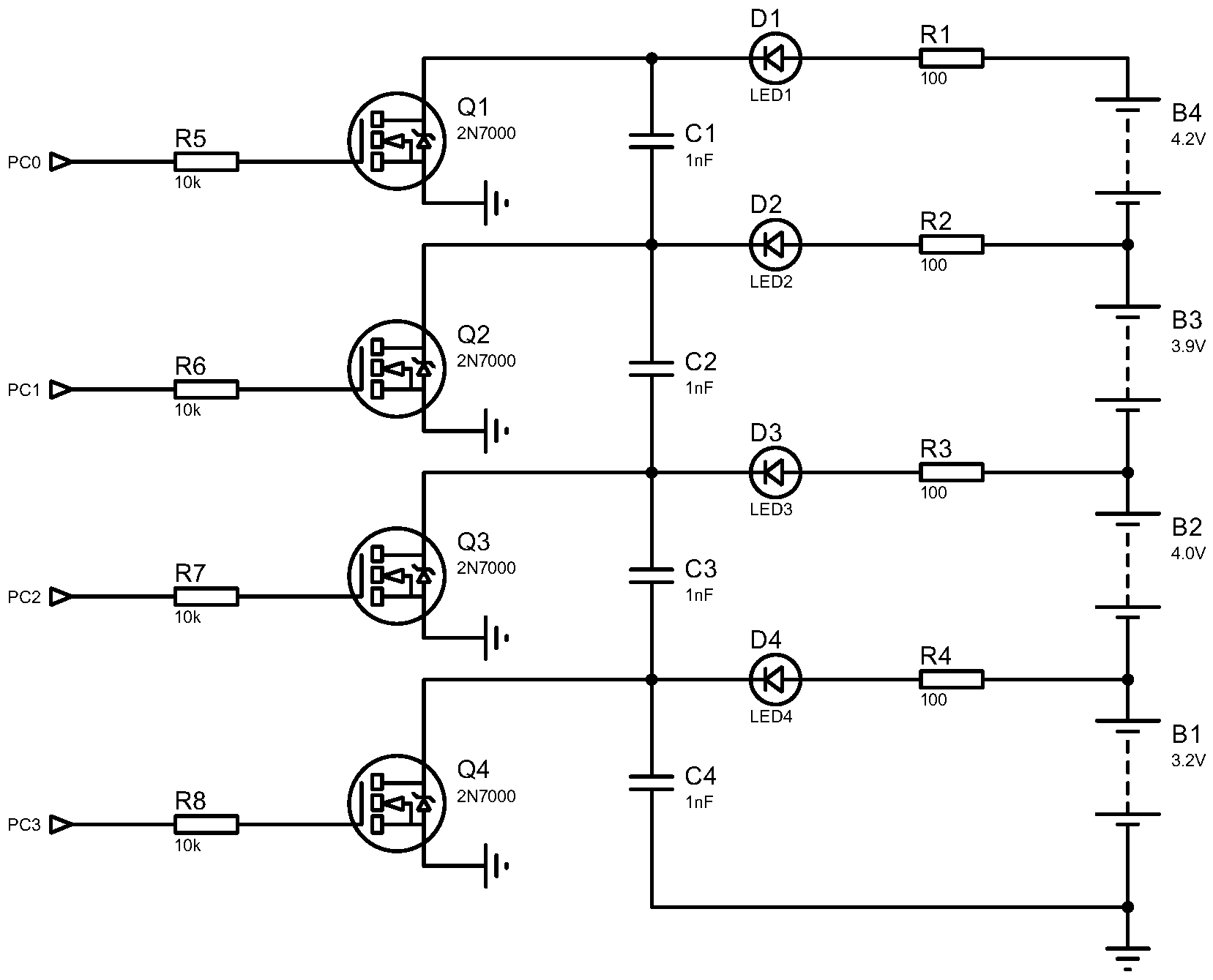
Figure 14 shows the proposed cell-balancing circuit diagram. PC0–PC3 pins are used to activate the battery equalisation circuit. When the voltage difference between cells exceeds the permitted value, the STM32 triggers the corresponding 2N7000 NPN MOSFET (ON Semiconductor, Phoenix, AZ, USA) to discharge the cell with a higher voltage. The 100 $\Omega$ resistance is the discharging resistance. Each cell is associated with an LED that lights on when balancing is activated.

4. Results and Discussions

4.1. Validation of the Proposed Battery Model

The EHPPC test presented in Section 2.1 is used to extract the relationship between the battery SOC and OCV. During the test, the battery is subjected to a series of dynamic pulses with varying magnitudes typical of the loading conditions of an EV. The battery SOC is identified using the CC method, and then the relationship between the OCV and SOC is acquired. Instead of relying on a look-up table to find the corresponding OCV value, a new method is proposed. It uses a seventh-order polynomial function to fit the OCV–SOC curve deviation.

The proposed model is defined as follows:

$$\begin{gathered} V_{ocv}\left(SoC\right)={\alpha }_1·So{C}^7+{\alpha }_2·So{C}^6+{\alpha }_3·So{C}^5+ \\ {\alpha }_4·So{C}^4+{\alpha }_5·So{C}^3+{\alpha }_6·So{C}^2+{\alpha }_7·So{C}^1+{\alpha }_8 \end{gathered}$$

(34)

Figure 15 shows the derived and fitted battery OCV–SOC curve. The fitted OCV was able to depict the OCV response with an RMSE of 0.0122 V.

Following this, the urban dynamometer driving schedule (UDDS) is applied to evaluate the performance of the proposed battery model. It is a standardised driving schedule developed by the United States Environmental Protection Agency (EPA) to simulate urban driving conditions. This cycle test is characterised by frequent stops and starts, representing typical city driving behaviour. The UDDS has become a standard for validating electric vehicle battery models due to its realistic driving conditions. The voltage and current profiles are shown in Figure 16. The test is conducted at various ambient temperatures of −10 °C, 10 °C, 25 °C and 40 °C.

The model voltage response is compared to the actual battery voltage response for each temperature, and the results are shown in Figure 17. It can be deduced from Figure 17 that the proposed battery model can accurately predict the battery terminal voltage even under extreme operating conditions. The estimation errors are bounded within −0.06 V, 0.06 V at −10 °C, −0.04 V, 0.03 V at 10 °C, −0.025 V, 0.026 V at 25 °C and −0.02, 0.02 V at 40 °C.

To further evaluate the performance of the proposed battery model, we tested the response of an offline 2RC-ECM model for which the parameters are assumed to be constant. The terminal voltage response of the offline method at 25 °C is illustrated in Figure 18.

Under the same operating conditions as the proposed battery model, the offline approach was not able to accurately simulate the battery response, where the estimation errors were relatively high (−0.25 V, 0.43 V).

4.2. SOC Validation

This section investigates the performance of the AN-SMO in estimating the battery SOC based on the online battery model developed in this study. The proposed system integrates FFRLS for continuous real-time parameter identification with the ANSMO to ensure robust SOC estimation. As FFRLS dynamically updates the parameters of the 2RC-ECM model (resistances and capacitances), ANSMO uses this updated model to compensate for non-linearities and uncertainties in real time, ensuring reliable and accurate SOC tracking even under varying operating conditions and battery ageing. The SOC estimation results and the SOC error under the UDDS at 25 °C and an initial capacity of 3 Ah are plotted in Figure 19. It can be seen from the results that the SOC estimation obtained by our proposed approach was able to track the reference SOC accurately. The absolute maximum estimation error of SOC is 1.082%, which has verified the usefulness of the proposed enhanced battery model in simulating battery response and improving the accuracy of the estimation.

In addition to evaluating the AN-SMO approach, its performance was compared against the EKF for SOC estimation. The EKF is a widely used method for SOC estimation due to its ability to handle non-linearities and measurement noise. However, it relies on a fixed model structure and does not adapt to changes in battery parameters over time, which may lead to reduced accuracy as the battery ages or as operating conditions vary.

As shown in Figure 20, the AN-SMO, combined with FFRLS, outperformed the EKF in terms of SOC tracking accuracy and robustness. While EKF-based estimation showed satisfactory performance under stable conditions, it exhibited greater estimation error under dynamic load changes due to its fixed parameter setup. In contrast, the AN-SMO dynamically adapted to the changing battery parameters, allowing for more accurate and reliable SOC tracking. As shown in the results, the AN-SMO achieved a maximum absolute SOC error of 1.082%, whereas the EKF’s maximum absolute SOC error was notably higher at approximately 2.81% under the same test conditions.

This comparison highlights the advantages of integrating FFRLS with AN-SMO for SOC estimation in applications where the battery experiences varying operating conditions and ageing effects. The adaptability of the AN-SMO approach ensures better long-term SOC estimation accuracy, making it a superior choice over traditional EKF for electric vehicle applications.

4.3. Cell-Balancing

To evaluate the performance of the HMS balancer circuit, we conducted a test using four cells with initial voltage values of 3.93 V, 4.08 V, 4.09 V, and 4.2 V, respectively. The graph in Figure 21 shows how the voltage of these cells converged over time. The voltage of the three cells decays slowly at different rates depending on the power being dissipated while the voltage of the first cell remains constant. The balancing process for the second and third cells stops around 325 s when their voltage is equal to that of the weaker cell, while it takes around 360 s for the fourth cell to balance.

The controller activated the MOSFET for the second, third, and fourth cells, causing them to discharge through the bleeding resistors until their voltage equalled the first cell. During this process, the LED is turned on to indicate that the equivalent cell is discharging (see Figure 22).

4.4. Overcharging Protection

Herein, we test the overcharging protection function of the proposed HMS. During the charging process, HMS tracks the SOC of each cell, as illustrated in Figure 23. The four cells used to evaluate the charging protection circuit had different initial SOCs. The fourth cell, with the highest initial SOC, was the first to reach the upper limit voltage while the three other cells were still charging.

The charging protection circuit activates for the fourth, as shown in Figure 24, to stop current from flowing into the battery and switch on the equivalent LED to indicate to the user that the charging is interrupted.

4.5. Battery Health

The health of the NMC battery pack is monitored using the LSTM approach. The accuracy of the proposed method is tested using the experimental data collected from the SNL Laboratory, as mentioned in the previous section.

First, we study the ageing behaviour of the NMC battery by analysing the capacity change with the number of cycles. The battery is fully charged and discharged at a rate of 0.5 C using a constant current constant voltage (CCCV) protocol as shown in Figure 25.

Figure 26 shows the variation of the battery voltage vs. capacity at room temperature (25 °C). It can be seen that both the charge and discharge curves have a similar pattern: they both shift to the left as the number of cycles increases, indicating a loss of capacity. This is further illustrated in Figure 27, which shows the discharge capacity change over the ageing cycles at three different temperatures (15 °C, 25 °C and 35 °C).

With the cyclic increase, the porosity of the electrode decreases due to the formation and the growth of the SEI film. It is apparent in Figure 27 that the capacity fade rate increased with decreasing temperature. The NMC battery capacity exhibits a fast decline at the low temperature of 15 °C. The loss rate is above 53 % during the first 500 cycles, indicating a severe deterioration of the battery’s health.

The capacity estimation result using the LSTM method is illustrated in Figure 28. Observing the LSTM estimation error (Figure 29), we notice some glitches around the fourth cycle, where the capacity estimation error reaches a maximum value of 0.04 Ah. This is due to the abnormal variation in the battery charge capacity, where the discharging current rate changed from 0.5 C to 1 C, doubling the battery cycle (see Figure 30).

Overall, the LSTM method showed good estimation results with an RSME of 0.0118 thanks to the excellent management of time series data regression.

The goal of battery capacity estimation is to serve as an indicator of the present health of the battery SOH, which helps to know how much the battery has aged over time and how much time is left before it reaches the EOL state. The NMC battery SOH is presented in Figure 31.

5. Conclusions

This work presents an HMS to monitor a 4s2p NMC battery pack. The proposed HMS adopts a master–slave topology, enhancing the system’s reliability and scalability. The platform performs efficient cell balancing, ensures over-charge protection, and monitors key parameters, including individual cell voltage, current drawn from the battery pack, and temperature variations at six hot spots.

An enhanced online battery model has been developed. The time-varying model parameters are identified in real time using the FFRLS algorithm, which helps optimise the battery usage, extend its lifespan and improve the accuracy of model-based approaches. The nonlinear OCV–SOC relationship is captured using a seventh-order polynomial function. The model showed good performance under a wide range of conditions, where the estimation errors under the UDDS test are bounded within −0.06 V, 0.06 V at −10 °C, −0.04 V, 0.03 V at 10 °C, −0.025 V, 0.026 V at 25 °C and −0.02, 0.02 V at 40 °C. The proposed model furthermore proved its accuracy when compared to an offline model. Following this, the AN-SMO was applied to estimate the battery SOC based on the proposed battery model. The algorithm was tested, and its accuracy was validated where the absolute maximum estimation error did not exceed 0.01082.

The LSTM approach effectively tracks battery capacity fade, demonstrating highly accurate predictions with capacity estimates closely aligning with actual measurements. Quantitatively, the proposed approach reduced the capacity prediction error by 15% compared to conventional methods, demonstrating its effectiveness in real-world applications. These findings show that the proposed HMS and battery model not only improve battery management precision but also contribute to extending battery lifespan and reducing degradation, offering a more robust solution for electric vehicle and energy storage systems.