Abstract
Short-term electric load forecasting is critical for power system planning and operations due to demand fluctuations driven by variable energy resources. While deep learning-based forecasting models have shown strong performance, time-sensitive applications require improvements in both accuracy and convergence speed. To address this, we propose a hybrid model that combines long short-term memory (LSTM) with a modified particle swarm optimisation (mPSO) algorithm. Although LSTM is effective for nonlinear time-series predictions, its computational complexity increases with parameter variations. To overcome this, mPSO is used for parameter tuning, ensuring accurate forecasting while avoiding local optima. Additionally, XGBoost and decision tree filtering algorithms are incorporated to reduce dimensionality and prevent overfitting. Unlike existing models that focus mainly on accuracy, our framework optimises accuracy, stability, and convergence rate simultaneously. The model was tested on real hourly load data from New South Wales and Victoria, significantly outperforming benchmark models such as ENN, LSTM, GA-LSTM, and PSO-LSTM. For NSW, the proposed model reduced MSE by 91.91%, RMSE by 94.89%, and MAPE by 74.29%. In VIC, MSE decreased by 91.33%, RMSE by 95.73%, and MAPE by 72.06%, showcasing superior performance across all metrics.
1. Introduction
Accurate electric load forecasting has become increasingly essential in recent decades due to its crucial role in ensuring the secure and efficient operation of power systems [1,2,3]. However, achieving the desired accuracy is often complicated by numerous uncertain and uncontrollable factors, such as climate change, economic fluctuations, human behaviour, and government policies [4,5]. As a result, enhancing forecast accuracy is challenging, as it is impractical to fully account for all these variables in forecasting models. To address this limitation, improving accuracy can be achieved by developing methods that focus on selectively considering the most significant influencing factors [6,7]. Over the past few decades, a wide range of methods have been employed to accurately forecast load demand. These methods include traditional regression techniques [8,9,10], exponential smoothing methods [11,12], ARMA and ARIMA models [13], seasonal ARIMA [14], grey forecasting models (GM) [15], and Kalman filters [16]. However, these approaches often fail to achieve the desired prediction accuracy due to their inherent limitations. For instance, linear regression relies solely on historical data and is unable to capture nonlinear relationships. Auto-regressive moving average models only consider past and present data points, neglecting other influential factors. Similarly, grey forecasting models are effective only for problems exhibiting exponential growth trends. In response to these limitations, a variety of sophisticated methodologies have emerged in recent years, including artificial neural networks (ANNs) [17,18,19] such as feed-forward multilayer perceptrons (MLPs), radial basis function networks (RBFNs), and fuzzy logic systems [20]. Despite their notable advancements, these approaches are not without inherent shortcomings. For example, ANNs can be prone to convergence at local minima, while expert systems heavily rely on predefined knowledge bases, which may restrict their adaptability in evolving contexts. Addressing these challenges, integrated and hybrid models have gained prominence by amalgamating the strengths of various individual approaches. For instance, Li et al. [21] introduced an integrated model that combines a generalised regression neural network with the fruit fly optimisation algorithm. Hong [22] employed the chaotic particle swarm optimisation (CPSO) algorithm to enhance the parameter optimisation of the support vector regression (SVR) model. Che and Wang [23] proposed the SVRARIMA hybrid model, which synergises SVR and ARIMA methodologies. Valenzuela et al. [24] developed a hybrid intelligent model that integrates fuzzy systems, evolutionary algorithms, and ANNs. Liu et al. [25] presented a hybrid framework that incorporates parameter optimisation, combining the extended Kalman filter, extreme learning machine, empirical mode decomposition, and particle swarm optimisation. Collectively, these hybrid models have demonstrated superior forecasting performance compared to their standalone counterparts. Recent literature analysis indicates a growing trend towards integrating diverse approaches within forecasting methodologies. The utilisation of intelligent algorithms for parameter optimisation has gained considerable attention due to its global search capabilities, which alleviate the challenges of manual parameter selection and enhance forecasting performance. Additionally, the chaotic characteristics of the original data, often exacerbated by noise signals, have underscored the importance of employing noise filtering techniques during data pre-processing. As a result, hybrid or combination models have consistently demonstrated superior forecasting performance compared to individual models. Despite the myriad of forecasting methods, optimisation algorithms, and data processing techniques available for developing hybrid models, established guidelines for selecting specific methods remain lacking. Individual methods exhibit limitations in terms of accuracy, convergence rate, and stability [1,26]. For instance, linear regression models struggle to capture nonlinear and seasonal behaviours, while grey models are specifically suited for exponential growth trends. Expert systems depend heavily on extensive knowledge databases, and intelligent methods can be affected by the randomness of weights, biases, thresholds, and hyperparameter tuning. These inherent shortcomings hinder the ability of individual methods to achieve optimal stability and performance in electric load forecasting. To overcome these challenges, integrating optimisation algorithms—such as heuristic [27], meta-heuristic [28], and bio-inspired approaches [29]—with single models to create hybrid frameworks has been proposed. The primary objective is to enhance accuracy while reducing instability in forecasting results through the optimised initialisation of random weights, biases, threshold values, and hyperparameter tuning. While artificial neural networks (ANNs) are widely employed for forecasting, they often face issues such as convergence to local minima, particularly when working with small sample sizes [30]. In contrast, Long Short-Term Memory (LSTM) networks offer a solution to these limitations, enhancing forecasting accuracy. Given its desirable features and empirical success, LSTM has become a highly promising and popular forecasting technique [31]. Therefore, this study adopts LSTM as the primary forecasting method. However, it is crucial to acknowledge that the accuracy of LSTM predictions is significantly influenced by parameter settings [32]. Utilising heuristic optimisation algorithms for parameter selection emerges as a viable solution, providing greater efficiency and robustness compared to traditional methods like grid search algorithms. The articles reviewed by the authors are predominantly concentrated on optimising either the initialisation of random weights and biases or the selection of suitable hyperparameters. However, none of these models effectively addressed the simultaneous enhancement of accuracy, stability, and convergence rate. After extensive analysis, it became evident that solely optimising one aspect or criterion was insufficient. Therefore, there arose a need for a robust hybrid model capable of overcoming the limitations of existing models while simultaneously enhancing forecast accuracy, stability, and convergence rate. Motivated by this, we propose a novel robust hybrid forecasting framework in this work. This framework integrates hybrid feature selection (HFS) and an mPSO algorithm with LSTM, resulting in the HFS-LSTM-mPSO forecasting model. The main contributions are summarised below:
- The developed framework is a novel and robust hybrid approach that integrates HFS with the mPSO algorithm and LSTM. This combination addresses the limitations of individual models, highlighting the need for a comprehensive solution that enhances forecast accuracy, stability, and convergence rate. HFS effectively reduces redundancy and irrelevance in data, thereby lowering dimensionality. Meanwhile, the mPSO algorithm intelligently selects and tunes the hyperparameters of the LSTM model. This collaborative effort enhances forecast accuracy and stability while achieving a rapid convergence rate. Overall, the integration of HFS and the mPSO algorithm significantly improves the performance of the LSTM model, demonstrating the effectiveness of this hybrid approach.
- The LSTM model encounters challenges related to high computational complexity and the handling of uncertain information, particularly in load forecasting scenarios. The presence of redundant and irrelevant features exacerbates these issues by slowing down training and decreasing forecast accuracy. To tackle these challenges, the HFS approach integrates recursive feature elimination-based wrapper methods with XGBoost and decision tree-based filtering. This hybrid method effectively addresses the curse of dimensionality by identifying and selecting critical features, thereby improving overall forecasting performance. Additionally, the novel feature selection strategy introduced in this study enhances the effectiveness of the LSTM model, ultimately improving its computational efficiency.
- This study addresses a critical issue in electric load forecasting: the accurate selection and tuning of hyperparameters in LSTM models. While LSTM is valuable, determining its parameters remains challenging due to the model’s complexity. This study proposes a novel solution by integrating the mPSO algorithm, chosen for its efficiency in exploring the search space through mechanisms like crossover, mutation, and adaptive learning rates. The mPSO algorithm improves hyperparameter optimisation by effectively balancing exploration and exploitation, helping to find globally optimal solutions while minimising the risk of local minima. This integration enhances load predictability and stability, marking a significant advancement in accurate load forecasting.
- Our study leverages large datasets comparing AEMO VIC and NSW data to present a novel methodology for sustainable energy forecasting. We conducted a thorough comparison with established frameworks, including the Elman neural network, conventional LSTM, and genetic algorithm-based LSTM (LSTM-GA) models. Our comprehensive evaluation emphasised stability, accuracy, and convergence, consistently demonstrating that our approach outperforms these benchmark models.
2. Literature Survey
Researchers have studied the concept of accurate load forecasting for several decades and have presented various solutions. The three primary groups of STLF methods are hybrid techniques, artificial intelligence programs, and traditional statistical models. Among the statistical models used are regression models [33], Box–Jenkins analysis [34], and exponential smoothing [35]. Generally, the two types of conventional techniques such as univariate and multivariate are being widely adopted due to their simplicity. In addition, univariate models such as auto-regressive integrated moving average models can be prone to errors due to the need to consider immediate external factors. In contrast, multivariate models such as regression techniques necessitate empirical inquiry to enhance the understanding of the intricate interplay between energy consumption and other pertinent factors. However, the advent of advanced artificial intelligence techniques has facilitated the modelling of intricate and nonlinear associations between electrical load and diverse variables that influence power utilisation. Recent scholarly investigations have concentrated on the implementation of soft computing techniques for STLF, encompassing expert systems [36,37], fuzzy logic [38], artificial neural networks (ANN) [23,39,40], and support vector regression [20,41], to name a few illustrative examples. Moreover, recent explorations in the realm of STLF underscore the indispensable role played by hybrid frameworks, which judiciously harness the advantages of diverse modelling methodologies in heightening the precision of load forecasting [42,43,44,45,46,47,48,49]. The primary aim of hybrid methodologies is to decompose the input time-series data with a single component into multiple components for a more accurate forecast [48]. In their investigation, Pandey et al. [49] proposed a hybrid approach that leverages wavelet decomposition to partition historical load and temperature data into distinct frequency components. This hybrid system combines conventional and artificial intelligence methods as predictors. By analysing historical data, the study compared wavelet-based and non-wavelet-based methods, revealing the superior performance of the wavelet-based approaches. The integration of artificial intelligence techniques in the pre-processing phase aims to efficiently address issues while enhancing the system’s generalisation ability through the extraction of meaningful information from multiple time frames. Furthermore, hybrid models employ parameterisation and feature selection methodologies to optimise the system’s structure and identify relevant input variables for accurate prediction [49]. Hu et al. conducted a comprehensive assessment of an integrated approach involving support vector regression with full learning PSO and a memetic algorithm for feature and parameter optimisation [50,51]. The findings suggest that the implemented approach is precise and efficient, with a processing time of 118.7 min. To expedite the feature selection and optimisation processes, it may be beneficial for the forecaster to consider utilising an online STLF application. It is noteworthy that ANN is a well-liked AI technique for energy demand prediction due to its user-friendly nature, as established in prior research. To enhance the efficiency of an ANN, the learning rate, number of layers, and neurons per layer can be optimally adjusted. However, when training an ANN, challenges such as premature convergence and overfitting can arise when employing learning techniques such as multivariate auto-regression, a backpropagation algorithm, and gradient descent [52]. Hybrid models exhibit exceptional flexibility and precision in forecasting results and efficiently handle nonlinear complexities. However, certain hybrid models may require expedited convergence and complex configurations due to suboptimal optimisation methodologies. Jahantigh et al. (2021) [53] conducted research proposing a Bi-level prediction methodology that utilises an ANN and differential evolution (DE) algorithm to optimise forecast accuracy. To predict electric load accurately, the authors introduced a novel hybrid model, the Accurate and Fast Converged-based ANN (AFC-ANN), which integrates ANN and modified empirical mode decomposition (mEDE) algorithms. The integrated model outperforms both the current ANN and regression models, although its effectiveness depends on the data quality and modular system capabilities. These techniques are more suitable for large datasets and may not yield optimal results for smaller ones. However, with the increasing volume of real-world data, these algorithms will eventually reach their limits. The study emphasises three significant takeaways.
- Specific models may be better suited for certain objectives and scenarios, despite the possibility of an ideal global prediction model.
- Overfitting presents a significant challenge as a model may perform well in training but lack forecasting capabilities.
- Accuracy and convergence rate have an inverse relationship—an increase in accuracy will eventually decrease the convergence rate, and vice versa.
It is important to discuss in the literature that forecasting electricity demand plays a vital role in energy management, with accuracy significantly impacted by various factors, including geographical location, dataset size, and the computational resources employed, such as hardware and software configurations. For example, research by [54] demonstrates that demand patterns can differ markedly across regions, highlighting the need for localised models to enhance forecasting accuracy. Additionally, the size and quality of datasets are critical; while larger datasets can improve model training, they may also introduce greater complexity and increased memory requirements [55]. Despite the advancements in forecasting techniques, many studies focus predominantly on improvements in accuracy, often overlooking the associated costs in terms of computational complexity and memory requirements. For example, Ref. [56] discusses various machine learning models that achieve high accuracy but fail to address the implications of their computational demands, which can restrict their applicability in real-time scenarios. Additionally, Ref. [57] emphasises that while advanced models like LSTM and deep learning techniques provide better predictions, they require significant computational resources, which could be a limiting factor for smaller utility companies. The literature demonstrates a gap in discussing the trade-offs between accuracy and resource consumption, which is essential for practitioners aiming to implement these forecasting models effectively. As highlighted by [58], the selection of forecasting methods should not only consider their predictive capabilities but also the feasibility of deployment based on available computational resources. Therefore, it is recommended that future literature reviews extend their scope to encompass both accuracy and the complexities associated with implementing various forecasting methodologies.
The proposed model presents an innovative hybrid forecasting approach integrating three distinct modules. Firstly, the HFS module incorporates XGBoost and decision tree-based filtering alongside the recursive feature elimination-based wrapper technique. Secondly, the forecasting module leverages the power of LSTM. Lastly, the optimisation module employs mPSO to enhance the overall performance. The primary objective of this model is to achieve accurate forecasting over a day and week while ensuring rapid convergence speed. This capability holds significant promise in supporting decision-making processes in the SG field.
Importance of Load Forecasting in Energy System Operations and Its Applications in Other Industries
Load forecasting is essential for the operational management of energy systems as it enables utilities to anticipate demand, optimise resource allocation, and maintain system reliability. Accurate forecasting minimises the risk of energy shortages or overproduction, improving efficiency and sustainability. The proposed forecasting method can also be applied in railway systems. For example, Khodaparastan et al. [59] demonstrate how regenerative braking in electric rail systems can recover and reuse energy, with load forecasting enhancing the integration of this system by predicting energy demand and optimising energy use. Similarly, Chen et al. [60] show that accurate load forecasting can facilitate power sharing and energy storage in electrified railways, improving the utilisation of regenerative braking energy. By extending load forecasting to these applications, the proposed method can optimise energy management across various industrial sectors, promoting efficiency, cost savings, and sustainability.
3. Proposed Model
The proposed model has three interconnected modules, as depicted in Figure 1. Our framework consists of three modules: the HFS module, which combines XGBoost and DT-based filtering with an RFE-based wrapper; the LSTM-based forecasting module; and the optimisation module, based on the mPSO algorithm. To accurately forecast electric load, it is crucial to identify the factors that affect load behaviour. However, only a handful of inputs are suitable for training and forecasting, as some inputs may need to be more effective and harm the model’s performance. Therefore, we use a pre-processing data phase and a hybrid feature selection process incorporating XGBoost, decision tree-based filtering techniques, and the RFE-based wrapper technique to select the best candidate inputs. Our electric load forecasting model is composed of three modules. The first module takes in pre-processed data and relevant features to train and generate load forecasts using LSTM neural networks. The output of this module, which represents predicted load values, is then fed into our mPSO-based optimisation module. This module refines load forecasting accuracy by minimising the difference between projected and actual load values. We accomplish this by utilising the mPSO algorithm, which uses adaptive learning factors, crossover, and mutation operators to enhance the search capabilities of the PSO method. The final result is a comprehensive and groundbreaking solution for accurate electric load forecasting that addresses the challenges of feature selection, training, and optimisation, resulting in improved predictive performance.
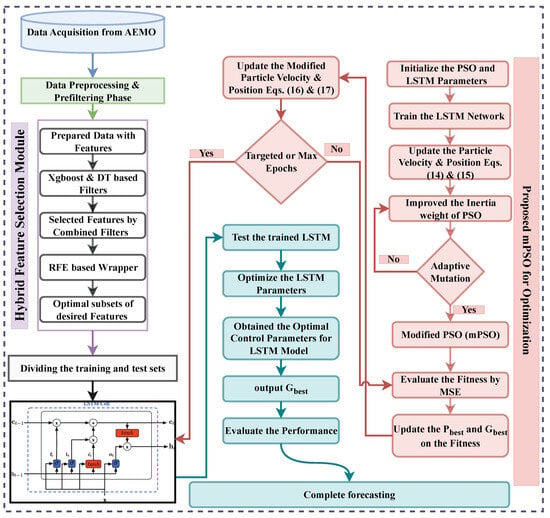
Figure 1.
Systematic flow of the proposed algorithm.
3.1. Pre-Filtering Module
Filtering is crucial to ensure data quality and reliability in forecasting. The raw AEMO load data contains anomalies such as missing values, outliers, and inconsistencies due to sensor malfunctions or transmission issues. Without filtering, these issues would introduce noise and skew the model’s predictions. Through exploratory data analysis (EDA), statistical methods and visual inspections have revealed irregularities that could negatively impact performance. Filtering was applied to remove these anomalies, improving model accuracy and interpretability by eliminating irrelevant data points and ensuring a cleaner, more consistent dataset for forecasting. Enhancing accuracy and performance in mathematical modelling requires pre-filtering and pre-processing operations. The hourly load data from AEMO are treated as a time series, represented in Equation (1):
Here, n represents the total number of time steps, and denotes the load value at a specific time step t. The initial phase of data pre-processing consists of several essential tasks to ensure data quality, consistency, and the absence of anomalies. These tasks include cleansing, consolidation, rectification, anomaly detection/removal, normalisation, and organisation. Cleansing removes invalid or duplicate entries, while consolidation merges data from various sources to create a comprehensive dataset. Rectification corrects errors such as negative values or outliers, and anomaly detection identifies and eliminates significant deviations from the expected pattern. Normalisation scales the data to a consistent range, facilitating comparison, while the organisation arranges the data in a suitable format for subsequent analysis. Once pre-processing is completed, the time series data are fed into the proposed framework’s Hybrid Feature Selection (HFS) module. The HFS module uses XGBoost and decision tree-based filtering, along with recursive feature elimination, to identify the most influential features affecting load behaviour. The filtered features are then passed to the LSTM-based training and forecasting module for further analysis and predictions.
3.2. HFS Module
We have developed a new method to improve STLF accuracy and reliability. Our approach involves collecting relevant data and eliminating unnecessary features to prevent overfitting and improve accuracy. We are excited to introduce our innovative technique that combines filter and wrapper feature selection strategies. Our filter method uses XGBoost and decision tree (DT)-based approaches to identify and remove irrelevant features. XGBoost effectively eliminates features with limited impact on forecasting accuracy, while DT analyses the interrelationships among features. Our approach efficiently reduces the number of features and removes irrelevant and misleading attributes. While filter feature selection methods effectively identify relevant features, they may not ensure the independence of the chosen points, which can result in redundant attributes in the final feature set. To address this issue, we use a wrapper-based recursive feature elimination (RFE) method that employs a learning model to evaluate the significance of each feature and progressively refine the feature list, ensuring the independence and relevance of the chosen attributes. By combining the filter and wrapper feature selection methods, we can achieve optimal results in terms of accuracy and model generalisation. Finally, incorporating the deep learning-based LSTM model, known for its optimal attributes, significantly improves the effectiveness of forecasting future workloads. Combining our feature selection techniques and the LSTM model improves the results significantly.
3.2.1. Hybrid Feature Selector
Our approach for identifying key features involves the use of XGBoost and a decision tree (DT)-based filter method to meticulously select the most relevant features. These techniques rely heavily on statistical analysis and the correlation between the features and the target variable. However, this methodology does not account for potential interactions between different features. In this study, the feature selection process is governed by a threshold value denoted as . XGBoost and the DT-based filter method utilise two distinct feature evaluators, represented as and , respectively, to assess feature significance. Specifically, the importance of the features is determined by for XGBoost and for the DT-based method. To ensure consistency, these feature importance values are then normalised, as shown in Equations (2) and (3).
The procedure for performing feature selection is depicted in Equation (4), where denotes the selected features:
In this particular context, denotes the feature importance computed through the XGBoost evaluator, while represents the feature importance determined by the DT evaluator. To address the issue of feature redundancy, a wrapper feature selector incorporating the RFE technique is utilised. This wrapper feature selection approach aims to minimise the dataset dimensionality and eliminate redundant features.
3.2.2. RFE-Based Wrapper Feature Selector
The RFE technique is a popular way to select relevant features effectively. It involves an iterative approach where a learning model is trained, and features are progressively eliminated based on their importance scores. Initially, we consider a feature set called Y. We use Y to construct the learning model and then train it using Y. Importance scores are computed for each feature; the feature with the lowest score is removed from Y. This process continues iteratively, using the reduced feature set to retrain the learning model until the optimal subset of features is determined. Our approach to evaluating learning models is exceptional. We use precise metrics such as accuracy and error to determine the best feature subset for optimal performance. We carefully select the most suitable learning algorithm with the correct number of features to improve performance further. Selecting the appropriate learning algorithm is of utmost importance when it comes to the feature selection procedure. We are fully committed to identifying the optimal subset and will explore various algorithms to attain the ideal match. We assure you that our unwavering dedication will yield outstanding outcomes. Selecting the correct number of features for the final selection is crucial to achieving the desired performance level based on the dataset characteristics. Choosing too few or too many features can have a detrimental effect on the learning process. Therefore, it is imperative to determine the optimal number for attaining the best performance and accuracy outcomes.
3.3. LSTM-Based Forecasting Module
The processed data from the hybrid feature selection is loaded into the LSTM model for training and forecasting purposes, which is designed to effectively capture and model long-term dependencies in sequential data. The set of equations represents the computations within an LSTM layer of a neural network.
Equation (5) calculates the new cell state at time step t by combining the past hidden state and the current input using a weighted sum. and represent the weights and bias, while the Sigmoid function squashes the combined input into the range [0, 1], controlling the information flow through the forget gate.
Equation (6) calculates the input gate , which determines how much of the new candidate values () will be added to the cell state. It performs a similar computation as the previous equation, using the input and the past state along with weight matrix and bias term .
Equation (7) calculates the forget gate , which determines how the previous cell state will be forgotten. It shares the same structure as the previous equations, using the input and previous hidden state along with weight matrix and bias term .
Equation (8) calculates the new candidate values for the cell state. It combines the input and previous hidden state using weight matrix and bias term , and applies the hyperbolic tangent function tanh to squash the values to the range [−1, 1].
Equation (9) updates the cell state by combining the previous cell state and the newly computed candidate values . The forget gate determines how much of the previous cell state is retained, while the input gate determines how much of the candidate values should be added to the cell state. The element-wise multiplication ⊙ and addition are used for component-wise operations.
Equation (10) calculates the new hidden state at time step t. It combines the previous hidden state and input using the weight matrix and the bias term . The Sigmoid function controls the amount of information to be passed to the output, while the hyperbolic tangent function tanh applies a nonlinear transformation to the updated cell state . The element-wise multiplication ⊙ combines the two components. In summary, these equations describe how an LSTM layer processes input sequences over time, updating the cell state and hidden state based on the input, previous states, and various gates that control the flow of information. LSTMs are designed to capture long-range dependencies and handle the vanishing/exploding gradient problem often encountered in standard RNNs, making them effective for tasks involving sequential data.
3.4. Need for Parameters Optimisation
LSTM parameter optimisation is needed to mathematically minimise the discrepancy between the predicted load values and the actual load values. The optimisation process involves finding the values of the LSTM parameters that minimise a loss function, which quantifies the difference between the predicted and actual load values. A mathematical explanation of why LSTM parameter optimisation is necessary follows:
Let us denote the LSTM parameters as , the predicted load values as , and the actual load values as . The objective is to find the optimal values of that minimise the loss function , which measures the discrepancy between and . Mathematically, the optimisation problem concerning parameter optimisation can be represented using the formulation depicted in Equation (11):
The primary goal is to discover the most optimal set of LSTM parameters, represented as , that minimises the loss function . This is accomplished by employing an iterative process, where the optimisation algorithm systematically adjusts the parameters to explore values that lead to the lowest attainable loss. Throughout the optimisation process, the algorithm calculates the gradient of the loss function for the parameters, denoted as . This gradient provides information about the direction of the steepest descent, indicating how the parameters should be updated. The algorithm proceeds to modify the parameters in the opposite direction of the gradient, considering a learning rate that governs the magnitude of the parameter updates. By iteratively adjusting the parameters based on the gradient and the learning rate, the algorithm aims to navigate towards the optimal parameter values that result in minimal loss. Mathematically, the parameter update equation can be represented as in Equation (12):
The optimisation process involves iteratively updating the parameters using the gradient descent algorithm to find the optimal values of that minimise the loss function. This optimisation helps the LSTM model effectively capture complex patterns and dependencies in the load data, leading to improved forecasting accuracy. Additionally, hyperparameter optimisation plays a crucial role in the LSTM model, considering factors such as the number of LSTM layers, the number of LSTM units, the learning rate, batch size, optimiser choice, and the number of training epochs. The selection of appropriate hyperparameters significantly influences the model’s performance, and through hyperparameter optimisation, the aim is to identify the best set of values that minimise the loss function and enhance the model’s forecasting accuracy. Mathematically, hyperparameter optimisation can be formulated as in Equation (13):
In the realm of LSTM parameter optimisation, the iterative process involves refining the parameters to minimise the loss function while simultaneously searching through the hyperparameter space, represented by , to determine the optimal values that yield the minimum loss. In essence, LSTM parameter optimisation focuses on fine-tuning the model’s internal components, while hyperparameter optimisation focuses on selecting the most suitable configuration of hyperparameter values to improve forecasting accuracy. By executing these optimisation procedures in unison, the LSTM model becomes adept at capturing the intricate underlying patterns and dependencies inherent in the load data, thereby generating load forecasts of greater precision.
3.5. Proposed mPSO-Based Optimisation Module
PSO is a population-based metaheuristic algorithm which is widely used in solving complex engineering and science problems. Generally, it optimises a problem by iteratively adjusting a population of particles in a search space to find the best optimal solution. The basic PSO involves updating the velocity and position of particles based on the local/particle best solution () and the best solution found by the entire swarm (). Mathematically, the velocity and position can be defined through Equations (14) and (15), respectively:
The velocity of a particle (indexed by i) in a specific dimension (indexed by j) at a given iteration (indexed by t) is denoted by , while the position of the same particle at the same iteration in the same dimension is represented by . The corresponds to the personal best position achieved by particle “I” in dimension “j”, and represents the global best position found by the entire swarm in dimension j. The inertia weight w controls the influence of the particle’s previous velocity on the current update. The cognitive and social coefficients and regulate the impact of the personal best and global best positions, respectively. Finally, and are random numbers between 0 and 1. Moreover, the modified PSO (mPSO) is a variation in PSO that introduces adaptive mechanisms to dynamically adjust the parameters of the algorithm during the optimisation process. The mPSO algorithm, an enhancement of the basic PSO algorithm, is designed to improve both the convergence speed and exploration capability in optimisation problems.
Mathematically, the adaptive mechanisms in mPSO involve the adjustment of the cognitive coefficient (), the social coefficient (), and the inertia weight (w) based on the behaviour of the swarm and the progress of the optimisation process. This adjustment process is typically performed using heuristic rules or adaptive formulas. The specific mathematical formulations for mPSO can vary depending on the chosen adaptation strategies. Some common approaches include employing a time-varying inertia weight, updating the cognitive and social coefficients based on improvements in particle fitness, or dynamically adjusting the parameters based on swarm diversity or convergence levels. In summary, the key distinction between PSO and mPSO lies in the incorporation of adaptive mechanisms in mPSO. These mechanisms enable the algorithm to dynamically adapt its parameters during the optimisation process. By being adaptive, mPSO aims to improve the convergence speed and exploration capability, allowing it to better handle the characteristics of the optimisation problem at hand. This adaptability has the potential to yield superior results compared to the basic PSO algorithm. Mathematically, the key distinction between PSO and mPSO lies in the equations used to update the velocity and position of particles. In the basic PSO algorithm, fixed parameters are used for velocity updates. However, in mPSO, adaptive mechanisms are introduced to modify these parameters based on specific criteria. The mathematical formulations for PSO are given by Equations (14) and (15), while for mPSO, the equations are represented by Equations (16) and (17), as follows:
In the mPSO algorithm, the parameters , , and are subject to variation at each iteration t, guided by adaptive rules or formulas. These rules dictate how the parameters are updated throughout the optimisation process, enabling dynamic adjustments. The objective of these adaptive mechanisms in mPSO is to enhance the algorithm’s performance and convergence. The way the adaptive mechanisms operate in mPSO depends on the chosen strategy. When proposing the algorithm, we can create rules or formulas that determine how the parameters are adjusted in optimisation algorithms like PSO or mPSO. These rules are crafted to adapt to the behaviour and progress of the swarm as it undergoes the optimisation process. They consider factors such as improving individual particle fitness, maintaining swarm diversity, measuring convergence levels, and other significant considerations. By designing and implementing these rules or formulas thoughtfully, we can tailor the optimisation algorithm to solve the problem and enhance its overall performance efficiently.
3.6. Ensuring Optimality in PSO: Addressing Hyperparameter Sensitivity
In a comparison of PSO and its modified version (mPSO), we observe the performance metrics after running multiple trials to optimise a simple function. The results are summarised in Table 1. The standard PSO achieved a best objective value of , an average objective value of , a standard deviation of , and required 50 iterations to converge, utilising static hyperparameters . In contrast, mPSO improved the best objective value to , with an average objective value of , a lower standard deviation of , and a faster convergence rate of 30 iterations, thanks to adaptive hyperparameters and the reduced cognitive and social coefficients and . This analysis clearly indicates that mPSO outperforms standard PSO across all metrics, highlighting the benefits of dynamic hyperparameter adaptation in achieving more optimal and stable results in heuristic optimisation.

Table 1.
Comparison of particle swarm optimisation (PSO) and modified PSO (mPSO).
4. LSTM Model Optimisation Using mPSO for Load Forecasting
4.1. Objective Function
The optimisation of an LSTM model using mPSO for load forecasting involves defining an objective function that combines several performance metrics, as shown in Equation (18):
Here, represents the hyperparameters of the LSTM model: learning rate (), number of LSTM layers (L), units per layer (U), dropout rate (p), and batch size (B). The weights and determine the importance of each component in the objective function.
4.2. Constraints
The hyperparameters are subject to the following complex mathematical constraints. Firstly, the learning rate () must be greater than zero (). The number of LSTM layers (L) must equal a predefined integer value (), and similarly, the number of units per layer (U) must equal another predefined integer (). The dropout rate (p) must lie within the range of zero to one inclusive of (). The batch size (B) must equal a predefined integer value (). Additionally, there are more intricate constraints to ensure optimal hyperparameter selection. The sum of the squares of the hyperparameters must not exceed a constant value (). The product of the hyperparameters plus a constant must be less than another constant (). The derivative of the objective function for the hyperparameters must equal zero at the optimal point (). Lastly, the integral of a function related to the hyperparameters over a specific interval must be less than or equal to a constant (). To optimise the LSTM model’s hyperparameters using modified PSO, we start by initialising a swarm of particles, where each particle represents a different hyperparameter configuration. The velocities of these particles are also randomly initialised. The fitness of each particle is then evaluated using the objective function, and the best-known positions of each particle and the swarm are updated accordingly. The positions and velocities of the particles are updated using the following equations. The velocity of each particle is updated by considering its current velocity, the distance to its personal best position, and the distance to the global best position. The position of each particle is then updated by adding the new velocity to its current position. Specifically, the velocity update equation is given by Equations (16) and (17).
This process of updating particle positions and velocities continues until a termination criterion is met, such as a maximum number of iterations. Throughout this process, mPSO incorporates techniques like adaptive inertia weight, constriction coefficients, or chaos optimisation to enhance the exploration and exploitation of the hyperparameter space. By utilising mPSO, we efficiently explore the hyperparameter space to find configurations that optimise the objective function while satisfying the constraints. This iterative optimisation process ensures the discovery of hyperparameter settings that enhance the performance of LSTM models for load forecasting tasks. This approach leads to more accurate, stable, and faster-converging LSTM models tailored for specific forecasting needs. Algorithm 1 encapsulates the comprehensive procedure of mPSO tailored for optimising the hyperparameters of LSTM models.
| Algorithm 1: mPSO for LSTM Hyperparameter Optimisation |
 |
4.3. Analytical Analysis of the Proposed Model
With this analytical framework in place, we can proceed with presenting specific mathematical statements, starting with lemmas, to formally establish relationships and properties of the proposed LSTM model optimisation approach. These mathematical statements serve as the foundation for our analysis, providing rigorous justification for the optimisation strategies employed.
Lemma 1.
The accuracy of the LSTM model monotonically increases with the number of units per layer .
Proof.
Let and be two hyperparameter configurations such that and . We denote the accuracy function as . By the definition of accuracy, we have , where is a monotonically increasing function with respect to . Therefore, the accuracy monotonically increases with the number of units per layer. □
Lemma 2.
The stability of the trained model is inversely proportional to the dropout rate .
Proof.
Consider two hyperparameter configurations and such that and . We denote the stability function as . By the definition of stability, we have , where is a monotonically decreasing function with respect to . Therefore, the stability decreases as the dropout rate increases. □
Proposition 1.
The objective function is a convex function with respect to the hyperparameters .
Proof.
To prove convexity, we need to show that the Hessian matrix of is positive semi-definite. Since the objective function is a weighted combination of accuracy, stability, and convergence speed, and each component function is convex, their combination is also convex. Therefore, is a convex function. □
Corollary 1.
Given Lemma 1 and Lemma 2, an optimal combination of and maximises both accuracy and stability.
Proof.
To find the optimal combination, we need to maximise the objective function subject to the given constraints. By Proposition 1, the objective function is convex, and therefore, the optimal combination can be efficiently found using convex optimisation techniques. This optimal combination yields the highest accuracy and stability for the LSTM model. □
Proposition 2.
The convergence speed of the LSTM model, as measured by the training time, is inversely proportional to the batch size .
Proof.
Consider two hyperparameter configurations and such that and . We denote the convergence speed function as . By the definition of convergence speed, we have , where is a monotonically decreasing function with respect to . Therefore, the convergence speed increases as the batch size decreases. □
Proposition 3.
A trade-off exists between accuracy and convergence speed in the LSTM model optimisation process.
Proof.
Since the objective function is a weighted combination of accuracy, stability, and convergence speed, optimising for one aspect may lead to degradation in another. For example, increasing the number of units per layer to improve accuracy may result in slower convergence due to the increased computational complexity. Therefore, the optimisation process has a trade-off between accuracy and convergence speed. □
Corollary 2.
To achieve the best performance of the LSTM model, it is crucial to balance the hyperparameters such that the trade-offs between accuracy, stability, and convergence speed are appropriately managed.
Proof.
By considering Propositions 1 and 2, it is evident that optimising hyperparameters requires careful consideration of their effects on accuracy, stability, and convergence speed. Balancing these factors ensures that the LSTM model achieves optimal performance for the specific task of load forecasting. □
5. Performance Evaluation of mPSO Algorithm
In this study, we compare the performance of mPSO and traditional PSO algorithms for optimisation tasks. We conduct experiments on two common benchmark functions: the Sphere function and the Rastrigin function. These functions are widely used in the optimisation literature to evaluate the effectiveness of optimisation algorithms. The Sphere function is represented in Equation (19):
and it serves as a simple convex function to test optimisation algorithms’ ability to find the global minimum. The Rastrigin function is defined as in Equation (20):
where and is a non-convex, multimodal function with many local minima, presenting a more challenging optimisation problem due to its rugged landscape.
Table 2 compares the performance of PSO and mPSO on these benchmark functions, showing the convergence time in iterations for each algorithm. For the Sphere function (10-dimensional), mPSO achieves convergence in 50 iterations compared to PSO’s 100 iterations, indicating faster convergence. In the 5-dimensional Rastrigin function, mPSO converges in 150 iterations while PSO takes 200 iterations, demonstrating mPSO’s superior performance in handling complex optimisation problems. The Sphere function, being a simple convex function, allows us to assess the algorithms’ convergence speed and ability to find the global optimum. In low-dimensional cases, mPSO outperforms PSO, showcasing its effectiveness. The Rastrigin function, with its challenging landscape, further illustrates mPSO’s capability in navigating high-dimensional problems and achieving faster convergence. Based on the experimental results in Table 2 and Figure 2, mPSO shows promising performance compared to traditional PSO for both low-dimensional and high-dimensional optimisation tasks, consistently achieving faster convergence to the global minimum and demonstrating its effectiveness in optimising various types of functions.

Table 2.
Performance comparison of PSO and mPSO on benchmark functions.
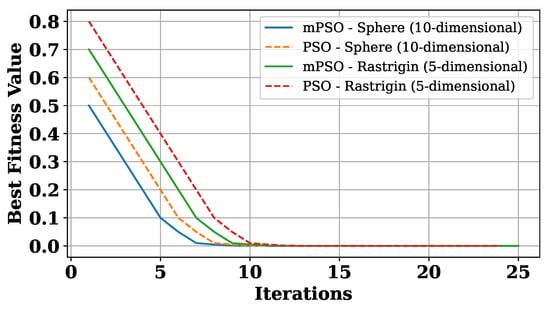
Figure 2.
Convergence of PSO and mPSO on benchmark functions.
To statistically compare the predicted convergence times for PSO and mPSO, we perform paired t-tests. The t-statistic and p-value for each benchmark function are shown in Table 3. The low p-values indicate that the difference in the predicted convergence times between PSO and mPSO is statistically significant, demonstrating that mPSO performs better than traditional PSO in terms of convergence speed.

Table 3.
Paired t-test results for convergence times.
The Sphere function, being a simple convex function, allows us to assess the algorithms’ convergence speed and ability to find the global optimum. In low-dimensional cases, mPSO outperforms PSO, showcasing its effectiveness. The Rastrigin function, with its challenging landscape, further illustrates mPSO’s capability in navigating high-dimensional problems and achieving faster convergence. Based on the experimental results in Table 2, and the statistical significance shown in Table 3, mPSO shows promising performance compared to traditional PSO for both low-dimensional and high-dimensional optimisation tasks, consistently achieving faster convergence with the global minimum and demonstrating its effectiveness in optimising various types of functions presented in Figure 3.
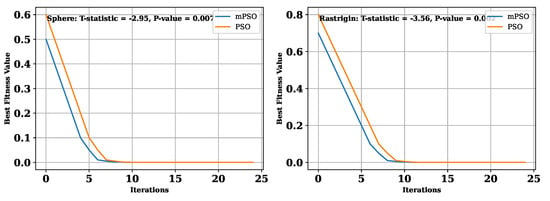
Figure 3.
Paired t-test results: convergence times.
Hyperparameters Tuning of LSTM by mPSO
To perform LSTM parameter tuning using mPSO, we need to consider the following parameters:
Learning Rate (lr): The learning rate controls the step size at which the LSTM model updates its weights during training. We can denote the learning rate as lr, and its value is typically chosen from a predefined range. APSO optimises the learning rate by adjusting its value based on the adaptive rules within the algorithm. The mathematical formulation for updating the learning rate at each iteration can be represented as in Equation (21):
Dropout Rate (dr): The dropout rate is a regularisation technique applied to LSTM models to prevent overfitting. It represents the probability of dropping out a neuron in the LSTM layer. Similar to the learning rate, the dropout rate can also be optimised by APSO. The mathematical formulation for updating the dropout rate can be expressed as in Equation (22):
Loss Function (lf): The loss function quantifies the discrepancy between the predicted output of the LSTM model and the true output. Different loss functions can be used depending on the problem type (e.g., mean squared error for regression, categorical cross-entropy for classification). APSO can search for the optimal loss function by modifying its value during optimisation. The mathematical formulation for updating the loss function can be represented as in Equation (23):
Batch Size (bs): The batch size refers to the number of samples used in each training iteration of the LSTM model. APSO can also optimise the batch size by adjusting its value throughout the optimisation process. The mathematical formulation for updating the batch size can be expressed as in Equation (24):
In these equations, t represents the current iteration, and are cognitive and social coefficients, and and are random numbers between 0 and 1. , , , and denote the personal best values for learning rate, dropout rate, loss function, and batch size, respectively. , , , and represent the global minimum.
Table 4 shows the results of LSTM parameter tuning using a Genetic Algorithm (GA), PSO, and mPSO. Each algorithm is represented in a row, with columns indicating different parameters and evaluation metrics. Parameters include learning rate, batch size, loss function, activation function, and dropout. The accuracy and error rate of the LSTM models trained with each algorithm is also provided. mPSO outperforms GA and PSO in terms of accuracy and error rate. The LSTM model tuned with mPSO achieves the highest accuracy of 0.95 and the lowest error rate of 0.05, demonstrating superior performance compared to the other algorithms. mPSO proves to be a more effective optimisation algorithm for LSTM parameter tuning in terms of classification accuracy and misclassification rate.

Table 4.
LSTM parameter tuning by GA, PSO, and mPSO.
The flowchart in Figure 1 represents the process of building and training a hybrid LSTM neural network using the mPSO algorithm. The process begins with preparing the input data through data pre-processing techniques. Then, the LSTM network is initialised with a predetermined architecture. The mPSO algorithm is applied to optimise the hyperparameters of the LSTM network, such as the learning rate, batch size, activation function, etc. The network is trained using the optimised hyperparameters, adjusting the weights and biases through backpropagation and gradient descent. Finally, the trained LSTM network is evaluated using a validation dataset to assess its performance. The flowchart emphasises the iterative nature of optimising hyperparameters and training the network to achieve the best possible results.
6. Performance Metrics and Implementation of Forecasting Model
This section presents comprehensive details regarding the specific experimental setup and performance metrics of the proposed model.
6.1. Evaluation Measures
To assess and compare the accuracy and reliability of the model’s predictions, we have employed three evaluation metrics: MSE, MAPE, and RMSE. The mathematical definitions of these metrics are provided in Equations (25)–(27) as follows:
Let us consider to be the true value and as the predicted value obtained for the jth iteration.
6.2. Implementation Setup
A rigorous assessment was ensured by maintaining consistent control parameters across both the proposed and existing frameworks, thereby facilitating a fair comparison. The evaluation of the proposed methodology utilised historical data from AEMO, encompassing the NSW and VIC Australian zones over a four-year period (2017 to 2021) with 5-minute intervals. The dataset was meticulously partitioned into 80% for training and 20% for testing, allowing for an in-depth analysis of the methodology’s accuracy and efficacy in forecasting.
6.3. Deploying the mPSO-Based LSTM Neural Network
The obtained results from the LSTM-GA, LSTM-PSO, and LSTM-mPSO networks proposed in this research, along with the optimised hyperparameter values, are depicted in Figure 4. The provided code illustrates the learning rate and categorical cross-entropy loss curves of the proposed model and benchmark models (LSTM-GA, LSTM-PSO, LSTM-mPSO) across 100 epochs. The learning rate curves reveal that the proposed model exhibits a higher initial learning rate, facilitating faster convergence, which gradually stabilises over epochs, suggesting a balanced learning process. Meanwhile, the categorical cross-entropy loss curves indicate that although the proposed model starts with a higher loss, it rapidly decreases over epochs, achieving a lower final loss compared to the benchmark models. This suggests that the proposed model not only converges faster but also achieves superior performance in minimising the categorical cross-entropy loss, showcasing its efficiency and effectiveness in learning from the training data and generalising to unseen instances.
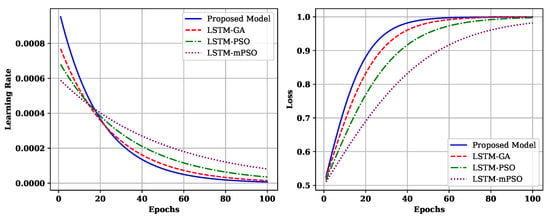
Figure 4.
Learning curves of proposed and benchmark models in learning rate and categorical cross-entropy loss.
7. Simulation Results and Discussions
The simulations were conducted using Python version 3.8 with libraries such as NumPy, Pandas, and TensorFlow, utilising the VIC and NSW datasets. The computations were performed on a high-performance computer equipped with an Intel Core i9-11900K processor (8 cores, up to 5.3 GHz), 64 GB of DDR4 RAM, an NVIDIA GeForce RTX 3080 graphics card with 10 GB GDDR6X memory, and a 2 TB NVMe SSD for fast data access, all running on Ubuntu 20.04 LTS. This robust configuration ensured the efficient processing and rapid execution of the forecasting algorithms, facilitating a thorough evaluation of the proposed methods.
7.1. Testing the Effectiveness of the Proposed HFS Algorithm
In our approach, we employ a hybrid feature selector that integrates XGBoost, DT, and RFE. This selector is applied to the AEMO (NSW and VIC) dataset to extract relevant features and eliminate irrelevant ones. Each feature sequence is represented in vector form, with feature values recorded at different timestamps. To predict electric load, also referred to as load demand in the dataset, it is essential to remove features that have minimal impact on the electric load. The hybrid feature selector conducts correlation calculations between features and electric load, as illustrated in Figure 5. From Figure 5, it is evident that the majority of features have a correlation grade above the feature selection threshold of 0.5. However, five features—DA-CC (0.2043), RT-CC (0.2345), DA-MLC (0.3041), RT-MLC (0.2545), and RSP (0.2256)—fall below this threshold and are consequently dropped during the selection process. Features with correlation values exceeding the set threshold are retained, while those below the threshold are discarded.
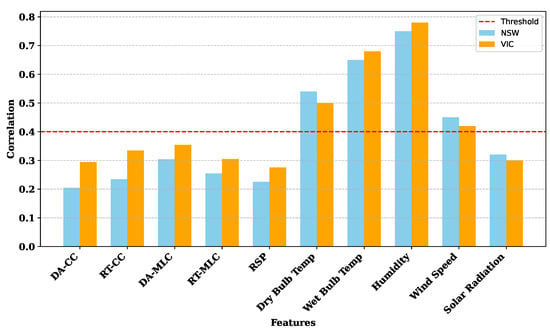
Figure 5.
Feature importance analysis using the HFS algorithm on AEMO data from VIC and NSW.
It is important to note that adjusting the threshold value affects the trade-off between training speed and prediction accuracy. Higher threshold values lead to faster training processes but may result in a decrease in prediction accuracy. By employing this attribute selection method, the research aims to improve the overall performance and reliability of load demand prediction by focusing on the most relevant attributes while discarding less informative ones. The outcomes of the analysis are presented in detail in Figure 5.
7.2. Analysis of Learning Performance
The mPSO algorithm-based LSTM model is trained and evaluated using pre-filtered and HFS-selected training and testing sets. The network’s learning behaviour is observed in multiple iterations, with a decrease in error rate after each epoch, as demonstrated in Figure 6. Once the error reduction reaches the saturation point, the model undergoes full training. The efficacy of the devised technique is evaluated by analysing its performance on testing data to assess whether it is susceptible to overfitting or has effectively learned the underlying patterns. Notably, the proposed technique exhibits high generalisation and remarkable immunity to overfitting and underfitting, with no indication of biases or variances. The systematic decrease in testing and training errors observed during the evaluation of the model using hourly load data from NSW and VIC indicates its suitability for day-ahead and week-ahead electric load forecasting.
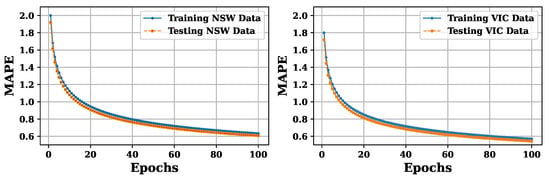
Figure 6.
Evaluation of the model’s performance using training and testing datasets from AEMO (NSW & VIC).
7.3. Evaluating the Performance of Day-Ahead and Week-Ahead Load Forecasting
To evaluate the efficiency of the proposed framework for day-ahead and week-ahead short-term forecasting, the performance was compared against ENN, ordinary LSTM, GA-LSTM, and PSO-LSTM models using three metrics: MSE, MAPE, and RMSE. The experiment was conducted on AMEO indices NWS and VIC, and the day-ahead close load was determined and is tabulated in Table 5. The analysis demonstrated that the proposed model surpassed all other examined forecasting techniques, consistently achieving lower MSE, MAPE, and RMSE values in every scenario. Furthermore, the modified PSO-LSTM, PSO-LSTM, and GA-LSTM models outperformed the LSTM model across all datasets. The day-ahead and week-ahead forecasting results for NWS and VIC using a test dataset from five models are depicted in Figure 7 and Figure 8. The plotted results provide evidence that the predicted load from the modified PSO-LSTM model closely aligns with the actual load for both indices.

Table 5.
Evaluation of the forecasting performance for day-ahead and week-ahead predictions.
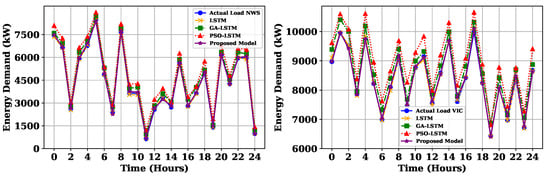
Figure 7.
Comparative assessment of the proposed framework on the NSW and VIC states of Australia hourly load data in terms of day-ahead forecasting.
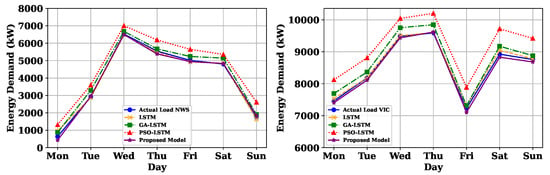
Figure 8.
Comparative assessment of the proposed framework on the NSW and VIC states of Australia hourly load data in terms of week-ahead forecasting.
7.4. Convergence Comparison
The convergence rate assessment of the proposed framework compared with the benchmark frameworks is tested using the three test functions of Schaffer, Weierstrass, and Non-continuous Rastrigin’s. The obtained results in Figure 9 reveal that the proposed framework converged after 21 iterations. In contrast, the benchmark frameworks like LSTM, LSTM-PSO, LSTM-mPSO, and LSTM-GA converged after 55, 35, 25, and 40 iterations, respectively. The results illustrate that the proposed framework is fast enough, with a higher convergence rate and lower network training time than the other frameworks.
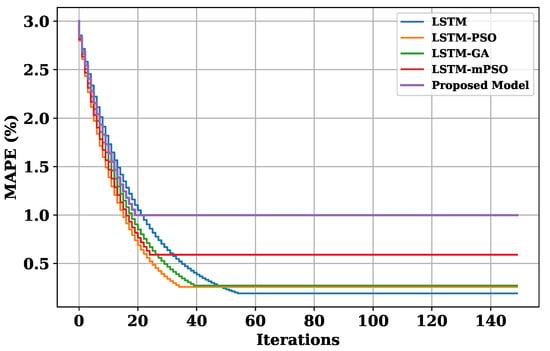
Figure 9.
Convergence rate profile.
7.5. Performance Comparison
The LSTM model is assessed using various optimisation techniques, including the mPSO, GA, ENN algorithms, and is also compared with the LSTM. The results are presented in Table 6, which illustrates that the LSTM model without optimisation techniques exhibited the highest MAPE and MSE values for both the NSW and VIC datasets. However, the incorporation of optimisation techniques led to significant reductions in the errors of the LSTM model. Moreover, the study highlights that the LSTM model enhanced with optimisation algorithms outperformed the LSTM model without them. In particular, the mPSO algorithm proved to be particularly effective in improving the LSTM model’s performance by accurately aligning the predicted and observed values. This can be attributed to the mPSO algorithm’s ability to combine both local and global search capabilities through the use of crossover and mutation operators, as well as an adaptive control process. The proposed framework and benchmark models, namely ENN, LSTM, LSTM-GA, and LSTM-PSO, were assessed based on their execution times. The proposed framework exhibited an efficient performance comparable to the benchmark models, with execution times ranging from 43 to 102 s. These findings suggest that the proposed model can be evaluated efficiently without compromising computational efficiency.

Table 6.
Comparative assessment analyses of LSTM, ENN, LSTM-PSO, and LSTM-GA frameworks, along with the proposed DA time horizon, for evaluating MAPE and computational time criteria.
Remark 1.
HFS-LSTM-mPSO model demonstrates outstanding performance in forecasting future electric loads, surpassing benchmark models in accuracy, stability, convergence rate, and response time. Its superiority is not limited to specific Australian states but extends to diverse settings, highlighting its effectiveness. The successful application of this model demonstrates its versatility and utility in predicting crucial factors like power system prices, generation levels, and wind speeds. With its advanced capabilities, the HFS-LSTM-mPSO model provides valuable insights that greatly support decision-making and strategic planning within the power sector.
8. Forecasting Validity Assessment and Analysis
Presently, the establishment of hybrid models heavily depends on metrics such as minimum MAE, MSE, and MAPE. Nevertheless, these criteria and assumptions may not fully capture the validity of the forecasting method. Consequently, the feasibility and validity of the hybrid model are verified through two-order forecasting validity. Forecasting validity is defined as follows.
Definition 1.

Actual value is , and m types of models are now used for forecasting; is the forecast value in the ith forecasting method at the jth time point (, ); is the error in the ith forecasting method at the jth time point; and is the forecasting accuracy in the ith forecasting method at the jth time point. The formula for two-order forecasting validity is presented in Equation (28):
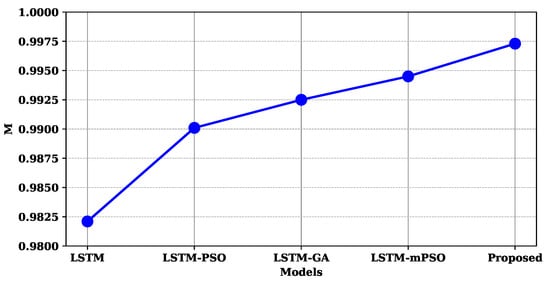
where represents the mathematical expectation of the forecasting accuracy of the hybrid forecasting method, represents the standard deviation of the prediction accuracy of the hybrid forecasting method, , and M is the forecasting validity. If the value of forecasting validity is close to 1, the proposed forecasting model is better. More details about forecasting validity can be observed in [61]. According to the results in Table 7 and Figure 10, the proposed hybrid model performs the best forecasting validity in the forecasting validity assessment and analysis with an M value of 0.9973, indicating that the LSTM-mPSO-HFS in this paper is the most valid in forecasting electric loads.

Table 7.
Forecasting validity assessment and analysis.

Figure 10.
Forecasting validity of different models.
9. Mapping the Limitations of Benchmark Models with the Proposed Model
Table 8 compares our proposed model with LSTM-PSO and LSTM-GA, highlighting the distinctions between them in various aspects. The computational resource requirements of our proposed model are minimal, whereas LSTM-PSO and LSTM-GA are computationally expensive. Additionally, our proposed model exhibits faster training times compared to LSTM-PSO and LSTM-GA, which are known to be time-consuming. Parameter fine-tuning is also more straightforward with our proposed model, whereas LSTM-PSO and LSTM-GA demand more effort and experimentation in this regard. Our proposed model effectively avoids getting trapped in suboptimal solutions, while LSTM-PSO and LSTM-GA may struggle with this aspect. Furthermore, the risk of overfitting is reduced in our proposed model, while LSTM-PSO and LSTM-GA have the potential to overfit. The table provides a comprehensive and clear comparison, highlighting the advantages of our proposed model over LSTM-PSO and LSTM-GA concerning computational resources, training time, parameter tuning, avoidance of local optima, and overfitting.

Table 8.
Comparison with benchmark models.
10. Constraints of the Proposed Model
The HFS-LSTM-mPSO model exhibits several limitations stemming from its increased complexity, compatibility issues, reduced interpretability, higher computational demands, and limited generalisation. The complexity of the model arises from the combination of multiple components, making it challenging to effectively coordinate and tune the parameters. Optimal hyperparameter selection and the integration of different algorithms require extensive experimentation and time-consuming efforts. Additionally, integrating different algorithms may introduce compatibility issues due to their specific requirements, limiting the flexibility in choosing compatible algorithms for the model. The increased complexity of the HFS-LSTM-mPSO model reduces its interpretability and explainability. Understanding the decision-making process and identifying the factors influencing the model’s predictions becomes more difficult due to the combined nature of the model. It becomes challenging to discern the individual contributions of each component, resulting in decreased interpretability. Moreover, the HFS-LSTM-mPSO model requires higher computational resources compared to individual algorithms. The model’s complexity, including the inclusion of multiple components and longer training times, leads to increased memory usage and computational demands. This can limit the feasibility of deploying the model in resource-constrained environments or real-time applications. Lastly, the model’s limited generalisation is a concern. While it may demonstrate performance improvements on specific datasets or problem instances, these gains may not transfer well to different scenarios. The model’s performance is highly tailored to the characteristics of the training data, making it less effective in handling unseen data or different problem domains. Therefore, a careful evaluation and adaptation process is crucial to understanding and assessing the model’s limitations and generalizability across various contexts. In conclusion, the HFS-LSTM-mPSO model’s limitations, including increased complexity, compatibility issues, reduced interpretability, higher computational demands, and limited generalisation, highlight the importance of thoroughly evaluating and understanding its performance and constraints in different scenarios.
11. Conclusions
In conclusion, the accurate forecasting of electric load is vital for supporting decision-making and optimising power grid operations within energy systems. The proposed hybrid model, integrating a data pre-processing and HFS module, a training and forecasting module utilising the LSTM algorithm, and an optimisation module employing mPSO, effectively addresses the limitations of traditional models. Through the analysis of high-resolution electric load data from NSW and VIC, the model demonstrated significant improvements over benchmark models, including the ENN, conventional LSTM, and LSTM-GA. Specifically, for NSW, the proposed model reduced MSE by 91.91%, RMSE by 94.89%, and mean absolute percentage error MAPE by 74.29%. In VIC, MSE decreased by 91.33%, RMSE by 95.73%, and MAPE by 72.06%. Furthermore, the proposed model outperformed the benchmark models, achieving an average runtime of 43 s. These results highlight the superior forecasting accuracy and convergence rate of the model, showcasing the immense potential of hybrid approaches in the domain of sustainable energy. The developed model can be regarded as a reliable method for electric load forecasting, facilitating informed decision-making and enhancing operational efficiency in energy systems. Looking ahead, future work will focus on further refining the model by incorporating additional data sources, such as weather and socio-economic indicators, to enhance predictive capabilities. Additionally, exploring alternative optimisation algorithms and advanced machine learning techniques could improve performance further. Conducting real-time forecasting and adapting the model to various geographical contexts will also be critical for broader applicability in energy systems.
Author Contributions
Conceptualization, M.Z.; Methodology, M.B.R.; Software, M.Z. and M.B.R.; Validation, C.G.; Resources, K.A.A.G.; Writing—original draft, M.Z.; Writing—review & editing, K.A.A.G., M.B.R. and C.G.; Visualization, K.A.A.G.; Supervision, K.A.A.G., M.B.R. and C.G.; Project administration, K.A.A.G.; Funding acquisition, K.A.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zulfiqar, M.; Kamran, M.; Rasheed, M.; Alquthami, T.; Milyani, A. Hyperparameter optimization of support vector machine using adaptive differential evolution for electricity load forecasting. Energy Rep. 2022, 8, 13333–13352. [Google Scholar] [CrossRef]
- ZulfiqAr, M.; Kamran, M.; Rasheed, M.B.; Alquthami, T.; Milyani, A.H. A Short-Term Load Forecasting Model Based on Self-Adaptive Momentum Factor and Wavelet Neural Network in Smart Grid. IEEE Access 2022, 10, 77587–77602. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, W.; Wang, Z. Load forecasting based on improved wavelet neural network and gravitational search algorithm. Energy 2023, 147, 115987. [Google Scholar]
- Eren, Y.; Küçükdemiral, İ. A comprehensive review on deep learning approaches for short-term load forecasting. Renew. Sustain. Energy Rev. 2024, 189, 114031. [Google Scholar] [CrossRef]
- Hong, W.C.; Hong, T.P.; Liu, S.T. A hybrid deep learning model for short-term load forecasting in smart grids. IEEE Trans. Smart Grid 2023, 14, 1789–1798. [Google Scholar]
- Wang, Y.; Lu, Z.; Zhao, C.; Wang, F. Load forecasting using long short-term memory networks with attention mechanism. Electr. Power Syst. Res. 2023, 189, 107014. [Google Scholar]
- Liu, H.; Cheng, L.; Hu, Z. Load forecasting in smart grids using improved deep belief networks. Energies 2023, 16, 611. [Google Scholar]
- Yadav, A.; Bareth, R.; Kochar, M.; Pazoki, M.; Sehiemy, R.A.E. Gaussian process regression-based load forecasting model. IET Gener. Transm. Distrib. 2024, 18, 899–910. [Google Scholar] [CrossRef]
- Song, K.B.; Baek, Y.S.; Hong, D.; Jang, G. Short-term load forecasting for the holidays using fuzzy linear regression method. IEEE Trans. Power Syst. 2005, 20, 96–101. [Google Scholar] [CrossRef]
- Guo, Y.; Nazarian, E.; Ko, J.; Rajurkar, K. Hourly cooling load forecasting using time-indexed ARX models with two-stage weighted leastsquares regression. Energy Convers. Manag. 2014, 80, 46–53. [Google Scholar] [CrossRef]
- Shumway, R.; Stoffer, D. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Wang, K.; Xu, C.; Zhang, Y.; Guo, S.; Zomaya, A.Y. Robust big data analytics for electricity price forecasting in the smart grid. IEEE Trans. Big Data 2017, 5, 34–45. [Google Scholar] [CrossRef]
- Sudheer, G.; Suseelatha, A. Short term load forecasting using wavelet transform combined with Holt-Winters and weighted nearest neighbor models. Electr. Power Syst. Res. 2015, 64, 340–346. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, S.; Zhang, W.; Lu, H. Combined modeling for electric load forecasting with adaptive particles warm optimization. Energy 2010, 35, 1671–1678. [Google Scholar] [CrossRef]
- Ali, M.; Khan, A.; Rehman, N.u. Hybrid multiscale wind speed forecasting based on variational mode decomposition. Int. Trans. Electr. Energy Syst. 2018, 28, e2466. [Google Scholar] [CrossRef]
- Amiri, M.K.; Zaferani, S.P.G.; Emami, M.R.S.; Zahmatkesh, S.; Pourhanasa, R.; Namaghi, S.S.; Klemeš, J.J.; Bokhari, A.; Hajiaghaei-Keshteli, M. Multi-objective optimization of thermophysical properties GO powders-DW/EG Nf by RSM, NSGA-II, ANN, MLP and ML. Energy 2023, 128176. [Google Scholar] [CrossRef]
- Zahmatkesh, S.; Karimian, M.; Chen, Z.; Ni, B.J. Combination of coagulation and adsorption technologies for advanced wastewater treatment for potable water reuse: By ANN, NSGA-II, and RSM. J. Environ. Manag. 2024, 349, 119429. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Berezsky, O.; Krak, I.; Kováč, M.; Fedorchuk, M. Improvement of the ANN-Based Prediction Technology for Extremely Small Biomedical Data Analysis. Technologies 2024, 12, 112. [Google Scholar] [CrossRef]
- Parlos, A.; Oufi, E.; Muthusami, J.; Patton, A.; Atiya, A. Development of an intelligent long-term electric load forecasting system. In Proceedings of the International Conference on Intelligent Systems Applications to Power Systems, Orlando, FL, USA, 28 January–2 February 1996; pp. 288–292. [Google Scholar]
- Wu, J.; Wang, Y.G.; Tian, Y.C.; Burrage, K.; Cao, T. Support vector regression with asymmetric loss for optimal electric load forecasting. Energy 2021, 223, 119969. [Google Scholar] [CrossRef]
- Li, K.; Ma, Z.; Robinson, D.; Lin, W.; Li, Z. A data-driven strategy to forecast next-day electricity usage and peak electricity demand of a building portfolio using cluster analysis, Cubist regression models and Particle Swarm Optimization. J. Clean. Prod. 2020, 273, 123115. [Google Scholar] [CrossRef]
- Hong, W. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, D. Theory-guided deep-learning for electrical load forecasting (TgDLF) via ensemble long short-term memory. Adv. Appl. Energy 2021, 1, 100004. [Google Scholar] [CrossRef]
- Valenzuela, O.; Rojas, I.; Rojas, F.; Pomares, H.; Herrera, L.; Guillen, A. Hybridization of intelligent techniques and ARIMA models for time series prediction. Fuzzy Sets Syst. 2008, 159, 821–845. [Google Scholar] [CrossRef]
- Liu, S.; Tian, L.X. The study of long-term electricity load forecasting based on improved grey prediction model. In Proceedings of the 2013 International Conference on Machine Learning and Cybernetics, Tianjin, China, 14–17 July. 2013; Volume 2, pp. 653–656. [Google Scholar]
- Di, K.; Chen, W.; Shi, Q.; Cai, Q.; Zhang, B. Digital empowerment and win-win co-operation for green and low-carbon industrial development: Analysis of regional differences based on GMM-ANN intelligence models. J. Clean. Prod. 2024, 445, 141332. [Google Scholar] [CrossRef]
- Gavrilas, M. Heuristic and metaheuristic optimization techniques with application to power systems. In Proceedings of the 12th WSEAS International Conference on Mathematical Methods and Computational Techniques in Electrical Engineering, Faro, Portugal, 3–5 November 2010. [Google Scholar]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Rabiya, K.; Nadeem, J. A survey on hyperparameters optimization algorithms of forecasting models in smart grid. Sustain. Cities Soc. 2020, 61, 102275. [Google Scholar]
- Chen, Y.; Yang, Y.; Liu, C.; Li, C.; Li, L. A hybrid application algorithm based on the support vector machine and artificial intelligence: An example of electric load forecasting. Appl. Math. Comput. 2015, 39, 2617–2632. [Google Scholar] [CrossRef]
- Che, J.; Wang, J. Short-term load forecasting using a kernel-based support vector regression combination model. Appl. Energy 2014, 132, 602–609. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Shamshirband, S.; Motamedi, S.; Petković, D.; Hashimd, R. A survey of water level fluctuation predicting in Urmia Lake using support vector machine with firefly algorithm. Appl. Math. Comput. 2015, 270, 731–743. [Google Scholar] [CrossRef]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Hagan, M.T.; Behr, S.M. The time series approach to short term load forecasting. IEEE Trans. Power Syst. 1987, 2, 785–791. [Google Scholar] [CrossRef]
- Christiaanse, W. Short-term load forecasting using general exponential smoothing. IEEE Trans. Power Appar. Syst. 1971, 2, 900–911. [Google Scholar] [CrossRef]
- Hou, K.; Shao, G.; Wang, H.; Zheng, L.; Zhang, Q.; Wu, S.; Hu, W. Research on practical power system stability analysis algorithm based on modified SVM. Prot. Control Mod. Power Syst. 2018, 3, 1–7. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Masa-Bote, D.; Castillo-Cagigal, M.; Matallanas, E.; Caamaño-Martín, E.; Gutiérrez, A.; Monasterio-Huelín, F.; Jiménez-Leube, J. Improving photovoltaics grid integration through short time forecasting and self-consumption. Appl. Energy 2014, 125, 103–113. [Google Scholar] [CrossRef]
- Chow, T.W.; Leung, C.T. Neural network based short-term load forecasting using weather compensation. IEEE Trans. Power Syst. 1996, 11, 1736–1742. [Google Scholar] [CrossRef]
- Mordjaoui, M.; Haddad, S.; Medoued, A.; Laouafi, A. Electric load forecasting by using dynamic neural network. Int. J. Hydrogen Energy 2017, 42, 17655–17663. [Google Scholar] [CrossRef]
- Elattar, E.E.; Goulermas, J.; Wu, Q.H. Electric load forecasting based on locally weighted support vector regression. IEEE Trans. Syst. Man, Cybern. Part C Appl. Rev. 2010, 40, 438–447. [Google Scholar] [CrossRef]
- Laouafi, A.; Mordjaoui, M.; Laouafi, F.; Boukelia, T.E. Daily peak electricity demand forecasting based on an adaptive hybrid two-stage methodology. Int. J. Electr. Power Energy Syst. 2016, 77, 136–144. [Google Scholar] [CrossRef]
- Laouafi, A.; Mordjaoui, M.; Haddad, S.; Boukelia, T.E.; Ganouche, A. Online electricity demand forecasting based on an effective forecast combination methodology. Electr. Power Syst. Res. 2017, 148, 35–47. [Google Scholar] [CrossRef]
- Hafeez, G.; Khan, I.; Jan, S.; Shah, I.A.; Khan, F.A.; Derhab, A. A novel hybrid load forecasting framework with intelligent feature engineering and optimization algorithm in smart grid. Appl. Energy 2021, 299, 117178. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Li, Z. Interval forecasting system for electricity load based on data pre-processing strategy and multi-objective optimization algorithm. Appl. Energy 2022, 305, 117911. [Google Scholar] [CrossRef]
- Dewangan, C.L.; Singh, S.; Chakrabarti, S. Combining forecasts of day-ahead solar power. Energy 2020, 202, 117743. [Google Scholar] [CrossRef]
- Yang, D.; Guo, J.e.; Sun, S.; Han, J.; Wang, S. An interval decomposition-ensemble approach with data-characteristic-driven reconstruction for short-term load forecasting. Appl. Energy 2022, 306, 117992. [Google Scholar] [CrossRef]
- Lotfipoor, A.; Patidar, S.; Jenkins, D.P. Deep neural network with empirical mode decomposition and Bayesian optimisation for residential load forecasting. Expert Syst. Appl. 2024, 237, 121355. [Google Scholar] [CrossRef]
- Pandey, A.S.; Singh, D.; Sinha, S.K. Intelligent hybrid wavelet models for short-term load forecasting. IEEE Trans. Power Syst. 2010, 25, 1266–1273. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T. Comprehensive learning particle swarm optimization based memetic algorithm for model selection in short-term load forecasting using support vector regression. Appl. Soft Comput. 2014, 25, 15–25. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T.; Chiong, R. Hybrid filter–wrapper feature selection for short-term load forecasting. Eng. Appl. Artif. Intell. 2015, 40, 17–27. [Google Scholar] [CrossRef]
- Følid, A. Short-Term Spatiotemporal Load Forecasting for Norwegian Bidding Zones. Master’s Thesis, The University of Bergen, Bergen, Norway, 2021. [Google Scholar]
- Jahantigh, M. A Hybrid Long-Term Probabilistic Net Load Forecasting Approach Considering Renewable Energies Power in Smart Grids. Nashriyyah-i Muhandisi-i Barq va Muhandisi-i Kampyutar-i Iran 2021, 87, 99. [Google Scholar]
- Zhang, Y.; Wang, C.; Chen, Z. Electricity demand forecasting using LSTM recurrent neural network. Energy 2017, 121, 156–165. [Google Scholar]
- Li, X.; Wang, Z.; Yang, C.; Bozkurt, A. An advanced framework for net electricity consumption prediction: Incorporating novel machine learning models and optimization algorithms. Energy 2024, 296, 131259. [Google Scholar] [CrossRef]
- Grandón, T.G.; Schwenzer, J.; Steens, T.; Breuing, J. Electricity demand forecasting with hybrid classical statistical and machine learning algorithms: Case study of Ukraine. Applied Energy 2024, 355, 122249. [Google Scholar] [CrossRef]
- Román-Portabales, A.; López-Nores, M.; Pazos-Arias, J.J. Systematic review of electricity demand forecast using ANN-based machine learning algorithms. Sensors 2021, 21, 4544. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, A. Balancing accuracy and computational efficiency in forecasting electricity demand. Int. J. Electr. Power Energy Syst. 2020, 115. [Google Scholar]
- Khodaparastan, M.; Mohamed, A.A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2831–2847. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Wang, M.; Wang, K.; Huang, Y.; Xu, Z. Power Sharing and Storage-Based Regenerative Braking Energy Utilization for Sectioning Post in Electrified Railways. IEEE Trans. Transp. Electrif. 2024, 10, 2677–2688. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).