Optimizing Models and Data Denoising Algorithms for Power Load Forecasting
Abstract
1. Introduction
2. Methods and Materials
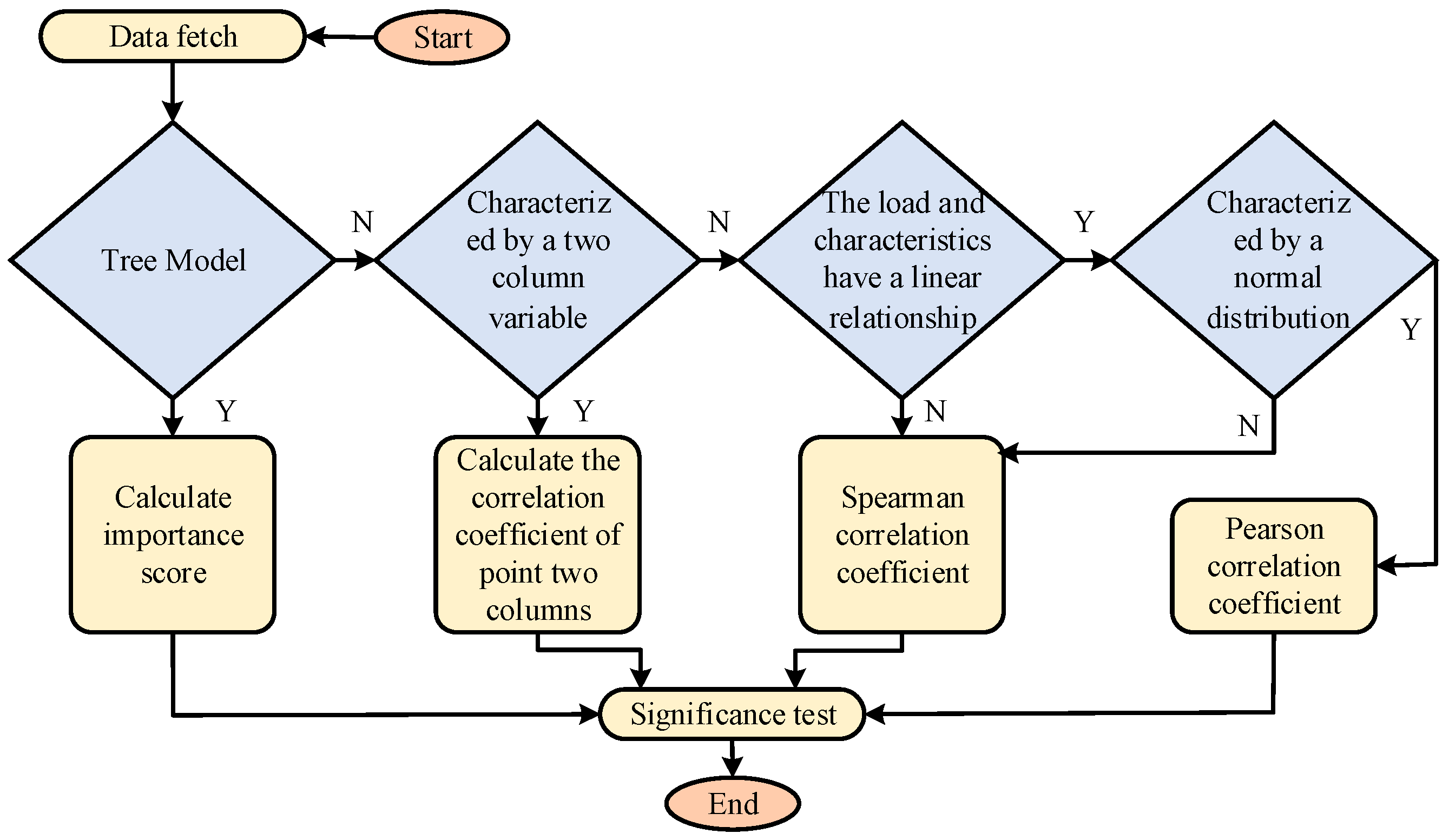
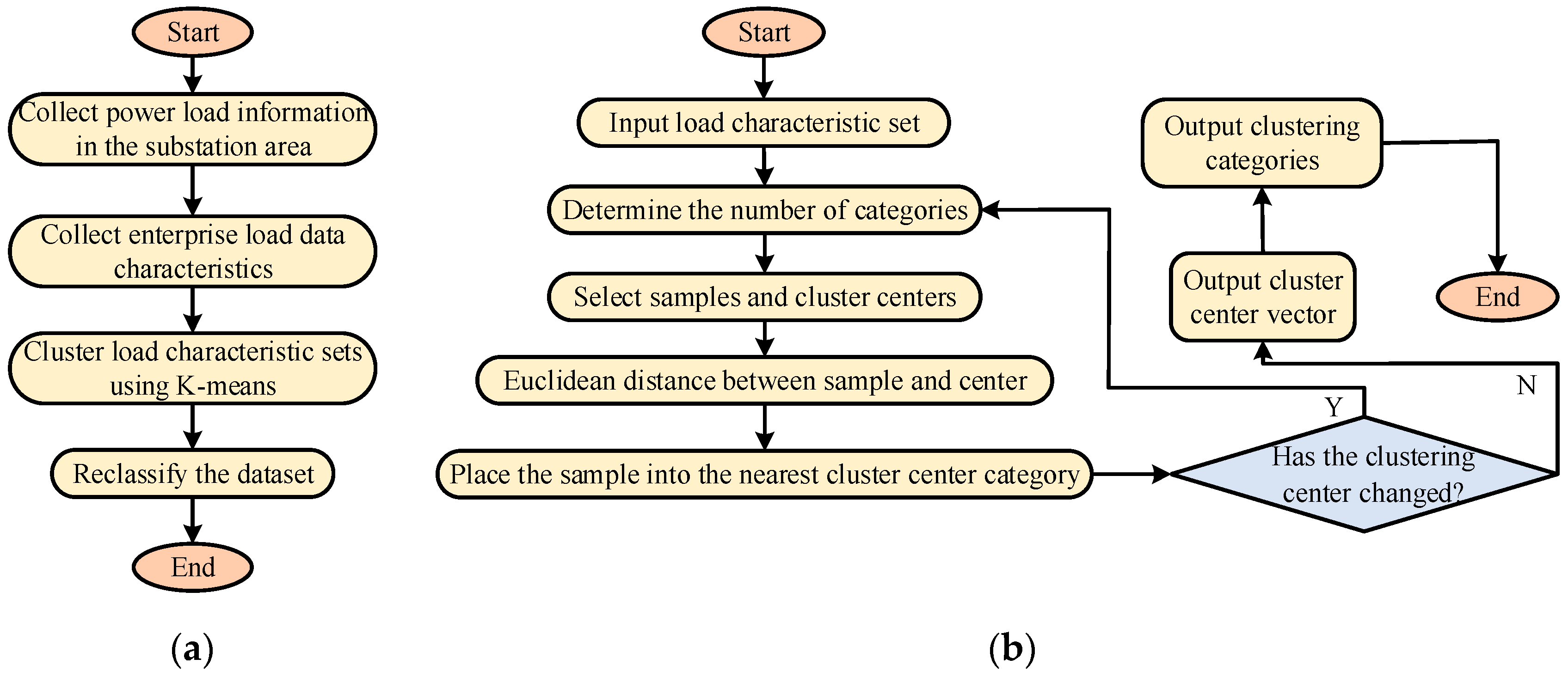
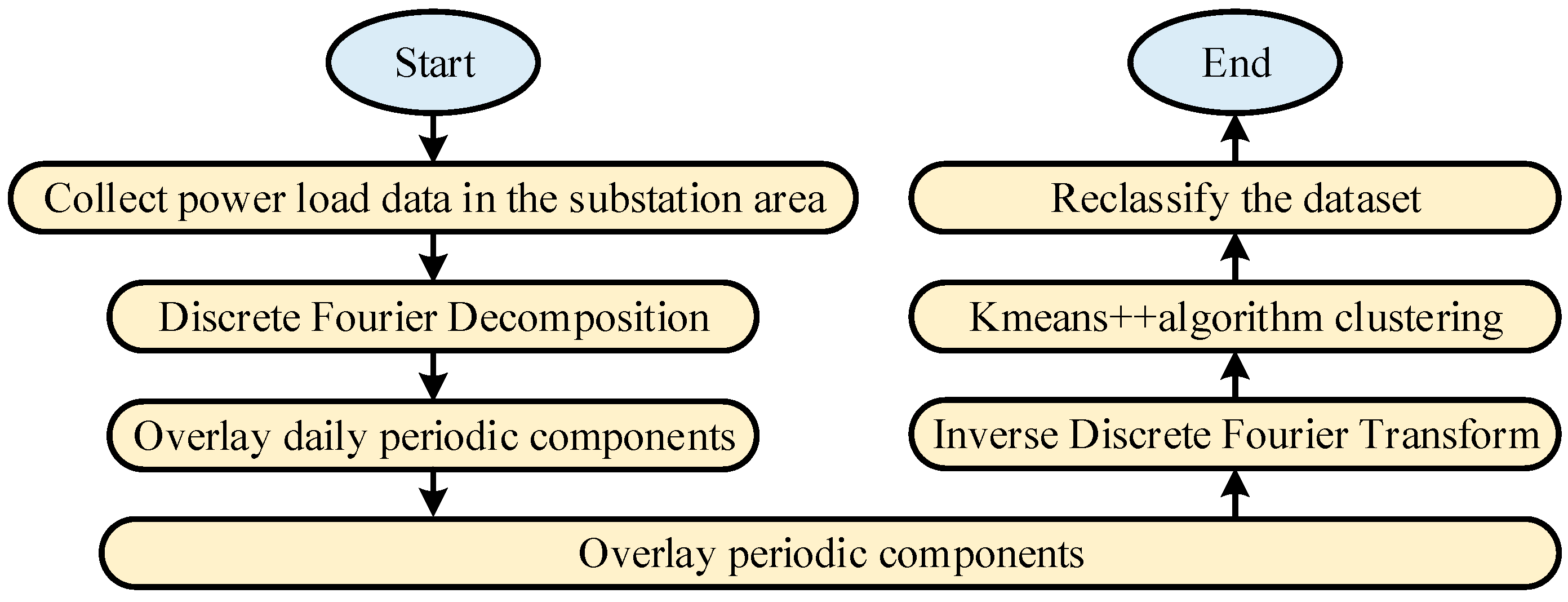
2.1. Data Processing and Noise Reduction Technology Design
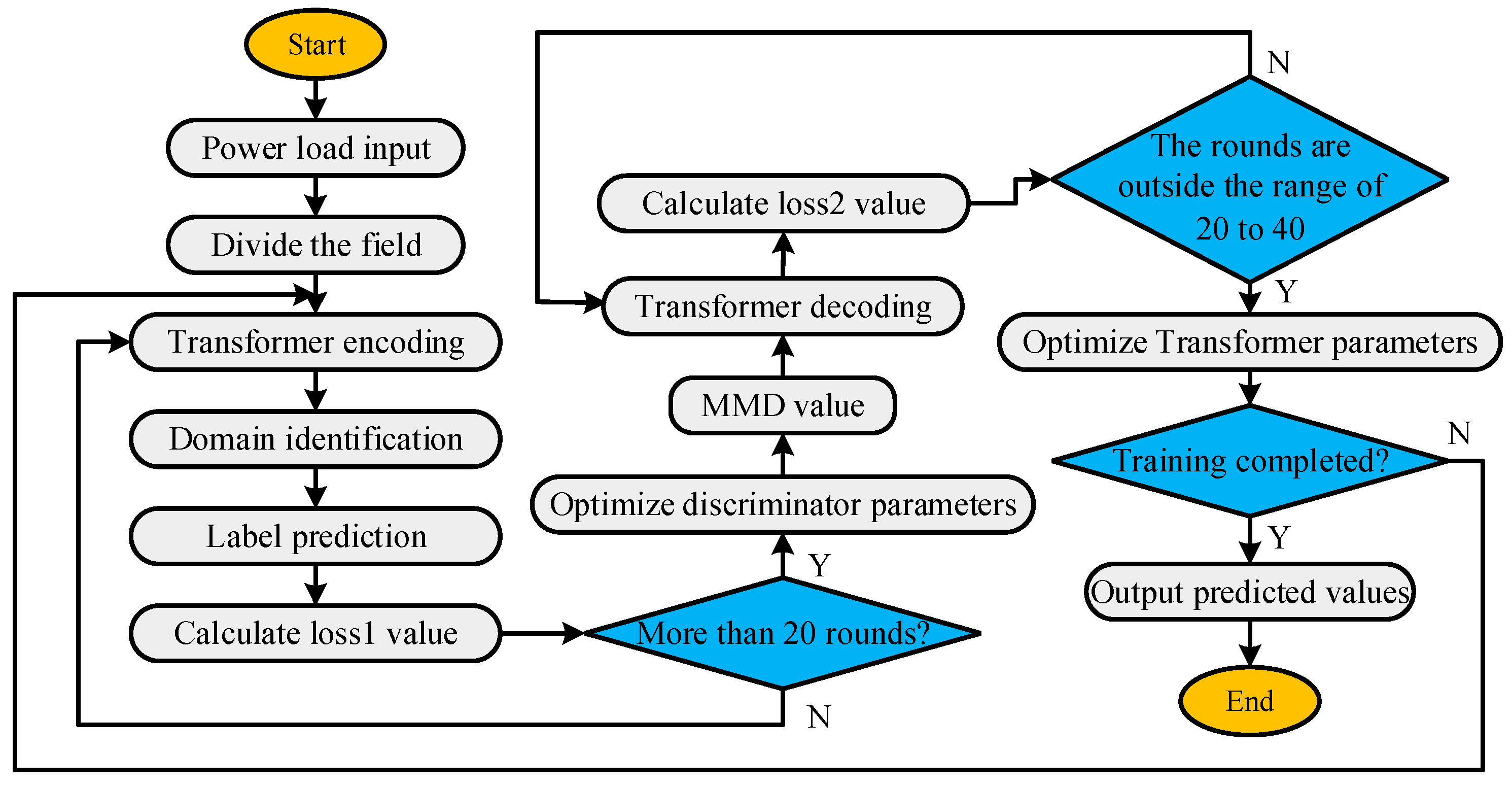
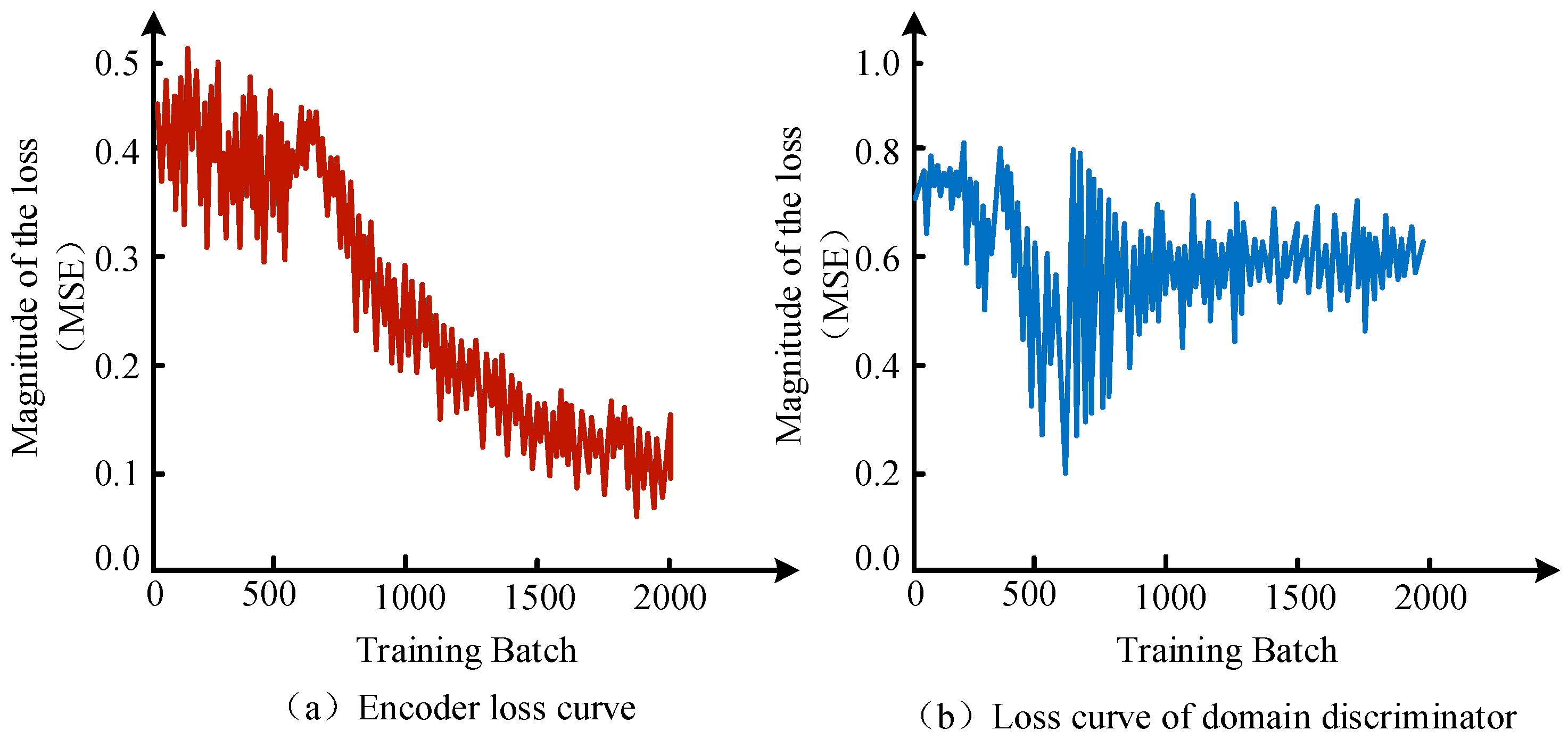
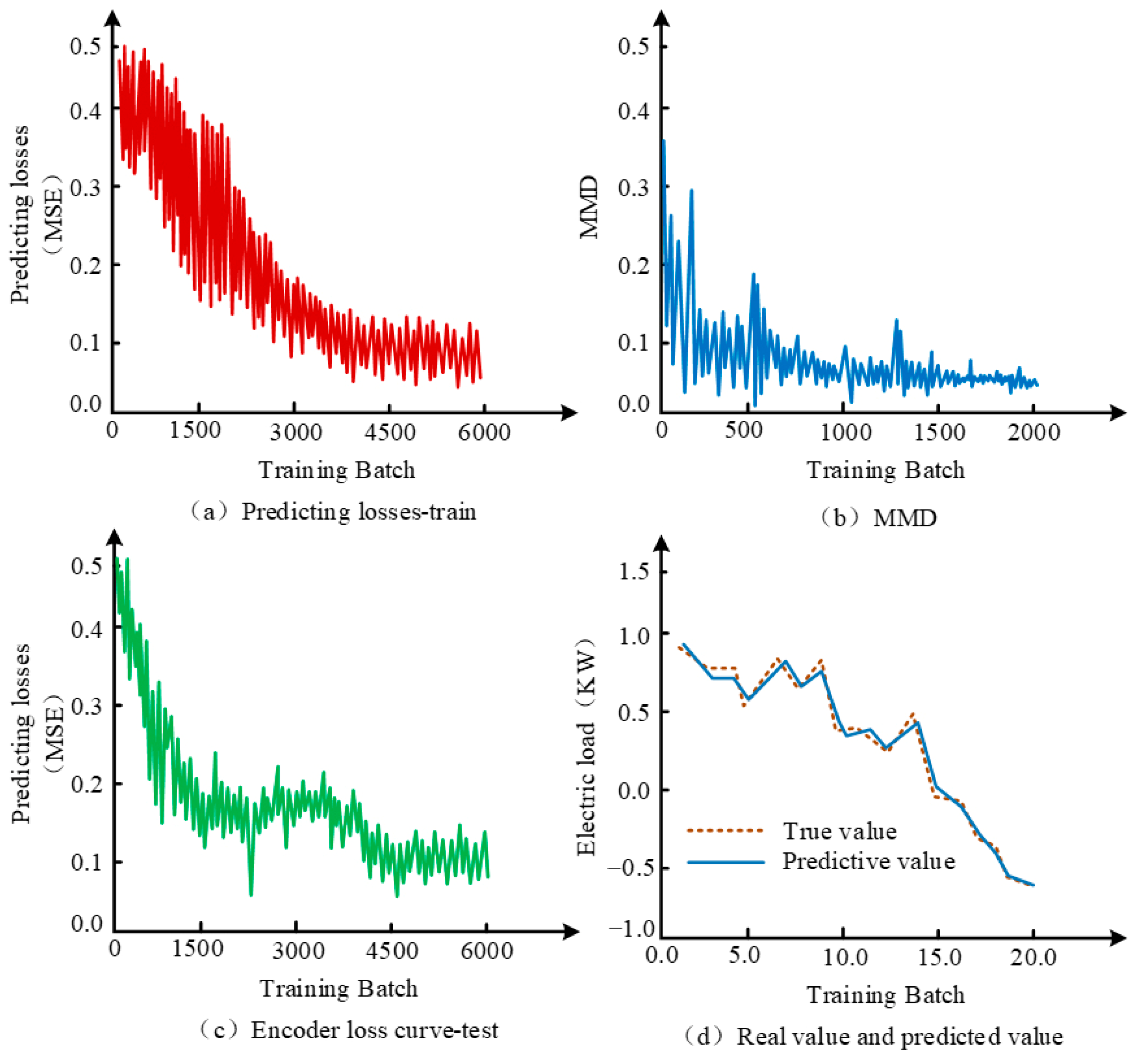
2.2. Adversarial Adaptive LF Model
3. Results
3.1. Analysis of Denoising Clustering Effect
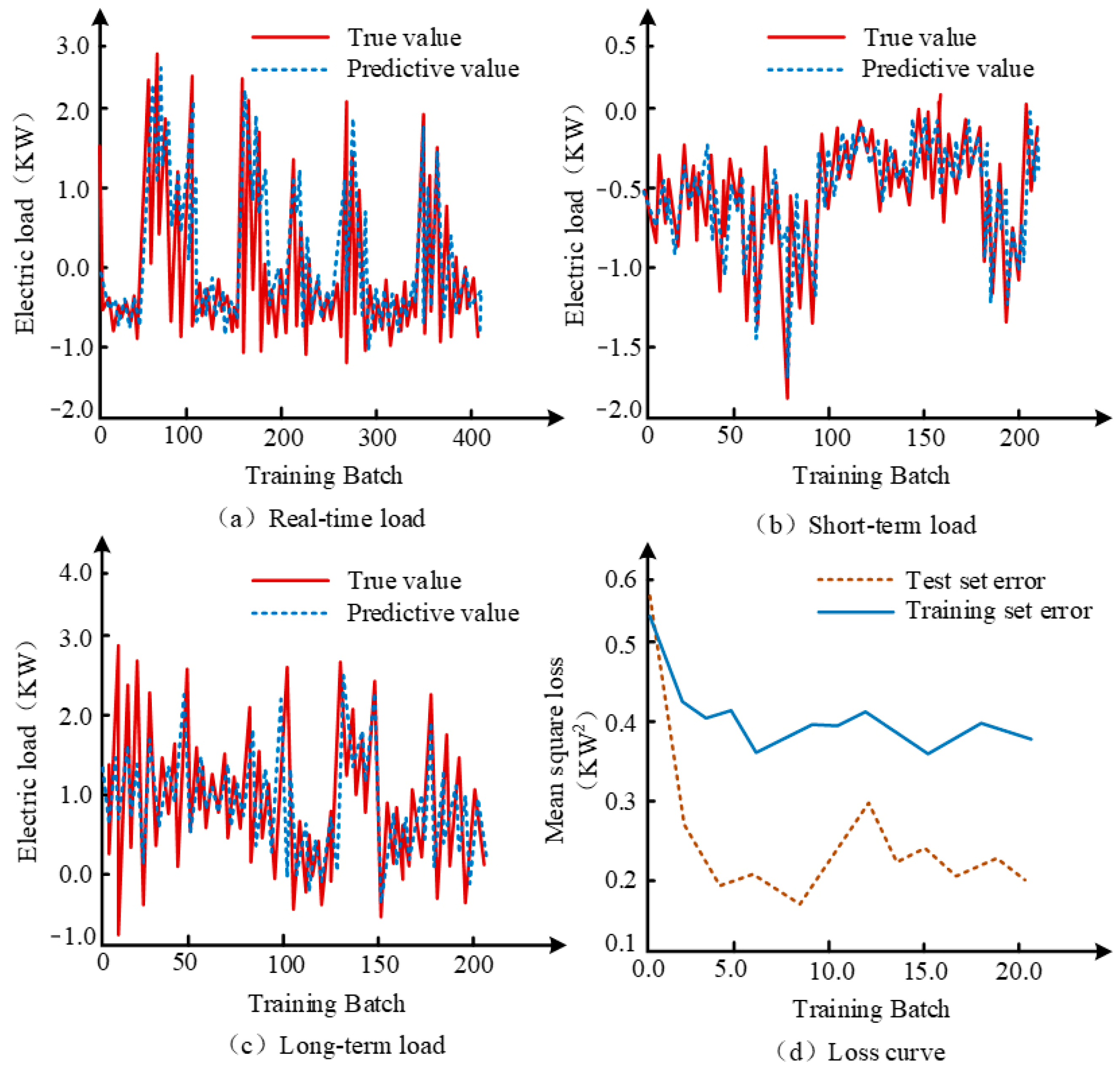
3.2. Analysis of LF Effectiveness
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farrag, T.A.; Elattar, E.E. Optimized deep stacked long short-term memory network for long-term load forecasting. IEEE Access 2021, 9, 68511–68522. [Google Scholar] [CrossRef]
- Chiu, M.C.; Hsu, H.W.; Chen, K.S.; Wen, C.Y. A hybrid CNN-GRU based probabilistic model for load forecasting from individual household to commercial building. Energy Rep. 2023, 9, 94–105. [Google Scholar] [CrossRef]
- Mubashar, R.; Awan, M.J.; Ahsan, M.; Yasin, A.; Singh, V.P. Efficient residential load forecasting using deep learning approach. Int. J. Comput. Appl. Technol. 2022, 68, 205–214. [Google Scholar] [CrossRef]
- Van den Ende, M.; Lior, I.; Ampuero, J.P.; Sladen, A.; Ferrari, A.; Richard, C. A self-supervised deep learning approach for blind denoising and waveform coherence enhancement in distributed acoustic sensing data. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3371–3384. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Han, Y. A Numerical Investigation on Kick Control with the Displacement Kill Method during a Well Test in a Deep-Water Gas Reservoir: A Case Study. Processes 2024, 12, 2090. [Google Scholar] [CrossRef]
- Xu, P.; Shin, I. Preparation and Performance Analysis of Thin-Film Artificial Intelligence Transistors Based on Integration of Storage and Computing. IEEE Access 2024, 12, 30593–30603. [Google Scholar] [CrossRef]
- Li, J.; Wei, S.; Dai, W. Combination of manifold learning and deep learning algorithms for mid-term electrical load forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2584–2593. [Google Scholar] [CrossRef]
- Ozer, I.; Efe, S.B.; Ozbay, H. A combined deep learning application for short term load forecasting. Alex. Eng. J. 2021, 60, 3807–3818. [Google Scholar] [CrossRef]
- Liu, Y.; Dutta, S.; Kong, A.W.K.; Yeo, C.K. An image inpainting approach to short-term load forecasting. IEEE Trans. Power Syst. 2022, 38, 177–187. [Google Scholar] [CrossRef]
- Zhu, Y.Q.; Cai, Y.M.; Zhang, F. Motion capture data denoising based on LSTNet autoencoder. J. Internet Technol. 2022, 23, 11–20. [Google Scholar] [CrossRef]
- Li, X.; Feng, S.; Hou, N.; Wang, R.; Li, H.; Gao, M.; Li, S. Surface microseismic data denoising based on sparse autoencoder and Kalman filter. Syst. Sci. Control Eng. 2022, 10, 616–628. [Google Scholar] [CrossRef]
- Feng, J.; Li, X.; Liu, X.; Chen, C.; Chen, H. Seismic data denoising based on tensor decomposition with total variation. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1303–1307. [Google Scholar] [CrossRef]
- Tibi, R.; Hammond, P.; Brogan, R.; Young, C.J.; Koper, K. Deep learning denoising applied to regional distance seismic data in Utah. Bull. Seismol. Soc. Am. 2021, 111, 775–790. [Google Scholar] [CrossRef]
- Dong, X.; Deng, S.; Wang, D. A short-term power load forecasting method based on k-means and SVM. J. Ambient Intell. Humaniz. Comput. 2022, 13, 5253–5267. [Google Scholar] [CrossRef]
- Veeramsetty, V.; Reddy, K.R.; Santhosh, M.; Mohnot, A. Short-term electric power load forecasting using random forest and gated recurrent unit. Electr. Eng. 2022, 104, 307–329. [Google Scholar] [CrossRef]
- Lv, L.; Wu, Z.; Zhang, J.; Zhang, L.; Tan, Z.; Tian, Z. A VMD and LSTM based hybrid model of load forecasting for power grid security. IEEE Trans. Ind. Inform. 2021, 18, 6474–6482. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, L.; Qiu, Y.; Wang, J.; Zhang, H.; Liao, Y. Short-term electric load forecasting based on improved Extreme Learning Machine Model. Energy Rep. 2021, 7, 1563–1573. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Song, X.F.; Zhang, Y.; Gong, D.W.; Gao, X.Z. A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data. IEEE Trans. Cybern. 2021, 52, 9573–9586. [Google Scholar] [CrossRef]
- Wang, S.; Celebi, M.E.; Zhang, Y.-D.; Yu, X.; Lu, S.; Yao, X.; Zhou, Q.; Miguel, M.-G.; Tian, Y.; Gorriz, J.M.; et al. Advances in data preprocessing for biomedical data fusion: An overview of the methods, challenges, and prospects. Inf. Fusion 2021, 76, 376–421. [Google Scholar] [CrossRef]
- Mastoi, M.S.; Zhuang, S.; Munir, H.M.; Haris, M.; Hassan, M.; Usman, M.; Bukhari, S.S.H.; Ro, J.-S. An in-depth analysis of electric vehicle charging station infrastructure, policy implications, and future trends. Energy Rep. 2022, 8, 11504–11529. [Google Scholar] [CrossRef]
- Verma, S.; Dwivedi, G.; Verma, P. Life cycle assessment of electric vehicles in comparison to combustion engine vehicles: A review. Mater. Today Proc. 2022, 49, 217–222. [Google Scholar] [CrossRef]
- Elberry, A.M.; Thakur, J.; Santasalo-Aarnio, A.; Larmi, M. Large-scale compressed hydrogen storage as part of renewable electricity storage systems. Int. J. Hydrogen Energy 2021, 46, 15671–15690. [Google Scholar] [CrossRef]
- Deng, J.; Deng, Y.; Cheong, K.H. Combining conflicting evidence based on Pearson correlation coefficient and weighted graph. Int. J. Intell. Syst. 2021, 36, 7443–7460. [Google Scholar] [CrossRef]
- Dufera, A.G.; Liu, T.; Xu, J. Regression models of Pearson correlation coefficient. Stat. Theory Relat. Fields 2023, 7, 97–106. [Google Scholar] [CrossRef]
- Hidayanti, A.A.; Mandalika, E.N.D. The Pearson Correlation Analysis of Production Costs on the Land Area of Salt Farmers in Bolo Sub-District, Bima District. J. Inovasi Pendidik. Sains 2021, 2, 119–127. [Google Scholar] [CrossRef]
- Amman, M.; Rashid, T.; Ali, A. Fermatean fuzzy multi-criteria decision-making based on Spearman rank correlation coefficient. Granul. Comput. 2023, 8, 2005–2019. [Google Scholar] [CrossRef]
- Abd Al-Hameed, K.A. Spearman’s correlation coefficient in statistical analysis. Int. J. Nonlinear Anal. Appl. 2022, 13, 3249–3255. [Google Scholar]
- Green, J.A. Too many zeros and/or highly skewed? A tutorial on modelling health behaviour as count data with Poisson and negative binomial regression. Health Psychol. Behav. Med. 2021, 9, 436–455. [Google Scholar] [CrossRef]
- Xu, P.; Liu, H.; Zhang, H.; Lan, D.; Shin, I. Optimizing Performance of Recycled Aggregate Materials Using BP Neural Network Analysis: A Study on Permeability and Water Storage. Desalination Water Treat. 2024, 317, 100056. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghadi, Y.; Adnan, M.; Ali, M. Load forecasting techniques for power system: Research challenges and survey. IEEE Access. 2022, 10, 71054–71090. [Google Scholar] [CrossRef]
- Geng, G.; He, Y.; Zhang, J.; Qin, T.; Yang, B. Short-term power load forecasting based on PSO-optimized VMD-TCN-attention mechanism. Energies 2023, 16, 4616. [Google Scholar] [CrossRef]




| Dataset | By Industry | Divided by Region | Fourier Transform Clustering | Load Characteristic Clustering |
|---|---|---|---|---|
| Collection 1 | 0.153 | 0.174 | 0.158 | 0.149 |
| Collection 2 | 0.170 | 0.158 | 0.171 | 0.172 |
| Collection 3 | 0.178 | 0.174 | 0.178 | 0.166 |
| Collection 4 | 0.173 | 0.167 | 0.164 | 0.177 |
| Collection 5 | 0.148 | 0.149 | 0.151 | 0.146 |
| Collection 6 | 0.122 | 0.134 | 0.129 | 0.121 |
| Collection 7 | 0.097 | 0.120 | 0.116 | 0.177 |
| Collection 8 | 0.260 | 0.202 | 0.180 | 0.258 |
| Collection 9 | 0.136 | 0.128 | 0.140 | 0.167 |
| average value | 0.160 | 0.156 | 0.154 | 0.170 |
| Dataset | Research Model | Adversarial Adaptive Module | MMD Module | Adversarial Adaptation and MMD Module | Attention Is Placed on the Encoder | Attention Is Placed on the Decoder |
|---|---|---|---|---|---|---|
| Collection 1 | 0.269 | 0.284 | 0.270 | 0.277 | 0.217 | 0.154 |
| Collection 2 | 0.260 | 0.263 | 0.261 | 0.265 | 0.260 | 0.210 |
| Collection 3 | 0.178 | 0.183 | 0.185 | 0.206 | 0.186 | 0.169 |
| Collection 4 | 0.375 | 0.390 | 0.379 | 0.418 | 0.390 | 0.189 |
| Collection 5 | 0.158 | 0.159 | 0.156 | 0.163 | 0.155 | 0.151 |
| Collection 6 | 0.143 | 0.148 | 0.145 | 0.149 | 0.132 | 0.125 |
| Collection 7 | 0.357 | 0.372 | 0.362 | 0.397 | 0.271 | 0.150 |
| Collection 8 | 0.439 | 0.458 | 0.439 | 0.453 | 0.330 | 0.262 |
| Collection 9 | 0.284 | 0.307 | 0.303 | 0.320 | 0.177 | 0.170 |
| Average value | 0.274 | 0.285 | 0.278 | 0.293 | 0.236 | 0.176 |
| Load Type | Dataset | DTW-LSTM | SVR | CART | XGB | LGB | Research Model |
|---|---|---|---|---|---|---|---|
| Long-term load | Collection 1 | 0.020 | 0.040 | 0.062 | 0.052 | 0.058 | 0.010 |
| Collection 2 | 0.008 | 0.038 | 0.038 | 0.045 | 0.035 | 0.026 | |
| Collection 3 | 0.105 | 0.101 | 0.031 | 0.117 | 0.050 | 0.043 | |
| Collection 4 | 0.090 | 0.092 | 0.013 | 0.060 | 0.074 | 0.026 | |
| Collection 5 | 0.079 | 0.071 | 0.133 | 0.177 | 0.346 | 0.162 | |
| Average value | 0.060 | 0.068 | 0.055 | 0.090 | 0.113 | 0.053 | |
| Short-term load | Collection 1 | 0.018 | 0.045 | 0.058 | 0.049 | 0.056 | 0.012 |
| Collection 2 | 0.016 | 0.032 | 0.035 | 0.046 | 0.034 | 0.027 | |
| Collection 3 | 0.103 | 0.096 | 0.029 | 0.107 | 0.056 | 0.041 | |
| Collection 4 | 0.095 | 0.083 | 0.014 | 0.062 | 0.268 | 0.025 | |
| Collection 5 | 0.064 | 0.068 | 0.115 | 0.169 | 0.341 | 0.157 | |
| average value | 0.059 | 0.065 | 0.050 | 0.087 | 0.151 | 0.052 | |
| Real-time load | Collection 1 | 0.028 | 0.022 | 0.024 | 0.026 | 0.006 | 0.016 |
| Collection 2 | 0.085 | 0.085 | 0.055 | 0.086 | 0.104 | 0.009 | |
| Collection 3 | 0.707 | 3.527 | 1.296 | 0.801 | 0.552 | 0.688 | |
| Collection 4 | 0.251 | 0.493 | 0.361 | 0.306 | 0.286 | 0.261 | |
| Collection 5 | 0.082 | 0.117 | 0.157 | 0.098 | 0.209 | 0.101 | |
| Average value | 0.231 | 0.849 | 0.378 | 0.263 | 0.231 | 0.215 |
| Dataset (MMD) | MMD = 0.45 | MMD = 0.25 | MMD = 0.18 | MMD = 0.07 | MMD = 0.02 | MMD = 0.01 | MMD = 0.00 | Average Value |
|---|---|---|---|---|---|---|---|---|
| Research model | 0.076 | 0.120 | 0.089 | 0.119 | 0.149 | 0.114 | 0.136 | 0.113 |
| XGB | 0.186 | 0.147 | 0.235 | 0.148 | 0.26 | 0.203 | 0.204 | 0.221 |
| SVR | 0.332 | 0.190 | 0.343 | 0.249 | 0.565 | 0.427 | 0.251 | 0.321 |
| LR | 0.331 | 0.178 | 0.279 | 0.258 | 0.495 | 0.386 | 0.249 | 0.288 |
| RF | 0.331 | 0.151 | 0.264 | 0.245 | 0.444 | 0.377 | 0.229 | 0.286 |
| LGBM | 0.211 | 0.137 | 0.199 | 0.100 | 0.312 | 0.204 | 0.228 | 0.215 |
| CART | 0.385 | 0.172 | 0.349 | 0.326 | 0.527 | 0.433 | 0.233 | 0.333 |
| DTW-LSTM | 0.091 | 0.137 | 0.098 | 0.192 | 0.192 | 0.053 | 0.193 | 0.127 |
| CNN-LSTM | 0.093 | 0.133 | 0.116 | 0.076 | 0.129 | 0.095 | 0.168 | 0.129 |
| Transformer | 0.092 | 0.168 | 0.258 | 0.181 | 0.122 | 0.114 | 0.171 | 0.15 |
| Data Sources | Research Model | CNN-LSTM | CNN-GRU | |
|---|---|---|---|---|
| Predictive accuracy | Digital 1 | 98.4% | 93.5% | 95.2% |
| Digital 2 | 97.6% | 91.4% | 93.1% | |
| Digital 3 | 93.5% | 89.6% | 90.4% | |
| Digital 4 | 98.1% | 95.3% | 96.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ugli, I.N.R.; Ugli, Y.I.H.; Lee, T.; Kim, T.-K. Optimizing Models and Data Denoising Algorithms for Power Load Forecasting. Energies 2024, 17, 5513. https://doi.org/10.3390/en17215513
Li Y, Ugli INR, Ugli YIH, Lee T, Kim T-K. Optimizing Models and Data Denoising Algorithms for Power Load Forecasting. Energies. 2024; 17(21):5513. https://doi.org/10.3390/en17215513
Chicago/Turabian StyleLi, Yanxia, Ilyosbek Numonov Rakhimjon Ugli, Yuldashev Izzatillo Hakimjon Ugli, Taeo Lee, and Tae-Kook Kim. 2024. "Optimizing Models and Data Denoising Algorithms for Power Load Forecasting" Energies 17, no. 21: 5513. https://doi.org/10.3390/en17215513
APA StyleLi, Y., Ugli, I. N. R., Ugli, Y. I. H., Lee, T., & Kim, T.-K. (2024). Optimizing Models and Data Denoising Algorithms for Power Load Forecasting. Energies, 17(21), 5513. https://doi.org/10.3390/en17215513








