Aerodynamic Performance and Numerical Validation Study of a Scaled-Down and Full-Scale Wind Turbine Models
Abstract
1. Introduction
2. Methodology
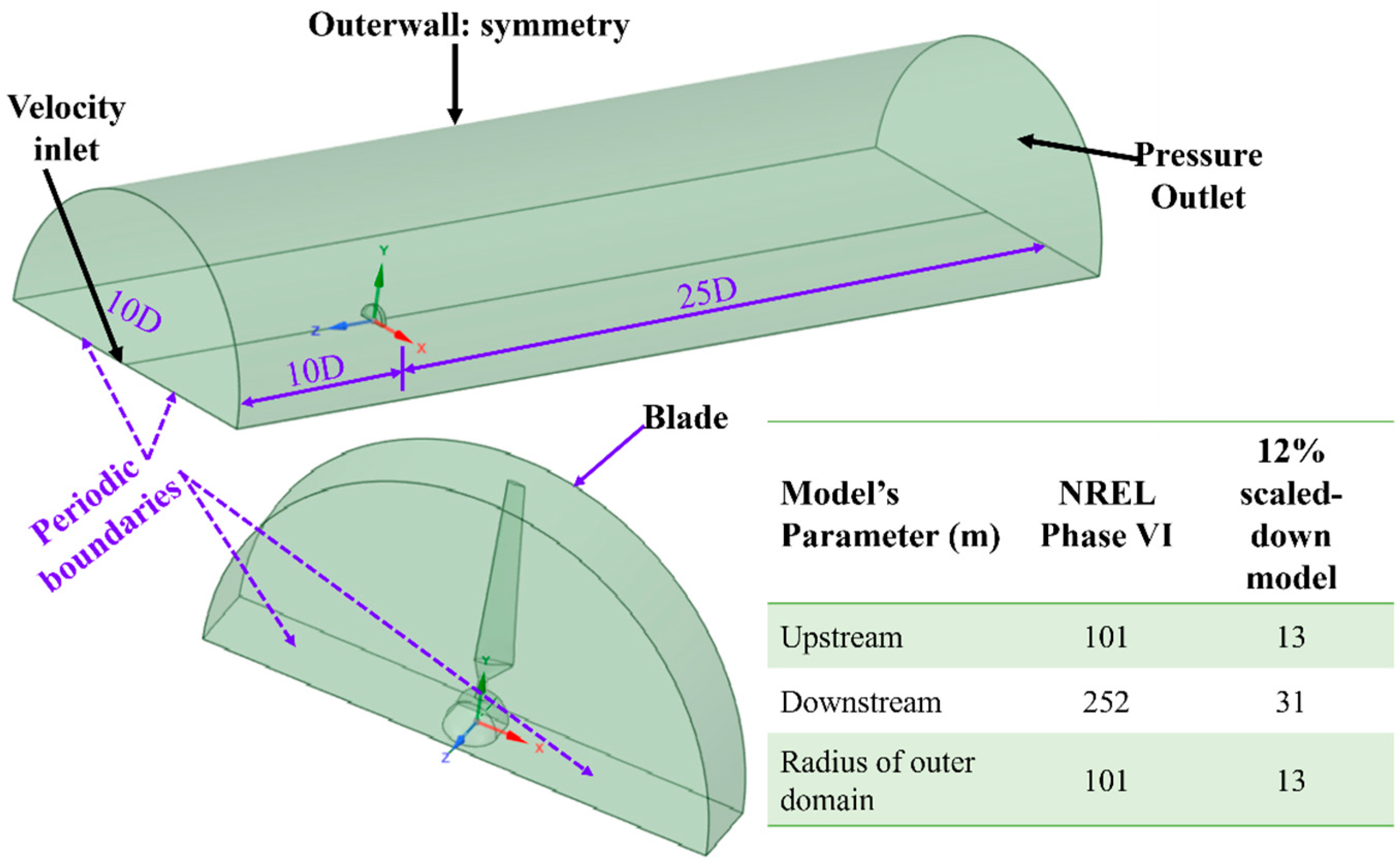
2.1. Computational Models
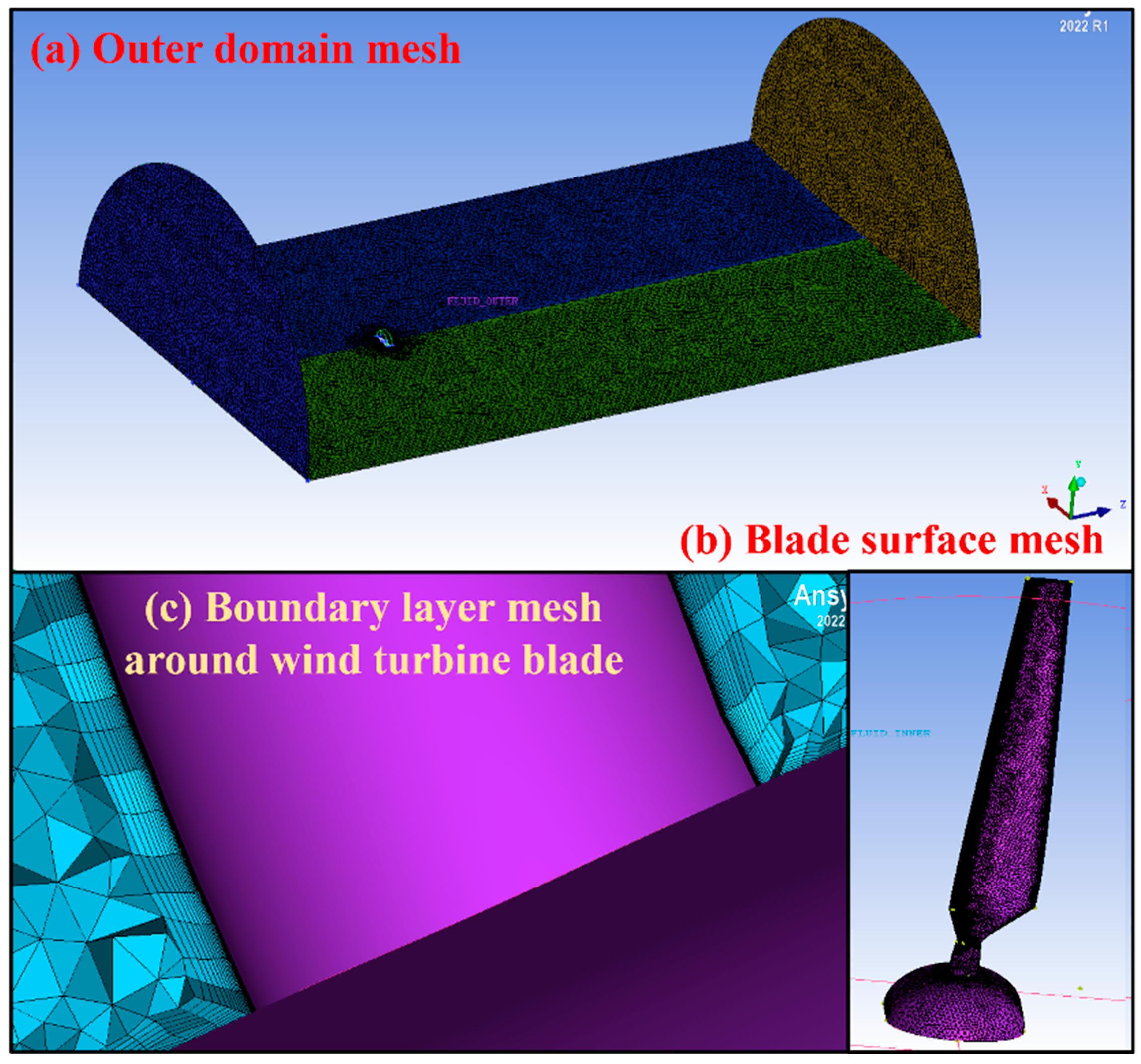
2.2. Meshing for CFD Simulation
2.3. Governing Equations and Theories of Turbulence
2.4. Computational Parameters and Boundary Conditions
2.5. Mesh Sensitivity Analysis
3. Results and Discussion
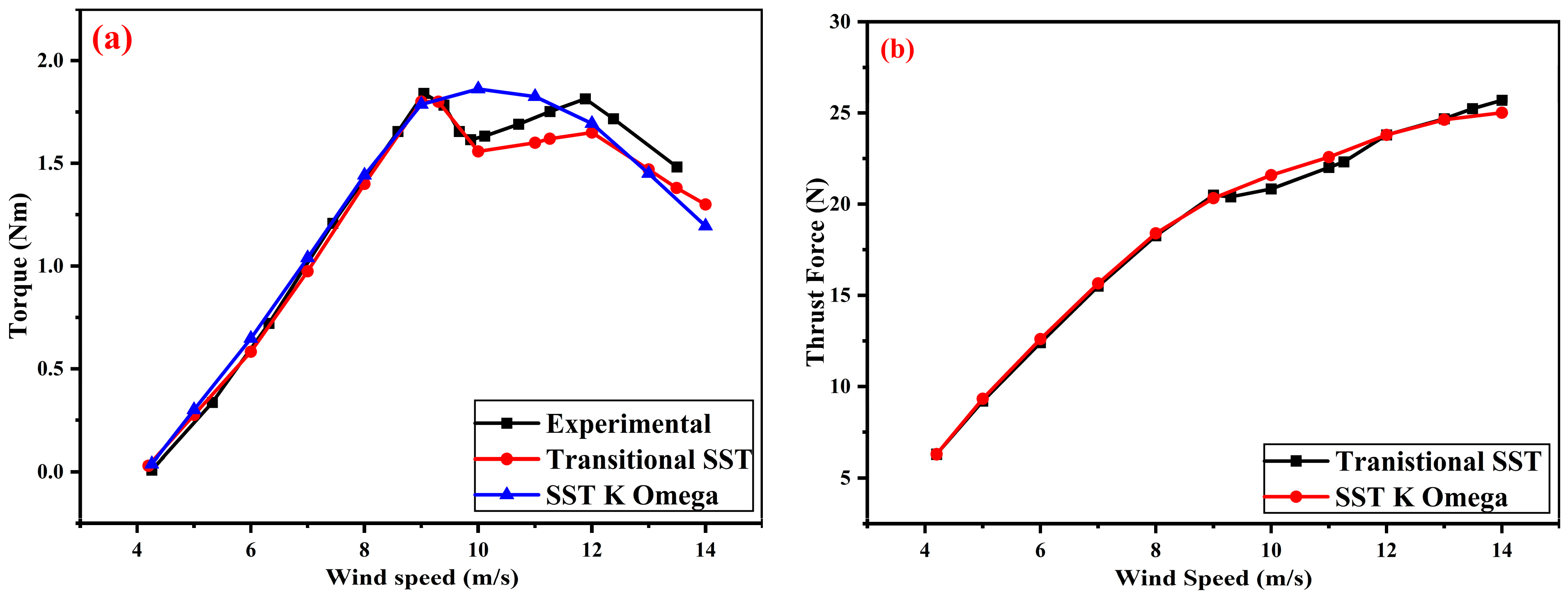
3.1. Torque and Thrust Force
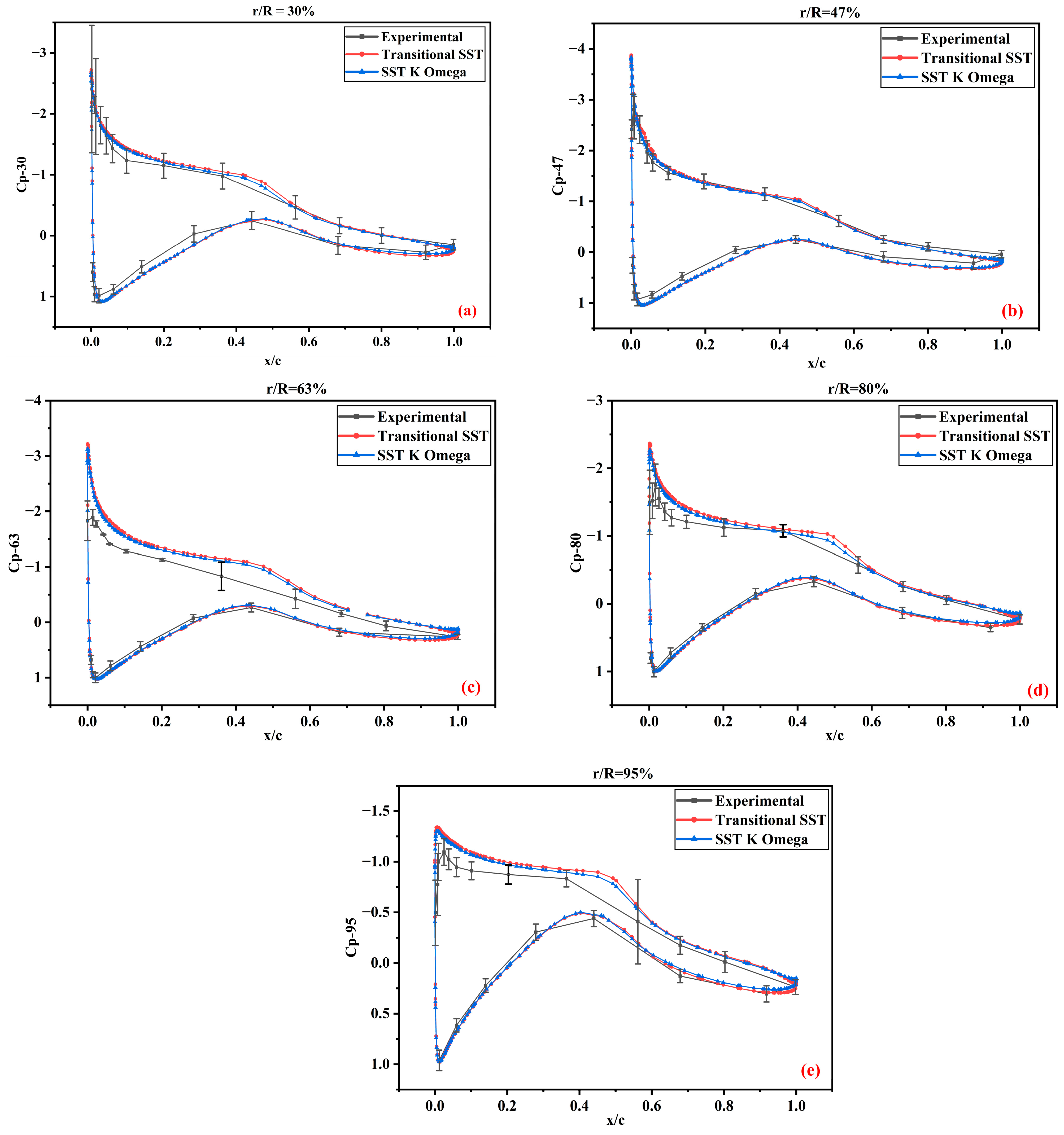
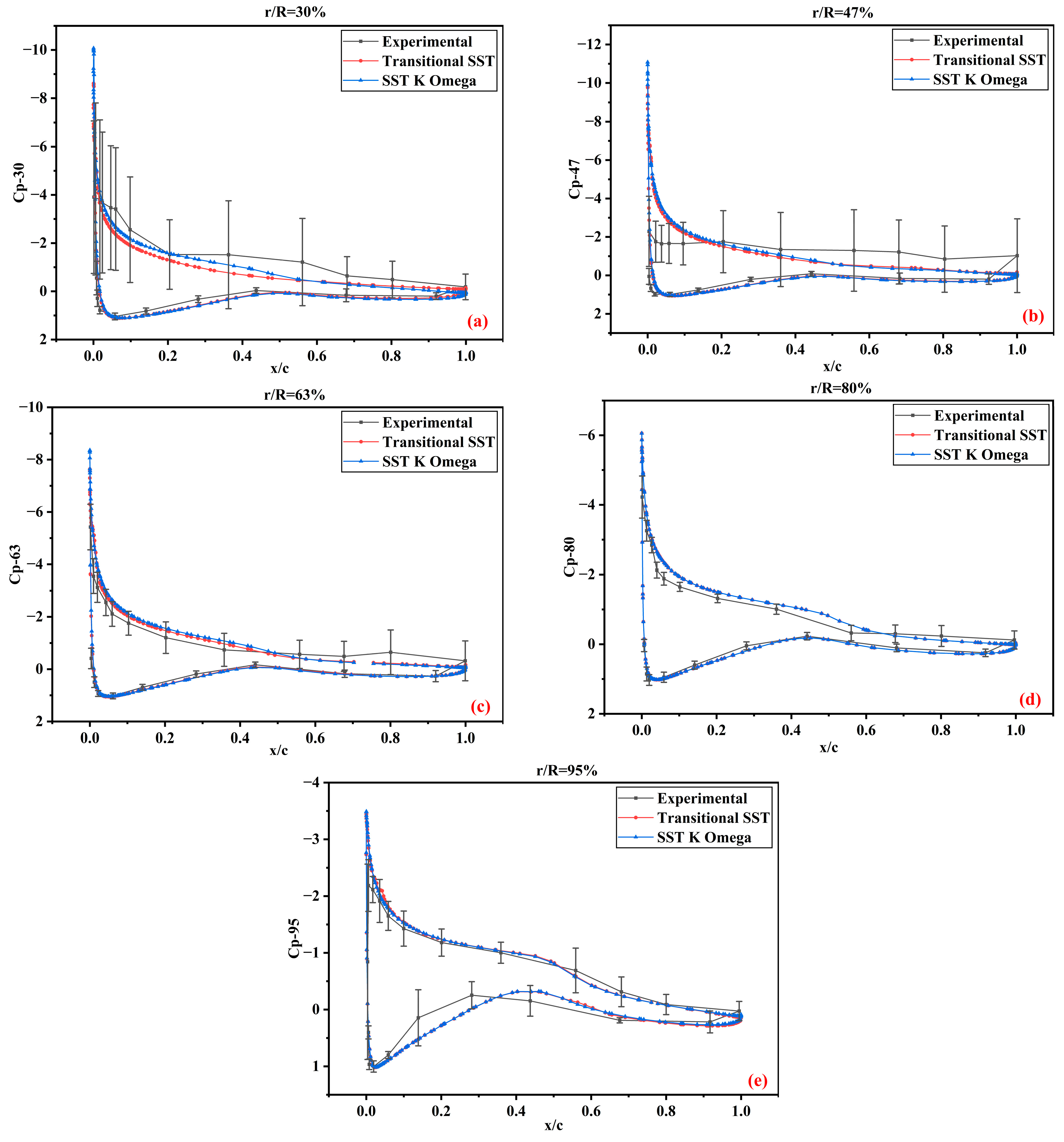
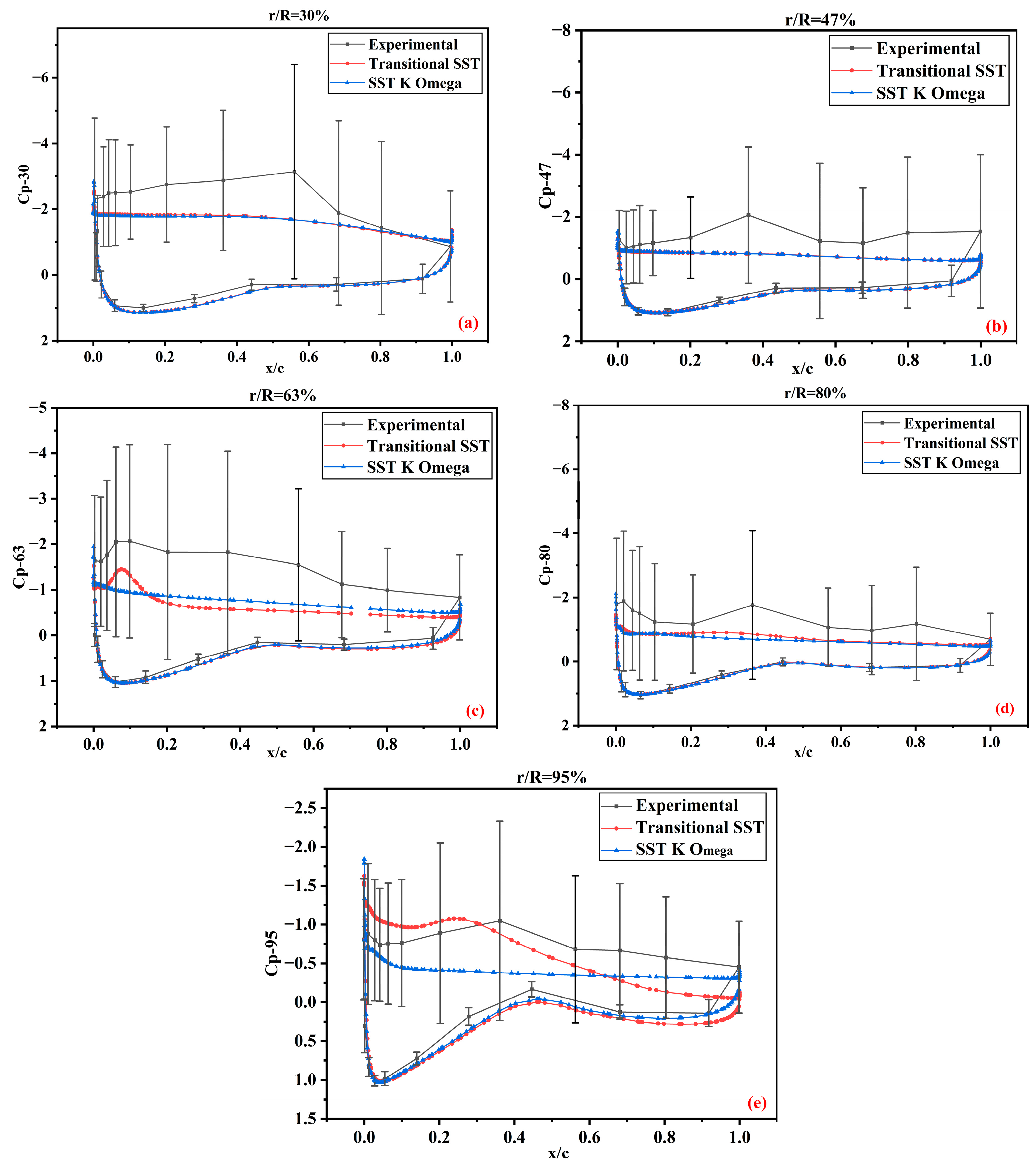
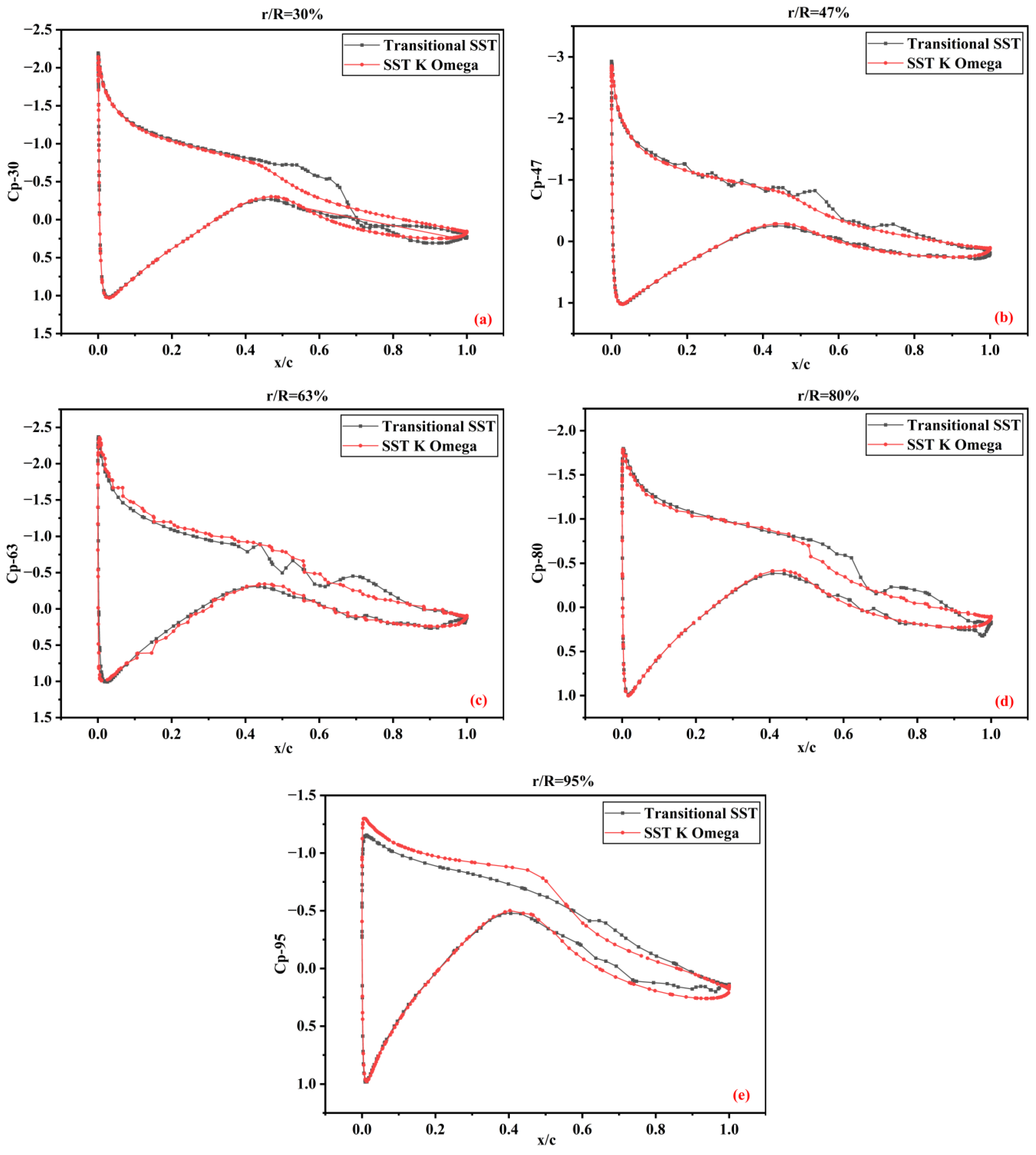
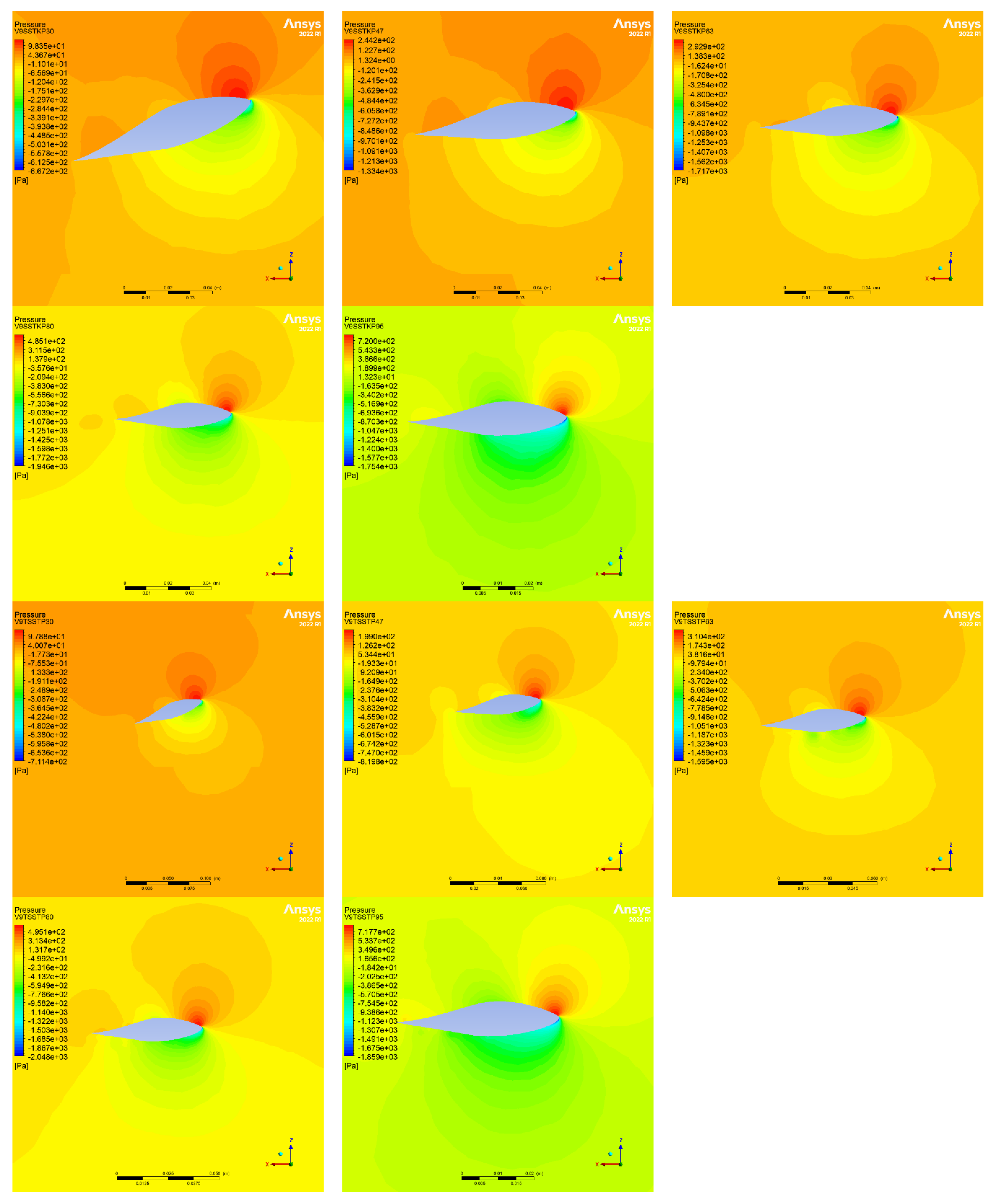
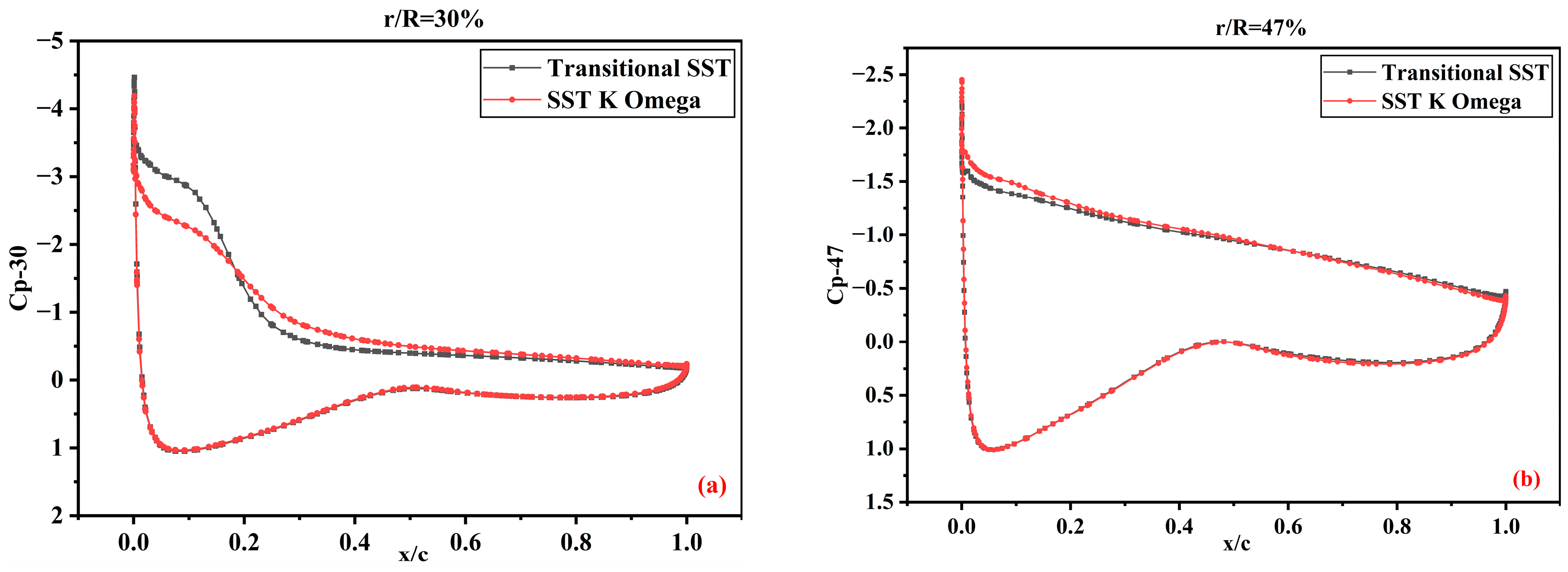
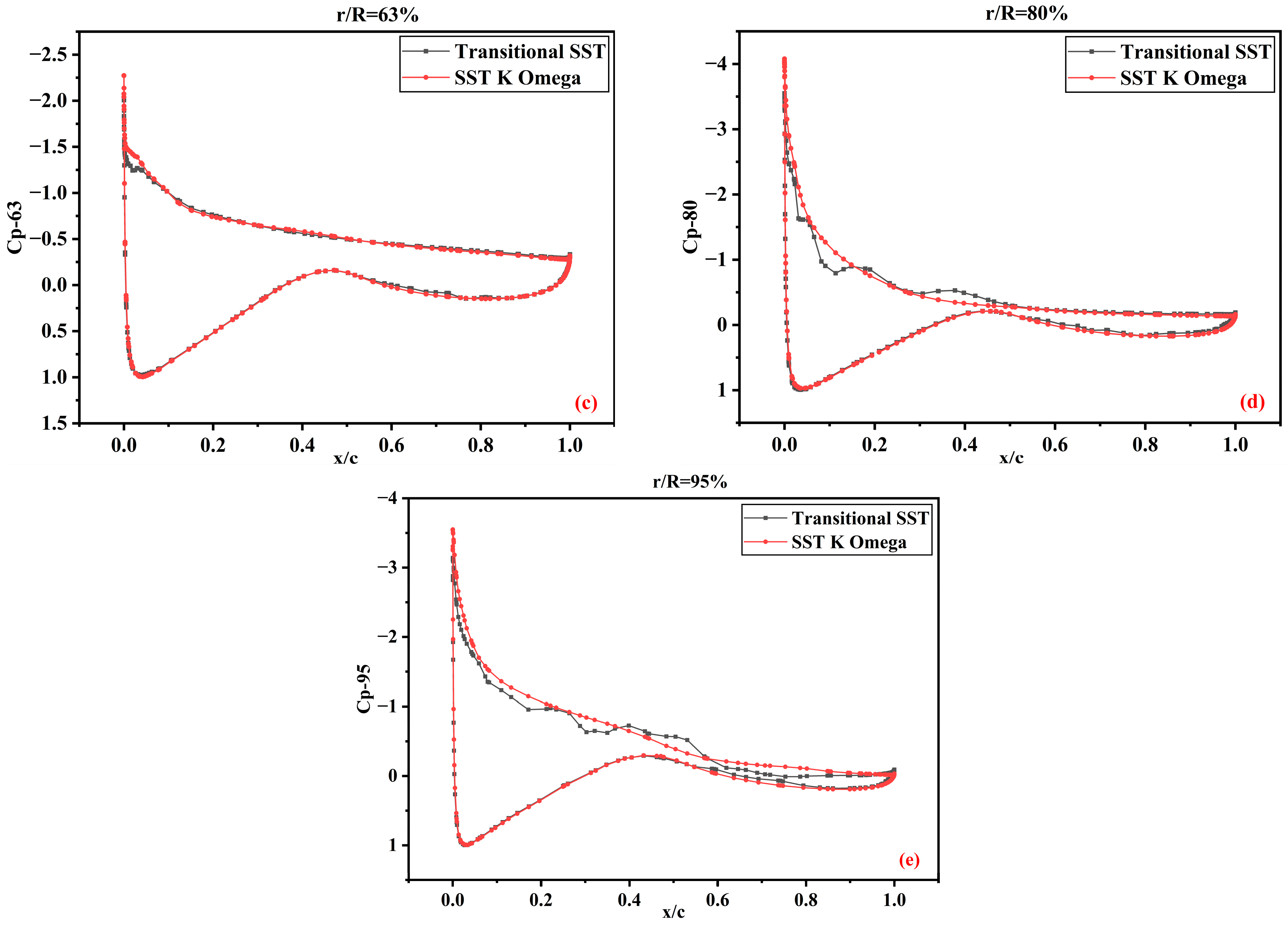
3.2. Pressure Coefficients
3.2.1. NREL Phase VI Validation
3.2.2. The 12% Scaled-Down Model
At Wind Speed = 7 m/s
At Wind Speed = 9 m/s
At Wind Speed = 12 m/s
4. Conclusions
- For wind flow velocities in the range of 5–10 m/s, the numerical simulation results of the transitional SST and SST K-Omega models matched well with the experimental data of the torque and thrust force. At a wind velocity of 10 m/s, both turbulence models overestimated the torque and thrust force values. Likewise, the torque values estimated by both turbulence models for a 12% scaled-down model up to a wind speed of 9 m/s displayed excellent trends with the experimental results. At a wind speed of 9 m/s, flow separation from the blade surface was observed, and the numerical solutions of the transitional SST and SST K-Omega deviated from the experimental data. Overall, the transitional SST model matched reasonably well with the experimental trend and slightly underestimated the torque values after a wind speed of 10 m/s, with a difference of less than 6%.
- The pressure coefficients predicted by the transitional SST and SST K-Omega models show satisfactory agreement with the experimental data, except for some deviations at high speeds, but lie within the standard deviation of the experimental data.
- The numerical results for the pressure coefficient curves obtained from the turbulence models were similar. The variation primarily occurred on the suction side, extending from the base to the blade tip. In the boundary layer region, the transitional SST model captured the flow phenomena better than the shear stress transport K-Omega model in the transition from the laminar to turbulent layers. Likewise, advancing from the leading edge to the trailing edge of the blade, the transitional SST model demonstrated an improved predicted flow separation. The simulation results of this study were limited to the specific flow regimes considered in the analysis.
5. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Ilinca, A.; Perron, J. Review of performance optimization techniques applied to wind turbines. Appl. Energy 2015, 142, 361–388. [Google Scholar] [CrossRef]
- Veers, P.; Bottasso, C.L.; Manuel, L.; Naughton, J.; Pao, L.; Paquette, J.; Robertson, A.; Robinson, M.; Ananthan, S.; Barlas, T.; et al. Grand challenges in the design, manufacture, and operation of future wind turbine systems. Wind Energy Sci. 2023, 8, 1071–1131. [Google Scholar] [CrossRef]
- Zhong, J.; Li, J. Aerodynamic performance prediction of NREL phase VI blade adopting biplane airfoil. Energy 2020, 206, 118182. [Google Scholar] [CrossRef]
- Ye, M.; Chen, H.-C.; Koop, A. Verification and validation of CFD simulations of the NTNU BT1 wind turbine. J. Wind. Eng. Ind. Aerodyn. 2023, 234, 105336. [Google Scholar] [CrossRef]
- Geng, X.; Liu, P.; Hu, T.; Qu, Q.; Dai, J.; Lyu, C.; Ge, Y.; Akkermans, R.A. Multi-fidelity optimization of a quiet propeller based on deep deterministic policy gradient and transfer learning. Aerosp. Sci. Technol. 2023, 137, 108288. [Google Scholar] [CrossRef]
- Schreck, S.J. IEA Wind Annex XX: HAWT Aerodynamics and Models from Wind Tunnel Measurements; Final Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2008. [Google Scholar]
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2001. [Google Scholar]
- Giguère, P.; Selig, M.S. Design of a Tapered and Twisted Blade for the NREL Combined Experiment Rotor; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1999. [Google Scholar]
- Lyu, C.; Liu, P.; Hu, T.; Geng, X.; Qu, Q.; Sun, T.; Akkermans, R.A.D. Hybrid method for wall local refinement in lattice Boltzmann method simulation. Phys. Fluids 2023, 35, 017103. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, P.; Hu, T.; Geng, X.; Sun, T.; Akkermans, R.A. A sliding mesh approach to the Lattice Boltzmann Method based on non-equilibrium extrapolation and its application in rotor flow simulation. Aerosp. Sci. Technol. 2022, 128, 107755. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wilcox, D.C.; Suga, K. Turbulence Modelling for CFD; DCW Industries Inc.: La Cañada, CA, USA, 1993; p. 460. [Google Scholar]
- Lee, K.; Huque, Z.; Kommalapati, R.; Han, S.-E. Fluid-structure interaction analysis of NREL phase VI wind turbine: Aerodynamic force evaluation and structural analysis using FSI analysis. Renew. Energy 2017, 113, 512–531. [Google Scholar] [CrossRef]
- Song, Y.; Perot, J.B. CFD Simulation of the NREL Phase VI Rotor. Wind. Eng. 2015, 39, 299–309. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Q.; Li, C.; Miao, W.; Yue, M.; Xu, Z. Investigation of the aerodynamic characteristics of horizontal axis wind turbine using an active flow control method via boundary layer suction. Renew. Energy 2022, 198, 1032–1048. [Google Scholar] [CrossRef]
- Dias, M.M.G.; Ramirez Camacho, R.G. Optimization of NREL phase VI wind turbine by introducing blade sweep, using CFD integrated with genetic algorithms. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 52. [Google Scholar] [CrossRef]
- Lee, M.-H.; Shiah, Y.C.; Bai, C.-J. Experiments and numerical simulations of the rotor-blade performance for a small-scale horizontal axis wind turbine. J. Wind. Eng. Ind. Aerodyn. 2016, 149, 17–29. [Google Scholar] [CrossRef]
- Sedighi, H.; Akbarzadeh, P.; Salavatipour, A. Aerodynamic performance enhancement of horizontal axis wind turbines by dimples on blades: Numerical investigation. Energy 2020, 195, 117056. [Google Scholar] [CrossRef]
- Ke, W.; Hashem, I.; Zhang, W.; Zhu, B. Influence of leading-edge tubercles on the aerodynamic performance of a horizontal-axis wind turbine: A numerical study. Energy 2022, 239, 122186. [Google Scholar] [CrossRef]
- Menegozzo, L.; Monte, A.D.; Benini, E.; Benato, A. Small wind turbines: A numerical study for aerodynamic performance assessment under gust conditions. Renew. Energy 2018, 121, 123–132. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Turbines–Part 2: Design Requirements for Small Wind Turbines; Technical Report 61400-2; International Electrotechnical Commission: Geneva, Switzerland, 2013. [Google Scholar]
- Radünz, W.C.; Sakagami, Y.; Haas, R.; Petry, A.P.; Passos, J.C.; Miqueletti, M.; Dias, E. Influence of atmospheric stability on wind farm performance in complex terrain. Appl. Energy 2021, 282, 116149. [Google Scholar] [CrossRef]
- Seim, F.; Gravdahl, A.R.; Adaramola, M.S. Validation of kinematic wind turbine wake models in complex terrain using actual windfarm production data. Energy 2017, 123, 742–753. [Google Scholar] [CrossRef]
- Subramanian, B.; Chokani, N.; Abhari, R. Aerodynamics of wind turbine wakes in flat and complex terrains. Renew. Energy 2016, 85, 454–463. [Google Scholar] [CrossRef]
- Zhao, F.; Gao, Y.; Wang, T.; Yuan, J.; Gao, X. Experimental Study on Wake Evolution of a 1.5 MW Wind Turbine in a Complex Terrain Wind Farm Based on LiDAR Measurements. Sustainability 2020, 12, 2467. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.; Guo, H.; Hu, T. Experimental investigations of turbulent decaying behaviors in the core-flow region of a propeller wake. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 319–329. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part I: Model Formulation. J. Turbomach. 2004, 128, 413–422. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. Wind turbine CFD modeling using a correlation-based transitional model. Renew. Energy 2013, 52, 31–39. [Google Scholar] [CrossRef]
- Sihag, S.; Kumar, M.; Tiwari, A.K. CFD Validation and Aerodynamic Behaviour of NREL Phase VI Wind Turbine. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1248, 012063. [Google Scholar] [CrossRef]
- Ji, B.; Zhong, K.; Xiong, Q.; Qiu, P.; Zhang, X.; Wang, L. CFD simulations of aerodynamic characteristics for the three-blade NREL Phase VI wind turbine model. Energy 2022, 249, 123670. [Google Scholar] [CrossRef]
- Langtry, R.; Gola, J.; Menter, F. Predicting 2D Airfoil and 3D Wind Turbine Rotor Performance using a Transition Model for General CFD Codes. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Blocken, B.; van Druenen, T.; Toparlar, Y.; Andrianne, T. Aerodynamic analysis of different cyclist hill descent positions. J. Wind. Eng. Ind. Aerodyn. 2018, 181, 27–45. [Google Scholar] [CrossRef]
- Kato, M. The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders. In Proceedings of the 9th International Symposium on Turbulent Shear Flows, Kyoto, Japan, 16–18 August 1993. [Google Scholar]
- Shaik, M.; Subramanian, B. Computational investigation of NREL Phase-VI rotor: Validation of test sequence-S measurements. Wind Eng. 2023, 47, 973–994. [Google Scholar] [CrossRef]
- Amiri, M.M.; Shadman, M.; Estefen, S.F. URANS simulations of a horizontal axis wind turbine under stall condition using Reynolds stress turbulence models. Energy 2020, 213, 118766. [Google Scholar] [CrossRef]
- Moshfeghi, M.; Song, Y.J.; Xie, Y.H. Effects of near-wall grid spacing on SST-K-ω model using NREL Phase VI horizontal axis wind turbine. J. Wind. Eng. Ind. Aerodyn. 2012, 107–108, 94–105. [Google Scholar] [CrossRef]
- Younoussi, S.; Ettaouil, A. Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed. Fluids 2023, 8, 192. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Stern, F.; Wilson, R.; Shao, J. Quantitative V&V of CFD simulations and certification of CFD codes. Int. J. Numer. Methods Fluids 2006, 50, 1335–1355. [Google Scholar]
- Cho, T.; Kim, C.; Lee, D. Acoustic measurement for 12% scaled model of NREL Phase VI wind turbine by using beamforming. Curr. Appl. Phys. 2010, 10 (Suppl. S2), S320–S325. [Google Scholar] [CrossRef]
- Hartwanger, D.; Horvat, A. 3D Modelling of a Wind Turbine Using CFD. In Proceedings of the NAFEMS UK Conference “Engineering Simulation: Effective Use and Best Practice”, Cheltenham, UK, 10–11 June 2008. [Google Scholar]





| Model Name | Mesh | Mesh Size (Million) | Torque (Nm) | RC |
|---|---|---|---|---|
| NREL Phase VI | : Coarse | 19.3 | 1607.68 | 0.035 |
| : Medium | 20.9 | 1686.50 | ||
| : Fine | 21.6 | 1689.32 | ||
| 12% Scaled Down | : Coarse | 36.5 | 0.710664 | 0.030 |
| : Medium | 38.6 | 0.834985 | ||
| : Fine | 42.5 | 0.849573 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, Z.; Wang, Z.; Zhang, X.; Shen, G. Aerodynamic Performance and Numerical Validation Study of a Scaled-Down and Full-Scale Wind Turbine Models. Energies 2024, 17, 5449. https://doi.org/10.3390/en17215449
Mehmood Z, Wang Z, Zhang X, Shen G. Aerodynamic Performance and Numerical Validation Study of a Scaled-Down and Full-Scale Wind Turbine Models. Energies. 2024; 17(21):5449. https://doi.org/10.3390/en17215449
Chicago/Turabian StyleMehmood, Zahid, Zhenyu Wang, Xin Zhang, and Guiying Shen. 2024. "Aerodynamic Performance and Numerical Validation Study of a Scaled-Down and Full-Scale Wind Turbine Models" Energies 17, no. 21: 5449. https://doi.org/10.3390/en17215449
APA StyleMehmood, Z., Wang, Z., Zhang, X., & Shen, G. (2024). Aerodynamic Performance and Numerical Validation Study of a Scaled-Down and Full-Scale Wind Turbine Models. Energies, 17(21), 5449. https://doi.org/10.3390/en17215449






