Parametrical Choice of the Optimized Fusion System for a FFHR

Abstract

Fusion–fission hybrid reactors are concepts of subcritical reactors based on the coupling of fusion and fission devices. In this case, the fusion reactor would work as an external neutron supplier for the fission core of the machine. Such systems could, in principle, operate as multi-purpose machines, such as energy generators, breeders and waste burners. The large availability of fusion and fission technologies makes the choice of devices to couple quite chaotic. In fact, most of the concepts proposed in the literature are based on attempts without real optimization. The purpose of this paper is to propose a parameter which could provide practical information regarding the choice or the design of the fusion system of an FFHR. An engineering approach based on the estimation of the energy efficiency of FFHRs was used. An evaluation of the parameter and some of its possible practical applications are shown. Obtained results indicate that, from a geometrical point of view, compact machines would need lower Q-values to reach high neutron source performance.

1. Introduction

The conceptual study of fusion–fission hybrid reactors (FFHRs) has gained relevance in recent years, as, if developed, they could represent a sort of intermediate step before pure fusion energy production [1]. In fact, FFHRs are coupled systems composed of fission subcritical reactors driven by a fusion device through the production of high-energy neutrons (14.1 MeV in the case of a D+T reaction, 2.45 in the case of a D+D reaction) [2]. In this case, the purpose of fusion reactors is to work as external neutron sources and not as energy generators [3]. The less demanding parameters of the relatively low-power fusion reactor (considering also Q < 1) in hybrid systems with respect to pure fusion and the availability of a controlled source of high-energy neutrons make this solution attractive. FFHRs also open up new ways for the discussion of those concepts which are not currently considered leading candidates for a practical fusion reactor [4].

Hybrid reactors can be designed for different applications: nuclear waste “burn”, generation of energy, production of radioisotopes for medicine and industry, and last but not least, tritium production for future fusion reactors. FFHRs have very interesting characteristics as transmuters, since the subcritical nature of these systems allows for the consideration of complex neutronic setups [5,6]. With the fission blanket being subcritical, the chain reaction is not self-sustained (i.e., it needs an external neutron source), and so, there is a strong margin of prompt criticality (setting the reactor’s k_eff around 0.95–0.96). This last feature allows for a subcritical reactor to contain large amounts of nuclear waste isotopes without having issues linked to the smaller fraction of delayed neutrons (fundamental in a critical assembly). This is not the case for critical reactors such as LWRs (Light Water Reactors), HTRs (High Temperature Reactors), or FRs (Fast Reactors) [7,8].

Complex neutronic setups or future fissile fuel composition may increase the efficiency of transmutation/conversion processes in FFHRs.

The large amount of different potential usages of FFHRs make it difficult to quantify the efficiency of this type of reactor. Moreover, the large availability of designs for fusion [9] and fission [10] machines makes the choice of devices to couple quite chaotic. Lots of FFHR concepts presented in the literature are often based on attempts or collaborations resulting in the coupling of many different fusion and fission technologies without real optimization.

The focus of this article regards the choice of a fusion machine as the neutron source of an FFHR using an engineering approach which takes into account the orders of magnitude of the relevant quantities. Fusion machines can be considered the real core of an FFHR, and their selection should be accurate and should guarantee the best possible performance in terms of neutron flux emission. A proposal for a possible strategy will be described in the following sections. The purpose of this work is to provide a parameter which could contribute information for the design of new FFHRs and the classification of the quality of existent fusion technologies as neutron sources in FFHRs. This step is fundamental for organizing the research regarding this topic. Possible applications of the proposed parameter are discussed in the Conclusions.

2. Neutron Production Scheme in a Fusion–Fission Hybrid Reactor

The main idea of a fusion–fission hybrid reactor is to combine the pros (and to limit the cons) of fusion and fission technologies. Fusion systems are high-intensity neutron sources, but they are complex machines, and up-to-date net energy generator fusion machines are not available; fission systems are excellent neutron multiplicators, but some arguments against their use, like those regarding the production of nuclear waste or the acceptance of the public, cannot be ignored. FFHRs could help with the industrialization of fusion devices, as fusion cores could be simpler machines than pure fusion devices (although issues regarding the construction of a full nuclear fusion device would not be fully mitigated). FFHRs could also, at the same time, limit the issues regarding fission systems. In fact, a subcritical reactor is generally safer as reactivity accidents are prevented, and it could help reduce the size of nuclear waste storage due to its fuel consumption properties.

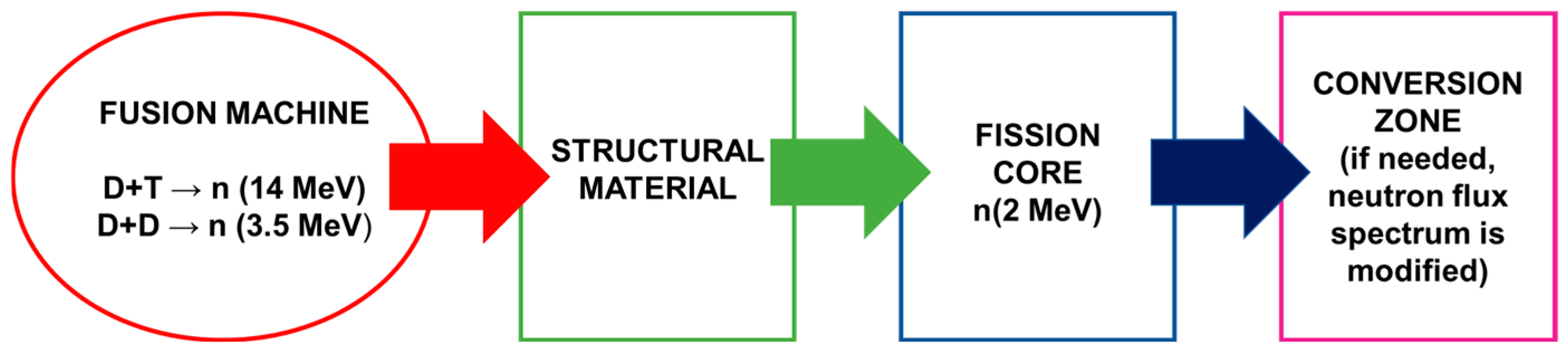
In principle, an FFHR could be designed considering the coupling of any fusion or fission system. In any case, the scheme of neutron production is always the same:

• Neutrons are generated by fusion reactions (D + T => n + α + 17.6 MeV or D + D => n + He³ + 3.5 MeV);
• They lose some of their energy (or get lost) passing through structural materials;
• They enter the fission blanket, where they induce fission reactions (or get lost);
• Depending on fission blanket technology, neutrons can be moderated or not.

Neutrons are generated in the fusion core with a defined energy depending on the fusion reaction. After the subcritical multiplication, their energy spectrum shape tends toward a fission one (mean energy ≈ 2 MeV). Previous results [4] showed that fusion neutrons hardly represent 2–3% of the total neutrons in a hybrid’s fission blanket. Therefore, the performances of FFHRs as multi-purpose systems will be similar to that of fission reactors. The pros of FFHRs lie in their safety parameters: the subcritical setup of the fission blanket gives FFHRs flexibility in core design and fuel management.

Neutron flux amplitude inside the blanket of an FFHR, as well as in other subcritical systems, depends mainly on two points:

• The available neutron source from fusion (S_ext);
• The subcritical multiplication factor M = 1/(1 − k_eff), where k_eff is the neutron multiplication factor which represents the ratio between the number of neutrons in two consecutive generations.

The reactor is subcritical when k_eff < 1. In this case, in the presence of an external neutron source, the reactor’s power output reaches a plateau after a characteristic time. The multiplication factor k_eff is usually set to ≈ 0.95–0.97 to guarantee a large subcriticality and prevent reactivity accidents. This means that M has a value in the range of 20–35, depending on the fission blanket design approach. As an example, let us suppose that k_eff is 0.97 (M = 33.3), that the neutron flux on the first wall of the fusion device is 5∙10¹² n cm⁻² s⁻¹ and that no neutron is lost on the path to the fission blanket. Then, the neutron flux inside the blanket is of the order of 1.7∙10¹⁴ n cm⁻² s⁻¹.

Fission blankets may have a multi-zone neutronic design [11], and isotope conversion may occur inside the actual fission core or at other locations (conversion zones). Figure 1 presents a simple scheme of neutron production.

3. A Proposal for an FFHR Fusion Source Figure of Merit

FFHRs are multi-purpose reactors which can be described as isotope converters: neutron–nuclei reactions occurring inside the fission blanket can be used to generate energy or to produce desired isotopes (for example, tritium). Generally, isotopes’ conversion by neutron irradiation relies on the irradiating neutron fluence and the neutron energy spectrum. In particular, the higher the available neutron fluence, the better. Therefore, the conversion performance depends on the external neutron source amplitude, the time of operation (duty cycle), the multiplication factor and neutron moderation. The first two parameters depend on the fusion core design and operation, while the last two are controlled via the fission blanket design. Neutron production is consequently a relevant characteristic for the fusion core of an FFHR.

A well-known figure of merit for fusion reactors is the Q factor, defined as

$$\mathrm{Q}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{F}\mathrm{U}\mathrm{S}}}{{\mathrm{P}}_{\mathrm{E}\mathrm{X}\mathrm{T}}}}$$

(1)

where P_FUS is the power generated from fusion reactions and P_EXT is the additional external power needed to operate the fusion reactor. Q is a function of many parameters of the fusion machine [12], including the dimensions and the operation mode (magnetic field, external power, plasma density and so on). Since the functional dependence may vary for different machines, it was not included in the formulas. Generally, bigger machines have higher Q-values.

To estimate the efficiency of a hybrid reactor, one could use a similar idea. For example, Hans Bethe in [13] defined the Q-factor of a fissile fuel breeder FFHR by adding the contribution of the power of the fuel burnt in external “satellites” fission reactors. A similar idea of power comparison can be used in the case of an FFHR focused on power production or fuel supply, and the Q factor of a, FFHR can be defined as

$${\mathrm{Q}}_{\mathrm{H}\mathrm{Y}\mathrm{B}\mathrm{R}}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{i}}}{{\mathrm{P}}_{\mathrm{E}\mathrm{X}\mathrm{T}}}}=\mathrm{Q}+{\mathrm{N}}_{\mathrm{b}}{\displaystyle \frac{{\sum }_{\mathrm{i}=2}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{i}}}{{\mathrm{P}}_{\mathrm{E}\mathrm{X}\mathrm{T}}}}$$

(2)

where P_i is the ith generated power contribution term, P₁ indicates the power generated from the fusion core of the FFHR and N_b is the number of modular blankets.

The terms P₂…P_n depend strictly on the neutron flux at the conversion locations. For these terms, it is possible to write an estimation formula, such as

$${\mathrm{P}}_{\mathrm{i}}={\mathrm{E}}_{\mathrm{i}}·{\mathsf{\Phi }}_{\mathrm{i}}{\sum }_{\mathrm{j}=1}^{\mathrm{K}}{\mathsf{\Sigma }}_{\mathrm{j}}·{\mathrm{V}}_{\mathrm{j}}$$

(3)

where Φ_i is the neutron flux at the conversion location, Σ_j is the macroscopic cross section of the conversion reaction, V_j is the volume of the converted material and E_i is the energy generated from the converted material.

V_j is an estimate of the proper volume of the isotope of interest and considers the volume of the conversion zone, the enrichment of the isotope of interest and the volume fraction of the material of interest.

For example, if tritium breeding from lithium is considered, Φ_i is the neutron flux at the conversion location, Σ_j is one of the tritium breeding reactions (such as Li⁶(n,α)T), V_j is the volume of the isotope of interest (for example, the proper volume of Li⁶) and E_i is the energy released by fusion reactions involving the produced tritium, which may be quantified as 3/5 of 17.6 MeV (energy released by a D+T fusion reaction).

Φ_i is the result of the multiplication process occurring in the device, as described in Section 2. It can be quantified as

$${\mathsf{\Phi }}_{\mathrm{i}}\approx \mathrm{M}·{\mathrm{f}}_1·{\mathrm{f}}_{2\mathrm{i}}·{\mathsf{\Phi }}_{\mathrm{S}}$$

(4)

where M is the subcritical multiplication factor of the fission blanket, f₁ is the fraction of source neutrons reaching the multiplication zone, f_2i is the fraction of multiplicated neutrons reaching the conversion zone (which could be different from the multiplication zone, otherwise f_2i = 1) and Φ_S is the neutron flux at the fraction of interest of the first wall of the fusion machine.

Assuming a neutron emission from a ring source, the term Φ_S can be defined as

$${\mathsf{\Phi }}_{\mathrm{s}}\approx {\displaystyle \frac{\left(\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\right)·{\mathrm{V}}_{\mathrm{P}\mathrm{C}}}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{F}\mathrm{U}\mathrm{S}}}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}·{\mathrm{E}}_{\mathrm{F}\mathrm{U}\mathrm{S}}}}$$

(5)

where V_PC is the plasma chamber volume, S_FW is the surface of the first wall, f_Θ is the first wall surface fraction reached by emitted neutrons and E_FUS is the energy released from a fusion reaction.

Therefore, it is possible to define the Q_HYBR as

$${\mathrm{Q}}_{\mathrm{H}\mathrm{Y}\mathrm{B}\mathrm{R}}=\mathrm{Q}+{\mathrm{N}}_{\mathrm{b}}·{\displaystyle \frac{{\mathrm{P}}_{\mathrm{F}\mathrm{U}\mathrm{S}}·{\mathrm{f}}_1·{\sum }_{\mathrm{i}=2}^{\mathrm{n}}{\sum }_{\mathrm{j}=1}^{\mathrm{K}}{{\mathrm{M}·\mathrm{E}}_{\mathrm{i}}·{\mathrm{f}}_{2\mathrm{i}}·\mathsf{\Sigma }}_{\mathrm{j}}·{\mathrm{V}}_{\mathrm{j}}}{{\mathrm{P}}_{\mathrm{E}\mathrm{X}\mathrm{T}}{·\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}·{\mathrm{E}}_{\mathrm{F}\mathrm{U}\mathrm{S}}}}$$

(6)

N_b can be defined as

$${\mathrm{N}}_{\mathrm{b}}=2\mathsf{\pi }{\mathrm{R}}_0·{\mathrm{n}}_{\mathrm{b}}$$

(7)

where R₀ is the major radius and ${\mathrm{n}}_{\mathrm{b}}$ is the number of blankets for a unit of length and depends on the blanket design, which is supposed to be the same for each blanket as a means of simplification.

The terms N_b, M, f₂ and Σ depend on the neutronic design of the blanket, E and E_FUS are constant, and V can be considered as independent from the fusion design if the blanket dimension (L³) is assumed to be adequately smaller than the fusion device one (L << R₀), because in that case, the dimensions are set by reactivity requirements. Therefore, the Q_HYBR definition can be rewritten as

$${\displaystyle \frac{{\mathrm{Q}}_{\mathrm{H}\mathrm{Y}\mathrm{B}\mathrm{R}}}{\mathrm{Q}}}=1+{\displaystyle \frac{{\mathrm{R}}_0·{\mathrm{f}}_1}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}{\sum }_{\mathrm{i}=2}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{i}}$$

(8)

where C_i includes all the constants and the terms of Equation (6) which are independent from the fusion device design and operation.

Q_HYBR is then the result of Q multiplied by a certain factor which depends on the hybrid reactor design. This “amplification factor” is of the order of some tens, depending on the scope and design of the reactor. This means that to reach the Q-value of a practical fusion reactor (Q > 25–30), the fusion reactor of an FFHR could be characterized by a Q of the order of 1–5.

For an FFHR, it could be possible to consider ${\mathrm{R}}_0{\displaystyle \frac{{\mathrm{f}}_1}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}{\sum }_{\mathrm{i}=2}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{i}}\gg 1$, so that

$${\mathrm{Q}}_{\mathrm{H}\mathrm{Y}\mathrm{B}\mathrm{R}}\approx {\displaystyle \frac{\mathrm{Q}·{\mathrm{R}}_0·{\mathrm{f}}_1}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}{\sum }_{\mathrm{i}=2}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{i}}$$

(9)

Equation (9) shows that once the ratio Q_HYBR/Q is set, the geometric design of the fusion system is determined by the fission blanket parameters.

Considering the sum of Equation (7) as a constant, Q_HYBR is at its maximum when F = ${\displaystyle \frac{\mathrm{Q}·{\mathrm{R}}_0·{\mathrm{f}}_1}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}$ is at its maximum. All these terms provide important information about the characteristics of fusion device design and operation: Q is the efficiency of the machine, S_FW is linked to the geometry design, f₁ represents the simplicity of the radial design of the machine and f_Θ defines the anisotropy of neutron emission. Two good first guesses of S_FW and f₁ could be

$${\mathrm{S}}_{\mathrm{F}\mathrm{W}}\approx 4{\mathsf{\pi }}^2{\mathrm{R}}_0·\mathrm{r}\sqrt{{\displaystyle \frac{1+{\mathrm{k}}^2}{2}}}$$

(10)

$${\mathrm{f}}_1\approx {\displaystyle \frac{\mathrm{r}}{\mathrm{r}+\mathrm{d}}}·{\displaystyle \frac{\mathsf{\lambda }}{\mathrm{d}}}$$

(11)

where R₀ is the major radius of the fusion system, r is the minor radius, k is the elongation of the torus section, d is the distance between the first wall of the fusion device and the fission blanket, and λ is the neutron mean free path in the fusion machine structural materials.

Through these approximations, it is possible to write F as

$$\mathrm{F}={\displaystyle \frac{\mathrm{Q}·{\mathrm{R}}_0·{\mathrm{f}}_1}{{\mathrm{S}}_{\mathrm{F}\mathrm{W}}·{\mathrm{f}}_{\mathsf{\Theta }}}}={\displaystyle \frac{\mathrm{Q}·\mathsf{\lambda }}{{\mathrm{f}}_{\mathsf{\Theta }}·(\mathrm{r}+\mathrm{d})·\mathrm{d}\sqrt{\frac{1+{\mathrm{k}}^2}{2}}}}$$

(12)

which is at its maximum for maximum Q and λ and for minimum d, r, k and f_Θ.

There is no explicit dependence from R₀ since it is eliminated through the ratio N_b/S_FW. Q is a Q(R,r,k …), and generally, it grows with the dimensions of the machine. This has to be considered to set up a compromise between the Q-value and the dimensions of the machine. In the case of Tokamaks (ITER scaling [14]), Q grows almost linearly with R₀.

During the design process of the fusion device for an FFHR, such an F factor could be used to set neutron source optimization conditions based on the geometry and the type of operation.

Obviously, the design goals will also depend on engineering and economic performance. A possible upgrade of the F formula could be the introduction of correction parameters to consider the costs and complexity of the devices. One could assume they depend on dimensions and the mode of operation (e.g., the presence of superconductors or a high duty cycle). In any case, these evaluations were not the main purpose of this work, and therefore, they are not included in this paper.

4. Classification of Fusion Machines through the Proposed Figure of Merit

The decision of the approach to FFHR design will depend on different aspects. For example, one could decide to start from the beginning and optimize the design, or to use mature technologies to cut development and building time [15]. Both approaches could be valid and justified. The factor F defined in Equation (12) could be used both to set conditions for new designs and to classify existent machines.

The following

Table 1. Characteristic parameters for various fusion machines [16,17].

MACHINE	R0 [m]	SFW [102 m2]	R0/SFW [10−2 m−1]	Q	F [10−2m−1]
DEMO	8.77	13	0.67	25	16.75
ITER	6.2	7	0.88	>10	8.88
STEP	4	8.81	0.45	10	4.5
RFX-modII	4	1.26	3.17	≈1	3.17
JET	2.96	1.55	1.90	0.67	1.27
DTT	2.19	0.77	2.84	1	2.84
ST-F1	1.4	0.8	1.75	3	5.25

shows an example classification of fusion machine projects through the proposed F parameter. The data listed here are estimations and serve just to show the orders of magnitude of the involved parameters.

It is important to note that most of the following machines are experimental and not designed for industrial operation. The Table aims to show how the different parameters affect the results.

As a means of simplification, f₁ and 1/f_Θ were set to 1 so that F (f₁ = 1/f_Θ = 1) = Q∙R₀/S_FW. These factors could be computed by neutronic codes once the geometry of the system and the neutron emission characteristics are known. Nevertheless, one could expect their values to be higher for machines whose sections have higher elongation (k). S_FW data are estimated from Equation (10).

Table 1 shows how geometric aspects of fusion devices and Q-values influence neutron source performance.

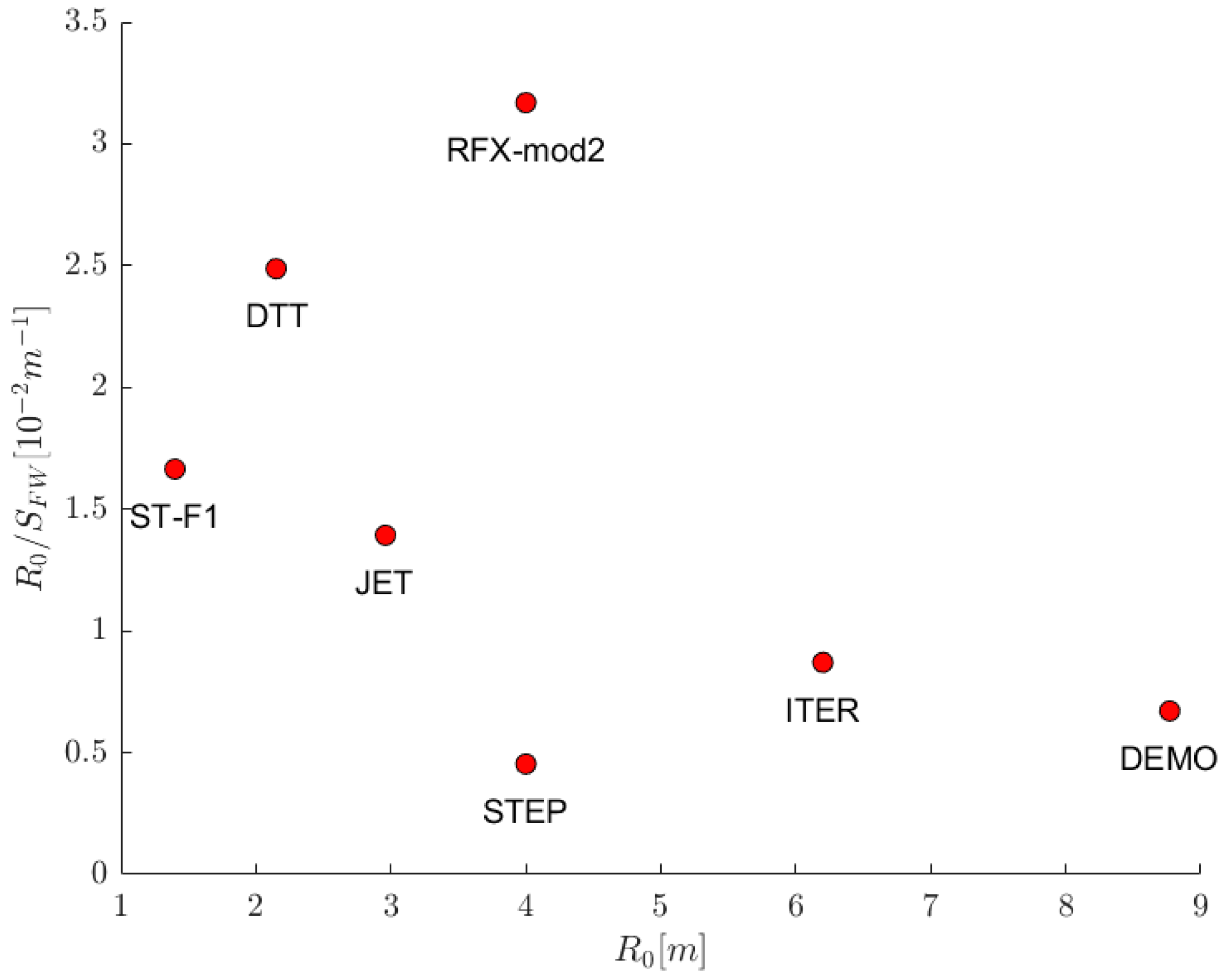
Machines with a larger F have better performances from the source neutronic point of view. ITER and DEMO are particularly favored by their high estimated Q-values. For other machines, the ratio R0/S_FW plays an important role for the computed values of F.

The table shows that there is a clear dependence of Q on the dimensions, which has to be taken into account. Data indicate that a compromise between Q, R0 and SFW has to be found.

ITER and DEMO are listed as references for other devices’ properties. Machines with such high Q-values (the designs’ Q-values are, respectively, 10 and 25) are probably not good fits for FFHRs since they are too high-performing and demanding. As a first estimate, it is possible to state that a commercial FFHR would need a fusion device with a Q-value of order of 1–5. The geometric parameter R₀/S_FW is proportional to 1/(r ∙ k), and thus, compact machines, or machines characterized by a relatively small minor radius and elongation, appear to be good fits as neutron sources for FFHRs. On the other hand, compact machines may have issues regarding heat flux on structures and should compensate for the dependence of Q on the dimensions.

RFP machines, which are characterized by high aspect ratios, show good performance as neutron sources even though they generally show lower performance as standalone fusion reactors compared to other technologies. Spherical machines (STEP, ST-F1) could be interesting fits for FFHRs since they can achieve relatively high Q-values with a compact setup. Tokamaks are somewhere between RFPs and Spherical Tokamaks (ST); their R₀/S_FW ratios are smaller than the RFP ones and higher than STs ones, and they can achieve high Q-values, but their designs are generally less compact. A compromise has to be found between Q, which also depends on the dimensions, and the size of the machine.

In selecting the right machine, one should look also at other characteristics like economics, the guaranteed time of operation and the complexity of the systems.

Figure 2 shows a graph for the geometry aspect factor R₀/S_FW versus R₀. It illustrates how fusion devices with a smaller minor radius and elongation are favored; i.e., they need a smaller Q to reach high neutron source performances.

5. Conclusions

The present work describes an approach to the evaluation of the energy efficiency of an FFHR and a proposal for a parameter useful in describing the quality of a fusion device as a neutron source for an FFHR.

The analysis of efficiency was performed considering the possible multiple contributions of such reactors, such as in energy production, tritium breeding and fissile fuel production. This is a very important point since FFHRs could operate not only as energy generators but also as breeders/converters. As a first estimate, it is possible to state that a commercial FFHR would need a fusion device with a Q-value of the order of 1–5.

This approach shows that a good factor for a fusion source figure of merit would be $F={\displaystyle \frac{Q·R_0·f_1}{S_{FW}·f_{\Theta }}}$, where Q is the Q-value of the fusion device, R₀ and S_FW are its major radius and first wall surface, and f₁ and f_Θ are correction factors which take into account, respectively, the complex of the radial development of the machine and the angle of neutron emission. These two factors may be computed by neutronic code once the geometry and emission characteristics of the machine are known. The F parameter indicates that, from a geometrical point of view, compact machines would need lower Q-values to reach high neutron source performance.

The proposed figure of merit could have practical applications during a design process or in classifying existent fusion technologies’ neutron source properties. In fact, there are two possible strategies for the design of FFHRs:

• To start from the beginning and develop a proper fusion machine design (in this case, the equation of the F parameter could be used in the equation system of the design process);
• To couple and adapt the designs of mature technologies.

Both strategies have their own pros and cons and need an accurate selection process of fusion and fission systems. For a commercial FFHR, engineering and economic choices would also play an important role in the design process.