Next Article in Journal
Electrochemical Behavior of Tantalum Nitride Protective Layers for PEMFC Application
Previous Article in Journal
Application of a GIS-Based Multi-Criteria Decision-Making Approach to the Siting of Ocean Thermal Energy Conversion Power Plants: A Case Study of the Xisha Sea Area, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 17
Issue 20
10.3390/en17205098
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Improvement of the Source Current Quality for a Shunt Active Power Filter Operating Using Hysteresis Technique with Stabilized Switching Frequency

by
Andrzej Szromba
Faculty of Electrical and Computer Engineering, Cracow University of Technology, 31-155 Cracow, Poland
Energies 2024, 17(20), 5098; https://doi.org/10.3390/en17205098
Submission received: 19 August 2024 / Revised: 23 September 2024 / Accepted: 8 October 2024 / Published: 14 October 2024
(This article belongs to the Topic Power Electronics Converters, 2nd Edition)
Browse Figures
Versions Notes

Abstract

:
Determining the current reference for a shunt active power filter (SAPF) can be carried out in many ways. Once the reference is determined, it can be shaped by SAPF switches with the use of pulse width modulation (PWM)/hysteresis control techniques. There are many variants of shaping the compensation waveform using these techniques. Nevertheless, regardless of the PWM/hysteresis technique adopted, a switching frequency current component appears in the system. It acts as a carrier used to inject a compensating current into the grid. Once the compensating current has been entered into the grid, the switching component should be reduced in it. This can be performed using RLC passive filters in various variants. The article discusses a variable/stabilized frequency hysteresis current control technique adapted for SAPF regulation with the use of current closed-loop control (source current direct control). For this technique, the passive filter should be placed outside the current control loop. The article focuses on examining the effectiveness of the interaction of the RLC filter with SAPF acting with such a control technique.

1. Introduction

In classic reactive power compensation systems, there is the possibility of immediately generating a smooth compensating current waveform using a capacitor/inductor. For non-linear/time-variable loads, this is no longer possible because, using linear/time-invariant devices, it is impossible to create a compensating waveform of a complex shape. A device that automatically follows the time-variable load, for example, SAPF, is needed. A broad review of devices used for improving power quality and the principles of their operation is collected, e.g., in [1,2,3,4,5].
However, the use of SAPF is associated with an inherent problem: SAPF injects to the grid not only the desired basic waveform, compensating for the load inactive current, but also the high-frequency waveform, which is a kind of carrier wave for this basic waveform. It is the result of switching the PWM/hysteresis controller. Since this high-frequency component has a negative impact on the grid and the devices powered by it, e.g., additional energy losses, electromagnetic interference, device overheating, etc., the amount of high-frequency component injected into the grid by SAPF should be limited.
Generally, there are two ways to limit this high-frequency component in the source branch current. The first one involves shaping the compensation waveform in a narrow band given by the PWM/hysteresis control parameters. This is usually associated with an increase in the pulsing frequency of the SAPF switches and, therefore, with an increase in the energy dissipated in them. If, for some reason, it is impossible to obtain a sufficiently low content of the high-frequency component in the source branch in this way, a passive filter should be used.
A number of interesting articles discussing the theory and practice of passive filters can be found in the literature. In particular, their structures, the effectiveness of their operation, methods of damping energy oscillations [6,7,8,9,10,11,12], and the cost of their production and operation [12] are discussed.
It can be considered that the basic structures of passive filters are classic RC and RLC circuits. The advantages of these filters are their compact structure, simplicity of design, and the presence of a physical resistor R. It can effectively suppress the inevitable oscillations of the energy stored in passive filters with inertial objects operating in the grid.
Recently, structures have been developed in which these oscillations can be damped by a “software” equivalent of the real resistor through so-called virtual resistance. Both the design process of virtual elements and their real-time control can reach high complexity. A well-documented example of designing a virtual element to achieve system stability in difficult conditions of the power supply environment can be found, e.g., in [13].
However, leaving the physical resistor in use preserves the important advantages of the RLC passive filter. Namely, its “infinite” speed of operation is maintained and, obviously, it is not affected by the imperfections of its adjustment to the ongoing need. However, these advantages come at the cost of its basic, inherent disadvantage: it dissipates energy. For the systems discussed below, power losses in the passive filter range from about a half watt to several watts, depending on the filter structure and the operating mode of the SAPF hysteresis controller. This range of power losses is within the ranges reported in the literature [6,14,15].
The SAPF device discussed in this article directly shapes the source branch current to the form of active current. This type of control is known in the literature as control in the current closed loop or source current direct control [16,17,18,19,20,21,22,23,24,25]. The properties of this control are described as precise and resistant to disturbances and changes in grid parameters.
At this point, it is appropriate to emphasize the basic scope of this article. Due to the closed-loop control of SAPF, i.e., with the regulation of the fundamental active current component and the use of the hysteresis controller directly in the supply source branch [26,27,28,29,30], the passive filter is placed outside this current control loop. Therefore, a SAPF-and-passive filter configuration is created, which is different from most structures with SAPF control in an open structure, in which the inductance of the SAPF output choke is used as one of the inductances of LCL/LLCL filters [11,31,32,33,34,35,36,37]. Nevertheless, there are exceptions to this generally encountered approach. In the literature, systems can be found with an LCL filter placed inside the SAPF current feedback loop with the source current, but operating with an additional SAPF current control loop (dual-loop current control: grid current loop and inverter-side current loop) [38,39]. It should also be noted here that the research topic described in this paragraph applies to both the two- and three-state hysteresis control methods of the SAPF filter (considered in Section 4).
The rest of the paper is organized as follows. Section 2 describes the hysteresis control technique for the variable (used so far) and then for the constant (considered in this paper) switching frequency for the SAPF under study. The reduction in the switching component in the source current for the classic, two-state operation mode of the hysteresis controller is discussed in Section 3. Section 4 shows the reduction in the switching component of the source current for a modified three-state hysteresis controller operation mode. Section 5 contains summaries and conclusions and is followed by the list of references.

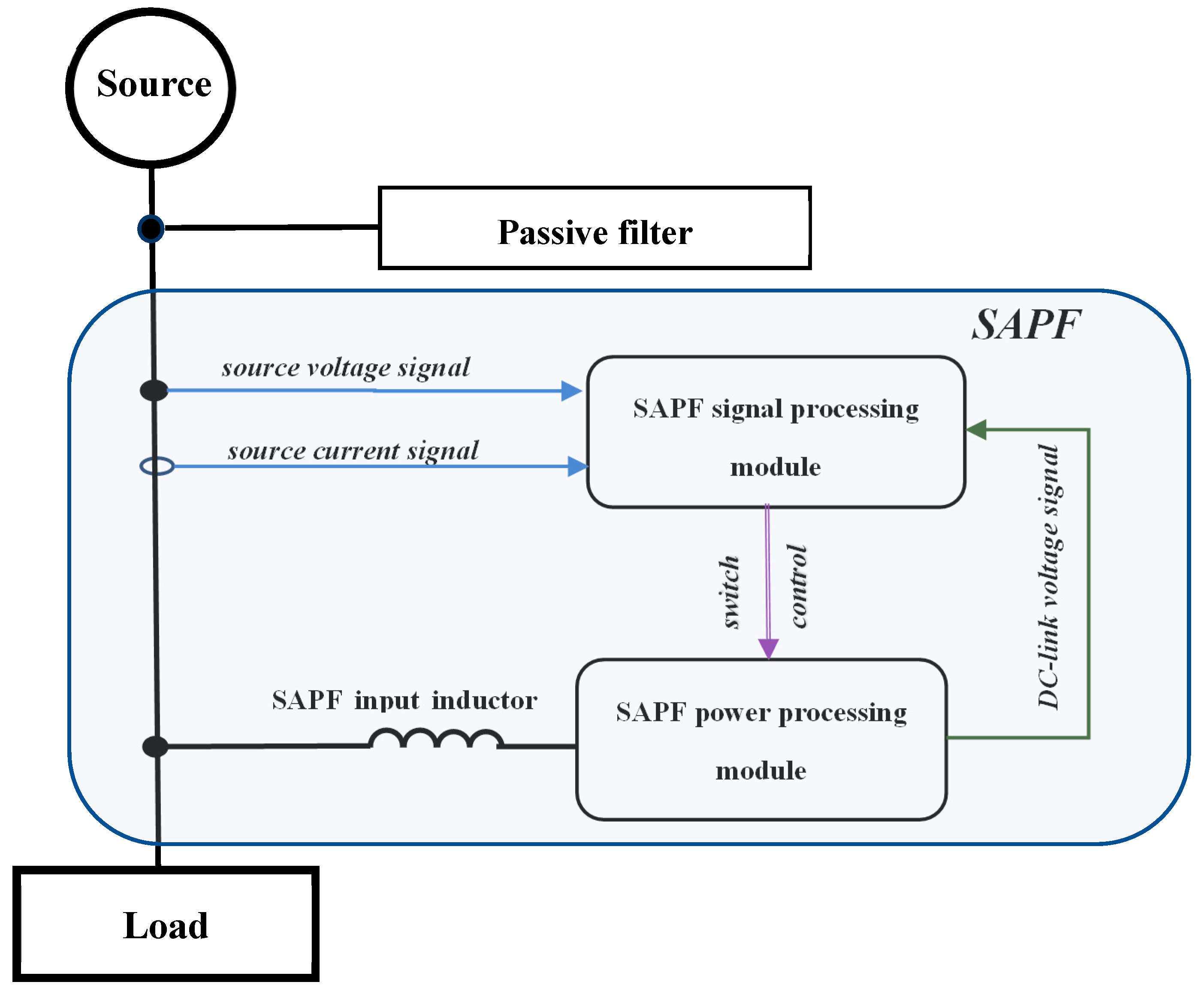
2. SAPF Hysteresis Controller with Variable or Stabilized Switching Frequency

In [40,41], broad information regarding the structure and operating principle of the SAPF considered here is included. Therefore, in order to avoid excessive length of this article, both in terms of real length, i.e., in the sense of too many pages, and in terms of content, i.e., in the sense of not repeating previously widely discussed matters, only information necessary for a clear presentation of the SAPF-and-passive filter system is given here. At the same time, for convenience, the articles [40,41] are consistently referred to in places that may require more extensive explanations.
The block structure of the discussed SAPF-and-passive filter system and its connection to the source-load line is shown in Figure 1.
The system shown in Figure 1 operates as follows. The SAPF device is built based on a voltage source inverter. By tracking the source voltage signal and the DC-link voltage signal, the SAPF signal processing module calculates the reference for the source current and generates switch control signals that control the operation of the SAPF switches. These switches are included in the SAPF power processing module. The current generated in the SAPF power processing module is injected into the source-to-load line through the SAPF input inductor L. The switching component of the SAPF current is separated by the Passive filter, reducing its amplitude in the source current.

2.1. Variable Switching Frequency Operation

In [40,41], it is shown that for the discussed SAPF, the pulse frequency of its switches can be described by the following relationship:
f i m p , var = v C 2 − v S 2 4 Δ I c o n s t L v C
where: vC is the instantaneous DC-link voltage; vS is the instantaneous source voltage; ∆Iconst is the fixed constant width of the hysteresis loop; and L is the inductance of the SAPF input choke.
For the studies presented in the paper, the DC-link voltage (i.e., voltage across SAPF’s voltage source inverter capacitor, 4 mF) varies from the initial value of 500 V, i.e., at no-load conditions, to 470 V at full SAPF loading; the source voltage consists of the sinusoidal EMF source, 230 V rms, and 50 Hz in series with 200 μH inductance and 2 mΩ resistance; ∆Iconst is 0.5 A or 1 A in the paper; and the inductance of the SAPF input choke L is 5 mH.
The source current is shaped by the SAPF hysteresis controller in a classic manner:
iST(n) ϵ (iT(n)* + ∆I, iT(n)* − ∆I)
where:
iT(n)* = GT(n-1)vS
where iST(n) is the instantaneous source current; iT(n)* is the active current reference; and GT(n) is the load equivalent conductance for n-th period of the source voltage cycle: GT(n) = PT(n)/VS2.
As it results from Equation (1), the pulse frequency of SAPF switches is variable. It depends on SAPF parameters, i.e., on the width of the hysteresis loop ∆I and the inductance of the input choke L, as well as on some signals, i.e., on the ongoing magnitudes of the source voltage vS and the DC-link capacitor voltage vC. It should be noted that, for the discussed SAPF, the voltage vC depends on the instantaneous load power: vC = f (pLoad = vSiLoad); therefore, the load power affects the switching frequency of the SAPF hysteresis controller [40,41]. The range of switching frequency variability, according to (1), at ∆I = 1 A changes in the range of 14.4 kHz–25.0 kHz at no-load conditions and in the range of 12.6 kHz–23.5 kHz at full-load conditions.
Depending on the mentioned parameters and signals, the switching frequency (1) can vary widely. In particular, which is important from the perspective of this article’s topic, the use of a smaller/larger hysteresis loop width ∆I results in a shift of the amplitude–frequency characteristic (spectrum) of the SAPF current. This effect can be seen by analyzing Equation (1), where, as a result of reducing the ∆I loop width from 1 A to 0.5 A, the SAPF current spectrum shifts from a range of about 14.5 kHz–25 kHz to a range of about 29 kHz–50 kHz.
It can therefore be stated that a characteristic of the discussed SAPF control method is the wide spectrum of switching frequency of its hysteresis controller. Such a spectrum can make it difficult to reduce the switching component in the source current through passive filtration. Therefore, it is justified to consider the possibility of operating the hysteresis controller with a stabilized switching frequency of the SAPF switches.

2.2. Stabilized Switching Frequency Operation

By transforming Expression (1), one can obtain a dependency on the time-varying hysteresis loop width as a function of the DC-link capacitor voltage and the source voltage for the required switching frequency fimp,const and the applied choke inductance L:
Δ I var = v C 2 − v S 2 4 f i m p , c o n s t L v C
Expression (4) can be used to change the mode of operation of the SAPF hysteresis controller from the constant band/variable frequency mode to the stabilized frequency/variable band mode.
The source current is still shaped according to the relations (2) and (3), but the width of the hysteresis loop ∆I is not constant. The range of variability of this loop width, according to (4), at fimp = 20 kHz changes in the range of 0.72 A to 1.25 A at no-load conditions and in the range of 0.63 A to 1.18 A at full-load conditions.
For simplicity in describing the principles of the discussed method and interpreting the obtained results, this section and Section 4.1 assume zero power of the compensated load, or no-load conditions. Therefore, a reference situation is discussed here, in which the SAPF current is a pure high-frequency current or a carrier wave for the compensating current, unaffected by either the level of or steep changes in load power. However, it should be noted that the mere activation of the SAPF imposes a certain active power load on the source. This is equal to the power losses in the SAPF power module, which, in practice, are significantly lower than the active power of the compensated load.
The operation of the SAPF under conditions of significant load current compensation, resulting in substantial variability of the voltage vC and an increase in its impact on ∆Ivar (see Expression (4)), is presented later in the article.
In Figure 2, the reference signal for the hysteresis loop width ∆Ivar, calculated according to Expression (4), and the resulting switching component of the SAPF current are shown. The constant switching frequency fimp,const is assumed to be 20 kHz.
Figure 3 compares the frequency–amplitude characteristics of the SAPF current for a system with variable versus stabilized switching frequency of the SAPF controller, i.e., according to Equation (1) versus (4). For the system with variable frequency, the band ∆Iconst was set to 1 A (see waveform 1). Next, to achieve an average ∆Ivar band of 1 A for the system controlled according to (4), the constant frequency fimp,const was set to 20 kHz (see waveform 2).
Based on the observation of waveforms 1 and 2 in Figure 3, it can be confirmed that, by changing the control method from a constant to a variable hysteresis loop width, described by Equations (1) and (4), respectively, a significant narrowing of the high-frequency spectrum of the SAPF current was achieved. This effect can be beneficial from the perspective of the efficiency of eliminating high-frequency components from the source current through passive filtration.

3. Reduction in High-Frequency Components in the Source Current Using a Passive Filter

It has been shown in the literature that SAPF can cooperate with various types of passive filters. This section considers the combination of SAPF with a circuit that can be considered basic in the family of tuned passive filters: a series RLC filter. It is tuned to the frequency fimp,const, given in formula (4), for pulsing the SAPF switches.

3.1. Filtration of the Pure Switching Component of the SAPF Current

First, for the reason given in the previous section of this paper, the SAPF-and-passive filter cooperation is presented for the pure switching current SAPF, i.e., without load current (no-load conditions). In order to reduce this current in the source branch, an RLC filter with resistance Rfpas = 1 Ω, inductance Lfpas = 19 μH, and capacitance Cfpas = 3.3 μF is used.
In Figure 4, the following are shown in sequence: the SAPF current, the passive RLC filter current (tuned to the frequency fimp,const = 20 kHz, i.e., for pulsing SAPF switches), and the source current.
The effective values of the currents shown in Figure 4 are 0.58 A, 0.68 A, and 0.25 A, respectively. The mutual relationships of these quantities, particularly the higher effective value of the RLC passive filter current compared to the SAPF current, require a comment. The passive filter current and the source current contain a capacitive component at the fundamental frequency, i.e., 50 Hz. This results from the resistive–capacitive type of the RLC one-port circuit at this frequency. The capacitive reactance is XCfpas = 965 Ω, and it dominates both the inductive reactance XLfpas = 6 μΩ and the series resistance Rfpas = 1 Ω. Therefore, XCfas determines both the type and amplitude of the fundamental current component in the RLC filter branch, and—due to no-load conditions and with the switching component filtered out—also the kind and amplitude of the current in the source branch. It is capacitive, with an rms of 0.24 A.
In Figure 5, the frequency–amplitude characteristics of the currents from Figure 4 are shown, with the color correspondence of the waveforms maintained in both figures. Comparing characteristics 2 and 3, it can be stated that there is a practical absence of the switching component in the source current.
If necessary, the capacitive component of the RLC filter (see graph no. 3 in Figure 4 and Figure 5) can be eliminated from the source branch. It can be sensed in the RLC filter branch and then generated by the SAPF as a compensating current. In the first approximation, i.e., for relatively small resistance and inductance of the RLC filter, their influence can be neglected, and the total current of the RLC filter can be considered as the waveform to be compensated. This generation of the compensating current is carried out in an open-loop control technique. To implement this compensation, an additional measurement and control circuit is placed in the SAPF signal processing module. It should be noted that this additional compensation slightly increases the energy dissipation in the SAPF power processing module.
To evaluate the efficiency of the SAPF-and-passive filter system, a certain cost indicator for filtering the switching component of the SAPF current can be applied. Given the common assertion that the main drawback of filter with a damping resistor is the relatively high power dissipation, let this indicator be the amount of this power. In the example discussed above, this power is about 0.5 W. The results obtained regarding this issue in the following sections are summarized in Table 1 in Section 5.

3.2. Operation of the SAPF-and-Passive Filter System for a Highly Distorted Load Current

The use of LC elements in passive filters is associated with the undesirable phenomenon of energy oscillation of a resonant nature, even in the presence of a damping resistor. To discuss this problem, this section shows the operation of the SAPF system with a “difficult” load current. It is generated in such a way that it should cause problems in SAPF operation as well as in the filtering of the oscillatory component by the passive filter. In particular, this current contains a constant component, an inertial component, and a pulse component with steep edges and high amplitudes. The latter component can excite energy oscillations in the system. Figure 6 shows the waveform of this load current, where all the mentioned components can be identified.
Since the dynamic of the SAPF is limited by its input inductor, the appearance of an abrupt load current slope causes a spike in the source current (see see Figure 7, Figure 8 and Figure 9, especially Figure 8). The switching action of the hysteresis controller is halted for the duration of this spike. The SAPF switches stop in a position that reduces the source current control error, i.e., in a position that forces it back into the band defined by the hysteresis loop width [40,41]. In the paper, load steep power changes with significant energy are used to cause current spikes and excite energy oscillation.
Indeed, such oscillations occur at load switching moments, here at t1 = 65 ms and t2 = 75 ms, as shown in Figure 6, Figure 7, Figure 8 and Figure 9. Their frequency is about 6 kHz, which corresponds to the resonant frequency of the capacitance Cfpas and the internal inductance of the supply voltage source. Thanks to energy dissipation in the source–RLC filter circuit, mainly in the resistor Rfpas of this filter, they are effectively damped and practically disappear after two periods of this resonant oscillation.
In Figure 8, the resonance phenomena described above are shown in the current waveform of the source, first in the system without the RCL filter, waveform 1, and then in the system with this filter, waveform 2.
For the sake of completeness, it can be added that a well-known method to reduce both the amplitude and steepness of the source current spike involves using an inductor (choke) in the load branch. An example of the results achievable by this method are shown in Figure 9. It can be observed that not only are the amplitude and duration of the spike in the source current waveform reduced, but the amplitude of the oscillations in the passive RLC filter current is as well.

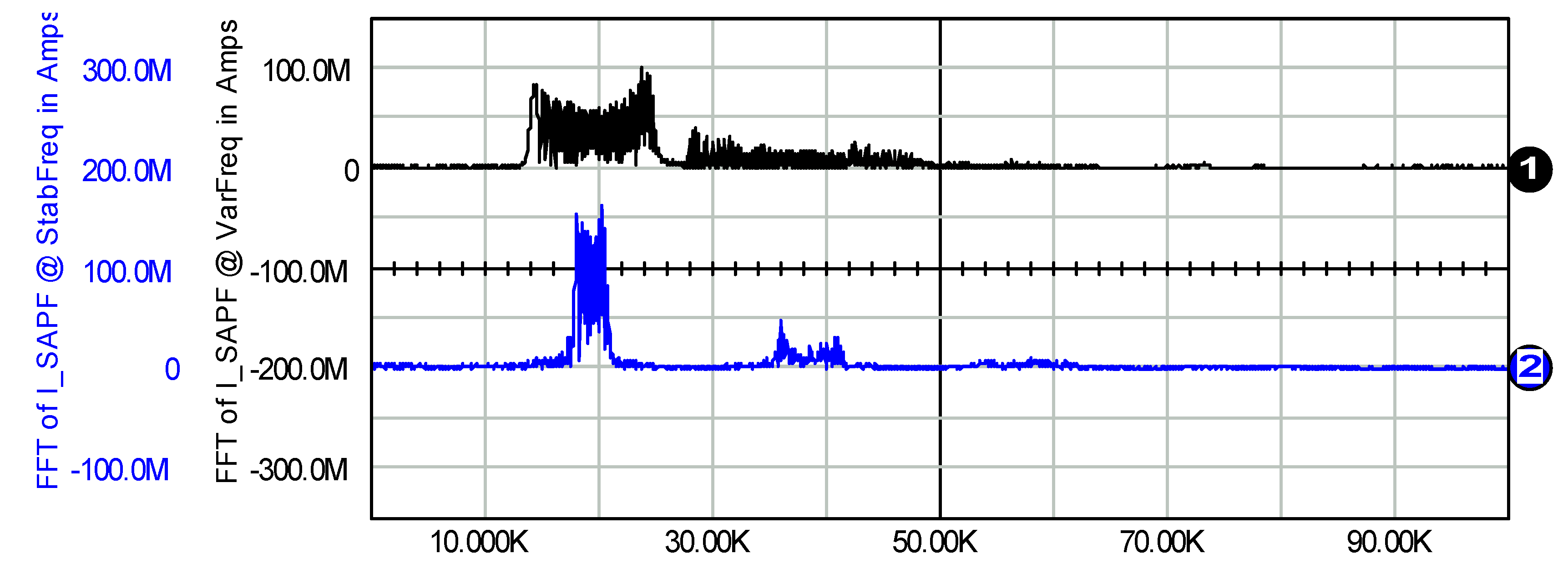
4. Reduction in the Switching Component in Source Current for Three-State Hysteresis SAPF Control

Extending the classical two-state hysteresis control method of SAPF to a three-state mode allows for a reduction in energy dissipation related to the switching of its transistors [40]. This involves eliminating a certain number of switches by extending some cycles of the SAPF hysteresis controller. This achieves a reduction in the switching frequency. In particular, this effect occurs for the source voltage around zero (see Figure 10). However, from the perspective of this paper, this reduction in switching frequency has a significant drawback, as it is associated with a broadening of the switching component spectrum of the SAPF current. This spectrum broadening occurs towards lower frequencies, making the use of a tuned RLC filter problematic, and the term “high-frequency” component in the SAPF current ambiguous.

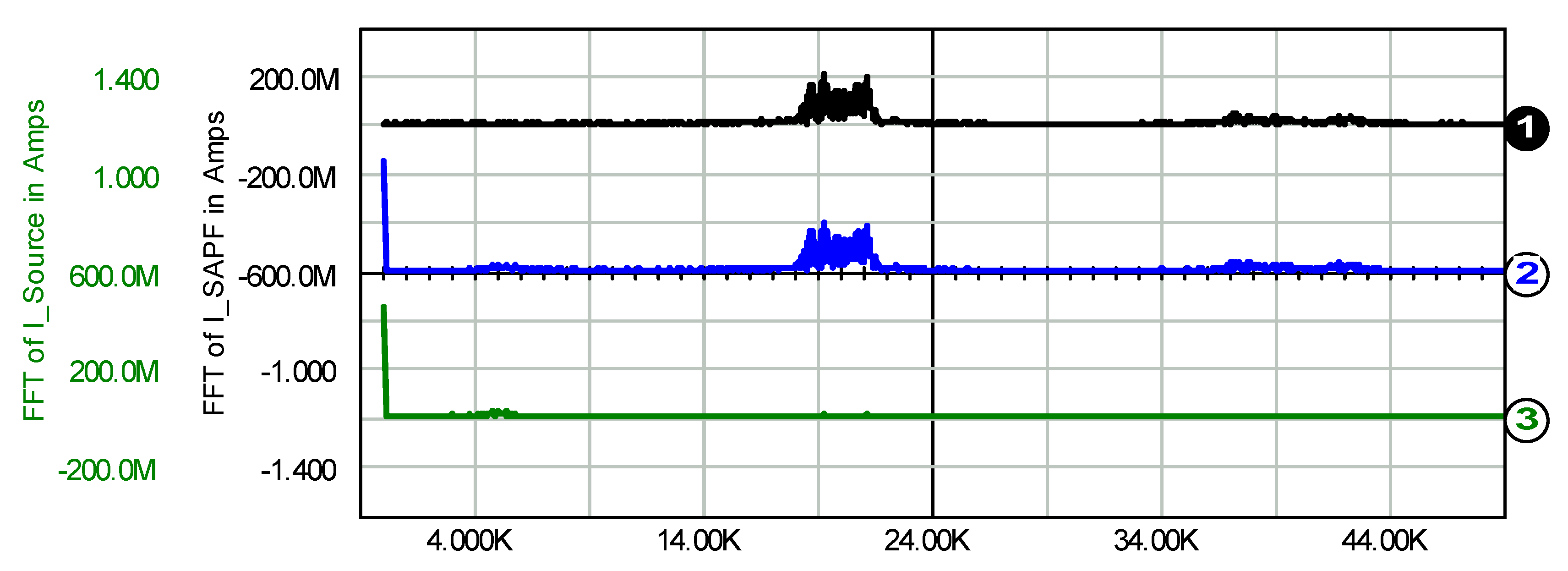
4.1. Permanent Three-State Hysteresis Control, No-Load Conditions

In the three-state control mode, despite controlling the operation of the switches according to Expression (4), the switching frequency is not stabilized. Figure 10 shows this situation, namely, the SAPF current waveform and its spectral characteristic in no-load conditions (see the justification in the Section 2.1, 3rd paragraph after Equation (4)). Of course, in no-load conditions, the source current and its characteristic are identical to those shown in Figure 10.
Due to the wide spectrum of the three-state hysteresis controller action, a broadband filter should be used. The basic solution is to use a simple series CR filter. Figure 11 shows the effect of using such a filter with elements Cfpas = 3.3 μF and Rfpas = 1 Ω. This filter is like a broadband version of the previously used RLC filter, that is, with the “turned off” tuning to a given frequency by skipping the Lfpas element.
As it turns out, when the hysteresis controller operates in the three-state mode, the SAPF-and-passive filter system is much more susceptible to energy oscillations than when the controller operates in the two-state mode. This already applies to the operation with only the pure switching component of the SAPF current, i.e., for no-load conditions. Figure 11 shows the current waveforms, in the order 1–3: SAPF (0.67 A rms), passive filter (1.42 A rms), source current (1.26 A rms), and the source voltage waveform. Significant energy oscillations can be identified in the source-and-passive filter circuit in a certain voltage environment, with the source voltage crossing through zero.

4.2. Alternate Two-/Three-State Hysteresis Control, No-Load Conditions

The amplitude of the oscillations visible in Figure 11 can be reduced by making changes both on the SAPF side and on the passive filter side. Figure 12 shows the waveforms after the following modifications: on the SAPF side, the hysteresis control mode was changed from three-state to two-state in the critical source voltage range (see waveform 4), and on the RC filter side, the resistance of the damping resistor was increased to Rfpas = 5 Ω and the capacitance of the capacitor was increased to Cfpas = 10 μF. Comparing the waveforms shown in Figure 11 and Figure 12, it can be concluded that, as a result of the changes made, the switching component in the source branch was significantly reduced, and the energy oscillations were practically eliminated.
From the comparison of the rms values of the currents shown in Figure 11 and Figure 12, it follows that the SAPF current increased from 0.67 A to 0.93 A. Almost entirely, this increase resulted from generating a compensation current for the capacitive current of the RC filter. On the other hand, the current of the RC passive filter decreased from 1.42 A to 0.93 A, which resulted from the reduction in energy oscillations.
The goal of the changes made in the SAPF-and-RC passive filter system was achieved: The switching component of the current in the source branch was reduced from 1.26 A to 0.16 A, with the simultaneous elimination of oscillations. The energy cost of achieving this goal, measured by the amount of energy losses during the operation of the RC filter, was about 4.5 W. This resulted both from the presence of the reactive component of its current, here with an amplitude of about 1 A, and from the switching component. To this cost, the increased energy dissipation in SAPF, associated with compensating for the reactive component of the RC filter current, should be added.
Commenting on the obtained results, it should be stated that balancing the relationship between the effects of reducing the switching component in the source current and the total costs of energy consumed for this purpose is an element of selecting the operating strategy of the SAPF-and-passive filter system, and can be optimized for the current needs.

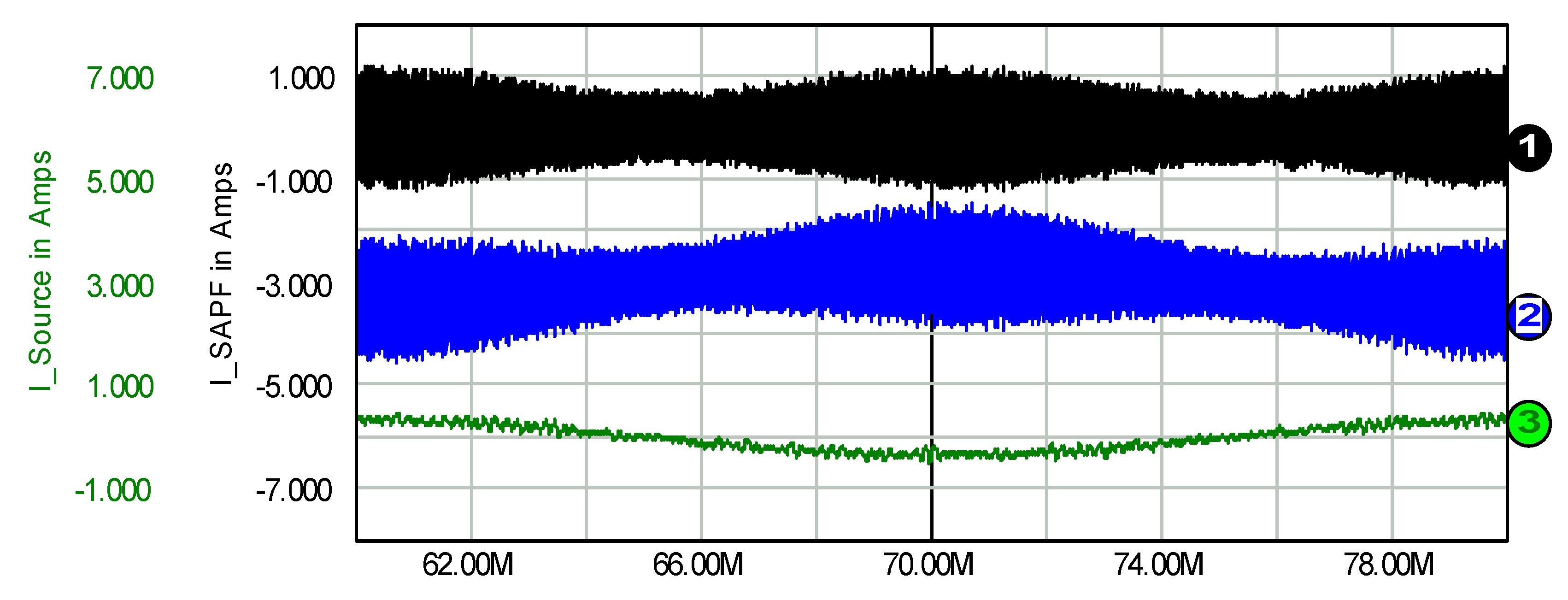
4.3. Alternate Two-/Three-State Hysteresis Control, Full-Load Conditions

Figure 13 shows the operation of the final SAPF-and-RC filter system with compensation for the “difficult” load current, which is the same as that shown in Figure 6. In particular, as a result of spikes occurring in this current, there are strong excitations to energy oscillations of a resonant nature. However, as can be seen from the waveforms of both the source current and the RC filter, these oscillations practically do not occur. This indicates the correct operation of the entire system.
The energy cost of operating an RC passive filter is about 6 W and is of a similar magnitude as in the case of filtering the pure switching component of the SAPF current. This is primarily due to the presence of a reactive component of the same amplitude, i.e., about 1 A, in the RC filter current. As already mentioned, balancing the relationship between the effects of passive filtering and the total dissipated energy costs can be carried out according to ongoing needs.

5. Summary

The article discusses a variable/stabilized frequency hysteresis current control technique combined with a two- or three-state mode of hysteresis controller operation. It is specific for SAPF regulation for the source current direct control method, with emphasis on cooperation with tuned RLC or wideband RC passive filters. It has been shown that the SAPF-and-passive filter cooperation can be effective, and the energy cost of filtering the switching component of SAPF current can be relatively low even with the use of a simple, classic RLC or RC filter.
In the considered system configuration, shown in Figure 1, the passive filter causes a capacitive reactive current in the source branch. However, as shown in the paper, if necessary, this current can be compensated by adding a new current reference to be generated by the SAPF.
Table 1 summarizes the obtained results. The first column refers to the discussed operating modes of the hysteresis controller, defined by expressions (1) and (4). Then, the frequency ranges of the hysteresis controller action, the ranges of its hysteresis loop variation, and the power dissipated in the passive filter resistor are compared. These data are given with separation into no-load and full-load conditions, in accordance with the reasoning in the paper.
Higher-order passive filters, which are widely considered in the literature, can operate at the lower edge of energy dissipation. However, the costs of their design, manufacturing, and control can be significantly higher, especially for SAPF when it controls the source current directly.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Baros, J.; Sotola, V.; Bilik, P.; Martinek, R.; Jaros, R.; Danys, L.; Simonik, P. Review of Fundamental Active Current Extraction Techniques for SAPF. Sensors 2022, 22, 7985. [Google Scholar] [CrossRef]
  2. Alfonso, J.L.; Tanta, M.; Pinto, J.G.; Monteiro, L.F.; Machado, L.; Sousa, T.J.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
  3. Garcia, O.; Cobos, J.; Prieto, R.; Alou, P.; Uceda, J. Single Phase Power Factor Correction: A Survey. IEEE Trans. Power Electron. 2003, 18, 749–755. [Google Scholar] [CrossRef]
  4. Revuelta, P.S.; Litran, S.P.; Thomas, J.P. Active Power Line Conditioners Design, Simulation and Implementation for Improving Power Quality; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
  5. Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Control algorithms for shunt active power filter for harmonics mitigation: A review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef]
  6. Buyuk, M.; Tan, A.; Bayindir, K.C.; Tumay, M. Analysis and comparison of passive damping methods for shunt active power filter with output LCL filter. In Proceedings of the 9th International Conference on Modelling, Identification and Control, Kunming, China, 10–12 July 2017. [Google Scholar]
  7. Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, L.C. A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef]
  8. Liu, T.; Liu, J.; Liu, Z.; Liu, Z. A Study of Virtual Resistor-Based Active Damping Alternatives for LCL Resonance in Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 247–262. [Google Scholar] [CrossRef]
  9. Tang, W.; Ma, K.; Song, Y. Critical Damping Ratio to Ensure Design Efficiency and Stability of LCL Filters. IEEE Trans. Power Electron. 2021, 36, 315–325. [Google Scholar] [CrossRef]
  10. He, W.; Li, Y.W. Generalized Closed-Loop Control Schemes with Embedded Virtual Impedances for Voltage Source Converters with LC or LCL Filters. IEEE Trans. Power Electron. 2012, 27, 1850–1861. [Google Scholar] [CrossRef]
  11. Routimo, M.; Tuusa, H. LCL Type Supply Filter for Active Power Filter—Comparison of an Active and a Passive Method for Resonance Damping. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2939–2945. [Google Scholar]
  12. Abdel Aleem, S.H.E.; Zobaa, A.F.; Sung, A.C.M. On the Economical Design of Multiple-Arm Passive Harmonic Filters. In Proceedings of the 47th International Universities Power Engineering Conference (UPEC), Uxbridge, UK, 4–7 September 2012. [Google Scholar]
  13. Li, X.; Fang, J.; Tang, Y.; Wu, X. Robust design of LCL filters for single-current-loop-controlled grid-connected power converters with unit PCC voltage feedforward. IEEE J. Emerg. Sel. Topics Power Electron. 2018, 6, 54–72. [Google Scholar] [CrossRef]
  14. Pena-Alzola, R.; Liserre, M.; Blaabjerg, F.; Sebastian, R.; Dannehl, J.; Fuchs, F.W. Analysis of the Passive Damping Losses in LCL-Filter-Based Grid Converters. IEEE Trans. Power Electron. 2013, 28, 2642–2646. [Google Scholar] [CrossRef]
  15. Wu, W.; He, Y.; Tang, T.; Blaabjerg, F. A new design method for the passive damped LCL and LLCL filter-based single-phase grid-tied inverter. IEEE Trans. Ind. Electron. 2013, 60, 4339–4350. [Google Scholar] [CrossRef]
  16. Mattavelli, P. A closed loop selective harmonic compensation for active filters. IEEE Trans. Ind. Appl. 2001, 37, 81–89. [Google Scholar] [CrossRef]
  17. Wang, X.; Guo, X.; Wang, F. Closed-Loop Control Method and Implementation of Selective Harmonic Type Active Power Filters. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
  18. Mattavelli, P.; Tenti, P. High performance active filters using selective harmonic control. In Proceedings of the IEEE 2000 Power Society Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000. [Google Scholar]
  19. Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
  20. Sun, X.; Li, N.; Wang, B.; Li, X. Improvement for the closed-loop control of shunt Active Power Filter. In Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
  21. Ribeiro, R.L.; Azevedo, C.C.; Sousa, R.M. A Robust Adaptive Control Strategy of Active Power Filters for Power Factor Correction Harmonic Compensation and Balancing of Nonlinear Loads. IEEE Trans. Power Electron. 2012, 27, 718–730. [Google Scholar] [CrossRef]
  22. Mariethoz, S.; Rufer, A. Open loop and closed loop spectral frequency active filtering. IEEE Trans. Power Electron. 2002, 17, 564–573. [Google Scholar] [CrossRef]
  23. Yi, H.; Zhuo, F.; Zhang, Y.; Li, Y.; Zhan, W.; Chen, W.; Liu, J. A Source-Current-Detected Shunt Active Power Filter Control Scheme Based on Vector Resonant Controller Active Power Filter. IEEE Trans. Ind. Appl. 2014, 50, 1953–1965. [Google Scholar] [CrossRef]
  24. Chen, Z.; Luo, Y.; Chen, M. Control and Performance of a Cascaded Shunt Active Power Filter for Aircraft Electric Power System. IEEE Trans. Ind. Electron. 2012, 59, 3614–3623. [Google Scholar] [CrossRef]
  25. Mattavelli, P.; Pinhabel, F. Repetitive-based control for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2004, 51, 1018–1024. [Google Scholar] [CrossRef]
  26. Fei, J.; Li, T.; Zhang, S. Indirect current control of active power filter using novel sliding mode controller. In Proceedings of the IEEE 13th Workshop on Control and Modeling for Power Electronics (COMPEL), Kyoto, Japan, 10–13 June 2012. [Google Scholar]
  27. Buso, S.; Malesani, L.; Mattavelli, P. Comparision of Current Control Techniques for Active Filter Applications. IEEE Trans. Ind. Electron. 1998, 45, 722–729. [Google Scholar] [CrossRef]
  28. Kale, M.; Ozdemir, E. An adaptive hysteresis band current controller for shunt active power filter. Electr. Power Syst. Res. 2005, 73, 113–119. [Google Scholar] [CrossRef]
  29. Awasthi, A.; Patel, D. Implementation of Adaptive Hysteresis Current Control Technique for Shunt Active Power Conditioner and Its Comparison with Conventional Hysteresis Current Control Technique. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Kollam, India, 8–10 August 2017. [Google Scholar]
  30. Kazmierkowski, M.; Malesani, L. Current Control Techniques for Three-Phase Voltage-Source PWM Converters: A Survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
  31. Buyuk, M.; Tan, A.; Inci, M.; Tumay, A. A notch filter based active damping of LLCL filter in Shunt Active Power Filter. In Proceedings of the 19th International Symposium on Power Electronics, Novi Sad, Serbia, 19–21 October 2017. [Google Scholar]
  32. Said-Romdhane, M.B.; Naouar, M.W.; Belkhodja, I.S.; Monmasson, E. An Improved LCL Filter Design in Order to Ensure Stability without Damping and Despite Large Grid Impedance Variations. Energies 2017, 10, 336. [Google Scholar] [CrossRef]
  33. Liu, C.; Dai, K.; Duan, K.; Wang, X.; Kang, Y. Application of an LLCL Filter on Three-Phase Three-Wire Shunt Active Power Filter. In Proceedings of the Intelec 2012, Scottsdale, AZ, USA, 30 September–4 October 2012. [Google Scholar]
  34. Yang, L.; Liu, D.; Zhang, Z.; Yang, M.; Zhao, L.; Chen, X.; Xu, L.; Fu, Y.; Ma, C. Improving the Current Control Performances of LCL-Type Shunt Active Power Filters with High-Pass Inverter-Side Current Feedback Active Damping. In Proceedings of the IEEE 6th International Electrical and Energy Conference, Hefei, China, 12–14 May 2023. [Google Scholar]
  35. Buyuk, M.; Inci, M.; Tumay, M. Performance evaluation of LLCL filter for active power filter. In Proceedings of the IEEE 16th International Conference on Environment and Electrical Engineering, Florence, Italy, 7–10 June 2016. [Google Scholar]
  36. Ge, H.; Zhen, Y.; Wang, Y.; Wang, D. Research on LCL filter active damping strategy in active power filter system. In Proceedings of the 9th International Conference on Modelling, Identification and Control, Kunming, China, 10–12 July 2017. [Google Scholar]
  37. Zheng, Z.; Jiaqiang, Y.; Niangchang, Y. Research on PI and Repetitive Control Strategy for Shunt Active Power Filter with LCL-Filter. In Proceedings of the IEEE 7th International Power Electronics and Motion Control Conference—ECCE, Harbin, China, 2–5 June 2012. [Google Scholar]
  38. Yang, L.; Yang, J.; Gao, M.; Watson, A.; Wheeler, P. Current Control of LCL-Type Shunt APFs: Damping Characteristics, Stability Analysis, and Robust Design Against Grid Impedance Variation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5026–5042. [Google Scholar] [CrossRef]
  39. Yang, L.; Yang, J. Robust Current Control Method for LCL-Type Shunt Active Power Filters with Inverter-Side Current Feedback Active Damping. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018. [Google Scholar]
  40. Szromba, A. Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter? Energies 2021, 14, 6031. [Google Scholar] [CrossRef]
  41. Szromba, A. Improving the Efficiency of the Shunt Active Power Filter Acting with the Use of the Hysteresis Current Control Technique. Energies 2023, 16, 4080. [Google Scholar] [CrossRef]
Energies 17 05098 g001
Figure 1. Block structure of SAPF-passive filter system and its connection to the source-load line.
Figure 1. Block structure of SAPF-passive filter system and its connection to the source-load line.
Energies 17 05098 g001
Energies 17 05098 g002
Figure 2. SAPF current: waveform 1 and the ∆I signal waveform according to (2.4): waveform 2.
Figure 2. SAPF current: waveform 1 and the ∆I signal waveform according to (2.4): waveform 2.
Energies 17 05098 g002
Energies 17 05098 g003
Figure 3. Characteristics of the active filter current for variable frequency with ∆Iconst = 1 A: waveform 1 and for stabilized frequency with mean ∆Ivar for 1 A: waveform 2.
Figure 3. Characteristics of the active filter current for variable frequency with ∆Iconst = 1 A: waveform 1 and for stabilized frequency with mean ∆Ivar for 1 A: waveform 2.
Energies 17 05098 g003
Energies 17 05098 g004
Figure 4. SAPF current: waveform 1; passive RLC filter current: waveform 2, and source current: waveform 3.
Figure 4. SAPF current: waveform 1; passive RLC filter current: waveform 2, and source current: waveform 3.
Energies 17 05098 g004
Energies 17 05098 g005
Figure 5. Characteristic of the SAPF current for variable frequency with ∆Iconst = 1 A: waveform 1; for passive RLC filter: waveform 2; and for source current: waveform 3.
Figure 5. Characteristic of the SAPF current for variable frequency with ∆Iconst = 1 A: waveform 1; for passive RLC filter: waveform 2; and for source current: waveform 3.
Energies 17 05098 g005
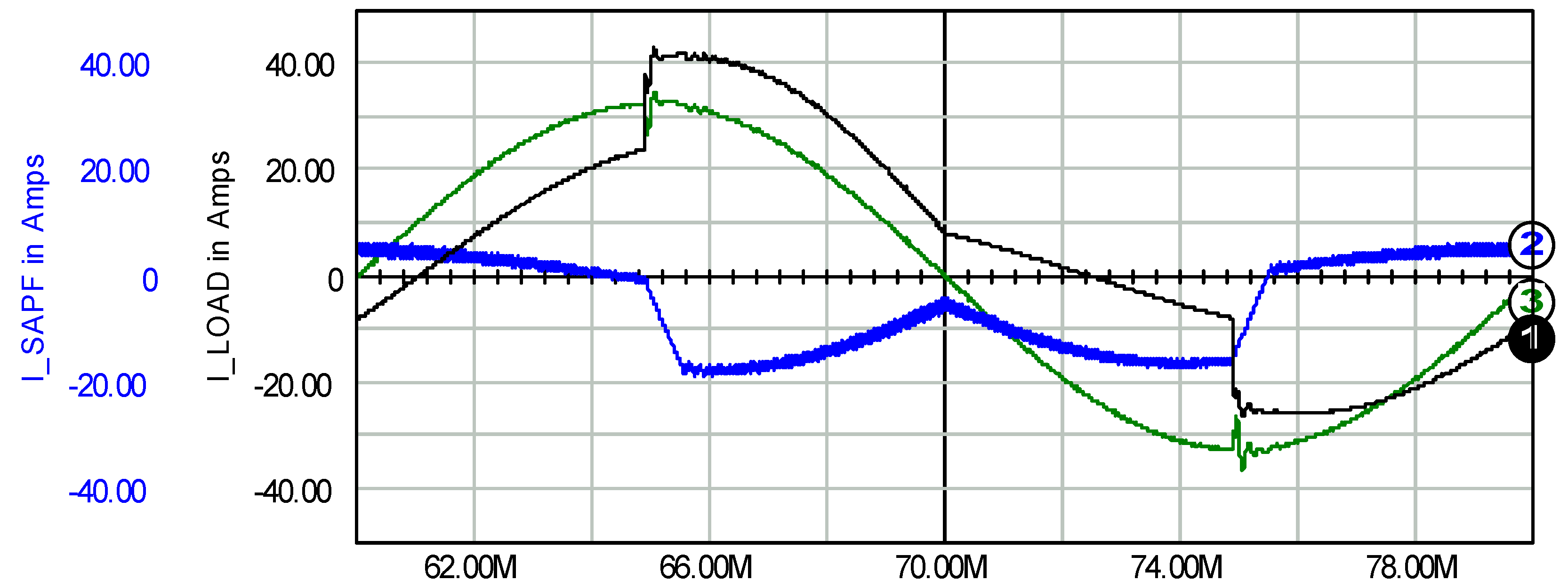
Energies 17 05098 g006
Figure 6. Load current: waveform 1; SAPF current: waveform 2; and source voltage: waveform 3.
Figure 6. Load current: waveform 1; SAPF current: waveform 2; and source voltage: waveform 3.
Energies 17 05098 g006
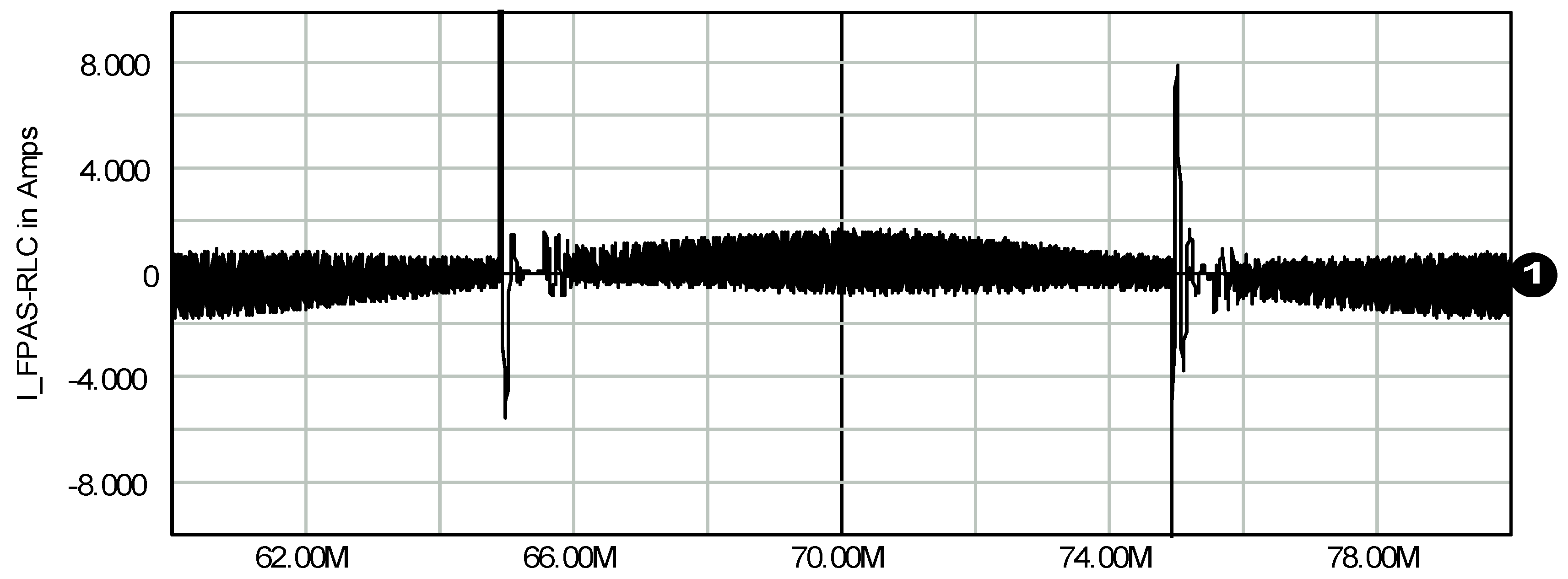
Energies 17 05098 g007
Figure 7. Oscillations in RLC filter current.
Figure 7. Oscillations in RLC filter current.
Energies 17 05098 g007
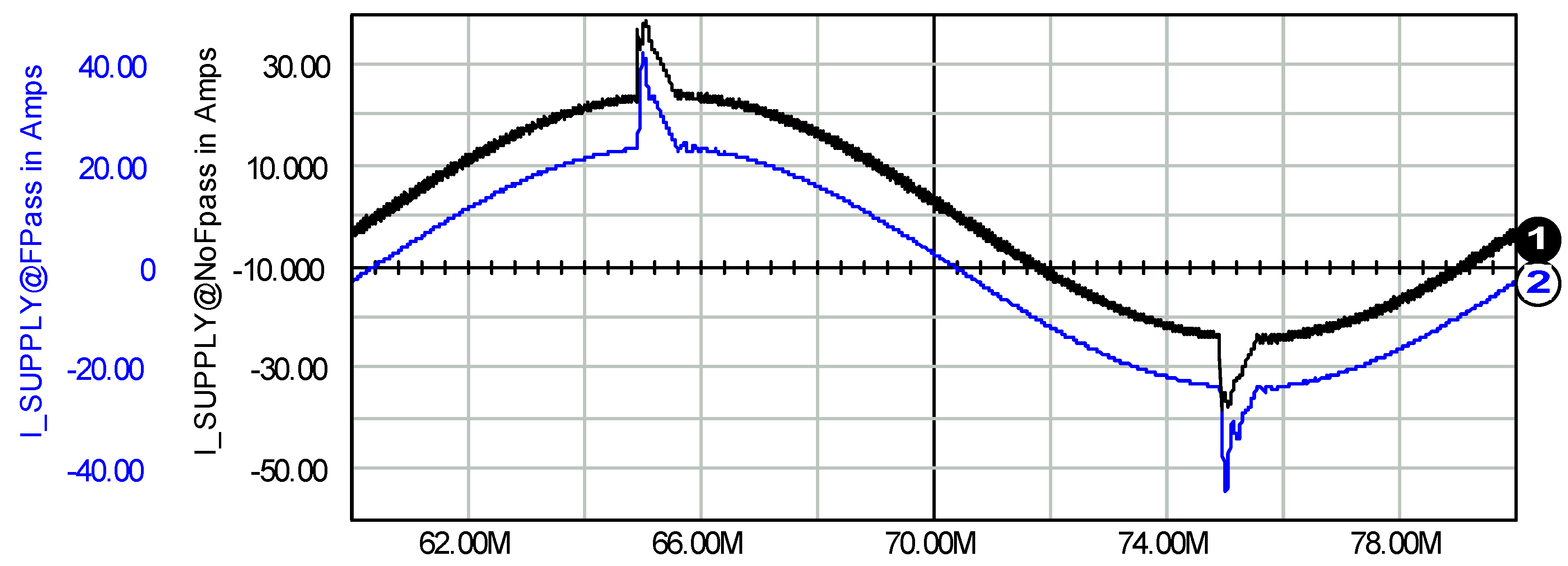
Energies 17 05098 g008
Figure 8. Source current with and without passive filtration: waveforms 1 and 2, respectively.
Figure 8. Source current with and without passive filtration: waveforms 1 and 2, respectively.
Energies 17 05098 g008
Energies 17 05098 g009
Figure 9. Reduction in energy oscillation by an inductor in the load branch. Source current and RLC filter current at no choke: waveforms 1 and 2, respectively; source current and RLC filter current at 1 mH choke: waveforms 3 and 4, respectively. Source and RLC filter currents are shown on the same scales, respectively.
Figure 9. Reduction in energy oscillation by an inductor in the load branch. Source current and RLC filter current at no choke: waveforms 1 and 2, respectively; source current and RLC filter current at 1 mH choke: waveforms 3 and 4, respectively. Source and RLC filter currents are shown on the same scales, respectively.
Energies 17 05098 g009
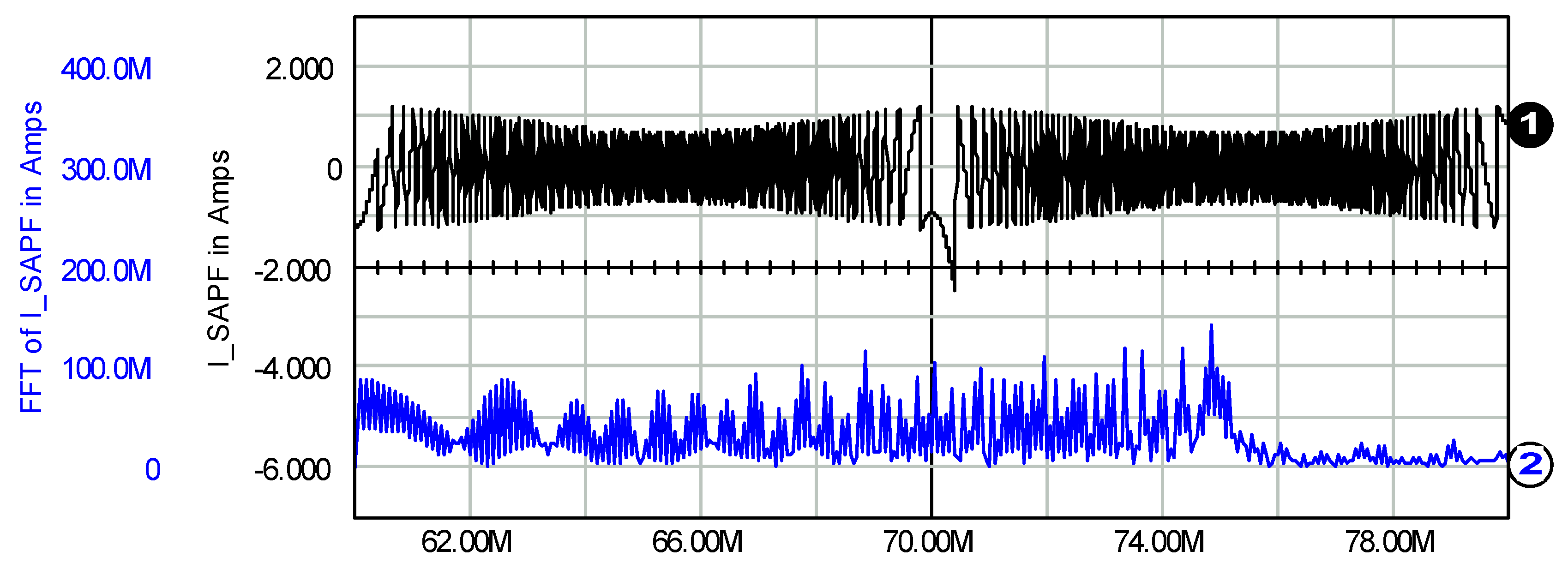
Energies 17 05098 g010
Figure 10. SAPF current: waveform1 and its spectrum: waveform 2. Axis range is 0–20 kHz.
Figure 10. SAPF current: waveform1 and its spectrum: waveform 2. Axis range is 0–20 kHz.
Energies 17 05098 g010
Energies 17 05098 g011
Figure 11. Permanent three-state hysteresis control at Cfpas = 3.3 μF and Rfpas = 1 Ω. SAPF. RC passive filter and source current: waveforms 1, 2, and 3, respectively. Source voltage: waveform 4. Vertical scale for all currents is 2 A/div.
Figure 11. Permanent three-state hysteresis control at Cfpas = 3.3 μF and Rfpas = 1 Ω. SAPF. RC passive filter and source current: waveforms 1, 2, and 3, respectively. Source voltage: waveform 4. Vertical scale for all currents is 2 A/div.
Energies 17 05098 g011
Energies 17 05098 g012
Figure 12. Reduction in energy oscillations for the combined three-state/two-state hysteresis control mode. SAPF current: waveform 1, rms 0.93 A; RC passive filter current: waveform 2, rms 0.93 A; source current: waveform 3, rms 0.16 A; signal activating the three-state control mode: waveform 4, activity at the high state; source voltage: waveform 5. Vertical axis scale for all currents: 2 A/div.
Figure 12. Reduction in energy oscillations for the combined three-state/two-state hysteresis control mode. SAPF current: waveform 1, rms 0.93 A; RC passive filter current: waveform 2, rms 0.93 A; source current: waveform 3, rms 0.16 A; signal activating the three-state control mode: waveform 4, activity at the high state; source voltage: waveform 5. Vertical axis scale for all currents: 2 A/div.
Energies 17 05098 g012
Energies 17 05098 g013
Figure 13. SAPF-and-RC filter system action at full-load condition. Load current: waveform 1, rms 21.0 A; SAPF current: waveform 2, rms 9.6 A; source current: waveform 3, rms 17.7 A; RC passive filter current: waveform 4, rms 1.1 A. Vertical axis scale for all currents: 10 A/div.
Figure 13. SAPF-and-RC filter system action at full-load condition. Load current: waveform 1, rms 21.0 A; SAPF current: waveform 2, rms 9.6 A; source current: waveform 3, rms 17.7 A; RC passive filter current: waveform 4, rms 1.1 A. Vertical axis scale for all currents: 10 A/div.
Energies 17 05098 g013
Table 1. Summary of the results obtained.
Table 1. Summary of the results obtained.
Control MethodNo-Load Conditions
Range f [kHz] Range ∆I [A] PRfpass [W]		Full-Load Conditions
Range f [kHz] Range ∆I [A] PRfpass [W]
fvar (according to Expression (1))14.4–25.01 (const.)no passive filter12.6–23.51 (const.)no passive filter
fstab/two-state (according to Expression (4))20.0 (const.)0.7–1.30.516.1 (1)–18.90.6–1.11
fstab/three-state (2) (according to Expression (4))10.0–20.00.7–1.34.37.1 (1)–18.60.6–1.16
(1) Neglecting oscillation caused by a steep change in load power, (2) discussed in Section 4.2 and Section 4.3.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Szromba, A. Improvement of the Source Current Quality for a Shunt Active Power Filter Operating Using Hysteresis Technique with Stabilized Switching Frequency. Energies 2024, 17, 5098. https://doi.org/10.3390/en17205098

AMA Style

Szromba A. Improvement of the Source Current Quality for a Shunt Active Power Filter Operating Using Hysteresis Technique with Stabilized Switching Frequency. Energies. 2024; 17(20):5098. https://doi.org/10.3390/en17205098

Chicago/Turabian Style

Szromba, Andrzej. 2024. "Improvement of the Source Current Quality for a Shunt Active Power Filter Operating Using Hysteresis Technique with Stabilized Switching Frequency" Energies 17, no. 20: 5098. https://doi.org/10.3390/en17205098

APA Style

Szromba, A. (2024). Improvement of the Source Current Quality for a Shunt Active Power Filter Operating Using Hysteresis Technique with Stabilized Switching Frequency. Energies, 17(20), 5098. https://doi.org/10.3390/en17205098

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop