A Novel Formula for Calculating the Dynamic Torque of an Engine Based on Its Geometric Parameters and Static Measurements

Abstract

Torque is the fundamental working parameter of the internal combustion engine (ICE). In a spark ignition (SI) ICE, static torque is a function of rotational speed and throttle angle. However, ICE inertia, the distance between the throttle and cylinders, the time interval between subsequent intake strokes and increased oil viscosity in the warm-up phase limit the use of this characteristic in dynamic states. The novel and simple formula for calculating ICE torque in dynamic working states, presented in the article, includes all the mentioned factors. The new formula is based on ICE static tests where the torque, speed, throttle angle and airflow are measured. On the basis of the intake manifold geometry, the phenomena occurring in this component are described to determine the delay in the ICE response to throttle position changes. Moreover, the influence of ICE inertia is included. Finally, the formula includes the ICE warm-up period, which is characterized by high friction losses that decrease ICE torque. The proposed formula is validated by comparing model performance in dynamic working states with measurements. The results show a high level of accuracy: the delay in ICE response differs by less than 0.01 s, and the calculated torque differs by less than 5%.

1. Introduction

ICE torque, a crucial working parameter, plays a significant role in shaping vehicle dynamics, driving comfort [1,2] and the quality of gear changes in an automatic transmission [3]. An ICE may work in a static state when working parameters, such as the speed, throttle position and torque, are constant or in dynamic states where these parameters vary [4,5].

Although dynamic states are common in real traffic, static states are the basis for most ICE characteristics. They do not include dynamic phenomena, such as inertia and the delay in ICE reaction to control signals. However, they allow superficial two- or three-dimensional characteristics to be created, such as torque vs. speed and throttle angle, spark advance angle calibration [6] or the design of modified fuel injectors, allowing a reduction in emissions [7]. In [8], the authors determine power and torque vs. speed as well as brake-specific fuel consumption vs. the speed characteristics of an armored vehicle, which gives a quick overview of the ICE’s performance. Basic static characteristics are also used when the main analysis concerns transmission components, such as the gearwheels, synchronizers or electric components of a hybrid drivetrain, and the ICE is defined with a simple static lookup table. In [9], the authors analyze in depth the impact of the downshifting process in a two-speed series-parallel hybrid transmission. Even though the problem concerns a dynamic process lasting tenths of a second, no aspect of ICE dynamics is mentioned. In [10], the authors analyze the influence of the battery state-of-charge in a hybrid drivetrain on system efficiency under a strong dynamic US06 test. A genetic algorithm used for this purpose utilizes a static ICE characteristic of torque vs. speed and throttle angle. In [11], where the authors study a low-voltage alternator-generator that enables engine boosting and downsizing, realizing mild hybrid functions, the static efficiency characteristics of the ICE and electric motor are also used.

The drawback of the above-listed applications of static characteristics is that, in dynamic working states, which dominate in real traffic, the ICE moment of inertia influences its effective torque significantly. The inertia J_ICE includes rotating masses, such as the crankshaft, connecting rods, pistons, camshafts and flywheel, as well as the oil and coolant that increase linear speed. Coolant and oil have a low linear speed and low density in relation to the metal components in reciprocating motion, so their influence on ICE inertia is negligible. The J_ICE factor is easily taken into account according to Formula (7). The drawback of this attempt is that it requires a detailed three-dimensional modeling process of the ICE components. Such an approach is presented in many research studies to make models closer to the real phenomena occurring in the ICE. This is especially important in the analysis of gear changes in all types of stepped automatic transmissions, such as dual-clutch transmissions (DCT), automated mechanical transmissions (AMT), hydrokinetic automatic transmissions (AT) or hybrid transmissions. DCT has two friction clutches that carry out quick gear changes without interrupting the torque to the wheels. Each gear change can be divided into two phases. In the first one, the so-called torque phase, the actual clutch disengages and the clutch of the following gear engages. Then, the inertia phase takes place, where the ICE speed decreases suddenly to match the target gear speed. In this phase, the throttle is closed, and the ICE inertia propels the vehicle with the feeling of uninterrupted driving force. In [12], the authors propose a method for combined speed and torque control of vehicle powertrains with dual-clutch transmissions (DCT) for both the engine and clutches. The authors expect the limited influence of higher frequency pulses from the ICE on the control of engine speed and propose the ICE model as a lookup table of speed and torque using the throttle angle to control the output torque. In [13], a Kalman filter is used to estimate each clutch torque characteristic without torque variations, which can be implemented in a high-performance production car equipped with a wet DCT. In [14,15], the authors use the static torque characteristic to control a DCT during the gear-change process, which is a strong dynamic state and lasts a tenth of a second. In such a dynamic process, inertia plays a crucial role, so including J_ICE is inevitable. In [16], the authors use basic signals of an AT: ICE speed, turbine speed and output speed to investigate a robust shift control strategy for the powertrain of a heavy-duty vehicle. The dynamic model of the powertrain includes the inertia of the ICE, turbine and external load. In [17], the authors consider a predictive control model for an AMT gearbox. The dynamic model (7) is used to apply a clutch micro-slip that reduces acceleration oscillations. In [18], the authors propose mode transition control that uses traffic information to improve the vehicle dynamics and driving comfort of a hybrid electric vehicle. Another example where a basic dynamic ICE model (7) is used is [19], where the authors analyze the optimal system efficiency of a fully hybrid electric vehicle with a single motor based on a DCT, which can take advantage of the distinctive hybrid electric vehicle structure and advantages of DCTs.

The models listed in the above paragraph include an important factor—inertia J_ICE; however, the delay in ICE response is still not included. It is a serious drawback of the model (7), especially in the case of DCTs, where the gear change is counted in milliseconds. This problem can be solved in three ways. The first solution is given in [20], where through the application of the Taylor method [21], a model of ICE torque derived from piston-by-piston firing and inertia variation in the pistons and connecting rods is developed as a function of crank angle and speed, taking into account the firing order. A linear interpolation is used to vary the piston head pressure for the purpose of throttle control, with the percent throttle determined for each piston at the beginning of the intake stroke. This model introduces a delay in engine control that is not present in the lookup table models as a result of the throttle input delaying the output torque. The second attempt is shown in [22], where the authors indicate that, after a sudden throttle angle change, the ICE needs some time to reach a new torque value. This is caused by the time intervals between the individual combustions. In the case of four-stroke, four-cylinder ICEs, it takes two crankshaft revolutions before new torque is developed. This assumption is only true for throttle openings. After the throttle closes, the ICE reaction may take longer than two crankshaft revolutions. The third solution is presented in [4,23,24], where the authors use artificial neural networks (ANN) to create dynamic characteristics of the ICE. Such an attempt includes all phenomena, including the delay, and the ICE performance is represented very precisely; however, time and cost-consuming measurements are required to implement an ANN with high computing accuracy. However, in the case of an ANN, there is no need to model the ICE rotating components because the inertia is included in the measurement data and then in the ANN.

The third factor, which is not described in either of the two above paragraphs but influences the ICE performance in both static and dynamic working states, is the oil viscosity. A low oil temperature decreases the ICE’s effective torque significantly in the warm-up period. None of the above-mentioned publications include the ICE warm-up phase, which may last for a dominant percentage of time in the case of short-distance, low-speed winter city driving. The aspects of oil viscosity influence on ICE torque were taken into account in [25], where the authors also used a static characteristic, but the formula for the ICE effective torque included a constant component of friction torque, pump torque and the coefficient of viscous friction. Unfortunately, these aspects are not presented in detail in the article; thus, the usefulness of the presented formula in such a form is troublesome.

The key contribution of the following study is that the novel formula for ICE torque includes all the above-mentioned factors: ICE inertia, the delay in ICE response to throttle position change (opening and closing) and increased oil friction, which have a significant impact on ICE torque in dynamic working states. What is important is that this formula is based on two static characteristics, which are relatively cheap and easy to obtain (contrary to dynamic measurements).

The structure of the article is as follows: Section 2 presents the engine test bed measurements, which allow the data for two basic static characteristics that are the basis for further analysis to be obtained. Section 3 formulates the problem of ICE dynamics and provides an initial description of the solution. Section 4 describes in detail the calculation of the influence of the throttle opening, throttle closing, ICE inertia and warm-up period on its dynamic performance. Section 5 presents simulations of different working states, proving the suitability of the presented model. Section 6 compares the presented ICE model with measurements from real working states. Section 7 presents the conclusions.

2. ICE Static Characteristics

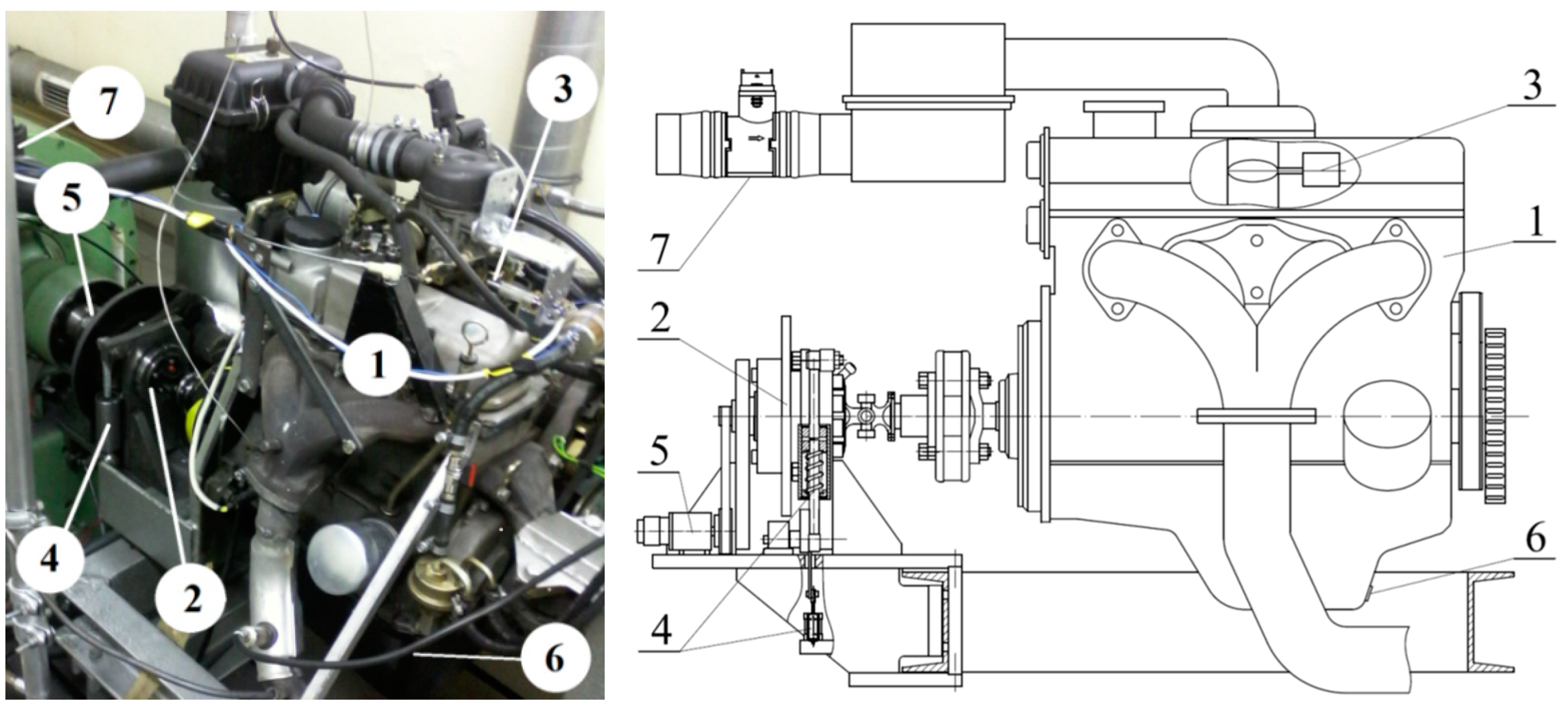
ICE parameters are commonly measured on stationary test stands in static working states where the speed, resistance torque and throttle position are constant. The presented model of dynamic torque will be created and validated on an SI ICE; thus, all the characteristics presented in the article concern a particular ICE, which is presented in Figure 1.

Table 1. ICE technical specification [26].

No	Parameter	Symbol, Value, Unit
1	ICE code	170 A1.000
2	Displacement	VICE = 899 cm3
3	Number of cylinders	nc = 4
4	Nominal power/speed	29 kW/5500 rpm
5	Nominal torque/speed	65 Nm/3000 rpm
6	Compression ratio	CR = 9.0
7	Cylinder bore	B = 65.0 mm
8	Piston stroke	S = 67.7 mm
9	Intake manifold volume	Vint = 0.4 dm3
10	Diameter of the main bearing	Dm = 51 mm
11	Diameter of connecting rod bearing	Dc = 40 mm

presents the basic technical parameters of the tested ICE.

The hydraulically controlled friction brake (Figure 1) was designed to generate drag torque (M_stat > 0 in Figure 2), which enables measurements to be performed in static and dynamic states.

The five following working parameters were measured: brake drag torque (M = 0–65 Nm), throttle opening angle (α = 0–90°), ICE speed (n = 800–5500 rpm), airflow in the intake manifold (Q_m = 8–120 kg/h) and crankcase temperature (t_crk = 15–95 °C). A warm-up period was included to take into account the additional friction in the piston-cylinder and crankshaft assemblies.

To design a characteristic that allows dynamic torque to be calculated (Section 4), two basic static characteristics are required. The first one (Figure 2) is a torque characteristic:

$$M_{\mathrm{stat}}=f\left(n,\mathsf{\alpha }\right)$$

(1)

which presents the ICE static torque M_stat vs. speed n and throttle angle α. This characteristic is based on the measurements performed at the nominal working temperatures of the coolant and oil. The presented engine brake (Figure 1) cannot propel the ICE, so the negative torque M_stat cannot be measured. However, in Figure 2, some parts of the plot take negative values of M_stat. These values are calculated based on Formula (7) and the data from the measurements where the ICE speed decreases with the throttle closed (α = 0°), and no external load is applied (M_d = 0). A known value of J_ICE and measured angular deceleration ε allows a negative M_stat to be calculated.

The second characteristic is the mass airflow Q_m to the cylinders vs. speed n and torque M_stat

$$Q_{\mathrm{m}}=f\left(n,M_{\mathrm{stat}}\right),$$

(2)

which is presented in Figure 3. This characteristic is similar to the one presented in Figure 2, based on the measurements performed at static working states at the nominal working temperature of the coolant and oil of about 90 °C. This characteristic is necessary to determine the intake manifold pressure p_int (3), which, in turn, allows a delay after throttle closing to be calculated (Section 3.3).

The basic thermodynamic relationship, after differentiation and taking the units into account, is presented as follows:

$$p_{\mathrm{int}}·Q_{\mathrm{v}}=0.001·Q_{\mathrm{m}}·R·T$$

(3)

where

$$Q_{\mathrm{v}}=V_{\mathrm{ICE}}·n/120$$

(4)

is the volumetric airflow [dm³/s], p_int is the intake manifold pressure [kPa], R is the air constant [J/kgK], and T is the air temperature [K].

Figure 4 presents the intake pressure p_int vs. α and p_int vs. M for n = 3000 rpm. It can be noticed that p_int does not change linearly, so relationship (2) must have been determined for the whole working range of the ICE.

The model (3) will be used further in Section 4.

3. Problem Formulation

3.1. ICE Geometry

The delay in the ICE response to the control signals must be analyzed separately for the throttle opening and throttle closing. In the case of the throttle opening, the ambient pressure before the throttle pushes the air into the intake manifold in a very short time. However, when the throttle is closed, an intake manifold vacuum is created in subsequent intake strokes, which requires more time. These two factors are described in more detail in two further sections. The common factor is that, in both cases, the ICE needs three additional strokes (in the case of a four-cylinder ICE) to equalize the torque in all cylinders to the new value after the new throttle position is reached.

The volume of the intake manifold geometry plays an important role. Figure 5 presents all the necessary geometrical parameters used in further calculations.

3.2. ICE Delay after Throttle Opening

The ICE delay after the throttle opening results from two factors, which are described below in more detail. The first factor concerns the pressure equalization in the intake manifold. When the throttle is opened, the pressure between the throttle and valves rises, resulting from the pressure difference before and after the throttle and the distance from the throttle to the inlet valves. Air temperature has an insignificant influence on such phenomena in the range occurring in real working conditions. Figure 6 presents how the simulation of the airflow and pressure rise was designed.

It is assumed that the throttle opening is an impulse that increases the pressure on the right side and compresses the subsequent section of the air on the left side. The simulation shows that, for the length of 200 mm, the time between the impulse and pressure increase at the left end (on intake valves) is shorter than 0.001 s. Due to losses p_loss that occur during airflow, the airspeed is lower than the speed of sound in the air. This situation takes place when the throttle angle increases. Considering the real angular speed of the throttle (up to 90° per 0.1 s), it can be assumed that the intake manifold pressure, during the throttle opening, changes immediately.

The second factor resulting in the ICE delay after the throttle opening is that two strokes, intake and compression, are required to start the generation of torque, resulting from a new throttle position, and another three strokes are required to burn the old mixture and equalize the torque in all four cylinders with regard to the new amount of mixture in cylinders.

3.3. ICE Delay after Throttle Closing

In the case of the throttle closing, the ICE reaction may be longer than in the case of the throttle opening. This is due to the fact that the throttle itself cannot generate a vacuum in the intake manifold. It is the pistons that create a vacuum in subsequent intake strokes. This phenomenon is described in Figure 7. According to the adiabatic transformation:

$$p_{\mathrm{int}1}\cdot V_{\mathrm{int}}^{\kappa }=p_{\mathrm{int}2}\cdot {\left(V_{\mathrm{int}}+V_{\mathrm{cyl}}\right)}^{\kappa }$$

(5)

The pressure in the intake manifold can decrease in one intake stroke of

$$p_{\mathrm{int}2}=p_{\mathrm{int}1}·{\left({\displaystyle \frac{V_{\mathrm{int}}}{V_{\mathrm{int}}+V_{\mathrm{cyl}}}}\right)}^{\mathsf{\kappa }}=p_{\mathrm{int}1}·k_{\mathrm{int}}$$

(6)

In one intake stroke, the intake manifold pressure can decrease by coefficient k_int. In the case of this particular ICE, k_int = 0.55. This means that the sudden throttle closing from fully opened to fully closed will result in two intake strokes to decrease the pressure in the intake manifold. Similarly to the throttle opening, three additional strokes are required to equalize the torque in all cylinders.

3.4. Inertia of Rotating Components

The ICE inertia influences the developed torque available for vehicle propulsion. Some part of the ICE torque M is consumed by its rotating elements; thus, the dynamic torque M_d is expressed by the following basic dynamic equation:

$$M_{\mathrm{d}}=M_{\mathrm{stat}}-J_{\mathrm{ICE}}·{\displaystyle \frac{\mathrm{d}\omega }{\mathrm{d}t}}$$

(7)

where ω is the ICE speed in [rad/s]. Based on the real construction of a 0.9 dm³ ICE, spatial models of the rotating components have been created, as presented in Figure 8. The numbers describing the particular components are listed in Table 1.

Table 2. Specifications of piston-crankshaft assembly elements.

No	Element (Abbreviation)	Mass [kg]	Moment of Inertia [kg·mm2]
1	Flywheel (fwl)	6.807	48,370
2	Crankshaft (crk)	8.869	9362
3	Gearwheel 1 (gr1)	0.132	52
4	Camshaft (cms)	1.525	142
5	Gearwheel 2 (gr2)	0.617	667
6	Connecting rod (cnr)	0.578	-
7	Piston assembly (pst)	0.278	-
8	Chain	0.375	-

presents the masses and moments of inertia of the main rotating components.

In the case of the considered ICE, the inertia is J_ICE = 0.07 kg·m². The ICE flywheel has the largest impact on the ICE moment of inertia:

$$J_{\mathrm{ICE}}=J_{\mathrm{crk}}+J_{\mathrm{fwl}}+J_{\mathrm{gr}1}+{\displaystyle \frac{1}{4}}·\left(J_{\mathrm{cms}}+J_{\mathrm{gr}2}\right)+n_c·{\displaystyle \frac{3}{4}}·m_{\mathrm{cnr}}·{\left({\displaystyle \frac{S}{2}}\right)}^2+{\displaystyle \frac{1}{2}}·n_c·\left(m_{\mathrm{pst}}+{\displaystyle \frac{1}{4}}·m_{\mathrm{cnr}}\right)·{\left({\displaystyle \frac{S}{2}}\right)}^2$$

(8)

It is important that J_ICE includes the inertia of the flywheel but without the single plate dry clutch cover and clutch pressure plate, which are mentioned in [27,28,29,30] and increase J_ICE significantly. They are not included because the test stand (Figure 1) does not include this part in its design. This is the reason the obtained result of J_ICE may be different from the values mentioned in the literature. However, the inertia of the friction brake is taken into account and equals J_brk = 0.04 kg·m².

3.5. ICE Warm-Up Period

The ICE static torque characteristic (Figure 2) is created on the basis of static measurements when both the coolant and oil temperatures have nominal values of about 90 °C. However, at low ambient temperatures, especially in urban driving, oil generates additional resistance torque for quite a large percentage of the ICE working. Thus, this factor cannot be ignored while creating a dynamic torque characteristic. To include this factor, the Patton friction model [31] is used to calculate the friction torque M_fr.

The torque characteristic (Figure 2) includes oil friction when the ICE and oil have nominal working temperatures. Thus, to calculate the ICE dynamics (13) at a lower oil temperature, only those factors dependent on oil viscosity are considered:

$$M_{\mathrm{fr}}={\displaystyle \frac{V_{\mathrm{ICE}}}{12.56}}·\left\{\sqrt{{\displaystyle \frac{k_{\mathrm{oil}}·\exp \left[{\mathit{\theta }}_1/\left({\mathit{\theta }}_2+{temp}_{\mathrm{oil}}\right)\right]}{\mathit{\nu }\left(100°\mathrm{C}\right)}}}-1\right\}·\left[{fm\mathrm{e}\mathrm{p}}_{\mathrm{crk}1}\left(\nu \right)+{fmep}_{\mathrm{pst}1}\left(\nu \right)+{fmep}_{\mathrm{cam}1}\left(\nu \right)\right]$$

(9)

All the fmep factors [31] connected with the mechanical friction phenomena in the area of the crankshaft (_crk), pistons (_pst) and camshafts (_cam) are the following:

$${fmep}_{\mathrm{crk}1}\left(\mathsf{\nu }\right)=3.03·{10}^{-4}·n·B·\gamma ·\left(0.129·{\displaystyle \frac{n_c+1}{n_c}}+0.096\right)$$

(10)

$${fmep}_{\mathrm{pst}1}\left(\mathsf{\nu }\right)=0.0098·{\displaystyle \frac{n}{\gamma }}+4·{\displaystyle \frac{M·bmep(n_{\mathrm{M}})}{M\left(n\right)}}+2.07$$

(11)

$${fmep}_{\mathrm{cam}1}\left(\nu \right)=84·\left[5.08·{\displaystyle \frac{n·\left(n_c+2\right)·\gamma }{B^3·n_c}}+{\displaystyle \frac{\sqrt{n}·\gamma }{B^2}}\right]$$

(12)

where

• γ—bore-to-stroke ratio (B/S) [-].

The characteristics of the 10W-40 oil used in this particular ICE are presented in

Table 3. Specifications of 10W-40 oil [32].

Oil	ν (40 °C) [mm2/s]	ν (100 °C) [mm2/s]	koil [mm2/s]	Θ1 [°C]	Θ2 [°C]
10W-40	79	12	0.088	1133	124.6
ν(tempoil) = koil·exp[θ1/(θ2 + tempoil)]

.

To show how important the increased oil friction is at a low temperature, Figure 9 presents the friction torque M_fr for three ICE speeds in a wide range of oil temperatures. For this particular ICE, the friction torque may be up to 50% of the nominal torque of 65 Nm at a nominal torque speed of 3000 rpm during cold starts at 0 °C.

It is clear that additional friction torques, occurring quite a long time after a cold start until the oil reaches the nominal working temperature, have a significant influence on the ICE’s performance.

4. New Dynamic ICE Model

The factors influencing ICE torque in dynamic working states are described in detail in the previous sections. Now, all this information is combined together to create a final formula. The main conclusions are:

• Two strokes are required to react to the throttle position opening;
• Three additional strokes are required to equalize the torque in all cylinders after throttle opening;
• One or two strokes are required to decrease the torque after throttle closing;
• Three additional strokes are required to equalize the torque in all cylinders after throttle closing;
• Oil friction may consume over 50% of the static ICE torque.

In the proposed attempt, the ICE’s performance is analyzed in constant time intervals dt, which can be set freely. In the simulation below, dt = 0.005 s is set. The time of one stroke equals 30/n [s] in the case of a four-cylinder ICE. The red line (Figure 10) represents the boundary condition for a dynamic torque calculation, where the intake manifold pressure drops to the minimum value of p₀·k_int. When the throttle closes in a very short time, and the position change is large (case 1 in Figure 10), the single intake stroke cannot keep up with the pressure decrease, and the pressure in the intake manifold is higher than the static characteristic. This is the reason why the additional variables p_real and M_real are introduced because, in some cases, the pressure and torque resulting from static characteristics (1) and (2) are smaller than the real pressure and torque (which is presented in Figure 10).

It should be noted that this formula includes moments before actual time t, so relevant matrices of n, p, M_stat and M_real, including the values of these parameters in every moment of time, must be created.

The final formula for the ICE torque calculation in dynamic working states is the following:

$$M_{\mathrm{dyn}}\left(t\right)={\displaystyle \frac{{\sum }_{i=A}^B{M}_{\mathrm{real}}(t-i·\mathrm{d}t)}{(B-A)/\mathrm{d}t}}-M_{\mathrm{fr}}-J_{\mathrm{ICE}}·{\displaystyle \frac{\mathrm{d}\omega }{\mathrm{d}t}}$$

(13)

where

$$A=-\mathrm{floor}\left[st{r}_1·\left(30/n\right)/\mathrm{d}t\right]$$

(14)

$$B=-\mathrm{floor}\left[st{r}_2·\left(30/n\right)/\mathrm{d}t\right]$$

(15)

This situation (case 1 in Figure 10) occurs when the following condition is met:

$${\displaystyle \frac{p_{\mathrm{stat}}\left(t\right)-p_{\mathrm{real}}(t-\mathrm{d}t)}{\mathrm{d}t}}<-{\displaystyle \frac{\left(1-k_{\mathrm{int}}\right)·p_{\mathrm{real}}\left(t-\mathrm{d}t\right)}{30/n}}$$

(16)

In such a case, the parameters in moment t are calculated in the following way:

$$\begin{gathered} M_{\mathrm{real}}\left(t\right)=M_{\mathrm{real}}\left(t-\mathrm{d}t\right)-\left[M_{\mathrm{real}}\left(t-\mathrm{d}t\right)-M_{\mathrm{stat}}\left(t\right)\right]· \\ {\displaystyle \frac{p_{\mathrm{real}}\left(t-\mathrm{d}t\right)-\left(1-k_{\mathrm{int}}\right)·p_{\mathrm{real}}\left(t-\mathrm{d}t\right)·\mathrm{d}t/\left(30/n\right)}{p_{\mathrm{real}}\left(t-\mathrm{d}t\right)-p_{\mathrm{stat}}\left(t\right)}} \end{gathered}$$

(17)

$$p_{\mathrm{real}}\left(t\right)=p_{\mathrm{real}}\left(t-\mathrm{d}t\right)-\left(1-k_{\mathrm{int}}\right)·p_{\mathrm{real}}\left(t-\mathrm{d}t\right)·\mathrm{d}t/\left(30/n\right)$$

(18)

str₁ = 6 and str₂ = 3.

If condition (16) is not met (case 2 and case 3 in Figure 10) and intake strokes keep up with a pressure decrease at throttle closing or the throttle just opens, which results in an immediate pressure change, the parameters are the following:

$$M_{\mathrm{real}}\left(t\right)=M_{\mathrm{stat}}\left(t\right)$$

(19)

$$p_{\mathrm{real}}\left(t\right)=p_{\mathrm{stat}}\left(t\right)$$

(20)

str₁ = 5 and str₂ = 2.

5. Simulations of the Developed Model

Formula (13) for dynamic torque M_dyn, presented in Section 4, is now compared to the static characteristic M_stat with a modification including the ICE’s inertia (7). The simulation in Figure 11 is performed for a constant ICE speed of 1500 rpm. According to the basic dynamic Equation (7), M_dyn should equal M_stat because the inertia factor equals zero. However, the changes are noticeable because they result from a delay in the ICE response to the throttle changes.

In Section 4, the ICE delay always refers to the number of strokes, so if the duration of one stroke is 30/n, it can now be converted to time. The throttle opening at 0.8 s results in a sudden torque increase in the case of the static characteristic. However, the green plot, created based on the dynamic model, increases about 0.1 s later. It is similar in the time interval of 1.0–1.2 s, where the ICE torque decreases. An important moment in the plot is at 1.6 s, where the throttle is suddenly closed from wide open to almost closed. It can be easily noticed in the second plot that the intake pressure does not decrease immediately. Two strokes are required to decrease the intake under pressure to the target value. The same situation occurs at 2.6 s. The plot in Figure 11 is created for the ICE speed of 1500 rpm. At this speed, the ICE delay is 0.15 s. In the analysis of gear changes in a dual-clutch transmission that lasts tenths of a second, ignoring such a delay may result in serious control problems, e.g., vehicle jerking.

6. Validation of a New Dynamic Model with ICE Test Bed Measurements

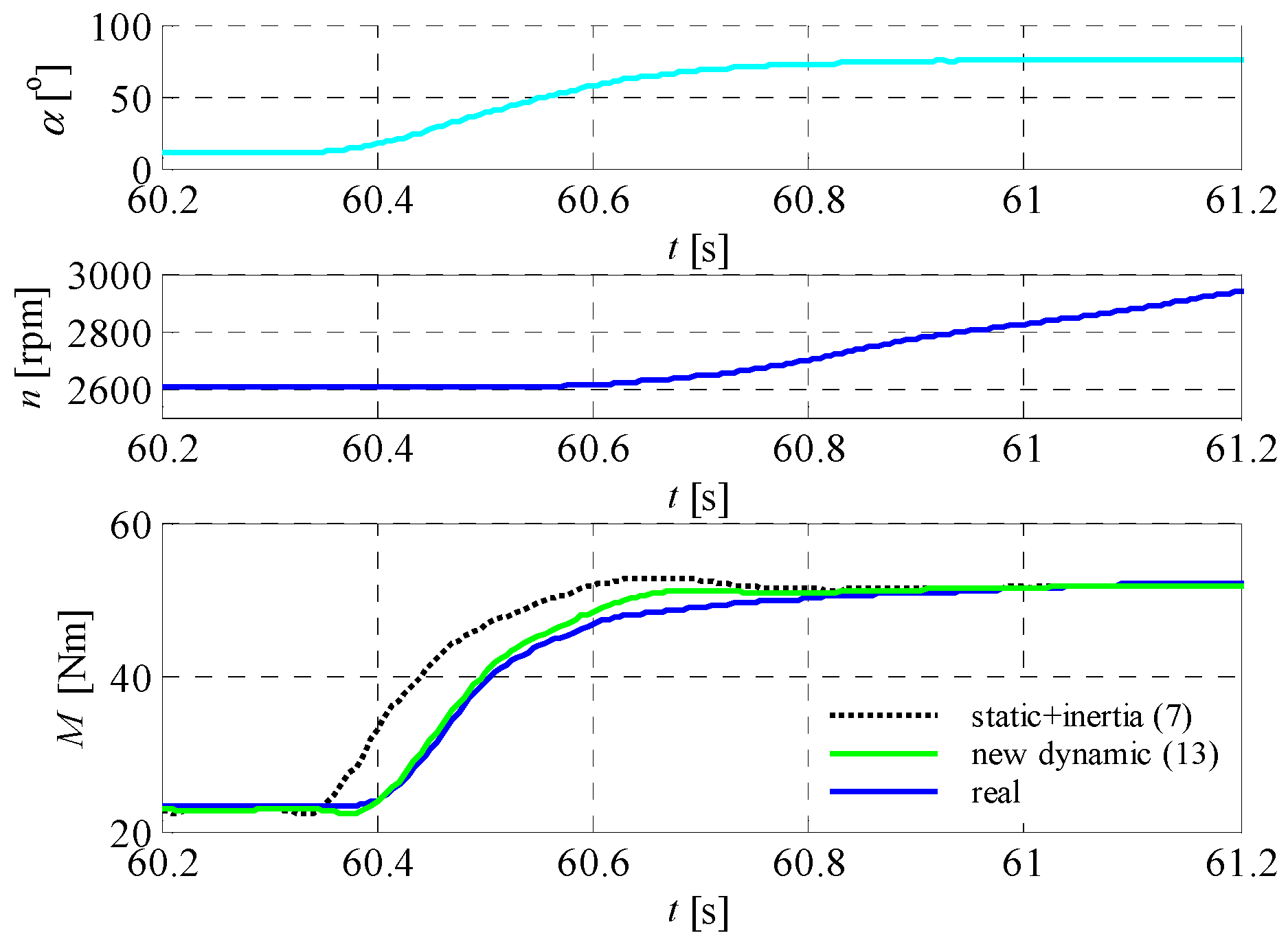
In this section, the developed formula for calculating the dynamic torque M_dyn (13) is compared with the real ICE torque measured in different working states on the ICE presented in Section 2. In Figure 12, Figure 13 and Figure 14, the first and second subplots represent the measured ICE speed and throttle angle, respectively. The third subplot represents the measured (blue line) torque and calculated torque, while the black one is calculated with the use of a static characteristic (7) and the green one is calculated with the use of a dynamic model (13).

It can be clearly noticed that, according to the static characteristic (1), the torque increase occurs exactly at the moment of throttle opening, whereas in reality, the delay is 0.06 s. The dynamic model (13) presents a delay of 0.055 s, which is only 0.005 s of the difference in relation to the measured torque.

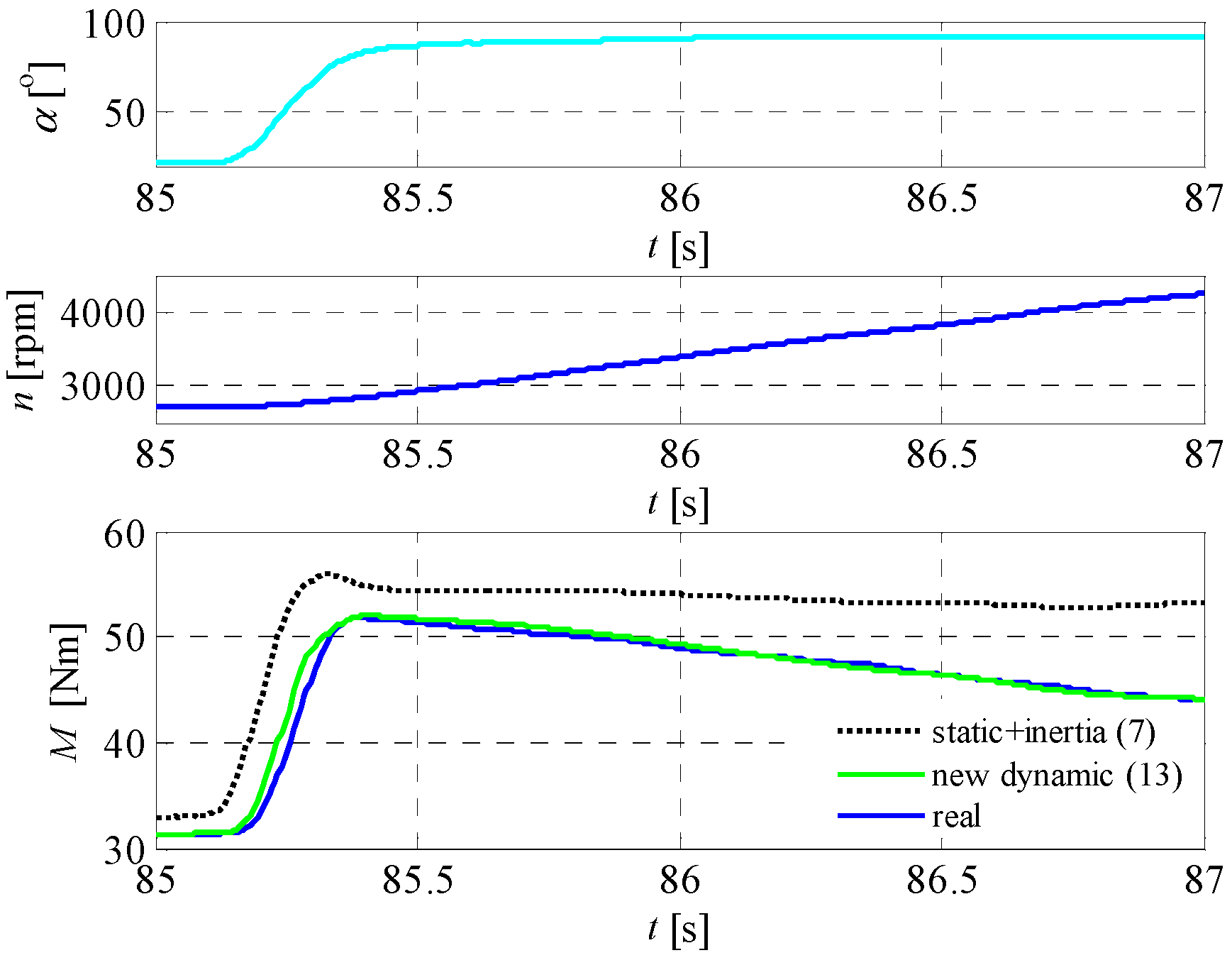
Figure 13 presents the ICE torque after sudden throttle closing. In this case, the results are similar. The static characteristic gives a premature signal of torque decrease. In reality, the torque starts to decrease 0.05 s later.

Figure 14 presents the ICE’s performance with an oil temperature of 20 °C. In the presented range of speed (2500–4500 rpm), the additional friction torque varies 2–7 Nm, which gives a 7–15% relative difference in comparison to the characteristic (7), which does not take into account this factor.

The presented simulations show the correctness of the newly developed dynamic model in terms of both ICE delay and torque decrease when the oil temperature is low. In Figure 12, Figure 13 and Figure 14, the calculated value of M_dyn (13) is much closer to M_real than M_stat corrected by including the ICE’s inertia (7). However, the real torque delay is always larger than M_dyn. This may be due to the fact that the mixture forming before the throttle needs more time to flow into the cylinders.

7. Conclusions

This article introduces an original formula for the ICE torque calculation in any working state that may occur during normal vehicle exploitation in any road conditions. The proposed formula, based on static measurements, is not only cost-effective but also less time-consuming than the measurements in dynamic working states. However, the detailed geometry of rotating components and intake manifold must be taken into consideration.

The validation of the dynamic model, developed through real ICE measurements (Figure 12, Figure 13 and Figure 14), is a crucial step. It shows a high level of correlation, with the calculated torque consistently leading the measured one by 0.005–0.006 s, in contrast to the 0.05 s delay in the case of the static characteristic. The difference in calculated torque is less than 5%, further confirming the accuracy and reliability of the new formula.

Differences in the case of a low oil temperature may result from the fact that the oil temperature was measured through the oil pan. However, the temperature of the oil supplied to the crankshaft bearings and piston may be different because of the heat exchange processes between the sensor and the supply spot.

The limitation of the presented formula is that it applies only to naturally aspirated ICEs. In the case of turbocharged ICEs, the so-called ‘turbolag’, connected with long air ducts and turbocharger inertia, must be considered.

Another limitation of the proposed model is that it utilizes the mean value of torque in a time interval, which means that the harmonics, crucial for the analysis of harsh noise-vibration phenomena in a drivetrain, are not taken into consideration.

Figure 4 presents an almost linear correlation between the intake manifold pressure and torque, so the simplification of the proposed model to only one ICE torque characteristic may be explored in future research.