Assessing Stability in Renewable Microgrid Using a Novel-Optimized Controller for PVBattery Based Micro Grid with Opal-RT-Based Real-Time Validation

Abstract

This paper focuses on the distributed generation (DG) controller of a PV-based microgrid. An independent DG controller (IDGC) is designed for PV applications to improve Maximum-Power Point Tracking (MPPT). The Extreme-Learning Machine (ELM)-based MPPT method exactly estimates the controller’s reference input, such as the voltage and current at the MPP. Feedback controls employ linear PI schemes or nonlinear, intricate techniques. Here, the converter controller is an IDGC that is improved by directly measuring the converter duty cycle and PWM index in a single DG PV-based MG. It introduces a fast-learning Extreme-Learning Machine (ELM) using the Moore–Penrose pseudo-inverse technique and online sequential ridge methods for robust control reference (CR) estimation. This approach ensures the stability of the microgrid during PV uncertainties and various operational conditions. The internal DG control approach improves the stability of the microgrid during a three-phase fault at the load bus, partial shading, irradiance changes, islanding operations, and load changes. The model is designed and simulated on the MATLAB/SIMULINK platform, and some of the results are validated on a hardware-in-the-loop (HIL) platform.

1. Introduction

The attempt to reduce our greenhouse gas and fossil fuel reliance has become possible by adapting renewable energy sources (RESs) like PV and wind generation to modern power systems while considering energy loss and sustainability [1,2]. Microgrid (MG) operations emphasize the integration of local loads into a distribution network to improve power quality and system reliability. Distributed Generation (DG), which includes converter stations and their associated components, ensures a stable and reliable power distribution as an alternative to conventional electricity generation. DG, powered by renewable and non-renewable energy sources, can function in both on-grid and off-grid modes, enhancing the flexibility and resilience of power infrastructure [3]. The utilization of solar photovoltaics, wind, fuel cells, combined heat and power (CHP) systems, biofuels, and micro-turbines offers significant benefits for localized grids, such as reduced emissions and dynamic power regulation, particularly in countries with abundant sunlight like India.

PV-based DG is extensively documented in the literature [4,5,6] and matches the IEEE 1547 standards for both grid-interactive and islanded generation modes [4]. As suggested in [5,6], hierarchical control structures for the effective management of PV-based DG systems are suggested in the ISA-95 standards, which endorse hierarchical structures at the distribution level. PV–DG solutions and rooftop PV installations facilitate coordinated distribution control. Through these applications, PV operates at maximum-power points with the MPPT algorithm [7,8,9,10]. Conventional MPPT control algorithms like P&O, INC, and Hill Climbing are the most suitable due to their simplicity and low operational cost. However, they are not good performers in partial-shading conditions [7]. Other methods, like fuzzy-based MPPT, need prerequisite information and have a high computational burden [8]. Besides this, Artificial Neural Network (ANN)-based MPPT enables high-speed computation and performs well in shaded conditions [9]. The adoption of artificial neural networks (ANNs) in small-scale PV solutions is hindered by challenges with their learning architecture, such as feedback bias. Adhering to the ISA-95 standards, the ordered controller integrates a Primary Controller (PC) and Independent Distributed Generation Controllers (IDGCs), which are essential for effective energy management in DG systems [11,12]. IDGCs act as closed-loop feedback controllers, managing converter stations on the PV side through duty-cycle calculations for PV–DC operations and PWM-based Phase-Locked Loop (PLL) operations [13,14]. This coordination within distributed PV systems follows standardized protocols, ensuring efficient system management. Cost-effective solutions for managing local loads in PV-based DG applications are crucial, where independent DG controllers incorporate Maximum-Power Point Tracking (MPPT) and feedback control for duty measurements to support stability analyses.

ANN-based control algorithms offer a promising solution to computational complexity, utilizing solar irradiation and PV panel temperature as their control inputs to optimize the duty reference for DC voltage-boost operations. This optimized approach, implemented in each iteration with a precise computational clock interval, reduces computational overheads while enhancing the stability and efficiency of PV-based DG systems [15,16]. A novel MPPT controller for PV-based microgrids, discussed in [17], employs a two-step process: data dimension reduction and optimized MPPT for precise control. Built for numerous locally connected PV generators, it uses Extreme-Learning Machine (ELM) for dimensionality reduction and a ridge regression-based ELM for MPPT error estimation at the tertiary control level, enhancing computational efficiency. In [18,19,20,21,22], the authors propose a soft computing approach using fuzzy logic to track MPP variations in solar PV systems. They introduce a variable-step radial basis functional controller fused with fuzzy logic to improve upon conventional fuzzy controllers in partially shaded conditions. This hybrid controller combines the strengths of fuzzy logic and artificial neural networks (ANNs) to optimize MPPT [23]. While fuzzy logic and ANN methods are effective, they can be computationally burdensome. Integrating these methods offers a robust solution to nonlinear problems, enhancing MPPT’s efficiency in challenging conditions. To overcome the challenges faced by a fuzzy and ANN-based MPPT controller, this paper introduces a streamlined approach using a single-layer feed-forward ELM to enhance computation time efficiency [24].

Contributions

• This paper introduces a novel IDGC for PV-based microgrids, integrating Maximum-Power Point Tracking (MPPT) and feedback control. This approach is designed to comply with the ISA-95 and IEEE-1547 standards.
• This study employs an ELM to enhance the accuracy and efficiency of MPPT in dynamic solar environments. The ELM-based IDGC uses the Moore–Penrose pseudo-inverse technique for training, ensuring rapid convergence and reduced computational complexity.
• The performance of the proposed IDGC is validated through MATLAB simulations and hardware-in-the-loop (HIL) testing. The results confirm the controller’s superiority in managing PV microgrid stability under various conditions, such as partial shading and irradiance changes.
• The paper demonstrates significant improvements in microgrid stability during fault conditions, load changes, and islanding operations using the proposed ELM–IDGC, outperforming conventional MPPT controllers in both response time and stability.
• The proposed ELM–IDGC minimizes computational overhead by streamlining the learning process, reducing the need for iterative calculations, and optimizing real-time data-processing for enhanced microgrid performance.

Here, the online sequential learning method, with ridge regression regularization, is applied to optimize the training output weights for ELM–IDGC. The motivation, problem formulation, and literature survey are discussed in Section 1. Section 2 describes the architecture of a PV-based microgrid with detailed specifications. This section also covers boost operations with linear PI control-based duty measurement. The ELM-based IDGC operation is outlined in Section 3, emphasizing online training methods. Section 4 validates the performance of this control approach, presenting MATLAB-based results that demonstrate improved stability with the proposed ELM–IDGC. Finally, Section 5 offers an overall discussion and summary of the research findings.

2. Considered PV-Based DG

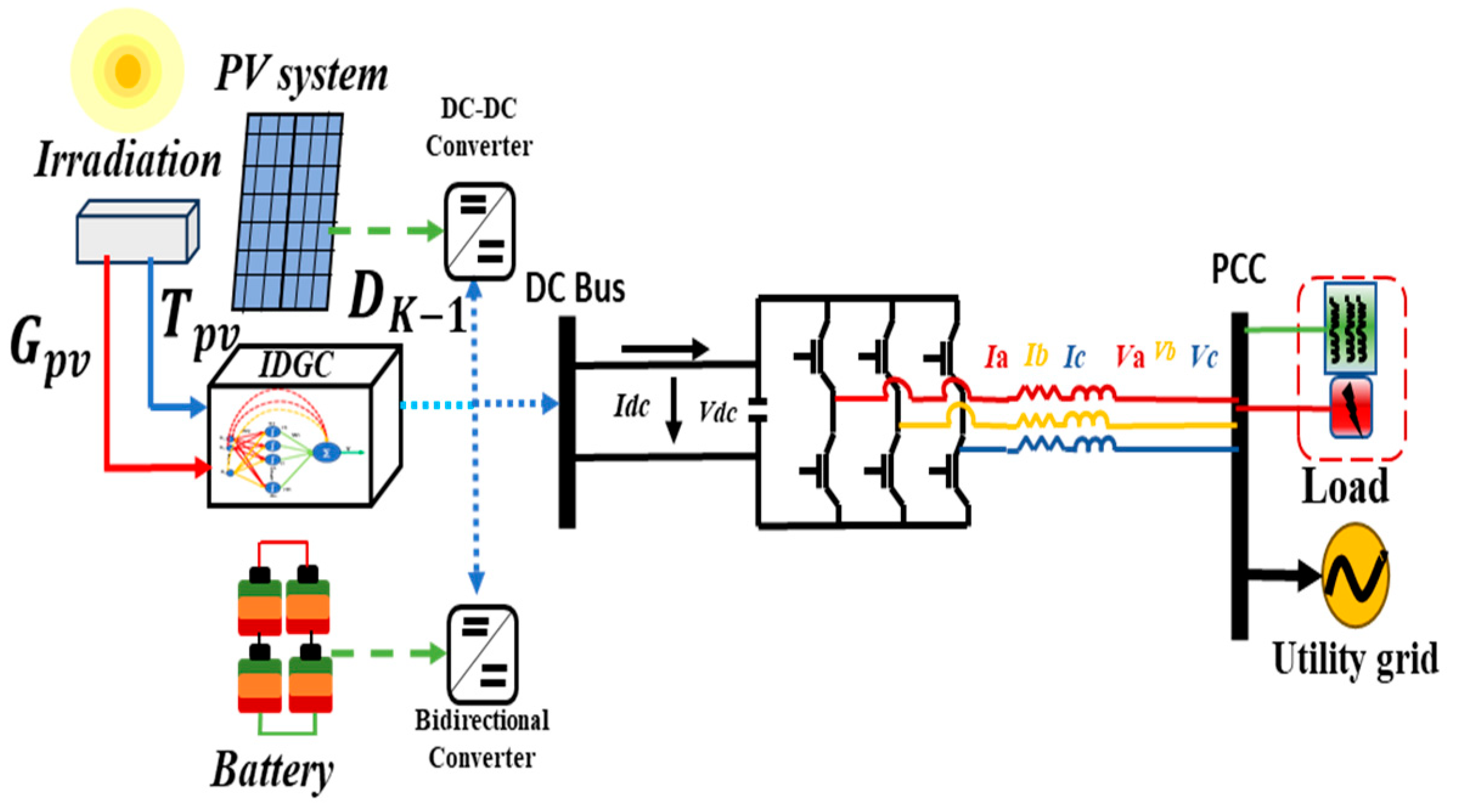
Photovoltaic energy is a popular RES that employs cells or modules arranged in series and parallel to form arrays tailored to load needs. These arrays, integrated into local distribution networks as a DG, utilize DC–DC and/or DC–AC converters. This section models PV-based DG, integrating converter dynamics for feedback control.

The PV system under consideration is rated at 140 kW with a voltage of 17 volts under standard test conditions (STC: 1000 W/m², 25 °C). Prior to grid-power dispatch, it is integrated with a DC–DC converter station (Figure 1). This study focuses on the DC voltage-boost operation $u_{bo}$ to maintain a consistent DC bus voltage profile $u_{dck}$, where “k” represents the control-operation instant. The primary objective is to assess the CR error and its impact on DG stability. Therefore, a voltage feedback control, or IDGC, is devised to estimate duty cycles for the DC $u_{bo}$ operation.

2.1. Modeling with Conventional MPPT

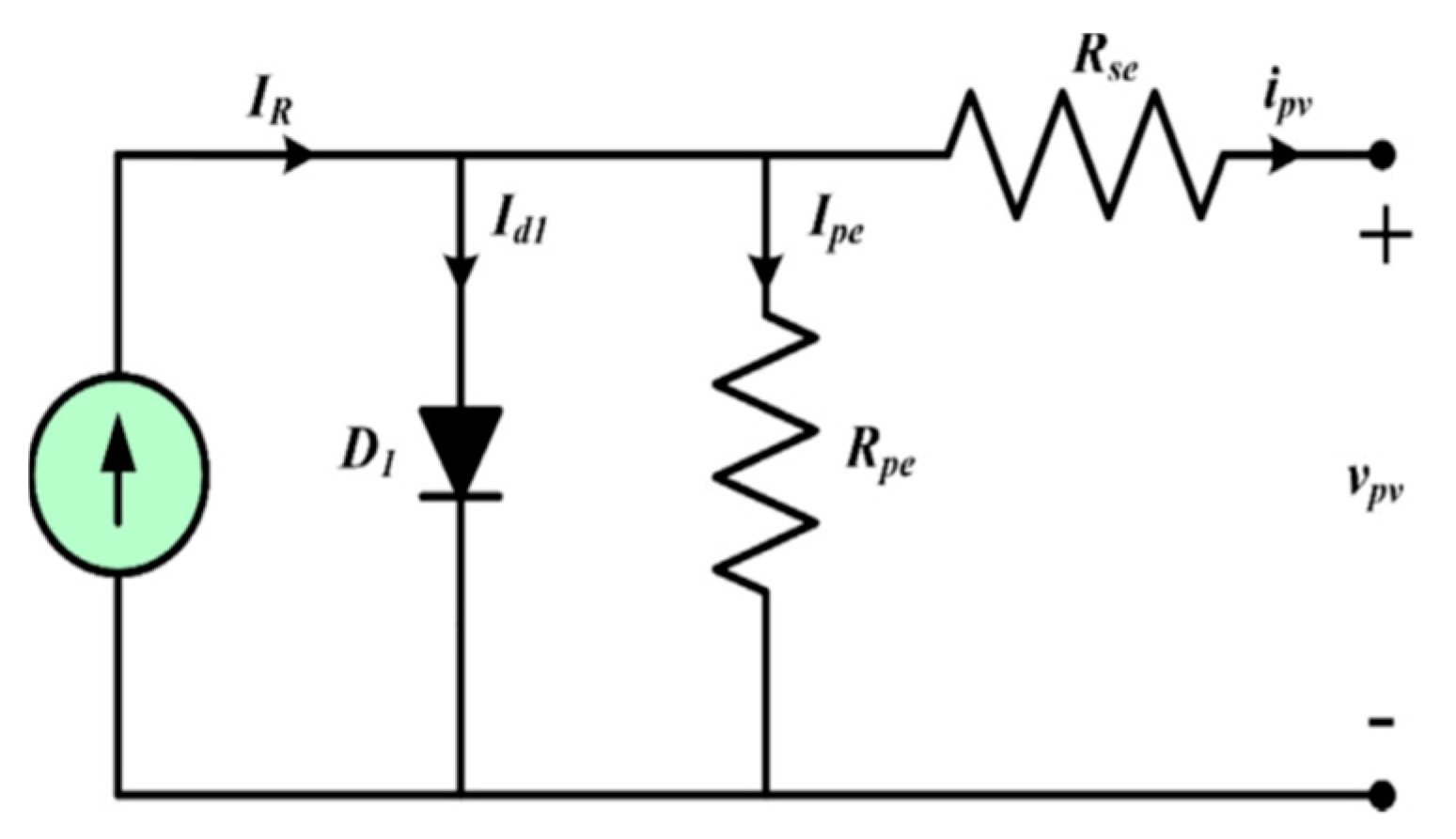
Here, a prototype real-world PV module (140 watts, 17 volts) is designed with a single diode and standard specifications [5]. The circuit contains series and parallel resistances. For generalized PV cells, the initial voltage drops and internal resistance $ir$ are considered. From Kirchhoff’s Current Law (KCL) in the PV circuit, Equation (1) derives the cell’s output current.

$$i=i_{ph}-i_{rst}\left[\exp \left({\displaystyle \frac{u+i{r}_s}{a{u}_T}}\right)-1\right]-\left({\displaystyle \frac{u+i{r}_s}{r_{sh}}}\right)$$

(1)

For a common PV cell, $r_s$ and $r_{sh}$ range from 0.02 to 0.13 Ω and 210 to 487 Ω, respectively. $i_{ph}$ is determined as

$$i_{ph}=0.01\times G_{PV}\times [i_{sc}+k_i({{\Gamma }_{PV}}^{*}-{\Gamma }_{PV})]$$

(2)

$G_{PV}$ signifies solar irradiation (W/m²) and $k_i$ is the short-circuit current temperature coefficient attainable from the datasheet. ${{\Gamma }_{PV}}^{*}$ and ${\Gamma }_{PV}$ indicate temperatures at the STC and the cell’s operational temperature, respectively. The back-saturation current $i_{rst}$ is stated as

$$i_{rst}=i_{rr}{\left({\displaystyle \frac{{\Gamma }_{PV}}{{{\Gamma }_{PV}}^{*}}}\right)}^2\times \exp \left[{\displaystyle \frac{q\times E_g}{k\times a}}\left({\displaystyle \frac{1}{{\Gamma }_{PV}}}-{\displaystyle \frac{1}{{{\Gamma }_{PV}}^{*}}}\right)\right]$$

(3)

PV cells are arranged in series and parallel to form PV modules, which are then connected similarly to achieve the desired power and voltage ratings. The PV system configuration, considering the number of series connected cells $n_{se}$ and parallel connected cells $n_{pp}$, is expressed as

$$\begin{array}{ll}{i}_{PV}^k=& n_{pp}{i}_{ph}^k-n_{pp}{i}_{rst}^k\left[\exp \left({\displaystyle \frac{1}{u_{T}a}}\times \left({\displaystyle \frac{u_{PV}^k+i_{PV}^{k-1}{r}_s}{n_{se}}}\right)\right)-1\right]\\ & -\left({\displaystyle \frac{\left(n_{se}/n_{pp}\right) u_{PV}^k+i_{PV}^{k-1}{r}_S}{r_{sh}}}\right)\end{array}$$

(4)

This section presents manufacturer details for a single 140 W PV module. The PV module is formed by connecting 3 modules in series, each rated at 3485.7 W and 317 V. Additionally, 13 shunt strings are created, with 2 modules in series per string. The PV output features, namely $u_{PVk}$ (voltage) vs. $P_{PVk}$ (power) or $u_{PVk}$ (voltage) vs. $i_{PVk}$ (current), exhibit nonlinear behavior. To maximize power $p_{MP{P}_k}$, the DC voltage $u_{bo}$ input should match the voltage at $P_{MP{P}_k}$, $u_{MPP}$ depicted in Figure 2.

The specifications of a WS-140 PV panel are $p_{\max }=140\hspace{0.17em}\hspace{0.17em}\mathrm{watt}$, $u_{MPP}=18\hspace{0.17em}\mathrm{volt}$, $i_{MPP}=7.85\hspace{0.17em}\mathrm{amp}$, open circuit voltage = 22 V, SC current = 8.95 A. The current temperature coefficient is (0.065 0.015)%/°C, which, for voltage, is 10 mV/°C; NOCT = 47 2 °C.

PV systems employing DC operation require MPPT algorithms. Traditional linear MPPT methods (like P&O and Hill Climbing) offer iterative, exact findings but may inaccurately track under multiple, such as partial-shading conditions. Partial shading occurs when certain PV modules are unable to receive full exposure, impacting overall system efficiency. Nonlinear MPPT methods, like fuzzy logic [13] and ANN approaches [14], are well documented. However, they impose computational burdens on PV–DG applications. Hence, this paper aims to enhance conventional iterative, backpropagation learning for a simpler solution.

2.2. Boost Converter Operation with Linear Feedback

The maximum power $p_{mp{p}^k}$ and voltage at MPP $u_{mp{p}^k}$ are the two inputs for designing a converter controller. The output of the converter is $p_{d{c}^k}$ and $u_{d{c}^k}$ is the converter power and voltage. The PV voltage and currents are expressed as

$${\dot{u}}_{\mathrm{dc}}^{\mathrm{k}}={\displaystyle \frac{1}{u_{\mathrm{dc}}^{\mathrm{k}}{C}_{\mathrm{dc}}}}\left[u_{\mathrm{dc}}^{\mathrm{k}}{\displaystyle \sum _{n=1}^N{i}_{\mathrm{dc},n}^{\mathrm{k}}(1-d_{\mathrm{MPP}}^{\mathrm{k}})}-p_{\mathrm{dc}}^{\mathrm{k}}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(5)

$${\dot{i}}_{\mathrm{dc},n}^{\mathrm{k}}={\displaystyle \frac{1}{L_{\mathrm{dc},\mathrm{n}}}}\left({\displaystyle \frac{u_{MPP}^{\mathrm{k}}}{1-d_{MPP}^{\mathrm{k}}}}-u_{\mathrm{dc}}^{\mathrm{k}}\right)\hspace{0.17em}\hspace{0.17em}$$

(6)

Here, n = 1, 2, … N, PV numbers $L_{dc}$ and $C_{dc}$ are converter inductance and capacitance. The $d_{mp{p}^k}$ is the $k_{th}$ sampling instant for converter duty. The $u_{bo}$ operation is guaranteed by the feedback path, which is given by Equation (7).

$$d_{\mathrm{mpp}}^{\mathrm{k}}=d_{\mathrm{MPP}}^{\mathrm{k}-1}\pm \left[{\kappa }_{\mathrm{P},\mathrm{dc}}\left(e_{\mathrm{dc}}^{\mathrm{k}}\right)+{\kappa }_{\mathrm{I},\mathrm{dc}}\left(e_{\mathrm{dc}}^{\mathrm{k}}-e_{\mathrm{dc}}^{\mathrm{k}-1}\right)\times \Delta {\Gamma }_{\mathrm{s}}\right]$$

(7)

Considered to be a control error, $e_{\mathrm{dc}}^{\mathrm{k}}=u_{\mathrm{dc}}^{*}-u_{\mathrm{mpp}}^{\mathrm{k}}$, and a simple PI is implemented. $\Delta {\Gamma }_s$ is the sampling time. The considered duty cycle is then processed for IGBT switching in the DC converter. Dynamic equations for the DC converter are derived to design a stable output-profile controller. A closed-loop feedback response is necessitated for the feedback controller/IDGC, adhering to ISA-95. Complying with IEEE 1547 ensures that the mode of operations of IDGC is prioritized for operational flexibility. The IDGC feedback path using a linear 2nd-order PI control is described here.

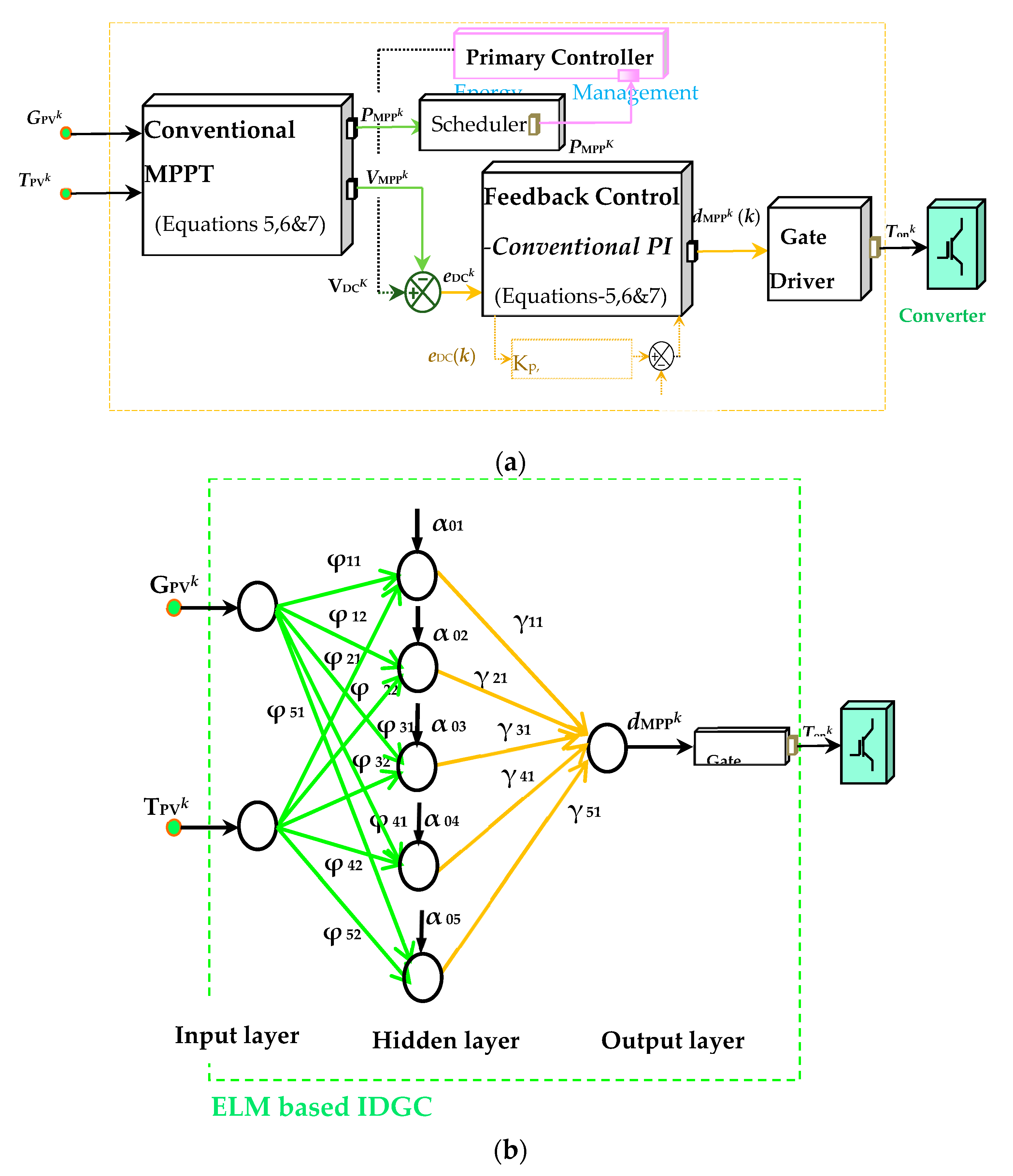
3. Proposed DG Controller

The IDGC, integrating MPPT and closed-loop PI control for duty assessment, can benefit from a computationally efficient approach using Artificial Neural Network (ANN)-based algorithms. Input parameters such as solar irradiation $G_{PV}$ and PV panel heat ${\Gamma }_{PV}$, with output as duty reference for DC boost operation $d_{mpp}$, streamline computations by directly converting $G_{PV}$ and ${\Gamma }_{PV}$ to $d_{mpp}$, omitting intermediate steps like $u_{mpp}$, $p_{mpp}$, and $e_{dc}$. This reduction in calculations per iteration enhances the accuracy of calculating control references (CRs).

To address the limitation of ANN-based IDGCs in real-time feasibility due to weight matrix estimation, a non-iterative Moore–Penrose pseudo-inverse $MPPI$ technique is employed for training. This technique, unlike conventional iterative methods, such as backpropagation, enhances efficiency and is applied to feed-forward ANNs like ELM [9].

In Figure 3a, the traditional IDGC (following the ISA-95 standard) involves two-step duty-cycle designs that are prone to control reference (CR) errors, potentially compromising DC bus stability. In contrast, the proposed ELM–IDGC (Figure 3b) streamlines computational steps and minimizes iterative learning, reducing computational delays. The fast-learning approach MPPiis advised for the ELM–IDGC and aims to enhance stability. The linear relationship between the duty cycle $d_{mp{p}^k}$ and MPP voltage (VMPPk), depicted in Figure 3, indicates predictable behavior. Variations in irradiation yield are different $u_{mp{p}^k}$ (Figure 3a) and $d_{mp{p}^k}$ (Figure 3b). By leveraging linear functionality instead of nonlinear nodes, the proposed IDGC anticipates improved stability. The ELM learning strategy is poised to reduce errors swiftly and robustly.

ELM is a feed-forward neural network typically structured with a single hidden layer. The defining characteristic of ELM is its non-iterative training process, which contrasts sharply with traditional neural networks that rely on iterative methods like backpropagation.

3.1. Training Process

In the ELM algorithm, the input weights and biases of the hidden nodes are randomly assigned and are not updated during the training process. The primary task is to determine the output weights analytically using the Moore–Penrose pseudo-inverse of the hidden-layer output matrix. This approach eliminates the need for iterative learning, leading to a faster training process. The training of ELM is straightforward:

• Initialization: Randomly assign input weights and biases.
• Computation of hidden-layer output: The hidden-layer output matrix is calculated using the input data.
• Output weight determination: The output weights are computed analytically using the pseudo-inverse of the hidden-layer output matrix.

3.2. Training Speed

One of the most significant advantages of ELM is its rapid training speed. By avoiding iterative adjustments and relying on an analytical solution for the output weights, ELM drastically reduces computational time. This makes ELM particularly suitable for real-time applications where quick model updates are necessary.

3.3. Generalization Capability

ELM has shown robust generalization capabilities even with minimal training data. This is partly due to its ability to avoid overfitting, which is a common issue in traditional neural networks that undergo extensive iterative training. The randomization of input weights and the use of the pseudo-inverse technique help ELM generalize well across different datasets and environmental conditions.

3.4. Unique Features Compared to Traditional Neural Networks

• Non-iterative training: Unlike traditional neural networks that require multiple iterations to adjust weights and biases, ELM uses a single step to compute the output weights.
• Fast Learning: ELM’s training speed is significantly faster because it avoids the iterative nature of backpropagation, making it ideal for applications requiring rapid learning and real-time processing.
• Simple architecture: ELM typically uses a single hidden layer, simplifying the network structure compared to deep neural networks with multiple layers.
• Good generalization: Despite its simplicity, ELM can generalize well with minimal data, making it effective in environments with varying conditions, such as fluctuating solar irradiance in photovoltaic systems.

3.5. Application in PV-Based Microgrids

In the context of the paper, ELM is employed for Maximum-Power Point Tracking (MPPT) in photovoltaic (PV) systems. The ELM-based Independent Distributed Generation Controller (IDGC) uses the Moore–Penrose pseudo-inverse technique for training, ensuring rapid convergence and reducing computational complexity. This method enhances the stability of the microgrid under various conditions, such as partial shading and irradiance changes. The application of ELM in this context demonstrates its superiority in terms of computational efficiency and response time compared to conventional MPPT controllers. It also showcases ELM’s ability to maintain system stability during dynamic environmental changes. This combination of features makes ELM a powerful tool in modern control systems, particularly where speed and adaptability are critical. In ANN literature, numerous constructional and working enhancements are explored, ranging from basic feed-forward structures to complex architectures incorporating feedback bias. Operational methods span from traditional backpropagation and least-square solutions to contemporary non-iterative (NI) techniques, enriching control algorithms’ operational perspectives [9]. The MPPT algorithm proposed by the authors outperforms conventional methods by offering faster convergence, reduced computational burden, and enhanced stability under varying conditions like partial shading and irradiance changes, ensuring more efficient energy harvesting in photovoltaic systems. The proposed MPPT algorithm does provide the necessary speed for PV operation. It achieves this through rapid convergence and reduced computational delay, which is crucial for maintaining system stability under varying conditions, such as irradiance changes, partial shading, and load variations. The algorithm’s efficiency is demonstrated in multiple scenarios, including fault conditions and islanding operations, where it consistently outperforms conventional methods in terms of convergence speed and transient response. The Artificial Neural Network (ANN) was implemented in the microcontroller by applying a computationally efficient algorithm that uses solar irradiation and PV panel temperature as inputs to calculate a duty reference for DC voltage-boost operations. This implementation reduces computational complexity, enhancing stability and performance in PV-based DG systems by directly streamlining the necessary control calculations. To ensure proper operation of the proposed MPPT algorithm, a microcontroller with sufficient computational power (32 GB RAM, NVIDIA Quadro GPU, and DAQ-1.8 GB/s system bandwidth NI my-DAQ, multiple modules) is necessary to handle the real-time processing of data, rapid convergence, and adaptive learning. The microcontroller should efficiently execute the Extreme-Learning Machine (ELM) algorithm, which requires a balance between computational speed and minimal overhead, especially during varying environmental conditions like irradiance changes and partial shading.

4. Ridge Regression-Based ELM

ELM has gained prominence as a feed-forward neural network (FFNN) in the past decade [23]. Because of its straightforward construction, different training techniques, such as least-square solutions, are recommended for strong valuation of error reduction. In PV-based DG applications, literature predominantly focuses on either MPPT algorithms alone or feed-forward IDGC structures, where $G_{PVk}$ and ${\Gamma }_{PVk}$ are functions of $d_{mppk}$ derived from linear MPPT data. However, adhering to ISA-95 and IEEE 1547 standards (Figure 3a), the entire operation, including traditional two-step MPPT tracing and closed-loop duty assessment, must be employed at the IDGC level. Hence, trained data for the proposed IDGC is acquired according to normal performance.

The structure of ELM comprises input, hidden, and output Layers ($i_L$, $h_L$ and $o_L$), respectively, to derive preferred probable control references (CRs), such as $d_{mppk}$ (Figure 3b). The general ELM is single-layered, and training employs an $mp{p}_i$ inverse method [24]. IL nodes connect arbitrarily, while γ is derived from non-iterative training. Despite arbitrariness, ELM can be designed with minimal $e_{IDGCk}$ during training, outperforming conventional techniques. Unlike methods requiring both φ and γ from initial randomness in training, ELM exhibits improved generalized performance [25]. The input layer node is given by

$${\left[{\chi }_{iL}\right]}_{1\times A}^k=\left[{\chi }_{iL,1}^k,{\chi }_{iL,2}^k,{\chi }_{iL,2}^k\dots \dots \dots {\chi }_{iL,A}^k\right]$$

(8)

and the output layer node is presented as

$${\left[{\gamma }_{oL}\right]}_{1\times A}^k=\left[{\gamma }_{oL,1}^k,{\gamma }_{oL,2}^k,{\gamma }_{oL,2}^k\dots \dots \dots {\gamma }_{oL,B}^k\right]$$

(9)

Here, A and B are input and output data sizes. The hidden-layer matrix is expressed as

$$\begin{array}{ll}[hL{]}_{1\times C}^{\mathrm{k}}& =\left[\begin{array}{cccc}{h}_{ \mathrm{L},1}^{\mathrm{k}}& h_{ \mathrm{L},2}^{\mathrm{k}}& \dots & h_{ \mathrm{L},C}^{\mathrm{k}}\end{array}\right]\\ & ={\left[\begin{array}{c}\sin \mathrm{h}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{A}}\left({\varphi }_{ \mathrm{i}}^1\times {\chi }_{ \mathrm{IL},1}^{\mathrm{k}}\right)+{\lambda }_{\mathrm{i}}}\right)\\ \sin \mathrm{h}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{A}}\left({\varphi }_{ \mathrm{i}}^2\times {\chi }_{ \mathrm{IL},1}^{\mathrm{k}}\right)+{\lambda }_{\mathrm{i}}}\right)\\ :\\ \sin \mathrm{h}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{A}}\left({\varphi }_{ \mathrm{i}}^{\mathrm{C}}\times {\chi }_{ \mathrm{IL},1}^{\mathrm{k}}\right)+{\lambda }_{\mathrm{i}}}\right)\end{array}\right]}^T\end{array}$$

(10)

Initially, ${\left[\varphi \right]}_{A\times C}$ is arbitrarily chosen from 0–1 during training. The sine hyperbolic activation function is employed for its adaptability to large $e_{IDGCk}$ signatures. Post-training estimated CR $d_{MPPk}$ is derived from the output layer node for real-time performance.

$${\left[E_{OL}\right]}_{1\times B}^k={\left[h_L\right]}_{1\times C}^k\times {\left[\gamma \right]}_{C\times B}^k$$

(11)

The $MPPI$ is utilized for finalizing the γ C × B with training data samples as

$${\left[\gamma \right]}_{\mathrm{C}\times \mathrm{B}}^{\mathrm{k}}={\left[{\left({\mathrm{hL}}^T\times \mathrm{hL}\right)}^{-1}{\mathrm{hL}}^T+{\displaystyle \frac{I}{R_C}}\right]}_{\mathrm{C}\times 1}^{\mathrm{k}}\times {\left[{\Gamma }_{\mathrm{OL}}\right]}_{1\times \mathrm{B}}^{\mathrm{k}}$$

(12)

During supervised learning, the OL layer outputs training samples with a minimization formulation.

$$\min {\zeta }_{\gamma }^{\mathrm{k}}={\displaystyle \frac{I}{2}}{‖\begin{array}{l} {\left[{\left({\mathrm{hL}}^T\times \mathrm{hL}\right)}^{-1}{\mathrm{hL}}^T\right]}_{\mathrm{C}\times 1}^{\mathrm{k}}\\ \times [{\Gamma }_{\mathrm{OL}}{]}_{1\times \mathrm{B}}^{\mathrm{k}}-[E_{\mathrm{OL}}{]}_{1\times B}^{\mathrm{k}}\end{array}‖}^2+{\displaystyle \frac{r_C}{2}}{‖e_{\mathrm{IDGC}}^{\mathrm{k}}‖}^2$$

(13)

The regularization coefficient is measured from [14].

$\varphi ,\hspace{0.17em}{h}_L,\gamma ,\hspace{0.17em}\alpha$ are the usual abbreviations for input weights, hidden-layer output matrix output weight, and bias in the output layer. $R_{c1}$, $e_{IDG{C}^k}$ are the regularization and control references.

Implementing an Extreme-Learning Machine (ELM) for Maximum-Power Point Tracking (MPPT) in photovoltaic systems introduces both opportunities and challenges. The complexity primarily arises from the need to optimize the ELM’s architecture, including selecting an appropriate number of hidden neurons and ensuring the model generalizes well to varying environmental conditions like irradiance and temperature. Unlike traditional MPPT methods, which may rely on simpler control algorithms, ELM-based MPPT requires careful training with diverse datasets to ensure robustness and accuracy. Additionally, real-time processing demands and the need for rapid convergence without overfitting add to the implementation complexity [26]. The balance between achieving fast convergence and maintaining minimal computational overhead is critical for efficient operation in dynamic solar environments. Despite these challenges, ELM offers the advantage of high-speed learning and reduced computational cost, making it a promising approach for adaptive and intelligent MPPT controllers. Extreme-Learning Machine (ELM) distinguishes itself from traditional neural networks in MPPT controllers by offering significantly faster training speeds and simplified learning processes. Unlike conventional neural networks, which require iterative backpropagation and extensive tuning, ELM assigns random weights and biases to the hidden layer and solves for the output weights analytically. This leads to rapid learning and a reduced computational overhead. Moreover, ELM’s ability to generalize well with minimal training data makes it highly efficient for real-time applications like MPPT, where swift and accurate adaptation to changing environmental conditions is crucial for optimizing energy harvest.

Robust Estimation Enhanced via Online Learning, Refining Models Dynamically for Resilient Data Analysis and Accurate Parameter Estimation

Dynamic control enactment necessitates a state–inform agenda to maintain balanced working conditions in PV–DG applications. The ELM-based IDGC is trained via online sequential learning, where training data is not entirely processed upfront. Instead, successive gaps (N data chunks) are treated iteratively, enhancing adaptability to changing conditions and facilitating real-time adjustments for improved performance.

$${\left[\gamma \right]}_{\mathrm{C}\times \mathrm{B}}^{\mathrm{k}+1}={\left[\gamma \right]}_{\mathrm{C}\times \mathrm{B}}^{\mathrm{k}}+\left(\begin{array}{l}{\left[{\left({\mathrm{hL}}^T\times \mathrm{hL}\right)}^{-1}{\mathrm{hL}}^T+{\displaystyle \frac{I}{r_C}}\right]}_{\mathrm{C}\times 1}^{\mathrm{k}}\\ \times {\left[{\Gamma }_{\mathrm{OL}}\right]}_{1\times \mathrm{B}}^{\mathrm{k}}\end{array}\right)-{\left[E_{\mathrm{OL}}\right]}_{1\times \mathrm{B}}^{\mathrm{k}}$$

(14)

In connection with the input layer node ${\left[{\chi }_{iL}\right]}_{1\times A}^k={\left[G_{PV},{\Gamma }_{PV}\right]}_{1\times A/2}^k$ and output layer node $\left[{\gamma }_{OL}^k\right]={\left[d_{mpp}\right]}_{1\times B}^k$, the ELMIDG is operated with PV–DG, as shown in Figure 1. To improve the training performance of optimal ${\left[\gamma \right]}_{C\times B}^{k+1}$ with error $e_{IDGC}^k$ reduction, online sequential learning is applied.

5. Results and Analysis

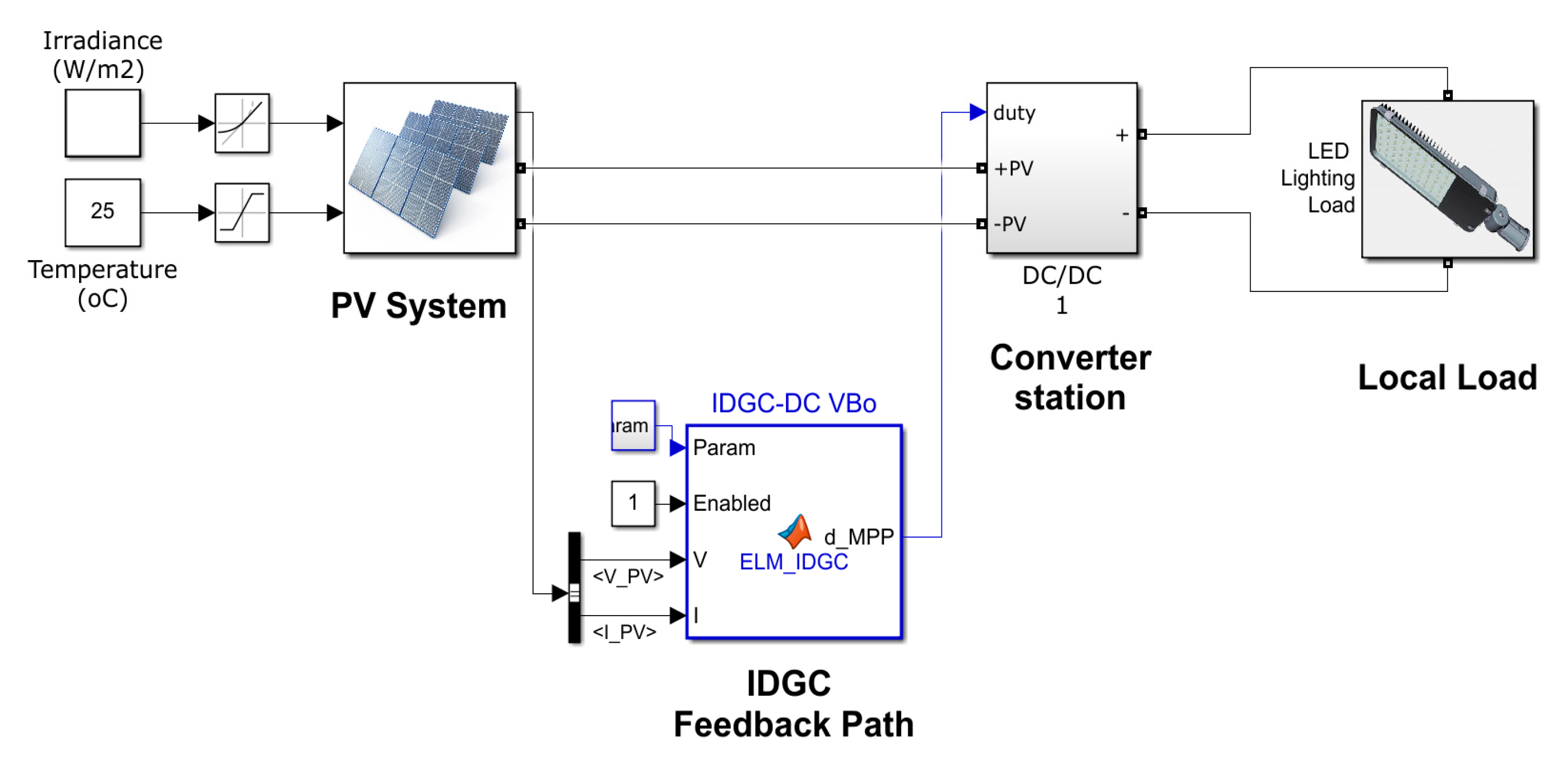
Here, a single DG-based microgrid is designed in the MATLAB/SIMULINK platform. The model details are given in this section. The proposed ELM–IDGC controller as shown in Figure 4 has been applied to a 10 kW PV application. The model is simulated for 10, 40, and 60 s, and the results are compared with the conventional method.

The enactment is evaluated through various operating conditions like MPPT error minimization, irradiance change, partial shading, and islanding operation three-phase fault and load change. The microgrid parameters are 12 kW, 100 V DC, DC link voltage 150 V DC, 230 V, and 50 Hz AC conversion, and the load rating is 10 kW, 0.784 Ω LEDs. The converter to PCC impedance is 2 km $0.1184+j0.0042$ Ω.

5.1. Scenario 1: MPPT Error Minimization

During the operation, the accuracy and computational burden are two major parameters to be measured. The efficacy of the proposed MPPT model is compared with the traditional linear and nonlinear techniques. Solar irradiance and the panel temperature are the two major input data to the MPPT. The RES dataset is divided into different sets based on the seasons. During considered events like partial shading, the seasonal data are resampled for RES–PPV and VPV estimation, with uncertainty. The training and testing ratio of irradiance data is 7:3. Various performance matrices are described to estimate the MPPT error, which is formulated as follows:

$$\begin{array}{l}MAPE=\left[{\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N\frac{\left|P_k-{\Gamma }_k\right|}{P_k}}\right]\ast 100\\ RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N{\left|P_k-{\Gamma }_k\right|}^2}}\\ MAE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N\left|P_k-{\Gamma }_k\right|}\end{array}$$

(15)

Here, the total samples are N and P_k and T_k are the actual value and predictable value of the MPPT. From the DAS data validation and the PCC of microgrid parameters, the performance of the proposed MPPT is judged. The DAS data with 5 min intervals measure various error responses such as RMSE and MAPE. For long time intervals, the MPP will be erroneous, which is why the 5-minute interval is considered. Here, the proposed ELM-based IDGC has been implemented to estimate maximum power in a microgrid. Its performance is compared with a basic MPPT controller. All the PV data are classified into different seasons, and here, only the summer data profile is validated. 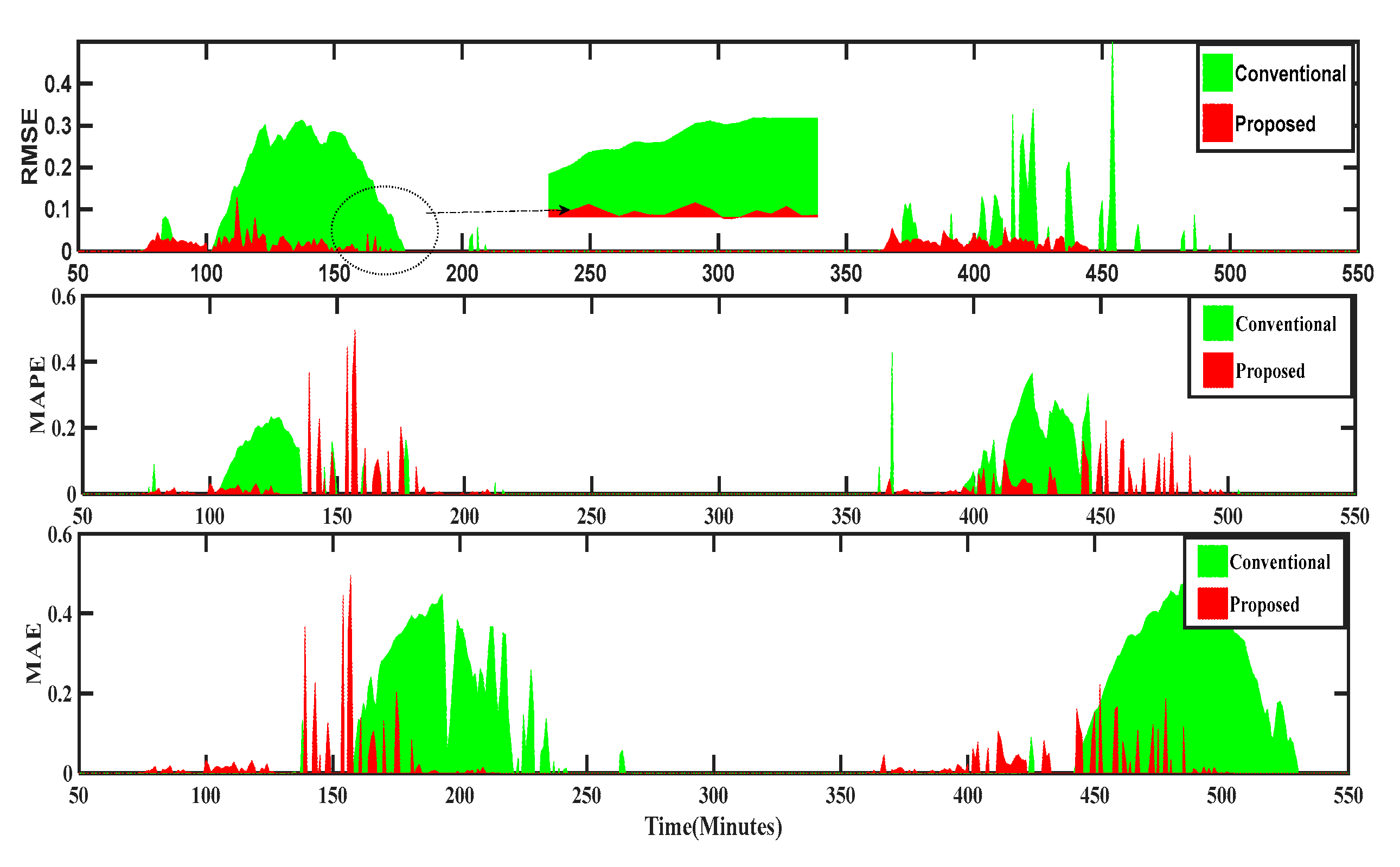Figure 5 depicts RMSE 0.061–0.88% and MAPE 2.48–4.48%. The conventional and proposed RMSE are given in Pu 0.032–0.0038, respectively. The ranges of MAPEs in Pu are 0.0412–0.0622 and 0.1053–0.2348 for the conventional and proposed ELM, respectively. The proposed MPPT performs effectively better than the conventional MPPT.

5.2. Scenario 2: Performance under Irradiation Variation

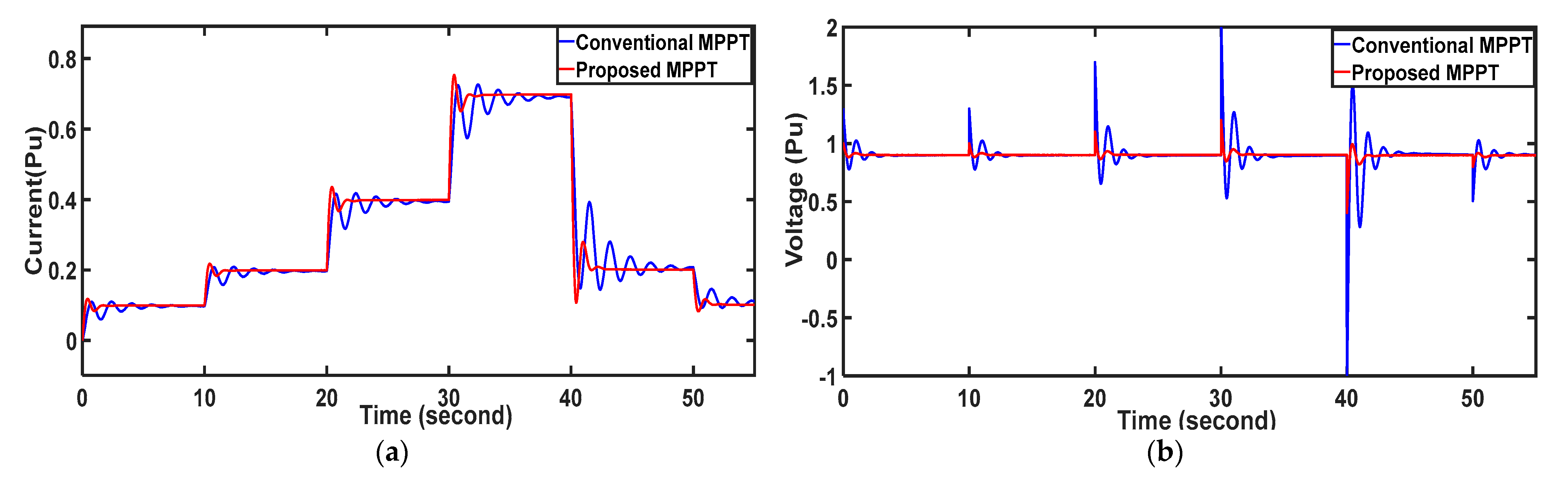
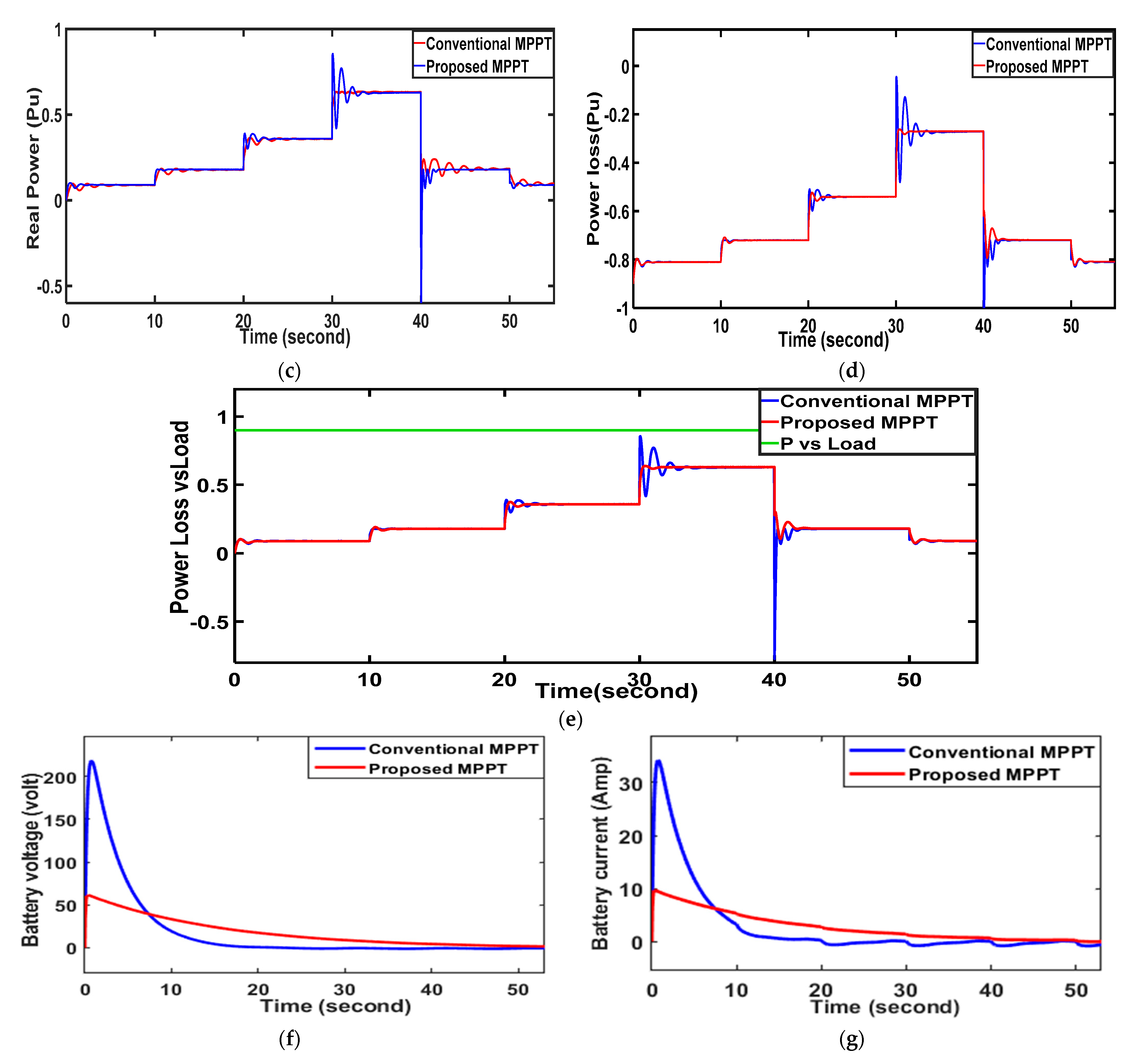
The PV-generated voltage and power are affected by the solar irradiance change due to its intermittent nature. The irradiance depends upon the weather conditions. In sunny weather, a substantial amount of irradiance is produced, and the PV generates its rated power and voltage. But in rainy season and foggy weather, the PV generation is affected. To compensate for this challenge, battery energy storage (BES) is connected to the system. The intermittent nature of irradiance influences the DC link voltage and other parameters of MG. The presentation of the proposed controller is investigated during irradiance variance through AC bus parameter disturbance. The fault-clearance time is measured in seconds and cycles. The performances are listed in

Table 1. Comparison of MPPT controller with 3 states.

MPPT Technique	State 1	State 2	State 3
Voltage ripple (V)
Conventional	3.98	2.87	3.88
Proposed	0.08	0.04	0.03
Current ripple (A)
conventional	0.93	0.49	0.054
Proposed	0.35	0.26	0.003
Convergence time (s)
Conventional	0.051	0.042	0.045
proposed	0.0062	0.0084	0.003
Tracking efficiency (%)
Conventional	96.98	96.92	97.10
Proposed	99.2	99.32	99.91
Overall efficiency
Conventional	94.93	92.85	91.51
Proposed	97.93	97.83	97.81
RSME MPPT error
Conventional	0.00481	0.02471	0.03166
Proposed	0.00061	0.00181	0.00287
MAE error
Conventional	0.00561	0.02971	0.01861
Proposed	0.00049	0.00187	0.00297
MAPE error
Conventional	0.5289	2.831	4.105
Proposed	0.0812	0.198	0.536

From Figure 6, it is observed that the irradiance changed in three states. In each state, the fault is mitigated within 1 s (50 cycles), but the conventional MPPT mitigates the fault in 10 s (200 cycles) in each state. The PV and IV characteristics of the PV cell are shown in Figure 6a,b, respectively, during various states. The instability created in the MG is balanced by the auxiliary power supply from the battery system given by Equation (16)

$$\begin{array}{l}if\hspace{0.17em}{p}_{pv}<p_{dcref}\\ if\hspace{0.17em}40<soc<80\\ p_{batt}=p_{dcref}-p_{pv}(discharging)\\ else\\ soc<40\\ p_{batt}=0\\ end\\ else\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}{p}_{pv}>p_{dcref}\\ if\hspace{0.17em}\hspace{0.17em}soc<80\\ p_{batt}=-(p_{dc}-p_{pv})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}charging\\ else\hspace{0.17em}\hspace{0.17em}soc>80\\ p_{batt}=0\\ end\\ end\end{array}$$

(16)

Figure 6f,g display the battery voltage and current fluctuations amid irradiance changes, showcasing the superior performance of the suggested IDGC over conventional methods. The proposed method exhibits minimized power oscillation and transient variation during fault incidents. This confirms IDGC’s superiority in managing system dynamics, offering improved stability and efficiency compared to traditional techniques. In this study, the irradiance varies at different time samples in each 10 s interval. The irradiance increased by 50 w/m², 100 w/m², and 200 w/m² at different time intervals, as shown in Figure 6. The irradiance was reduced after 40 s in various time intervals.

5.3. Scenario 3: Partial Shading

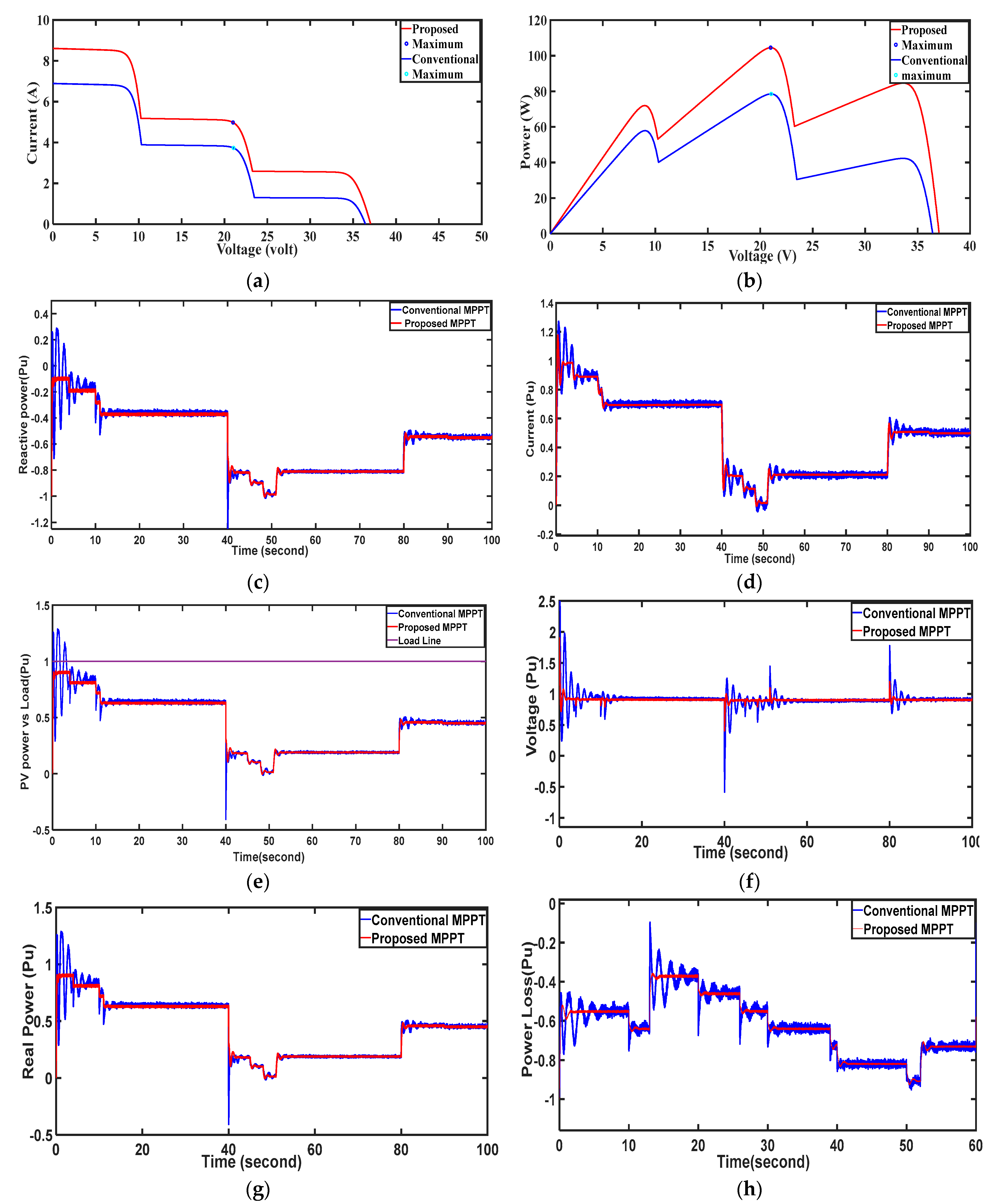
To achieve the rated power for a Multipanel Photovoltaic System (MPVS), the arrangement of PV panels in series and/or parallel configurations is crucial. A series connection boosts the output voltage, while a parallel connection increases the PV array output current. Accurate modeling of the PV array necessitates reproducing the actual current–voltage (I–V) characteristic curve of the PV cells. In the literature, single- and double-diode models are commonly employed. The single-diode model, simpler and less computationally intensive, is often favored, particularly for demonstrating partial-shading effects, offering satisfactory results with minimal complexity. Under non-uniform irradiation, the power–voltage (P–V) characteristics of the PV array exhibit multiple peaks, as shown in Figure 7a,b. The highest peak is termed the global maximum (GM) point, and the lowest is the local maximum (LM) point; however, from the above Table 1, all the real-time data will be found. The number of peaks correlates with the number of panels receiving varying power or irradiance levels, while the position of the GM depends on the intensity of irradiance and the arrangement of panels. In this case, a multicell PV array is used as a distributed generator of an MG. A 100 W PV panel is taken with a total of 60 cells (connected 40 series and 20 parallel). As depicted in Figure 7, partial shading is achieved by disconnecting individual cells. Here, each cell is of 0.15 V and 1.5 W. At t = 5 s, 2 cells (3 W), at t = 10, 2 cells (3 W), and at t = 40 s to 50 s, 6 cells (0.9 V, 9 W) are disconnected. Furthermore, at t = 80 s, two cells (0.3 V, 3 W) are included. The disconnection of cells results in the partial-shading operation of the PV module. The cell reduction produces a disturbance in the PV output and microgrid system. Given these types of disturbances, the DC voltage fluctuates by approximately 2.5 Pu. Current fluctuated within 0.4 Pu. Similarly, the deviation of real power, reactive power, and active power loss by both MPPT controllers are shown in Figure 7. From the results, it is confirmed that the proposed IDGC MPPT controller reduces the deviations more quickly than the conventional controller.

5.4. Scenario 4: Three-Phase Fault at Bus 1

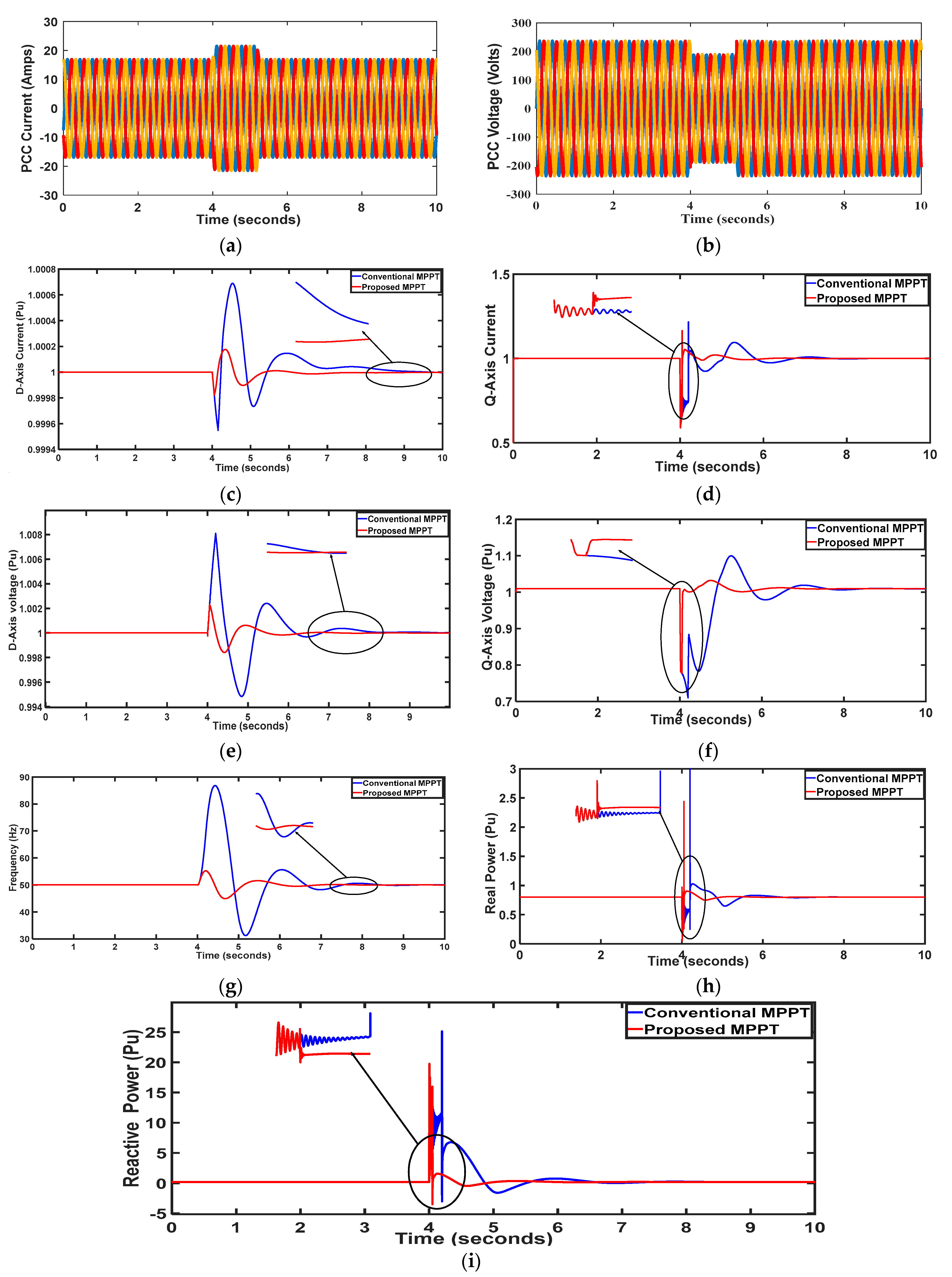
The efficacy of the system with increased strength undergoes scrutiny in a three-phase fault scenario at Bus 1 (PCC). Figure 8 illustrates the response of various grid and auxiliary power supply parameters. At t = 0.5 s, a five-cycle three-phase fault is introduced at the PCC. The IDGC technique swiftly damps oscillations, stabilizing the system within 2 s or 100 cycles. In contrast, conventional MPPT requires nearly 4 s (200 cycles), respectively, for system restoration post-fault occurrence. Figure 8e,f depicts the DC link voltage between the PV system’s back-to-back converters, revealing notable stability with the proposed technique. Convergence of the cost function is achieved in merely 9 iterations with the proposed IDGC. Optimal gain parameters yield reduced transients and an optimally responsive system. Overall, the proposed approach ensures efficient system stability and rapid response during fault scenarios, outperforming traditional methods in both damping capability and convergence speed. Furthermore, as shown by the results depicted in Figure 8, the direct-axis voltage and current have been simulated. Three-phase fault sustains for 1 s (4 s to 5 s). In all the following simulation results, the conventional MPPT controller settles the system within 4 s, whereas the proposed IDGC technique achieves steady state condition within 1 s. Thus, the proposed IDGC proves its superiority over the conventional MPPT controller in overshoot and settling time.

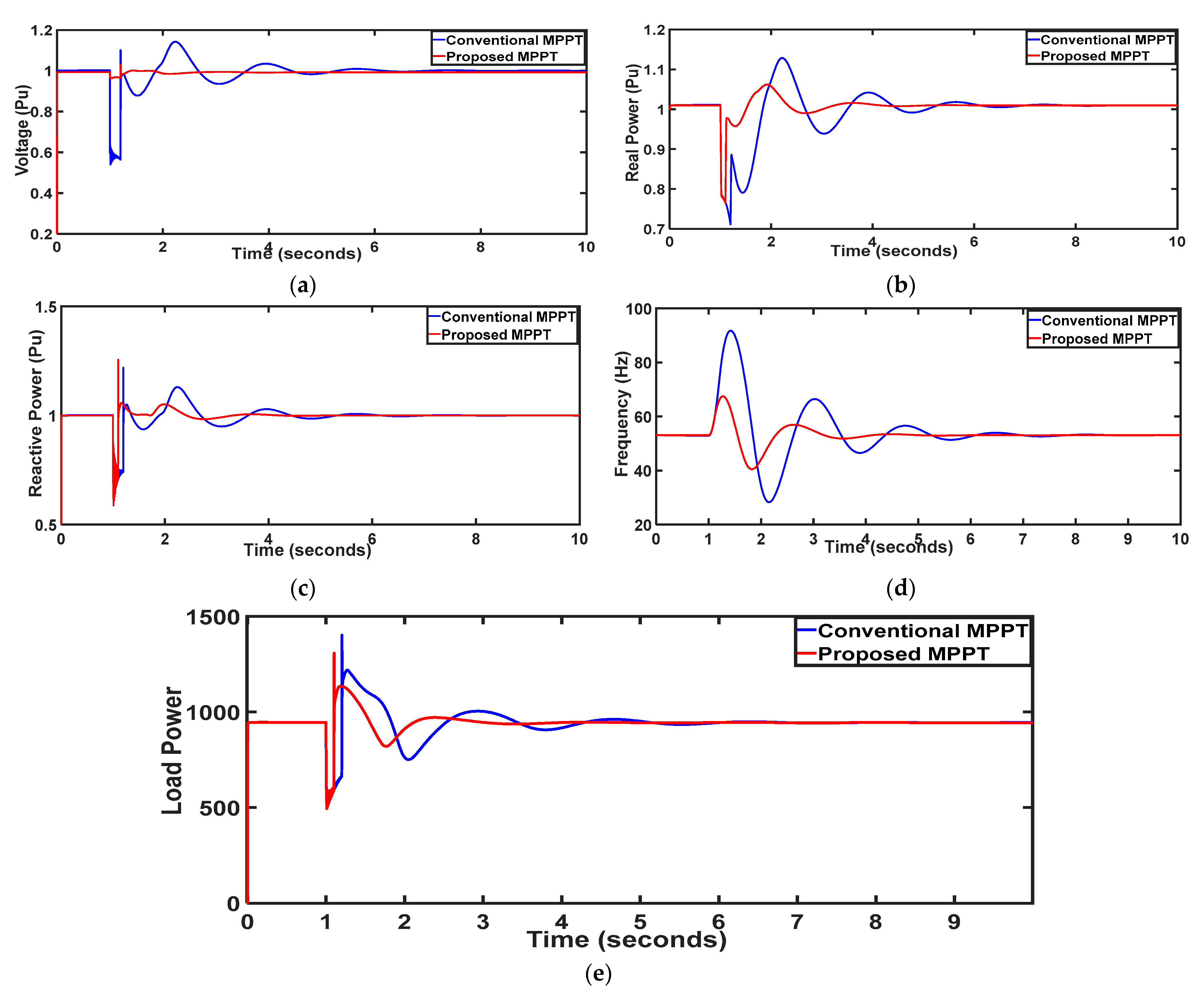
5.5. Scenario 5: Islanding Operation

The microgrid behavior is investigated with the proposed controller during an islanding situation. At t = 1 s, intentional islanding is initiated via switch s1, as depicted in Figure 9, focusing on the responses of PCC parameters. During islanding, the combined output from PV and battery adequately meets local load demand, ensuring stable Bus-1 voltage through distributed generation (DG) supply amid uncertainties. Notably, the proposed IDGC controller achieves system stabilization within a swift 0.5-s span, equivalent to 25 cycles (Figure 9a). In comparison, alternative methods require more cycles: the conventional MPPT controller-based Phase-Locked Loop (PLL) controller demands 100 cycles (2 s); the proposed controller exhibits heightened damping, resulting in diminished transient oscillations. Figure 9 illustrates convergence graphs of optimization methods, showcasing the proposed controller’s rapid convergence (merely 5 generations) with minimal error content. This underscores the efficacy of the proposed approach in swiftly stabilizing the system during intentional islanding, outperforming conventional methods in both convergence speed and transient response.

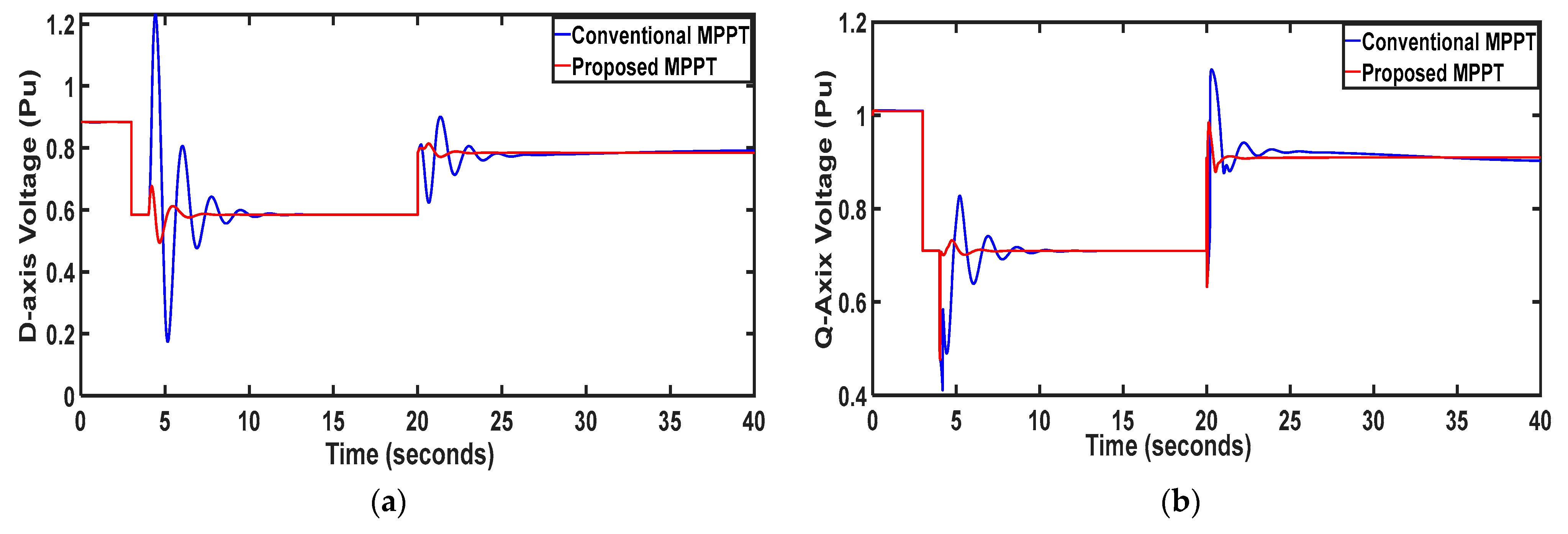
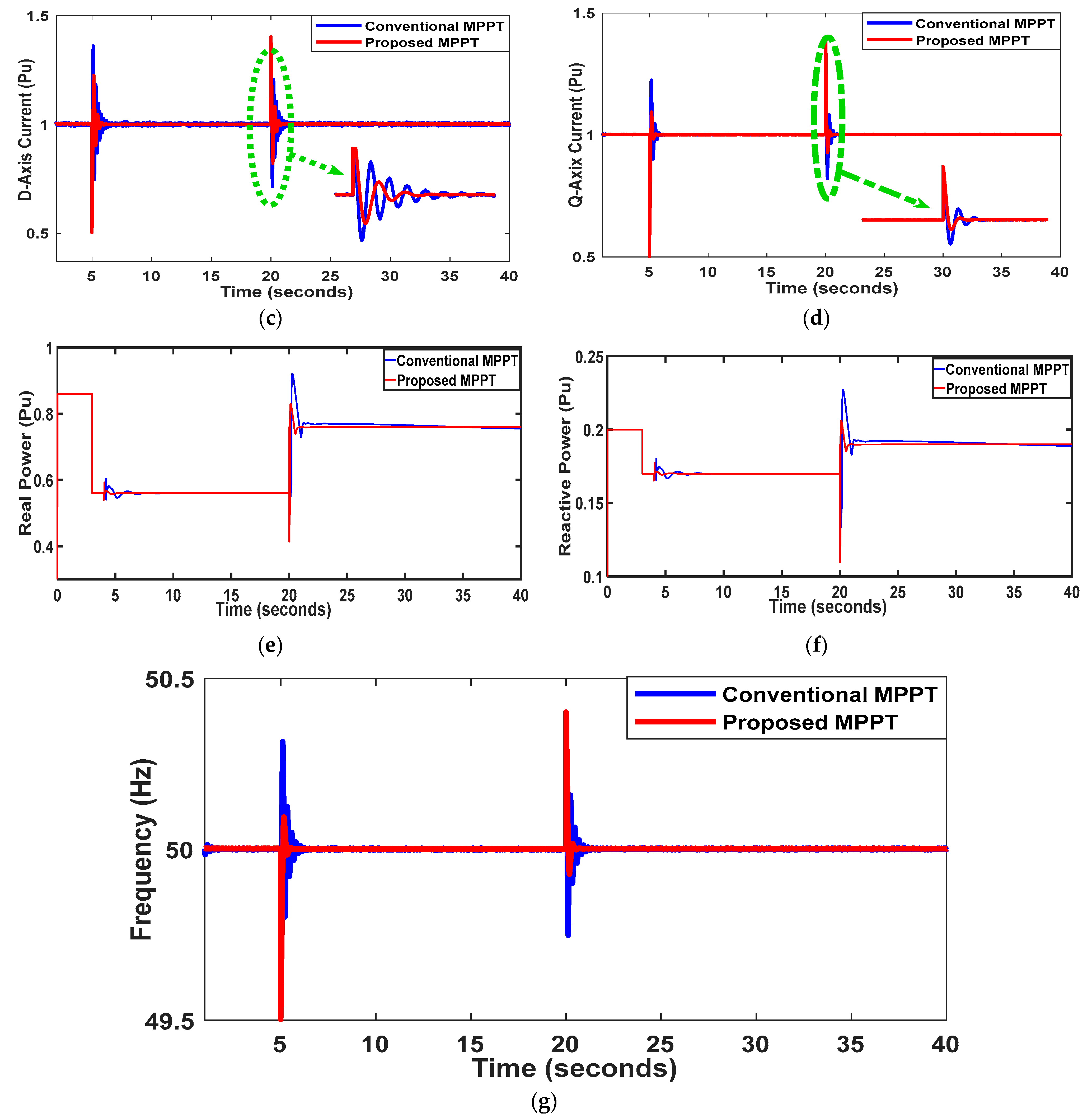
5.6. Scenario 6: Load Change

The performance evaluation extends to variations in load parameters, specifically at (PCC), where a 30% decrease occurs at t = 5 s followed by a 10% increase at t = 20 s, as depicted in Figure 10. The load current, as illustrated in Figure 10c,d, exhibits a corresponding decrease and subsequent increase in line with the load variation. Notably, despite these fluctuations, Figure 10a,b showcases the remarkable constancy of Bus-1 voltage, indicative of effective controller operation, resulting in minimal deviation. Conversely, Figure 10e,f reveals the real and reactive power trend opposite to that of load current. The system’s restoration time with the proposed IDGC controller stands at a mere 25 cycles (0.5 s), a notable improvement compared to the conventional technique requiring 50 cycles (1 s). Furthermore, transient oscillations are notably subdued in the proposed method compared to the conventional techniques. Employing the optimal IDGC method results in a system exhibiting a superior transient profile and optimal functionality. The combination of reduced restoration time minimized transient oscillations, and swift convergence of optimization underscores the effectiveness of the proposed approach in enhancing system stability and performance amid load variations, offering significant advantages over conventional methods.

5.7. Scenario 7: Hardware Validation

The validation of the performance of the proposed IDGC in a microgrid involves a hardware-in-the-loop (HIL) simulation using advanced tools such as the OPAL-RT real-time simulator and the Eco Sense PV Emulator. In this setup as displayed in Figure 11, the microgrid system, comprising a standard model with solar PV and battery energy storage (BES), is simulated in real time using MATLAB Simulink integrated with OPAL-RT. The OPAL-RT simulator, specifically the OP5600 model (see Appendix A for detailed hardware specifications), enables precise real-time simulation and hardware interfacing, facilitating the emulation of dynamic microgrid conditions. The PV-based distributed generation (DG) system is emulated using the Eco Sense PV Emulator, which replicates the behavior of a prototype solar plant. This emulator is interfaced with Simulink as a controlled voltage source, allowing for the accurate simulation of PV system characteristics under various environmental conditions. Real-time data as illustrated in Figure 12, including irradiation variation and partial-shading effects, are captured using the data-acquisition system extension boards (ADC C5: OPA350 Master PPC library), which are crucial for ensuring the accurate representation of real-world conditions within the simulation. The performance of the Point of Common Coupling (PCC) within the microgrid is continuously monitored by recording the RMS voltage and current using the data-acquisition system integrated within the OPAL-RT framework. To optimize the system’s performance, the controller gains are finely tuned using MATLAB script-based analysis. These optimized gains are then implemented within the Simulink model to ensure precise control of the microgrid under varying operational conditions. The irradiation profile for the PV emulator varies at specific time intervals to simulate different environmental scenarios. Data acquisition and processing are facilitated by a digital-to-analog converter (DAC) within the OPAL-RT system, connected to a high-speed digital signal processor (DSP) via the embedded USB JTAG. The collected data are visualized using a digital storage oscilloscope (DSO) (e.g., Tektronix TBS1022) through a Toshiba TLP 250 gate driver, allowing for real-time analysis of system performance. During the simulation, the conventional MPPT controller exhibited significant performance issues, with the system manifesting 150 cycles of dynamic oscillation. In contrast, the proposed IDGC controller, when tested under similar conditions, demonstrated superior performance, as depicted in Figure 10. The IDGC controller, compared to conventional Phase-Locked Loop (PLL) controllers, significantly reduced oscillations and enhanced system damping, leading to quicker stabilization of the microgrid system. In summary, the HIL simulation, utilizing OPAL-RT and the Eco Sense PV Emulator, validates the effectiveness of the proposed IDGC in mitigating uncertainties and efficiently stabilizing the microgrid system. This validation is supported by real-time emulation and detailed performance analysis, showcasing the IDGC’s capability to maintain system stability under challenging environmental conditions.

6. Conclusions

A new IDGC is suggested, utilizing an Extreme-Learning Machine (ELM) for PV-based Distributed Generator (DG) operations. Compliant with ISA-95 and IEEE-1547 standards, it integrates MPPT and feedback control for standalone or grid-connected operation. The ELM-based IDGC aims to outperform traditional architectures by minimizing computation errors like $e_{mppk}$ through reduced computational complexity. It replaces iterative ANN learning with the MPPI technique, cutting computational delays. Regularization is achieved with a novel ridge regression estimated coefficient (RC), enhancing robustness against initial randomness. It is observed that the applied controller is more suitable and robust towards stability improvements in PV-based MG. The proposed controller is tested in six case studies, namely error minimization, irradiance change, partial shading, three-phase fault, load change, and islanding operations. The results are obtained in a MATLAB environment. It is observed that the proposed IDGC controller proved superior as compared to the conventional method. Finally, the performance in irradiance changes and partial shading is validated in a hardware-in-the-loop (HIL) environment.