A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization
Abstract
1. Introduction
1.1. Literature Review
1.2. Main Contribution and Highlights
- This study employs a flexible, sustainable power system model, taking into account the impact and unpredictability resulting from RESs. It is possible to solve the LFC problem quite quickly using thorough explanations of several mathematical representations of renewable energy.
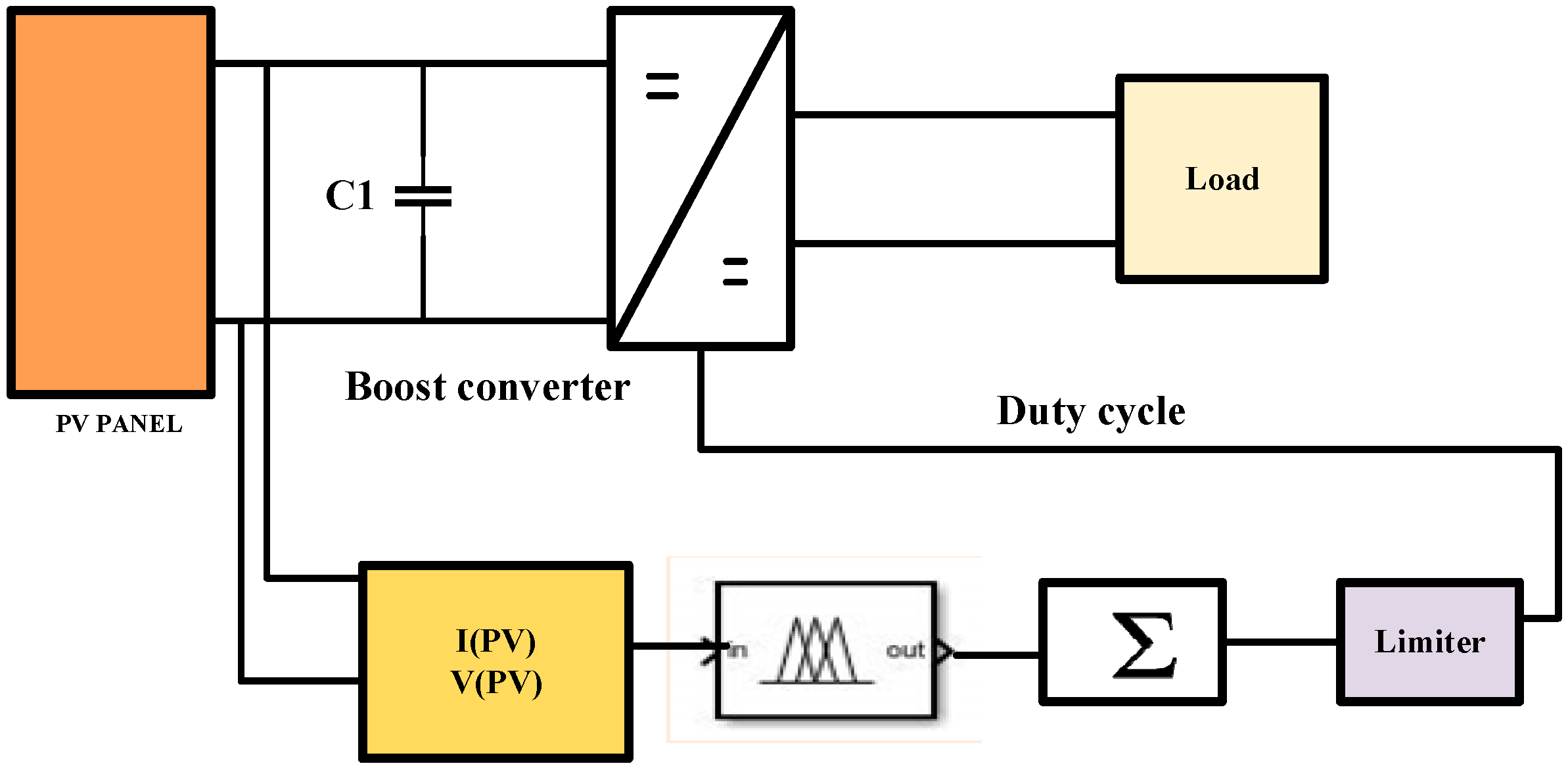
- To design a model of a one-area power network with multiple sources, this research included a fuzzy-based MPPT solar power system and PMSG-based wind power system using P & O MPPT technique and a model of the fuel cell.
- A model of a double-area power network interlinked via tie line is designed.
- The PSO approach is utilized to optimize the parameter values of the PID controller.
- The steady-state error is brought to zero after load variation.
- By varying system values throughout a range of around ±50% and variations in load for double-area tie-line IPS, the efficiency of the PSO-PID controller for multi-source one-area and dual-area tie-line IPS is analyzed in various scenarios.
- It is dependable and generates better results than a conventional PID control system. In every situation this research examines, the suggested system control technique has less undershoot, overshoot, and settling time than the traditional PID controller model.
1.3. Structure of Article
2. Proposed Power Structure Modeling
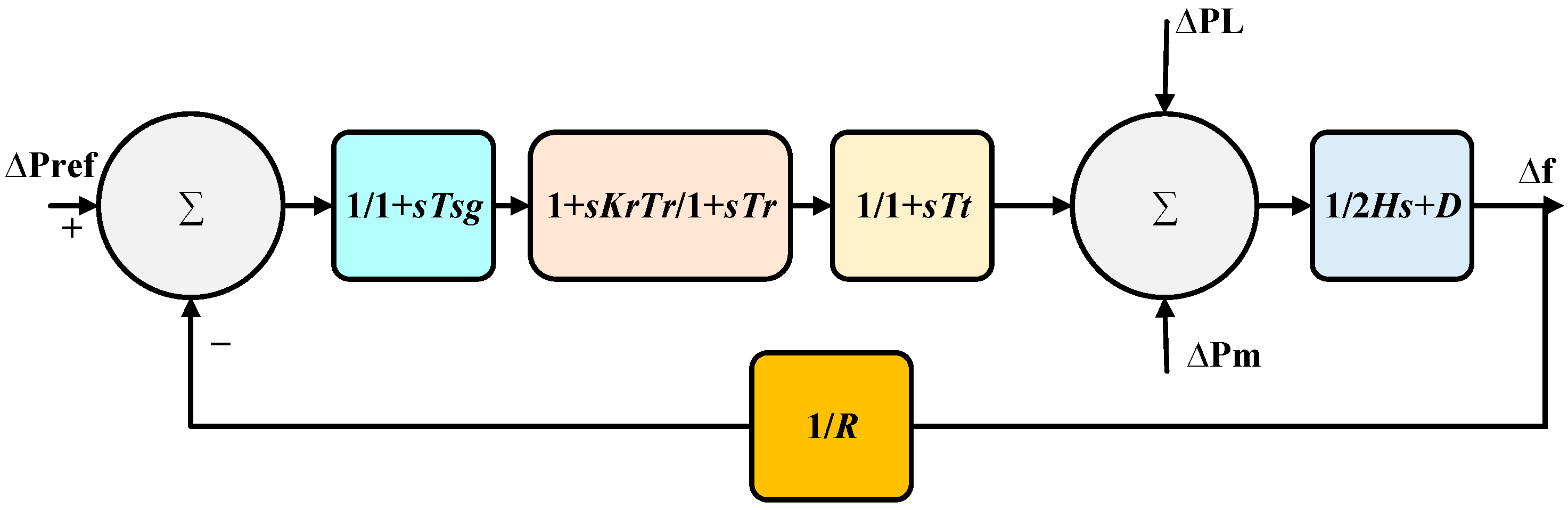
2.1. Thermal Power System Mathematical Modeling
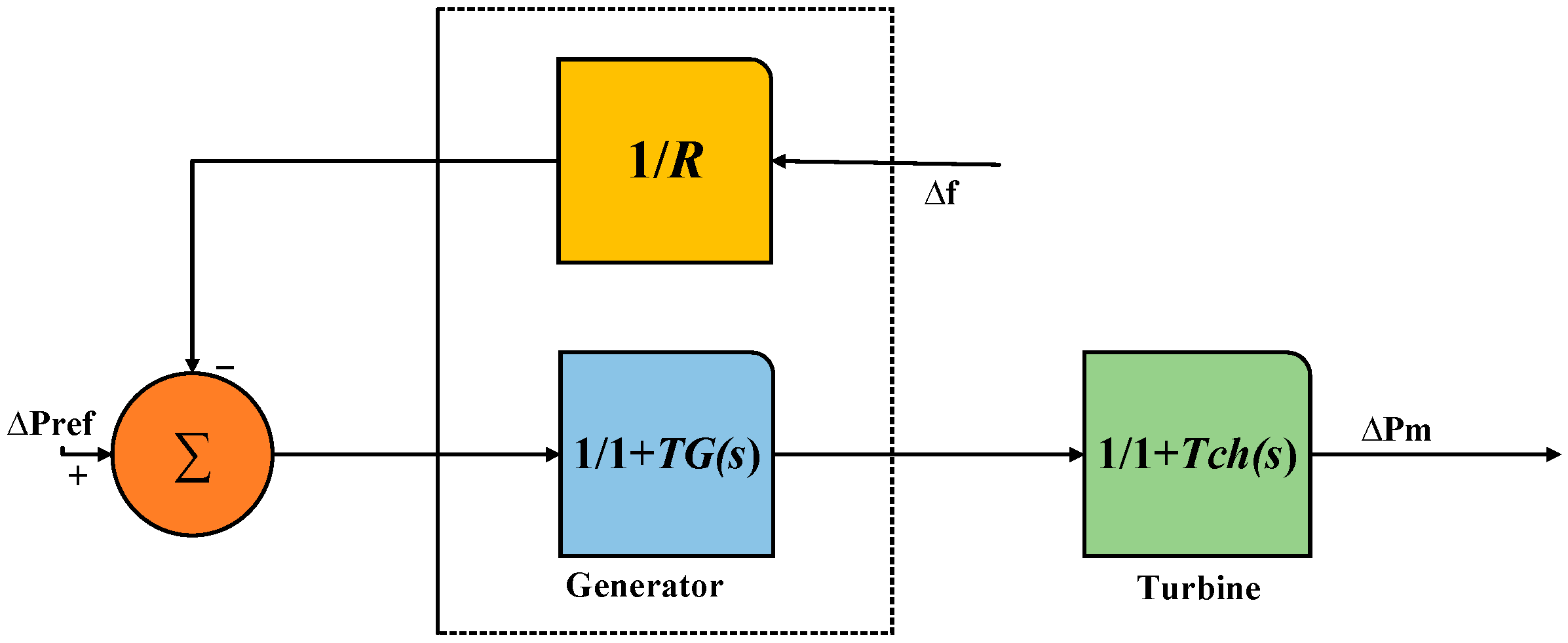
2.1.1. Governor
2.1.2. Turbine
2.1.3. Load
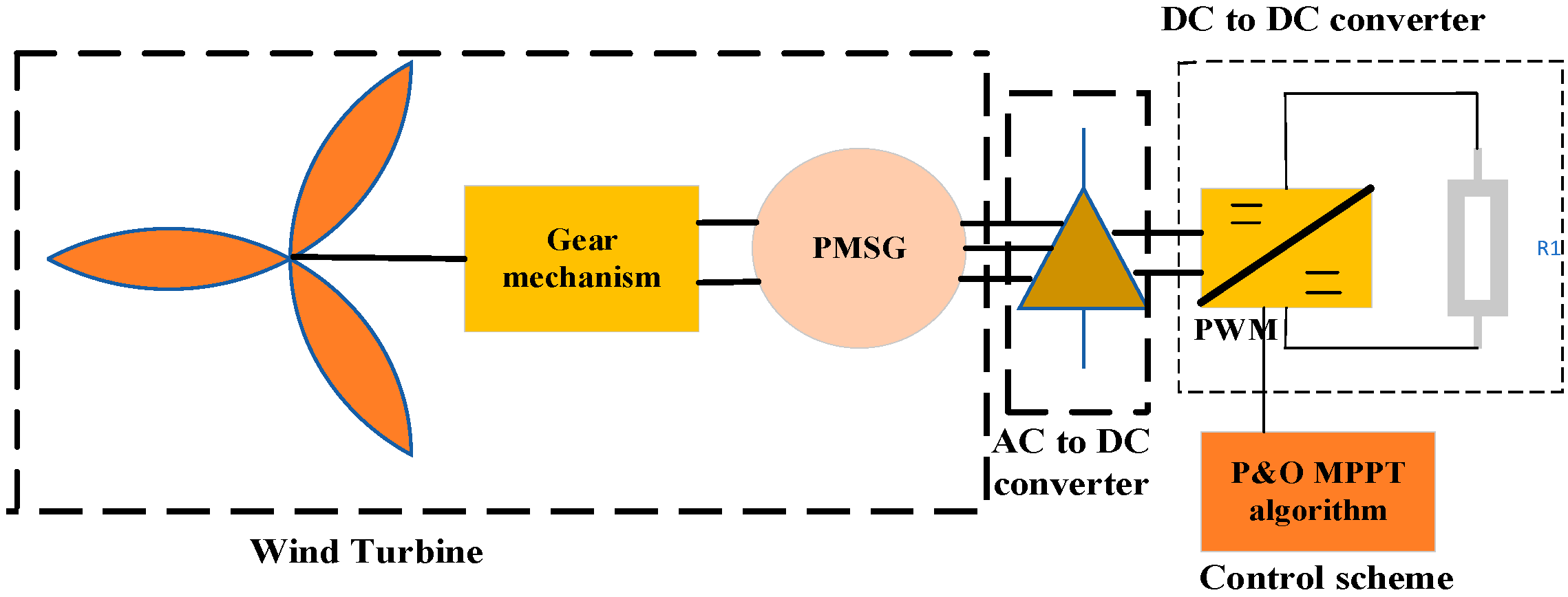
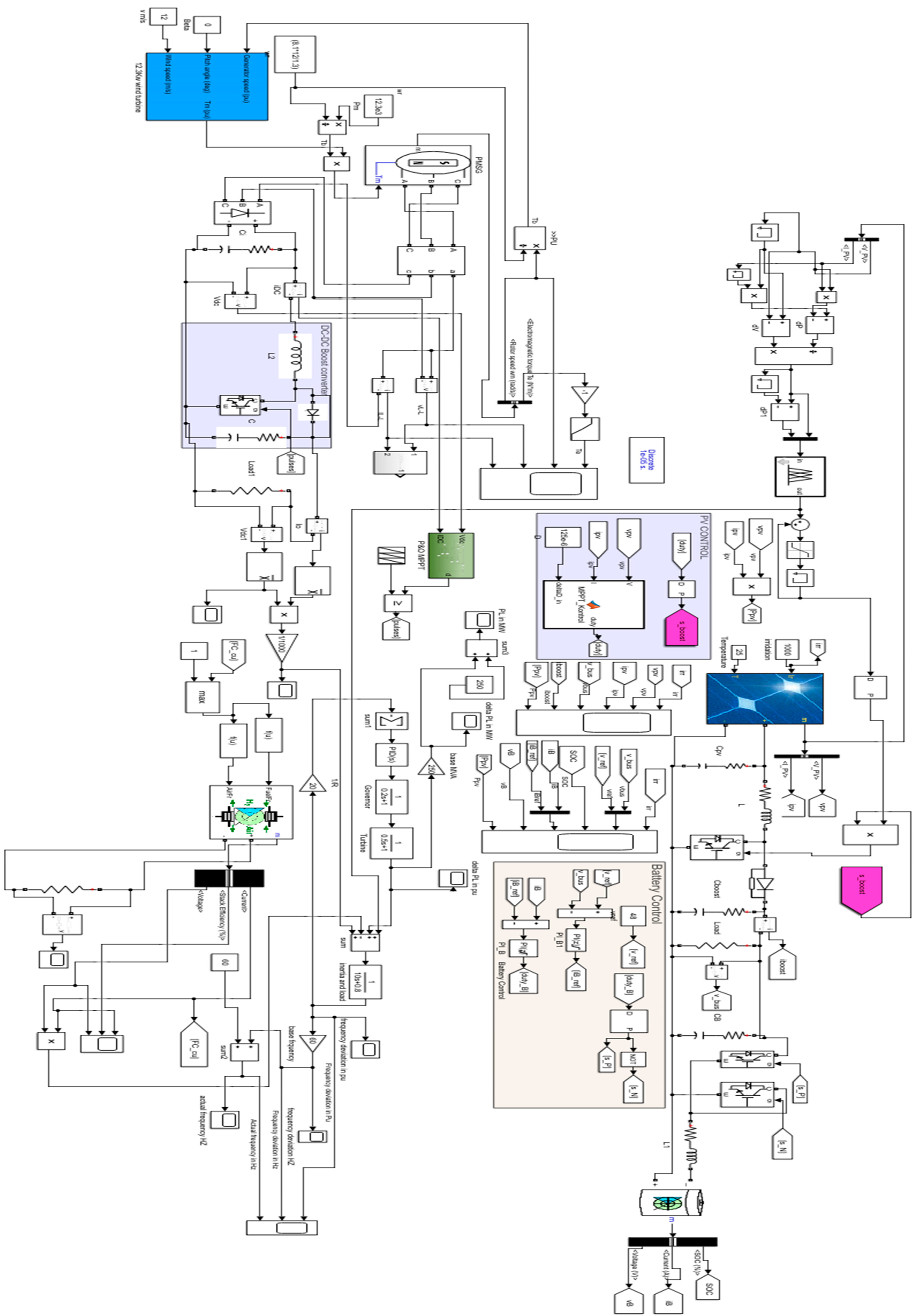
2.2. Mathematical Modeling of Wind Power System
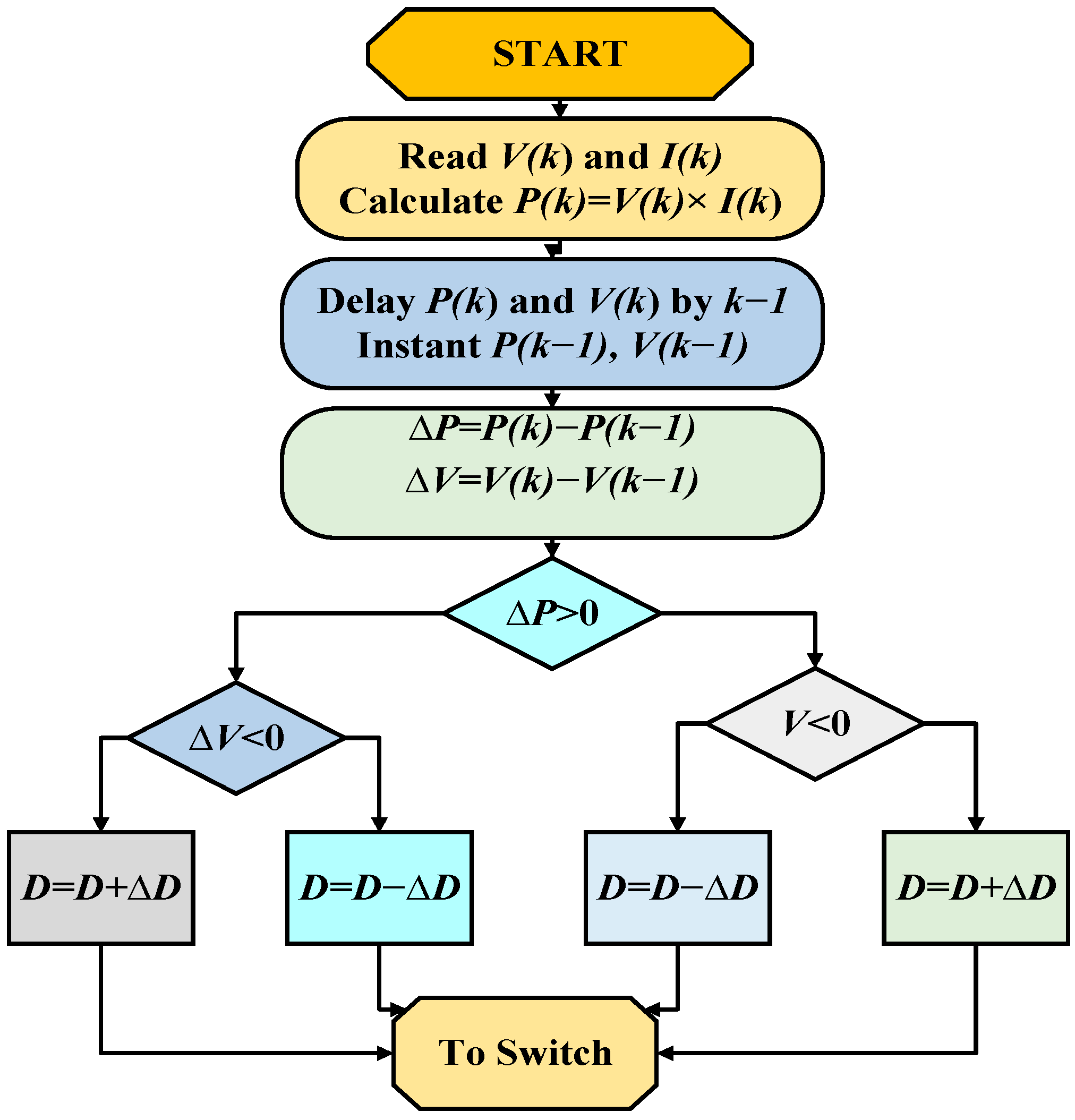
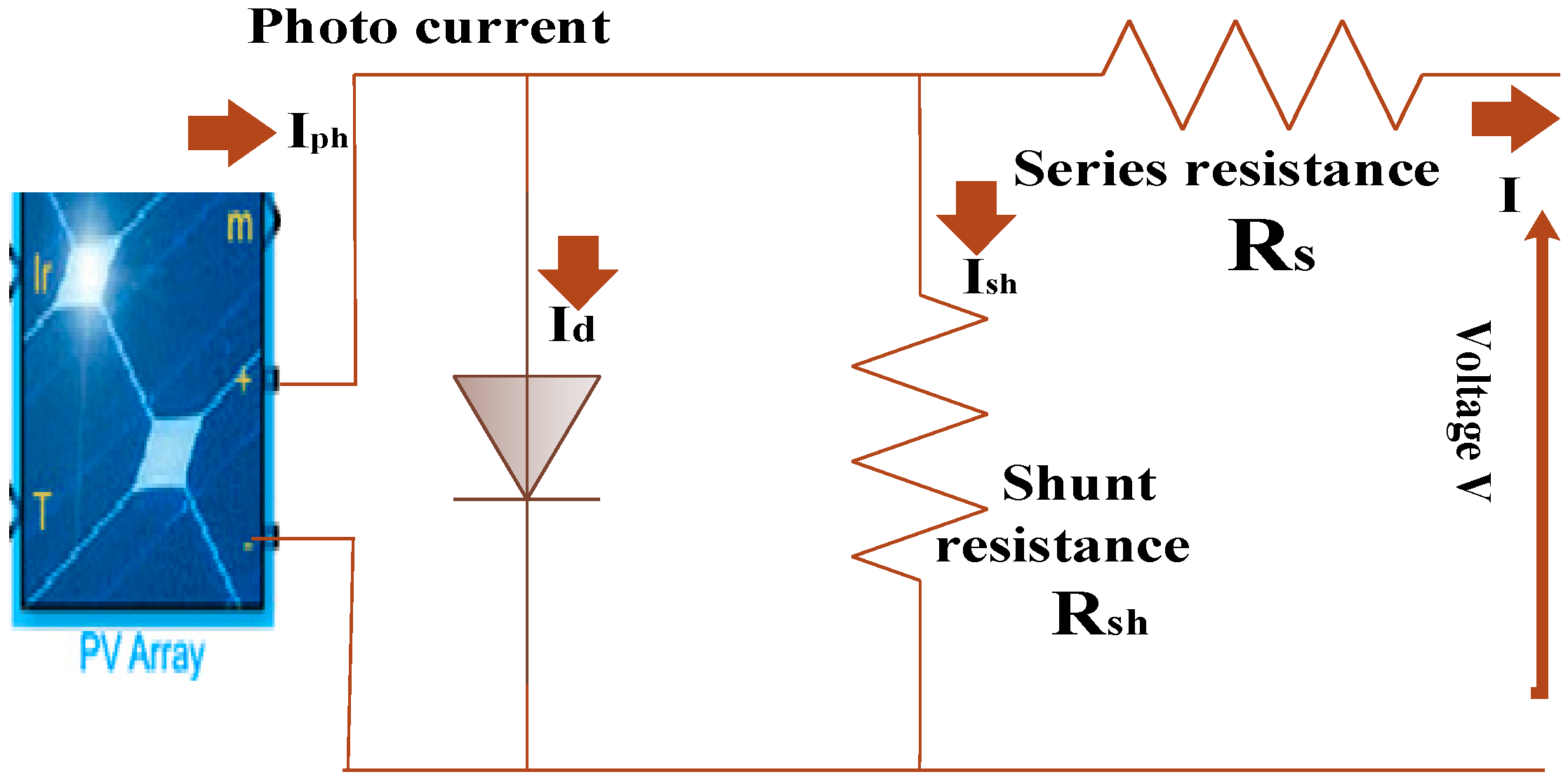
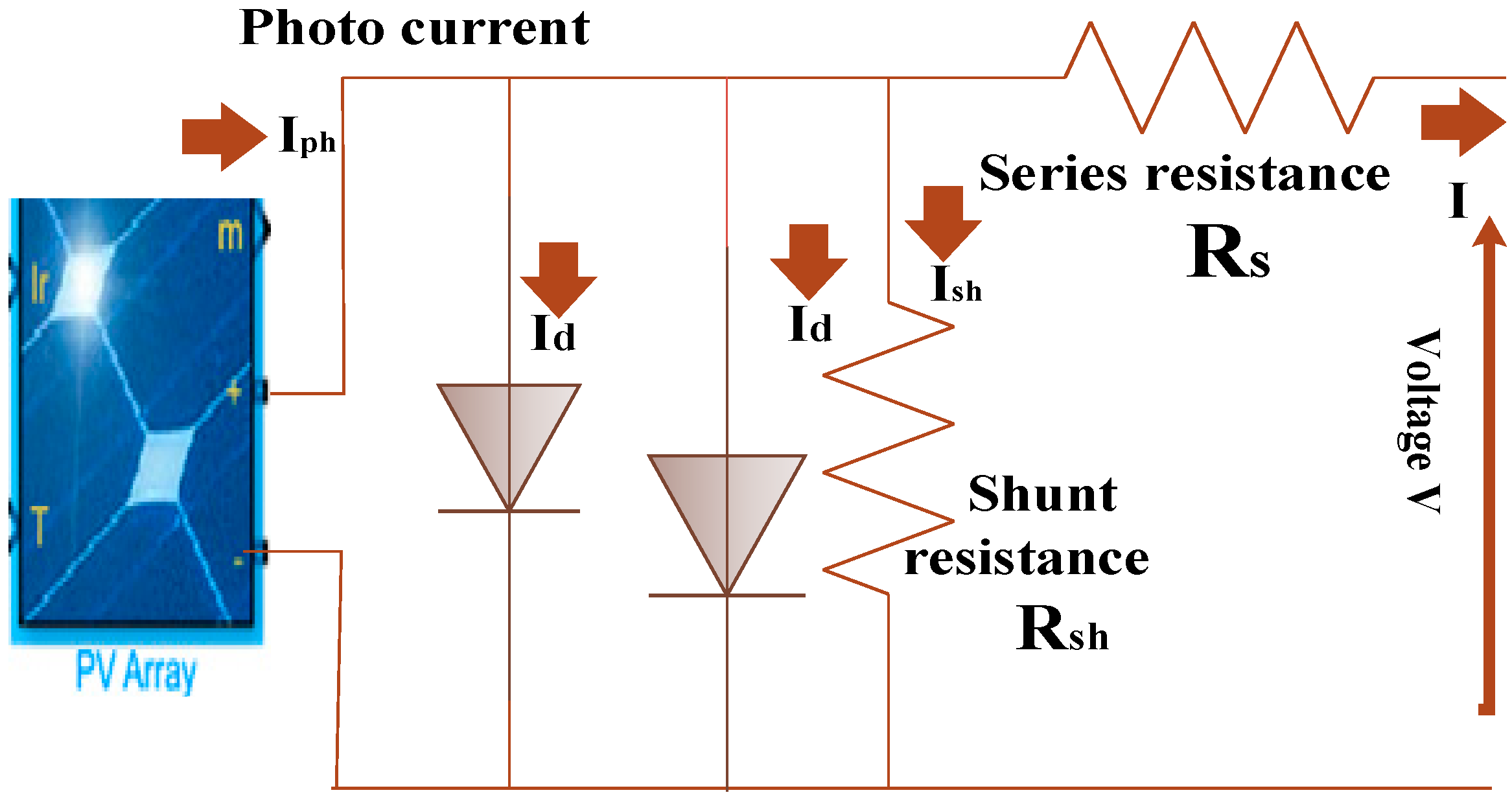
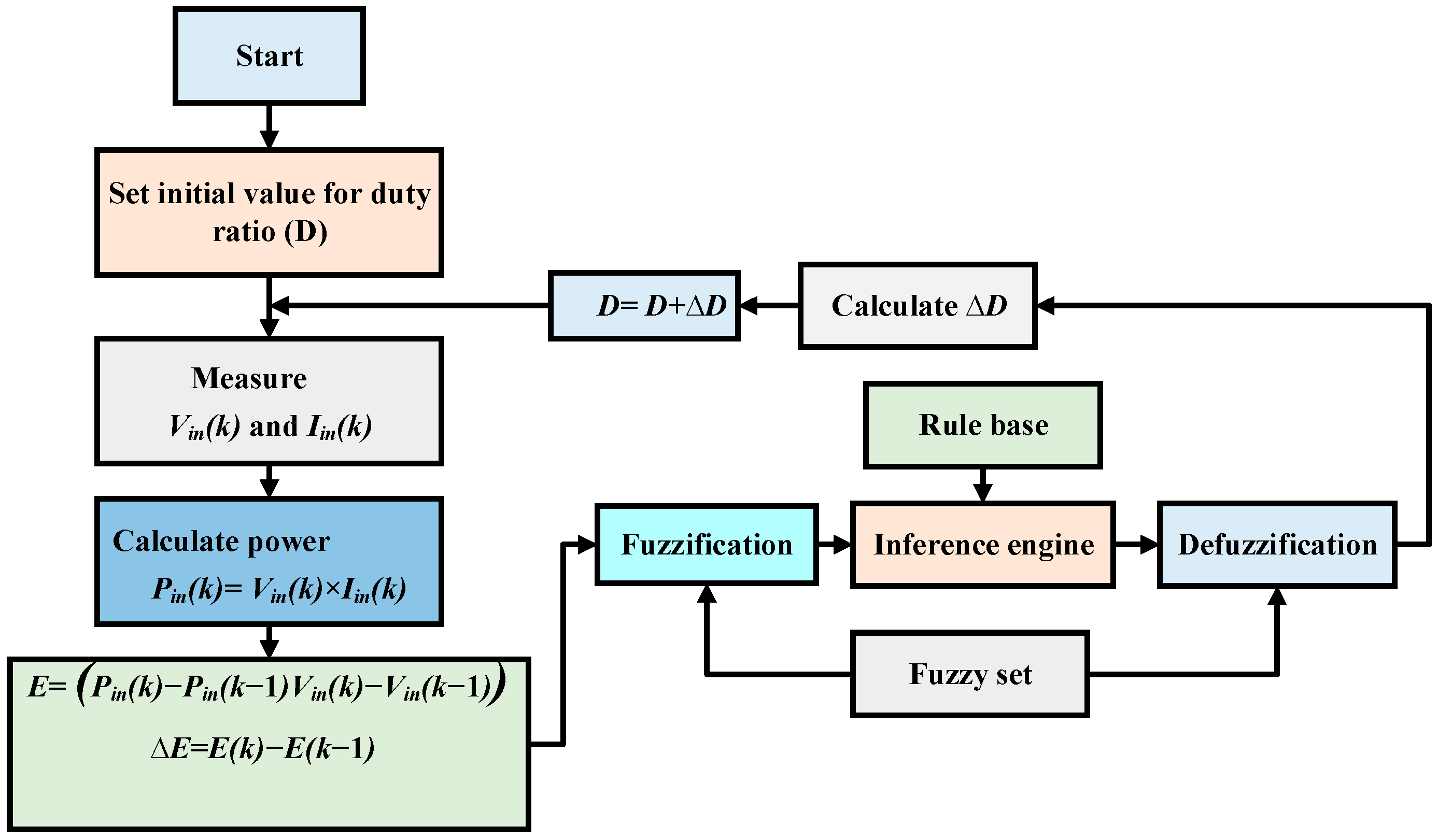
2.3. Mathematical Modeling of Solar Power System
2.4. Fuel Cell Dynamic Modeling
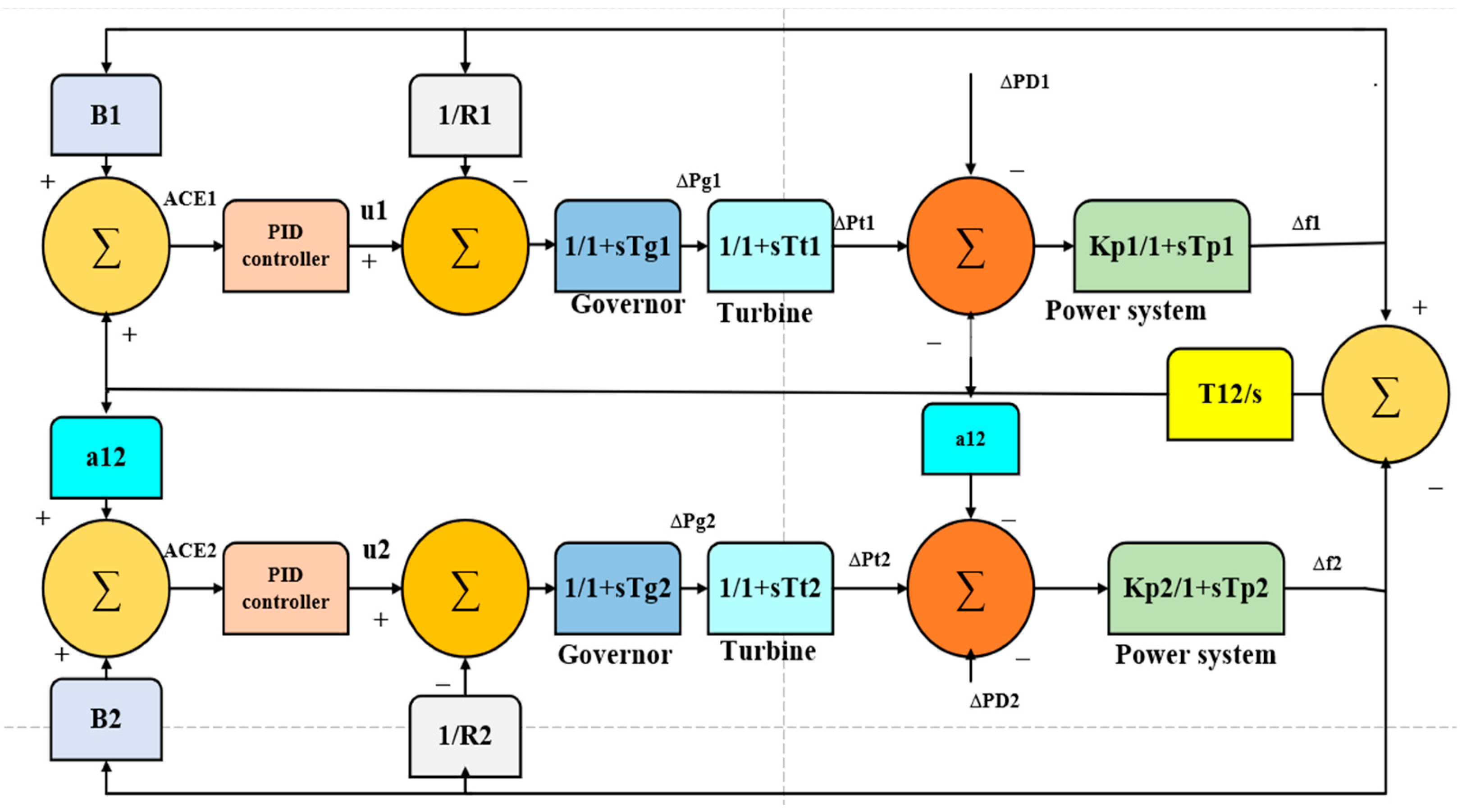
2.5. Two-Area Tie-Line Modeling
3. Proposed Control Strategy
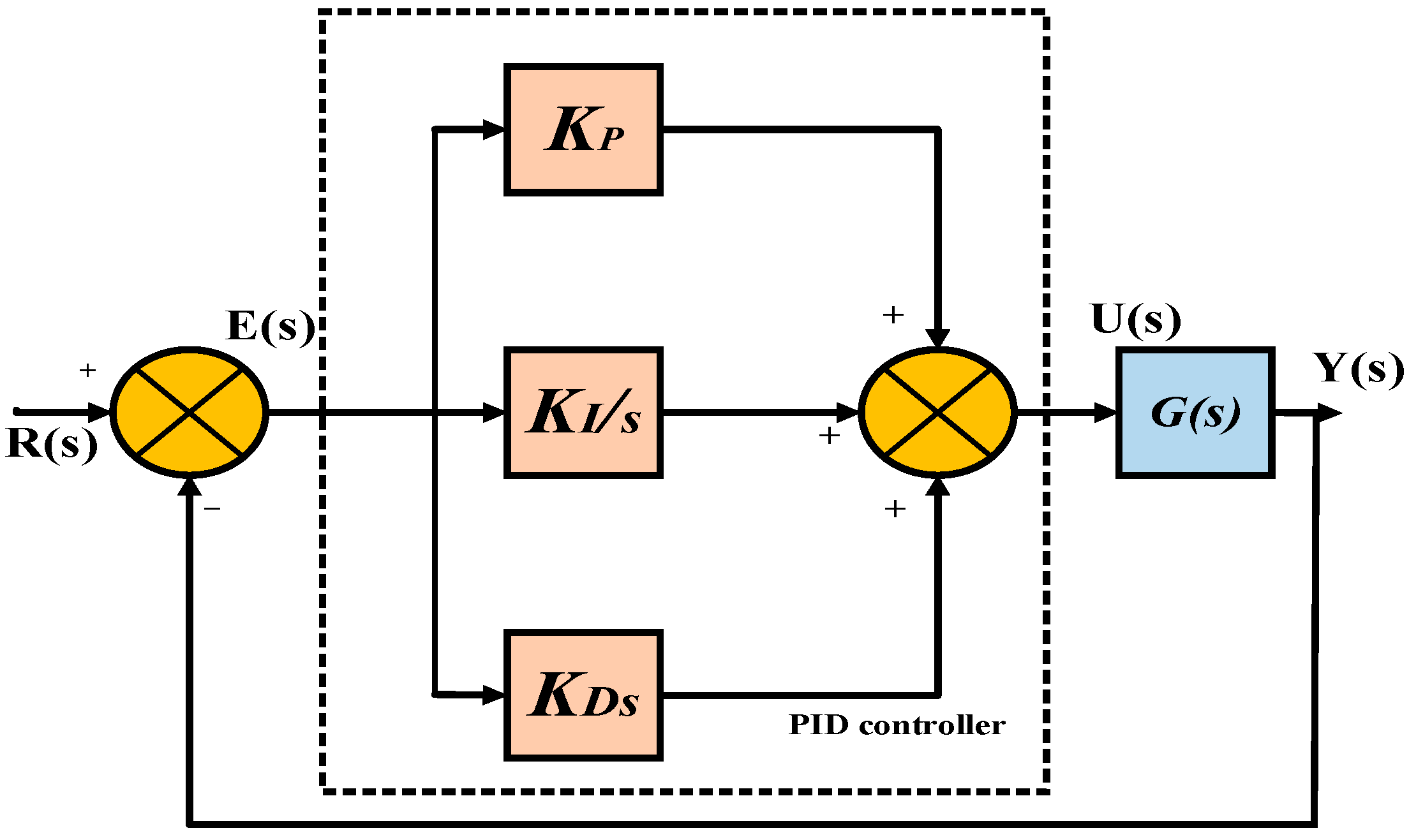
3.1. PID Controller
3.2. Objective Function
3.3. Multi-Source Single-Area Power Network
3.4. LFC in an Interlined Dual-Area Tie-Line Power Network
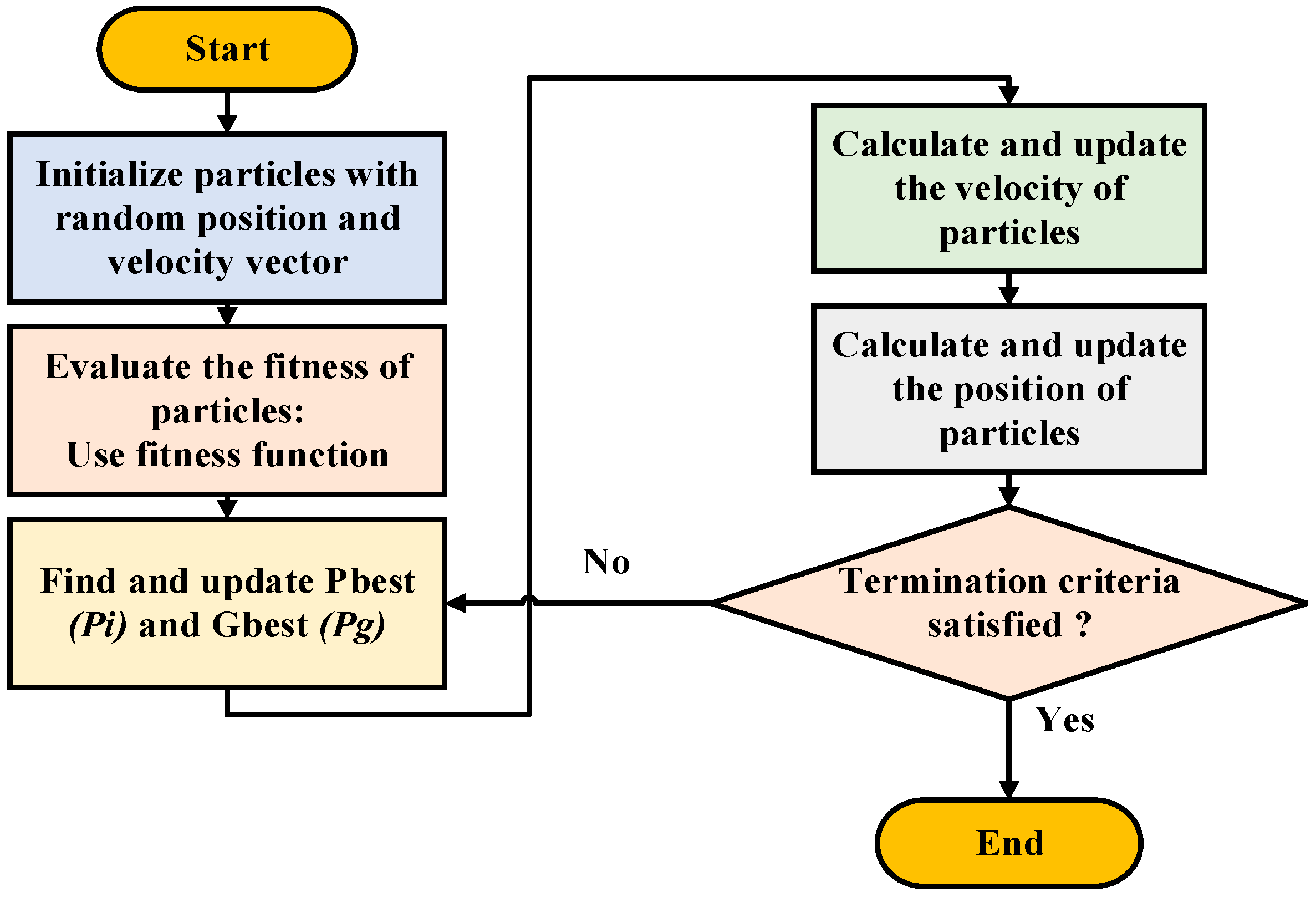
3.5. Proposed Algorithm Particle Swarm Optimization (PSO)
4. Simulation Results
- System parameter variations in one-area multi-source power network and dual-area tie-linked power system.
- Load variations are in double-area tie-line linked power systems only.
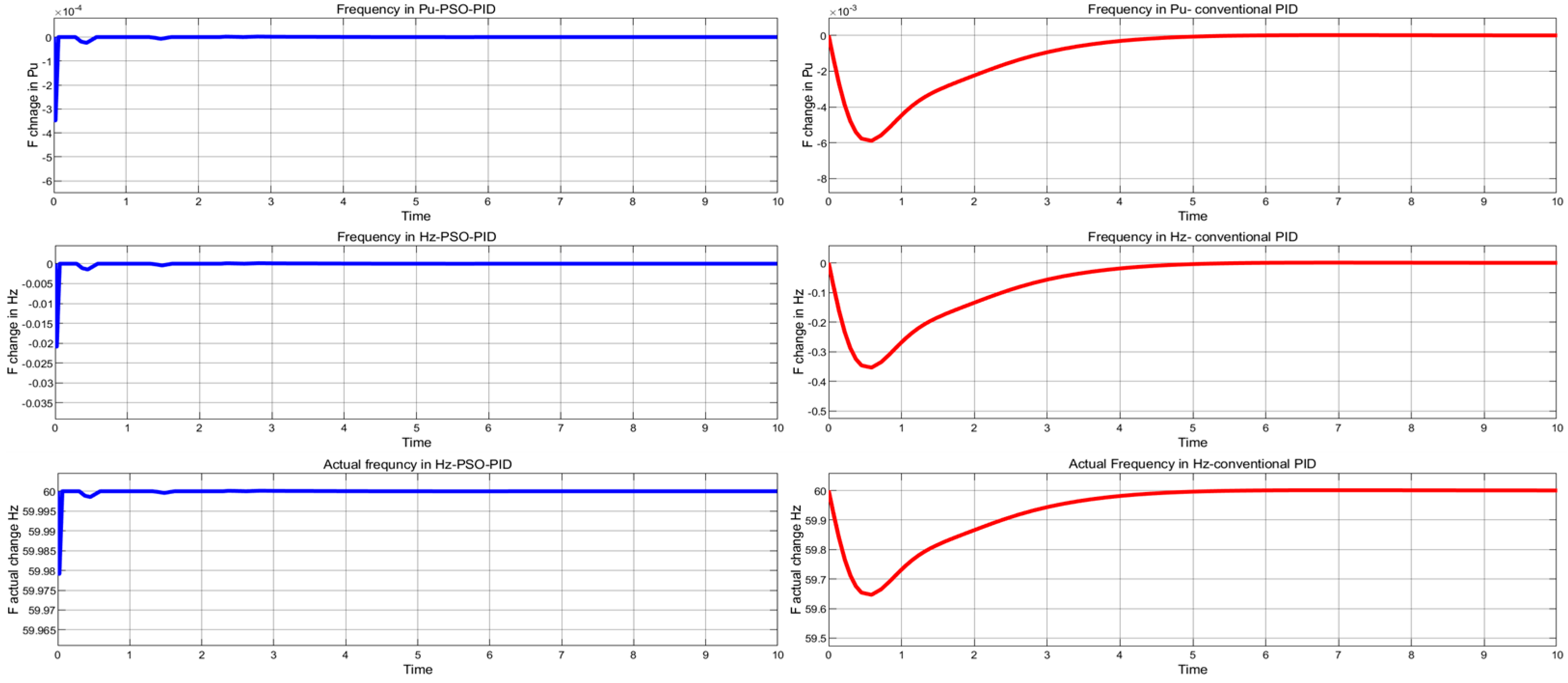
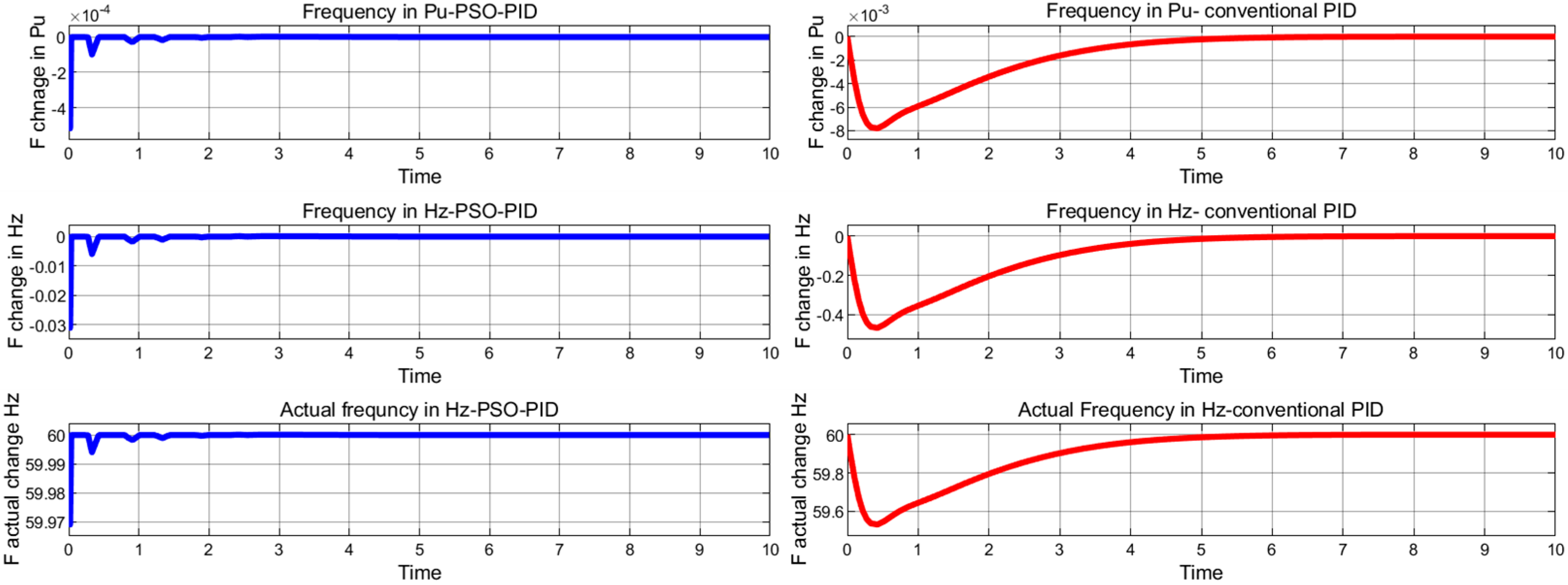
4.1. Multi-Source One-Area Power Network
Robustness Evaluations (Case Study 1)
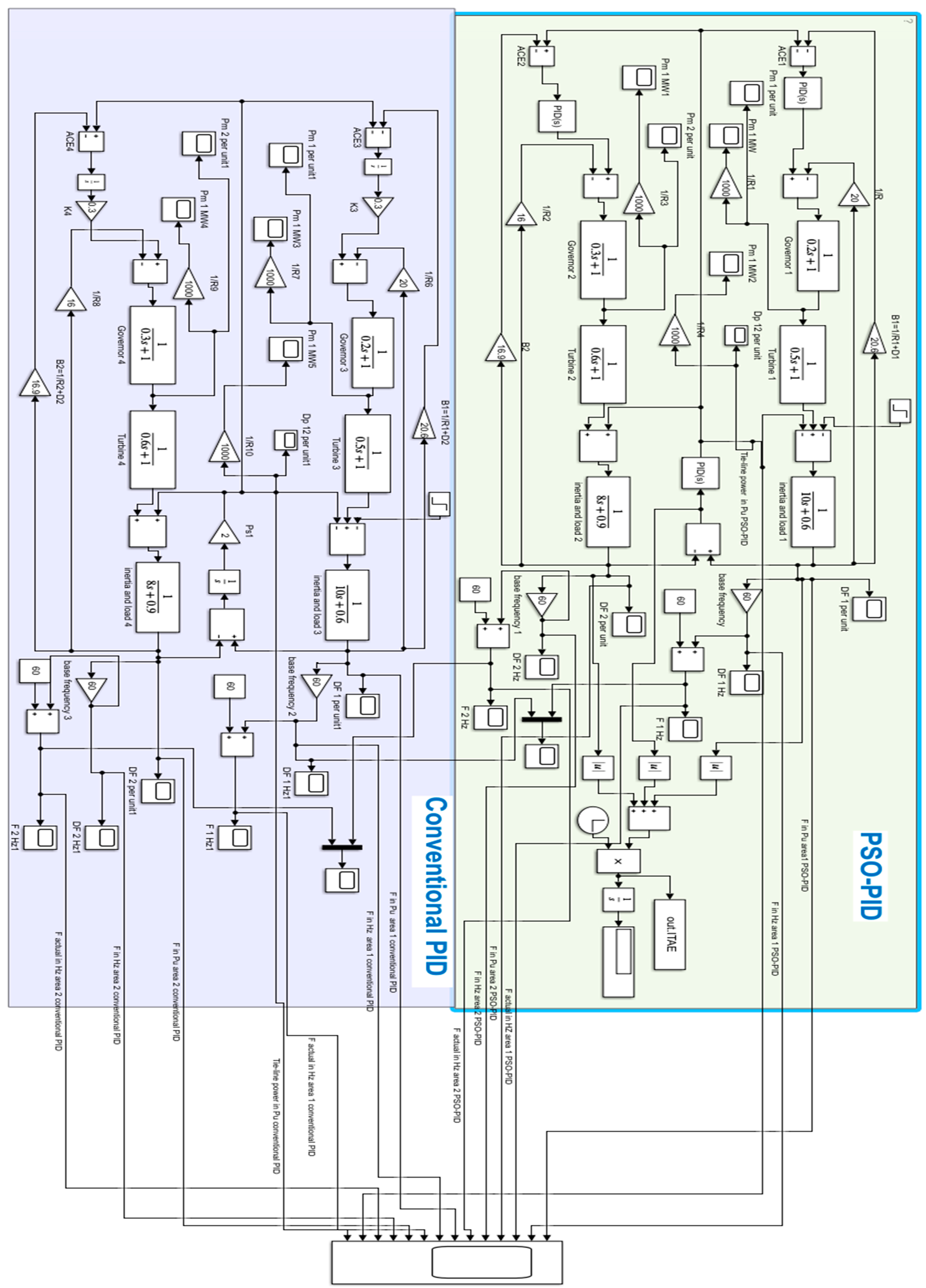
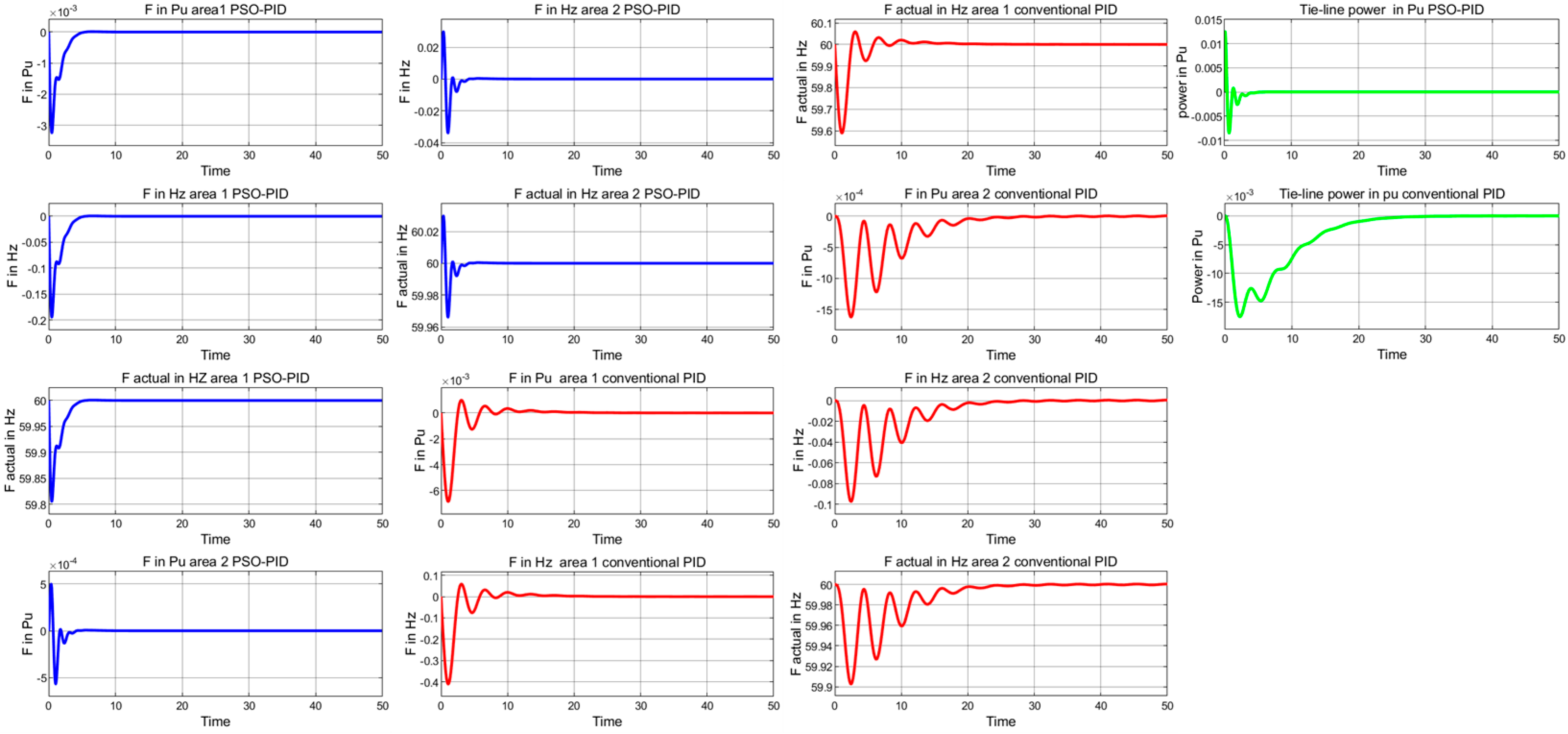
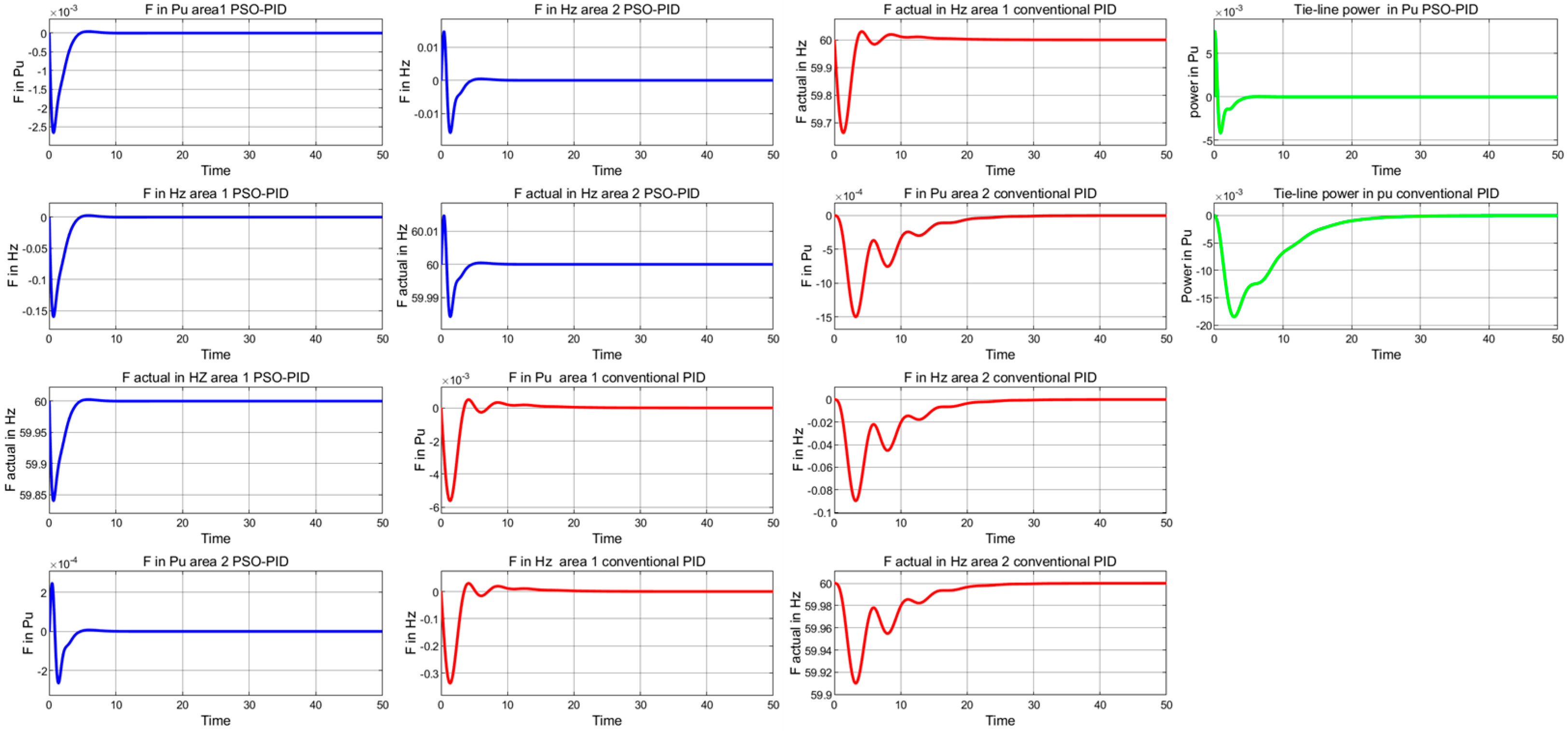
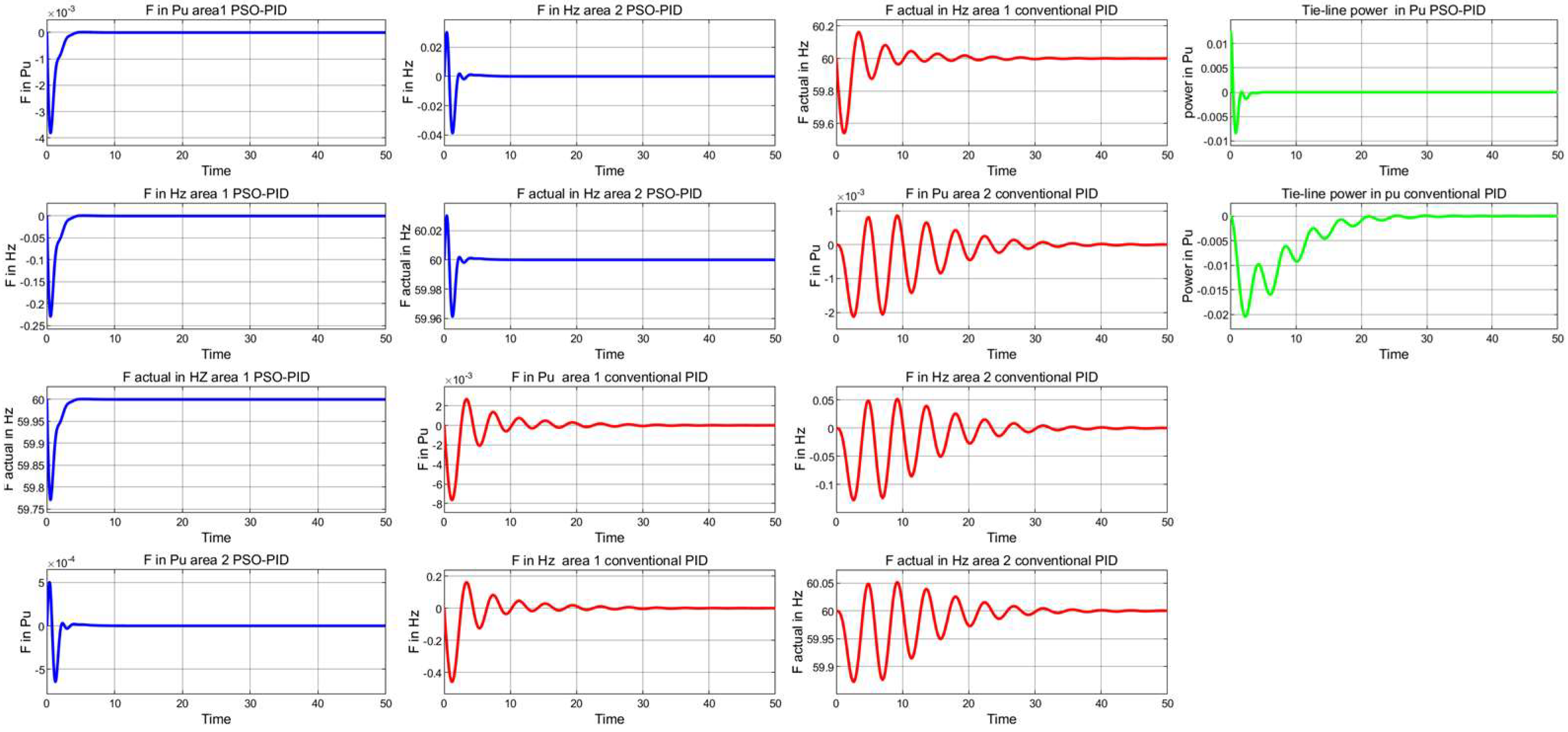
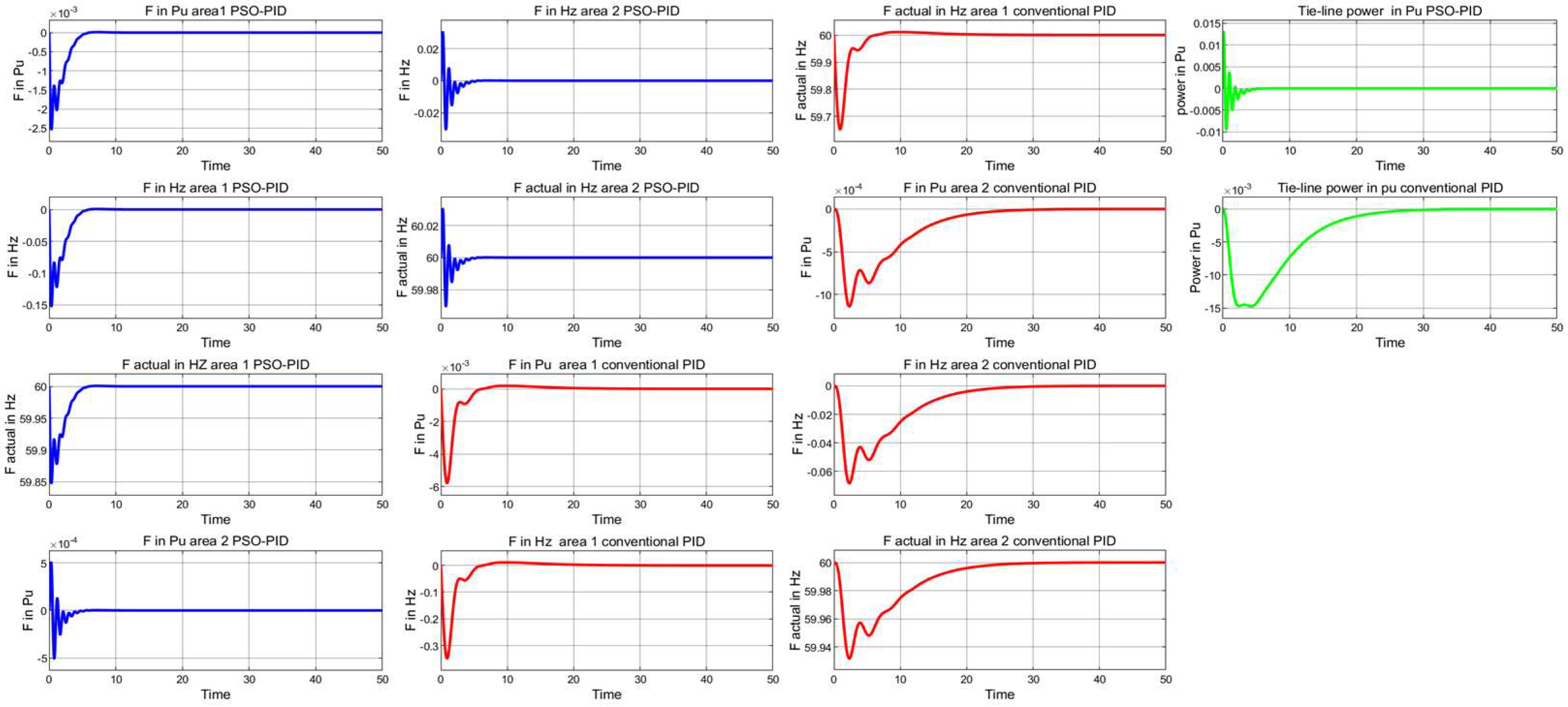
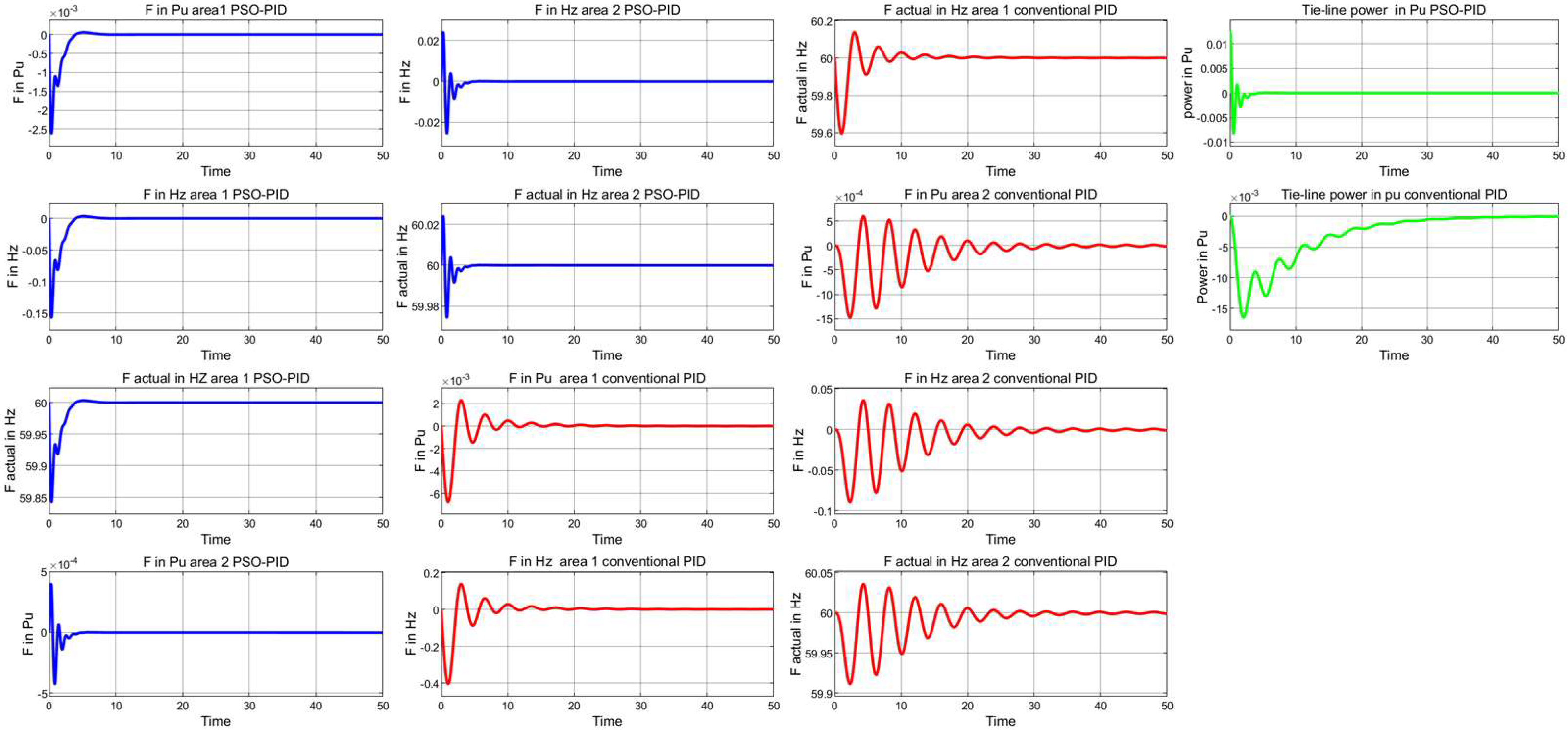
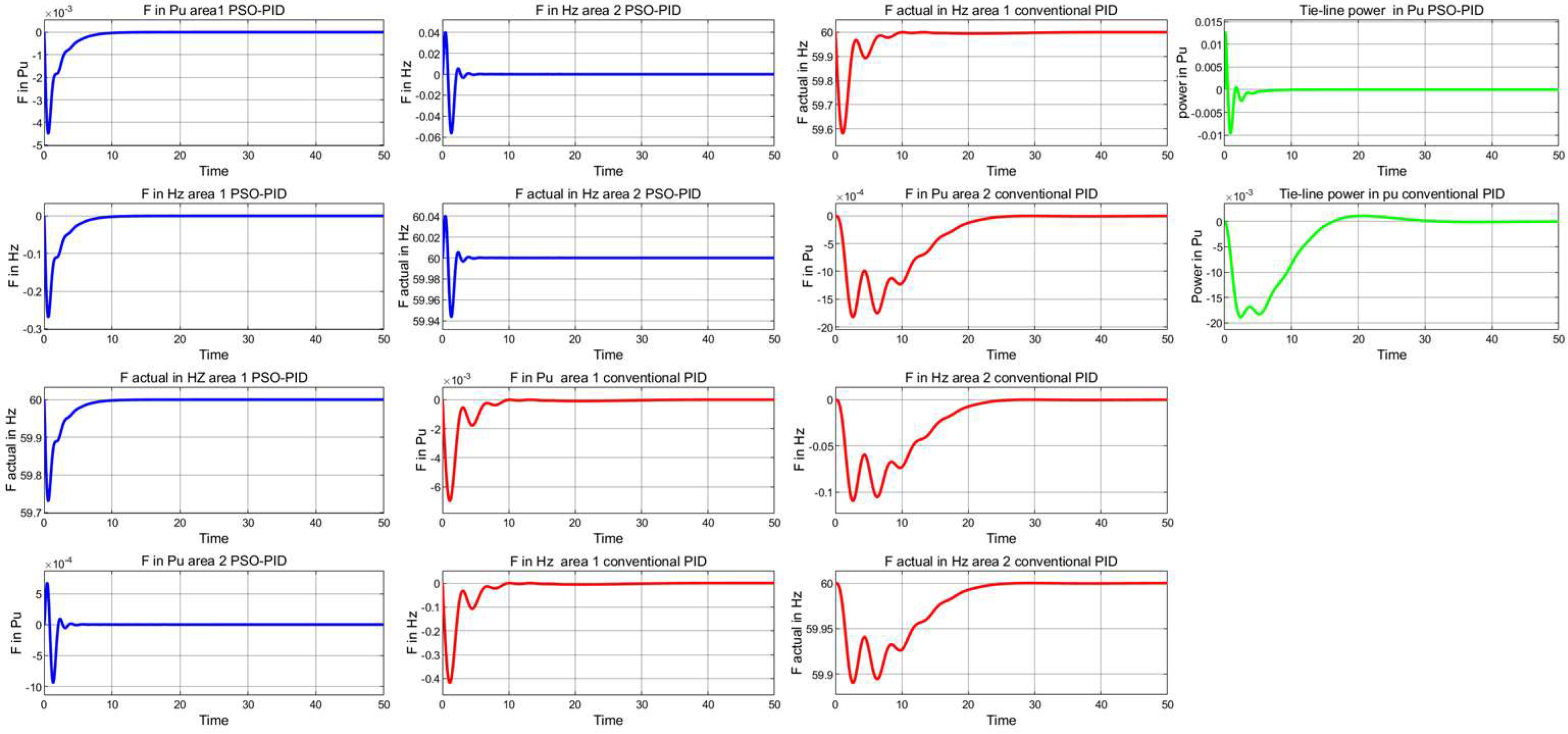
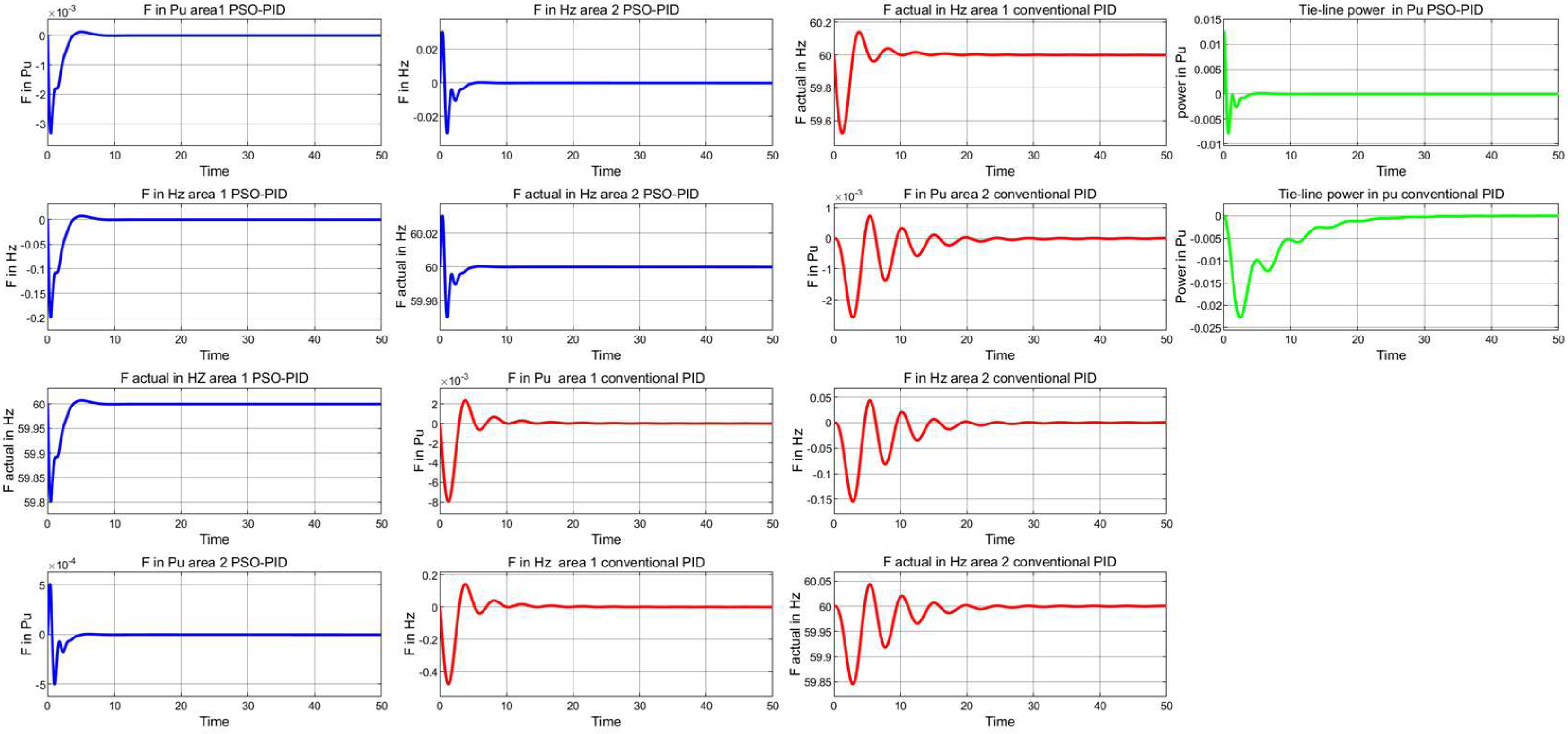
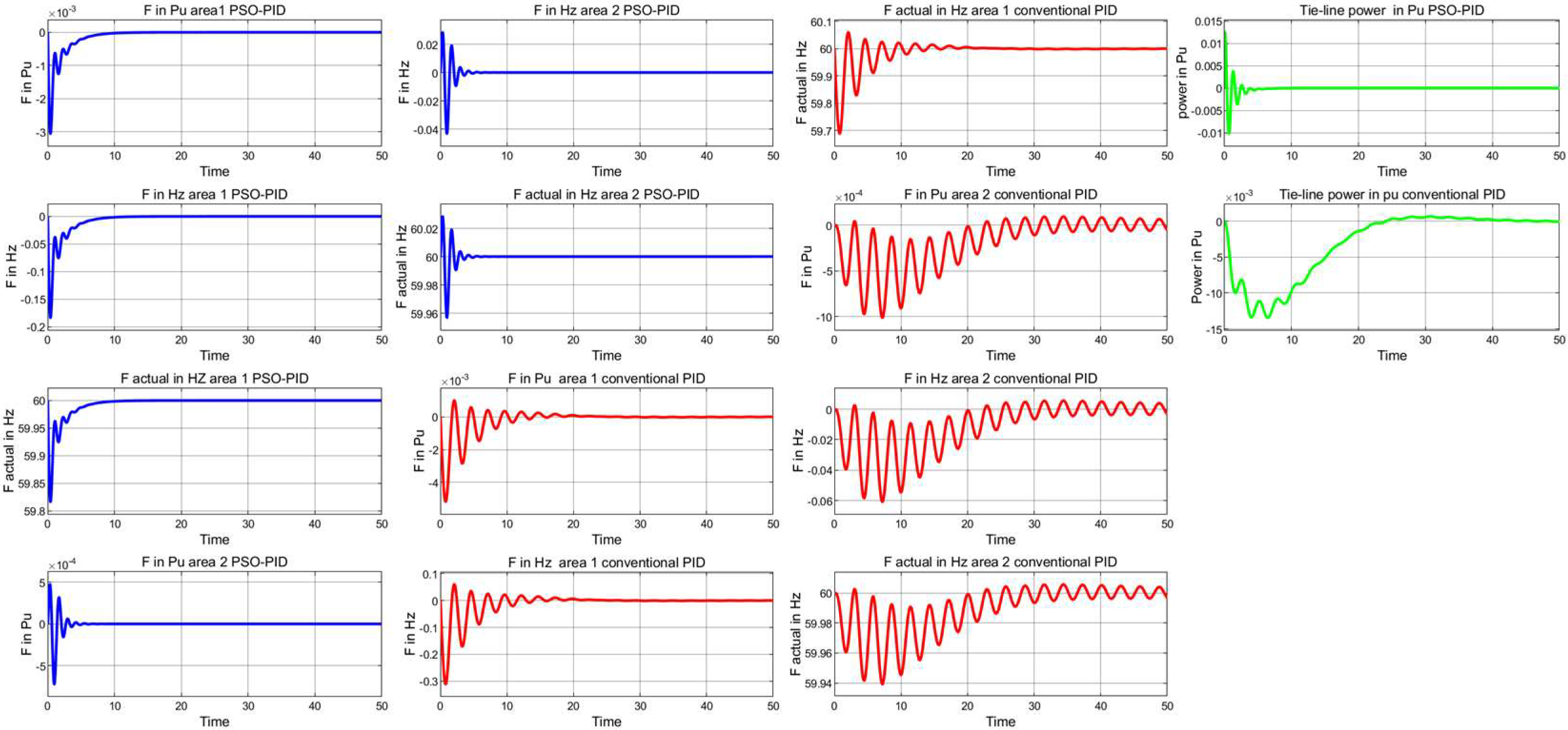
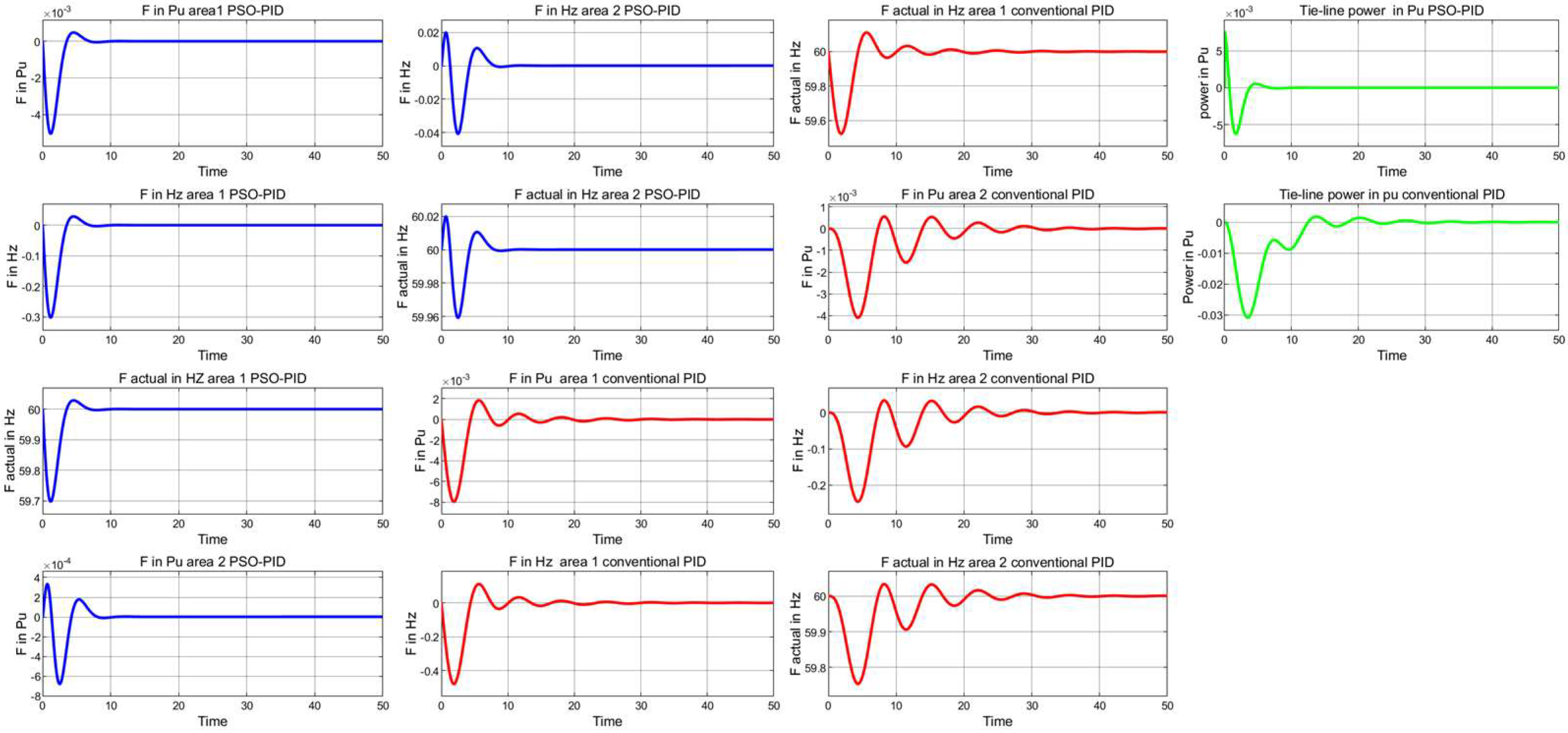
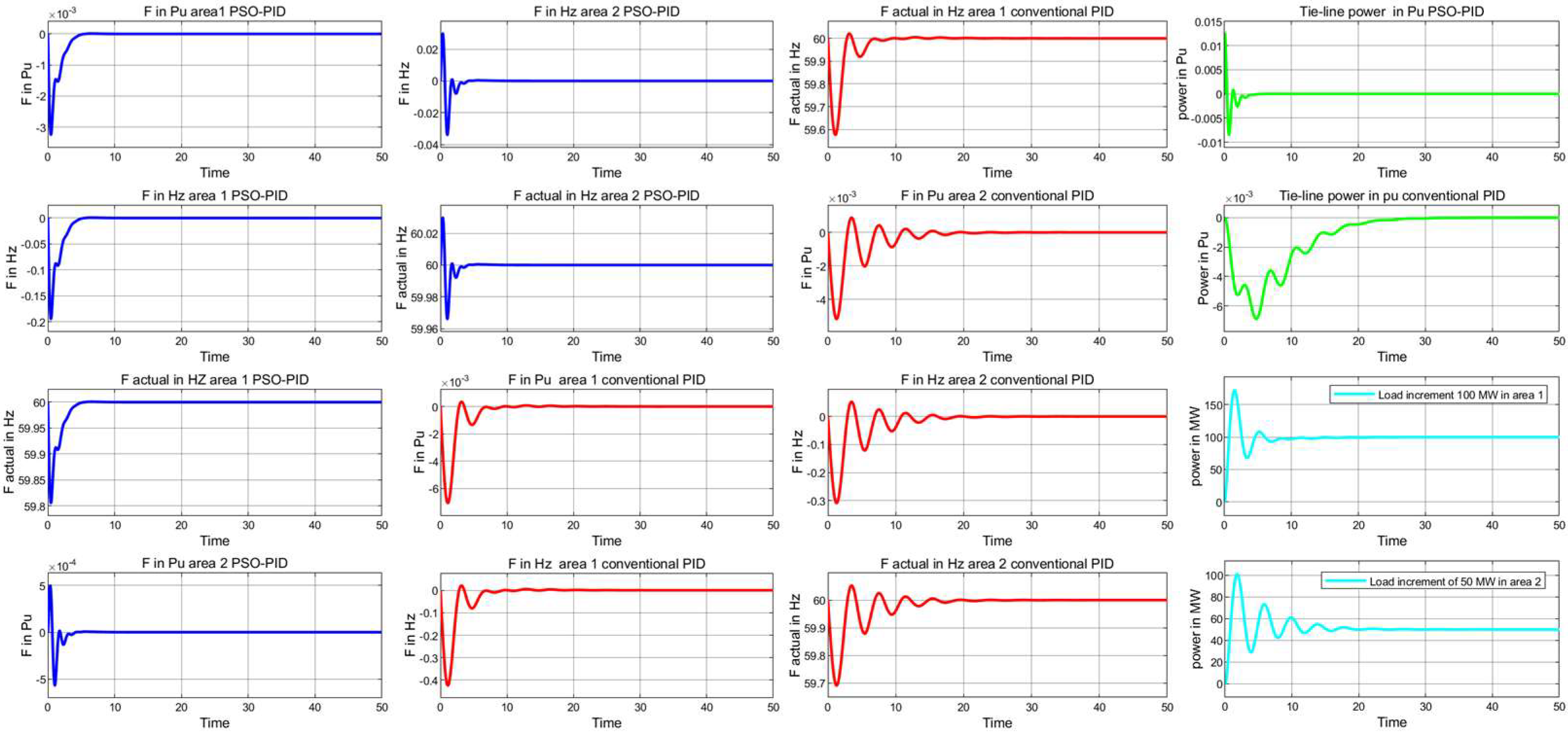
4.2. Two-Area Tie-Line Interconnected Power System
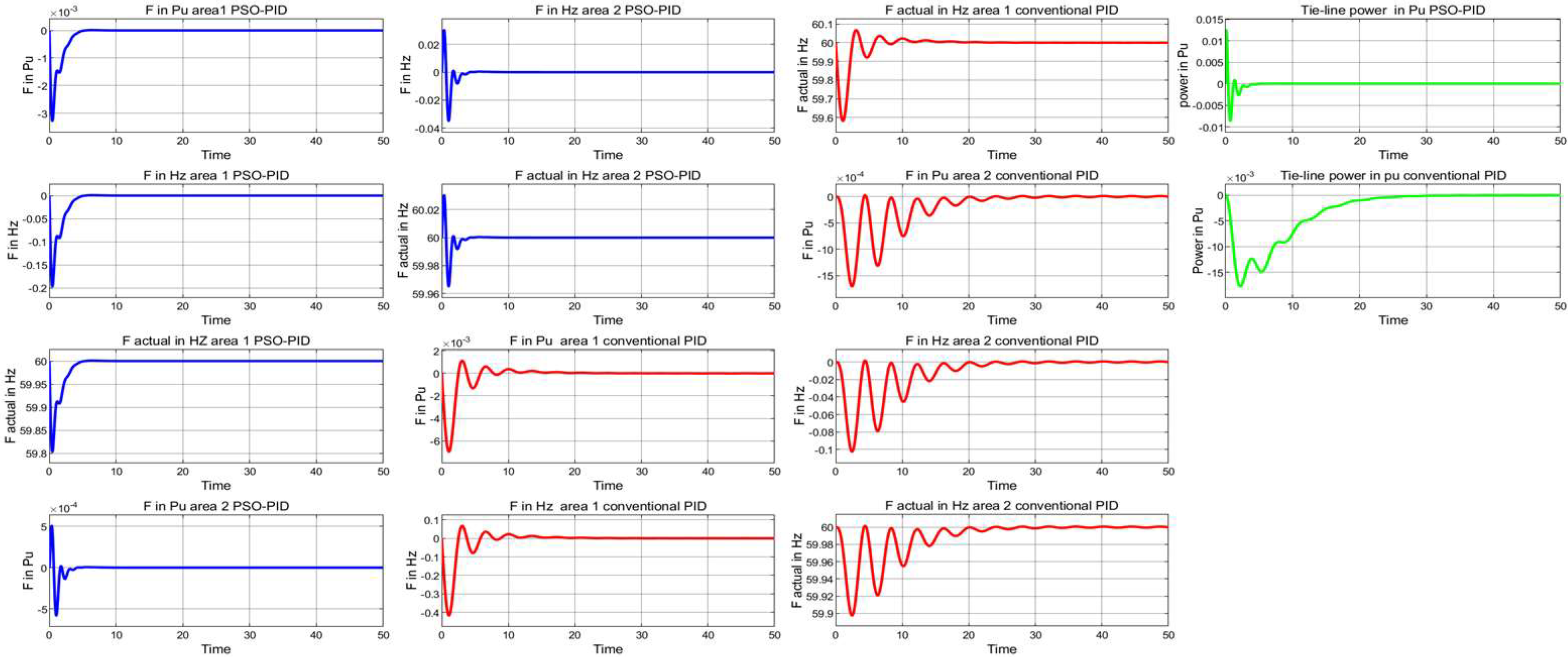
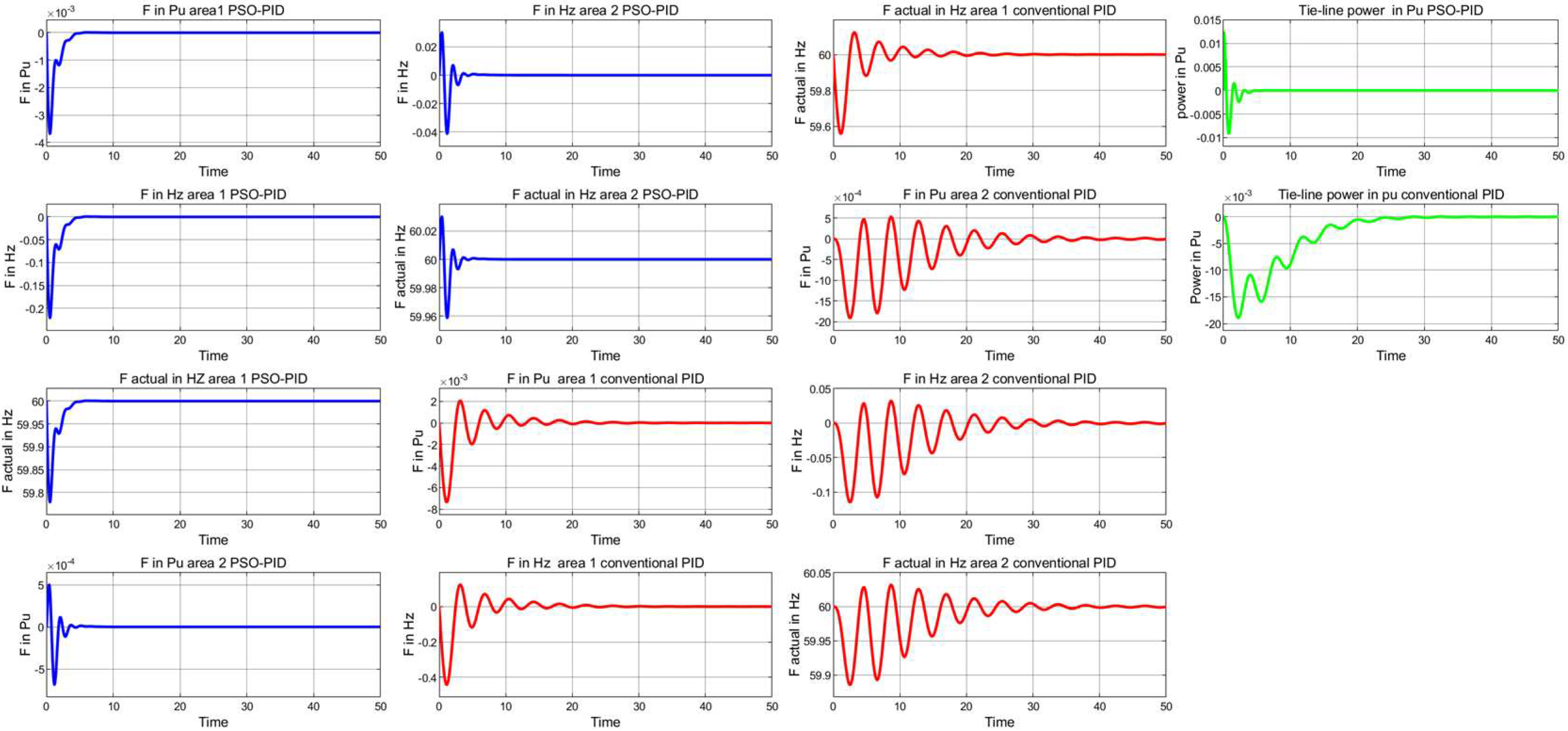
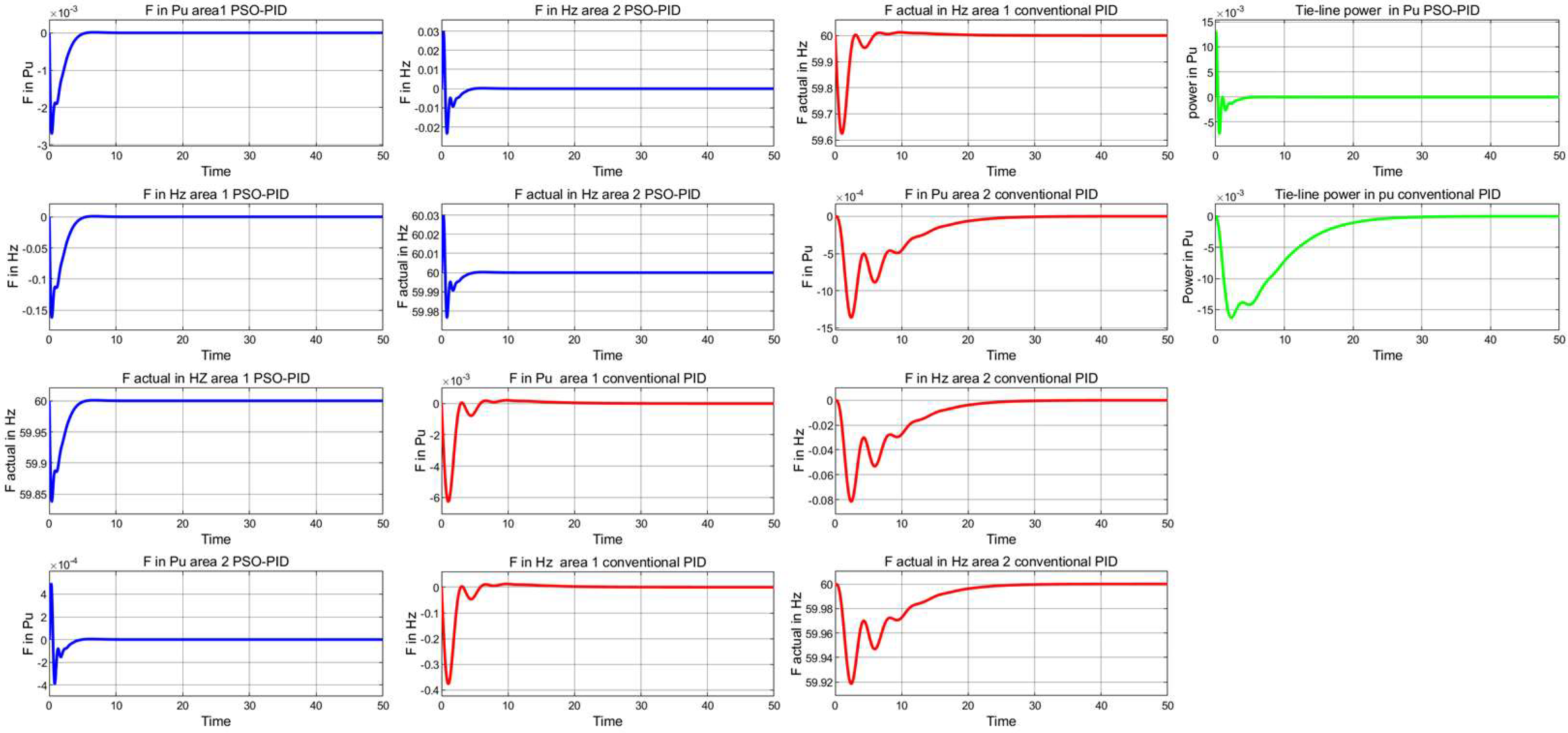
4.2.1. Robustness Evaluations (Case Study 1)
4.2.2. Load Variations (Case Study 2)
5. Conclusions and Future Directions
5.1. Conclusions
5.2. Future Directions
- Renewable energy: a number of previously unusable renewable energy sources have gradually been produced for power systems as a result of ongoing research into renewable energy. The power system’s connected renewable energy sources have a variety of power outputs, which adds uncertainty and complexity to the fluctuation of power generation. This poses difficulties for LFC power systems that are combined with RESs in terms of stabilization. Furthermore, integrating various renewable energy sources necessitates the employment of additional electrical equipment. LFC power systems will inevitably have obstacles related to ensuring device matching, efficient information transfer, and other matters.
- Flexibility: Since renewable energy sources require significant penetration and networking requirements, an extremely flexible and secure integrated power system is required. A higher percentage of RESs can facilitate the transformation of the current energy production mix. This will increase the flexibility and dependability of multi-area power systems and lead to the creation of new intelligent algorithms for control, storage, and market strategies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RESs | Renewable energy sources |
| LFC | Load frequency control |
| IPS | Interconnected power system |
| HC | Hill climbing |
| GA | Genetic algorithm |
| ACO | Ant colony optimization |
| PV | Photovoltaic |
| MARL | Multi-agent reinforcement learning |
| FPA | Flower pollination algorithm |
| FOFPID | Fractional order fuzzy PID |
| ARA | Artificial rabbits algorithm |
| MAPS | Multi-area power systems |
| BESSO | Bald eagle sparrow search optimization |
| BBO | Biogeography-based optimization |
| GBO | Gradient-based optimizer |
| TID | Tilt integral derivative |
| AGC | Automatic generation control |
| R | Governor speed droop characteristics |
| H | Inertia constant |
| D | Coefficient of damping |
| ACE | Area control error |
| ΔPD | Power change in the demand |
| B | Factor of frequency bias |
| u | Input for governor control |
| Tg | Constant governor time |
| ΔPg | Variations in the governor’s valve position |
| Tt | Constant turbine time |
| WTG | Wind turbine generator |
| ΔPL | Changes in load power |
| ΔPm | Changes in mechanical power |
| ΔPt | Variations in turbine output power |
| KP, KI & KD | PID controller gains |
| Δf | Change in system frequency |
| ΔPtie | Tie-line power change |
| a12 | Constant |
Appendix A
| System Parameter | Parameter Value |
|---|---|
| Time Constant Turbine | 0.5 s |
| Time Constant Governor | 0.2 s |
| Generator Constant of Inertia | 5 s |
| Governor’s Speed Regulation | 0.05 per unit |
| Turbine power rating | 250 MW |
| Frequency | 60 hertz |
| Duty ratio D | 0.8 |
Appendix B
| Electrical Characteristics of 1Soltech 1STH-215-P Solar Module | |
|---|---|
| strings in parallel | 50 |
| Modules connected in series for each string | 50 |
| Maximum output power | 213.15 W |
| Voltage of open circuit | 36.3 V |
| Voltage at the point of maximum power | 29 V |
| Coefficient of temperature for open circuit voltage | −0.36099 |
| Each module’s cells | 60 |
| Current on short circuit | 7.84 A |
| Current at the point of maximum power | 7.35 A |
| Temperature coefficient | 0.102 |
| Specified temperature | 25 °C, 1000 (W/m2) |
| Ideality factor of diode | 0.98117 |
| Resistance of shunt | 313.3991 Ohms |
| resistance in series | 0.39383 Ohms |
| PMSG wind turbine specifications | |
| The mechanical output power nominally | 100 Kw |
| The electrical generator’s base power | 100 Kw/0.9 |
| Maximum power (Pu of nominal mechanical power) at base wind speed | 0.85 |
| Rotational base speed (Pu of the generator speed at base) | 1.2 |
| PMSG’s stator phase resistance | 0.0485 ohms |
| Wind speed | 12 m/s |
| Fuel cell parameters | |
| Function 1: 1.36908036 atomic mass units | 60,000 × 8.3145 × (273 + 95) × 400 × u (1)/(2 × 96,485 × (3 × 101,325) × 0.919 × 0.995) |
| Function 2: 5.89420573 atomic mass units | 60,000 × 8.3145 × (273 + 95) × 400 × u (1)/(4 × 96,485 × (3 × 101,325) × 0.5057 × 0.21) |
| Stack power (Watts) | 25,200 |
| Fuel cell resistance (ohms) | 4.2142 |
| Nerst voltage of one cell (V) | 0.9835 |
| Exchange current (A) | 0.27591 |
| Exchange coefficient | 0.78812 |
| System temperature (K) | 1133 |
| Fuel supply pressure (bar) | 1.2 |
| Air supply pressure (bar) | 1 |
Appendix C
| Operator | Operator Value |
|---|---|
| Solver | ode23s (stiff/Mod.Rosenbrock) |
| Fitness function | ITAE |
| Number of variables | 3 |
| Number of iterations | 100 |
| Number of particles | 15 |
| Limit | 0.1000 |
| c1= c2 | 2 |
| wmax | 1 |
| wmin | 0.1 |
Appendix D
| System Parameters | Area 1 | Area 2 |
|---|---|---|
| Speed regulation R | 0.05 | 0.0625 |
| Duty ratio D | 0.6 | 0.9 |
| Inertia constant H | 5 | 4 |
| Base power | 1000 MVA | 1000 MVA |
| Gt | 0.2 s | 0.3 s |
| Tt | 0.5 s | 0.6 s |
Appendix E
| Operator | Operator Value |
|---|---|
| Solver | ode23s (stiff/Mod.Rosenbrock) |
| Fitness function | ITAE |
| Number of variables | 9 |
| Number of iterations | 100 |
| Number of particles | 15 |
| Limit | 0.1000 |
| c1= c2 | 2 |
| wmax | 1 |
| wmin | 0.1 |
References
- Arya, Y.; Dahiya, P.; Çelik, E.; Sharma, G.; Gözde, H.; Nasiruddin, I. AGC performance amelioration in multi-area interconnected thermal and thermal-hydro-gas power systems using a novel controller. Eng. Sci. Technol. Int. J. 2021, 24, 384–396. [Google Scholar] [CrossRef]
- Elkasem, A.H.; Khamies, M.; Hassan, M.H.; Agwa, A.M.; Kamel, S. Optimal design of TD-TI controller for LFC considering renewables penetration by an improved chaos game optimizer. Fractal Fract. 2022, 6, 220. [Google Scholar] [CrossRef]
- Ameli, A.; Hooshyar, A.; El-Saadany, E.F.; Youssef, A.M. Attack detection and identification for automatic generation control systems. IEEE Trans. Power Syst. 2018, 33, 4760–4774. [Google Scholar] [CrossRef]
- Mohammadikia, R.; Aliasghary, M. A fractional order fuzzy PID for load frequency control of four-area interconnected power system using biogeography-based optimization. Int. Trans. Electr. Energy Syst. 2019, 29, e2735. [Google Scholar] [CrossRef]
- Ali, T.; Malik, S.A.; Hameed, I.A.; Daraz, A.; Mujlid, H.; Azar, A.T. Load frequency control and automatic voltage regulation in a multi-area interconnected power system using nature-inspired computation-based control methodology. Sustainability 2022, 14, 12162. [Google Scholar] [CrossRef]
- Ali, T.; Malik, S.A.; Daraz, A.; Aslam, S.; Alkhalifah, T. Dandelion optimizer-based combined automatic voltage regulation and load frequency control in a multi-area, multi-source interconnected power system with nonlinearities. Energies 2022, 15, 8499. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Particle swarm optimisation-based parameters optimisation of PID controller for load frequency control of multi-area reheat thermal power systems. Int. J. Adv. Intell. Paradig. 2017, 9, 464–489. [Google Scholar] [CrossRef]
- Dhanasekaran, B.; Siddhan, S.; Kaliannan, J. Ant colony optimization technique tuned controller for frequency regulation of single area nuclear power generating system. Microprocess. Microsyst. 2020, 73, 102953. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Al-Gahtani, S.F. Fractional. Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems. Fractal Fract. 2023, 7, 97. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.-G. Design of cascaded controller based on coyote optimizer for load frequency control in multi-area power systems with renewable sources. Control Eng. Pract. 2022, 121, 105058. [Google Scholar] [CrossRef]
- Alayi, R.; Zishan, F.; Seyednouri, S.R.; Kumar, R.; Ahmadi, M.H.; Sharifpur, M. Optimal load frequency control of island microgrids via a PID controller in the presence of wind turbine and PV. Sustainability 2021, 13, 10728. [Google Scholar] [CrossRef]
- Vedik, B.; Kumar, R.; Deshmukh, R.; Verma, S.; Shiva, C.K. Renewable energy-based load frequency stabilization of interconnected power systems using quasi-oppositional dragonfly algorithm. J. Control Autom. Electr. Syst. 2021, 32, 227–243. [Google Scholar] [CrossRef]
- Mohanty, B.; Panda, S.; Hota, P. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2014, 54, 77–85. [Google Scholar] [CrossRef]
- Panwar, A.; Sharma, G.; Bansal, R.C. Optimal AGC design for a hybrid power system using hybrid bacteria foraging optimization algorithm. Electr. Power Compon. Syst. 2019, 47, 955–965. [Google Scholar] [CrossRef]
- Bharti, K.K.; Singh, V.P.; Singh, S. PSO-based: MARL approach for frequency regulation of multi-area power system. J. Electr. Eng. Technol. 2020, 15, 1529–1539. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N.; Santhi, V.; Ashour, A.S.; Balas, V.E. Application of flower pollination algorithm in load frequency control of multi-area interconnected power system with nonlinearity. Neural Comput. Appl. 2017, 28, 475–488. [Google Scholar] [CrossRef]
- Kumarakrishnan, V.; Vijayakumar, G.; Boopathi, D.; Jagatheesan, K.; Saravanan, S.; Anand, B. Optimized PSO technique based PID controller for load frequency control of single area power system. Solid State Technol. 2020, 63, 7979–7990. [Google Scholar]
- Gupta, D.K.; Jha, A.V.; Appasani, B.; Srinivasulu, A.; Bizon, N.; Thounthong, P. Load frequency control using hybrid intelligent optimization technique for multi-source power systems. Energies 2021, 14, 1581. [Google Scholar] [CrossRef]
- Ram Babu, N.; Bhagat, S.K.; Saikia, L.C.; Chiranjeevi, T.; Devarapalli, R.; García Márquez, F.P. A comprehensive review of recent strategies on automatic generation control/load frequency control in power systems. Arch. Comput. Methods Eng. 2023, 30, 543–572. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Davoodkhani, I.F.; Kamyab, H.; Ali, R.R. Load-frequency control in an islanded microgrid PV/WT/FC/ESS using an optimal self-tuning fractional-order fuzzy controller. Environ. Sci. Pollut. Res. 2023, 30, 71677–71688. [Google Scholar] [CrossRef]
- Hu, C.; Bi, L.; Piao, Z.; Wen, C.; Hou, L. Coordinative optimization control of microgrid based on model predictive control. Int. J. Ambient. Comput. Intell. 2018, 9, 57–75. [Google Scholar] [CrossRef]
- Bhattacharya, H.; Chattopadhyay, S.; Chattopadhyay, M.; Banerjee, A. Storage and bandwidth optimized reliable distributed data allocation algorithm. Int. J. Ambient. Comput. Intell. 2019, 10, 78–95. [Google Scholar] [CrossRef]
- Choudhary, R.; Rai, J.; Arya, Y. Automatic generation control for single area power system using GNA tuned PID controller. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1478, p. 012011. [Google Scholar]
- Raj, T.D.; Kumar, C.; Kotsampopoulos, P.; Fayek, H.H. Load Frequency Control in Two-Area Multi-Source Power System Using Bald Eagle-Sparrow Search Optimization Tuned PID Controller. Energies 2023, 16, 2014. [Google Scholar] [CrossRef]
- Dhanasekaran, B.; Kaliannan, J.; Baskaran, A.; Dey, N.; Tavares, J.M.R. Load Frequency Control Assessment of a PSO-PID Controller for a Standalone Multi-Source Power System. Technologies 2023, 11, 22. [Google Scholar] [CrossRef]
- Ali, T.; Malik, S.A.; Daraz, A.; Adeel, M.; Aslam, S.; Herodotou, H. Load frequency control and automatic voltage regulation in four-area interconnected power systems using a gradient-based optimizer. Energies 2023, 16, 2086. [Google Scholar] [CrossRef]
- Debnath, M.K.; Agrawal, R.; Tripathy, S.R.; Choudhury, S. Artificial neural network tuned PID controller for LFC investigation including distributed generation. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2740. [Google Scholar] [CrossRef]
- Kumarakrishnan, V.; Vijayakumar, G.; Jagatheesan, K.; Boopathi, D.; Anand, B.; Kanendra Naidu, V. PSO optimum design-PID controller for frequency management of single area multi-source power generating system. In Contemporary Issues in Communication, Cloud and Big Data Analytics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 373–383. [Google Scholar]
- Wang, Z.; Liu, Y.; Yang, Z.; Yang, W. Load frequency control of multi-region interconnected power systems with wind power and electric vehicles based on sliding mode control. Energies 2021, 14, 2288. [Google Scholar] [CrossRef]
- Eisa, S.A. Modeling dynamics and control of type-3 DFIG wind turbines: Stability, Q Droop function, control limits and extreme scenarios simulation. Electr. Power Syst. Res. 2019, 166, 29–42. [Google Scholar] [CrossRef]
- Eisa, S.A.; Wedeward, K.; Stone, W. Wind turbines control system: Nonlinear modeling, simulation, two and three time scale approximations, and data validation. Int. J. Dyn. Control. 2018, 6, 1776–1798. [Google Scholar] [CrossRef]
- Eisa, S.A. Nonlinear modeling, analysis and simulation of wind turbine control system with and without pitch control as in industry. In Advanced Control and Optimization Paradigms for Wind Energy Systems. Power Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–40. [Google Scholar]
- Sobhy, M.A.; Abdelaziz, A.Y.; Hasanien, H.M.; Ezzat, M. Marine predators algorithm for load frequency control of modern interconnected power systems including renewable energy sources and energy storage units. Ain Shams Eng. J. 2021, 12, 3843–3857. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M. A novel deep reinforcement learning controller based type-II fuzzy system: Frequency regulation in microgrids. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 5, 689–699. [Google Scholar] [CrossRef]
- Ginidi, A.; Ghoneim, S.M.; Elsayed, A.; El-Sehiemy, R.; Shaheen, A.; El-Fergany, A. Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 2021, 13, 9459. [Google Scholar] [CrossRef]
- Kouba, N.E.Y.; Menaa, M.; Hasni, M.; Boudour, M. LFC enhancement concerning large wind power integration using new optimised PID controller and RFBs. IET Gener. Transm. Distrib. 2016, 10, 4065–4077. [Google Scholar] [CrossRef]






| Technique for Optimization/Secondary Controller | Power Source | Work | Reference |
|---|---|---|---|
| PSO/PID | Generating source thermal | Compared outcomes with GA and HC | [7] |
| ARA/PID | Two-area non-reheat thermal systems | Compared results with PSO, DE, JAYA optimizer | [9] |
| GA/PID | Source of thermal generation | Performance of PI and PID with and without GRC | [23] |
| BESSO/PID | Hydro, Gas, and thermal | Analyzed the controller efficacy and compared the findings with conventional PID controller | [24] |
| PSO/PID | Thermal, Hydro, and Gas | Results compared with DE and GA | [25] |
| DE/PID | Thermal, Hydro, and Gas | Analyzed controller efficiency utilizing I, PI, and PID | [13] |
| HBFOA/PID | Thermal and PV | PSO and BFO results examined | [14] |
| GBO/PID | Gas, Thermal, Hydro, Solar, and Wind | Results compared with GBO-I-PD, GBO-TID, and GBO-I-P | [26] |
| ANN/PID | Distributed power sources (WTG, DEG, AE, FC) | The superiority of the proposed approach was achieved by applying the Grasshopper optimization algorithm. | [27] |
| PSO/PID | PV, Nuclear, Hydro, Gas, and Thermal | Comparison of PSO-PID and ordinary PID controller outcomes | [17] |
| PSO/PID | Thermal, Solar, and Wind | Performance comparison of standard I, PI, and PID controllers | [28] |
| ΔVpv × (o/p) | ΔVpv(i/p) | |||||
|---|---|---|---|---|---|---|
| ΔPpv(i/p) | NB | NS | ZE | PS | PB | |
| NB | PS | PB | NB | NB | NS | |
| NS | PS | PS | NS | NS | NS | |
| ZE | ZE | ZE | ZE | ZE | ZE | |
| PS | NS | NS | PS | PS | PS | |
| PB | NS | NB | PB | PB | PS | |
| Input/Output | No. of Membership Function | Range of Membership Function | Type of Membership Function |
|---|---|---|---|
| Input 1 | 5 membership functions | Range (−8.5 to 8.5) | Triangular mf |
| Input 2 | 5 membership functions | Range (−1.6 to 1.6) | Triangular mf |
| Output | 5 membership functions | Range (−1.6 to 1.6) | Triangular mf |
| PID Gain Parameters | KP | KI | KD |
| Conventional-PID | 10 | 30 | 50 |
| PSO-PID | 2 | 1 | 1 |
| Area 1 | Area 2 | Tie-Line | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PSO-PID | P | I | D | P | I | D | P | I | D |
| 0.80744 | 0.78184 | −0.33167 | 0.39749 | −0.604380 | −0.938918 | 0.48814 | 4.40 × 10−05 | −0.040155 |
| Scenarios | Specifications | Value at Nominal | Range of Variation | New Value after Variation |
|---|---|---|---|---|
| Scenario 1 | Tg | 0.2 | +50% | 0.3 |
| H | 5 | +50% | 10 | |
| D | 0.8 | −50% | 0.4 | |
| R | 0.05 | −50% | 0.025 | |
| Scenario 2 | Tg | 0.2 | −50% | 0.1 |
| H | 5 | −50% | 2.5 | |
| D | 0.8 | +50% | 1.2 | |
| R | 0.05 | +50% | 0.075 |
| Frequency Responses | |||||||
|---|---|---|---|---|---|---|---|
| Controller | Undershoot % | Overshoot % | Settling Time s | Fall Time ms | Error | Pre-Shoot % | High/Low Hz |
| Conventional PID | 0.505 | 1.576 | 6 | 327.339 | 0.2797 | 0.241 | 60/59.65 |
| PSO-PID | 0.505 | −0.505 | 0.0075 | 16.962 | 0.0008 | −0.11 | 60/59.98 |
| Scenario 1 | |||||||
| PSO-PID | 0.532 | −0.532 | 0.0085 | 16.869 | 0.0211 | 0.033 | 60/59.99 |
| Conventional PID | 0.505 | 1.735 | 3.3 | 370.198 | 0.2525 | 0.291 | 60/59.80 |
| Scenario 2 | |||||||
| PSO-PID | 0.505 | −0.505 | 0.0079 | 14.777 | 0.0005 | 0.039 | 60/59.97 |
| Conventional PID | 42.143 | 0.325 | 4.2 | 128.502 | 0.3004 | 0.640 | 60/59.67 |
| Case Number | Parameters | Nominal Values | Variation Range | New Values | ||
|---|---|---|---|---|---|---|
| Area 1 | Area 2 | Area 1 | Area 2 | |||
| 1 | H | 5 | 4 | +50% | 7.5 | 6 |
| 2 | H | 5 | 4 | −50% | 2.5 | 2 |
| 3 | Tt | 0.5 | 0.6 | +50% | 0.75 | 0.9 |
| 4 | Tt | 0.5 | 0.6 | −50% | 0.25 | 0.3 |
| 5 | B | 20.6 | 16.9 | +50% | 30.9 | 25.35 |
| 6 | B | 20.6 | 16.9 | −50% | 10.3 | 8.45 |
| 7 | D | 0.6 | 0.9 | +50% | 0.9 | 1.35 |
| 8 | D | 0.6 | 0.9 | −50% | 0.3 | 0.45 |
| 9 | Tg | 0.2 | 0.3 | +50% | 0.3 | 0.45 |
| 10 | Tg | 0.2 | 0.3 | −50% | 0.1 | 0.15 |
| 11 | R | 0.05 | 0.0625 | +50% | 0.075 | 0.0937 |
| 12 | R | 0.05 | 0.0625 | −50% | 0.025 | 0.0312 |
| 13 | B | 20.6 | 16.9 | −50% | 10.3 | 8.45 |
| H | 5 | 4 | +50% | 7.5 | 6 | |
| R | 0.05 | 0.0625 | +50% | 0.075 | 0.0937 | |
| D | 0.6 | 0.9 | −50% | 0.3 | 0.45 | |
| Tt | 0.5 | 0.6 | +50% | 0.75 | 0.9 | |
| Tg | 0.2 | 0.3 | +50% | 0.3 | 0.45 | |
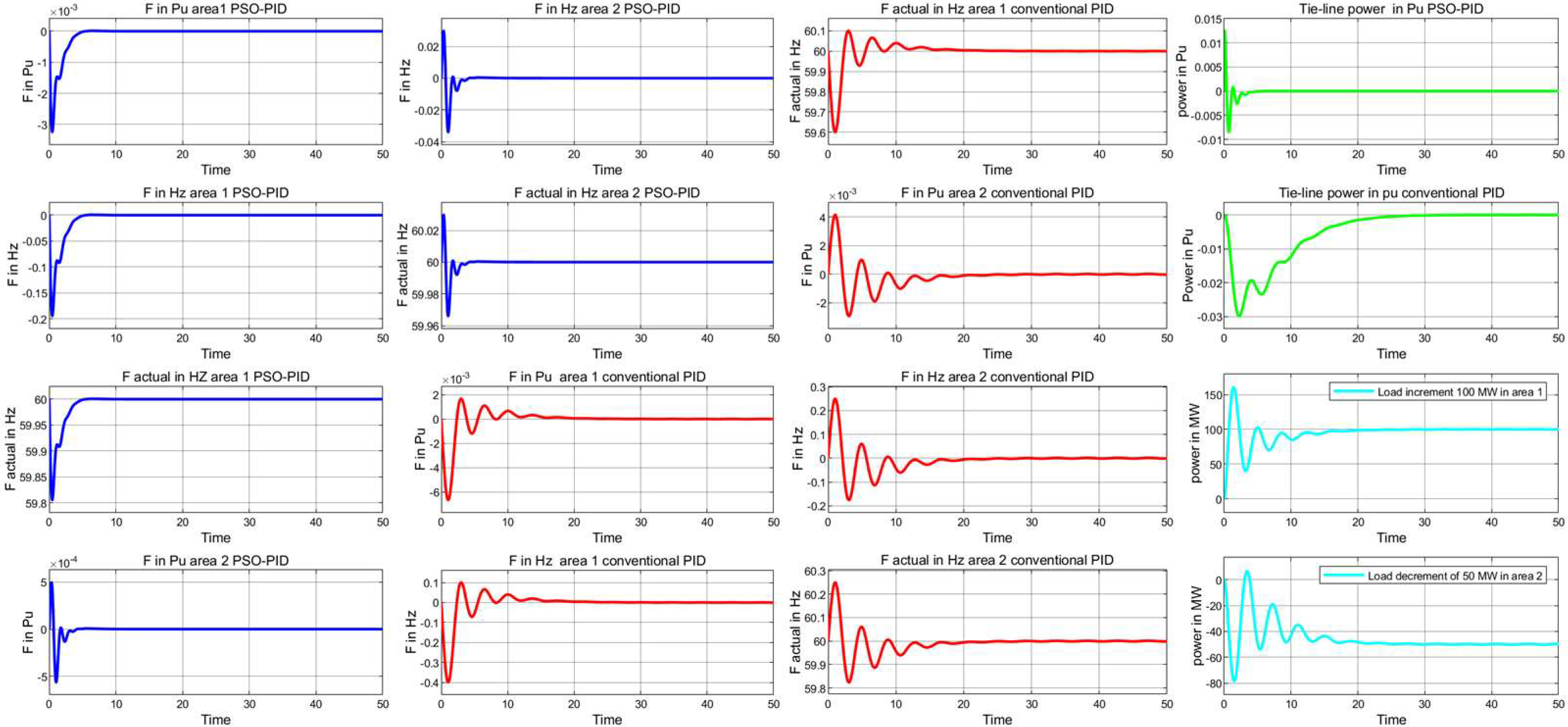
| Frequency Responses Area 1 | Frequency Responses Area 2 | Tie-Line Power (Pu) Response | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Controller | Ush % | Osh % | Psh % | H/L Hz | Ush % | Osh % | Psh % | H/L Hz | Ush % | Osh % | Psh % | Fall Time ms |
| PSO-PID | 0.50 | 1.05 | 0.11 | 60/59.81 | 137.04 | −5.31 | 74.56 | 60/60 | 68.64 | −7.40 | 0.84 | 207.96 |
| Conventional PID | 0.57 | 1.82 | −0.11 | 60/59.59 | 50.75 | 92.90 | 0.11 | 60/59.94 | 36.30 | 2.16 | 0.61 | 895.73 |
| Case no 1 | ||||||||||||
| PSO-PID | 7.06 | 0.41 | −0.10 | 60/59.85 | 0.98 | 0.20 | 95.09 | 60/59.98 | 55.46 | 1.19 | 0.78 | 282.64 |
| Conventional PID | 0.54 | 1.76 | 0.23 | 60/59.66 | 91.34 | 1.19 | 0.96 | 60/59.95 | 36.30 | 0.84 | 0.68 | 1147 |
| Case no 2 | ||||||||||||
| PSO-PID | 0.50 | 0.47 | 0.22 | 60/59.79 | 84.47 | −9.47 | 121.58 | 60/59.99 | 74.56 | −9.57 | 0.87 | 190.03 |
| Conventional PID | 0.58 | 1.92 | −0.08 | 60/59.57 | 9.44 | 1.10 | 2.09 | 60/59.92 | 14.36 | 18.65 | 0.48 | 995.140 |
| Case 3 | ||||||||||||
| PSO-PID | 0.50 | 0.42 | 0.11 | 60/59.77 | 0.89 | −0.89 | 77.67 | 60/59.96 | 68.64 | −4.15 | 0.84 | 254.17 |
| Conventional PID | 0.68 | 1.36 | 0.61 | 60/59.54 | 92.47 | −10.13 | 68.85 | 60/59.95 | 0.50 | 0.82 | −0.01 | 1328 |
| Case 4 | ||||||||||||
| PSO-PID | 25.94 | 21.43 | −0.04 | 60/59.88 | 163.21 | −163.21 | 509.89 | 60/60 | 74.56 | 1.54 | 0.87 | 146.19 |
| Conventional PID | 1.79 | 0.50 | 0.50 | 60/59.65 | 0.50 | 1.28 | 0.50 | 60/59.93 | 0.50 | 1.70 | 0.50 | 1272 |
| Case 5 | ||||||||||||
| PSO-PID | 95 | −6.87 | 0.68 | 60/59.92 | 172.88 | −17.26 | 97.62 | 60/60 | 68.64 | 0.08 | 68.64 | 173.81 |
| Conventional PID | 0.67 | 1.02 | 0.09 | 60/59.60 | 94.88 | −7.71 | 59.20 | 60/59.96 | 95.09 | −4.11 | 0.98 | 652.40 |
| Case 6 | ||||||||||||
| PSO-PID | 0.50 | 1.13 | 0.50 | 60/59.73 | 0.86 | 1.74 | 71.55 | 60/59.94 | 77.67 | −0.94 | 0.89 | 258.51 |
| Conventional PID | 0.50 | 1.11 | 0.50 | 60/59.58 | 84.25 | −5.33 | 0.92 | 60/59.94 | 2.71 | 8.20 | −0.073 | 1309 |
| Case 7 | ||||||||||||
| PSO-PID | 0.50 | 0.98 | 0.15 | 60/59.81 | 138.28 | −6.39 | 66.79 | 60/60 | 68.64 | −8.45 | 0.84 | 206.75 |
| Conventional PID | 0.56 | 1.78 | 0.23 | 60/59.60 | 0.50 | 1.12 | 0.16 | 60/59.91 | 32.66 | 1.85 | 0.61 | 917.64 |
| Case 8 | ||||||||||||
| PSO-PID | 0.50 | 1.12 | 0.07 | 60/59.80 | 135.47 | −0.14 | 82.35 | 60/59.99 | 68.64 | −6.32 | 0.84 | 209.14 |
| Conventional PID | 0.58 | 1.88 | −0.49 | 60/59.58 | 0.51 | 1.90 | 0.07 | 60/59.90 | 19.88 | 16.66 | 0.52 | 1010 |
| Case 9 | ||||||||||||
| PSO-PID | 0.50 | 0.48 | 0.13 | 60/59.78 | 93.30 | −28.50 | 143.28 | 60/59.99 | 74.56 | −15.36 | 0.87 | 243.408 |
| Conventional PID | 0.64 | 1.09 | −0.47 | 60/59.56 | 0.64 | 1.89 | −0.59 | 60/59.89 | 19.88 | 31.31 | 0.33 | 1032 |
| Case 10 | ||||||||||||
| PSO-PID | 42.14 | −7.40 | −0.02 | 60/59.89 | 172.68 | −1.07 | 153.10 | 60/60 | 57.93 | −9.67 | 0.79 | 161.879 |
| Conventional PID | 0.52 | 1.75 | 0.27 | 60/59.63 | 57.93 | 35.93 | 0.79 | 60/59.95 | 14.36 | 2.72 | 0.57 | 1071 |
| Case 11 | ||||||||||||
| PSO-PID | 85.75 | −2.87 | −0.19 | 60/59.89 | 97.24 | 0.09 | 40.22 | 60/60 | 63.11 | −3.98 | 0.82 | 214.27 |
| Conventional PID | 0.64 | 1.75 | −0.56 | 60/59.53 | 46.56 | 0.25 | 25.87 | 60/59.92 | 0.50 | 1.89 | 0.46 | 1421 |
| Case 12 | ||||||||||||
| PSO-PID | 25.94 | 0.56 | 0.63 | 60/59.85 | 0.83 | 1.90 | 65.83 | 60/59.96 | 84.25 | −17.73 | 0.92 | 192.19 |
| Conventional PID | 0.60 | 1.17 | 0.39 | 60/59.69 | 44.40 | 12.01 | 3.69 | 60/59.97 | 0.52 | 16.90 | −0.29 | 3132 |
| Case 13 | ||||||||||||
| PSO-PID | 1.66 | 0.98 | −0.14 | 60/59.70 | 0.74 | −0.74 | 48.50 | 60/59.96 | 84.25 | 1.36 | 0.92 | 476.575 |
| Conventional PID | 0.61 | 1.06 | −0.34 | 60/59.53 | 0.57 | 1.18 | 0.54 | 60/59.76 | 0.53 | 0.74 | −0.10 | 2013 |
| Case No | Area 1 | Area 2 |
|---|---|---|
| 1 | 100 MW increment | - |
| 2 | 100 MW increment | 50 MW increment |
| 3 | 100 MW increment | 50 MW decrement |
| Frequency Responses Area 1 | Frequency Responses Area 2 | Tie-Line Power (Pu) Response | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Controller | Ush % | Osh % | Psh % | H/L Hz | Ush % | Osh % | Psh % | H/L Hz | Ush % | Osh % | Psh % | Fall Time ms |
| Case no 1 | ||||||||||||
| PSO-PID | 0.50 | 1.05 | 0.11 | 60/59.81 | 137.04 | −5.31 | 74.56 | 60/60 | 68.64 | −7.40 | 0.84 | 207.96 |
| Conventional PID | 0.57 | 1.82 | −0.11 | 60/59.59 | 50.75 | 92.90 | 0.11 | 60/59.94 | 36.30 | 2.16 | 0.61 | 895.73 |
| Case no 2 | ||||||||||||
| PSO-PID | 0.50 | 1.05 | 0.11 | 60/59.81 | 137.04 | −5.31 | 74.56 | 60/60 | 68.64 | −7.40 | 0.84 | 207.96 |
| Conventional PID | 0.57 | 1.82 | −0.11 | 60/59.80 | 50.75 | 92.90 | 0.11 | 60/59.97 | 36.30 | 2.16 | 0.61 | 895.73 |
| Case 3 | ||||||||||||
| PSO-PID | 0.50 | 1.05 | 0.11 | 60/59.81 | 137.04 | −5.31 | 74.56 | 60/60 | 68.64 | −7.40 | 0.84 | 207.96 |
| Conventional PID | 14.36 | 18.69 | 0.57 | 60.2/60 | 0.71 | 2.37 | 50.75 | 60/60.03 | 2.16 | 36.30 | 0.61 | 897.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Younis, W.; Wang, Y.; Georgievitch, P.M. A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization. Energies 2024, 17, 517. https://doi.org/10.3390/en17020517
Qu Z, Younis W, Wang Y, Georgievitch PM. A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization. Energies. 2024; 17(2):517. https://doi.org/10.3390/en17020517
Chicago/Turabian StyleQu, Zhengwei, Waqar Younis, Yunjing Wang, and Popov Maxim Georgievitch. 2024. "A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization" Energies 17, no. 2: 517. https://doi.org/10.3390/en17020517
APA StyleQu, Z., Younis, W., Wang, Y., & Georgievitch, P. M. (2024). A Multi-Source Power System’s Load Frequency Control Utilizing Particle Swarm Optimization. Energies, 17(2), 517. https://doi.org/10.3390/en17020517





