A Novel Approach to Using Dual-Field Excited Synchronous Generators as Wind Power Generators
Abstract
1. Introduction
2. Modeling of DESG
2.1. Mathematical Model
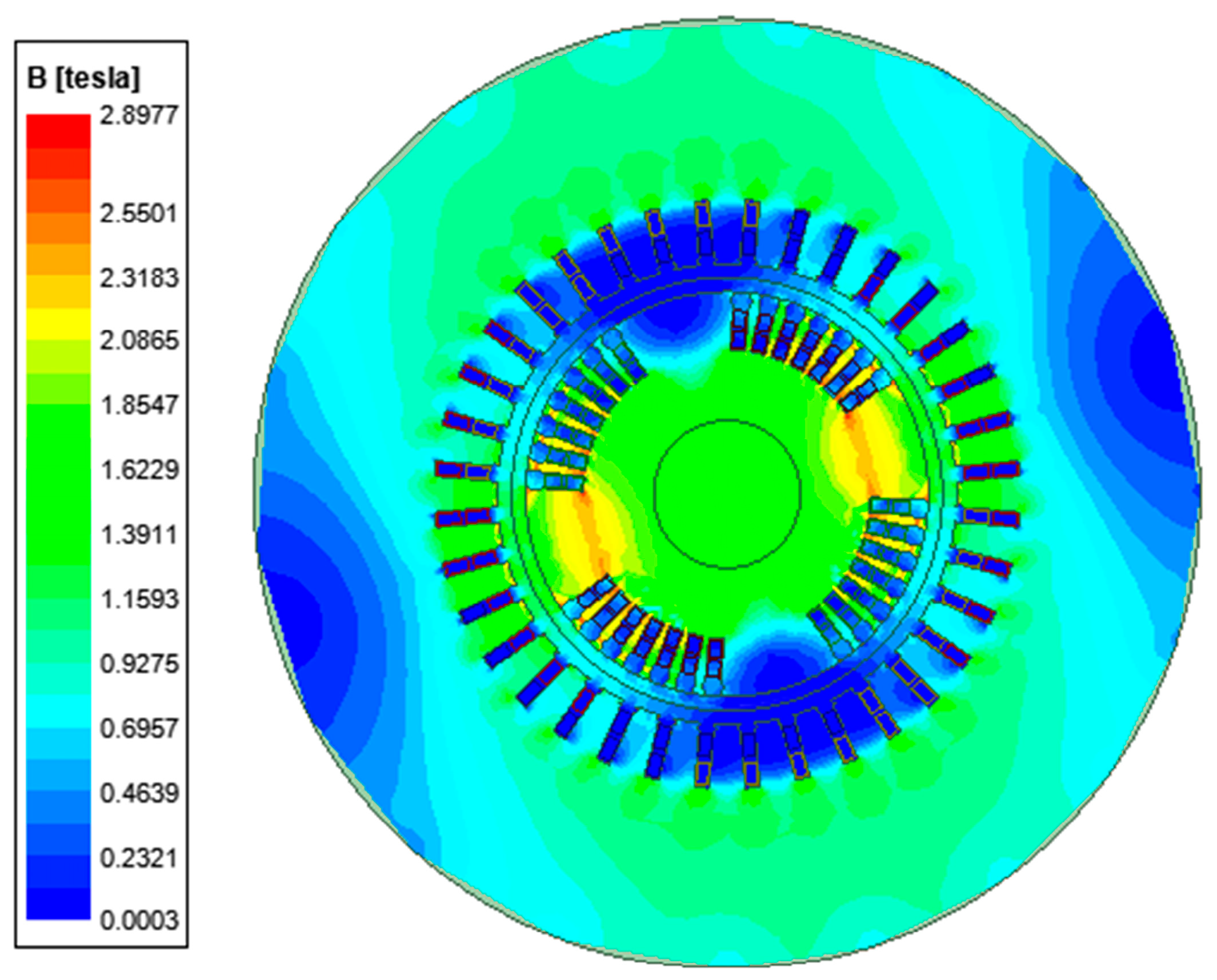
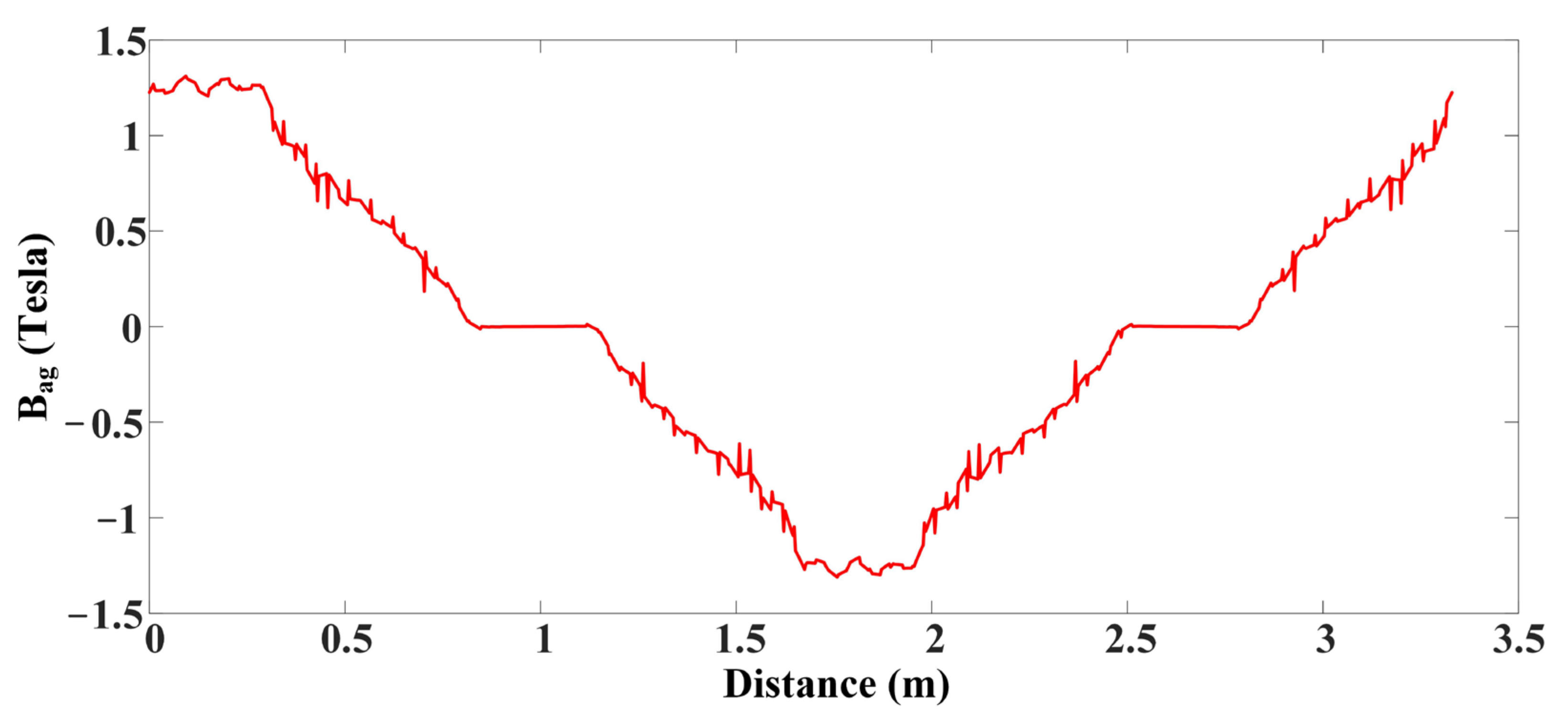
2.2. Maxwell Design
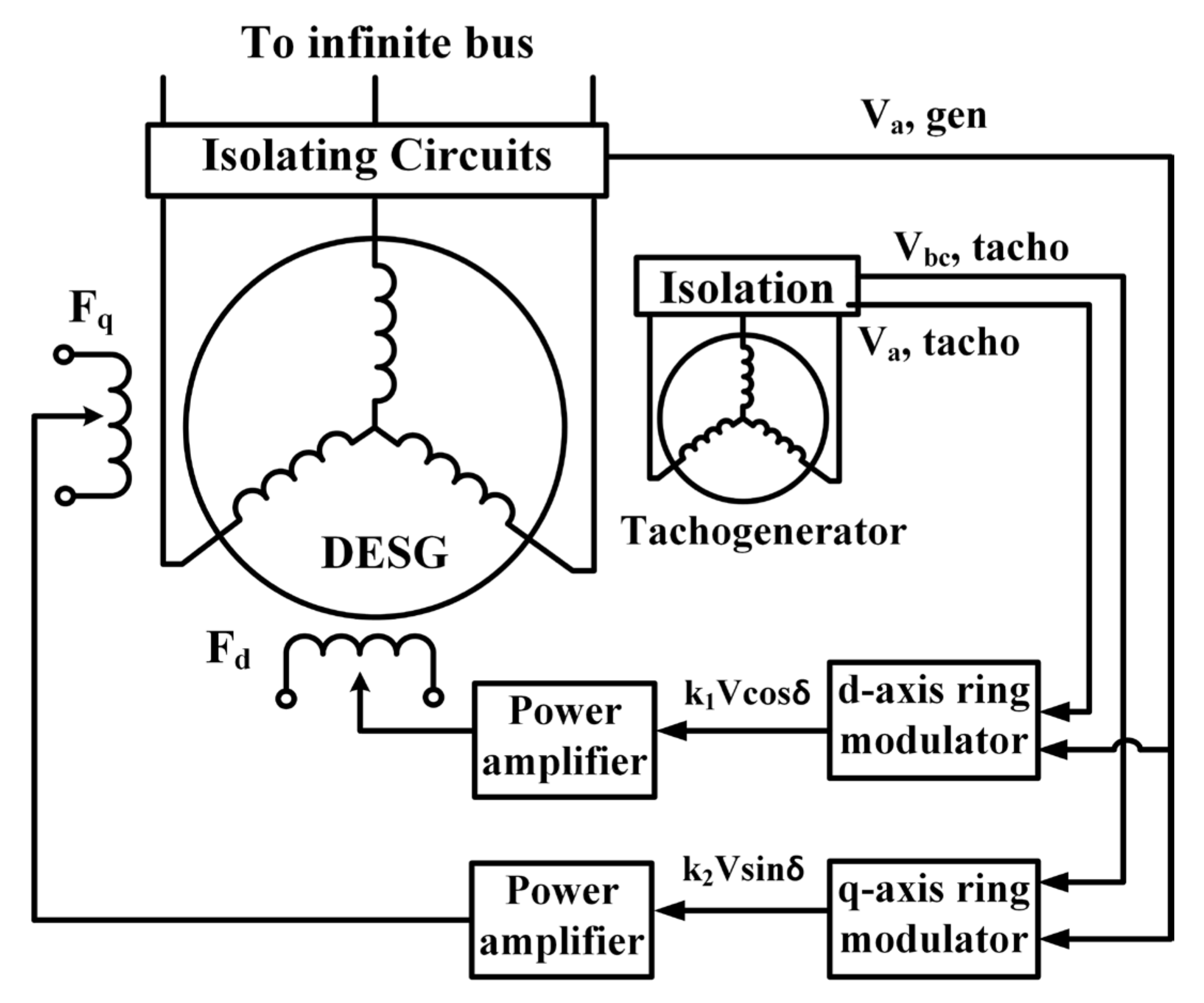
3. Control Strategy for DESG
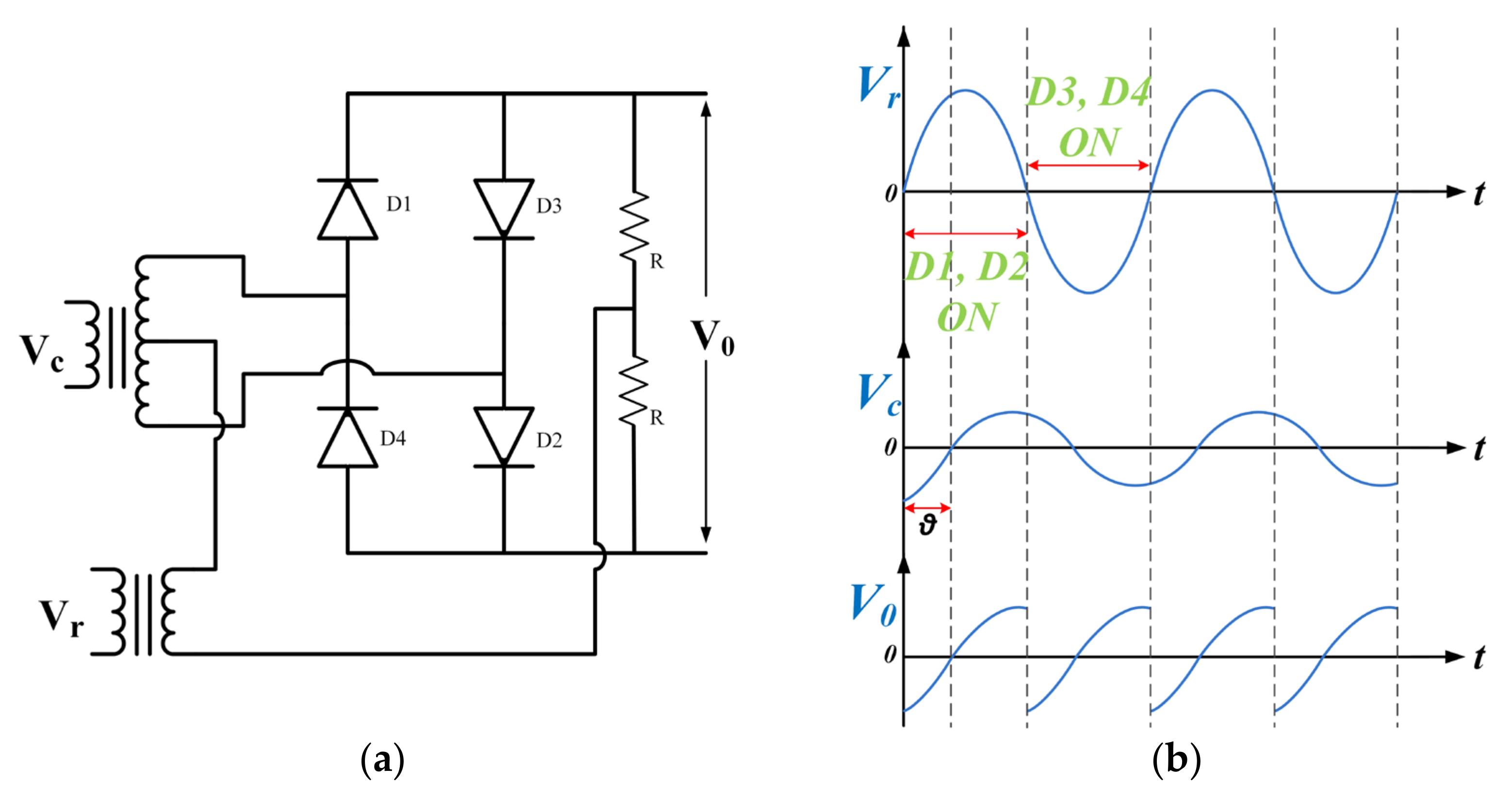
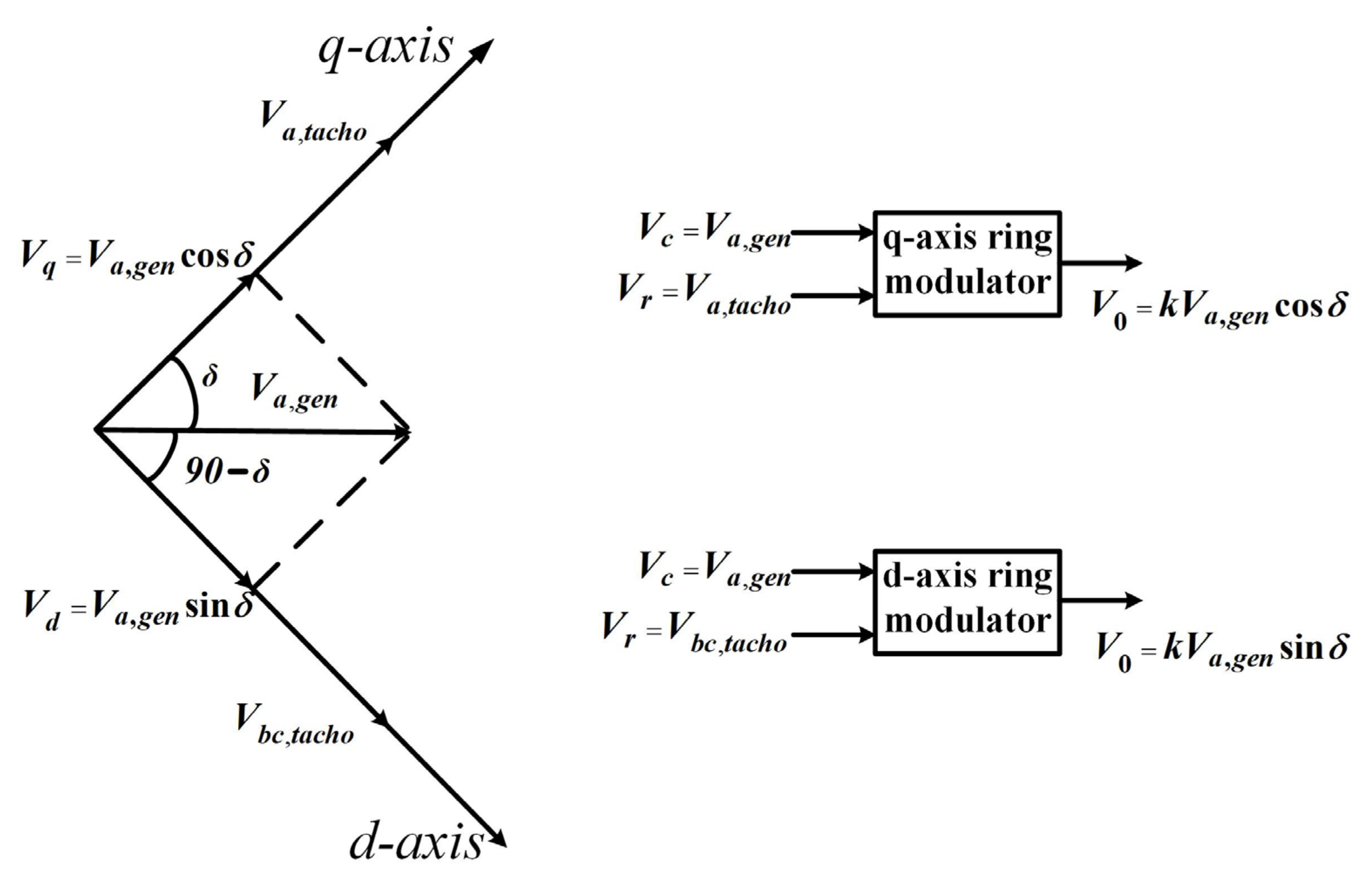
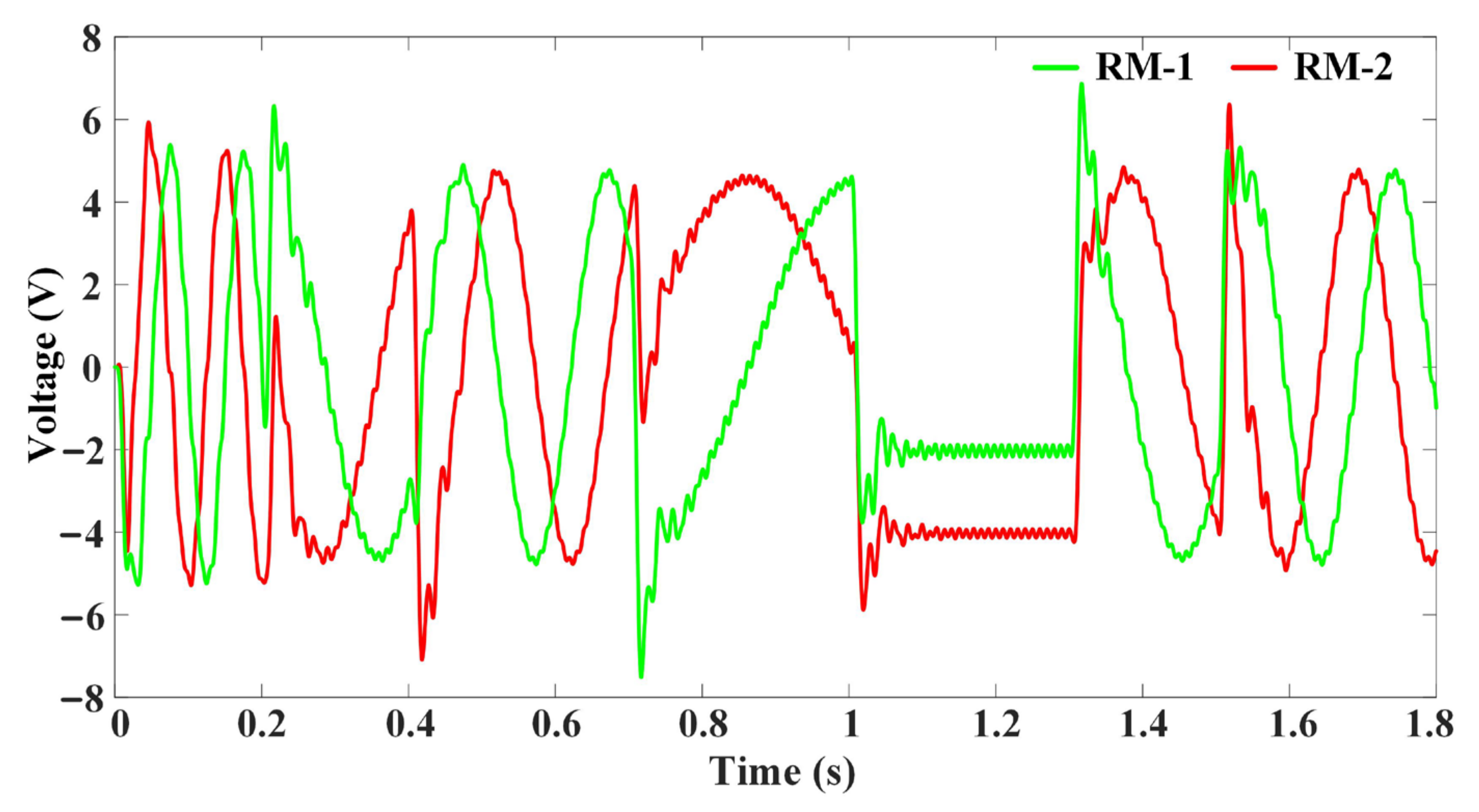
3.1. Ring Modulator and Its Operation
3.2. Control of DESG Using Ring Modulator
4. System Analysis and Discussion
4.1. Analysis of DESG as Wind Generator
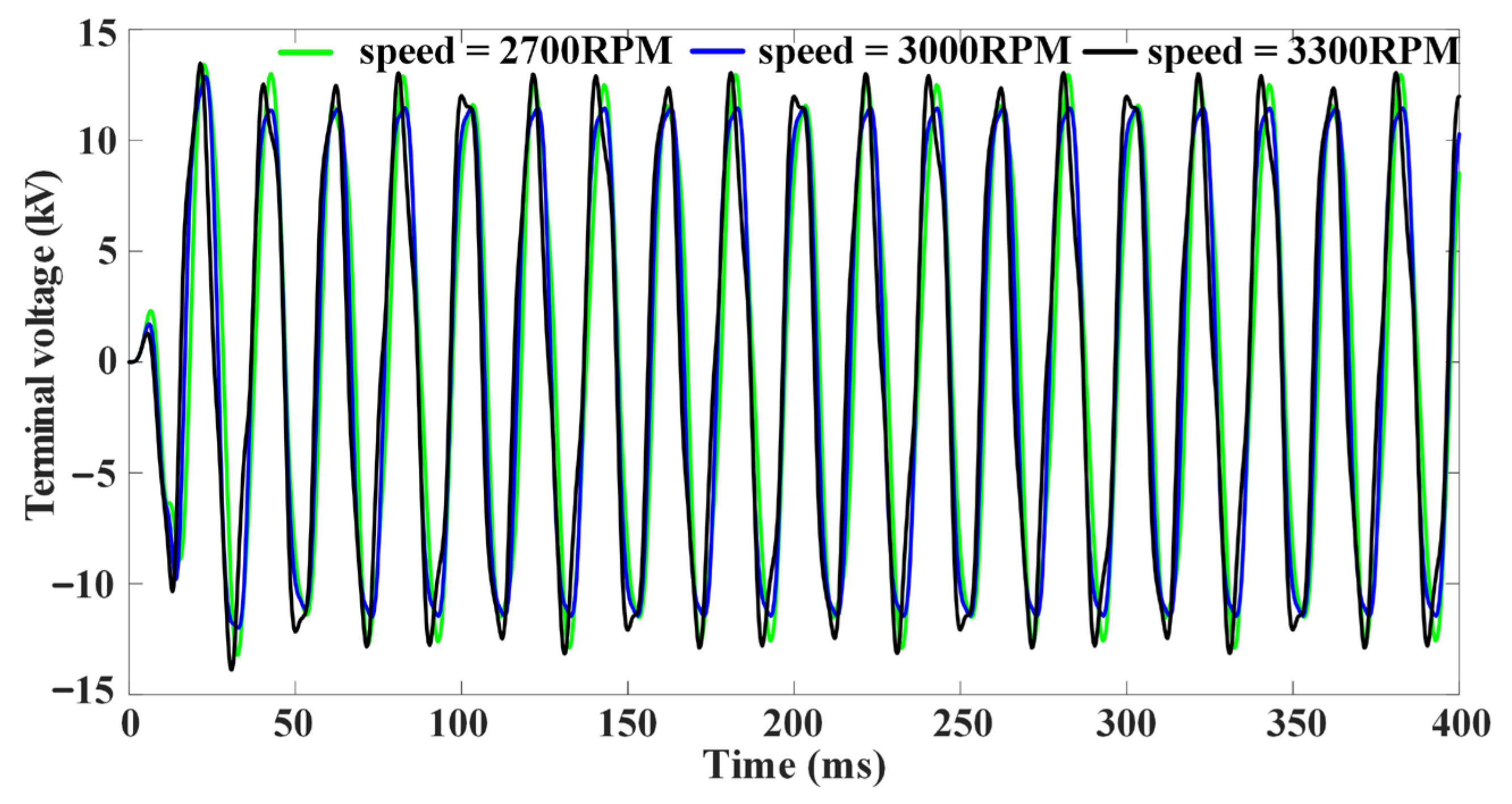
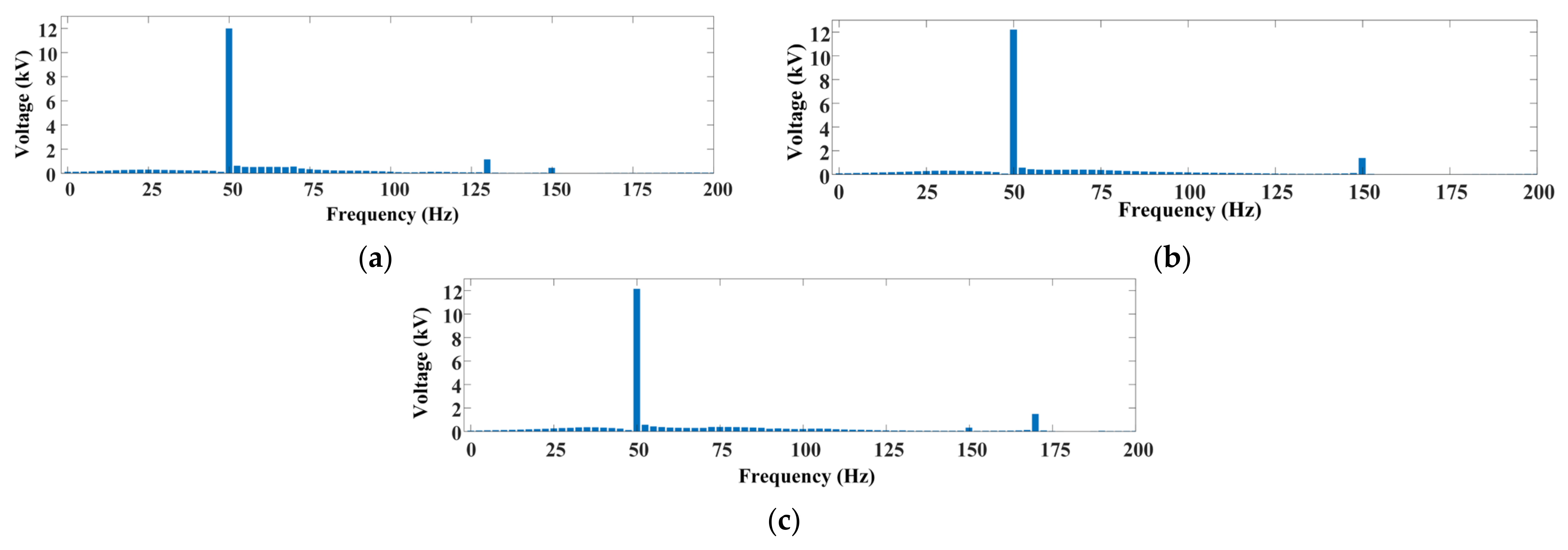
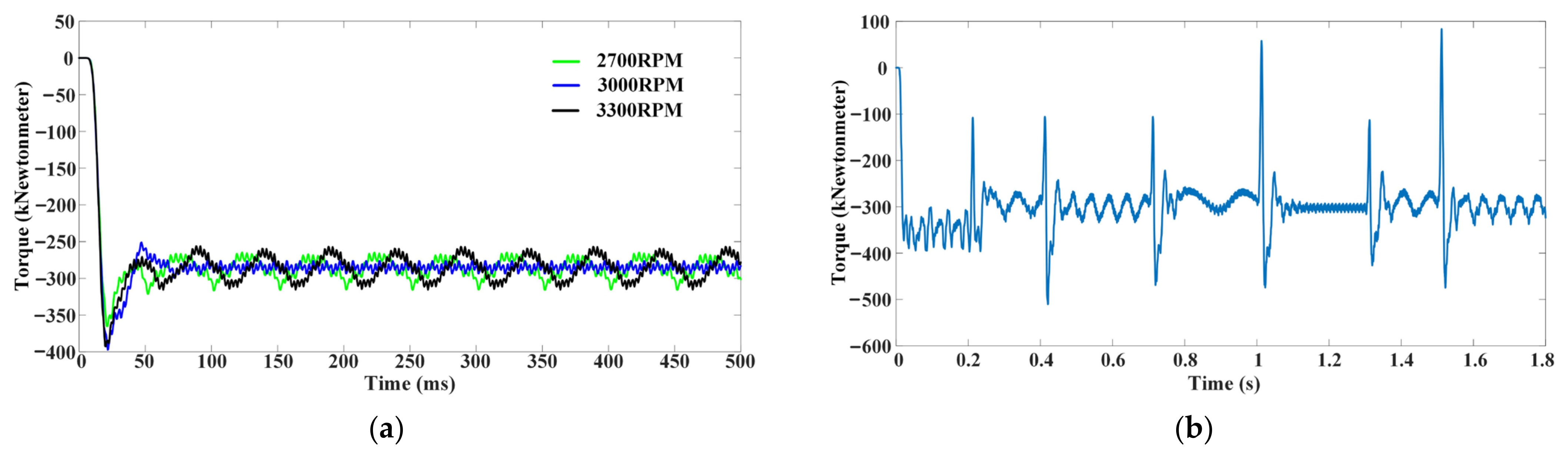
4.1.1. Constant-Speed Operation
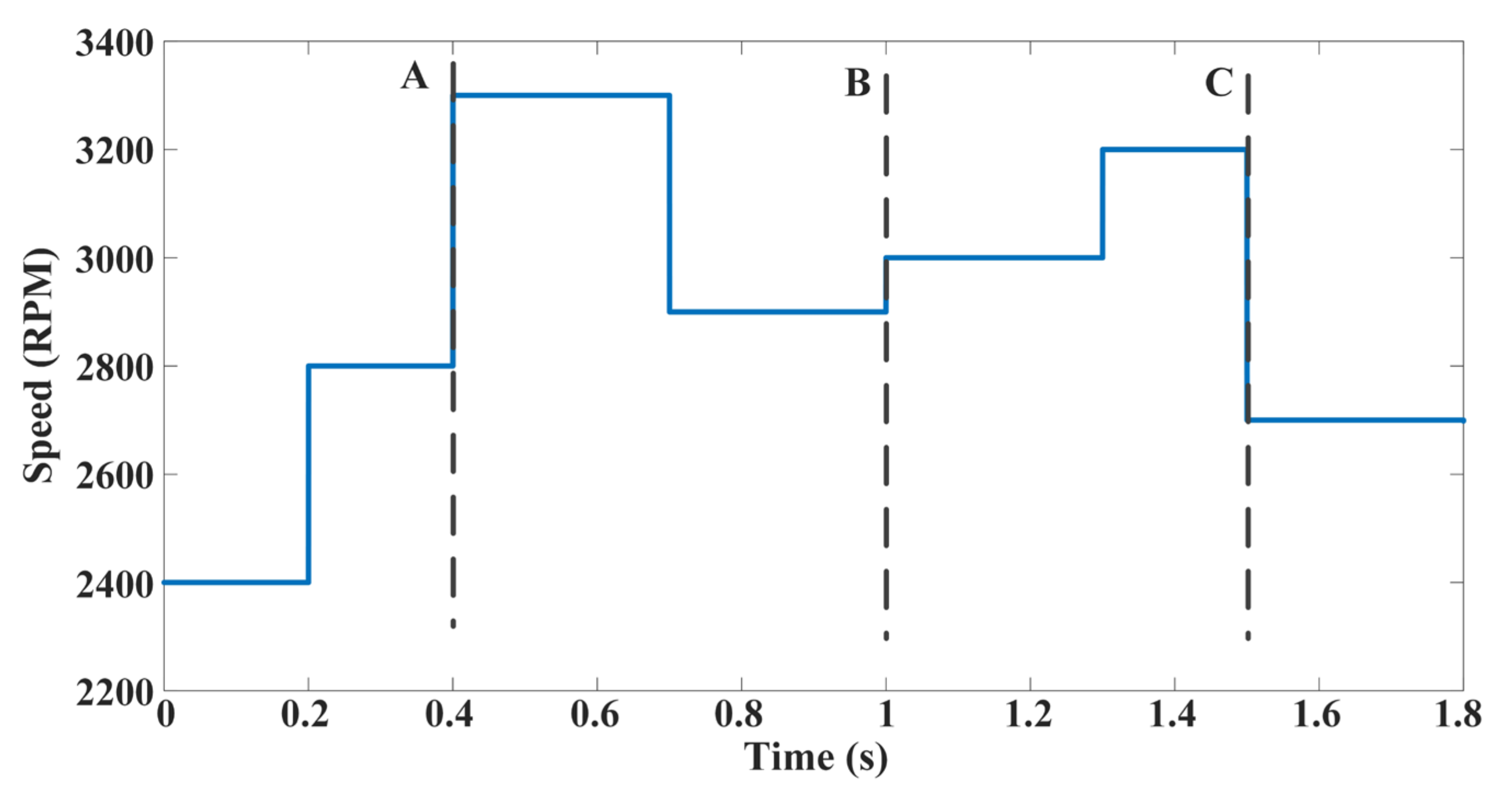
4.1.2. Variable-Speed Operation
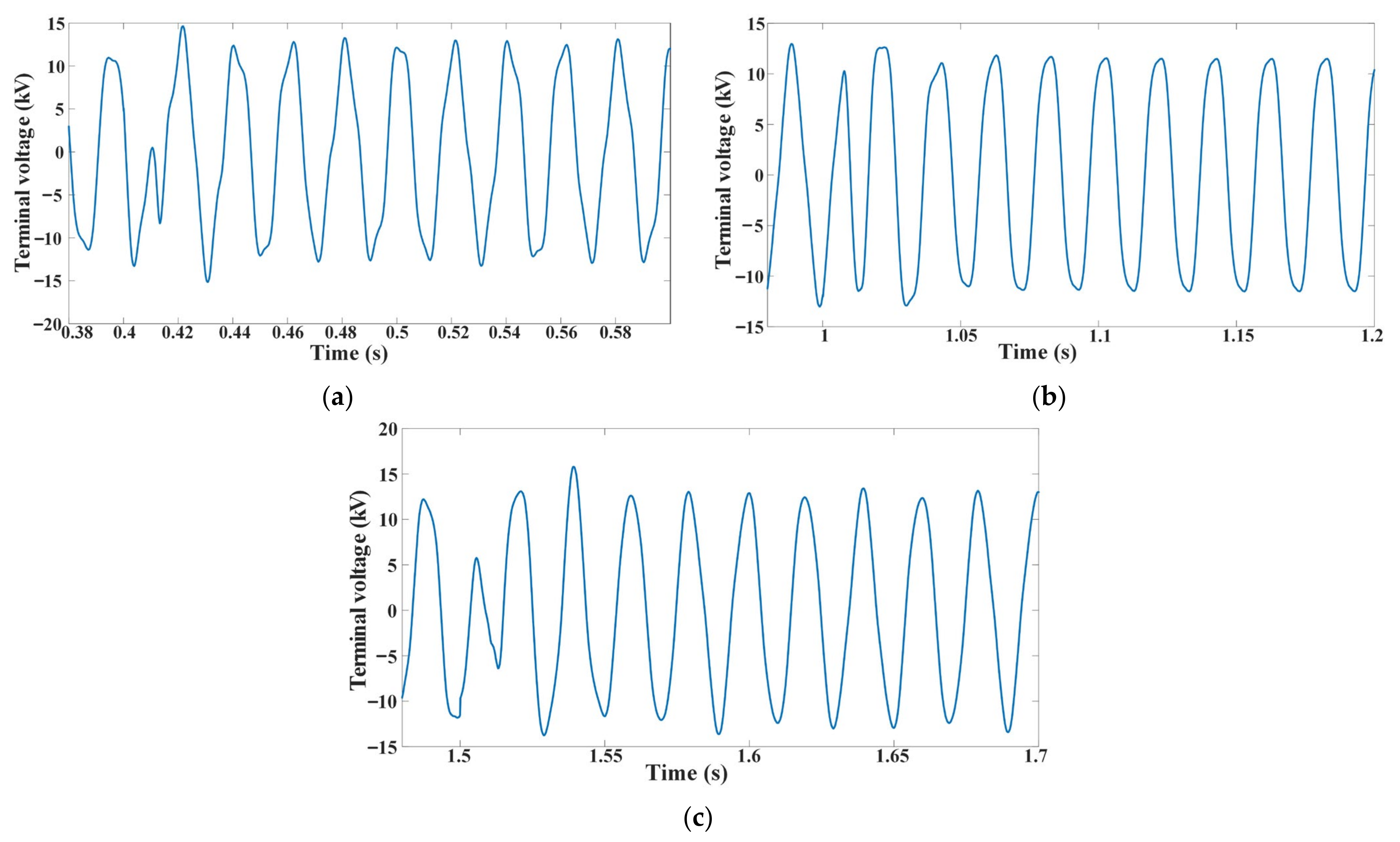
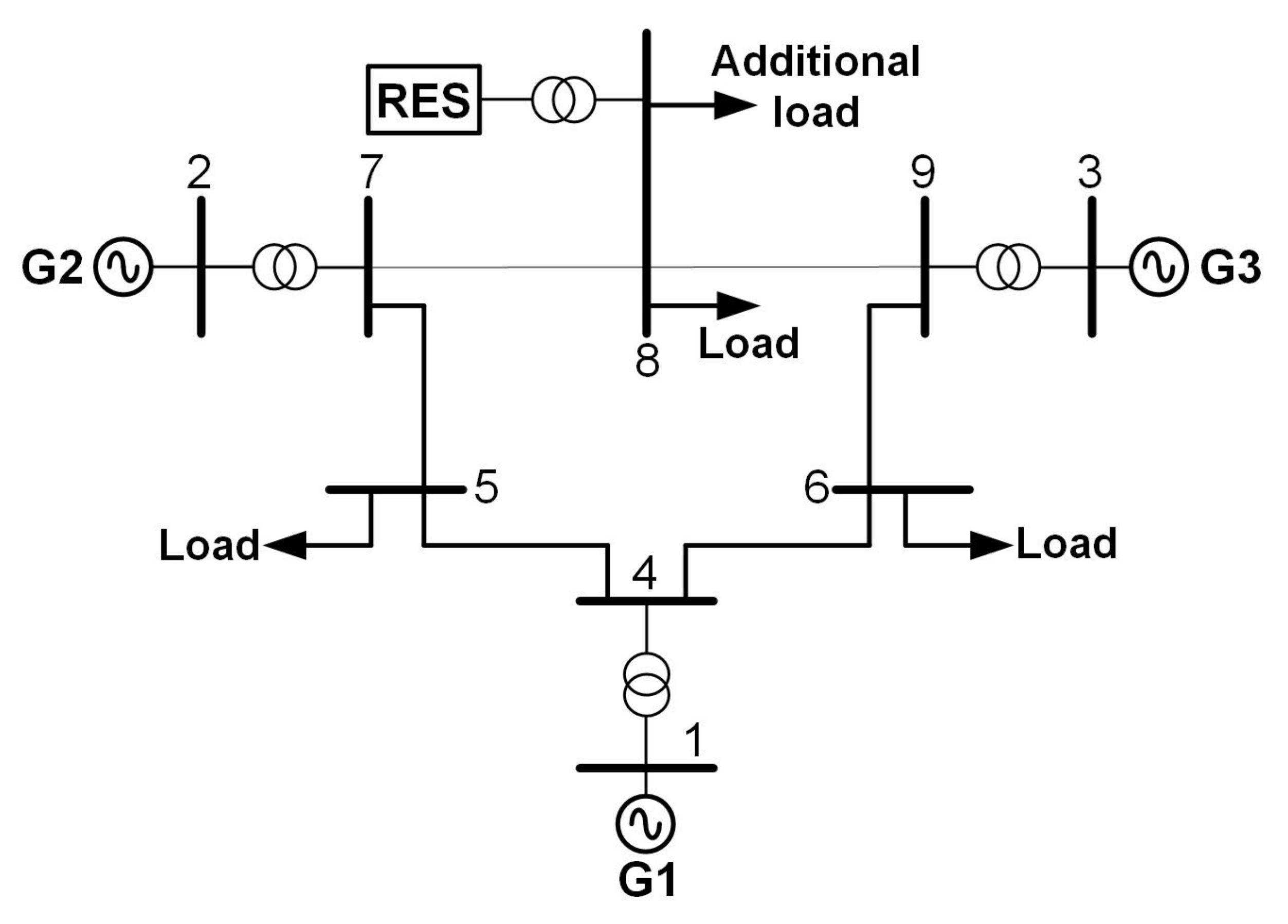
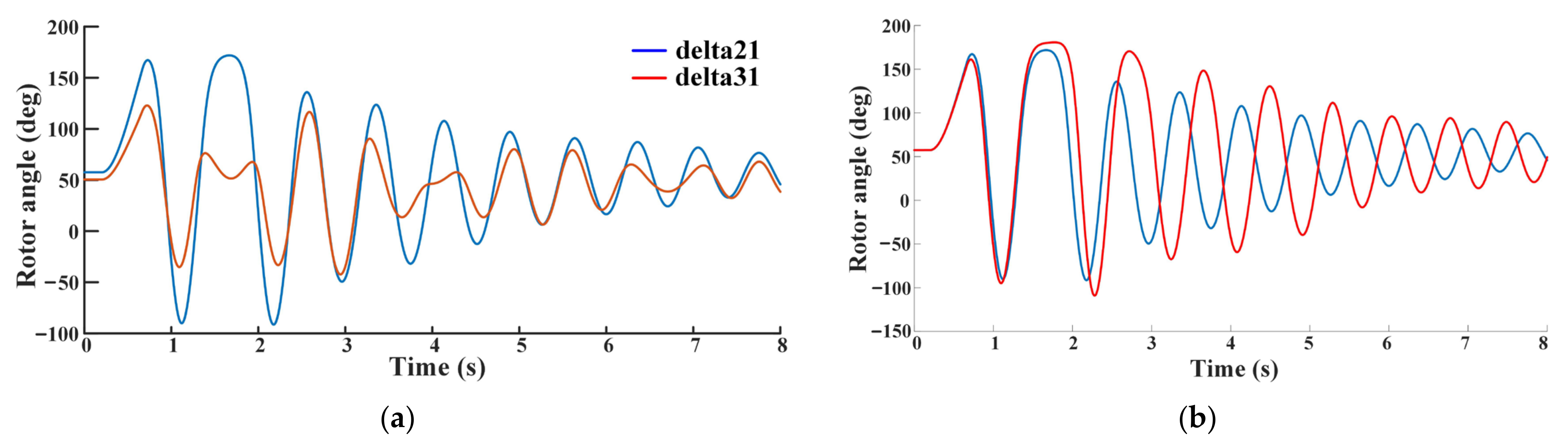
4.2. Multi-Machine System Analysis
4.2.1. Constant-Speed Operation
4.2.2. Variable-Speed Operation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| DESG | Dual-Field Excited Synchronous Generator |
| PMSG | Permanent Magnet Synchronous Generator |
| DFIG | Doubly Fed Induction Generator |
| RM-1 and RM-2 | Ring Modulator-1 and Ring Modulator-2 |
| CCT | Critical Clearing Time |
| G2 and G3 | Generator-2 and Generator-3 |
| Va,tacho, Vbc,tacho | A-Phase Voltage and Line-Line Voltage of Tacho-Generator |
| Vr, Vc | Reference and Control Input Voltages to the Ring Modulator |
| Va,gen | A-Phase Voltage of DESG |
| θ | Phase Shift in Vr with Respect to Vc |
| δ | Rotor Angle |
| and | Flux Linkage Vectors of Stator and Rotor, Respectively |
| , , and | Voltage and Current Vectors of Stator and Rotor, Respectively |
| and Xm | Stator Impedance and Mutual Reactance |
| s | Machine Slip |
References
- Saidur, R.; Islam, M.R.; Rahim, N.A.; Solangi, K.H. A Review on global wind energy policy. Renew. Sustain. Energy Rev. 2010, 14, 1744–1763. [Google Scholar] [CrossRef]
- Gualtieri, G. A comprehensive review on wind resource extrapolation models applied in wind energy. Renew. Sustain. Energy Rev. 2019, 102, 215–233. [Google Scholar] [CrossRef]
- Zeng, Z.; Yang, H.; Zhao, R.; Cheng, C. Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement: A comprehensive review. Renew. Sustain. Energy Rev. 2013, 24, 223–270. [Google Scholar] [CrossRef]
- Duan, Y.; Harley, R.G. Present and future trends in wind turbine generator designs. In Proceedings of the 2009 IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Yin, M.; Xu, Y.; Shen, C.; Liu, J.; Dong, Z.Y.; Zou, Y. Turbine Stability-Constrained Available Wind Power of Variable Speed Wind Turbines for Active Power Control. IEEE Trans. Power Syst. 2016, 32, 2487–2488. [Google Scholar] [CrossRef]
- Ngamroo, I. Review of DFIG wind turbine impact on power system dynamic performances. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 301–311. [Google Scholar] [CrossRef]
- Kaloi, G.S.; Wang, J.; Baloch, M.H. Active and reactive power control of the doubly fed induction generator based on wind energy conversion system. Energy Rep. 2016, 2, 194–200. [Google Scholar] [CrossRef]
- Yunus, A.M.S.; Abu-Siada, A.; Masoum, M.A.S.; El-Naggar, M.F.; Jin, J.X. Enhancement of DFIG LVRT Capability During Extreme Short-Wind Gust Events Using SMES Technology. IEEE Access 2020, 8, 47264–47271. [Google Scholar] [CrossRef]
- Polinder, H.; van der Pijl, F.; de Vilder, G.-J.; Tavner, P. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.-R.I. Assessment and Enhancement of a Full-Scale PMSG-Based Wind Power Generator Performance Under Faults. IEEE Trans. Energy Convers. 2016, 31, 728–739. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, S.; Wang, Y.; Jin, S.; Jovanovic, M.G. Design and Performance Comparisons of Brushless Doubly Fed Generators With Different Rotor Structures. IEEE Trans. Ind. Electron. 2019, 66, 631–640. [Google Scholar] [CrossRef]
- Strous, T.D.; Polinder, H.; Ferreira, J.A. Brushless doubly-fed induction machines for wind turbines: Developments and research challenges. IET Electr. Power Appl. 2017, 11, 991–1000. [Google Scholar] [CrossRef]
- Cheng, M.; Hua, W.; Zhang, J.; Zhao, W. Overview of Stator-Permanent Magnet Brushless Machines. IEEE Trans. Ind. Electron. 2011, 58, 5087–5101. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S. Design, Modeling, and Control of a Novel Hybrid-Excited Flux-Bidirectional-Modulated Generator-Based Wind Power Generation System. IEEE Trans. Power Electron. 2018, 33, 3086–3096. [Google Scholar] [CrossRef]
- Kjaer, A.B.; Korsgaard, S.; Nielsen, S.S.; Demsa, L.; Rasmussen, P.O. Design, fabrication, test, and benchmark of a magnetically geared permanent magnet generator for wind power generation. IEEE Trans. Energy Convers. 2020, 35, 24–32. [Google Scholar] [CrossRef]
- Smith, O.J.M. Synchronous-flux generator. Electr. Eng. 1958, 77, 605–610. [Google Scholar] [CrossRef]
- Morsy, M.S.; Amer, H.H.; Badr, M.A.; El-Serafi, A.M. Transient Stability of Synchronous Generators with Two-Axis Slip Frequency Excitation. IEEE Power Eng. Rev. 1983, PER-3, 27–28. [Google Scholar] [CrossRef]
- Krause, P.C.; Towle, J.N. Synchronous machine damping by excitation control with direct and quadrature axis field windings. IEEE Trans. Power Appar. Syst. 1969, PAS-88, 1266–1274. [Google Scholar] [CrossRef]
- Harley, R.G.; Adkins, B. Stability of synchronous machine with divided-winding rotor. Proc. IEE 1970, 117, 933–947. [Google Scholar] [CrossRef]
- Subramaniam, P.; Malik, O. Dynamic-stability analysis of d.w.r. synchronous generator with feedback-stabilised voltage and angle regulators. Proc. Inst. Elect. Eng. 1971, 118, 1768–1774. [Google Scholar] [CrossRef]
- Reddy, A.A.; Bhat, S.S.; Ugale, R.T. Design and FEM analysis of dual excited synchronous generator. In Proceedings of the 2017 National Power Electronics Conference (NPEC), Pune, India, 18–20 December 2017; pp. 302–306. [Google Scholar]
- Xu, G.; Wang, Z.; Liu, B.; Zhan, Y.; Li, W.; Zhao, H.; Huang, H.; Yu, H. Finite-element calculation of electromagnetic characteristics and steady-state stability of dual-excited synchronous generator. IET Electr. Power Appl. 2021, 15, 1300–1313. [Google Scholar] [CrossRef]
- Xu, G.; Hu, Y.; Hao, X.; Zhan, Y.; Zhao, H.; Liu, X.; Luo, Y. The Relationship of Magnetomotive Force Under Different Excitation Modes of Dual-Excited Synchronous Generator. IEEE Trans. Magn. 2017, 54, 8200704. [Google Scholar] [CrossRef]
- Nakamura, M. Electric Vehicle Control Device. Japan Patent JPWO2011135777A1, 18 June 2013. [Google Scholar]
- Hunt, S.R. Calibrated Slip Synchronous Machine. U.S. Patent US10587176B2, 10 March 2020. [Google Scholar]
- D’Arco, S.; Piegari, L.; Tricoli, P. A novel control of Dual-Excited Synchronous machines for variable-speed wind turbines. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Piegari, L.; Rizzo, R.; Tricoli, P. High Efficiency Wind Generators with Variable Speed Dual-Excited Synchronous Machines. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 795–800. [Google Scholar]
- Yonah, Z.O.; El-Serafi, A.M.; Krause, A.E. Regulation of terminal voltage and output frequency of a variable-speed dual-excited synchronous generator by using a computer-based two-phase excitation system. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Vancouver, BC, Canada, 14–17 September 1993; Volume 2, pp. 1165–1168. [Google Scholar]
- Yonah, Z.O.; El-Serafi, A.M.; Krause, A.E. Computer-controlled VSCF generating system using a dual-excited synchronous generator. In Proceedings of the IEEE Pacific Rim Conference on Communications, Computers, and Signal Processing, Victoria, BC, Canada, 17–19 May 1995; pp. 619–622. [Google Scholar]
- Smith, I.R.; Creighton, G.K.; Kaynak, M.O. Theoretical and Experimental Study of an Asynchronized Synchronous Machine. IEEE Trans. Ind. Electron. Control Instrum. 1975, IECI-22, 501–506. [Google Scholar] [CrossRef]
- Reddy, A.A.; Bhat, S.S. Modeling of Dual Excited Synchronous Generator with slip frequency excitation. In Proceedings of the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Yassin, H.M.; Abdel-Wahab, R.R.; Hanafy, H.H. Active and Reactive Power Control for Dual Excited Synchronous Generator in Wind Applications. IEEE Access 2022, 10, 29172–29182. [Google Scholar] [CrossRef]
- Abdel-Wahab, R.R.; Yassin, H.M.; Hanafy, H.H. Dual Excited Synchronous Generator a Suitable Alternative for Wind Applications. In Proceedings of the 2020 IEEE 14th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Setubal, Portugal, 8–10 July 2020; pp. 352–357. [Google Scholar] [CrossRef]
- Mitra, A.; Chatterjee, D. Active Power Control of DFIG-Based Wind Farm for Improvement of Transient Stability of Power Systems. IEEE Trans. Power Syst. 2015, 31, 82–93. [Google Scholar] [CrossRef]
- Agarala, A.; Bhat, S.S.; Mitra, A.; Zychma, D.; Sowa, P. Transient Stability Analysis of a Multi-Machine Power System Integrated with Renewables. Energies 2022, 15, 4824. [Google Scholar] [CrossRef]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]



| Specification | Value |
|---|---|
| Outer diameter (mm) | 2350 |
| Inner diameter (mm) | 1140 |
| Slots | 36 |
| Coil pitch (slots) | 14 |
| Core length | 3450 |
| Slots/pole/phase | 6 |
| Air gap (mm) | 70 |
| Poles | 2 |
| Winding | Double layer (Lap) |
| Specification | Value |
|---|---|
| Outer diameter (mm) | 1000 |
| Inner diameter (mm) | 365 |
| Indexed slots | |
| Actual slots | 28 |
| Core length | 3500 |
| Slots/pole/phase | 7 |
| Poles | 2 |
| Winding | Double layer (Lap) |
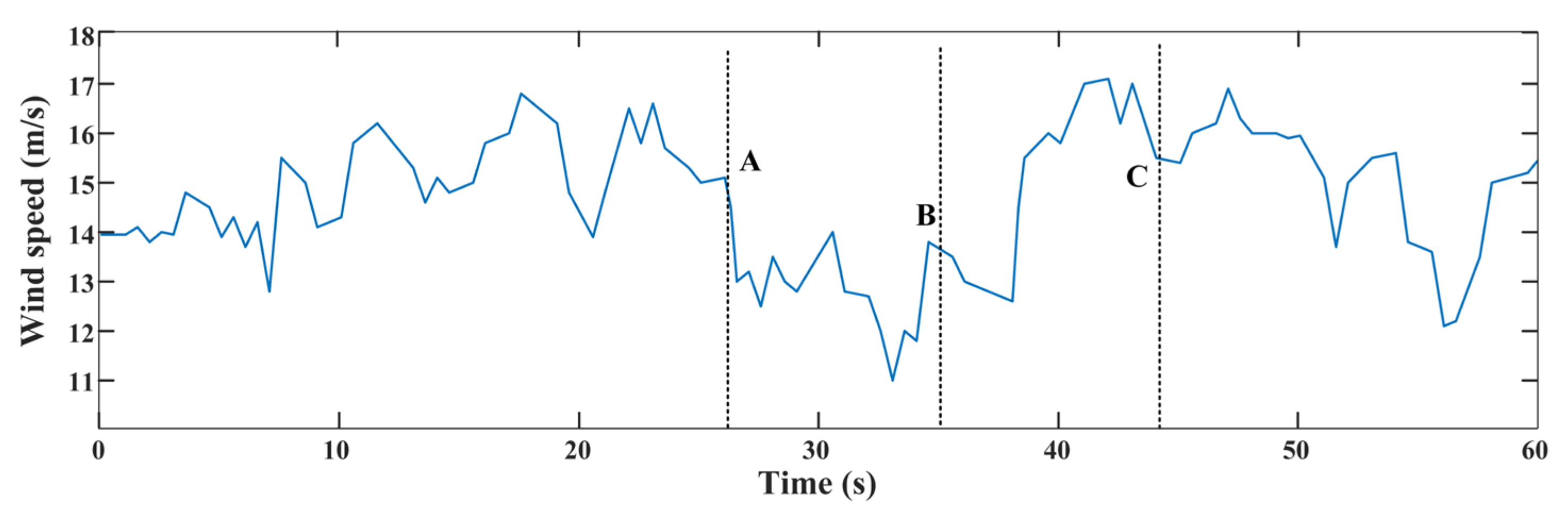
| Fault Instance | At A (26.25 s) | At B (35 s) | At C (44.2 s) |
|---|---|---|---|
| DFIG | 454 ms | 468 ms | 456 ms |
| DESG | 503 ms | 498 ms | 486 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarala, A.; Bhat, S.S.; Zychma, D.; Sowa, P. A Novel Approach to Using Dual-Field Excited Synchronous Generators as Wind Power Generators. Energies 2024, 17, 456. https://doi.org/10.3390/en17020456
Agarala A, Bhat SS, Zychma D, Sowa P. A Novel Approach to Using Dual-Field Excited Synchronous Generators as Wind Power Generators. Energies. 2024; 17(2):456. https://doi.org/10.3390/en17020456
Chicago/Turabian StyleAgarala, Ajaysekhar, Sunil S. Bhat, Daria Zychma, and Pawel Sowa. 2024. "A Novel Approach to Using Dual-Field Excited Synchronous Generators as Wind Power Generators" Energies 17, no. 2: 456. https://doi.org/10.3390/en17020456
APA StyleAgarala, A., Bhat, S. S., Zychma, D., & Sowa, P. (2024). A Novel Approach to Using Dual-Field Excited Synchronous Generators as Wind Power Generators. Energies, 17(2), 456. https://doi.org/10.3390/en17020456






