Abstract
Recently, the implementation of software/hardware systems based on advanced artificial intelligence techniques for continuous monitoring of the electrical parameters of intelligent networks aimed at managing and controlling energy consumption has been of great interest. The contribution of this paper, starting from a recently studied DC-MG, fits into this context by proposing an intuitionistic fuzzy Takagi–Sugeno approach optimized for the energy management of isolated direct current microgrid systems consisting of a photovoltaic and a wind source. Furthermore, a lead-acid battery guarantees the stability of the DC bus while a hydrogen cell ensures the reliability of the system by avoiding blackout conditions and increasing interaction with the loads. The fuzzy rule bank, initially built using the expert’s knowledge, is optimized with the aforementioned procedure, maximizing external energy and minimizing consumption. The complete scheme, modeled using MatLab/Simulink, highlighted performance comparable to fuzzy Takagi–Sugeno systems optimized using a hybrid approach based on particle swarm optimization (to structure the antecedents of the rules) and minimum batch squares (to optimize the output).
1. Introduction
Recently, global energy policy has been increasingly oriented towards the exploitation of renewable energy sources (RESs) to reduce carbon dioxide emissions (mainly responsible for the reduction of the ozone layer in the atmosphere, which protects the earth from the harmful action of UV rays) [1,2,3]. In this framework, microgrids (MGs), smaller local electricity networks that can also be operated individually, have established themselves as solutions for managing energy flows from RESs for future smart networks [4,5,6]. MGs, depending on the operating mode, can be divided into direct current (DC-MG) [7,8,9] and alternative current (AC-MG) microgrids. Compared to the AC-MGs, the DC-MGs, which also operate in isolated mode, provide better performance regarding the management of energy flows coming from RESs (photovoltaic (PV), wind (WT), fuel cell (FC) [10]) with storage systems [11] towards electrical loads both civil and industrial without the need for DC/AC converters for the integrated system and without requiring synchronization operations [12,13,14].
Recent works of scientific literature propose efficient algorithms for the control and management of energy flow, ensuring maximum power transfer (through the use of maximum point power (MPPT) directly in the algorithms [15,16]), even in adverse or otherwise changing weather conditions [17,18,19,20]. However, it should be noted that the scale limitations and the limited capacity of the accumulator do not allow AC-MGs to provide long-term energy, so it is necessary to use modular FCs to guarantee adequate power with continuity and with rapid response to load variations (common diesel generators are to be excluded because they are polluting and characterized by reduced efficiency) [21,22]. Stationary FCs stand out among them as they can be used in contexts where the quantity of energy required is significant [23,24,25].
Obviously, the energy management system (EMS) is the core of an MG which should be able, on the one hand, to standardize the power exchanged between RESs and loads (in compliance with the respective constraints) and, on the other, to reduce costs and increase the lifetime of the MG [26,27,28].
Furthermore, EMSs, in case of interruption of the primary power supply, should be able to start the backup power supply by starting the FC which, coupled to an electrolyzer, produces the fuel (for example, hydrogen ()) on demand [29,30,31].
Now, many authors are busily engaged in the design and validation of EMSs for DC-MGs with high reliability and performance. There is no lack of theoretical studies of physical-mathematical modeling of MGs with certainly interesting results, but almost all are based on the resolution of systems of differential equations [32,33]. However, it is worth noting that the systems of differential equations that describe the dynamic behaviors of PV and WT powers have different operating times and therefore suffer from synchronization problems [34,35,36,37]. A possible solution would require the adaptive insertion of delay times into each of the equations, resulting in the challenge of obtaining numerical solutions within a reasonable time. It follows that the mathematical models for this MG are currently not very efficient [38,39,40].
Recently, a considerable number of works have been produced reporting interesting DC-MG studies which also propose sophisticated topologies with latest-generation energy storage and production elements [41,42,43] equipped with multi-level hierarchical control systems to optimize any fuel consumption [44,45].
With the widespread diffusion of approaches based on artificial intelligence (AI), scientific production in the DC-MG field has recently achieved important results thanks to the strong peculiarity of these techniques in the processing of large quantities of data for the process of decision making. In fact, machine learning techniques have opened wide frontiers, especially in the study of stability (regression [26,46,47], random forest tree [26,48,49], convolutional neural networks [26,50,51] and others [52,53,54]). However, these techniques, although promising in performance and results obtained, have the flaw of being black-box type procedures so, on the one hand, they are difficult to understand by non-experts and, on the other, they do not allow updates except in the case of substantial interventions.
In AI, soft computing comes into play and, in particular, fuzzy systems (FSs) which represent flexible evolutionary models that solve non-linear problems (difficult to solve using equations and/or mathematical algorithms) where human intelligence is required [55]. FSs, by formulating “...” banks of fuzzy rules, solve problems in which the data used are affected by uncertainties and/or inaccuracies [56,57,58]. With the help of these techniques, numerous EMSs have been designed and tested for DC-MGs with PV and WT power generation with the integration of a battery storage and FC with the aim of reducing costs by maximizing power. However, even if the results appear valuable, in some cases the naive approach makes performance inefficient [26,59,60]. Obviously, there is no shortage of significant advances regarding the fuzzy EMS control procedure of DC-MGs, based on automatic extraction of the fuzzy rule bank [61,62,63], fault detection and classification [64,65,66].
However, to consider any uncertainties in writing the membership functions, only recently have significant works been produced on the management and control of EMSs in DC-MGs using fuzzy systems based on intuitionistic fuzzy sets without, however, considering any need to adaptively optimize the fuzzy membership functions (FMFs) [67,68,69]. To our knowledge, until now no significant work has been published regarding this important task for the DC-MGs of the future.
With this objective in mind (i.e., reducing consumption to a minimum and maximizing the power of the RESs), we start with the DC-MG in island mode (Figure 1) proposed in [26] which, through a Mamdani fuzzy EMS, managed the power supply of domestic users with RESs (PV/WT) and a lead-acid storage system supported by a cell in which the inputs were the net power and state of charge (SoC) of the battery and the output was the power of the cell. As detailed in Figure 1, the system is composed of a load connected to the RESs via electronic converters acting as a connection between the system devices and the backup system (lead-acid battery and production/consumption). Furthermore, each subsystem is accompanied by a local control device (based on decentralized architecture) and an EMS characterized by centralized supervision.
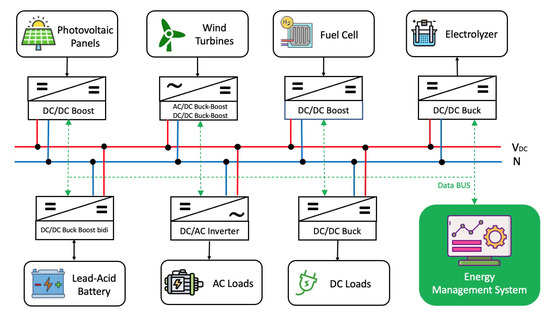
Figure 1.
Block-diagram of the stand-alone DC-MG.
Even if the results in [26] were noteworthy (since they reduced hydrogen consumption by increasing the power extractable from the RESs), no adaptive procedure was recognized regarding the writing of the fuzzy rules (in particular, of the FMFs) which, in that case, were built through experience gained over the years by the authors without any optimized tuning process.
Therefore, starting from the aforementioned EMS, in this work, to consider any uncertainties in the membership values, we rewrite the bank of fuzzy rules according to an innovative optimized intuitionistic Takagi–Sugeno (TS) approach exploiting a procedure based on the subtractive cluster technique able to optimize the FMFs.
The main contributions of this paper are summarized in the following list.
- The fuzzy (heuristic) Mamdani model proposed in [26], although it does not require a mathematical model to structure the EMS allowing for easy upgradeability, does not provide a detailed description of the process. It also does not allow the use of design techniques in the form of rules with optimization of the shape and position of the membership functions for each variable involved. Finally, Mamdani’s approach, which has limited validity to the data intervals used for its definition, does not allow guidelines for the definition of the model’s characteristics (i.e., order, number and form of qualifiers, number and content of the rules).Since the problem under study has two inputs and one output (MISO), the fuzzy model studied in [26] was rewritten according to the TS approach. This fuzzy approach, regarding the fuzzification and application of connectives, maintains the same steps as the Mamdani inference. Furthermore, the output is structured as a set of singletons which, appropriately combined, provide functional (deterministic) consequences.
- It can be immediately observed that the fuzzy rules presented in [26] arise from the expert’s knowledge, which is essentially derived from the behavior of the individual elements that constitute the MG. The behavior of many of them (unfortunately not all) is described deterministically by a system of evolutionary differential equations whose solutions provide indications to the expert for the composition of the fuzzy rules. However, to reduce the risk of fuzzy rule banks with numerous rules, and at the same time start evaluating any fuzzy assumptions for stability, it appears necessary to verify that these evolutionary models admit a single solution (thus ensuring that, at least in principle, the outputs of fuzzy systems do not represent ghost solutions [70,71]). So, in this article, before proceeding with the design of fuzzy systems, this verification was performed using analytical techniques now consolidated in the literature.
- The main reason why it was chosen to transform the Mamdani model studied in [26] concerns the great potential that TS models have in the clustering of the antecedents (to determine the number of rules) and in the structuring of the consequent (which culminates in functional deterministic expression of the output), as well as providing banks of fuzzy rules and inferences that are completely general and not limited to a few inputs and rules. Particularly, to structure the antecedents of each rule, an AI heuristic iterative technique based on particle swarm optimization (PSO) was exploited, as required by the specifications of the Tech4You Project. The proposed approach can identify “optimum candidates” in the search space based on specific quality measures. Even if the most recent scientific literature proposes innovative alternative techniques for the intended objective, the PSO, by not making any assumptions on the problem, allows the exploration of considerable solution spaces. Furthermore, by not using differential operators during the optimization process, differentiability of the issue under study is not required, opening up broad prospects of success for that entire class of irregular, noisy concerns with uncertainties and/or inaccuracies.
- As regards the structuring of the consequent, an approach based on batch least squares (BLS) was used which, in synergy with the PSO, determines the optimal allocation of the output singletons with a limited computational complexity.
- While obtaining promising results following the use of the EMS managed by the optimized fuzzy TS, it is appropriate to consider any additional uncertainties contained in each membership function involved in each fuzzy rule. With this objective in mind, the optimized TS fuzzy model was generalized considering both membership and non-membership values, inducing the formulation of a respective degree of hesitation. The proposed procedure allowed us to build a fuzzy TS (intuitionistic) system which, through clustering of the antecedents, also determines the number of rules (with a high performance estimated using an appropriate index).
The three EMSs obtained (managed by the aforementioned fuzzy systems) were tested in an area located in southern Italy (38715.138 N/153955.315 E) in correspondence with the buildings of the DICEAM Departments of the “Mediterranea” University of Reggio Calabria (Italy) now involved in the activities of the aforementioned Project (Tech4You Spoke 2 Project—Goal 2.1—PP1—Action 9). The results obtained, in maximizing the power provided by the RESs and reducing the production of , are fully comparable with the performances obtained through the TS type formulation of the model in [26] optimized using the combined particle swarm approach optimization (PSO) and batch least squares (BLS), but with better performance results and CPU-time, which is interesting for any real-time applications and technological transfer as well.
The remainder of the paper is structured as follows. After briefly describing the configuration of the DG-MG studied in [26] (Section 2), the physical-mathematical characteristics of the RESs used are detailed, highlighting that the evolutionary differential models for managing the exchange of information with the DC bus are well posed (Section 3). Next, Section 4 details the peculiar characteristics of the starting EMS that uses the Mamdani approach, including the bank of fuzzy rules that manages the control. Then, Section 5 details the steps that allow the formulation of the optimized TS approach, while Section 6 describes the structure of the optimized fuzzy system which exploits the intuitionistic approach. Once the electrical loads have been described by outlining the meteorological parameters and power profiles of the RESs considered as reported in Section 7, the implementation aspects are highlighted in Section 8 introducing the initial relevant results. Section 9 is dedicated to discussing the performance while the conclusions and possible future perspectives conclude the paper. As a summary of the entire work, an appendix contains the proofs of the theorems that establish the well-posedness of each evolutionary differential model.
2. DC-MG Structure: An Overview
As can be seen from Figure 1, the starting DC-MG considered in this paper, as in [26], is made up of two primary renewable sources, PV and WT, operating in MPTT mode generating 100 kW and 50 kW, respectively. Furthermore, a FC functions as a secondary source and guarantees, if necessary, enough energy (50 kW at nominal state, 60 kW at maximum power) to avoid blackout situations. And again, a 50 kW battery stabilizes the voltage on the DC bus, providing energy to the grid if necessary and absorbing any excess energy, while a dump-load electrolyzer (DC charge) absorbs excess energy if the generated power exceeds that of the load with an SoC over . Finally, some DC and AC domestic loads complete the MG. In particular, as regards the wind turbine, a double AC/DC and DC/DC converter has been inserted in a single block so that the second converter acts as an interface with the DC bus. Furthermore, the electrolyzer has been positioned to interact with the fuel cell allowing the DC-powered electrolyzer to produce hydrogen during the accumulation phase by storing it in tanks. The fuel cell converts the hydrogen back into electrical energy in DC during peak absorption. As regards the connection lines, in Figure 1, the power flows have been indicated by arrows. In particular, the red/blue lines indicate the DC bus, while the green dotted line indicates the data bus to monitor the operation of the DC-MG (power flows, voltages, currents⋯). Finally, the black lines indicate the power flows of the various elements. As is known [26], the power balance equation for the aforementioned MG is the following:
Furthermore, 50 kW represents the maximum charge/discharge power of the battery; when it is discharged, the energy comes from the RESs. In any case, it will absorb extra energy until the SoC reaches 80%, using the surplus energy to produce in an electrolyzer. Table 1 lists the complete parameters of the DC-MG as reported in [26].

Table 1.
Characteristics of the DC-MG.
3. Some Important Physical-Mathematical Details
3.1. PV System and MPPT Control
The PV system consists of a certain number of panels connected to the DC bus via a DC/DC boost converter [26]. The output power can be evaluated using the following relationship
where is the output power (W) and is the solar irradiance (W/m2); moreover, represents the rated power (W) of the module at standard test condition (STC) and denotes the dimensionless temperature coefficient. Finally, is the cell temperature at STC and represents the ambient temperature .
The PV system is connected to the DC bus via a boost converter, whose behavior is described evolutionary by the following dynamic model [26]:
where and represent the PV system current and DC bus voltage, respectively. Furthermore, C and L are the capacitance and inductance of the boost converter, while R is the load resistance and represents the control input of the boost converter.
Remark 1.
Regarding the optimization of the output power of the PV system, as in [26], an iterative MPPT algorithm based on Perturb and Observe (P&O) was used, since it is simple to adapt and d is quite accurate. The approach, in principle, perturbs the operating voltage at regular intervals by oscillating around the point (i.e., MPPT).
Remark 2.
In [26], a fuzzy system for EMS control was proposed by structuring a fuzzy inference without checking the feasibility of the approach. To be sure that the EMS can be structured in terms of stable fuzzy inference, it is not enough to build a bank of fuzzy rules whose inference models the behavior exhibited by the available data. It is necessary to be sure that the differential equations governing evolutionary behavior admit a system of fuzzy rules whose inference is equivalent to the starting differential system. Setting (physical parameters directly linked to the power delivered) as proved in [72], the if-only-if model (3) admits a unique solution; it also admits a fuzzy plant rule in the form:
where N is the number of inference rules; , and are fuzzy sets, while and represent the system state and control input, respectively, and, finally, , and . Furthermore, and are the k-models as formulated in [72],
Therefore, denoting by , with , for the membership function, after calculations, one achieves
such that
Therefore, by fuzzy blending, the global fuzzy dynamic model is writable as [72]
having denoted for brevity, where and .
Then, the following Proposition presents the first important result in this paper.
Proposition 1.
Proof of Proposition 1.
See Appendix A. □
3.2. WT System and MPPT Control
In this work, as in [11,26], we use a permanent magnet synchronous generator (PMSG) connected directly to the WT (always operating below the rated speed) whose mechanical power can be quantified as follows:
where is the air density (), R is the blade radius (m), is the wind speed (m/s) and expresses the link between the tip speed ratio () and the pitch angle (). As in [11,26], we consider the usual equations for the currents of both d and q axis, structured as follows:
in which , , and represent the current and voltage of d and q axis. Moreover, the angular frequency of the generator, whose inductances are and with P number of pole pairs and as the magnetic flux linkage, is indicated by .
Remark 3.
As in Section 3.1, the next Proposition verifies that (10) admits a unique solution.
Proposition 2.
Proof of Proposition 2.
See Appendix B. □
The WT, connected to the DC bus via a buck-boost DC/DC converter, exhibits dynamic behavior governed by the following system of differential equations:
in which L and are the buck-boost parameters, and D is the duty cycle.
Remark 4.
As in [26], we propose a control approach that involves only the calculation of the power output, without the need for wind speed measurement or other electromechanical considerations. In any case, the operation is carried out when the ratio of the change in power to the interpretation of speed is equal to zero (i.e., ).
Remark 5.
As in the previous cases, by applying the procedure proposed in Remark 2, it is verifiable that (11) admits an equivalent fuzzy system, provided that it admits the uniqueness of the solution.
Proposition 3.
Proof of Proposition 3.
See Appendix C. □
3.3. Lead-Battery Acid Modeling and Its Control
Since the optimal contribution of RESs in an MG is not achievable due to their variability and instability, energy storage systems stabilize energy demand against irregular generation. Lead batteries currently represent the most used electrochemical storage systems in this field, even if they are characterized by a short life cycle and low efficiency. Currently, many researchers are working hard on studies analyzing the performance of MGs with alternative storage systems (i.e., lithium-ion batteries) with higher efficiency. However, for reasons of opportunity linked to the Tech4You project, the study area is represented by the Engineering Departments of the “Mediterranea” University of Reggio Calabria (Italy), in which a lead-acid storage system already exists. Particularly, in this work, the batteries exploited are lead-acid and rechargeable with reversible redox semi-reactions at the electrodes. In particular, the anode is made up of lead immersed in concentrated sulfuric acid, while the cathode is made up of a lead foil covered in lead dioxide immersed in concentrated sulfuric acid. During the discharge phase, i.e., when the accumulator supplies electric current, the direct reaction occurs, while in the charging phase the reverse reaction occurs. In this paper, we represent the battery by a controlled voltage source in series with an internal constant resistance. Therefore, indicating by the battery current, the voltage of the battery’s output, , is evaluated as follows,
in which E and represent the open circuit voltage and its internal resistance, respectively. Moreover, the open circuit voltage, E, is evaluated as follows,
in which is the battery constant voltage and is the battery capacity. Furthermore, k is the polarization voltage and, being the current in the battery, it follows that represents the actual battery charge. Finally, A is the exponential zone amplitude and B is the exponential zone time constant inverse. The bank of batteries is connected to the DC bus via a bidirectional buck-boost DC/DC converter whose dynamic model, as proposed in [10,26], is the following:
in which and are the instantaneous values of inductor current voltage and capacitor voltage, respectively; is the total power, the power generated and load demand power; is the nominal battery voltage; and R is the load resistance while is the equivalent series resistor of the BDC inductor. Finally, C and L are the capacitance and inductance of the converter, respectively.
To limit the degradation of the battery to the benefit of its life, its capacity must be kept within certain limits:
in which and represent the minimum and maximum battery capacity, respectively. Finally, the of the battery can be evaluated as follows
The battery efficiency does not reach 100%, and only a part of the charging amp hours can be returned. In particular, we assume that the battery range is between 20 and 80%. Finally, using a proposed hysteresis control [26], two complementary PWM signals are generated, controlling the switches of the bidirectional buck-boost DC/DC converter to regulate the charge/discharge operations and maintain the DC bus value at 400 V.
Remark 6.
Finally, it is easily verifiable that (14) admits an equivalent fuzzy system, as detailed in Remark 2.
Proposition 4.
Proof of Proposition 4.
See Appendix D. □
Remark 7.
It is worth observing that energy supplies, whose dynamic behaviors are governed by systems of differential equations, highlight different action times, which raises the issue of synchronization. A possible solution would require the adaptive insertion of delay times into each of the equations, resulting in challenges to numerical solution in a reasonable time. It follows that the mathematical models for these smart grids are difficult to use.
3.4. Fuel Cell Modeling and Its Control
Regarding fuel cells, recent studies have identified how solid oxide cells have broad applicability in various MG systems, including grid-connected, backup and autonomous configurations that achieve high efficiencies. However, since the selected study area already had a hydrogen cell (in accordance with the Tech4You Project), the FC used in this work is a proton exchange membrane cell (PEMFC) for converting chemical energy into electrical energy through the electrochemical combustion of hydrogen and oxygen, with the production of electricity, water and heat development. The anode and cathode, loaded with the catalyst, are separated by an electrolyte. The fuel arrives at the anode (where the oxygen oxidizes, releasing negative ions) while the oxygen, supplied by the air, arrives at the cathode where it absorbs electrons. In order to maintain the stability of the system, it is imperative that the electron flow is externally directed through an electrical circuit [6]. The open-circuit voltage of the FC, , depends strongly on the Gibbs free energy which is influenced by the type, pressure and concentration of the reactants and by the types of reaction products. The ideal is provided by the following contribution
In (17), represents the rated voltage constant while indicates the electromotive forces under standard pressure; T is the operating temperature and z and F are the transferring electron number and the Faraday constant, respectively. Moreover, and indicate the gas pressures, respectively.
However, in practice this voltage is less than its theoretical value due to some voltage drop that affects the reversible voltage-current density curve (see Figure 2 in [73]). In particular, due to the conversion of products into reactants in the catalytic state, an activation voltage drop, , occurs. It can be evaluated as follows [26,73],
in which is the cell output current; and N are the dynamic response time constant and the number of cells, respectively.
Furthermore, due to the transport of ions through the membranes and the internal resistances of the materials, a further voltage drop, , occurs, which can be calculated as follows:
where represents the inner resistance of the stack and is the cell output current.
Remark 8.
It is worth noting that, as the chemical reactions proceed, the concentration of hydrogen and oxygen on the electrodes varies significantly, resulting in a further mass transport voltage drop. However, in this paper, such a voltage drop is not considered.
As regards control of the FC, the EMS generates a reference current compared to the actual current produced by the FC so that a proportional-integral-derivative PID regulates the error. The controller, the PWM signal generated in controlling the boost converter, sees its average value precedent [26].
4. The Energy Management Systems: A Mamdani Fuzzy Approach
In this work, we start with the EMS based on a fuzzy Mamdani multi-input single-output (MISO) system studied in [26], and structured through a rule bank based on the expert’s knowledge (considering any limitations and non-linear behaviors that each component highlighted). The system ensured a uniform power profile of the islanded DC-MG, reducing power fluctuations and peaks. As shown in Figure 2, the system inputs are , which subtracts the power of the renewable sources from the load power, and the SoC of the accumulator considering the reference power FC as production. The MISO fuzzy system depicted in Figure 2 represents the EMS of the MG under study, whose MatLab/Simulink scheme is displayed in Figure 3.
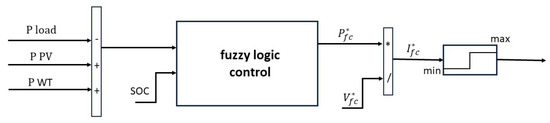
Figure 2.
MISO fuzzy system: (W) is the sum of the power supplied by the renewable sources and the difference between the rate obtained from the sum and the power requested by the load, while the SoC (%) represents the state of charge of the battery.
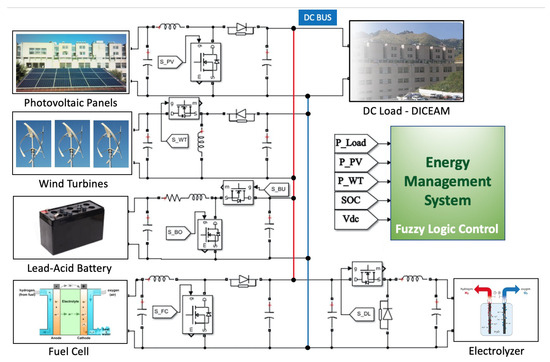
Figure 3.
MatLab/Simulink scheme of the proposed DC-MG.
In particular, the FIS considered in [26] treated and through linguistic subsets operating on the respective universes of discourse. The range of possible values for each variable (universe of discourse, ), as specified in [26], are:
Moreover, for each variable, trapezoidal/triangular FMFs have been formulated to fuzzify each variable, , as follows
As detailed in Table 2, for , five FMFs were considered (High-Negative, , Negative, , Medium, , Positive, , High-Positive, ); for , three MFs have been considered (Low, , Medium, , High, ); finally, for four FMFs have been considered (Very-Low, , Low, , Medium, , High, ).

Table 2.
Characterization of FMFs for the fuzzy MISO system in [26].
The criterion with which the fuzzy rules were constructed (see Table 3) is based on the following assumptions:

Table 3.
Fuzzy rule bank for the MISO system proposed in [26].
- (a)
- If the has a low value and the has a strongly negative value, the is certainly high, so the FC should deliver maximum power while, if the has a negative value, the has a medium and therefore the cell would deliver half the power;
- (b)
- In the case in which the has a low value and stands at average values, should be low so that the cell delivers reduced power, unlike the case where stands at positive (highly positive) values, requiring low (very low) values;
- (c)
- The situation is a little more complex when stands at average values. In these cases, if is clearly negative (negative, highly positive), would settle at average values (low, very low) and therefore the cell would deliver an average value (low, very low, very low) of power;
- (d)
- If has a high value and has a highly negative value (negative, positive, highly positive), has a medium value (medium, very low, very low); then, the FC delivers half (reduced percentage, reduced percentage) of the power that can be delivered.
A fuzzy inference applies the rules to each input, obtaining a composite fuzzy set generated by the union of two or more MFs (depending on the number of activated rules) via a t-norm based on the evaluation of the minimum value of the membership degrees involved. Finally, the centroid was extracted from the aforementioned composite fuzzy set to obtain a crisp value of the output. However, it is worth noting that Mamdani-type FISs, even though they are characterized by precise fuzzifications and linguistically interpretable rules (hence adaptable to human input), provide less flexibility in the design of EMSs. This is because they provide moderately discontinuous surface output, requiring quantified .
5. The Energy Management System: A TS Optimized Approach
Fuzzy inference (or fuzzy reasoning) is used in a fuzzy rule to determine the result starting from the inputs. The fuzzy rules, as a whole, represent the control strategy starting from knowledge and/or experience. In each rule, the information assigned to the input variables (via the antecedent) is transferred to the consequent via fuzzy inference. To remedy the disadvantages of an EMS designed with the Mamdani approach, in this paper we reformulate the problem for TS inference, typical of MISO systems, where the antecedent parts of the fuzzy rules, regarding the Mamdani formulation, remain unchanged. As presented in [26], a fuzzy Mamdani rule is made up of two fundamental sections: the first section, which precedes “THEN”, represents its antecedent while what follows “THEN” represents its consequent. After fuzzifying the data, the rule applies the fuzzy “and” operator (i.e., Mamdani minimum inference or drastic product inference) to the resulting operations on the membership values in the rule, obtaining a combined fuzzy membership value that is the result obtained from the antecedent of the same rule. Then, the “THEN” operator represents the inference of the rule as it transfers the information from the antecedent to the consequent. In particular, the Mamdani procedure cuts the output fuzzy set to the fuzzy membership value obtained by applying the “and” connective (i.e., the combined value obtained above) [26]. Obviously, each rule provides its cut fuzzy set as explained above. These cut fuzzy sets are then aggregated together, usually through superposition and consequent envelope, whose center of gravity is the real number representing the defuzzified value of the output.
For TS fuzzy rules, while maintaining the same steps as Mamdani’s inference regarding fuzzification and connective application, the output is structured as a set of singletons and a typical fuzzy rule assumes the following form
in which the output is performed via linear polynomial combination of the inputs, and , even if higher-degree polynomials can be taken into account with significant increase in computational complexity. In (23), and represent the FMFs, affected by the k-th fuzzy rule, of the two inputs, respectively. Moreover, and indicate the model parameters to be trained. Then, for a generic fuzzy rule, we indicate by and the membership values of to and to , respectively, and since the “and” connective is present, the output will be activated at the value . Therefore, the output, y, is achieved by applying the generalized defuzzifier,
To better understand how (24) works, consider as an example the fuzzy inference illustrated in Figure 4 whose fuzzy rules are structured as in (23). It is worth noting that not all fuzzy rules are always activated. For example, by choosing (at random) and as input variables, it is easy to verify that only some rules are activated (in this case, rules 3, 4, 8, 12 and 13 are activated). From Figure 4, we can easily see that activates the first rule with an activation degree while activates the first rule with an activation degree . Since a fuzzy rule is stable when the output is activated with [72], it follows that the first fuzzy rule does not participate in the definition of the output. Table 4 displays all the activation coefficients for each inference rule depicted in Figure 4.
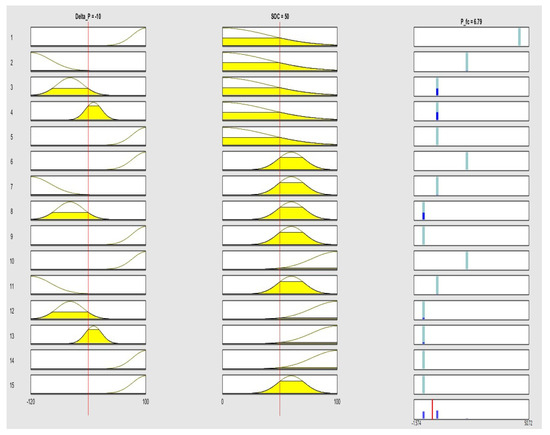
Figure 4.
TS optimized approach: the structure of the inference and output generation for two specific values of inputs ( and ).

Table 4.
Activation coefficients for each inference rule depicted in Figure 4.
Therefore, according to Table 4, (24) becomes
in which the weights and are determined by the procedure described below.
The system was trained using PSO to obtain the parameters of the fuzzy sets associated with the antecedents, while the BLS-based approach was exploited to obtain the polynomial coefficients of the output. In particular, in each iteration of the PSO procedure, each particle of the swarm contains the characteristic parameters of the Gaussian membership functions (peaks and widths) which, through the BLS approach, determine the consequent of the fuzzy rules. As the iterations proceed, the particles move in the definition space, generating a new set of parameters which will generate as many consequences. The best solution is obtained by minimizing an objective function.
Such FSs have greater flexibility in design by obtaining continuous surface outputs. Finally, a tuning procedure has been exploited to optimize the localization for each FMF.
5.1. PSO for Structuring the Antecedents of Each Fuzzy Rule
PSO considers a group of particles dispersed in a given search space. Let d be the dimension of this space. A generic particle, equipped with position, , and velocity, , with the best local position, , accesses the best global position , identified from the swarm, through the optimization of an objective function based on the PSO algorithm in which the velocity and position of the particles are calculated as follows [74]:
in which and represent two vectors with uniformly distributed random numbers in , i is the current iteration number and and are positive constants. In (26), the addends inertial considers the tendency of the particle to move in the same direction, the cognitive considers the attraction towards their best personal positions and the social considers possible movements towards the best positions previously found by any particle [74].
5.2. BLS for Optimizing the Fuzzy Output
Indicating by [74]
the fuzzy basic functions (FBFs), the output of the system can be written as follows,
Furthermore, setting (modified FBFs)
we finally achieve
Output (31) can be written in matrix form. In fact, indicating by
we easily achieve:
in which
To obtain the model parameters, consider n training observations, , , from which to construct the following regression model
We introduce the following cost function to minimize:
in which is the output (31), which represents a measure of precision to determine the accuracy of the model (the lower this value, the more accurate the performance).
Therefore, if , the optimal solution is given by
in which is the input data matrix. Obviously, if the problem is an ill-posed one, (38) is rewritten in the following more convenient form
where is a positive regularization parameter and, as usual, is the identity matrix. Thus, for the cost function (37), we need to add the addend obtaining:
5.3. BLS and PSO: Steps of the Procedure
The approach we propose starts by setting both the maximum number of iterations, , and the number of particles.
Each particle represents a peak or the width of each Gaussian representing a fuzzy set. Thus, the particles for each rule are [74]
Each particle is initialized by the following assumptions:
in which
and
with, ,
Furthermore, recent scientific literature suggests the following good position [74]
The next step, starting from and , and , updates and by
respectively, in which “rand” is a randomly generated number belonging to . Moreover, and represent the widths of the initialization ranges for the peaks. Furthermore,
and
with .
Exploiting (35), , are determined which contain the modified fuzzy basis functions as defined in (30).
Next, the regression matrix (36) is computed to then determine the polynomial coefficients (38). Obviously, if is a singular matrix, (39) is used instead of (38) (using an appropriate ), then calculating the RMSE,
For particles that exhibit repeating peaks, a penalty is applied by assigning them a high value of the objective function.
Next, and are updated based on the evaluation of the objective function. Therefore, by (26) and (27), both the velocity and the position are updated.
At this point, we limit the peaks and into the intervals, and ; just as and are limited in the intervals and .
Finally, the whole procedure repeats until the number of iterations reaches . Then, the obtained provides the best solution. Figure 5 displays the flow diagram showing all the steps of the procedure.
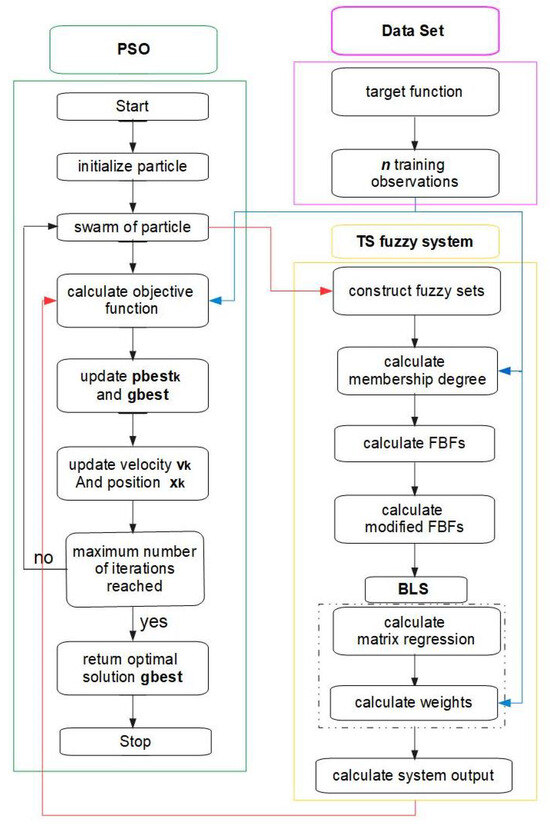
Figure 5.
The PSO-BLS method: the steps pertaining to the PSO are grouped in green; the steps concerning the training observations are in purple, while the steps concerning the TS fuzzy system, in which the BLS approach is also developed, are in yellow.
6. The Energy Management System: A TS Intuitionistic Fuzzy Approach
An IF set is an object in structured in the following form:
where and , such that
and
represent the membership and non-membership functions. Moreover, it is also defined as another function,
which represents the hesitation part (the larger , the greater the decision maker’s margin of hesitation), increasing the accuracy in the management of uncertainties. Then, the need arises to construct two FISs: one relating to the function , whose k-th rule takes the form:
another, relative to the function , where the k-th rule becomes:
Each fuzzy rule produces two outputs, and , which, similarly to what was done in the TS approach (non-intuitionistic), can be written as follows
Finally, the convex combination of and produces the final output of the intuitionistic FIS:
in which represents the weight of .
Remark 9.
Obviously, if , the system becomes a classical TS; if , only the non-membership component impacts the TS system. In this paper, to equally consider the components (membership and non-membership), we set .
As is known, Mamdani fuzzy systems build the fuzzy rule bank through manual inspection, resulting in a limitation to recognizing all the rules. To determine the number and antecedents of the fuzzy rules, we use a Subtractive Clustering Algorithm (SCA) so that the cluster centers determine N and the antecedents. In particular, the real data provided by the Technical Physics research group of the DICEAM Department has been structured into two technical sheets (one for inputs and one for output) made up of a single column and with an adequate number of rows for containing all the linguistic information associated with each input and the output (translated into ASCII format).
Next, it is necessary to set a constant positive that governs the spatial influence of the cluster, : high values of generate few fuzzy rules; small values of could produce a high number of cluster centers producing the overfitting phenomenon. Then, the optimization of the parameters , , ⋯, , and , , ⋯, , with in both (59) and (60) determine the consequent of each rule. In SCA, each data point is considered a potential cluster center. The extent of the potential of each point , here, is quantified via the following formulation,
in which and represent two generic data points. Therefore, there will exist a data point, relative to many points close to it, that exhibits the maximum value of ; this data point represents the first cluster center, .
Next, on this first cluster center, a new radius is fixed, , which determines its neighborhood; thus, if is the potential of ,
represents the quantity to subtract from to obtain its updated value, that is, becomes
The procedure is repeated until all the data points are associated with one or more clusters. Obviously, each will be decomposed into two component vectors; , which contains the first n elements of (i.e., input data), and , which contains the output component. Since the intuitionistic system considered is first-order, it makes sense to compute the output as
where is a constant vector and is a real constant (even zero). To easily understand the approach for parameter estimation, it will be sufficient to interpret the procedure as the least squares estimate of the form where is an array of output values, is a constant array and is an array of parameters to estimate. To compute , minimize . Alternatively, it is possible by computing the pseudo-inverse of , that is,
Since the calculation of is quite onerous, we look for two orthogonal matrices and and a matrix tridiagonal such that . The Householder approach easily allows us to decompose into . Then, we look for the spectral decomposition of (symmetric tridiagonal) that is simplest to determine (computational cost of the order of ). In this case, the Bauer–Fike theorem is applicable and provides a particular increase in the absolute error, which confirms the sensitivity of the eigenvalues from the condition number of the eigenvector matrix. This allows the creation of stable fuzzy TS systems [72].
Table 5 summarizes some differences between the exploited fuzzy inferences.

Table 5.
Main differences between the three adopted power management procedures.
7. RES Characteristics and Load Profile
7.1. Location and Meteorological Parameters
In this paper, the EMS described above, implemented in MatLab/Simulink Toolbox R2023a, refers to a DC-MG (equipped with WT and PV sources on lead-acid battery and cell) in stand-alone mode for the community academics of the Department of Civil, Energy, Environmental and Materials Engineering (DICEAM) of the “Mediterranea” University of Reggio Calabria (geographical coordinates, 38715.138 N/153955.315 E) located on the Messina Channel in southern Italy. The location is affected by mild winters and very hot summers and considering that teaching, research and third-mission activities at DICEAM are interrupted for only twenty days in the month of August, it makes sense to evaluate the effectiveness and efficiency of the intuitionistic fuzzy EMS designed in July. The training and testing of real meteorological parameters (sampled by special control units located in the study area) were provided by members of the Technical Physics Research group of the DICEAM Department. They considered solar radiation which exceeds 900 W/m2 in the early afternoon hours with a temperature well above 40 °C (see Figure 6 where the 24 h are displayed on a 100 s scale). The wind speed in the chosen location highlights a high potential for energy exploitation as highlighted in Figure 6. These data were used for the training of the proposed TS systems, while for testing, an additional database of real data with the same characteristics was set up.
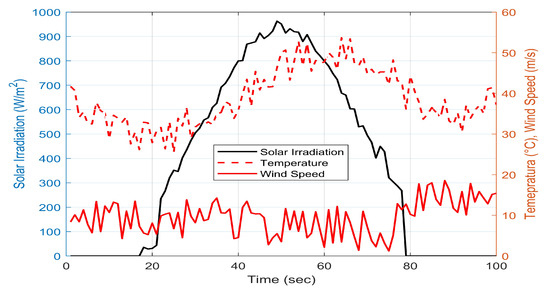
Figure 6.
Solar irradiation (W/m2), temperature (°C) and wind speed (m/s) of the selected location (20 July 2023).
7.2. Load and RES Power Profiles
The real load data (both training and testing), following a specific request, were provided by the energy supply company, while the real RES data were provided by both the Technical Physics Research group and the Electrical Systems Research group. Figure 7, in relation to the case study, highlights the trend of the load power requested during the entire observation period. Through analysis of the aforementioned figure, it can be seen that the load power is minimal at the beginning of the day as well as in the early hours of the afternoon where there is a real collapse in consumption, mainly due to the interruption of the canteen service and the educational activities that, in the summer periods, are limited exclusively to midday. The peak power of over 135 kW was reached around 1.30 p.m. However, in the late afternoon there was an increase in consumption due to preparations for a party organized by the student associations, a level of consumption which lasted almost all night.
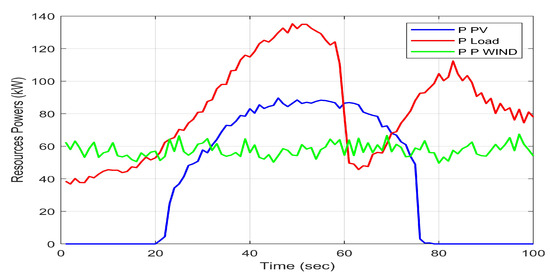
Figure 7.
Power evolution of load side and PV/WT (20 July 2023).
As regards the power supplied by the PV system, it stands at a maximum value of just over 89 kW (but significantly lower than the peak power of the load) where the maximum solar radiation is evident (the high-temperature values will, however, influence the efficiency of the power delivered). This power is drastically reduced in the afternoon hours due to the sharp drop in solar radiation. Regarding the power provided by the wind source, since the wind speed is significant (although not constant), it fluctuates between 49 and 67 kW with a significant increase in the evening hours due to the strong breeze blowing from the sea (see Figure 7).
From Figure 8, it can be seen how the generated power, for long periods, exceeds the load power. In particular, until around five in the morning this condition is verified as well as after five thirty in the morning until 6 pm. Afterward, due to the lack of solar source and the increasing load, this condition is no longer verified. Obviously, an additional database of real data with the same characteristics has also been set up for the load and RES power profiles.

Figure 8.
Trend of power of the renewable sources, of the load and of the (20 July 2023).
8. Some Implementation Aspects
8.1. Optimized TS System: Some Relevant Results
The Mamdani-type fuzzy system proposed in [26] and described in Section 4, through the Fuzzy Toolbox of MatLab R2023b, has been preliminarily transformed into a TS fuzzy system with the same rules but with Gaussian FMFs for the inputs. The input tuning phase was performed by the PSO technique as described in Section 5.1 while the outputs were optimized using the BLS proposed in Section 5.2, with . For the tuning operation, real data provided by the weather stations present at the DICEAM and by the power sensors near each renewable source over the 24 h of the day examined were used. Even after the tuning phase, the number of rules remained unchanged compared to the system proposed in [26], still respecting the fuzzy rule bank detailed in Table 3, confirming that the experts’ knowledge poured into [26] was adequate. Figure 9a,b display the MFMs of the inputs obtained following the tuning operation from which it can be deduced that, compared to the FMFs in [26], the modification of the localization on the respective universes of the discourses has produced a clear improvement in both continuity and regularity of the control surface (see Figure 10a,b).
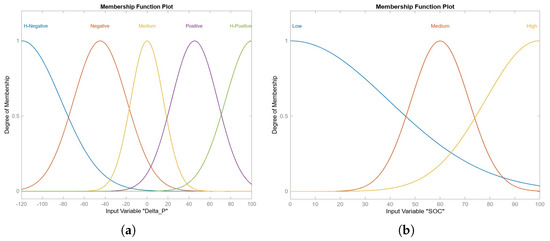
Figure 9.
FMFs for (a) and (b) in TS optimized approach.
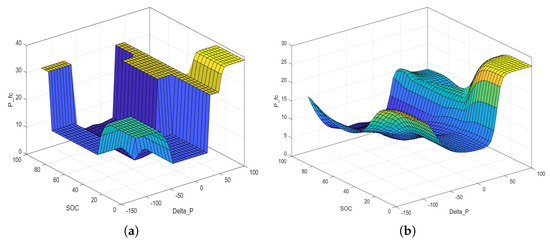
Figure 10.
Control surface achieved by (a) Mamdani model in [26] and by (b) TS optimized approach.
Figure 4 displays the fuzzy inference structure of the optimized TS system. It should be noted that, whatever the values of the inputs, not all the fuzzy rules are necessarily activated; only a few rules, for each pair of inputs, participate in the quantification of the output.
8.2. Optimized Intuitionistic TS System: Some Relevant Results
Using SCA, the TS intuitionistic fuzzy system was set up by choosing the number of rules and the number of FMFs and non-FMFs through an appropriate selection of the value to avoid overfitting phenomena. In particular, we tested different values of belonging to the interval obtaining a hesitation level (with ), confirming the values usually suggested by the scientific literature [75,76]. Then, and can be formulated as follows:
in which and are its peak and width, respectively. A suitable number of simulations were carried out to optimize the value of which, increasing in , will make weigh more than . Obviously, the selected is the one that produces the minimum root-mean-square error (RMSE). As can be seen from Table 6, in our case, the optimal value is .

Table 6.
Optimized intuitionistic TS system: RMSE on benchmark datasets.
This system has been implemented by MatLab Toolbox R2023b using the joint BLS and PSO approach to obtaining an optimized intuitionistic FS whose FMFs of the inputs are, respectively, displayed in Figure 11a,b. Finally, Figure 12 depicts the control surface which, in addition to maintaining the characteristics of regularity and continuity required for stable control, highlights a greater differentiation of the control action at the extremes of each variable.
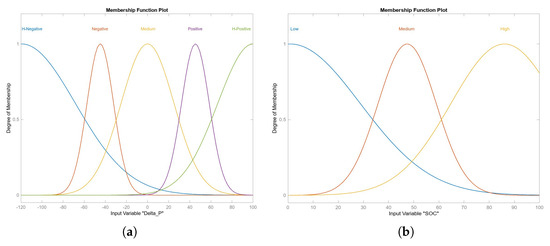
Figure 11.
FMFs for (a) and (b) in intuitionistic TS optimized approach.
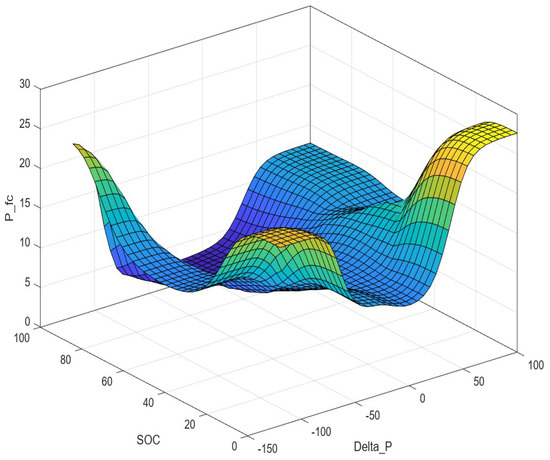
Figure 12.
Control surface achieved by intuitionistic TS optimized approach.
8.3. Evaluation of the Model Quality
To compare the performance of both models, since the dataset is small, we used leave-one-out cross-validation (LOOCV) [77]. In particular, as in [74], we evaluated the square root of the mean square error defined as:
in which denotes the output of the model achieved in the i-th step of the validation process. Particularly, in the step of the BLS-PSO approach, the data are removed from the training data so that the parameters to be determined in the consequent of each fuzzy rule are calculated using the BLS approach without the above data. This allows a reliable evaluation while avoiding any overfitting.
Table 7 displays the numerical values obtained for . It is highlighted that the intuitionistic approach offers significantly higher performance than the other two approaches, with completely comparable CPU-time, even if there is a substantial increase in the number of rules compared to the Mamdani approach studied in [26]. This is because the intuitionistic approach, unlike Mamdani’s method, constructs a linear function as output, whose coefficients have already been determined in the training phase.

Table 7.
Cross-validation error, number of rules and CPU-time for each fuzzy approach.
9. Relevant Results and Discussion
Let us preliminarily observe that both the optimized TS system and the optimized intuitionistic TS system showed significant performance by covering the demand represented by the load, whatever the operating conditions. This is because the number of rules and their structuring in terms of localization and shape of the FMFs are obtained with deep-learning techniques directly from real data, without relying on expert knowledge, considerably reducing the risk of neglecting any MG behaviors. However, some differences in behavior regarding both the use of the battery and the FC should be highlighted. In all the cases discussed, it is clear that the battery is charged both at the beginning of the day and in the early afternoon hours, so that when the load is less than the energy production, the excess power is stored, also guaranteeing the stability of the bus by balancing the entire system. The battery discharge process occurs in the meridian period or when the generated power is not enough to cover the load (essentially due to the lack of solar energy). As in [26], backup devices step in to share the missing power. As regards the FC, until late afternoon, its activation is negligible in all cases treated. However, using the Mamdani system, when the battery power drops, the FC is forced to deliver substantial amounts of power with consequent consumption of . This phenomenon is significantly mitigated if both optimized TS systems work. In particular, the intuitive approach offers a slight performance increase compared to the optimized TS, but without considering the uncertainty in the FMFs. Finally, the excess power is well recovered for hydrogen production (for details, see Figure 13, Figure 14 and Figure 15).
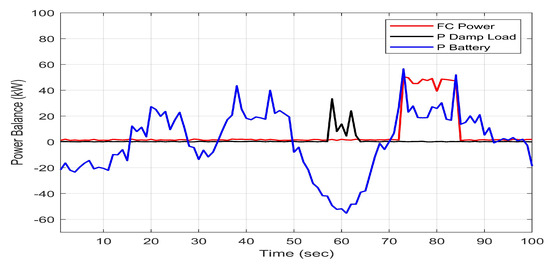
Figure 13.
The power balance of battery/FC/Electrolyzer for Mamdani approach in [26].
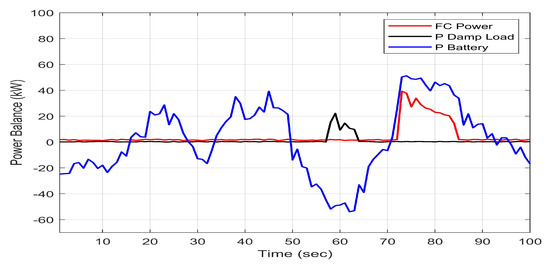
Figure 14.
The power balance of battery/FC/Electrolyzer for TS optimized approach [26].
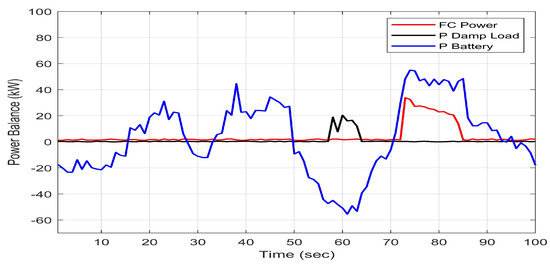
Figure 15.
The power balance of battery/FC/Electrolyzer for intuitionistic TS optimized approach [26].
Regarding the percentage variation of the battery SOC over 24 h, as in [26], there are no large differences in performance when the fuzzy approach used varies. This is due to the switching mode implemented in the simulation phase, as is done in [26]. However, Mamdani’s approach confirms a consistent charging–discharging trend of the battery, as already highlighted in [26], since the use of energy coming from the FC is more marked compared to both implemented TS systems, which have better performance in SoC percentages (see Figure 16). This is highlighted even more by the fact that the air and hydrogen consumption of the FC stands at around 111.14 Ipm for the Mamdani system while for the optimized and intuitionistic TS systems they stand at around 44.26 Ipm and 39.18 Ipm, highlighting that the TS approaches proposed require less battery consumption.
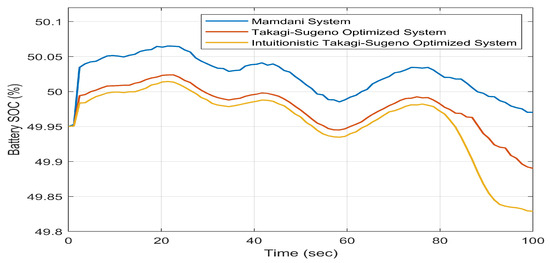
Figure 16.
Battery SoC.
Finally, it is worth underlining the fact that the optimization procedures concern exclusively the localization of the membership functions (and, in the case of the intuitionistic approach, of the non-membership functions and consequent hesitation functions). It follows that the runner tiles of each fuzzy approach used, being all rules of the same structure, have completely comparable execution times (and, in any case, are dependent on the type of workstation used).
10. Conclusions and Perspectives
The most recent guidelines for the design of DC-MGs (equipped with appropriate converters) for the management of energy flows from renewable sources direct designers towards comparative studies of potential control techniques for strategic energy management. Furthermore, the ever-increasing diffusion of AI techniques makes it possible to exploit innovative techniques which also involve any uncertainties and/or inaccuracies present in the data. In this work, starting from a well-known EMS managed via a Mamdani-type fuzzy rule bank (in which the fuzzy rule bank is built exclusively through expert knowledge), the dynamic performance has been improved, minimizing consumption of fuel, using optimized TS approaches together with intuitionistic formulations. The results obtained are encouraging, especially if we compare the SOC obtained and the consumption of . The better performance can be attributed to the optimized intuitionistic approach of the TS, which also demonstrates efficient response times that are still dependent on the available workstation. This allows for effective collaboration with the Research Units involved in the Tech4You Project, with which we share some common objectives. It should be underlined that the proposed approach, in addition to exhibiting interesting results and performance, is independent of the type of data processed. In other words, the design steps of an intuitionistic fuzzy TS system, with the technique used in this article, do not change when considering different geographic locations. Obviously, for larger and more diverse DC-MG systems, the number of inputs will change with a consequent increase in the number of rules; however, given that the proposed formulation is general both in terms of input and in terms of rules (especially regarding the deep-learning techniques used for optimization), the transferability of the approach is ensured. Furthermore, the proposed approach is to be considered as a preliminary basis for the development of an industrial prototype which aims to unmask inaccuracies by proposing model-free chips and processors which require a lower number of rules to function compared to traditional processors (based on boolean methods). This allows you to structure forecasting models in which the fuzzy aspect is based on the possibility of managing partially true statements without falling into contradictions. Certainly, in the near future, we believe it is appropriate to proceed with the optimization of intuitionistic functions through the joint use of intuitionistic fuzzy systems with multilayer neural networks. This allows the use of back-propagation learning algorithms (or other more advanced ones) in order to size the weights of the synapses based on the intended use of the MG, making its use in real applications more flexible.
Author Contributions
Conceptualization, M.V. and F.L.F.; methodology, M.V. and F.L.F.; software, M.V. and F.L.F.; validation, M.V. and F.L.F.; formal analysis, M.V. and F.L.F.; investigation, M.V. and F.L.F.; resources, M.V. and F.L.F.; data curation, M.V. and F.L.F.; writing—original draft preparation, M.V. and F.L.F.; writing—review and editing, M.V. and F.L.F.; visualization, M.V. and F.L.F.; supervision, M.V. and F.L.F.; project administration, M.V. and F.L.F.; funding acquisition, M.V. and F.L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Next Generation EU—Italian NRRP, Mission 4, Component 2, Investment 1.5, call for the creation and strengthening of ‘Innovation Ecosystems’, building ‘Territorial R&D Leaders’ (Directorial Decree n. 2021/3277)—project Tech4You—Technologies for climate change adaptation and quality of life improvement, n. ECS0000009 (in particular, action 9 of Spoke 2—Goal 2.1—Pilot Project 1). This work reflects only the authors’ views and opinions; neither the Ministry for University and Research nor the European Commission can be considered responsible for them.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article material, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC-MG | Alternative Current Microgrid System |
| AI | Artificial Intelligence |
| BLS | Batch Least Square |
| DC-MG | Direct Current Microgrid System |
| EMS | Energy Management System |
| ESS | Electrolyzer (Dump-Load) |
| FBF | Fuzzy Basis Function |
| FC | Fuel Cell |
| FS | Fuzzy System |
| MF | Membership Function |
| MG | Microgrid |
| MISO | Multi-Input Single-Output |
| MPP | Maximum Power Point |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| PMSG | Permanent Magnet Synchronous Generator |
| P&O | Perturb and Observe |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic Panel |
| RES | Renewable Energy Resources |
| SCA | Subtractive Clustering Algorithm |
| SoC | State of Charge of the Battery |
| WT | Wind Turbine |
Appendix A. Proof of Proposition 1
To prove the existence and uniqueness of the solution for (3), we will use the following result known in the literature [78].
Theorem A1.
Let us consider a continuous function on with and T bounded. So, if there exists a positive constant K such that the inequality
holds for every , (i.e., is Lipschitzian in ), then for every there exists a unique continuous and differentiable for every solution of the following Cauchy’s problem:
Appendix B. Proof of Proposition 2
As in Proposition 1 (see Appendix A), indicating by , considering that both and are bounded functions, (A1) is verified with
Therefore, model (11), by way of Theorem A1, admits a unique solution.
Appendix C. Proof of Proposition 3
Retracing the same steps of the proof of Proposition 1 (see Appendix A), indicating by , (A1) is verified with . Therefore, it follows that model (11), by Theorem A1, admits a unique solution.
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilina, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Succetti, F.; Rosato, A.; Araneo, R.; Di Lorenzo, G.; Panella, M. Challenges and Perspectives of Smart Grid Systems in Islands: A Real Case Study. Energies 2023, 16, 583. [Google Scholar] [CrossRef]
- Chen, Z.; Amani, A.M.; Yu, X.; Jalili, M. Control and Optimisation of Power Grids Using Smart Meter Data: A Review. Sensors 2023, 23, 2118. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Arya, Y. Jaya-ITDF control strategy-based frequency regulation of multi-microgrid utilizing energy stored in high-voltage direct current-link capacitors. Soft Comput. 2023, 27, 5951–5970. [Google Scholar] [CrossRef]
- Yong, L.; Mingmin, Z.; Yijia, C. Stability Analysis, Flexible Control and Optimal Operation of Microgrid; Springer: Singapore, 2023. [Google Scholar]
- Dahale, S.; Das, A.; Pindoriya, N.M.; Rajendran, S. An Overview of DC-DC Converter Topologies and Controls in DC Microgrid. In Proceedings of the 7th Int Conf Power Syst (ICPS), Pune, India, 21–23 December 2017; pp. 410–415. [Google Scholar] [CrossRef]
- Alam, S.; Saleh Al-Ismail, F.; Fahad, A.; Al-Sulaiman Mabito, M.A. Energy management in DC microgrid with an efficient voltage compensation mechanism. Electr. Power Syst. Res. 2023, 214, 108842. [Google Scholar] [CrossRef]
- Afifi, M.A.; Marei, M.I.; Mohamad, A.M.I. Modelling, Analysis and Performance of a Low Inertia AC-DC Microgrid. Appl. Sci. 2023, 13, 3197. [Google Scholar] [CrossRef]
- Abadi, S.A.G.K.; Khalili, T.; Habibi, S.I.; Bidram, A.; Guerrero, J.M. Adaptive control and management of multiple nano-grids in an islanded DC microgrid system. IET Gener. Transm. Distrib. 2023, 17, 1799–1815. [Google Scholar] [CrossRef]
- Soumeur, M.A.; Gasbaoui, B.; Abdelkhalek, O.; Ghouili, J.; Toumi, T.; Chakar, A. Comparative Study of Energy Management Strategies for Hybrid Proton Exchange Membrane Fuel Cell Four-Wheel Drive Electric Vehicle. J. Power Sources 2020, 462, 228167. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J.M. A Coordinated Control of Hybrid ac/dc Microgrids With PV-Wind-Battery Under Variable Generation and Load Conditions. Int. J. Electr. Power Energy Syst. 2019, 104, 583–592. [Google Scholar] [CrossRef]
- Das, S.; Singh, B. Self-Synchronizing Control Enabling Disruption-Free Operation and Seamless Mode Transitions in Wind–Solar Based Hybrid AC/DC Microgrid. IEEE Trans. Ind. Appl. 2023, 59, 4797–4807. [Google Scholar] [CrossRef]
- Pires, V.F.; Pires, A.; Cordeiro, A. DC Microgrids: Benefits, Architectures, Perspectives and Challenges. Energies 2023, 16, 1217. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 13154–36172. [Google Scholar] [CrossRef]
- Martinez-Barbosa, A.; Guerrero-Ramirez, G.; Calleja-Gjumlich, J.; Guerrero-Ramirez, E.; Adam-Medina, M.; Aguilar-Castillo, C.; Aguayo-Alquicira, J. Modeling and Control of an Air Conditioner Powered by PV Energy and the Grid Using a DC Microgrid. Processes 2023, 11, 1547. [Google Scholar] [CrossRef]
- El-Shahat, A.; Sumaiya, S. DC-Microgrid System Design, Control, and Analysis. Electronics 2019, 8, 124. [Google Scholar] [CrossRef]
- Puchalapalli, S.; Singh, B.; Das, S. Grid-Interactive Smooth Transition Control of Wind-Solar-DG Based Microgrid at Unpredictable Weather Conditions. IEEE Trans. Ind. Appl. 2023, 12, 1–11. [Google Scholar] [CrossRef]
- Wei, D.; Zhang, L.; Zhang, N.; Fang, J.; Qian, Q. Optimal Generation Planning in a Micro-Grid for Supplying Electrical and Thermal Loads in Order to Reduce Pollutant Emissions. J. Clean. Prod. 2023, 421, 138531. [Google Scholar] [CrossRef]
- Ibraheem, M.I.; Edrisi, M.; Gholipour, M.; Alhelou, H.H. A Novel Frequency Rgulation in Islanded Microgrid Using Sliding Mode Control with Disturbance Observers Considering Storages and EVs. Comput. Electr. Eng. 2023, 105, 108537. [Google Scholar] [CrossRef]
- Pathak, P.K.; Yadav, A.K.; Shastri, A.; Alvi, P.A. BWOA Assisted PIDF-(1+ I) Controller for Intelligent Load Frequency Management of Standalone Micro-grid. ISA Trans. 2023, 132, 387–401. [Google Scholar] [CrossRef]
- Mumtaz, F.; Yahaya, N.Z.; Meraj, S.T.; Singh, N.S.S.; Rahman, M.S.; Hossain Lipu, M.S. A High Voltage Gain Interleaved DC-DC Converter Integrated Fuel Cell for Power Quality Enhancement of Microgrid. Sustainability 2023, 15, 7157. [Google Scholar] [CrossRef]
- Kamel, A.; Rezk, A.; Shehata, N.; Thomas, J. Energy Management of a DC Microgrid Composed of Photovoltaic/Fuel Cell/Battery/Supercapacitor Systems. Batteries 2019, 5, 63. [Google Scholar] [CrossRef]
- Jouili, Y.; Garraoui, R.; Ben Hamed, M.; Sbita, L. Self-Adaptive PI-FLC for BLDC Motor Speed Supplied by PEM Fuel Cell Stack Optimized by MPPT. Arab. J. Sci. Eng. 2023, 2, 1–17. [Google Scholar] [CrossRef]
- Li, R. Protection and Control Technologies of Connecting to the Grid for Distributed Power Resources. Distrib. Power Resour. 2019, 6, 121–144. [Google Scholar]
- Samadhiya, A.; Namrata, K.; Kumar, N. An Experimental Performance Evaluation and Management of a Dual Energy Storage System in a Solar Based Hybrid Microgrid. Arab. J. Sci. Eng. 2023, 48, 5785–5808. [Google Scholar] [CrossRef]
- Hafsi, O.; Abdelkhalek, O.; Mekhilef, S.; Soumeur, M.A.; Hartani, M.A.; Chakar, A. Integration of Hydrogen Technology and Energy Management Comparison for DC-Microgrid Including Renewable Energies and Energy Storage System. Sustain. Energy Technol. Assess. 2022, 52 Pt B, 102121. [Google Scholar] [CrossRef]
- Elmorshedy, M.F.; Subramaniam, U.; Mohamed Ali, J.S.; Almakhles, D. Energy Management of Hybrid DC Microgrid with Different Levels of DC Bus Voltage for Various Load Types. Energies 2023, 16, 5438. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Allam, S.M.; Shaheen, A.M.; Nagem, N.A.; Sharaf, A.M. Renewable Energy Micro-Grid Interfacing: Economic and Environmental Issues. Electronics 2022, 11, 815. [Google Scholar] [CrossRef]
- Mancera, J.J.C.; Saenz, J.L.; López, E.; Andújar, J.M.; Manzano, F.S.; Vivas, F.J.; Isorna, F. Experimental Analysis of the Effects of Supercapacitor Banks in a Renewable DC Microgrid. Appl. Energy 2022, 308, 118355. [Google Scholar] [CrossRef]
- Alam, M.S.; Al-Ismail, F.S.; Rahman, S.M.; Shafiullah, M.; Hossain, M.A. Planning and Protection of DC Microgrid: A Critical Review on Recent Developments. Eng. Sci. Technol. Int. J. 2023, 41, 101404. [Google Scholar] [CrossRef]
- Rashad, M.; Ashraf, M.; Bhatti, A.I.; Minhas, D.M. Mathematical Modeling and Stability Analysis of DC Microgrid Using SM Hysteresis Controller. Int. J. Electr. Power Energy Syst. 2018, 95, 507–522. [Google Scholar] [CrossRef]
- Modu, B.; Abdullah, M.P.; Sanusi, M.A.; Hamza, M.F. DC-Based Microgrid: Topologies, Control Schemes, and Implementations. Alex. Eng. J. 2023, 70, 61–92. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; Mosalam, H.A.; Amer, R.A. Optimal Control Design and Management of Complete DC-Renewable Energy Microgrid System. Ain Shams Eng. J. 2023, 14, 101964. [Google Scholar] [CrossRef]
- Negero, N.T.; Duressa, G.F. Uniform Convergent Solution of Singularly Perturbed Parabolic Differential Equations with General Temporal-Lag. Iran. J. Sci. Technol. Trans. A Sci. 2022, 46, 507–524. [Google Scholar] [CrossRef]
- He, J.; Liang, Y.; Hao, X.; Yang, F.; Pan, Q. A Quadratic Convex Framework with Bigger Freedom for the Stability Analysis of a Cyber-Physical Microgrid System. Sci. China Inf. Sci. 2023, 66, 122202. [Google Scholar] [CrossRef]
- Gong, X.; Wang, X. A Novel Koopman-Inspired Method for the Secondary Control of Microgrids with Grid-Forming and Grid-Following sources. Appl. Energy 2023, 333, 120631. [Google Scholar] [CrossRef]
- Munafò, C.F.; Palumbo, A.; Versaci, M. An Inhomogeneous Model for Laser Welding of Industrial Interest. Mathematics 2023, 11, 3357. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, G.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Meta-Learning Based Voltage Control Strategy for Emergency Faults of Active Distribution Networks. Appl. Energy 2023, 349, 121399. [Google Scholar] [CrossRef]
- Rafati, A.; Joorabian, M.; Mashhour, E. An Efficient Hour-Ahead Electrical Load Forecasting Method Based on Innovative Features. Energy 2020, 201, 117511. [Google Scholar] [CrossRef]
- Uzair, M.; Li, L.; Eskandari, M.; Hossain, J.; Zhu, J.G. Challenges, Advances and Future Trends in AC Microgrid Protection: With a Focus on Intelligent Learning Methods. Renew. Sustain. Energy Rev. 2023, 178, 113228. [Google Scholar] [CrossRef]
- Yin, C.; Wu, H.; Locment, F.; Sechilariu, M. Energy Management of DC Microgrid Based on Photovoltaic Combined with Diesel Generator and Supercapacitor. Energy Convers. Manag. 2017, 132, 14–27. [Google Scholar] [CrossRef]
- Puchalapalli, S.; Tiwari, S.K.; Singh, B.; Goel, P.K. A Microgrid Based on Wind-Driven DFIG, DG, and Solar PV Array for Optimal Fuel Consumption. IEEE Trans. Ind. Appl. 2020, 56, 4689–4699. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Javanshir, F.; Kargarzadeh, A. Economic Analysis and Optimal Design of Hydrogen/Diesel Backup System to Improve Energy Hubs Providing the Demands of Sport Complexes. Int. J. Hydrog. Energy 2021, 46, 14109–14129. [Google Scholar] [CrossRef]
- Sedaghati, R.; Shakarami, M.R. A Novel Control Strategy and Power Management of Hybrid PV/FC/SC/Battery Renewable Power System-Based Grid-Connected microgrid. Sustain. Cities Soc. 2019, 44, 830–843. [Google Scholar] [CrossRef]
- Fathy, A.; Ferahtia, S.; Rezk, H.; Yousri, D.; Abdelkareem, M.A.; Olabi, A.G. Optimal Adaptive Fuzzy Management Strategy for Fuel Cell-Based DC Microgrid. Energy 2022, 247, 123447. [Google Scholar] [CrossRef]
- Bello, I.A.; McCulloch, M.D.; Rogers, D.J. A Linear Regression Data Compression Algorithm for an Islanded DC Microgrid. Sustain. Energy Grids Netw. 2022, 32, 100901. [Google Scholar] [CrossRef]
- Montoya, R.; Poudel, B.P.; Bidram, A.; Reno, M.J. DC Microgrid Fault Detection Using Multiresolution Analysis of Traveling Waves. Int. J. Electr. Power Energy Syst. 2022, 135, 107590. [Google Scholar] [CrossRef]
- Poudel, S.; Sun, H.; Nikovski, D.; Zhang, J. Resilient Restoration of Power Distribution System Based on Minimum Spanning Forest. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Grcic, I.; Pandzic, H.; Novosel, D. Fault Detection in DC Microgrids Using Short-Time Fourier Transform. Energies 2021, 14, 277. [Google Scholar] [CrossRef]
- Jeyaraj, P.R.; Asokan, S.P.; Karthiresan, A.C. Optimum Power Flow in DC Microgrid Employing Bayesian Regularized Deep Neural Network. Electr. Power Syst. Res. 2022, 205, 107730. [Google Scholar] [CrossRef]
- Baidya, S.; Nandi, C.A. Comprehensive Review on DC Microgrid Protection Schemes. Electr. Power Syst. Res. 2022, 210, 108051. [Google Scholar] [CrossRef]
- Nallolla, C.A.; P, V.; Chittathuru, D.; Padmanaban, S. Multi-Objective Optimization Algorithms for a Hybrid AC/DC Microgrid Using RES: A Comprehensive Review. Electronics 2023, 12, 1062. [Google Scholar] [CrossRef]
- Kumar, P.; Kannaiah, S.K.; Choudhury, S.R.; Rajasekar, N. Genetic Algorithm-Based Modeling of PEM Fuel Cells Suitable for Integration in DC Microgrids. Electr. Power Compon. Syst. 2017, 45, 1152–1160. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity 2022, 3, 346–364. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Sugeno, M. (Eds.) Fuzzy Systems: Modeling and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Boubaker, S.; Do, D.T.; Hammami, H.; Ly, K.C. The Role of Bank Affiliation in Bank Efficiency: A Fuzzy Multi-Objective Data Envelopment Analysis Approach. Ann. Oper. Res. 2022, 311, 611–639. [Google Scholar] [CrossRef]
- Setyanugraha, N.; Al Aziz, S.; Harmoko, I.W.; Fianti, F. Study of a Weather Prediction System Based on Fuzzy Logic Using Mamdani and Sugeno Methods. Phys. Commun. 2022, 6, 61–70. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Fuzzy Time Series Approach for Disruption Prediction in Tokamak Reactors. IEEE Trans. Magn. 2003, 39, 1503–1506. [Google Scholar] [CrossRef]
- Meliani, M.; El Barkany, A.; El Abbassi, I.; Mahmoudi, M. Energy Management of a Fuzzy Control System in a Microgrid. Proc. E3S Web Conf. 2022, 353, 2002. [Google Scholar] [CrossRef]
- Aysar, M.; Alsayed, M.F. Fuzzy Logic Power Management for a PV/Wind Microgrid with Backup and Storage Systems. Int. J. Electr. Comput. Eng. 2021, 11, 2876–2888. [Google Scholar]
- Shakeel, F.M.; Malik, O.P. ANFIS Based Energy Management System for V2G Integrated Micro-Grids. Electr. Power Compon. Syst. 2022, 50, 584–599. [Google Scholar] [CrossRef]
- Aloo, L.A.; Kihato, P.K.; Kamau, S.I.; Orenge, R.S. Modeling and Control of a Photovoltaic-Wind hybrid Microgrid System Using GA-ANFIS. Heliyon 2023, 9, e14678. [Google Scholar] [CrossRef]
- Cerne, G.; Dovzan, D.; Skrjanc, I. Short-Term Load Forecasting by Separating Daily Profiles and Using a Single Fuzzy Model Across the Entire Domain. IEEE Trans. Ind. Electron. 2018, 65, 7406–7415. [Google Scholar] [CrossRef]
- Ferahtia, S.; Djerioui, A.; Zeghlache, S.; Houari, A. A Hybrid Power System Based on Fuel Cell, Photovoltaic Source and Supercapacitor. SN Appl. Sci. 2020, 2, 940–950. [Google Scholar] [CrossRef]
- Rahman Fahim, S.K.; Sarker, S.; Muyeen, S.M.; Sheikh, M.R.I.; Das, S.K. Microgrid Fault Detection and Classification: Machine Learning Based Approach, Comparison, and Reviews. Energies 2020, 13, 3460. [Google Scholar] [CrossRef]
- Rafi, S.H.; Masood, N.A.; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Yang, M.-S.; Pamucar, D. Aczel-Alsina Aggregation Operators on T-Spherical Fuzzy (TSF) Information With Application to TSF Multi-Attribute Decision-Making. IEEE Access 2022, 10, 26011–26023. [Google Scholar] [CrossRef]
- Naseem, A.; Ullah, K.; Akram, M.; Bozanic, D.; Cirovic, G. Assessment of Smart Grid Systems for Electricity Using Power Maclaurin Symmetric Mean Operators Based on T-Spherical Fuzzy Information. Energies 2022, 15, 7826. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Munda, J.L.; Hamam, Y. Triangular Intuitionistic Fuzzy Aggregating and Ranking Function Approach for the Rating of Battery ‘End-of-Life’Handling Alternatives. Energies 2022, 15, 2248. [Google Scholar] [CrossRef]
- Versaci, M.; Jannelli, A.; Morabito, F.C.; Angiulli, G. A Semi-Linear Elliptic Model for a Circular Membrane MEMS Device Considering the Effect of the Fringing Field. Sensors 2021, 21, 5237. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Numerical Approaches for Recovering the Deformable Membrane Profile of Electrostatic Microdevices for Biomedical Applications. Sensors 2023, 23, 1688. [Google Scholar] [CrossRef]
- Zhong, Z. Modeling, Control Estimation, and Optimization for Microgrids; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2023. [Google Scholar]
- Benmouiza, K.; Cheknane, A. Analysis of Proton Exchange Membrane Fuel Cells Voltage Drops for Different Operating Parameters. Int. J. Hydrog. Energy 2018, 43, 3512–3519. [Google Scholar] [CrossRef]
- Wiktorowicz, K.; Krzeszowski, T. Training High-Order Takagi-Sugeno Fuzzy Systems Using Batch Least Squares and Particle Swarm Optimization. Int. J. Fuzzy Syst. 2020, 22, 22–34. [Google Scholar] [CrossRef]
- Olej, V.; Hajek, P. Comparison of Fuzzy Operators for IF-Inference Systems of Takagi- Sugeno Type in Ozone Prediction. In Artificial Intelligence Applications and Innovations. EANN/AIAI 2011; Part II. IFIP AICT; Iliadis, L., Maglogiannis, I., Papadopoulos, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 364, pp. 92–97. [Google Scholar]
- Hajek, P.; Olej, V. Adaptive Intuitionistic Fuzzy Inference Systems of Takagi-Sugeno Type for Regression Problems. In Artificial Intelligence Applications and Innovations: 8th IFIP WG 12.5 International Conference, AIAI 2012, Halkidiki, Greece, 27–30 September 2012; Part I 8; Springer: Berlin/Heidelberg, Germany, 2012; pp. 206–216. [Google Scholar]
- Aslot, S.; Celisse, A. A Survey of Cross-Validation Procedures for Model Selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar]
- Georgiev, S.; Vulkov, L. Determination of a Time-Varying Point Source in Cauchy Problems for the Convection–Diffusion Equation. Appl. Sci. 2023, 13, 4536. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).