Enhancing Loadability of Transmission Lines Using Static Synchronous Series Compensator Devices: A Case Study of the Syrian Network
Abstract
1. Introduction
- Detailed and accurate modeling of the Syrian transmission network based on real data. This involves incorporating crucial parameters such as transmission line lengths, conductor types, generation capacities, and peak loads.
- Proposing the deployment of SSSC units for contingency management by preventing the overloading of transmission lines, thereby enhancing the overall stability and reliability of the Syrian transmission network.
- Achieving the optimal placement of SSSCs is through the utilization of the particle swarm optimization (PSO) algorithm. This ensures efficient and effective sizing and allocation, leading to the lowest possible active power loss value. The performance of the PSO algorithm is also compared with two algorithms, namely genetic algorithm (GA) and firefly algorithm (FFA).
2. Overview of the Syrian Electrical Network
3. Proposed Solution to Enhance Loadability of the Syrian Electrical Network
3.1. Statistic Synchronous Series Compensator
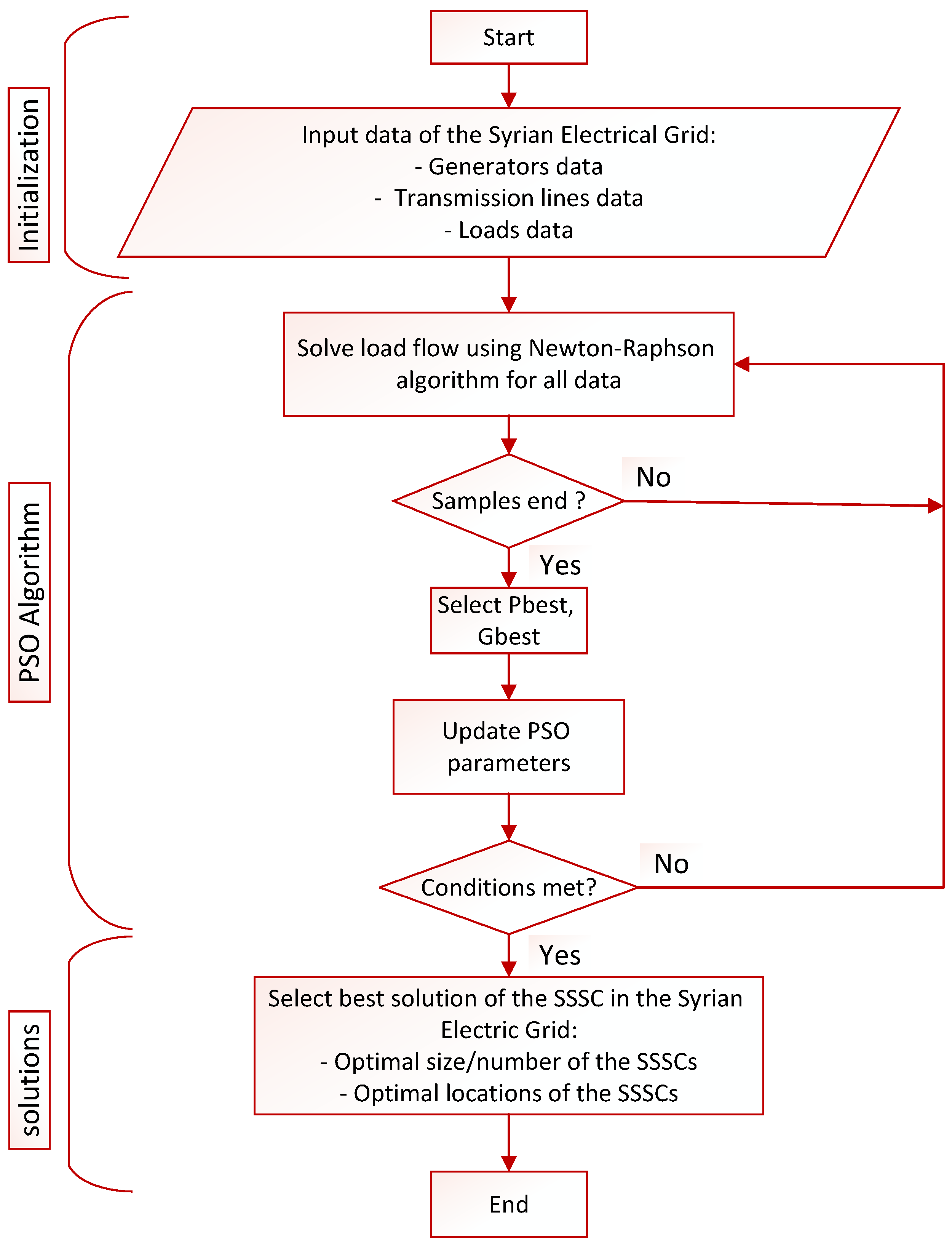
3.2. Optimal SSSC Sizing and Allocation Using PSO Algorithm
4. Results
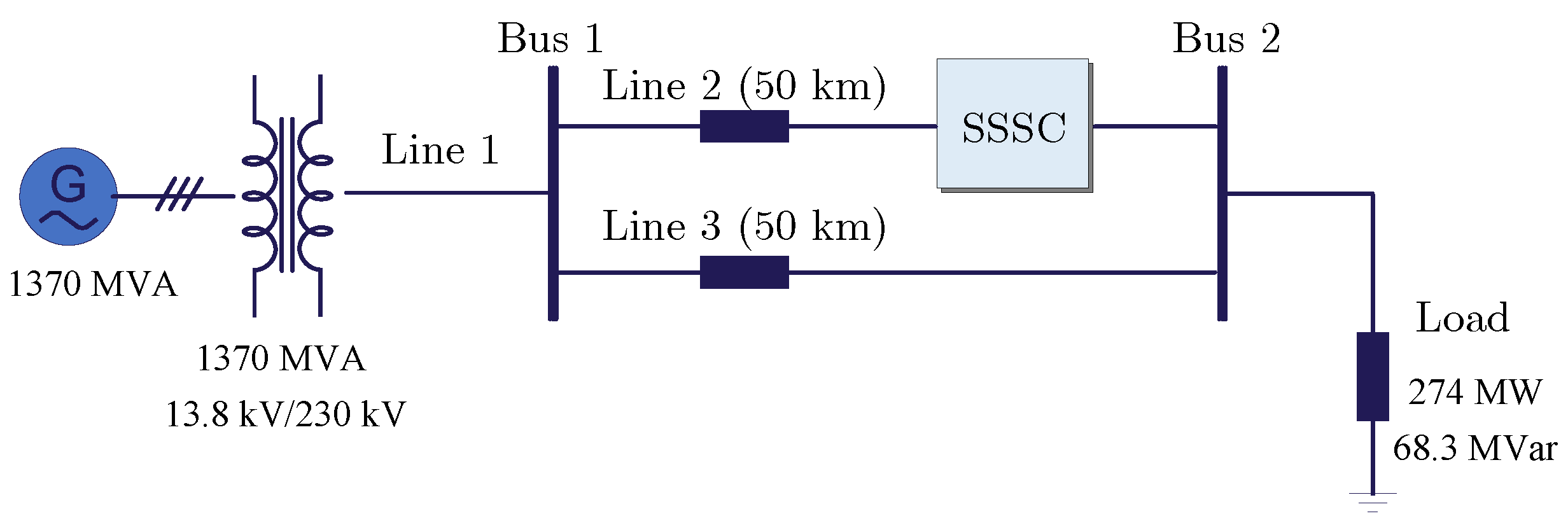
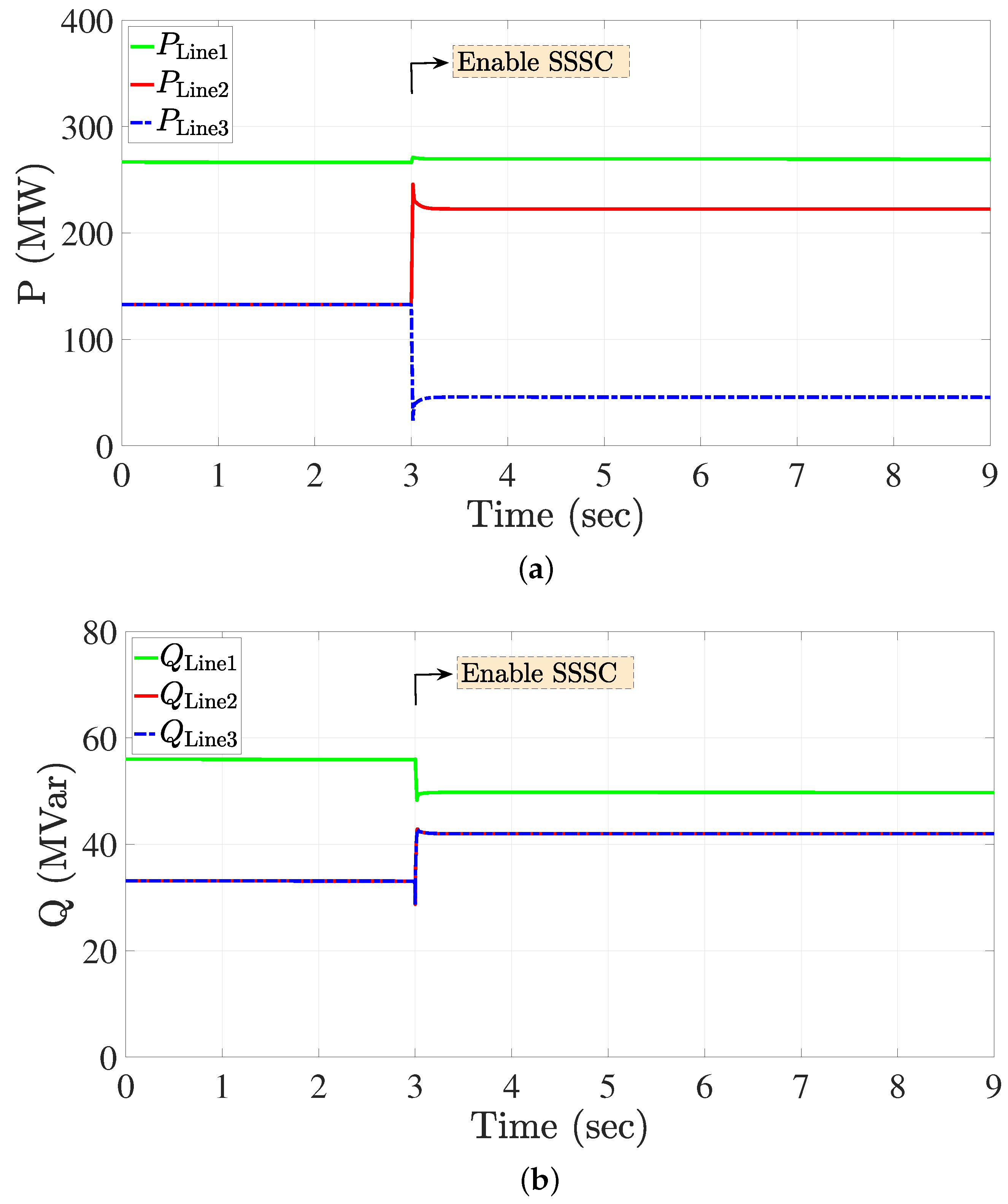
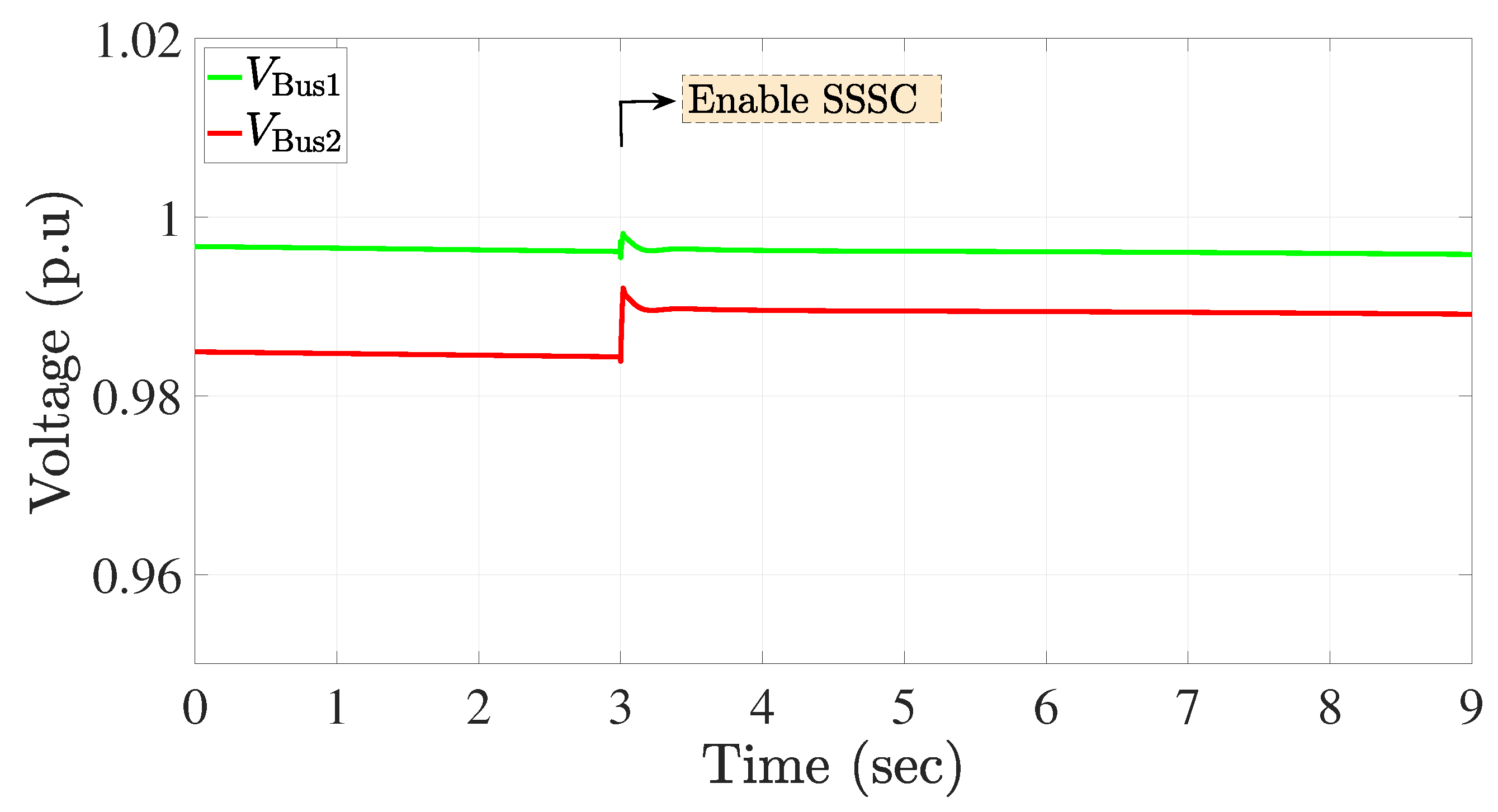
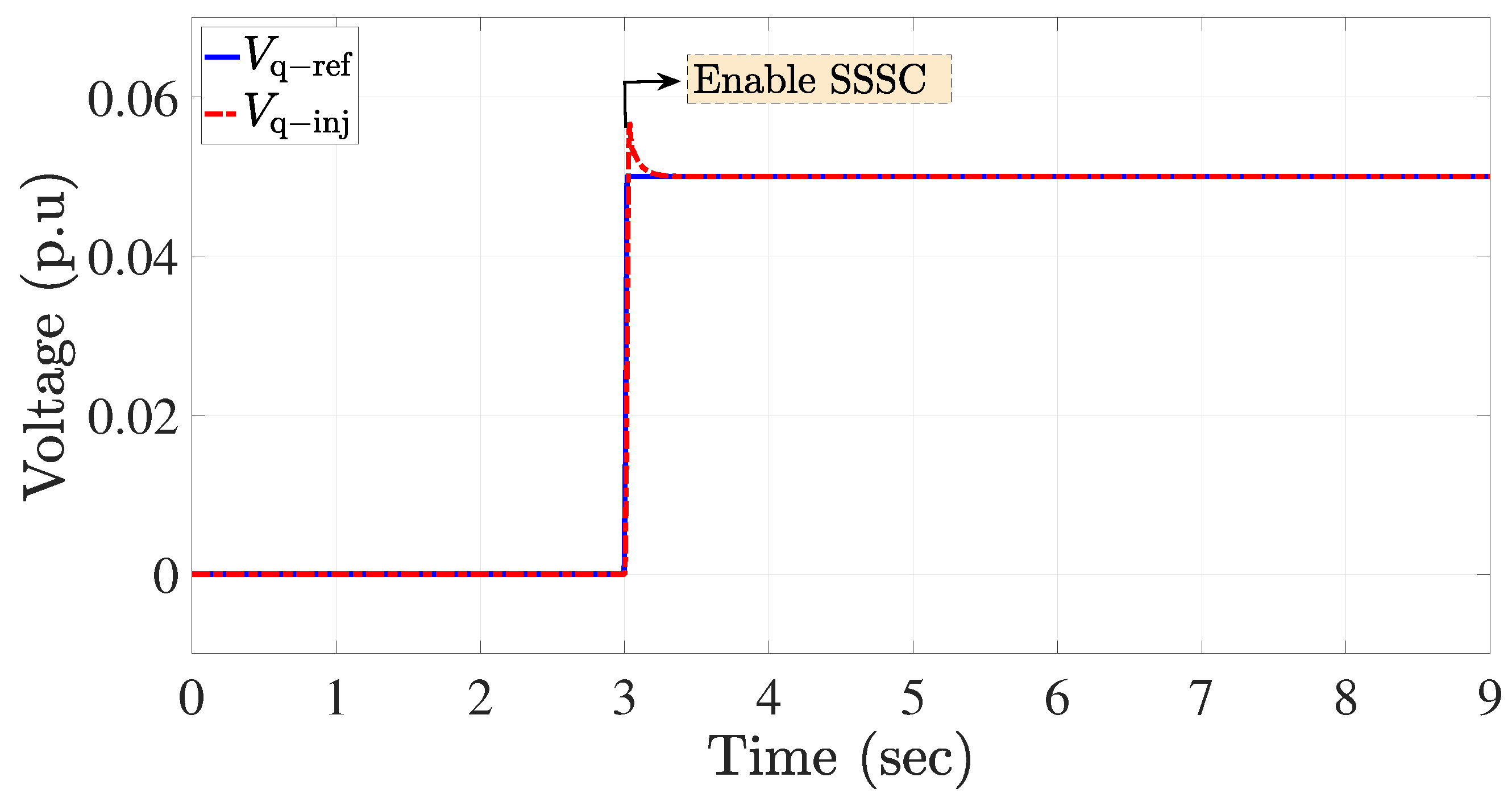
4.1. Case 1: Integrating the SSSC into a Two-Bus Transmission System
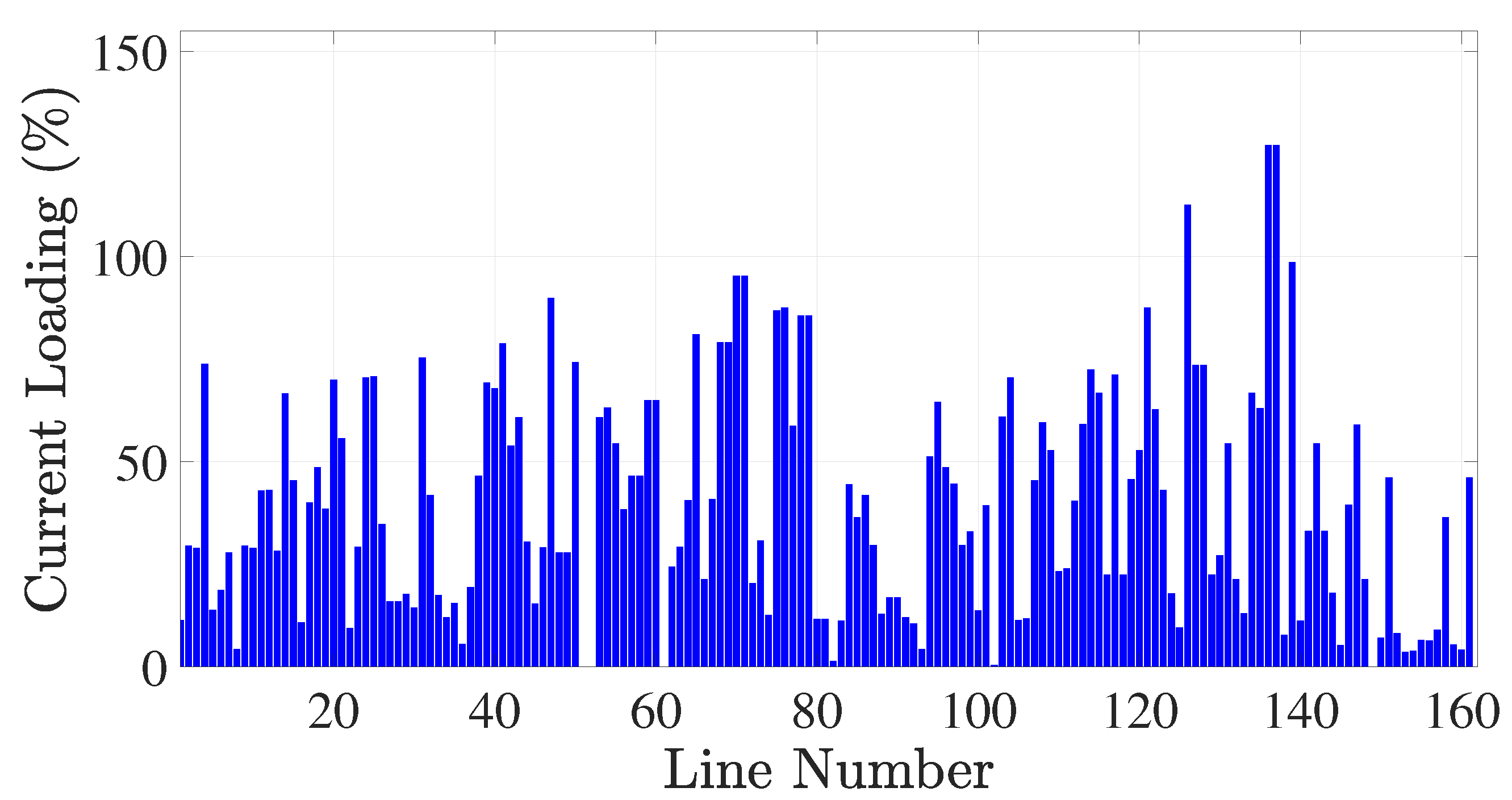
4.2. Case 2: Overloading before Adding SSSCs to the Syrian Electrical Network
4.3. Case 3: Enhancing Loadability of the Syrian Electrical Network via SSSCs
4.3.1. Optimal Sizing and Allocation of SSSCs for the Syrian Electrical Network
4.3.2. Cost Comparison: New Transmission Line vs. SSSCs Deployment
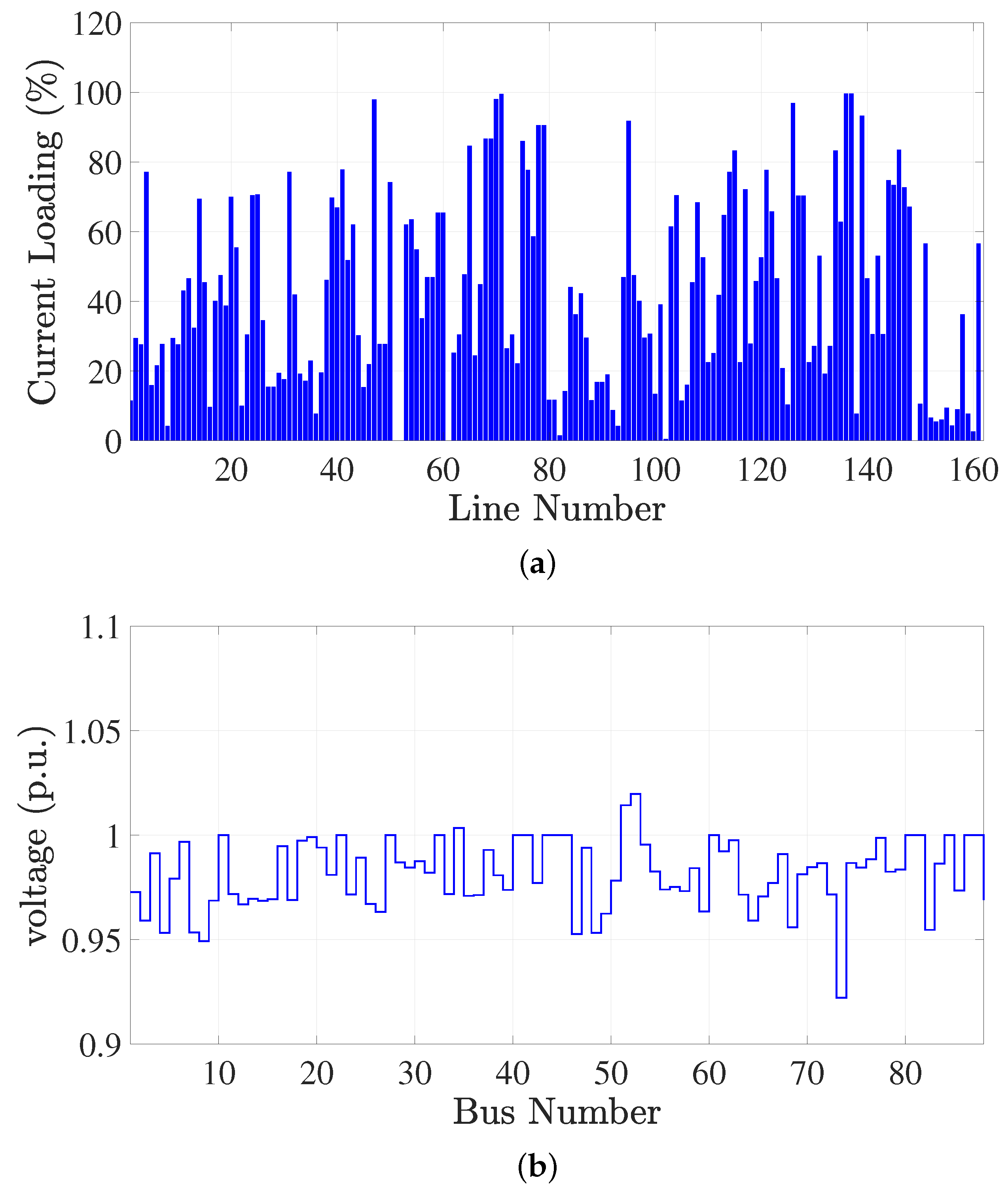
4.3.3. Performance of the Syrian Electrical Network after Adding the SSSCs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Transformation, G.E. Global Energy Transformation: A Roadmap to 2050; IRENA: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- Lopes, J.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- Amani, A.M.; Jalili, M. Power grids as complex networks: Resilience and reliability analysis. IEEE Access 2021, 9, 119010–119031. [Google Scholar] [CrossRef]
- Hingorani, N.G.; Gyugyi, L. Understanding FACTS: Concepts and Technology of Flexible AC Transmission Systems; Wiley-IEEE Press: Hoboken, NJ, USA, 2000. [Google Scholar]
- Hamache, A.; Bensidhoum, M.; Ouslimani, A. UPFC Power Flow Tracking using Decentralized Discrete-Time Quasi-Sliding Mode Control. In Proceedings of the 2019 8th International Conference on Systems and Control (ICSC), Marrakesh, Morocco, 23–25 October 2019; pp. 164–169. [Google Scholar]
- Yang, D.; Chou, H.M.; Thomas, K.; Kynev, S.; Rye, R. STATCOM Performance Evaluation Using Operation Data from Digital Fault Recorder. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Venkateswarlu, S.; Velpula, S.; Janaki, M.; Thirumalaivasan, R. Analysis of SSR with SSSC using FPA based Voltage Controller. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019; Volume 1, pp. 1–6. [Google Scholar]
- Rinat, K.R.; Oleg, K.N. Determination of tuning parameters of SVC controllers using D-decomposition method. In Proceedings of the 2020 21st International Symposium on Electrical Apparatus & Technologies (SIELA), Bourgas, Bulgaria, 3–6 June 2020; pp. 1–4. [Google Scholar]
- Sen, K.K. SSSC-static synchronous series compensator: Theory, modeling, and application. IEEE Trans. Power Deliv. 1998, 13, 241–246. [Google Scholar] [CrossRef]
- Rao, H.G.; Prabhu, N.; Mala, R. Adaptive distance protection for transmission lines incorporating SSSC with energy storage device. IEEE Access 2020, 8, 156017–156026. [Google Scholar] [CrossRef]
- Golov, V.; Kormilicyn, D.; Churkina, Y. Controlled Series Compensation Law of Control Selection Procedure. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 25–29 March 2019; pp. 1–6. [Google Scholar]
- Zhang, X.P. Advanced modeling of the multicontrol functional static synchronous series compensator (SSSC) in Newton power flow. IEEE Trans. Power Syst. 2003, 18, 1410–1416. [Google Scholar] [CrossRef]
- Barik, S.K.; Mohapatra, S.K.; Patra, A.K. Application of MOL algorithm for SSSC based damping controller design with modified local input signal. In Proceedings of the 2018 Technologies for Smart-City Energy Security and Power (ICSESP), Bhubaneswar, India, 28–30 March 2018; pp. 1–6. [Google Scholar]
- Lone, A.H.; Yousuf, V.; Prakash, S.; Bazaz, M.A. Load frequency control of two area interconnected power system using SSSC with PID, Fuzzy and Neural Network Based Controllers. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 108–113. [Google Scholar]
- Fadhil, S.T.; Vural, A.M. Comparison of dynamic performances of TCSC, Statcom, SSSC on inter-area oscillations. In Proceedings of the 2018 5th International conference on electrical and electronic engineering (ICEEE), Istanbul, Turkey, 3–5 May 2018; pp. 138–142. [Google Scholar]
- Wang, X.; Wu, D.; Wei, M.; Li, J.; Wang, H.; Li, Q. The capacitor voltage balancing control strategy based on hierarchical theory in Cascaded H-bridge SSSC. In Proceedings of the 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–6 November 2018; pp. 40–44. [Google Scholar]
- Kumar, L.S.; Ghosh, A. Modeling and control design of a static synchronous series compensator. IEEE Trans. Power Deliv. 1999, 14, 1448–1453. [Google Scholar] [CrossRef]
- Rashitov, P.A.; Vershanskiy, E.A.; Gorchakov, A.V. The Techniques of Reactance Regulation by the Distributed Static Synchronous Series Compensator in Power Lines. In Proceedings of the 2019 20th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 29 June–3 July 2019; pp. 469–475. [Google Scholar]
- Gu, L.; Zhou, X.; Liu, M.; Shi, H. Nonlinear control of SSSC for power system stability enhancement. In Proceedings of the 2010 International Conference on Power System Technology, Zhejiang, China, 24–28 October 2010; pp. 1–6. [Google Scholar]
- Farahani, M.; Ganjefar, S.; Alizadeh, M. Intelligent control of SSSC via an online self-tuning PID to damp the subsynchronous oscillations. In Proceedings of the 20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran, 15–17 May 2012; pp. 336–341. [Google Scholar]
- Bagha, G.; Kumar, A. Voltage profile enhancement for IEEE-14 bus system using UPFC, TCSC and SSSC. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 267–272. [Google Scholar]
- Pandey, R.; Chaitanya, D. An effective approach for ATC enhancement with FACTS device-A case study. In Proceedings of the 2012 International Conference on Advances in Power Conversion and Energy Technologies (APCET), Mylavaram, India, 2–4 August 2012; pp. 1–6. [Google Scholar]
- BV, A.; AO, E. Enhancing Loadability of Transmission Lines Using Series Compensation (Facts) Device in Nigeria Network. Iconic Res. Eng. J. 2018, 2, 12–22. [Google Scholar]
- Gyugyi, L.; Edris, A.A.; Eremia, M. Static synchronous series compensator (SSSC). In Advanced Solutions in Power Systems: HVDC, FACTS, and Artificial Intelligence: HVDC, FACTS, and Artificial Intelligence; Wiley: Hoboken, NJ, USA, 2016; pp. 527–557. [Google Scholar]
- Gandhar, S.; Ohri, J.; Singh, M. Application of SSSC for compensation assessment of interconnected power system. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–5. [Google Scholar]
- Divan, D.; Johal, H. Distributed FACTS-A new concept for realizing grid power flow control. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 8–14. [Google Scholar]
- Dahat, S.A.; Dhabale, A. Co-ordinated Control of Combination of SSSC and SVC for Enhancement of Power System Voltage Stability. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar]
- Mohammed, N.; Ciobotaru, M. Adaptive power control strategy for smart droop-based grid-connected inverters. IEEE Trans. Smart Grid 2022, 13, 2075–2085. [Google Scholar] [CrossRef]
- Saadat, H. Power System Analysis; McGraw-Hill: New York, NY, USA, 1999; Volume 2. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Baldick, R.; O’Neill, R.P. Estimates of comparative costs for uprating transmission capacity. IEEE Trans. Power Deliv. 2009, 24, 961–969. [Google Scholar] [CrossRef]

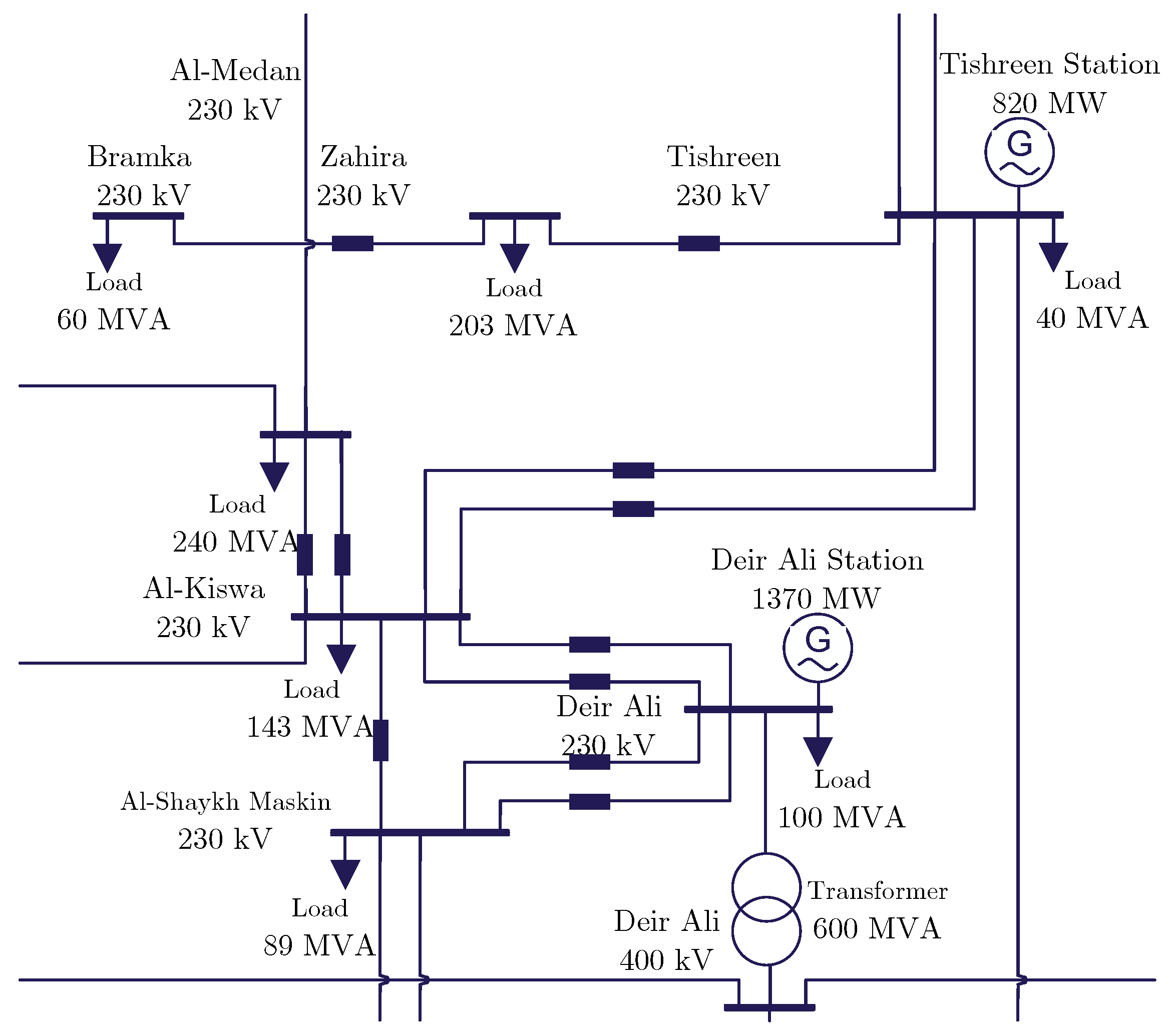
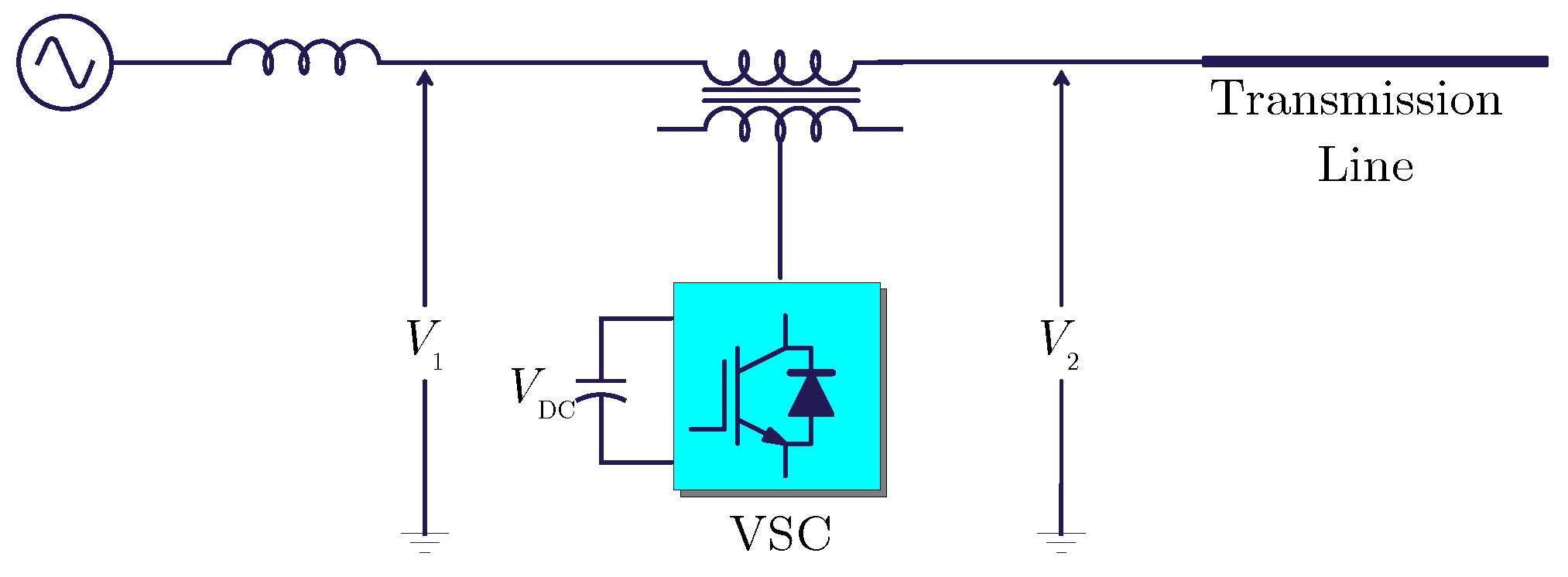
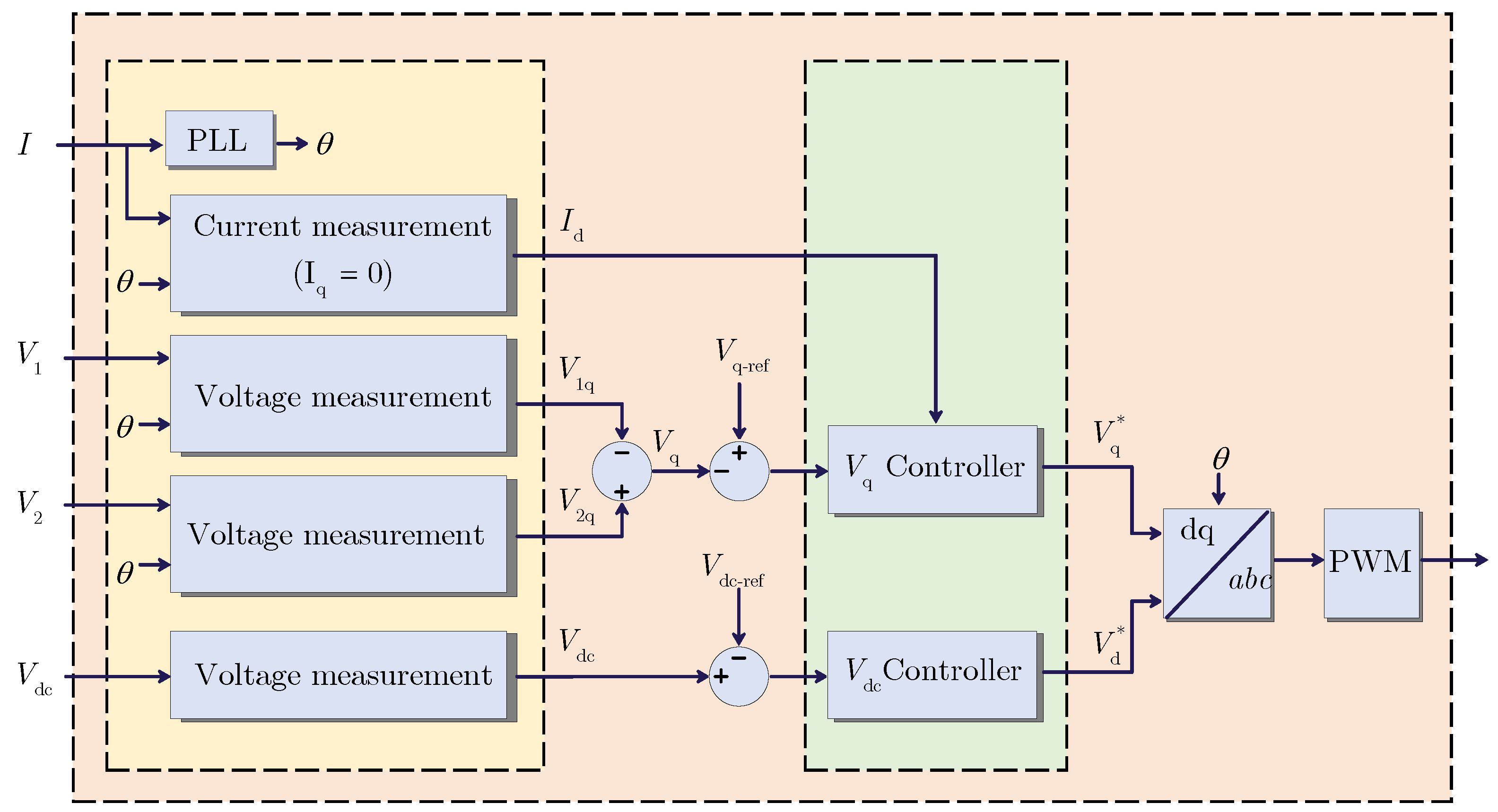
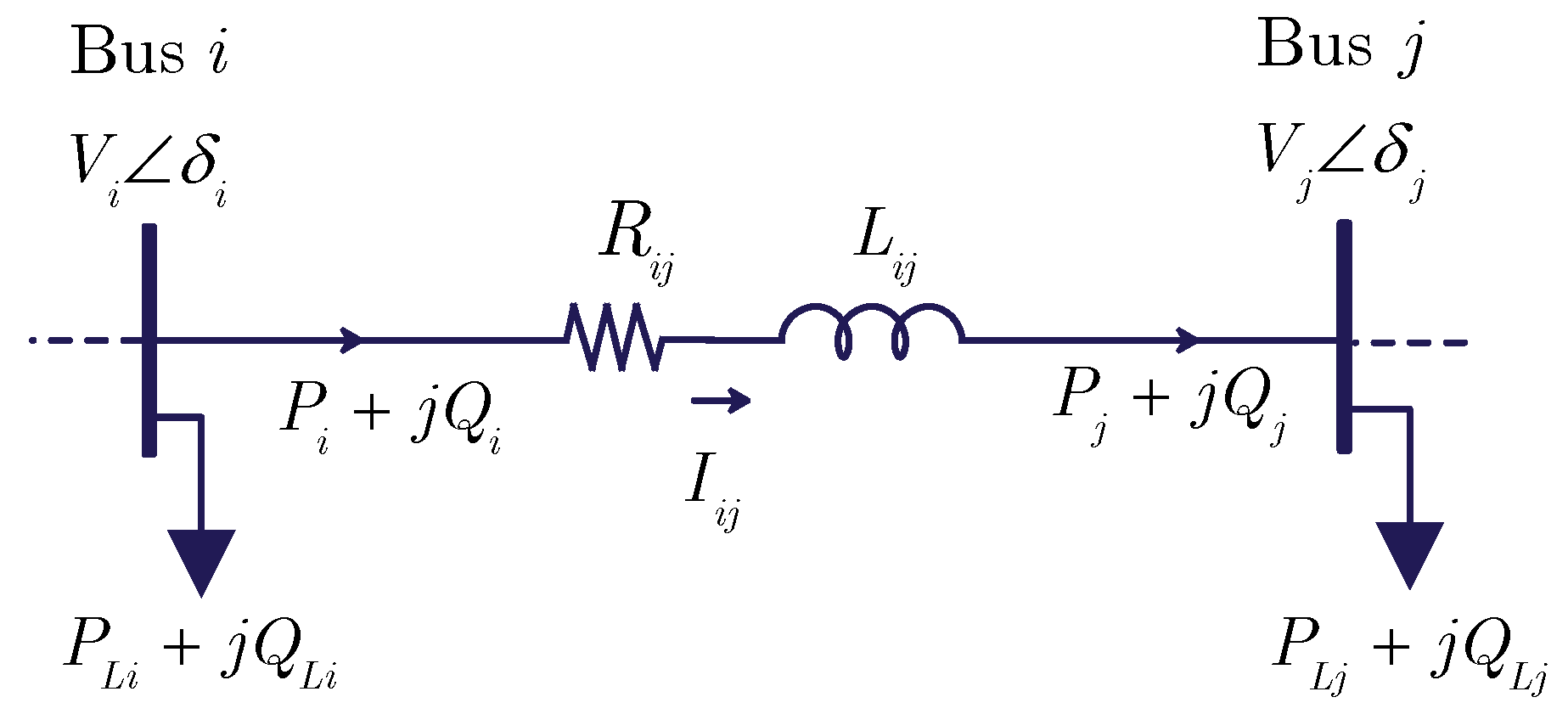
| Station Name | Nominal Capacity (MW) | Station Name | Nominal Capacity (MW) |
|---|---|---|---|
| Deir Ali | 1370 | Jandar | 600 |
| Aleppo | 1150 | Mehardeh | 530 |
| Banias | 940 | Nasserieh | 480 |
| Tishreen Dam | 820 | Zayzoun | 384 |
| Tishreen | 820 | Swediah | 170 |
| Al-Thawrah | 700 | Thayyem | 100 |
| Al-Zara | 660 | Baath | 50 |
| Algorithm | No. of SSSC Units | Size of Each SSSC Unit | Active Power Losses |
|---|---|---|---|
| GA | 9 | 5.07% | 1330 |
| FFA | 12 | 4.24% | 1000 |
| PSO | 10 | 3.65% | 1200 |
| Variable | Case 1 | Case 2 |
|---|---|---|
| Number of Samples | 250 | 500 |
| Number of Iterations | 60 | 100 |
| C1 | 2 | 2 |
| C2 | 2 | 2 |
| W | 1 | 1 |
| Buses | Volume (kVar) | Buses | Volume (kVar) |
|---|---|---|---|
| 10 | 1200 | 75 | 1200 |
| 12 | 1200 | 42 | 1200 |
| 72 | 1200 | 23 | 1200 |
| 79 | 1200 | 33 | 1200 |
| 18 | 1200 | 84 | 1200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asper, H.; Shabaan, F.; Kherbek, T.; Mohammed, N. Enhancing Loadability of Transmission Lines Using Static Synchronous Series Compensator Devices: A Case Study of the Syrian Network. Energies 2024, 17, 390. https://doi.org/10.3390/en17020390
Asper H, Shabaan F, Kherbek T, Mohammed N. Enhancing Loadability of Transmission Lines Using Static Synchronous Series Compensator Devices: A Case Study of the Syrian Network. Energies. 2024; 17(2):390. https://doi.org/10.3390/en17020390
Chicago/Turabian StyleAsper, Hussam, Faisal Shabaan, Tarek Kherbek, and Nabil Mohammed. 2024. "Enhancing Loadability of Transmission Lines Using Static Synchronous Series Compensator Devices: A Case Study of the Syrian Network" Energies 17, no. 2: 390. https://doi.org/10.3390/en17020390
APA StyleAsper, H., Shabaan, F., Kherbek, T., & Mohammed, N. (2024). Enhancing Loadability of Transmission Lines Using Static Synchronous Series Compensator Devices: A Case Study of the Syrian Network. Energies, 17(2), 390. https://doi.org/10.3390/en17020390







