Abstract
More and more microgrids, energy storage systems, and other emerging entities are integrated into active distribution networks. However, a microgrid is characterized by autonomous operation and privacy protection. The rapid development of equipment such as shared energy storage brings strong uncertainty to a traditional dispatcher. The observability and controllability of the distribution system decrease, and traditional regulatory methods are no longer applicable. To deal with the above challenges, a distributed collaborative operation optimization method of multilateral participants is proposed. Guided by the dynamic time-of-use electricity price, the collaborative operation of multilateral participants can be realized. Firstly, the cooperative operation architecture is established considering the dynamic time-of-use electricity price. In this architecture, the residual capacity of shared energy storage is used for arbitrage by storing electricity at low electricity prices and generating electricity at high electricity prices. Then, the optimization operation models of a microgrid alliance, shared energy storage, and an active distribution network are established. The final operation scheme and the dynamic time-of-use price of the distribution network are formulated through the cyclic iteration among the three participants. Finally, a case study is carried out to analyze the optimization effect of each participant with the proposed method. It is found that the overall interests and the interests of each participant can be taken into account effectively and the consumption of renewable energy can be promoted by the method proposed in the paper. In addition, an oscillation phenomenon is found during the distributed collaborative operation, and the strategy to eliminate the oscillation phenomenon is given.
1. Introduction
With the implementation of China’s carbon neutrality strategy, an increasing number of emerging entities have been integrated into the distribution network [1]. The impact of large-scale renewable energy integrated into the distribution grid can be effectively reduced with a microgrid operation control strategy for renewable energy and load. At present, high-efficiency microgrids are mainly based on distributed energy storage applications. The charging and discharging behavior of the energy storage of multiple microgrids connected to the same distribution network is disorderly from an overall perspective, resulting in a waste of energy storage resources [2]. The energy storage, microgrid operators, and active distribution network share the electrical connection. The output fluctuation in renewable energy in a microgrid can be suppressed by making full use of the complementary characteristics of different microgrid loads. The impact on the active distribution network can also be reduced. The cooperative operation method for multiple microgrids, shared energy storage, and an active distribution network has become a research hotspot [3].
A microgrid can effectively improve the consumption of distributed new energy. However, the new energy generation within the microgrid is still volatile [4]. When multiple microgrids are connected to the active distribution network, the timing power of the tie line between the active distribution network and the microgrids must be coordinated to improve the overall power supply reliability and operation economy of the system [5]. The existing research on new energy microgrids and active distribution networks is mostly focused on meeting the energy balance constraints and grid operation constraints, taking economic and environmental optimization as the optimization objectives to optimize the relevant indicators. Ref. [6] takes the optimal economic benefit of the supplier as the objective function and constructs a microgrid operation optimization model of the coupled thermoelectric system. In ref. [7], the objective optimal scheduling model of a large electric vehicle microgrid is established with the goal of environmental protection cost. The study presented in [8] established a collaborative optimization architecture based on load demand, energy storage technology, and a renewable energy microgrid and reduced the operating cost of the microgrid on the premise of ensuring the reliability of the microgrid. In [9], various energy storage systems in multi-energy microgrids are analyzed in depth, and an optimization model is established, which helps determine the optimal grid-connected position of energy storage systems in microgrids to achieve the economic optimum. However, the existing research lacks the exploration of the power interaction behavior of multiple microgrids from the overall perspective and does not consider the cooperative operation of multiple microgrids, resulting in the waste of energy storage resources.
Energy storage is an important means of stabilizing the fluctuation in new energy in microgrids [10,11]. Using the fast charging and discharging characteristics of energy storage can reduce the impact of a microgrid on the distribution network and improve the absorptive capacity of the active distribution network. When multiple microgrids jointly lease and share energy storage, they can make full use of the complementarity of each microgrid’s demand for energy storage charging and discharging and improve the energy storage efficiency [12,13]. In the existing research on the optimization of energy storage systems, a single technical index or economic index is often used as the configuration target, and the optimization is carried out on this basis. Ref. [14] proposed an efficient and economical multi-microgrid hybrid storage and energy-sharing model, whereby multiple microgrids can cooperatively share energy via hybrid energy storage systems. This model can effectively improve the utilization of renewable energy and bring considerable economic benefits. Ref. [15] established a two-stage evaluation framework to analyze the impact of shared energy storage on the self-sufficiency ratio and power quality under different photovoltaic power penetration levels. Ref. [16] established an optimal configuration model of energy storage capacity with the goal of maximizing the annual value of the system, considering the balance of energy flow, the utilization rate of new energy, the number of delivery channels, and the operation constraints of the energy storage system. In addition, when shared energy storage and its users participate in the joint scheduling of a microgrid alliance and distribution network, the rental price of the shared energy storage must be formulated [17,18]. With the continuous improvement of the electricity market, users can directly participate in electricity market transactions via point-to-point transactions. Ref. [19] proposed a business model of sharing energy storage operators to provide offset insurance services for new energy sources. The research results show that this model greatly improves the energy storage utilization efficiency and the economic benefits of energy storage operators. Considering the market price and battery degradation, ref. [20] proposed a price-based shared energy storage leasing mechanism composed of two parts and established a joint optimal market bidding model for virtual power plants with new energy to maximize daily profits. In [21], a joint optimization method for the capacity planning and operation of a large-scale photovoltaic-integrated 5G base station and shared energy storage system is proposed, and a dynamic capacity leasing model of a shared energy storage system is established. Ref. [22] proposed a day-ahead real-time market bidding scheduling strategy for wind power participation based on shared energy storage. In the first stage, aiming at the maximum profit of wind farms in the day-ahead market, the quantum genetic algorithm is used to obtain the optimal bidding power of each wind farm in the daytime market. The second stage maximizes the net income of multiple wind farms in the day-ahead real-time market by coordinating the charging and discharging services of each wind farm using shared energy storage power stations. In the existing research, although the energy storage optimization configuration models established for different optimization objectives and constraints have different emphases, energy storage only passively accepts the charging and discharging schemes formulated by the users and does not fully exploit its remaining capacity to improve its own benefits.
In view of the difference and complementarity in the charging and discharging behavior of multi-microgrid energy storage in time and space, researchers have carried out a game study between the capacity configuration of microgrid hybrid energy storage and the operation of active distribution networks. Ref. [23] proposed a joint planning method based on a two-stage multi-cooperative game. In the first stage, a joint planning model of a local integrated energy system alliance and shared energy storage providers is established. In the second stage, a shared energy storage cost allocation model for the local integrated energy system alliance is proposed alongside a solution algorithm based on constraint generation technology. Shared energy storage is crucial in realizing the sustainable development of community energy systems based on renewable energy. Ref. [24] proposed a coordinated design method for community energy systems and shared energy storage. Based on the bounded rationality theory, the pricing mechanism of energy storage sharing is established, and the Stackelberg game is introduced to consider the storage sharing between energy systems at the design stage. The uncertainties of solar radiation, wind speed, and electricity demand on both sides of supply and demand are also considered. Ref. [25] establishes a master–slave game optimization model to coordinate the source, network, load, and storage of microgrids to minimize the overall operating cost within the microgrids and achieve the highest power quality in the upper grid. The example analysis shows that this method can effectively balance the interests of multiple parties. Ref. [26] proposed a hybrid energy storage capacity optimization configuration method based on a non-cooperative game. Taking hybrid energy storage and a tie line as participants, a non-cooperative game model was established. The breeding mechanism and mutation operator in the invasive weed algorithm were introduced to improve the genetic algorithm and solve the problem. The economy of hybrid energy storage and the smoothing effect of tie-line power fluctuation were comprehensively balanced. However, most of the existing studies regard shared energy storage as an entity belonging to microgrid users and fail to construct an operation optimization model of trilateral subjects such as shared energy storage, multi-microgrid users and an active distribution network.
In summary, many studies on shared energy storage have been carried out at home and abroad. However, the multilateral game problem involving multi-microgrids with shared energy storage has not been solved. This paper proposes an optimization method for the distributed collaborative operation of multilateral entities considering a dynamic time-of-use electricity price in an active distribution network. A collaborative optimization model including three entities, i.e., a microgrid alliance, shared energy storage, and active distribution network, is established. The overall efficiency can be improved by optimizing the operation scheme of each entity in turn. The main innovations of this research include the following:
- (1)
- A trilateral distributed cooperative operation optimization model considering the dynamic time-of-use electricity price of the active distribution network is established. The power exchange scheme of the microgrid alliance and shared energy storage and the electricity price optimization scheme of the active distribution network can be formulated via the cyclic iterative solution of three linear programming models.
- (2)
- The economic benefits of sharing energy storage and trilateral entities can be improved via peak–valley price arbitrage while considering the measure of sharing energy storage, using the remaining capacity to participate in the peak shaving of the active distribution network.
- (3)
- The possible oscillation phenomenon of trilateral agents in the process of distributed cooperative operation is found, and an optimization strategy is proposed to suppress the oscillation of the results.
The structure of this paper is as follows: The framework of the coordinated operation of the microgrid alliance–shared energy storage–active distribution network is set in Section 2. The optimization model of the trilateral entity and the overall iterative optimization strategy are given in Section 3. In Section 4, an example analysis is carried out, the possible oscillation phenomenon in the cooperative operation process is found, and the strategy to suppress the oscillation is given. Finally, the work in this paper is summarized, and future work is proposed.
2. Distributed Cooperative Operation Architecture of Trilateral Subjects
The three-sided main system structure diagram of the microgrid alliance–shared energy storage–active distribution network is shown in Figure 1. The microgrid users with distributed photovoltaics are aggregated to form a multi-microgrid alliance. The multi-microgrid alliance is connected to the active distribution system as well as having an electrical connection with the shared energy storage. The shared energy storage also has an electrical connection with the active distribution network. The main operation modes are introduced as follows:
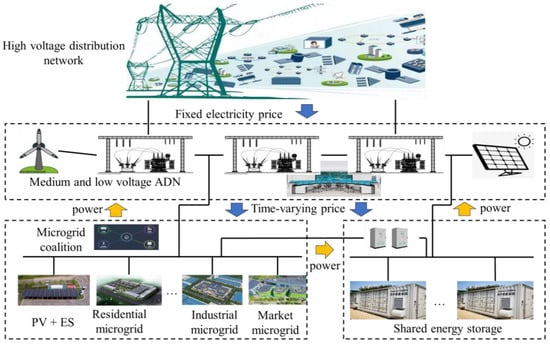
Figure 1.
Microgrid alliance–shared energy storage–active distribution network trilateral main system structure diagram.
- (1)
- The microgrid alliance is responsible for integrating the information of each microgrid and generating power surplus and shortage based on the priority of the distributed photovoltaic output to support the microgrid load. The microgrid alliance aims at the lowest operating cost or the maximum profit. It can choose to stabilize the net load fluctuation by sharing the energy storage leasing, charging, and discharging service or interacting with the active distribution network. The charging and discharging scheme between the microgrid alliance and the shared energy storage and the power interaction scheme between the microgrid alliance and the active distribution network are formulated and submitted to the two parties, respectively.
- (2)
- Firstly, the shared energy storage must meet the charging and discharging interaction requirements of the microgrid alliance and provide energy storage leasing services to the multi-microgrid alliance. On this basis, the shared energy storage uses its remaining capacity to optimize the power interaction scheme between itself and the active distribution network according to the time-of-use electricity price information of the active distribution network. The profit is realized via low storage and high discharge, and the charging and discharging power demand is reported to the active distribution network.
- (3)
- Based on the fixed electricity price, the active distribution network buys/sells electricity from/to the urban high-voltage distribution network to meet the self-load demand of the active distribution network, the purchase and sale power demand of the microgrid alliance, and the charge and discharge power demand of the shared energy storage. The purchase and sale electricity price information between the downstream microgrid alliance and the shared energy storage is re-established to maximize its benefits.
The active distribution network delegates the updated electricity price information to the microgrid alliance and the shared energy storage. They will then reformulate the purchase and sale power scheme and the charge and discharge power scheme. The three entities must carry out cyclic iteration until the convergence criterion is satisfied, i.e., the two adjacent time-of-use electricity price data are the same or the benefits of each side are no longer changed.
3. Distribution Network Optimization Based on Trilateral Game
3.1. Optimization Model of Trilateral Subjects
According to the cooperative operation architecture of the trilateral subjects established in Section 2, the trilateral subjects are iteratively optimized in the order of ‘microgrid coalition → shared energy storage → active distribution network → microgrid coalition →…. Each subject has its own optimization objectives. In this section, their respective optimization models are established, and the distributed cooperative operation strategy is given.
3.1.1. Optimization Model and Solution of Microgrid Coalition
Assuming there are N microgrid users in the multi-microgrid coalition, the net power demand of the microgrid user i on the next day is as follows:
where is the net power demand of the microgrid user i on the next day, is the load forecast value of the microgrid user i on the next day, and is the distributed power output forecast value of the microgrid user i on the next day.
- (1)
- The optimization goal of microgrid coalition
The microgrid users report the net power demand to the management center of the microgrid coalition, and the microgrid coalition summarizes the net power demand of N microgrids. According to the time-of-use electricity price information of the active distribution network and the configuration information of the shared energy storage, the power interaction scheme between the microgrid coalition and the active distribution network and the charging and discharging scheme between the microgrid coalition and the shared energy storage are optimized. The objective function is as follows:
where is the power interaction income between the microgrid coalition and the active distribution network and is the service fee paid by the microgrid coalition to obtain charging and discharging services from the shared energy storage. The specific calculation methods of and are as follows:
where and represent the electricity purchase price and electricity sale price of the active distribution network at time t, respectively. and represent the power of the microgrid coalition to sell and buy electricity to and from the active distribution network at time t, respectively. represents the unit power service fee paid by the microgrid coalition using the shared energy storage service at time t, and and represent the power of the microgrid coalition to charge and discharge the shared energy storage at time t, respectively.
- (2)
- Constraint conditions of microgrid coalition optimization
The microgrid coalition needs to meet the following power balance constraints:
where represents the total net power demand of N microgrid users summarized by the microgrid coalition at time t.
The microgrid coalition needs to meet the tie-line constraints with the active distribution network:
where is the upper limit of the tie-line power between the microgrid coalition and the active distribution network; and are the sign variables of the microgrid coalition selling and purchasing electricity to and from the active distribution network. Users can only sell electricity to the grid or purchase electricity from the grid, and the two operations cannot be carried out at the same time.
The microgrid coalition needs to satisfy the interactive power constraint with the shared energy storage:
is the maximum value of the charging and discharging power of the shared energy storage used by the microgrid coalition; and are the charging and discharging state bits of the shared energy storage used by the microgrid coalition. The shared energy storage can discharge or charge to the microgrid coalition at any time, but both operations cannot be carried out at the same time. ensures that the microgrid coalition can use the shared energy storage charging service only when the total photovoltaic output is greater than the total load.
Shared energy storage needs to meet sequential constraints:
is the remaining power of the shared energy storage at time t; and represent the charging and discharging efficiency of the shared energy storage, respectively; and and represent the minimum and maximum states of charge of the shared energy storage, respectively. ensures that the shared energy storage can provide long-term stable charging or discharging services.
The model established above is a linear model that can be quickly solved by mature mathematical optimization methods to obtain the power interaction scheme and between the microgrid coalition and the active distribution network and the charging and discharging scheme and between the microgrid coalition and the shared energy storage, which are passed to the active distribution network and the shared energy storage operator, respectively.
3.1.2. Optimization Model of Shared Energy Storage
- (1)
- Objective function
The shared energy storage accepts the charging and discharging scheme provided by the microgrid coalition and formulates the power interaction scheme between the shared energy storage and the active distribution network according to the time-of-use electricity price information provided by the active distribution network. The power interaction target of the shared energy storage and active distribution network is
where and represent the power of the shared energy storage to sell and purchase electricity to and from the active distribution network at time t, respectively. is the unit power lease maintenance cost of the shared energy storage participating in the active distribution network transaction at time t.
- (2)
- Constraint condition
The tie-line constraints are also satisfied between the shared energy storage and the active distribution network:
where is the upper limit of the power of the tie line between the shared energy storage and the active distribution network, and are the sign variables for the shared energy storage to sell electricity to the active distribution network, and the shared energy storage cannot sell electricity to the grid and purchase electricity from the grid at the same time.
Since the microgrid coalition only provides the power interaction demand for the shared energy storage itself, when designing the power interaction scheme between the shared energy storage and the active distribution network, it is only necessary to ensure that the remaining capacity can meet the charging and discharging needs of the microgrid coalition at any time within the capacity limit range. Assuming that the actual remaining capacity of the shared energy storage at time t is , then there is the following:
where and are the optimized charging and discharging schemes of the microgrid coalition in Section 3.1.1.
The above model is a 0–1 mixed integer optimization model, which can be solved quickly using mature mathematical optimization methods, so the shared energy storage can optimize the power interaction schemes and between itself and the active distribution network according to the above objective function and constraint conditions and report them to the distribution network control center.
3.1.3. Optimization Model of Active Distribution Network
The active distribution network obtains power vectors and , where contains the interactive power and between the microgrid coalition and the active distribution network; contains the interactive power and between the shared energy storage and the active distribution network:
- (1)
- Objective function
The active distribution network also aims to optimize its own operating efficiency. Under the premise of fully accepting the interaction scheme of the microgrid coalition and shared energy storage reporting, the purchase and sale price of electricity is reasonably set again. The objective function of the active distribution network optimization is as follows:
is the unit price of power purchase from the active distribution network to the upstream urban high-voltage distribution network at time t.
- (2)
- Constraint condition
Because the active distribution network has independent pricing power, to avoid maliciously adjusting the downstream purchase and sale price when improving its own economic benefits, user protection constraints are established:
where and represent the upper limit of the average selling price and the lower limit of the average purchasing price, respectively.
To achieve the economy, reliability, and sustainability of the overall system operation by flexibly adjusting the electricity price, the active distribution network should adopt a reasonable electricity price optimization strategy. First, the electricity price of the active distribution network at any time is greater than the purchase price of the active distribution network at the same time, which allows better coping with market fluctuations and promotes the response of the microgrid coalition and shared energy storage to changes in electricity prices:
Then, the time-of-use price reflects the cost and demand differences in the power system in different periods. Ensuring the peak price of the purchase and sale price ≥ flat price ≥ valley price helps to improve system efficiency and sustainability:
where , , and represent the electricity selling price of the active distribution network at peak, normal, and valley times, respectively; , , and represent the electricity purchase price of the active distribution network at peak, normal, and valley times, respectively.
3.2. Optimization Model Solution Process Based on Trilateral Game Theory
The microgrid coalition, shared energy storage, and active distribution network in the system belong to different stakeholders, which have self-seeking attributes. Based on game theory, the following solution process is set up:
Step 1: Microgrid users predict and report power interaction requirements to the microgrid coalition.
Step 2: The microgrid coalition formulates the charging and discharging scheme between the microgrid coalition and the shared energy storage and the power interaction scheme between the microgrid coalition and the active distribution network through the optimization model established in Section 3.1.1 and the set solution process and submits them to the shared energy storage operator and the distribution network control center, respectively.
Step 3: The shared energy storage determines the power interaction scheme between itself and the active distribution network via the optimal configuration method and reports it to the active distribution network to achieve ‘peak–valley arbitrage’.
Step 4: According to the optimization model in Section 3.1.3, the active distribution network formulates the electricity purchase/sale price information between the downstream microgrid coalition and the shared energy storage and sends the electricity price information to the microgrid coalition and the shared energy storage.
Step 5: Whether the convergence condition is satisfied is determined. If yes, the optimal solution is output; otherwise, return to step 1.
The overall optimization process is shown in Figure 2.
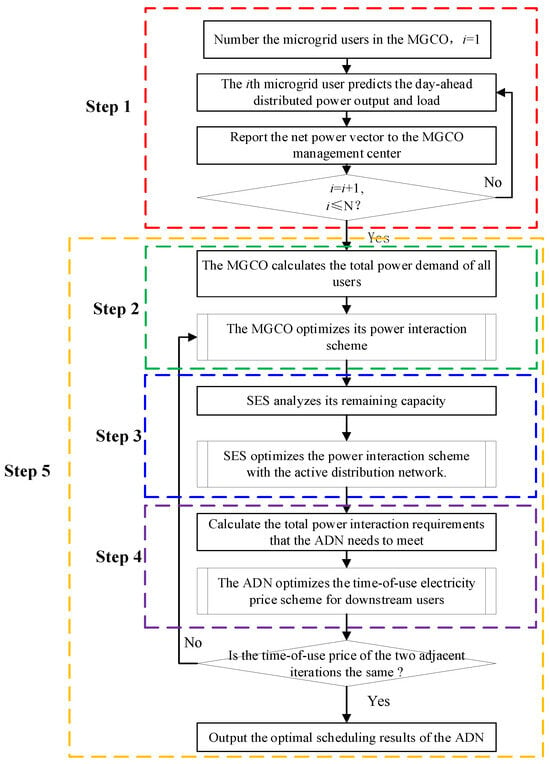
Figure 2.
The solving process of trilateral agent distributed cooperative operation scheme.
4. Example Analysis
4.1. Parameter Introduction
In the trilateral main system of the microgrid coalition–shared energy storage–active distribution network constructed in this paper, the load of the microgrid coalition is 4 MW, 6 MW photovoltaic is installed. Load and photovoltaic predicted output of microgrid coalition are shown in Figure 3. And the tie-line capacity between the microgrid coalition, the active distribution network, and the shared energy storage is 4 MW. The rated capacity of the shared energy storage power station is 10 MWh, the maximum charge and discharge power is 4 MW, the initial and cut-off values of the daily state of charge are 0.5, the minimum state of charge is 0.1, and the charge and discharge efficiency is 0.95. The service fee paid by the microgrid coalition using the energy storage charge and discharge service is 0.15 CNY/kWh. The capacity lease maintenance cost of the shared energy storage participating in the active distribution network transaction is 0.1 CNY/kWh, and the tie-line power between the active distribution network is 4 MW. The power load of the active distribution network is 50 MW, and the fixed time-of-use price is adopted between the active distribution network and the superior advanced distribution network, as shown in Figure 4. The daily average selling price and purchasing price issued to the downstream components are 21/24 CNY/kWh and 15/24 CNY/kWh, respectively. In this paper, the simulation calculation is solved by using matlabR2018b software combined with Yalmip module to call CPLEX solver.
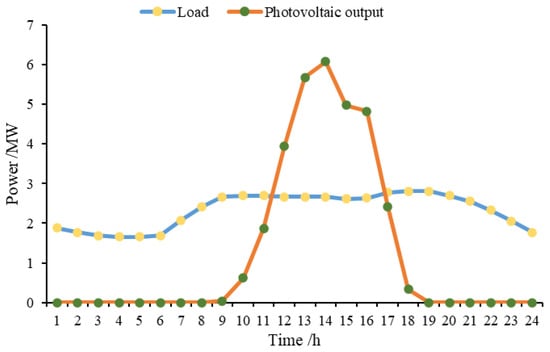
Figure 3.
Load and photovoltaic predicted output of microgrid coalition.
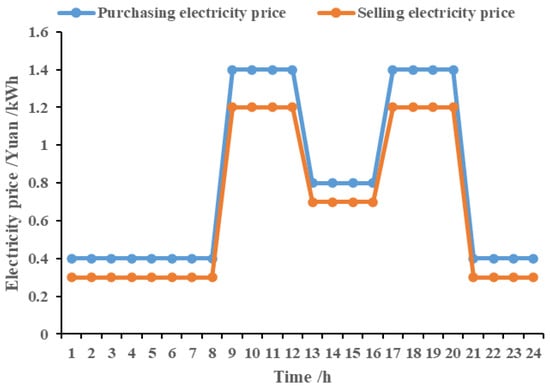
Figure 4.
Electricity purchase/sale price between active distribution network and superior power grid [27].
4.2. Analysis of the Optimization Results of the Trilateral Participants
Based on the initial electricity purchase and sale price of the active distribution network and the load and photovoltaic output data of the microgrid coalition, the microgrid coalition takes its maximum operating efficiency as the objective function and carries out optimal control to complete the first round of the electricity purchasing/selling scheme and charging/discharging scheme optimization. The optimized power interaction scheme of the microgrid coalition is shown in Figure 5. In the period of 00:00–08:00, the photovoltaic output in the microgrid coalition is basically zero, and the load demand of the microgrid coalition is satisfied by purchasing electricity from the active distribution network. From 08:00, the photovoltaic output of the microgrid coalition gradually increases, but it does not yet cover the load demand in the microgrid coalition. Furthermore, the net load of the microgrid coalition is still satisfied by the purchase of electricity from the active distribution network. During the period of 11:00–16:00, the photovoltaic output is further increased and reaches the maximum at 14:00. The microgrid coalition sells excess power to the active distribution network for economic benefits or charges the shared energy storage to meet future needs. During the period of 17:00–24:00, the photovoltaic output of the microgrid coalition is less than the load demand until it is basically zero. Combined with the energy storage margin and the power purchase price of the active distribution network, the load demand of the microgrid coalition is satisfied by the energy storage discharge or the power purchase of the active distribution network.
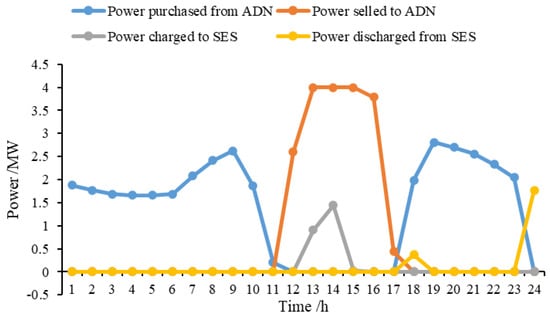
Figure 5.
Power interaction demand of the first round of microgrid coalition.
At this time, the electricity price between the active distribution network and the downstream components is fixed, the purchase price of the active distribution network is lower than the sale price at any time, and the shared energy storage cannot arbitrage with the remaining capacity. The active distribution network optimizes the new time-of-use price setting according to the power interaction scheme provided by the microgrid coalition, as shown in Figure 6.
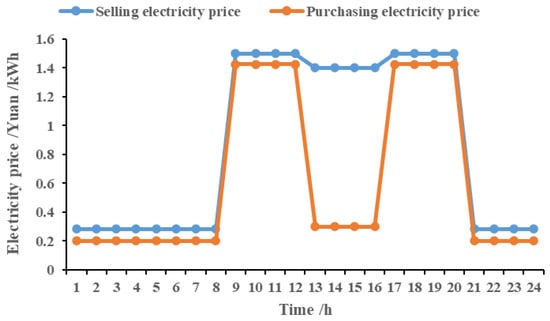
Figure 6.
Time-of-use price setting of active distribution network after the first round is completed.
In the new time-of-use price setting, the peak, normal, and valley prices of electricity sold in the active distribution network are 1.5000 CNY/kWh, 1.4000 CNY/kWh, and 0.2833 CNY/kWh, respectively, and the peak, normal, and valley prices of electricity purchased are 1.4250 CNY/kWh, 0.3000 CNY/kWh, and 0.2000 CNY/kWh, respectively. Since there is no interaction between the shared energy storage and the active distribution network in this round of optimization, the active distribution network chooses 12:00–16:00, which is the maximum photovoltaic output period of the microgrid coalition, and sets the purchasing price at a low level of 0.3833 CNY/kWh to reduce the cost of purchasing a large amount of electricity from the microgrid coalition. Due to the user protection constraints and electricity purchase/sale price constraints, the active distribution network integrates the electricity purchasing demand of the microgrid coalition at peak and valley times to complete the electricity price setting that maximizes its benefits.
The microgrid coalition re-optimizes its power interaction scheme under the new time-of-use electricity price setting. The updated power interaction scheme of the microgrid coalition is shown in Figure 7. Compared with the power interaction scheme of the first round, due to the setting of the time-of-use price of the active distribution network, the microgrid coalition chooses to purchase electricity from the active distribution network to meet its net power demand during the valley price periods of 00:00–08:00 and 20:00–24:00. In the periods of 08:00–12:00 and 16:00–20:00, when the electricity price of the active distribution network is at peak times, the microgrid coalition chooses to use more shared energy storage to stabilize its net load demand. For example, at 09:00 and 18:00, the net load demand of the microgrid coalition is 2624.8 kW and 2362.4 kW. In the first round of the proposed interaction scheme, the demand is mainly satisfied by the power purchased from the active distribution network. In the second round of the interaction scheme, the demand is completely satisfied by the energy storage discharge. During the 12:00–16:00 period of high photovoltaic power generation—especially at 13:00 and 14:00, when the photovoltaic output is the largest—due to the low purchasing price of the active distribution network, the microgrid coalition chooses to store more residual energy in the shared energy storage to meet the reduction in new energy output in the evening to expand its benefits.
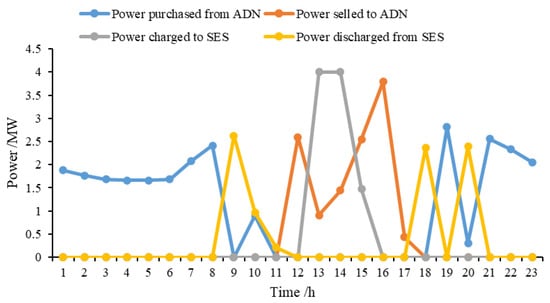
Figure 7.
Secondary wheel power interaction demand of microgrid coalition.
On this basis, the shared energy storage fully explores its remaining capacity and participates in the profit of electricity purchasing and selling transactions with the active distribution network. The remaining capacity under the demand of the microgrid coalition and the shared energy storage is shown in Figure 8. In the case where only the microgrid coalition uses the shared energy storage charging and discharging service, the microgrid coalition chooses to use the energy storage charging service during the first peak electricity price period of the active distribution network, and it charges the energy storage to the maximum capacity of 10 MWh of the energy storage when the photovoltaic power generation is high. This abundant electricity is gradually released during the 17:00–20:00 period, reducing the amount of electricity purchased during the second peak electricity price period of the active distribution network. Overall, the charging and discharging demand of the microgrid coalition for shared energy storage is once a day, and the shared energy storage can explore its available residual capacity. During the period of 00:00–08:00, the microgrid coalition does not lease the charging and discharging service of the shared energy storage, The valley electricity purchase price period of the active distribution network occurs at this time. The shared energy storage is charged to the maximum capacity of 10 MWh via the active distribution network within the range of capacity. In the period of 08:00–12:00, it sells the electricity to the active distribution network at a higher price while meeting the discharge demand of the microgrid coalition. During the 12:00–16:00 period, the shared energy storage accepts the charging service of the microgrid coalition and increases the remaining capacity to 10 MWh once again. Since the peak purchase price of the active distribution network is greater than the valley sale price, during the period of 17:00–20:00, the shared energy storage sells electricity to the active distribution network for the second time while discharging to the microgrid coalition, and it purchases electricity at a lower price within 20:00–24:00 to meet the capacity balance in one day.
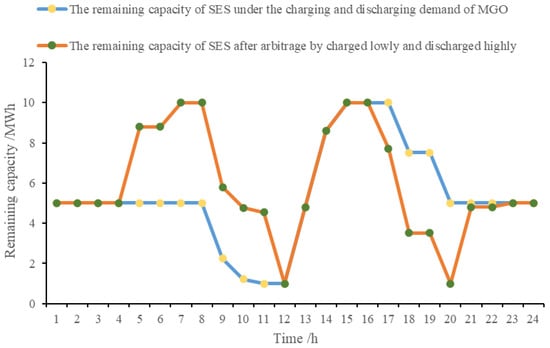
Figure 8.
Residual power of shared energy storage.
To only meet the charging and discharging needs of the microgrid coalition, the shared energy storage increases an arbitrage behavior of low charging and high discharging and realizes two charging and discharging behaviors per day, which improves the utilization rate and economic benefits of the shared energy storage.
4.3. The Iterative Optimization Results of Trilateral Subjects
4.3.1. The Analysis of Iterative Optimization Results
After several rounds of optimization, the electricity price of the active distribution network is no longer changed, and the benefits of the trilateral subjects of the microgrid coalition–shared energy storage–active distribution network are convergent. The change in the electricity purchase and sale price of the active distribution network is shown in Figure 9. Due to the introduction of the interaction between the shared energy storage and the active distribution network after the time-of-use electricity price is set, the shared energy storage purchases electricity from the active distribution network at 00:00–08:00 and 20:00–24:00 when the microgrid coalition does not rent the charging and discharging service, and the discharge time is at the peak selling times of 08:00–12:00 and 17:00–20:00. Therefore, compared with the first time-of-use electricity price setting, the electricity purchase prices in peak, normal, and valley periods of the active distribution network under the final electricity price setting are 1.2583 CNY/kWh, 0.3833 CNY/kWh, and 0.2833 CNY/kWh, and the electricity sale prices in peak, normal, and valley periods are still 1.5000 CNY/kWh, 1.4000 CNY/kWh, and 0.2833 CNY/kWh, which maintain the benefits.
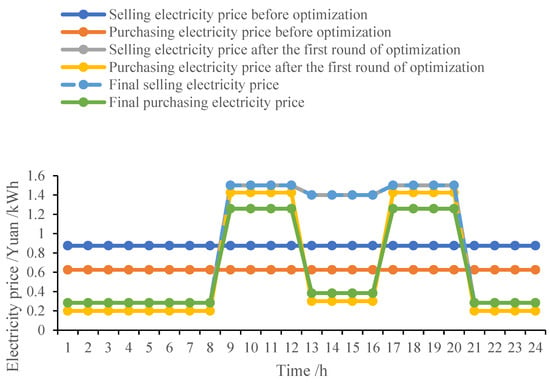
Figure 9.
Electricity price information of active distribution network.
The changes in the efficiency of the trilateral subjects are shown in Table 1. Under the initial electricity price setting, the benefits of the active distribution network, microgrid coalition, and shared energy storage and the total benefits are CNY 84,318, CNY −18,626.2, CNY 677.59, and CNY 66,369.39, respectively. The benefit space of the microgrid coalition and the shared energy storage has not been fully explored. After the active distribution network adopts the time-of-use electricity price setting, the two greatly improve their operating efficiency by adjusting their interaction behavior. The operating efficiency of the microgrid coalition reaches CNY −8466.01, and the operating efficiency of the shared energy storage reaches CNY 10,400.72. Subsequently, the active distribution network continues to update the time-of-use electricity price setting for the trilateral subjects until the benefits are convergent. Finally, the benefits of the active distribution network, microgrid coalition, and shared energy storage and the total benefits are CNY 83,420.44, CNY −8246.75, CNY 8975.72, and CNY 84,149.41, respectively.

Table 1.
The benefit optimization results of the trilateral subjects (unit: CNY).
4.3.2. Comparison of the Results of Different Electricity Price Optimization Strategies
In Table 1, the time-of-use electricity price of the active distribution network and the trilateral subjects’ benefits are convergent and are obtained under various strategic constraints. If the electricity price setting strategy is changed, a stable electricity price optimization result may not be obtained, and the benefits of each subject and the total benefits oscillate, as shown in Figure 10. In this case, the benefits of the trilateral subjects of the microgrid coalition–shared energy storage–active distribution network and the total benefits have oscillated since the beginning of the second iteration process.
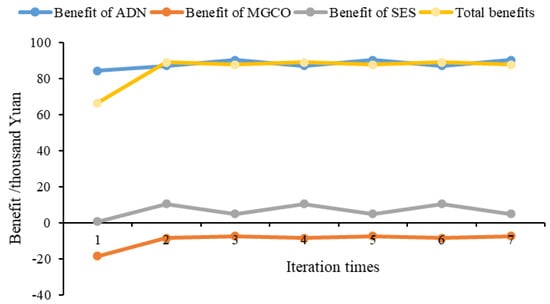
Figure 10.
The benefit evaluation results of the trilateral subjects after canceling the restriction that the purchase price is lower than the sale price.
The optimization results in the fifth and sixth iterations are shown in Figure 11, Figure 12 and Figure 13. The microgrid coalition always tends to choose to purchase electricity when the selling price of the active distribution network is low. When the selling price of the active distribution network is high, it can meet its load demand as much as possible via the energy storage. The shared energy storage uses any period of time with the possibility of low charging and high discharging to complete arbitrage. If the constraint that the purchasing price of the active distribution network is lower than the selling price is canceled, to ensure its benefits under the current downstream interaction scheme, the active distribution network formulates a period when the purchasing price is higher than the selling price, which will lead to the alternate occurrence of the purchasing or selling demand of the microgrid coalition and the shared energy storage during this period. With the time-of-use electricity price of the active distribution network, behavior similar to low charging and high discharging is generated, which leads to the continuous adjustment of the active distribution network to the original electricity price setting. Then, the process is repeated continuously, which results in the model’s non-convergence.
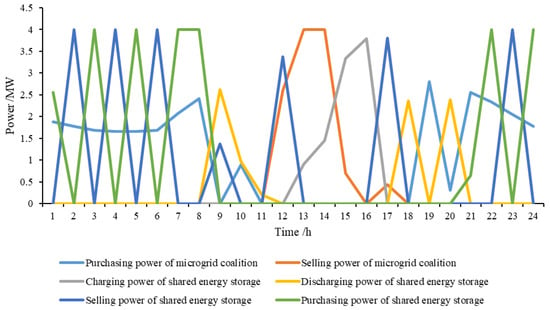
Figure 11.
The fifth-generation optimization results in the process of oscillation.
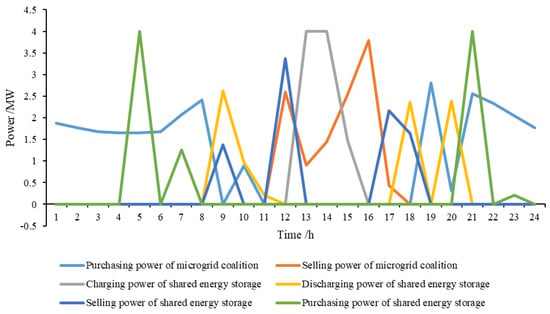
Figure 12.
The sixth-generation optimization results in the process of oscillation.
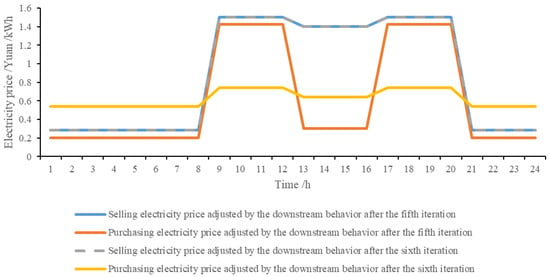
Figure 13.
The electricity sale/purchase price adjusted by the downstream behavior after the fifth/sixth iteration.
In addition, if the constraint that the microgrid coalition can sell electricity to the active distribution network or charge to the energy storage merely when the photovoltaic output is greater than its own load demand is canceled, oscillation may also occur. If the peak–normal–valley electricity price model is canceled but the electricity price of 24 periods is allowed to fluctuate arbitrarily between the upper and lower limits, oscillation will also occur. The causes of the oscillation are similar and will not be repeated here.
4.4. Comparison with Existing Research
In order to prove the effectiveness of the method in this paper, according to the methods in the existing research: ① shared energy storage only interacts with the microgrid and no longer uses the residual capacity for arbitrage [28]; ② the fixed time-of-use electricity price is used for optimization [29]. Under the condition that other parameters remain unchanged, the relevant indicators are analyzed after the convergence of the optimization iteration process. The optimization results obtained are shown in Table 2. It can be seen that due to the more reasonable time-of-use electricity price, the method in the paper has greater advantages than Methods 1 and 2 in reducing the cost of unit power supply. At the same time, the mining of remaining capacity greatly improves the benefit space of shared energy storage.

Table 2.
The comparison of indices for different methods.
5. Conclusions
An optimization method for the distributed collaborative operation of multilateral participants in an active distribution network is proposed in the paper. Dynamic time-of-use electricity price is used as the driving force for collaborative operation, and the residual capacity of shared energy storage is used to obtain greater benefits. The operation optimization models of trilateral participants are established, and a solution process based on cyclic iteration is designed. The iterative optimization is in the order of ‘microgrid coalition → shared energy storage → active distribution network → microgrid coalition →… until the optimization results of each participant no longer change. The power exchange scheme between each participant and the time-of-use electricity price between the active distribution network and downstream components can be obtained. In the proposed method, the requirements of autonomous operation and privacy protection of the microgrid alliance and shared energy storage can be satisfied. Through the example given, the following results were found:
- (1)
- The collaborative operation scheme of the trilateral participants can be obtained with only 3–5 iterative calculations. The solution efficiency of the model is high.
- (2)
- The equipment utilization rate of shared energy storage has been improved. All the benefits of trilateral participants are increased by coordinated operation.
- (3)
- An oscillation phenomenon may occur during the cyclic iteration. Appropriate operation constraints should be set to avoid the occurrence of oscillation.
Author Contributions
Conceptualization, G.L. and B.S.; methodology, G.L.; software, Z.Z.; validation, G.L. and Y.W.; formal analysis, B.S.; investigation, G.L.; resources, G.L.; data curation, G.L.; writing—original draft preparation, B.S.; writing—review and editing, Z.Z.; visualization, G.L.; supervision, Y.W.; project administration, Z.Z.; funding acquisition, B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Grid science and technology project, grant number (SGTJDL00DKJS2300674).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Gang Liang was employed by Jinghai Power Supply Branch of State Grid Tianjin Electric Power Company. Author Yu Wang was employed by Dongli Power Supply Branch of State Grid Tianjin Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ma, M.; Huang, H.; Song, X.; Peña-Mora, F.; Zhang, Z.; Chen, J. Optimal sizing and operations of shared energy storage systems in distribution networks: A bi-level programming approach. Appl. Energy 2022, 307, 118170. [Google Scholar] [CrossRef]
- Mansouri, S.; Ahmarinejad, A.; Nematbakhsh, E.; Javadi, M.; Nezhad, A.E.; Catalão, J. A sustainable framework for multi-microgrids energy management in automated distribution network by considering smart homes and high penetration of renewable energy resources. Energy 2022, 245, 123228. [Google Scholar] [CrossRef]
- Deng, H.; Wang, J.; Shao, Y.; Zhou, Y.; Cao, Y.; Zhang, X.; Li, W. Optimization of configurations and scheduling of shared hybrid electric-hydrogen energy storages supporting to multi-microgrid system. J. Energy Storage 2023, 74, 109420. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Predictive power management strategy for PV/battery hybrid unit based islanded AC microgrid. Int. J. Electr. Power Energy Syst. 2019, 110, 487–496. [Google Scholar] [CrossRef]
- Han, Y.; Chen, W.; Li, Q.; Yang, H.; Zare, F.; Zheng, Y. Two-level energy management strategy for PV-Fuel cell-battery-based DC microgrid. International Journal of Hydrogen Energy. Int. J. Hydrog. Energy 2019, 44, 19395–19404. [Google Scholar] [CrossRef]
- Lu, Z.; Gao, Y.; Xu, C. Evaluation of energy management system for regional integrated energy system under interval type-2 hesitant fuzzy environment. Energy 2021, 222, 119860. [Google Scholar] [CrossRef]
- Tend, Y.; Sun, P.; Hui, Q. Optimal operation model of micro-energy network considering classification and disposal of biomass waste. Autom. Electr. Power Syst. 2021, 45, 55–63. [Google Scholar]
- Hu, Q.; Zhao, G.; Hu, J.; Razmjooy, N. Maximizing energy storage in Microgrids with an amended multi-verse optimizer. Heliyon 2023, 11, e21471. [Google Scholar] [CrossRef]
- Shahbazbegian, V.; Dehghani, F.; Shafiyi, M.A.; Shafie-khah, M.; Laaksonen, H.; Ameli, H. Techno-economic assessment of energy storage systems in multi-energy microgrids utilizing decomposition methodology. Energy 2023, 283, 128430. [Google Scholar] [CrossRef]
- Jian, J.; Zhao, J.; Ji, H.; Bai, L.; Xu, J.; Li, P.; Wu, J.; Wang, C. Supply restoration of data centers in flexible distribution networks with spatial-temporal regulation. IEEE Trans. Smart Grid 2023, 15, 340–354. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z.; Yu, H.; Ji, H.; Li, P.; Xi, W.; Yan, J.; Wang, C. Cloud-Edge Collaboration-Based Local Voltage Control for DGs with Privacy Preservation. IEEE Trans. Ind. Inform. 2023, 19, 98–108. [Google Scholar] [CrossRef]
- Shuai, X.; Ma, Z.; Wang, X.; Guo, H.; Zhang, H. Optimal Operation of Shared Energy Storage and Integrated Energy Microgrid Based on Leader-follower Game Theory. Power Syst. Technol. 2023, 47, 679–687. [Google Scholar]
- Xi, C.; Wenlong, F.; Hairong, Z.; Yunning, Z.; Renming, W.; Jiayu, L. Optimal Dispatching Strategy of Shared Energy Storage and Multi-Microgrid Considering the Uncertainty of New Energy Generation. Power Syst. Technol. 2023; in press. [Google Scholar]
- Cao, W.; Xiao, J.W.; Cui, S.C.; Liu, X.K. An efficient and economical storage and energy sharing model for multiple multi-energy microgrids. Energy 2022, 244, 123124. [Google Scholar] [CrossRef]
- Tercan, S.M.; Demirci, A.; Gokalp, E.; Cali, U. Maximizing self-consumption rates and power quality towards two-stage evaluation for solar energy and shared energy storage empowered microgrids. J. Energy Storage 2022, 51, 104561. [Google Scholar] [CrossRef]
- Li, P.; Han, P.; Liu, S.; Zhang, J. Capacity coordinated optimization of battery, thermal and hydrogen storage system for multi-energy complementary power system. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023. [Google Scholar]
- Wang, C.; Zhang, X.; Wang, Y.; Xiong, H.; Ding, X.; Guo, C. Pricing method of electric-thermal heterogeneous shared energy storage service. Energy 2023, 281, 128275. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Zhou, W.; Chen, Y.; Zheng, F. Joint Optimal Operation and Bidding Strategy of Scenic Reservoir Group Considering Energy Storage Sharing. J. Electr. Eng. 2023, 18, 219–227. [Google Scholar] [CrossRef]
- Xu, X.; Li, G.; Yang, H.; Liu, D.; Wang, J.; Zhang, Z.; Zhao, L.; Zhang, X. Pricing method of shared energy storage bias insurance service based on large number theorem. J. Energy Storage 2023, 69, 107726. [Google Scholar] [CrossRef]
- Zhang, T.; Qiu, W.; Zhang, Z.; Lin, Z.; Ding, Y.; Wang, Y.; Wang, L.; Yang, L. Optimal bidding strategy and profit allocation method for shared energy storage-assisted VPP in joint energy and regulation markets. Appl. Energy 2023, 329, 120158. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Liao, H.; Zhou, Z.; Ma, X.; Yin, X.; Wang, Z.; Liu, Y.; Lu, Z.; Lv, G. Optimal capacity planning and operation of shared energy storage system for large-scale photovoltaic integrated 5G base stations. Int. J. Electr. Power Energy Syst. 2023, 147, 108816. [Google Scholar] [CrossRef]
- Yang, X.; Fan, L.; Li, X.; Meng, L. Day-ahead and real-time market bidding and scheduling strategy for wind power participation based on shared energy storage. Electr. Power Syst. Res. 2023, 214, 108903. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, Y.; Zhang, T.; Li, Q.; Li, Z.; Liang, H.; Liu, C.; Ma, Y.; Lin, Z.; Yang, L. Two-stage multiple cooperative games-based joint planning for shared energy storage provider and local integrated energy systems. Energy 2023, 284, 129114. [Google Scholar] [CrossRef]
- Li, L.; Peng, K.; Yang, X.; Liu, K. Coordinated design of multi-stakeholder community energy systems and shared energy storage under uncertain supply and demand: A game theoretical approach. Sustain. Cities Soc. 2024, 100, 105028. [Google Scholar] [CrossRef]
- Guo, T.; Guo, Q.; Huang, L.; Guo, H.; Lu, Y.; Tu, L. Microgrid source-network-load-storage master-slave game optimization method considering the energy storage overcharge/overdischarge risk. Energy 2023, 282, 128897. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, L.; Han, Y. Capacity configuration method of hybrid energy storage system in microgrids based on a non-cooperative game model. J. Glob. Energy Interconnect. 2021, 4, 454–463. [Google Scholar]
- Polaris Energy Storage Network. Summary of the Largest Peak Valley Electricity Price Difference in China in July 2022! Available online: https://news.bjx.com.cn/html/20220628/1236774.shtml (accessed on 28 June 2022).
- Li, L.; Xu, Q.S.; Wang, X.J.; Ling, J.; Sun, H. Optimal economic scheduling of industrial customers on the basis of sharing energy-Storage Station. Electr. Power Constr. 2020, 41, 100–107. [Google Scholar]
- Sun, B.; Jing, R.; Zeng, Y.; Li, Y.; Chen, J.; Liang, G. Distributed optimal dispatching method for smart distribution network considering effective interaction of source-network-load-storage flexible resources. Energy Rep. 2023, 9, 148–162. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).