Enhancing Heat Storage Cooling Systems via the Implementation of Honeycomb-Inspired Design: Investigating Efficiency and Performance
Abstract
1. Introduction
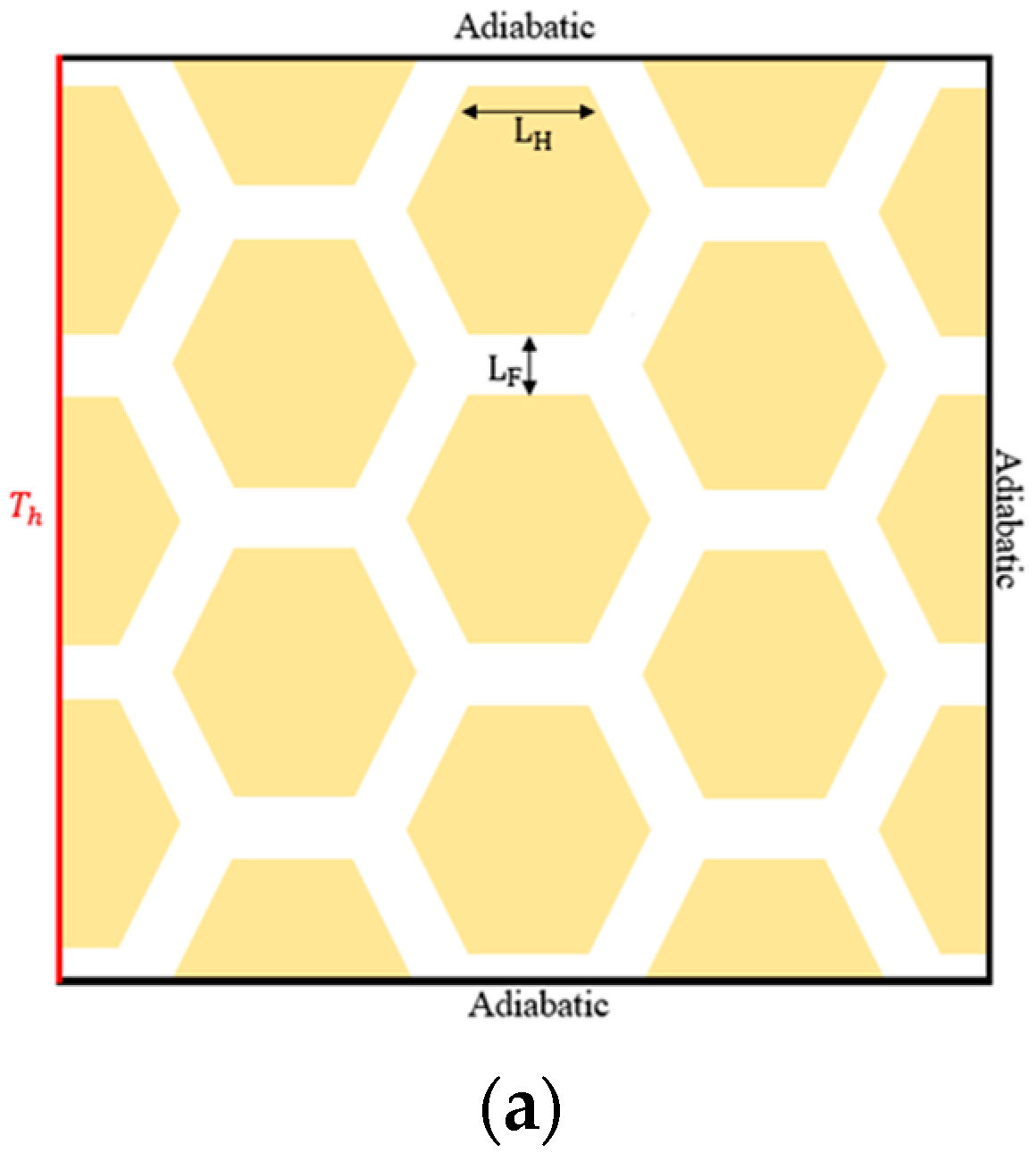
2. Honeycomb Cooling Structure
Geometry
3. Governing Equations
3.1. Lattice Boltzmann Method
3.2. Boundary Conditions
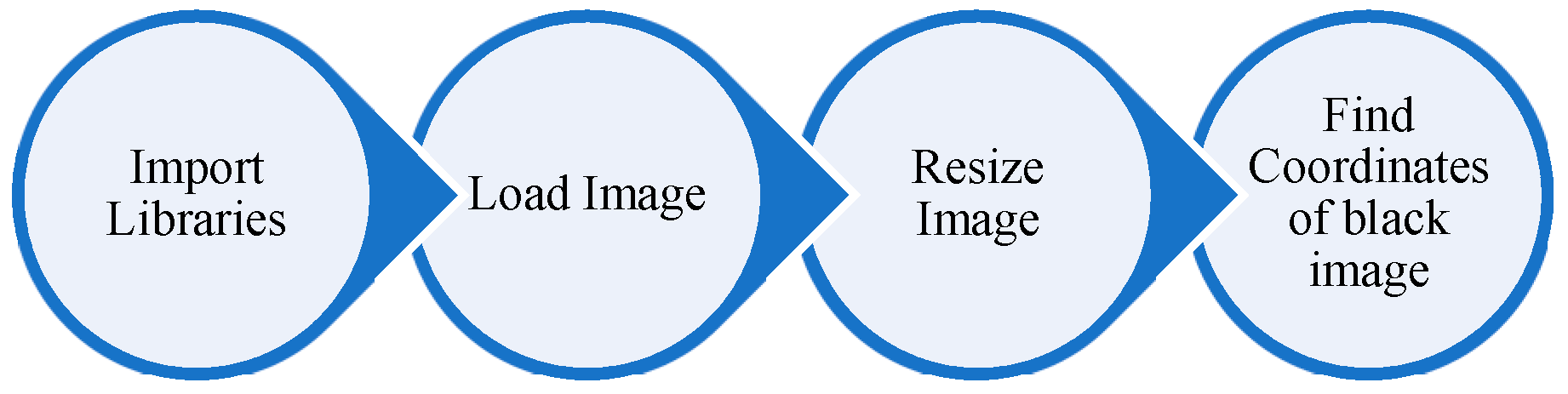
3.3. Image Processing Algorithms
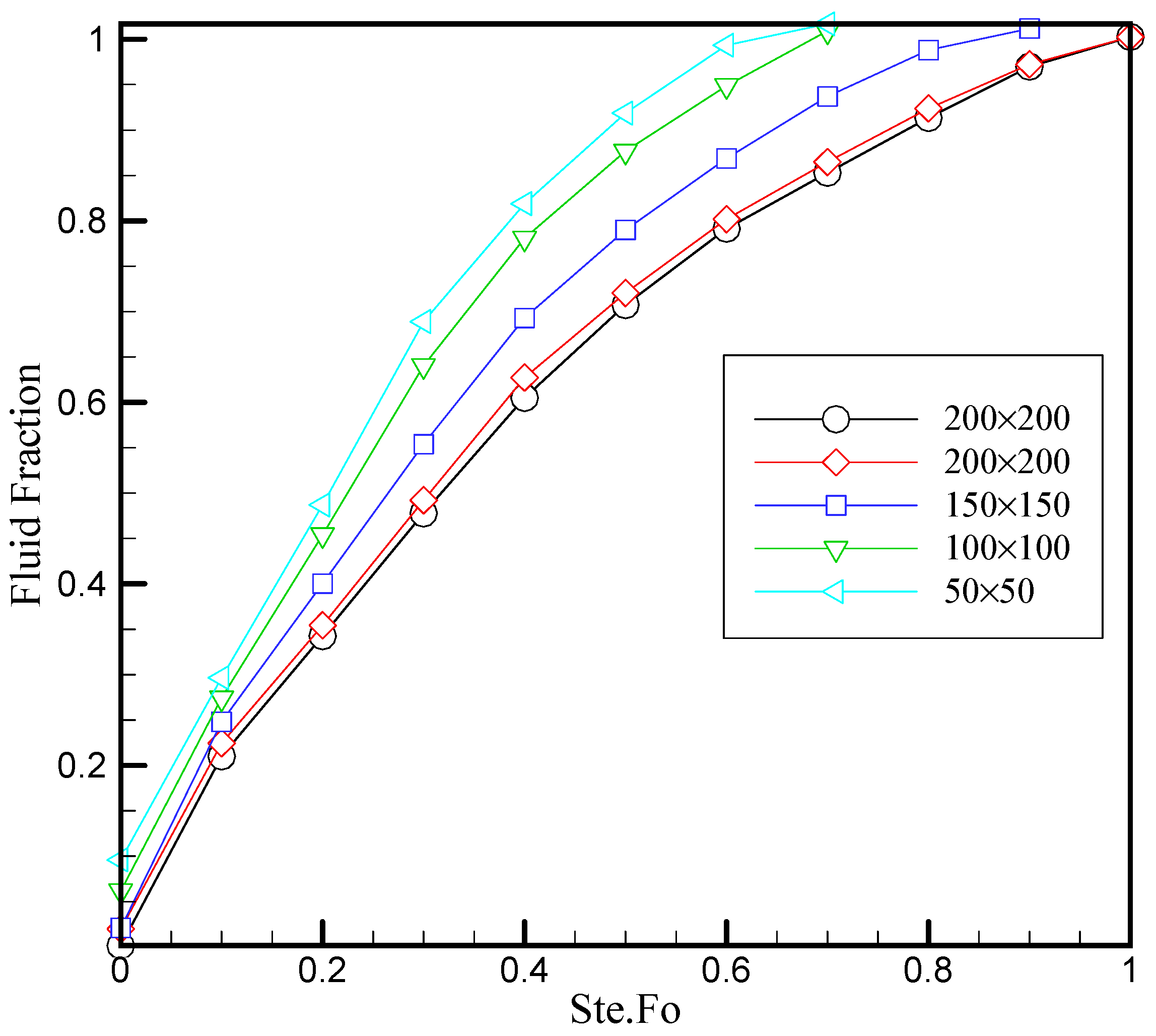
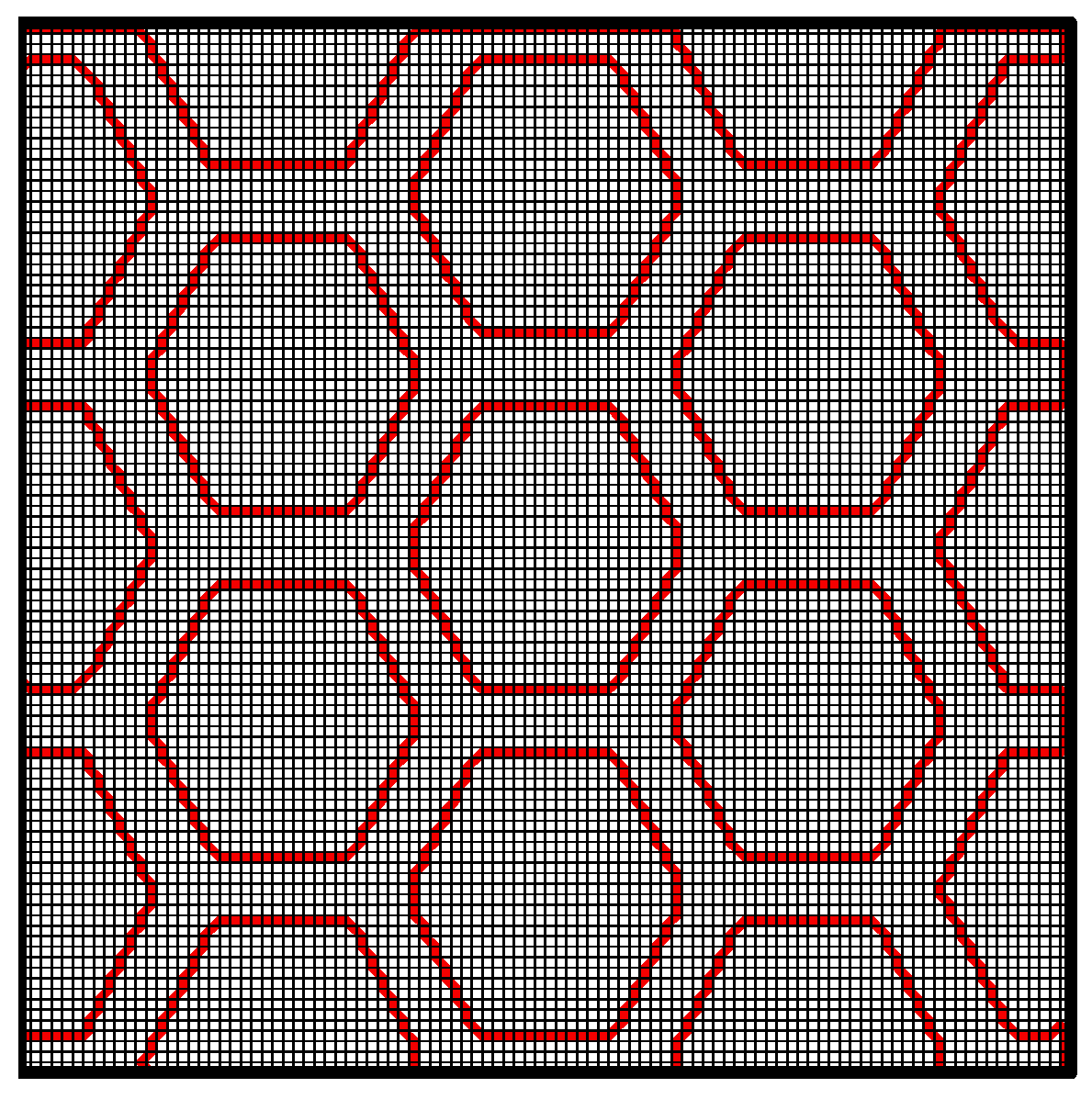
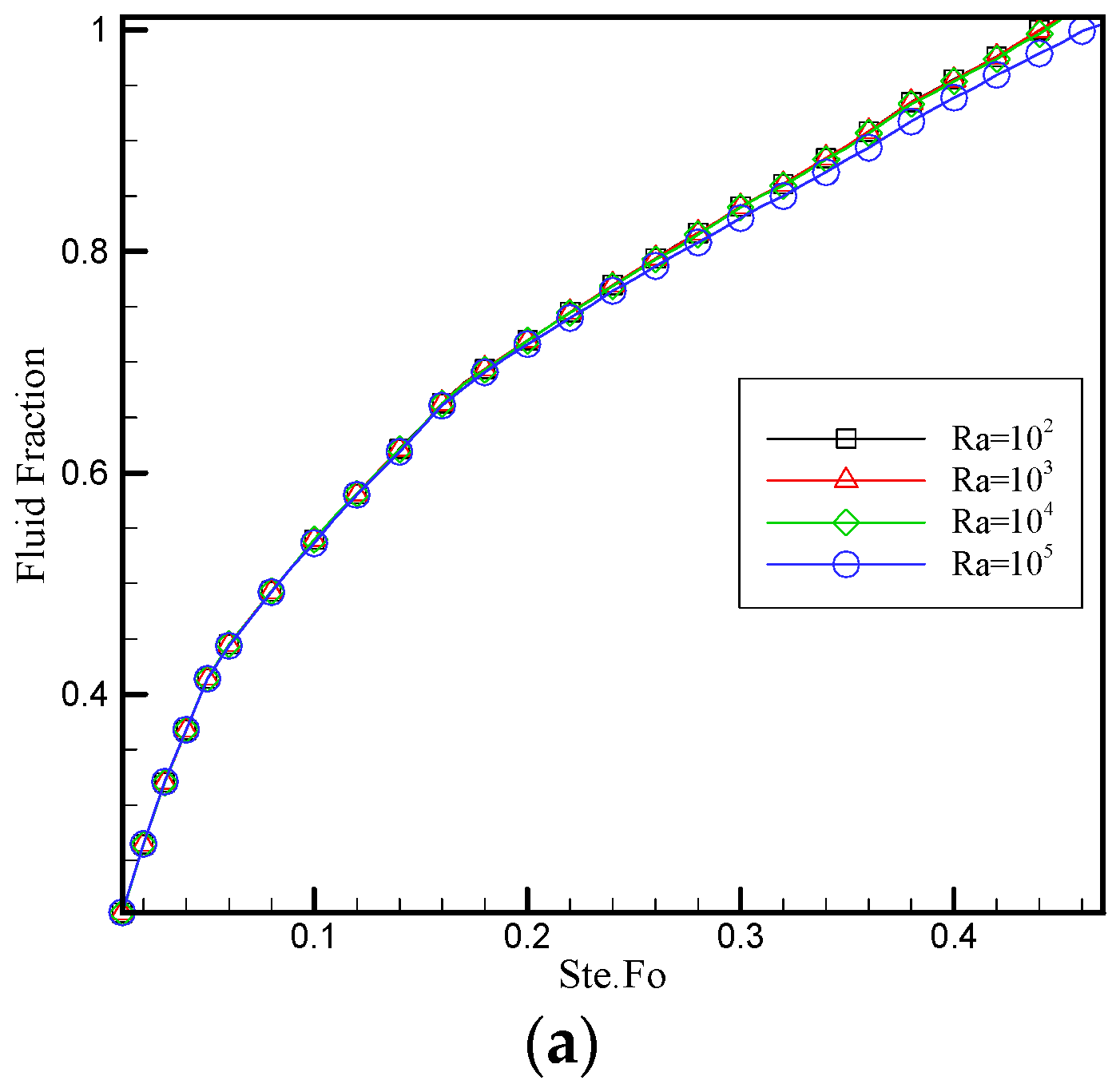
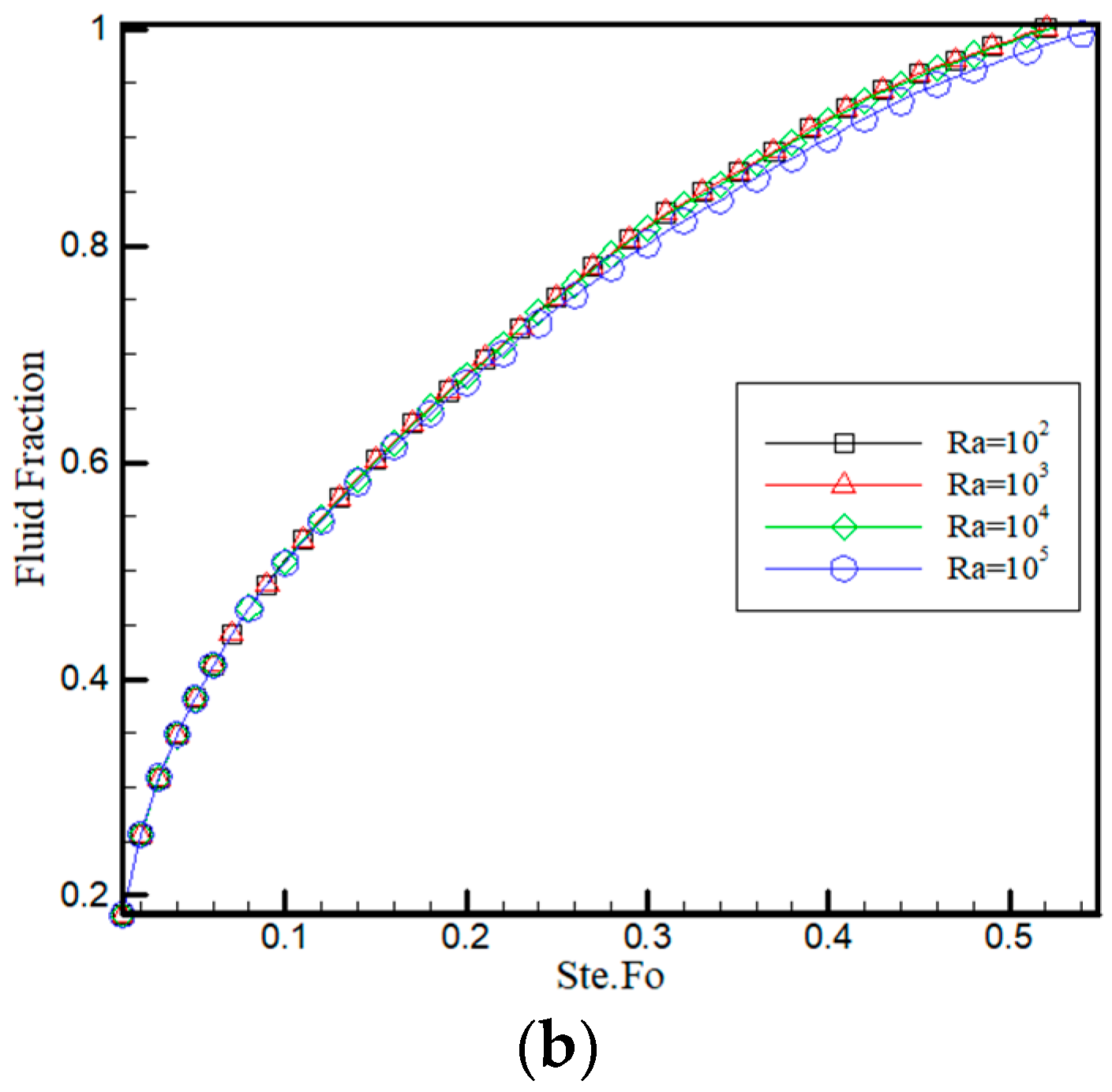
4. Grid Study
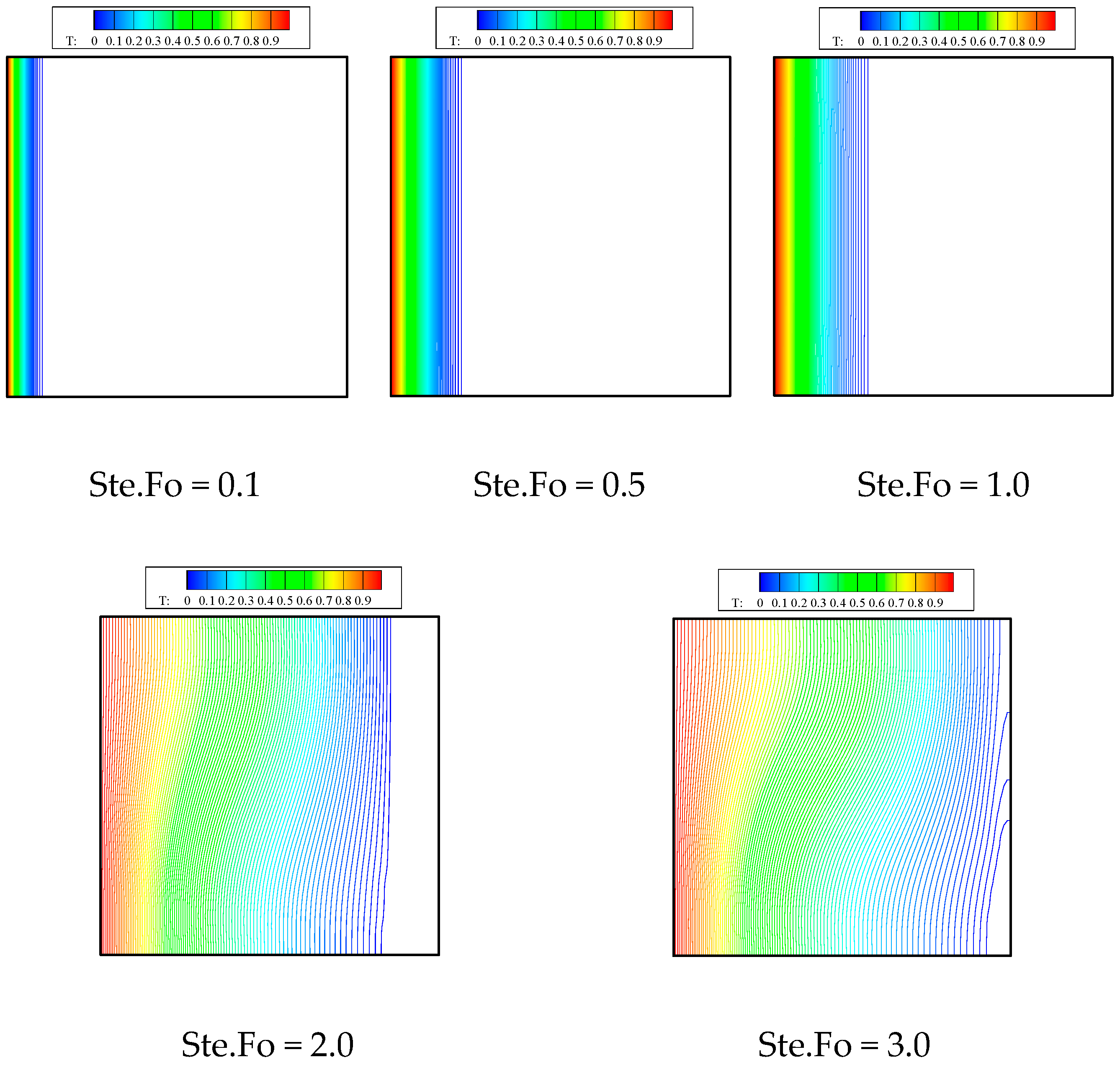
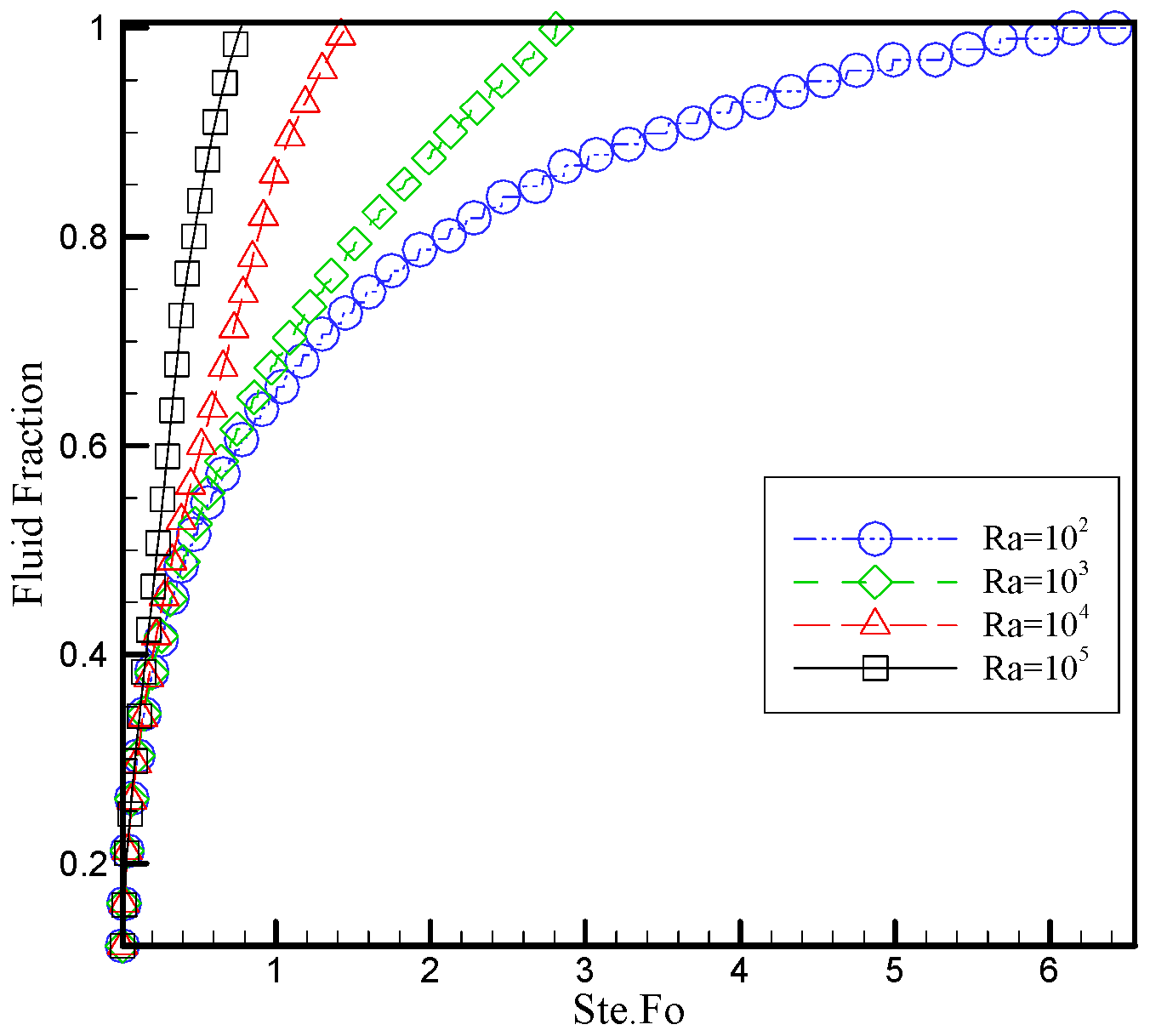
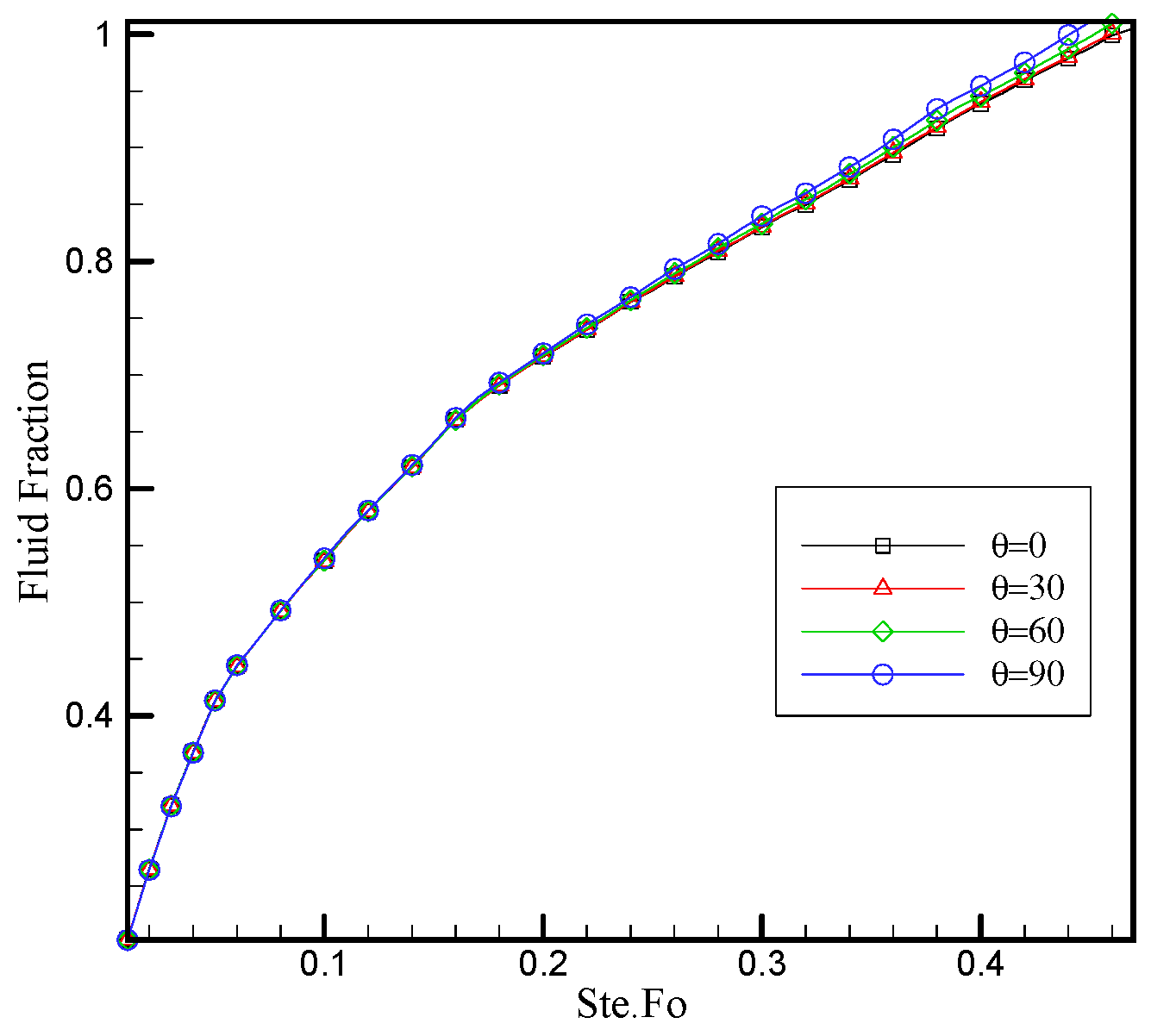
5. Validation
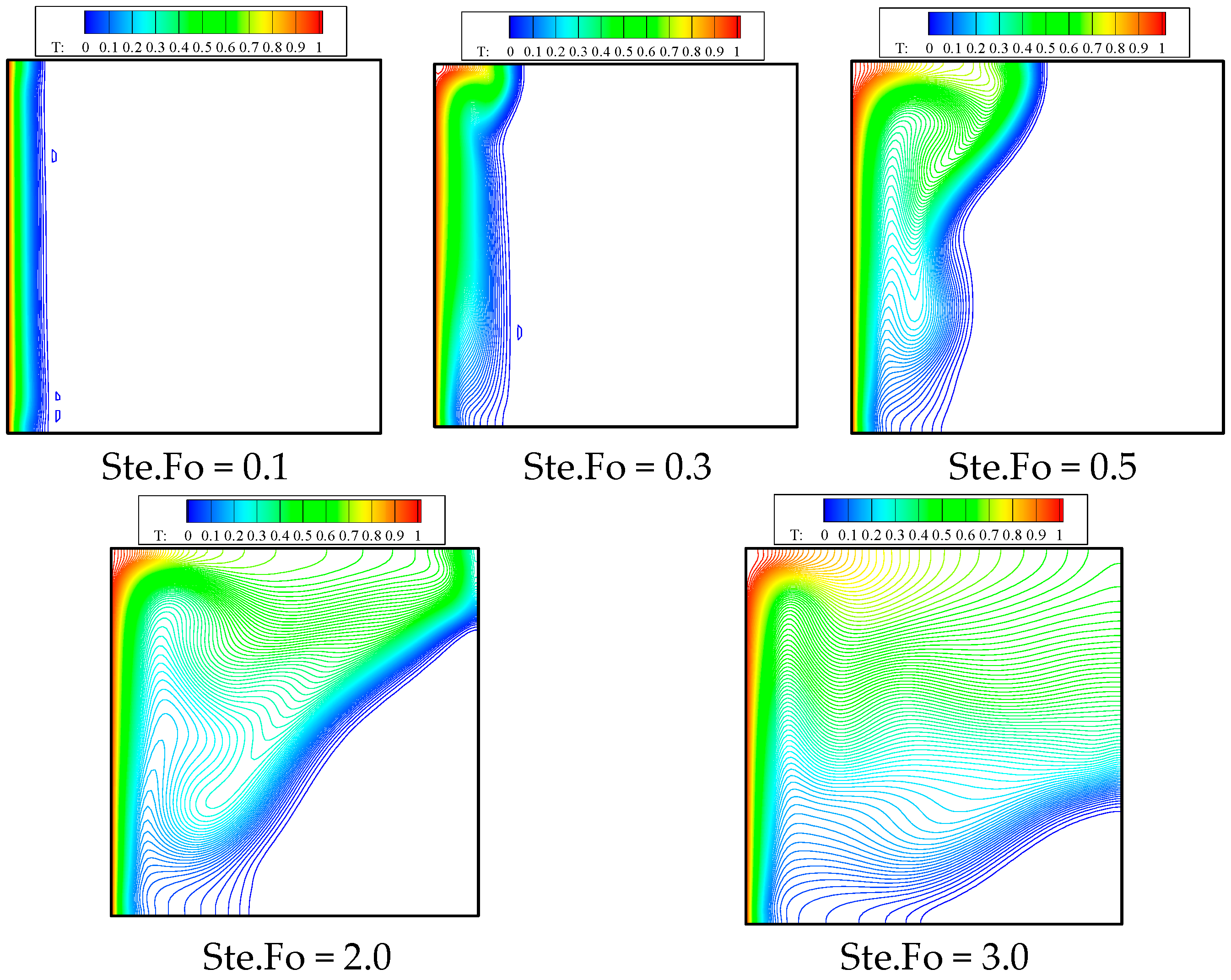
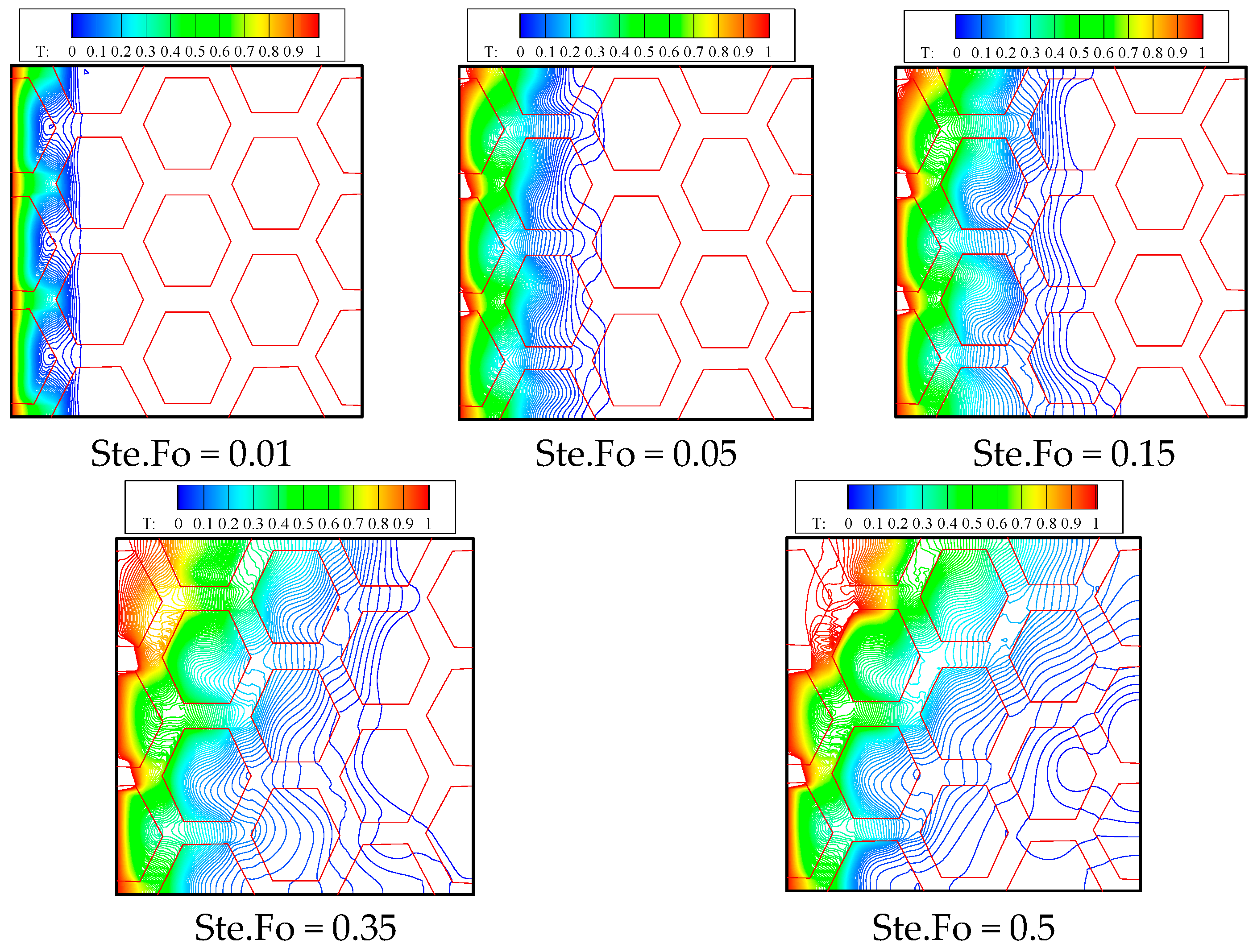
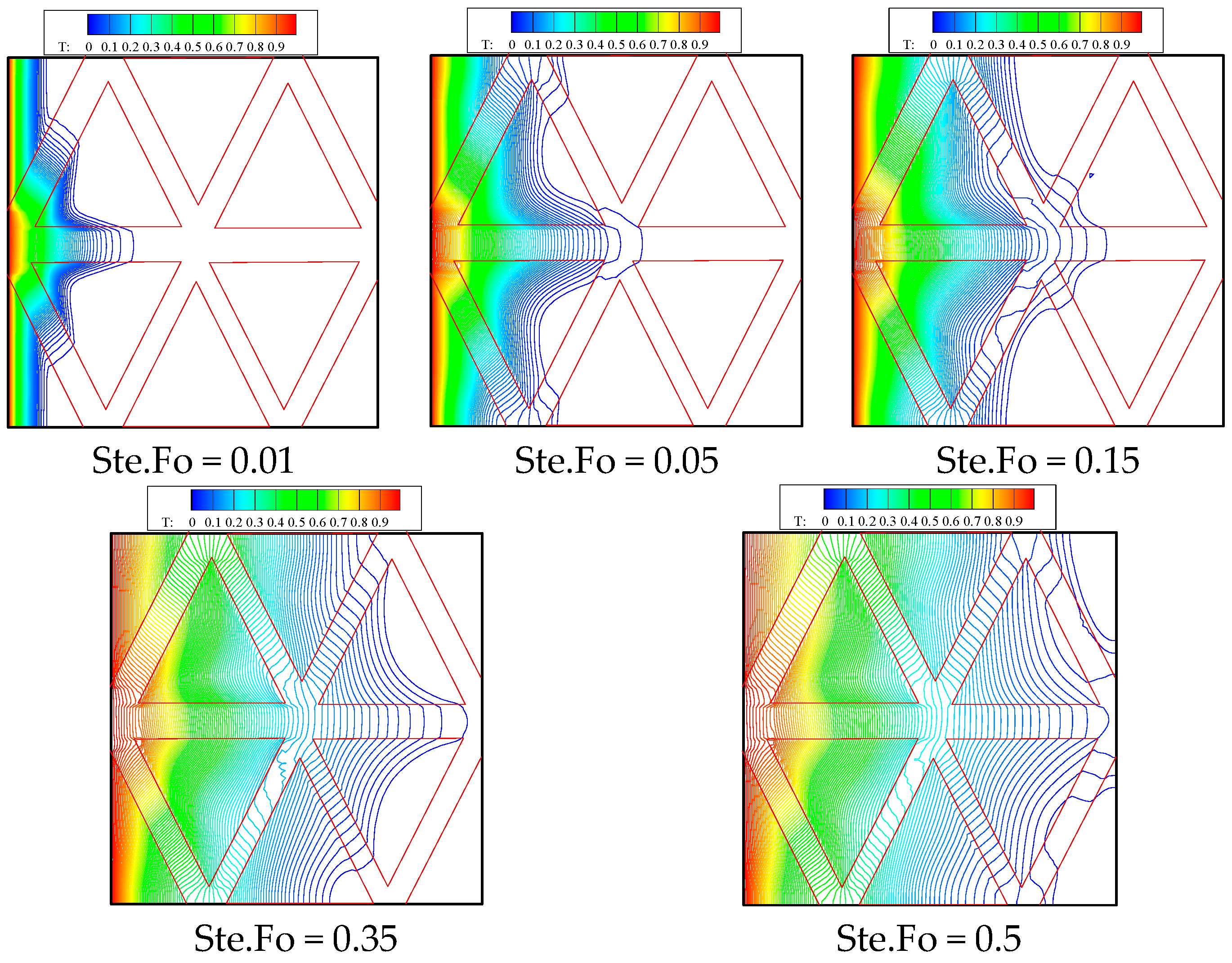
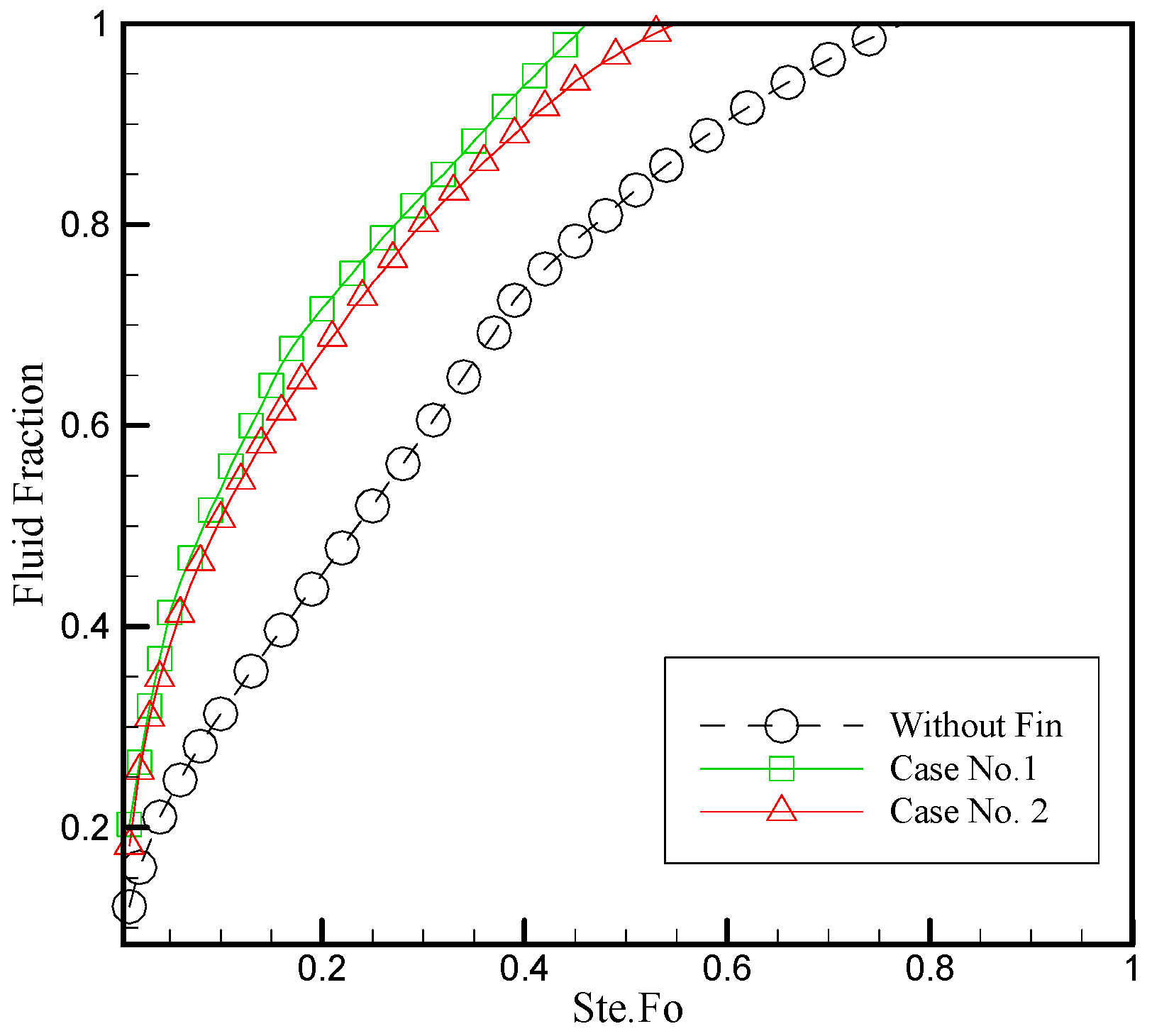
6. Results
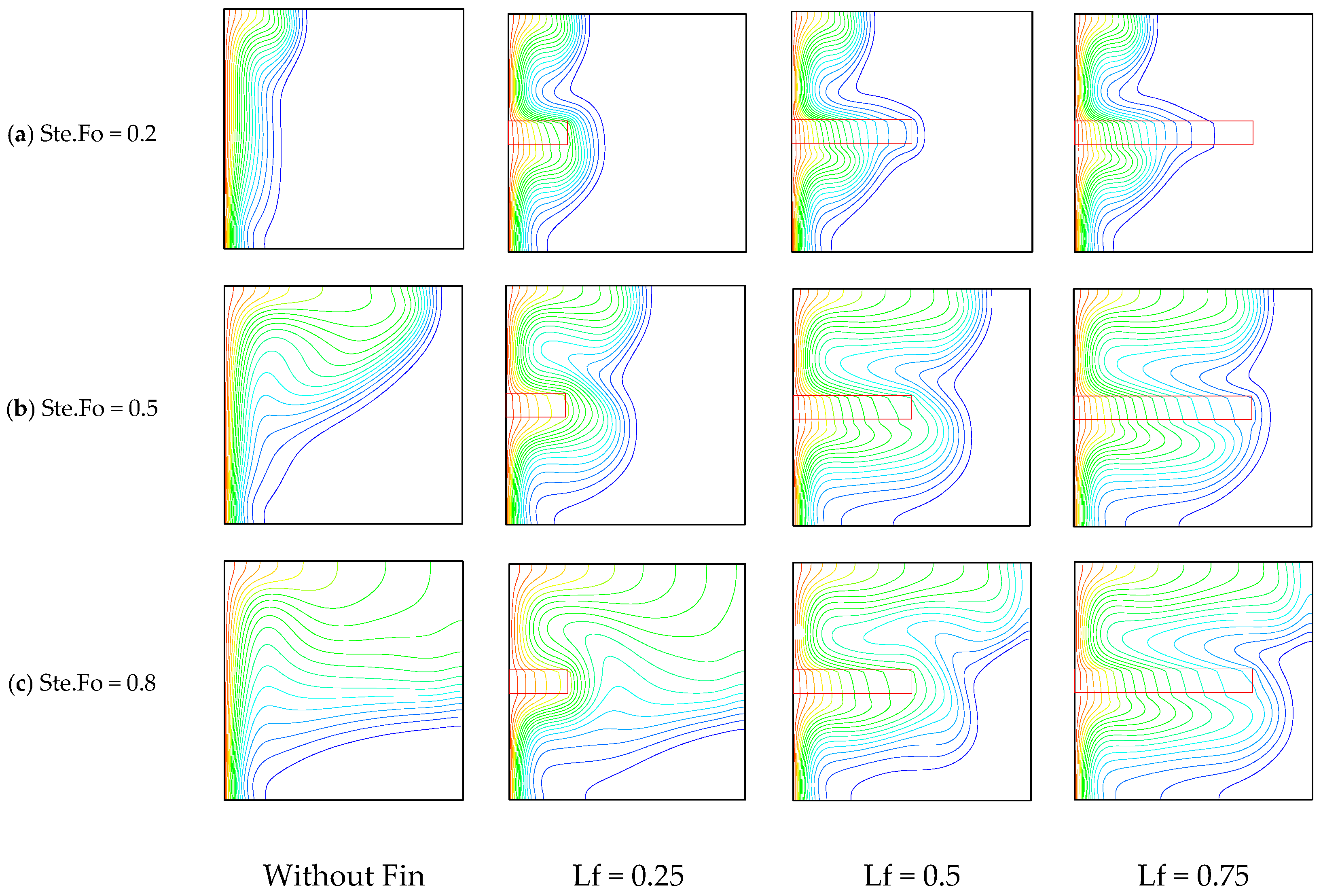
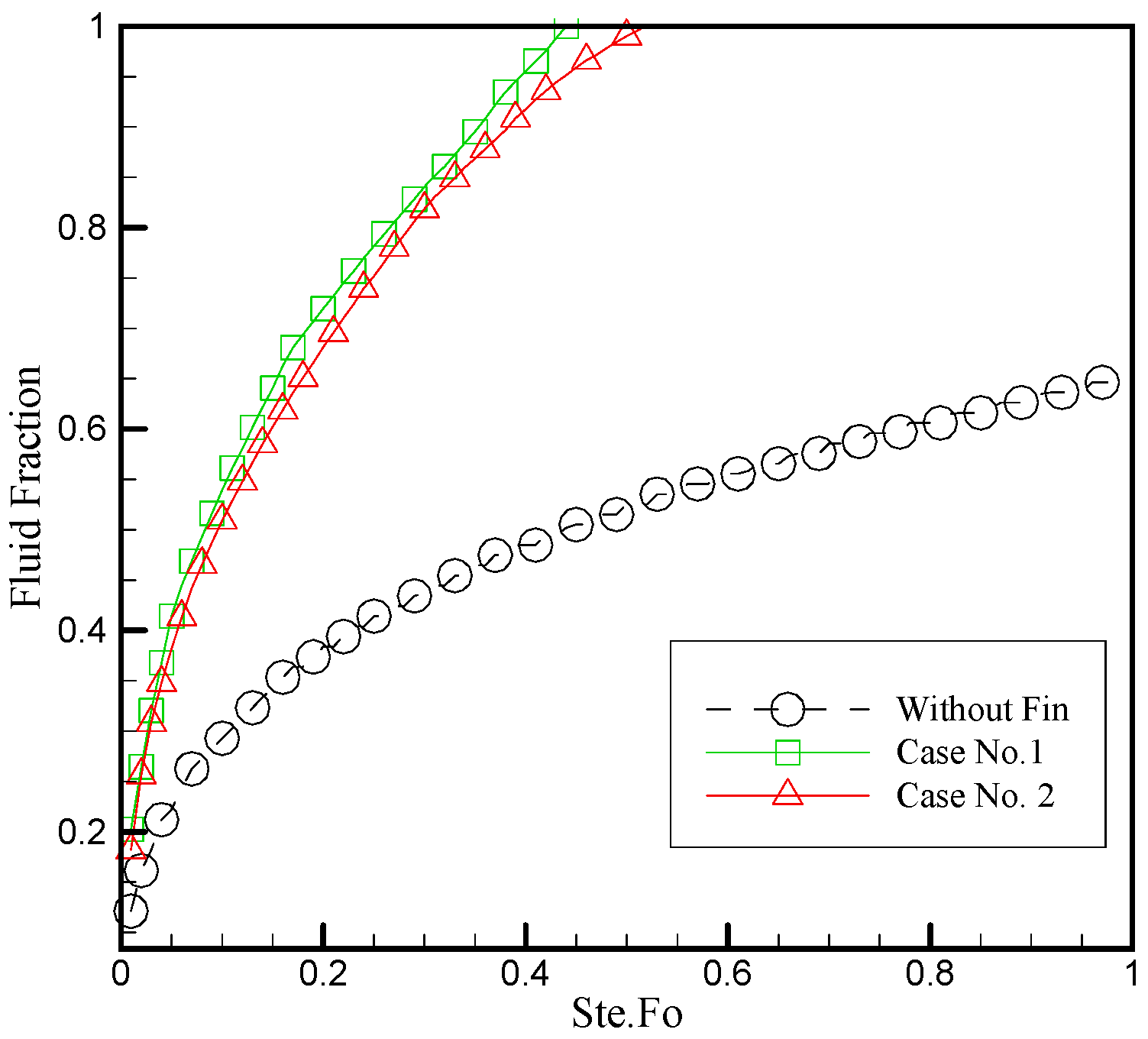
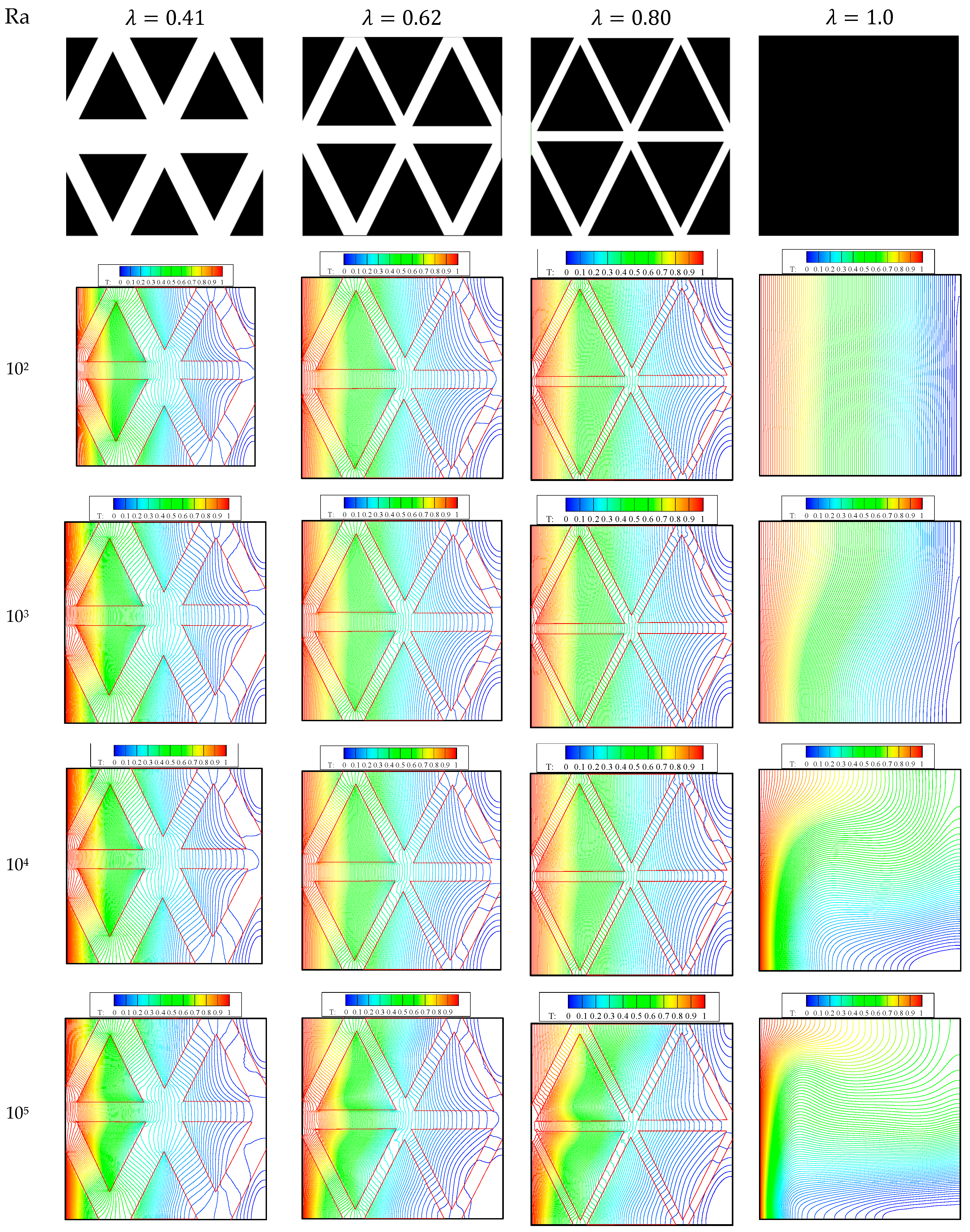
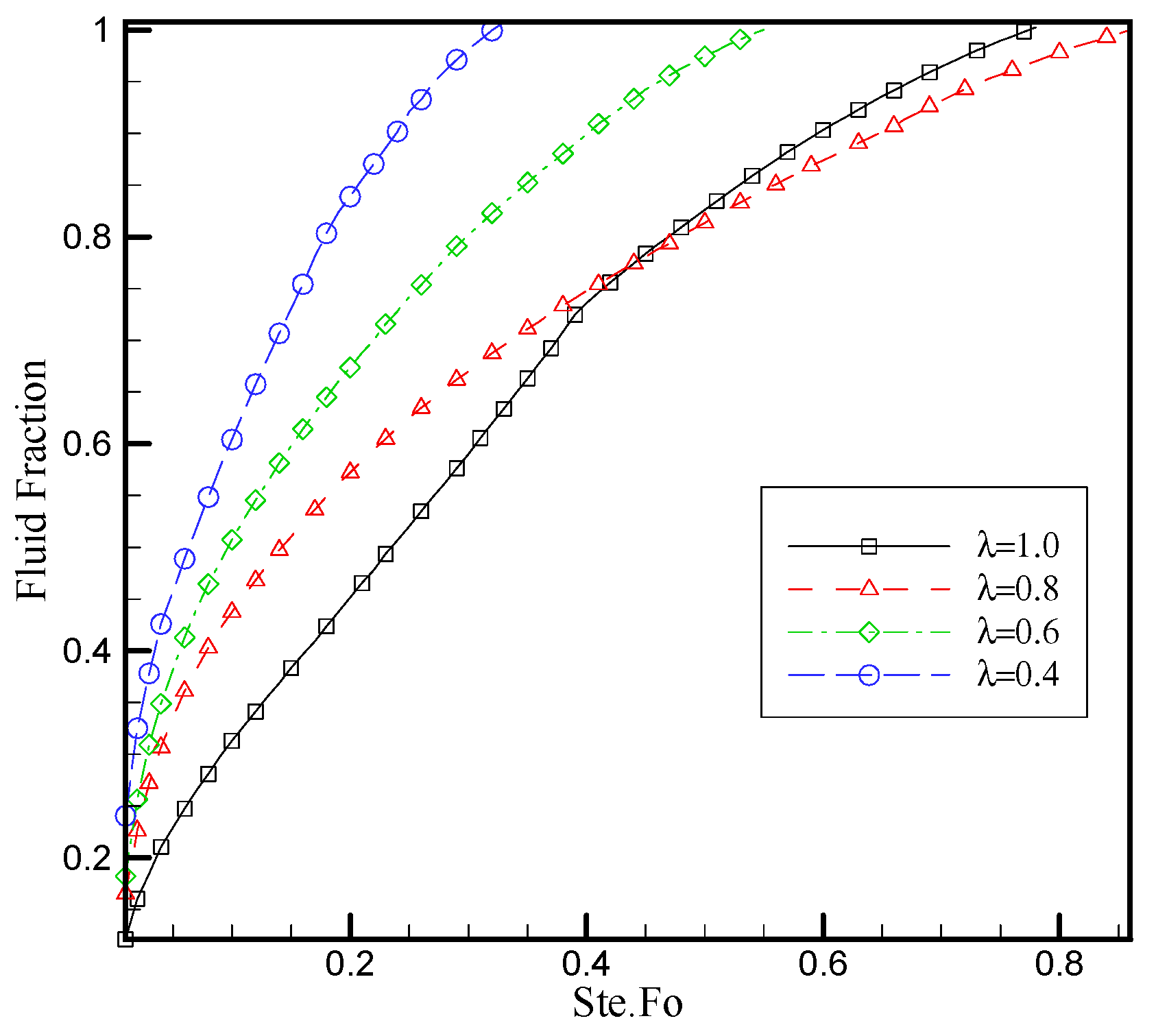
6.1. Effect of the Honeycomb Fin Structure
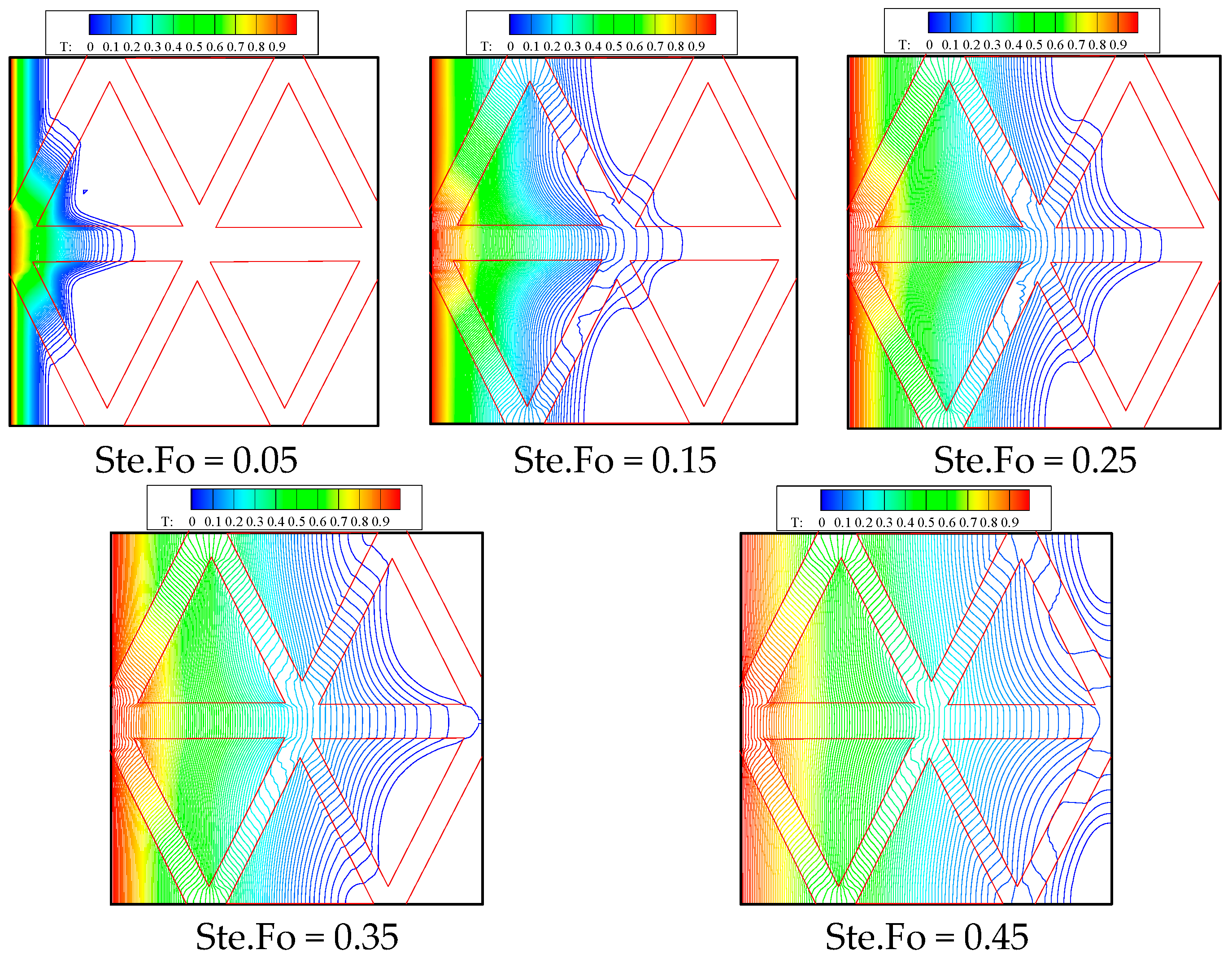
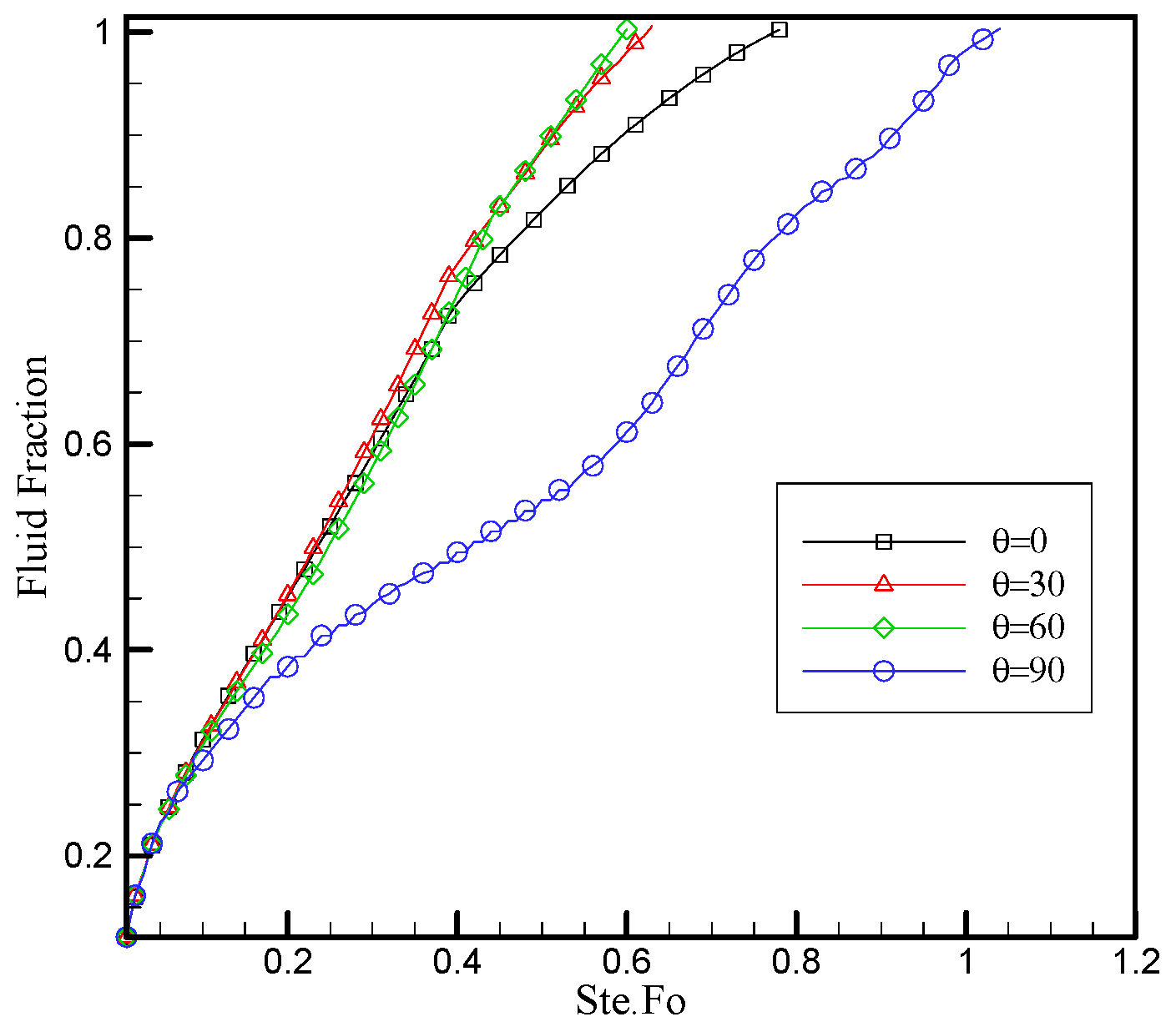
6.2. The Effect of Honeycomb Structure on Inclined Cavities
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| (m/s) | the discrete velocity of Boltzmann grid |
| () | specific heat at constant pressure |
| (m/s) | sound speed |
| buoyancy force | |
| the distribution function | |
| fluid fraction at time step n and iteration k | |
| the local equilibrium distribution function | |
| the gravitational acceleration | |
| temperature distribution function | |
| the local equilibrium distribution function of temperature | |
| Grashof number | |
| ( | conduction heat transfer coefficient |
| (m) | the width of the cavity |
| Latent heat | |
| Prandtl number | |
| Rayleigh number | |
| (K) | temperature |
| (s) | time |
| (m/s) | velocity component in the x-direction |
| velocity component in the y-direction | |
| the velocity of the top wall | |
| the weight function of the ith direction | |
| Greek | |
| thermal diffusivity | |
| viscosity | |
| ) | density |
| the relaxation time of the flow field | |
| the relaxation time of the temperature field | |
| kinematic viscosity | |
| Footnotes | |
| fluid | |
| wall | |
| Abbreviations | |
| PCM | phase change material |
| LBM | lattice Boltzmann method |
References
- Tripathi, B.M.; Shukla, S.K.; Rathore, P.K.S. A comprehensive review on solar to thermal energy conversion and storage using phase change materials. J. Energy Storage 2023, 72, 108280. [Google Scholar] [CrossRef]
- Cui, H.; Zou, Y.; Yang, H.; Bao, X. Thermal-mechanical behaviors of concrete with innovative salt hydrate PCM-based thermal energy storage aggregate. Energy Convers. Manag. 2023, 293, 117477. [Google Scholar] [CrossRef]
- Chavan, S.; Venkateswarlu, B.; Prabakaran, R.; Salman, M.; Joo, S.W.; Choi, G.S.; Kim, S.C. Thermal runaway and mitigation strategies for electric vehicle lithium-ion batteries using battery cooling approach: A review of the current status and challenges. J. Energy Storage 2023, 72, 108569. [Google Scholar] [CrossRef]
- Mubarrat, M.; Mashfy, M.M.; Farhan, T.; Ehsan, M.M. Research Advancement and Potential Prospects of Thermal Energy Storage in Concentrated Solar Power Application. Int. J. Thermofluids 2023, 20, 100431. [Google Scholar] [CrossRef]
- Liu, Z.; Du, J.; Steere, R.; Schlegel, J.P.; Khayat, K.H.; Meng, W. Cement-Based Materials with Solid–Gel Phase Change Materials for Improving Energy Efficiency of Building Envelope. J. Mater. Civ. Eng. 2023, 35, 04023425. [Google Scholar] [CrossRef]
- Yang, T.; Ding, Y.; Li, B.; Athienitis, A.K. A review of climate adaptation of phase change material incorporated in building envelopes for passive energy conservation. Build. Environ. 2023, 244, 110711. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Le, T.L.; Duong, X.Q.; Le, V.V.; Nguyen, D.T.; Nguyen, P.Q.P.; Rajamohan, S.; Vo, A.V.; Le, H.S. Application of phase change materials in improving the performance of refrigeration systems. Sustain. Energy Technol. Assess. 2023, 56, 103097. [Google Scholar] [CrossRef]
- Hu, C.; Sha, L.; Huang, C.; Luo, W.; Li, B.; Huang, H.; Xu, C.; Zhang, K. Phase change materials in food: Phase change temperature, environmental friendliness, and systematization. Trends Food Sci. Technol. 2023, 140, 104167. [Google Scholar] [CrossRef]
- Dardouri, S.; Mankai, S.; Almoneef, M.M.; Mbarek, M.; Sghaier, J. Energy performance based optimization of building envelope containing PCM combined with insulation considering various configurations. Energy Rep. 2023, 10, 895–909. [Google Scholar] [CrossRef]
- Nikolaidis, P. Solar Energy Harnessing Technologies towards De-Carbonization: A Systematic Review of Processes and Systems. Energies 2023, 16, 6153. [Google Scholar] [CrossRef]
- Odoi-Yorke, F.; Opoku, R.; Davis, F.; Obeng, G.Y. Optimisation of thermal energy storage systems incorporated with phase change materials for sustainable energy supply: A systematic review. Energy Rep. 2023, 10, 2496–2512. [Google Scholar] [CrossRef]
- Soodmand, A.M.; Azimi, B.; Nejatbakhsh, S.; Pourpasha, H.; Farshchi, M.E.; Aghdasinia, H.; Mohammadpourfard, M.; Heris, S.Z. A comprehensive review of computational fluid dynamics simulation studies in phase change materials: Applications, materials, and geometries. J. Therm. Anal. Calorim. 2023, 148, 10595–10644. [Google Scholar] [CrossRef]
- Quan, L.; Pan, Z. Investigating the thermal behavior of phase change materials of ethylene glycol-filled SiO2 plates in the presence of solar radiation by molecular dynamics simulation. Eng. Anal. Bound. Elem. 2023, 150, 1–6. [Google Scholar] [CrossRef]
- Yan, G.; Alizadeh, A.; Rahmani, A.; Zarringhalam, M.; Shamsborhan, M.; Nasajpour-Esfahani, N.; Akrami, M. Natural convection of rectangular cavity enhanced by obstacle and fin to simulate phase change material melting process using Lattice Boltzmann method. Alex. Eng. J. 2023, 81, 319–336. [Google Scholar] [CrossRef]
- Triki, R.; Chtourou, S.; Baccar, M. Heat transfer enhancement of phase change materials PCMs using innovative fractal H-shaped fin configurations. J. Energy Storage 2023, 73, 109020. [Google Scholar] [CrossRef]
- Zhang, T.; Huo, D.; Wang, C.; Shi, Z. Review of the modeling approaches of phase change processes. Renew. Sustain. Energy Rev. 2023, 187, 113724. [Google Scholar] [CrossRef]
- Moreira, M.; Silva, T.; Dias-de-Oliveira, J.; Neto, F.; Amaral, C. Numerical modelling of radiant systems and phase change materials in building applications—A review. Appl. Therm. Eng. 2023, 234, 121342. [Google Scholar] [CrossRef]
- Pignata, A.; Minuto, F.D.; Lanzini, A.; Papurello, D. A feasibility study of a tube bundle exchanger with phase change materials: A case study. J. Build. Eng. 2023, 78, 107622. [Google Scholar] [CrossRef]
- Rashid, F.L.; Eisapour, M.; Ibrahem, R.K.; Talebizadehsardari, P.; Hosseinzadeh, K.; Abbas, M.H.; Mohammed, H.I.; Yvaz, A.; Chen, Z. Solidification enhancement of phase change materials using fins and nanoparticles in a triplex-tube thermal energy storage unit: Recent advances and development. Int. Commun. Heat Mass Transf. 2023, 147, 106922. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Chao, H. Machine learning and computational fluid dynamics based optimization of finned heat pipe radiator performance. J. Build. Eng. 2023, 78, 107612. [Google Scholar] [CrossRef]
- Li, S.J.; Zhu, L.T.; Zhang, X.B.; Luo, Z.H. Recent Advances in CFD Simulations of Multiphase Flow Processes with Phase Change. Ind. Eng. Chem. Res. 2023, 62, 10729–10786. [Google Scholar] [CrossRef]
- Rocha, T.T.M.; Teggar, M.; Trevizoli, P.V.; de Oliveira, R.N. Potential of latent thermal energy storage for performance improvement in small-scale refrigeration units: A review. Renew. Sustain. Energy Rev. 2023, 187, 113746. [Google Scholar] [CrossRef]
- Hu, Y.; Jasim, D.J.; Alizadeh, A.A.; Rahmani, A.; Al-Shati, A.S.; Zarringhalam, M.; Shamsborhan, M.; Nasajpour-Esfahani, N. Simulation of heat transfer in a nanoparticle enhanced phase change material to design battery thermal management systems: A lattice Boltzmann method study. J. Taiwan Inst. Chem. Eng. 2023, 152, 105137. [Google Scholar] [CrossRef]
- Nasehi, P.; Jamekhorshid, A. Simulation and optimization of a modified geometry LHTES system using needle-shaped fins. Multiscale Multidiscip. Model. Exp. Des. 2023, 1–14. [Google Scholar] [CrossRef]
- Nedumaran, M.S.; Gnanasekaran, N.; Hooman, K. Extensive analysis of PCM-based heat sink with different fin arrangements under varying load conditions and variable aspect ratio. J. Energy Storage 2023, 73, 108870. [Google Scholar] [CrossRef]
- Palacios, A.; Navarro-Rivero, M.E.; Zou, B.; Jiang, Z.; Harrison, M.T.; Ding, Y. A perspective on Phase Change Material encapsulation: Guidance for encapsulation design methodology from low to high-temperature thermal energy storage applications. J. Energy Storage 2023, 72, 108597. [Google Scholar] [CrossRef]
- Sarath, K.P.; Osman, M.F.; Mukhesh, R.; Manu, K.V.; Deepu, M. A review of the recent advances in the heat transfer physics in latent heat storage systems. Therm. Sci. Eng. Prog. 2023, 42, 101886. [Google Scholar] [CrossRef]
- Kumar, S.; Panda, D.; Ghodke, P.; Gangawane, K.M. Lattice Boltzmann method for heat transfer in phase change materials: A review. J. Therm. Anal. Calorim. 2023, 148, 9263–9287. [Google Scholar] [CrossRef]
- Ahn, J.; Song, J.C.; Lee, J.S. An Immersed Boundary Method for Conjugate Heat Transfer Involving Melting/Solidification. Int. J. Aeronaut. Space Sci. 2023, 24, 1–10. [Google Scholar] [CrossRef]
- Huber, C.; Parmigiani, A.; Chopard, B.; Manga, M.; Bachmann, O. Lattice Boltzmann model for melting with natural convection. Int. J. Heat. Fluid. Flow. 2008, 29, 1469–1480. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, X.; Huo, Y.; Rao, Z. The lattice Boltzmann model for the heat and mass transfer of latent functional thermal fluid using enthalpy-transforming method. J. Energy Storage 2023, 64, 107189. [Google Scholar] [CrossRef]
- Peng, W.; Sadaghiani, O.K. Thermal function improvement of phase-change material (PCM) using alumina nanoparticles in a circular-rectangular cavity using Lattice Boltzmann method. J. Energy Storage 2021, 37, 102493. [Google Scholar] [CrossRef]
- Li, D.; Yu, Z. Natural convection melting in a cubic cavity with internal fins: A lattice Boltzmann study. Case Stud. Therm. Eng. 2021, 25, 100919. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Sheremet, M.; Raizah, Z.; Akkurt, N.; Ghalambaz, M. Latent heat thermal energy storage in a shell-tube design: Impact of metal foam inserts in the heat transfer fluid side. J. Energy Storage 2023, 73, 108893. [Google Scholar] [CrossRef]
- Reddy, B.D.; Rahul, S.V.S.; Harish, R. Impact of fin number and nanoparticle size on molten salt NanoPCM melting in finned annular space. J. Energy Storage 2023, 72, 108705. [Google Scholar] [CrossRef]
- Subasi, A.; Subasi, S.; Bayram, M.; Sarı, A.; Hekimoğlu, G.; Ustaoglu, A.; Gencel, O.; Ozbakkaloglu, T. Effect of carbon nanotube and microencapsulated phase change material utilization on the thermal energy storage performance in UV cured (photoinitiated) unsaturated polyester composites. J. Energy Storage 2023, 61, 106780. [Google Scholar] [CrossRef]
- Zhao, C.; Opolot, M.; Liu, M.; Bruno, F.; Mancin, S.; Hooman, K. Numerical study of melting performance enhancement for PCM in an annular enclosure with internal-external fins and metal foams. Int. J. Heat. Mass. Transf. 2020, 150, 119348. [Google Scholar] [CrossRef]
- Lashgari, S.; Mahdavian, A.R.; Arabi, H.; Ambrogi, V.; Marturano, V. Preparation of acrylic PCM microcapsules with dual responsivity to temperature and magnetic field changes. Eur. Polym. J. 2018, 101, 18–28. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Jourabian, M.; Farhadi, M. Melting and solidification of PCM enhanced by radial conductive fins and nanoparticles in cylindrical annulus. Energy Convers. Manag. 2016, 118, 253–263. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. GPU accelerated numerical study of PCM melting process in an enclosure with internal fins using lattice Boltzmann method. Int. J. Heat. Mass. Transf. 2016, 100, 522–535. [Google Scholar] [CrossRef]
- Ren, Q.; Guo, P.; Zhu, J. Thermal management of electronic devices using pin-fin based cascade microencapsulated PCM/expanded graphite composite. Int. J. Heat. Mass. Transf. 2020, 149, 119199. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, Z.; Zhou, Y.; Lu, B.; Zhang, Y. Numerical study using lattice Boltzmann method on melting and solidification of NEPCM placed inside a rectangular cavity with a new double-fin arrangement. Appl. Therm. Eng. 2023, 219, 119619. [Google Scholar] [CrossRef]
- Alizadeh, M.; Shahavi, M.H.; Ganji, D.D. Performance enhancement of nano PCM solidification in a hexagonal storage unit with innovative fin shapes dealing with time-dependent boundary conditions. Energy Rep. 2022, 8, 8200–8214. [Google Scholar] [CrossRef]
- Sultan, M.; Mostafa, H.; El Boz, A.M.; Elngiry, E. Effect of Inlet and Geometrical Parameters on the Melting of PCM Capsules of Elliptical Cross Section. ERJ. Eng. Res. J. 2021, 44, 11–20. [Google Scholar] [CrossRef]
- Jourabian, M.; Farhadi, M.; Darzi, A.A.R. Simulation of natural convection melting in an inclined cavity using lattice Boltzmann method. Sci. Iran. 2012, 19, 1066–1073. [Google Scholar] [CrossRef]
- Rahmani, A.; Dibaj, M.; Akrami, M.; Akrami, M. Computational investigation of magnetohydrodynamic flow and melting process of phase change material in a battery pack using the lattice Boltzmann method. J. Energy Storage 2024, 78, 110046. [Google Scholar] [CrossRef]





| Properties | Unit | Paraffin-Wax |
|---|---|---|
| 2000 | ||
| 800 | ||
| 0.2 | ||
| 275 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmani, A.; Dibaj, M.; Akrami, M. Enhancing Heat Storage Cooling Systems via the Implementation of Honeycomb-Inspired Design: Investigating Efficiency and Performance. Energies 2024, 17, 351. https://doi.org/10.3390/en17020351
Rahmani A, Dibaj M, Akrami M. Enhancing Heat Storage Cooling Systems via the Implementation of Honeycomb-Inspired Design: Investigating Efficiency and Performance. Energies. 2024; 17(2):351. https://doi.org/10.3390/en17020351
Chicago/Turabian StyleRahmani, Amin, Mahdieh Dibaj, and Mohammad Akrami. 2024. "Enhancing Heat Storage Cooling Systems via the Implementation of Honeycomb-Inspired Design: Investigating Efficiency and Performance" Energies 17, no. 2: 351. https://doi.org/10.3390/en17020351
APA StyleRahmani, A., Dibaj, M., & Akrami, M. (2024). Enhancing Heat Storage Cooling Systems via the Implementation of Honeycomb-Inspired Design: Investigating Efficiency and Performance. Energies, 17(2), 351. https://doi.org/10.3390/en17020351







