Numerical Investigations of the Cooling Performance of an R410A Closed-Loop Spray Cooling System
Abstract
1. Introduction
2. Physical and Mathematical Model
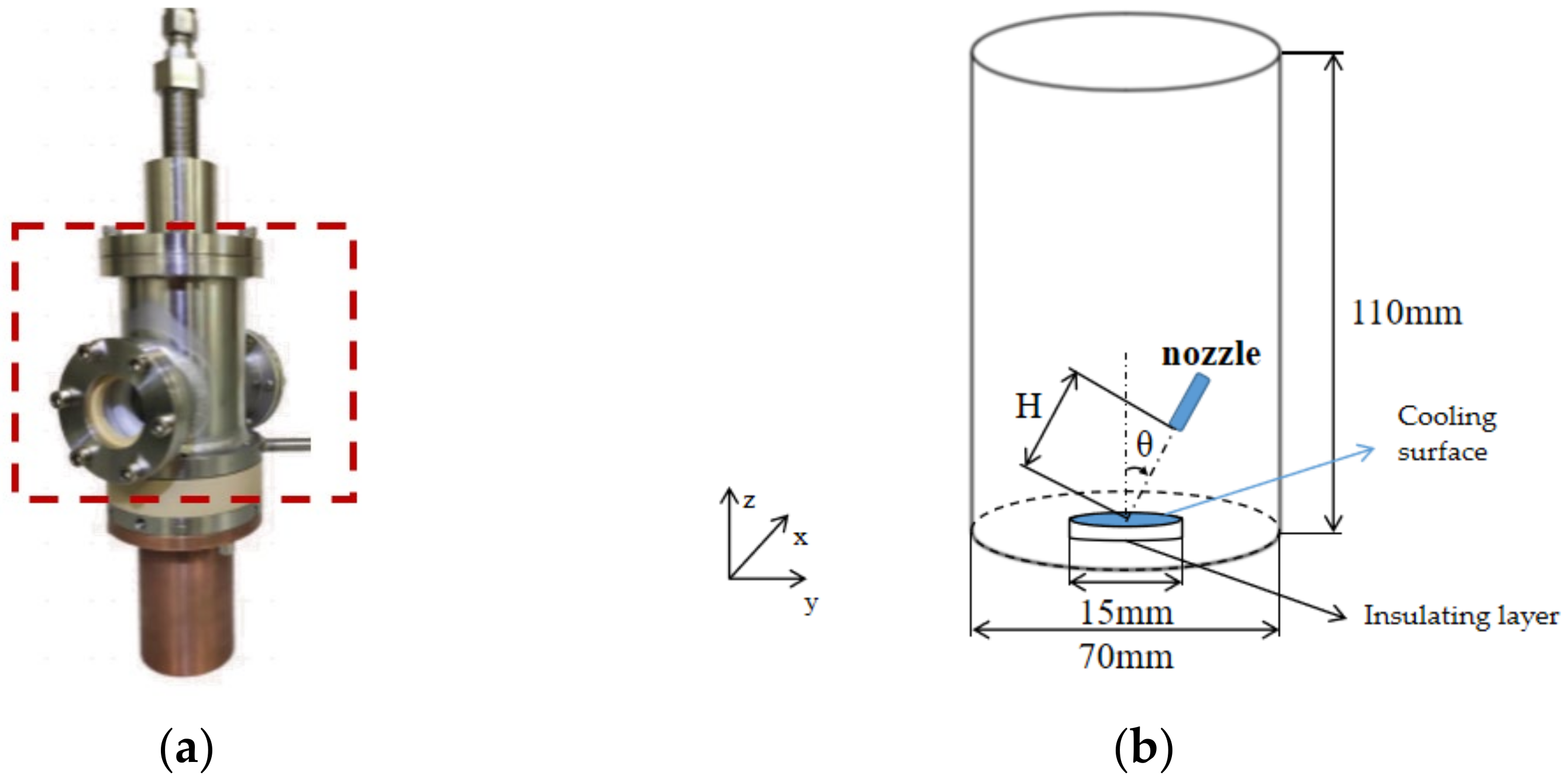
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Continuous Phase Model
2.2.2. Discrete Phase Model
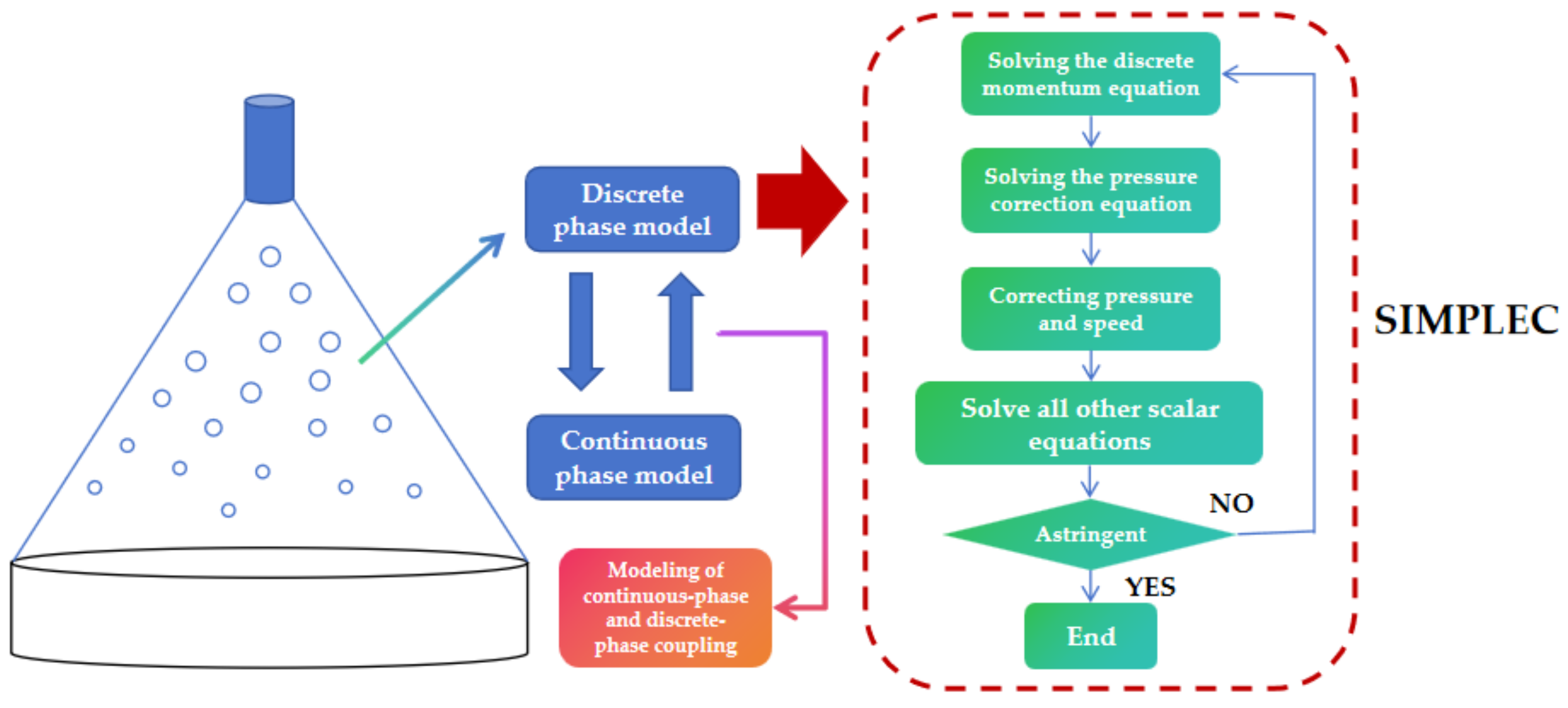
2.2.3. Coupling between the Continuous and Discrete Phase Models
2.2.4. Thermal Properties and Boundary Conditions
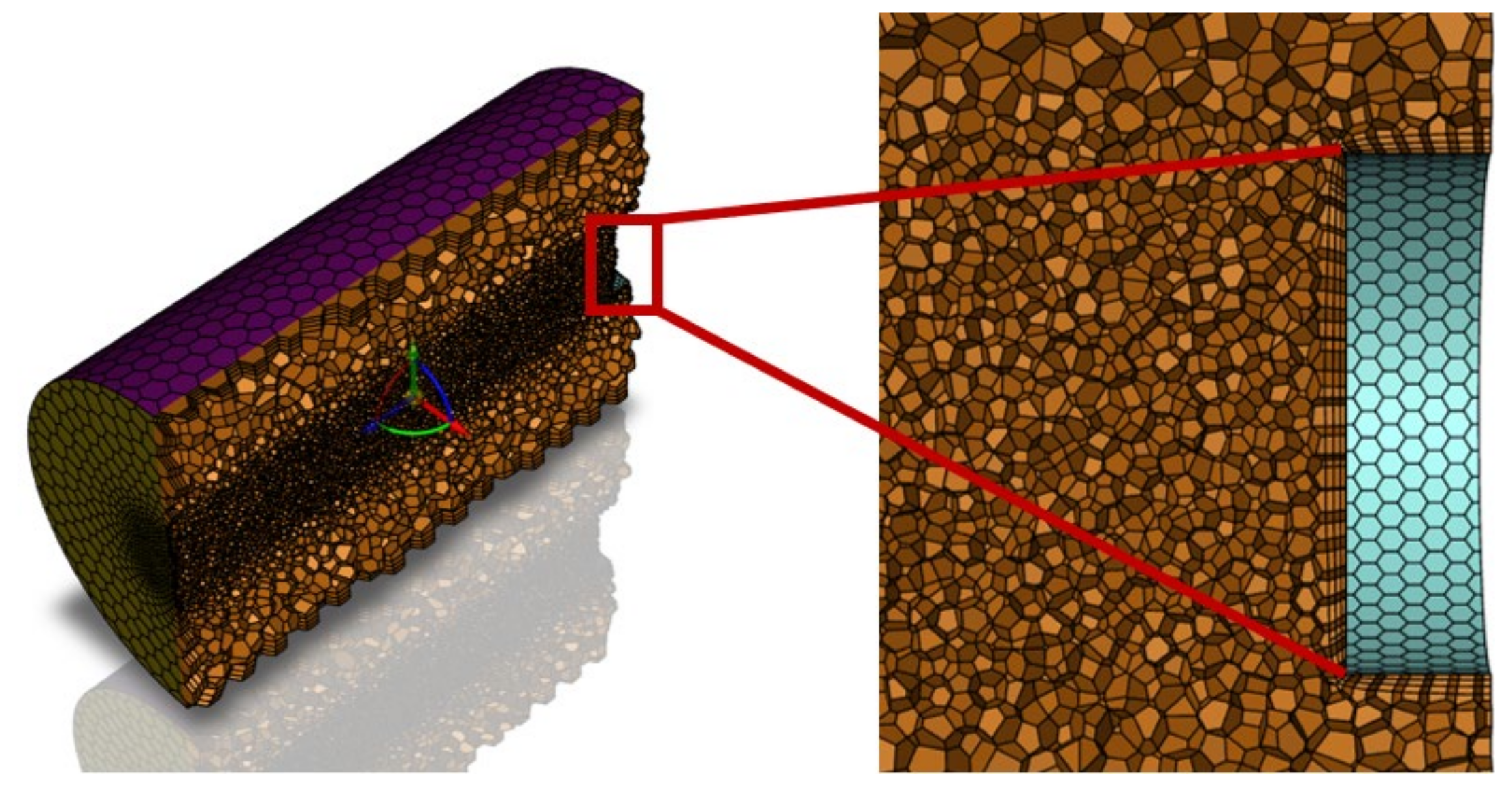
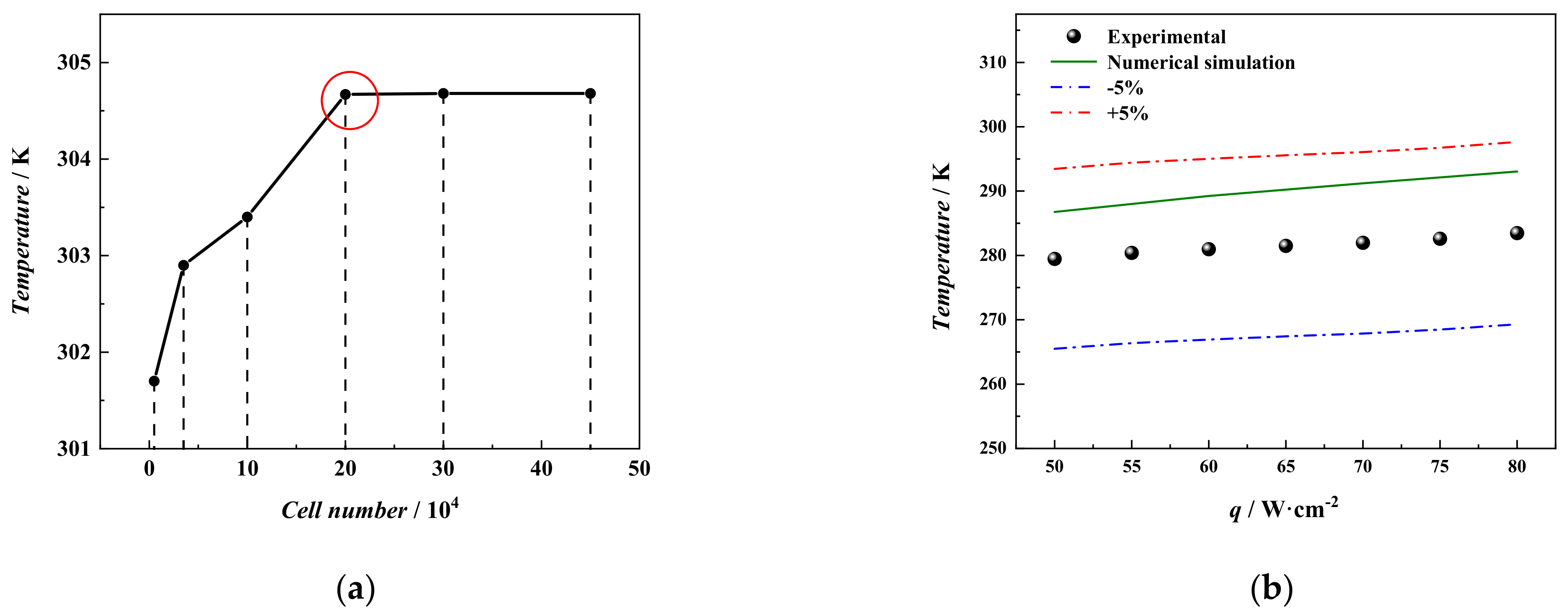
3. Model Validation
4. Results and Discussion
4.1. Cooling Characteristics
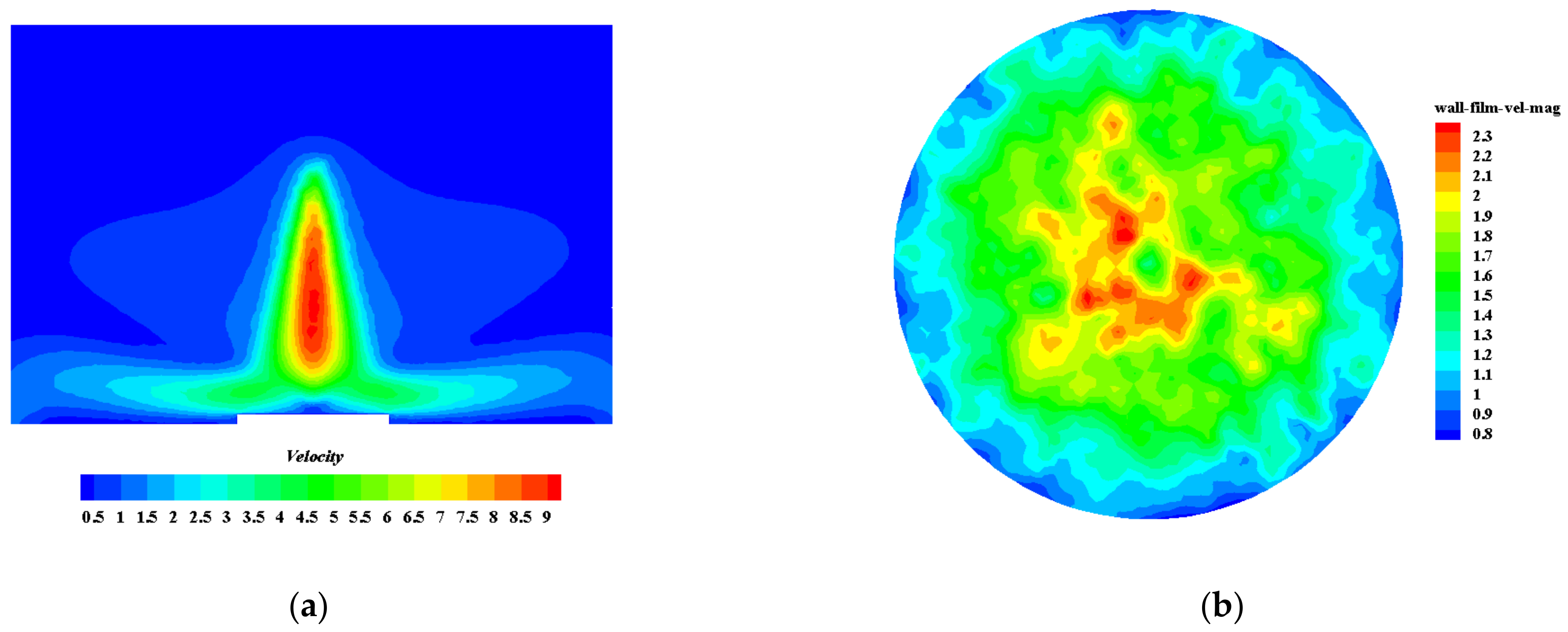
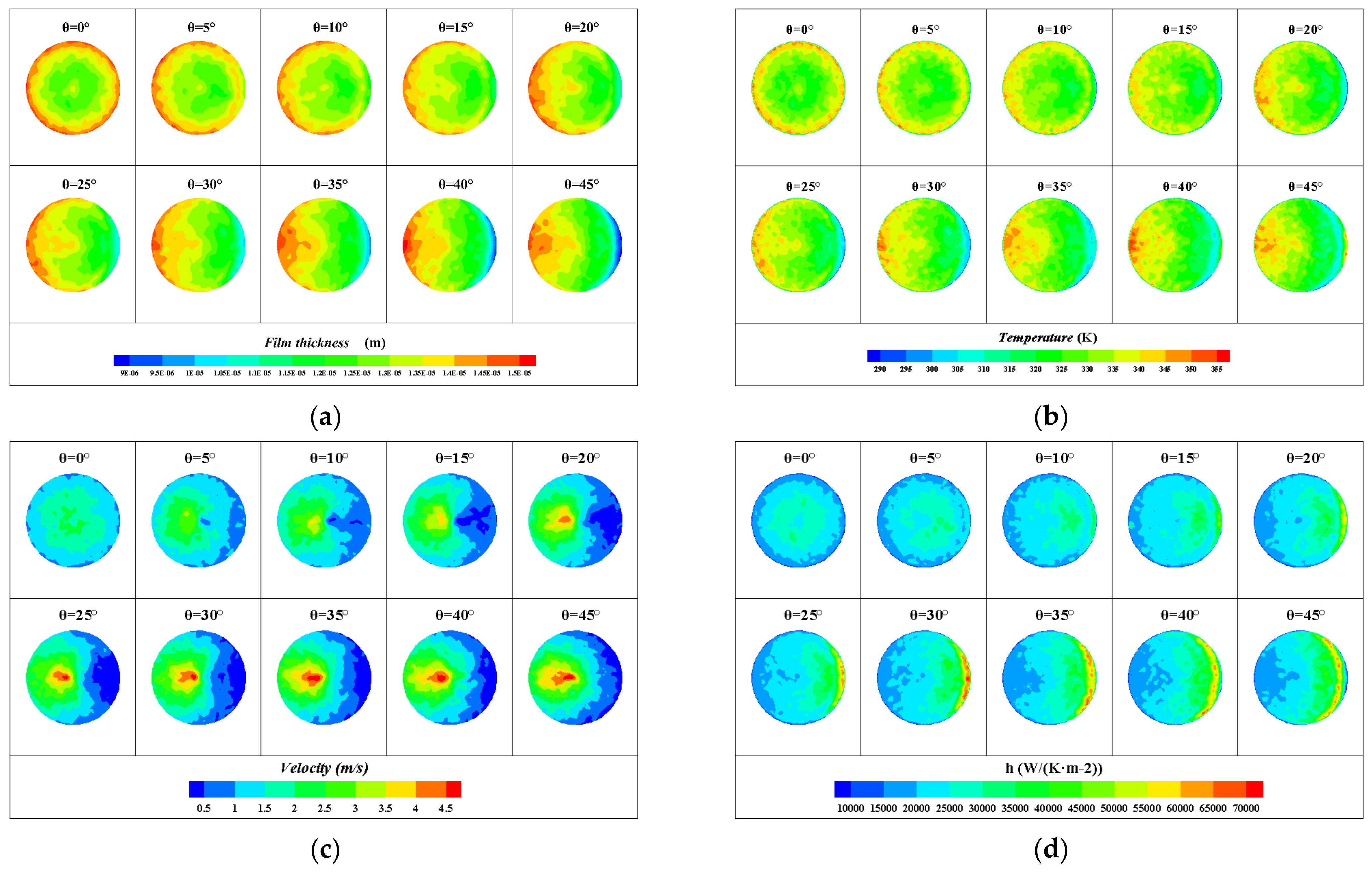
4.1.1. Spray Morphology and Velocity
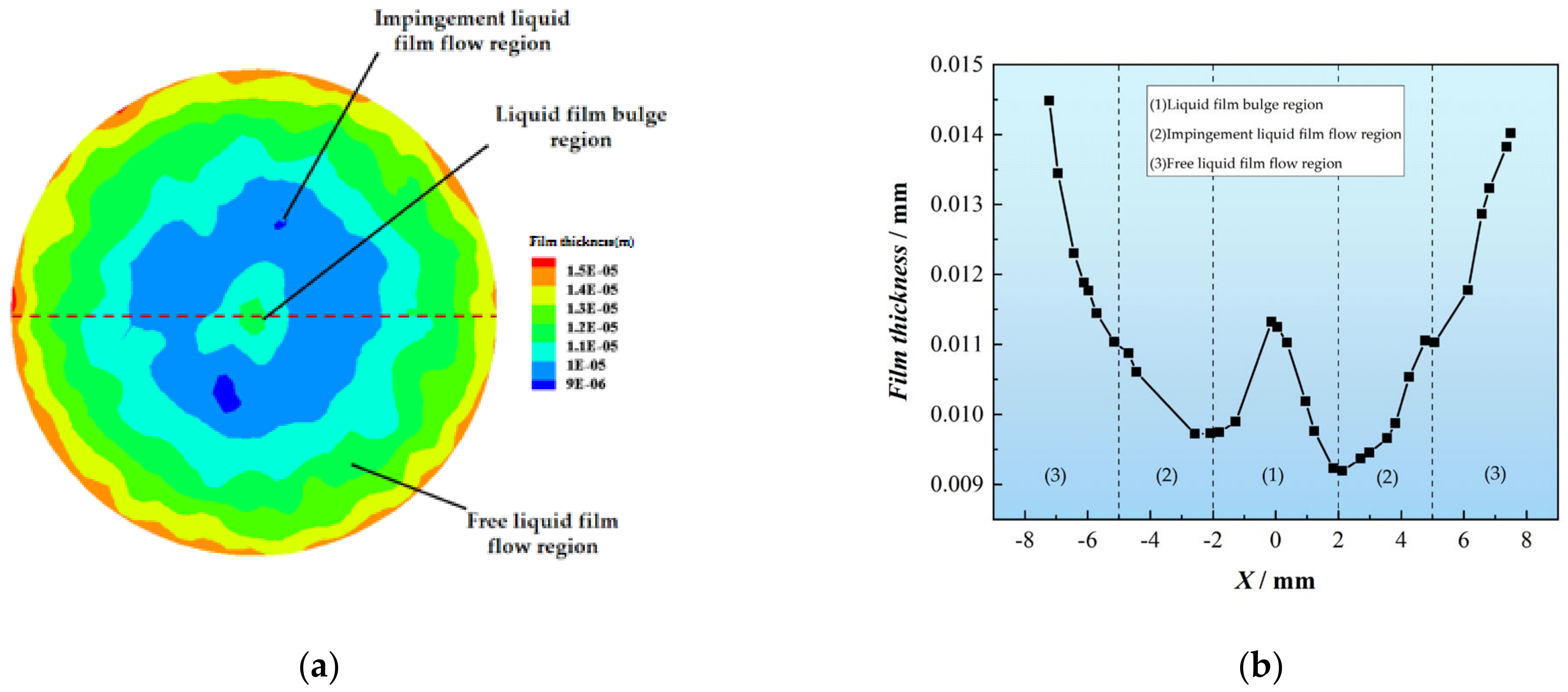
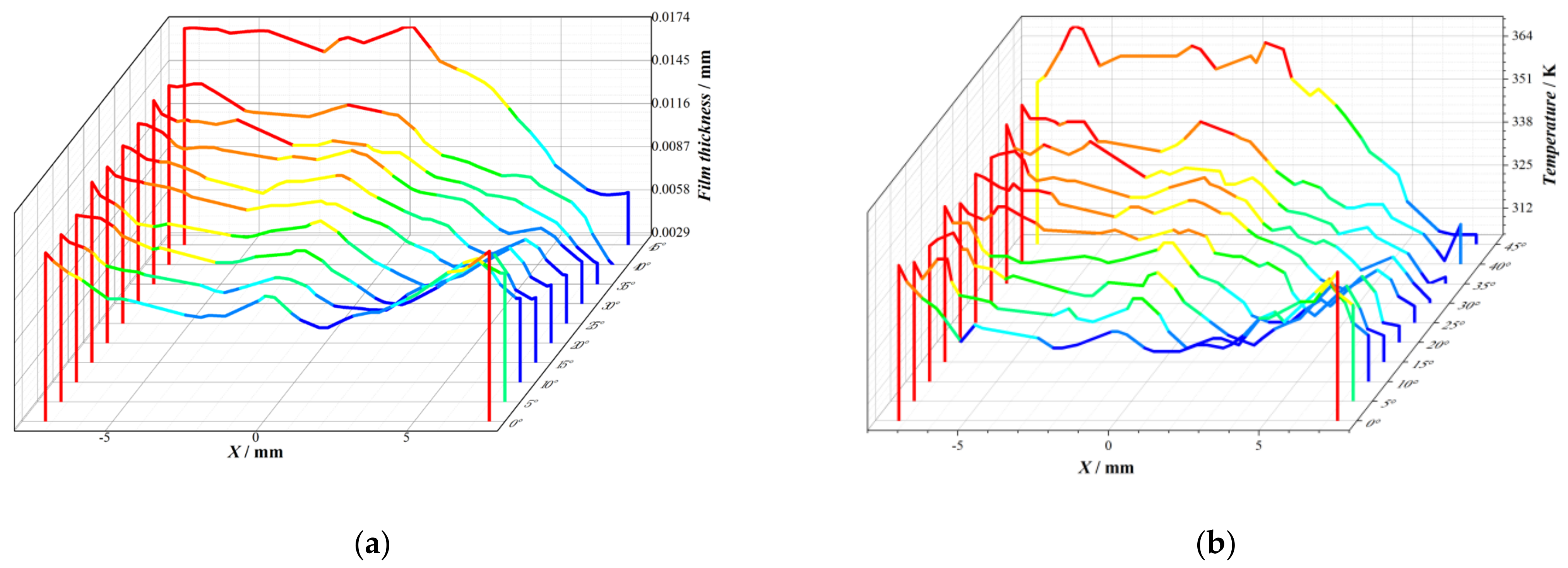
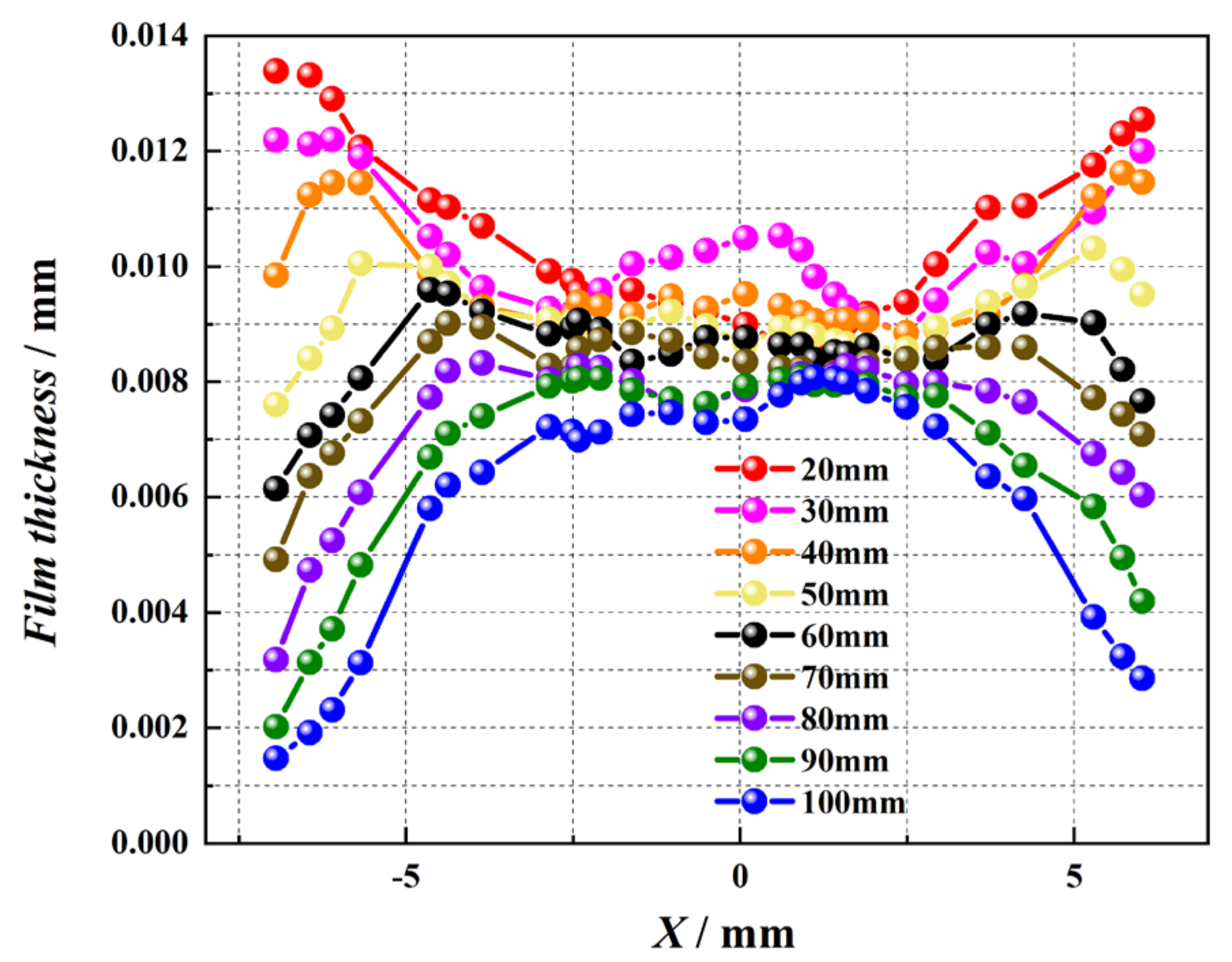
4.1.2. The Distribution of Liquid Film Height
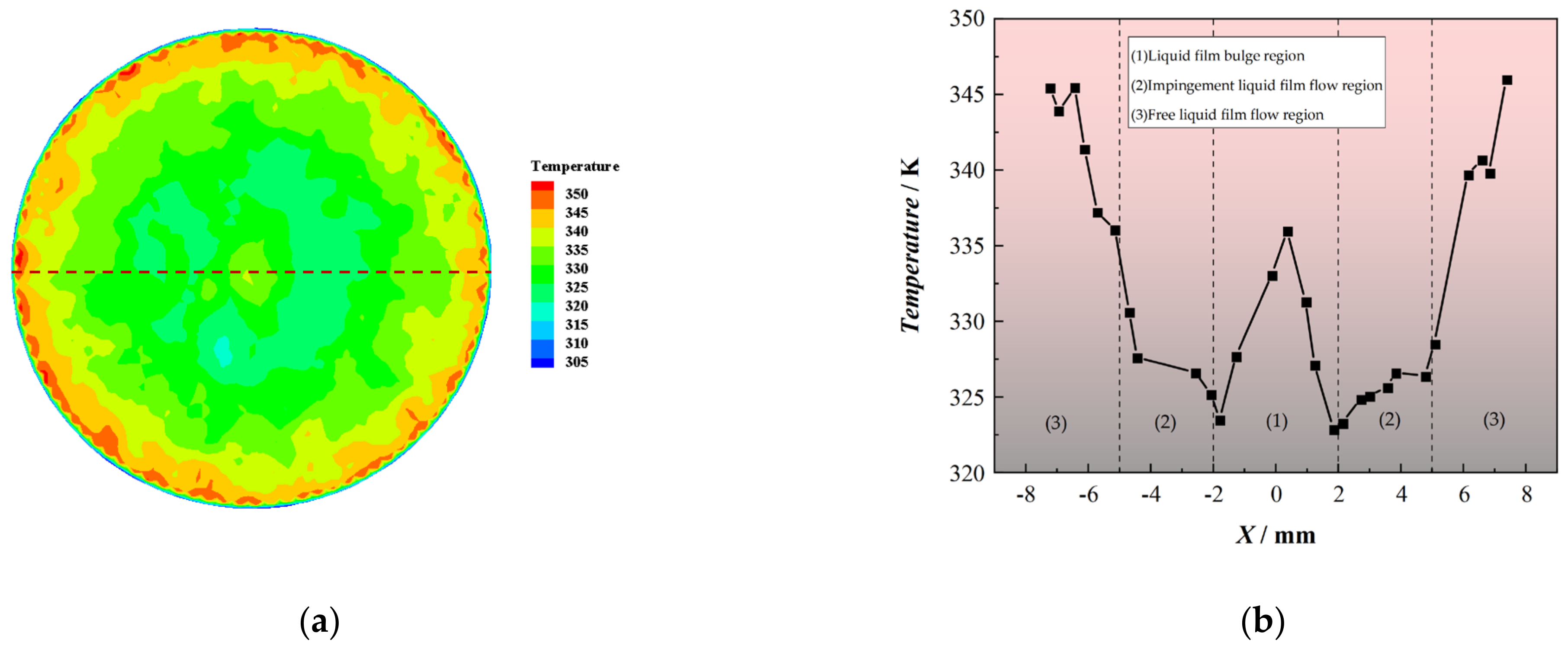
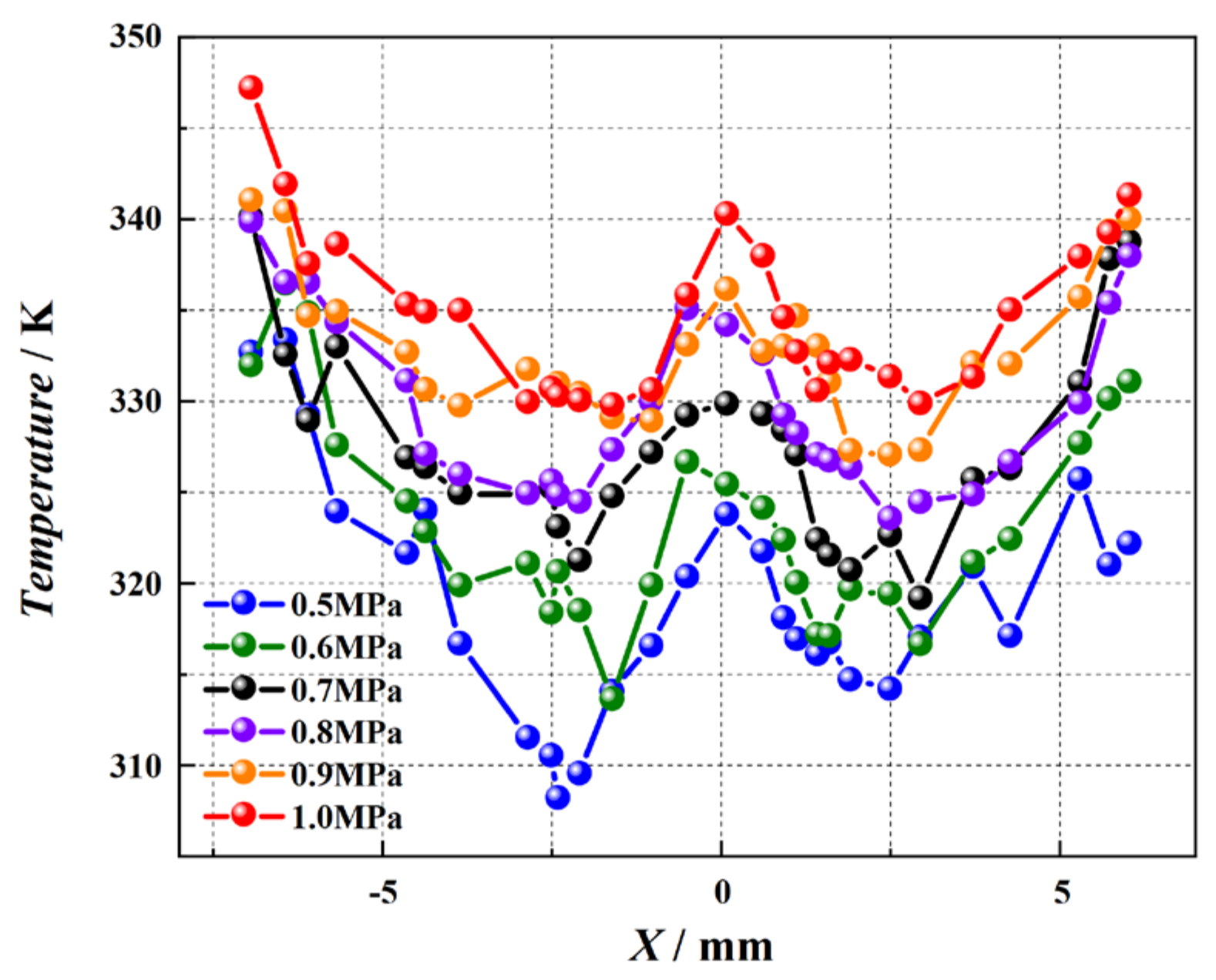
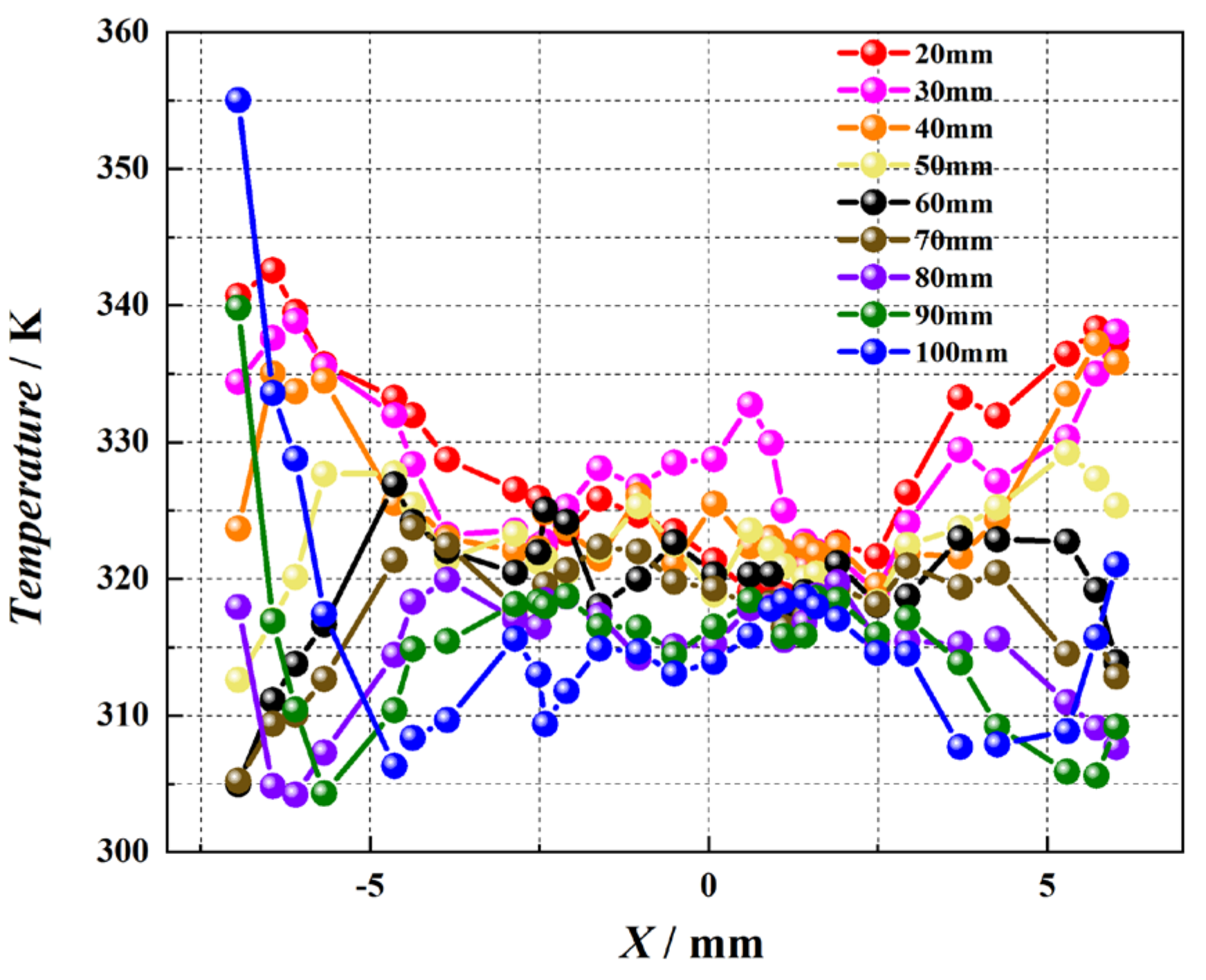
4.1.3. Temperature Distribution on the Cooling Surface
4.2. The Influence of Spray Parameters on the Heat Transfer Performance
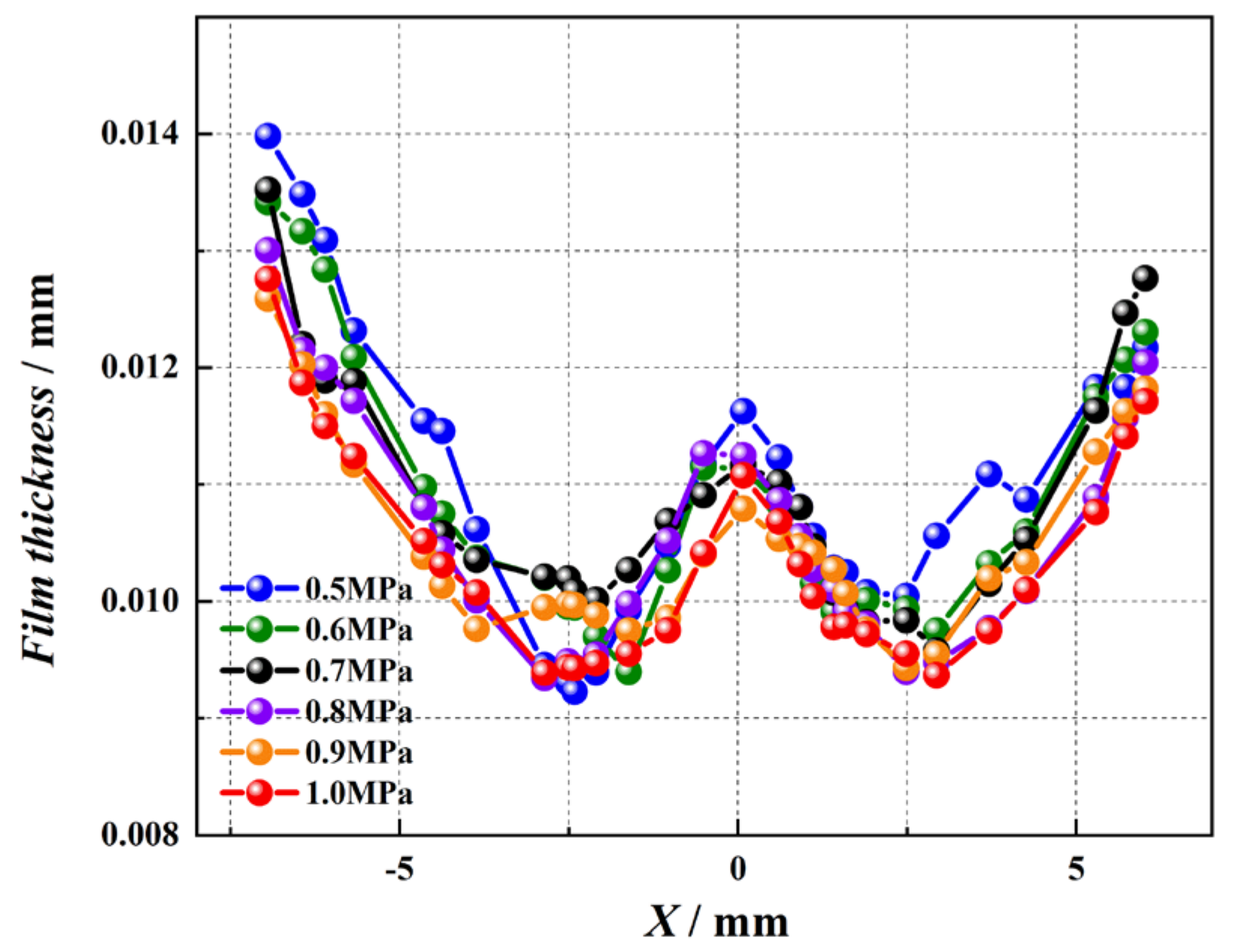
4.2.1. The Impact of Spray Pressure
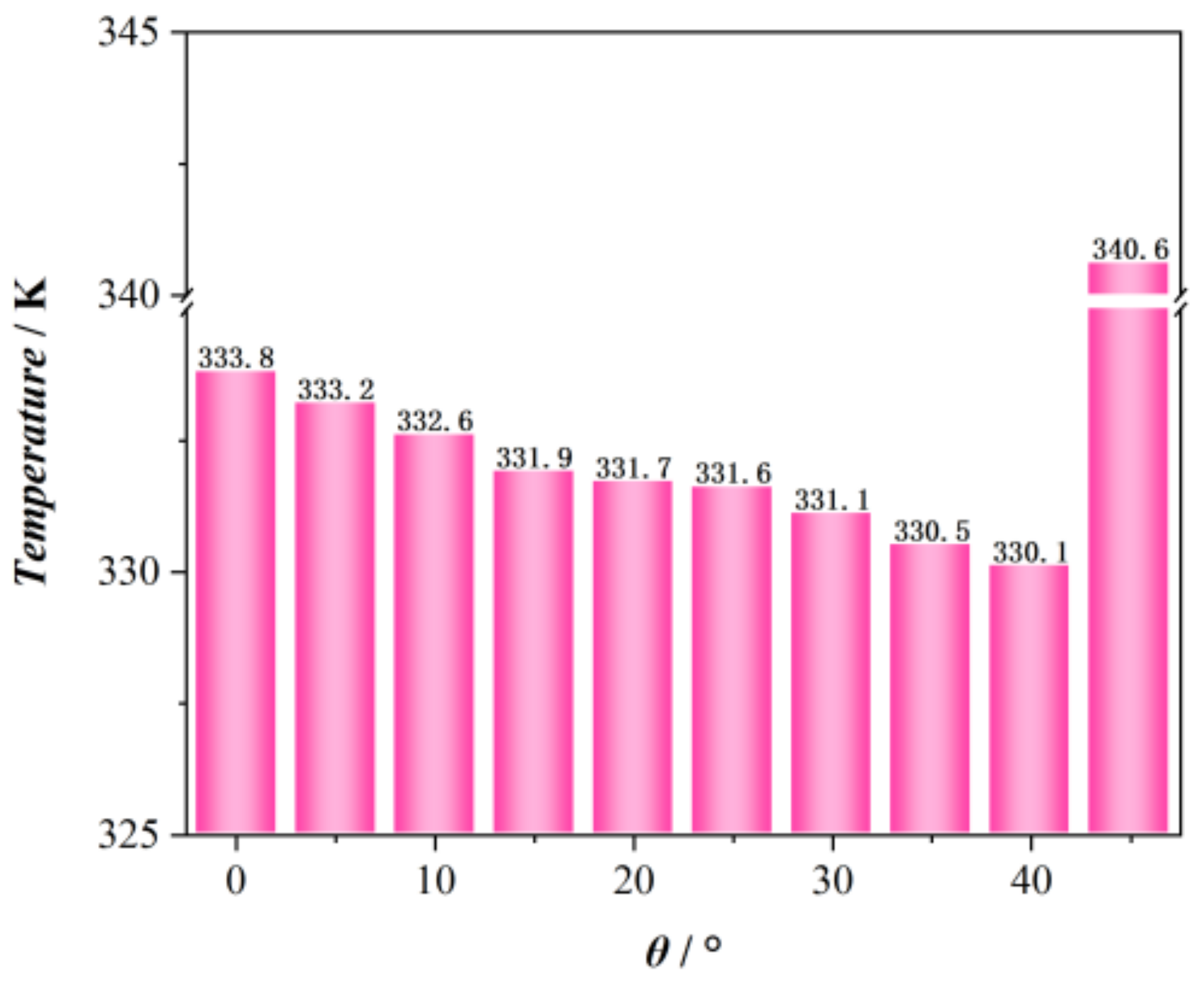
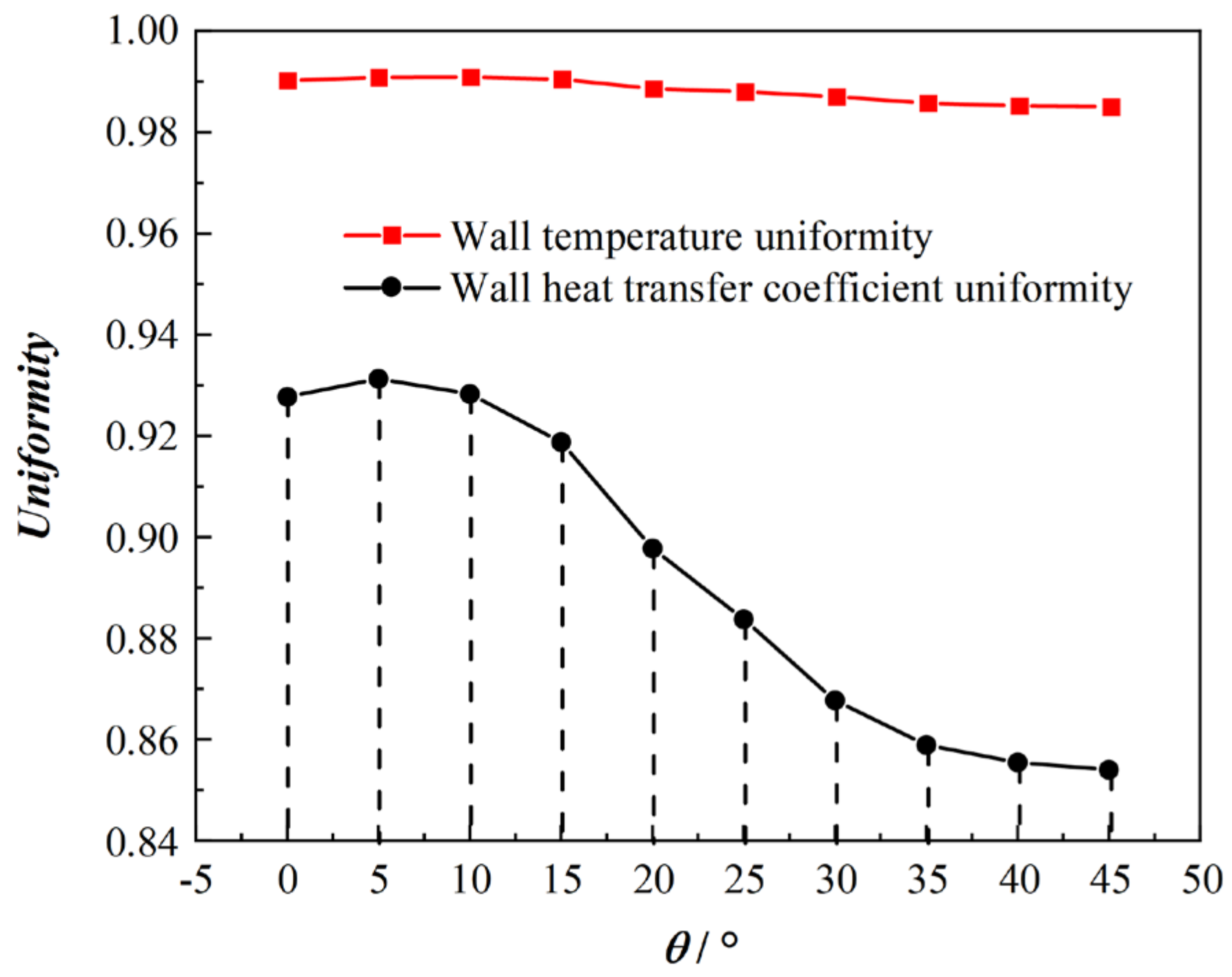
4.2.2. The Impact of Spray Tilt Angle
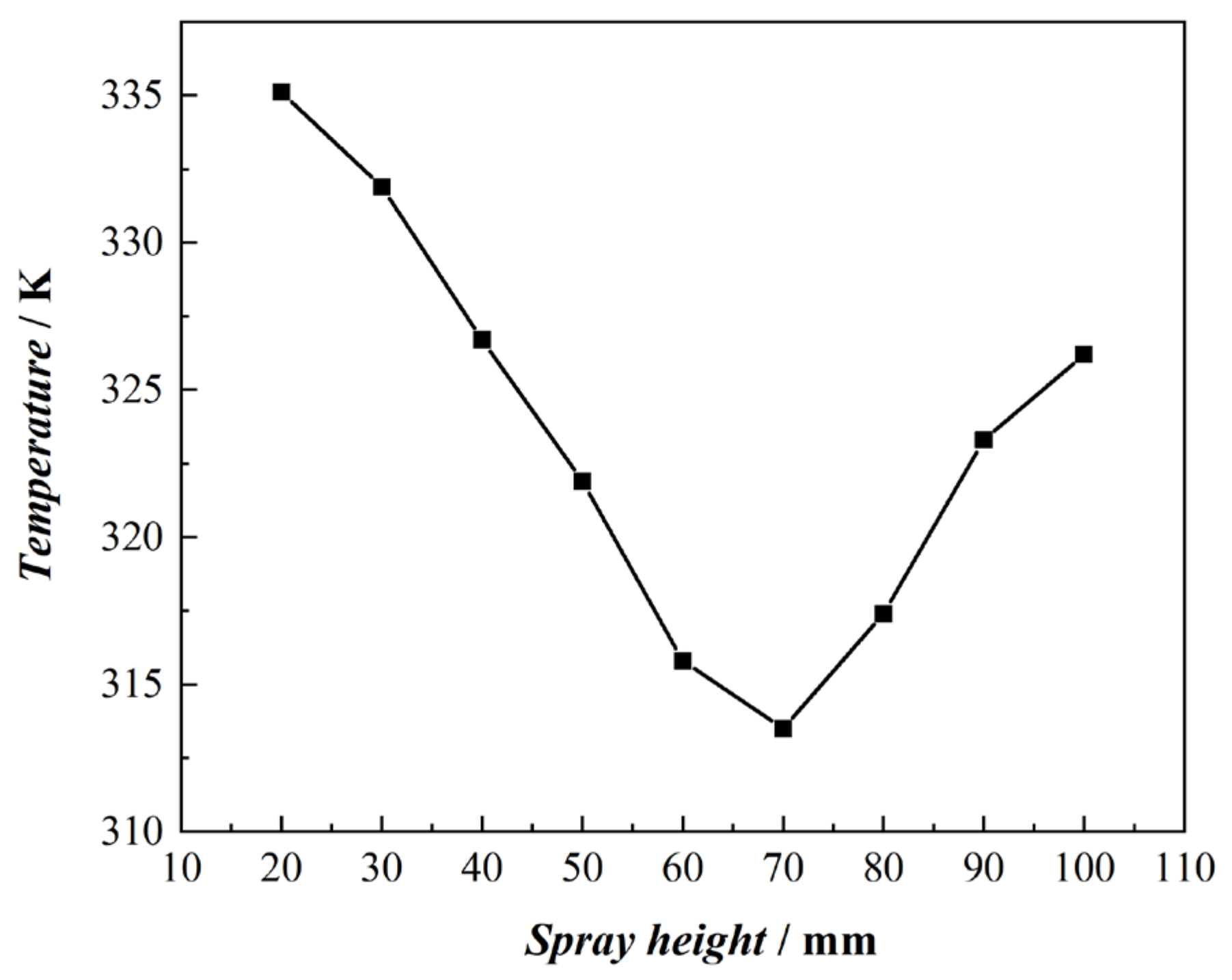
4.2.3. The Impact of Spray Height
5. Conclusions
- (1)
- The spray pattern is conical, with the center velocity significantly higher than that at the edge, and the liquid film velocity gradually decreases from a central stagnation point to the periphery of the cooling surface.
- (2)
- The temperature distribution of the cooling surface and liquid film height both exhibit a “W” shape.
- (3)
- The surface temperature gradually increases with an increase in spray chamber pressure, and considering the average cooling surface temperature, the optimal tilt angle is 40° with an average surface temperature of 330.1 K. When considering wall temperature and wall heat transfer coefficient uniformity, however, the optimal tilt angle is 10°, leading to the average surface temperature of 332.6 K.
- (4)
- There is an optimal liquid film height of approximately 5μm, at which the cooling surface temperature is the lowest. The optimal spray height is around 70 mm, where the average cooling surface temperature is 313.4 K. Correspondingly, the spray area utilization rate at the optimal spray height ranges from 9.8% to 17.4%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| t | Time, s |
| The velocity of the continuous phase fluid, M·s−1 | |
| T | Thermodynamic temperature, K |
| p | Pressure, Pa |
| g | Gravitational acceleration, m·s−2 |
| Sm | Mass of the continuous phase gas, kg |
| E | Internal energy of the continuous phase fluid, kJ |
| Continuous change in momentum, kg·m·s−1 | |
| Gk | Turbulent kinetic energy generated by mean velocity gradients, m2·s−2 |
| Gb | Turbulent kinetic energy generated by buoyancy forces, m2·s−2 |
| ud | The velocity vector of a droplet, m·s−1 |
| dd | Droplet diameter, m |
| Cd | Drag coefficient for a droplet |
| Cd,s | Drag coefficient for a spherical droplet |
| Re | Reynolds number |
| y | Shape correction factor for a droplet |
| Δt | Time step |
| Initial mass flow rate of liquid droplets, kg·s−1 | |
| Initial mass of a droplet | |
| Mass of a droplet as it enters the continuous phase grid, kg | |
| Mass of a droplet as it leaves the continuous phase grid, kg | |
| Specific heat of a particle, J·kg−1·K−1 | |
| Temperature of a liquid droplet upon entering the continuous phase grid, K | |
| Temperature of a liquid droplet upon leaving the continuous phase grid, K | |
| Latent heat of vaporization, J·kg−1 | |
| q | Heat flux, W·cm−2 |
| X | Coordinate position, mm |
| h | Heat transfer coefficient, W·K−1·m−2 |
| Greek letters | |
| The density of continuous phase fluid, kg·m−3 | |
| Fluid thermal conductivity, W·m−1·K−1 | |
| Viscosity, kg·m−1·s−1 | |
| Turbulent viscosity, kg·m−1·s−1 | |
| d | Droplet density, kg·m−3 |
| θ | Spray tilt angle, 0 |
References
- Smakulski, P.; Pietrowicz, S. A review of the capabilities of high heat flux removal by porous materials, microchannels and spray cooling techniques. Appl. Therm. Eng. 2016, 104, 636–646. [Google Scholar] [CrossRef]
- Shende, M.D.; Mahalle, A. Cooling of Electronic Equipments with Heat Sink: A Review of Literature. IOSR J. Mech. Civ. Eng. 2013, 5, 56–61. [Google Scholar] [CrossRef]
- Wang, J.X.; Guo, W.; Xiong, K.; Wang, S.N. Review of aerospace-oriented spray cooling technology. Prog. Aerosp. Sci. 2020, 116, 100635. [Google Scholar] [CrossRef]
- Tauseef-ur-Rehman, A.H.M. Experimental investigation on paraffin wax integrated with copper foam based heat sinks for electronic components thermal cooling. Int. Commun. Heat Mass Transf. 2018, 98, 155–162. [Google Scholar] [CrossRef]
- Zhou, W.; Dong, K.; Sun, Q.; Luo, W.; Zhang, B.; Guan, S.; Wang, G. Research progress of the liquid cold plate cooling technology for server electronic chips: A review. Int. J. Energy Res. 2022, 46, 11574–11595. [Google Scholar] [CrossRef]
- Wei, J.J.; Liu, L.; Yang, X.P. Research Progress on Loop Heat Pipes for Thermal Management of High Heat Flux Electronic Devices. J. Chem. Eng. Chin. Univ. 2023, 74, 60–73. [Google Scholar]
- Shen, G.Y. Research on Water Cooling Technology. Refrig. Air Cond. 1999, 43–45. [Google Scholar]
- Xu, H.J.; Wang, J.F.; Tian, J.M.; Zhang, Y.; Zhao, T.Y. Heat Transfer Characteristics of Ethanol Electrostatic Spray Cooling under Different Atomization Modes. J. Eng. Thermophys. 2021, 42, 2559–2565. [Google Scholar]
- Wang, H.; Wu, J.J.; Yang, Q.; Zhu, X.; Liao, Q. Heat transfer enhancement of ammonia spray cooling by surface modification. Int. J. Heat Mass Transf. 2016, 101, 60–68. [Google Scholar] [CrossRef]
- Visaria, M.; Mudawar, I. Effects of high subcooling on two-phase spray cooling and critical heat flux. Int. J. Heat Mass Transf. 2008, 51, 5269–5278. [Google Scholar] [CrossRef]
- Liu, Z.M. Alternative Technologies for R22 Refrigerant. Refrig. Air Cond. 2001, 47–53+27. [Google Scholar]
- Jin, W.F.; Xue, T.D.; Yuan, X.Y.; Wang, Z.Q. Experimental Study on Concentration Distribution and Indoor Safety of R32 Refrigerant Leakage at Different Locations. J. Refrig. 2022, 43, 114–121. [Google Scholar]
- Zhou, Z.F.; Lin, Y.K.; Tang, H.L.; Fang, Y.; Chen, B.; Wang, Y.C. Heat transfer enhancement due to surface modification in the close-loop R410A flash evaporation spray cooling. Int. J. Heat Mass Transf. 2019, 139, 1047–1055. [Google Scholar] [CrossRef]
- Zhou, Z.F.; Lin, X.W.; Ji, R.J.; Zhu, D.Q.; Chen, B.; Wang, H.; Lu, Y.J. Enhancement of heat transfer on micro-and macro-structural surfaces in close-loop R410A flashing spray cooling system for heat dissipation of high-power electronics. Appl. Therm. Eng. 2023, 223, 119978. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Sang, X.; Chen, B.; Romeos, A. Coupling dynamic thermal analysis and surface modification to enhance heat dissipation of R410A spray cooling for high-power electronics. Energy 2023, 284, 129224. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Comparative analysis of microfin vs. smooth tubes in R32 and R410A condensation. Int. J. Refrig. 2021, 128, 218–231. [Google Scholar] [CrossRef]
- Pan, Y.Q.; Du, Y.J.; Zhang, C.C.; Yu, L. Numerical Simulation of Single-Phase Heat Transfer Characteristics in Small Spray Cooling Systems. J. Chem. Eng. Chin. Univ. 2022, 36, 8. [Google Scholar]
- Cai, C.; Liu, H.; Jia, M.; Yin, H.; Xie, R.; Yan, P. Numerical investigation on heat transfer of water spray cooling from single-phase to nucleate boiling region. Int. J. Therm. Sci. 2020, 151, 106258. [Google Scholar] [CrossRef]
- Tian, J.; Chen, B.; Zhou, Z.; Li, D. Theoretical Study on Cryogen Spray Cooling in Laser Treatment of Ota’s Nevus: Comparison and Optimization of R134a, R404A and R32. Energies 2020, 13, 5647. [Google Scholar] [CrossRef]
- Giannadakis, A. Spray Cooling as a High-Efficient Thermal Management Solution: A Review. Energies 2022, 15, 8547. [Google Scholar]
- Wu, T.; Wang, C.; Hu, Y.; Fan, X.; Fan, C. Research on spray cooling performance based on battery thermal management. Int. J. Energy Res. 2022, 46, 8977–8988. [Google Scholar] [CrossRef]
- Hu, K.; Li, Z.B. Detailed Explanation of ANSYS ICEM CFD Engineering Examples; CAE Analysis Series; People’s Posts and Telecommunications Press: Beijing, China, 2014; 421p. [Google Scholar]
- Liu, H.; Cai, C.; Yan, Y.A.; Jia, M.; Yin, B. Numerical simulation and experimental investigation on spray cooling in the non-boiling region. Heat Mass Transf. 2018, 54, 3747–3760. [Google Scholar] [CrossRef]
- Wang, X.Z.; Cui, X.Y.; Deng, L. Obtaining Refrigerant Thermophysical Data in Application Programs. Refrig. Air Cond. 2010, 24, 40–44. [Google Scholar]
- Hu, B.M.; Zuo, J.Z. Numerical Simulation of Ultra-Fast Cooling by Liquid Nitrogen Spray. Energy Conserv. 2022, 41, 40–43. [Google Scholar]
- Guo, Y.X. Theory of Liquid Film Flow in Spraying and Experimental Study on Spray Cooling of Electronic Devices. Ph.D. Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2009. [Google Scholar]


| Temperature (K) | Density (kg/m3) | Thermal Conductivity (mW/(m·K)) | Latent Heat of Vaporization (kJ/kg) | Viscosity Coefficient (μPa·s) | |
|---|---|---|---|---|---|
| Liquid | 150~340 | 1560.40~714.47 | 175.35~69.67 | 344.05~73.01 | 1201.00~54.37 |
| Vapor | 0.017~275.27 | 6.11~46.46 | 6.62~20.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Sang, X.; Chen, B.; Li, D. Numerical Investigations of the Cooling Performance of an R410A Closed-Loop Spray Cooling System. Energies 2024, 17, 339. https://doi.org/10.3390/en17020339
Yang W, Sang X, Chen B, Li D. Numerical Investigations of the Cooling Performance of an R410A Closed-Loop Spray Cooling System. Energies. 2024; 17(2):339. https://doi.org/10.3390/en17020339
Chicago/Turabian StyleYang, Wenbo, Xuehao Sang, Bin Chen, and Dong Li. 2024. "Numerical Investigations of the Cooling Performance of an R410A Closed-Loop Spray Cooling System" Energies 17, no. 2: 339. https://doi.org/10.3390/en17020339
APA StyleYang, W., Sang, X., Chen, B., & Li, D. (2024). Numerical Investigations of the Cooling Performance of an R410A Closed-Loop Spray Cooling System. Energies, 17(2), 339. https://doi.org/10.3390/en17020339






