Analytical Study of Permeability Properties of Loose Sandstone Based on Thermal-Hydraulic-Mechanical (THM) Coupling
Abstract
1. Introduction
2. Test Introduction
2.1. Test Sample
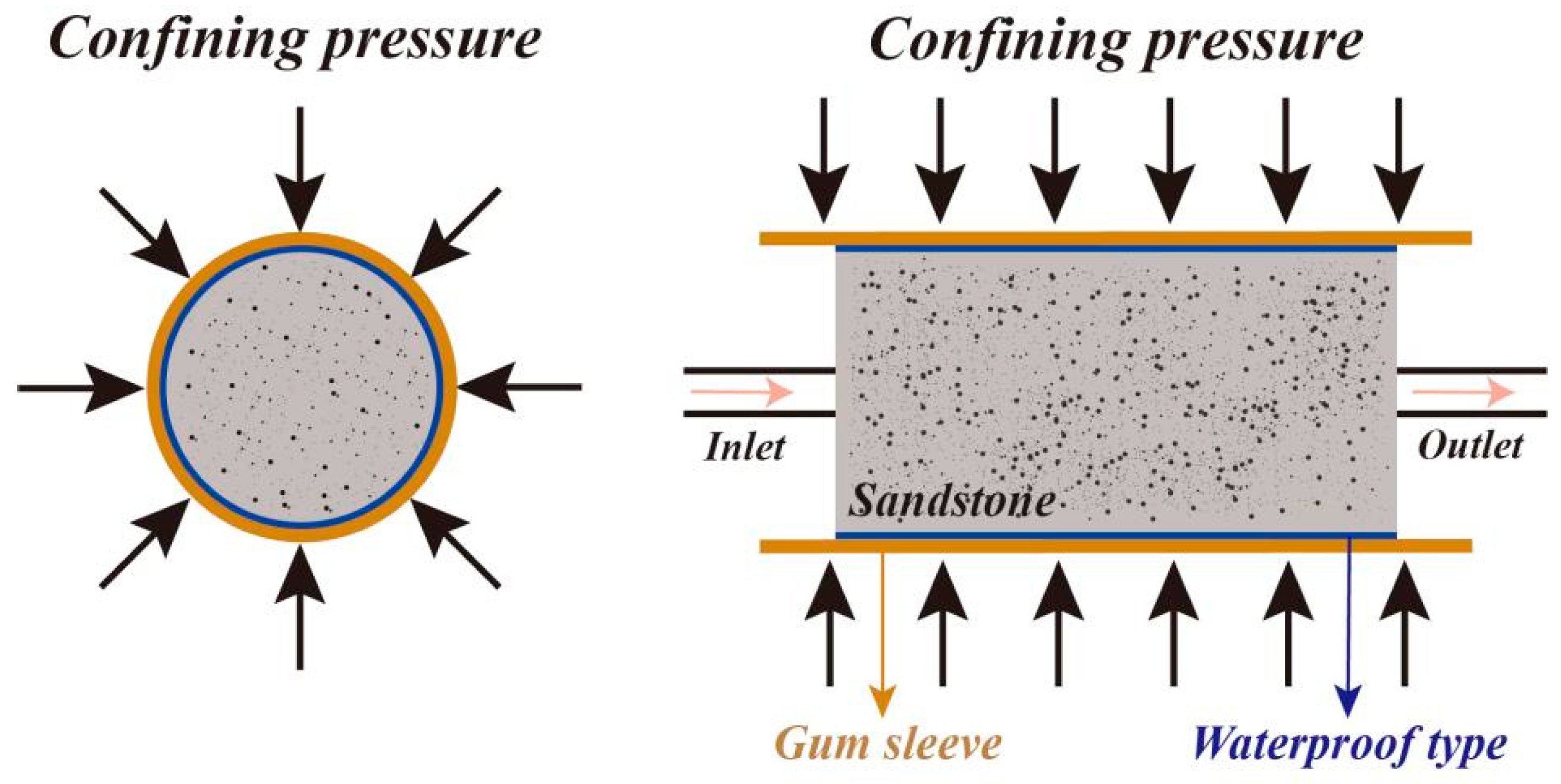
2.2. Test System
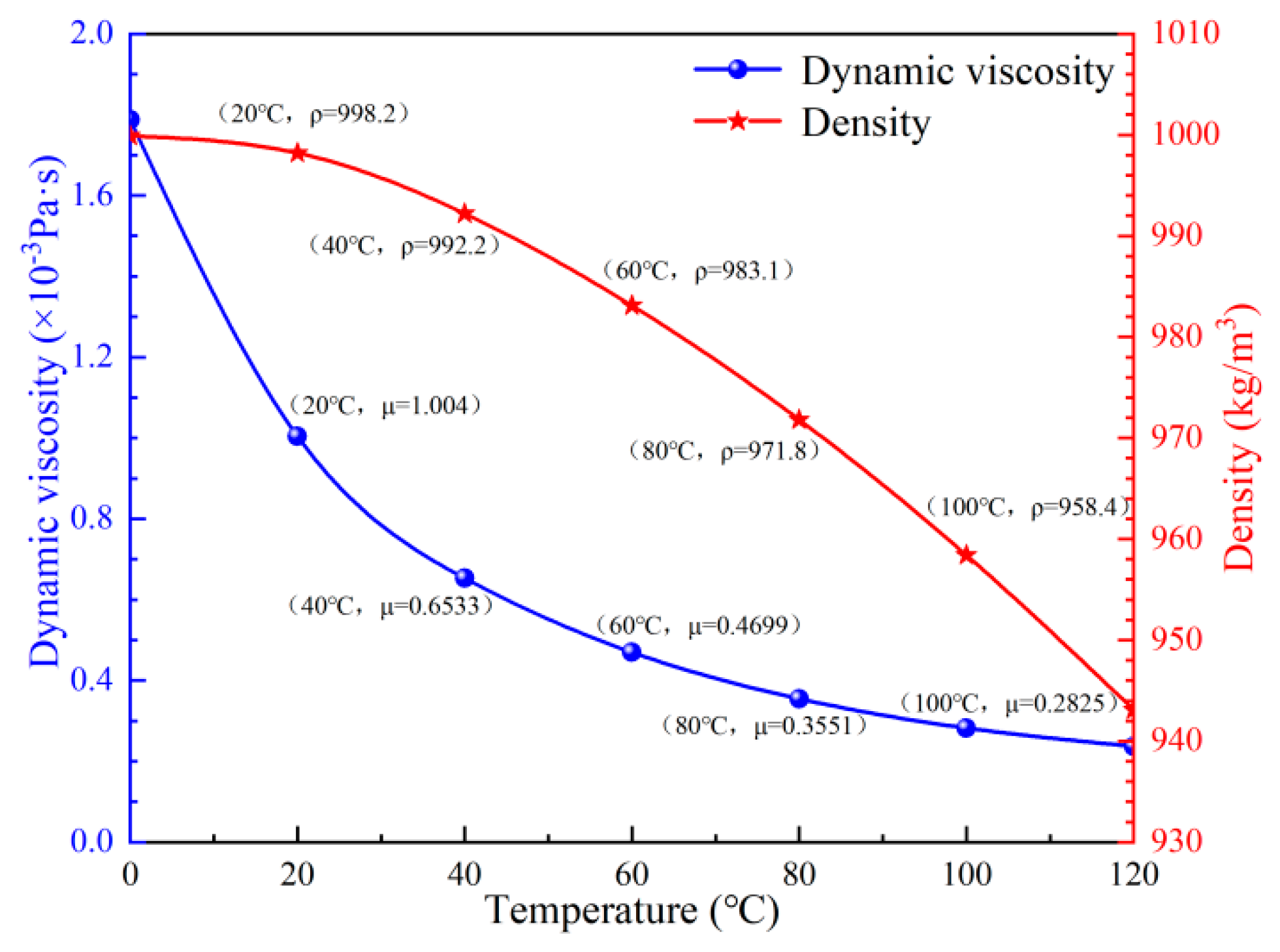
2.3. Computing Formula
3. Test Results and Analysis
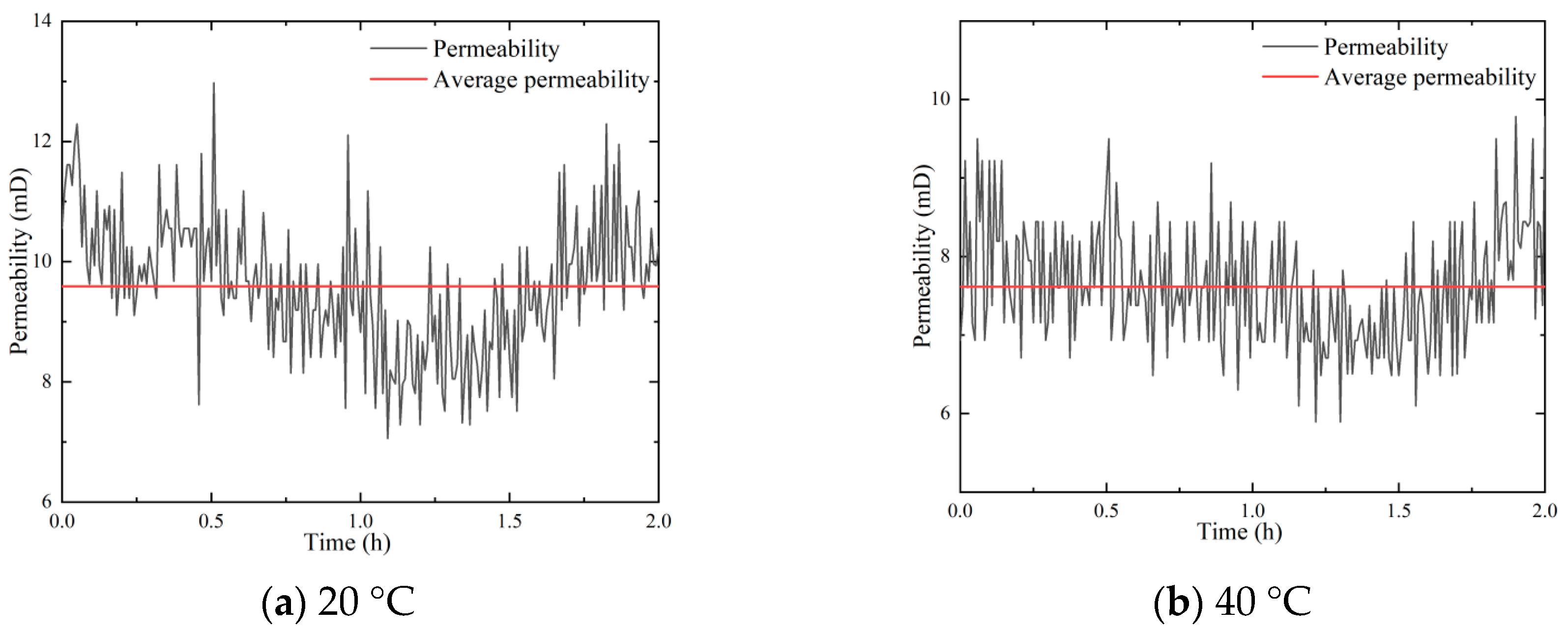
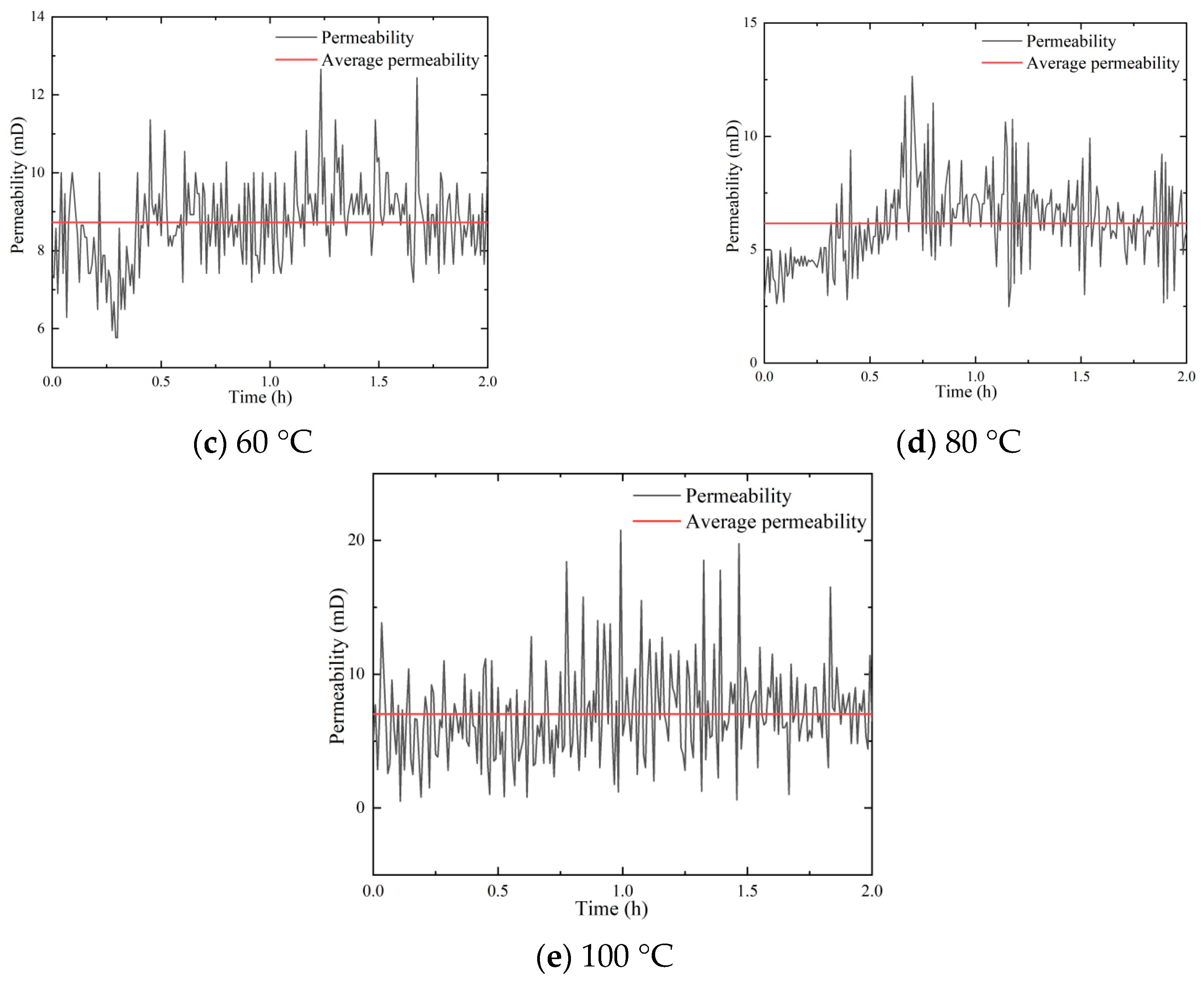
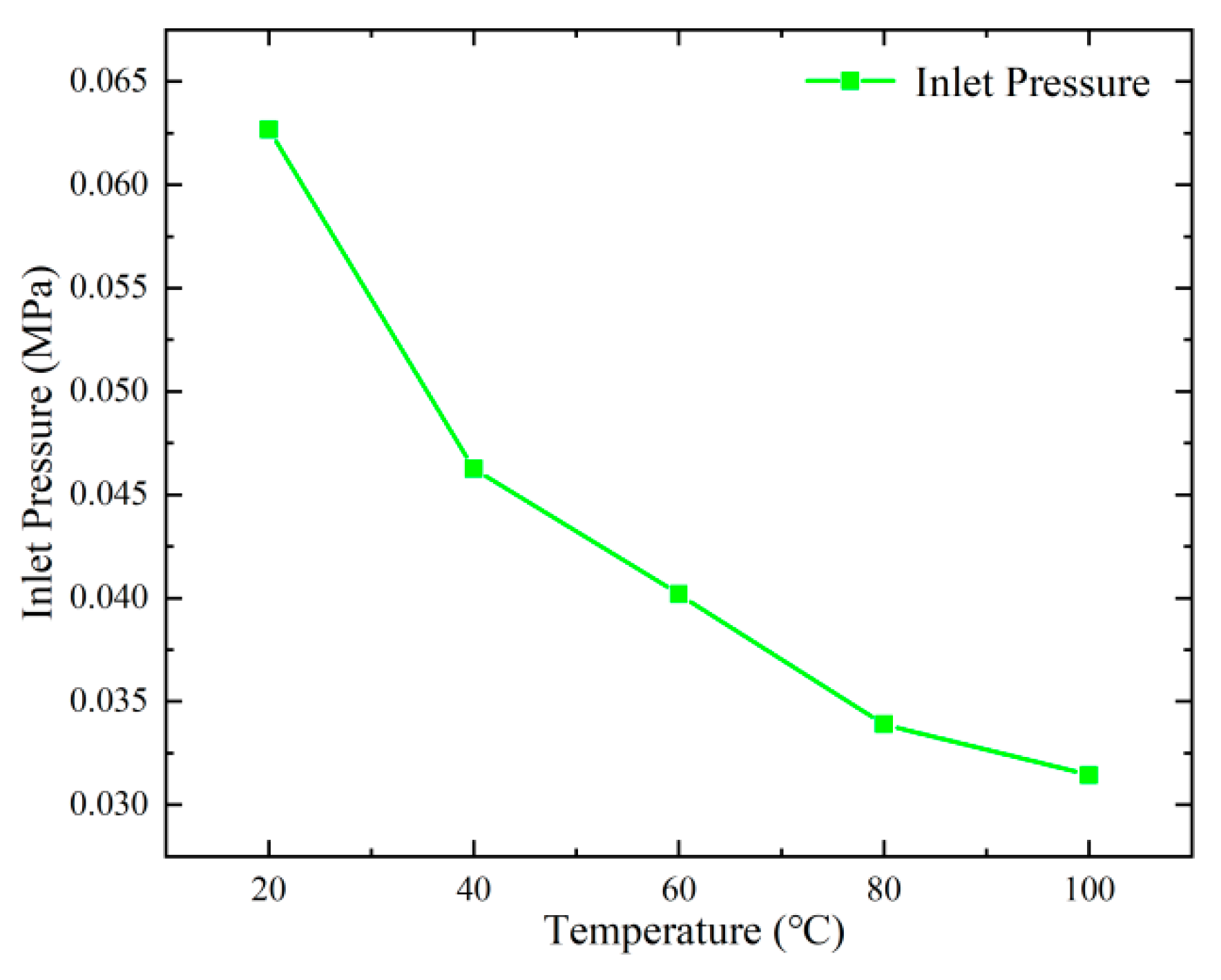
3.1. Effect of Temperature on Permeability of Sandstone Aquifer
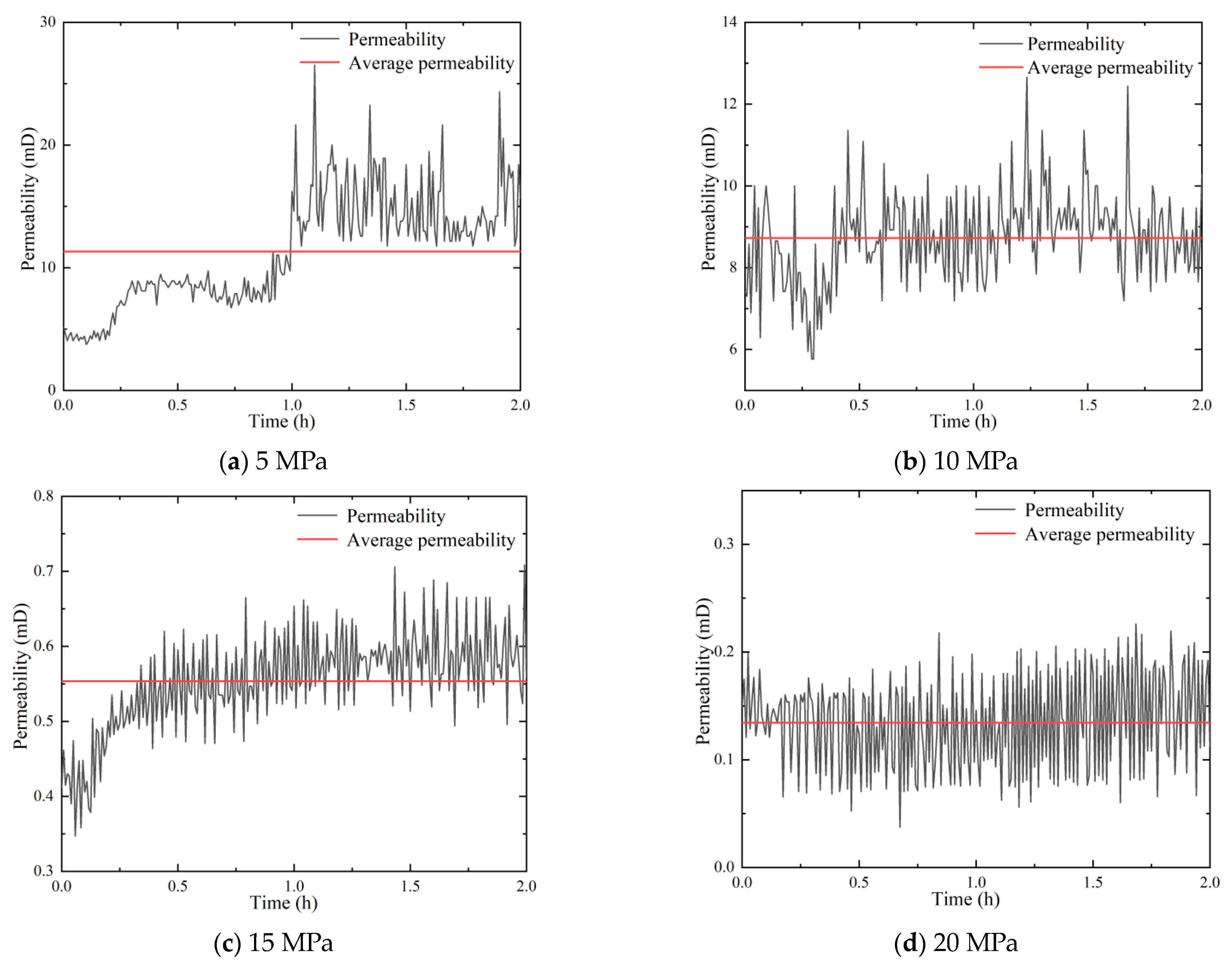
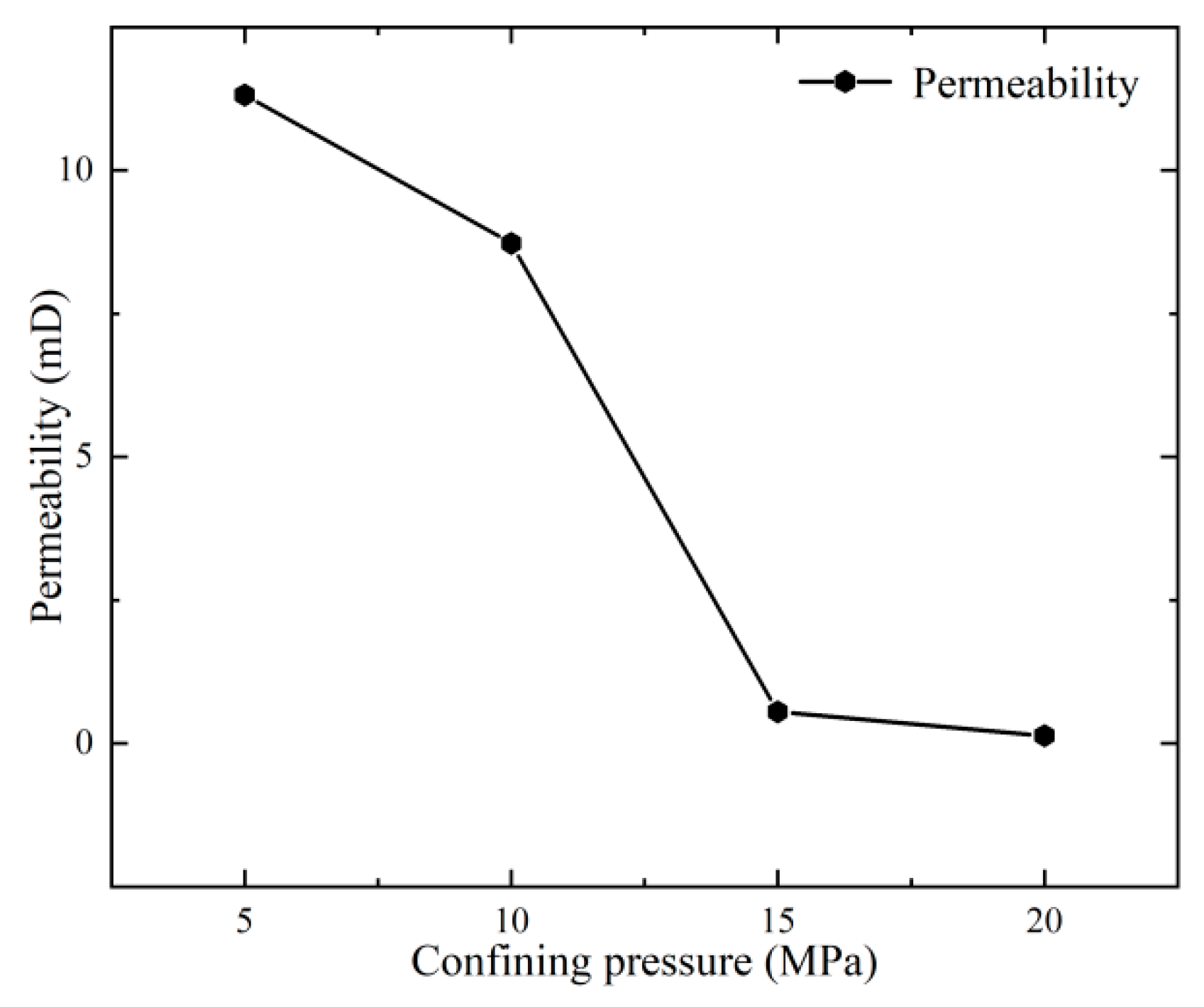
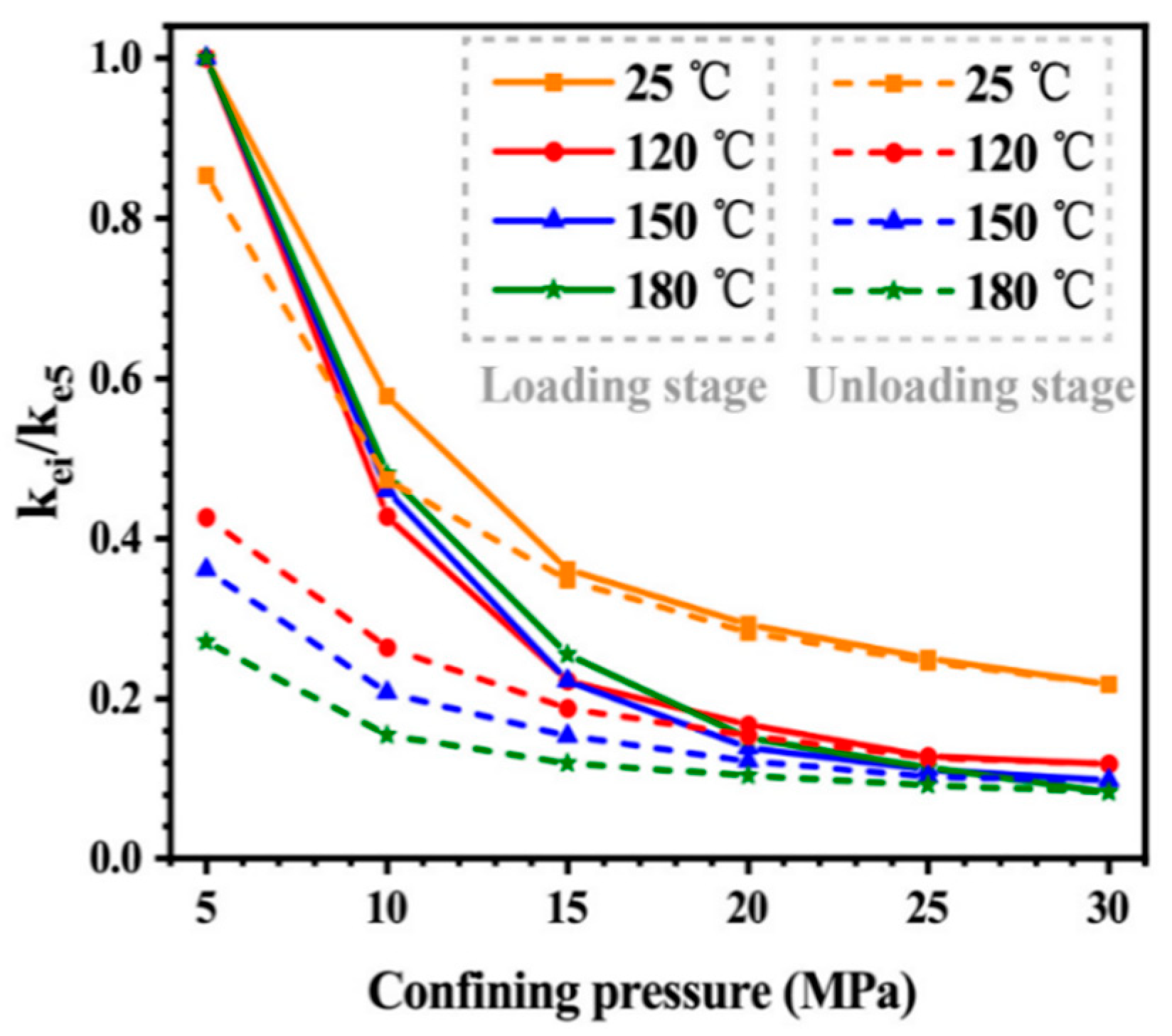
3.2. Effect of Confining Pressure on Permeability of Sandstone Aquifer
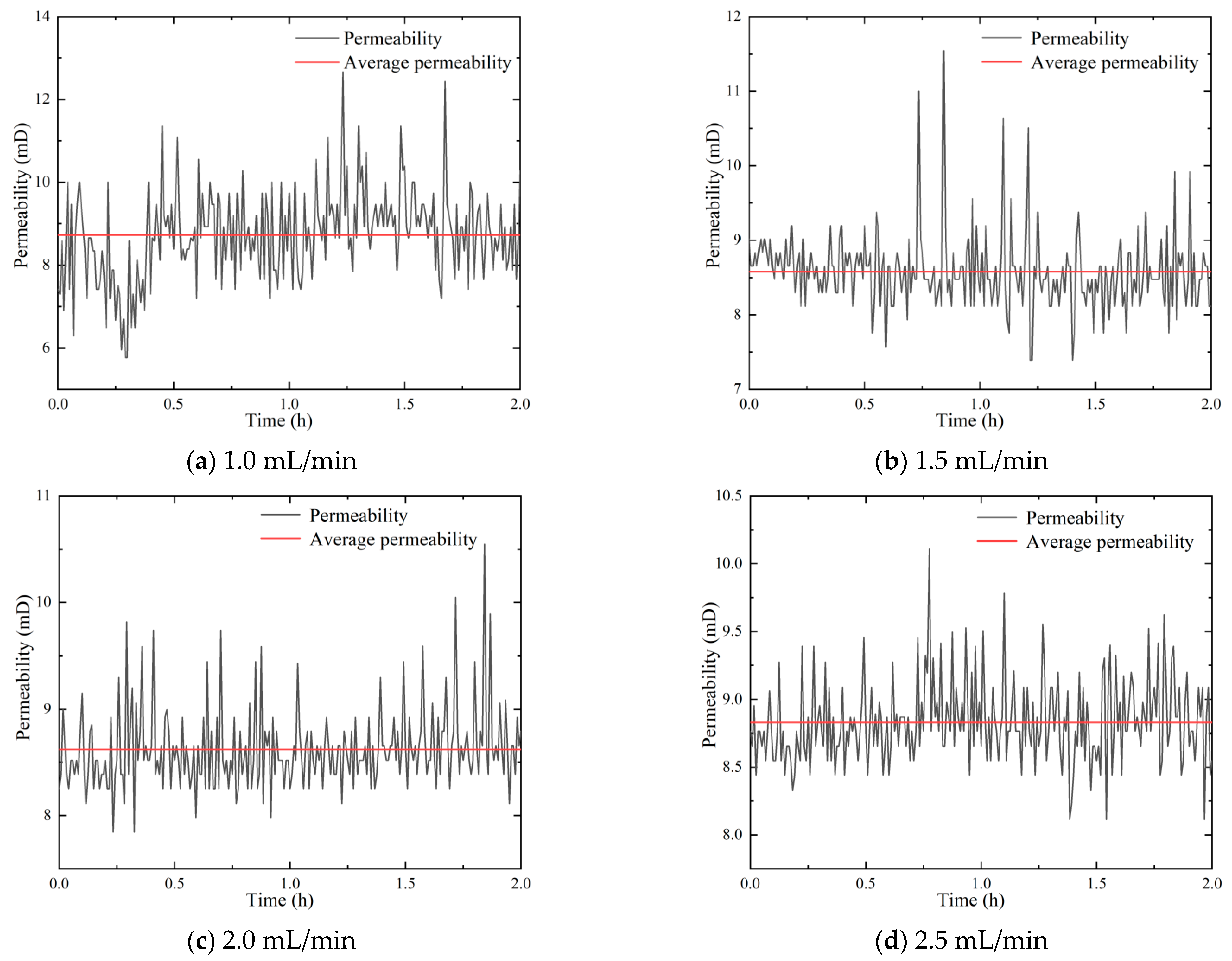
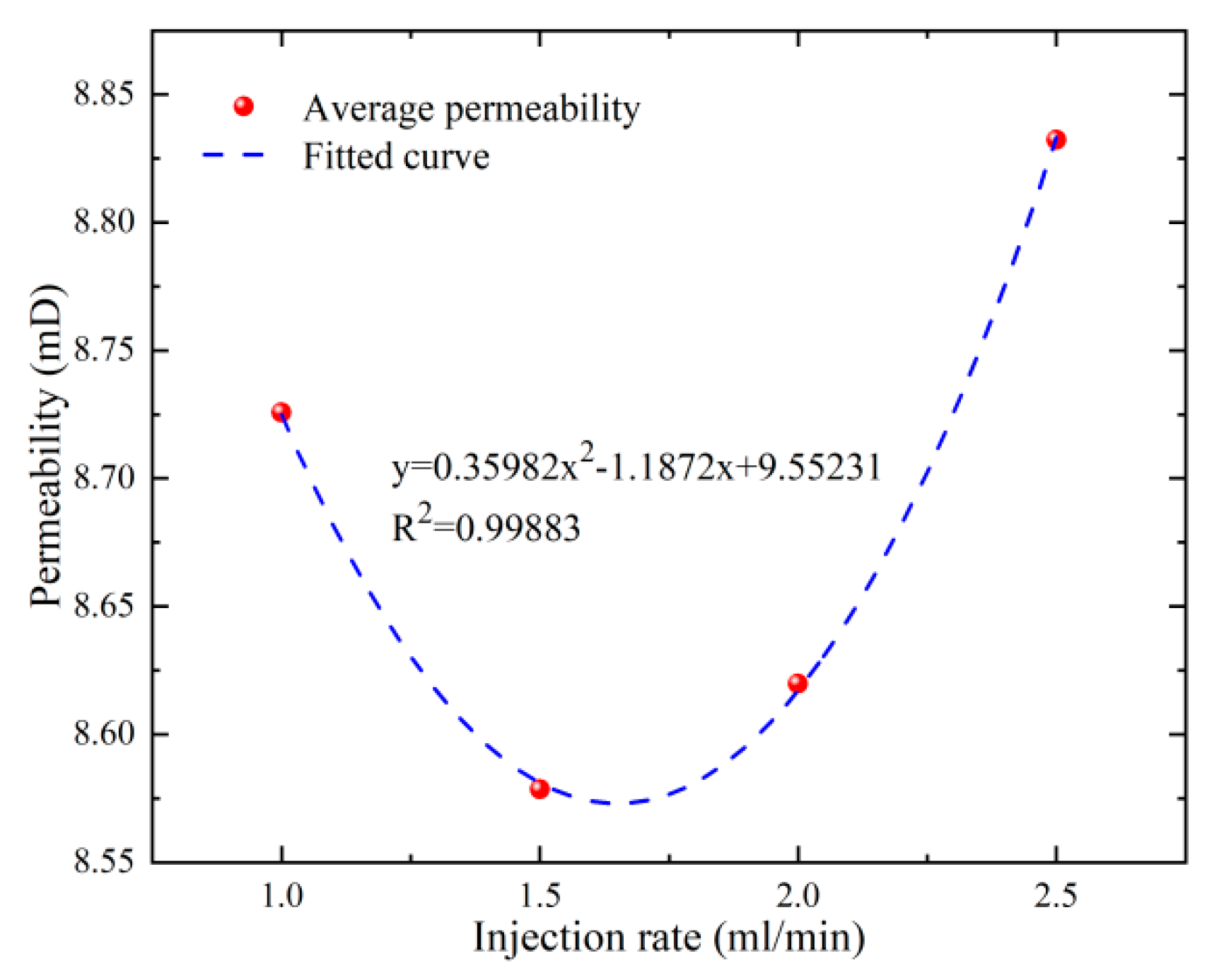
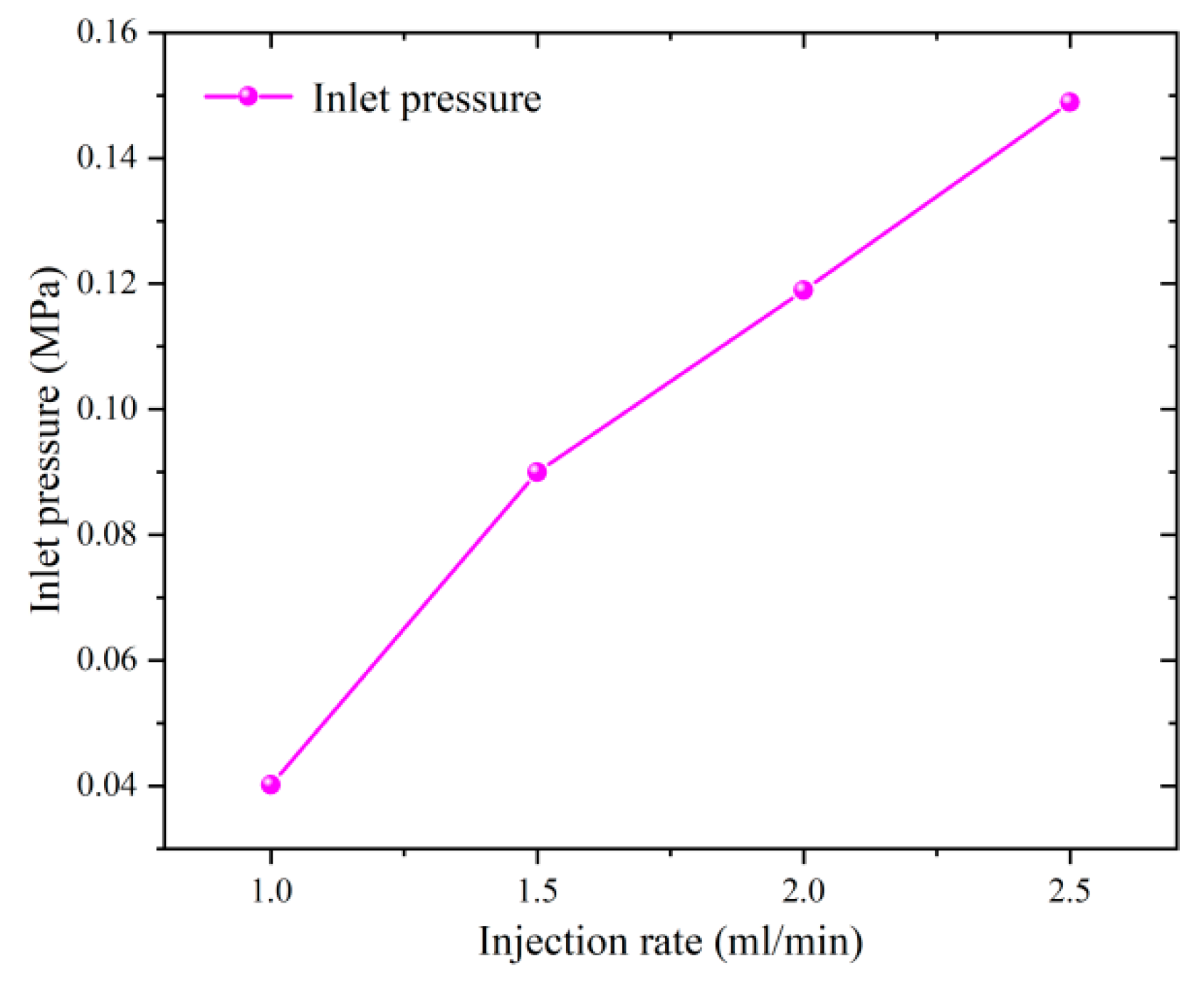
3.3. Effect of Injection Rate on Permeability of Sandstone Aquifer
3.4. Effect of Cyclic Loading and Unloading on Permeability of Sandstone Aquifer
4. Conclusions
- The influence of temperature on the permeability of unconsolidated sandstone is primarily manifested in two aspects. Firstly, as the temperature increases, the overall tendency of permeability decreases. This trend is primarily attributed to the reduction in internal pore volume of the sandstone samples due to the influence of thermal expansion. Secondly, the higher the temperature, the greater the amount of gravel outflow.
- The critical pressure for the internal pore closure of the original unconsolidated sandstone in Zijiao Town is approximately 15 MPa.
- Compared to temperature and confining pressure, the effect of low injection rate on permeability is negligible. However, the higher the injection rate, the greater the amount of gravel carried by the fluid, which requires the selection of an appropriate injection rate during geothermal extraction. The injection rate selected in this test is low, and it is reasonable to believe that this type of sandstone will show different permeability properties when injected with a large flow rate.
- Under the condition of loading and unloading, the permeability ratio curve of the unloading stage at three temperatures is almost a straight line. The higher the temperature, the smaller the slope, and the permeability at 20 °C with the highest recovery degree is only about 50% of the initial one.
- Under laboratory-scale conditions, temperature and injection rate are the most direct factors affecting sand production, while confining pressure has a relatively small impact. Future research should focus on changes in the permeability of unconsolidated sandstone under higher temperature and high injection rate conditions. Moreover, the rock samples used in this experiment had a relatively small size of φ25 mm × 50 mm. Future research should increase the sample size and further investigate the influence of different conditions on the permeability of unconsolidated sandstone, in order to guide the exploitation of geothermal resources in similar types of reservoirs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- George, A.; Shen, B.; Craven, M.; Wang, Y.; Kang, D.; Wu, C.; Tu, X. A Review of Non-Thermal Plasma Technology: A novel solution for CO2 conversion and utilization. Renew. Sustain. Energy Rev. 2021, 135, 109702. [Google Scholar] [CrossRef]
- Moya, D.; Aldás, C.; Kaparaju, P. Geothermal energy: Power plant technology and direct heat applications. Renew. Sustain. Energy Rev. 2018, 94, 889–901. [Google Scholar] [CrossRef]
- Usman, M.; Khalid, K.; Mehdi, M.A. What determines environmental deficit in Asia? Embossing the role of renewable and non-renewable energy utilization. Renew. Energy 2021, 168, 1165–1176. [Google Scholar] [CrossRef]
- Pastor-Martinez, E.; Rubio-Maya, C.; Ambriz-Díaz, V.; Belman-Flores, J.; Pacheco-Ibarra, J. Energetic and exergetic performance comparison of different polygeneration arrangements utilizing geothermal energy in cascade. Energy Convers. Manag. 2018, 168, 252–269. [Google Scholar] [CrossRef]
- Chen, B. Study on Numerical Methods for Coupled Fluid Flow and Heat Transfer in Fractured Rocks of Doublet System. Ph.D. Dissertation, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Pan, S.-Y.; Gao, M.; Shah, K.J.; Zheng, J.; Pei, S.-L.; Chiang, P.-C. Establishment of enhanced geothermal energy utilization plans: Barriers and strategies. Renew. Energ. 2019, 132, 19–32. [Google Scholar] [CrossRef]
- Feng, Z.; Wan, Z.; Zhao, Y.; Li, G.; Zhang, Y.; Wang, C.; Zhu, N. Experimental study of permeability of anthracite and gas coal masses under high temperature and triaxial stress. Chin. J. Rock Mech. Eng. 2010, 29, 689–696. [Google Scholar]
- Zhao, Y.; Wan, Z.; Zhang, Y.; Zhang, N.; Feng, Z.; Dong, F.; Wu, J.; Qu, F. Experimental study of related laws of rock thermal cracking and permeability. Chin. J. Rock Mech. Eng. 2010, 29, 1970–1976. [Google Scholar]
- Xi, B.; Cheng, Z.; He, S.; Yang, X.; Liu, J. Experimental study on permeability characteristics and its evolution of granite after high temperature. Chin. J. Rock Mech. Eng. 2021, 40 (Suppl. S1), 2716–2723. [Google Scholar]
- Chaki, S.; Takarli, M.; Agbodjan, W. Influence of thermal damage on physical properties of a granite rock: Porosity, permeability and ultrasonic wave evolutions. Constr. Build. Mater. 2008, 22, 1456–1461. [Google Scholar] [CrossRef]
- Brace, W.F.; Walsh, J.; Frangos, W. Permeability of granite under high pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Xu, J.; Tao, Y.; Yin, G.; Peng, S.; Li, B. Coupled Modeling and Experimental Study of THM in Gas-Bearing Coal; Science Press: Beijing, China, 2012. [Google Scholar]
- Xu, J.; Zhang, D.; Peng, S.; Nie, W.; Wang, L.; Chen, Y. Experimental research on impact of temperature on seepage characteristics of coal containing methane under triaxial stress. Chin. J. Rock Mech. Eng. 2011, 30, 1848–1854. [Google Scholar]
- Yin, G.; Jiang, C.; Wang, J.-G.; Xu, J. Combined effect of stress, pore pressure and temperature on methane permeability in anthracite coal: An experimental study. Transp. Porous Media 2013, 100, 1–16. [Google Scholar] [CrossRef]
- Dou, H.; Bai, X. Stress sensitivity consists in low permeability and middle-high permeability reservoirs. Oil Drill. Prod. Technol. 2009, 31, 121–124. [Google Scholar]
- Liu, S.; Li, H.; Zhou, X. Relationship between sedimentary microfacies and reservoir productivity in Da12—Da66 wellblock, Daniudi gas field. Oil Gas Geol. 2012, 33, 45–49+60. [Google Scholar]
- Pan, W.; Lun, Z.; Wang, W.; Liu, H. Experimental study of stress sensitivity in abnormal overpressure gas reservoir. Pet. Geol. Exp. 2011, 33, 212–214. [Google Scholar]
- Yang, P.; Chen, M.; Hou, B.; Jin, Y.; Liu, X.; Zhang, W. The study of stress sensitivity for fractured and matrix carbonate rocks before and after sealing. Pet. Drill. Tech. 2011, 39, 31–34. [Google Scholar]
- Ru, T.; Liu, Y.; Fan, Y.; Li, B.; Yu, J. Pressure-sensitive effect in development of low permeability sandstone gas reservoir. Fault-Block Oil Gas Field 2011, 18, 94–96. [Google Scholar]
- Xiao, Z.; Pu, C.; Qin, W. Experimental study on pressure sensitivity in low permeability sandstone reservoir. Drill. Prod. Technol. 2008, 3, 97–98+113+157. [Google Scholar]
- Wang, X.; Ling, M.; Li, S.; Wang, B.; Zhang, B.; Zhang, L. Experimental Study of Sand Producing Law of Lower S3, Pan’er Area in Linpan Oilfield. Fault-Block Oil Gas Field 2003, 10, 67–70+93. [Google Scholar]
- Gao, B.; Zeng, M. Causes and prevention measures of clogging in the reinjection well of a geothermal double-well system. Hydrogeol. Eng. Geol. 2007, 2, 75–80. [Google Scholar]
- Bouwer, H. Role of groundwater recharge in treatment and storage of wastewater for reuse. Water Sci. Technol. 1991, 24, 295–302. [Google Scholar] [CrossRef]
- Li, Y. The Exploration Potential Zoning Evaluation of Shandong Province Deep Geothermal Resources. Master’s Dissertation, Shandong Jianzhu University, Jinan, China, 2016. [Google Scholar]
- Liu, C.; Wang, W.; Wei, Z. Analysis of hydrothermal geothermal resources and its prospect of development and utilization in Shandong. Geol. Surv. China 2018, 5, 51–56. [Google Scholar]
- Zhao, J. The Geothermal Resource Evaluation for GuanTao Geothermal Reservoir in Dezhou City. Master’s Dissertation, China University of Geosciences, Beijing, China, 2007. [Google Scholar]
- Luo, J. Reservoir Characteristics, Tracer Test and Optimization of Laoling Geothermal Field. Ph.D. Dissertation, The University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Sedov, L.I.; Shen, Q. Similarity Method and Dimensional Theory in Mechanics; Science Press: Beijing, China, 1982. [Google Scholar]
- Xie, Y.; Chen, Z. Experiment study on permeability sensitivity in loose sandstone gas reservoir. Fault-Block Oil Gas Field 2013, 20, 488–491. [Google Scholar]
- Qiao, M. Study on Deformation and Seepage of Reservoir during Re-injection of Tail Water in Sandstone Geothermal Engineering. Master’s Dissertation, Taiyuan University of Technology, Taiyuan, China, 2021. [Google Scholar]
- Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G.; Sengers, J.V.; Assael, M.J.; Metaxa, I.N.; Vogel, E.; Mareš, R.; Miyagawa, K. New international formulation for the viscosity of H2O. J. Phys. Chem. Ref. Data 2009, 38, 101–125. [Google Scholar] [CrossRef]
- Rivkin, S.; Akhundov, T. Experimental determination of the specific volumes of heavy water at high pressures and temperatures. Sov. At. Energy 1964, 14, 609–611. [Google Scholar] [CrossRef]
- Qu, Z.-q.; Zhang, W.; Guo, T.-k. Influence of different fracture morphology on heat mining performance of enhanced geothermal systems based on COMSOL. Int. J. Hydrogen Energy 2017, 42, 18263–18278. [Google Scholar] [CrossRef]
- Kariznovi, M.; Nourozieh, H.; Abedi, J. Experimental measurements and predictions of density, viscosity, and carbon dioxide solubility in methanol, ethanol, and 1-propanol. J. Chem. Thermodyn. 2013, 57, 408–415. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, Y.a.; Zhao, J.; Zhang, L.; Liu, S.; Liu, Z.; Feng, B.; Feng, G.; Yue, G. Heat extraction performance and optimization for a doublet-well geothermal system in Dezhou, China. Energy Explor. Exploit. 2022, 40, 619–638. [Google Scholar] [CrossRef]
- Baujard, C.; Genter, A.; Dalmais, E.; Maurer, V.; Hehn, R.; Rosillette, R. Temperature and hydraulic properties of the Rittershoffen EGS reservoir. In Proceedings of the European Geothermal Congress, Strasbourg, France, 19–24 September 2016; pp. 1–8. [Google Scholar]
- Song, W. Study on Prediction of Rockburst with Water Injection into Coal Seam in Fuxin Mine District. Ph.D. Dissertation, Liaoning Technical University, Fuxin, China, 2004. [Google Scholar]
- Schubert, H.; Herrmann, W.; Rumpf, H. Deformation behaviour of agglomerates under tensile stress. Powder Technol. 1975, 11, 121–131. [Google Scholar] [CrossRef]
- Wang, Y. Reservoir sand production rule and its influence on permeability. Inn. Mong. Petrochem. Ind. 2006, 12, 179–180. [Google Scholar]
- Chen, T. Feasibility Evaluation of Fracturing Sand Control in Unconsolidated Sandstone. Master’s Dissertation, China University of Petroleum (East China), Qingdao, China, 2019. [Google Scholar]
- Zhong, C.; Xu, T.; Yuan, Y.; Cui, G.; Gherardi, F.; Li, X. Coupled effects of elastic and plastic deformation on hydraulic properties of the geothermal fracture induced by cyclic loading-unloading processes. Eng. Geol. 2023, 313, 106929. [Google Scholar] [CrossRef]




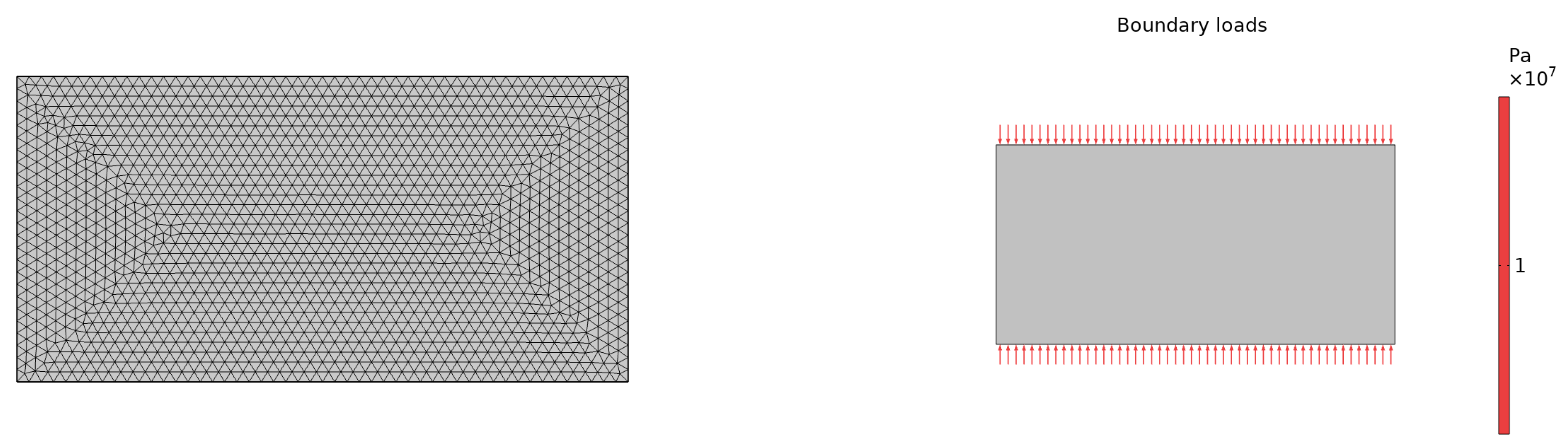
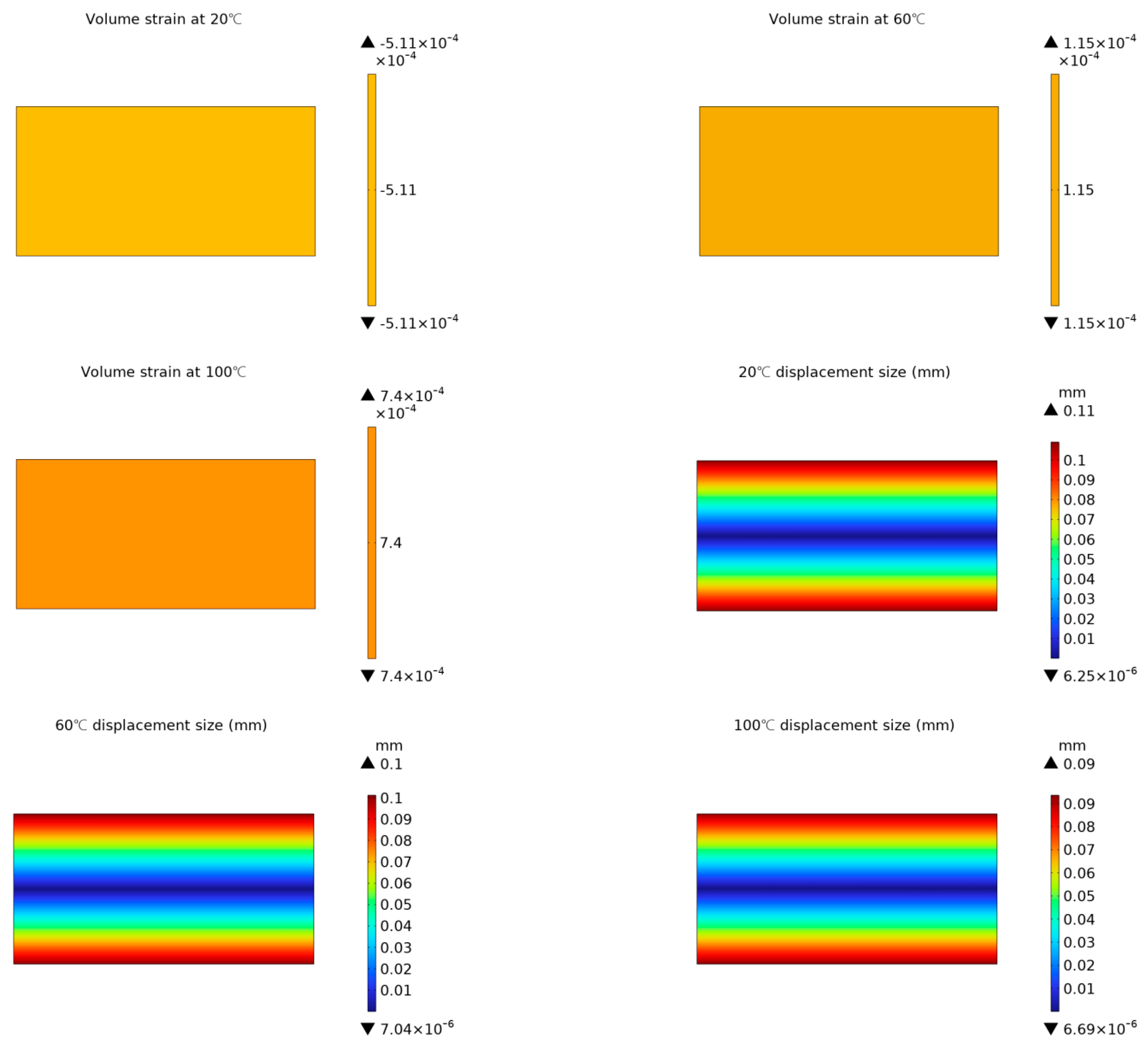
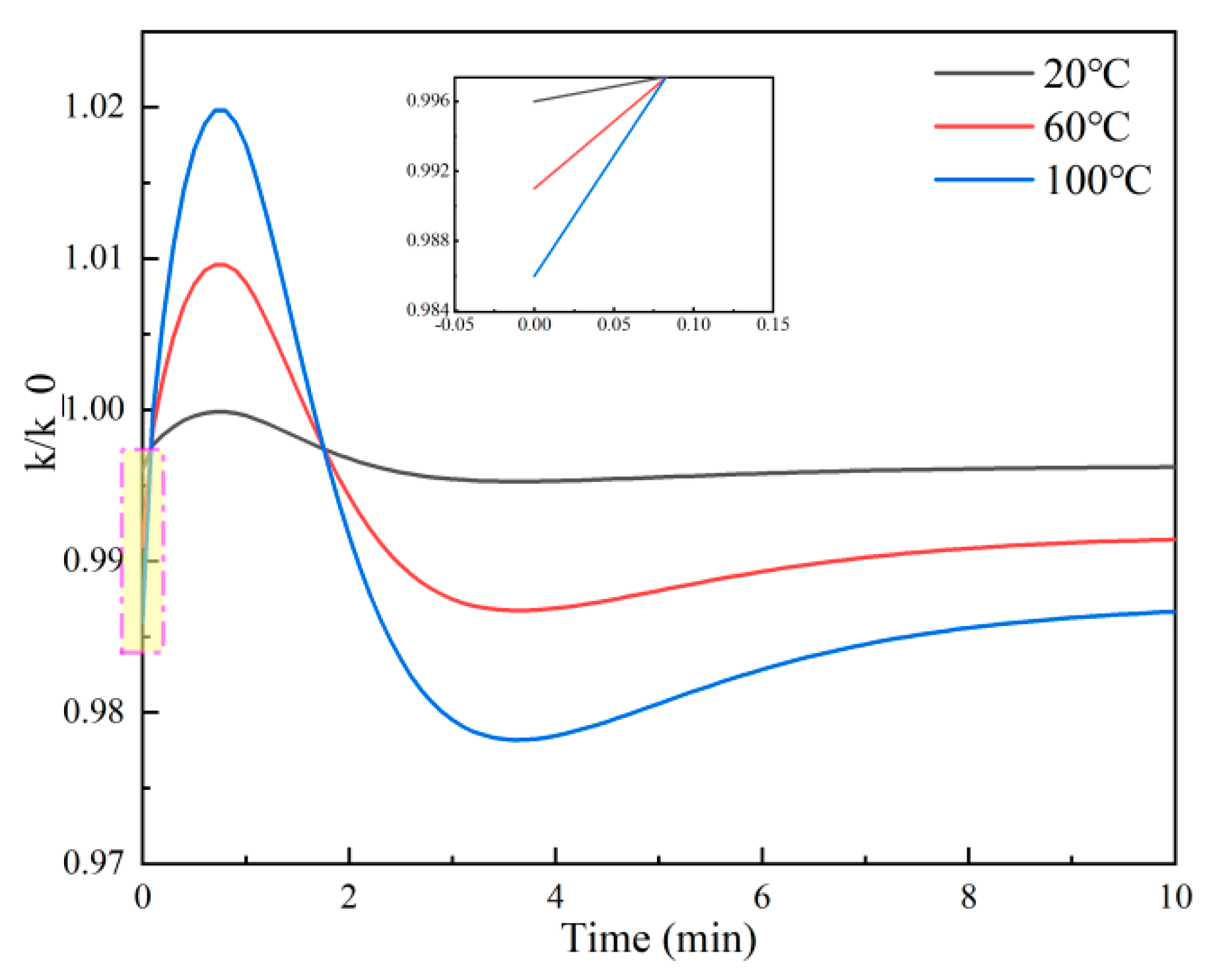
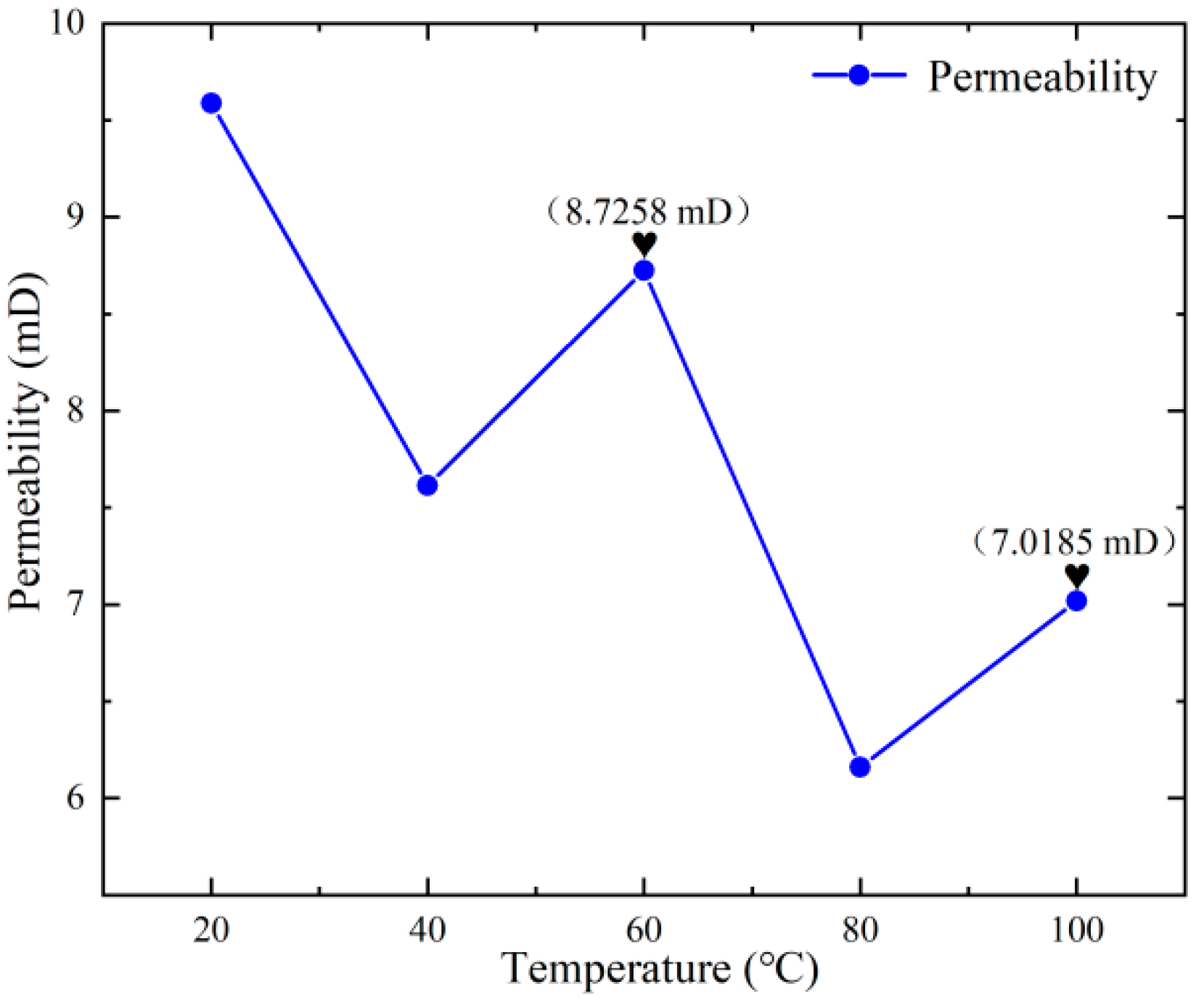



| Test Number | Temperature (°C) | Confining Pressure (Mpa) | Injection Rate (mL/min) |
|---|---|---|---|
| 1 | 20 | 10 | 1.0 |
| 2 | 40 | 10 | 1.0 |
| 3 | 60 | 10 | 1.0 |
| 4 | 80 | 10 | 1.0 |
| 5 | 100 | 10 | 1.0 |
| Parameters | Numerical Value | Unit |
|---|---|---|
| Injection temperature | 10 | °C |
| Confining pressure | 10 | MPa |
| Thermal expansivity (αT) | 1 × 10−5 | K−1 |
| Thermal conductivity of rock (λs) | 2.1 | W m−1 K−1 |
| Thermal conductivity of water (λw) | 0.5 | W m−1 K−1 |
| Specific heat capacity of rock (cs) | 909 | J (kg−1 K−1) |
| Specific heat capacity of water (cw) | 4200 | J (kg−1 K−1) |
| Density of rock (ρ) | 2000 | kg m−3 |
| Young’s modulus (E) | 1 | GPa |
| Poisson ratio (v) | 0.22 | 1 |
| Bulk modulus of rock skeleton (Ks) | 1.701 | GPa |
| 0.20 | 1 | |
| Initial permeability (k0) | 1 × 10−14 | m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, R.; Feng, B.; Duan, X.; Zhao, J.; Yang, Y.; Feng, S.; Yuan, Y. Analytical Study of Permeability Properties of Loose Sandstone Based on Thermal-Hydraulic-Mechanical (THM) Coupling. Energies 2024, 17, 327. https://doi.org/10.3390/en17020327
Cui R, Feng B, Duan X, Zhao J, Yang Y, Feng S, Yuan Y. Analytical Study of Permeability Properties of Loose Sandstone Based on Thermal-Hydraulic-Mechanical (THM) Coupling. Energies. 2024; 17(2):327. https://doi.org/10.3390/en17020327
Chicago/Turabian StyleCui, Rui, Bo Feng, Xiaofei Duan, Jichu Zhao, Yabin Yang, Shoutao Feng, and Yilong Yuan. 2024. "Analytical Study of Permeability Properties of Loose Sandstone Based on Thermal-Hydraulic-Mechanical (THM) Coupling" Energies 17, no. 2: 327. https://doi.org/10.3390/en17020327
APA StyleCui, R., Feng, B., Duan, X., Zhao, J., Yang, Y., Feng, S., & Yuan, Y. (2024). Analytical Study of Permeability Properties of Loose Sandstone Based on Thermal-Hydraulic-Mechanical (THM) Coupling. Energies, 17(2), 327. https://doi.org/10.3390/en17020327







