Abstract
The utilization of geological formations, distinguished by natural porosity and permeability and protected by low-permeability caprock, has emerged as an effective strategy for carbon dioxide (CO2) storage. This method significantly contributes to mitigating anthropogenic greenhouse gas emissions and addressing the challenges of climate change. Recent research has unveiled the potential of CO2 to enhance geothermal heat energy extraction in geothermal reservoirs by acting as a subsurface heat exchange fluid. This review paper explores the viability of CO2 in augmenting geothermal heat energy extraction, comparing it to conventional water-based geothermal systems. Special emphasis is placed on CO2 plume geothermal (CPG) systems, characterized by rapid deployment and long-term utilization of geothermal energy resources. With the overarching objective of establishing net-zero energy communities, the analysis of such systems offers a comprehensive understanding of their features, providing a fresh perspective on extracted energy within the context of energy supply in integrated, sustainable energy in built systems. Notably, these systems demonstrate efficacy in meeting the power requirements of an energy community, spanning both distinct heating and electricity needs. However, the key challenge lies in selecting suitable locations. This scientific review aims to comprehend the characteristics of CPG under specific temperature and pressure conditions while optimizing subsurface permeability. This insight is pivotal for identifying future locations for CPG operations with the intent of powering small energy communities.
1. Introduction
1.1. Background
Following the industrial revolution, global warming and energy shortages have emerged as the most widely discussed challenges [1]. The Earth’s increasing temperature is primarily attributed to greenhouse gases, with carbon dioxide (CO2) being a major contributor. Unlike other pollutants, CO2 can be significantly eliminated since it is primarily emitted by specific sources, mainly from human industrial processes [2]. One effective method to address this is “carbon capture and sequestration” (CCS) in geological formations. While CCS is considered the primary approach for reducing CO2 in the environment, its implementation faces an important challenge: the associated cost [3].
Geothermal energy provides environmentally friendly, steady, and reliable electrical power without the need for large-scale energy storage on the grid, distinguishing it from many other renewable energy options. The extensive harnessing of deep geothermal energy holds the potential to substantially contribute to decarbonization of the power, heating, and cooling industries [4]. Although this idea has reached a high “technological readiness level” (TRL), the availability of hydrothermal resources is restricted to specific geologically advantageous areas. Therefore, a heightened emphasis on petrothermal projects will be crucial for the meaningful integration of deep geothermal energy into the global energy system’s transformation in the upcoming decades.
To tap into the abundant geothermal energy for human use, various approaches have been proposed to create or expand fractures within hot, dry, and impermeable crystalline basement rocks. This process aims to establish artificial geothermal reservoirs of relatively small size that can facilitate the flow of fluids and extraction of heat. This system, known as an enhanced or “engineered geothermal system” (EGS) (Section 2.2), commonly employs water to fracture the rocks and extract heat through advection. However, there have been proposals to use CO2 as the working fluid [1,5]. While EGS holds promise for improving access to geothermal resources, there are several challenges that need to be addressed through technological advancements before this system can effectively extract significant amounts of energy [6]. Some of the shortcomings associated with EGS include low heat extraction efficiency, potential of rock mineral precipitation and dissolution, substantial energy demands for water circulation, and issues of water scarcity in certain regions [7]. These limitations highlight the need for further research and development to overcome these obstacles and optimize the performance of EGS for large-scale energy extraction.
The utilization of CO2 as a heat carrier has garnered increasing attention from both academia and industry over the past two decades. Recently, the findings of an initial larger research demonstration project have been published [8]. Integrating CCS with geothermal energy production can lower greenhouse gas emissions, contributing to climate change mitigation [9]. Furthermore, it can enhance the economic viability of CCS [10], leveraging the advantageous thermodynamic and fluid mechanical properties of “supercritical CO2” (sCO2) (Section 2.3). Additionally, the superior heat extraction efficiency of CO2 compared to water or brine becomes especially advantageous in regions with low-to medium-grade geothermal heat resources. In such areas where traditional geothermal electricity production may not be economically feasible, this approach has the capability to substantially expand global geothermal electricity generation [11].
Until now, investigations into electric power generation utilizing CO2 as the subsurface working fluid have mainly concentrated on EGS reservoirs within a restricted range of conditions [12,13,14]. Atrens [13] computed exergy production, representing the maximum theoretical surface plant electric power production, for both subsurface CO2 and water using a specific set of parameters. These parameters included a temperature of 225 °C, a depth of 5 km, a reservoir with fixed permeability modeled using the Darcy equation, and injection and production well diameters of 0.23 m. Beckers et al. [14] conducted calculations on electric power production and the “levelized cost of electricity” (LCOE) for EGS using fixed mass flow rates. This involved varying multiple parameters, such as depth, geothermal well diameter, temperature gradient, and surface plant design. However, EGS has faced substantial socio-political resistance, as evidenced by the termination of several EGS projects in 2009, including the Basel project in Switzerland [15].
Although the application of CO2 was initially described in the context of EGS [1,12,16], Randolph and Saar [10,17,18,19] advanced the concept by integrating geothermal energy production with geological carbon dioxide sequestration. They termed their concept the “CO2 plume geothermal” (CPG) system, distinguishing it from CO2-based EGS approaches (Section 2.3). The CPG concept has been extensively explored and discussed in various publications after Randolph and Saar, including those by Adams et al. [20,21,22], Garapati et al. [23,24,25,26], Ezekiel et al. [27,28,29], and Fleming et al. [30,31].
In the CPG approach, sCO2 is injected into pre-existing naturally porous and permeable geologic formations. As it traverses through the geologic reservoir, it undergoes geothermal heating. A portion of the heated CO2 is subsequently extracted back to the surface, using an appropriate well configuration system. This recovered CO2 can be applied for direct heat applications or used to produce electric power through a direct CPG turbomachinery power plant [21,27,28]. The primary purpose of CPG is to recover geothermal energy from these formations, and as a secondary benefit, the originally injected CO2 can be permanently stored underground, transforming the process into a “CO2 capture, utilization, and storage” (CCUS) technology [10,17,18,19].
1.2. Overview of Past Research on CPG Studies
The primary focus of research on CPG technology revolves around reservoir and wellbore fluid dynamics, subsurface heat transfer, and the surface components of the system. Numerous numerical models have been developed to simulate CPG systems, taking into account different reservoir parameters and CO2 injection rates. These models play a crucial role in helping researchers to analyze and optimize CPG’s performance under diverse conditions.
Garapati et al. [23,24,25,26] have conducted extensive research on CPG technology. In their study [23], they observed that increasing reservoir thickness, permeability, and porosity lead to higher total heat energy output. The contribution of thermal energy from CO2 increases with temperature and CO2 mass fraction, while the contribution from the rock matrix decreases. Furthermore, their analysis of CPG performance in multi-layered geologic reservoirs [24] revealed that the CO2 mass fraction depends on higher-permeability layers, while horizontal layers act as conductors for CO2 flow. Permeability heterogeneity affects the pressure drop and heat energy extraction rate, with low-permeability layers leading to greater pressure drops.
Additionally, Garapati et al. [25] explored the impact of CO2 injection on brine displacement. Their findings showed that the initial CO2 injection increases with well spacing, permeability, and reservoir depth, but diminishes for higher geothermal gradients. The rates of heat extraction vary depending on the depth of the reservoir, gradient, and circulation rate. Lastly, in their evaluation of electric power generation potential between two geothermal-hybrid systems, Garapati et al. [26] observed that direct CPG systems generate more power at low turbine inlet temperatures, while indirect brine-hybrid systems perform best at low-to-moderate temperatures. Optimal turbine inlet temperatures and heat fractions play crucial roles in maximizing the hybrid power ratio.
The research undertaken by Adams et al. [20,21,22] further expanded the knowledge of CPG technology and its impact on various aspects of the system. Adams et al.’s [20] focus was on highlighting the significance of the “thermosiphon effect” in CPG systems (Section 2.3), analyzing the influencing factors, and developing a mathematical model based on thermodynamics and fluid mechanics. They found that CO2 has lower pressure losses, a larger thermosiphon-induced mass flow rate (compared to brine), higher heat extraction rates, and requires less pumping power. It performs well at shallow depths and has optimal benefits between depths of 0.5 km and 3 km.
In addition, their comparative analysis of CPG and brine geothermal systems under varied reservoir conditions [21] showed that CO2 experiences less pressure loss than brine in sedimentary reservoirs and demonstrates higher power generation capacity at lower-to-moderate depths and permeabilities. In hot and deep reservoirs, CO2 direct systems outperform brine systems by producing significantly more power.
Furthermore, Adams et al.’s [22] study investigated the impact of heat depletion on CPG systems in sedimentary basins, emphasizing the importance of considering heat depletion in system design. The findings highlighted the optimal reservoir radius for maximizing power generation and sustaining it over time. The study also addressed the trade-off between energy extraction and long-term reservoir sustainability, emphasizing the impact of reservoir thickness and well pipe diameter on power generation and heat depletion rates.
Expanding on the groundwork established by Adams et al., the investigations carried out by Ezekiel et al. [27,28,29] introduced another innovation in the CPG system. In their study [27], they explored the use of sCO2 as a working fluid for “enhanced gas recovery” (EGR) and extracting geothermal energy from deep natural gas reservoirs. The system aimed to capture and store CO2 while optimizing power output. Numerical simulations indicated that integrating CO2 injection for gas recovery and establishing a CO2 plume for geothermal energy leads to an augmentation in energy production. This approach improves overall gas field performance and extends its lifespan, making it suitable for geologic CO2 storage and geothermal energy extraction.
Moreover, Ezekiel et al. [28] explored the potential synergy of utilizing CO2 for EGR and CPG from natural gas reservoirs. Their results demonstrated that optimal overall energy recovery performance was achieved by overlapping “CO2-enhanced gas recovery” (CO2-EGR) and CPG stages with a brief CO2 injection period. Sensitivity analysis revealed that permeability anisotropy and reservoir temperature influence EGR, while reservoir temperature and wellbore diameter affect geothermal power generation. In their recent work [29], they emphasized the importance of optimizing the fluid production flow rate to minimize water entry, maintain annular flow, and maximize CPG power generation. They conducted a flow pattern transition analysis for CO2-brine systems, discussing minimum CO2 velocity, case study insights, and sensitivity analyses of operational and reservoir parameters.
Delving deeper into the understanding of the CPG field, Fleming et al.’s [30,31] studies have made crucial and notable contributions. Specifically, Fleming et al. [30] investigated the potential for increased power generation in CPG power plants through exothermic water exsolution. Wet CO2 models, considering water dissolved in CO2, led to higher wellhead fluid temperatures and resulted in a noteworthy rise in turbine electric power output in comparison to dry CO2 assumptions. Furthermore, the concept of a “flexible CPG” (CPG-F) facility [31], which combined dispatchable power generation and energy storage using geologically stored CO2, generated higher instantaneous power compared to a traditional CPG power plant but had lower daily energy production. However, the “CPG-F facility” designed for different energy storage durations incurred a higher capital cost but yielded more power.
Following the aforementioned inquiries, it is crucial to underscore and examine some supplementary and up-to-date research on CPG technology. To begin, the simulation of multi-fluid and multi-level geothermal systems using brine and CO2 as working fluids has shown that integrated reservoir systems could extend reservoir lifespans, generate more electricity, reduce fluid-induced seismicity risk, and offset the expenses associated with CCS (Saar et al. [32]). In this research, a model of a generic system was developed over a span of 100 years using the “NUFT numerical simulator,” considering factors like heat transfer, pressure changes, flow dynamics, and other parameters. Moreover, Hefny et al.’s [33] investigation focused on geologic CO2 storage in the Nubian sandstone formation in the Gulf of Suez, Egypt, utilizing synchrotron X-ray computed microtomography to create a high-resolution 3D pore network model of the rock. A numerical simulator was developed to predict the characteristics of two-phase flow and investigate CO2 trapping mechanisms. The findings demonstrated the efficiency and capacity of Nubian sandstone for CO2 storage and contributed to the development of effective CCS strategies.
Finally, yet importantly, the works by Brummen et al. [34], Schifflechner et al. [35], and Norouzi et al. [36] have to be mentioned as the most recent studies in the CPG field. Brummen et al. [34] explored the feasibility of utilizing CPG power plants and “CPG-F facilities” combined with wind and solar energy sources to tackle the challenges posed by variability and intermittency. They employed plant-scale and power grid-level optimization models to determine the optimal power capacities under different scenarios. The results indicated that while CPG power plants may face limitations on hot days and might require curtailment when combined with renewables, “CPG-F facilities” equipped with long-duration energy storage can alleviate system capacity needs and mitigate these limitations. Schifflechner et al. [35] assessed various configurations of CPG plants for “combined heat and power” (CHP) production. They concluded that CPG plants are suitable for CHP applications, but necessitate larger reservoir depths compared to water-based systems. The two-staged serial concept demonstrated the highest net power output, while thermosiphon systems exhibited the potential for significant revenue increases. Consequently, CHP applications can enhance the overall efficiency of CPG systems.
Conversely, Norouzi et al. [36] assessed the feasibility and efficiency of CPG systems in generating power from 3D fluvial aquifers, revealing that the CO2 injection rate, aquifer thermal depletion, and fluvial heterogeneity significantly impact system performance. Supercritical CO2 production and parallel well orientations yielded better results. Homogeneous cases outperformed heterogeneous cases in terms of cumulative power generation. High mass flow rates were necessary for acceptable power output, suggesting the need for alternative scenarios like depleted oil reservoirs or smaller-scale applications.
Several research endeavors have explored the benefits and challenges of integrating CPG systems with “carbon capture and storage” (CCS) in various locations. However, some researchers have primarily focused on investigating the feasibility of CPG systems in India and Germany. Gupta and Vashistha [37] discussed the technical and economic advantages of CPG systems in India, while McDonnell et al. [38] conducted a comprehensive feasibility study in Germany. The findings unveiled the significant geothermal potential in India, the economic competitiveness of geothermal energy compared to other renewable sources, and the scalability and capability of CPG systems to deliver a stable power supply. Similarly, Germany’s geologic formations were found to be favorable for CPG systems and CO2 utilization. The economic analysis conducted in both studies demonstrated promising returns on investment, highlighting the potential economic viability of CPG systems in these regions.
1.3. Objectives of the Paper
In this paper, particular attention is given to the methodologies employed by Randolph and Saar in their extensive CPG technology research [10,17,18,19]. The researchers devised sophisticated models to simulate CPG technology operations under specific conditions. The paper critically assesses the rates of energy recovery and production achieved by CPG systems, employing a comparative analysis against EGS systems. Additionally, it scrutinizes the simulation methodologies of using H2O and brine versus CO2 as working fluids in CPG systems for energy comparison. This comparative approach sheds light on the relative effectiveness of CPG in meeting the energy demands within a built environment.
A key focus of the evaluation is the simulation methodologies employed by Randolph and Saar, particularly regarding the use of different working fluids—H2O and brine versus CO2—in CPG systems. This comparative analysis aims to provide insight into the energy efficiency and potential benefits associated with utilizing CO2 as a working fluid in CPG systems. Understanding these simulation approaches is crucial for future optimization of CPG technology, especially in addressing the power and heating needs of an energy-efficient building community.
As the broader goal of this paper aligns with creating net-zero energy communities, the findings from Randolph and Saar’s methodologies contribute significantly to the ongoing discourse on sustainable and renewable energy solutions. By emphasizing the role of CO2 in CPG systems and its impact on energy efficiency, this review adds a valuable perspective to the quest for optimal methods to strengthen the power heating requirements of energy-efficient built environments.
2. Utilizing CO2 as the Working Fluid in Geothermal Power Plants
To delineate the attributes of CO2-based geothermal systems, particularly the technology of CPG systems, a brief overview of the fundamental operations of a geothermal plant will be presented.
2.1. Introduction to Geothermal Power Plants
The production of geothermal energy is contingent on extracting thermal energy from the Earth’s subsurface. A geothermal reservoir is a volume of rock in the subsurface, the exploitation of which in terms of heat can be economically profitable. Due to several geomorphological and other rock properties and parameters, such as location, depth, thermal mass, and reservoir flow, the operating temperature of a geothermal plant varies. Thus, three main technologies can be distinguished for electricity production from geothermal resources: (a) flash steam, (b) dry steam, and (c) the binary cycle, which is used for lower-temperature geothermal resources [39,40,41]. The commonly used working fluid to circulate geothermal heat is water (H2O) [42]. In the binary cycle, a second working fluid is required to drive the power loop. The most common fluids for this purpose are propane, butane, pentane, and ammonia (NH3) [40].
Geothermal systems typically utilize injected “cold” water to transport heat from the subsurface to the surface, where it is converted into electricity via turbines and generators [42]. The binary cycle operates in two separated loops:
- The geothermal loop involves the absorption of heat from the hot rock, which is then transferred to the evaporator. This process leads to the transformation of the secondary working fluid into saturated steam through heat exchange.
- The power loop involves the second working fluid undergoing expansion in the turbine to generate electricity in the generator [40,41,42].
- Geothermal systems operate through a continuous circulation of mass and heat fluid [43].
2.2. Enhanced Geothermal System (EGS)
An enhanced or “engineered geothermal system” (EGS) represents a highly efficient method for achieving electricity production through high-temperature geothermal technology. EGS involves creating an artificial geothermal reservoir by injecting fluid at high pressure into hot, impermeable rock formations. This is particularly beneficial when natural permeability is low or when the hot rock lacks sufficient fluid saturation. Commonly, sedimentary zones and regions with “hot dry rock” (HDR) characteristics are used to stimulate the flow of heat to the surface.
“Hot dry rock” (HDR) is a type of EGS technology that involves creating artificial geothermal reservoirs in dry or impermeable rock formations. Designed to overcome the limitations of traditional geothermal systems, which rely on naturally occurring hot water or steam, HDR technology enables the extraction of heat from areas lacking such reservoirs. With HDR technology, it is possible to extract heat from areas that do not have naturally occurring geothermal reservoirs. These reservoirs typically exist at depths ranging from 2 to 10 km below the Earth’s surface, and the rock’s permeability and porosity are typically low, often with few or no fractures. Fractures are mechanical breaks in rocks involving discontinuities in displacement across surfaces or narrow zones [42].
The HDR process involves hydraulic fracturing (or hydro-fracturing) to create fractures in impermeable rock, enhancing water circulation. During the hydro-fracturing process, water is injected at high pressure through an injection well into the rock formation, creating small cracks and fractures [44,45]. These fractures are then held open using proppants like sand or ceramic particles, preventing them from closing once the injection pressure is released. Additionally, the water used in the hydro-fracturing process is typically mixed with a small amount of chemical additives, such as acids or polymers, to dissolve or break down minerals in the rock and increase the permeability of the fractures.
Once the fractures are created, water is circulated through the newly formed channels and heated by the surrounding hot rock. This heated water is then pumped back to the surface through a separate production well, where it is utilized to generate electricity in a geothermal power plant. This process establishes pathways for heat exchange between the HDR and working fluid. A system of production and injection wells is constructed to circulate the geothermal fluid and extract the heat [5].
Certainly, improving EGS involves addressing the expenses related to drilling and water loss [42]. Nevertheless, the advancement of EGS may present environmental impacts such as air and water pollution, induced seismicity (resulting from the intentional surpassing of critical fracture stresses [46,47]), and increased water consumption, hindering its worldwide application. Besides potential environmental impacts, various institutional, regulatory, technological, and financial factors pose challenges to the deployment of EGS [48].
The hydro-fracturing process is a vital element of HDR geothermal systems and EGS, enabling the creation of an artificial reservoir in dry or impermeable rock formations and enhancing the efficiency of heat transfer between the rock and circulating fluid. However, it is important to note that the use of hydraulic fracturing has been controversial due to concerns about its potential environmental impact, including the risk of groundwater contamination and seismic activity. Therefore, proper environmental safeguards and monitoring should be implemented to ensure the safe and sustainable use of this technology.
2.3. CO2-Based Geothermal Systems
As mentioned above, CO2 has recently been proposed as a geothermal working fluid due to its enhanced thermodynamic supercritical properties compared to H2O-based systems, introducing an opportunity for geological storage [49]. Brown [1,5] describes several promising advantages of using CO2 as a potential heat carrier compared to H2O. Thus CO2:
- Is an ionic and less effective solvent for rock minerals, minimizing scaling issues;
- Has lower kinematic viscosity (or higher mobility), allowing for high flow velocities that would lead to greater mass extraction rates for a given pressure gradient;
- Exhibits a higher heat exchange rate compared to H2O, enabling faster heat extraction;
- Has large compressibility and expansibility (high-density variation) that cause a strong buoyancy effect, resulting in a high self-driven mass flow rate without requiring a pump (referred to as the “thermosiphon effect”);
- Enables sequestration of CO2 in the deep subsurface.
CO2-based geothermal systems require reservoirs located deeper than 800 m with a low-permeability caprock to prevent CO2 migration to the surface. Injecting CO2 as a supercritical fluid (sCO2) is crucial to maintaining the necessary pressure and temperature values for CO2 storage. Supercritical CO2 is a state in which CO2 is at a temperature and pressure above its “critical point” (CP), exhibiting high-density properties similar to those of a liquid while retaining the fluid-like properties of a gas. This makes it an efficient working fluid for generating electricity from geothermal energy.
The critical temperature (Tcritical = 31.03 °C) and critical pressure (Pcritical = 71.778 bar) of CO2 ensure that it remains a supercritical fluid. Supercritical fluid is a single phase that can continuously transform from gas to liquid and vice versa with no phase boundaries [37]. Its volume is significantly smaller than its volume as a gas at the surface and can shrink to 2.7 m3 at a depth of 2 km, making it an attractive option for large-scale storage.
One significant advantage of using supercritical CO2 (sCO2) as a working fluid in geothermal systems is the density-driven “thermosiphon effect.” This natural process occurs when injected fluids, such as H2O or CO2, circulate due to differences in density caused by temperature variations. As the fluid is heated by the Earth’s crust, it expands and becomes less dense than the cooler fluid in the surrounding rocks. This density difference creates a buoyancy force that causes the hotter fluid to rise and cooler fluid to sink, resulting in a natural flow [12,20].
The thermosiphon effect is essential for the efficiency and sustainability of geothermal systems as it maintains a constant flow of heat from the Earth’s crust to the surface, usable for power generation or other applications. Using sCO2 as a subsurface working fluid has the advantage of high mobility, characterized by low kinematic viscosity and high thermal expansibility compared to H2O. This results in a strong thermosiphon effect that eliminates the need for parasitic pumping, thereby reducing energy requirements and improving overall system efficiency [12,20].
However, sCO2 has a lower specific heat capacity than H2O, which can be a drawback. The specific heat capacity of a fluid is the amount of heat energy needed to increase its temperature by a particular amount. Nevertheless, this drawback is compensated by the lower viscosity of sCO2 [5,50], allowing most of the pressure to be utilized in the production well rather than for moving the fluid [51]. It is worth noting that the effectiveness of the thermosiphon effect depends on various factors, including the temperature gradient, fluid properties, and geological conditions of the system. Moreover, the elimination of parasitic pumping requirements may not always be possible to maintain the desired flow rates in the system. Factors such as the distance between injection and production wells, the permeability of the surrounding rock formations, and the temperature gradient in the reservoir can all affect the intensity of the thermosiphon effect and overall efficiency of the geothermal system. It is essential to carefully consider all of these factors when designing and operating a geothermal system to ensure optimal efficiency and sustainability.
This paper discusses two CO2-based geothermal systems: CO2-EGS and the CPG system. When comparing CO2-EGS with the CPG system, the former requires the artificial creation of highly permeable reservoirs, which still demonstrates limited CO2 storage capacity. Furthermore, EGS is commonly developed by hydraulic fracturing or stimulation of low natural permeability rock, a process that may trigger seismicity because of intentionally exceeding the critical fracture stresses in geologic formations (Section 2.2) [46,47]. On the other side of the spectrum, the CPG system uses natural high permeability sedimentary formations with high CO2 storage capacity, which therefore eliminates the need for fracturing the rock (Section 2.4). The size of these natural reservoirs is generally much larger than that of hydro-fractured reservoirs [10]. For example, reservoirs in the Williston Basin, USA, span hundreds of kilometers [52], whereas the EGS site in Soultz, France, covers an extent of a few hundred meters [53]. Hence, the CO2 sequestration potential of the described CPG system is considerably greater than that of EGS.
2.4. CO2 Plume Geothermal (CPG)
The CO2 plume geothermal (CPG) energy capture and conversion cycle begins by capturing CO2 gas from an emitter, such as a fossil fuel power plant. This process results in a negative carbon footprint, and the plant functions as a CO2 sequestering geothermal power plant [10]. The captured CO2 is subsequently injected into a high-permeability sedimentary reservoir in its supercritical state. The reservoir has a confining layer called “caprock”, a rock of very low permeability that acts as an upper seal to prevent fluid flow out of a reservoir. This caprock is a common formation worldwide, and it ensures that the CO2 remains trapped within this layer [54]. Because of the larger contacting surfaces of sedimentary basins, the CO2 heat exchange is more efficient and favorable [55].
When CO2 is injected into a deep geologic formation, it displaces the native formation fluid (e.g., H2O), creating a large subsurface plume of supercritical CO2. This plume is then heated naturally either by the high underground temperatures or by the Earth’s geothermal heat flux (the amount of heat moving steadily outward from the interior of the earth through a unit area in unit time [56]), through conduction heat transfer from geological formations. Eventually, the heated sCO2 plume returns back to the surface through the production well system and can be used in two ways: either it can be directed through a turbine, generating power for a generator and producing electricity, or it can be employed in a heat exchanger to supply energy for both electricity production and district heating in a binary cycle. After circulating in the abovementioned manner, the sCO2 is cooled and re-injected back into the reservoir [10,21]. The injection and production processes occur through the specific design of an injection and production drilling system.
As sCO2 circulates in a closed-loop cycle without additional CO2, this prevents the release of CO2 into the atmosphere. This feature enhances the system’s flexibility, allowing it to operate with a limited quantity of CO2 stored underground. As a result, it minimizes the need for continuous injection and geological CO2 storage, especially when such practices are unfeasible or unprofitable under certain conditions [24]. Another advantage of the system is its ability to control the amount of CO2 produced. By controlling the thermosiphon effect, the rate of heat depletion within the reservoir can be decelerated. The rate of heat depletion depends not only on the transport of free-phase CO2 and dissolved CO2 but also on the sensitivity of permeability changes. Thus, optimizing this rate for a specific location in a geologic reservoir can increase the system’s longevity and provide significant economic and environmental benefits [23].
CPG technology can increase the efficiency of electricity generation by eliminating the need for parasitic power requirements to maintain pumping circulation, as discussed earlier in Section 2.3. This is achieved through the sCO2 thermosiphon effect [26]. Moreover, locating the CPG facility near established CO2 sequestration sites enhances the effectiveness of CO2 geological sequestration and geothermal heat extraction, making CPG a CCS (carbon capture and storage) technology. Utilizing CO2 as a resource for electricity generation can assist in reducing the costs associated with sequestration [18] and spread the cost of subsurface exploration across different activities [57]. It should be noted, however, that it might be necessary to use parasitic pumping in certain cases in order to maintain the desired flow rates in the system.
Conventional H2O-based geothermal development has three geologic requirements that need to be satisfied:
- A substantial amount of H2O;
- A permeable formation that allows for H2O extraction and reinjection;
- Sufficient subsurface temperatures.
To increase the probability of geothermal heat extraction, EGS artificially induces the second requirement and either supplies water (in H2O-based EGS) or prevents it (in CO2-based EGS) [1,5]. Conversely, closed-loop CPG systems are designed to maximize the heat extraction efficiency by exploiting the high mobility of CO2. Unlike H2O-based systems, CPG systems eliminate the need for a substantial amount of water (first requirement) and can operate at lower minimum subsurface temperatures (third requirement), reducing the technical and economic feasibility thresholds [10].
In a CPG system, the low viscosity of CO2 facilitates smoother flow through the small pores in the reservoir rock. This increases the contact area between the fluid and rock, thereby enhancing heat transfer. This results in higher rates of heat extraction from the reservoir compared to traditional H2O-based systems, particularly at deeper reservoir depths where temperatures are higher.
CPG systems can extract more heat from the reservoir for medium-low permeability values, typically ranging from 0.1–2 [×10−14 m2], compared to H2O-based systems. However, for higher permeability values above 5 × 10−14 m2, the advantage of using CO2 becomes less significant as the difference in permeability between CO2 and H2O is less pronounced [17,21]. It is essential to note that the optimal permeability range for CPG systems may vary depending on the specific geology of the reservoir.
As a reliable and predictable source of energy, CPG systems can produce either dispatchable or baseload “carbon-neutral” electricity, making them an attractive option for renewable energy. Furthermore, the CO2 used in the process can be recycled, making CPG systems more sustainable than other forms of geothermal energy. CPG systems can also be modified to provide energy storage, increasing their versatility and potential applications in the energy sector [58].
All of the above information is analyzed in the following Section 3, covering the overall CPG system, its model characteristics, system parameters, and simulation results, as described by Randolph and Saar. The analysis is conducted in comparison with CO2-EGS not only to contrast the two systems but also to provide extensive details on the development of CPG numerical models.
3. CPG Model Configuration
3.1. General System Parameters
When comparing the CPG system and CO2-EGS, it is essential to identify certain critical characteristics (e.g., reservoir permeability, temperature, pressure, size, injection/production fluid rate, etc.) for thermal energy extraction. The Base Case parameters for the model configuration were set by Randolph and Saar [10,17,18,19]. These general system parameters encompassed the CPG formation parameters, injection/production model specifications, as well as initial and boundary conditions. To determine the reservoir conditions for CPG technology, investigating the standard values of worldwide geothermal power plants is crucial. Water-based geothermal systems are primarily situated in areas with relatively high temperatures (>150 °C) and high heat flow (>90 mW/m2, approximately) [18]. In contrast, CO2-based geothermal systems require larger reservoirs that are not often ideal for high temperature processes. The established lower limit of the initial temperature for geothermal electricity production in a subsurface system is T = 100 °C [59].
Considering the above information, for CPG modeling, Randolph and Saar [10,18] selected a geologic reservoir with non-extreme thermal characteristics, typical of most areas around the Earth’s surface. As the geologic formation parameters, they set a reservoir map-view area of 1 km2 with a thickness of 305 m, rock grain density of 2650 kg/m3, rock specific heat of 1000 J/kg/°C, thermal conductivity of 2.1 W/m/°C, and heat source of 90 mW/m2. Two different permeability values were taken into account: 5 × 10−14 m2 for direct comparison with reservoir system simulations and 2.5 × 10−14 m2, which better reflected practical EGS implementations (see Section 3.2).
Randolph and Saar introduced the EGS technology features as outlined by Pruess (2006) [5] to optimize the functionality of their CPG model. Subsequently, they adjusted their simulations for naturally porous and permeable systems. Instead of employing an “injector-producer doublet,” which is a combination of a production and injection well working in double pairs, they adopted the 5-spot well configuration (square-shaped) from EGS. Its high degree of symmetry reduced the modeling requirements to 1/8th of the system domain (Figure 1), simplifying the modeling problem. In this configuration, 4 production wells and 1 injection well are positioned. The injection well is located at the center of the square, while the production wells are situated at the four corners, respectively. The two-dimensional 5-point grid has a basic pattern area of 1 km2 (reservoir map-view area) and comprises 36 grid main blocks, each with a side length of 70.71 m (well separation). Drawing inspiration from several CO2 sequestration basins (e.g., Williston Basin), the blocks consist of a continuous porous medium matrix with a porosity of 20%. The temperature of the injected fluid was set at 20 °C, the injection/production rate was set at 300 kg/s (variable), and the total injection/production duration was set at 25 years. The downhole injection temperature exceeds the surface heat rejection temperature (specified in Section 4.1), attributed to Joule–Thomson heating taking place in the injection well. Additionally, the downhole injection and production pressures were set at 260 and 240 bar, respectively (Base Case). All of these parameters characterized the injection and production conditions of the model.
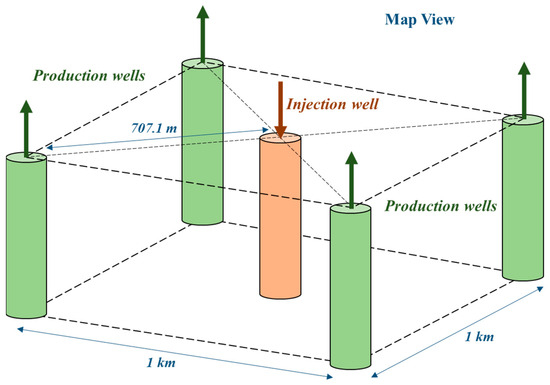
Figure 1.
A 3D view of a 5-spot well configuration.
Furthermore, as the initial conditions, Randolph and Saar defined 100 °C and 250 bar as the initial reservoir temperature (T) and pressure (P), respectively. These values corresponded to a formation depth of 2.5 km under a low-to-moderate geothermal gradient of 30–35 °C/km (Base Case), varying with the local mean annual surface temperature and fluid rock thermal conductivity. The reservoir fluid was only CO2. Such initial conditions are prevalent in several sites worldwide suitable for CO2 sequestration, including the Williston Basin in North Dakota (USA) and Alberta Basin (Canada) [52]. As for the boundary conditions, they assumed no fluid or heat flow at the top and sides and no fluid flow or heat conduction at the bottom of the reservoir configuration.
Besides the Base Case parameters, Randolph and Saar [10,18] examined several additional permeability, temperature, and pressure scenarios to explore the parameter space. The parameter space encompasses the range of potential parameter values that define a specific mathematical model, typically representing a subset of finite-dimensional Euclidean space. These scenarios were part of the Additional Case parameters for the CPG model configuration, with all other parameters remaining the same as those for the Base Case. The cases examined included CPG, CO2-EGS, H2O reservoir (where H2O reservoir refers to a traditional geothermal system with H2O as the working fluid and no fracture spacing is applied), and H2O-EGS. Cases 1–4 were applied to all, while Case 5 was specific to CO2-EGS. Cases 6* and 7* were modified for specific CPG reservoir requirements [18]. Case 6* was specifically designed for a reservoir with considerable depth and moderate geothermal heat flux, such as the aforementioned Williston Basin [52]. Case 7* was utilized for shallow reservoirs with high geothermal heat flux, particularly in regions like the western USA [18]. More analytically, the formation temperatures and pressures are respectively represented below:
- Case 1: 120 °C, 250 bar
- Case 2: 140 °C, 250 bar
- Case 3: 100 °C, 200 bar
- Case 4: 100 °C, 300 bar
- Case 5: 100 °C, 250 bar
- Case 6*: 150 °C, 400 bar
- Case 7*: 100 °C, 100 bar
Monitoring the production well is crucial for system operation, as both the heat extraction rate (H) and fluid flow rate (Q) can be controlled. The heat extraction rate (H) is defined as:
where h and h0 are the fluid enthalpies of the produced and injection (at 20 °C) conditions, respectively.
The rock characteristics used generally reflected those of the EGS site in Soultz. Pruess et al. (2006) [5] examined an idealized fractured reservoir design with parameters adjusted to mimic the conditions of the European EGS site at Soultz, France [53]. Similar values may be encountered at various potential geologic CO2 sequestration sites, such as the Williston Basin in North Dakota (USA) and Alberta Basin (Canada) [52]. Randolph and Saar completed their simulations using the reservoir simulator TOUGH2 [60] with the fluid property module ECO2N (equation-of-state module) [61]. CO2 was assumed to be the only subsurface working fluid in the system, while the displacement of natural brine and formation of other fluids by CO2 were important to be examined (Section 4).
3.1.1. Permeability
The permeability (k) of geothermal formations is a vital parameter for CPG system operation. In line with permeability values found in commonly known CO2 sequestration sites such as the Illinois Basin (with permeability values ranging from 3 to 10 [×10−14 m2] [62]) and the saline aquifer systems of Alberta, Saskatchewan, North and South Dakota, and Montana (with permeability values ranging from 9.3 × 10−15 to 9.3 × 10−12 m2 [52]), the rock thermal permeability was set at 5 × 10−14 m2. However, due to the limited number of EGS production facilities, defining representative reservoir-scale permeability values for CO2-EGS simulations is relatively challenging. As a result, two approaches for determining kEGS permeability were developed [19].
In Approach 1, it was considered that the reservoir permeability values were the same for both EGS and CPG models (5 × 10−14 m2). This allowed for an easy comparison of thermal energy extraction, directly achieved without the impact of hydraulic effects between the two systems. The only drawback is to what extent these values reflect actual EGS sites. To address this, fracture permeability modeling for hydraulically stimulated basement rocks (hydro-fracturing, as discussed in Section 2.2) was established in Approach 2 [19]. This analytical approach aimed to estimate the reservoir-scale permeability of a hydraulically stimulated basement rock reservoir from “core-scale” pre-stimulated basement rock samples. A core sample is a roughly cylindrical piece of subsurface material removed by a special drilling process and brought to the surface for examination. The sample is analyzed to determine porosity, permeability, fluid content, geologic age, etc. [63]. This method provides at least a more indicative value of actual EGS implementations.
The analytical permeability calculation in Approach 2 for a specific fracture is based on electrical resistance theory in the 5-spot EGS grid, applying “Kirchhoff’s 1st Law” to a fracture network. To be more specific, Ohm’s Law (2) is analogous to Darcy’s Law (3), as for constant ρ and μ values (4), resistance (R) is analogous to permeability (k).
where I is the current, ΔV is the voltage difference, R is the electrical resistance, q is Darcy’s velocity, ∇h is the hydraulic head gradient, K is the hydraulic conductivity, ρ is the fluid density, g is Earth’s gravitational acceleration, k is the permeability, and μ is the dynamic fluid viscosity [64].
According to the “multiple interacting continua” (MINC) method [65], connections between fractures and adjacent grid blocks are created, even if they already exist along the boundaries of the primary grid blocks. A fracture connection network is formed, enclosing the permeable domain of 5-point EGS grid and smaller fracture segments are connected in grid block nodes (Figure 2). Applying Kirchhoff’s law for each node, assuming that ΔV is analogous to ∇h and R is analogous to k for an individual fracture (except the injection well, ∇h = 0), a linear system with 35 unknown hydraulic heads is created. For a given individual fracture—considering ΔV as the “voltage difference” (hydraulic head) between production and injection wells and I = 1 A as the “current” (fluid flow) across each fracture—the “resistance” (permeability) is calculated as 5.4 times the permeability of a fracture.
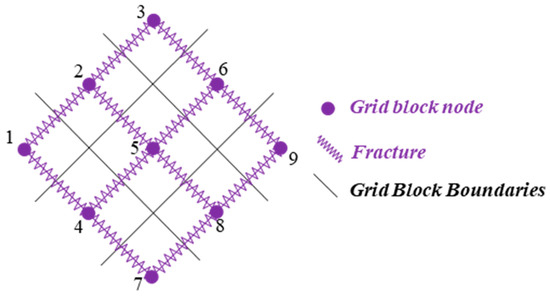
Figure 2.
Enlarged view of a section of the 2D fracture connection network that encloses the permeable domain of the EGS model. Numbers indicate the nodes per grid block boundary.
The core samples from the Soultz site and the “midcontinental rift system” (MRS) have permeabilities ranging from 10−18 to 10−16 m2. The MRS is a geological rift in the North American continent that spans 2,000 km and formed around 1.1 billion years ago during the Mesoproterozoic era [46,66]. In the MRS, especially at depths greater than 3.5 km, the average permeability is 10−18 m2. Randolph and Saar [19] selected a pre-hydraulic-stimulation permeability value of 10−17 m2. Assuming that hydraulic stimulation augments permeability by a factor of 200 (Soultz [46]), they chose a core-scale EGS permeability of 2 × 10−15 m2.
Using Approach 2, they calculated an effective system-scale permeability of 1.1 × 10−14 m2, obtained by multiplying the core-scale permeability by a factor of 5.4 (2 × 10−15 [m2] × 5.4 = 10.8 × 10−15 [m2] ≈ 1.1 × 10−14 [m2]). For numerical exercise purposes, they averaged this value with the EGS permeability in Soultz, France. Determining the permeability in Soultz for CO2-based EGS simulations is challenging due to the lack of production-scale (water-based) EGS facilities. However, a post-stimulation, reservoir-scale value of 6 × 10−14 m2 is provided by the EGS site in Soultz, France [46]. This averaging process resulted in a fracture system permeability of 3.5 × 10−14 m2, which was utilized to compare the CPG system and CO2-EGS.
3.2. Energy Recovery versus EGS
According to Randolph and Saar [19], two approaches were established for CPG modeling, as mentioned in Section 3.1.1. In Approach 1, all simulations for CPG and CO2-EGS reservoirs were performed with the same system permeability of 5 × 10−14 m2 to ensure identical mass flow rates [10]. Four cases were considered: one for CPG and three for EGS. The three cases of EGS corresponded to fracture spacings of 70.71 m, 141.42 m (2 × 70.71 m), and 212.13 m (3 × 70.71 m), as shown in Figure 3, respectively. All model parameters and constraints for each case were the same as those for the Base Case. According to Berkowitz (2002), percolation theory, primary path analysis, and field testing frequently demonstrate that systems may have dense fracture networks, but only a small fraction of the fractures accommodate the majority of the fluid flow. As such, discrete fracture networks provide logical approximations of the main fluid flow conduits and heat extraction from fracture-dominated systems [67].
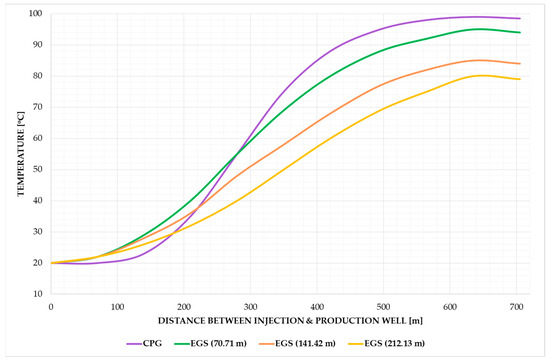
Figure 3.
Temperature profiles from injection to production wells. The production well temperature of the CPG case is higher than that of the EGS cases, indicating more extensive heat mining in the CPG scenario.
With the simulation time set to 10 years of CO2 injection and production, Figure 3 displays the temperature profiles along a line based on the distance from the injection to production wells. It is observed that the temperature at the CPG case’s production well tends to be closer to the initial reservoir temperature of 100 °C compared to that of the EGS case production wells. Furthermore, as the fracture spacing increases, the temperature at the EGS cases’ production wells decreases. These results indicate an augmented heat flow rate in the CPG case compared to the EGS cases, suggesting that CO2 has better and larger contact with the specific surface area of reservoir rock or sediment in the CPG system [10].
To incorporate time-based operations in simulation software, time series are formed. Within a time series, simulation controllers are used to update the values of different elements in each time step of a loop. Two such elements in these cases are the pumping and injection times and rates at the production and injection wells, respectively. All rates were provided for the full 5-spot domain, with a total simulation time of 25 years. The system permeability was 5 × 10−14 m2, except for EGS fracture spacing of 70.71 m, which was shown by both permeability values of 5 × 10−14 m2 and 3.5 × 10−14 m2 (Section 3.1.1) for comparison. EGS fracture spacing of 70.71 m was utilized as the investigated spacing [10], with heat-sweeping characteristics most similar to the CPG reservoir case.
It is noted that when the reservoir’s heat diminishes and the temperature at the production well gradually decreases, there is a decline in the rate of heat extraction, even though the mass flow rate generally remains stable. This result indicates that the CPG system provides more extensive heat extraction compared to EGS, maintaining higher temperatures in the production well for a more extended duration. As the EGS fracture spacing increases, there is reduced contact between the heat exchange fluid and reservoir materials. Consequently, this leads to a higher rate of temperature drop in the produced fluid over time [19]. In Approach 2, where the EGS permeability was lower (3.5 × 10−14 m2), lower mass flow rates were observed. This resulted in lower heat extraction rates, leading to slower cooling of the formation compared to EGS with similar fracture spacing and a permeability of 5 × 10−14 m2 [10].
In developing Approach 2, Randolph and Saar [10] incorporated a new reported value from the EGS field site in Ogachi, Japan (10−15 to 10−14 m2) [68]. The new fracture system permeability was defined as kEGS = 2.5 × 10−14 m2, representing the averaged value of Soultz (6 × 10−14 m2), Ogachi, and a system-scale permeability of 1.1 × 10−14 m2. This value was utilized for the purpose of CPG Additional Case parameters (Section 3.1).
Observations revealed that as temperature and pressure decrease over time, the CPG system demonstrates higher heat extraction rates compared to H2O-based systems (EGS and reservoir). This indicates that the CPG approach is notably beneficial in, although not limited to, relatively shallow geologic formations. However, to guarantee adequate subsurface temperatures at which CO2 remains in its supercritical phase, minimum depths are required [10].
3.2.1. Numerical Analysis Findings
The simulation results regarding the heat extraction rates (H) for both Base/Additional Cases of different systems, including CPG, H2O reservoir, CO2-based EGS, and H2O-based EGS, on average in a 5-spot well system, are represented in Figure 4 [10]. It is observed that the Base Case of the CPG model (100 °C/250 bar) has a significant heat extraction rate of about 47 MW, which is very close to Case 5 of the CO2-EGS model (100 °C/250 bar) with H = 45.8 MW. However, the highest H is noted in Case 2 of the CPG model (140 °C/250 bar) with H = 68.8 MW. The two Additional Cases (Cases 6* and 7*) of the CPG model also generate high levels of heat extraction rate with H = 62.6 MW and H = 64.1 MW, respectively. The total simulation results for the traditional H2O reservoir and H2O-EGS show relatively smaller average H for Cases 1–4, while CO2-EGS approaches CPG.
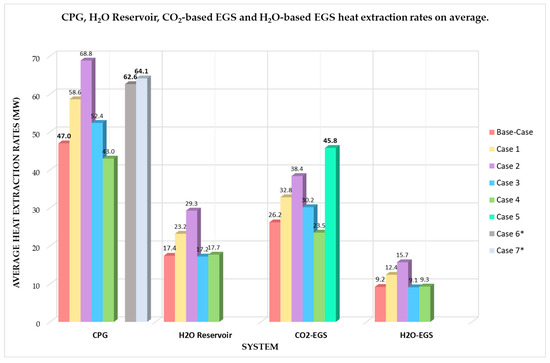
Figure 4.
Average simulation results for the heat extraction rate (H) across all parameter cases of CPG, H2O reservoir, CO2-based EGS, and H2O-based EGS over the 25-year life of the system.
While it is possible to employ technology to tap into geothermal resources with water temperatures below 100 °C, around 90% of the installed capacity in the United States predominantly utilizes dry steam or flash power systems, requiring subsurface temperatures exceeding 150 °C. According to Randolph and Saar’s [10] model simulations, it is noticed that the heat extraction energy for the Base Case parameters of a traditional H2O-based geothermal reservoir system, installed in a single 5-spot well configuration at 150 °C and a depth of 2.5 km with an averaged permeability of 5 × 10−14 m2, is approximately 46 MW. This corresponds to 5.2 MW of electricity, as calculated by Carnot with a 10 °C average annual heat rejection temperature and 50% power system efficiency (modified after [69]). It is observed that a CPG system with identical parameters has the potential to generate equivalent electrical production at a geologic temperature as low as 98.2 °C. Similarly, the geologic temperature of 100 °C in H2O-based geothermal reservoir systems corresponds to the required temperature of 65.8 °C for CPG systems for the same production of electricity.
These results illustrate that in regions with comparatively low geothermal temperatures and heat flow rates, where adequate reservoirs are available, CPG offers viable geothermal energy resources for electricity production. Under a wide range of circumstances, it significantly surpasses the performance of CO2-EGS, not to mention conventional H2O-based reservoirs or H2O-EGS approaches, all the while concurrently storing CO2 [10]. In Figure 5 and Figure 6, the ratios of the average heat extraction (H) and mass flow (MF) rates of the CPG-H2O reservoir, CO2-EGS, and H2O-EGS are represented, respectively. It is crucial to highlight that the CPG difference in heat extraction ratio for all simulation cases on average is 1.8 times higher than that of CO2-EGS, 2.6 times higher than that of the traditional H2O geothermal reservoir, and 4.9 times higher than that of H2O-EGS, as seen in the trendlines in Figure 5.
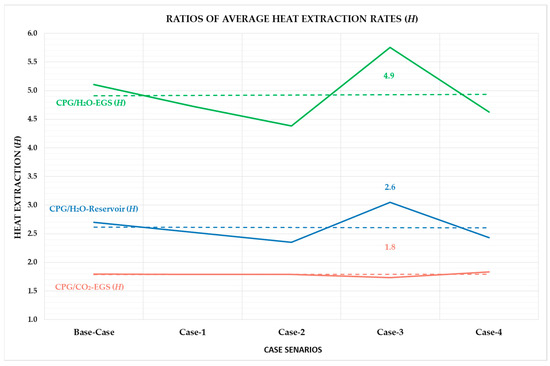
Figure 5.
Simulation results as CPG ratios of average heat extraction rate (H) to H2O reservoir, CO2-based EGS, and H2O-based EGS for Cases 1–4.
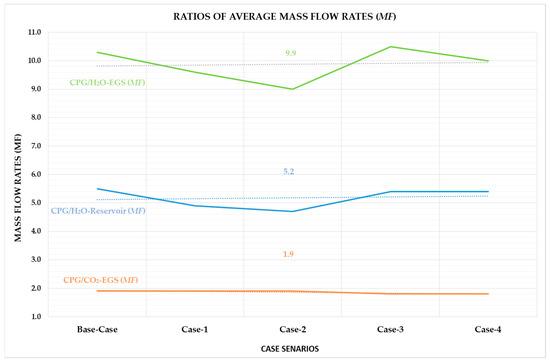
Figure 6.
Simulation results as CPG ratios of average mass flow rate (MF) to H2O reservoir, CO2-based EGS, and H2O-based EGS for Cases 1–4.
3.2.2. CO2 Mobility
As mentioned in Section 2.3, CO2 has higher mobility than water, providing several advantageous characteristics as a working fluid in geothermal systems. Mobility describes the tendency of a fluid to maintain its momentum during flow. It can be defined by dividing fluid density by the inverse of kinematic viscosity (or dynamic viscosity). Despite CO2 having a lower thermal capacity than H2O under the same temperature and pressure conditions, its higher mobility leads to increased fluid mass flow, resulting in higher heat extraction. This minimizes the permeability threshold at which heat advection tends to dominate over conduction [70].
The use of a CPG working fluid, characterized by its higher mobility (3.5 times higher, on average) compared to H2O, broadens the spectrum of natural formation permeability. Consequently, this reduces the economically and technologically viable subsurface temperature threshold. Therefore, the development of CPG has the potential to facilitate the expansion of geothermal energy in reservoirs with lower permeabilities than those that are feasible with water-based geothermal systems [17].
3.2.3. CPG Electricity Production Calculation
Calculating the value of energy captured by CPG (electricity production) in relation to CCS is crucial for enhancing the economic feasibility of the CO2 sequestration component in deep saline aquifers. For this reason, Randolph and Saar [18] estimated the value of energy captured per ton of injected CO2. This paper only focuses on the methodology they used to calculate power production (W). Gross revenue (R) is not analyzed here.
To be more specific, they first determined the total amount of CO2 sequestered over a 25-year period of CPG power plant operation by applying the parameters relevant to the Base Case scenario (Section 3.1). The examined geothermal reservoir (Base Case) had to be filled with CO2 in 10% of its total area prior to the production process (pre-injection process). This corresponded to around 6 months under a continuous injection rate of 280 kg/s [18]. However, the production well configuration could not recover all of the injected CO2 during operation of the power plant. Thus, 7% of the average injection rate (non-recoverable) had to be regularly refilled. This non-recoverable CO2 (fluid loss) represents the system’s CO2 sequestration component, and it is thought to be permanently stored within the geologic formation (CO2 storage). It is essential to underline that, according to Pruess [5], these fluid losses (initially higher during early plant operation and gradually diminishing over time) are considered to account for about 5% of the injection rate throughout the extended operation of CO2-based EGS. Anticipated higher fluid loss values are expected in naturally permeable formations and were taken into account in the CPG system simulation.
Ultimately, since the CO2 circulating through the above-ground power plant system is reinjected, all of the CO2 injected into the reservoir is permanently sequestered (except for the upward leakage through the caprock, if any) [18]. Therefore, in the Base Case, the overall CO2 sequestration over the 25-year simulation of the CPG power plant was theoretically 2 × 107 tons.
To begin with, applying the Carnot efficiency (C)—representing the maximum theoretical amount of thermal energy that can be converted into mechanical work—along with the mechanical system utilization efficiency (E) and energy extraction rate (H), electricity production (W) is defined in the following Equation (5):
In terms of Carnot efficiency (6) for the Base Case, Treservoir was equal to 373.15 K (100 °C + 273.15) and Trejection was equal to 283 K (10 °C + 273.15), determined by the approximate average yearly surface temperature in the northern United States [71]. So, calculating C = 0.24 and applying H = 47 MW (Figure 4) and E = 50% (modified after [69]) to Equation (5), the total electricity production for the Base Case was calculated to be W = 5.7 MWe [18]. Similar calculations were also made for the CPG Additional Cases, and their results are presented in Table 1. The maximum value of electricity production corresponded to Case 2 (140 °C, 250 bar) with W = 10.8 MWe. However, the elevated temperature of 140 °C may pose a limitation, as it might not be accessible in most locations.

Table 1.
Calculated CPG electricity production (W) for all case parameters, applying Carnot efficiency.
4. CO2 versus H2O and Native Brine
Randolph and Saar [17] also conducted a simulation to distinguish the impact of reservoir permeability on geothermal energy production from natural reservoirs. This involved the selection of a subsurface working fluid, with options including CO2, water, and native brine.
4.1. Numerical Simulation Methodology
To begin, numerous assumptions and simplifications were required to specify the reservoir fluid behavior. Specifically, Randolph and Saar [17] assumed there was sufficient geologic formation injectivity and productivity in the bottom-hole area around the wells to determine the injection/production rate. Although injectivity and productivity are crucial factors, the emphasis was on reservoir-scale features.
Under several permeability selections (ranging from 5 × 10−16 m2 to 5 × 10−12 m2 [52,62]), the simulation was conducted using the following working fluids:
- CO2
- Pure water (H2O)
- 20% mass fraction NaCl brine (brine)
Similar to other CPG investigations (Section 3), each numerical model’s pore space used one only fluid. All simulations were conducted using the reservoir simulator TOUGH2 [60] with the fluid property module ECO2N [61].
The Base Case parameters for the simulation models of the three examined working fluids were identical to those for the CPG Base Case (Section 3.1), with the exception of reservoir porosity (10%), heat extraction rate (43.6 MW), average annual surface temperature (12 °C), and heat rejection surface temperature (22 °C). It is important to note that heat rejection surface temperature assumes a prudent value for the heat rejection efficiency of binary geothermal systems [72]. This temperature is typically 10 °C above the average annual atmospheric temperature [71]. Hydrostatic pressures occur under reservoir conditions characterized by such low temperatures and heat flow rates [73]. The geothermal power system is considered a binary system due to its low resource temperatures (T < 150 °C) [73], often employing a variation of the “Organic Rankine Cycle” (OCR). Nevertheless, because of the low critical point of CO2 (31.03 °C, 71.778 bar), it is utilized directly in a turbine.
The fluid production temperature was assumed to be constant, and the pressure drop through the surface equipment was ignored [17]. Furthermore, to maintain single-phase conditions in surface equipment, the surface pressure of CO2 injection was adjusted to be 10 bar above the saturation pressure (60 bar) at the wellhead temperature during injection [17]. Newtonian iteration was employed to estimate the T and P profiles for CO2 in the injection well, starting with the T and p values at the surface. It is essential to highlight that, for a more realistic perspective of long-term fluid behavior in the injection and production wells, fluid flow was considered to be isenthalpic for the temperature and pressure conditions [5]. This approximation takes into account temperature changes resulting from the (de-)compression of fluids, commonly referred to as the “Joule–Thomson effect” [74]. This effect is important in CO2 simulations due to the large compressibility of sCO2 (Section 2.3). In contrast, H2O and brine were characterized as relatively incompressible liquids under the examined conditions, exhibiting practically isothermal flow within the well.
As stated by Randolph and Saar [17]: “in certain CPG systems, a throttling valve could be used to sufficiently decrease pressure between injection and production wellheads, whereas in H2O/brine and other CPG cases (e.g., very low reservoir permeability), additional pumping may be needed.”
Therefore, the injection/production pumping power (p) had to be calculated [75]:
where q is the total flow, ΔP is the necessary pressure to ensure the q rate, ρ is the fluid density, and η is the pump efficiency.
Applying η = 0.9 (modified from [73]) and assuming the use of downhole shaft pumps, the pump depth was constrained to 450 m [73]. Consequently, in models involving H2O and brine, the presumption of hydrostatic reservoir conditions sets a lower limit of about 205 bar on the pressure at the bottom-hole production well, ensuring that the fluid reaches the downhole production pump [17]. In simulations, any extra pressure difference between the injection and production wells must originate from the injection side, and the production bottom-hole pressure is not allowed to drop below 210 bar [17]. In CPG models, ppump = 0 if the pressure at the production wellhead is greater than the pressure at the injection wellhead (see Section 2.3, thermosiphon effect) [17].
Some other constraints established in the system included a constant bottom-hole pressure difference between the injection and production wells and a constant production mass flow rate across all fluids. However, to distinguish the effects of reservoir permeability (k) from variations in fluid mobility (inverse kinematic viscosity, Section 3.2.2) and heat capacity, it is significant to establish the heat energy extraction rate from the reservoir between fluids for a specific reservoir permeability [17,18,19]. The Base Case simulations were applied to calculate the mass flow rate for each working fluid at the same permeability of 5 × 10−14 m2. It is important to note that these simulations do not optimize power plant electricity production for each permeability and fluid, but compare various reservoir fluids at various permeabilities over constant fluid flow-mass rates. The pressure drops through the reservoir, starting with the CO2 case with a pressure drop of 20 bar, determine the mass flow rate for each fluid. This mass flow rate then remains constant by adjusting the pressure drop while the permeability changes in the H2O/brine case [17].
4.2. Electricity Efficiency versus Permeability
Electricity efficiency (e) at the production process is defined by the following Equation (8):
where Wnet is the net electricity production rate, Htotal is the total heat energy extraction rate, W is the total electricity production rate, p is the injection/production pumping power, and m is the total mass flow.
In Figure 7, it is demonstrated how the properties of sCO2 (mobility, heat capacity, compressibility) collaborate to enhance the electricity production efficiency (e) at different reservoir permeabilities versus H2O and NaCl brine. More specifically, for:
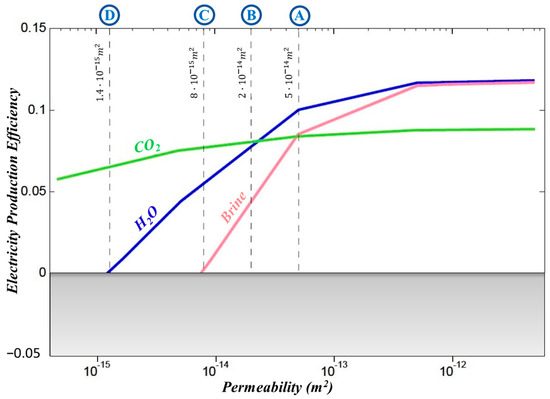
Figure 7.
Numerical simulation results of electricity production efficiency (e) related to reservoir permeability (k) for the three examined working fluids (CO2, H2O, and 20% NaCl brine).
- k < 10−15 m2: Water has negative efficiency, but CO2 is generally stable (Figure 7D);
- k = 8 × 10−15 m2: CO2 produces an efficiency that is around 50% greater than H2O, while brine moves into the negative efficiency zone (Figure 7C);
- k > 2 × 10−14 m2: Pure H2O is more efficient than CO2 (Figure 7B);
- k > 5 × 10−14 m2: NaCl brine provides higher power efficiency than CO2 (Figure 7A).
It is observed that for larger permeabilities (k > 2 × 10−14 m2), H2O and NaCl brine have slightly higher power efficiencies than CO2 due to their relatively high heat capacities and low compressibilities. Particularly, above extremely high permeabilities (k > 5 × 10−14 m2), H2O’s and brine’s pumping powers approach zero and their power production efficiencies (e) stabilize (stop varying with k). Conversely, at moderate-to-low permeabilities (10−16 < k < 10−14 m2) the high mobility of CO2 becomes advantageous, diminishing pumping power needs and leading to higher mass flow rates. Moreover, net power production from H2O, let alone brine, is not feasible, while the efficiency of CO2 is slightly reduced [17]. Considering specific hydraulic head gradients, kinematic water viscosities, and water heat capacities at the relevant temperatures and pressures, the minimum permeability range required for heat advection in H2O or brine is 5 × 10−17 < kmin < 10−15 m2 [70,76].
To investigate the impact of permeability on electricity production efficiency (e) under various temperature and pressure conditions, Randolph and Saar [17] conducted a multitude of simulations at numerous points along two different geothermal gradients (35 and 60 °C/km).
4.3. Simulation Results
In light of the observations presented above and simulations of geothermal development in sedimentary basins [17], the recommended reservoir permeability for economical geothermal developments is k < 2 × 10−14 m2 (moderate-to-low permeability formations). This value is influenced by the compaction of sediments and hydrothermal alteration, leading to pore space clogging [52,62]. Moreover, even at swallower depths, k can be exceptionally low in crystalline rocks [17].
For the Base Case parameters T, P, and k (100 °C, 250 bar, and 5 × 10−14 m2, respectively), the net electricity production rate (Wnet) and thermal utilization efficiency, were calculated to be 3664 kW and 8.4%, respectively. Assuming 90% system efficiency and 93% turbine efficiency, Wnet became 4170 kW and the thermal utilization efficiency was 9.6% for the direct, Base Case CO2 system [17]. The direct system efficiency may be proportionately much greater at higher resource temperatures and pressures, especially when the wellhead pressure difference is significantly increased.
5. Sustainable Energy Communities
Energy communities represent a forward-thinking approach to residential development, emphasizing sustainability and community engagement [6]. These innovative neighborhoods prioritize energy efficiency and environmental consciousness, employing renewable energy sources, energy-efficient technologies, and eco-friendly construction practices. Architectural designs incorporate passive solar principles, advanced insulation, and ventilation systems. The integration of solar panels, wind turbines, and geothermal systems ensures clean and sustainable power generation, reducing reliance on traditional fossil fuels and minimizing the community’s carbon footprint [77]. Geothermal systems, in particular, play a crucial role by harnessing Earth’s natural heat for heating and cooling, offering significant energy savings and a lower environmental impact compared to conventional systems [78]. The longevity and lower maintenance requirements of geothermal systems contribute to the overall sustainability and resilience of these communities.
Implementing geothermal technology in energy communities aligns with the principles of sustainable development, providing a reliable, eco-friendly, and cost-effective solution for heating and cooling needs [79]. This approach requires a comprehensive feasibility study and collaboration with experienced professionals to ensure successful integration into the community’s infrastructure [6]. By prioritizing renewable energy sources and embracing environmentally conscious practices, energy communities set a precedent for responsible and sustainable living, fostering a harmonious coexistence between human habitation and environmental preservation.
A relevant example of an energy-efficient community is the “Beddington Zero Energy Development” (BedZED) in the UK. Situated in Hackbridge, South London, BedZED is an environmentally friendly housing development consisting of 100 homes, community facilities, and sufficient workspace for 100 people. This pioneering eco-village incorporates various renewable energy sources, including solar panels (777 m2) and wind turbines, to generate electricity for the entire community. The average electricity consumption per square meter (m2) here does not exceed 34.4 kWh/year, while the average heating and hot water consumption does not exceed 48 kWh/year, respectively [80].
The Vauban neighborhood in Freiburg, Germany, serves as another model of sustainable urban planning, emphasizing passive house design principles. Boasting well-insulated buildings and efficient ventilation systems, it minimizes reliance on conventional heating and cooling methods. Additionally, Vauban incorporates renewable energy sources, significantly reducing its dependence on non-renewable energy. Situated on a 380,404 m2 site that was once a French military base, its thriving community has nearly 5100 residents living in around 2000 buildings. The average electricity consumption per square meter (m2) in Vauban is an impressive 15 kWh/year. This transformation highlights the successful adaptive reuse of a former military facility, showcasing how urban spaces can evolve to meet modern environmental and social challenges [81].
Additionally, Malmö, Sweden, deserves recognition for its commitment to sustainability, with a focus on the “Western Harbour (Västra Hamnen)” district. A notable showcase of sustainable urban development in this district is the “Flagghusen block”, covering an area of 40,000 m2 and featuring 16 buildings with around 600 residences, of which two-thirds are available for public rentals. The construction project prioritized housing diversity, specifically aiming to provide affordable options for low- and middle-income residents. The design of the buildings was guided by community preferences, including a height restriction of under 25 m. Notably, energy conservation measures were implemented, with a stipulation that the energy consumption per square meter (m2) should not exceed 120 kW/year, underscoring a strong commitment to sustainability [82].
Assuming an average consumption for these examples of approximately 56 kWh/m2/year and average residence area of 50 m2, it is calculated that the average annual consumption for a household is approximately 3 MWh, enough to be captured by a CPG system with an annual average electricity production of 5 × 104 MWh.
It is imperative to acknowledge that the calculations presented herein serve as approximate estimates, and real-world outcomes may deviate due to an array of factors. Notable among these factors are the efficiency of the geothermal system, considerations related to maintenance practices, and losses incurred during the distribution of power. Furthermore, it is pertinent to recognize that the assumption of continuous, uniform power production, while useful for illustrative purposes, diverges from the nuanced reality of geothermal systems, where variations in operational states and power production levels are commonplace.
5.1. CPG Challenges
While the energy data presented above are theoretical, a detailed examination is necessary due to its practical complexities. Achieving a comprehensive understanding of community energy consumption involves considerations such as architectural design, renewable energy integration, and advanced technologies like combined heat and power systems. A holistic approach to assessing and improving energy consumption in a community involves considering the interplay of these factors. Each community may have unique characteristics, and a tailored strategy based on local conditions and priorities is often essential. Regular monitoring, evaluation, and adaptation of strategies are crucial for the long-term sustainability of energy communities.
CPG plays a substantial role in energy communities, particularly in addressing distinct heating and electricity power needs. The critical parameter influencing its effectiveness is the location’s proximity. The sustainable scenario for optimal CPG operation is closely tied to the community’s location, a challenge given Earth’s geothermal heat flux limitations in specific areas. Regions considered CPG-viable might be conservative, not factoring in the efficiency benefits associated with using CO2 instead of water in a power cycle. For instance, CO2 turbines can operate at higher pressure, potentially boosting efficiency. Moreover, CO2 freezing at temperatures below 0 °C in cool climates could enhance electricity production potential. The potential of a CO2 thermosiphon and its impact on pumping costs are not explored in this analysis [12].
Furthermore, CPG technology may pose some other certain limitations that need to be highlighted. In CPG research, it is thought that the produced fluid from production wells may not contain native brine or H2O, a parameter that does not occur in real life. In the initiation of a new CPG approach, the subsurface reservoir might be filled with brine or retain residual brine, leading to the potential co-production of water and CO2 in the production well. However, a significant challenge lies in preventing the occurrence of CO2 mixtures within the thermosiphon. The production of wet CO2, containing dissolved H2O, can elevate fluid temperatures and pressures at production wellheads due to the exothermic release of H2O from CO2 [30]. Although the circulation of dry CO2 strengthens the thermosiphon effect, the production of mixed fluids may weaken it. Despite this, the higher temperatures and pressures associated with wet CO2 can enhance electric power output by 15–25% compared to 100% CO2.
Moreover, sedimentary formations exhibit heterogeneities in porosity, permeability, mineralogy, thickness, and other parameters. Previous modeling has assumed homogeneous reservoirs, neglecting variations in these properties that may have a substantial impact on the overall heat extraction. Further exploration of the complexity of such systems by considering geological heterogeneity or assuming a multi-layered reservoir, as described by Garapati et al. [24], represents an important direction for advancing research in geothermal heat extraction. This aspect will be analyzed in future work.
The subsurface variations in sedimentary basin aquifers play a crucial role in heat transfer, affecting facility performance. Three-dimensional unconformities and permeability variations create “thief zones” with higher permeability, allowing increased heat extraction. However, regions with lower permeability can hinder flow rates and reduce heat extraction efficiency. Key questions remain regarding optimal heat extraction rates, CO2 replenishment, and their impact on geothermal power generation. Uncertainties in CO2 supplies may present challenges or opportunities for geological carbon sequestration (GCS). The effects of reservoir characteristics on operational costs and energy storage efficiency are not adequately considered. Addressing these challenges could unlock significant CO2 mitigation and power system service potential [83].
6. Conclusions
In light of the studies and analyses presented above, it is indisputable that, according to fluid-mechanical simulations, CO2 is a really interesting heat exchange fluid due to its consistently higher mobility than H2O under the specific temperature and pressure conditions of interest. CPG systems demonstrate higher geothermal heat extraction rates compared to both hydrothermal and water-based EGS, even at lower temperatures and pressures, under the consideration that there are sufficient temperatures at these depths and CO2 remains in its supercritical form. CPG heat mining is more extensive than EGS mainly because it sustains higher temperature profiles for a longer time period at geothermal production wells. Other advantages over EGS include:
- It does not rely on hydraulic fracturing or rock stimulation to improve permeability but utilizes existing highly permeable and porous geological reservoirs, thereby avoiding microseismicity.
- Natural reservoirs are considerably larger in size than those formed through hydraulic fracturing.
As analyzed in Section 4, subsurface formation permeability (k) has a considerable impact on the net generation of geothermal power. Numerical simulations have shown that for low-to-moderate reservoir permeabilities (k < 2 × 10−14 m2), CO2 provides higher power generation efficiencies than H2O and NaCl brine systems, and slightly lower efficiencies for higher permeability values (k > 5 × 10−14 m2) always depend on formation temperature and pressure. Furthermore, CPG reservoir temperatures of about 65.8 °C and 98.2 °C may yield the same electrical power as H2O-based reservoir temperatures of 100 °C and 150 °C, respectively, under the same reservoir parameters and injection/production pressure conditions (Section 3.2.1). This means that CPG systems can offer higher electricity generation than traditional geothermal systems under given temperature and pressure conditions.
According to the energy demands of the buildings in energy communities, CPG systems utilizing CO2 as a working fluid present a highly efficient and environmentally friendly solution for powering these sustainable environments. With superior energy capture efficiency compared to traditional geothermal methods, as mentioned above, the CPG system ensures reliable and continuous electricity generation. Its reduced environmental impact aligns with sustainability goals, contributing to lower greenhouse gas emissions. The technology’s adaptability to various geological settings enhances its applicability, while integration with smart grids optimizes energy distribution. Community engagement and education initiatives can further promote the technology’s acceptance. Assessing economic viability is crucial for its long-term success.
In conclusion, CPG emerges as a promising and scalable solution, poised to play a key role in powering the sustainable communities of the future. However, further research in this field is needed to overcome the limitations described in Section 5.1.
7. Future Objectives
The goal of this review paper was to present some of the CPG specifications discussed in the scientific community, providing a new perspective on the extracted energy in comparison with the demands of an integrated energy built environment system. While the paper primarily explores conventional CPG technologies, it is important to note that certain advancements, such as integrating CPG with direct air CO2 [84,85] or coupling it with natural gas recovery [27,74], could potentially enhance energy outputs, although these are not analyzed in this paper.
In future research, the CPG system, as suggested by Randolph and Saar, will be optimized with the intention of providing sustainable and renewable methods tailored for the creation of net-zero energy communities. Achieving net-zero energy status involves a holistic approach that integrates CPG systems seamlessly into the built environment. Key parameters to be considered in this optimization process include the necessary CO2 volume for CPG system formation, operating temperature, depth, desired power production ratio, 5-spot reservoir impedance, and heat losses. Furthermore, the optimal location for CPG construction to achieve the best performance in a nearly sustainable built community will be thoroughly analyzed. These aspects will be subject to further simulation analysis to refine and improve CPG technologies. The success of this endeavor relies on meticulous planning, efficient energy extraction, and minimizing environmental impacts.
In summary, this review paper not only presents current CPG specifications but also sets the stage for future research endeavors geared towards optimizing these systems. The overarching aim is to contribute to the development of sustainable and renewable energy solutions, ultimately paving the way for the realization of net-zero energy communities.
Author Contributions
Conceptualization, G.A.; methodology, G.A.; software, G.A.; validation, G.A.; formal analysis, G.A.; investigation, G.A.; resources, I.K.; writing—original draft preparation, G.A.; writing—review and editing, I.K.; visualization, G.A.; supervision, I.K.; project administration, I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any external funding.
Data Availability Statement
Available after request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, D.W. A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 January 2000. [Google Scholar]
- Bielinski, A. Numerical Simulation of CO2 Sequestration in Geological Formations; Mitteilungen; Institut für Wasserbau, Universität Stuttgart: Stuttgart, Germany, 2007; ISBN 978-3-933761-58-3. [Google Scholar]
- Davison, J. Performance and Costs of Power Plants with Capture and Storage of CO2. Energy 2007, 32, 1163–1176. [Google Scholar] [CrossRef]
- Lee, I.; Tester, J.W.; You, F. Systems Analysis, Design, and Optimization of Geothermal Energy Systems for Power Production and Polygeneration: State-of-the-Art and Future Challenges. Renew. Sustain. Energy Rev. 2019, 109, 551–577. [Google Scholar] [CrossRef]
- Pruess, K. Enhanced Geothermal Systems (EGS) Using CO2 as Working Fluid—A Novel Approach for Generating Renewable Energy with Simultaneous Sequestration of Carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Massachusetts Institute of Technology (Ed.) The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century: An Assessment; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; ISBN 978-0-615-13438-3. [Google Scholar]
- Pruess, K.; Spycher, N. Enhanced Geothermal Systems (EGS) with CO2 as Heat Transmission Fluid—A Scheme for Combining Recovery of Renewable Energy with Geologic Storage of CO2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2010. [Google Scholar]
- Adams, B.; Fleming, M.R.; Bielicki, J.M.; Garapati, N.; Saar, M.O. An Analysis of the Demonstration of a CO2-Based Thermosiphon at the SECARB Cranfield Site. In Proceedings of the 46th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 16–18 February 2021. 9p. [Google Scholar]
- Socolow, R.H.; Pacala, S.W. A Plan to Keep Carbon in Check. Sci. Am. 2006, 295, 50–57. [Google Scholar] [CrossRef]
- Randolph, J.B.; Saar, M.O. Combining Geothermal Energy Capture with Geologic Carbon Dioxide Sequestration. Geophys. Res. Lett. 2011, 38, L10401. [Google Scholar] [CrossRef]
- Adams, B.; Ogland-Hand, J.; Bielicki, J.M.; Schädle, P.; Saar, M. Estimating the Geothermal Electricity Generation Potential of Sedimentary Basins Using genGEO (The Generalizable GEOthermal Techno-Economic Simulator). Chemistry 2021. [Google Scholar] [CrossRef]
- Atrens, A.D.; Gurgenci, H.; Rudolph, V. CO2 Thermosiphon for Competitive Geothermal Power Generation. Energy Fuels 2009, 23, 553–557. [Google Scholar] [CrossRef]
- Atrens, A.D.; Gurgenci, H.; Rudolph, V. Electricity Generation Using a Carbon-Dioxide Thermosiphon. Geothermics 2010, 39, 161–169. [Google Scholar] [CrossRef]
- Beckers, K.F.; Lukawski, M.Z.; Anderson, B.J.; Moore, M.C.; Tester, J.W. Levelized Costs of Electricity and Direct-Use Heat from Enhanced Geothermal Systems. J. Renew. Sustain. Energy 2014, 6, 013141. [Google Scholar] [CrossRef]
- Glanz, J. Deep in Bedrock, Clean Energy and Quake Fears. New York Times, 23 June 2009. [Google Scholar]
- Pruess, K. Role of Fluid Pressure in the Production Behavior of EnhancedGeothermal Systems with CO2 as Working Fluid; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2007; p. LBNL--62611. [Google Scholar]
- Randolph, J.B.; Saar, M.O. Impact of Reservoir Permeability on the Choice of Subsurface Geothermal Heat Exchange Fluid: CO2 versus Water and Native Brine. Geotherm. Resour. Counc. Trans. 2011, 35, 521–526. [Google Scholar]
- Randolph, J.B.; Saar, M.O. Coupling Carbon Dioxide Sequestration with Geothermal Energy Capture in Naturally Permeable, Porous Geologic Formations: Implications for CO2 Sequestration. Energy Procedia 2011, 4, 2206–2213. [Google Scholar] [CrossRef]
- Randolph, J.B.; Saar, M.O. Coupling Geothermal Energy Capture with Carbon Dioxide Sequestration in Naturally Permeable, Porous Geologic Formations: A Comparison with Enhanced Geothermal Systems. GRC Trans. 2010, 34, 433–438. [Google Scholar]
- Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Randolph, J.B.; Saar, M.O. On the Importance of the Thermosiphon Effect in CPG (CO2 Plume Geothermal) Power Systems. Energy 2014, 69, 409–418. [Google Scholar] [CrossRef]
- Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Randolph, J.B.; Saar, M.O. A Comparison of Electric Power Output of CO2 Plume Geothermal (CPG) and Brine Geothermal Systems for Varying Reservoir Conditions. Appl. Energy 2015, 140, 365–377. [Google Scholar] [CrossRef]
- Adams, B.M.; Vogler, D.; Kuehn, T.H.; Bielicki, J.M.; Garapati, N.; Saar, M.O. Heat Depletion in Sedimentary Basins and Its Effect on the Design and Electric Power Output of CO2 Plume Geothermal (CPG) Systems. Renew. Energy 2021, 172, 1393–1403. [Google Scholar] [CrossRef]
- Garapati, N.; Randolph, J.B.; Saar, M.O. Total Heat Energy Output From, Thermal Energy Contributions To, and Reservoir Development of CO2 Plume Geothermal (CPG) Systems. In Proceedings of the Thirty-Ninth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24 February 2014. [Google Scholar]
- Garapati, N.; Randolph, J.B.; Valencia, J.L.; Saar, M.O. CO2-Plume Geothermal (CPG) Heat Extraction in Multi-Layered Geologic Reservoirs. Energy Procedia 2014, 63, 7631–7643. [Google Scholar] [CrossRef]
- Garapati, N.; Randolph, J.B.; Saar, M.O. Brine Displacement by CO2, Energy Extraction Rates, and Lifespan of a CO2-Limited CO2-Plume Geothermal (CPG) System with a Horizontal Production Well. Geothermics 2015, 55, 182–194. [Google Scholar] [CrossRef]
- Garapati, N.; Adams, B.M.; Fleming, M.R.; Kuehn, T.H.; Saar, M.O. Combining Brine or CO2 Geothermal Preheating with Low-Temperature Waste Heat: A Higher-Efficiency Hybrid Geothermal Power System. J. CO2 Util. 2020, 42, 101323. [Google Scholar] [CrossRef]
- Ezekiel, J.; Ebigbo, A.; Adams, B.M.; Saar, M.O. Combining Natural Gas Recovery and CO2-Based Geothermal Energy Extraction for Electric Power Generation. Appl. Energy 2020, 269, 115012. [Google Scholar] [CrossRef]
- Ezekiel, J.; Kumbhat, D.; Ebigbo, A.; Adams, B.M.; Saar, M.O. Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems. Energies 2021, 14, 6122. [Google Scholar] [CrossRef]
- Ezekiel, J.; Adams, B.M.; Saar, M.O.; Ebigbo, A. Numerical Analysis and Optimization of the Performance of CO2-Plume Geothermal (CPG) Production Wells and Implications for Electric Power Generation. Geothermics 2022, 98, 102270. [Google Scholar] [CrossRef]
- Fleming, M.R.; Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Saar, M.O. Increased Power Generation Due to Exothermic Water Exsolution in CO2 Plume Geothermal (CPG) Power Plants. Geothermics 2020, 88, 101865. [Google Scholar] [CrossRef]
- Fleming, M.R.; Adams, B.M.; Ogland-Hand, J.D.; Bielicki, J.M.; Kuehn, T.H.; Saar, M.O. Flexible CO2-Plume Geothermal (CPG-F): Using Geologically Stored CO2 to Provide Dispatchable Power and Energy Storage. Energy Convers. Manag. 2022, 253, 115082. [Google Scholar] [CrossRef]
- Saar, M.O.; Buscheck, T.A.; Jenny, P.; Garapati, N.; Randolph, J.B.; Karvounis, D.C.; Chen, M.; Sun, Y.; Bielicki, J.M. Numerical Study of Multi-Fluid and Multi-Level Geothermal System Performance. In Proceedings of the World Geothermal Congress, New Zealand, Australia, 16–24 April 2015. [Google Scholar]
- Hefny, M.; Qin, C.; Saar, M.O.; Ebigbo, A. Synchrotron-Based Pore-Network Modeling of Two-Phase Flow in Nubian Sandstone and Implications for Capillary Trapping of Carbon Dioxide. Int. J. Greenh. Gas Control 2020, 103, 103164. [Google Scholar] [CrossRef]
- Van Brummen, A.C.; Adams, B.M.; Wu, R.; Ogland-Hand, J.D.; Saar, M.O. Using CO2-Plume Geothermal (CPG) Energy Technologies to Support Wind and Solar Power in Renewable-Heavy Electricity Systems. Renew. Sustain. Energy Transit. 2022, 2, 100026. [Google Scholar] [CrossRef]
- Schifflechner, C.; Wieland, C.; Spliethoff, H. CO2 Plume Geothermal (CPG) Systems for Combined Heat and Power Production: An Evaluation of Various Plant Configurations. J. Therm. Sci. 2022, 31, 1266–1278. [Google Scholar] [CrossRef]
- Norouzi, A.M.; Pouranian, F.; Rabbani, A.; Fowler, N.; Gluyas, J.; Niasar, V.; Ezekiel, J.; Babaei, M. CO2-Plume Geothermal: Power Net Generation from 3D Fluvial Aquifers. Appl. Energy 2023, 332, 120546. [Google Scholar] [CrossRef]
- Gupta, N.; Vashistha, M. Carbon Dioxide Plume Geothermal (CPG) System-A New Approach for Enhancing Geothermal Energy Production and Deployment of CCUS on Large Scale in India. Energy Procedia 2016, 90, 492–502. [Google Scholar] [CrossRef]
- McDonnell, K.; Molnár, L.; Harty, M.; Murphy, F. Feasibility Study of Carbon Dioxide Plume Geothermal Systems in Germany–Utilising Carbon Dioxide for Energy. Energies 2020, 13, 2416. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, J.; Gong, Y.; Wang, Y.; Ma, W. Energy Efficiency Comparison between Geothermal Power Systems. Therm Sci 2017, 21, 2633–2642. [Google Scholar] [CrossRef]
- Moya, D.; Aldás, C.; Kaparaju, P. Geothermal Energy: Power Plant Technology and Direct Heat Applications. Renew. Sustain. Energy Rev. 2018, 94, 889–901. [Google Scholar] [CrossRef]
- Muffler, P.; Cataldi, R. Methods for Regional Assessment of Geothermal Resources. Geothermics 1978, 7, 53–89. [Google Scholar] [CrossRef]
- Gallup, D.L. Production Engineering in Geothermal Technology: A Review. Geothermics 2009, 38, 326–334. [Google Scholar] [CrossRef]
- Barbier, E. Geothermal Energy Technology and Current Status: An Overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Von Jouanne, A.; Brekken, T.K.A. Ocean and Geothermal Energy Systems. Proc. IEEE 2017, 105, 2147–2165. [Google Scholar] [CrossRef]
- Sanyal, S.K. Future of geothermal energy. In Proceedings of the Thirty-Fifth Workshop on Geothermal Reservoir Engineering; Stanford University, Stanford, CA, USA, 1–3 February 2010. [Google Scholar]
- Evans, K.F.; Moriya, H.; Niitsuma, H.; Jones, R.H.; Phillips, W.S.; Genter, A.; Sausse, J.; Jung, R.; Baria, R. Microseismicity and Permeability Enhancement of Hydrogeologic Structures during Massive Fluid Injections into Granite at 3 Km Depth at the Soultz HDR Site: Induced Seismicity and Flow in Deep Granite. Geophys. J. Int. 2004, 160, 389–412. [Google Scholar] [CrossRef]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced Seismicity Associated with Enhanced Geothermal Systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Pan, S.-Y.; Gao, M.; Shah, K.J.; Zheng, J.; Pei, S.-L.; Chiang, P.-C. Establishment of Enhanced Geothermal Energy Utilization Plans: Barriers and Strategies. Renew. Energy 2019, 132, 19–32. [Google Scholar] [CrossRef]
- Sun, F.; Yao, Y.; Li, G.; Li, X. Performance of Geothermal Energy Extraction in a Horizontal Well by Using CO2 as the Working Fluid. Energy Convers. Manag. 2018, 171, 1529–1539. [Google Scholar] [CrossRef]
- Tianfu, X.; Guanhong, F.; Yan, S.; Hongwu, L. Use of CO2 as Heat Transmission Fluid to Extract Geothermal Energy: Advantages and Disadvantages in Comparison with Water. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19 April 2015. [Google Scholar]
- Biagi, J.; Agarwal, R.; Zhang, Z. Simulation and Optimization of Enhanced Geothermal Systems Using CO2 as a Working Fluid. Energy 2015, 86, 627–637. [Google Scholar] [CrossRef]
- Steadman, E.N.; Daly, D.J.; Silva, L.L.; Harju, J.A.; Jensen, M.D.; Peck, W.D.; O’Leary, E.M.; Smith, S.A.; Sorensen, J.A. Plains CO2 Reduction (Pcor) Partnership (Phase I) Final Report; Energy & Environmental Research Center, University of North Dakota: Grand Forks, ND, USA, 2006; p. 887132. [Google Scholar]
- Dezayes, C.; Genter, A.; Hooijkaas, G.R. Deep-Seated Geology and Fracture System of the EGS Soultz Reservoir (France) Based on Recent 5 km Depth Boreholes. In Proceedings of the World Geothermal Congress 2005, Antalya, Turkey, 24 April 2005. [Google Scholar]
- Metz, B.; Davidson, O.; Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK, 2005; p. 443. [Google Scholar]
- Zhang, L.; Ezekiel, J.; Li, D.; Pei, J.; Ren, S. Potential Assessment of CO2 Injection for Heat Mining and Geological Storage in Geothermal Reservoirs of China. Appl. Energy 2014, 122, 237–246. [Google Scholar] [CrossRef]
- National Snow and Ice Data Center Cryosphere Glossary. Available online: https://nsidc.org/learn/cryosphere-glossary/geothermal-heat-flux (accessed on 9 December 2023).
- Quattrocchi, F.; Boschi, E.; Spena, A.; Buttinelli, M.; Cantucci, B.; Procesi, M. Synergic and Conflicting Issues in Planning Underground Use to Produce Energy in Densely Populated Countries, as Italy. Appl. Energy 2013, 101, 393–412. [Google Scholar] [CrossRef]
- Fleming, M.R.; Adams, B.M.; Randolph, J.B.; Ogland-Hand, J.D.; Kuehn, T.H.; Buscheck, T.A.; Bielicki, J.M.; Saar, M.O. High Efficiency and Large-Scale Subsurface Energy Storage with CO2. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 12 February 2018. [Google Scholar]
- Hulen, J.; Wright, P. Geothermal Energy: Clean, Sustainable Energy for the Benefit of Humanity and the Environment, Energy & Geoscience Institute; University of Utah: Salt Lake City, UT, USA, 2001. [Google Scholar]
- Pruess, K. The TOUGH Codes—A Family of Simulation Tools for Multiphase Flow and Transport Processes in Permeable Media. Vadose Zone J. 2004, 3, 738–746. [Google Scholar] [CrossRef]
- Pruess, K. ECO2N: A TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005; p. LBNL--57952. [Google Scholar]
- Finley, R. An Assessment of Geological Carbon Sequestration Options in the Illinois Basin; National Energy Technology Laboratory: Pittsburgh, PA, USA; Morgantown, WV, USA, 2005. [Google Scholar]
- Britannica, T. Editors of Encyclopaedia, Encyclopedia Britannica. Available online: https://www.britannica.com/technology/core-sampling (accessed on 9 December 2023).
- Fatt, I. The Network Model of Porous Media. Trans. AIME 1956, 207, 144–181. [Google Scholar] [CrossRef]
- Pruess, K.; Narasimhan, T.N. A Practical Method for Modeling Fluid and Heat Flow in Fractured Porous Media. Soc. Pet. Eng. J. 1985, 25, 14–26. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Audigane, P.; Royer, J.-J. Large-Scale In Situ Permeability Tensor of Rocks from Induced Microseismicity. Geophys. J. Int. 1999, 137, 207–213. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing Flow and Transport in Fractured Geological Media: A Review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. Impact of Enhanced Geothermal Systems on US Energy Supply in the Twenty-First Century. Phil. Trans. R. Soc. A 2007, 365, 1057–1094. [Google Scholar] [CrossRef]
- Sanyal, S.K.; Butler, S.J. An Analysis of Power Generation Prospects from Enhanced Geothermal Systems. In Proceedings of the World Geothermal Congress 2005, Antalya, Turkey, 24 April 2005. [Google Scholar]
- Saar, M.O. Review: Geothermal Heat as a Tracer of Large-Scale Groundwater Flow and as a Means to Determine Permeability Fields. Hydrogeol. J 2011, 19, 31–52. [Google Scholar] [CrossRef]
- U.S.A. Department of Commerce (DOC); National Oceanic and Atmospheric Administration (NOAA); National Environmental Satellite, Data, and Information Service (NESDIS); National Climate Data Center (NCDC). U.S.A. Climate Normals (1971–2000); 2000. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00115 (accessed on 9 December 2023).
- DiPippo, R. Ideal Thermal Efficiency for Geothermal Binary Plants. Geothermics 2007, 36, 276–285. [Google Scholar] [CrossRef]
- Sanyal, S.K.; Morrow, J.W.; Butler, S.J. Net power capacity of geothermal wells versus reservoir temperature—A practical perspective. In Proceedings of the Thirty-Second Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 22 January 2007. [Google Scholar]
- Katz, D.L.; Lee, R.L. Natural Gas Engineering: Production and Storage (MCGRAW HILL CHEMICAL ENGINEERING SERIES); McGraw-Hill Economics Dept: New York, NY, USA, 1991; ISBN 0-07-033352-1. [Google Scholar]
- Entingh, D.J.; Pike, R.; Lane, S. DOE Geothermal Electricity Technology Evaluation Model (GETEM): Volume I—Technical Reference Manual; Department of Energy: Washington, DC, USA; The National Renewable Energy Laboratory: Golden, CO, USA, 2006. [Google Scholar]
- Manning, C.E.; Ingebritsen, S.E. Permeability of the Continental Crust: Implications of Geothermal Data and Metamorphic Systems. Rev. Geophys. 1999, 37, 127–150. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications and Case Studies, 2nd ed.; Reprint; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 978-0-7506-8620-4. [Google Scholar]
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct Utilization of Geothermal Energy 2010 Worldwide Review. Geothermics 2011, 40, 159–180. [Google Scholar] [CrossRef]
- Rybach, L. Geothermal Energy: Sustainability and the Environment. Geothermics 2003, 32, 463–470. [Google Scholar] [CrossRef]
- Hodge, J.; Haltrecht, J. BedZED Monitoring Report 2007; BioRegional: London, UK, 2007. [Google Scholar]
- Coates, G.J. The Sustainable Urban District of Vauban in Freiburg, Germany. Int. J. DNE 2013, 8, 265–286. [Google Scholar] [CrossRef]
- Lu, H. Malmo, Sweden. In Eco-Cities and Green Transport; Elsevier: Amsterdam, The Netherlands, 2020; pp. 347–362. ISBN 978-0-12-821516-6. [Google Scholar]
- Bielicki, J.M.; Leveni, M.; Johnson, J.X.; Ellis, B.R. The Promise of Coupling Geologic CO2 Storage with Sedimentary Basin Geothermal Power Generation. iScience 2023, 26, 105618. [Google Scholar] [CrossRef]
- Adams, B.; Sutter, D.; Mazzotti, M.; Saar, M.O. Combining Direct Air Capture and Geothermal Heat and Electricity Generation for Net-Negative Carbon Dioxide Emissions. In Proceedings of the World Geothermal Congress 2020, Reykjavik, Iceland, 26 April–2 May 2020. [Google Scholar] [CrossRef]
- Leveni, M.; Bielicki, J.M. A Potential for Climate Benign Direct Air CO2 Capture with CO2-Driven Geothermal Utilization and Storage (DACCUS). Environ. Res. Lett. 2024, 19, 014007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).