Abstract
To monitor temperature as a function of varying inductance and resistance, we propose a data-driven digital twin approach for the rapid and efficient real-time estimation of the rotor temperature in an induction motor. By integrating differential equations with online signal processing, the proposed data-driven digital twin approach is structured into three key stages: (1) transforming the nonlinear differential equations into discrete algebraic equations by substituting the differential operator with the difference quotient based on the sampled voltage and current; (2) deriving approximate analytical solutions for rotor resistance and stator inductance, which can be utilized to estimate the rotor temperature; and (3) developing a general procedure for obtaining approximate analytical solutions to nonlinear differential equations. The feasibility and validity of the proposed method were demonstrated by comparing the test results with a 1.5 kW AC motor. The experimental results indicate that our method achieves a minimum estimation error that falls within the standards set by IEC 60034-2-1. This work provides a valuable reference for the overheating protection of induction motors where direct temperature measurement is challenging.
1. Introduction
Accurate temperature estimation is very important for the overheating protection of an induction motor, which is difficult to measure directly [,]. Considering nonlinear parameter perturbation, such as the inductance and resistance, which is an implicit function of the temperature of the induction motor [,], how to increase the estimation accuracy of the temperature is still a serious problem that it is urgent to solve. On the other hand, the inductance and resistance of an induction motor cannot be measured directly due to the restriction of the mounting sensor or sampling signal transmission. Also, the influence of the harmonic current produced by the inverter on identifying the temperature of the induction motor should be considered (as shown in Table 1). As discussed above, it is necessary to develop an approach for estimating the temperature that can overcome the influence of the varying inductance and resistance of an induction motor.

Table 1.
Influence of harmonic current on estimating the temperature of the induction motor.
Investigations show that there are many methods that are suitable for estimating the temperature of the induction motor. As shown in Table 2, several representative methods are Recursive Least Squares (RLS), Stator Windings Resistance (SWR) measurement method, Model Reference Adaptive System (MRAS), Extended Kalman Filter (EKF) algorithm, Proximal Policy Optimization-Reinforcement Learning (PPO-RL) algorithm and Intelligent algorithms. The above-mentioned methods have been used to estimate the motor temperature directly or indirectly already, which can serve as the research base of this paper. But, considering the rapidity and effectiveness requirements for the overheating protection in an induction motor, there are still many issues that should be solved: (1) it is generally difficult to obtain the closed-form solution of the temperature that is associated with the sampling voltage and sampling current of the induction motor; (2) the harmonics current caused by the inverter influences the estimation accuracy of the motor’s temperature; and (3) the inductance and resistance of the stator and the rotor are nonlinearly changing with the temperature of the motor. Therefore, deriving an analytical expression of the temperature to the varying inductance and varying impedance may be a suitable method of estimating the temperature of the induction motor. The difficulty of this work is to research a method for solving the general differential equations with varied coefficients associated with the varying inductance and resistance of the induction motor based on online sampling voltage and current.

Table 2.
Summarized temperature estimation algorithms of the induction motor.
As discussed above, the main goal of this paper is to develop an approach that can be used to find analytical solutions to nonlinear differential equations. Empirical studies show that the classical methods make it difficult to solve the nonlinear differential equations in a real-time-based on-chip system (as shown in Table 3). As Table 3 shows, there are successful methods for solving differential equations. But, for obtaining the analytical solution of a differential equation in real time, there are still some problems that should be solved. For example, among all the proposed algorithms to approximate the influence maximization, some are time-consuming, some inaccurate, and some include too many assumptions. However, the accurate monitoring temperature of the induction motor requires an analytical expression of the temperature due to the following reasons: (1) it needs to be executed rapidly and precisely; and (2) this approach should be realized in an on-chip system. Also, considering that the overwhelming majority of nonlinear differential equations are not solvable analytically, we should explore a suitable path to realize this research work. Therefore, it is necessary to develop an approach to obtaining the analytical solution for the motor temperature corresponding to Table 3.

Table 3.
Summarized classical methods for solving the differential equations.
As mentioned above, this paper aims to explore the use of the data-driven digital twin approach for temperature estimation in induction motors. Here, we propose a data-driven digital twin approach [,] that can effectively be used for the online identification of the varying inductance and resistance of induction motors, addressing the limitations of the traditional methods in terms of the accuracy and speed of deriving expressions. The structure of the paper includes the following: (1) establishing simplified differential equations related to the induction motor; (2) transforming the differential equations into time-difference algebraic equations by analyzing the sampled voltage and current of the induction motor; (3) deriving an analytical expression for the motor temperature by solving the difference algebraic equations; and (4) developing a data-driven digital twin processing procedure that can be implemented in an on-chip system. The feasibility and validity of the proposed method were demonstrated by comparing the test results with a 1.5 kW AC motor. As the induction motor is powered by an inverter, this results in a high harmonic current, which is one of the causes of the increased temperature in the motor. To estimate the current, it is necessary to extract the fundamental component of the current. To ensure the accuracy of voltage acquisition, inductors are used for filtering. The experimental results show that the estimation accuracy of the rotor temperature achieved by this method is below °C and meets the expected standards.
2. Modelling and Analyzing the Induction Motor
The differential equations that describe the temperature of an induction motor are taken as an example to demonstrate the proposed approach. The state equation of an induction motor in coordinate is shown as follows []
where the detailed parameters of (1) are shown in Table 4. The coefficient matrices and are shown in (2) and (3). It means that, since the parameters , , , and are functions of the temperature, system (1) can be viewed as a time-varying nonlinear system of differential equations.
Let us rewrite system (1) as follows
Corresponding parameters of (1–7) are shown in Table 4. System (4–7) illustrates the relationship between the leakage inductance and the stator current of the induction motor. In order to eliminate the flux leakage vectors and that cannot be measured directly, we differentiate (4) and (5) with respect to time. We obtain

Table 4.
Corresponding parameters of Equations (1)–(29).
By substituting (6) and (7) into (8) and (9), we eliminate and . Then, (8) and (9) can be rewritten as
Although (10) and (11) incorporate second-order differential equations, we can still eliminate the flux leakage vectors and by adding and to obtain new functions and substituting (4) and (5) into them as follows
When the motor is in a stable working state or the motor speed has a small variation range, it can be assumed that . Rewrite (12) and (13) in a matrix form:
Here, are the induction motor system parameters:
Since and , there are only two independent variables, and , in (15). We should find and from (15) using the mutual inductance, , whereas the rotor inductance, , will be obtained and employed below to calculate the rotor temperature of the induction motor.
Since the motor temperature is a function of the parameters , , , , and , it is necessary to derive the analytical expression of the above-mentioned parameters from (14). The parameters , , , , and are varying with the current in real time, and this computational process needs to be performed in an on-chip system; therefore, the numerical methods, as well as semi-analytical methods, do not quite meet this computing demand.
3. Data-Driven Digital Twin Model
In order to use the sampling current and voltage to estimate the temperature of the induction motor, a data-driven digital twin model has been derived. The core work is to transform differential Equation (14) into algebraic difference equations by replacing the differential operator with the differential quotient, which is described by the derivative of two adjacent sampling data to the sampling period.
Moreover, for obtaining the analytic expressions for variables and , the stator current and and the stator voltage and can be rewritten as follows based on the discretization of the differential operator:
where m, (m + 1) and (m + 2) denote mth, (m + 1)th and (m + 2)th sampling periods, respectively. In order to avoid measurement errors caused by numerical differentiation, it is necessary to use a filter to obtain a smooth waveform before measurement. Considering the measurement error level for the current, after the current has been measured by the sensor, the should be delivered to the CPU, which takes some time –. Due to this delay time, the true current becomes . So, the measurement error is equal to . The voltage is the same; the measurement errors can be .
By substituting (16) into (14), the following system of algebraic equations can be obtained
Equation (18) includes two characteristic sets associated with the variables and . Based on the above analysis, the expressions of and can be obtained.
Analytic expressions of and are provided in (A2) to (A3a,b) in Appendix A. Then, we can find variables and as follows
where and can be written as the following expressions
As a supplement, the impedance and the inductance of the motor can be provided by the previous research [,]
where denotes the initial value of the stator resistance at the ambient temperature ; denotes the resistance coefficient, and is the rotor temperature. The middle variable is
where and are the sampling current and the sampling voltage of the motor stator, respectively; is the phase difference between the stator voltage and the stator current . As shown in Figure 1, the x-axis is aligned with the current phasor . The positive sequence voltage can be described by and .
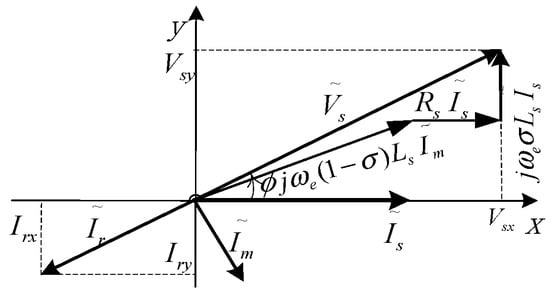
Figure 1.
Phasor diagram of the equivalent circuit of the induction motor.
According to (19) and (24), the rotor impedance , the rotor inductance , and the rotor temperature can be derived and expressed as follows
where denotes the initial impedance of the rotor at ambient temperature and the sign denotes the resistance constant.
Assuming the voltage vector and the current vector correspond to the stator voltage and the stator current in the coordinate system, the transformation of the stator voltage and the stator current in the coordinate system to the coordinate system can be described as
As discussed above, we have developed a data-driven digital twin model of an induction motor. The topology analysis and algorithmic procedure for this model are summarized in Figure 2 and Algorithm 1 respectively.

Figure 2.
Data-driven digital twin model of the induction motor.
As shown in Algorithm 1, The main steps of the analytic solution of the rotor temperature is summarized in Table 5.
| Algorithm 1: Algorithm of proposed data-driven digital twin model |
| 0: Modeling an induction motor by the differential equations, providing |
| 1: Call (14), and replace the differential operator with (16) |
| 2: Differential equations were transformed into algebraic equations (17) |
| 3.1: Solving characteristic algebraic equation (17) |
| 3.2: Extract accuracy fundamental voltage and current and eliminate intermediate variable based on sampling data |
| 3.3: Obtain analytic solutions , based on (21) and (22) |
| 4.1: k = 1 |
| 4.2: , calculate power factor angle , , |
| 4.3: , , |
| 4.4: Call (18) derive |
| 4.6: Call (17) and (20) obtain |
| 4.7: Call (26) and (27) calculate |
| 4.8: Obtain by calling (28) |
| 4.9: k = k + 1 and repeat above process 4.2–4.8 |
| 5.0: End |

Table 5.
Main steps to find the analytic solution of the rotor temperature of an induction motor.
4. Experiment Validation
As shown in Figure 3, in order to verify the estimation accuracy and efficiency of the proposed approach, we have designed an experimental system that consists of a 1.5 kW induction motor (as the power source) and a 2.0 Hp DC motor (as the load). The electric–dynamic phenomena and the rotor temperature of the induction motor can be illustrated in (1) to (14) and (28). The parameters of this AC motor are as follows: , °C, °C, , , , .

Figure 3.
Experiment device of 1.5 kW induction motor, where the original cooling fan of the AC motor has been removed in order to obtain and analyze the extreme temperatures of the stator and rotor. The detailed parameters are listed in Table 6.

Table 6.
Introduction of the experiment system.
Table 6.
Introduction of the experiment system.
| Order | Part of the Experiment | Parameters | Note |
|---|---|---|---|
| 1 | (1) AC motor | 1.5 kW/AC380V | We should estimate the rotor temperature of this motor due to it being used to drive a coaxial DC motor. |
| 2 | (2) DC motor | 2.0 Hp/DC180V | It is a load generator for the AC motor. |
| 3 | (3) Inverter | 5 kW/AC380V | It is used to power the AC motor. |
| 4 | (4) Signal conditioning circuit | 0–3.3 V output voltage | 6 channels for sampling; 3 phases of voltage and 3 phases of voltage |
| 5 | (5) Power Analyzer | 3 current sensors and 3 voltage sensors | It is used to test the stator voltage and current of the AC motor |
| 6 | (6) TMP-A temperature instrument | 4 thermocouples | It is used to measure the temperature between the stator and rotor of the AC motor. |
Figure 4 shows the diagram of the experiment system. The temperature can be obtained by the voltage , and the current , , which is derived by transforming the sampling voltage and sampling current based on (29).
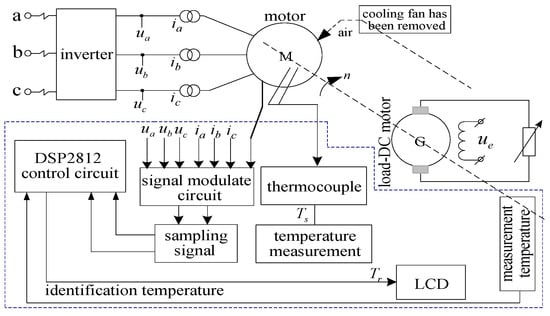
Figure 4.
Schematic diagram of proposed experiment system, where four thermocouples belong to the TMP-A temperature instrument, which is used to measure the temperature between the stator and rotor of the AC motor.
Figure 5 shows the measured instantaneous voltage and current of the induction motor. It denotes that, due to the control errors of the inverter that is chosen as the power supply of the induction motor, there are considerable aberrance and distortions in the stator current. It can also be proven in Figure 6 that the total harmonic distortion of the stator current (THDi) exceeds standard [].
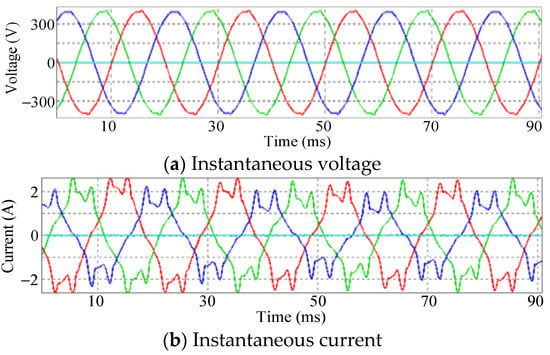
Figure 5.
The measured voltage and current of the AC motor, where (a,b) are the instantaneous voltage and instantaneous current, respectively. Blue solid line, green solid line, and red solid line denote the stator voltage and current of phase A, phase B, and phase C of the AC motor, respectively. We found that the stator current from the AC motor is greatly distorted, which should be considered for estimating the rotor temperature.
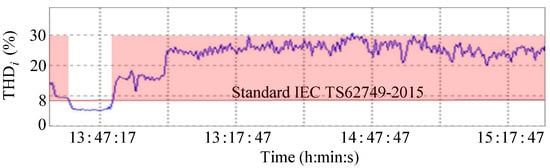
Figure 6.
Measured THDi of the stator current of the AC motor obtained by Power Analyzer. It denotes that the actual value described by the blue solid line is far over 8%, which is the limit value of standard [].
Considering that only the fundamental current is useful for identifying the temperature of the motor, the FFT (Fast Fourier Transform) algorithm has been used to extract the fundamental current and its spectrum, which are shown in Figure 6 and Figure 7, respectively. The correctness of Figure 7 can be illustrated by comparing Figure 8 with Figure 9.
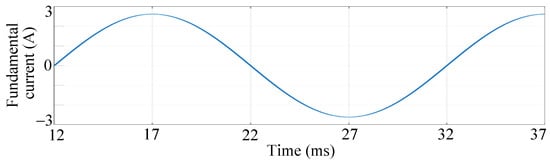
Figure 7.
Fundamental current obtained by FFT. This work is used to extract accurate fundamental current based on Figure 5, which is the basis for estimating the rotor temperature of the AC motor.
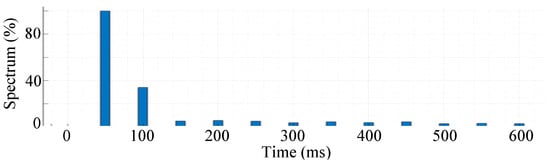
Figure 8.
The spectrum of stator currents obtained by FFT is based on Figure 5. There are remarkable aspects of the second harmonic, third harmonic, fifth harmonic, etc., which have a negative influence on estimating the rotor temperature of the AC motor.
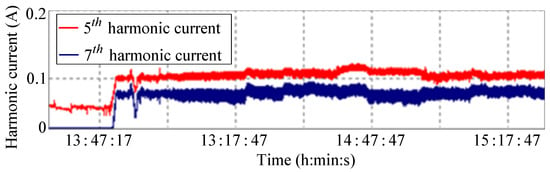
Figure 9.
The fifth harmonic and seventh harmonic currents of the stator currents obtained by the Power Analyzer, which correspond to Figure 5b.
Based on the above sampling voltage and current of the induction motor, the estimated stator inductance, estimated rotor impedance, and estimated rotor temperature are shown in Figure 10, Figure 11 and Figure 12. Figure 10 and Figure 11 show that the stator inductance and the rotor impedance increase with the running time, which influences the temperature of the induction motor.
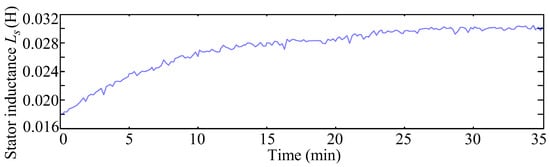
Figure 10.
Estimated stator inductance of the induction motor.
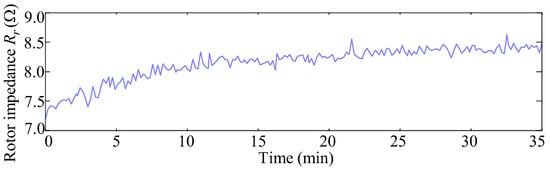
Figure 11.
Estimated rotor impedance of the induction motor.
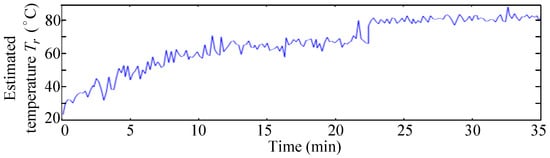
Figure 12.
The estimated rotor temperature of the induction motor.
Figure 12 and Figure 13 show the estimated rotor temperature and measured rotor temperature, respectively. Comparison of Figure 12 and Figure 13 shows that the estimated rotor temperature conforms exactly to the measured temperature of the induction motor. Both the estimated and measured values significantly increased from °C to °C within 35 min.
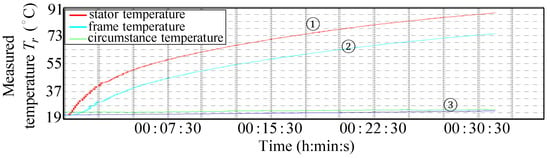
Figure 13.
The measured stator temperature of the induction motor, where ① denotes the stator temperature; ② denotes the frame temperature; ③ denotes the circumstance temperature.
It should be noted that, in order to emphasize the estimation effect, the cooling fan has been removed, which is the reason why the rotor temperature has increased to about °C within 35 min. In addition, because the rotor is located on the central axis of the stator coil, its temperature is slightly higher than the stator coil. It is the reason why the measured stator temperature is lower, °C, than the estimated rotor temperature of the induction motor. Moreover, Figure 14 shows the temperature obtained by the infrared camera, which is very close to the estimated rotor temperature of the induction motor. The motor is composed of iron, and its emissivity used for the thermographic picture is 0.6.

Figure 14.
The measured stator temperature of the induction motor by using FLIR infrared camera at time 00:30:30 of Figure 13.
The error between the measured temperature and the estimated temperature is shown in Table 7. It is defined as .

Table 7.
Error of proposed approach regarding measured temperature (°C).
Table 7 shows that the estimation error of the temperature was lower, °C, which can satisfy the demand for the overheating protection of the induction motor. It means that we can use (20) to monitor the temperature of the induction motor based on sampling the stator voltage and current.
For this work, we have proposed and demonstrated the configuration of a data-driven digital twin model for an induction motor, as shown in Figure 15.
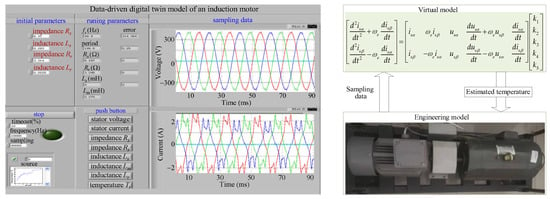
Figure 15.
Configuration of the proposed data-driven digital twin model.
5. Conclusions
This paper proposes a data-driven digital twin approach to estimate the real-time temperature of an induction motor. The main contribution of this work is to derive the analytical expressions of the rotor temperature from the nonlinear differential equations used to describe the response phenomena of the induction motor. Due to our work, as shown in the experimental results, when the induction motor is driven by a variable-frequency drive (VFD), approximately 25% THDi is generated, and these harmonics are a significant cause of motor heating. Additionally, the inductance and resistance also increase. By identifying the resistance and inductance, the temperature is indirectly estimated, resulting in a final estimation error of 1.8%, and the minimum error for testing the temperature of the induction motor is less than °C, which has reached the standard of standard [].
At the algorithm level, an approach that can be used to obtain the analytical solution to the nonlinear differential equations has been proposed based on modeling the data-driven digital twin. The procedure for substituting the differential operator by the differential quotient was provided and used to obtain the discretization algebraic equations. This work is suitable for deriving an analytical solution to differential equations with varying coefficients, which is the basis of the proposed data-driven digital twin approach.
At the engineering level, in order to suppress the interturn short circuit in an induction motor caused by overheating, we have developed a protection technology that efficiently and rapidly estimates the rotor temperature of an induction motor. So far, this technology has been used to monitor the temperature of the wind power generator and electrical submersible motor. This work can provide a reference for generating a solution for increasing the security and reliability of a nonlinear dynamic system. Furthermore, if different operating conditions or motor types can be mathematically transformed into similar differential equation problems, relevant algorithms can be developed. After the proper validation of the corresponding models, these algorithms would enable rapid and accurate temperature estimation.
Author Contributions
Conceptualization, L.W.; Methodology, Y.L. and D.S.; Software, Y.L. and L.W.; Validation, L.W., A.D. and E.C.; Formal analysis, L.W. and E.C.; Investigation, L.W.; Resources, Y.L.; Data curation, Y.L. and L.W.; Writing—original draft, Y.L. and L.W.; Writing—review & editing, D.S., A.D. and E.C.; Supervision, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was partly supported by the Science and Technology Project of Beijing of China (MH20210194) and the Ministry of Science and Higher Education of the Russian Federation, project FZZS-2024-0003.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Equations (21), (22) and (A1)–(A3) have been obtained by eliminating elements of the time discretization algebraic equations based on the software Maple (23.07.180256).
References
- Chertovskih, R.; Pogodaev, N.; Staritsyn, M.; Aguiar, A.P. Optimal Control of Diffusion Processes: Infinite-Order Variational Analysis and Numerical Solution. IEEE Control. Syst. Lett. 2024, 8, 1469–1474. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Liu, M.-Y.; Song, H.; Li, C.; Yang, X.-L. A Temperature and magnetic field-based approach for stator inter-turn fault detection. IEEE Sens. J. 2022, 22, 17799–17807. [Google Scholar] [CrossRef]
- Vitale, G.; Lullo, G.; Scire, D. Thermal Stability of a DC/DC Converter with Inductor in Partial Saturation. IEEE Trans. Ind. Electron. 2021, 68, 7985–7995. [Google Scholar] [CrossRef]
- Scirè, D.; Lullo, G.; Vitale, G. Assessment of the Current for a Non-Linear Power Inductor Including Temperature in DC-DC Converters. Electronics 2023, 12, 579. [Google Scholar] [CrossRef]
- Yamazaki, K.; Suzuki, A.; Ohto, M.; Takakura, T. Harmonic Loss and Torque Analysis of High-Speed Induction Motors. IEEE Trans. Ind. Appl. 2012, 48, 933–941. [Google Scholar] [CrossRef]
- Yamazaki, K.; Suzuki, A.; Ohto, M.; Takakura, T.; Nakagawa, S. Equivalent Circuit Modeling of Induction Motors Considering Stray Load Loss and Harmonic Torques Using Finite Element Method. IEEE Trans. Magn. 2011, 47, 986–989. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, H.; Zhao, H.; Wu, T. A Fast Identification Method for Rotor Flux Density Harmonics and Resulting Rotor Iron Losses of Inverter-Fed Induction Motors. IEEE Trans. Ind. Electron. 2018, 65, 5384–5394. [Google Scholar] [CrossRef]
- Wu, C.; Nian, H.; Zhou, Q.; Cheng, P.; Pang, B.; Sun, D. Harmonic Impedance Modeling of DFIG Considering Dead Time Effect of Rotor Side Converter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 950–955. [Google Scholar]
- Pengcheng, D.; Dianguo, X.; Bo, W.; Yong, Y. Offline Parameter Identification Strategy of Permanent Magnet Synchronous Motor Considering the Inverter Nonlinearities. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar]
- Yang, Y.; Zhang, G.; Zhou, Y.; Chen, B.; Ma, R.; Li, Z. A Review of Permanent Magnet Synchronous Motor Parameter Iden-tification Research. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023. [Google Scholar]
- Geravandi, M.; CheshmehBeigi, H.M. Stray Load Losses Determination Methods of Induction Motors-A Review. In Proceedings of the 2022 30th International Conference on Electrical Engineering (ICEE), Tehran, Iran, 17–19 May 2022; pp. 1033–1038. [Google Scholar]
- Ma, Z.; Zhang, W.; He, J.; Jin, H. Multi-Parameter Online Identification of Permanent Magnet Synchronous Motor Based on Dynamic Forgetting Factor Recursive Least Squares. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 27–29 May 2022; pp. 4865–4870. [Google Scholar]
- Li, Z.; Feng, G.; Lai, C.; Li, W.; Kar, N.C. Current injection-based simultaneous stator winding and PM temperature estimation for dual three-phase PMSMs. IEEE Trans. Ind. Appl. 2021, 57, 4933–4945. [Google Scholar] [CrossRef]
- Geravandi, M.; CheshmehBeigi, H.M. Stator Windings Resistance Estimation Methods of In-Service Induction Mo-tors-A Review. In Proceedings of the 2023 31st International Conference on Electrical Engineering (ICEE), Tehran, Iran, 9–11 May 2023. [Google Scholar]
- Fang, H.; Duan, X.; Yang, Y.; Wang, Y.; Luo, G. Deadbeat Control of Permanent Magnet Synchronous Motor Based on MRAS Parameter Identification. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020. [Google Scholar]
- Xiao, Q.; Liao, K.; Shi, C.; Zhang, Y. Parameter identification of direct-drive permanent magnet synchronous generator based on EDMPSO-EKF. IET Renew. Power Gener. 2022, 16, 1073–1086. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, D.; Li, Y. Parameter identification of permanent magnet synchronous motor based on modified-fuzzy particle swarm optimization. Energy Rep. 2023, 9, 873–879. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, H. Induction-motor stator and rotor winding temperature estimation using signal injection method. IEEE Trans. Ind. Appl. 2006, 42, 1038–1044. [Google Scholar]
- Jing, H.; Chen, Z.; Wang, X.; Wang, X.; Ge, L.; Fang, G.; Xiao, D. Gradient Boosting Decision Tree for Rotor Temperature Estimation in Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 10617–10622. [Google Scholar] [CrossRef]
- Chu, L.; Zhu, P.; Chang, C. Research on Full Brake-By-Wire System and Clamping Force Estimation Strategy Based on Redundant Drive Motors. IEEE Access 2023, 11, 124098–124113. [Google Scholar] [CrossRef]
- Zhao, H.; Eldeeb, H.H.; Wang, J.; Kang, J.; Zhan, Y.; Xu, G.; Mohammed, O.A. Parameter Identification Based Online Noninvasive Estimation of Rotor Temperature in Induction Motors. IEEE Trans. Ind. Appl. 2021, 57, 417–426. [Google Scholar] [CrossRef]
- Jin, L.; Wei, L.; Li, S. Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans. Autom. Control. 2023, 68, 620–627. [Google Scholar] [CrossRef]
- Ahmad, J.; Iqbal, A.; Hassan, Q.M.U. Study of nonlinear fuzzy integral differential equations using mathematical methods and applications. Int. J. Fuzzy Log. Intell. Syst. 2021, 21, 76–85. [Google Scholar] [CrossRef]
- Shams, M.; Kausar, N.; Agarwal, P.; Momani, S.; Shah, M.A. Highly efficient numerical scheme for solving fuzzy system of linear and non-linear equations with application in differential equations. Appl. Math. Sci. Eng. 2022, 30, 777–810. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; Butterworth-Heinemann: Oxford, UK, 2000; Volume 2. [Google Scholar]
- Dangal, T.; Chen, C.; Lin, J. Polynomial particular solutions for solving elliptic partial differential equations. Comput. Math. Appl. 2017, 73, 60–70. [Google Scholar] [CrossRef]
- Raza, A.; Farid, S.; Amir, M.; Yasir, M.; Danyal, R.M. A study on convergence analysis of Adomian decomposition method applied to different linear and non-linear equations. Interface J. Sci. Eng. Res. 2020, 11, 1358–1378. [Google Scholar]
- Wang, B.; Duan, N.; Sun, K. A time–power series-based semi-analytical approach for power system simulation. IEEE Trans. Power Syst. 2019, 34, 841–851. [Google Scholar] [CrossRef]
- Xu, X.; Yao, R.; Sun, K.; Qiu, F. A Semi-analytical solution approach for solving constant-coefficient first-order partial differential equations. IEEE Control. Syst. Lett. 2022, 6, 704–709. [Google Scholar] [CrossRef]
- Shams, M.; Kausar, N.; Alayyash, K.; Al-Shamiri, M.M.; Arif, N.; Ismail, R. Semi-analytical scheme for solving intuitionistic fuzzy system of differential equations. IEEE Access 2023, 11, 33205–33223. [Google Scholar] [CrossRef]
- Shams, M.; Kausar, N.; Kousar, S.; Pamucar, D.; Ozbilge, E.; Tantay, B. Computationally semi-numerical technique for solving system of intuitionistic fuzzy differential equations with engineering applications. Adv. Mech. Eng. 2022, 14. [Google Scholar] [CrossRef]
- Xu, S.; Guan, X.; Peng, Y.; Liu, Y.; Cui, C.; Chen, H.; Ohtsuki, T.; Han, Z. Deep reinforcement learning based data-driven mapping mechanism of digital twin for internet of energy. IEEE Trans. Netw. Sci. Eng. 2024, 11, 3876–3890. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, D.; Jia, S.; Yang, L.; Yang, S. Incipient inter-turn short-circuit fault diagnosis of permanent magnet synchronous motors based on the data-driven digital twin model. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3514–3524. [Google Scholar] [CrossRef]
- Wang, T.; Chiang, H.-D. Neighboring Stable Equilibrium Points in Spatially-Periodic Nonlinear Dynamical Systems: Theory and Applications. IEEE Trans. Autom. Control. 2015, 60, 2390–2401. [Google Scholar] [CrossRef]
- Wang, L.G.; Zhang, X.; Xu, D.; Huang, W. Study of a differential control method for solving chaotic solutions of a nonlinear dynamic system. Nonlinear Dyn. 2011, 67, 2821–2833. [Google Scholar] [CrossRef]
- IEC TS62749; Assessment of Power Quality—Characteristics of Electrics Supplied by Public Networks. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- IEC 60034-2-1; Standard Methods for Determining Losses and Efficiency from Tests (Excluding Machines for Traction Vehicles). International Electrotechnical Commission: Geneva, Switzerland, 2014.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).