Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis
Abstract
1. Introduction
2. Related Work
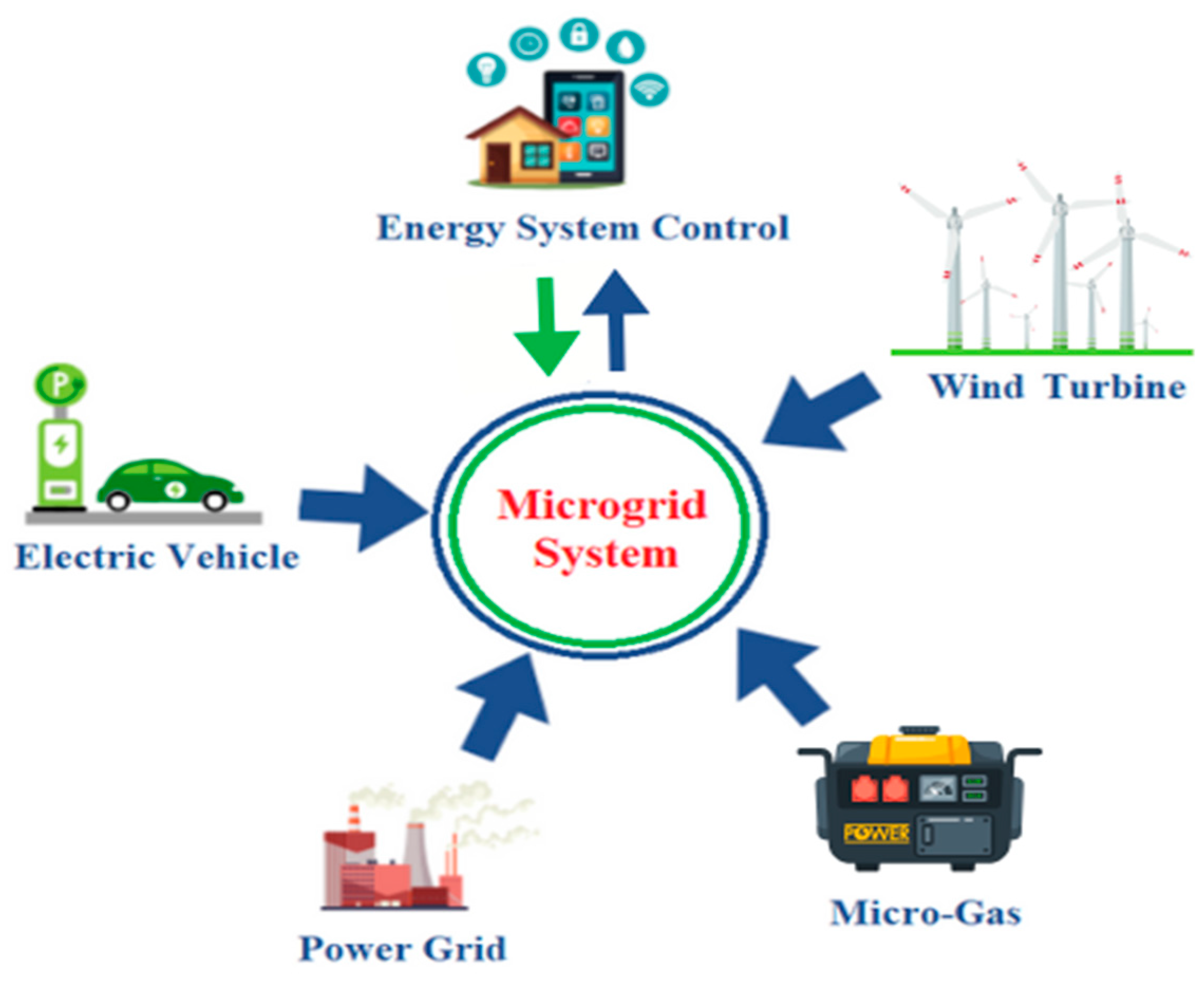
2.1. Description of Microgrid
2.2. Carbon Cost Model
3. Proposed Model
3.1. The Objective Function
3.2. Constraints
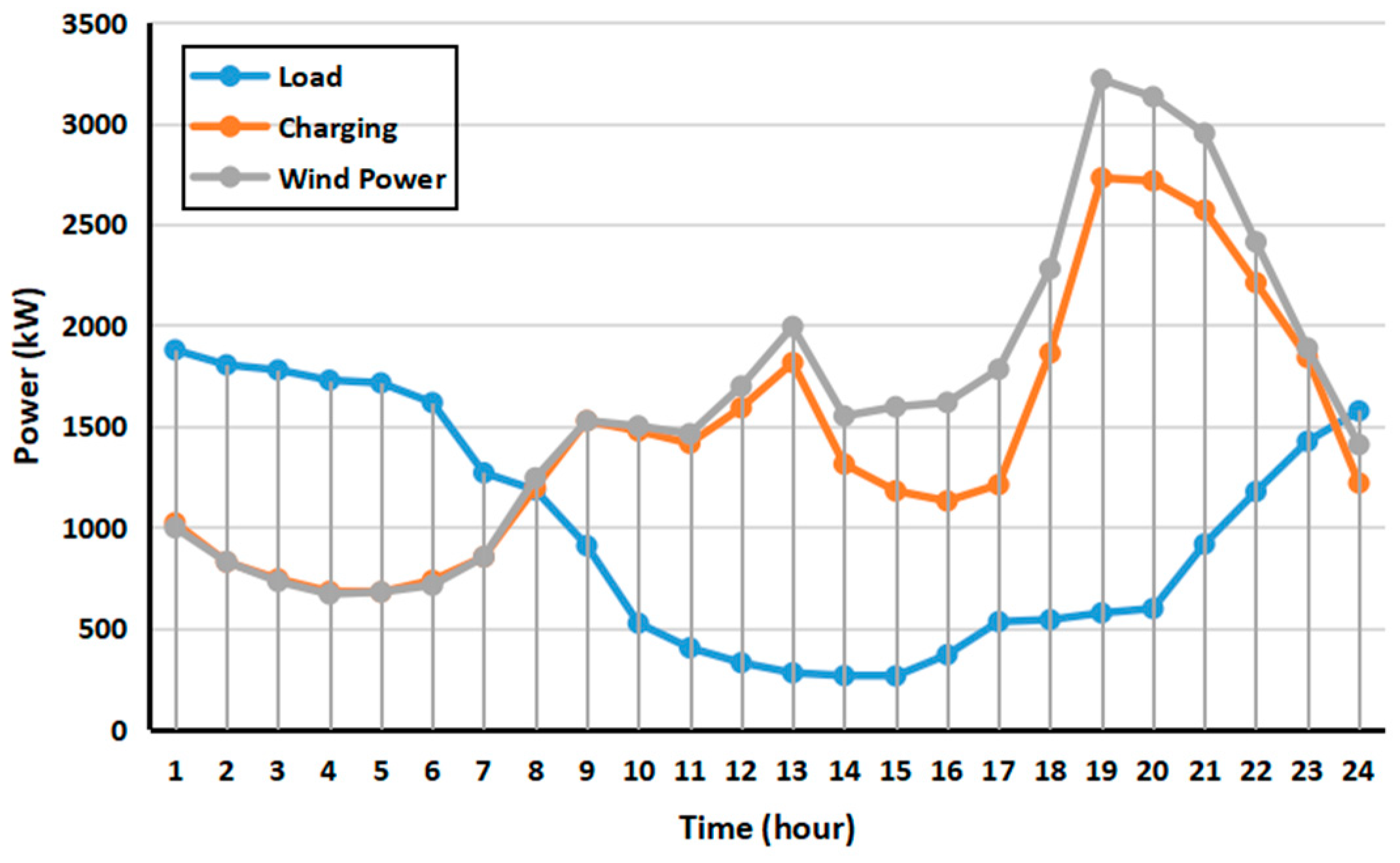
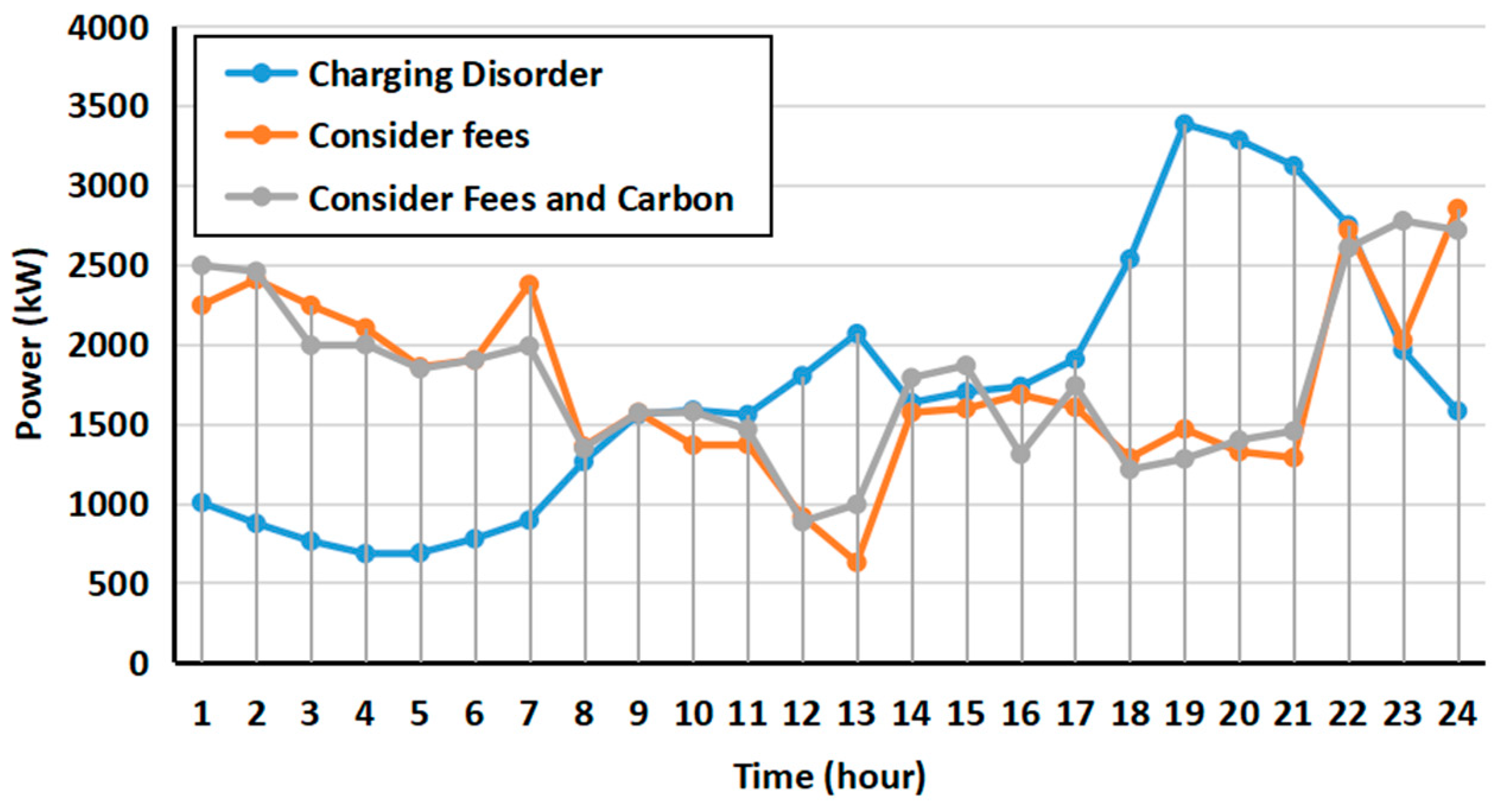
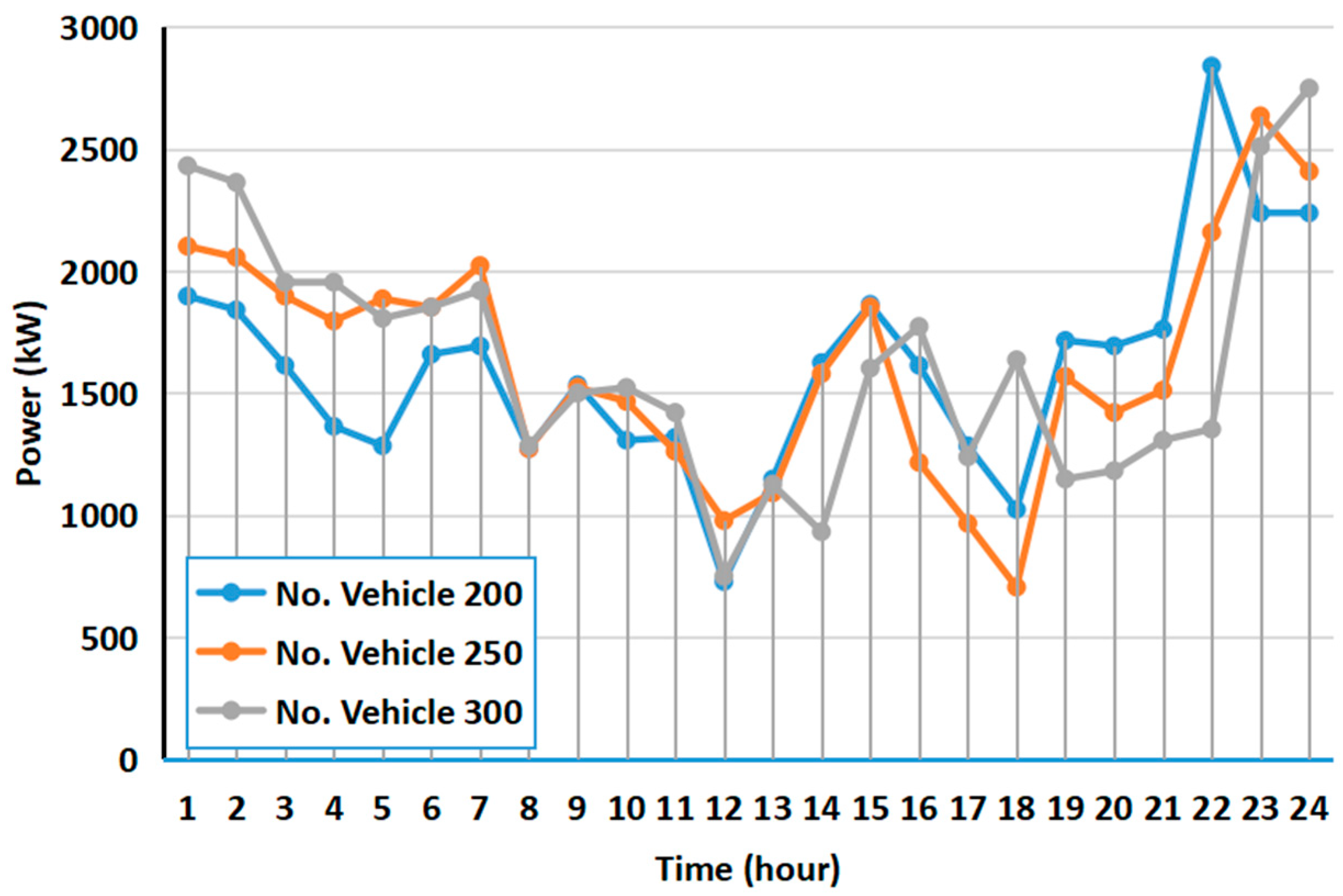
4. Results and Discussion
5. Conclusions
- The implementation of the dual incentive strategy, incorporating EVs into the carbon trading system, resulted in a 31.12% reduction in peak–valley differences compared to the original load curve. When compared to the single time-of-use electricity pricing strategy, the reduction was 19.26%, and user income doubled. This highlights significant improvements in the peak–valley management while also increasing the user participation in microgrid dispatching.
- The use of dynamic carbon pricing and reward–punishment mechanisms proved to be more adaptable to the variability of wind power compared to static carbon quota pricing. This effectively smoothed the load curve. Moreover, increasing the number of EVs by 50 can reduce the peak–valley difference by approximately 7%, contributing to the optimal dispatch of the microgrid.
- A broader range of scenarios across typical days should be considered to enhance the general applicability of the strategy and ensure its effectiveness under various conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Datta, J.; Das, D. Energy management of multi-microgrids with renewables and electric vehicles considering price-elasticity based demand response: A bi-level hybrid optimization approach. Sustain. Cities Soc. 2023, 99, 104908. [Google Scholar] [CrossRef]
- Huang, Y.; Masrur, H.; Lipu, M.S.H.; Howlader, H.O.R.; Gamil, M.M.; Nakadomari, A.; Mandal, P.; Senjyu, T. Multi-objective optimization of campus microgrid system considering electric vehicle charging load integrated to power grid. Sustain. Cities Soc. 2023, 98, 104778. [Google Scholar] [CrossRef]
- Sun, J.; Ruze, N.; Zhang, J.; Shi, J.; Shen, B. Capacity planning and optimisation for integrated energy system in industrial park considering environmental externalities. Renew. Energy 2021, 167, 56–65. [Google Scholar] [CrossRef]
- Rangu, S.K.; Lolla, P.R.; Dhenuvakonda, K.R.; Singh, A.R. Recent trends in power management strategies for optimal operation of distributed energy resources in microgrids: A comprehensive review. Int. J. Energy Res. 2020, 44, 9889–9911. [Google Scholar] [CrossRef]
- Mulvey, J.M.; Vanderbei, R.J.; Zenios, S.A. Robust optimisation of large-scale systems. Oper. Res. 1995, 43, 264–281. [Google Scholar] [CrossRef]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of Fuzzy Logic in Renewable Energy Systems—A Review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Nazir, M.S.; Din, S.U.; Shah, W.A.; Ali, M.; Kharal, A.Y.; Abdalla, A.N.; Sanjeevikumar, P. Optimal Economic Modelling of Hybrid Combined Cooling, Heating, and Energy Storage System Based on Gravitational Search Algorithm-Random Forest Regression. Complexity 2021, 2021, 5539284. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P.; Guo, Q.; Sun, H. A stochastic bi-level optimal allocation approach of intelligent buildings considering energy storage sharing services. IEEE Trans. Consum. Electron. 2024. [Google Scholar] [CrossRef]
- Rudberg, M.; Waldemarsson, M.; Lidestam, H. Strategic perspectives on energy management: A case study in the process industry. Appl. Energy 2013, 104, 487–496. [Google Scholar] [CrossRef]
- Cinar, D.; Kayakutlu, G. Scenario analysis using Bayesian networks: A case study in energy sector. Knowl. Based Syst. 2010, 23, 267–276. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Zidan, A. Modeling, evaluation, and optimisation of gas-power and energy supply scenarios. Front. Energy 2016, 10, 393–408. [Google Scholar] [CrossRef]
- Kiriyama, E.; Kajikawa, Y. A multilayered analysis of energy security research and the energy supply process. Appl. Energy 2014, 123, 415–423. [Google Scholar] [CrossRef]
- Faccio, M.; Gamberi, M.; Bortolini, M.; Nedaei, M. State-of-art review of the optimisation methods to design the configuration of hybrid renewable energy systems (HRESs). Front. Energy 2018, 12, 591–622. [Google Scholar] [CrossRef]
- Aghaei, J.; Shayanfar, H.; Amjady, N. Joint market clearing in a stochastic framework considering power system security. Appl. Energy 2009, 86, 1675–1682. [Google Scholar] [CrossRef]
- Nandini, K.K.; Jayalakshmi, N.S.; Jadoun, V.K. Risk-based dynamic pricing by metaheuristic optimization approach for electric vehicle charging infrastructure powered by grid integrated microgrid system. Electr. Power Syst. Res. 2024, 230, 110250. [Google Scholar]
- Rasheed, M.B.; Llamazares, Á.; Oca, M.; Revenga, P. A game-theoretic approach to mitigate charging anxiety for electric vehicle users through multi-parameter dynamic pricing and real-time traffic flow. Energy 2024, 304, 132103. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Mallik, A.; Chen, Y. Dynamic pricing strategy for electric vehicle charging stations to distribute the congestion and maximize the revenue. Electr. Power Energy Syst. 2024, 158, 109946. [Google Scholar] [CrossRef]
- Moses Babu, V.S.; Chakraborty, P.; Pal, M. Planning of fast charging infrastructure for electric vehicles in a distribution system and prediction of dynamic price. Electr. Power Energy Syst. 2024, 155, 109502. [Google Scholar]
- Hussain, S.; Prasad Teni, A.; Hussain, I.; Hussain, Z.; Pallonetto, F.; Eichman, J.; Irshad, R.R.; Alwayle, I.M.; Alharby, M.; Hussain, A.; et al. Enhancing electric vehicle charging efficiency at the aggregator level: A deep-weighted ensemble model for wholesale electricity price forecasting. Energy 2024, 308, 132823. [Google Scholar] [CrossRef]
- Misconel, S.; Zimmermann, F.; Mikurda, J.; Möst, D.; Kunze, R.; Gnann, T.; Kühnbach, M.; Speth, D.; Pelka, S.; Yu, S. Model coupling and comparison on optimal load shifting of battery electric vehicles and heat pumps focusing on generation adequacy. Energy 2024, 305, 132266. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, M.; Chen, D.; Huo, Y.; Lu, W. Dynamic grouping control of electric vehicles based on improved k-means algorithm for wind power fluctuations suppression. Glob. Energy Interconnect. 2024, 6, 542–553. [Google Scholar] [CrossRef]
- Srithapon, C.; Månsson, D. Predictive control and coordination for energy community flexibility with electric vehicles, heat pumps, and thermal energy storage. Appl. Energy 2023, 347, 121500. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H.; Yang, J.; Feng, J.; Li, Y.; Zhang, S.; Okoye, M.O. Electric vehicle clusters scheduling strategy considering real-time electricity prices based on deep reinforcement learning. Energy Rep. 2022, 8, 695–703. [Google Scholar] [CrossRef]
- Seo, M.; Kodaira, D.; Jin, Y.; Son, H.; Han, S. Development of an efficient vehicle-to-grid method for massive electric vehicle aggregation. Energy Rep. 2024, 11, 1659–1674. [Google Scholar] [CrossRef]
- Shatanawi, M.; Alatawneh, A.; Mészáros, F. Implications of static and dynamic road pricing strategies in the era of autonomous and shared autonomous vehicles using simulation-based dynamic traffic assignment: The case of Budapest. Res. Transp. Econ. 2022, 95, 101231. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Peng, P.; Chen, Z. Toward efficient smart management: A review of modeling and optimization approaches in electric vehicle-transportation network-grid integration. Green Energy Intell. Transp. 2024. [Google Scholar] [CrossRef]
- Ziemsky, V.; Biedenbach, F. Attractiveness and business model potential of the spot market optimized charging of electric vehicles. Transp. Res. Procedia 2023, 70, 99–106. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Paredes, Á.; González, J.M.; Aguado, J.A. A three-layer game theoretic-based strategy for optimal scheduling of microgrids by leveraging a dynamic demand response program designer to unlock the potential of smart buildings and electric vehicle fleets. Appl. Energy 2023, 347, 121440. [Google Scholar] [CrossRef]
- Bilbao, E.; Barrade, P.; Etxeberria-Otadui, I.; Rufer, A.; Luri, S.; Gil, I. Optimal Energy Management Strategy of an Improved Elevator with Energy Storage Capacity Based on Dynamic Programming. IEEE Trans. Ind. Appl. 2013, 50, 1233–1244. [Google Scholar] [CrossRef]
- Sheibani, M.R.; Yousefi, G.R.; Latify, M.A.; Dolatabadi, S.H. Energy storage system expansion planning in power systems: A review. IET Renew. Power Gener. 2018, 12, 1203–1221. [Google Scholar] [CrossRef]
- Abdulla, K.; de Hoog, J.; Muenzel, V.; Suits, F.; Steer, K.; Wirth, A.; Halgamuge, S. Optimal Operation of Energy Storage Systems Considering Forecasts and Battery Degradation. IEEE Trans. Smart Grid 2016, 9, 2086–2096. [Google Scholar] [CrossRef]
- Javadi, M.A.; Khodabakhshi, S.; Ghasemiasl, R.; Jabery, R. Sensitivity analysis of a multi-generation system based on a gas/hydrogen-fueled gas turbine for producing hydrogen, electricity and freshwater. Energy Convers. Manag. 2022, 252, 115085. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Ju, Y.; Nazir, M.S.; Tao, H. A Robust Economic Framework for Integrated Energy Systems Based on Hybrid Shuffled Frog-Leaping and Local Search Algorithm. Sustainability 2022, 14, 10660. [Google Scholar] [CrossRef]



| Carbon Quota-Related Parameters | Value (kg/kW) |
|---|---|
| Micro-gas turbine | 0.6113 |
| Electricity generated by the micro-gas turbine | 0.7110 |
| Emissions per kilometer of fuel vehicles | 0.1962 |
| Power purchased by the grid | 0.7202 |
| Purchased from the grid | 0.8892 |
| Case | Considers Time-of-Use Electricity Prices | Considers Carbon Trading |
|---|---|---|
| 1 | × | × |
| 2 | √ | × |
| 3 | √ | √ |
| Case | Load Peak and Valley Difference (kW) | User Income (USD) | Microgrid Operating Cost (USD) |
|---|---|---|---|
| case 1 | 2655.6 | - | 54,353 |
| case 2 | 2280.2 | 1549.3 | 57,262 |
| case 3 | 1856.2 | 3683.2 | 54,390 |
| Vehicles | Peak to Valley Difference (kW) | Daily Load Variance (kW) |
|---|---|---|
| 200 | 2180.2 | 137,370.0 |
| 250 | 1998.7 | 110,740.0 |
| 300 | 1856.2 | 51,962.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdi, M.A.; Abdalla, A.N.; Liu, L.; Ji, R.; Bian, H.; Hai, T. Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis. Energies 2024, 17, 4994. https://doi.org/10.3390/en17194994
Mahdi MA, Abdalla AN, Liu L, Ji R, Bian H, Hai T. Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis. Energies. 2024; 17(19):4994. https://doi.org/10.3390/en17194994
Chicago/Turabian StyleMahdi, Mahdi A., Ahmed N. Abdalla, Lei Liu, Rendong Ji, Haiyi Bian, and Tao Hai. 2024. "Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis" Energies 17, no. 19: 4994. https://doi.org/10.3390/en17194994
APA StyleMahdi, M. A., Abdalla, A. N., Liu, L., Ji, R., Bian, H., & Hai, T. (2024). Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis. Energies, 17(19), 4994. https://doi.org/10.3390/en17194994






