Decentralized Goal-Function-Based Microgrid Primary Control with Voltage Harmonics Compensation

Abstract

This paper proposes goal-function-based decentralized control of microgrids. In addition to being an instrument for maintaining the grid voltage and frequency stability, each grid-tie inverter generates a current component with the aim of compensating for voltage distortion in the node where it is connected. The designed goal-function does not need to rely on the assumption that a microgrid is dominantly inductive or resistive to derive its control law, as is mostly the case with the droop-based approach. The priorities of the proposed scheme can be adjusted according to user preferences. In addition, the control algorithm is independent of network topology, can be applied in both islanded and non-islanded microgrids, and secure system scalability. The proposed method is verified by detailed simulations.

1. Introduction

A microgrid (MG) can be defined as an entity in which generation sources are connected to the AC power system through power electronic interface converters to meet both grid-connected and islanding operations [1,2]. Among others, the following problems inevitably arise during MG operation: (1) The lack of natural system inertia caused by the high penetration of renewables can result in significant frequency variation in islanded MGs; (2) The power exchange between the MG nodes is strongly coupled with frequency and voltage variation and thus affects MG stability; (3) Distribution grids and MGs are characterized by small X/R ratios, limiting the applicability of traditional control methods. Furthermore, the loads connected in a microgrid can be both linear and nonlinear. Nonlinear loads deteriorate the power quality by drawing harmonic currents. Drawing nonlinear currents will make the voltage waveform non-sinusoidal, which may prove harmful for other loads connected to the system [3]. To improve power quality and mitigate higher voltage and current harmonics in microgrids [4], several methods inspired by solutions applied in a low voltage distribution network, such as passive and active filters, D-STATCOM, and D-FACTS [5], have been proposed. In [6], D-STATCOM using a reinforcement learning algorithm for enhancing power quality in MG was presented. Methods for active power filtering and reactive power compensation with optimized control parameters have been offered in [7,8]. Ref. [9] proposes a control architecture of distributed generator inverters and shunt active power filters in microgrids to compensate voltage harmonics in a coordinated way. In [10], a wideband series harmonic voltage compensator as an extension to series active power filter has been proposed. Its function aims to form virtually zero high-frequency impedance at the output of the paralleled grid-tied inverter to assure system stability under any operating conditions.

The state-of-the-art tendency is to employ multifunctional capabilities of grid-tied converters, such as inverters, interfacing distribution generation to deal with power quality issues. The main role of the distribution generation (DG) inverter is to adjust the output voltage phase angle and amplitude in order to control the active and reactive power flow. However, compensation of power quality problems, such as voltage harmonics and unbalance, can also be achieved through proper control strategies [11]. In this way, grid-tied converters become multifunctional [12,13].

In the literature, the MG control algorithm has been generally divided into different hierarchical levels, usually referred to as primary, secondary and tertiary control levels. Since the primary control level has the fastest response and can be operated without any communication links, it is widely preferred for implementing harmonic mitigation methods. In [14], harmonic mitigation methods have been classified into 5 groups: Modified Droop Controller, Harmonic Droop Controller, Virtual Impedance, PR Controller, Repetitive Controller and Other Methods.

Harmonic Droop Controller [15,16] and Modified Droop Controller in combination with Harmonic Droop Controller [17,18] are used to modify the voltage reference generated by a standard droop control (P-f and Q-V) to compensate for voltage harmonics at the point of common coupling with loads. The virtual impedance method [19,20,21] is based on the modification of the grid-tie inverter current, which is then added to the inverter voltage. The aim is to reshape the output impedance in the direction of harmonic suppression. Adaptive virtual impedance methods [22,23] have been developed to improve the control robustness regarding system parameters. Feeder impedance estimation based on the microgrid central controller and inherent harmonic signals introduced by a nonlinear or unbalanced load was proposed in [24]. In [25], a combination of virtual impedance with droop control was proposed, where droop distributed virtual impedance among distributed generation units. In order to reconcile the issue between harmonic residual capacity (inverter capacity to share harmonic power) and virtual impedance, a nonlinear droop scheme was proposed in [26]. Regarding so-called Virtual Synchronous generator (VSG)-based microgrids, several methods for voltage harmonics mitigation have been developed. The method of reducing the impedance of VSG in order to prevent a significant voltage distortion induced by a non-linear load in the islanded microgrid was proposed in [27]. Another method for VSG-based microgrids, which can separately mitigate the grid harmonic current caused by nonlinear loads and grid background harmonics, was proposed in [28]. A decentralized inverter control scheme with an advanced voltage injection technique that minimizes the voltage unbalance factor and reduces voltage total harmonic distortion in a low-voltage AC microgrid using Pareto multi-objective optimization was proposed in [29]. A distributed and selective harmonic current compensation without interfering with the converter’s power exchange based on master/slave architecture was proposed in [30]. There has also been growing literature about the application of machine learning in solving power quality challenges in a distribution grid and microgrids [31,32].

The method proposed in this paper is based on a goal function with the aim of addressing several microgrid control objectives. It extends the self-stabilizing primary control of microgrids proposed in [33], which itself cannot cope efficiently with the higher harmonics by means of the ability to compensate the voltage distortion. The proposed method maintains the advantages from [33], such as: (1) Voltage and frequency deviations are strictly kept within predefined but adjustable limits. This is in accordance with the grid operator demands and future MG code requirements and hence contributes to the MG reliability and stability; (2) The goal function approach provides active power production consistent with predetermined power-exchange requirements, without compromising the MG stability; (3) Plug-and-play capability is ensured, and the control framework is MG topology-agnostic (only nodal parameters are required), supporting the system’s scalability. Additionally, the proposed controller is apt for both grid-connected and islanded MG operational modes; (4) The proposed control algorithm can be easily integrated with hierarchically higher control levels (e.g., secondary and tertiary control). These advantages combined with the ability to limit total harmonic distortion (THD) are inherent for the method proposed in this paper. In addition, the priorities of the proposed scheme (voltage deviation, frequency deviation, harmonics distortion) can be adjusted according to user preference, which contributes to the high level of flexibility.

In the continuation, this paper is organized as follows: In Section 2, the main idea behind the so-called “Decentralized self-stabilizing primary control of microgrids” [33] is briefly explained for the purpose of readability, since it is a base upon which the proposed harmonic compensation method proposed in this paper is built. The derivation of the proposed method and the implementation of the overall control system are presented in Section 3. The verification through simulation results is given in Section 4, followed by the conclusions in Section 5.

2. Decentralized Self-Stabilizing Primary Control of Microgrids

The strategy proposed in this paper extends the concept of the decentralized self-stabilizing primary control of microgrids proposed in [33] with harmonic mitigation capability. For the sake of readability, the main points of this concept are briefly explained here.

Frequency and voltage stability are the two most important goals for a microgrid’s smooth operation. This becomes even more apparent when peer-to-peer energy exchange among microgrid prosumers is required. Consequently, volatile power flows pose an additional challenge for microgrid stability.

Obviously, there are several conflicting goals at hand: voltage and frequency stability and free power exchange. One solution to coping with such a challenge might be to quantify all the goals of interest by one goal function.

For each microgrid node $l$ (Figure 1), a local goal function $V_{0l}$ was proposed

$$V_{0l}=\mathsf{\alpha }\left(P_l-P_l^{ref}\right)+\beta \left(v_l-v^{ref}\right),$$

(1)

where $P_l$ is the net active power output of the node $l$, $P_l^{ref}$ is the node’s net active power reference, $v_l$ is the node’s voltage, $v^{ref}$ is the node’s reference voltage, $\mathsf{\alpha }$ and $\beta$ are weight functions that determine a weight of relative deviation of the active power and voltage:

$$\mathsf{\alpha }\left(\Delta P_l\right)={\displaystyle \frac{1}{2}}{\alpha }_0\Delta P_l^2,{ \Delta P}_l=P_l-P_l^{ref},$$

(2)

$$\beta \left(\Delta v_l\right)={\displaystyle \frac{1}{2}}{\beta }_0{\displaystyle \frac{\Delta v_l^2}{\Delta v_{\max }^2-\Delta v_l^2}}, \Delta v_l=v_l-v^{ref},$$

(3)

where ${\alpha }_0$ and ${\beta }_0$ are control parameters, while $\Delta v_{max}$ is the maximal permittable voltage deviation. Note that the output of function $\beta$ grows rapidly when the voltage deviation approaches its limit, in contrast to function $\alpha$. Obviously, voltage stability is a much more important goal than achieving a desired power exchange. In this way, the control strategy defined by (1) has embedded voltage stabilization. It is assumed that grid nodes have different power references in accordance with the requirement for free energy exchange, while the voltage reference is the same for all nodes. The mechanism for frequency self-stabilization, which is of the utmost importance, will be explained in the continuation.

The voltage RMS $v$ and phase angle $\theta$ should be controlled at each grid node so that the node $l$ open-loop dynamics is given as

$$\begin{array}{rr}\dot{v_i}& =w_l\\ \dot{{\theta }_i}& ={\omega }_l\end{array},$$

(4)

where $w_l$ and ${\omega }_l$ are the control variables. Note that when only the fundamental voltage harmonic is considered, as is the case at this moment, voltage magnitude and its RMS are mutually replaceable (by the multiplication coefficient $\sqrt{2}$), so instead of voltage magnitude, RMS can be introduced in (4).

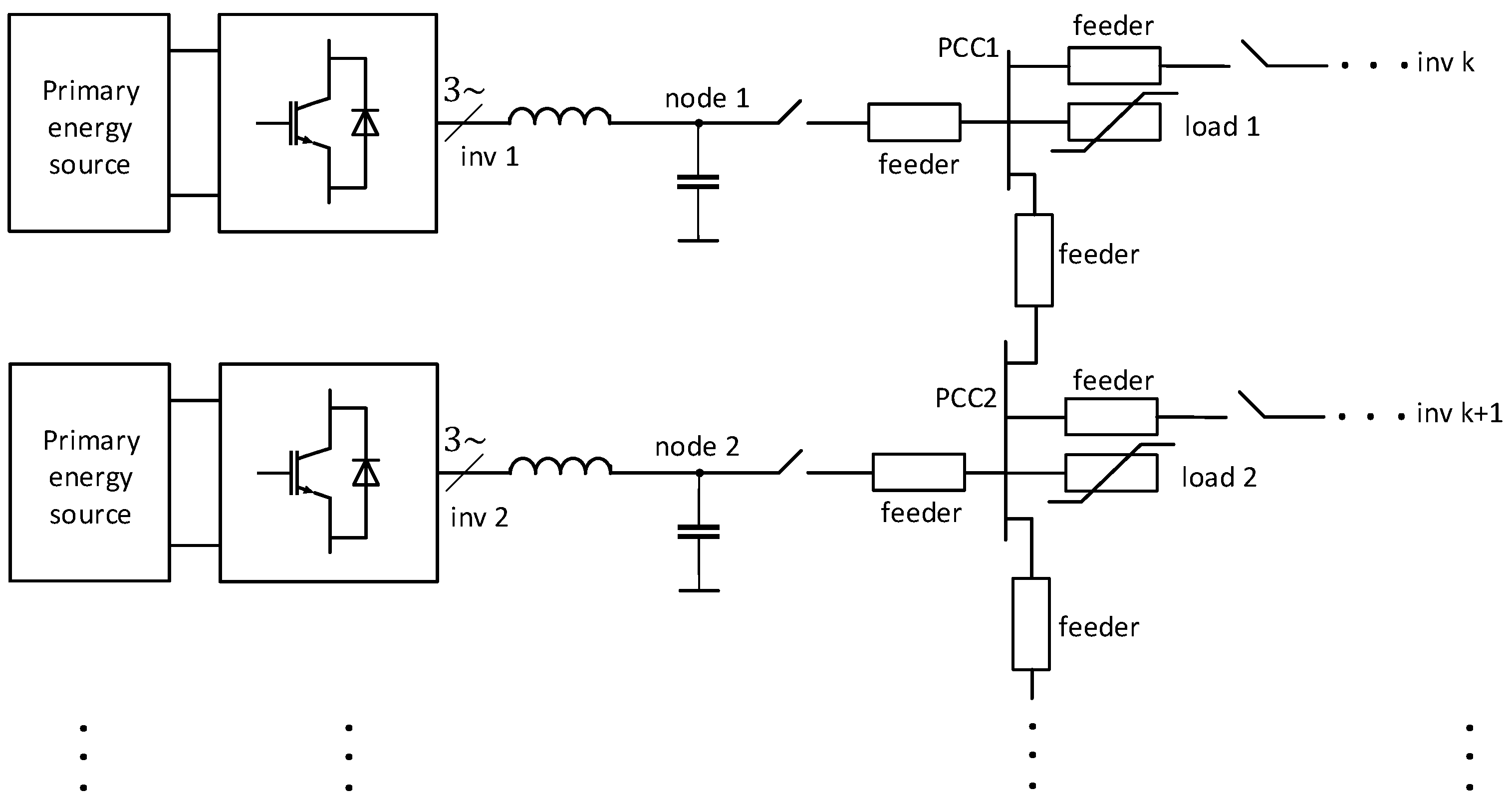
It is assumed that every microgrid node can be controlled by an inverter in the role of interface between a primary energy source (solar, wind, energy storage) and the microgrid. Therefore, a microgrid at hand could be depicted in a more detailed level, as displayed by Figure 2.

Note that the term “node” is employed for the output of any inverter, i.e., an output of its LC filter, because this point is directly controlled throughout an inverter operation, while the point where loads and inverter systems are connected is designated as a Point of Common Coupling (PCC).

Following Equations (1) and (4), the control law for node $l$ was defined as

$$\begin{array}{ll}{\dot{v}}_l& =w_l=-k_{v_l}{\displaystyle \frac{\partial V_{0l}}{\partial v_l}},\\ {\dot{\theta }}_l& ={\omega }_l=-\eta \left(k_{{\theta }_l}{\displaystyle \frac{\partial V_{0l}}{\partial {\theta }_l}}\right)+{\omega }^{ref},\end{array}$$

(5)

where local node parameters $k_{v_l}$ and $k_{{\theta }_l}$ are positive real coefficients which can affect the dynamics of the voltage and frequency change.

Note the $\eta \left(k_{{\theta }_l}{\displaystyle \frac{\partial V_{0l}}{\partial {\theta }_l}}\right)$ represents the frequency deviation from the nominal (reference) frequency ${\omega }^{ref}$.

$$\eta \left(a\right)=\Delta {\omega }_{max}\tan \mathrm{h}\left({\displaystyle \frac{\alpha }{{\alpha }_0}}\right),$$

(6)

The function $\eta$ belongs to a barrier-type functions which imposes a limit on a control variable because it is of the outmost importance to keep frequency stability.

The output, per-phase active and reactive power of the node $l$ can be calculated as in [34]:

$$\begin{gathered} P_l=\sum _{k\ne l}{v}_l^2{G}_{lk}-v_l{v}_k{G}_{lk}\cos \left({\theta }_l-{\theta }_k\right)+v_l{v}_k{B}_{lk}\sin \left({\theta }_l-{\theta }_k\right), \\ {Q}_l=\sum _{k\ne l}{v}_l^2{B}_{lk}-v_l{v}_k{G}_{lk}\sin \left({\theta }_l-{\theta }_k\right)-v_l{v}_k{B}_{lk}\cos \left({\theta }_l-{\theta }_k\right), \end{gathered}$$

(7)

where $G_{lk}$ and $B_{lk}$ are a conductance and susceptance between any two neighboring nodes $l$ and $k$ respectively, $v_l$ and $v_k$ are voltage RMS values while ${\theta }_l$ and ${\theta }_k$ are phase angles of nodes $l$ and $k$.

Taking this into account and following Equations (1), (5) and (6), the control law can be rewritten as

$$w_l=\dot{v_i}=-k_{v_l}\left[{\alpha }^{\prime }\left({\Delta P}_l\right)\left({\displaystyle \frac{P_l}{v_l}}+v_l{G}_l\right)+{\beta }^{\prime }\left({\Delta v}_l\right)\right],$$

(8)

$${\omega }_l=\dot{{\theta }_i}=-\eta \left[{k_{{\theta }_l}\alpha }^{\prime }\left({\Delta P}_l\right)\left(-Q_l+v_l^2{B}_l\right)+{\omega }^{ref}\right],$$

(9)

where $G_l=\sum _{k\ne l}{G}_{lk}$ and $B_l=\sum _{k\ne l}{B}_{lk}$. Expressions (8) and (9) essentially define the value of voltage phasor in each microgrid node to be achieved in order to fulfill the required goals.

The stability proof of the control law defined by Expressions (8) and (9) can be found in [33,35].

3. The Proposed Goal-Function-Based Harmonics Mitigation

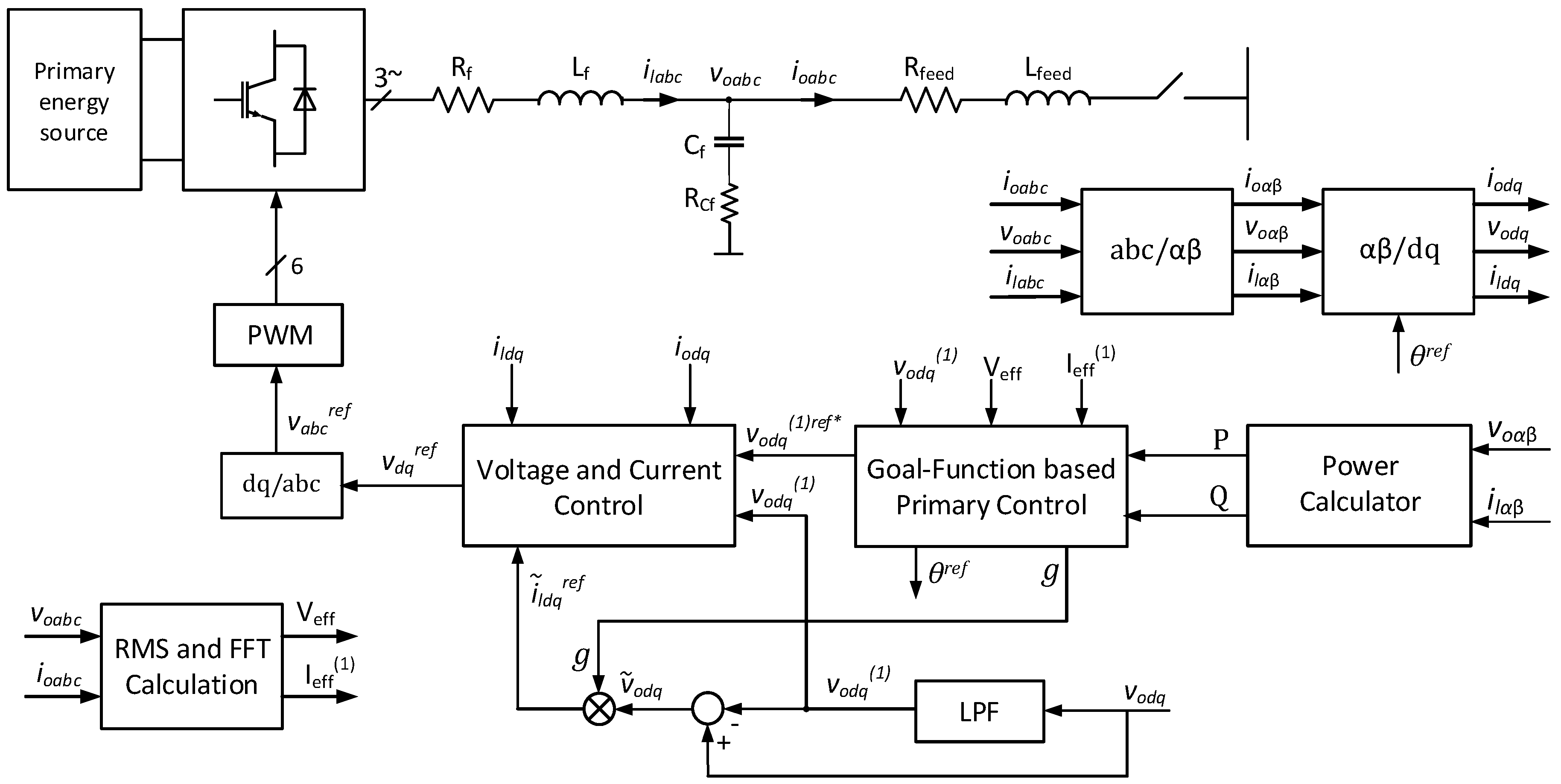
The proposed control concept is decentralized; therefore, the system control description (Figure 3) will be explained on a single inverter system taken from the microgrid depicted in Figure 2.

The core of the overall control structure is the Goal-Function-Based Primary Control, which gives the key control variables: the fundamental harmonic of the node reference volage phasor $v_{0dq}^{\left(1\right)ref}$ and a gain $g$ used to compensate for higher harmonic components of that voltage.

The control law defined in Section 2 deals only with power at the fundamental frequency (fundamental harmonic). Therefore, to improve voltage quality in the case of higher harmonics (e.g., produced by non-linear loads), the control law must be extended by an additional goal that will suppress higher voltage harmonics in microgrid nodes and points of common coupling. Therefore, in Section 3.1, the power of higher harmonics will be calculated, followed by a derivation of the proposed controlled law in Section 3.2. Finally, its step-by-step implementation based on Figure 3 will be presented in Section 3.4 and Section 3.5.

3.1. The Power of Higher Harmonics

The apparent power can be expressed as

$$S^2=P^2+Q^2+H^2,$$

(10)

where $P$ and $Q$ are active and reactive power at the fundamental harmonic, while $H$ presents the “harmonics power”, essentially an undesired component that should be mitigated.

In a three-phase balanced AC system, the power values per phase are

$$S=V_{eff}{I}_{eff}, P=V_{eff}^{\left(1\right)}{I}_{eff}^{\left(1\right)}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1, Q=V_{eff}^{\left(1\right)}{I}_{eff}^{\left(1\right)}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1,$$

(11)

where $V_{eff}$ and $I_{eff}$ are RMS values of the voltage and current respectively, $V_{eff}^{\left(1\right)}$ and $I_{eff}^{\left(1\right)}$ are RMS values of the first voltage and current harmonic, while ${\phi }_1$ is the phase shift between the fundamental harmonic of voltage and current.

The harmonics power $H$ can then be calculated as

$$H^2{=S}^2-P^2-Q^2=V_{eff}^2{I}_{eff}^2-{\left(V_{eff}^{\left(1\right)}\right)}^2{\left(I_{eff}^{\left(1\right)}\right)}^2.$$

(12)

Volage and current RMS value, $V_{eff}$ and $I_{eff}$, can be decomposed [36] on RMS value of the fundamental harmonic and RMS value of the rest of higher harmonics

$$V_{eff}^2={\left(V_{eff}^{\left(1\right)}\right)}^2+{\tilde{V}}_{eff}^2, {\tilde{V}}_{eff}^2=\sum _{h=2}{\left(V_{eff}^{\left(h\right)}\right)}^2,$$

(13)

$$I_{eff}^2={\left(I_{eff}^{\left(1\right)}\right)}^2+{\tilde{I}}_{eff}^2, {\tilde{I}}_{eff}^2=\sum _{h=2}{\left(I_{eff}^{\left(h\right)}\right)}^2,$$

(14)

where $V_{eff}^{\left(h\right)}$ and $I_{eff}^{\left(h\right)}$ are the voltage and current RMS values of the h—th harmonic, respectively.

The value of H can be calculated by combining (12) with (13) and (14)

$$\begin{gathered} H^2=\left({\left(V_{eff}^{\left(1\right)}\right)}^2+{\tilde{V}}_{eff}^2\right)\left({\left(I_{eff}^{\left(1\right)}\right)}^2+{\tilde{I}}_{eff}^2\right)-{\left(V_{eff}^{\left(1\right)}\right)}^2{\left(I_{eff}^{\left(1\right)}\right)}^2= \\ {\left(V_{eff}^{\left(1\right)}\right)}^2{\tilde{I}}_{eff}^2+{\left(I_{eff}^{\left(1\right)}\right)}^2{\tilde{V}}_{eff}^2+{\tilde{V}}_{eff}^2{\tilde{I}}_{eff}^2. \end{gathered}$$

(15)

The last term of the equation, ${\tilde{V}}_{eff}^2{\tilde{I}}_{eff}^2$ is significantly smaller than the remaining ones and can be neglected for all practical purposes, so

$$H^2={\left(V_{eff}^{\left(1\right)}\right)}^2{\tilde{I}}_{eff}^2+{\left(I_{eff}^{\left(1\right)}\right)}^2{\tilde{V}}_{eff}^2.$$

(16)

3.2. The Control Law Formulation

The control variable $g$ will be defined such that

$${\tilde{I}}_{eff}^2=g^2{\tilde{V}}_{eff}^2$$

(17)

Employing (17), (16) can be formulated as

$$H^2={\tilde{V}}_{eff}^2\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{\left(V_{eff}^{\left(1\right)}\right)}^2\right)=\left(V_{eff}^2-{\left(V_{eff}^{\left(1\right)}\right)}^2\right)\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{\left(V_{eff}^{\left(1\right)}\right)}^2\right)$$

(18)

Now, an additional term, $\mathsf{\gamma }\left(H^2\right)$ will be included in the goal function (1). This term will make the controlling agent aware of the harmonic disturbance and will make the states in which the harmonic disturbance is lower preferable.

$$V=\mathsf{\alpha }\left(\Delta P\right)+\beta \left(\Delta v\right)+\mathsf{\gamma }\left(H^2\right),$$

(19)

where

$$\mathsf{\gamma }\left(H^2\right)={\mathsf{\gamma }}_0{H}^2,$$

(20)

and ${\mathsf{\gamma }}_0$ is a real coefficient, i.e., $\mathsf{\gamma }\left(H^2\right)$ is a linear function with the argument $H^2$. Note that other functions could have been chosen for $\mathsf{\gamma }\left(H^2\right)$. It is only important that they grow slower than $\mathsf{\alpha }\left(\Delta P\right)$ and $\beta \left(\Delta v\right)$ defined by (2) and (3), so that the relative importance of harmonic mitigation is lower than that of keeping the network stable and achieving desired power exchange. Note that the node’s index l was omitted from (19) for the sake of simplicity. Keeping all this in mind, the new goal function can be presented as

$$V=V_0+\mathsf{\gamma }\left(H^2\right),$$

(21)

where $V_0$ is “the old” goal function defined by (1).

Applying (5), the control variables $w$ and $\omega$ are now calculated as follows:

$$w=-k_v{\displaystyle \frac{\partial V}{\partial v}}=-k_v{\displaystyle \frac{\partial V_0}{\partial v}}-k_v{\displaystyle \frac{\partial \mathsf{\gamma }\left(H^2\right)}{\partial v}}=-k_v{\displaystyle \frac{\partial V_0}{\partial v}}-k_v{\displaystyle \frac{\partial \mathsf{\gamma }\left(H^2\right)}{\partial \left(H^2\right)}}·{\displaystyle \frac{\partial \left(H^2\right)}{\partial v}}.$$

(22)

Note that the term $-k_v{\displaystyle \frac{\partial V_0}{\partial v}}$ is already defined by (8).

The second term from (22) becomes $k_v{\displaystyle \frac{\partial \mathsf{\gamma }\left(H^2\right)}{\partial \left(H^2\right)}}·{\displaystyle \frac{\partial \left(H^2\right)}{\partial v}}=k_v{\mathsf{\gamma }}_0·{\displaystyle \frac{\partial \left(H^2\right)}{\partial v}}$.

To calculate the term ${\displaystyle \frac{\partial \left(H^2\right)}{\partial v}}$, the harmonics power from (16) must be reformulated by means of variable $v$

$$H^2=\left(V_{eff}^2-v^2\right)\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{v}^2\right),$$

(23)

and therefore

$${\displaystyle \frac{\partial \left(H^2\right)}{\partial v}}=2v\left[g^2\left(V_{eff}^2-v^2\right)-\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{v}^2\right)\right].$$

(24)

Finally,

$$w=-k_v{\displaystyle \frac{\partial V_0}{\partial v}}-{2k}_v{\mathsf{\gamma }}_{0}v\left[g^2\left(V_{eff}^2-v^2\right)-\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{v}^2\right)\right],$$

(25)

where $-k_v{\displaystyle \frac{\partial V_0}{\partial v}}$ can be calculated as in (8).

The value of control variable $\omega$ can be obtained as

$$\mathsf{\omega }=-k_{\theta }{\displaystyle \frac{\partial V}{\partial \theta }}=-k_{\theta }{\displaystyle \frac{\partial \left(V_0+\mathsf{\gamma }\left(H^2\right)\right)}{\partial \theta }}=-k_{\theta }{\displaystyle \frac{\partial V_0}{\partial \theta }}-k_{\theta }{\displaystyle \frac{\partial \left(\mathsf{\gamma }\left(H^2\right)\right)}{\partial \theta }},$$

(26)

where $-k_{\theta }{\displaystyle \frac{\partial V_0}{\partial \theta }}$ has been already given by (9) and $\mathsf{\gamma }\left(H^2\right)$ is defined by (20).

Since (23) does not depend on θ, ${\displaystyle \frac{\partial \left(H^2\right)}{\partial \theta }}\equiv 0$.

Therefore,

$$\mathsf{\omega }=-k_{\theta }{\displaystyle \frac{\partial V_0}{\partial \theta }}=-\eta \left[{k_{\theta }\alpha }^{\prime }\left(∆P\right)\left(-Q+v^{2}B\right)+{\omega }^{ref}\right].$$

(27)

Finally, in analogy with $\omega =\dot{\theta }$ and $w=\dot{v}$, a new variable $a$ is defined as

$$a=\dot{g}.$$

(28)

At the other side, the variable $a$ is calculated from the goal function as

$$a=-k_g{\displaystyle \frac{\partial V}{\partial g}}=-k_g{\displaystyle \frac{\partial V_0}{\partial g}}-k_g{\displaystyle \frac{\partial \mathsf{\gamma }\left(H^2\right)}{\partial \left(H^2\right)}}·{\displaystyle \frac{\partial \left(H^2\right)}{\partial g}}=-{2k}_g{\mathsf{\gamma }}_0{v}^{2}g\left(V_{eff}^2-v^2\right).$$

(29)

Variables $v$ and $\theta$ define the voltage phasor reference value, while $g$ directs the higher harmonics compensation, as will be described in detail in Section 3.5. To summarize, Equations (4), (25), (27)–(29) are implemented as a key part of the Goal-Function-Based Primary Control (GFBPC) for achieving a decentralized primary microgrid control with higher harmonics suppression. The implemented equations are listed in

Table 1. GFBPC equations.

Core Control Equations

$∆P=P-P^{ref}$ $∆v=v-v^{ref}$ $\begin{array}{l}w=-k_v\left[{\alpha }_0∆P\left({\displaystyle \frac{P}{v}}+Gv\right)+{\beta }_0{\displaystyle \frac{\Delta v_{\max }^2∆v}{\Delta v_{\max }^2-∆v^2}}\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -{2k}_v{\mathsf{\gamma }}_{0}v\left[g^2\left(V_{eff}^2-v^2\right)-\left({\left(I_{eff}^{\left(1\right)}\right)}^2+g^2{v}^2\right)\right]\end{array}$ $\mathsf{\omega }=-\eta \left[{k_{\theta }\alpha }_0∆P\left(-Q+v^{2}B\right)+{\omega }^{ref}\right]$ $\dot{g}=-{2k}_g{\mathsf{\gamma }}_0{v}^{2}g\left(V_{eff}^2-v^2\right)$ $\begin{array}{rr}\dot{v}& =w\\ \dot{\theta }& =\omega \end{array}$

.

In the Appendix A it is shown that the proposed decentralized control strategy guarantees the boundedness of both voltage and frequency deviation, as well as the boundedness of harmonic distortions.

3.3. Goal-Function-Based Primary Control Implementation

Figure 4 shows the Goal-Function-Based Primary Control elements.

The variable $v$ is obtained via the magnitude of the node’s voltage fundamental harmonic $V_{0max}^{\left(1\right)}$ in the following way:

$$V_{0max}^{\left(1\right)}=\sqrt{{\left(v_{0d}^{\left(1\right)}\right)}^2+{\left(v_{0q}^{\left(1\right)}\right)}^2,}$$

(30)

while $v_{0d}^{\left(1\right)}$ and $v_{0q}^{\left(1\right)}$ are filtered values of the voltage components $v_{od}$ and $v_{oq}$ procured from the three phase voltages $v_{oabc}$ by means of dq transform, where the transformation angle is one of the Goal-Function outputs. After applying the magnitude invariant abc/dq transformation on the signal with the fundamental and higher harmonics, the fundamental harmonic will be transformed into a DC value, while higher harmonics will still be at higher frequencies. Therefore, the fundamental harmonic can be extracted by employing a low-pass filter, such as

$$LPF\left(s\right)={\displaystyle \frac{{\omega }_c}{s+{\omega }_c}},$$

(31)

where ${\omega }_c$ is chosen as a compromise between the satisfactory harmonics’ attenuation and filter dynamics.

Inputs in the Equations Calculator, P and Q are obtained from the Power Calculator block, while $V_{eff}$ and $I_{eff}^{\left(1\right)}$ are calculated (Figure 3) as a RMS of the voltage $v_{0abc}$ and applying FFT to the current $i_{0abc}$ respectively. The input $P^{ref}$ is set to the value of zero. In the case when the secondary control would be included, this variable would be fed from the secondary control subsystem.

The Equations Calculator outputs $V_{max}^{\left(1\right)ref}$ and ${\theta }^{ref}$ are employed to set the reference value of the voltage fundamental harmonic $V_{0dq}^{\left(1\right)ref*}$ which is fed to the Voltage and Current Control block. The angle ${\theta }^{ref}$ is used as an input for all abc/dq and dq/abc transformations.

3.4. Goal-Function-Based Primary Control Implementation

Inverter apparent power $\widehat{S}$ can be calculated using magnitude invariant $\alpha \beta$ reference frame as

$$\begin{array}{l}\widehat{S}={\displaystyle \frac{3}{2}}\left(v_{0\alpha }+j{v}_{0\beta }\right){\left(i_{l\alpha }+j{i}_{l\beta }\right)}^{*}={\displaystyle \frac{3}{2}}\left(v_{0\alpha }{i}_{l\alpha }+v_{0\beta }{i}_{l\beta }\right)+j{\displaystyle \frac{3}{2}}\left(-v_{0\alpha }{i}_{l\beta }+v_{0\beta }{i}_{l\alpha }\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =P_{tot}+j{Q}_{tot},\end{array}$$

(32)

and consequently

$$P_{tot}={\displaystyle \frac{3}{2}}\left(v_{0\alpha }{i}_{l\alpha }+v_{0\beta }{i}_{l\beta }\right), Q_{tot}={\displaystyle \frac{3}{2}}\left(-v_{0\alpha }{i}_{l\beta }+v_{0\beta }{i}_{l\alpha }\right).$$

(33)

Variables $P_{tot}$ and $Q_{tot}$ could contain power components at higher harmonics $\tilde{P}$ and $\tilde{Q}$, beside the desired active and reactive power $P$ and $Q$, i.e.,

$$P_{tot}=\tilde{P}+P, Q_{tot}=\tilde{Q}+Q.$$

(34)

Therefore, active and reactive power $P$ and $Q$ are obtained by filtering $P_{tot}$ and $Q_{tot}$ applying (31).

3.5. Voltage and Current Control

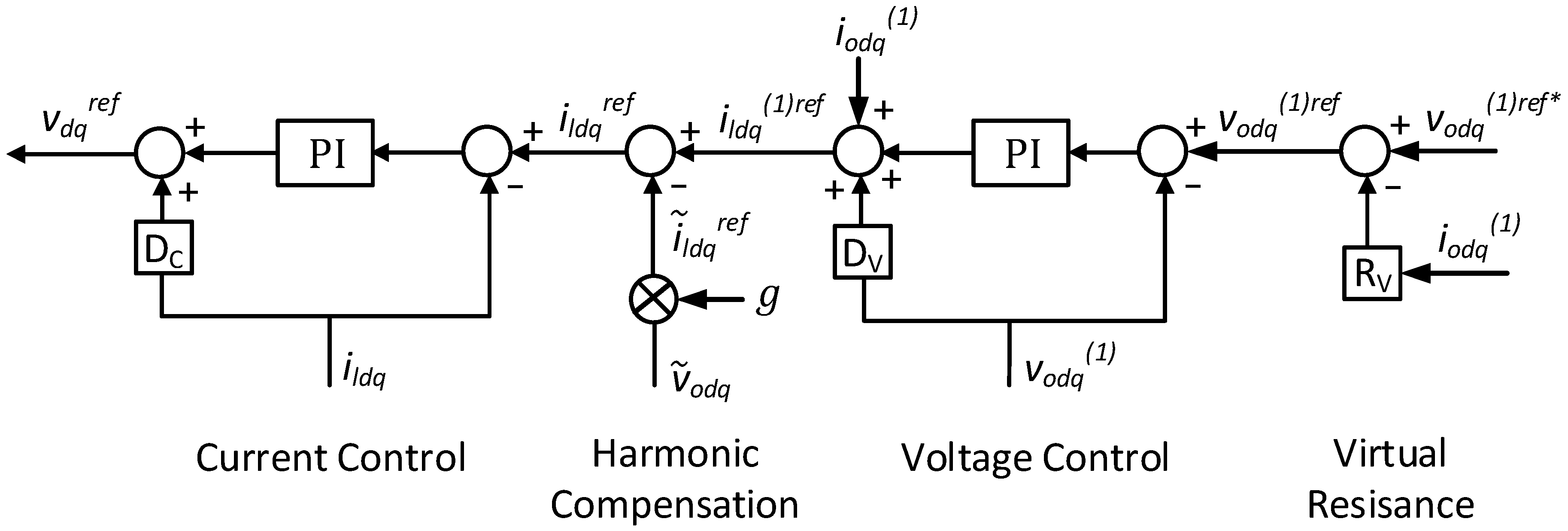
The inverter local voltage and current structure shown in Figure 5 is implemented in the rotating (dq) system. It consists of four main elements: Virtual Resistance, Voltage Control, Harmonic Compensation and Current Control.

The virtual resistance $R_v$ increases the system oscillation damping [37], which is a particularly convenient feature in a microgrid. When droop control is applied, a very often approach is to design a virtual inductance beside a virtual resistance. The role of virtual inductance (reactance) is to improve active and reactive power decoupling [38]. Namely, the droop-oriented primary control is based on a linear (droop) approximation of expressions for active and reactive power flow between any two nodes, as presented in (7). When the grid is purely resistive or inductive, such an approximation works rather satisfactorily. However, when the values of line reactance and resistance are comparable, an additional solution must be adopted. One such solution is the inclusion of a virtual reactance. In this paper, there is no need to employ a virtual reactance because the proposed method is not based on linear approximations, and it is one of its important advantages.

The voltage fundamental harmonic reference $v_{0dq}^{\left(1\right)ref}$ which is to be fed to the voltage controller is calculated from the voltage $v_{0dq}^{\left(1\right)ref*}$ as an output of the Goal-Function by subtracting the voltage drop on the virtual resistance:

$$v_{0dq}^{\left(1\right)ref}=v_{0dq}^{\left(1\right)ref*}-R_v·i_{0dq}^{\left(1\right)}.$$

(35)

The Voltage Controller contains a PI regulator accompanied by a decoupling element ${\widehat{D}}_v=j{\omega }_0{C}_f{v}_{0dq}$, where $C_f$ is a capacitor of the LC filter (see Figure 3). Namely, neglecting the voltage drop on $R_{Cf}$ as an equivalent series resistance of $C_f$,

$$C_f{\displaystyle \frac{d{v}_{0\alpha \beta }}{dt}}=i_{l\alpha \beta }-i_{0\alpha \beta }.$$

(36)

After applying dq transform to arbitrary variable $v_{0\alpha \beta }$, $v_{0\alpha \beta }=v_{0dq}{e}^{j\omega t}$, Equation (36) becomes

$$C_f{\displaystyle \frac{d{v}_{0dq}}{dt}}+j\omega C_f{v}_{0dq}=i_{ldq}-i_{0dq},$$

(37)

i.e., control of the fundamental voltage harmonic is obtained as

$$i_{ldq}^{\left(1\right)ref}=PI\left(v_{0dq}^{\left(1\right)}\right)+j\omega C_f·v_{0dq}^{\left(1\right)}+i_{0dq}^{\left(1\right)},$$

(38)

where d and q current components $i_{0dq}^{\left(1\right)}$ are filtered out from $i_{0dq}$ by applying (31).

The output of the voltage controller is the reference to the inverter’s fundamental current harmonic $i_{ldq}^{\left(1\right)ref}$. However, the currents $i_{0dq}$ (i.e., $i_{0abc}$) due to non-linear loads might contain components at higher “lower harmonics”, such as fifth and seventh. High-order harmonics as a consequence of PWM switching are not considered by means of control structure since the LC filter is designed to deal with them. In order to address the lower harmonics, the Harmonics Compensation block (Figure 5) is added. It measures the harmonics component of the volage $v_{0dq}$, ${\tilde{v}}_{0dq}$. The voltage ${\tilde{v}}_{0dq}$ is obtained by subtracting the fundamental harmonic component $v_{0dq}^{\left(1\right)}$ from the overall voltage $v_{0dq}$ (Figure 3). Multiplying ${\tilde{v}}_{0dq}$ by the control variable $g$ from (28) and (29), aimed to suppress the total harmonic power; the harmonic current ${\tilde{i}}_{ldq}^{ref}$ is generated. Addition of ${\tilde{i}}_{ldq}^{ref}$ to the $i_{ldq}^{\left(1\right)ref}$ with the negative sign is set to compensate for the distorted currents responsible for the voltage harmonic distortion.

Finally, the current controller consists of a PI regulator with a decoupling element ${\widehat{D}}_c=j{\omega }_0{L}_f{i}_{ldq}$, in a similar way as it was the case with the Voltage Controller.

4. Simulation Results

The proposed harmonics mitigation control strategy is tested in Matlab/Simulink (https://www.mathworks.com/products/matlab.html, 18 September 2024) on the system with two inverter units (Figure 6) with two points of common coupling, PCC1 and PCC2, where both non-linear and linear loads in different moments are connected. It is assumed that both inverters have identical parameters, which are given in

Table 2. Inverter nominal system parameters.

Apparent Power [kVA]	Line Voltage [V]	Switching Frequency [kHz]	DC Bus Voltage [V]
10	400	10	650

.

LC output filter is designed following the guidelines [39] according to which the filter inductance $L_f$ should be chosen based on the maximal permissible inverter current ripple (generally 15–25%, in this paper 18% is chosen), while as a rule of thumb

$$10f_g<f_{res}\ll f_{sw}.$$

(39)

While $f_g$ is a nominal grid frequency, $f_g=50$ Hz, $f_{sw}$ is a switching frequency from Table 2, and $f_{res}$ is an LC filter resonance frequency

$$f_{res}={\displaystyle \frac{1}{2\pi \sqrt{L_f{C}_f}}}.$$

(40)

For LC filter damping, passive damping is chosen, with damping resistor $R_{C_f}$ given as

$$R_{C_f}=\xi \sqrt{{\displaystyle \frac{L_f}{C_f}}},$$

(41)

where ξ is a damping factor, chosen as ξ = 0.6.

Parameters of the LC filter are given in

Table 3. LC filter, load and feeder’s parameters.

${\mathit{L}}_{\mathit{f}}\left[\mathbf{m}\mathbf{H}\right]$	${\mathit{C}}_{\mathit{f}}\left[\mathsf{\mu }\mathbf{H}\right]$	${\mathit{R}}_{{\mathit{C}}_{\mathit{f}}}\left[\mathit{\Omega }\right]$	${\mathit{Z}}_{\mathit{f}\mathit{e}\mathit{e}\mathit{d}1}\left[\mathit{\Omega }\right]$	${\mathit{Z}}_{\mathit{f}\mathit{e}\mathit{e}\mathit{d}2}\left[\mathit{\Omega }\right]$	${\mathit{Z}}_{\mathit{f}\mathit{e}\mathit{e}\mathit{d}12}\left[\mathit{\Omega }\right]$	${\mathit{Z}}_{\mathit{L}\mathit{o}\mathit{a}\mathit{d}1}\left[\mathit{\Omega }\right]$
1.8	25	5	0.6 + j1.6965	0.2 + j0.5655	0.1 + j0.056	50 + j12.56

together with feeders’ and linear load (Load1) parameters.

Note that the feeder impedances have comparable inductive and resistive components, where the Feeder 12 is predominantly resistive, while other two are predominantly inductive. Feeder 1 has exactly three times greater impedance than Feeder 2, i.e., the distance between Inverter 1 and its point of common coupling (PCC1) is three times longer than the distance between Inverter 2 and PCC2.

Non-linear loads (Load 1 and Load 2) are three-phase diode rectifiers, chosen here because they are very common consumer components and because they are among the highest harmonic polluters. The value of the DC bus capacitors of each rectifier is set to 1 mF, while they are loaded with a resistive load of 100 Ω.

Control system parameters, such as Goal-Function-Based Harmonic Mitigation (GFBHM) parameters, are given in

Table 4. GFBHM parameters.

${\mathsf{\alpha }}_0$	${\mathsf{\beta }}_0$	${\mathsf{\gamma }}_0$	${\mathit{G}}_1$$\left[\mathit{S}\right]$	${\mathit{G}}_2\left[\mathit{S}\right]$	${\mathit{B}}_1\left[\mathit{S}\right]$	${\mathit{B}}_2\left[\mathit{S}\right]$	$\Delta {\mathit{v}}_{\mathit{m}\mathit{a}\mathit{x}}\left[\mathit{V}\right]$
${10}^{-8}$	$100$	${2·10}^{-9}$	$3$	$1.25$	$1$	$0.65$	$10$

, while voltage and current PI controller parameters are given in

Table 5. Voltage and current controller parameters.

Voltage Control PI Controller		Current Control PI Controller		Virtual Resistance
$k_{pv}$	$k_{iv}$	$k_{pc}$	$k_{ic}$	$R_v \left[\Omega \right]$
$2$	$50$	$10$	$1000$	$1$

.

All parameter values have been determined empirically. Parameters ${\mathsf{\alpha }}_0$ and ${\mathsf{\gamma }}_0$ have rather small values since they are multiplied with the square value of power, as defined in (2) and (20), respectively. In addition, note that the value of ${\mathsf{\gamma }}_0$ is an order of magnitude lower than ${\mathsf{\alpha }}_0$ since, the goal of preserving voltage stability is of much higher importance than harmonics suppression. Furthermore, GFBHM parameters $k_v$, $k_{\theta }$ and $k_g$ are all set to the value 1. Parameters B and G, although expressed in [S], S = 1/Ω, are the controller parameters.

The simulation sequence is designed as follows:

• GFBHM control is off at the start;
• Load 1 (a linear load) is connected from the start;
• At the moment t = 0.3 s, Load 2 (a non-linear load) is connected. GFBHM control is still off;
• At the moment t = 0.75 s, GFBHM control is on;
• At the moment t = 1.2 s, Load 3 (a non-linear load) is connected;
• At the moment t = 1.7 s, Load 2 and Load 3 are disconnected, Load 2 is still connected, and GFBHM control is still on;
• The simulation ends at the moment t = 2 s.

Figure 7 presents the active power generated from both inverter units (P₁ and P₂) and system frequency. Inverters (inv. 1 and inv. 2 from Figure 6) share the load according to their GFBHM parameters, which are set equally. Since the impedance of Feeder 1 is three times bigger than the impedance of Feeder 2 and more than six times bigger than the impedance of the interconnecting Feeder 12, inverter 2 takes a higher share. In Figure 7b, reference frequencies generated by GFBHM control of each inverter system (Ref. Freq 1 and Ref. Freq. 2) are displayed together with the frequency measured by the PLL (PLL Frequency). It can be noticed that due to the goal function’s highest priority of keeping the frequency stable, frequency is kept very tightly to the reference value of 50 Hz, safely into the borders of 50 Hz +/−1%.

In Figure 8, voltages V_o1 and V_o2 are shown. From their RMS values, it can be seen that the voltage drop is less than 10 V. At the beginning, THD is very small, around 1%. Then, when non-linear Load 2 (three-phase rectifier is plugged in, it rises to 18% for Vo1 and 16% for Vo1. With the start of harmonic compensation, THD falls to a couple percent. When non-linear Load 2 is plugged in at the moment of 1.2 s, THD rises slightly since the compensation is still active.

Similar qualitative conclusions can be drawn for voltages in the points of common coupling V_pcc1 and V_pcc2 (Figure 9), with the difference that points of common coupling are a feeder away from the inverters and therefore they experience somewhat higher voltage drop and THD in the whole process.

However, THD is less than 8% when both non-linear loads are connected.

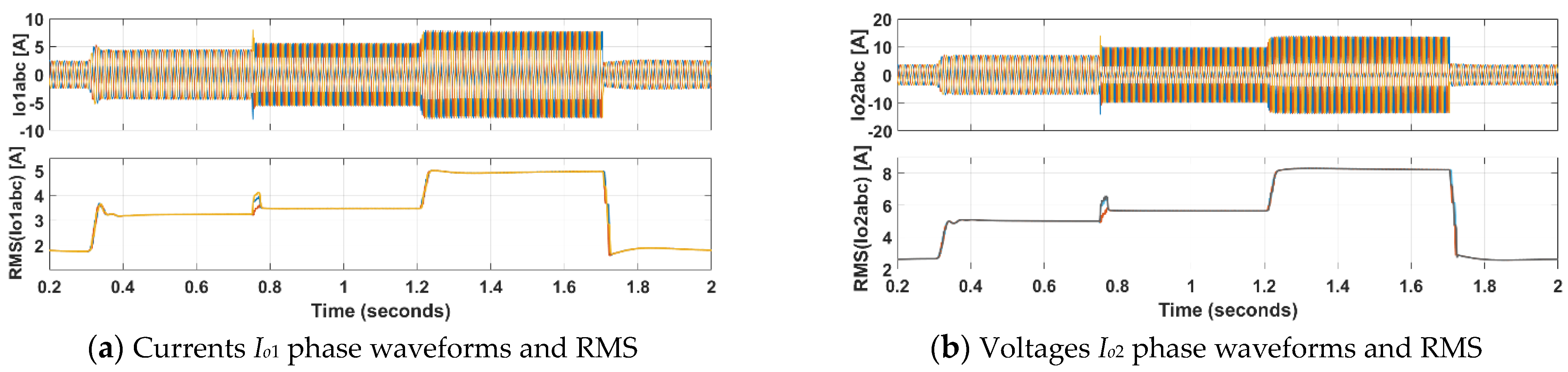
In Figure 10, inverter output currents after filtering, I_o1 and I_o2 are shown. They generally follow the pattern of respective active power from Figure 7a.

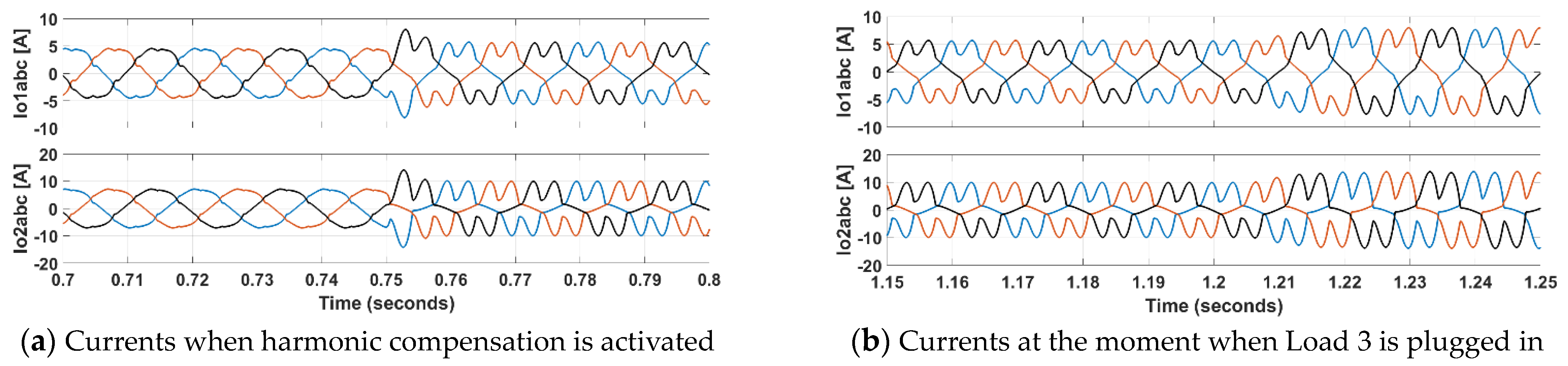
Figure 11 presents two details from Figure 10 around the moment of 0.7 s when the harmonic compensation is activated and another detail around the moment of 1.2 s when a non-linear load, Load 3, is plugged in, while compensation is still on. It is noticeable that the current waveform deteriorates further at the moment of starting the harmonic compensation because inverters generate recognizable distorted current components to deal with the rectifier current.

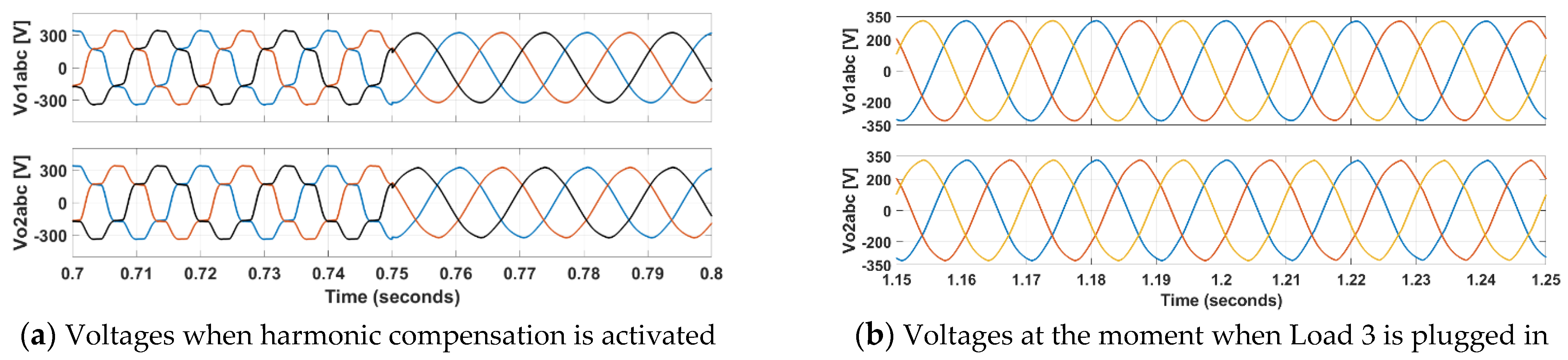
In Figure 12, voltages V_o1 and V_o2 can be observed at the same moments as in Figure 11. Before the harmonic compensation started (Figure 12a), voltages are highly distorted, as already indicated from their THD values (Figure 8). From the moment 0.75 s when harmonic compensation starts, their waveforms are much improved. At the moment of 1.2 s (Figure 12b), a non-linear load, Load 3 is plugged in, which slightly affects waveforms since the compensation is still active.

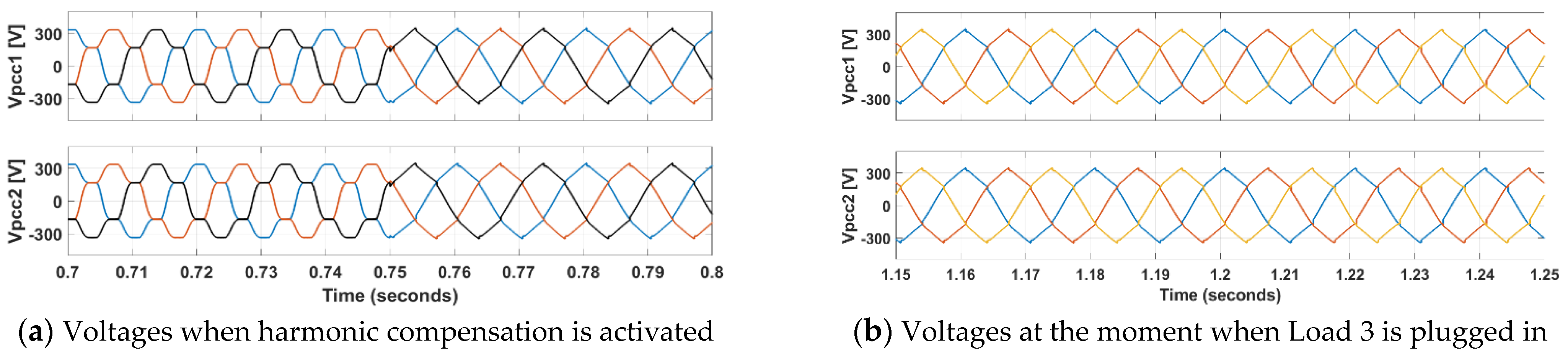
A very similar qualitative analysis applies for voltages of the points of common coupling V_pcc1 and V_pcc2 (Figure 13), with the remark that their waveforms are more distorted since they are a feeder or two away from one or another inverter.

5. Conclusions

This paper proposes a goal function-based decentralized control of microgrids with an arbitrary X/R feeders ratio and grid topology. The proposed approach ensures that the main microgrid stability indicators, voltage and frequency will remain within the predetermined boundaries. Furthermore, an additional goal was set to reduce voltage harmonics in the grid nodes where the grid-tied converters are located. A grid-tied converter as an interface between distribution generation and a grid was controlled in such a way as to compensate for distorted currents produced by non-linear loads, thus improving voltage THD. The priorities of the proposed scheme could be adjusted according to user preferences. Although the proposed derivation of the control law is not trivial, its final form is simple, facilitating simple implementation in practice. The performance of the proposed method was validated through simulations and the results of all relevant indicators. Voltage distortion at the nods where grid-tied inverters are located was reduced decisively, while the microgrid frequency was kept tightly around the pre-set value with a voltage magnitude drop in accordance with the expectations. Similarly, although slightly deteriorated, the situation was at the point of common coupling with loads. In future research, the control law should be extended to include compensation for unbalanced non-linear loads.