Distributed Optimization Strategy for New Energy Stations and Energy Storage Stations Considering Multiple Time Scales
Abstract
1. Introduction
2. Problem Formulation
2.1. Model Establishment
2.2. Constraint Condition
- (1)
- Power balance constraints
- (2)
- Generator output constraint
- (3)
- Wind and photovoltaic output constraints
- (4)
- ES charge/discharge constraints
- (5)
- State of charge constraint
2.3. Objective Function
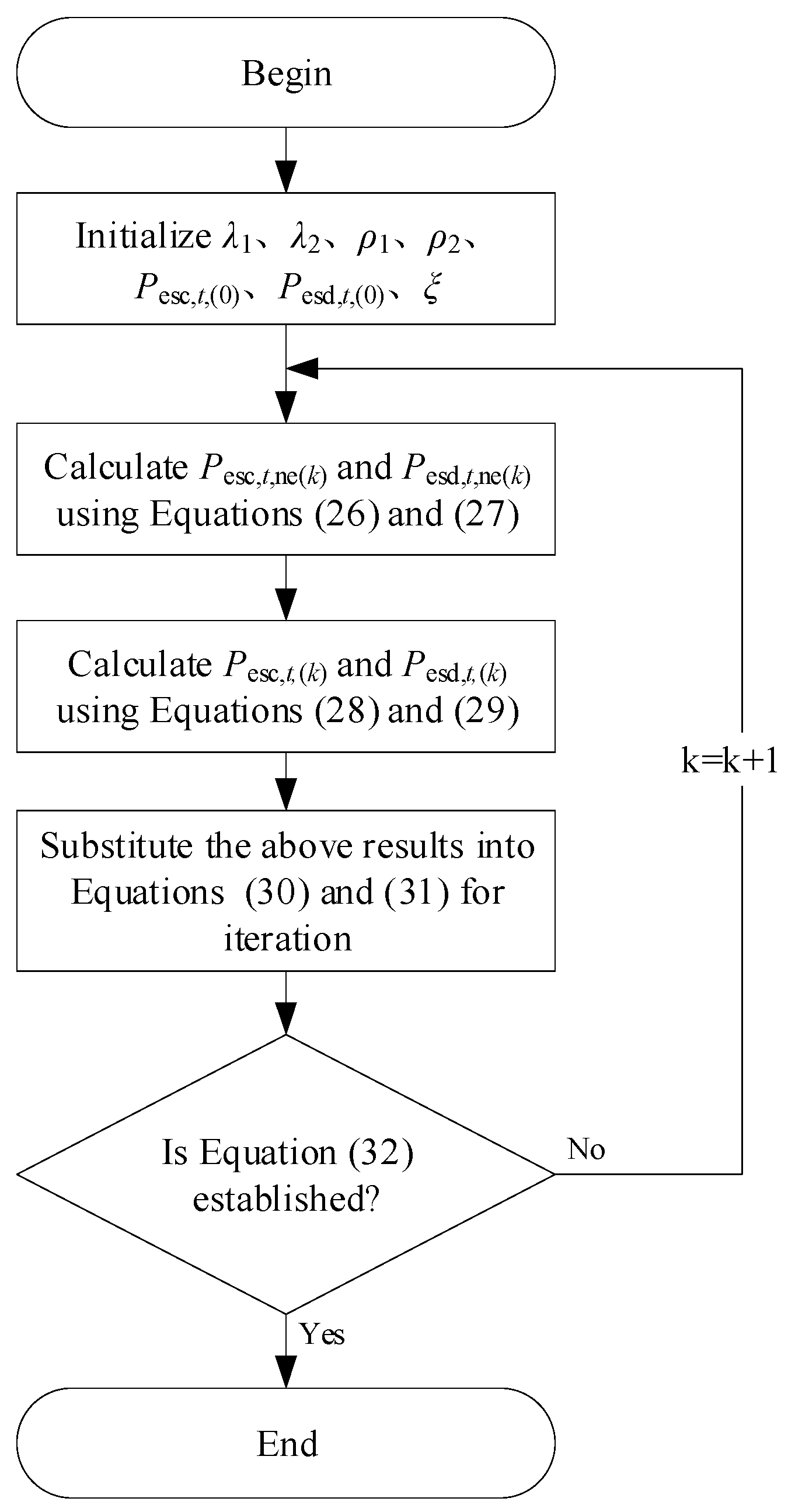
3. Solving the Objective Function
3.1. Alternate Direction Multiplier Method (ADMM)
3.2. Distributed Optimization of NESs
3.3. Distributed Optimization of ESSs
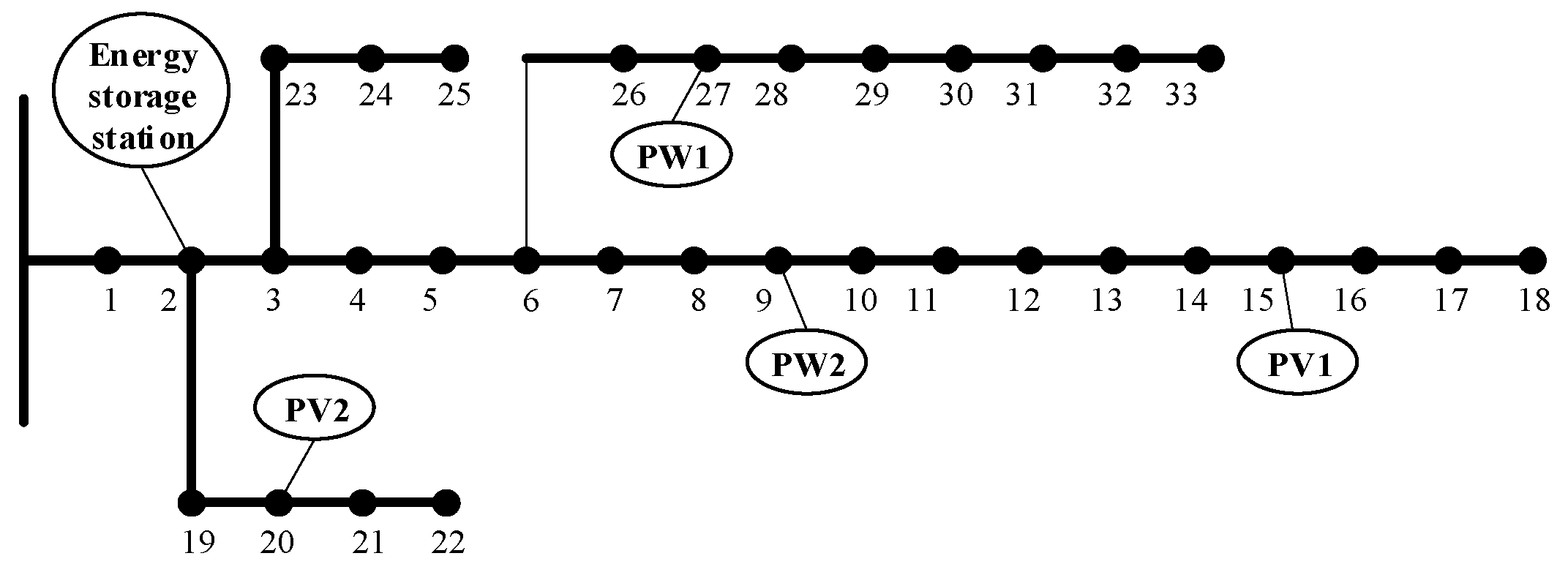
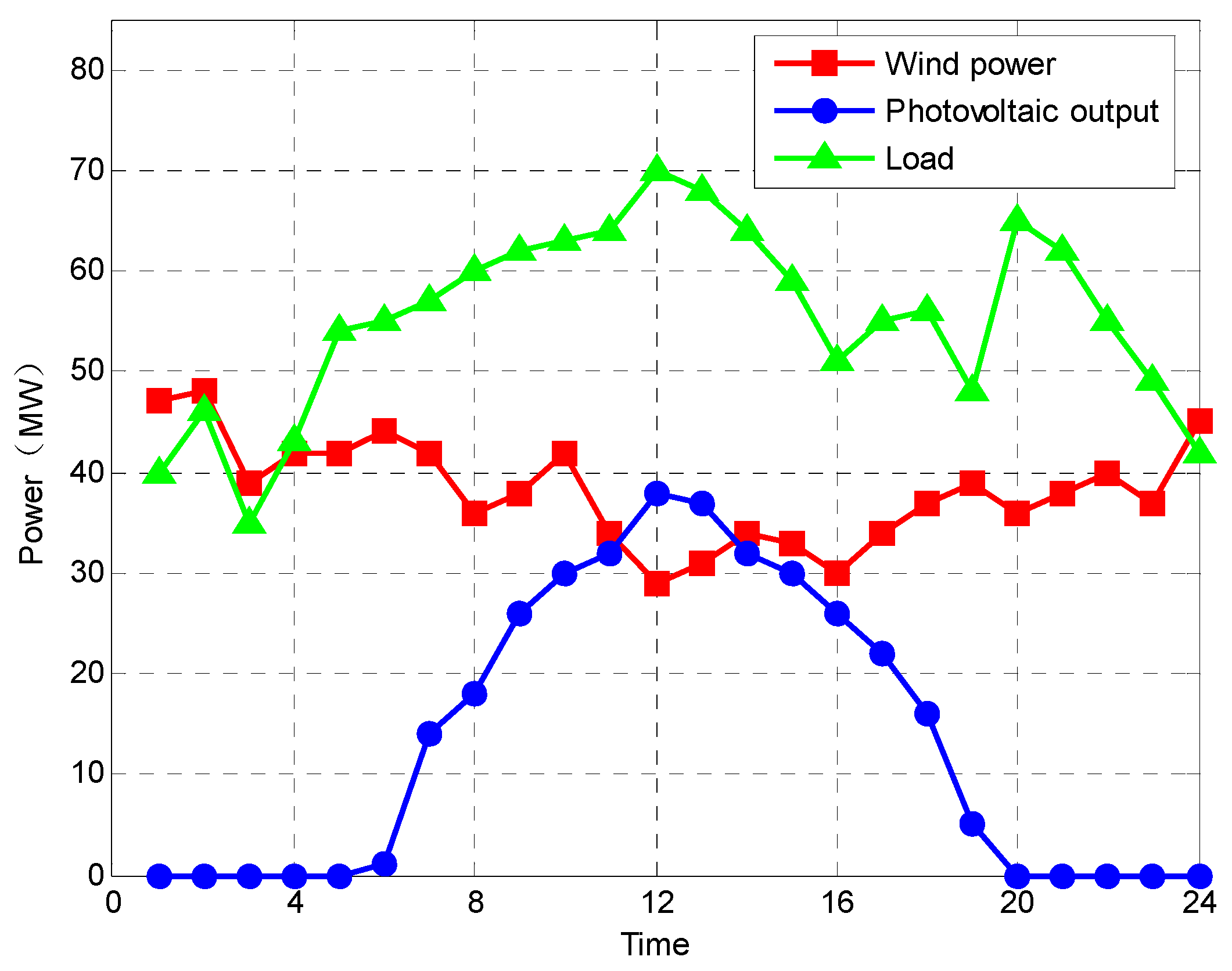
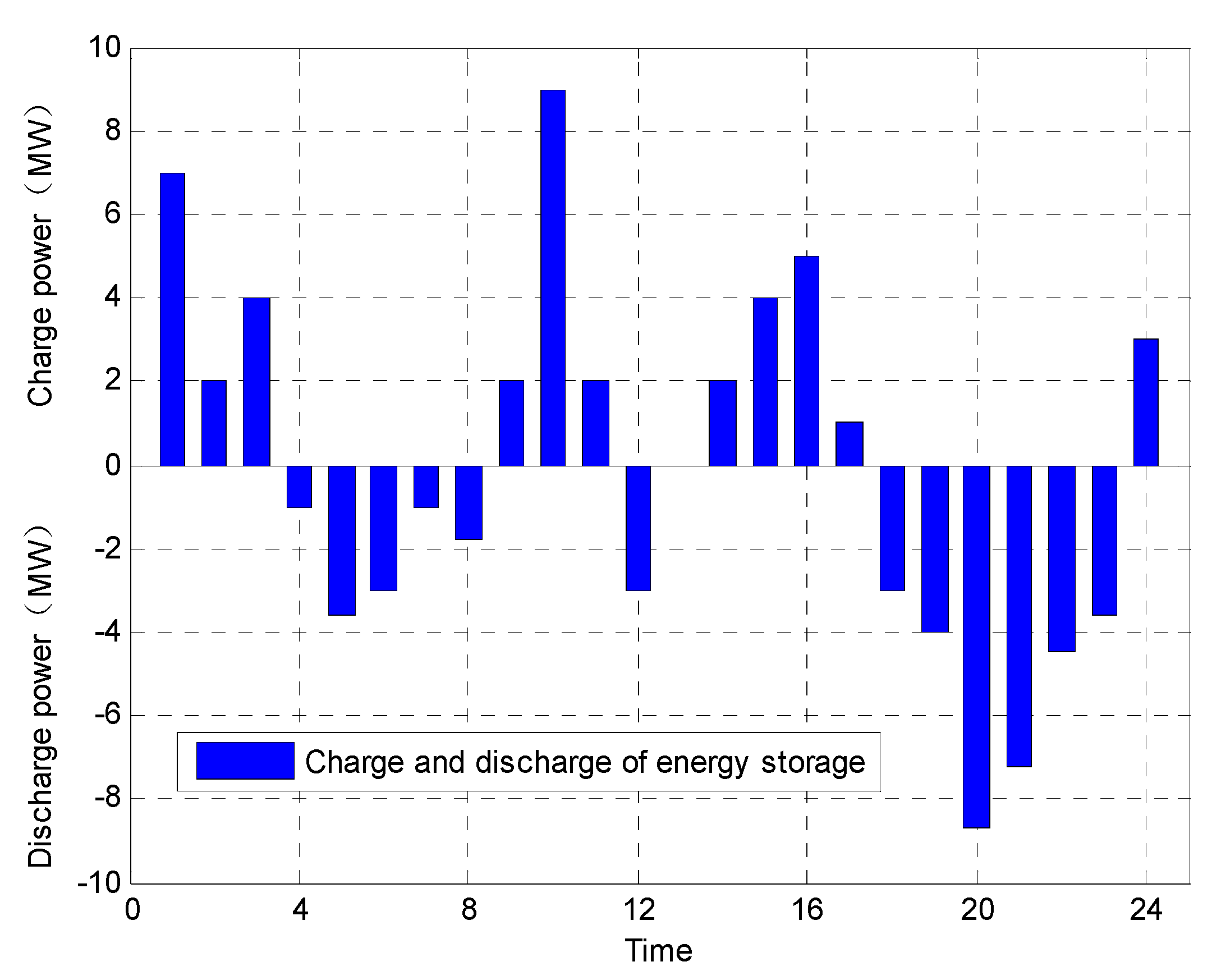
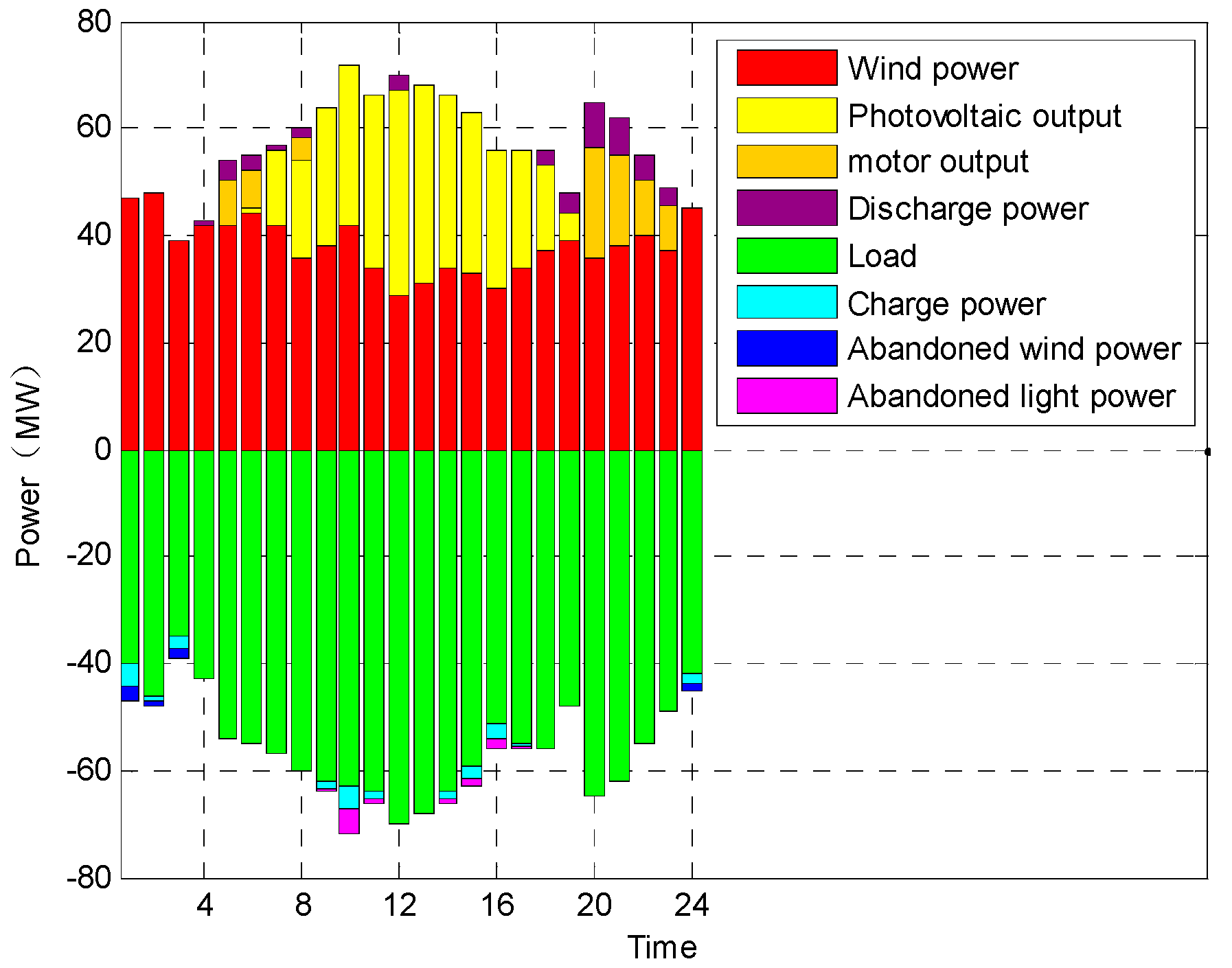
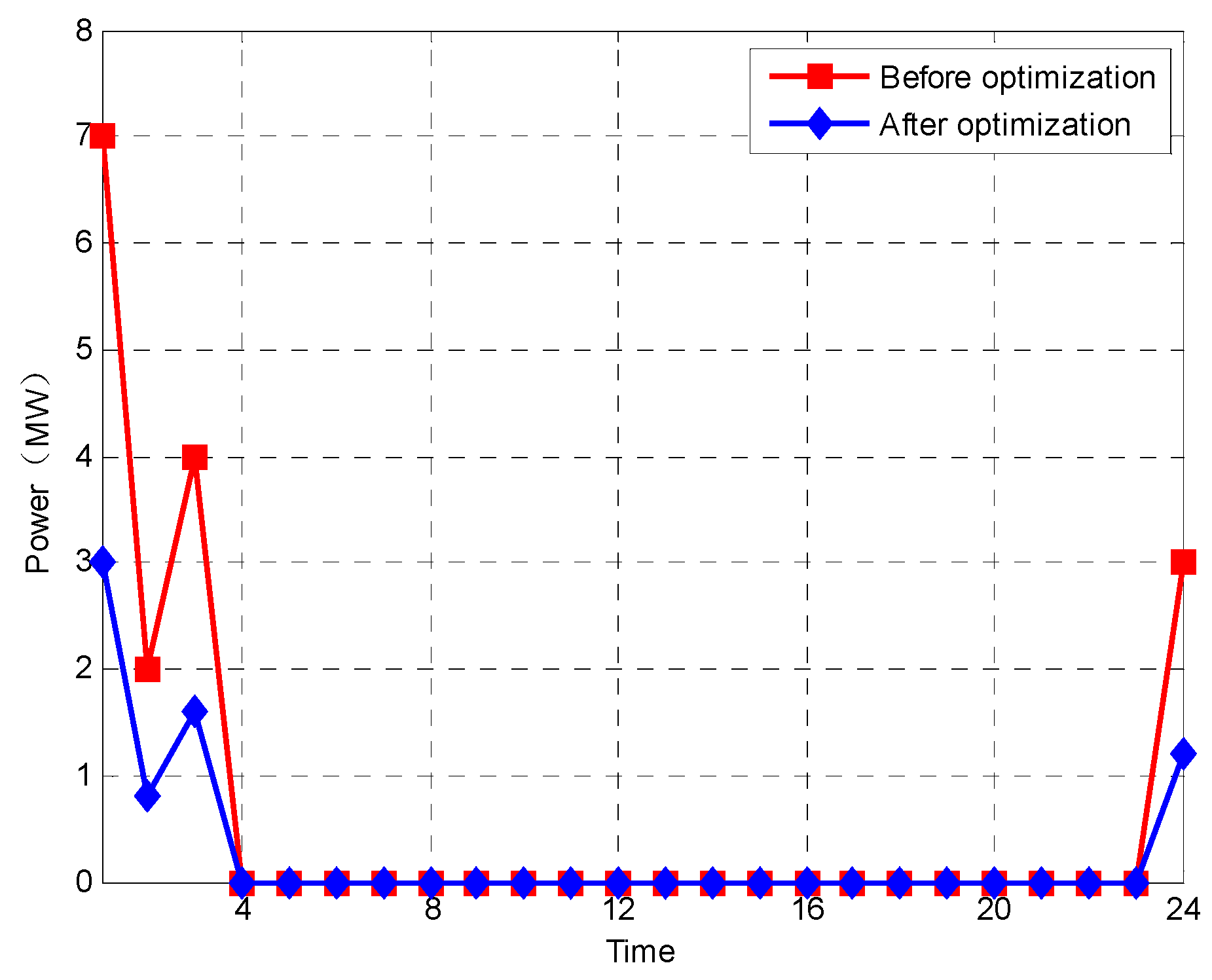
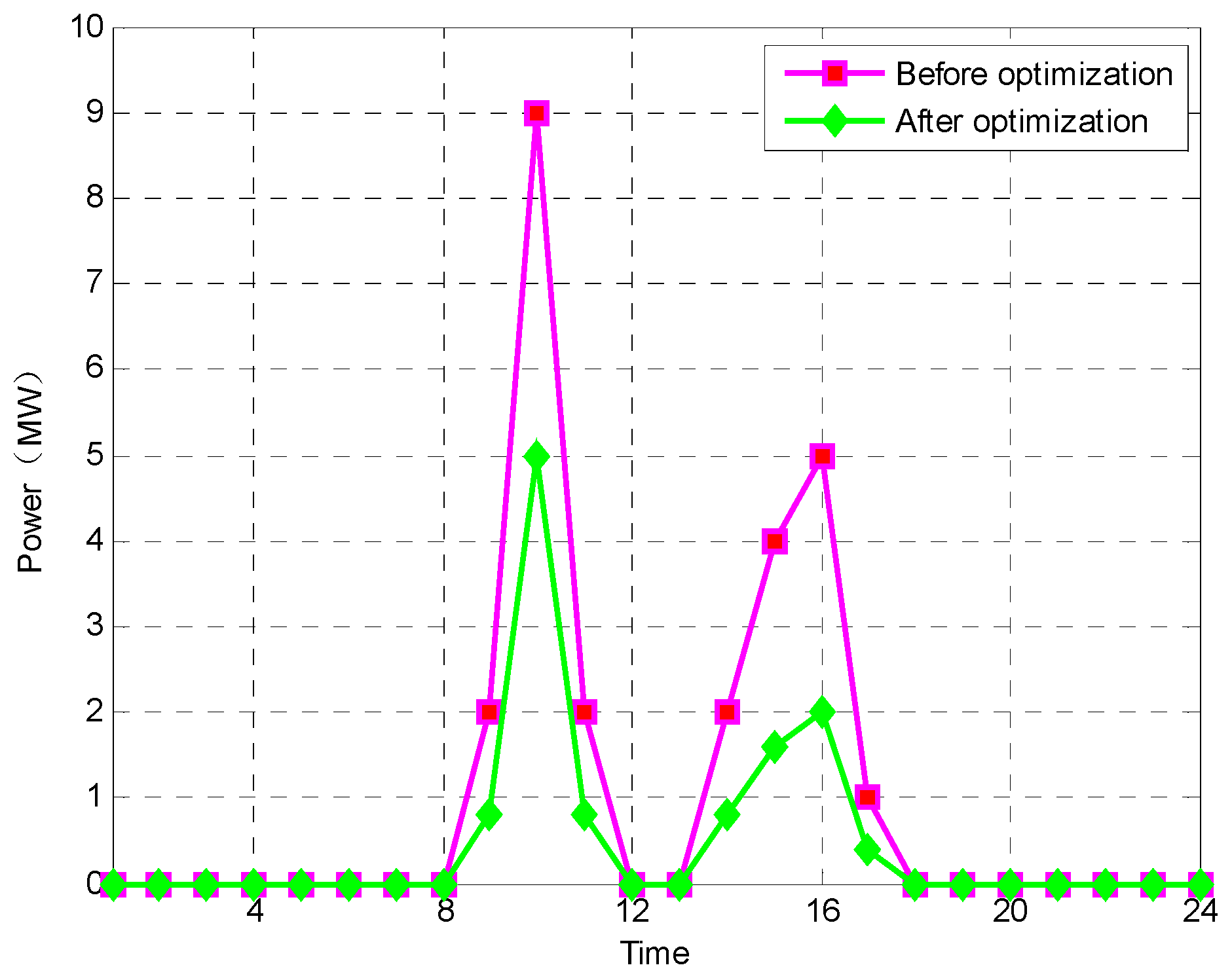
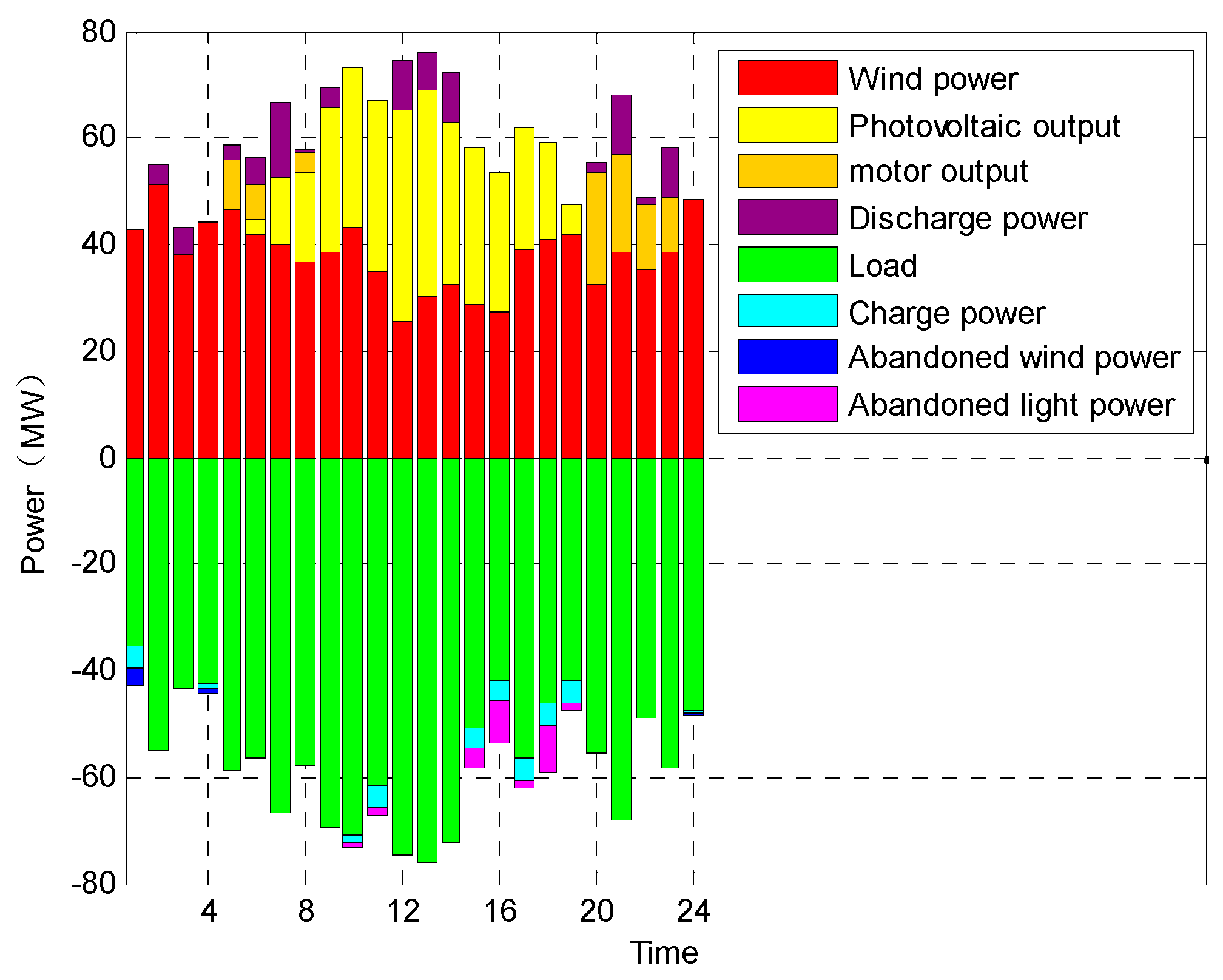
4. Example Analysis
4.1. Result Analysis
4.2. Revenue Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Li, B.; Zhao, T.; Zhao, W.; Xu, P.; Xie, H. Transient angle instability mode and mechanism of distributed synchronous condensers in renewable energy station. Autom. Electr. Power Syst. 2023, 47, 12–18. [Google Scholar]
- Rosales-Asensio, E.; Diez, D.B.; Cabrera, P.; Sarmento, P. Effectiveness and efficiency of support schemes in promoting renewable energy sources in the Spanish electricity market. Int. J. Electr. Power Energy Syst. 2024, 158, 109926. [Google Scholar] [CrossRef]
- Long, Y.; Liu, X. Optimal green investment strategy for grid-connected microgrid considering the impact of renewable energy source endowment and incentive policy. Energy 2024, 295, 131073. [Google Scholar] [CrossRef]
- Bi, T.; Li, Y.; Jia, K.; Yang, Q. Transient current waveform similarity based pilot protection for transmission lines connected to renewable energy power plants. Proc. CSEE 2018, 38, 2012–2019. [Google Scholar]
- Yang, G.; Fan, P.; Wang, C.; Yu, Y.; Lv, P.; Liang, Y.; Zhang, Z. Pilot protection based on energy distribution for transmission line connected to renewable power plants. Power Syst. Technol. 2023, 47, 1415–1422. [Google Scholar]
- Zheng, L.; Jia, K.; Bi, T.; Fang, Y.; Yang, Z. Cosine similarity based pilot protection of teed transmission line connected to renewable energy power plant. Autom. Electr. Power Syst. 2019, 43, 111–119. [Google Scholar]
- Ruban, N.; Rudnik, V.; Askarov, A.; Maliuta, B. Frequency control by the PV station in electric power systems with hydrogen energy storage. Int. J. Hydrog. Energy 2023, in press. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J. Optimum integration of solar energy with battery energy storage systems. IEEE Trans. Eng. Manag. 2022, 69, 697–707. [Google Scholar] [CrossRef]
- Yuan, B.; Li, X.; Yin, C.; Liu, R. Mechanism and suppression strategy of high-frequency oscillation caused by integration of islanded renewable energy station into MMC-HVDC system. Autom. Electr. Power Syst. 2023, 47, 133–141. [Google Scholar]
- Sun, H.; Xu, S.; Xu, T.; Guo, Q.; He, J.; Zhao, B.; Yu, L.; Zhang, Y.; Li, W.; Zhou, Y.; et al. Definition and index of short circuit ratio for multiple renewable energy stations. Proc. CSEE 2021, 41, 497–505. [Google Scholar]
- Li, X.; Chen, L.; Sun, F.; Hao, Y.; Du, X.; Mei, S. Share or not share, the analysis of energy storage interaction of multiple renewable energy stations based on the evolution game. Renew. Energy 2023, 208, 679–692. [Google Scholar] [CrossRef]
- Tan, C.; Tan, Z.; Yin, Z.; Wang, Y.; Geng, S.; Pu, L. Study on grid price mechanism of new energy power stations considering market environment. Renew. Energy 2023, 203, 177–193. [Google Scholar] [CrossRef]
- Sun, H.; Li, J.; Li, W.; Guo, J.; Guo, Q.; He, J. Research on model structures and modeling methods of renewable energy station for large-scale power system simulation (part I): Model structure. Proc. CSEE 2023, 43, 1379–1388. [Google Scholar]
- Fu, X.; Zhang, Y.; Liu, X.; Liu, Z. Stable power supply system consisting of solar, wind and liquid carbon dioxide energy storage. Renew. Energy 2024, 221, 119730. [Google Scholar] [CrossRef]
- Cao, M.; Yu, J. Sales channel classification for renewable energy stations under peak shaving resource shortage. Int. J. Electr. Power Energy Syst. 2024, 160, 110115. [Google Scholar] [CrossRef]
- Ju, L.; Bai, X.; Li, G.; Gan, W.; Qi, X.; Ye, F. Two-stage robust transaction optimization model and benefit allocation strategy for new energy power stations with shared energy storage considering green certificate and virtual energy storage mode. Appl. Energy 2024, 362, 122996. [Google Scholar] [CrossRef]
- Moradzadeh, M.; Abdelaziz, M. A new MILP formulation for renewables and energy storage integration in fast charging stations. IEEE Trans. Transp. Electrif. 2020, 6, 181–198. [Google Scholar] [CrossRef]
- Amry, Y.; Elbouchikhi, E.; Le Gall, F.; Ghogho, M.; El Hani, S. Optimal sizing and energy management strategy for EV workplace charging station considering PV and flywheel energy storage system. J. Energy Storage 2023, 62, 106937. [Google Scholar] [CrossRef]
- Li, X.; Ma, R.; Gan, W.; Yan, S. Optimal dispatch for battery energy storage station in distribution network considering voltage distribution improvement and peak load shifting. J. Mod. Power Syst. Clean Energy 2021, 10, 131–139. [Google Scholar] [CrossRef]
- Li, G.; Hu, A.; Yang, T.; Zhang, L.; Shui, H.; Fang, C. Research on the control technologies of battery energy storage station for plug and play operation. Electr. Meas. Instrum. 2021, 58, 59–67. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Li, C.; Kang, L.; Yue, G. Research on coordinated scheduling method of new energy power station based on fair power generation. Electr. Meas. Instrum. 2020, 57, 76–85. [Google Scholar]
- Lu, M.; Li, X.; Li, F.; Xiong, W.; Cheng, S. Strategy of energy storage leasing configuration of photovoltaic power station cluster based on bi-level game optimization. Proc. CSEE 2022, 42, 5887–5898. [Google Scholar]
- Li, Z.; Li, P.; Xia, J.; Liu, X. Optimization for micro-energy grid dispatch based on non-supplementary fired compressed air energy storage aided energy hub and hybrid hyper-spherical search. J. Mod. Power Syst. Clean Energy 2022, 10, 1009–1020. [Google Scholar] [CrossRef]
- Zhu, H.; Yuan, S.; Li, C. Control strategy and analysis of virtual synchronous motor of photovoltaic power plant with energy storage link. Electr. Meas. Instrum. 2023, 60, 45–50. [Google Scholar]
- Li, J.; Hou, T.; Yan, G.; Li, C.; Mu, G. Two-layer optimization of frequency modulation power in multi-battery energy storage system considering frequency modulation cost and recovery of state of charge. Proc. CSEE 2021, 41, 8020–8032. [Google Scholar]
- Dai, Y.; Li, C.; Xia, S.; He, H.; Wang, P.; Jing, J. Collaborative optimization of distribution network and 5G base stations considering its communication load migration and energy storage dynamic backup flexibility. Int. J. Electr. Power Energy Syst. 2024, 160, 110124. [Google Scholar] [CrossRef]
- Mouratidis, P. Augmenting electric vehicle fast charging stations with battery-flywheel energy storage. J. Energy Storage 2024, 97, 112957. [Google Scholar] [CrossRef]
- Nagem, N.; Ebeed, M.; Alqahtani, D.; Jurado, F.; Khan, N.H.; Hafez, W.A. Optimal design and three-level stochastic energy management for an interconnected microgrid with hydrogen production and storage for fuel cell electric vehicle refueling stations. Int. J. Hydrog. Energy 2024, 87, 574–587. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, X.; Ding, B.; Zhang, Z.; Gao, Q. Cooperative game-based energy storage planning for wind power cluster aggregation station. Energy Rep. 2024, 11, 4021–4031. [Google Scholar] [CrossRef]
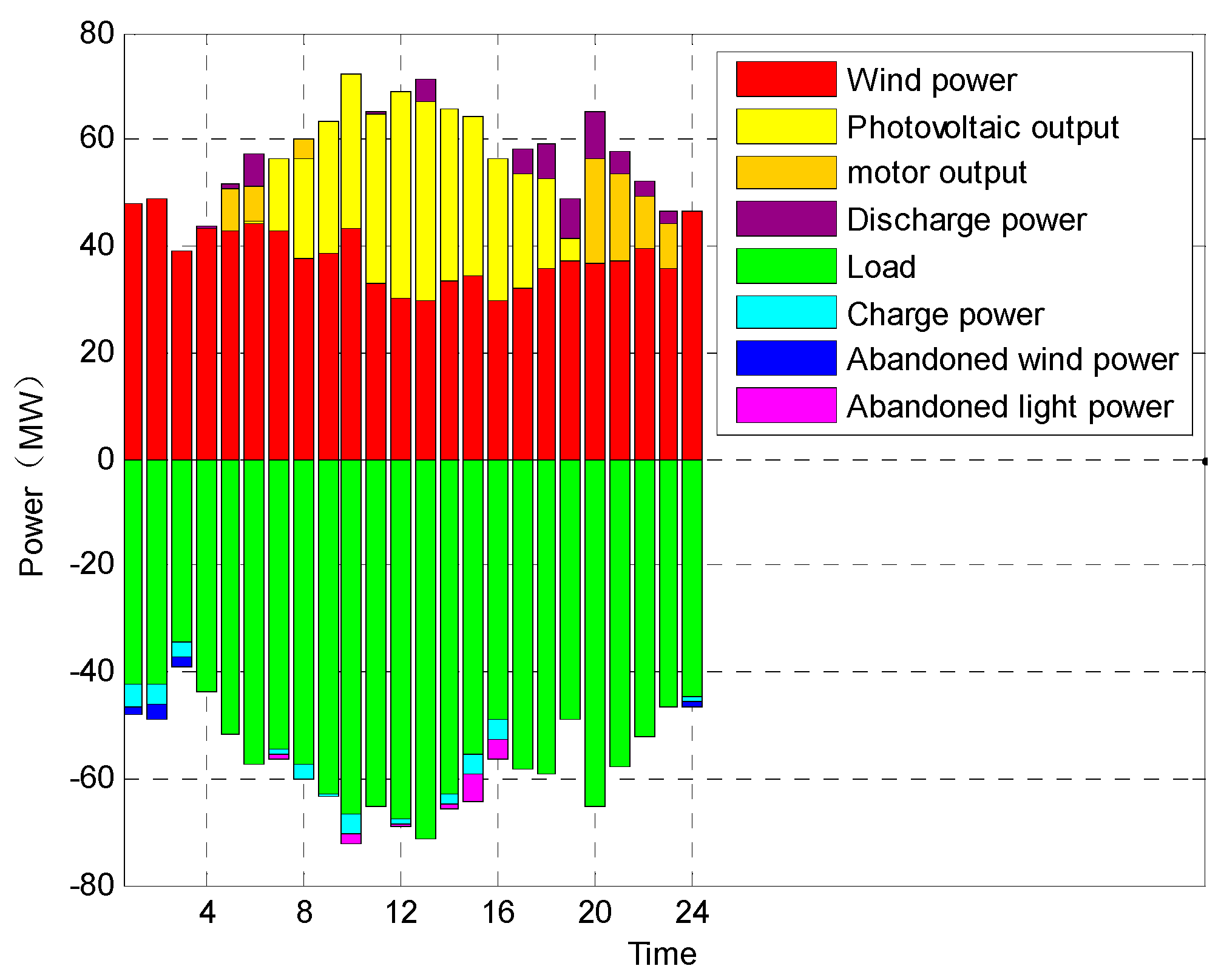
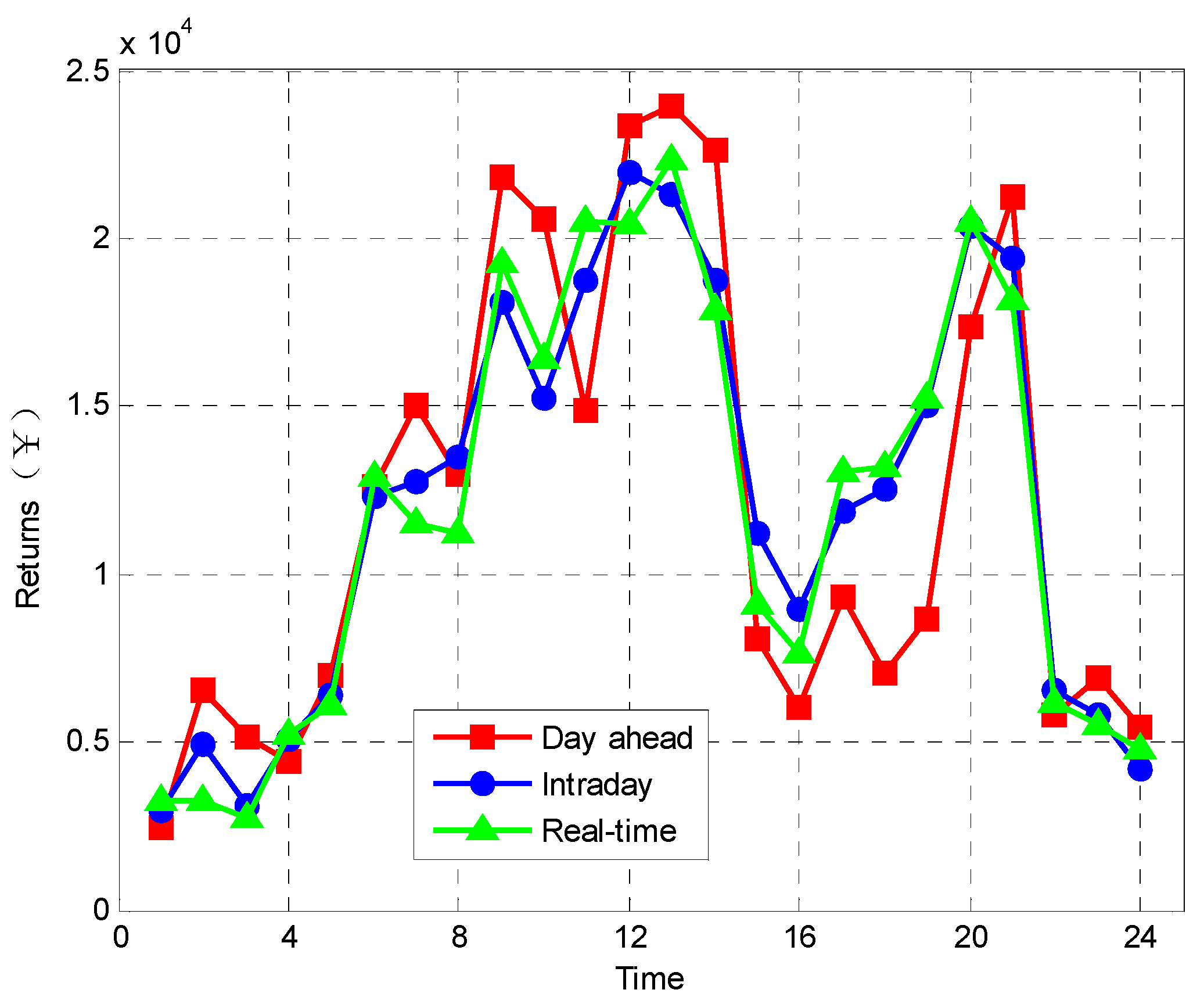

| Time Periods | Symbol | Electricity Purchase Price (¥·(kWh)−1) | Electricity Selling Price (¥·(kWh)−1) |
|---|---|---|---|
| Peak load periods | 8:00–14:00, 18:00–21:00 | 1.12 | 0.95 |
| Normal load periods | 5:00–8:00, 14:00–18:00 | 0.83 | 0.68 |
| Low load periods | 0:00–5:00, 21:00–24:00 | 0.45 | 0.36 |
| Before Optimization | After Optimization | |||||
|---|---|---|---|---|---|---|
| Markets | Daily | Intraday | Real-Time | Daily | Intraday | Real-Time |
| Revenues (Ten thousand yuan) | 28.906 | 29.115 | 28.649 | 33.68 | 32.257 | 32.498 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, S.; Li, W.; Zheng, C.; Wang, W. Distributed Optimization Strategy for New Energy Stations and Energy Storage Stations Considering Multiple Time Scales. Energies 2024, 17, 4923. https://doi.org/10.3390/en17194923
Zhai S, Li W, Zheng C, Wang W. Distributed Optimization Strategy for New Energy Stations and Energy Storage Stations Considering Multiple Time Scales. Energies. 2024; 17(19):4923. https://doi.org/10.3390/en17194923
Chicago/Turabian StyleZhai, Suwei, Wenyun Li, Chao Zheng, and Weixin Wang. 2024. "Distributed Optimization Strategy for New Energy Stations and Energy Storage Stations Considering Multiple Time Scales" Energies 17, no. 19: 4923. https://doi.org/10.3390/en17194923
APA StyleZhai, S., Li, W., Zheng, C., & Wang, W. (2024). Distributed Optimization Strategy for New Energy Stations and Energy Storage Stations Considering Multiple Time Scales. Energies, 17(19), 4923. https://doi.org/10.3390/en17194923





