Adaptive Current Angle Compensation Control Based on the Difference in Inductance for the Interior PMSM of Vehicles
Abstract
1. Introduction
- (1)
- To ensure the stability of the system at the same time of improving transient response, some papers have indeed achieved faster results, but these methods are always accompanied by negative effects.
- (2)
- The accurate identification of sensitive parameters has attracted more attention, but it is difficult to achieve.
- (3)
- Simplifying the procedure to make the control process easier to achieve in control chips.
- (1)
- The proposed method is supposed to have faster performance than traditional methods.
- (2)
- It eliminates the need to identify inductance in the d-q axes. There is no need for a complex derivation process, and it can still obtain the optimization results.
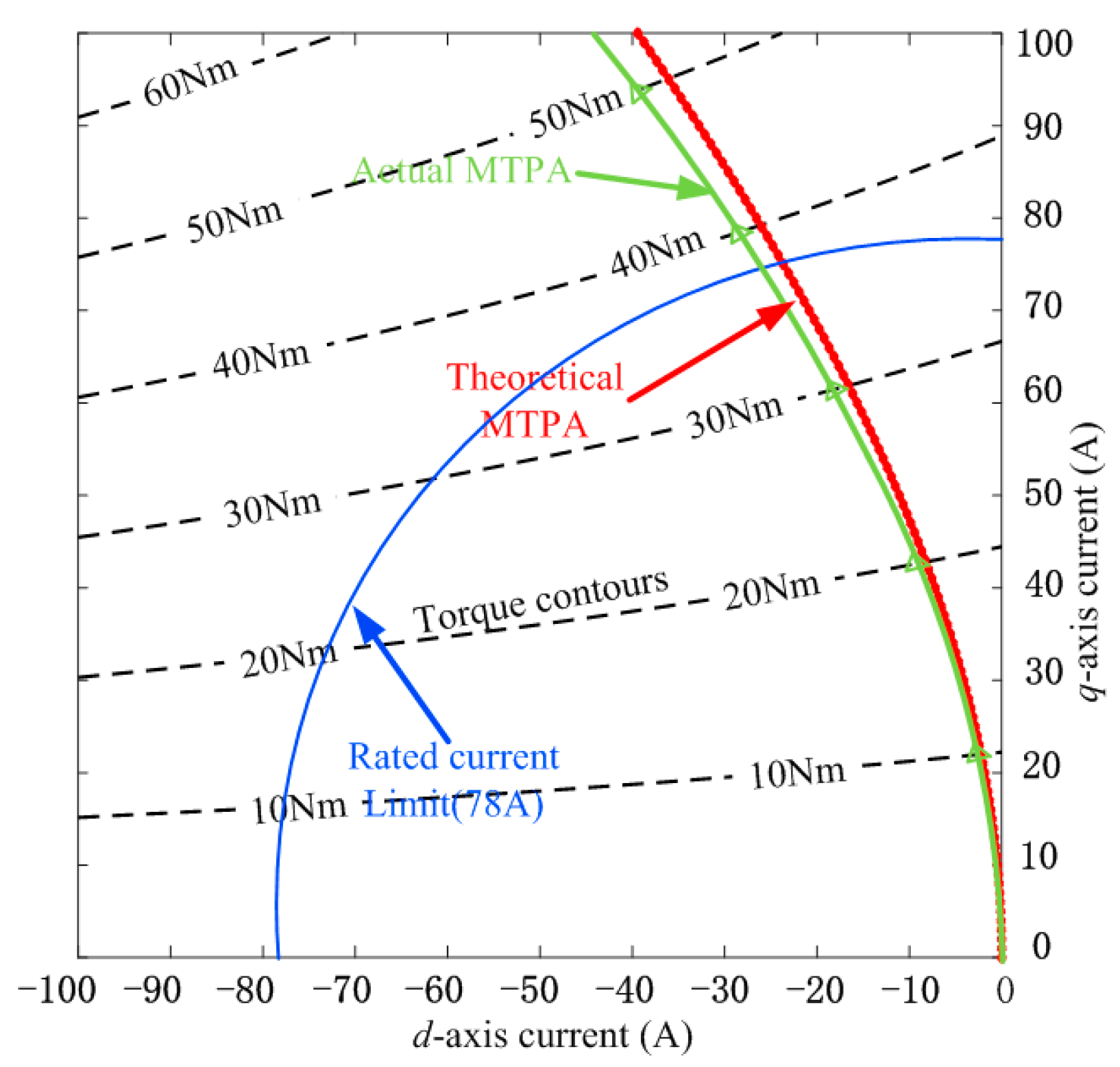
2. Model of IPMSM and MPTA Control
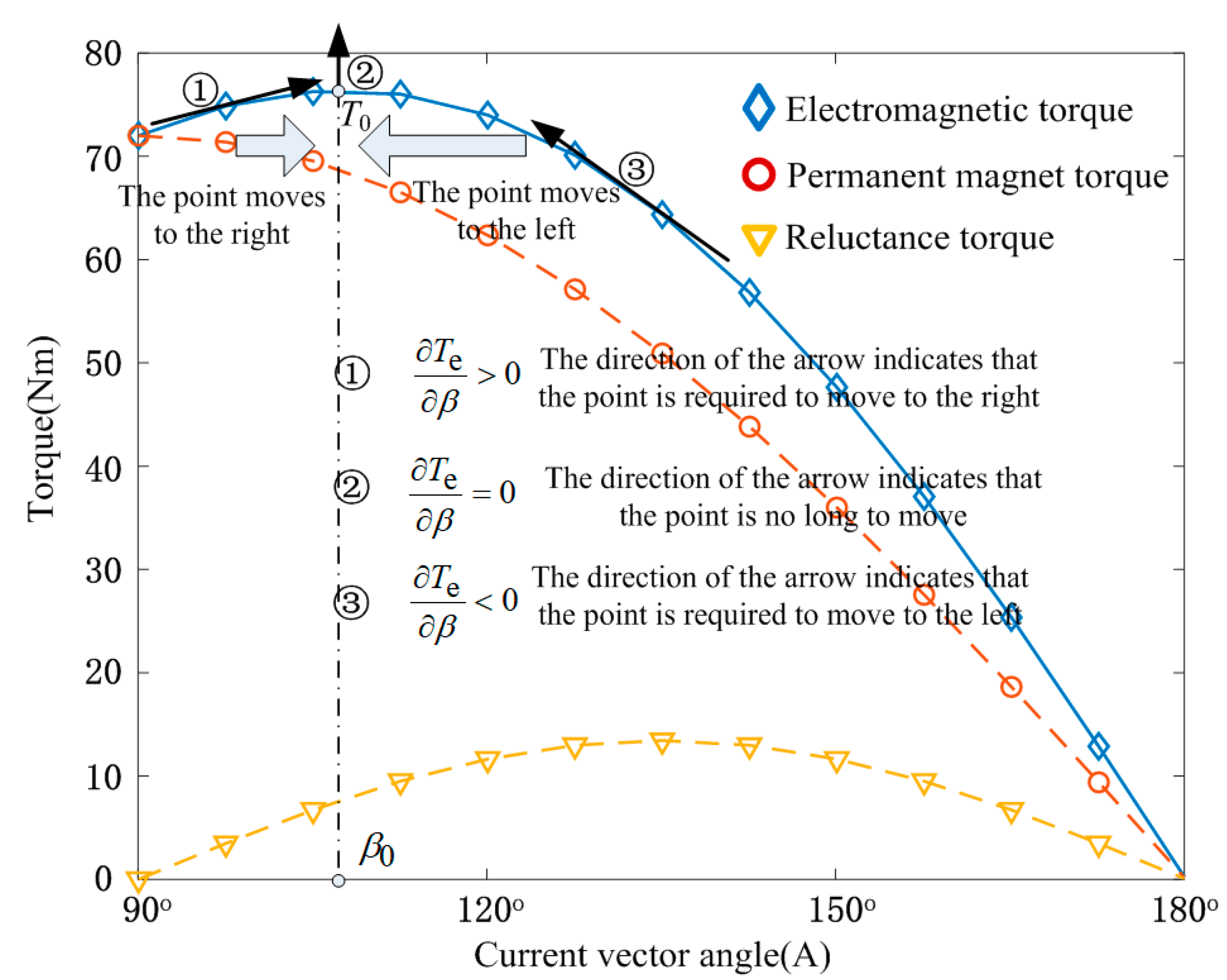
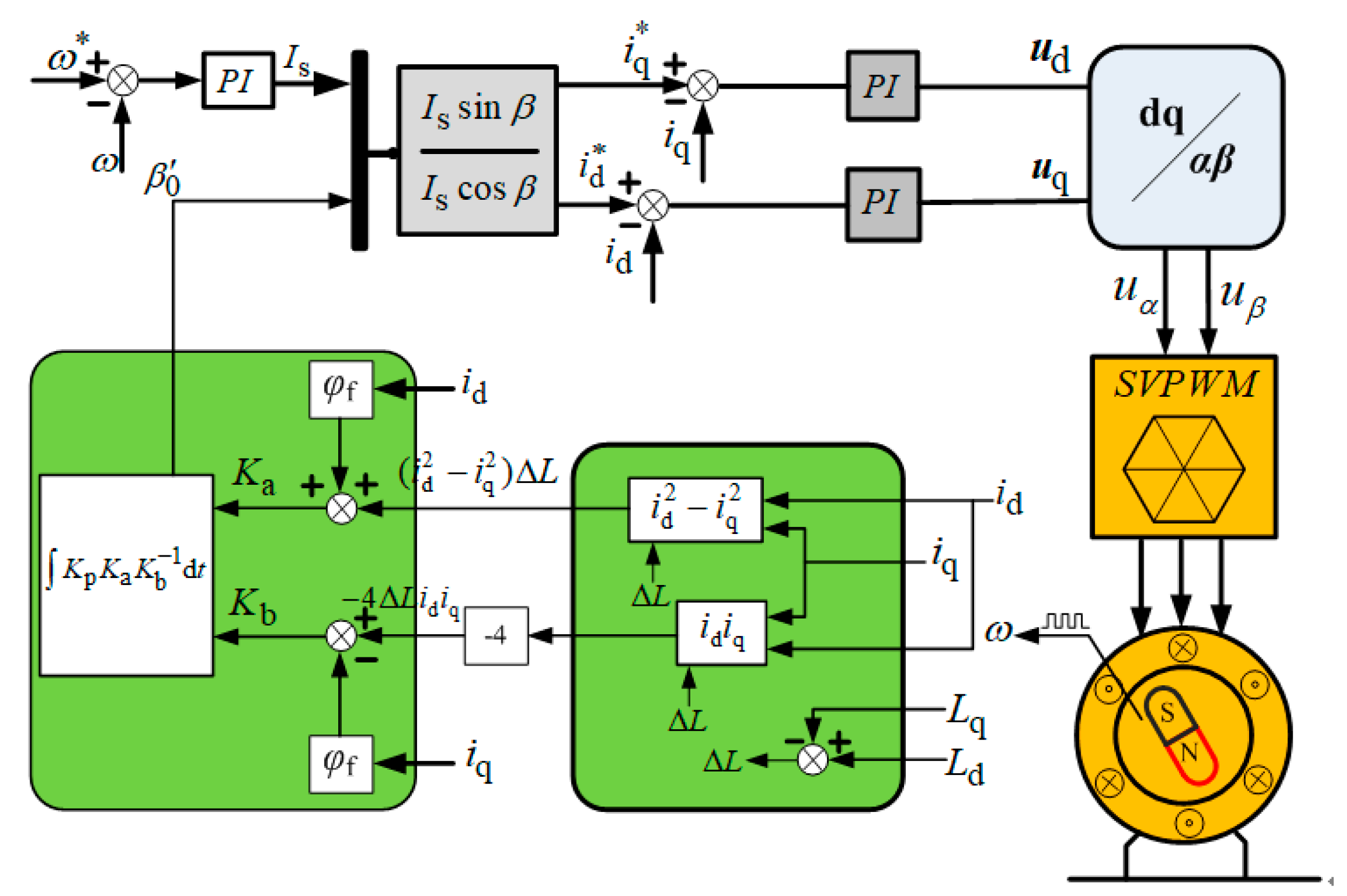
3. Current Vector Angle Compensation Control
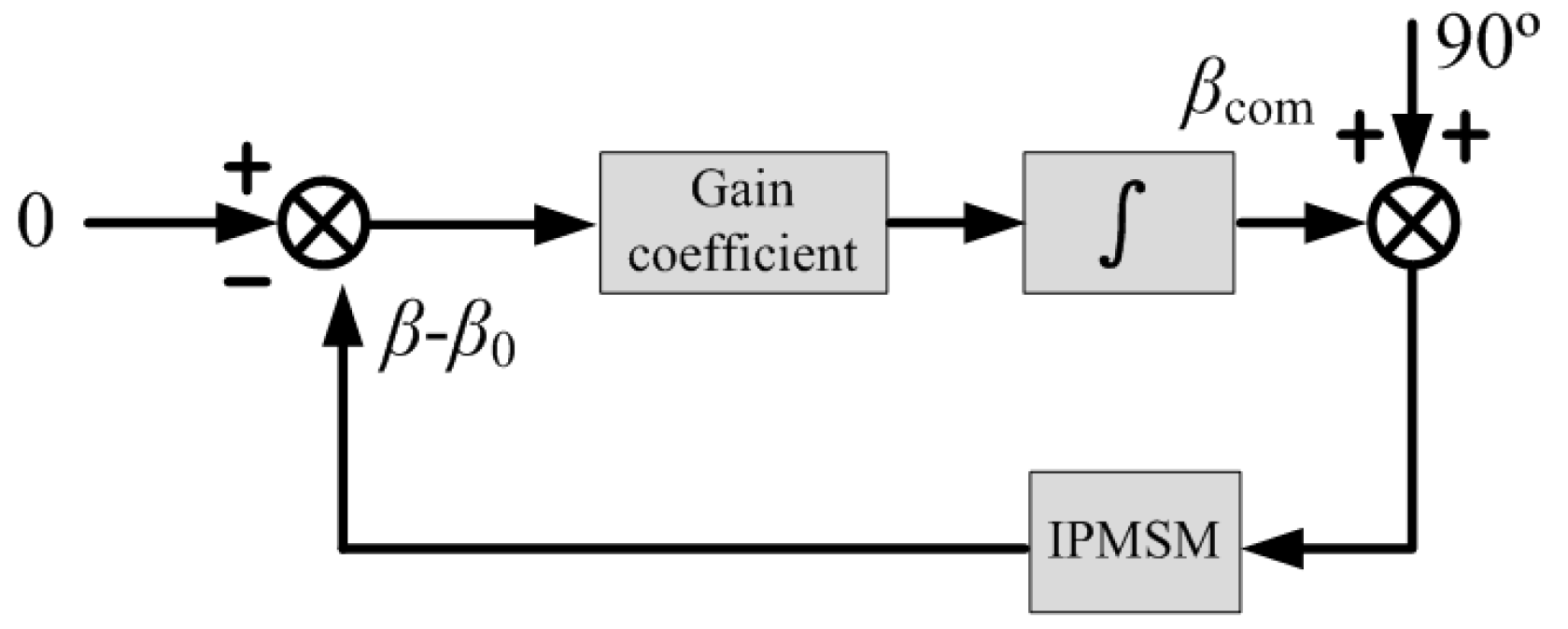
3.1. Current Vector Angle Compensation with Variable Gain
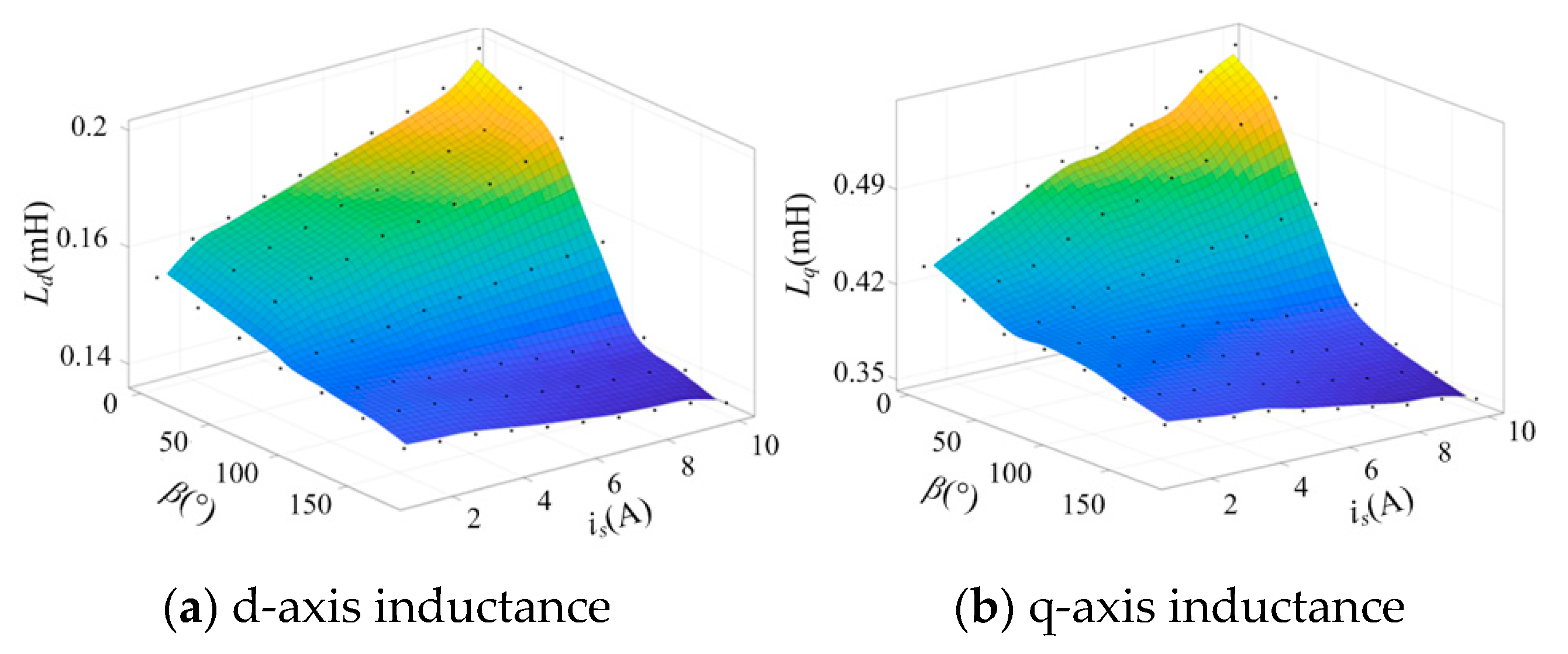
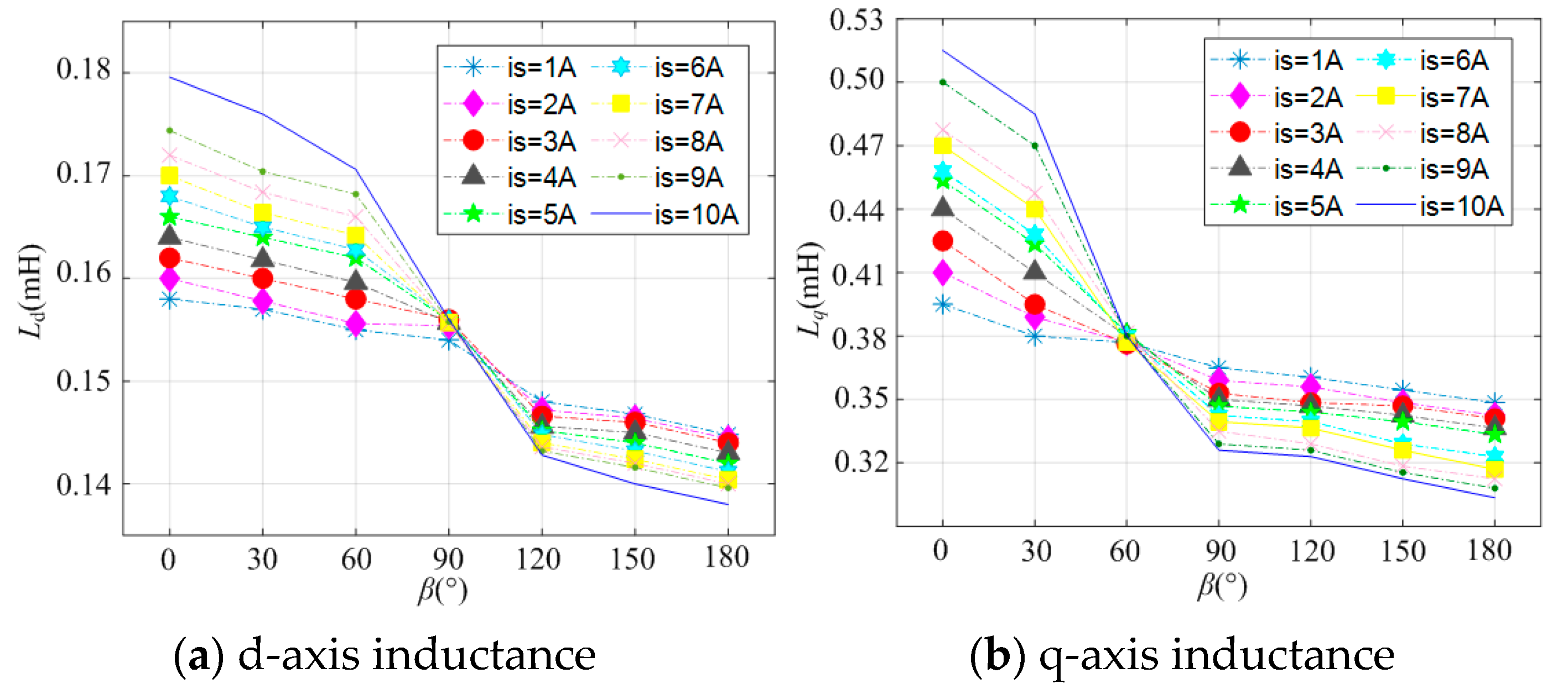
3.2. Coupling Analysis of DQ Axes Inductance Parameters
3.2.1. Difference Estimation of Inductance in DQ-Axis
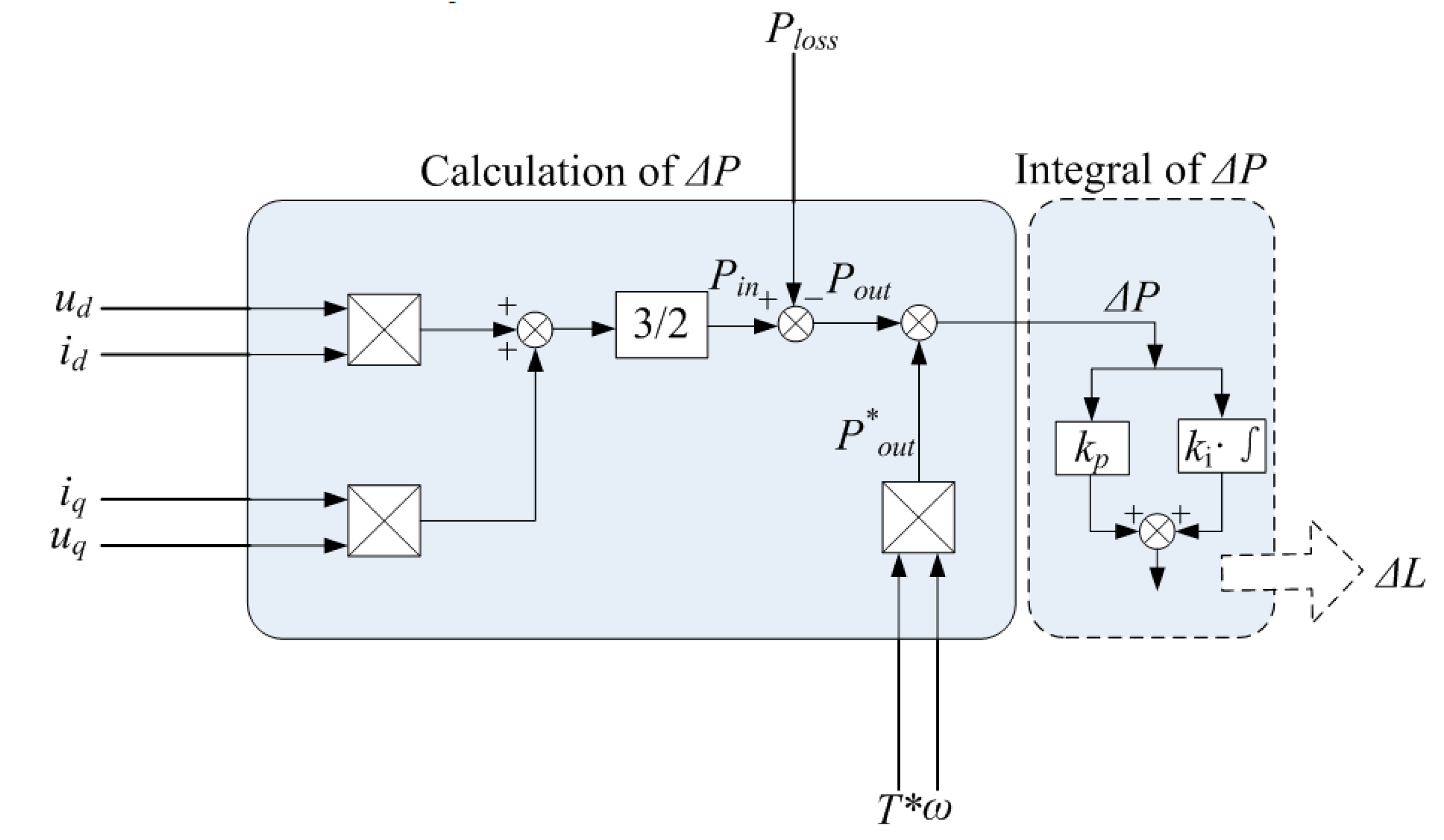
3.2.2. Estimation of Ploss
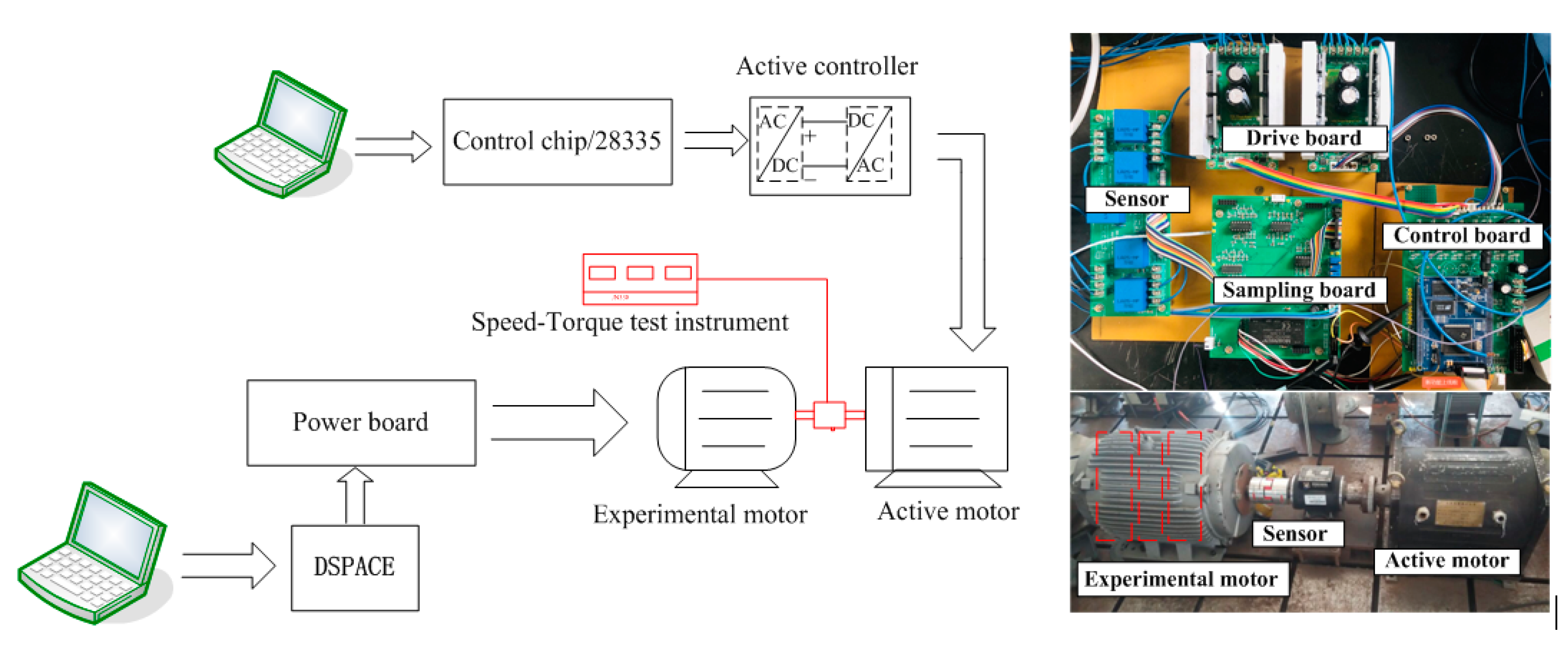
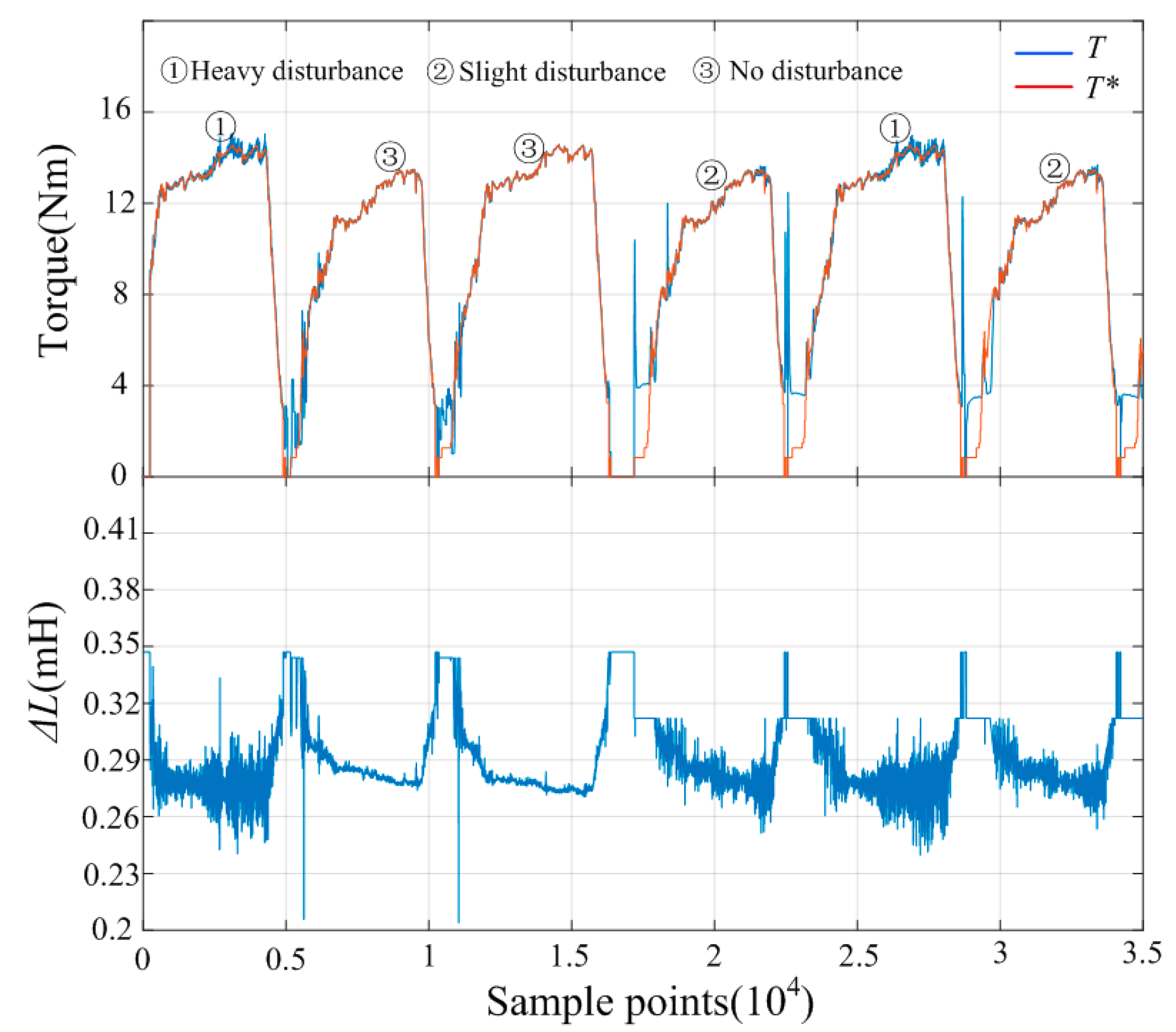
4. Verification and Analysis
4.1. Estimation of ΔL
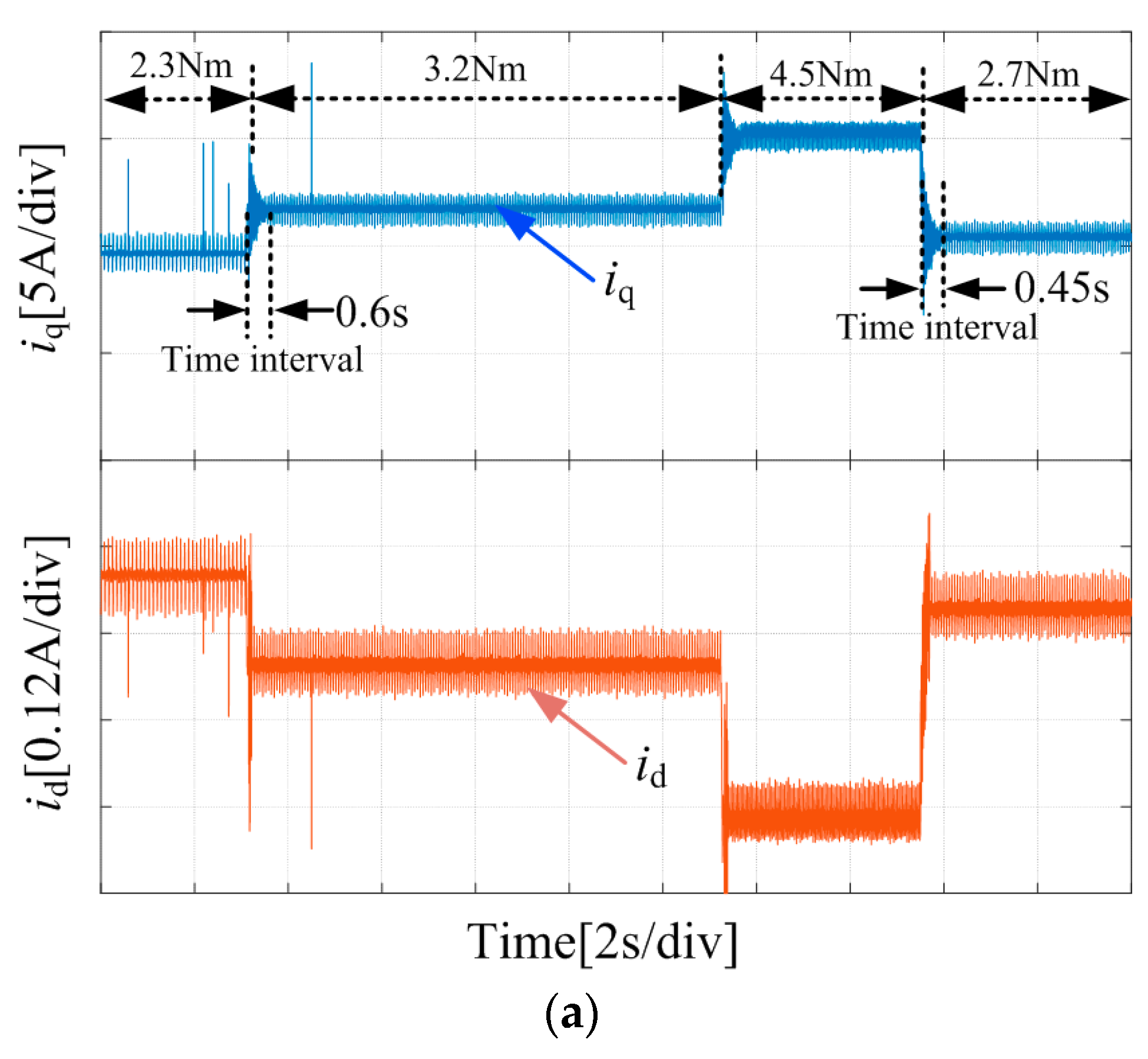
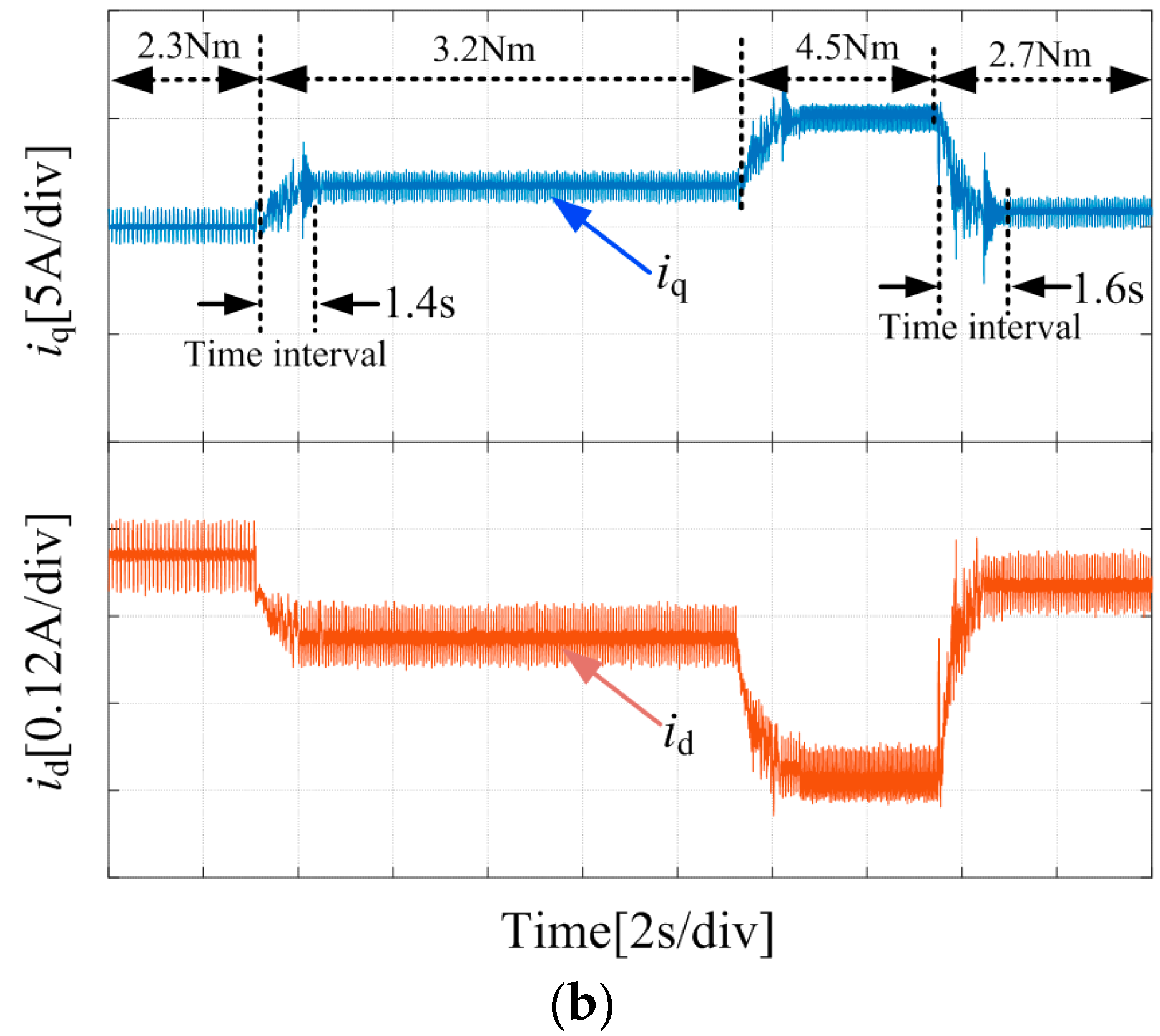
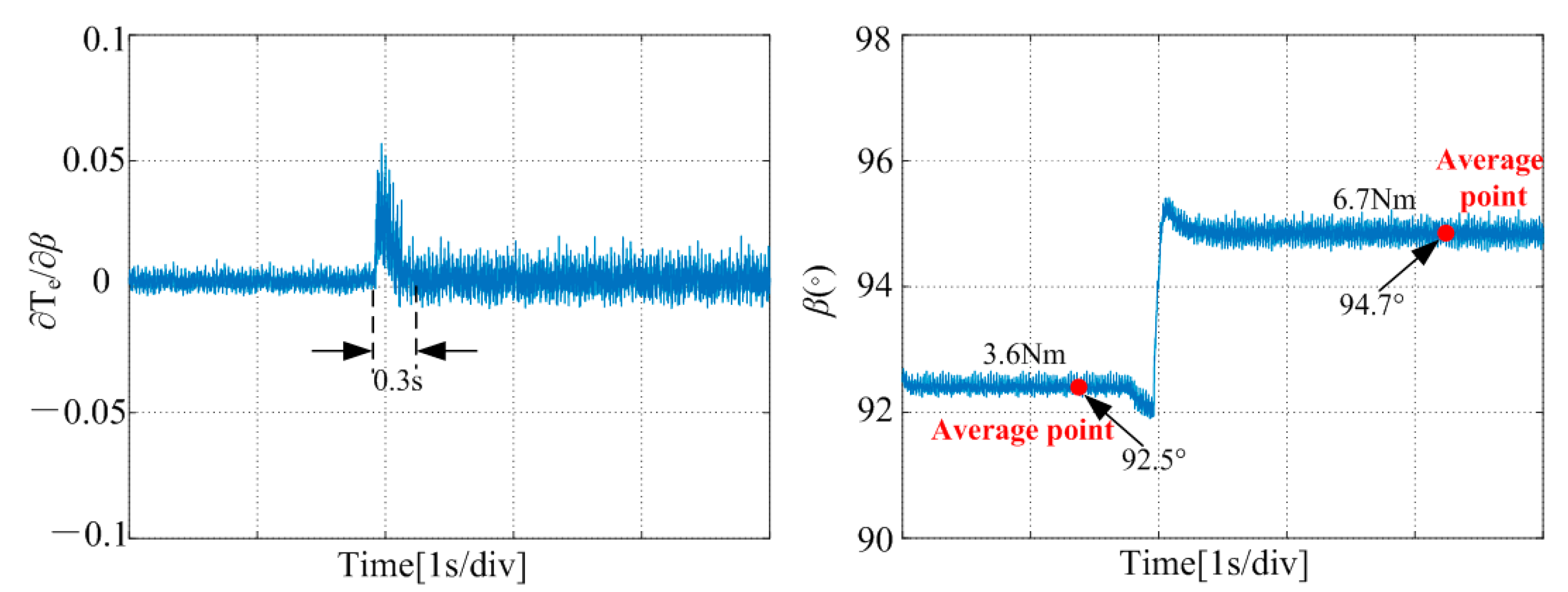
4.2. Results of Control Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Han, D.; Sarlioglu, B. Modeling of interior permanent magnet machine considering saturation, cross coupling, spatial harmonics, and temperature effects. IEEE Trans. Transport. Electrif. 2017, 3, 682–693. [Google Scholar] [CrossRef]
- Khayamy, M.; Chaoui, H. Current sensorless MTPA operation of interior pmsm drives for vehicular applications. IEEE Trans. Veh. Technol. 2018, 67, 6872–6881. [Google Scholar] [CrossRef]
- Han, Z.; Liu, J.; Yang, W.; Pinhal, D.B.; Reiland, N.; Gerling, D. Improved online maximum-torque-per-ampere algorithm for speed controlled interior permanent magnet synchronous machine. IEEE Trans. Ind. Electron. 2020, 67, 3398–3408. [Google Scholar] [CrossRef]
- Sun, J.; Lin, C.; Xing, J.; Jiang, X. Online MTPA Trajectory Tracking of IPMSM Based on a Novel Torque Control Strategy. Energies 2019, 12, 3261. [Google Scholar] [CrossRef]
- Ni, R.; Xu, D.; Wang, G.; Ding, L.; Zhang, G.; Qu, L. Maximum efficiency per ampere control of permanent-magnet synchronous machines, IEEE Trans. Ind. Electron. 2015, 62, 2135–2143. [Google Scholar] [CrossRef]
- Dianov, A.; Anuchin, A. Adaptive maximum torque per ampere control of sensorless permanent magnet motor drives. Energies 2020, 13, 5071. [Google Scholar] [CrossRef]
- Li, J.C. Analytical model of the cross magnetizing effect in saturated synchronous machines. Electr. Power Syst. Res. 1996, 37, 19–28. [Google Scholar] [CrossRef]
- Meessen, K.J.; Thelin, P.; Soulard, J.; Lomonova, A. Inductance calculation of permanent magnet synchronous machines including flux and self and cross saturation. IEEE Trans. Magn. 2008, 44, 2324–2331. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y. Maximum torque per ampere (MTPA) control for IPMSM drives based on a variable-equivalent-parameters MTPA control law. IEEE Trans. Power Electron. 2019, 34, 7092–7102. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, C.; Li, L.; Zhang, J.; Wang, M. Maximum Efficiency per Torque Control of permanent-magnet Synchronous Machines. Appl. Sci. 2016, 6, 425. [Google Scholar] [CrossRef]
- Tang, Q.P.; Shen, A.W.; Luo, P.; Shen, H.L.; Li, W.H.; He, X.N. IPMSMs Sensorless MTPA Control Based on Virtual q-Axis Inductance by Using Virtual High-Frequency Signal Injection. IEEE Trans. Ind. Electron. 2020, 67, 136–146. [Google Scholar] [CrossRef]
- Sun, T.F.; Koc, M.; Wang, J. MTPA control of IPMSM drives based on virtual signal injection considering machine parameters variations. IEEE Trans. Ind. Electron. 2018, 65, 6089–6098. [Google Scholar] [CrossRef]
- Liu, Q.; Hameyer, K. High-Performance adaptive torque control for an IPMSM with real-time MTPA Operation. IEEE Trans. Energy Conv. 2017, 32, 571–581. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Scelba, G.; Testa, A. Steady-state and transient operation of IPMSMs under maximum-torque-per-ampere control. IEEE Trans. Ind. Appl. 2010, 46, 121–129. [Google Scholar] [CrossRef]
- Mohamed, Y.A.-R.I.; Lee, T.K. Adaptive self-tuning MTPA vector controller for IPMSMdrive system. IEEE Trans. Energy Conv. 2006, 21, 636–644. [Google Scholar] [CrossRef]
- Hajime, H.; Yoshio, T.; Keiji, K. Novel sensorless control for pmsynchronous motors based on maximum torque control frame. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Inoue, T.; Inoue, Y.; Morimoto, S.; Sanada, M. Maximum torque per ampere control of a direct torque-controlled PMSM in a stator flux linkage synchronous frame. IEEE Trans. Ind. Appl. 2016, 52, 2360–2367. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Bai, C.; Wang, G.; Liu, J. A rotor position and speed estimation method using an improved linear extended state observer for IPMSM sensorless drives. IEEE Trans. Power Electron. 2021, 36, 14062–14073. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, S.G.; Liu, Y.T.; Chen, S.Y. A power perturbation-based MTPA control with disturbance torque observer for IPMSM drive system. Trans. Inst. Meas. Control 2018, 40, 3179–3288. [Google Scholar] [CrossRef]



| Symbol | Explanation | Value and Unit |
|---|---|---|
| p | Number of pole pairs | 4 |
| Ld | D-axis inductance | 0.18 mH |
| Lq | Q-axis inductance | 0.53 mH |
| R | Resistance | 10.2 mΩ |
| nN | Rated speed | 3000 rpm |
| PN | Rated power | 5 kW |
| TN | Rated torque | 16 Nm |
| Torque | Proposed Method | Conventional Method |
|---|---|---|
| 2.3 Nm | 91.91° | 91.6° |
| 3.2 Nm | 92.36° | 92.05° |
| 4.5 Nm | 92.92° | 92.63° |
| 2.7 Nm | 92.08° | 91.65° |
| Comparison Item | Description |
|---|---|
| Response speed | The proposed method has a faster response, although with a transient impact when the load changes. |
| Accuracy | More accurate results can be obtained from the method proposed, though they are not optimal. |
| Implementation | The algorithm is indeed simple, less calculation, and low complexity. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Cui, Z.; Hou, T.; Zhang, R.; Hao, W.; Song, L. Adaptive Current Angle Compensation Control Based on the Difference in Inductance for the Interior PMSM of Vehicles. Energies 2024, 17, 4905. https://doi.org/10.3390/en17194905
Zhang L, Cui Z, Hou T, Zhang R, Hao W, Song L. Adaptive Current Angle Compensation Control Based on the Difference in Inductance for the Interior PMSM of Vehicles. Energies. 2024; 17(19):4905. https://doi.org/10.3390/en17194905
Chicago/Turabian StyleZhang, Liying, Zongze Cui, Tingchen Hou, Rui Zhang, Wei Hao, and Liwei Song. 2024. "Adaptive Current Angle Compensation Control Based on the Difference in Inductance for the Interior PMSM of Vehicles" Energies 17, no. 19: 4905. https://doi.org/10.3390/en17194905
APA StyleZhang, L., Cui, Z., Hou, T., Zhang, R., Hao, W., & Song, L. (2024). Adaptive Current Angle Compensation Control Based on the Difference in Inductance for the Interior PMSM of Vehicles. Energies, 17(19), 4905. https://doi.org/10.3390/en17194905






