Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization
Abstract
1. Introduction
2. Assessment of Probabilistic Power and Energy Balance Characteristics and Risk Indicators for Supply–Demand Equilibrium
2.1. Analysis of Probability Balance Characteristics
2.2. Indicators of Supply and Demand Equilibrium Risk
3. Probabilistic Balancing Analysis Model for New Energy Power Systems Based on Distributed Robust Optimization
3.1. A New Energy Power System Balance Analysis Model Based on Risk Assessment Indicators
- (1)
- The objective function
- (2)
- Equations governing power flow
- (3)
- Limitations on the commencement and termination of operations for thermal power units
- (4)
- Restrictions on the output limitation of thermal power units
- (5)
- Limitations on the Spinning Reserve Capacity of Thermal Power Units
- (6)
- Limitations on the ramp rate of thermal power units
3.2. Wasserstein Fuzzy Sets for Characterizing Uncertainty in Wind and Solar Resources
4. Transformation of the Model
4.1. Linearization of Trends
4.2. The Dual Transformation of a Distributionally Robust Model
5. Simulation Study
5.1. Systematic Probabilistic Analysis of Supply and Demand Balance
5.2. Analyzing the Influence of Varying Confidence Levels on Scheduling Outcomes
5.3. Analyzing Scheduling Outcomes Employing Various Optimization Techniques
6. Conclusions
- Tailored safety and economic risk indicators for modern power systems’ power and energy balance have been proposed, which can be used in scheduling decisions to achieve operational equilibrium between safety and economic risks.
- By fully considering the flexible ramping reserves provided by coal-fired power plants, the results of probabilistic risk assessment can guide the rational planning of flexible resources such as energy storage and demand-side response within the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Unit Number | Access Node | ai/ (CNY/MW2.h) | bi/ (CNY/MWh) | ci/ (CNY/MW.h) | riup, ridown/ (MW/h) | / MW | / MW | / h |
|---|---|---|---|---|---|---|---|---|
| G1 | 10 | 0.003264 | 110.092 | 6800 | 200 | 455 | 150 | 8 |
| G2 | 12 | 0.003264 | 110.092 | 6800 | 200 | 455 | 150 | 8 |
| G3 | 26 | 0.002108 | 117.368 | 6596 | 200 | 455 | 150 | 8 |
| G4 | 46 | 0.002108 | 117.368 | 6596 | 200 | 455 | 150 | 8 |
| G5 | 49 | 0.027064 | 133.96 | 3060 | 100 | 162 | 25 | 6 |
| G6 | 59 | 0.027064 | 133.96 | 3060 | 100 | 162 | 25 | 6 |
| G7 | 61 | 0.014348 | 112.2 | 4624 | 80 | 130 | 20 | 5 |
| G8 | 66 | 0.0136 | 112.88 | 4760 | 80 | 130 | 20 | 5 |
| G9 | 80 | 0.0136 | 112.88 | 4760 | 80 | 130 | 20 | 5 |
| G10 | 87 | 0.048416 | 151.368 | 2516 | 72 | 80 | 20 | 3 |
| G11 | 89 | 0.005372 | 188.632 | 3264 | 80 | 85 | 25 | 3 |
References
- National Energy Administration The National Energy Administration Released the Statistical Data of the National Power Industry in 2023. 2024. Available online: https://www.nea.gov.cn/2024-01/26/c_1310762246.htm (accessed on 26 January 2024).
- Liu, C.; Huang, Y.; Shi, W.; Li, X. Production Simulation of New Energy Power System; China Electric Power Press: Beijing, China, 2019. [Google Scholar]
- Gill, L.; Gutierrez, A.; Weeks, T. 2021 SB 100 Joint Agency Report Achieving 100 Percent Clean Electricity in California: An Initial Assessment; California Energy Commission: Sacramento, CA, USA, 2021.
- Chen, G.; Dong, Y.; Liang, Z. Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition. Proc. CSEE 2020, 40, 5493–5505. [Google Scholar]
- Lu, B.; Blakers, A.; Stocks, M.; Do, T.N. Low-cost, low-emission 100% renewable electricity in Southeast Asia supported by pumped hydro storage. Energy 2021, 236, 121387. [Google Scholar] [CrossRef]
- Wu, J.; Luh, P.B.; Chen, Y.; Bragin, M.A.; Yan, B. A novel optimization approach for sub-hourly unit commitment with large numbers of units and virtual transactions. IEEE Trans. Power Syst. 2022, 37, 3716–3725. [Google Scholar] [CrossRef]
- Wei, L.; Ai, X.; Fang, J.; Lou, Y.; Liao, S.; Wen, J. Chronological operation simulation for power system with peak regulation ancillary service market in China: Formulation, solving, and validation. Int. J. Electr. Power Energy Syst. 2023, 152, 109156. [Google Scholar] [CrossRef]
- Tan, Y. Power System Planning and Design Technology; China Electric Power Press: Beijing, China, 2012. [Google Scholar]
- Verástegui, F.; Lorca, A.; Olivares, D.E.; Negrete-Pincetic, M.; Gazmuri, P. An adaptive robust optimization model for power systems planning with operational uncertainty. IEEE Trans. Power Syst. 2019, 34, 4606–4616. [Google Scholar] [CrossRef]
- Wan, C.; Qian, W.; Zhao, C.; Song, Y.; Yang, G. Probabilistic forecasting based sizing and control of hybrid energy storage for wind power smoothing. IEEE Trans. Sustain. Energy 2021, 12, 1841–1852. [Google Scholar] [CrossRef]
- Da Costa, L.C.; Thomé, F.S.; Garcia, J.D.; Pereira, M.V. Reliability-constrained power system expansion planning: A stochastic risk-averse optimization approach. IEEE Trans. Power Syst. 2021, 36, 97–106. [Google Scholar] [CrossRef]
- Wang, J.; Shahidehpour, M.; Li, Z. Security-constrained unit commitment with volatile wind power generation. IEEE Trans-Actions Power Syst. 2008, 23, 1319–1327. [Google Scholar] [CrossRef]
- Wang, C.; Fu, Y. Fully parallel stochastic security-constrained unit commitment. IEEE Trans. Power Syst. 2016, 31, 3561–3571. [Google Scholar] [CrossRef]
- Power Planning Decision Support System Gopt; Tsinghua University: Beijing, China, 2005.
- GE VERNOVA. Multi Area Production Simulation Software. 2023. Available online: https://www.gevernova.com/content/dam/Energy_Consulting/global/en_US/pdfs/GEA35096B-GE-MAPS_Brochure_R3.pdf (accessed on 26 January 2024).
- Li, Z.M.; Wu, L.; Xu, Y. Risk-averse coordinated operation of a multi-energy microgrid considering voltage/var control and thermal flow: An adaptive stochastic approach. IEEE Trans. Smart Grid 2021, 12, 3914–3927. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Mohammadi-Ivatloo, B.; Zare, K.; Khalili, T.; Bidram, A. Economic-emission dispatch problem in power systems with carbon capture power plants. IEEE Trans. Ind. Appl. 2021, 57, 3341–3351. [Google Scholar] [CrossRef]
- Alshammari, M.E.; Ramli, M.A.M.; Mehedi, I.M. Hybrid chaotic maps-based artificial bee colony for solving wind energy-integrated power dispatch problem. Energies 2022, 15, 4578. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Daneshvar, M.; Mohammadi-Ivatloo, B.; Zare, K.; Anvari-Moghaddam, A. Optimal Robust Energy Management of Microgrid with Fuel Cells, Hydrogen Energy Storage Units and Responsive Loads. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Zheng, L.; Xie, D.; Bai, X. Robust optimal power flow based on Predictive & Prescriptive frame-work. Electr. Power Autom. Equip. 2023, 43, 175–181. [Google Scholar]
- Yang, H.; Yi, B.; Meng, K.; Yu, H.; Zhou, N.; Xu, Z. Distributed Robust Optimal Scheduling of the New Interconnected Power System with the Inter-province and Intra-province Considering Moment Uncertainty of Source Load Power. Electr. Power Constr. 2023, 44, 98–110. [Google Scholar]
- Wang, H.; Bie, C. Distributionally robust economic dispatch of flexible ramping reserve considering physical boundaries of uncertainty. Autom. Equip. 2023, 43, 59–68. [Google Scholar]
- Ye, X.; Lu, Z.; Qiao, Y. Time-varying probabilistic model and dispatch performance indices for wind farm cluster virtual power generator—Part II: Dispatch performance indices. Proc. CSEE 2015, 35, 5395–5404. [Google Scholar]
- Lorca, Á.; Sun, X.A. Multistage robust unit commitment with dynamic uncertainty sets and energy storage. IEEE Trans. Power Syst. 2017, 32, 1678–1688. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-driven stochastic unitcommitment for integrating wind generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W. A distributionally robust optimization model for real-time power dispatch in distribution networks. IEEE Trans. Smart Grid 2018, 10, 3743–3752. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, H.; Xu, Y.; Li, Z.; Lin, Z.; Liang, Z. A mixed-integer SDP solution to distributionally robust unit commitment with second order moment constraints. CSEE J. Power Energy Syst. 2020, 6, 374–383. [Google Scholar]
- Zhao, C.; Guan, Y. Data-driven risk-averse stochastic optimization with wasserstein metric. Oper. Res. Lett. 2018, 46, 262–267. [Google Scholar] [CrossRef]


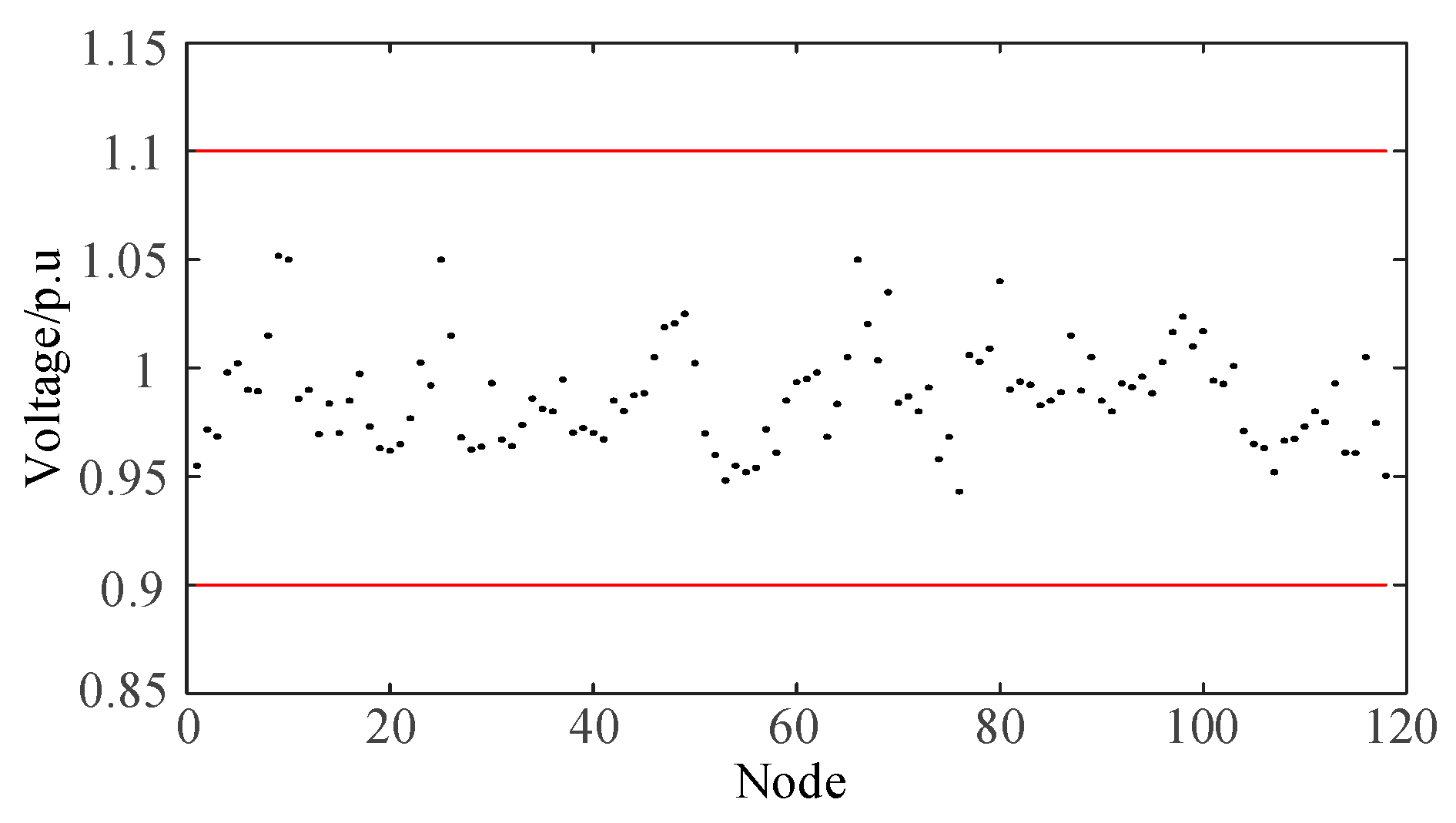
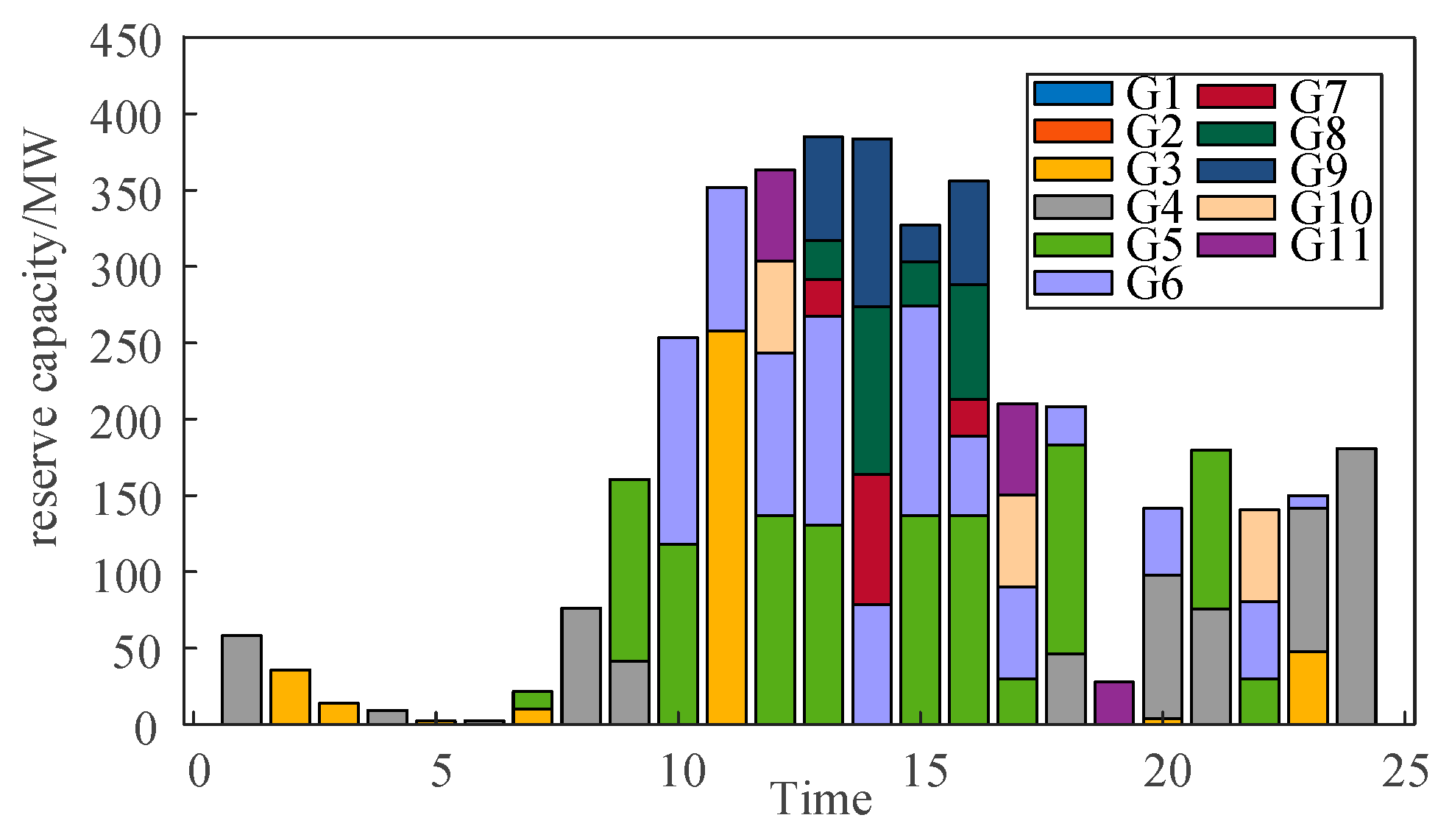

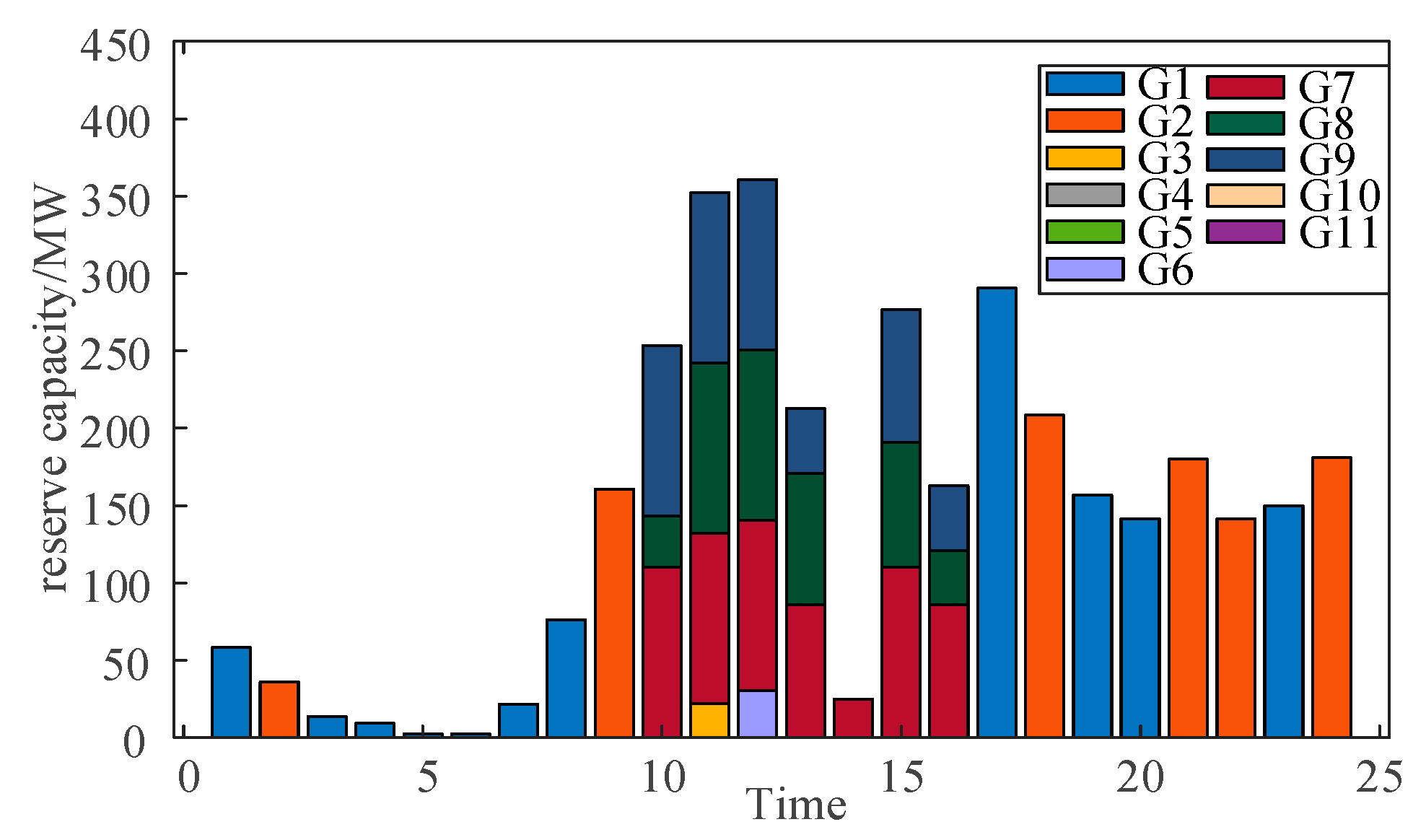

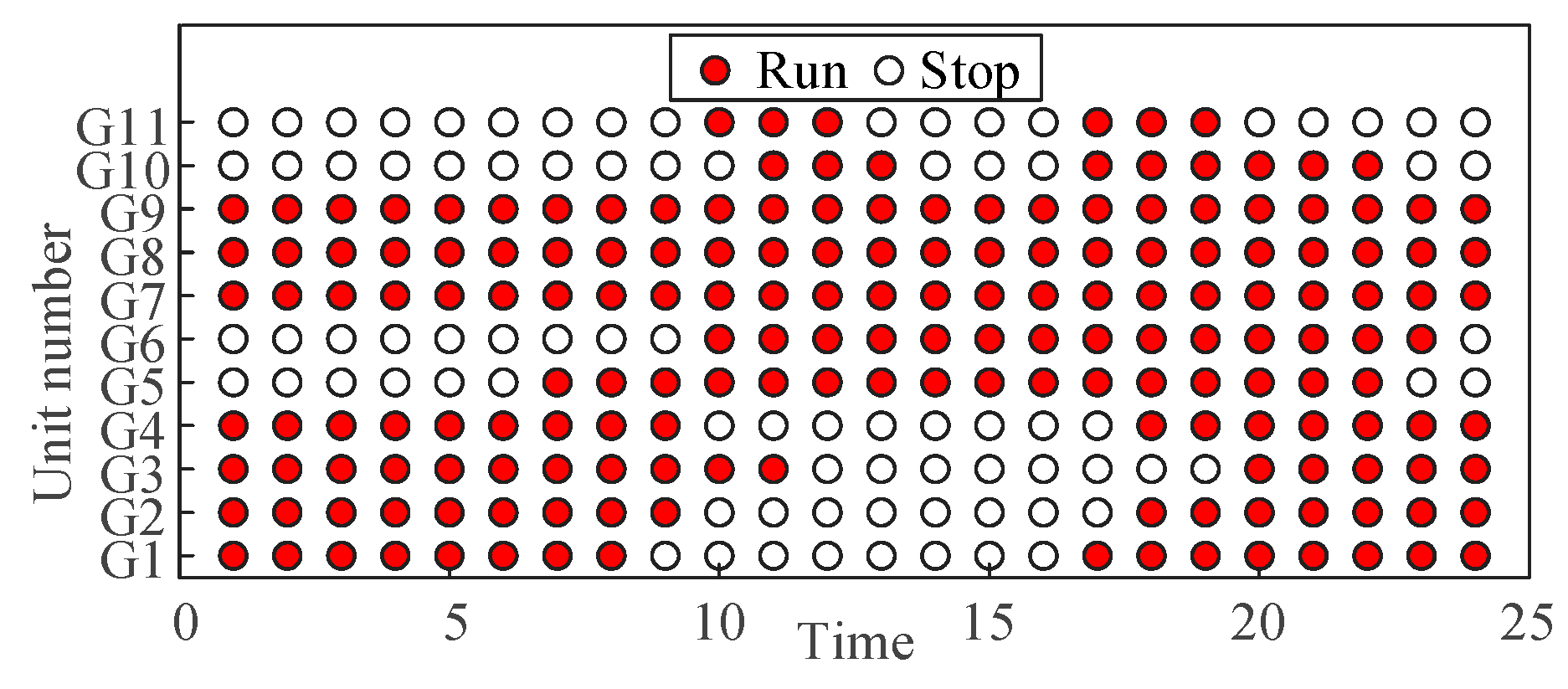
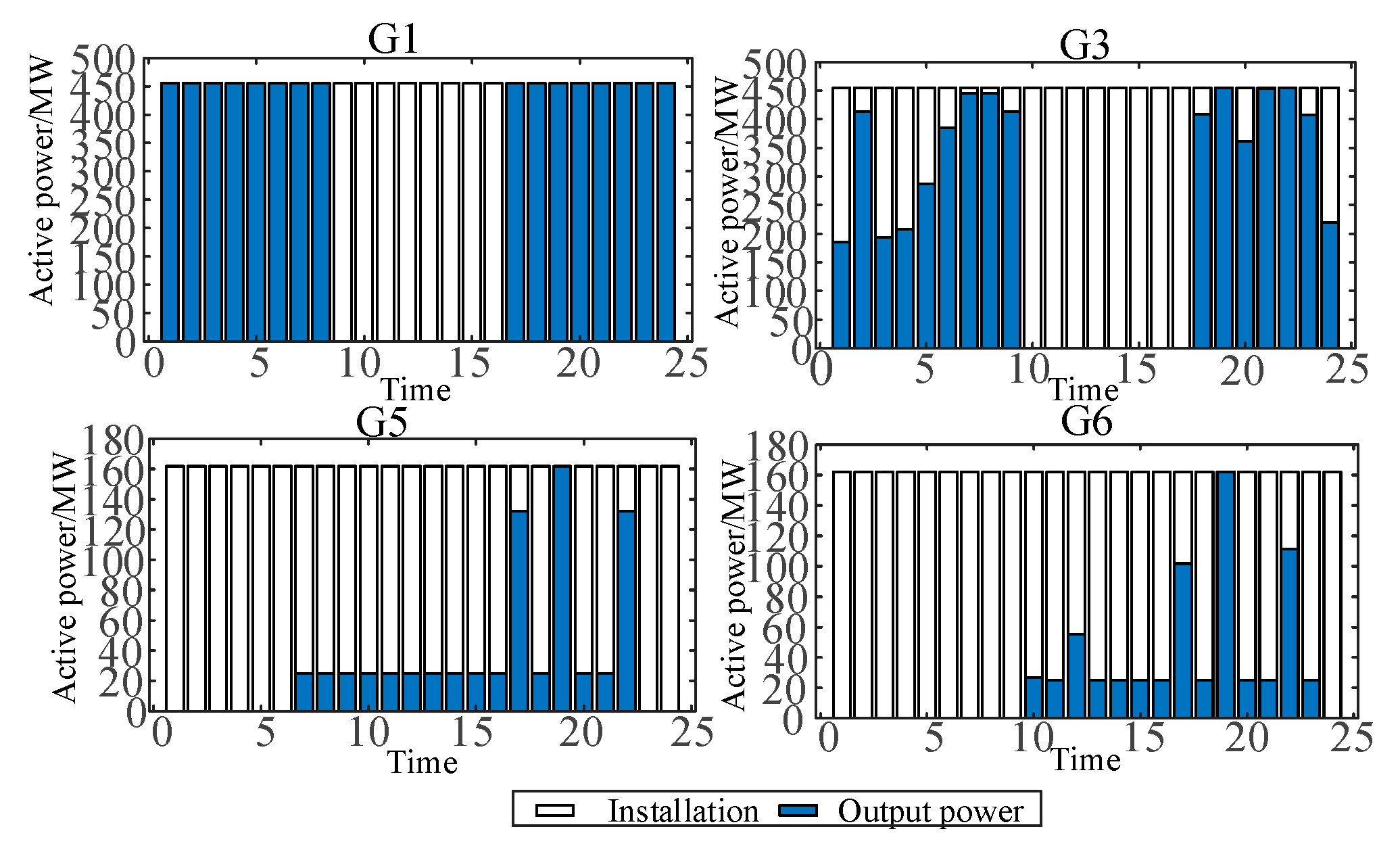


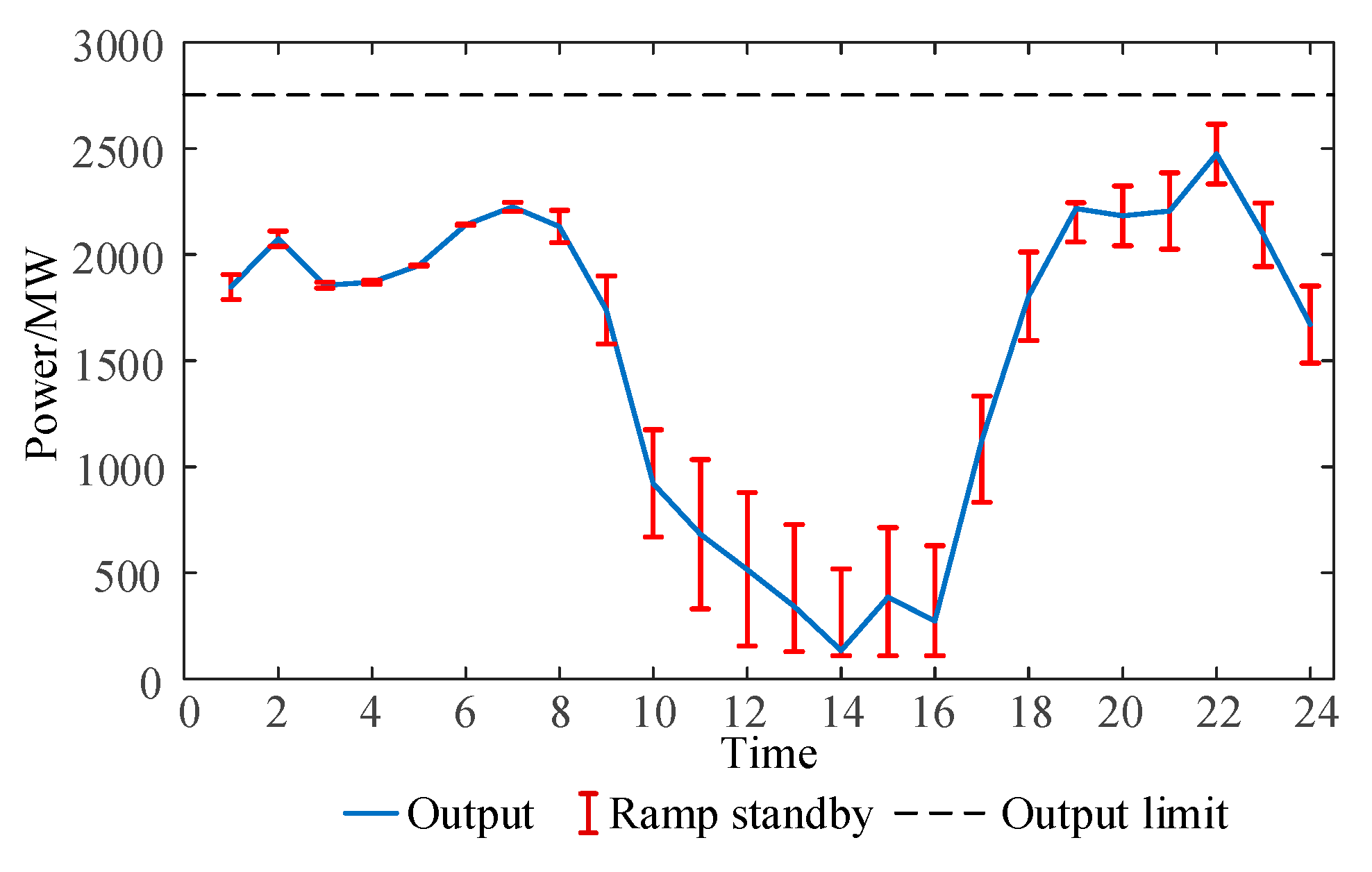

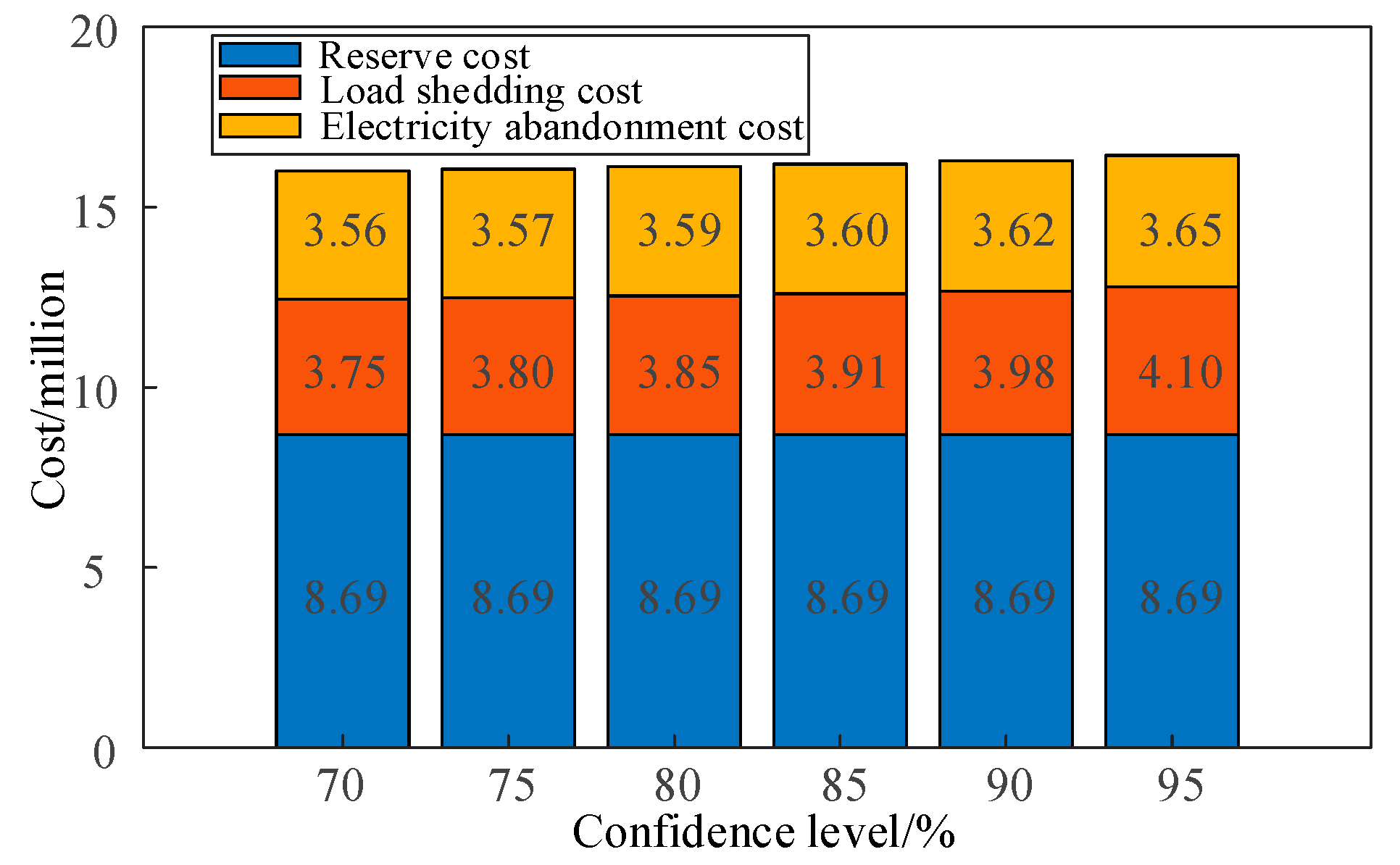
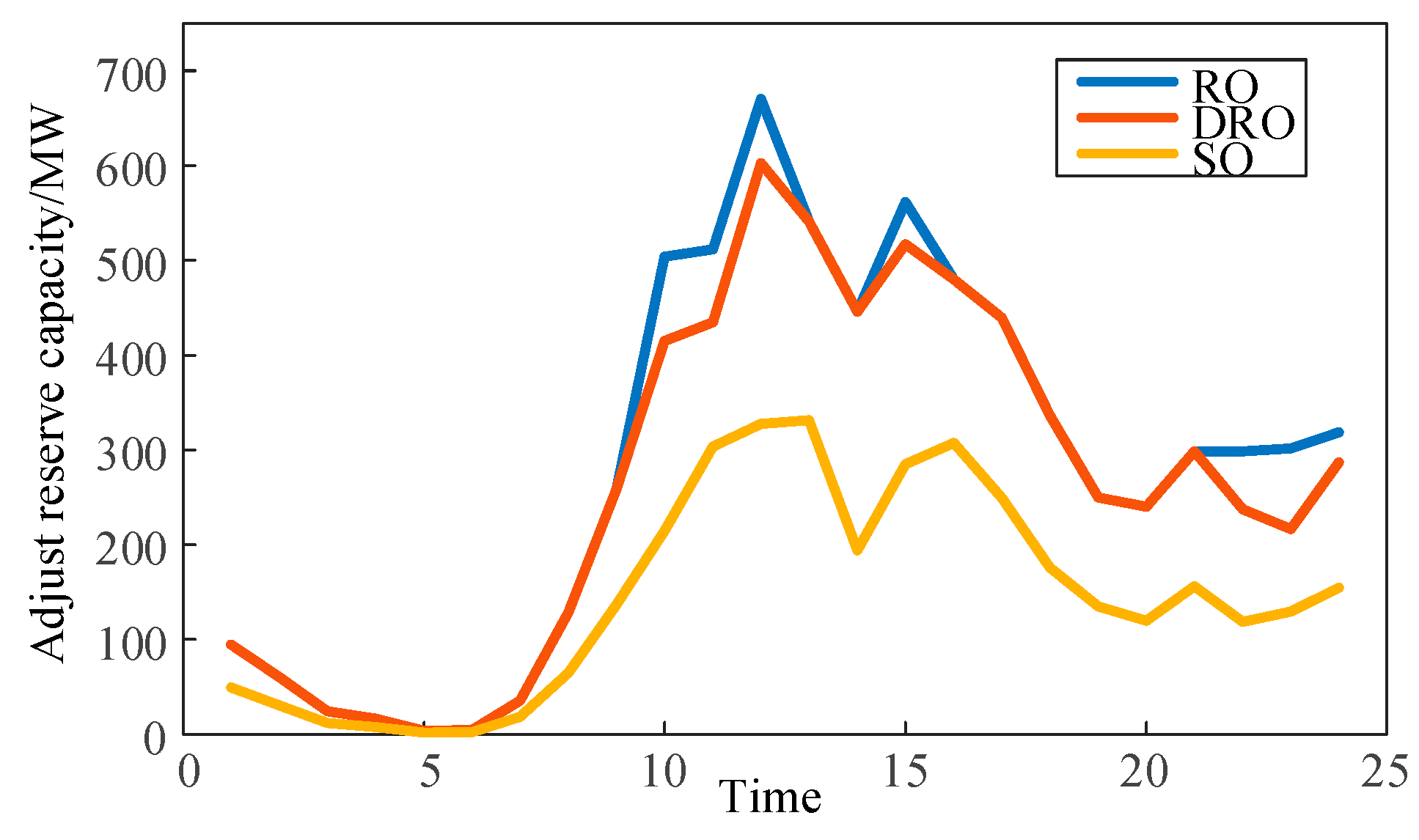
| Interconnection | Adjustable Resources | Adjust the Source of Demand |
|---|---|---|
| Mains side | Thermal power and hydropower | New energy output prediction error |
| Load side | Adjustable load | Non-adjustable load |
| Energy storage side | Short-term and long-term energy storage | / |
| Case | Costs of Scheduling/10,000 CNY | Up Reserve Demand/MW | Down Reserve Demand/MW | Electricity Abandonment Probability/% | Load Shedding Probability/% | Expected Curtailed Electricity/MWh | Expected Load Shedding/MWh |
|---|---|---|---|---|---|---|---|
| RO | 560.00 | 3661.48 | 3161.74 | 0.38 | 2.25 | 45.48 | 3.16 |
| SO | 555.09 | 1860.27 | 1649.25 | 9.13 | 11.46 | 104.84 | 63.38 |
| DRO | 559.38 | 3656.45 | 2711.23 | 0.46 | 2.83 | 50.98 | 3.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Qin, J.; Li, H.; Li, Z.; Ge, Y.; Liu, B. Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization. Energies 2024, 17, 4894. https://doi.org/10.3390/en17194894
Shi J, Qin J, Li H, Li Z, Ge Y, Liu B. Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization. Energies. 2024; 17(19):4894. https://doi.org/10.3390/en17194894
Chicago/Turabian StyleShi, Jing, Jianru Qin, Haibo Li, Zesen Li, Yi Ge, and Boliang Liu. 2024. "Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization" Energies 17, no. 19: 4894. https://doi.org/10.3390/en17194894
APA StyleShi, J., Qin, J., Li, H., Li, Z., Ge, Y., & Liu, B. (2024). Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization. Energies, 17(19), 4894. https://doi.org/10.3390/en17194894






