An Integrated Frequency Regulation Method Based on System Frequency Security Posture
Abstract
1. Introduction
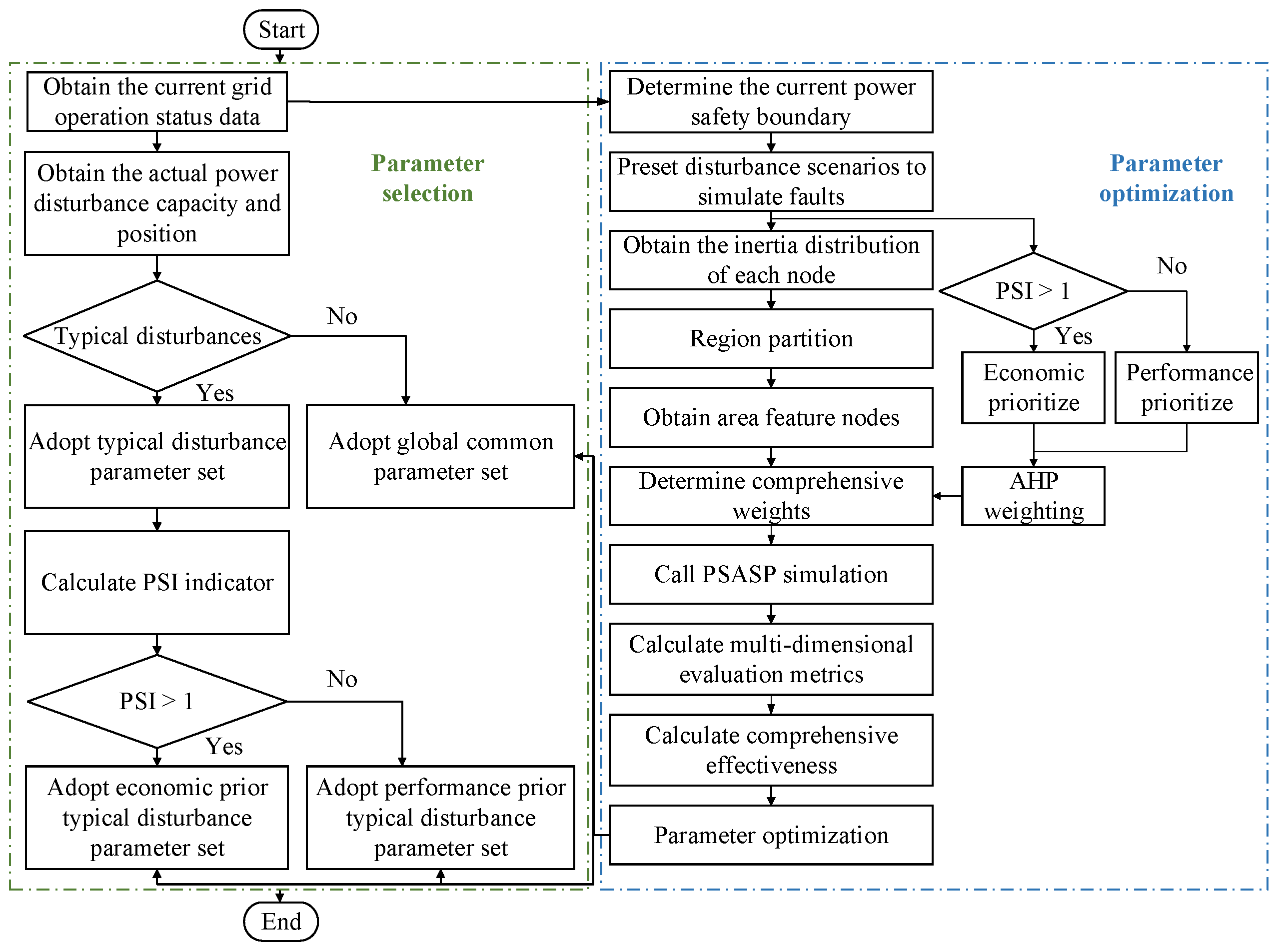
2. System Frequency Security Posture Assessment Method Considering Spatial Distribution Characteristics
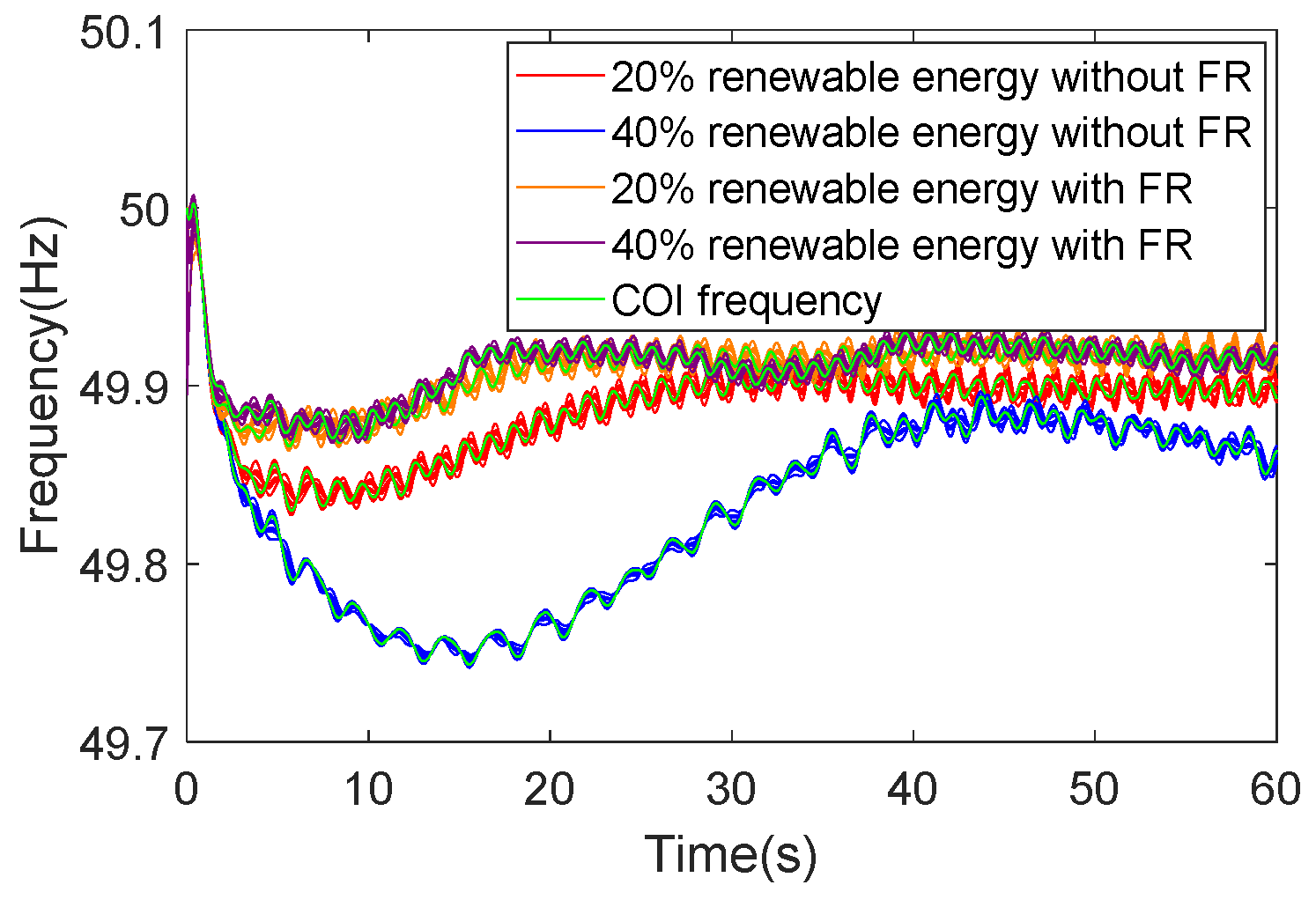
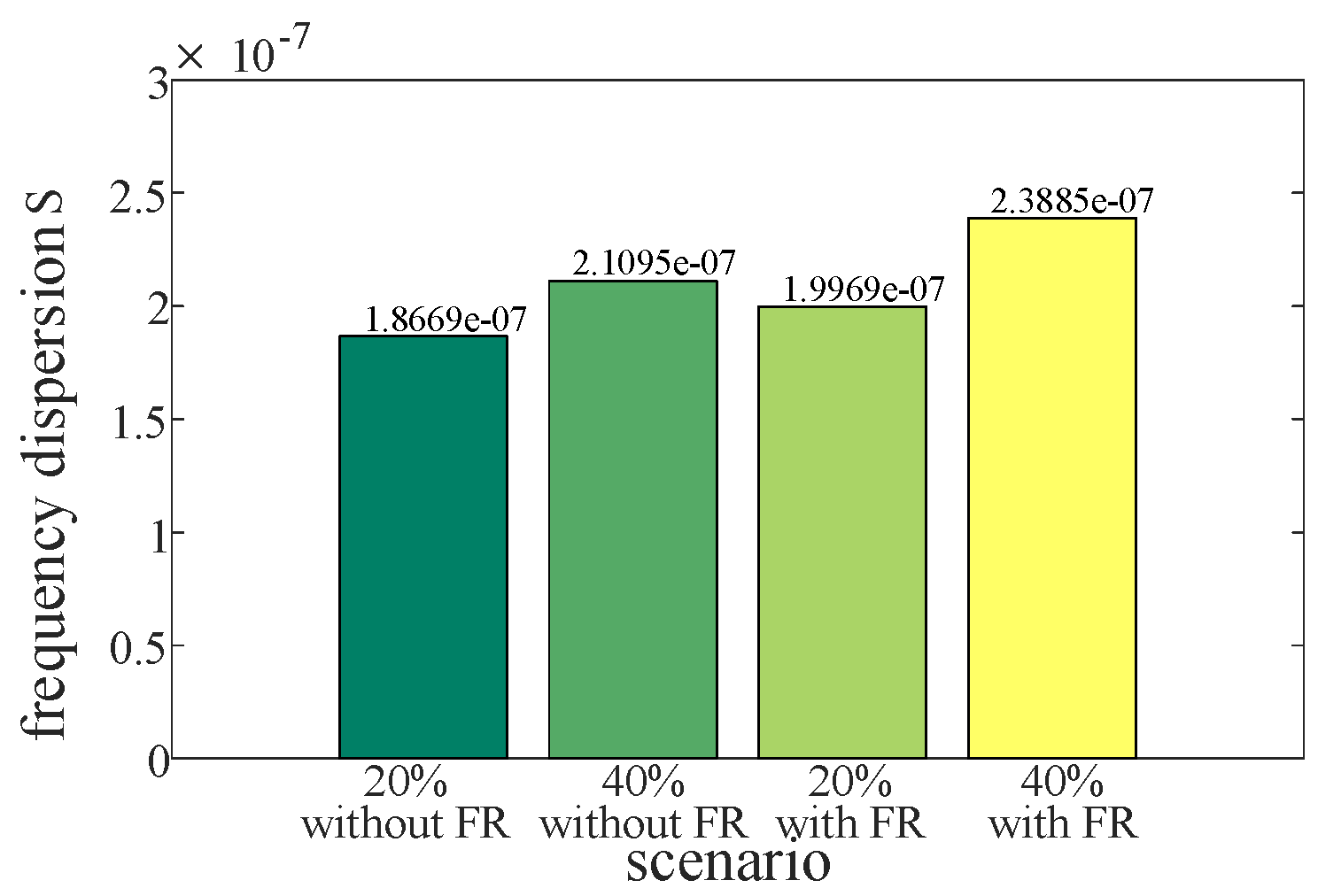
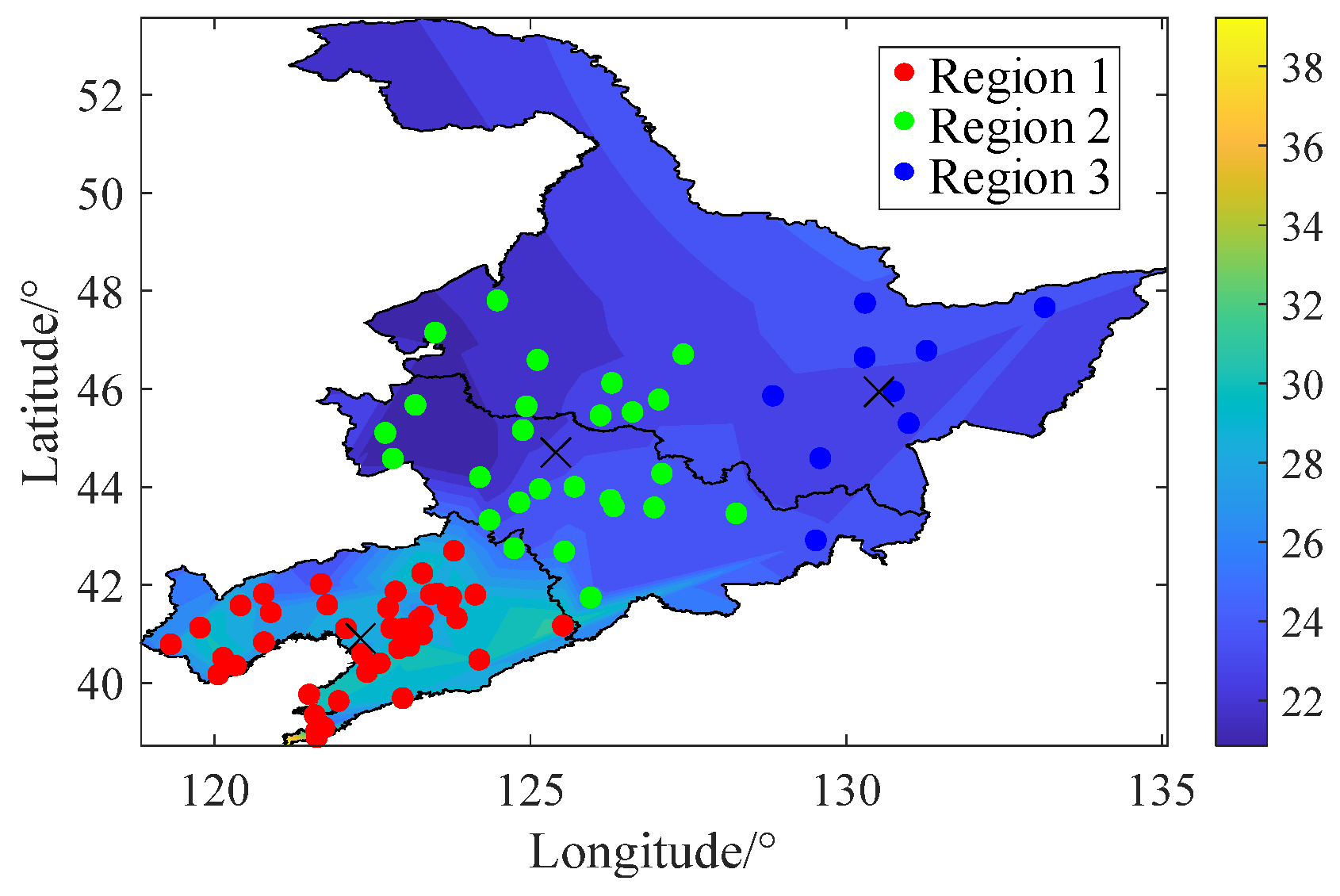
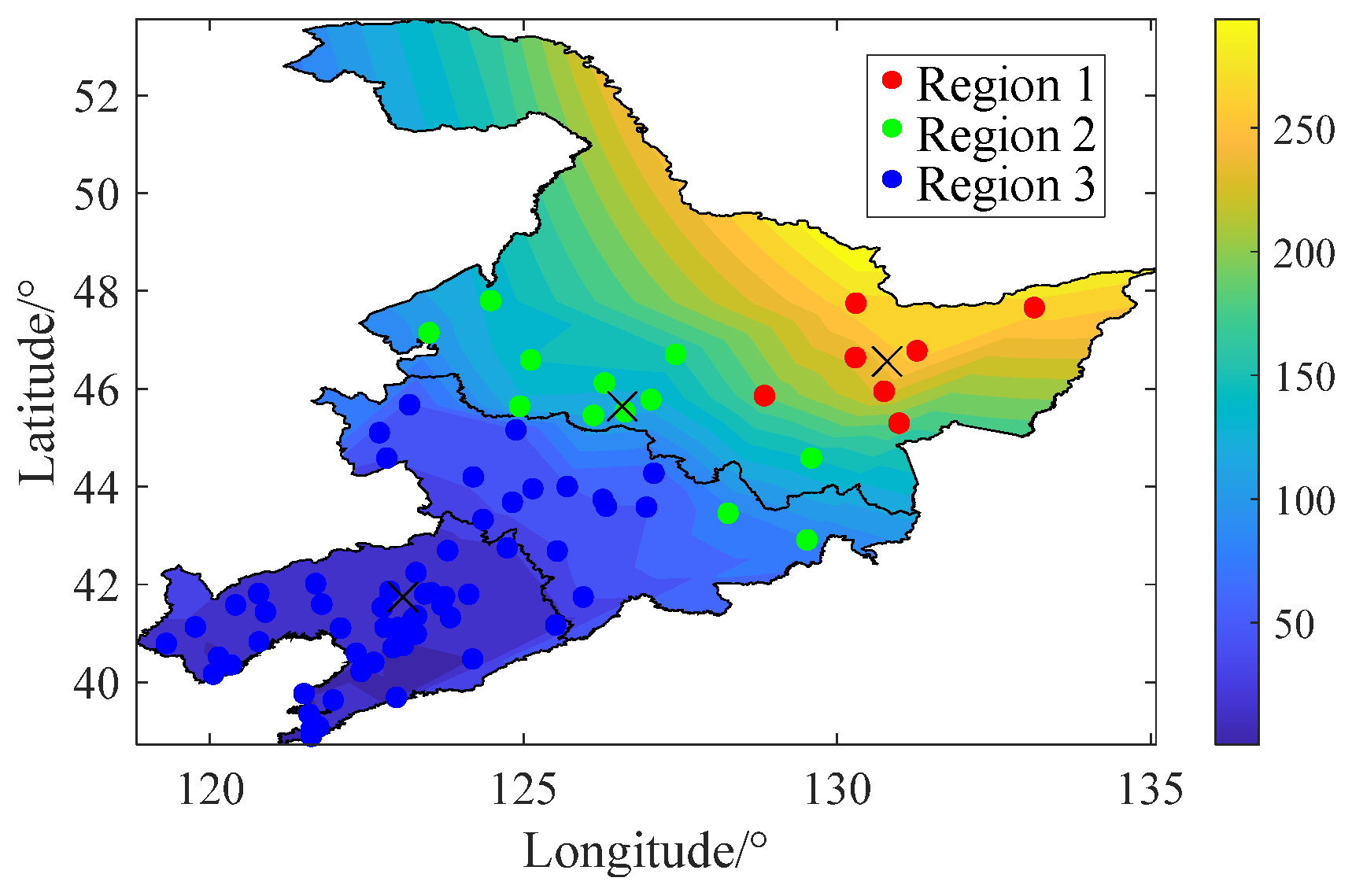
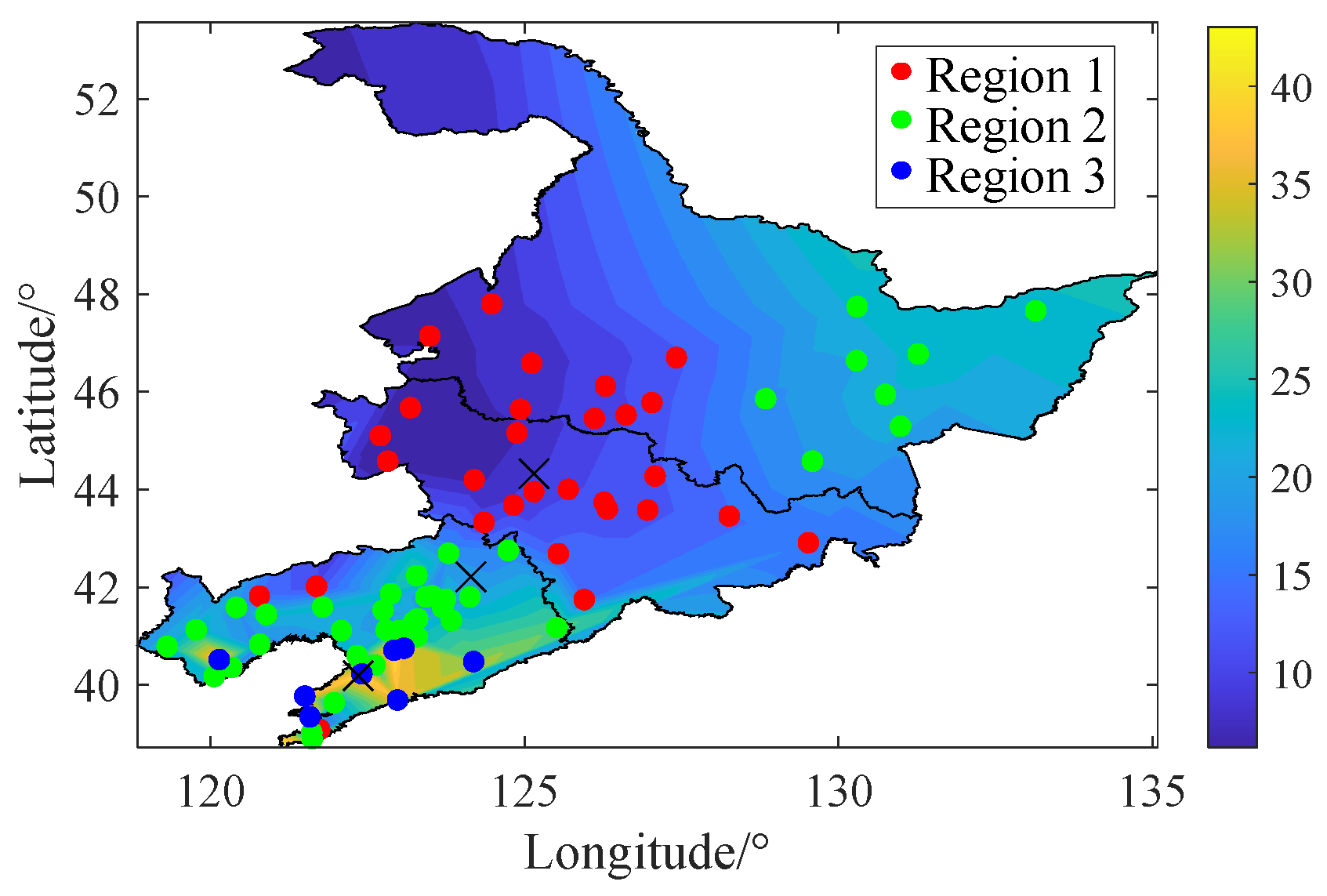
2.1. Quantitative Analysis of System Frequency Spatial Distribution Characteristics Based on Actual Grid Models
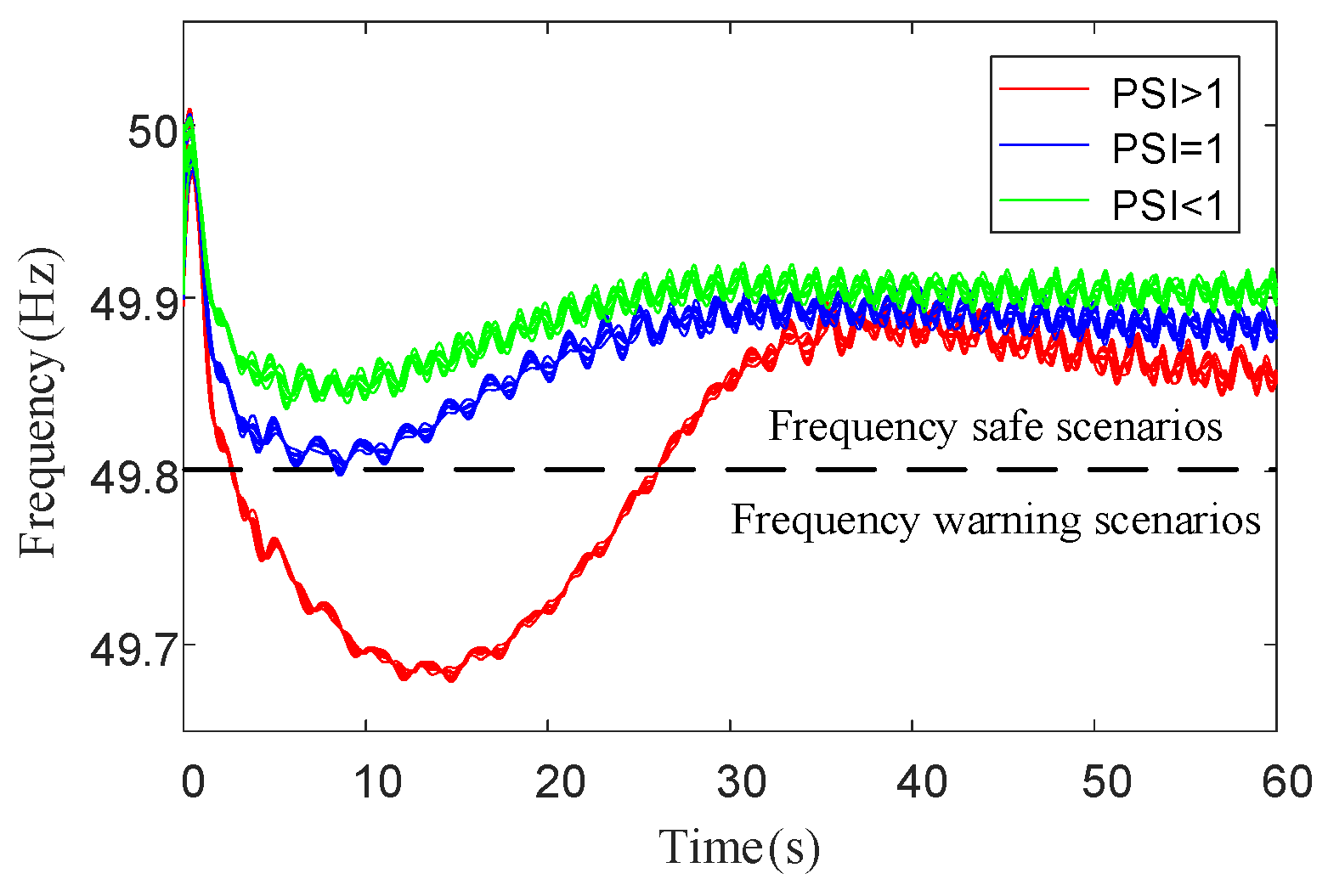
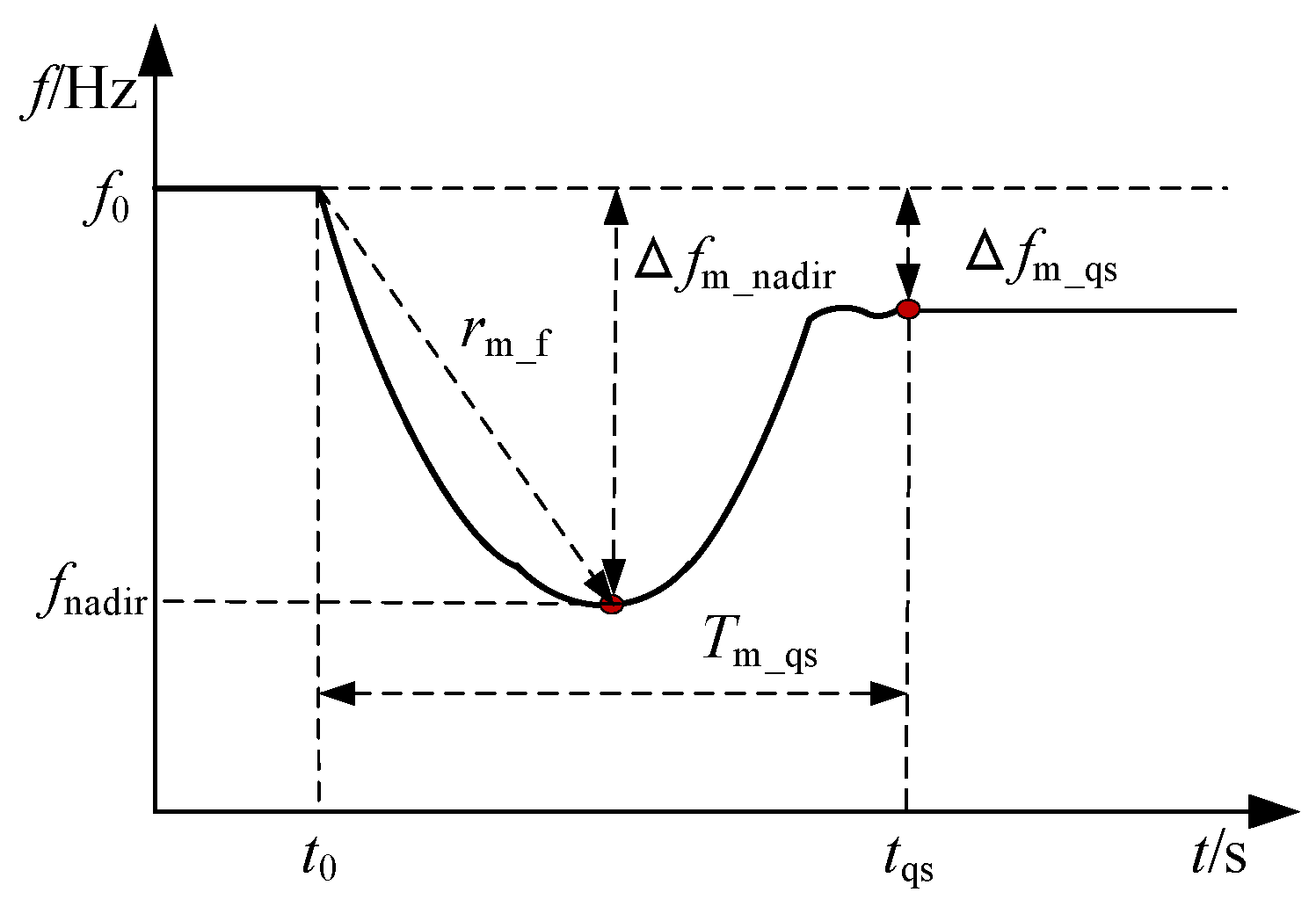
2.2. Frequency Security Posture Assessment Method
3. The Integrated Frequency Regulation Method Based on System Frequency Security Posture
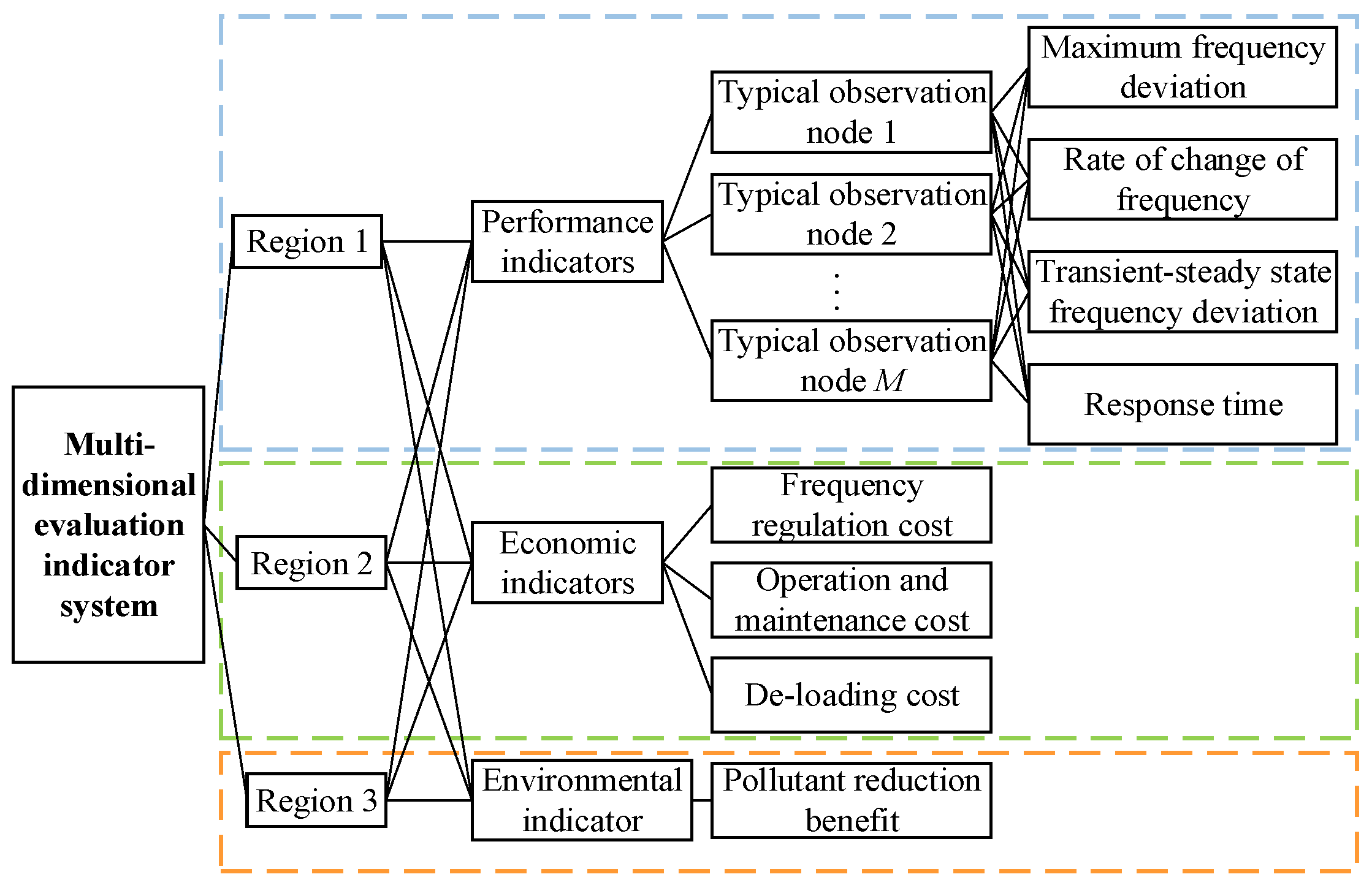
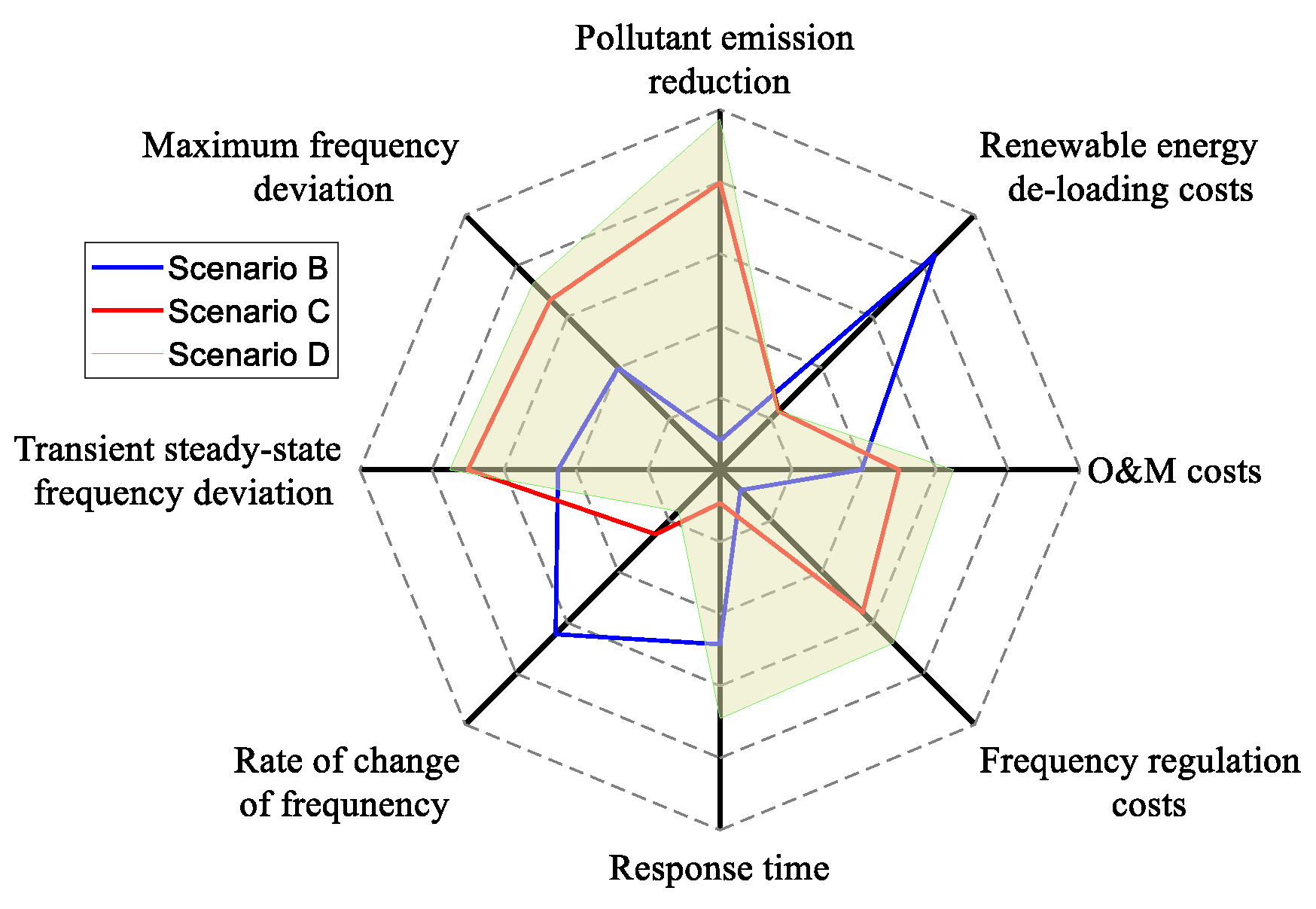
3.1. Comprehensive Evaluation Method for Frequency Regulation Effectiveness
- Performance indicators
- 2.
- Economic indicators
- 3.
- Environmental indicators
3.2. Parameter Optimization Method for Diversified Frequency Regulation Resources
- Mutation: First, mutated new individuals are obtained based on adaptive mutation factors by evaluating the better individuals from the original population:where represents the value of the ith individual variant at the g + 1st iteration; , and are the values of the r 1st, r 2nd, and r 3rd individuals in the population at the gth iteration, respectively; r1, r2, and r3 are integers randomly chosen to be mutually exclusive with i at NP population size; F is the variational operator, which serves to equalize the local and global searches; F0 is the initial variation operator; and Gm is the total number of iterations.
- Crossover: This step involves simulating a genetic algorithm to construct a preparatory population by combining the original population with mutated individuals based on random probabilities.where and are the parameter values of the jth term in the ith individual subjected to crossover and mutation at the g + 1st iteration, respectively; CR is a cross-operator; n is the total number of parameters; and is the preparatory population for g + 1st iterations.
- Boundary condition processing: Individual data are adjusted for new populations based on parameter group ranges:where and are the maximum and minimum value of the jth parameter range; is the value of the preparatory population for the jth parameter in the ith individual of the g + 1st iteration.
- Selection: Based on the assessment results of the original and preparatory populations, a new population is constructed based on merit:where is the final parameter value obtained in the g + 1st iteration; and represents the assessment results when and are used as a selection variable, respectively.
3.3. Integrated Frequency Regulation Method for Diversified Resources
4. Simulation Verification
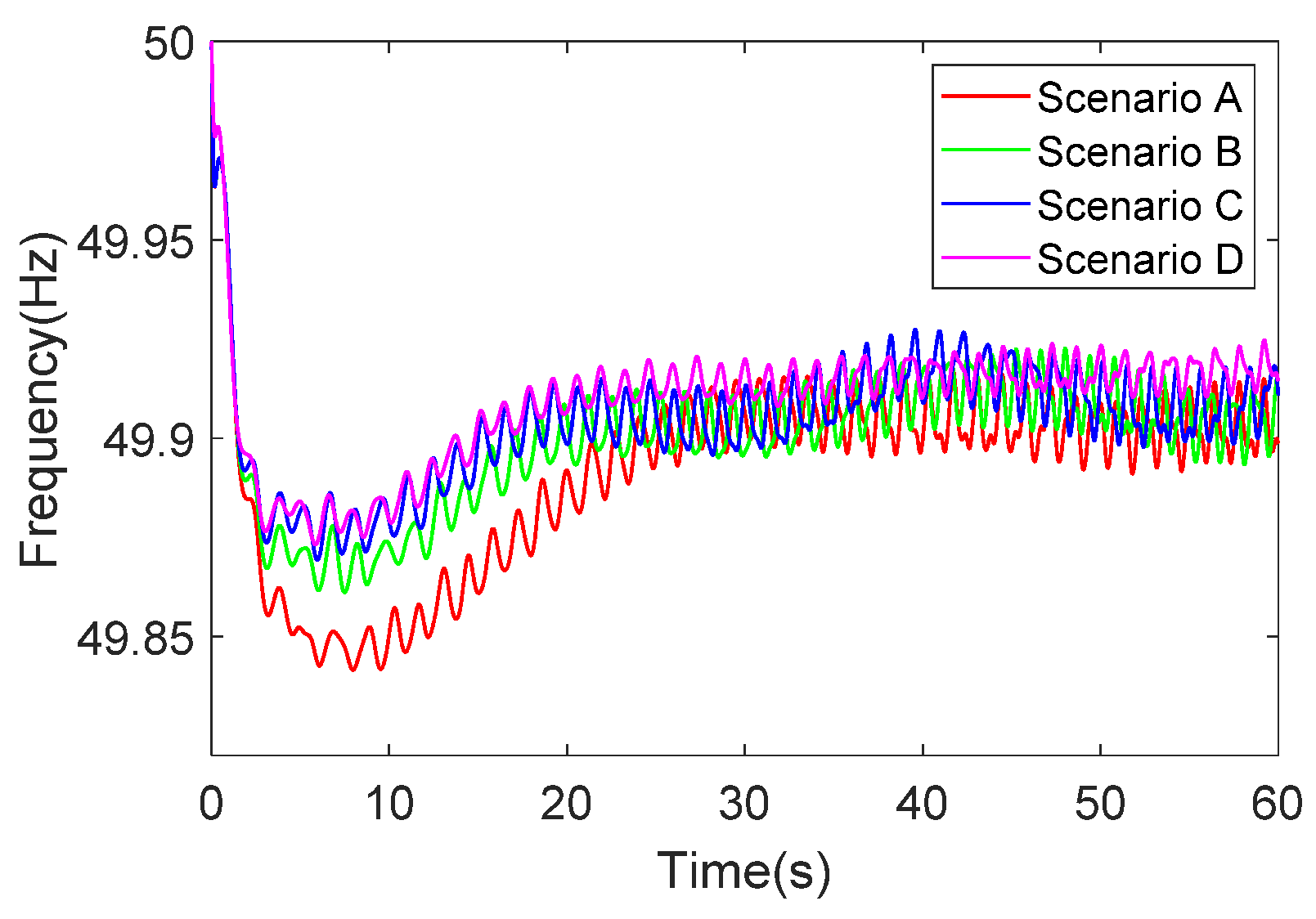
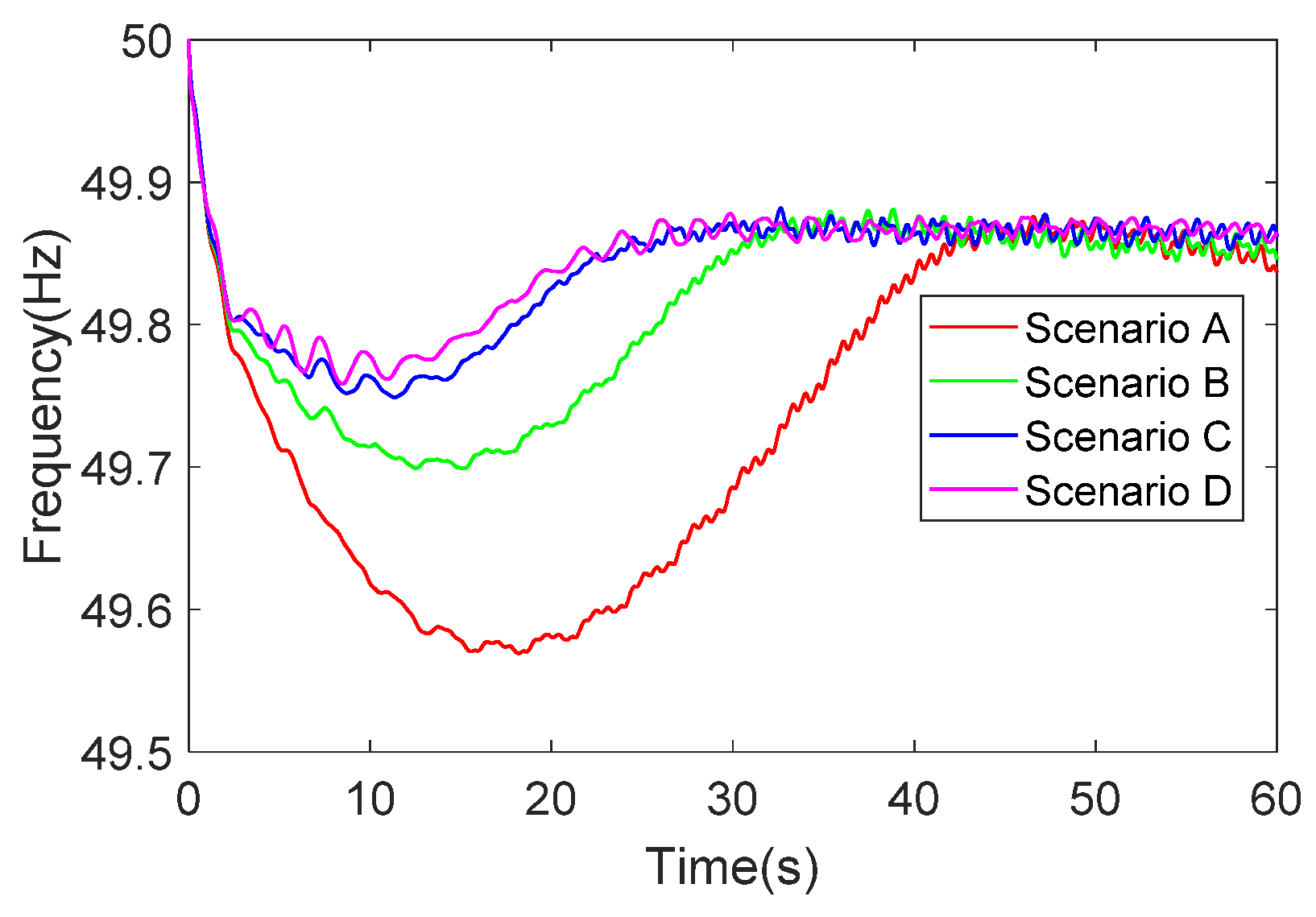
4.1. Typical Disturbance Condition I
4.2. Typical Disturbance Condition II
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Region | Wind Power Units | Photovoltaic Units | Energy Storage System | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dead Zone | Droop Coefficient | De-Loading Coefficient | Virtual Inertia Coefficient | Dead Zone | Droop Coefficient | De-Loading Coefficient | Dead Zone | Droop Coefficient | |
| 1 | 0.071 | 7.36 | 0.019 | 8.96 | 0.041 | 18.85 | 0.035 | 0.038 | 138 |
| 2 | 0.051 | 23.15 | 0.069 | 9.04 | 0.022 | 21.49 | 0.050 | 0.048 | 110 |
| 3 | 0.043 | 18.47 | 0.058 | 9.45 | 0.049 | 9.30 | 0.089 | 0.040 | 105 |
| Region | Wind Power Units | Photovoltaic Units | Energy Storage System | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dead Zone | Droop Coefficient | De-Loading Coefficient | Virtual Inertia Coefficient | Dead Zone | Droop Coefficient | De-Loading Coefficient | Dead Zone | Droop Coefficient | |
| 1 | 0.041 | 41.261 | 0.02 | 9.72 | 0.048 | 43.73 | 0.04 | 0.049 | 41 |
| 2 | 0.056 | 37.351 | 0.07 | 8.98 | 0.045 | 40.37 | 0.05 | 0.038 | 146 |
| 3 | 0.078 | 36.275 | 0.06 | 9.51 | 0.049 | 25.59 | 0.09 | 0.032 | 110 |
| Region | Wind Power Units | Photovoltaic Units | Energy Storage System | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dead Zone | Droop Coefficient | De-Loading Coefficient | Virtual Inertia Coefficient | Dead Zone | Droop Coefficient | De-Loading Coefficient | Dead Zone | Droop Coefficient | |
| 1 | 0.069 | 10.35 | 0.02 | 9.76 | 0.026 | 49.89 | 0.04 | 0.040 | 149 |
| 2 | 0.038 | 18.35 | 0.07 | 9.42 | 0.054 | 24.88 | 0.05 | 0.039 | 145 |
| 3 | 0.061 | 24.03 | 0.06 | 9.09 | 0.028 | 41.60 | 0.09 | 0.038 | 83 |
References
- Hamada, H.; Kusayanagi, Y.; Tatematsu, M.; Watanabe, M.; Kikusato, H. Challenges for a reduced inertia power system due to the large-scale integration of renewable energy. Glob. Energy Interconnect. 2022, 5, 266–273. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, N.; Du, E.; Kang, C.; Wang, Z. Review and Countermeasures on Frequency Security Issues of Power Systems with High Shares of Renewables and Power Electronics. Proc. Chin. Soc. Electr. Eng. 2022, 42, 1–24. [Google Scholar]
- Shao, S.; Li, M.; Cai, H.; Liu, B.; Xu, X.; Guo, C. The Influence of Measured Trajectory Based Model Parameters Correcting on Simulation Precision of Power System Dynamic Frequency. Electr. Meas. Instrum. 2014, 51, 46–52. [Google Scholar]
- Ma, N.; Xie, X.; Qin, X.; Su, L. Space-time Distribution Characteristics of Frequency in Power Systems with Renewable Energy Generators. In Proceedings of the 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), Virtual, 9–11 October 2021; pp. 227–232. [Google Scholar]
- You, C.; Zhao, Y.; Hou, S.; Zhang, Y.; Lv, Y. Research on Centre of Inertia Based Frequency Sampling and System Frequency Distribution Characteristics. IEEE Access 2024, 12, 71371–71378. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, J.; Zhou, Y.; Qu, S. Online Identification of Inertia Distribution in Normal Operating Power System. IEEE Trans. Power Syst. 2020, 35, 3301–3304. [Google Scholar] [CrossRef]
- Dhara, P.K.; Rather, Z.H. A New Generator Clustering Approach for Power System Inertia Estimation with Reduced Number of Frequency Monitoring Nodes. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), 56th Annual Meeting of the IEEE-Industry-Applications-Society (IAS), Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar]
- Ekanayake, J.; Jenkins, N. Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Shi, L.; Lao, W.; Wu, F.; Zheng, T.; Lee, K.Y. Frequency Regulation Control and Parameter Optimization of Doubly-Fed Induction Machine Pumped Storage Hydro Unit. IEEE Access 2022, 10, 102586–102598. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, T.; Wang, S.; Dong, Y.; Chen, Z. Comprehensive Coordinated Control Strategy of PMSG-Based Wind Turbine for Providing Frequency Regulation Services. IEEE Access 2019, 7, 63944–63953. [Google Scholar] [CrossRef]
- Sun, M.; Min, Y.; Xiong, X.; Chen, L.; Zhao, L.; Feng, Y.; Wang, B. Practical Realization of Optimal Auxiliary Frequency Control Strategy of Wind Turbine Generator. J. Mod. Power Syst. Clean Energy 2022, 10, 617–626. [Google Scholar] [CrossRef]
- Kheshti, M.; Ding, L.; Bao, W.; Yin, M.; Wu, Q.; Terzija, V. Toward Intelligent Inertial Frequency Participation of Wind Farms for the Grid Frequency Control. IEEE Trans. Ind. Inform. 2020, 16, 6772–6786. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Y. Coordinated Control Strategy of a Battery Energy Storage System to Support a Wind Power Plant Providing Multi-Timescale Frequency Ancillary Services. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), IEEE-Power-and-Energy-Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Li, D.; Chen, Z.; Xu, B.; Li, P.; Chen, H. Mechanism analysis and optimal dead zone parameter of wind-storage combined frequency regulation considering primary frequency regulation dead zone. Power Syst. Prot. Control 2024, 52, 38–47. [Google Scholar]
- Liang, C.; Wang, P.; Han, X.; Qin, W.; Billinton, R.; Li, W. Operational Reliability and Economics of Power Systems with Considering Frequency Control Processes. IEEE Trans. Power Syst. 2017, 32, 2570–2580. [Google Scholar] [CrossRef]
- Li, J.; Guo, Z.; Ma, S.; Zhang, G.; Wang, H. Overview of the “Source-grid-load-storage” Architecture and Evaluation System Under the New Power System. High Volt. Eng. 2022, 48, 4330–4341. [Google Scholar]
- Xue, J.; Wang, D.; Tao, Y.; Qi, J.; Liao, S.; Mao, B.; Yao, L. Evaluation of Frequency Regulation Performance of Energy Storage Power Plants Based on Correlation Analysis and Combined Weighting Method. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 349–354. [Google Scholar]
- Zhao, Y.; Xie, K.; Shao, C.; Lin, C.; Shahidehpour, M.; Tai, H.; Hu, B.; Du, X. Integrated Assessment of the Reliability and Frequency Deviation Risks in Power Systems Considering the Frequency Regulation of DFIG-Based Wind Turbines. IEEE Trans. Sustain. Energy 2023, 14, 2308–2326. [Google Scholar] [CrossRef]
- Guo, Q.; Song, B.; Guo, C.; Liu, J.; Chen, H.; Jia, Y.; Wang, Z. Evaluation of the Performance of Energy Storage System Participating in Grid Frequency Regulation. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 4205–4209. [Google Scholar]
- Li, J.; Lu, J.; Qian, M.; Tang, B.; Chen, N.; Peng, P. Research on System Partition Method of High Proportion Renewable Energy Power System Considering Dynamic Frequency Spatiotemporal Characteristics. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023; pp. 750–755. [Google Scholar]
- GB/T40595-2021; Guide for Technology and Test on Primary Frequency Control of Grid-Connected Power Resource. China Electricity Council: Beijing, China, 2021.
- Terzija, V.V. Adaptive underfrequency load shedding based on the magnitude of the disturbance estimation. IEEE Trans. Power Syst. 2006, 21, 1260–1266. [Google Scholar] [CrossRef]


| Scenario | ||||||||
|---|---|---|---|---|---|---|---|---|
| B | 0.138 | 0.091 | 7.709 | 42.734 | 1.992 | 16.214 | 1.747 | 1.457 |
| C | 0.130 | 0.086 | 8.494 | 48.612 | 1.944 | 16.006 | 1.931 | 1.958 |
| D | 0.128 | 0.085 | 8.675 | 39.648 | 1.932 | 15.705 | 1.931 | 2.081 |
| Scenario | ||||||||
|---|---|---|---|---|---|---|---|---|
| B | 0.302 | 0.146 | 3.305 | 36.391 | 3.528 | 28.612 | 0.968 | 0.334 |
| C | 0.252 | 0.138 | 5.835 | 29.646 | 3.543 | 29.065 | 1.931 | 0.708 |
| D | 0.240 | 0.136 | 4.609 | 28.690 | 3.691 | 29.775 | 1.931 | 1.128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wang, C.; Song, W.; Chao, P.; Jin, Y.; Zeng, H.; Li, P.; Liu, W. An Integrated Frequency Regulation Method Based on System Frequency Security Posture. Energies 2024, 17, 4886. https://doi.org/10.3390/en17194886
Zhang Q, Wang C, Song W, Chao P, Jin Y, Zeng H, Li P, Liu W. An Integrated Frequency Regulation Method Based on System Frequency Security Posture. Energies. 2024; 17(19):4886. https://doi.org/10.3390/en17194886
Chicago/Turabian StyleZhang, Qiang, Chao Wang, Wenting Song, Pupu Chao, Yonglin Jin, Hui Zeng, Ping Li, and Wansong Liu. 2024. "An Integrated Frequency Regulation Method Based on System Frequency Security Posture" Energies 17, no. 19: 4886. https://doi.org/10.3390/en17194886
APA StyleZhang, Q., Wang, C., Song, W., Chao, P., Jin, Y., Zeng, H., Li, P., & Liu, W. (2024). An Integrated Frequency Regulation Method Based on System Frequency Security Posture. Energies, 17(19), 4886. https://doi.org/10.3390/en17194886






