Electrothermal Modeling of Photovoltaic Modules for the Detection of Hot-Spots Caused by Soiling
Abstract
1. Introduction
2. The State of the Art
2.1. Thermal Models
2.2. Modeling of Hot-Spots
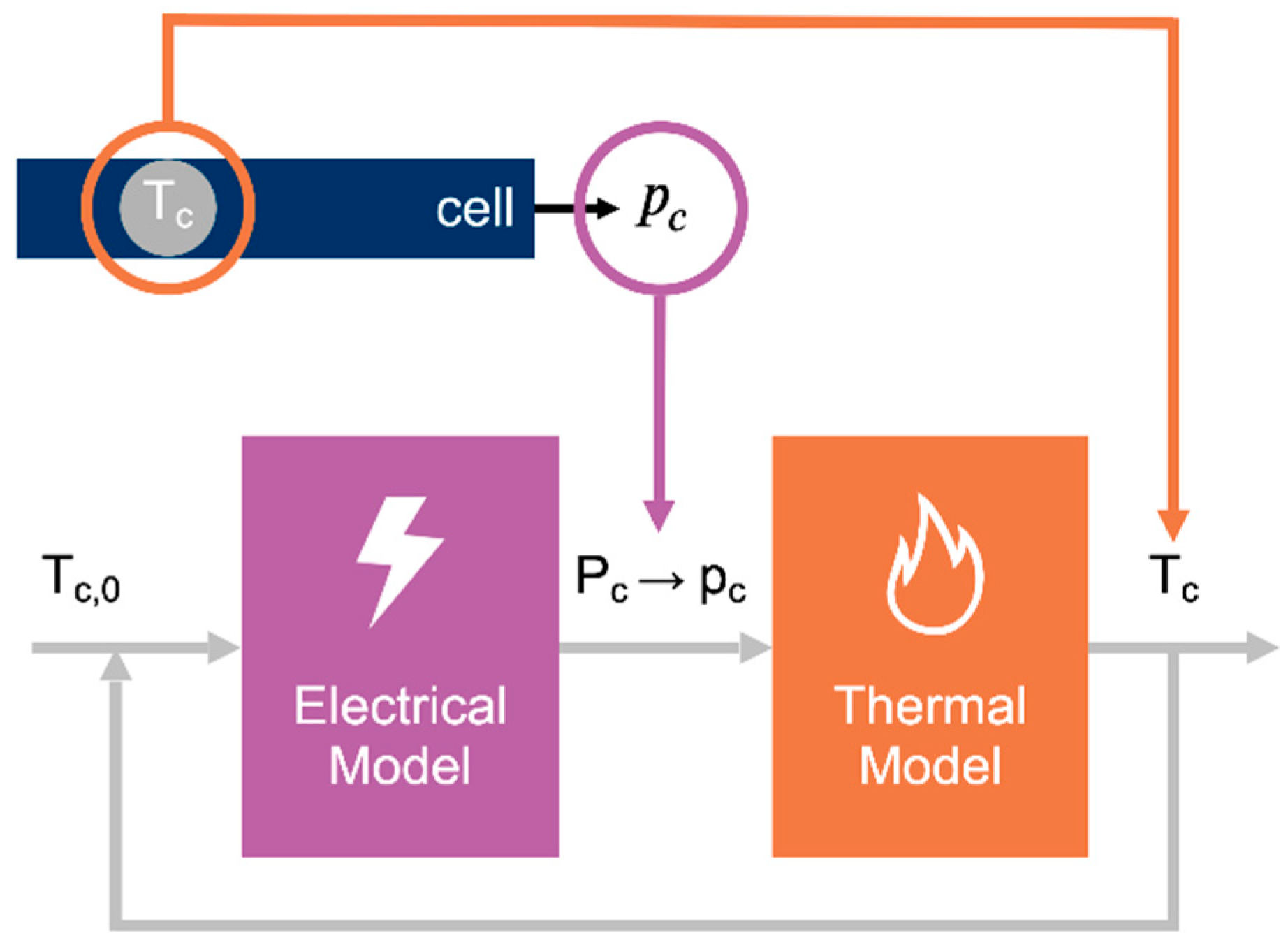
3. Description of the New Electrothermal Model
3.1. Thermal Model
3.2. Material Properties of Layers
3.3. Electrical Model and Combination to Electrothermal Model
3.4. Non-Linear System of Equations
3.5. Thermal Inertia
4. Experimental Validation and Discussion
4.1. Experiment with Clean PV Modules
4.2. Experiment with Soiled PV Modules
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaics |
| IRT, IR | Infrared thermography, Infrared |
| EL | Electroluminescence |
| RGB image | Red, Green, Blue image (image type) |
| IV curve | Current-voltage curve |
| UV light/radiation | Ultraviolet light/radiation |
| CNN | Convolutional Neural Network |
| STC | Standard test conditions |
| NOCT | Normal operating condition temperature |
| RMSE | Root mean square error |
| MAE | Mean average error |
| MBE | Mean bias error |
| Symbols | |
| Conductive heat transfer | |
| Convective heat transfer | |
| Specific heat capacity | |
| Electrical power | |
| Cell area | |
| Temperature | |
| Irradiance | |
| Wind speed | |
| Convective heat transfer coefficient | |
| Elementary charge | |
| Resistance | |
| Diode ideality factor | |
| Module efficiency | |
| Thermal radiation | |
| Thermal conductivity | |
| Hemispherical reflectance | |
| Absorptance | |
| Emissivity | |
| Hemispherical Transmittance | |
| Kinematic viscosity |
Appendix A

Appendix B
| Quantity | Value |
|---|---|
| Breakdown factor | 0.002 |
| Breakdown voltage | −14 V |
| Trigger voltage of the bypass diode | −0.5 |
| Breakdown exponential factor | 3 |
| Efficiency | 0.17622% |
| Short circuit current under STC | 9.61 A |
| Open circuit voltage under STC | 47.13 V |
| Power under STC | 349 W |
| MPP current under STC | 9.26 A |
| MPP voltage under STC | 37.80 V |
| Temperature coefficient of the power | −0.37 %/K |

References
- Bouckaert, S.; Pales, A.F.; McGlade, C.; Remme, U.; Wanner, B.; Varro, L.; D’Ambrosio, D.; Spencer, T. Net Zero by 2050: A Roadmap for the Global Energy Sector; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2021; p. 224. [Google Scholar]
- Gielen, D.; Gorini, R.; Wagner, N.; Leme, R.; Gutierrez, L.; Prakash, G.; Asmelash, E.; Janeiro, L.; Gallina, G.; Vale, G. Global Energy Transformation: A Roadmap to 2050; International Renewable Energy Agency (IRENA): Masdar City, United Arab Emirates, 2019; p. 52. [Google Scholar]
- Honrubia-Escribano, A.; Ramirez, F.J.; Gómez-Lázaro, E.; Garcia-Villaverde, P.M.; Ruiz-Ortega, M.J.; Parra-Requena, G. Influence of solar technology in the economic performance of PV power plants in Europe. A comprehensive analysis. Renew. Sustain. Energy Rev. 2018, 82, 488–501. [Google Scholar] [CrossRef]
- Deitsch, S.; Christlein, V.; Berger, S.; Buerhop-Lutz, C.; Maier, A.; Gallwitz, F.; Riess, C. Automatic classification of defective photovoltaic module cells in electroluminescence images. Sol. Energy 2019, 185, 455–468. [Google Scholar] [CrossRef]
- Köntges, M.; Kurtz, S.; Packard, C.; Jahn, U.; Berger, K.A.; Kato, K.; Friesen, T.; Liu, H.; Van Iseghem, M.; Wohlgemuth, J. Review of Failures of Photovoltaic Modules; Istituto Sostenibilità Applicata All’ambiente Costruito: Mendrisio, Switzerland, 2014. [Google Scholar]
- IEC 61215(04); Crystalline Silicon Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval. International Standard IEC: Geneva, Switzerland, 2005.
- Polo, J.; Martín-Chivelet, N.; Sanz-Saiz, C.; Alonso-Montesinos, J.; López, G.; Alonso-Abella, M.; Battles, F.J.; Marzo, A.; Hanrieder, N. Modeling soiling losses for rooftop PV systems in suburban areas with nearby forest in Madrid. Renew. Energy 2021, 178, 420–428. [Google Scholar] [CrossRef]
- Smestad, G.P.; Germer, T.A.; Alrashidi, H.; Fernández, E.F.; Dey, S.; Brahma, H.; Sarmah, N.; Ghosh, A.; Sellami, N.; Hassan, I.A. Modelling photovoltaic soiling losses through optical characterization. Sci. Rep. 2020, 10, 58. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Xu, Z.; Wang, Y.; Li, C.; Zhang, J.; Zhang, K.; Wei, H. Temperature Estimation of Partially Shaded Photovoltaic Modules Using a Multiphysics Model. IEEE J. Photovolt. 2022, 12, 1243–1251. [Google Scholar] [CrossRef]
- Pavan, A.M.; Mellit, A.; De Pieri, D. The effect of soiling on energy production for large-scale photovoltaic plants. Sol. Energy 2011, 85, 1128–1136. [Google Scholar] [CrossRef]
- Ilse, K.; Micheli, L.; Figgis, B.W.; Lange, K.; Daßler, D.; Hanifi, H.; Wolfertstetter, F.; Naumann, V.; Hagendorf, C.; Gottschalg, R. Techno-economic assessment of soiling losses and mitigation strategies for solar power generation. Joule 2019, 3, 2303–2321. [Google Scholar] [CrossRef]
- Maghami, M.R.; Hizam, H.; Gomes, C.; Radzi, M.A.; Rezadad, M.I.; Hajighorbani, S. Power loss due to soiling on solar panel: A review. Renew. Sustain. Energy Rev. 2016, 59, 1307–1316. [Google Scholar] [CrossRef]
- Lamaamar, I.; Tilioua, A.; Zaid, Z.B.; Babaoui, A.; Ettakni, M.; Alaoui, M.A.H. Evaluation of different models for validating of photovoltaic cell temperature under semi-arid conditions. Heliyon 2021, 7, e08534. [Google Scholar] [CrossRef]
- Vumbugwa, M.; Crozier McCleland, J.; Van Dyk, E.; Vorster, F.; Serameng, T. Effects of current mismatch due to uneven soiling on the performance of multi-crystalline silicon module strings. J. Energy S. Afr. 2020, 31, 62–72. [Google Scholar] [CrossRef]
- Winkel, P.; Wilbert, S.; Röger, M.; Krauth, J.J.; Algner, N.; Nouri, B.; Wolfertstetter, F.; Carballo, J.A.; Alonso-Garcia, M.C.; Polo, J. Cell-Resolved PV Soiling Measurement Using Drone Images. Remote Sens. 2024, 16, 2617. [Google Scholar] [CrossRef]
- Qasem, H.; Mnatsakanyan, A.; Banda, P. Assessing dust on PV modules using image processing techniques. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016. [Google Scholar]
- Hwang, P.C.; Ku, C.C.-Y.; Chan, J.C.-C. Soiling detection for photovoltaic modules based on an intelligent method with image processing. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), Taoyuan, Taiwan, 28–30 September 2020. [Google Scholar]
- Li, X.; Yang, Q.; Chen, Z.; Luo, X.; Yan, W. Visible defects detection based on UAV-based inspection in large-scale photovoltaic systems. IET Renew. Power Gener. 2017, 11, 1234–1244. [Google Scholar] [CrossRef]
- Cipriani, G.; D’Amico, A.; Guarino, S.; Manno, D.; Traverso, M.; Di Dio, V. Convolutional neural network for dust and hotspot classification in PV modules. Energies 2020, 13, 6357. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Touati, F.; Chowdhury, N.A.; Benhmed, K.; Gonzales, A.J.S.P.; Al-Hitmi, M.A.; Benammar, M.; Gastli, A.; Ben-Brahim, L. Long-term performance analysis and power prediction of PV technology in the State of Qatar. Renew. Energy 2017, 113, 952–965. [Google Scholar] [CrossRef]
- Busquet, S.; Kobayashi, J. Modelling daily PV performance as a function of irradiation, ambient temperature, soiling, wind speed, and aging-Applied to PV modules operating in Maui. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018. [Google Scholar]
- Mittag, M.; Vogt, L.; Herzog, C.; Neuhaus, H. Thermal modelling of photovoltaic modules in operation and production. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition (EUPVSEC), Marseille, France, 9–13 September 2019. [Google Scholar]
- Tuncel, B.; Ozden, T.; Balog, R.; Akinoglu, B. Dynamic thermal modelling of PV performance and effect of heat capacity on the module temperature. Case Stud. Therm. Eng. 2020, 22, 100754. [Google Scholar] [CrossRef]
- Olukan, T.A.; Emziane, M. A comparative analysis of PV module temperature models. Energy Procedia 2014, 62, 694–703. [Google Scholar] [CrossRef]
- Ross, R. Design techniques for flat-plate photovoltaic arrays. In Proceedings of the 15th Photovoltaic Specialists Conference, Orlando, FL, USA, 12–15 May 1981. [Google Scholar]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model; Citeseer: University Park, PA, USA, 2004; Volume 8. [Google Scholar]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Gilman, P. SAM Photovoltaic Model Technical Reference; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015. [Google Scholar]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2009, 34, 23–29. [Google Scholar] [CrossRef]
- Qian, J.; Thomson, A.; Blakers, A.; Ernst, M. Comparison of half-cell and full-cell module hotspot-induced temperature by simulation. IEEE J. Photovolt. 2018, 8, 834–839. [Google Scholar] [CrossRef]
- Solheim, H.J.; Fjær, H.G.; Sørheim, E.A.; Foss, S.E. Measurement and simulation of hot spots in solar cells. Energy Procedia 2013, 38, 183–189. [Google Scholar] [CrossRef][Green Version]
- Rossi, D.; Omaña, M.; Giaffreda, D.; Metra, C. Modeling and detection of hotspot in shaded photovoltaic cells. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 23, 1031–1039. [Google Scholar] [CrossRef]
- Geisemeyer, I.; Fertig, F.; Warta, W.; Rein, S.; Schubert, M. Prediction of silicon PV module temperature for hot spots and worst case partial shading situations using spatially resolved lock-in thermography. Sol. Energy Mater. Sol. Cells 2014, 120, 259–269. [Google Scholar] [CrossRef]
- Winkel, P.; Wilbert, S.; Wolfertstetter, F.; Röger, M.; Krauth, J.J.; Algner, N.; Zarzalejo, L.; Martinez, D.; Polo, J.; Alsonso García, M.C.; et al. Zell-aufgelöste Bestimmung der Verschmutzung von PVModulen mit bildgebenden Verfahren. In Proceedings of the PV Symposium, Freiburg im Breisgau, Germany, 21–23 June 2022. [Google Scholar]
- Tool, C.; Burgers, A.; Manshanden, P.; Weeber, A.; Van Straaten, B. Influence of wafer thickness on the performance of multicrystalline Si solar cells: An experimental study. Prog. Photovolt. Res. Appl. 2002, 10, 279–291. [Google Scholar] [CrossRef]
- Lorenz, A.; Münzer, A.; Lehner, M.; Greutmann, R.; Brocker, H.; Reinecke, H.; Clement, F. High-throughput front and rear side metallization of silicon solar cells using rotary screen printing. Energy Procedia 2017, 124, 680–690. [Google Scholar] [CrossRef]
- Zheng, D.; Hunt, E.R., Jr.; Running, S.W. A daily soil temperature model based on air temperature and precipitation for continental applications. Clim. Res. 1993, 2, 183–191. [Google Scholar] [CrossRef]
- Xu, C.; Qu, J.J.; Hao, X.; Zhu, Z.; Gutenberg, L. Surface soil temperature seasonal variation estimation in a forested area using combined satellite observations and in-situ measurements. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102156. [Google Scholar] [CrossRef]
- Araghi, A.; Mousavi-Baygi, M.; Adamowski, J.; Martinez, C.; van der Ploeg, M. Forecasting soil temperature based on surface air temperature using a wavelet artificial neural network. Meteorol. Appl. 2017, 24, 603–611. [Google Scholar] [CrossRef]
- Zhou, J.; Yi, Q.; Wang, Y.; Ye, Z. Temperature distribution of photovoltaic module based on finite element simulation. Sol. Energy 2015, 111, 97–103. [Google Scholar] [CrossRef]
- Pfreundt, A.; Yucebas, D.; Beinert, A.; Verissimo Mesquita, L.; Pitta Bauermann, L.; Romer, P.; Mittag, M. Post-processing thickness variation of PV module materials and its impact on temperature, mechanical stress and power. In Proceedings of the 36th EU PV Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019. [Google Scholar]
- Hoang, P.; Bourdin, V.; Liu, Q.; Caruso, G.; Archambault, V. Coupling optical and thermal models to accurately predict PV panel electricity production. Sol. Energy Mater. Sol. Cells 2014, 125, 325–338. [Google Scholar] [CrossRef]
- Priyadarshini, B.G.; Sharma, A.K. Design of multi-layer anti-reflection coating for terrestrial solar panel glass. Bull. Mater. Sci. 2016, 39, 683–689. [Google Scholar] [CrossRef]
- Notton, G.; Cristofari, C.; Mattei, M.; Poggi, P. Modelling of a double-glass photovoltaic module using finite differences. Appl. Therm. Eng. 2005, 25, 2854–2877. [Google Scholar] [CrossRef]
- Lee, B.; Liu, J.; Sun, B.; Shen, C.; Dai, G. Thermally conductive and electrically insulating EVA composite encapsulants for solar photovoltaic (PV) cell. Express Polym. Lett. 2008, 2, 357–363. [Google Scholar] [CrossRef]
- Wolf, A.; Pohl, P.; Brendel, R. Determination of thermophysical properties of thin films for photovoltaic applications. In Proceedings of the Conference Record of the Thirty-first IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005. [Google Scholar]
- Solar, J. 395W PERC Module, J.S. 375-395/PR, Editor. 2024.
- United States Committee on Extension to the Standard Atmosphere. US Standard Atmosphere, 1976; National Oceanic and Amospheric [sic] Administration: Washington, DC, USA, 1976. [Google Scholar]
- Siebers, D.L. Experimental Mixed Convection Heat Transfer from a Large, Vertical Surface in a Horizontal Flow; Stanford University: Stanford, CA, USA, 1983. [Google Scholar]
- Kreith, F.; Kreider, J.F. Principles of Solar Engineering; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Cole, R.; Sturrock, N. The convective heat exchange at the external surface of buildings. Build. Environ. 1977, 12, 207–214. [Google Scholar] [CrossRef]
- Bell, C. Fluid Dynamics Component of Chemical Engineering Design Library (ChEDL). 2023. Available online: https://github.com/CalebBell/fluids (accessed on 1 March 2023).
- Ilse, K.K.; Figgis, B.W.; Naumann, V.; Hagendorf, C.; Bagdahn, J. Fundamentals of soiling processes on photovoltaic modules. Renew. Sustain. Energy Rev. 2018, 98, 239–254. [Google Scholar] [CrossRef]
- Devi, A.; Satheesh, S.K. Global maps of aerosol single scattering albedo using combined CERES-MODIS retrieval. Atmos. Chem. Phys. 2022, 22, 5365–5376. [Google Scholar] [CrossRef]
- Rubio, E.; Caselles, V.; Badenas, C. Emissivity measurements of several soils and vegetation types in the 8–14 μm Wave band: Analysis of two field methods. Remote Sens. Environ. 1997, 59, 490–521. [Google Scholar] [CrossRef]
- Hamdhan, I.N.; Clarke, B.G. Determination of thermal conductivity of coarse and fine sand soils. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- The Engineering ToolBox. Surface Emissivity Coefficients. 2003. Available online: https://www.engineeringtoolbox.com/emissivity-coefficients-d_447.html (accessed on 14 June 2024).
- The Engineering ToolBox. Plastics—Thermal Conductivity Coefficients. 2011. Available online: https://www.engineeringtoolbox.com/thermal-conductivity-plastics-d_1786.html (accessed on 14 June 2024).
- Sutha, S.; Suresh, S.; Raj, B.; Ravi, K. Transparent alumina based superhydrophobic self–cleaning coatings for solar cell cover glass applications. Sol. Energy Mater. Sol. Cells 2017, 165, 128–137. [Google Scholar] [CrossRef]
- Bishop, J. Computer simulation of the effects of electrical mismatches in photovoltaic cell interconnection circuits. Sol. Cells 1988, 25, 73–89. [Google Scholar] [CrossRef]
- Post, D.; Fimbres, A.; Matthias, A.; Sano, E.; Accioly, L.; Batchily, A.; Ferreira, L. Predicting soil albedo from soil color and spectral reflectance data. Soil Sci. Soc. Am. J. 2000, 64, 1027–1034. [Google Scholar] [CrossRef]
- Enriquez, R.; Zarzalejo, L.; Jiménez, M.; Heras, M. Ground reflectance estimation by means of horizontal and vertical radiation measurements. Sol. Energy 2012, 86, 3216–3226. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Andrews, R.W.; Lorenzo, A.T.; Stein, J.S. PVLIB python 2015. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015. [Google Scholar]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Restrepo-Cuestas, B.J.; Montano, J.; Ramos-Paja, C.A.; Trejos-Grisales, L.A.; Orozco-Gutierrez, M.L. Parameter estimation of the bishop photovoltaic model using a genetic algorithm. Appl. Sci. 2022, 12, 2927. [Google Scholar] [CrossRef]
- Dobos, A.P. An Improved Coefficient Calculator for the California Energy Commission 6 Parameter Photovoltaic Module Model; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Restrepo-Cuestas, B.J.; Montano, J. Bishop model parameter estimation in photovoltaic cells using metaheuristic optimization techniques. Sol. Energy 2024, 270, 112410. [Google Scholar] [CrossRef]
- The SciPy Community. scipy.optimize.fsolve. 2014. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html (accessed on 29 July 2014).
- Jessen, W.; Wilbert, S.; Gueymard, C.A.; Polo, J.; Bian, Z.; Driesse, A.; Habte, A.; Marzo, A.; Armstrong, P.R.; Vignola, F. Proposal and evaluation of subordinate standard solar irradiance spectra for applications in solar energy systems. Sol. Energy 2018, 168, 30–43. [Google Scholar] [CrossRef]
- Winter, S.; Friedrich, D.; Sperling, A. Effects of the new standard IEC 60904-3: 2008 on the calibration results of common solar cell types. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009. [Google Scholar]











| Quantity | Symbol | Unit | Source |
|---|---|---|---|
| Solar irradiance in the module plane | W m−2 | SOZ-03 reference cell by NES Sensors GmbH (Damme, Germany) | |
| Thermal sky radiation | W m−2 | CGR4 Pyrgeometer by Kipp & Zonen (Delft, The Netherlands), serial number IRCGR4-120446 | |
| Wind speed | m s−2 | NRG 200 m wind wane by NRG Systems (Hinesburg, VT, USA) | |
| Ambient temperature | °C | CS215-L thermometer | |
| Ground temperature | °C | Estimated from ambient temperature | |
| Surface power density | W m−2 | Electrical model | |
| Absorptance | - | Literature [41,42,43,44] | |
| Reflectance | ρ | - | Literature [41,42,43,44] |
| Transmittance | - | Literature [41,42,43,44] | |
| Emissivity | - | Literature [41,42,43,44] | |
| Thermal conductivity | W m−1 K−1 | Literature [41,42,45,46,47] | |
| Layer thickness | mm | PV data sheet [48] | |
| Cell area | m2 | PV data sheet [48] | |
| Stefan–Boltzmann constant | W m−2 K−4 | Natural constant | |
| Atmospheric pressure | Pa | Barometer | |
| Elevation | m | Google Maps | |
| Atmospheric density | kg m−3 | Literature [49] | |
| Thermal conductivity of air | W m−1 K−1 | Literature [49] | |
| Kinematic viscosity of air | m2 s−1 | Literature [49] | |
| Specific heat capacity of air | J kg−1 K−1 | Literature [49] | |
| Characteristic length, module height | m | PV data sheet [48] |
| Hemispherical Reflectance | Hemispherical Transmittance | Emissivity | Thermal Conductivity | Thickness | |
|---|---|---|---|---|---|
| [-] | [-] | [-] | [W m−1 K−1] | d [mm] | |
| Soiling layer (dust) | [55] | Optically measured | 0.903 [56] | 0.27 [57] | 0.01 * |
| 0.907 [56] | 3.34 [57] | ||||
| Artificial soiling (foil stack) | Optically measured | Optically measured | 0.92 [58] | 0.2 [59] | Measured |
| Glass | 0.08 [41,44] | 0.92 [41,44] | 0.837 [42] 0.85 [41] 0.9 [45] | 0.98 [46] | 3.0 [42] |
| 1.0 [42] | |||||
| 0.04 [43] | 0.95 [43,60,61] | 1.8 [45] | 3.2 [41] | ||
| 2.0 [41] | |||||
| Silicon | 0.07 [43] | 0 * | - | - | - |
| 0.08 [41] | |||||
| Back sheet | 0.86 [41] | 0.1[41] | 0.769 [42] | 0.15 [41] | 0.3 [41] |
| 0.9 [41,43] | 0.155 [42] | 0.35 [42] | |||
| 0.56 [47] |
| Model | RMSE [K] | MAE [K] | MBE [K] |
|---|---|---|---|
| Ross | 9.4 | 8.7 | 8.6 |
| Sandia | 4.0 | 3.6 | 3.4 |
| Faiman | 2.7 | 1.9 | 0.5 |
| NOCT | 2.9 | 2.1 | 0.2 |
| Developed model | 2.6 | 2.2 | −1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkel, P.; Smretschnig, J.; Wilbert, S.; Röger, M.; Sutter, F.; Blum, N.; Carballo, J.A.; Fernandez, A.; Alonso-García, M.d.C.; Polo, J.; et al. Electrothermal Modeling of Photovoltaic Modules for the Detection of Hot-Spots Caused by Soiling. Energies 2024, 17, 4878. https://doi.org/10.3390/en17194878
Winkel P, Smretschnig J, Wilbert S, Röger M, Sutter F, Blum N, Carballo JA, Fernandez A, Alonso-García MdC, Polo J, et al. Electrothermal Modeling of Photovoltaic Modules for the Detection of Hot-Spots Caused by Soiling. Energies. 2024; 17(19):4878. https://doi.org/10.3390/en17194878
Chicago/Turabian StyleWinkel, Peter, Jakob Smretschnig, Stefan Wilbert, Marc Röger, Florian Sutter, Niklas Blum, José Antonio Carballo, Aránzazu Fernandez, Maria del Carmen Alonso-García, Jesus Polo, and et al. 2024. "Electrothermal Modeling of Photovoltaic Modules for the Detection of Hot-Spots Caused by Soiling" Energies 17, no. 19: 4878. https://doi.org/10.3390/en17194878
APA StyleWinkel, P., Smretschnig, J., Wilbert, S., Röger, M., Sutter, F., Blum, N., Carballo, J. A., Fernandez, A., Alonso-García, M. d. C., Polo, J., & Pitz-Paal, R. (2024). Electrothermal Modeling of Photovoltaic Modules for the Detection of Hot-Spots Caused by Soiling. Energies, 17(19), 4878. https://doi.org/10.3390/en17194878









