Impact of Adding Fast Switching Fault Current Limiter (FSFCL) to the Neutral Point of 220 kV Transformer
Abstract
1. Introduction
2. Materials and Methods
2.1. Working Principle of FSFCL
2.2. Short-Circuit Current Calculation Method
3. Results and Discussion
3.1. Analysis of the Neutral Point Fault Current Limiter Connection Method
3.1.1. Analysis of the Current-Limiting Reactor Installation at the High-Voltage Neutral Point
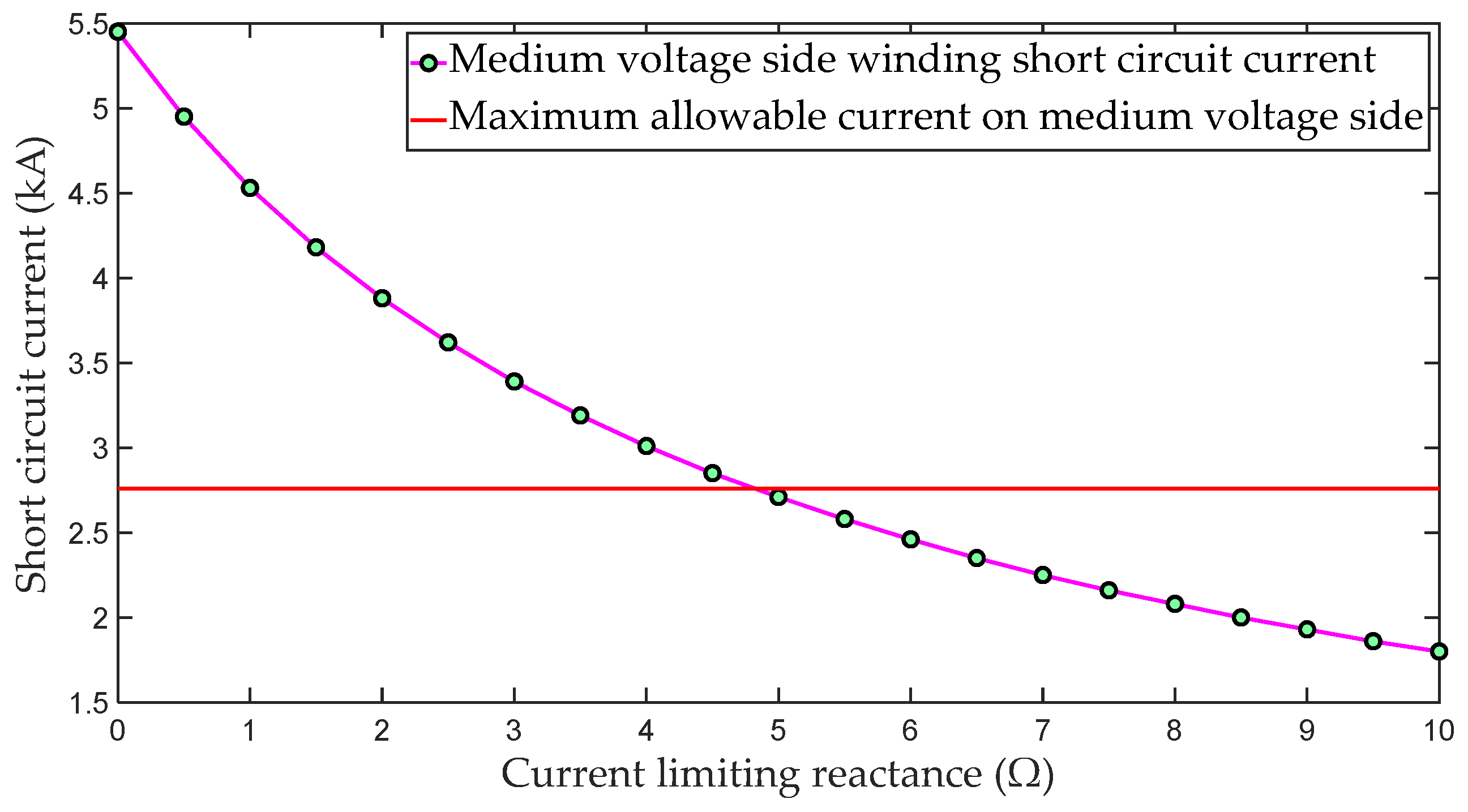
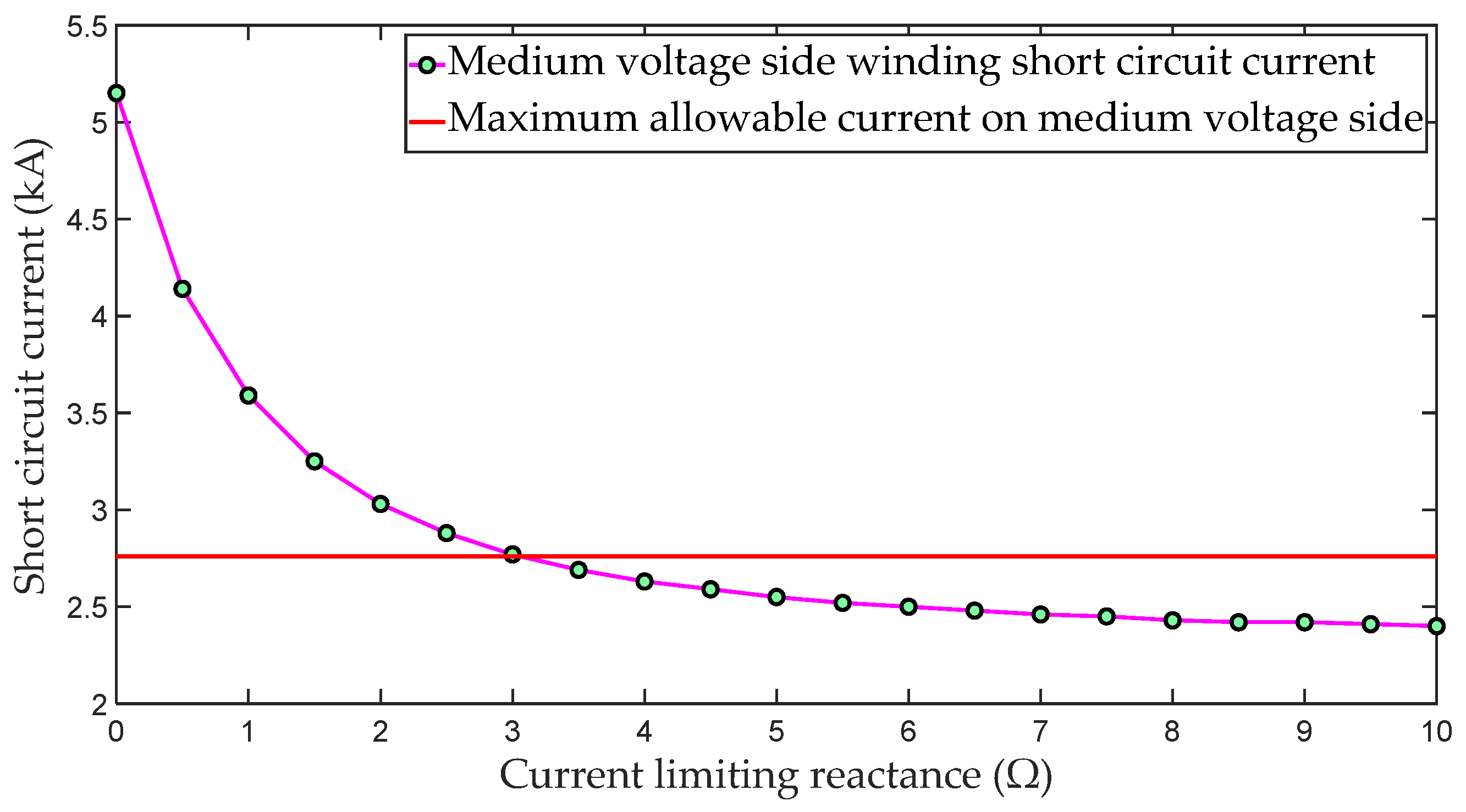
3.1.2. Adding a Limiting Reactor to the Neutral Point on the Medium-Voltage Side
3.2. Effect of Different Current-Limiting Reactance Values on Fault Current under Various Fault Conditions
3.2.1. Evaluation of the Limiting Effect during Single-Phase Ground Faults
3.2.2. Evaluation of the Limiting Effect during Two-Phase Ground Faults
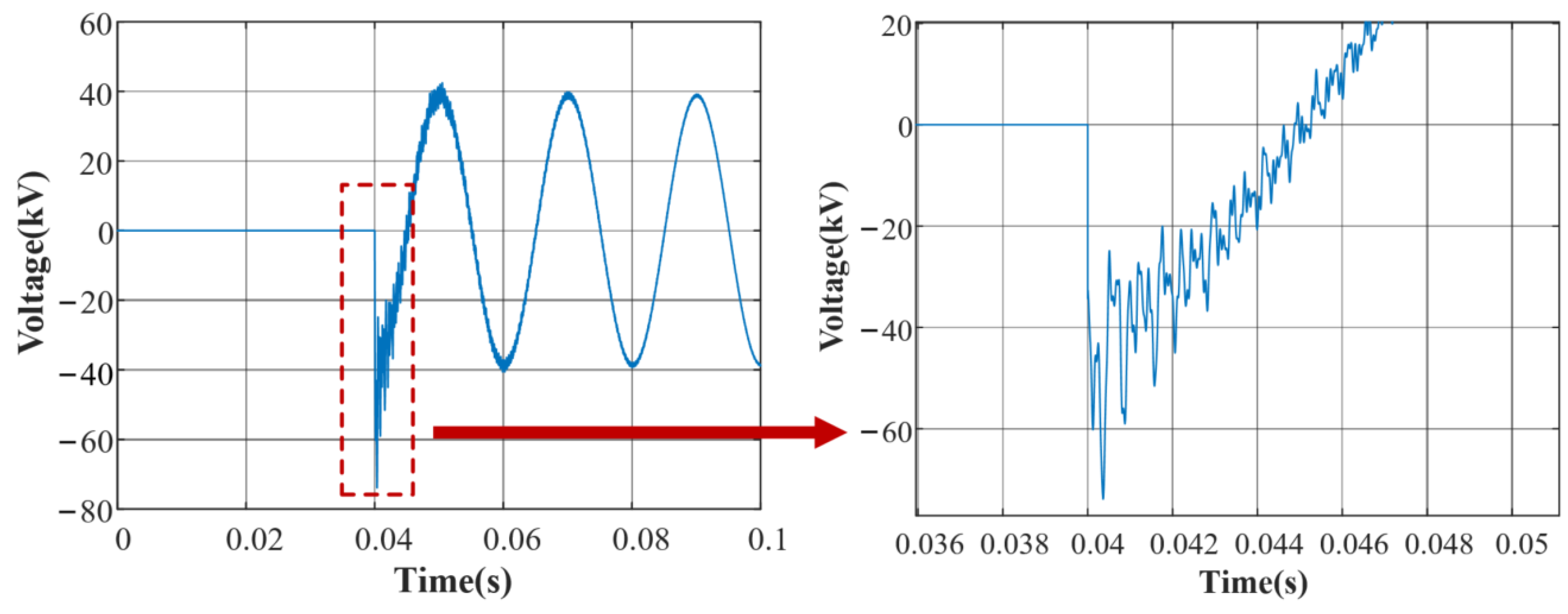
3.3. Overvoltage Simulation Analysis
3.3.1. Simulation Model Construction
- (1)
- The 220 kV high-voltage side power grid utilized a three-phase ideal voltage source and three symmetrical parallel resistors for equivalent representation, with a phase voltage peak value of 179.6 kV.
- (2)
- Transformers were modeled using the BCT (Bipolar Charge Transformer) model, with a capacity of 120 MVA and rated voltages of 220/121/10.5 kV. Two transformers operated in parallel on the high- and medium-voltage sides, while the low-voltage side operated independently, and only one transformer was grounded. The excitation and short-circuit losses were set based on actual values.
- (3)
- The fault current limiter was simplified to a current-limiting reactor.
- (4)
- Asymmetrical faults were simulated at the medium-voltage side exit of the transformer with two scenarios: one involved phase A grounding through a 0.01 Ω small resistor, and the other involved phases B and C grounding through a 0.01 Ω small resistor.
- (5)
- The 110 kV medium-voltage side power grid comprised three transmission lines, all using the LCC (Line Commutated Converter) model, with lengths of 23.33 km, 5.73 km, and 21.53 km, respectively. The ends of these lines were equivalently loaded with three-phase symmetrical Y-connected grounding resistors.
- (6)
- The 10.5 kV low-voltage side power grid was equivalently represented by three-phase symmetrical Y-connected grounding resistors.
3.3.2. Simulation Results Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, L.; Zhang, L.; Hu, Y.; Yang, H.; Xiang, B.; Yao, X. Zero-crossing prediction method of short-circuit current based on long-term and short-term memory network. High Volt. Eng. 2023, 49, 5022–5031. [Google Scholar]
- Huang, F.; Huang, C.; Jing, X.; Zen, Y.; Wang, H.; Wang, X. Analysis of 110kV side grounding mode of main transformer in 220kV substation. High Volt. Eng. 2007, 12, 157–161. [Google Scholar]
- Xu, Z.; Li, P.; Zhang, S.; Wang, Z.; Cheng, H. Transformer winding deformation location technology based on distributed optical fiber sensing. Grid Technol. 2022, 46, 3224–3230. [Google Scholar]
- Bagheri, S.; Moravej, Z.; Gharehpetian, B.G. Effect of transformer winding mechanical defects, internal and external electrical faults and inrush currents on performance of differential protection. IET Gener. Transm. Distrib. 2017, 11, 2508–2520. [Google Scholar] [CrossRef]
- Han, B.; Chen, W.; Chang, N.; Jin, Y.; Qie, X.; Han, Y.; Zhu, B.; Tan, S.; Yu, Y.; Zhang, J.; et al. Research on short-circuit current limitation method based on system topology dynamic adjustment. Grid Technol. 2021, 45, 1158–1166. [Google Scholar]
- Zhao, E.; Han, Y.; Liu, Y.; Zalhaf, A.S.; Wang, C.; Yang, P. Feasibility analysis of neutral grounding by small reactor of HVDC converter transformer. Energy Rep. 2022, 8 (Suppl. S1), 392–399. [Google Scholar] [CrossRef]
- Chen, T.; Li, B.; Han, Y.; Li, Q.; Wang, J.; Jing, J. Research on fault line selection of small current grounding system considering zero sequence unbalanced current. Electr. Porcelain Light. Arrester 2022, 4, 124–130. [Google Scholar]
- Lv, W.; Xu, Y.; Liu, Y.; Ge, J.; Xie, H.; Fang, T. Application research and development of high voltage fault current limiter system. High Volt. Electr. Appl. 2022, 58, 48–56. [Google Scholar]
- Chen, B.; Wei, L.; Lei, Y.; Tu, Z.; Yuan, J.; Chen, F.; Nie, D.; Pan, J. Multi-objective optimal configuration of high temperature superconducting fault current limiter Pareto based on immune algorithm. Power Grid Technol. 2015, 39, 1343–1350. [Google Scholar]
- Li, C.; Wu, Q.; Li, B.; Zhu, J.; Chen, P.; Wei, F.; Xin, Y. Design method of magnetic bias superconducting fault current limiter considering the influence of aperiodic components of short circuit current and analysis of its current limiting characteristics. Grid Technol. 2023, 47, 4887–4897. [Google Scholar]
- Xu, D. Research on Fault Current Limiter Based on Fast Switch. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar] [CrossRef]
- Xu, M. Research on Modeling and Application of Complex High Coupling Split Reactor for Fault Current Limiter. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2020. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, J.; Zhou, H.; Li, X.; Mo, Z. Parameter design of short-circuit fault current limiter for high voltage AC system considering transient component of short-circuit current. High Volt. Eng. 2024, 50, 3769–3785. [Google Scholar] [CrossRef]
- Han, N.; Jia, X.; Zhao, X.; Xu, J.; Zhao, C. A novel hybrid DC fault current limiter topology. Proc. Chin. Soc. Electr. Eng. 2019, 39, 1647–1658+1861. [Google Scholar]
- Gong, X.; Gao, C.; Long, Z.; Lin, Y.; Xu, L. Principle of adding small reactance to limit asymmetric short-circuit current at the neutral point of 500kV autotransformer. Electr. Power Constr. 2013, 34, 56–60. [Google Scholar]
- Lei, Y.; Li, P.; Xu, J.; Li, Q.; Zhao, L.; Song, Z. Mechanism and Suppression Methods of Neutral Point Current Differences in YY and YD Converter Transformers. South. Power Grid Technol. 2018, 12, 1–6. [Google Scholar] [CrossRef]
- Im, I.G.; Choi, H.S.; Jung, B.I. Limiting characteristics of the superconducting fault current limiter applied to the neutral line of conventional transformer. Phys. C Supercond. 2013, 494, 339–343. [Google Scholar] [CrossRef]
- Sahebi, A.; Samet, H. Discrimination between internal fault and magnetising inrush currents of power transformers in the presence of a superconducting fault current limiter applied to the neutral point. IET Sci. Meas. Technol. 2016, 10, 537–544. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Xu, Y.; Lv, W.; Yang, B.; Fang, T. Tank fast switch of 500 kV fast switching fault current limiter. High Volt. Eng. 2023, 49, 803–811. [Google Scholar]
- Hu, J.; Li, X.; Yang, Y.; Bao, X.; Li, J. Analysis of neutral grounding overvoltage of 220 kV transformer. Electr. Porcelain Light. Arrester 2019, 6, 152–158. [Google Scholar]
- Zhang, W.; Ding, Q.; Hu, G.; Qiao, Z.; Ma, X. Research on lightning overvoltage protection scheme of distribution transformer based on ATP-EMTP simulation analysis. Electr. Porcelain Light. Arrester 2020, 2, 86–92. [Google Scholar]
- Chinese National Standard GB 311.1-2012; Insulation Coordination Part 1: Definitions, Principles, and Rules. Standards Press of China: Beijing, China, 2012.
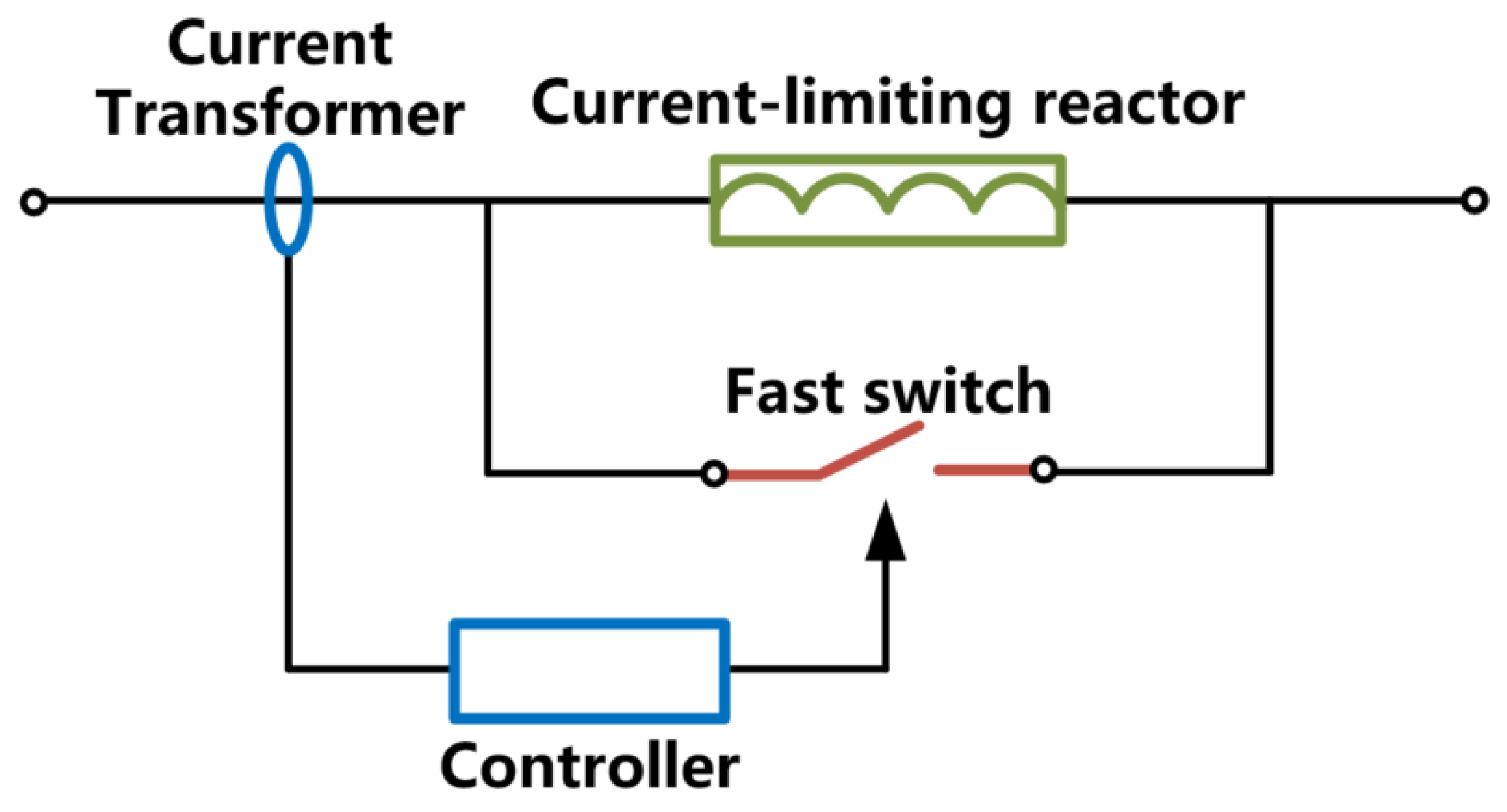
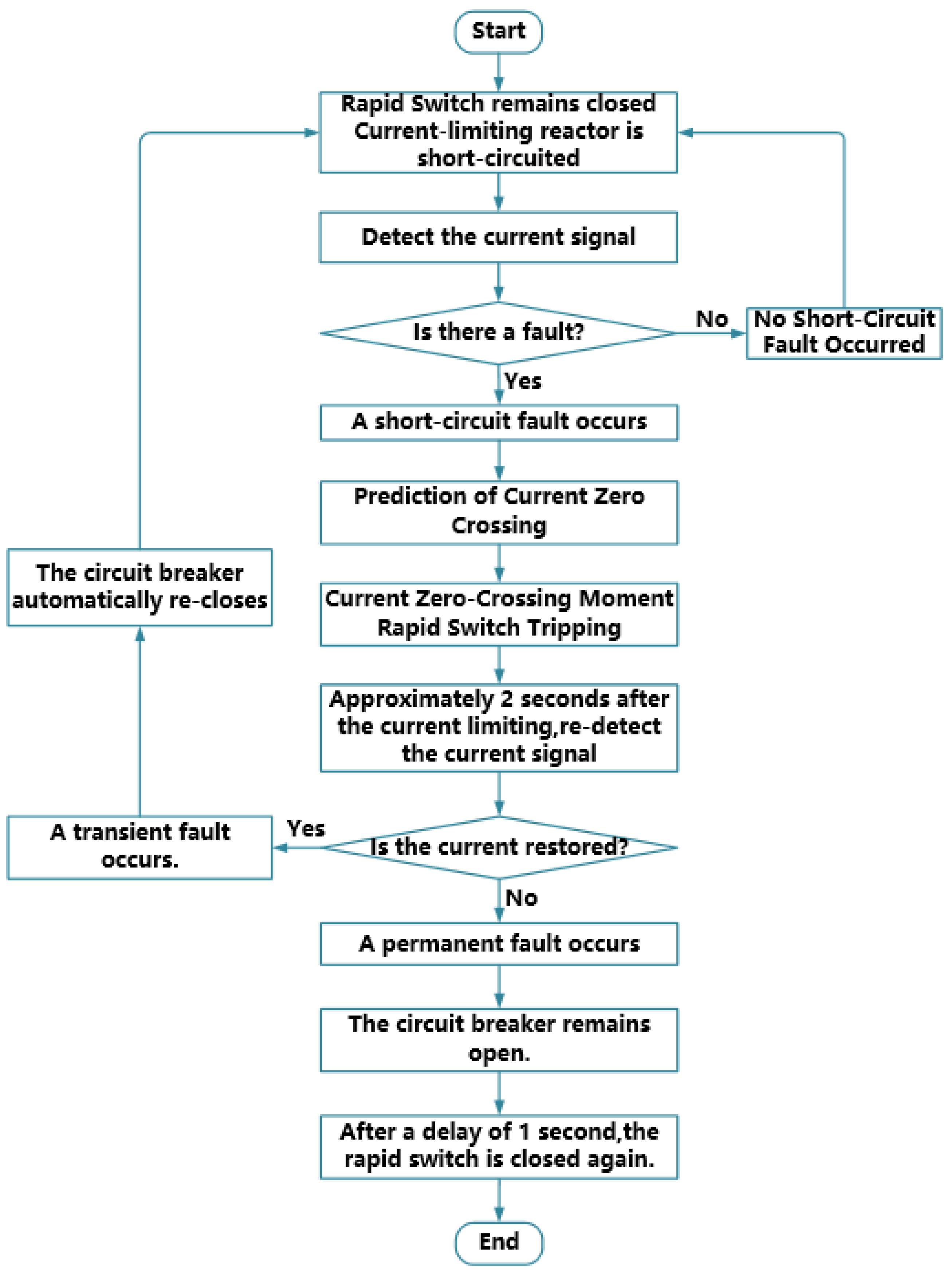
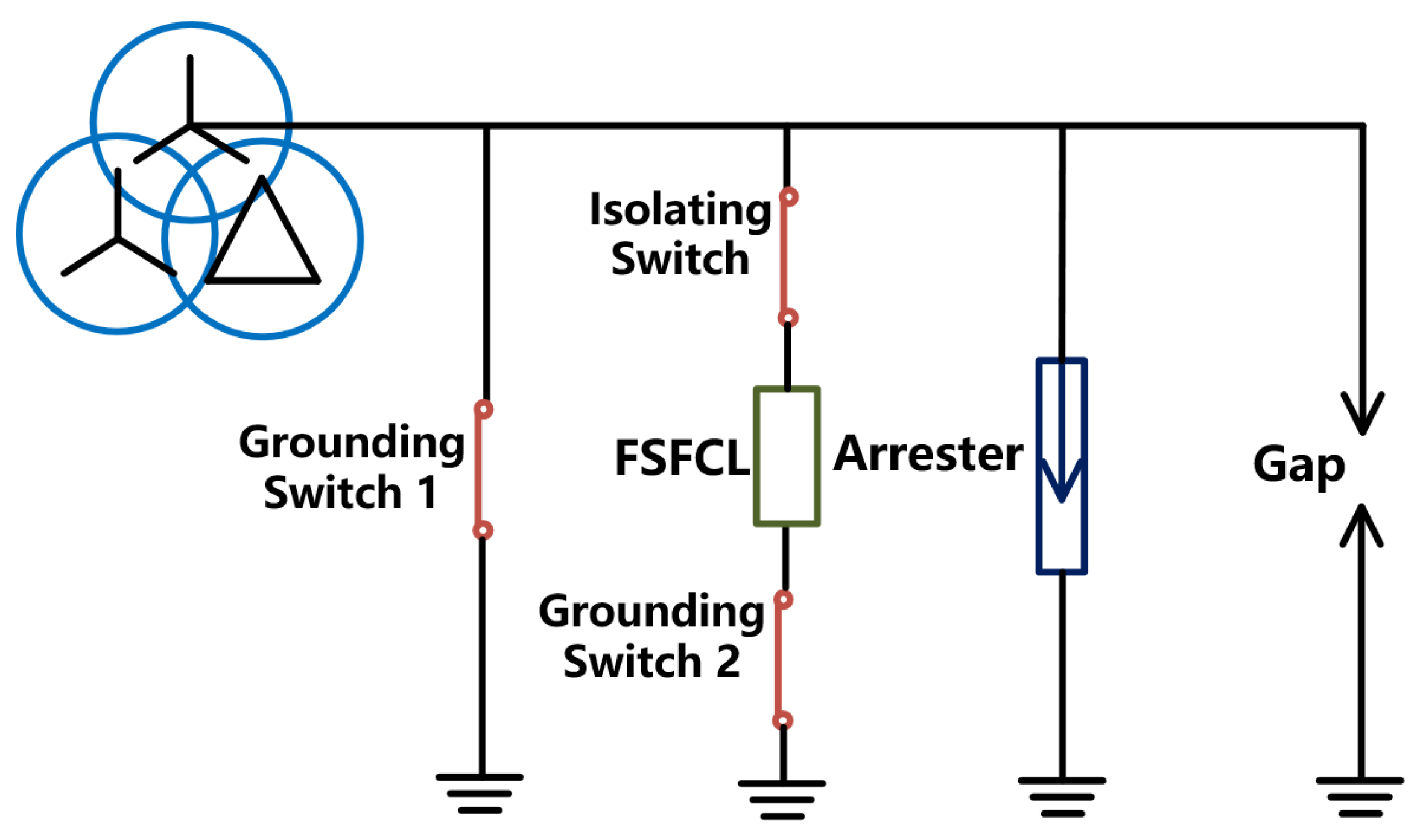


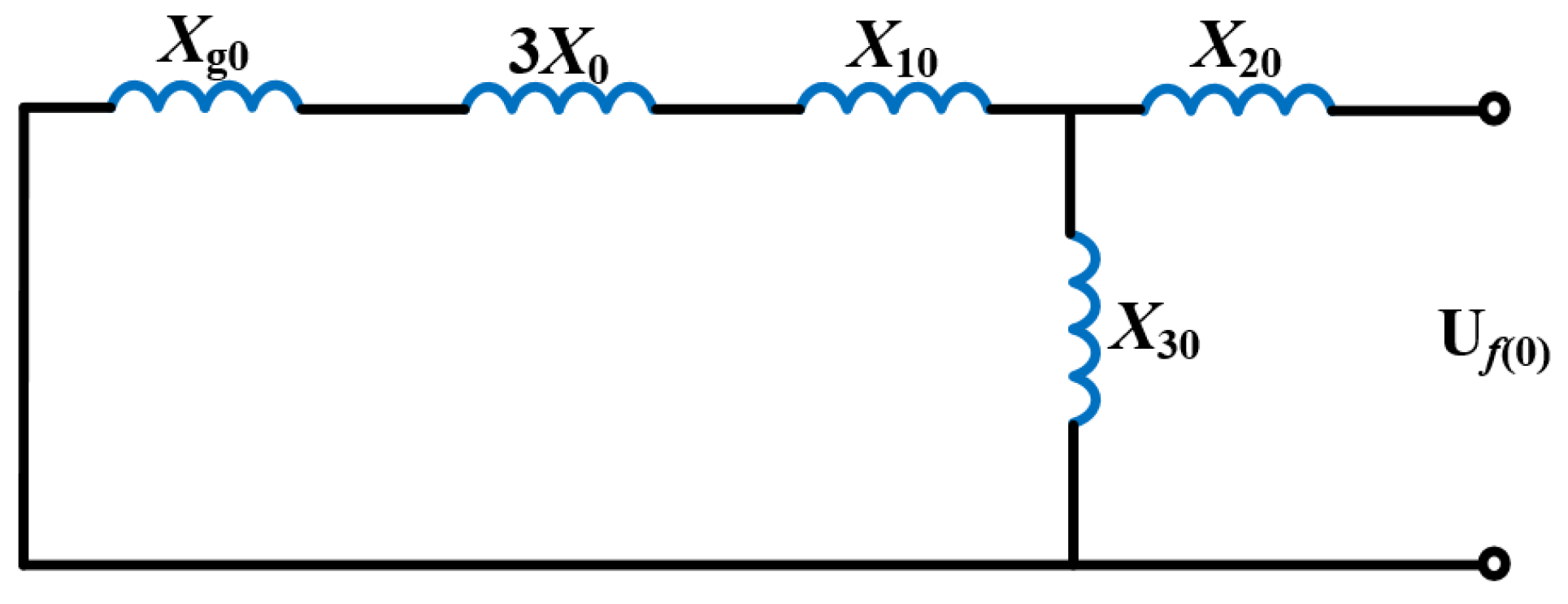
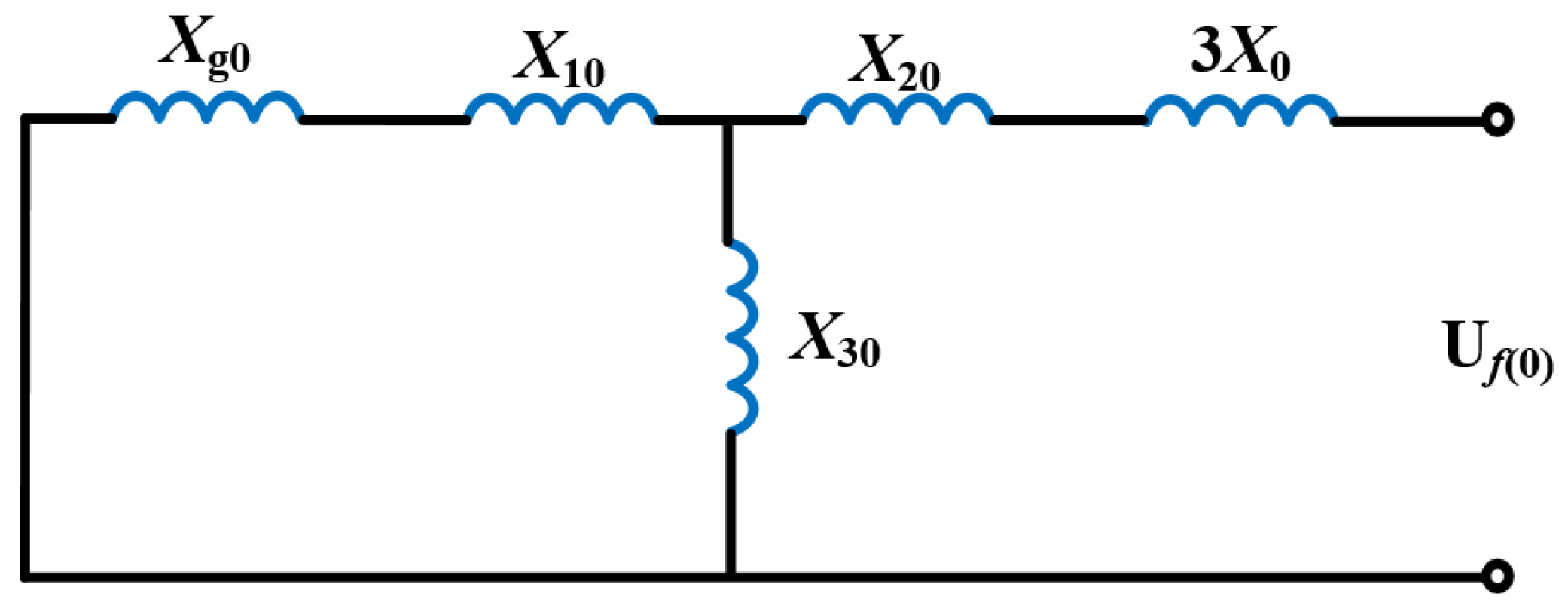

| Impedance Name | Transformer (p.u.) | System (p.u.) | ||||
|---|---|---|---|---|---|---|
| Positive Sequence | Zero Sequence | Maximum Operating Mode | Minimum Operating Mode | |||
| Positive Sequence | Zero Sequence | Positive Sequence | Zero Sequence | |||
| High Voltage | 0.1555 | 0.1423 | 0.0108 | 0.0252 | 0.0480 | 0.0900 |
| Medium Voltage | −0.0103 | −0.0093 | 0.0600 | 0.0360 | 0.2160 | 0.0960 |
| Low Voltage | 0.0843 | 0.0768 | / | / | / | / |
| Limiting Reactor (Ω) | Fault Point Zero Sequence | High-Voltage Side Winding Current (kA) | Medium-Voltage Side Winding Current (kA) | Low-Voltage Side Winding Current (kA) | |
|---|---|---|---|---|---|
| Impedance (p.u.) | Current (kA) | ||||
| 0 | 0.0434 | 2.72 | 1.97 | 5.45 | 12.43 |
| 2 | 0.0496 | 2.65 | 1.79 | 5.29 | 13.50 |
| Limiting Reactor (Ω) | Fault Point Zero Sequence | High-Voltage Side Winding Current (kA) | Medium-Voltage Side Winding Current (kA) | Low-Voltage Side Winding Current (kA) | |
|---|---|---|---|---|---|
| Impedance (p.u.) | Current (kA) | ||||
| 0 | 0.0434 | 2.72 | 1.97 | 5.45 | 12.43 |
| 2 | 0.1286 | 1.94 | 1.40 | 3.88 | 8.84 |
| Limiting Reactor (Ω) | Zero-Sequence Current (kA) | High-Voltage Winding Current (kA) | Medium-Voltage Winding Current (kA) | Low-Voltage Winding Current (kA) | ||
|---|---|---|---|---|---|---|
| High-Voltage Winding | Medium-Voltage Winding | Low-Voltage Winding | ||||
| 0 | 0.47 | 2.72 | 12.42 | 1.97 | 5.45 | 12.42 |
| 0.5 | 0.43 | 2.47 | 11.28 | 1.79 | 4.95 | 11.28 |
| 1 | 0.39 | 2.26 | 10.33 | 1.64 | 4.53 | 10.33 |
| 1.5 | 0.36 | 2.09 | 9.53 | 1.51 | 4.18 | 9.53 |
| 2 | 0.34 | 1.94 | 8.84 | 1.40 | 3.88 | 8.84 |
| 2.5 | 0.31 | 1.81 | 8.25 | 1.31 | 3.62 | 8.25 |
| 3 | 0.29 | 1.69 | 7.73 | 1.22 | 3.39 | 7.73 |
| 3.5 | 0.28 | 1.59 | 7.27 | 1.15 | 3.19 | 7.27 |
| 4 | 0.26 | 1.50 | 6.86 | 1.09 | 3.01 | 6.86 |
| 4.5 | 0.25 | 1.42 | 6.50 | 1.03 | 2.85 | 6.50 |
| 5 | 0.23 | 1.35 | 6.17 | 0.98 | 2.71 | 6.17 |
| 5.5 | 0.22 | 1.29 | 5.88 | 0.93 | 2.58 | 5.88 |
| 6 | 0.21 | 1.23 | 5.61 | 0.89 | 2.46 | 5.61 |
| 6.5 | 0.20 | 1.18 | 5.36 | 0.85 | 2.35 | 5.36 |
| 7 | 0.19 | 1.13 | 5.14 | 0.81 | 2.25 | 5.14 |
| 7.5 | 0.19 | 1.08 | 4.93 | 0.78 | 2.16 | 4.93 |
| 8 | 0.18 | 1.04 | 4.74 | 0.75 | 2.08 | 4.74 |
| 8.5 | 0.17 | 1.00 | 4.56 | 0.72 | 2.00 | 4.56 |
| 9 | 0.17 | 0.96 | 4.40 | 0.70 | 1.93 | 4.40 |
| 9.5 | 0.16 | 0.93 | 4.25 | 0.67 | 1.86 | 4.25 |
| 10 | 0.16 | 0.90 | 4.11 | 0.65 | 1.80 | 4.11 |
| High Voltage | Medium Voltage | Low Voltage | |
|---|---|---|---|
| Maximum allowable current (kA) | 2.00 | 2.76 | 13.40 |
| Limiting Reactor (Ω) | Single-Phase Ground Fault | Two-Phase Ground Fault | ||
|---|---|---|---|---|
| Steady State (kV) | Transient (kV) | Steady State (kV) | Transient (kV) | |
| 5 | 39.1 | 73.5 | 28.9 | 37.0 |
| 5.5 | 41.1 | 77.0 | 30.0 | 38.2 |
| 6 | 43.2 | 80.7 | 30.9 | 39.3 |
| 6.5 | 45.1 | 83.6 | 31.7 | 40.3 |
| 7 | 46.8 | 86.3 | 32.5 | 41.1 |
| 7.5 | 48.5 | 88.8 | 33.1 | 41.9 |
| 8 | 50.0 | 91.1 | 33.8 | 42.7 |
| 8.5 | 51.4 | 93.2 | 34.4 | 43.3 |
| 9 | 52.7 | 95.1 | 34.9 | 43.9 |
| 9.5 | 54.0 | 96.6 | 35.4 | 44.5 |
| 10 | 55.2 | 97.9 | 35.8 | 45.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, L.; Zhao, J.; Guo, M.; Gao, S.; Xiang, C.; Wei, B.; Qin, W.; Ma, G.; Tian, Y. Impact of Adding Fast Switching Fault Current Limiter (FSFCL) to the Neutral Point of 220 kV Transformer. Energies 2024, 17, 4862. https://doi.org/10.3390/en17194862
Dai L, Zhao J, Guo M, Gao S, Xiang C, Wei B, Qin W, Ma G, Tian Y. Impact of Adding Fast Switching Fault Current Limiter (FSFCL) to the Neutral Point of 220 kV Transformer. Energies. 2024; 17(19):4862. https://doi.org/10.3390/en17194862
Chicago/Turabian StyleDai, Lujian, Jun Zhao, Meng Guo, Shuguo Gao, Chenmeng Xiang, Bin Wei, Weiqi Qin, Guoming Ma, and Yuan Tian. 2024. "Impact of Adding Fast Switching Fault Current Limiter (FSFCL) to the Neutral Point of 220 kV Transformer" Energies 17, no. 19: 4862. https://doi.org/10.3390/en17194862
APA StyleDai, L., Zhao, J., Guo, M., Gao, S., Xiang, C., Wei, B., Qin, W., Ma, G., & Tian, Y. (2024). Impact of Adding Fast Switching Fault Current Limiter (FSFCL) to the Neutral Point of 220 kV Transformer. Energies, 17(19), 4862. https://doi.org/10.3390/en17194862






