A Novel Approach to Enhancing the Determination of Primary Indicators in Non-Idealised Absorption Chillers
Abstract
1. Introduction
- The electrical work of the Solution Circulation Pump;
- Entropy loss due to the Expansion Valves before the Evaporator and Absorber;
- Entropy changes resulting from superheating after the Evaporator and subcooling after the Condenser;
- Heat exchange between the machine components and the environment;
- Exergy losses associated with heat losses;
- Exergy destruction within the machine;
- The effects of the Solution Heat Exchanger.
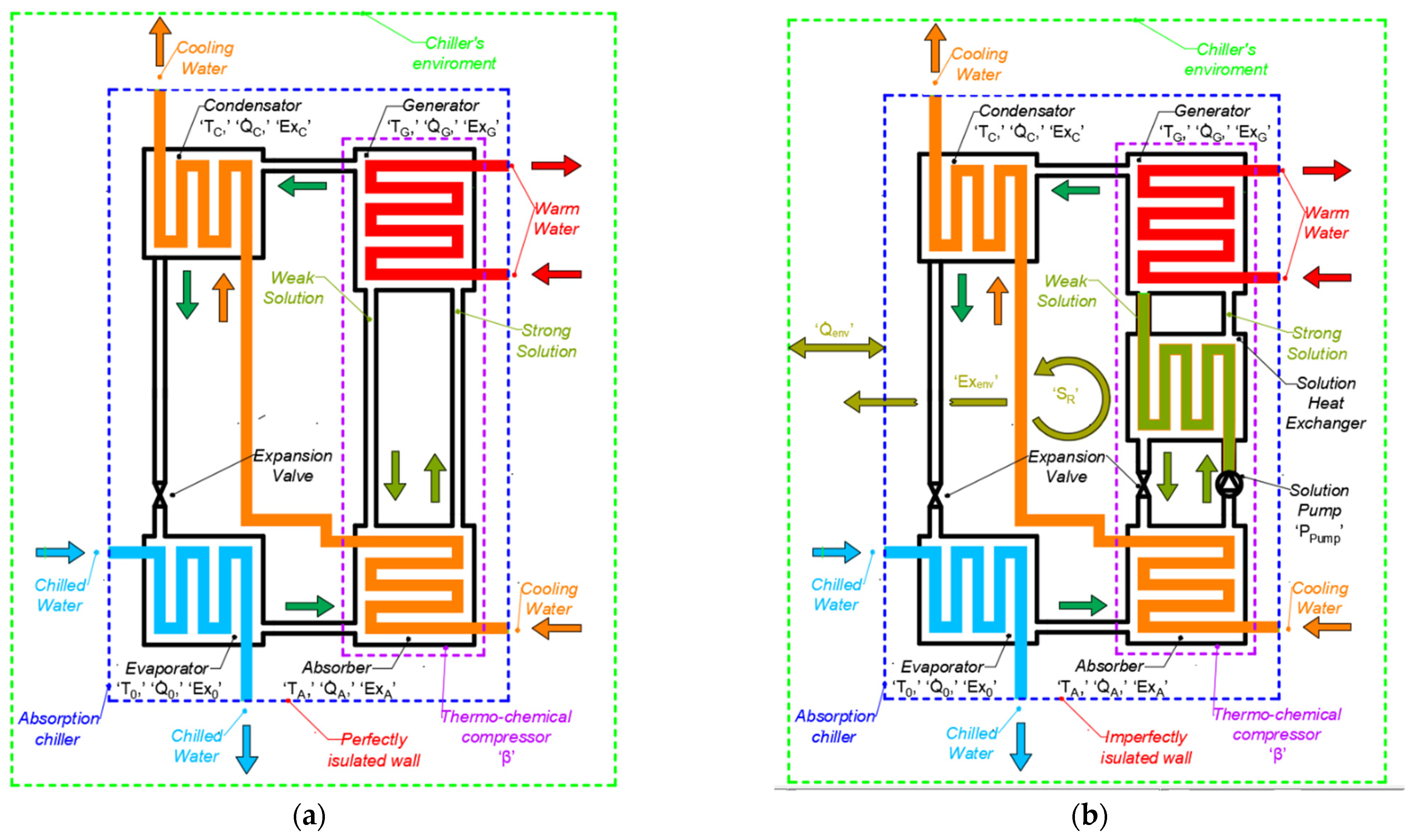
2. Material and Methods
3. Results
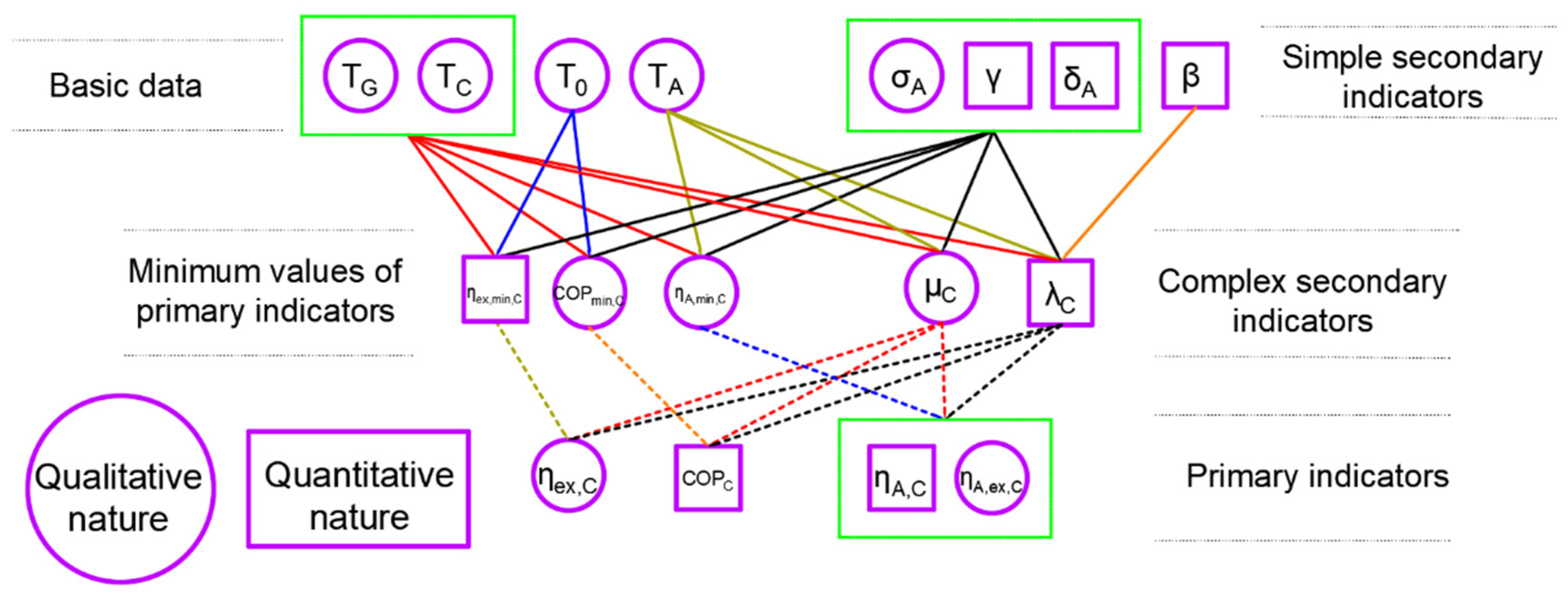
3.1. New Secondary Indicators
3.2. Connection Using the Balance Equations
3.3. A Novelty Description of the Primary Indicators
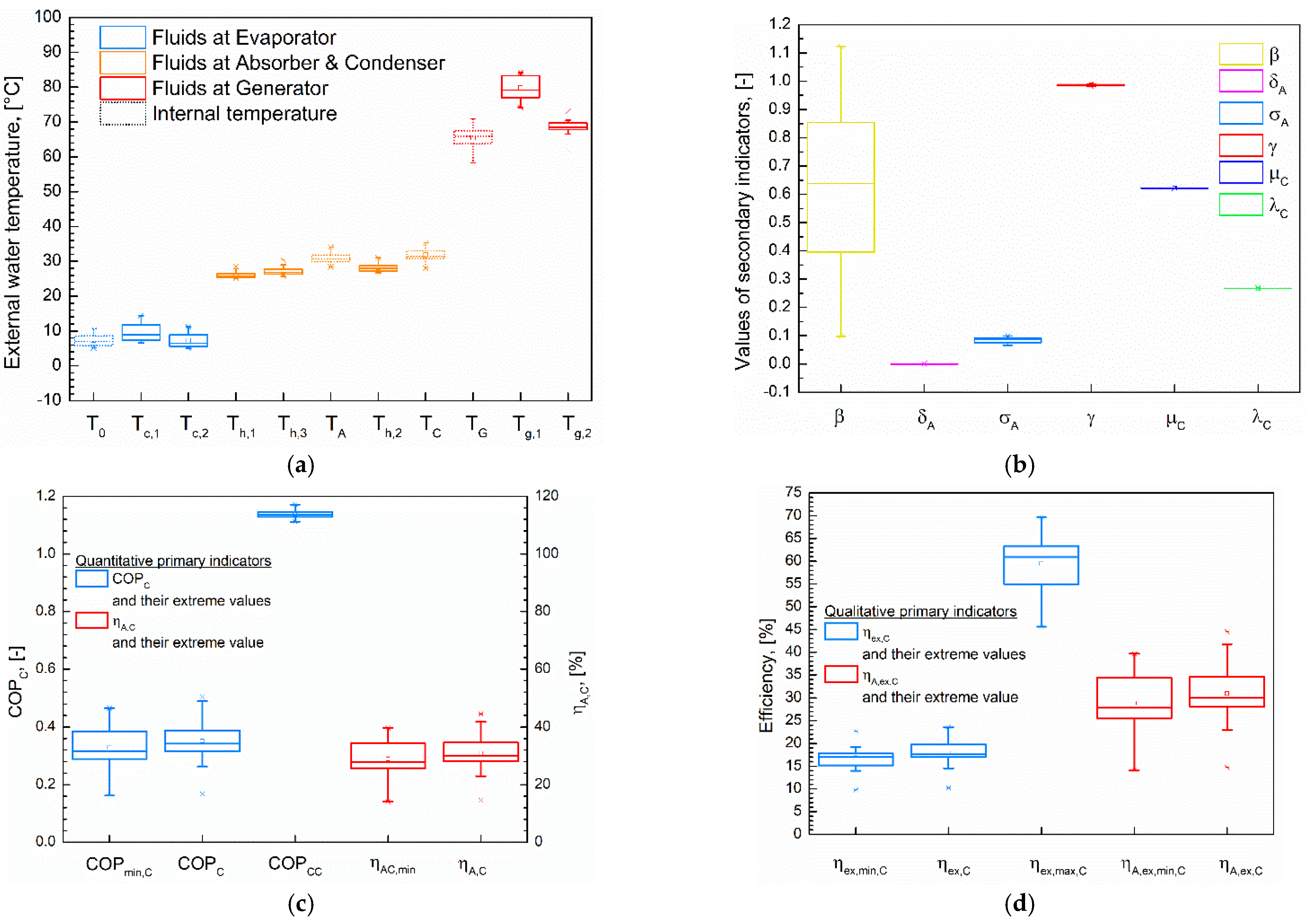
4. Validation
5. Discussion
5.1. Correlation and Significance Analysis
| Pearson Correlation | Significance | |||||
|---|---|---|---|---|---|---|
| COPC | ηex,C | ηA,C; ηA,ex,C | COPC | ηex,C | ηA,C; ηA,ex,C | |
| COPmin,C | 0.98373 | 0.90262 | 0.98248 | 0.00000 | 0.00001 | 0.00000 |
| COPCC | 0.20153 | 0.09270 | 0.14440 | 0.48964 | 0.75261 | 0.62235 |
| ηex,min,C | 0.81141 | 0.97655 | 0.81359 | 0.00043 | 0.00000 | 0.00040 |
| ηex,max,C | −0.78042 | −0.41638 | −0.78365 | 0.00099 | 0.13862 | 0.00091 |
| ηA,min,C; ηA,ex,min,C | 0.98091 | 0.90317 | 0.98327 | 0.00000 | 0.00001 | 0.00000 |
| Secondary Indicators | Pearson Correlation | Significance | |||||
|---|---|---|---|---|---|---|---|
| COPC | ηex,C | ηA,C; ηA,ex,C | COPC | ηex,C | ηA,C; ηA,ex,C | ||
| Simple | β | 0.83736 | 0.75826 | 0.83155 | 0.00019 | 0.00167 | 0.00023 |
| δA | −0.55504 | −0.48865 | −0.54258 | 0.03937 | 0.07622 | 0.04499 | |
| σA | −0.91356 | −0.75318 | −0.90144 | 0.00000 | 0.00187 | 0.00001 | |
| γ | −0.30883 | −0.49928 | −0.31318 | 0.28266 | 0.06912 | 0.27559 | |
| Complex | μC | −0.98091 | −0.90318 | −0.98327 | 0.00000 | 0.00001 | 0.00000 |
| λC | 0.58502 | 0.32680 | 0.58250 | 0.02798 | 0.25410 | 0.02883 | |
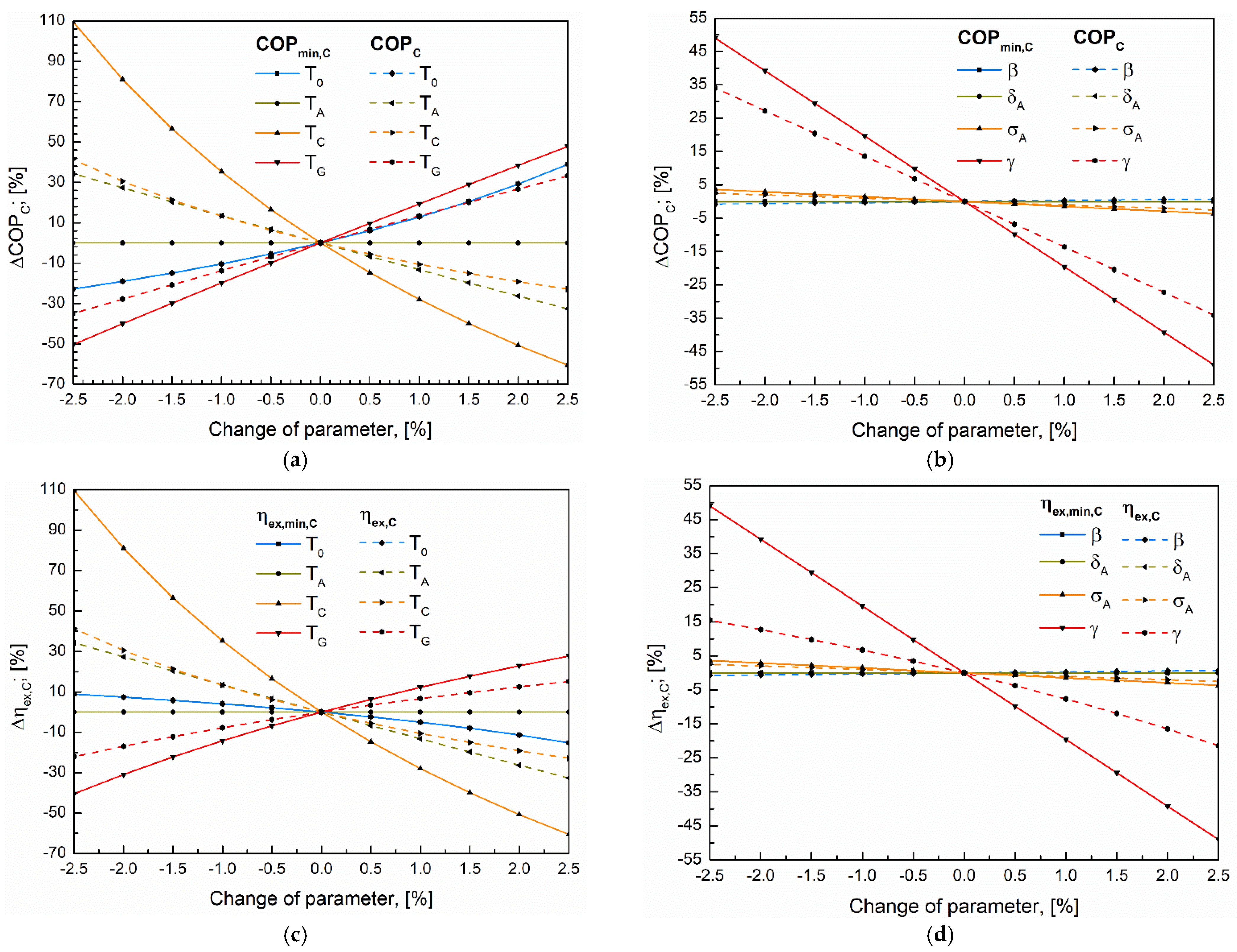
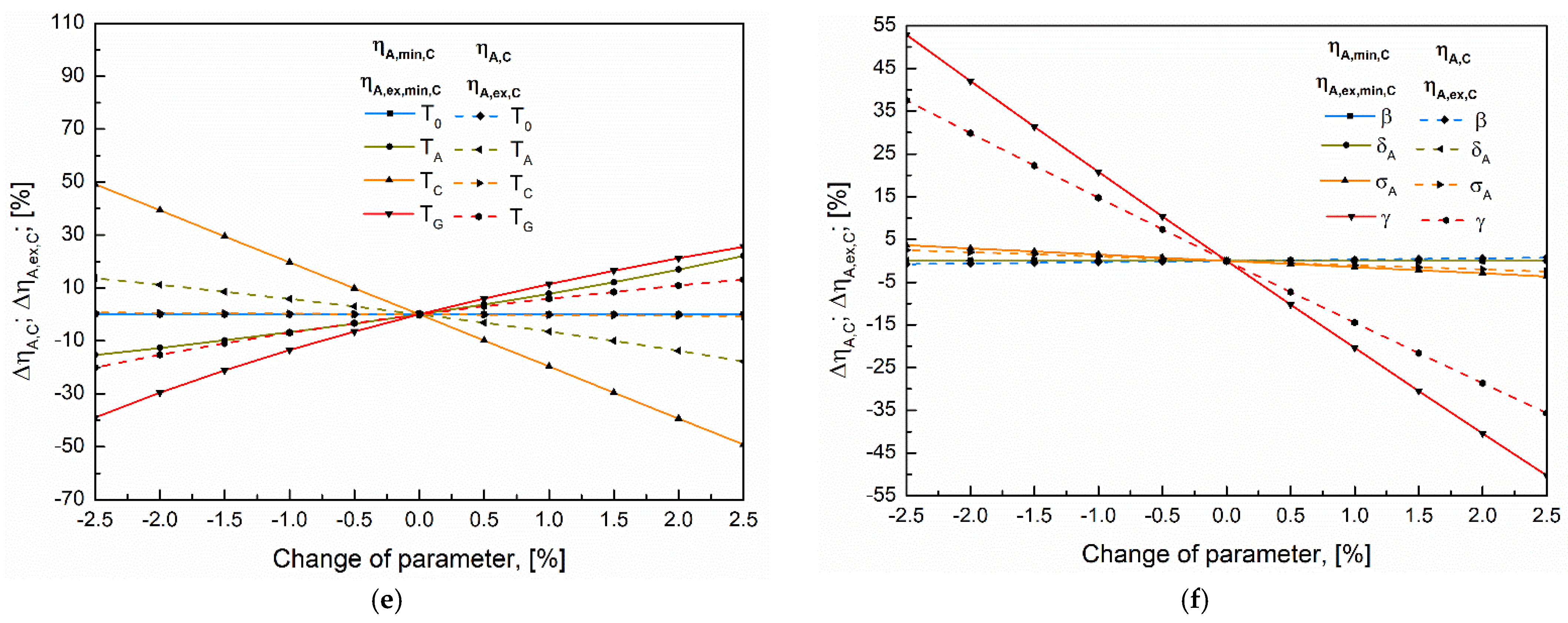
5.2. Sensitivity Analysis
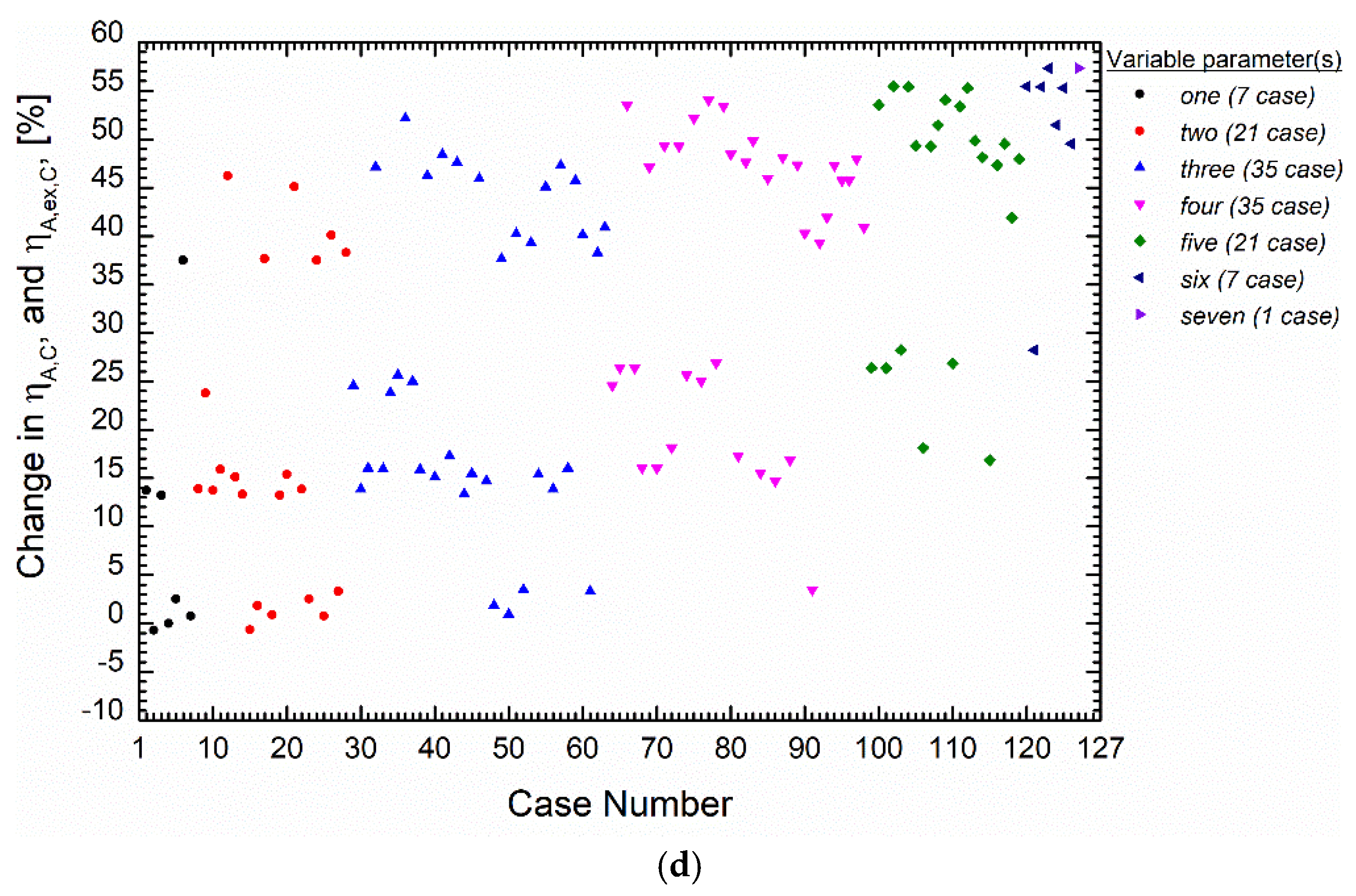
5.3. Analysis of the Convergence of Primary Indicators to Their Maximum Using the Extreme Values Proximity Index
5.4. The Qualitative and Quantitative Nature of Indicators and Their Included Parameters
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| is the cooling capacity, in W. | |
| is the heat released in the Absorber, in W. | |
| is the heat released in the Condenser, in W. | |
| is the heat consumed in the Generator, in W. | |
| is the total heat released in the Absorber and Condenser, in W. | |
| PPump | is the electric power consumed by the Solution Circulation Pump, in W. |
| is the heat exchange between parts of the machine and the environment, in W. | |
| SR | is the generated entropy within the refrigerant cycle, in W∙K−1. |
| Ex0 | is the exergy content of , in W. |
| ExA | is the exergy content of , in W. |
| ExC | is the exergy content of , in W. |
| ExG | is the exergy content of , in W. |
| Exenv | is the difference in the exergy contents, in W. |
| T0 | is the evaporation temperature, in K. |
| TA | is the temperature in the Absorber (absorption temperature), in K. |
| TC | is the condensation temperature, in K. |
| TG | is the temperature in the Generator (generator temperature), in K. |
| TX | is the reference temperature, in K. |
| Tc,1; Tc,2 | is the supply and return temperature of chilled water, in K. |
| Tg,1; Tg,2 | is the temperature of heating water entering and leaving the Generator, in K. |
| Th,1; Th,2 | is the supply and return temperature of cooling water, in K. |
| β | is the Thermo-Chemical Performance Index. |
| σA | is the Quality Loss Index (absorption chiller). |
| δA | is the Coefficient of Compensation for Entropy-Surplus (absorption machine), in K−1. |
| γ | is the Heat Fraction Factor. |
| μC | is the Thermo-Chemical Instability Index (cooling mode). |
| λC | is the Extreme Values Proximity Index (cooling mode). |
| COPC | is the Coefficient of Performance (cooling mode). |
| COPmin,C | is the value of Coefficient of Performance (cooling mode) when β=0. |
| COPCC | is the maximum value of Coefficient of Performance (cooling mode). |
| COPH | is the Coefficient of Performance (heating mode). |
| ηex,C | is the Exergetic Efficiency (cooling mode), in %. |
| ηEx,min,C | is the value of the Exergetic Efficiency (cooling mode) when β = 0, in %. |
| ηex,max,C | is the value of the Exergetic Efficiency (cooling mode) when COPC = COPCC, in %. |
| ηex,H | is the Exergetic Efficiency (heating mode), in %. |
| ηA,C | is the Thermo-Chemical Efficiency (cooling mode), in %. |
| ηA,min,C | is the value of the Thermo-Chemical Efficiency (cooling mode) when β = 0, in %. |
| ηA,ex,C | is the Exergetic Thermo-Chemical Efficiency (cooling mode), in %. |
| ηA,ex,min,C | is the value of the Exergetic Thermo-Chemical Efficiency (cooling mode) when β = 0, in %. |
References
- Santamouris, M. Cooling the buildings—Past, present and future. Energy Build. 2016, 128, 617–638. [Google Scholar] [CrossRef]
- Csáky, I. Analysis of daily energy demand for cooling in buildings with different comfort categories—Case study. Energies 2021, 14, 4694. [Google Scholar] [CrossRef]
- Kalmár, F.; Kalmár, T. Thermal comfort aspects of solar gains during the heating season. Energies 2020, 13, 1702. [Google Scholar] [CrossRef]
- European Commission. Energy—Roadmap 2050; Publications Office: Brussels, Belgium, 2012. [Google Scholar]
- Kostyák, A.; Szekeres, S.; Csáky, I. Investigation of Sensible Cooling Performance in the Case of an Air Handling Unit System with Indirect Evaporative Cooling: Indirect Evaporative Cooling Effects for the Additional Cooling System of Buildings. Buildings 2023, 13, 1800. [Google Scholar] [CrossRef]
- Nemogne, R.L.F.; Wouagfack, P.A.N.; Nouadje, B.A.M.; Tchinda, R. Exergetic, ecological and thermo-economic (3E) optimization of an absorption heat pump with heat resistance, heat leakage and two internal irreversibilities: Comparison. Int. J. Refrig. 2020, 112, 251–261. [Google Scholar] [CrossRef]
- Kalmár, T.; Szodrai, F.; Kalmár, F. Experimental study of local effectiveness in the case of balanced mechanical ventilation in small offices. Energy 2022, 244, 122619. [Google Scholar] [CrossRef]
- Kalmár, F.; Kalmár, T. Numerical evaluation of thermal discomfort in conditions of surface heating and asymmetric radiation. Int. Rev. Appl. Sci. Eng. 2019, 9, 175–179. [Google Scholar] [CrossRef]
- Wouagfack, P.A.N.; Tchinda, R. Finite-time thermodynamics optimization of absorption refrigeration systems: A review. Renew. Sustain. Energy Rev. 2013, 21, 524–536. [Google Scholar] [CrossRef]
- Feidt, M. Evolution of thermodynamic modelling for three and four heat reservoirs reverse cycle machines: A review and new trends. Int. J. Refrig. 2013, 36, 8–23. [Google Scholar] [CrossRef]
- Alhuyi-Nazari, M.; Mukhtar, A.; Yasir, A.S.H.M.; Ahmadi, M.H.; Kumar, R.; Luong, T.N.L. Applications of geothermal sources for absorption chillers as efficient and clean cooling technologies for buildings: A comprehensive review. J. Build. Eng. 2024, 82, 108340. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Ahmadi, A.; El Haj Assad, M.; Rosen, M.A. Investigation of an integrated system combining an Organic Rankine Cycle and absorption chiller driven by geothermal energy: Energy, exergy, and economic analyses and optimization. J. Clean. Prod. 2020, 258, 120780. [Google Scholar] [CrossRef]
- Leveni, M.; Cozzolino, R. Energy, exergy, and cost comparison of Goswami cycle and cascade organic Rankine cycle/absorption chiller system for geothermal application. Energy Convers. Manag. 2021, 227, 113598. [Google Scholar] [CrossRef]
- Er, D.; Göktun, S. Optimum performance of an irreversible solar-driven cogeneration heat pump system. Energy Convers. Manag. 2001, 42, 329–337. [Google Scholar] [CrossRef]
- De Francisco, A.; Illanes, R.; Torres, J.L.; Castillo, M.; De Bla, M.; Prieto, E.; García, A. Development and testing of a prototype of low-power water–ammonia absorption equipment for solar energy applications. Renew. Energy 2002, 25, 537–544. [Google Scholar] [CrossRef]
- Chahbani, M.H.; Labidi, J.; Paris, J. Modeling of adsorption heat pumps with heat regeneration. Appl. Therm. Eng. 2004, 24, 431–447. [Google Scholar] [CrossRef]
- Jeong, S.; Kang, B.H.; Karng, S.W. Dynamic simulation of an absorption heat pump for recovering low grade waste heat. Appl. Therm. Eng. 1998, 18, 1–12. [Google Scholar] [CrossRef]
- Míšek, P.; Adamovský, R.; Neuberger, P. Laboratory and operational analysis of air to water gas absorption heat pump cycle. Energy Build. 2023, 292, 113180. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, J.; Li, Z. Irreversibility characterization and analysis of coupled heat and mass transfer processes in an absorption system. Int. J. Heat Mass Transf. 2019, 133, 1121–1133. [Google Scholar] [CrossRef]
- Shirazi, A.; Taylor, R.A.; Morrison, G.L.; White, S.D. Solar-powered absorption chillers: A comprehensive and critical review. Energy Convers. Manag. 2018, 171, 59–81. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Said, S.A.M. A review of solar powered absorption systems. Renew. Sustain. Energy Rev. 2015, 42, 93–115. [Google Scholar] [CrossRef]
- Kim, D.S.; Ferreira, C.A.I. Solar refrigeration options—A state-of-the-art review. Int. J. Refrig. 2008, 31, 3–15. [Google Scholar] [CrossRef]
- Trutassanawin, S.; Groll, E.A.; Garimella, S.V.; Cremaschi, L. Experimental investigation of a miniature-scale refrigeration system for electronics cooling. IEEE Trans. Compon. Packag. Technol. 2006, 29, 678–687. [Google Scholar] [CrossRef]
- Konovalov, D.; Tolstorebrov, I.; Iwamoto, Y.; Kobalava, H.; Lamb, J.J.; Eikevik, T.M. Optimizing Low-Temperature Three-Circuit Evaporative Cooling System for an Electric Motor by Using Refrigerants. Energies 2024, 17, 3942. [Google Scholar] [CrossRef]
- Manu, S.; Chandrashekar, T.K. A simulation study on performance evaluation of single-stage LiBr–H2O vapor absorption heat pump for chip cooling. Int. J. Sustain. Built Environ. 2016, 5, 370–386. [Google Scholar] [CrossRef]
- Chiriac, V.; Chiriac, F. Absorption refrigeration method with alternative water-ammonia solution circulation system for microelectronics cooling. In Proceedings of the 2010 12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, ITherm 2010, Las Vegas, NV, USA, 2–5 June 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Wu, W.; Wang, B.; Shi, W.; Li, X. Absorption heating technologies: A review and perspective. Appl. Energy 2014, 130, 51–71. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, Y.; Fu, L.; Zhang, S. Experimental and theoretical investigation of a novel full-open absorption heat pump applied to district heating by recovering waste heat of flue gas. Energy Build. 2018, 173, 45–57. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E.; Shadloo, M.S. Energy and exergy analyses of a nanofluid based solar cooling and hydrogen production combined system. Renew. Energy 2019, 141, 1013–1025. [Google Scholar] [CrossRef]
- Liu, F.; Dong, F.; Li, Y.; Jia, L. Study on the heating performance and optimal intermediate temperature of a series gas engine compression-absorption heat pump system. Appl. Therm. Eng. 2018, 135, 34–40. [Google Scholar] [CrossRef]
- Le Lostec, B.; Galanis, N.; Millette, J. Experimental study of an ammonia-water absorption chiller. Int. J. Refrig. 2012, 35, 2275–2286. [Google Scholar] [CrossRef]
- Yi, Y.; Xie, X.; Zhang, H.; Jiang, Y. Thermodynamics and process studies on absorption cycle from the perspective of real solution with non-volatile solute. Energy 2024, 291, 130356. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, X.; Chen, Q. Heat current method-based modeling and optimization of the single effect lithium bromide absorption chiller. Appl. Therm. Eng. 2020, 175, 115345. [Google Scholar] [CrossRef]
- Chen, Y.; Han, W.; Jin, H. Thermodynamic performance optimization of the absorption-generation process in an absorption refrigeration cycle. Energy Convers. Manag. 2016, 126, 290–301. [Google Scholar] [CrossRef]
- Bhardwaj, P.K.; Kaushik, S.C.; Jain, S. Finite time optimization of an endoreversible and irreversible vapour absorption refrigeration system. Energy Convers. Manag. 2003, 44, 1131–1144. [Google Scholar] [CrossRef]
- Su, H.; Gong, G.; Wang, C.; Zhang, Y. Thermodynamic optimization of an irreversible Carnot refrigerator with heat recovery reservoir. Appl. Therm. Eng. 2017, 110, 1624–1634. [Google Scholar] [CrossRef]
- Bhardwaj, P.K.; Kaushik, S.C.; Jain, S. General performance characteristics of an irreversible vapour absorption refrigeration system using finite time thermodynamic approach. Int. J. Therm. Sci. 2005, 44, 189–196. [Google Scholar] [CrossRef]
- Qin, X.; Chen, L.; Ge, Y.; Sun, F. Thermodynamic modeling and performance analysis of the variable-temperature heat reservoir absorption heat pump cycle. Phys. A Stat. Mech. Its Appl. 2015, 436, 788–797. [Google Scholar] [CrossRef]
- Cardoso-Fernández, V.; Bassam, A.; Tzuc, O.M.; Ch, M.A.B.; de Jesús Chan-González, J.; Soberanis, M.A.E.; Velázquez-Limón, N.; Ricalde, L.J. Global sensitivity analysis of a generator-absorber heat exchange (GAX) system’s thermal performance with a hybrid energy source: An approach using artificial intelligence models. Appl. Therm. Eng. 2023, 218, 119363. [Google Scholar] [CrossRef]
- Fumagalli, M.; Sivieri, A.; Aprile, M.; Motta, M.; Zanchi, M. Monitoring of gas driven absorption heat pumps and comparing energy efficiency on primary energy. Renew. Energy 2017, 110, 115–125. [Google Scholar] [CrossRef]
- Browne, M.W.; Bansal, P.K. Transient simulation of vapour-compression packaged liquid chillers. Int. J. Refrig. 2002, 25, 597–610. [Google Scholar] [CrossRef]
- Szabó, G.L. Energy and Exergy Analysis of Radiant Cooling Systems in Buildings; University of Debrecen: Debrecen, Hungary, 2020. [Google Scholar]
- Szabó, G.L. Thermo-chemical instability and energy analysis of absorption heat pumps. Energies 2020, 13, 1966. [Google Scholar] [CrossRef]
- Szabó, G.L. Exergetic optimization of absorption chillers—A case study. Case Stud. Therm. Eng. 2021, 28, 101634. [Google Scholar] [CrossRef]
- Szabó, G.L. Energetic and exergetic study of a potential interconnection of a natural gas engine, heat pumps with a thermal and a mechanical compressor. Therm. Sci. Eng. Prog. 2022, 36, 101525. [Google Scholar] [CrossRef]
- Arora, C.P. Refrigeration and Air Conditioning, 3rd ed.; Tata McGraw-Hill Education Pvt. Ltd.: New Delhi, India, 2009. [Google Scholar]
- Balmer, R.T. Modern Engineering Thermodynamics; Elsevier Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Szabó, G.L. Az abszorpciós gépek jelzőszámai és ezek kapcsolata. Energiagazdálkodás 2018, 59, 38–42. [Google Scholar]


| Denomination | Notation | Value |
|---|---|---|
| Energy flow | //Ppump/; in kW | 910/1312.5/15.8/2154.6 |
| //; in kW | 1134.0/1020.6/83.7 | |
| Exergy | Ex0/ExG/Ppump; in kW | 60.68/162.93/15.8 |
| ExA/ExC/Exenv; in kW | 3.78/26.58/87.66 | |
| Temperature | T0/ TC; in °C | 7.3/34.0 |
| TA/TG; in °C | 27.0/68.4 | |
| Tc,1/Tc,2; in °C | 14.0/8.0 | |
| Tg,1/Tg,2; in °C | 85.0/70.0 | |
| Th,1/Th,2; in °C | 29.8/26.0 | |
| TX; in °C | 26.0 | |
| Volume flow | ; in m3/h (at the Evaporator) | 130 |
| ; in m3/h (at the Absorber and the Condenser) | 486 | |
| ; in m3/h (at the Generator) | 75 | |
| Simple secondary indicators | β | 0.864 |
| δA | −0.00001006 | |
| σA | 0.06599 | |
| γ | 0.9881 | |
| Complex secondary indicators | μC | 0.6217 |
| λC | 0.2674 | |
| Primary indicators | COPC/COPH | 0.685/1.622 |
| ηex,C/ηex,H; in % | 33.96/16.99 | |
| ηA,C/ηA,ex,C; in % | 54.46/54.46 |
| COPC; [−] | ηEx,C; [%] | |||||
|---|---|---|---|---|---|---|
| Date of Measurement | Based on Measure Data | Based on Model | Deviation | Based on Measure Data | Based on Model | Deviation |
| Equation (4) | Equation (18) | Equation (6) | Equation (19) | |||
| 13 May 2021 | 0.3441 | 0.3441 | −1.943 ∙ 10−15 | 19.778 | 19.778 | −1.279 ∙ 10−13 |
| 7 September 2020 | 0.5059 | 0.5059 | 3.664 ∙ 10−15 | 20.279 | 20.279 | 9.948 ∙ 10−14 |
| 29 August 2018 | 0.3147 | 0.3147 | 2.109 ∙ 10−15 | 16.986 | 16.986 | 1.101 ∙ 10−13 |
| 5 July 2017 | 0.3172 | 0.3172 | −2.165 ∙ 10−15 | 17.675 | 17.675 | −1.279 ∙ 10−13 |
| 27 September 2016 | 0.1686 | 0.1686 | 2.165 ∙ 10−15 | 10.242 | 10.242 | 1.261 ∙ 10−13 |
| 5 July 2016 | 0.3522 | 0.3522 | 2.665 ∙ 10−15 | 16.514 | 16.514 | 1.279 ∙ 10−13 |
| 25 August 2014 | 0.2625 | 0.2625 | 8.327 ∙ 10−16 | 14.523 | 14.523 | 5.684 ∙ 10−14 |
| 10 June 2014 | 0.3881 | 0.3881 | 0 | 17.533 | 17.533 | 0 |
| 9 September 2013 | 0.3404 | 0.3404 | −6.661 ∙ 10−16 | 18.724 | 18.724 | −4.263 ∙ 10−14 |
| 29 May 2013 | 0.3209 | 0.3209 | −3.164 ∙ 10−15 | 17.357 | 17.357 | −1.599 ∙ 10−13 |
| 27 June 2012 | 0.3637 | 0.3637 | 1.110 ∙ 10−15 | 17.653 | 17.653 | 9.237 ∙ 10−14 |
| 21 June 2011 | 0.4393 | 0.4393 | 0 | 23.584 | 23.584 | 0 |
| 31 May 2011 | 0.4897 | 0.4897 | 0 | 22.949 | 22.949 | 0 |
| 18 July 2008 | 0.3089 | 0.3089 | 1.998 ∙ 10−15 | 17.964 | 17.964 | 1.101 ∙ 10−13 |
| Pearson Correlation | Significance | |||||
|---|---|---|---|---|---|---|
| COPC | ηex,C | ηA,C; ηA,ex,C | COPC | ηex,C | ηA,C; ηA,ex,C | |
| T0 | 0.7044 | 0.33792 | 0.69137 | 0.00491 | 0.23734 | 0.00617 |
| TA | 0.72665 | 0.39009 | 0.7382 | 0.00324 | 0.16793 | 0.00257 |
| TC | 0.58126 | 0.17606 | 0.58728 | 0.02925 | 0.54713 | 0.02723 |
| TG | 0.39127 | 0.11736 | 0.41068 | 0.16654 | 0.68949 | 0.14467 |
| Pearson Correlation | Significance | |||||||
|---|---|---|---|---|---|---|---|---|
| T0 | TA | TC | TG | T0 | TA | TC | TG | |
| σA | −0.8067 | −0.6367 | −0.5747 | −0.2155 | 4.89 × 10−4 | 0.0143 | 0.0316 | 0.4594 |
| δA | −0.2977 | −0.3628 | −0.2706 | −0.3009 | 0.3013 | 0.2024 | 0.3495 | 0.2959 |
| μC | −0.6034 | −0.7183 | −0.5045 | −0.4128 | 0.0224 | 0.0038 | 0.0658 | 0.1424 |
| λC | 0.7482 | 0.4652 | 0.6628 | 0.1944 | 0.00208 | 0.0937 | 0.0098 | 0.5055 |
| COPmin,C | 0.6177 | 0.7059 | 0.4985 | 0.3915 | 0.0186 | 0.0048 | 0.0696 | 0.1662 |
| ηEX,min,C | 0.2108 | 0.3379 | 0.0602 | 0.1053 | 0.4695 | 0.2374 | 0.8381 | 0.7203 |
| ηA,min,C; ηA,ex,min,C | 0.6034 | 0.7183 | 0.5045 | 0.4128 | 0.0224 | 0.0038 | 0.0658 | 0.1424 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
L. Szabó, G. A Novel Approach to Enhancing the Determination of Primary Indicators in Non-Idealised Absorption Chillers. Energies 2024, 17, 4858. https://doi.org/10.3390/en17194858
L. Szabó G. A Novel Approach to Enhancing the Determination of Primary Indicators in Non-Idealised Absorption Chillers. Energies. 2024; 17(19):4858. https://doi.org/10.3390/en17194858
Chicago/Turabian StyleL. Szabó, Gábor. 2024. "A Novel Approach to Enhancing the Determination of Primary Indicators in Non-Idealised Absorption Chillers" Energies 17, no. 19: 4858. https://doi.org/10.3390/en17194858
APA StyleL. Szabó, G. (2024). A Novel Approach to Enhancing the Determination of Primary Indicators in Non-Idealised Absorption Chillers. Energies, 17(19), 4858. https://doi.org/10.3390/en17194858






