Convex Hull Pricing for Unit Commitment: Survey, Insights, and Discussions
Abstract
1. Introduction
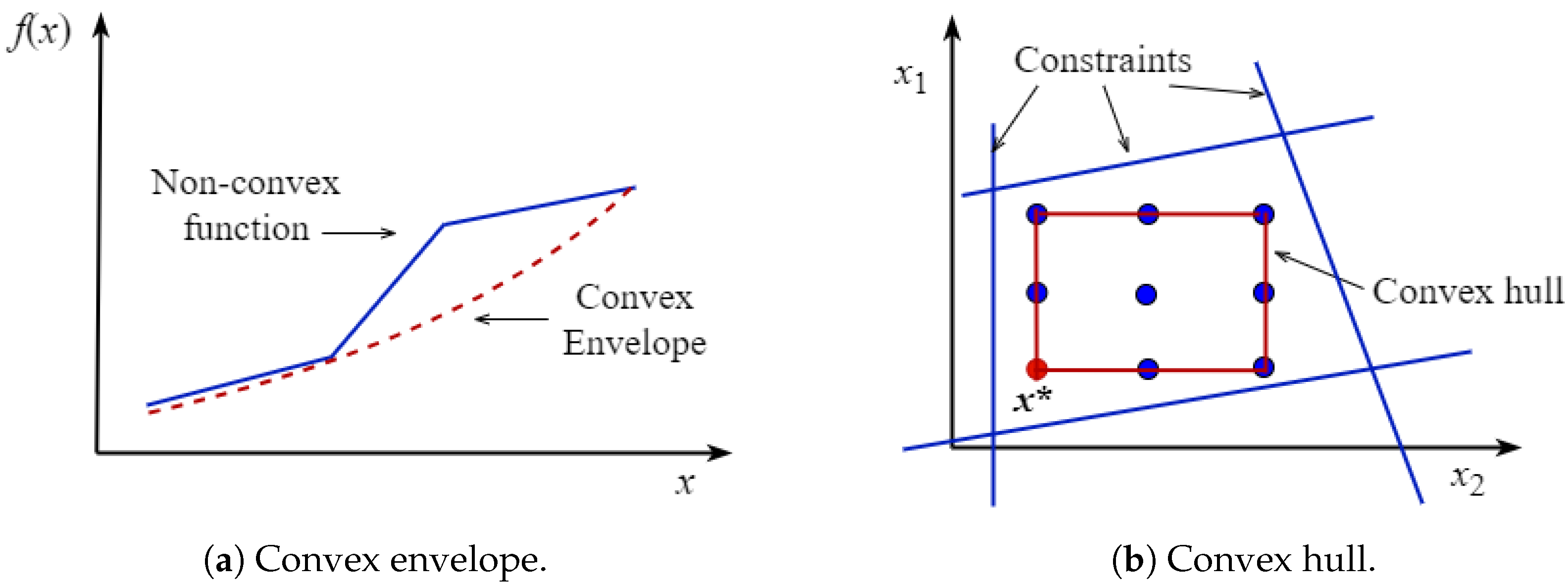
- The first type is to solve the convex hull pricing problem corresponding to convexified UC which requires the convex envelope of the total cost function over the convex hull of the problem, such a convexified problem can be equivalently formulated by using the convex envelope and the convex hull of each unit [7,8,9,10,11,12,13,14].
2. UC Problem and Its Convexification for Convex Hull Pricing
2.1. UC Problem
- (1)
- Objective function
- (2)
- System-level constraints
- (3)
- Unit-level constraints of unit g
- (3.1)
- Requirements on generation capacities: When unit g is online, its generation level must be between its minimum and maximum , i.e.,
- (3.2)
- Requirements on start-up: The binary start-up variable is one if unit g is online at time slot t, i.e.,Also, unit g cannot start up at time slot t if unit g is online at , i.e.,
- (3.3)
- Requirements for minimum up- and down-time: The unit g stays online (resp. offline) for its minimum-up (resp. minimum -down) time slots, i.e.,where and are the minimum up and down time of unit g, respectively.
- (3.4)
- Requirements on ramp rates: The change in generation levels between two consecutive time slots must not exceed the unit’s ramp rate, i.e.,where is the ramp-up/-down rate; is the start-up/shut-down ramp rate.
2.2. Convexified UC Problem for Convex Hull Pricing
3. Convex Hull Pricing Problem
- (1)
- (2)
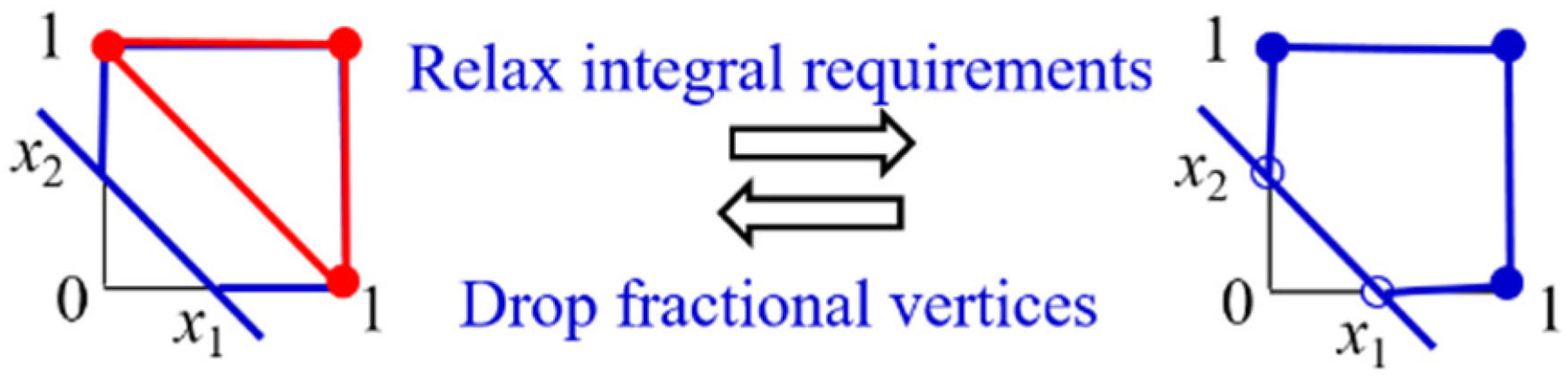
- Case 2. When a unit formulation is not tight, its convex hull can be formulated by various approaches, as discussed in [10,11,12,13,14], with a primary focus on convex hull formulation. However, solving the resulting convex hull pricing problems might increase the computational burden, as the complexity of accurately formulating a convex hull increases exponentially with the number of time slots [28];
- (3)
- Case 3. As a compromise, the employment of an approximate convex hull is also discussed in [8] when a unit formulation is not tight.
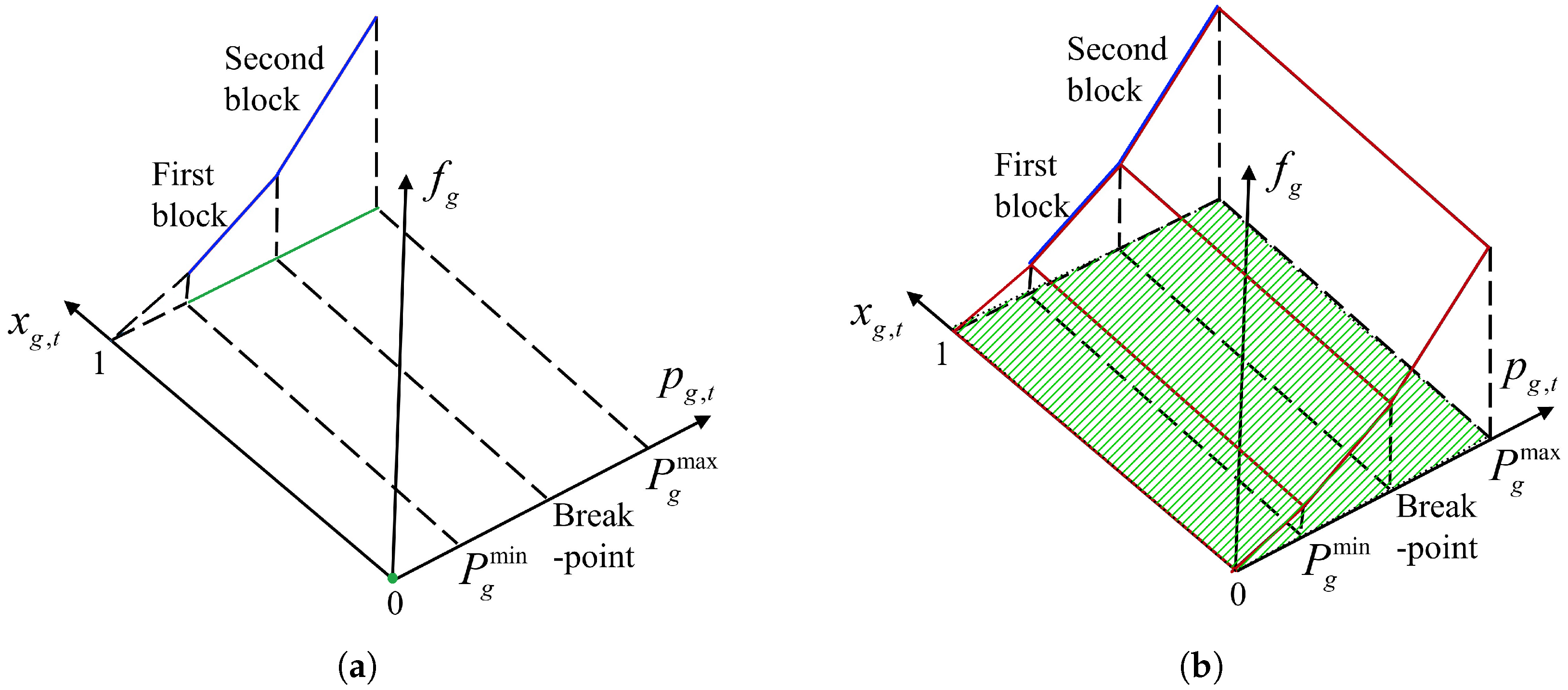
3.1. Convex Hull Pricing Problem from Each Unit
- Property 1: The convex envelope of a function is the double conjugate of the function itself.
- Property 2: Additivity applies to a conjugate function.
3.2. Convex Hull and Convex Envelope under a Tight Formulation
- (1)
- Network flow approach
- (2)
- Polyhedron approach
- (3)
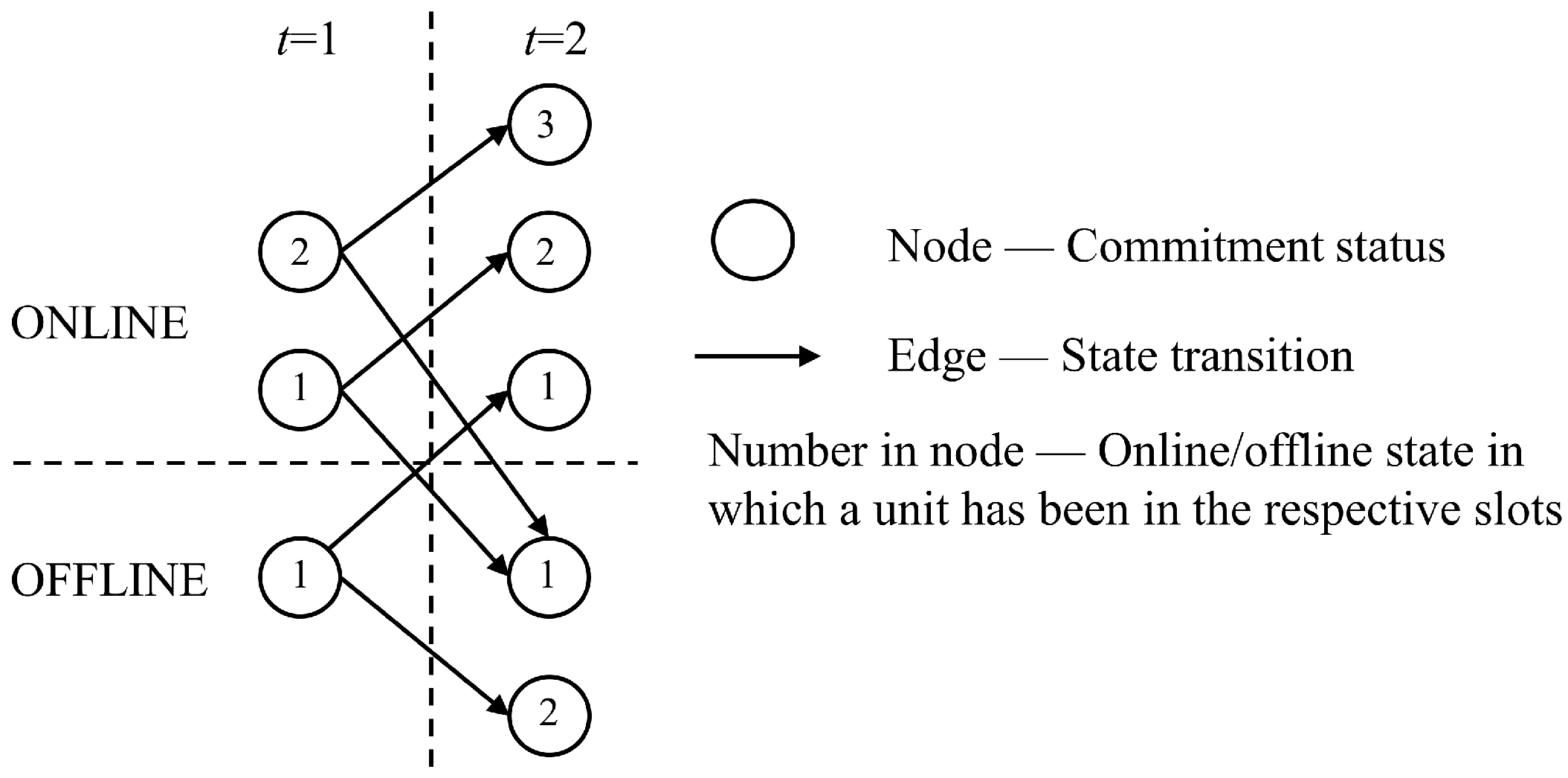
- State transition approach
- (1)
- No matter whether the fuel cost function of each unit is either convex or non-convex over the convex hull of each unit, the convex envelope of each unit can be obtained by integer relaxation because the cost function based on the state transition diagram is linear with and . This arises from the fact that changes the generation capacity from to (per unit). Therefore, the slope from zero to does not affect the convexity of the cost function.
- (2)
- No matter whether the coefficients of commitment costs are either constant or time-dependent, the convex envelope of each unit can be obtained by integer relaxation. This is because time-dependent coefficients of commitment costs are handled by that enumerates transitions of all the commitment statuses.
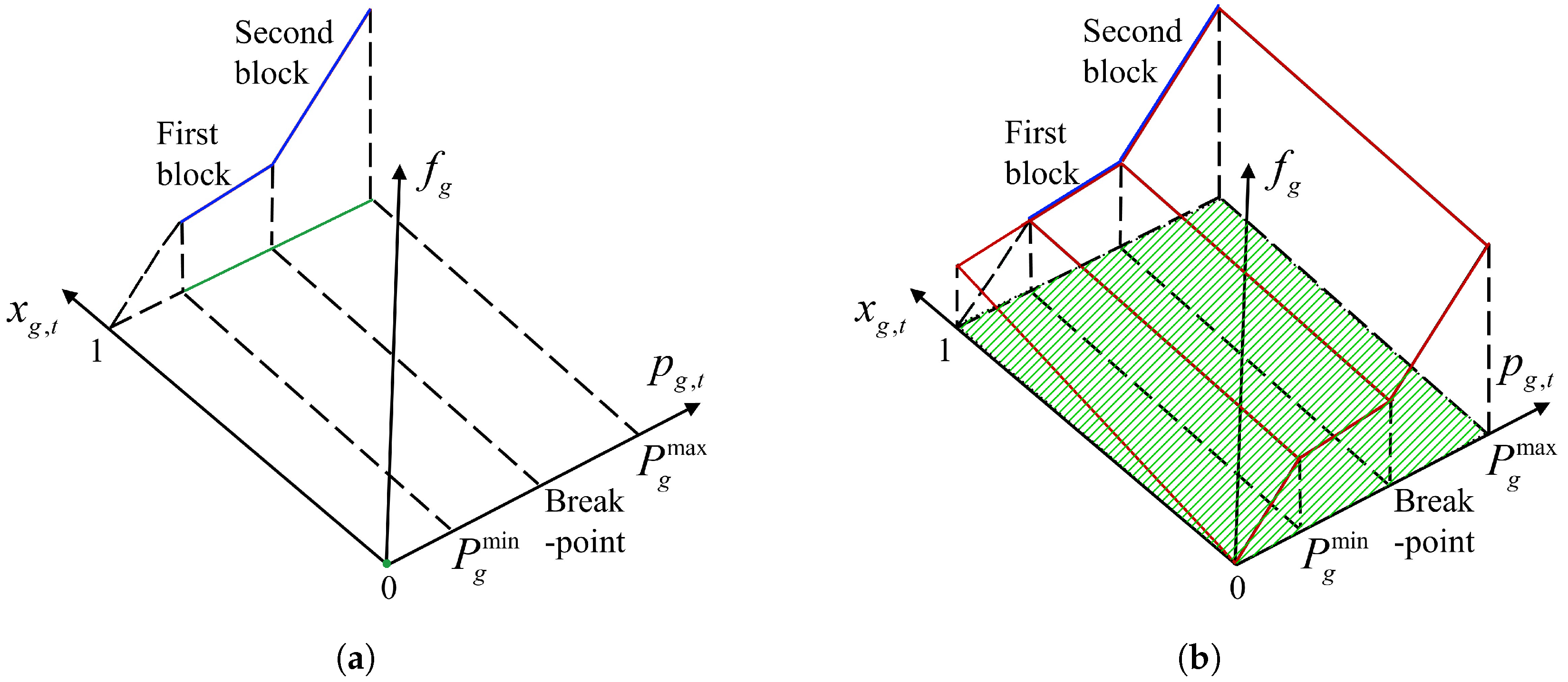
3.3. Convex Hull and Convex Envelope under a Unit Formulation Which Is Not Tight
- (1)
- Disjunctive programming approach
- (2)
- Interval concept approach
- (3)
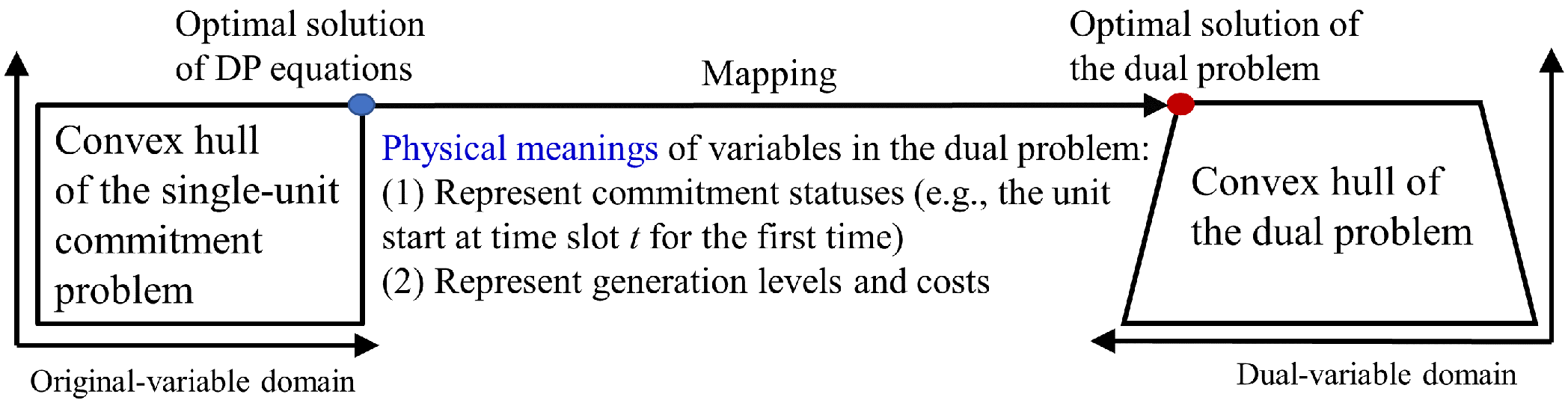
- Single-unit commitment approach
- (4)
- Dantzig-Wolfe (DW) decomposition approach
3.4. Approaches Using Approximate Convex Hulls
4. Convex Hull Pricing by the Lagrangian Dual Problem of a UC Problem
4.1. Convex Hull Pricing from the Lagrangian Dual Problem of the UC-Orig Problem
4.2. Approaches Using the UC-Orig-Lagrangian-Dual Problem
- (1)
- Subgradient simplex cutting plane approach
- (2)
- Extreme-point subdifferential approach
- (3)
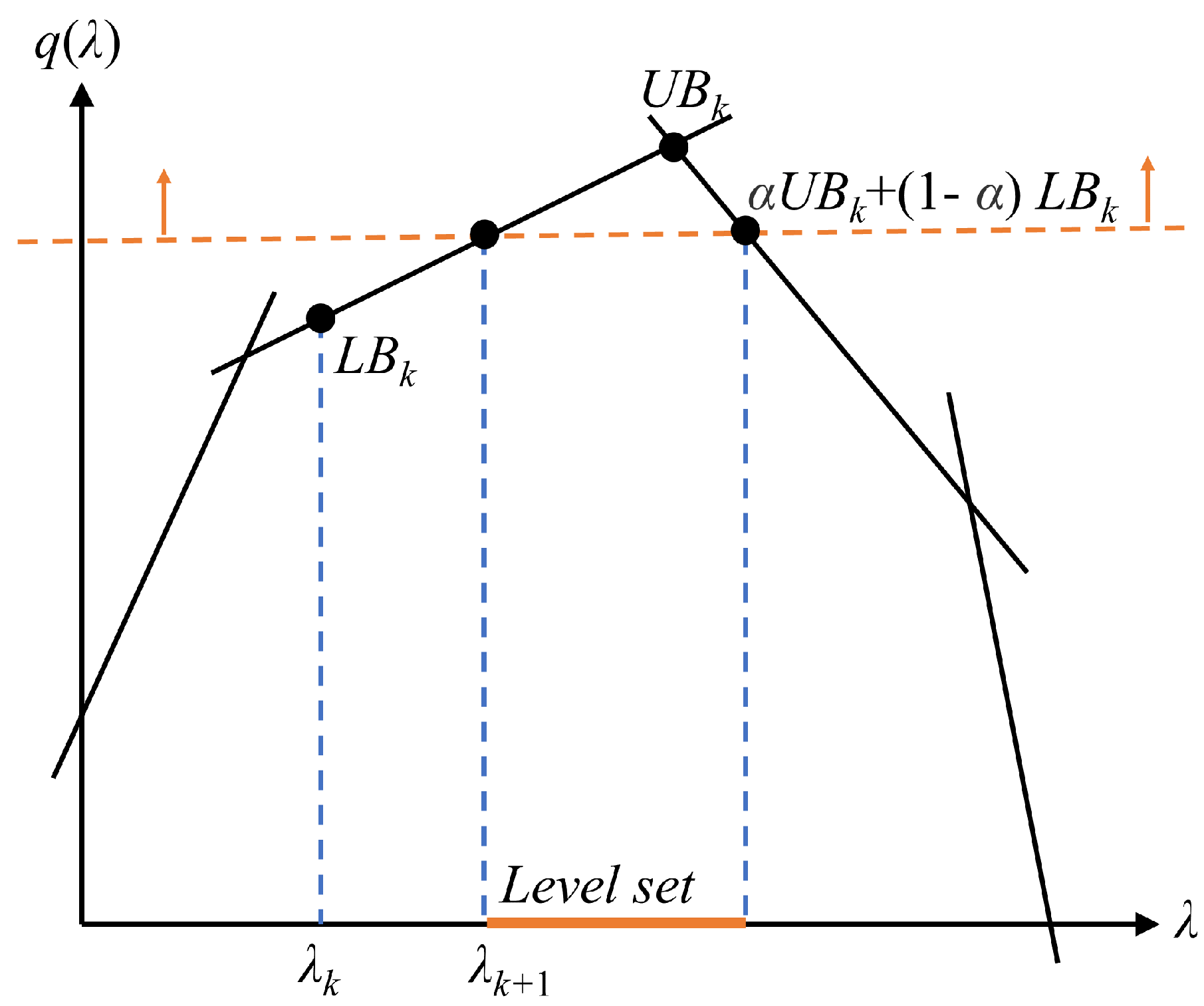
- Level method
4.3. Discussions on Convex Hull Pricing by Solving the Lagrangian Dual Problem through the SLR Method
- All the subproblems are not required to be solved optimally. Only the surrogate optimality condition must be satisfied, as demonstrated in (26). Consequently, computational efforts are reduced.
- The guesstimate of is not needed in the implementation. This avoids the slow convergence caused by inefficient adjustments of .
- The surrogate directions given by (25) are smoother, and zigzagging is eliminated.
5. Discussion and Insights
5.1. Remaining Limitations and Potential Improvements of Current Approaches
- Exact convex hull pricing approaches: For the primal category, the computational efficiency can be enhanced by bypassing the need for the exact convex hulls. This is inspired by the fact that the solution to a MILP problem is at one vertex of the convex hull, hence, only facets adjacent to the optimal solution needed to be delineated. For the dual category, the utilization of the linear convergence potential, as discussed in [42,43], can accelerate iteration-wise convergence, thereby enabling more efficient computations of convex hull pricing for large-scale problems.
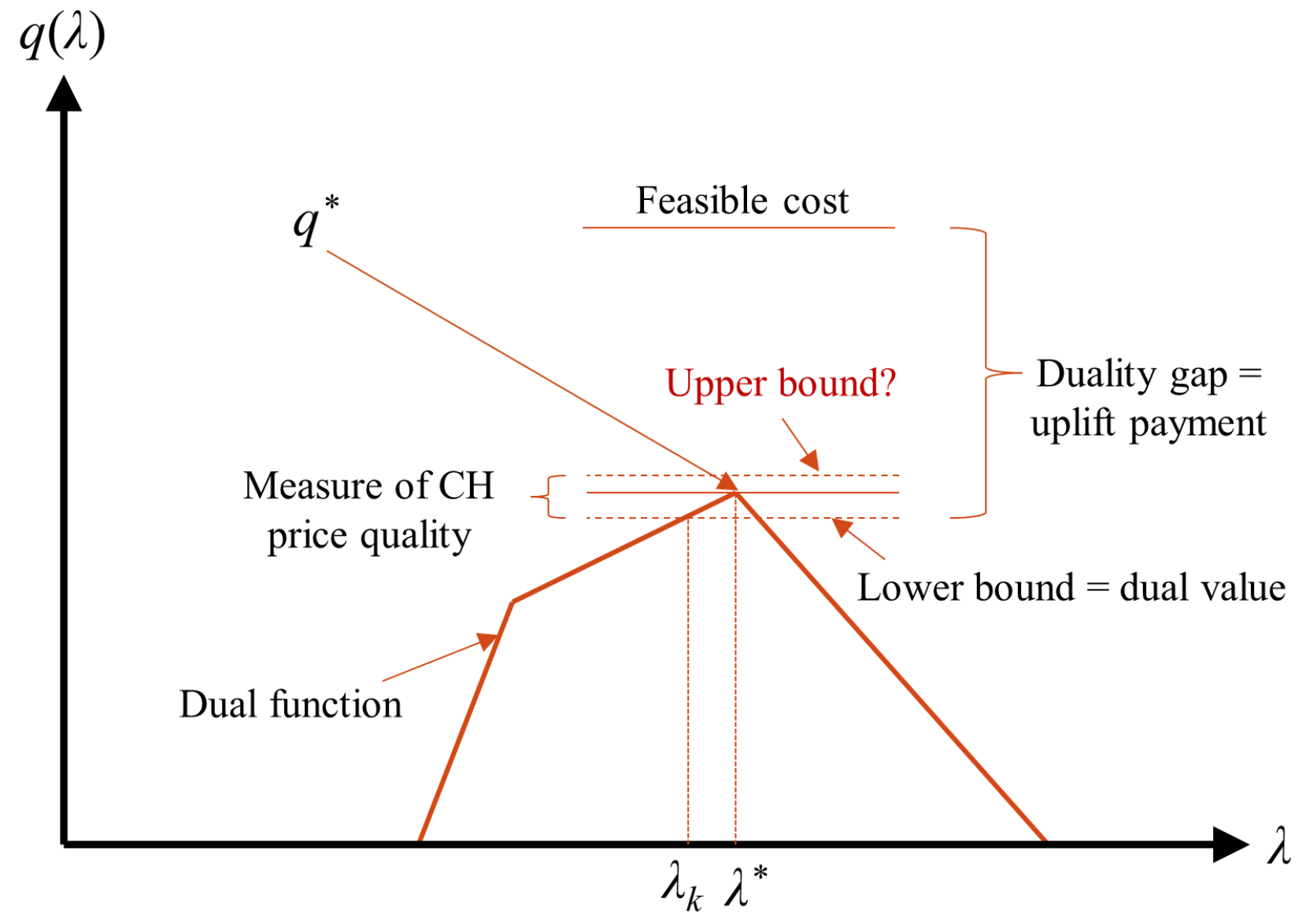
- Approximated convex hull pricing approaches: When calculating exact convex hull prices is not efficient for large-scale problems, approximated convex hull prices offer a viable alternative. In existing studies, the approximation accuracy is usually evaluated by the total uplift payments, i.e., the lower the value, the higher the accuracy. Beyond the existing system-level evaluation based on total uplift payments, a more detailed evaluation can be conducted at the unit level. This involves comparing the uplift payments for each unit across various approaches. For such unit-level analysis, metrics such as the root mean square errors, maximum errors, and minimum errors of each unit’s uplift payments could be used as standards.
5.2. New Challenges from Power System Decarbonization
- New binary variables: Looking to the future, at least two sources of new binary variables will be integrated into UC. The first source emerges from new components, such as energy storage. To mitigate the intermittency of variable renewable energy sources such as solar and wind, and to further decarbonize, energy storage is essential for maintaining a reliable and resilient grid operation. In modeling energy storage, binary variables are required to avoid simultaneous charging and discharging of the storage unit [45]. Recent studies developed a convex hull pricing model for pumped hydro storage units [46] and carbon-capture-utilization-and-storage (CCUS) systems [47]. However, further research on convex hull models for emerging chemical battery storage is desired. The second source of binary variables is associated with new, broader operational requirements at the system level. For example, stability constraints, have been encouraged in UC [48], often involving complex formulations. These stability constraints are currently interpreted using machine learning techniques, such as deep neural networks, which necessitate binary variables for their explicit representation [49]. Another source of binary variables is for reserve commitments where additional binary variables are used to ensure that a generator is committed to provide regulation reserves [50]. In our view, incorporating these binary variables necessitates addressing three key questions: (1) How do these new binary variables influence energy prices? (2) How can these effects be incorporated into the convex hull pricing framework? (3) What are the strategies for efficiently implementing convex hull pricing in the presence of new binary variables?
- Variable renewable generation uncertainties: One key feature of variable renewable energy is the uncertain nature of its fluctuations. However, current convex hull pricing majorly focuses on deterministic UC. A recent study [51] employed convex hull pricing as a way of pricing the uncertainty associated with wind production instead of incorporating several wind power generation scenarios into the UC problem. Convex hull prices were determined for different renewable energy penetration levels and added to the cost function. Thereby, transforming a stochastic UC problem into a deterministic problem. While this study uses convex hull pricing for risk mitigation, the impact of variable renewable generation uncertainties on convex hull pricing remains unclear. In addition, renewable energy sources can lead to transmission congestion as they are often located far from load centers. For example, in the state of Texas, most of the wind power is located in the Western region of the state but the population centers are in the East. The resulting network congestion affects convex hull prices throughout the Texas grid. It is thus critical to incorporate renewable uncertainties in convex hull pricing. From our understanding, convex hull pricing under renewable uncertainties may involve addressing four critical questions: (1) What types of renewable uncertainties (e.g., probabilistic distribution functions and uncertainty set) should be considered in electricity markets? (2) What modeling changes will be needed to incorporate renewable uncertainties in electricity markets? (3) What are the impacts of these modeling changes on convex hull pricing (e.g., impacts on the formulations of convex hulls and convex envelopes)? (4) How to address the impact of transmission congestion on convex hull prices?
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhattacharya, K.; Bollen, M.H.; Daalder, J.E. Operation of Restructured Power Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Litvinov, E.; Zhao, F.; Zheng, T. Electricity markets in the united states: Power industry restructuring processes for the present and future. IEEE Power Energy Mag. 2019, 17, 32–42. [Google Scholar] [CrossRef]
- Gribik, P.R.; Hogan, W.W.; Pope, S.L. Market-Clearing Electricity Prices and Energy Uplift; Harvard Electricity Policy Group: Cambridge, MA, USA, 2007; pp. 1–46. [Google Scholar]
- Hogan, W.W. Electricity market design and efficient pricing: Applications for New England and beyond. Electr. J. 2014, 27, 23–49. [Google Scholar] [CrossRef]
- Lin, X.; Wang, B.; Xiang, Z.; Zheng, Y. A review of market power-mitigation mechanisms in electricity markets. Energy Convers. Econ. 2022, 3, 304–318. [Google Scholar] [CrossRef]
- Chao, H.P. Incentives for efficient pricing mechanism in markets with non-convexities. J. Regul. Econ. 2019, 56, 33–58. [Google Scholar] [CrossRef]
- Hua, B.; Baldick, R. A convex primal formulation for convex hull pricing. IEEE Trans. Power Syst. 2016, 32, 3814–3823. [Google Scholar] [CrossRef]
- Alvarez, C.; Mancilla-David, F.; Escalona, P.; Angulo, A. A bienstock–zuckerberg-based algorithm for solving a network-flow formulation of the convex hull pricing problem. IEEE Trans. Power Syst. 2019, 35, 2108–2119. [Google Scholar] [CrossRef]
- Schiro, D.A.; Zheng, T.; Zhao, F.; Litvinov, E. Convex hull pricing in electricity markets: Formulation, analysis, and implementation challenges. IEEE Trans. Power Syst. 2015, 31, 4068–4075. [Google Scholar] [CrossRef]
- Knueven, B.; Ostrowski, J.; Castillo, A.; Watson, J.P. A computationally efficient algorithm for computing convex hull prices. Comput. Ind. Eng. 2022, 163, 107806. [Google Scholar] [CrossRef]
- Yu, Y.; Guan, Y.; Chen, Y. An integral formulation and convex hull pricing for unit commitment. arXiv 2019, arXiv:1906.07862. [Google Scholar]
- Guan, Y.; Pan, K.; Zhou, K. Polynomial time algorithms and extended formulations for unit commitment problems. IISE Trans. 2018, 50, 735–751. [Google Scholar] [CrossRef]
- Andrianesis, P.; Bertsimas, D.; Caramanis, M.C.; Hogan, W.W. Computation of convex hull prices in electricity markets with non-convexities using dantzig-wolfe decomposition. IEEE Trans. Power Syst. 2021, 37, 2578–2589. [Google Scholar] [CrossRef]
- Wang, C.; Peng, T.; Luh, P.B.; Gribik, P.; Zhang, L. The subgradient simplex cutting plane method for extended locational marginal prices. IEEE Trans. Power Syst. 2013, 28, 2758–2767. [Google Scholar] [CrossRef]
- Wang, G.; Shanbhag, U.V.; Zheng, T.; Litvinov, E.; Meyn, S. An extreme-point subdifferential method for convex hull pricing in energy and reserve markets—Part I: Algorithm structure. IEEE Trans. Power Syst. 2013, 28, 2111–2120. [Google Scholar] [CrossRef]
- Wang, G.; Shanbhag, U.V.; Zheng, T.; Litvinov, E.; Meyn, S. An extreme-point subdifferential method for convex hull pricing in energy and reserve markets—Part II: Convergence analysis and numerical performance. IEEE Trans. Power Syst. 2013, 28, 2121–2127. [Google Scholar] [CrossRef]
- Stevens, N.; Papavasiliou, A. Application of the level method for computing locational convex hull prices. IEEE Trans. Power Syst. 2022, 37, 3958–3968. [Google Scholar] [CrossRef]
- Liberopoulos, G.; Andrianesis, P. Critical Review of Pricing Schemes in Markets with Non-Convex Costs. Oper. Res. 2016, 64, 17–31. [Google Scholar] [CrossRef]
- Chen, Y.; O’Neill, R.; Whitman, P. A Comparison of Three Methods for ISO Pricing. IEEE Trans. Energy Mark. Policy Regul. 2024, 1–12. [Google Scholar] [CrossRef]
- Stevens, N.; Papavasiliou, A.; Smeers, Y. On some advantages of convex hull pricing for the European electricity auction. Energy Econ. 2024, 134, 107542. [Google Scholar] [CrossRef]
- Garcia, M.; Nagarajan, H.; Baldick, R. Generalized Convex Hull Pricing for the AC Optimal Power Flow Problem. IEEE Trans. Control Netw. Syst. 2020, 7, 1500–1510. [Google Scholar] [CrossRef]
- Li, N.; Gao, Y. Real-time pricing based on convex hull method for smart grid with multiple generating units. Energy 2023, 285, 129543. [Google Scholar] [CrossRef]
- Ito, N.; Takeda, A.; Namerikawa, T. Convex hull pricing for demand response in electricity markets. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 151–156. [Google Scholar]
- Borokhov, V. Modified convex hull pricing for power markets with price-sensitive load. Int. J. Electr. Power Energy Syst. 2018, 100, 422–437. [Google Scholar] [CrossRef]
- Yang, Z.; Lin, W.; Qiu, F.; Yu, J.; Yang, G. Correct the piecewise linearization error of quadratic objective function in DC OPF model. IEEE Trans. Power Syst. 2019, 34, 5083–5086. [Google Scholar] [CrossRef]
- Zhao, F.; Schiro, D.; Zhao, J.; Zheng, T.; Litvinov, E. On the Primal UC Formulation Dependence of Convex Hull Pricing. IEEE Trans. Energy Mark. Policy Regul. 2023, 1, 227–236. [Google Scholar] [CrossRef]
- Damcı-Kurt, P.; Küçükyavuz, S.; Rajan, D.; Atamtürk, A. A polyhedral study of production ramping. Math. Program. 2016, 158, 175–205. [Google Scholar] [CrossRef]
- Falk, J.E. Lagrange multipliers and nonconvex programs. SIAM J. Control 1969, 7, 534–545. [Google Scholar] [CrossRef]
- Fulkerson, D.R.; Ford, L.R. Flows in Networks; Rand Corporation: Santa Monica, CA, USA, 1962. [Google Scholar]
- Yu, Y.; Zhang, T.; Guan, Y. Network-Flow-Based Formulations for Convex Hull Pricing with Maximum Start-Ups. IEEE Trans. Power Syst. 2022, 37, 1198–1206. [Google Scholar] [CrossRef]
- Yan, B.; Luh, P.B.; Zheng, T.; Schiro, D.A.; Bragin, M.A.; Zhao, F.; Zhao, J.; Lelic, I. A systematic formulation tightening approach for unit commitment problems. IEEE Trans. Power Syst. 2019, 35, 782–794. [Google Scholar] [CrossRef]
- Balas, E. Disjunctive programming: Properties of the convex hull of feasible points. Discret. Appl. Math. 1998, 89, 3–44. [Google Scholar] [CrossRef]
- Pan, K.; Guan, Y. A polyhedral study of the integrated minimum-up/-down time and ramping polytope. arXiv 2016, arXiv:1604.02184. [Google Scholar]
- Hyder, F.; Yan, B.; Bragin, M.A.; Luh, P.B. Impacts of uc formulation tightening on computation of convex hull prices. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Bragin, M.A.; Luh, P.B.; Yan, J.H.; Yu, N.; Stern, G.A. Convergence of the surrogate Lagrangian relaxation method. J. Optim. Theory Appl. 2015, 164, 173–201. [Google Scholar] [CrossRef]
- Goffin, J.L.; Kiwiel, K.C. Convergence of a Simple Subgradient Level Method; Groupe d’études et de Recherche en Analyse des Décisions: Montréal, QC, Canada, 1998. [Google Scholar]
- Nedić, A.; Bertsekas, D. Convergence rate of incremental subgradient algorithms. In Stochastic Optimization: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 223–264. [Google Scholar]
- Bragin, M.A.; Luh, P.B.; Yan, B.; Sun, X. A scalable solution methodology for mixed-integer linear programming problems arising in automation. IEEE Trans. Autom. Sci. Eng. 2018, 16, 531–541. [Google Scholar] [CrossRef]
- Yang, L.; Qin, Q.; Chen, S.; Jian, J. Fully distributed convex hull pricing based on alternating direction method of multipliers. Comput. Oper. Res. 2025, 173, 106823. [Google Scholar] [CrossRef]
- Bragin, M.A.; Hyder, F.; Yan, B.; Luh, P.B.; Zhao, J.; Zhao, F.; Schiro, D.A.; Zheng, T. Novel Quality Measure and Efficient Resolution of Convex Hull Pricing for Unit Commitment. arXiv 2023, arXiv:2304.07990. [Google Scholar]
- Bragin, M.A. Survey on Lagrangian relaxation for MILP: Importance, challenges, historical review, recent advancements, and opportunities. Ann. Oper. Res. 2024, 333, 29–45. [Google Scholar] [CrossRef]
- Bragin, M.A.; Tucker, E.L. Surrogate “Level-Based” Lagrangian Relaxation for mixed-integer linear programming. Sci. Rep. 2022, 12, 22417. [Google Scholar] [CrossRef] [PubMed]
- International Energy Agency. Net Zero by 2050: A Roadmap for the Global Energy Sector. 2021. Available online: https://trid.trb.org/View/1856381 (accessed on 12 September 2024).
- Guo, Z.; Wei, W.; Chen, L.; Shahidehpour, M.; Mei, S. Economic value of energy storages in unit commitment with renewables and its implication on storage sizing. IEEE Trans. Sustain. Energy 2021, 12, 2219–2229. [Google Scholar] [CrossRef]
- Qu, M.; Ding, T.; Sun, Y.; Mu, C.; Pan, K.; Shahidehpour, M. Convex hull model for a single-unit commitment problem with pumped hydro storage unit. IEEE Trans. Power Syst. 2022, 38, 4867–4880. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, J.; Shahidehpour, M.; Bai, L.; Li, Z. Convex-Hull Pricing of Ancillary Services for Power System Frequency Regulation With Renewables and Carbon-Capture-Utilization-and-Storage Systems. IEEE Trans. Power Syst. 2024, 39, 6615–6635. [Google Scholar] [CrossRef]
- Wu, T.; Wang, J. Transient Stability-Constrained Unit Commitment Using Input Convex Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2023. [Google Scholar] [CrossRef]
- Tjeng, V.; Xiao, K.; Tedrake, R. Evaluating robustness of neural networks with mixed integer programming. arXiv 2017, arXiv:1711.07356. [Google Scholar]
- Yu, Y.; Zhang, T.; Guan, Y.; Chen, Y. Convex Primal Formulations for Convex Hull Pricing with Reserve Commitments. IEEE Trans. Power Syst. 2021, 36, 2345–2354. [Google Scholar] [CrossRef]
- Akhundov, N.; Bakhshi, M.; Ostrowski, J. Convex hull pricing as a risk mitigation device in unit commitment. Energy Syst. 2023, 1–22. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyder, F.; Yan, B.; Bragin, M.; Luh, P. Convex Hull Pricing for Unit Commitment: Survey, Insights, and Discussions. Energies 2024, 17, 4851. https://doi.org/10.3390/en17194851
Hyder F, Yan B, Bragin M, Luh P. Convex Hull Pricing for Unit Commitment: Survey, Insights, and Discussions. Energies. 2024; 17(19):4851. https://doi.org/10.3390/en17194851
Chicago/Turabian StyleHyder, Farhan, Bing Yan, Mikhail Bragin, and Peter Luh. 2024. "Convex Hull Pricing for Unit Commitment: Survey, Insights, and Discussions" Energies 17, no. 19: 4851. https://doi.org/10.3390/en17194851
APA StyleHyder, F., Yan, B., Bragin, M., & Luh, P. (2024). Convex Hull Pricing for Unit Commitment: Survey, Insights, and Discussions. Energies, 17(19), 4851. https://doi.org/10.3390/en17194851







