A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade
Abstract
1. Introduction
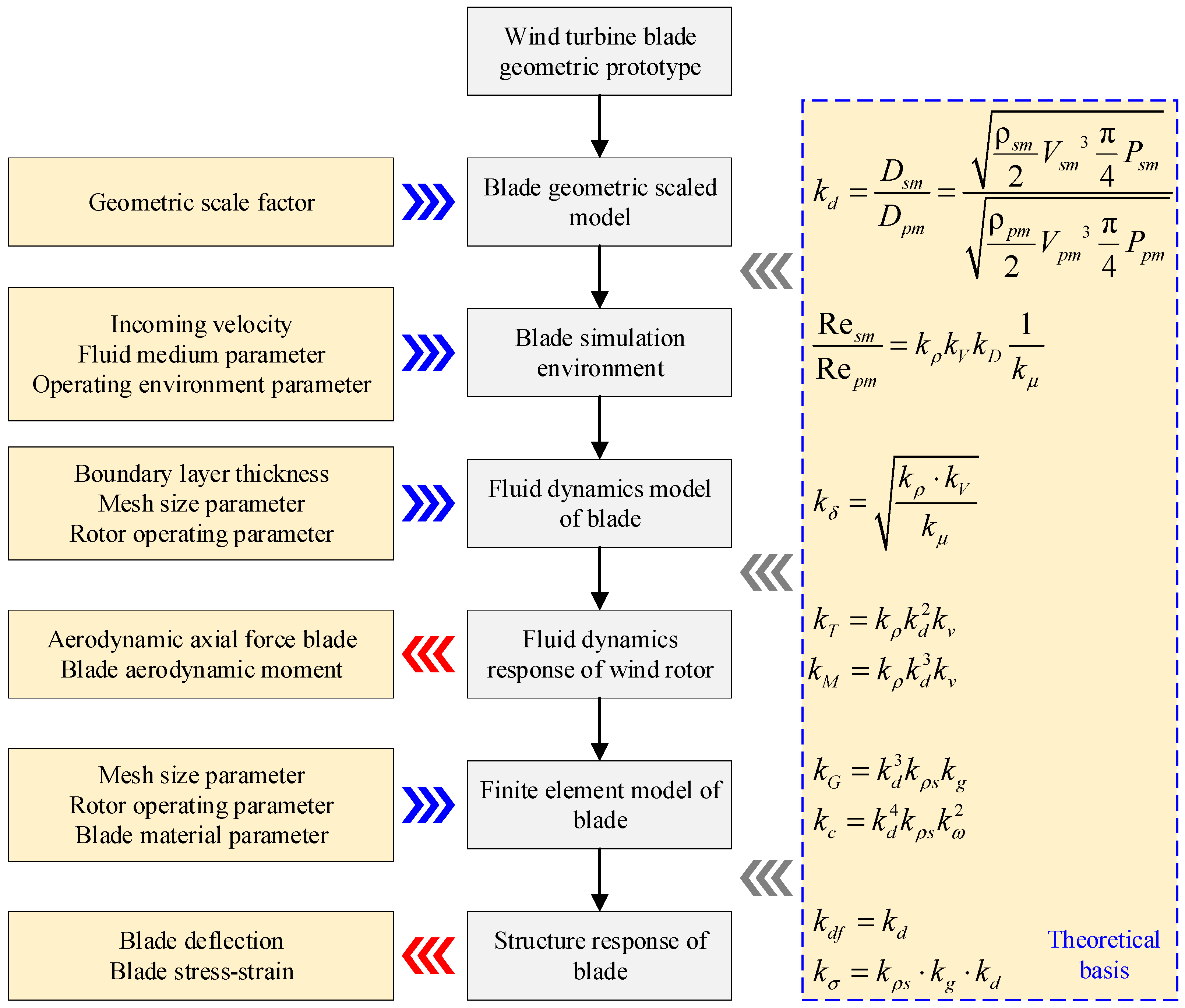
2. Dimensionally Scaled Model
3. Numerical Simulations of the Scaled Model
3.1. Material Similarity Model
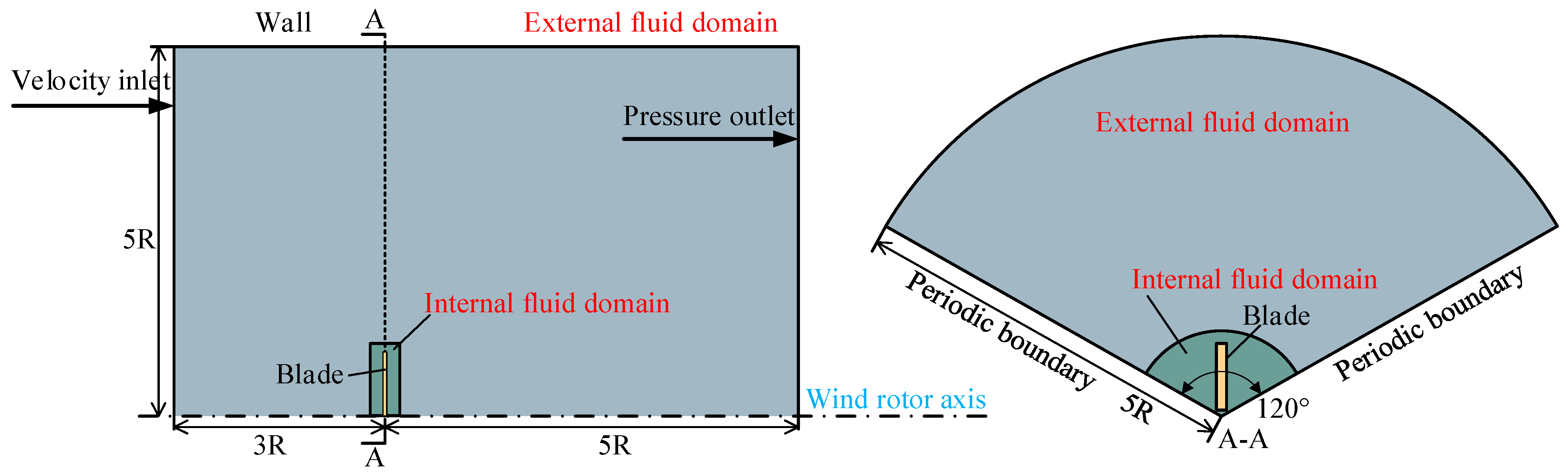
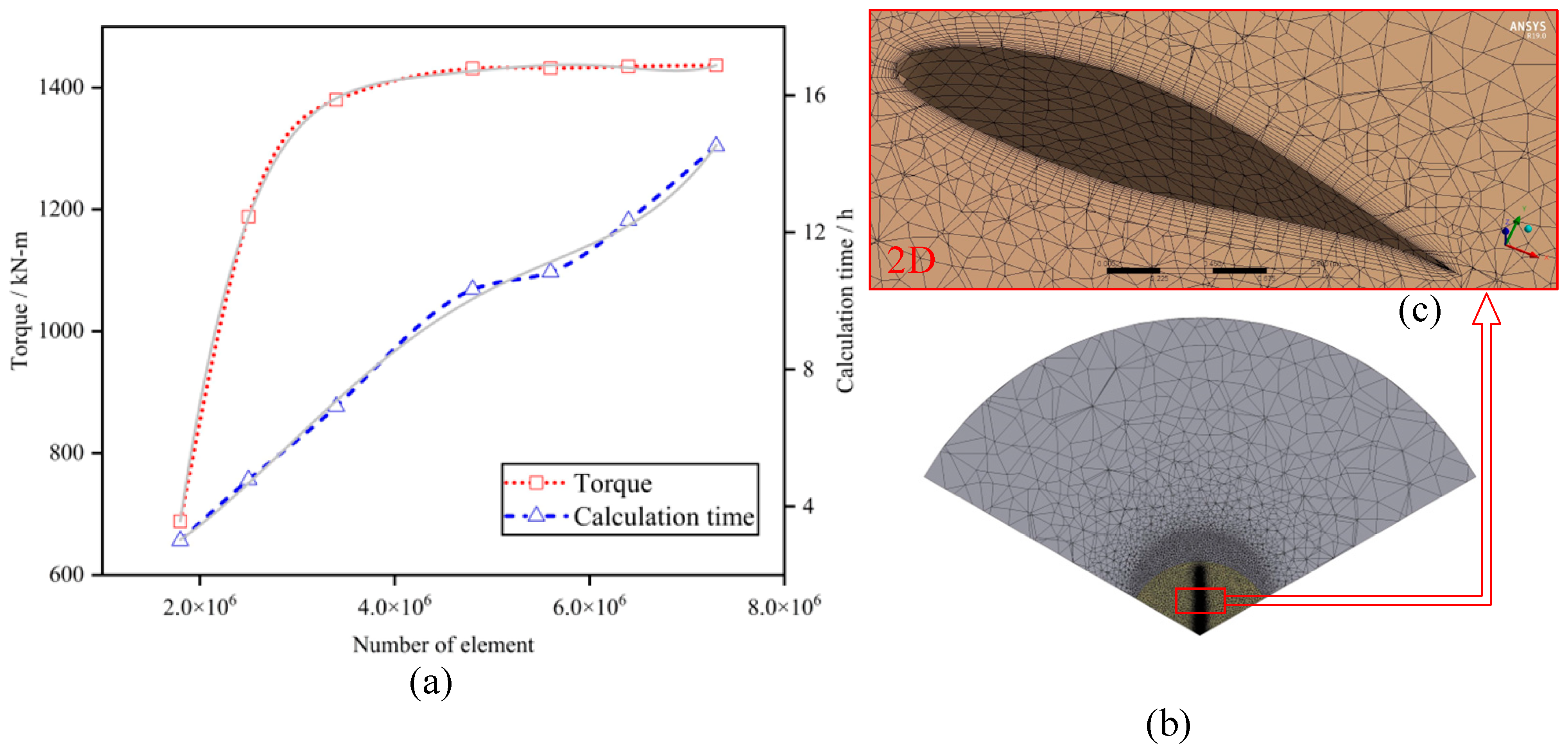
3.2. Mesh Generation
4. Load Similarity Model
4.1. Aerodynamic Load
4.2. Inertial Load
5. The Similarity Relationship of Structural Response
5.1. Scaled Model Response
5.2. Determine the Scaling Factors
5.3. The Process for Building a Scaled Model
- (1)
- A three-dimensional geometric model of large wind turbine blades is established from the data on airfoil, propeller blade angle, and chord length.
- (2)
- Select the appropriate scale factor to calculate the wind turbine diameter, blade thickness, chord length, and other parameters, and use these to establish the geometric scale model.
- (3)
- Under the premise that the flow pattern of the scaled model airfoil remains consistent with that of the prototype, the fluid dynamic simulation parameters, including the wind turbine incoming velocity, fluid medium density, and kinematic viscosity of the fluid medium, are determined.
- (4)
- The wind rotor fluid domain model is constructed based on the geometric scaling relationship. The boundary layer thickness variation is calculated to determine the thickness of the first boundary layer, which is used to generate the fluid domain mesh model.
- (5)
- Given the inlet wind speed and the rotation speed of the wind turbine’s rotating domain, select an appropriate turbulence model to perform the fluid dynamic simulation analysis of the wind rotor. This process will provide the blade pressure distribution, from which the aerodynamic axial force and aerodynamic moment of the wind turbine blade can be calculated.
- (6)
- According to the material parameter scale factor, composite layups are performed on the wind turbine blade scale model. The structural design of the airfoil’s leading edge, trailing edge, spar, and web is completed using glass fiber, carbon fiber, balsa wood, and PVC foam.
- (7)
- Aerodynamic loads are applied to the blade surface, and static simulation analysis is performed to determine the deflection and stress–strain response of the scale model blade. The mechanical response of the blade prototype is evaluated using the blade structural response factor.
6. Numerical Examples
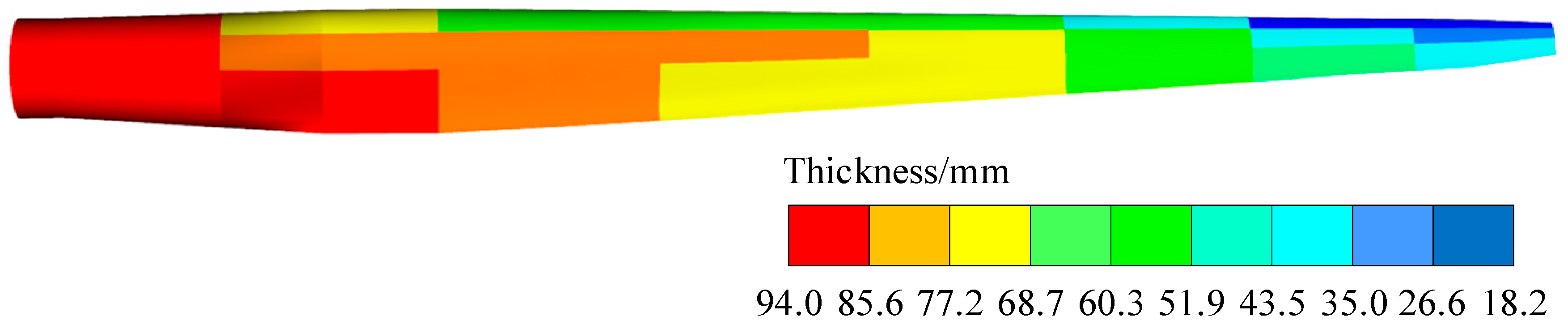
6.1. Blade Model
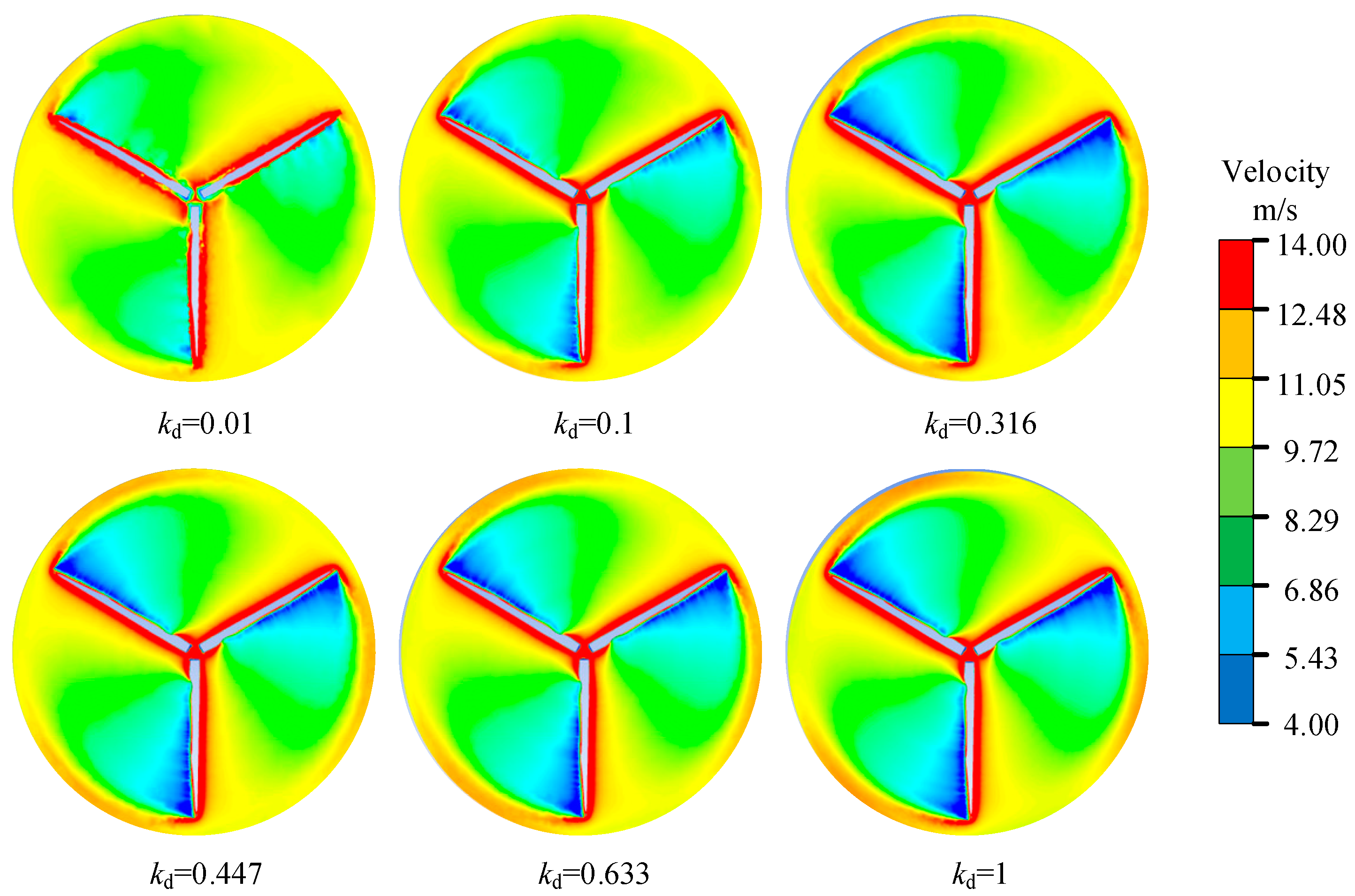
6.2. Aerodynamic Load
6.3. Static Analysis
6.4. Transient Analysis
7. Conclusions
- (1)
- The proposed method ensures that the blade scale model satisfies structural and fluid similarities. This is achieved by coordinating the scale relationship of the model operation parameters, numerical simulation environment parameters, and mechanical response parameters.
- (2)
- The numerical scale model constructed can improve the efficiency of aerodynamic analysis and guarantee the solution’s accuracy by selecting appropriate geometric scale factors. For a geometric scale factor of 0.316, the relative difference in maximum deflection is 4.52%, with a reduction in calculation time by 48.1%.
- (3)
- The scale model is suitable for aerodynamic load analysis, structural static analysis, and structural transient analysis, and the precision of the scale model is mainly related to the accuracy of aerodynamic analysis.
8. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ben Backwell, M.H.; Khinda, N.; Clarke, E.; Qiao, L.; Williams, R.; Tan, W.H.; Liang, W.; Esther, A.L.; Fang, M.R.; Ann Margret, T.V.B.; et al. Global Wind Report 2024; 2024. Available online: https://gwec.net/global-wind-report-2024/ (accessed on 16 April 2024).
- Ghiasi, P.; Najafi, G.; Ghobadian, B.; Jafari, A.; Mamat, R.; Ghazali, M.F. CFD-Study of the H-Rotor Darrius wind turbine performance in Drag-Lift and Lift Regime: Impact of type, thickness and chord length of blades. Alex. Eng. J. 2023, 67, 51–64. [Google Scholar] [CrossRef]
- Hijazi, A.; ElCheikh, A.; Elkhoury, M. Numerical investigation of the use of flexible blades for vertical axis wind turbines. Energy Convers. Manag. 2024, 299, 117867. [Google Scholar] [CrossRef]
- Eltayesh, A.; Castellani, F.; Burlando, M.; Hanna, M.B.; Huzayyin, A.; El-Batsh, H.M.; Becchetti, M. Experimental and numerical investigation of the effect of blade number on the aerodynamic performance of a small-scale horizontal axis wind turbine. Alex. Eng. J. 2021, 60, 3931–3944. [Google Scholar] [CrossRef]
- Khalafallah, M.G.; Ahmed, A.M.; Emam, M.K. The effect of using winglets to enhance the performance of swept blades of a horizontal axis wind turbine. Adv. Mech. Eng. 2019, 11, 1687814019878312. [Google Scholar] [CrossRef]
- Zheng, T.; Zhao, C.; He, J. Research on Fatigue Performance of Offshore Wind Turbine Blade with Basalt Fiber Bionic Plate; Structures 2023; Elsevier: Amsterdam, The Netherlands, 2023; pp. 466–481. [Google Scholar]
- Hand, B.; Kelly, G.; Cashman, A. Structural analysis of an offshore vertical axis wind turbine composite blade experiencing an extreme wind load. Mar. Struct. 2021, 75, 102858. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Behzad, M.; Moradi, H.; Haddadpour, H. Modal-based damage identification for the nonlinear model of modern wind turbine blade. Renew. Energy 2016, 94, 391–409. [Google Scholar] [CrossRef]
- Chen, Y.; Griffith, D.T. Blade mass imbalance identification and estimation for three-bladed wind turbine rotor based on modal analysis. Mech. Syst. Signal Process. 2023, 197, 110341. [Google Scholar] [CrossRef]
- Jayswal, S.; Bhattu, A. Structural and modal analysis of small wind turbine blade using three different materials. Mater. Today Proc. 2023, 72, 1347–1352. [Google Scholar] [CrossRef]
- Navadeh, N.; Goroshko, I.; Zhuk, Y.; Etminan Moghadam, F.; Soleiman Fallah, A. Finite element analysis of wind turbine blade vibrations. Vibration 2021, 4, 310–322. [Google Scholar] [CrossRef]
- Lipian, M.; Czapski, P.; Obidowski, D. Fluid-structure interaction numerical analysis of a small, urban wind turbine blade. Energies 2020, 13, 1832. [Google Scholar] [CrossRef]
- Marzec, Ł.; Buliński, Z.; Krysiński, T. Fluid structure interaction analysis of the operating Savonius wind turbine. Renew. Energy 2021, 164, 272–284. [Google Scholar] [CrossRef]
- Li, J.; Liu, R.; Yuan, P.; Pei, Y.; Cao, R.; Wang, G. Numerical simulation and application of noise for high-power wind turbines with double blades based on large eddy simulation model. Renew. Energy 2020, 146, 1682–1690. [Google Scholar] [CrossRef]
- Maizi, M.; Mohamed, M.; Dizene, R.; Mihoubi, M. Noise reduction of a horizontal wind turbine using different blade shapes. Renew. Energy 2018, 117, 242–256. [Google Scholar] [CrossRef]
- Moon, H.; Jeong, J.; Park, S.; Ha, K.; Jeong, J.-H. Numerical and experimental validation of vortex generator effect on power performance improvement in MW-class wind turbine blade. Renew. Energy 2023, 212, 443–454. [Google Scholar] [CrossRef]
- Siddiqui, M.S.; Rasheed, A.; Kvamsdal, T.; Tabib, M. Quasi-static & dynamic numerical modeling of full scale nrel 5mw wind turbine. Energy Procedia 2017, 137, 460–467. [Google Scholar]
- Zhang, Y.; Song, Y.; Shen, C.; Chen, N.-Z. Aerodynamic and structural analysis for blades of a 15MW floating offshore wind turbine. Ocean Eng. 2023, 287, 115785. [Google Scholar] [CrossRef]
- Gao, G.; Wang, H.; Li, E.; Li, G. An exact block-based reanalysis method for local modifications. Comput. Struct. 2015, 158, 369–380. [Google Scholar] [CrossRef]
- Jokar, H.; Mahzoon, M.; Vatankhah, R. Nonlinear dynamic characteristics of horizontal-axis wind turbine blades including pre-twist. Ocean Eng. 2022, 256, 111441. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.; Son, E.; Lee, S.; Lee, S. Aerodynamic noise analysis of large horizontal axis wind turbines considering fluid–structure interaction. Renew. Energy 2012, 42, 46–53. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Z.; Li, W.; Hu, G. LES simulation study of wind turbine aerodynamic characteristics with fluid-structure interaction analysis considering blade and tower flexibility. Energy 2023, 282, 128840. [Google Scholar] [CrossRef]
- Hu, Z.; Dang, C.; Wang, L.; Beer, M. Parallel Bayesian probabilistic integration for structural reliability analysis with small failure probabilities. Struct. Saf. 2024, 106, 102409. [Google Scholar] [CrossRef]
- Chasapi, M.; Antolin, P.; Buffa, A. Fast parametric analysis of trimmed multi-patch isogeometric Kirchhoff-Love shells using a local reduced basis method. Eng. Comput. 2024, 1–28. Available online: https://link.springer.com/article/10.1007/s00366-024-01980-6 (accessed on 24 September 2024). [CrossRef]
- Teng, D.; Feng, Y.-W.; Lu, C.; Keshtegar, B.; Xue, X.-F. Generative adversarial surrogate modeling framework for aerospace engineering structural system reliability design. Aerosp. Sci. Technol. 2024, 144, 108781. [Google Scholar] [CrossRef]
- Li, W.; Chen, S. Structural reanalysis method for local modifications based on system reduction and iterative solution. Eng. Struct. 2022, 273, 114977. [Google Scholar] [CrossRef]
- Luo, T.; Wu, G.; Zhang, P.; Zhang, H. A new similarity criterion for wind tunnel testing of floating wind turbines achieving dynamic aerodynamic characteristics similarity. Energy Convers. Manag. 2024, 301, 118015. [Google Scholar] [CrossRef]
- Wang, X.; Cai, C.; Chen, Y.; Chen, Y.; Liu, J.; Xiao, Y.; Zhong, X.; Shi, K. Numerical verification of the dynamic aerodynamic similarity criterion for wind tunnel experiments of floating offshore wind turbines. Energy 2023, 283, 129082. [Google Scholar] [CrossRef]
- Tschepe, J. On the prediction of boundary layer quantities at high Reynolds numbers. Fluids 2022, 7, 114. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report No. NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]

| Name of Method | Methodological Principle | Fields of Application | Case | Accurate |
|---|---|---|---|---|
| Parallel computing | Simultaneous computation is achieved by distributing tasks across multiple processors or compute nodes. | Modal analysis | Turbine blade structural model [23] | 95% |
| Reduced basis method | Model degeneracy | Analysis of the effect of geometric parameter variations on structural performance | Scordelis-Lo roof with holes [24] | 92% |
| Surrogate models | An approximation function is constructed using a finite sample of points from the original model to capture the relationship between inputs and outputs. | Modal analysis | Transient deterministic analysis for turbine blisk radial deformation [25] | 99.99% |
| Reanalysis | Rapid solution following local structural modifications. | Structural analysis | Two-dimensional plate with hole [26] | 71.40% |
| Scale models | Based on the similarity theory, the similarity ratio factor is constructed. | Structural analysis and flow field analysis | Verification for the NREL 5 MW [27] | 98.76% |
| Type of Physical Quantity | Physical Quantity | Relationship of Proportions | Proportional Value |
|---|---|---|---|
| Parameters of the wind rotor operating environment | Gravitational acceleration | kg | kd−1.0 |
| Parameters of the wind rotor operating environment | Density of fluid medium | kρ | 1.0 |
| Parameters of the wind rotor operating environment | Kinematic viscosity of fluid medium | kμ | kd |
| Parameters of blade geometry | Wind rotor diameter | kd | kd |
| Parameters of blade geometry | Blade thickness | kd | kd |
| Blade material parameter | Blade density | kρs | 1.0 |
| Blade material parameter | Blade elastic modulus | 1.0 | |
| Rotor operating patameter | Incoming velocity | kv | 1.0 |
| Rotor operating patameter | Rotational speed | kd−1.0 | |
| Rotor simulation parameter | Thickness of the first boundary layer | kd0.25 | |
| Rotor simulation parameter | Boundary layer thickness | kd−0.5 | |
| Rotor simulation parameter | Number of grids | kd0.5 | kd0.5 |
| Rotor load parameter | Aerodynamic axial force of blade | kd2 | |
| Rotor load parameter | Blade aerodynamic moment | kd3 | |
| Rotor load parameter | Blade gravity | kd2 | |
| Rotor load parameter | Blade centrifugal force | kd2 | |
| Response parameter of the blade structure | Blade deflection | kd | |
| Response parameter of the blade structure | Blade stress | 1.0 |
| Name | Density kg·m−3 | Ex MP | Ey MP | Ez MP | υxy - | υyz - | υxz - | Gxy MP | Gyz MP | Gxz MP |
|---|---|---|---|---|---|---|---|---|---|---|
| BALSA foam | 80 | 2070 | 2070 | 4000 | 0.02 | 0.16 | 0.02 | 106 | 200 | 106 |
| Two-way cloth glass fiber | 1900 | 12,500 | 11,300 | 10,000 | 0.626 | 0.626 | 0.14 | 6000 | 6000 | 3200 |
| Carbon fiber | 1560 | 136,000 | 11,900 | 11,900 | 0.29 | 0.29 | 0.4 | 4860 | 4860 | 4400 |
| One-way cloth glass fiber | 1930 | 33,190 | 11,120 | 10,120 | 0.23 | 0.11 | 0.11 | 3690 | 3000 | 3000 |
| Three-way cloth glass fiber | 1910 | 24,700 | 13,700 | 9120 | 0.413 | 0.355 | 0.13 | 5200 | 5000 | 3000 |
| Geometric Scale Factor kd | Theoretical Power kW | Total Number of Mesh - | Axial Force of Model N | Axial Force of Scale Model N | Torque of Model N·m | Torque of Scale Model N·m | Simulation Power kW | Calculation Time h |
|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.53 | 5.97 × 104 | 15.07 | 1.51 × 105 | 0.471 | 4.71 × 105 | 0.18 | 0.01 |
| 0.1 | 53.18 | 5.65 × 105 | 2346.84 | 2.35 × 105 | 1207.76 | 1.21 × 106 | 45.90 | 0.5 |
| 0.316 | 531.04 | 1.81 × 106 | 2.49 × 104 | 2.49 × 105 | 4.36 × 104 | 1.38 × 106 | 524.43 | 4.33 |
| 0.447 | 1062.59 | 2.29 × 106 | 5.02 × 104 | 2.51 × 105 | 1.25 × 105 | 1.39 × 106 | 1062.96 | 5.1 |
| 0.633 | 2130.87 | 2.97 × 106 | 1.01 × 105 | 2.52 × 105 | 3.57 × 105 | 1.41 × 106 | 2144.25 | 6.74 |
| 1.0 | 5318.02 | 4.80 × 106 | 2.58 × 105 | 2.58 × 105 | 1.43 × 106 | 1.43 × 106 | 5435.50 | 10.02 |
| Geometric Scale Factor kd | Maximum Deflection m | Maximum Deflection of Scale Model (m) | Maximum Equivalent Stress (N) | Relative Difference in Maximum Deflection (%) | Relative Difference in Maximum Equivalent Stress (%) |
|---|---|---|---|---|---|
| 0.01 | 0.0091424 | 0.91424 | 9.1446 × 107 | 43.77 | 34.67 |
| 0.1 | 0.14688 | 1.4688 | 1.3374 × 108 | 9.67 | 4.46 |
| 0.316 | 0.48592 | 1.6016 | 1.4159 × 108 | 5.42 | 2.37 |
| 0.447 | 0.73806 | 1.6511 | 1.4567 × 108 | 1.53 | 3.91 |
| 0.632 | 1.0161 | 1.6078 | 1.4251 × 108 | 1.11 | 1.78 |
| 1 | 1.6258 | 1.6258 | 1.3998 × 108 | - | - |
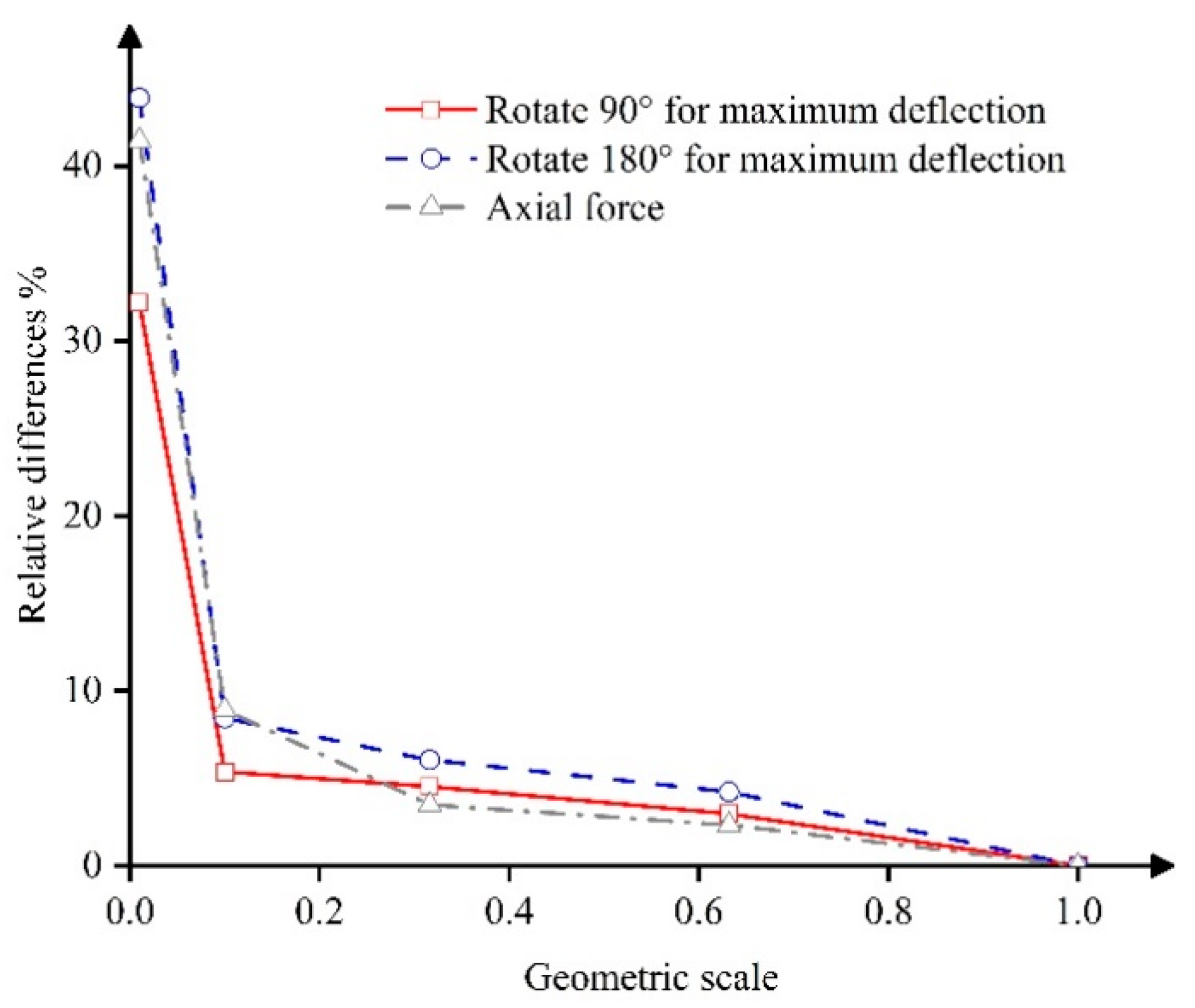
| Geometric Scale Factor kd | Rotate 90° for Maximum Deflection m | Rotate 90° for Calculation Time h | Rotate 180° for Maximum Deflection m | Rotate 180° for Calculation Time h |
|---|---|---|---|---|
| 0.01 | 0.9389 | 0.031 | 1.316 | 0.051 |
| 0.1 | 1.3102 | 0.117 | 2.147 | 0.26 |
| 0.316 | 1.3219 | 1.133 | 2.2032 | 2.48 |
| 0.632 | 1.3432 | 1.433 | 2.2462 | 3.75 |
| 1 | 1.3845 | 2.183 | 2.3451 | 6.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, G.; Shu, H.; Yi, Z.; Yang, S.; Dai, J.; Zhang, F. A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade. Energies 2024, 17, 4849. https://doi.org/10.3390/en17194849
Gao G, Shu H, Yi Z, Yang S, Dai J, Zhang F. A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade. Energies. 2024; 17(19):4849. https://doi.org/10.3390/en17194849
Chicago/Turabian StyleGao, Guoqiang, Hongsheng Shu, Zixin Yi, Shuyi Yang, Juchuan Dai, and Fan Zhang. 2024. "A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade" Energies 17, no. 19: 4849. https://doi.org/10.3390/en17194849
APA StyleGao, G., Shu, H., Yi, Z., Yang, S., Dai, J., & Zhang, F. (2024). A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade. Energies, 17(19), 4849. https://doi.org/10.3390/en17194849






