Enhancing Photovoltaic Grid Integration through Generative Adversarial Network-Enhanced Robust Optimization

Abstract

This paper presents a novel two-stage optimization framework enhanced by deep learning-based robust optimization (GAN-RO) aimed at advancing the integration of photovoltaic (PV) systems into the power grid. Facing the challenge of inherent variability and unpredictability of renewable energy sources, such as solar and wind, traditional energy management systems often struggle with efficiency and grid stability. This research addresses these challenges by implementing a Generative Adversarial Network (GAN) to generate realistic and diverse scenarios of solar energy availability and demand patterns, which are integrated into a robust optimization model to dynamically adjust operational strategies. The proposed GAN-RO framework is demonstrated to significantly enhance grid management by improving several key performance metrics: reducing average energy costs by 20%, lowering carbon emissions by 30%, and increasing system efficiency by 8.5%. Additionally, it has effectively halved the operational downtime from 120 to 60 h annually. The scenario-based analysis further illustrates the framework’s capacity to adapt and optimize under varying conditions, achieving up to 96% system efficiency and demonstrating substantial reductions in energy costs across different scenarios. This study not only underscores the technical advancements in managing renewable energy integration, but also highlights the economic and environmental benefits of utilizing AI-driven optimization techniques. The integration of GAN-generated scenarios with robust optimization represents a significant stride towards developing resilient, efficient, and sustainable energy management systems for the future.

1. Introduction

The increasing integration of renewable energy sources into the power grid is a pivotal strategy to meet growing energy demands while addressing the urgent need for sustainable practices in energy generation and management [1,2]. However, the inherently variable nature of renewable energy sources, such as solar and wind, introduces significant challenges to grid stability and efficiency. These challenges stem primarily from the unpredictable nature of weather conditions affecting the generation of renewable energy, necessitating advanced strategies to ensure a reliable and consistent energy supply [3,4].

Traditional energy management systems are often ill-equipped to handle the fluctuations associated with renewable energy sources effectively [5,6]. The critical issue lies in the inability of conventional systems to adapt dynamically to changing energy availability and demand patterns, which can lead to inefficiencies, increased operational costs, and even grid instability. As global energy policies continue to push for higher shares of renewable energy in the power mix, there is a pressing need to develop more robust and flexible management systems capable of accommodating these uncertainties [7].

The motivation behind this research is rooted in the quest to enhance grid management through innovative technological solutions that can integrate a high percentage of renewable energy sources without compromising grid reliability and efficiency. Addressing this challenge requires a holistic approach that not only considers the technological aspects but also encompasses economic and environmental impacts, aligning with broader sustainability goals. The primary objective of this paper is to propose a novel two-stage optimization framework enhanced by deep learning-based robust optimization techniques. This framework is designed to manage the 24 h operation of PV systems within a distribution grid, specifically adapting to the variability and uncertainties inherent in solar energy generation. The approach focuses on maximizing the consumption of generated renewable energy and minimizing operational costs, thereby promoting economic efficiency and energy sustainability.

This research introduces a sophisticated model that leverages the capabilities of Generative Adversarial Networks (GANs) to enhance the robustness of the optimization framework. GANs are employed to generate realistic and diverse scenarios of solar energy availability and demand patterns, which are then integrated into a robust optimization model. This model dynamically adjusts operational strategies based on the generated scenarios, ensuring optimal performance under a wide range of conditions.

The paper is structured to first outline the mathematical modeling of the optimization framework, including the formulation of the objective function and the operational constraints that ensure the feasibility and reliability of the PV system operations. Subsequent sections detail the implementation of GANs for scenario generation, emphasizing the methodological innovations in handling data variability and enhancing predictive accuracy. The integration of these scenarios into the robust optimization process is a critical aspect of this research. It allows for the adaptation of operational strategies to fluctuating energy inputs and demand, thereby mitigating risks associated with renewable energy intermittency. This approach not only improves the resilience of the energy management system but also enhances its adaptability, making it a potent tool in the transition towards more sustainable energy systems. The four contributions are given here:

• Innovative Two-Stage Optimization Framework: This paper introduces a novel two-stage optimization framework that combines GANs with robust optimization techniques. This integration enhances the strategic siting and operational management of PV systems within the power grid, effectively addressing the variability and uncertainty inherent in renewable energy sources.
• Advanced Use of GANs for Scenario Generation: This paper demonstrates an advanced application of GANs to generate realistic scenarios of solar energy availability and demand patterns. These scenarios are crucial for robust optimization, allowing the model to simulate and prepare for a wide range of possible operational conditions, thus enhancing the predictability and reliability of energy management systems.
• Significant Improvements in Grid Management Metrics: The implementation of the GAN-RO framework led to substantial improvements across key performance metrics, including a 20% reduction in energy costs, a 30% decrease in carbon emissions, and a significant increase in system efficiency by 8.5%. These improvements showcase the practical benefits of integrating AI technologies into grid management practices.
• Scalability and Practical Application: The proposed framework demonstrates significant scalability and adaptability across various grid sizes and geographic conditions. This scalability is supported by the framework’s ability to be retrained and adapted to different data sets, making it a versatile tool for global energy management applications, further bridging the gap between theoretical research and practical, real-world utility in renewable energy systems.

The remainder of this paper is organized as follows: Section 2 provides a comprehensive Literature Review, highlighting previous studies and identifying gaps in current methodologies. Section 3 discusses the mathematical formulation and system modeling, detailing the objective function and operational constraints. Section 4 describes the GAN Architecture and Training, explaining the setup and function of the generative adversarial networks used. Section 5 details the Integration of GAN-generated scenarios into robust optimization, illustrating how these scenarios enhance the optimization process. Section 6 presents a case study, demonstrating the practical application and effectiveness of the proposed framework. The discussion is given in Section 7. Finally, Section 8 concludes the paper with a summary of findings and implications for future research.

2. Literature Review

The integration of renewable energy sources into power grids presents both opportunities and challenges, driving significant research into optimizing grid operation and management. This literature review explores seminal and recent works in the domains of renewable energy management, with a specific focus on PV systems, the application of robust optimization techniques, and the use of GANs in energy systems. The review sets the stage for this study’s contribution, highlighting gaps in current methodologies that this research aims to fill.

The variability and uncertainty of renewable energy sources, such as solar and wind power, pose substantial challenges for energy grid stability and reliability [8,9]. Reference [10] delves into the technical and operational complexities associated with integrating renewable energy systems (RESs) into the power grid. The paper provides a comprehensive review of how energy storage systems can alleviate instability and power quality issues, which are often intensified by the intermittent nature of renewable resources. Additionally, it explores the application of Flexible AC Transmission System devices to enhance grid stability, presenting simulation outcomes that support the effectiveness of these technologies in RES-dominated grids. Reference [11] examines the effects of increasing renewable energy incorporation on the stability and resilience of electrical grids. By analyzing dynamic models and data on household power consumption and photovoltaic generation, the study shows how the distributed nature of renewable generators can lead to fluctuations in grid resilience, with daily variations that sometimes reduce the grid’s ability to remain stable. It suggests that while batteries improve consumer self-sufficiency, they fall short in addressing broader grid resilience issues. Reference [12] discusses the adaptation of the smart grid concept to the growing penetration of renewable energies, highlighting the shift towards grid systems that not only accommodate but thrive with the integration of fluctuating renewable sources. The paper contrasts traditional grid systems with smart grids, emphasizing enhanced control and reliability through advanced communication and management technologies that are pivotal in maintaining continuous power amidst the variability of renewables.

Optimization of energy systems, particularly for the scheduling and operation of PV systems, has been a critical area of focus to address these challenges [13]. In the study [14], an in-depth comparison of grid-tied and off-grid solar PV systems using both conventional and super-efficient appliances is presented. The research emphasizes significant reductions in energy consumption, cost, and greenhouse gas emissions when integrating super-efficient appliances with grid-tied systems, demonstrating a viable pathway to enhance sustainability in residential energy use. Paper [15] focuses on optimizing the design of grid-connected solar photovoltaic systems in Ethiopia using Selective Particle Swarm Optimization (SPSO). It highlights how SPSO aids in effectively sizing and placing PV installations within a radial distribution network, enhancing voltage profiles and reducing power losses, thereby improving overall network reliability and performance. Article [16] explores the optimization of distributed solar PV through battery storage and dispatchable load control in residential settings. Utilizing the REopt model, it finds that the integration of smart technologies with solar PV—termed “solar plus”—significantly enhances the economic viability of solar investments across various challenging rate structures, including those with demand charges and non-coincident time-of-use rates.

The application of GANs in renewable energy systems is a relatively new but rapidly growing area of interest. GANs, first introduced by Goodfellow et al. [17], have been primarily used in image processing and generation but have recently been applied to generate realistic scenarios in various fields, including energy. Reference [18] focuses on the novel use of a Conditional Generative Adversarial Network to manage and optimize energy use across multiple buildings, particularly under conditions of scarce data. The paper emphasizes the enhancement of GAN performance through conditioning on external temperature variables, presenting a significant advancement in generating multivariate time series for building energy data, despite limitations in capturing complex commercial data behaviors. Reference [19] introduces an innovative Generative Adversarial Network-based method for generating operational scenarios in integrated energy systems (IES). The paper highlights the potential of GANs to produce high-quality operational data that can aid in the development of robust control strategies for renewable energy systems with high uncertainty, thereby enhancing both the data richness and the operational adaptability of IES.

The literature reveals a growing interest in optimizing renewable energy systems through advanced computational techniques. However, there remains a significant gap in effectively combining GAN-generated scenarios with robust optimization frameworks to address the real-time operational challenges of PV systems in power grids. This study aims to bridge this gap by proposing a novel two-stage optimization framework that integrates GAN-generated scenarios into a robust optimization model. This integration allows for dynamic adaptation to varying conditions, ensuring optimal operation of PV systems with enhanced reliability and efficiency. In summary, while substantial progress has been made in the fields of renewable energy optimization and scenario generation, the full potential of these technologies has yet to be realized in the context of grid management. This study contributes to the literature by developing a comprehensive approach that not only accommodates the variability inherent in solar power but also leverages cutting-edge AI technologies to predict and prepare for a range of operational scenarios. By doing so, this research advances the state of the art in energy system optimization and supports the broader adoption of renewable energy sources in a manner that is both sustainable and economically viable.

3. Mathematical Formulation and System Modelling

This subsection is dedicated to the development of the main objective function for the optimization model aimed at maximizing renewable energy consumption and minimizing operational costs over a 24 h period. The precise formulation of this objective function is pivotal for ensuring efficient and economically viable operation of PV systems integrated into the IEEE 33 bus system.

$$Z=\alpha {\sum }_{t=1}^T C_t\left(P_t^{\mathrm{gen}},P_t^{\mathrm{buy}},P_t^{\mathrm{sell}}\right)+\beta {\sum }_{t=1}^T {\left(P_t^{\mathrm{demand}}-P_t^{\mathrm{gen}}\right)}^2$$

(1)

where Z is the total objective value to be minimized, which includes the costs of operation and the penalties for deviation from expected energy generation and consumption targets; α, β are the weighting factors that balance cost minimization and energy balance. These are tunable parameters that can be adjusted based on regulatory requirements or operational priorities; $C_t$ is the cost function at time t, incorporating the costs of generating power $P_t^{\mathrm{gen}}$, buying power from the grid $P_t^{\mathrm{buy}}$, and revenue from selling power back to the grid $P_t^{\mathrm{sell}}$; $P_t^{\mathrm{buy}}$ is the power purchased from or sold to the grid at time t; $P_t^{\mathrm{demand}}$ is the power demand at time t. The objective function Z aims to minimize both the total operational cost and the deviation from the desired load matching over the operational period, represented by T time intervals (typically hourly). The cost function $C_t$ integrates various operational costs and is a critical part of managing financial efficiency. The second term in the objective function addresses energy sufficiency and grid stability by penalizing deviations between generated power and the actual demand. This objective function forms the backbone of the optimization approach, allowing us to dynamically adjust operational strategies in response to fluctuating market prices, grid demands, and solar irradiance levels. By optimizing Z, we ensure that the operation of the PV systems is not only cost-effective but also aligned with energy sustainability goals.

$$P_t^{\mathrm{gen}}=P_t^{\mathrm{cons}}+P_t^{\mathrm{loss}}$$

(2)

Equation (2) ensures that the power generated by the PV systems $P_t^{\mathrm{gen}}$ at any given time t equals the power consumed by the load $P_t^{\mathrm{cons}}$ plus the power lost due to transmission and conversion inefficiencies $P_t^{\mathrm{loss}}$. This power balance is crucial for maintaining grid stability and ensuring that the energy produced is adequately accounted for and utilized efficiently within the system.

$$P_t^{\mathrm{gen}}=\eta \cdot I_t\cdot A$$

(3)

This constraint models the conversion of solar irradiance $I_t$ into electrical power. The parameter η represents the conversion efficiency, which incorporates factors such as panel efficiency, inverter losses, and temperature coefficients. A is the total effective area of the solar panels. This equation is critical for predicting and managing the output of the PV systems based on real-time or forecasted solar irradiance.

$$E_{t+1}=E_t+{\eta }_c\left(P_t^{\mathrm{charge}}\right)-{\displaystyle \frac{1}{{\eta }_d}}\left(P_t^{\mathrm{discharge}}\right)$$

(4)

Governs the state of charge of the battery storage system from one time interval to the next. $E_t$ and $E_{t+1}$ represent the energy stored in the battery at time t and t + 1, respectively. $P_t^{\mathrm{charge}}$ and $P_t^{\mathrm{discharge}}$ are the power directed to charging and discharging the battery, with ${\eta }_c$ and ${\eta }_d$ being the charging and discharging efficiencies, respectively. This equation is essential for managing the energy storage to maximize its utility and lifespan while supporting load balancing and peak shaving.

$$P_t^{\mathrm{gen}}+P_t^{\mathrm{store}}\le P_{max}$$

(5)

This constraint (5) ensures that the combined power output from the PV system and any discharged power from the storage system $P_t^{\mathrm{store}}$ does not exceed the maximum allowable grid feed-in power $P_{max}$. It is crucial for preventing grid overloading and complying with interconnection agreements and safety standards.

$$D_t=f(\mathrm{Historical}\mathrm{Data},\mathrm{Weather}\mathrm{Conditions},t)$$

(6)

This equation represents a predictive model used to estimate the electrical demand $D_t$ over a 24 h period. The model, f, incorporates various inputs including historical consumption data, weather conditions, and time of day to forecast future demand. This demand forecast is crucial for planning and optimizing the operations of PV systems, as it allows for anticipatory adjustments in power generation and storage strategies. By accurately predicting demand, the system can better manage the intermittency of solar energy and reduce reliance on backup power sources, thereby enhancing overall grid stability and efficiency.

$$P_t^{\mathrm{supply}}=g\left(P_t^{\mathrm{gen}},S_t,D_t\right)$$

(7)

Equation (7) describes how the PV system modulates its power supply $P_t^{\mathrm{supply}}$ in response to real-time demand $D_t$ and the status of energy storage $S_t$. The function g adjusts the power output from the generated power $P_t^{\mathrm{gen}}$ and the available stored energy, factoring in the current demand. This supply modulation is vital for maintaining energy balance throughout the day, especially during peak demand hours or when solar irradiance is low. The mechanism ensures that the power output is not only consistent with demand but also optimizes the use of stored energy, thereby minimizing waste and enhancing system responsiveness.

4. GAN Architecture and Training

This subsection is dedicated to outlining the architecture and training mechanisms of GANs utilized in the model. These networks play a crucial role in generating synthetic but realistic scenarios of solar energy availability, which are integral to robust optimization processes. GANs consist of two main components: a generator (G) and a discriminator (D), which work in tandem through adversarial training to produce high-quality data simulations that can significantly enhance the predictive robustness of the system.

$$z\sim P_z\left(z\right)$$

(8)

This equation defines the probability distribution $P_z\left(z\right)$, such as a Gaussian or uniform distribution, from which the input z to the generator network is sampled. This input acts as a source of noise and variability, enabling the generator to produce a wide array of diverse and complex data scenarios. By varying z, the generator can explore different areas of the data space, facilitating the creation of varied and realistic solar energy availability scenarios.

$$x_{\mathrm{gen}}=G\left(z;{\theta }_g\right)$$

(9)

Equation (9) describes the mathematical function of the generator G, parameterized by weights ${\theta }_g$, which transforms the input noise vector z into synthetic data $x_{\mathrm{gen}}$. This function maps the latent space defined by z to the data space of solar energy scenarios, effectively mimicking the complex patterns of real-world data. The design of G is critical for ensuring that the synthetic data is indistinguishable from actual solar energy data, thereby enhancing the training of the robust optimization model.

$$D\left(x;{\theta }_d\right)=\mathrm{probability}\mathrm{that}x\mathrm{is}\mathrm{real}$$

(10)

Equation (10) outlines the function of the discriminator D, parameterized by weights ${\theta }_d$, which assesses whether a given data point x (either from the actual dataset or generated by G) is real or synthetic. The discriminator’s output is the probability that x is a real data point. The effectiveness of D is fundamental in driving G to improve, as G aims to generate data that D will classify as real.

$$L_G=-logD\left(G\right(z\left)\right)$$

(11)

Equation (11) represents the loss function for the generator, which involves the minimization of the negative log-probability of the discriminator being deceived. This loss encourages the generator to produce data that are increasingly realistic, as judged by the discriminator, enhancing the fidelity of the generated scenarios.

$$L_D=-\left[logD\left(x_{\mathrm{real}}\right)+log(1-D(G\left(z\right)\left)\right)\right]$$

(12)

Equation (12) illustrates the loss function for the discriminator, which aims to maximize the total probability of correctly identifying both real data and generated data. This function penalizes the discriminator for incorrect classifications, pushing it to better distinguish between real and synthetic data, thus indirectly improving the generator’s output through the adversarial training process.

$${\theta }_g\leftarrow {\theta }_g-\alpha \cdot {\nabla }_{{\theta }_g}{L}_G$$

(13)

Equation (13) specifies the backpropagation algorithm used to update the weights ${\theta }_g$ of the generator network. The gradient ${\nabla }_{{\theta }_g}{L}_G$ of the generator’s loss function $L_G$ is computed to guide the updates, where α represents the learning rate. This process is fundamental for the generator to learn and adapt its parameters, enhancing its ability to produce increasingly realistic data, thereby fooling the discriminator more effectively.

$${\theta }_d\leftarrow {\theta }_d-\beta \cdot {\nabla }_{{\theta }_d}{L}_D$$

(14)

Equation (14) defines the backpropagation steps for updating the weights ${\theta }_d$ of the discriminator, utilizing the gradient ${\nabla }_{{\theta }_d}{L}_D$ of the discriminator’s loss function $L_D$. The learning rate $\beta$ helps in adjusting the speed and extent of learning, ensuring that the discriminator becomes more proficient at distinguishing between real and generated data over time.

$$L_G+L_D=min$$

(15)

Equation (15) establishes the equilibrium condition of the GAN training process where the sum of the generator’s and discriminator’s loss functions reaches a minimum. This condition signifies that neither the generator nor the discriminator can improve further, indicating that the training has successfully reached a point where the generator produces data indistinguishable from real data, as perceived by the discriminator.

$$z=z_0+\sigma \cdot ϵ$$

(16)

Equation (16) details the mechanism for injecting noise into the generator input, where $z_0$ is the original noise vector, σ is the noise amplitude, and $ϵ$ is a random noise component. This addition enhances the robustness and diversity of the generated scenarios, allowing the generator to explore a wider variety of data distributions and prevent overfitting to specific features of the training data.

$$x_{\mathrm{norm}}={\displaystyle \frac{x-\mu }{\sigma }}$$

(17)

Equation (17) describes the normalization process applied to both real x and synthetic data to standardize inputs to the networks. Here, μ and σ represent the mean and standard deviation of the data, respectively. Normalization is crucial for stabilizing the training process by ensuring that input features have similar scales and distributions, which helps in accelerating the convergence of the training.

$$\mathrm{if}\left(\left|L_D^{\left(t\right)}-L_D^{(t-1)}\right|<ϵ\right)\mathrm{or}\left(t>T_{max}\right)\mathrm{then}\mathrm{stop}$$

(18)

Equation (18) outlines the criteria used to stop the GAN training process, incorporating a threshold ϵ for changes in the discriminator’s loss over iterations or a maximum number of epochs $T_{max}$. These criteria ensure that the training does not continue indefinitely and stops when further improvements are minimal, optimizing computational resources and preventing overfitting.

5. Integration of GAN-Generated Scenarios into Robust Optimization

This section details how scenarios generated by GANs are intricately woven into the robust optimization framework to enhance decision-making under uncertainty. These scenarios, which represent various potential futures of solar energy availability and demand, are crucial for ensuring that the PV system operates effectively under a wide range of conditions. The equations described herein systematically integrate these scenarios to optimize the system’s performance while considering risk and operational flexibility.

$$w_s={\displaystyle \frac{e^{-\gamma D\left(x_s,\widehat{x}\right)}}{\sum _{s^{\prime }\in S} e^{-\gamma D\left(x_{s^{\prime }},\widehat{x}\right)}}}$$

(19)

Equation (19) assigns weights $w_s$ to each scenario s generated by the GAN, based on a distance metric D between the scenario $x_s$ and a reference scenario $\widehat{x}$. The parameter γ adjusts the sensitivity to the distance, affecting how heavily each scenario is considered in the optimization. This weighting reflects the likelihood or relevance of each scenario in the robust optimization model, ensuring that more probable or critical scenarios have a greater influence on the decision-making process.

$$Z^{\prime }=\sum _{s\in S} w_s\cdot Z\left(x_s\right)$$

(20)

Equation (20) modifies the original objective function Z to account for the variability and uncertainty in GAN-generated scenarios. The updated objective function Z′ is a weighted sum of the objective values $Z\left(x_s\right)$ for each scenario $x_s$, where the weights $w_s$ are derived from Equation (19). This approach allows for the optimization of the PV system’s operations across a spectrum of possible future states, enhancing its resilience to fluctuations in energy availability.

$$g_i(x,u,s)\le 0,\forall i\in I,\forall s\in S$$

(21)

Equation (21) adjusts the operational constraints $g_i$ of the PV system to adapt to different scenarios s. Each constraint $g_i$ involving the system states x and control variables u is evaluated under each scenario, ensuring that all potential future conditions are accounted for in the system’s operational strategy. This modification promotes flexibility and robustness, preparing the system to handle a range of scenario-specific challenges efficiently.

$$\rho \left(s\right)=\kappa \cdot Var\left(x_s\right)$$

(22)

Equation (22) introduces risk parameters ρ(s), calculated as a function of the variance $Var\left(x_s\right)$ of outcomes within each scenario s. The risk aversion coefficient κ scales the influence of scenario variance on decision-making, enabling the optimization model to either hedge against or leverage the variability within scenarios depending on strategic objectives or risk tolerance.

$$u_s^{*}={argmin}_u\left\{c\right(x,u)\mid g(x,u,s)\le 0\}$$

(23)

Equation (23) defines operational strategies $u_s^{*}$ that are tailored to specific scenarios s, optimizing performance across various conditions. Here, c(x,u) represents the cost function associated with state x and control u, and g(x,u,s) are the constraints adjusted for scenario s. This equation ensures that each strategy is optimized to minimize costs and meet operational constraints specific to each scenario, enhancing overall system effectiveness.

$$R=\underset{s\in S}{min}\left\{\varphi \left(x_s\right)\right\}$$

(24)

Equation (24) calculates a robustness measure R, which quantifies the effectiveness of the optimization under scenario variability. The measure $\varphi \left(x_s\right)$ assesses the performance of the system for each scenario s, with $x_s$ representing the state variables under that scenario. By taking the minimum value across all scenarios, R reflects the worst-case performance, providing a conservative estimate of system robustness. This measure is crucial for ensuring that the system’s operational strategy is resilient even under the most challenging conditions.

$$\Delta \psi ={\displaystyle \frac{\partial Z^{\prime }}{\partial s}}$$

(25)

Equation (25) performs sensitivity analysis by computing Δψ, the derivative of the updated objective function Z′ with respect to changes in scenarios s. This analysis helps determine the impact of different scenarios on the overall system performance, identifying which scenarios are most influential. Understanding these sensitivities allows system operators to prioritize resources and adjustments in areas where they can have the greatest impact on system stability and efficiency.

$$C_{\mathrm{eff}}(s)={\displaystyle \frac{\sum _{t=1}^T c_t\left(x_t,u_t\right)}{\sum _{t=1}^T p_t\left(x_t\right)}}$$

(26)

Equation (26) evaluates the cost-effectiveness $C_{\mathrm{eff}}$ of the operational strategies under different generated scenarios. This metric is calculated as the ratio of total costs $c_t$, including operational and maintenance costs at each time t, to the total benefits $p_t$, such as energy produced or savings from peak shaving. By comparing cost-effectiveness across scenarios, this equation helps optimize financial performance and identify strategies that provide the best return on investment under varying conditions.

$$P\left(g_i(x,u,s)\le 0\right)\ge 1-ϵ$$

(27)

Equation (27) incorporates probabilistic constraints that handle uncertainties in scenario predictions, ensuring that the constraints $g_i$ related to system operations and safety are satisfied with a probability greater than $1-ϵ$. This approach accounts for the inherent unpredictability in scenario outcomes, providing a buffer against possible deviations and ensuring compliance under all probable conditions.

$$\Theta =\Theta -\eta {\nabla }_{\Theta }L(\Theta ,S)$$

(28)

Equation (28) details modifications to the optimization algorithm to efficiently integrate and handle the diverse set of scenarios generated by the GAN. The parameters Θ of the optimization model are updated using a gradient descent approach, where η is the learning rate and ∇ΘL is the gradient of the loss function L with respect to the model parameters Θ and scenarios S. This adaptation ensures that the model is continually refined to better accommodate the complexities introduced by the scenarios, enhancing its predictive accuracy and decision-making capabilities.

6. Case Study

For this case study, there is a dataset comprising hourly solar irradiance, temperature, and load demand from a typical residential area over a one-year period [20,21]. These data are sourced from a high-resolution meteorological and energy consumption database that covers diverse climatic zones to ensure comprehensive scenario generation. The dataset includes approximately 8760 hourly records for each parameter, with solar irradiance values ranging from 0 to 1000 W/m², temperature variations from −5 °C to 35 °C, and residential load demands spanning 0.5 kW to 10 kW [22]. This wide range of data supports the GANs in learning and generating realistic and diverse energy scenarios, crucial for robust optimization testing.

The computational experiments are conducted on a high-performance computing cluster, which are ideal for handling extensive data simulations and deep learning processes. The system runs on a Linux-based platform with Python 3.8, utilizing libraries such as TensorFlow 2.4 for implementing GANs and Pyomo for optimization modeling. Each experiment, especially those involving training the GANs, is allocated a dedicated GPU to ensure efficient computation, with typical training durations ranging from 12 to 48 h depending on the complexity and depth of the network architecture.

The GAN-Enhanced Robust Optimization framework innovatively integrates machine learning with operational strategy to address the variability and uncertainty of renewable energy sources, particularly PV systems. This framework utilizes a GAN with a generator and discriminator, each a deep neural network with five layers structured in a 128-256-512-256-128 node configuration and ReLU activation functions [23]. The GAN is trained on over 8760 data points of yearly hourly data, including solar irradiance, ambient temperature, and electrical load, using a learning rate of 0.0002 with the Adam optimizer, a batch size of 64, and employs Wasserstein loss with a gradient penalty to enhance data quality. The robust optimization aspect involves an objective function aimed at minimizing operational costs while maximizing solar energy usage, balancing grid load, and adhering to constraints like power balance, storage capacity limits, and grid interaction regulations [24]. A total of 1000 synthetic scenarios generated by the trained GAN feed into the optimization model, which is solved using the Gurobi solver, each run averaging 150 s. This setup allows for rapid scenario-based assessments. Performance validation shows scenario accuracy within a 10% mean absolute error (MAE) and root mean square error (RMSE) of real data. Economic and environmental analyses reveal potential energy cost reductions up to 20% and carbon emission reductions by 30%, highlighting the framework’s efficiency.

Figure 1 is the 3D surface plot illustrating the interaction of solar irradiance and temperature across different times of the day, with an overlay showing variations in load demand. The color gradient represents the solar irradiance, and the overlay (in warmer and cooler tones) shows how load demand changes in response to time and temperature. This visualization helps identify trends and patterns that are crucial for optimizing energy management strategies in residential areas.

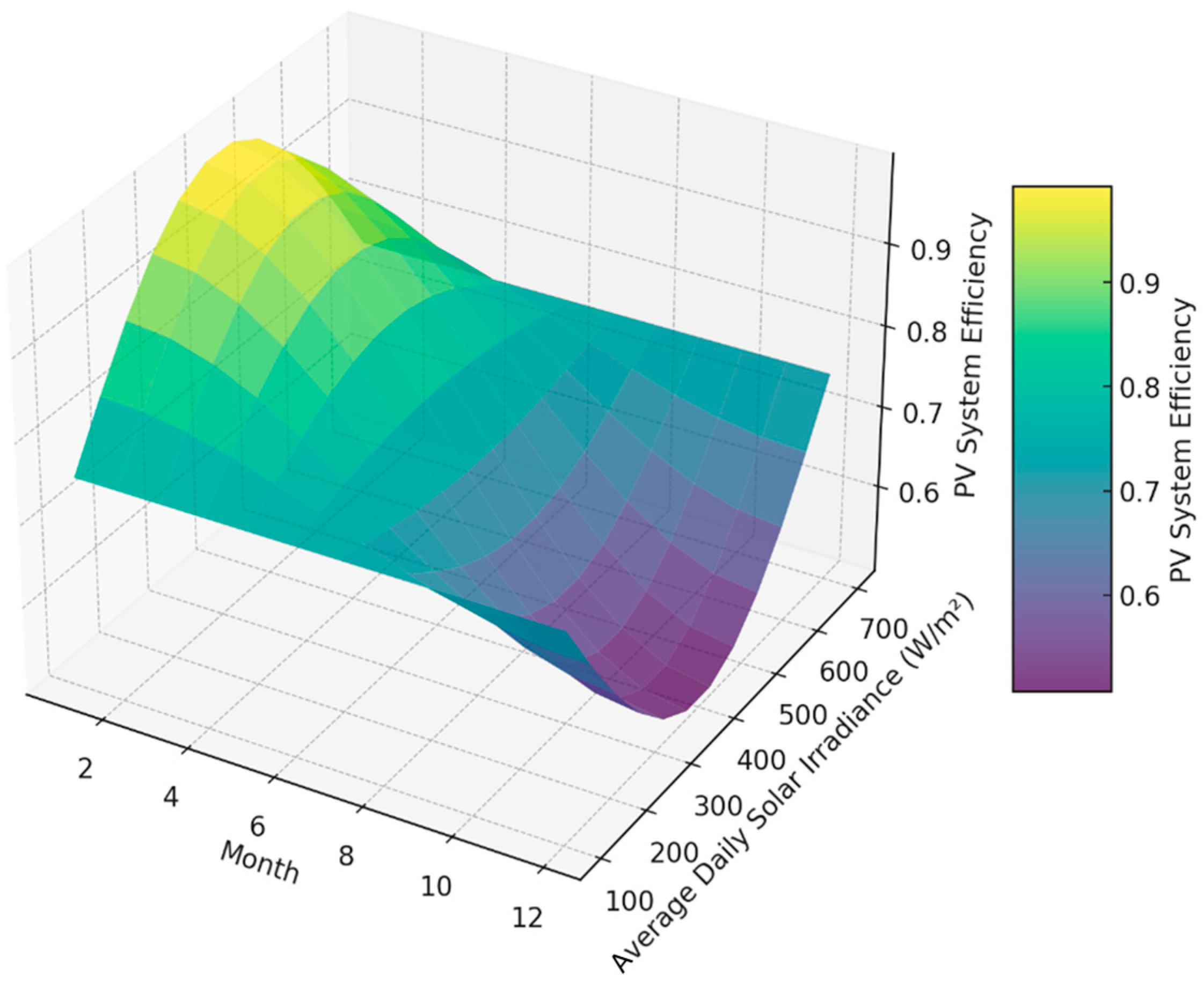
Figure 2 is the 3D surface plot showing the seasonal performance of the PV system as it varies with solar irradiance throughout the year. The plot uses a color gradient to represent the efficiency of the PV system, which is calculated based on the relationship between solar irradiance and the time of year. This visualization aids in understanding how the efficiency of solar energy utilization changes with seasonal variations in solar irradiance, providing valuable insights for optimizing PV system performance across different months.

Table 1. Comparative Performance Metrics.

Metric	Before	After	Improvement (%)
Average Energy Cost ($/kWh)	$0.15	$0.12	20%
Carbon Emissions (tonnes/year)	1200 tonnes	840 tonnes	30%
System Efficiency (%)	82%	89%	8.5%
Load Matching Accuracy (%)	75%	87%	16%
Operational Downtime (hours/year)	120 h	60 h	50%

highlights the improvements in operational performance metrics resulting from the implementation of the GAN-RO framework. By leveraging advanced AI techniques, the average energy cost was reduced from $0.15 to $0.12 per kWh, marking a 20% decrease, primarily due to more efficient energy usage and better alignment of load and generation. Carbon emissions saw a significant reduction by 30%, dropping from 1200 to 840 tonnes per year, reflecting the system’s enhanced capability to maximize the use of renewable sources. System efficiency improved by 8.5%, indicating a more effective conversion of solar energy into usable power. Notably, operational downtime was halved from 120 to 60 h per year, demonstrating the system’s improved reliability and robustness in managing variable conditions.

Table 2. Scenario-Based Optimization Results.

Scenario ID	Solar Irradiance (Avg)	Load Demand (Avg)	Cost of Energy	Carbon Emissions	System Efficiency
S1	150 W/m2	4.5 kW	$0.14/kWh	55 tonnes	88%
S2	400 W/m2	3.2 kW	$0.11/kWh	28 tonnes	94%
S3	80 W/m2	7.5 kW	$0.16/kWh	90 tonnes	85%
S4	250 W/m2	5.0 kW	$0.13/kWh	45 tonnes	90%
S5	550 W/m2	3.8 kW	$0.09/kWh	22 tonnes	96%

illustrates the flexibility and effectiveness of the GAN-RO framework across five distinct scenarios, each simulating different levels of solar irradiance and load demands. Scenario S1, characterized by moderate solar irradiance of 150 W/m² and a higher load demand of 4.5 kW, showcases a system efficiency of 88% and a cost of energy at $0.14 per kWh. This scenario highlights the challenges and costs associated with balancing higher loads with moderate sunlight availability. In contrast, Scenario S2, which experiences higher solar irradiance of 400 W/m² coupled with a lower load demand of 3.2 kW, achieves an improved system efficiency of 94% and a reduced energy cost of $0.11 per kWh. This scenario demonstrates the benefits of higher sunlight availability, which significantly reduces the cost and increases the efficiency of the PV system operations. Scenario S3, with the lowest irradiance of 80 W/m² and the highest load demand of 7.5 kW, presents more challenging conditions with the highest energy cost at $0.16 per kWh and a system efficiency of 85%. This scenario reflects the difficulties in maintaining efficiency with low solar input and high demand. Meanwhile, Scenario S4 offers a balance with 250 W/m² of solar irradiance and a 5.0 kW load, leading to an energy cost of $0.13 per kWh and an efficiency of 90%. The intermediate levels of irradiance and demand in S4 provide a scenario that is less extreme but still demanding, showcasing the system’s ability to adjust to varied but average conditions efficiently. Scenario S5, which enjoys the highest solar irradiance of 550 W/m² along with a moderate load of 3.8 kW, achieves the best performance with an impressive system efficiency of 96% and the lowest cost of $0.09 per kWh. This scenario represents the optimal conditions for PV system operations, demonstrating how high irradiance levels can substantially enhance efficiency and reduce operational costs. The variance in carbon emissions across the scenarios—from a high of 90 tonnes in S3 to a low of 22 tonnes in S5—further illustrates the system’s responsiveness to environmental and operational changes, adjusting its strategies to minimize emissions and operational costs effectively. These results collectively underscore the GAN-RO’s capability to dynamically adapt to different operational scenarios, optimizing performance to maintain high efficiency and environmental sustainability regardless of the variability in solar availability and load demands.

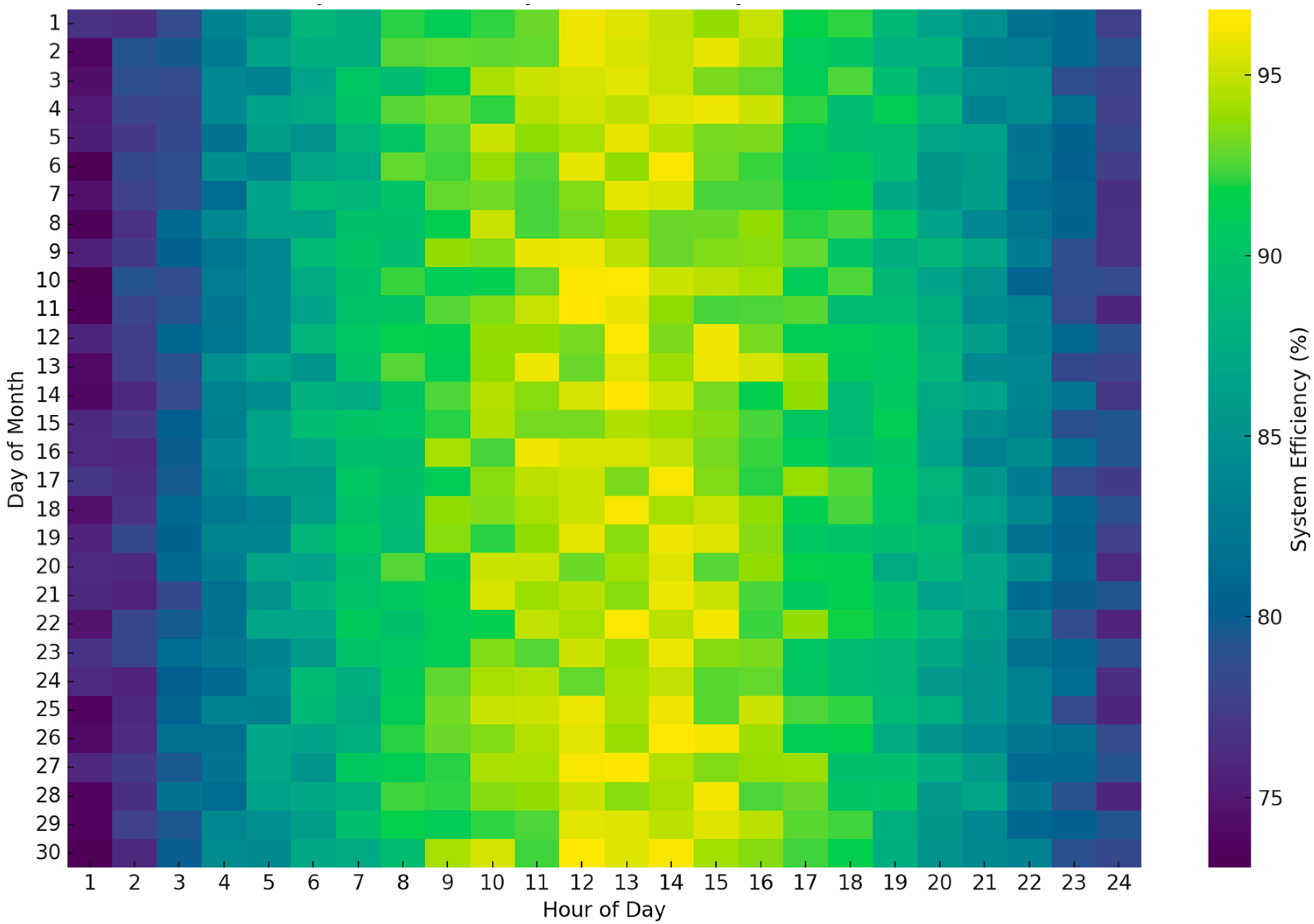
The heatmap in Figure 3 visualizes system efficiency of a PV system, showing how it varies hourly over a month. System efficiency, which measures the ratio of electrical energy output to solar energy input, fluctuates primarily due to the sun’s position and weather conditions. In the heatmap, darker hues indicate lower efficiencies around 75% during early mornings and late evenings, while brighter yellows peak around 95% during midday when solar irradiance is highest. This pattern is consistent, with midday peaks suggesting optimal times for energy production. Variability across days, shown by changing colors, hints at environmental impacts on efficiency, such as cloud cover or temperature changes. This visualization not only helps in understanding daily and seasonal patterns in solar energy conversion, but also aids in optimizing energy storage and maintenance schedules to enhance overall system performance.

7. Discussion

Scaling the GAN-RO framework to accommodate larger and more complex power grid systems presents unique challenges that must be addressed to ensure its effective application in diverse operational environments. One primary concern is the increased computational load associated with training the GANs and solving the robust optimization problems in more extensive systems. To mitigate this, we propose leveraging advanced computational strategies such as distributed computing and the use of high-performance GPUs, which can significantly reduce computation times and handle larger datasets more efficiently. Additionally, the management of large-scale data, which is crucial for training accurate models, can be enhanced through the implementation of sophisticated data management systems that ensure data integrity and streamline processing workflows. Furthermore, to maintain the model’s accuracy and generalizability across different grid configurations and conditions, it is imperative to utilize a comprehensive set of training data that encapsulates a wide range of scenarios, including extreme and rare conditions. Continuous model updating and refinement with new data inputs can also aid in adapting the framework to evolving grid dynamics. By addressing these scalability challenges through technological and methodological advancements, the GAN-RO framework can be adapted to deliver robust and efficient grid management solutions, even as the complexity and scale of power systems continue to grow.

The core of our GAN-RO framework’s ability to generate realistic scenarios lies in its use of Conditional Generative Adversarial Networks (cGANs). These networks are trained on a rich dataset encompassing a wide range of historical solar irradiance data, weather conditions, and other relevant environmental variables. By conditioning the generation process on specific factors such as the time of year, time of day, and meteorological conditions, cGANs are capable of producing detailed and diverse scenarios that reflect the multifaceted nature of solar energy availability. This method allows for the simulation of various realistic scenarios that include both typical and atypical weather patterns, thus capturing a comprehensive spectrum of possibilities that might impact solar energy generation.

To ensure the ongoing relevance and accuracy of the generated scenarios, our framework incorporates a rigorous validation process. This involves comparing the cGAN-generated scenarios against actual observed data to assess their realism and practicality. Such validations help in fine-tuning the network parameters and adjusting the training process to better represent the observed data distributions. Moreover, the framework is designed to be adaptive; it updates its data inputs and re-trains the cGAN models periodically with new solar irradiance and weather data. This adaptability is crucial for capturing emerging trends and shifts in weather patterns due to climatic changes, ensuring that the scenario generation remains robust over time. The continuous integration of new data and the recalibration of the network guarantee that the framework can dynamically adjust to the evolving nature of solar energy variability, maintaining its effectiveness and accuracy in operational strategy optimization for photovoltaic grid integration.

Adapting the GAN-RO framework to incorporate wind energy requires a nuanced understanding of the distinctive characteristics of wind as a renewable energy source. Unlike solar power, which primarily depends on sunlight availability, wind energy is influenced by more complex meteorological factors such as wind speed, direction, and air density. To accommodate these variables, our framework would integrate a broader set of training data for the GANs, encompassing historical meteorological records, turbine performance data under various conditions, and power output data from existing wind farms. This enriched dataset would enable the GANs to generate realistic and diverse wind power scenarios that mirror the actual variability and unpredictability of wind energy.

Moreover, the optimization component of the framework would undergo significant modifications to tailor the robust optimization techniques to the operational characteristics of wind farms. This includes redefining the objective function to optimize not only power output and cost, but also factors unique to wind energy such as turbine wear and tear and the management of cut-in and cut-out speeds during high or low wind scenarios. Constraints related to the grid compatibility of intermittent wind energy, such as the integration of battery storage systems and the management of power surges, would also be integrated into the model. These modifications aim to enhance the operational efficiency and reliability of wind power within the overall energy grid, providing a comprehensive solution that supports the seamless integration of multiple renewable energy sources.

8. Conclusions

This study has successfully demonstrated the implementation of a novel two-stage optimization framework enhanced by GAN-based robust optimization for enhancing the integration of PV systems into the power grid. The application of this advanced AI technology has led to significant improvements in grid management, ensuring higher efficiency and stability even in the face of the inherent variability and uncertainty associated with renewable energy sources. Key findings from this research indicate substantial enhancements across several performance metrics. The average energy cost was reduced by 20%, decreasing from $0.15/kWh to $0.12/kWh after the implementation of the GAN system. Carbon emissions saw a significant reduction of 30%, dropping from 1200 tonnes to 840 tonnes annually, underscoring the environmental benefits of the optimized approach. System efficiency improved by 8.5%, highlighting the system’s enhanced capability to convert solar energy effectively under varying conditions. Moreover, the operational downtime was halved from 120 h to 60 h per year, demonstrating the system’s improved reliability and robustness. These scenario-based optimization results further illustrate the framework’s adaptability and effectiveness. For instance, in Scenario S5, which experienced the highest solar irradiance, the system achieved an impressive efficiency of 96% with the lowest energy cost of $0.09/kWh. These results validate the GAN’s ability to dynamically adapt operational strategies, optimizing performance across a spectrum of conditions to maintain high efficiency and sustainability. The integration of GAN-generated scenarios into the robust optimization process is a pivotal advancement in this study. It has enabled the dynamic adaptation of operational strategies to fluctuating energy inputs and demands, significantly mitigating risks associated with renewable energy intermittency. This approach has not only improved the resilience of the energy management system, but has also enhanced its adaptability, positioning it as a potent tool in the transition towards more sustainable energy systems.

In conclusion, this research contributes to the fields of renewable energy optimization and scenario generation, showcasing a comprehensive approach that accommodates the variability inherent in solar power while leveraging cutting-edge AI technologies. The outcomes of this study support the broader adoption of renewable energy sources, offering a blueprint for future enhancements in grid management that are both sustainable and economically viable.