Abstract
The prevailing approach to the wind resistance design of transmission towers is rooted in the quasi-static method. However, this methodology faces criticism for neglecting tower-line coupling dynamics. Despite efforts to boost structural wind resilience, the research on tower failure mechanisms, especially under extreme winds considering tower-line coupling, is limited. To address this gap, the wind-induced dynamic failure modes of the transmission tower-line system are investigated in this paper. The consistent discrete random flow generation method is employed to simulate the fluctuating wind field for transmission lines. Incorporating the compressive buckling mode of angle steel, the plastic hinge model of the frame element is employed to simulate mechanical nonlinearity. A typical transmission tower-line system is concerned, with a finite element model established for a three-tower, four-line coupled configuration. The findings reveal that the wind-induced collapse of the transmission tower is directly triggered by the buckling failure of the compressed main members, with the vulnerable section located beneath the lower cross-arm. The transmission tower experiences bidirectional bending and compression instability under an unfavorable wind direction. In contrast, the traditional pushover collapse modes of the transmission tower cannot fully capture the characteristics of the collapse failure, mainly due to the ignorance of the transverse wind force action induced by the coupling effect. This research underscores the importance of incorporating lateral dynamic considerations into transmission tower designs and advocates for optimizing strategies to mitigate wind-induced collapse modes.
1. Introduction
Amidst the global push to reduce carbon emissions, the world’s energy structure is undergoing a transformation and upgrade. The power transmission system plays a crucial role, which is shifting from traditional centralized transmission systems to decentralized transmission systems enabled by renewable energy. As a high-voltage power transmission channel, the transmission line shoulders a significant historical mission. Building a robust transmission network and continuously enhancing disaster prevention and resilience are of utmost importance for sustainable development. In recent years, the frequent passage of typhoons in coastal areas and the frequent occurrence of severe convective weather in inland areas have significantly increased the vulnerability of infrastructure to strong wind disasters. Globally, transmission lines are exposed to severe wind hazards [1], with more than 80% of transmission line failures attributed to extremely strong wind conditions [2]. Current transmission lines are generally designed to withstand wind resistance. With ongoing research on the wind resistance of transmission lines, relevant design specifications are correspondingly being updated. However, accidents caused by wind-induced damage to transmission towers continue to occur.
Figure 1 depicts a crashed transmission tower in Guangdong Province, China, resulting from Typhoon Mujigae in 2015. The devastating storm, with a maximum wind speed of 50 m/s (Category 15 severe typhoon), underscores the challenges faced by transmission structures under extreme weather conditions. As shown in Figure 1, the primary damaged area of the tower is located in the middle and lower parts of the tower body, concentrated in the region below the lowest cross-arm, where buckling failures occurred in the main members and some diagonal members. Moreover, the damage to the upper part of the tower body is speculated to be primarily due to the bending failure of structural members caused by the impact of the collapsing tower hitting the ground. The tower legs, feet, and foundation connections remained largely undisplaced. The investigations could intuitively judge that the collapse was triggered by the integral instability of the tower under the strong wind.

Figure 1.
A typical case of wind-induced collapse of a transmission tower.
A transmission tower-line system exhibits characteristics of high flexibility. Under strong wind loads, the vibration response shows significant randomness and geometric nonlinearity. In extreme weather scenarios, a transmission tower may enter an elastic–plastic working state, which can result in structural dynamic instability and eventual collapse. Due to the combined effects of geometric and material nonlinearity, the study of the wind-induced collapse mechanisms of transmission tower-line systems has become a challenging problem in the field of structural wind resistance.
Rao et al. [3,4] and Shukla and Selvaraj [5] conducted pushover failure tests on angle steel transmission towers and discovered that the arrangement of diagonal members and other redundant components significantly affect the structural load-bearing capacity. Structural design codes may overestimate the buckling capacity of diagonal members, leading to a collapse before the structure reaches its expected ultimate bearing capacity. Tian et al. [6] and Fu et al. [7] conducted pushover tests on transmission towers under conditions such as broken wires, icing, and wind and discovered that structural failure originates from the buckling of main members. Xie et al. [8,9] conducted static loading failure tests on full-scale models of tower sections and reported that diagonal members are relatively weak and prone to buckling and proposed effective reinforcement measures. In the design, diagonal members are mainly used to reduce the calculated length of the main members and ensure the full utilization of their bearing capacity. However, full-scale tower pushover tests and actual structural collapse failure characteristics often do not follow this pattern, as the buckling of both diagonal and main members can potentially trigger overall structural failure. Full-scale tower pushover failure tests are the most direct means of revealing collapse evolution mechanisms, but they can only be simulated using pseudo-static loading methods. It is extremely challenging to develop effective dynamic loading methods that simulate extreme wind conditions.
Transmission towers are typical spatial truss structures that can be modeled using bar or frame elements for a nonlinear numerical simulation analysis of the structural collapse process. Based on classical beam–column elements, Eslamlou et al. [10], Gao et al. [11], and Zhang et al. [12] conducted nonlinear dynamic analyses of transmission towers by removing failed members to study the continuous collapse process of tower structures and the development of internal force redistribution. Wang et al. [13] adopted a multiscale simulation method that combines beam–column elements and shell elements. Shell elements were utilized to simulate target members or connection nodes, allowing for a more precise analysis of the overall structure. However, this approach also imposes greater demands on the coupling constraint technology among different elements, which significantly increases the complexity of the analysis. To comprehensively consider computational efficiency and accuracy, Tian et al. [6] and Zhang et al. [14] modified the steel constitutive relation by incorporating member stability coefficients to address the influence of member buckling on the ultimate bearing capacity of a structure. Li et al. [15] analyzed the failure modes of a typical 220 kV transmission tower through nonlinear static and dynamic methods, and they found that the collapse of the tower under strong wind loads was usually due to the large deformation caused by the elastic–plastic buckling of leg members. Zhu et al. [16] evaluated the fragility of transmission towers, incorporating the inherent uncertainty associated with wind-resistance capacity and the stochastic nature of wind load effects. Their findings indicate that a preponderance of initial buckling events is concentrated proximally to the initial section of the transmission towers; on the other hand, although the instability of diagonal members did not result in the immediate collapse of the tower structure, it would substantially diminish the stability of the primary structural members. Under strong winds, most standard transmission towers display structural vulnerabilities and modes of failure caused by wind, leading to poor resistance to sustained collapse. Current research on the wind-induced collapse mechanisms of transmission tower-line systems still fails to meet the requirements of practical structural engineering.
In transmission lines, transmission towers support the lines, while the lines connect individual towers to form a continuous system. The contribution of wind load effects on the lines to the structural responses (such as the axial force of main members, displacement of tower top, and so on) of the supporting tower can be more than 30~70% under strong winds [17,18]. Zhang et al. [19] conducted a wind-induced vibration analysis of a 500kV high-voltage transmission tower-line system through a comparison of finite element simulation and field measurements. It reveals that the coupling effect between the towers and lines under strong winds might result in the risk of structural premature failure. Liang et al. [18] and Chen et al. [20] conducted destructive wind tunnel test studies on the power transmission towers and compared them with the actual collapse cases. They found that coupling resonance occurs between the transmission tower and line, and the large vibration of the transmission line drives the large vibration of the transmission tower. The coupling between the transmission tower and lines, beyond altering the natural frequency and damping, also manifests as load transfer. Although an accumulating body of research paid attention to the coupling effect of the tower-line system, there is still a lack of effective quantification of the coupling effects on the collapse mechanism of transmission towers under severe wind conditions. Therefore, accurate simulation of the wind field and loading on the transmission lines is crucial for evaluating the wind-induced dynamic response of transmission line structures. Additionally, the tower-line coupling effect exacerbates the impact of conductors on the wind resistance of transmission towers.
This paper focuses on a typical transmission tower-line system and conducts a nonlinear dynamic analysis of the wind-induced collapse of transmission towers. The analysis takes into account the spatial wind field along the transmission line and the mechanical nonlinearity of the angle steel components. Under unfavorable wind direction conditions, this study explores the failure modes of transmission towers due to a wind-induced collapse. This paper further discusses the dynamic collapse failure mechanism that transmission towers should withstand under extreme wind loads. This research provides valuable information for the future structural optimization design of transmission towers. The rest is organized as follows. Section 2 establishes the finite element model of the coupling transmission tower-line system using SAP2000 software (version 22). Section 3 simulates the wind field, accounting for the extensive spatial scale of the lines, and determines the resulting wind load on the transmission tower-line system. Section 4 delves into structural nonlinear dynamic analysis, investigating the collapse mechanism of the transmission tower under intense wind conditions. Finally, conclusions and prospects are drawn in Section 5.
2. Finite Element Model of the Transmission Tower-Line
2.1. Investigation Description
This paper focuses on a transmission tower similar to the crashed one shown in Figure 1, which served in a 220 kV transmission line in China. The location of the transmission tower is classified as the B-type open-country terrain defined in the Chinese design code (GB 50009-2012) [21]. It is with a design wind speed of 37 m/s at 10 m height, an annual average temperature of 25 °C, and an average altitude of 25 m. In addition, the target transmission tower has been described in previous research [22]. As shown in Figure 2, the transmission tower has a height of 42.5 m. The primary structural bars of the tower legs, tower body, and cross arms are all made of Q345 equilateral angle steel, whereas the diagonal and auxiliary structural bars are made of Q235 equilateral angle steel. “L125 × 10” denotes the type of equilateral angle steel with side length 125 mm and thickness 10 mm, and the geometric dimensions of other types can be similarly derived. The mechanical parameters of the steel are shown in Table 1, in which σy is yield stress, E is the elastic modulus, ρ is the material density, and µ is the Poisson’s ratio.
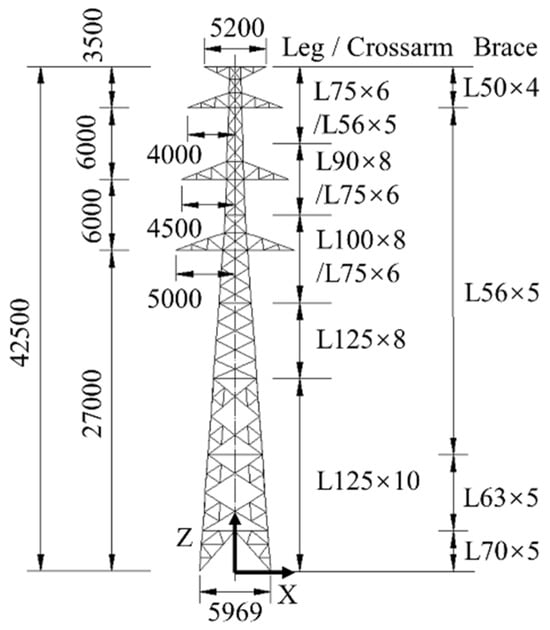
Figure 2.
Transmission tower structure (unit: mm).

Table 1.
Mechanical parameters of steel.
The tower supports a total of four layers of transmission lines. The uppermost layer is the ground wire, which is connected to the tower head cross-arm, and the next three layers are conductors. These conductors are connected to their respective cross-arms through suspension insulator strings. The ground wire is an OPGW optical cable, and the conductor is a double-split LGJX-300/40. The insulator string adopts a suspension I-type CA-874EY. Their physical parameters are listed in Table 2.

Table 2.
Physical parameters of wire.
2.2. Finite Element Model of a Transmission Tower
Based on the SAP2000 software (version 22), the structural model of the transmission tower is established in this paper, as illustrated in Figure 3. The angle steel members are simulated using L-shaped cross-section frame elements, and rigid connections are adopted between adjacent members and between the tower legs and the foundation. The direction of the L-shaped element cross-section is adjusted to align with the actual member conditions. Considering the influence of gusset plates and bolt masses, the material density is set as ρ0 = c0 × ρ, where c0 = 1.21 in this study. The origin of the coordinates is located at the geometric center of the tower foundation. The X-axis is parallel to the front of the cross-arm, the Y-axis is perpendicular to the front of the cross-arm, and the Z-axis is along the height direction of the transmission tower.
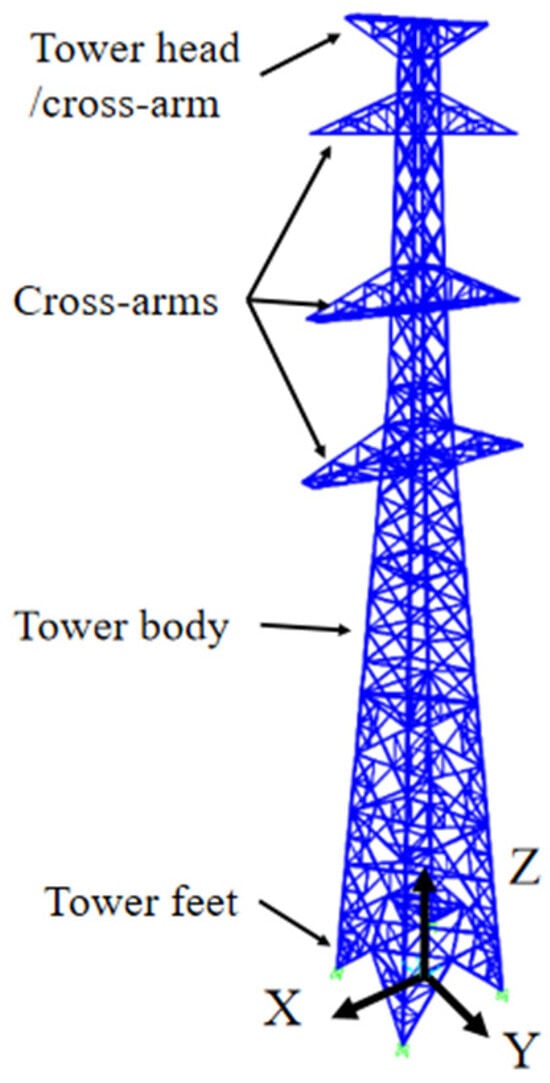
Figure 3.
Finite element model of the transmission tower.
Modal analysis of the single transmission tower model without lines is conducted using SAP2000 software, with its fundamental modal configurations illustrated in Figure 4. The frequencies of the bending modes in the X-direction and Y-direction are 2.013 Hz and 2.023 Hz, respectively, while the frequency of the torsional mode around the Z-axis is 6.678 Hz.
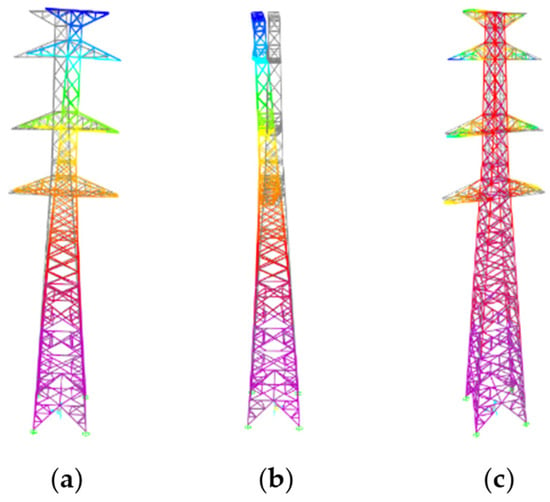
Figure 4.
Mode modes of the single transmission tower. (a) The first-order mode shape in the X-direction; (b) the first-order mode shape in the Y-direction; (c) the torsional mode.
2.3. Finite Element Model of the Transmission Tower-Line System
Based on the SAP2000 software, a structural model of a three-tower, four-line coupling system is established in this work, as depicted in Figure 5. Among them, Towers A, B, and C are of the same type, and Tower B in the middle is designated as the target object. At the end of the side span of the transmission line, a fixed support is used, while the end of the middle span is connected to the suspension points on the cross-arms.
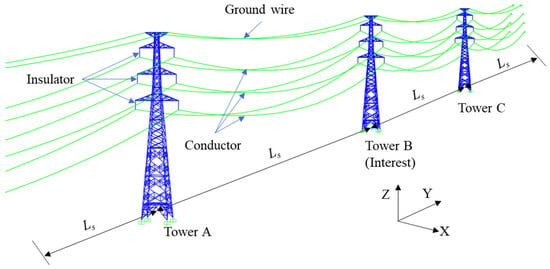
Figure 5.
Transmission tower-line coupling system.
The catenary cable element and shape calculator in the SAP2000 program (version 22) are employed to model the conductors and ground wires. The cable element incorporates the geometric nonlinearity of tensile-rigidification and large displacement effects, allowing for the consideration of both slack and tensioned states of the cables. The cable shape calculator initially assigns an undeformed initial shape to the transmission line based on the catenary equation. Subsequently, a static nonlinear analysis is conducted on the line under the combined effects of self-weight and preset tension to determine its geometric configuration and stiffness in a state of static equilibrium. When constrained by fittings such as spacers, the wind-induced vibration motion of multi-split conductors can generally be regarded as synchronized. In this paper, multi-split conductors are modeled as single suspension cables based on the principle of equal cross-sectional area. Suspension insulator strings serve as the main connecting component between the conductors and the transmission tower. They are mainly exposed to axial forces and can experience considerable swings or rotations during strong winds. In this study, the insulator strings are simulated using frame elements with rotational constraints released at both ends.
The span length Ls of the transmission line is set to 350 m as specified in Table 2. The average operating tension of the transmission line is designed to be 18% of its ultimate tensile strength [23]. Correspondingly, the calculated sags SL at the midspan of the ground wire and the conductor are 5.572 m and 10.242 m, respectively. Each span of the transmission line is discretized into 35 cable elements with equal spacing, resulting in a length of approximately 10 m for each cable element.
The Ritz vector method [24] is appropriate for solving the free vibration and dynamic response analysis of large complex systems. It takes into account the spatial distribution of loads and can ignore modes that do not participate in the dynamic response, such as local vibration modes. Compared with the exact eigenvector method, it is more applicable for seeking modes excited by specific loads. Concerning the large number of elements of the transmission tower-line system and the high flexibility of cable, the Ritz vector method is adopted to conduct modal analysis on the coupling transmission tower-line system model. The initial loading patterns include the structural self-weight, structural accelerations (in the X-, Y-, and Z-directions), and average wind force distribution on the structure. Figure 6 illustrates the primary vibration modes of the transmission tower in the tower-line system.
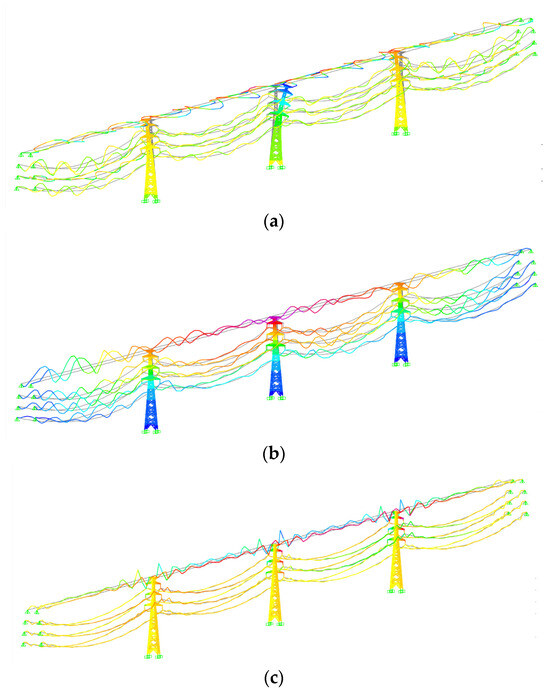
Figure 6.
Typical modes of towers in the transmission tower-line system. (a) Fundamental mode shape in the X-direction; (b) fundamental mode shape in the Y-direction; (c) torsional mode.
The first-order overall bending vibration frequencies of the target transmission tower in the X-direction and Y-direction are 1.729 Hz and 1.811 Hz, respectively. These frequencies are 14.1% and 10.5% lower than those of the single tower without lines hanging on. Additionally, the torsional vibration frequency is 3.680 Hz, which is 44.9% lower than that of the single tower. The results indicate that the tower-line coupling effect has a significant influence on the dynamic characteristics of the transmission tower, reducing the fundamental modal frequencies of the structure. A decrease in the fundamental frequency of the transmission tower can affect the resonance effect of the wind-induced vibration response of the structure.
3. Wind Field Simulation and Loading
3.1. Wind Field Simulation
Due to the large spatial span of transmission lines, the simulation area is typically divided into a finite number of closely spaced points to simulate the time history of fluctuating wind speeds. Considering the slender nature of transmission lines and their relatively small sag, only the longitudinal fluctuating component of the wind is taken into account for its contribution to the wind-induced vibration response of the lines. When the cross-arm length of the transmission tower (in this paper, ≤10 m) is relatively small, it is assumed that the wind speeds at two points along the same wind direction are consistent, thus simplifying the wind field space of the transmission lines into a two-dimensional Y-O-Z plane. Therefore, this paper simulates the longitudinal fluctuating component at discrete points on the Y-O-Z plane (shown in Figure 7) based on the structural characteristics of transmission lines.
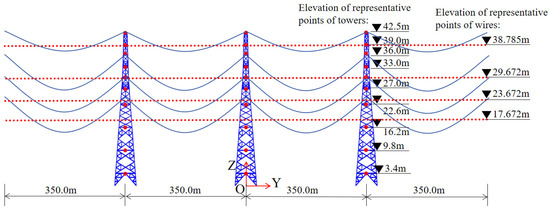
Figure 7.
Simulating points of the transmission tower-line system in the wind fields.
For the same transmission line, when the two ends of the line are at the same height, the effect of the average wind varying with height difference can be ignored. The effective height, He, is used as the reference height, where He = HL − 2/3SL. Here, HL represents the height from the ground to the suspension point of the transmission line, and SL represents the sag of the transmission line. For the typical transmission tower-line system selected in this paper, the four-layer transmission lines are discretized into 564 spatial points, with a horizontal spacing of approximately 10 m, which corresponds to the length of the cable element. The representative nodal positions (denoted as the red points) of the transmission tower-line system in the wind fields are shown in Figure 7. Faced with a large number of discrete points, traditional numerical simulation methods such as the harmonic synthesis technique [25] present significant memory requirements that might be challenging for standard computers to fulfill.
The consistent discrete random flow generation (CDRFG) method [26] is a series synthesis method based on the Fourier transform. It can strictly ensure the continuity conditions of the generated turbulence, satisfying the requirements of the target spectrum and spatial coherence function. Additionally, parallel computing can independently generate the turbulence time history for each coordinate point, thus demonstrating significant advantages in terms of computational efficiency. Therefore, the CDRFG method is adopted to simulate the fluctuating wind field for transmission lines.
This paper selects the mean wind profile and turbulence profile model for the B-type open-country terrain specified in the Chinese code [21]. The Von Karman model [27] is chosen for the wind speed spectrum, while the Shiotani model [28] is selected for the spatial correlation function of fluctuating wind speeds. Take the target wind field with a mean wind speed of = 30.0 m/s at the height of 10 m as an example. In Figure 8, subfigure (a) shows the simulated fluctuating wind speed at the top of Tower B, subfigure (b) displays the power spectral density of the simulated fluctuating wind speed, subfigure (c) illustrates the distribution of the simulated turbulence intensity, and subfigure (d) demonstrates the correlation of the simulated fluctuating wind field.
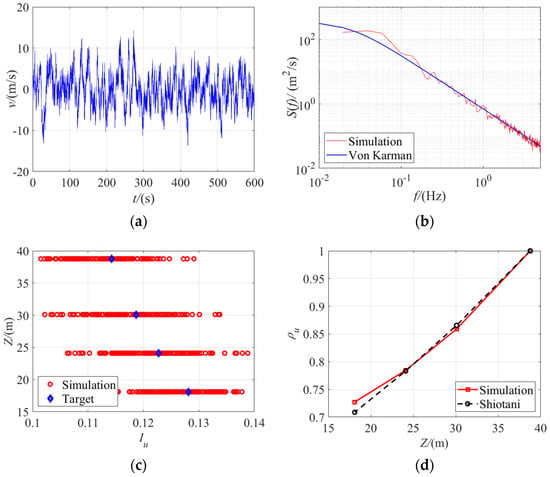
Figure 8.
Simulation result of the fluctuating wind field of the transmission line. (a) Time history; (b) power spectral density; (c) turbulence intensity; (d) correlation.
3.2. Dynamic Wind Loads on the Transmission Tower Line
3.2.1. Wind Loads on Transmission Lines
In a wind field, the dynamic effects on transmission lines can be divided into three components: the mean wind force, fluctuating wind force, and self-excited force generated by aerodynamic coupling. In this paper, the mean wind force and fluctuating wind force are calculated based on the quasi-steady aerodynamic formula, while the self-excited force resulting from aerodynamic coupling is converted into an aerodynamic damping force [29].
During structural dynamic analysis, the dynamic wind loads are applied to each segment of the transmission line at the respective nodes. For the i-th segment of the transmission line, the wind force FL,i(t) acting on the node is calculated using the following formula:
where ρa represents the air density; μsl is the shape coefficient of the transmission line; dc is the diameter of the transmission line; li is the length of the i-th segment of the transmission line; (zi) and u(zi,t) are the mean wind speed and fluctuating wind speed time histories at the i-th node, respectively; and θ is the angle between the wind speed and the transmission line.
3.2.2. Wind Loads on the Transmission Tower
The tower can be divided into several segments along its height according to its configuration characteristics. The average wind load of each segment can be calculated and then applied to each critical node. Based on the quasi-steady assumption, the wind load FT,i(t) on the i-th segment of the transmission tower can be expressed as
where As,i represents the effective projected area of the i-th segment perpendicular to the front direction of the cross-arm; μs,i is the wind force coefficient of the i-th segment; and αθ is the wind force distribution coefficient of the i-th segment corresponding to the wind direction θ, adopting the values specified in DL/T 5551-2018 [23].
4. Wind-Induced Failure Analysis of the Transmission Tower
4.1. Mechanical Nonlinearity of the Angle Steel Rod
In this paper, the yield or post-buckling behavior of the angle steel rod is defined using the axial force hinge model of bar elements, and its skeleton curve is shown in Figure 9. Here, the horizontal axis represents the displacement Δ, and the vertical axis represents the axial force FN. Segments A-B characterize the elastic phase. Point B represents the yield or buckling capacity of the member. Point C represents the ultimate tensile or compressive capacity of the member. Segments C-D characterize the unloading process after member failure, and point E indicates the complete loss of bearing capacity of the member. Length “a” characterizes the ductility of the member after yielding or buckling, length “b” represents the ultimate plastic deformation of the member, and height “c” represents the residual bearing capacity level of the member. Three performance points are assigned to the axial force hinge based on deformation: the immediate occupancy (IO) state, life safety (LS) state, and collapse prevention (CP) state.
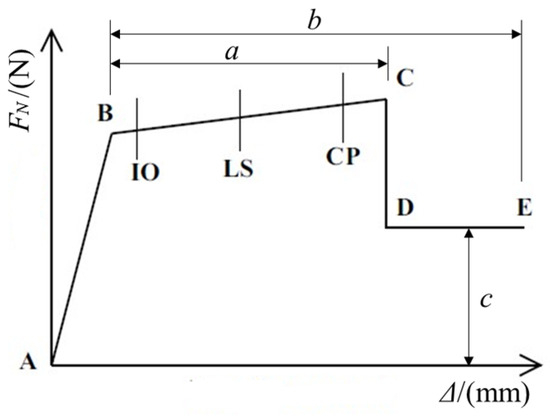
Figure 9.
Force-displacement relation diagram of the axial force hinge.
When strength failure occurs in the axial loading member, the strength of the angle steel member is determined according to the following formula:
where An represents the net cross-sectional area of the component excluding the bolt holes at the joints; δm is the strength reduction coefficient of the component; and fy is the standard value of the steel strength.
When buckling failure occurs in the axial compression member, the stability of the angle steel member is calculated according to the following formula:
where A0 represents the gross cross-sectional area of the angle steel member; φm is the stability factor of the compressed member, which is related to the slenderness ratio of the member; and δn is the strength reduction coefficient for the stability of the compression bar. Considering that various boundary or structural conditions can impact the stability capacity of compressed angle steel, a modified effective length should be utilized to calculate the slenderness ratio. It is important to note that the stability analysis of compressed angle steel members requires careful consideration of the specific loading and boundary conditions present in the application.
Based on Equations (3) and (4), two failure modes for the angle steel members of transmission towers are considered: tensile strength failure and compressive instability failure. The values of the undetermined parameters for the ultimate bearing capacity of the angle steel members in transmission towers are determined according to the design code of steel structures (GB 50017-2017 [30]) and the design code of overhead transmission line pole and tower structures (DL/T 5154-2012 [31]) in China. The displacement parameters of the axial force hinge model for the angle steel are determined according to the nonlinear analysis modeling parameters for compression braces and steel beam–column members, following the American code FEMA 356, as outlined in Table 3. Here, Δt represents the yield displacement of the tension member, and Δc represents the buckling displacement of the compression member.

Table 3.
Modeling parameters for nonlinear procedures of steel components.
Taking the typical angle steel members L125 × 10 (slenderness ratio = 64.5) and L90 × 8 (slenderness ratio = 84.3) as examples, the mechanical skeleton curve of the axial force hinge is expressed in terms of a stress–strain relationship, as shown in Figure 10. In this paper, it is assumed that the nonlinear behavior of the members occurs only within the plastic hinge zone of the bar, while the sections outside the plastic hinge zone undergo only linear elastic behavior. For the material constitutive model of the angle steel axial force hinge, an ideal elastic–plastic model is adopted on the tensile side, with the maximum stress taken as the nominal tensile strength of the steel. On the compressive side, the critical buckling stress strength of the member is considered. The axial force hinge utilizes an isotropic hysteretic model, disregarding factors such as steel stress stiffening that affect material strength. The unloading and reverse-loading paths of the hinge are parallel to the elastic segment.
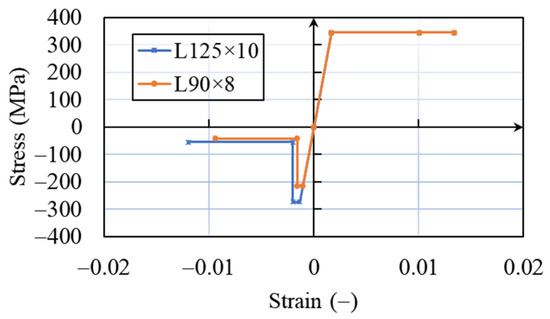
Figure 10.
Stress–strain relationship of the angle steel plastic hinge.
4.2. Analysis Method for the Wind-Induced Dynamic Response of a Transmission Line Structure
For the dynamic response analysis of the transmission tower-line system, the structural mass matrix and stiffness matrix can be directly constructed based on the physical space model of the structure. The relevant properties can be automatically incorporated by the finite element analysis program. Due to the significant difference in the damping characteristics between transmission towers and transmission lines, this paper specifies the structural damping of transmission towers and transmission lines separately by defining material damping. It is assumed that the damping of the transmission towers and transmission lines conforms to the Rayleigh damping model. The structural damping ratio of the transmission tower is set to 0.02, and the Rayleigh damping coefficient is determined based on the first two modal frequencies of the transmission tower in the tower-line system. The inherent damping effect of the transmission line itself is ignored, and only the aerodynamic damping contribution of the transmission line is considered. The modal aerodynamic damping ratio ξa is computed from Equation (5) as performed in [32],
where represents the average wind speed at the effective height He of the transmission line; mc is the mass per unit length of the transmission line; and ωl is the modal circular frequency of the transmission line.
Under strong winds, the steps for the dynamic analysis of the wind-induced vibration response in transmission tower-line systems are as follows:
- (1)
- Perform a static nonlinear analysis based on the structural dead load to obtain the structural gravity equilibrium configuration and stiffness.
- (2)
- Starting from the gravity equilibrium state, gradually apply the average wind load to the structure, and conduct a pseudo-static nonlinear analysis to obtain the structural quasistatic equilibrium configuration and stiffness.
- (3)
- Based on the quasistatic equilibrium state, a fluctuating wind load is applied, and a dynamic nonlinear analysis is conducted to determine the total wind-induced vibration response of the structure.
Using the SAP2000 program, geometric nonlinearities such as P-Δ and large displacement effects are considered in the established model of the transmission tower-line system. The α-Hilbert–Hughes–Taylor (α-HHT) incremental time integration method is adopted to analyze the wind-induced time-domain response of the transmission line structure [33]. Notably, the α-HHT method is unconditionally stable. In this research, the value of α is set to −0.05.
When the axial force of a member in the transmission tower reaches the critical compressive buckling force or tensile yield force, a plastic hinge occurs in the member, indicating the transition to a nonlinear material state. Once the number of plastic hinges reaches a certain threshold, the overall structure may form a mechanism or exhibit strong nonlinearities, leading to nonconvergence of the α-HHT algorithm. In such cases, the wind resistance capacity of the structure is considered to be ineffective.
4.3. Wind-Induced Failure Modes of the Transmission Tower
Generally, more unfavorable wind directions for transmission lines typically fall within the range of θ = 90° to 60°, where θ = 90° corresponds to the wind direction being perpendicular to the transmission line. In this study, the wind-induced collapse failure modes of transmission towers are analyzed under two wind direction conditions: θ = 90° and 60°. Additionally, the initial identification of the weak areas and critical member numbers of the transmission tower is presented in Figure 11.
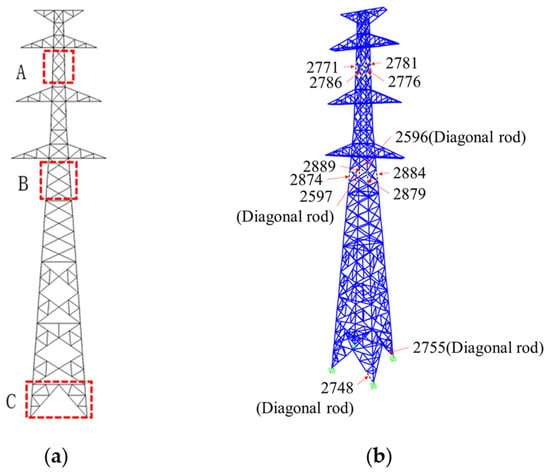
Figure 11.
Vulnerable sections of typical transmission towers. (a) Vulnerable section; (b) key members in vulnerable section.
4.3.1. Wind Direction θ = 90°
Under θ = 90° and 10 = 37.0 m/s, the displacement trajectory of the transmission tower top is shown in Figure 12, in which DX and DY represent the displacement along the X- and Y-directions respectively. Before the tower’s collapse, the structural dynamic responses centered predominantly around a quasi-static equilibrium point, specifically DX = 0.404 m and DY = 0 m. Here, DX experienced fluctuations within a range of approximately 0.371 m to 0.482 m, while DY exhibited similar variability, oscillating between −0.057 m and 0.045 m. This underscores the significant structural vibrations that were induced along the Y-axis, perpendicular to the incoming wind flow, which were of comparable intensity to those observed along the X-axis. As the structure approached its critical state, before the collapse, the displacements along both the X- and Y-directions surged rapidly. However, the ultimate failure manifested primarily along the X-direction, highlighting the predominant influence of forces acting in this direction at the time of collapse.
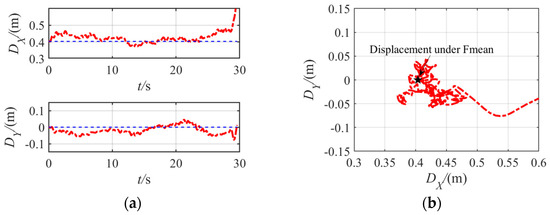
Figure 12.
Transmission tower top displacement under θ = 90° and 10 = 37 m/s. (a) Time history; (b) trajectory.
The axial force time history of the member at the weak point is presented in Figure 13. Regarding the members positioned on the same compressive side of the vulnerable section B, under quasi-static equilibrium conditions, Frames 2884 and 2879 exhibit equivalent axial forces. Nevertheless, under the influence of fluctuating wind loads, these values diverge, displaying a complementary fluctuation pattern: as the axial force in Frame 2879 diminishes, that of Frame 2884 intensifies, and the reverse occurs. An analogous behavior is observable in the primary tension members, Frames 2889 and 2874, attributable primarily to the transmission tower’s transverse vibrational dynamics. Among the selected diagonal members, Frames 2748 and 2755, and Frames 2596 and 2597, display synchronized fluctuations in their axial forces, indicating a coordinated response. However, as the structure approaches collapse, the compressive members, Frames 2879 and 2884, initially succumb in succession through buckling and unloading, followed by the diagonal members, Frames 2596 and 2597, which also fail due to buckling and unloading. This sequence underscores the structural vulnerabilities and failure mechanisms under extreme loading conditions.
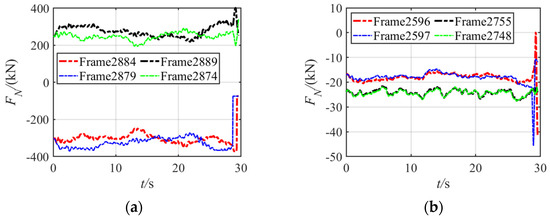
Figure 13.
Axial force of the member on the vulnerable sections of the transmission tower under θ = 90° and 10 = 37 m/s. (a) Main members at vulnerable section B; (b) diagonal members at vulnerable sections B and C.
Moreover, the evolution process of plastic hinges in the angle steel members of the transmission tower is illustrated in Figure 14. Overall, the wind-induced collapse evolution mechanism of the transmission tower under θ = 90° is described in terms of the tower top displacement, the internal forces of the main members, and the evolution of plastic hinges as follows:
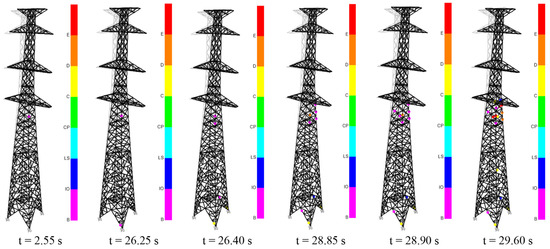
Figure 14.
Collapse mechanism of the transmission tower at θ = 90° and 10 = 37 m/s.
- (1)
- Before the transmission tower collapses, it primarily vibrates around the equilibrium state under the average wind force.
- (2)
- At t = 2.55 s, main member Frame 2879, which is located below the lowest cross-arm, reaches a critical state of compressive buckling and develops a plastic hinge into the IO state.
- (3)
- At t = 26.25 s, diagonal member Frame 2748 of the tower leg reaches a critical state of compressive buckling and develops a plastic hinge into the IO state. Subsequently, at t = 26.40 s, the plastic hinge enters a buckling unloading state into the plastic hinge C-D segment, and the adjacent bars to the main member Frame 2879 below the lowest cross-arm consecutively enter a critical state of compressive buckling and develop plastic hinges into the IO state.
- (4)
- At t = 28.85 s, the plastic hinge of Frame 2879 enters a buckled state and loses its strength in the plastic hinge D-E segment. Immediately afterward, plastic hinges in the IO state appear in the compressed main members on the other side. The tension in main member Frame 2889 on the tension side of the tower suddenly increases, while the tension in member Frame 2874 suddenly decreases. The Y-direction displacement at the top of the transmission tower also suddenly increases, indicating the critical state of collapse.
- (5)
- Starting at t = 28.90 s, plastic hinges appear in the compressed members below the lowest cross-arm of the transmission tower. The tension in main member Frame 2889 on the tension side begins to decrease, while the tension in Frame 2874 begins to increase. The Y-directional displacement at the tower top starts to decrease, while the X-directional displacement increases abruptly. This indicates that the lateral load-bearing capacity of the transmission tower has decreased.
4.3.2. Wind Direction θ = 60°
Under θ = 60° and 10 = 40.0 m/s, the displacement trajectory of the transmission tower top is shown in Figure 15. The difference with the previous case is that the structural quasi-static equilibrium state performs deflection along both the X- and Y-directions, i.e., DX = 0.407 m and DY = 0.062 m, which are elicited by the components of the mean wind load acting in their respective directions. Before the tower’s failure, the structural dynamic responses predominantly oscillate around this quasi-static equilibrium position, with DX varying within a range of approximately 0.382 m to 0.462 m, and DY exhibiting a narrower yet significant fluctuation between 0.011 m and 0.115 m. This underscores that despite the comparatively modest deflection along the Y-axis, the magnitude of vibration exceeds that observed along the X-axis. As the structure nears its critical point of collapse, the displacements along both axes undergo a rapid surge, ultimately culminating in the structure’s primary failure along the X-direction.
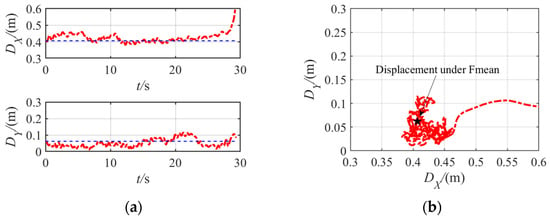
Figure 15.
Transmission tower top displacement under θ = 60° and 10 = 40 m/s. (a) Time history; (b) trajectory.
The axial force time history of the member at the weak point is presented in Figure 16. Analogous to the trends observed in Figure 13, the axial forces within members situated on the same compressive or tensile side of identical vulnerable sections exhibit a complementary fluctuation pattern. Specifically, for the designated diagonal members, Frames 2596 and 2597, their axial force fluctuations become desynchronized from approximately 17.2 s onwards, coinciding with Frame 2884 entering a critical buckling state. As the structure precariously approaches collapse, Frame 2884, being under compression, initially fails through buckling and subsequent unloading, followed by the buckling and unloading failures of the diagonal members, Frames 2596 and 2597.
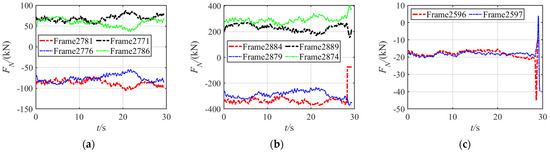
Figure 16.
Axial force of the member on the vulnerable sections of the transmission tower under θ = 60° and 10 = 40 m/s. (a) Main member at vulnerable section A; (b) main member at vulnerable section B; (c) diagonal member at vulnerable section B.
Moreover, the evolution process of plastic hinges in the angle steel members of the transmission tower is illustrated in Figure 17. Overall, the wind-induced collapse evolution mechanism of the transmission tower under θ = 60° is described in terms of the tower top displacement, the internal forces of the main members, and the evolution of plastic hinges as follows:
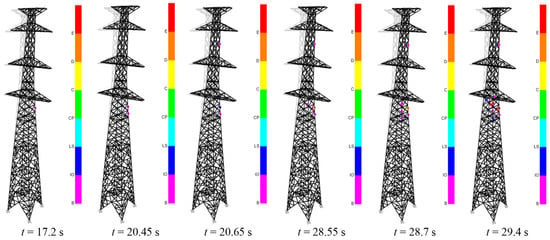
Figure 17.
Collapse mechanism of the transmission tower at θ = 60° and 10 = 40 m/s.
- (1)
- Before the collapse, the transmission tower primarily vibrates around the equilibrium state under the average wind force.
- (2)
- At t = 17.20 s, main member Frame 2884, which is located beneath the lowest cross-arm, enters a critical state of compressive buckling and develops a plastic hinge into the IO state.
- (3)
- At t = 20.45 s, the members adjacent to Frame 2884 also exhibit plastic hinges in the IO state.
- (4)
- At t = 20.65 s, compressed member Frame 2781, which is located in the middle section of the second and third cross-arms, reaches a critical state of compressive buckling and develops a plastic hinge into the IO state. Concurrently, the plastic hinge of Frame 2884 transitions to the LS state.
- (5)
- At t = 28.55 s, Frame 2884 enters a buckling unloading state, i.e., the plastic hinge D-E segment. The diagonal member Frame 2596, connected to this member, experiences a sudden increase in compression and subsequently develops a plastic hinge into the IO state, while the opposing diagonal member Frame 2597 undergoes sudden unloading.
- (6)
- At t = 28.70 s, the members adjacent to main member Frame 2879, which is located below the lowest cross-arm, develop plastic hinges.
- (7)
- At t = 29.40 s, Frame 2884 and 2596 undergo buckling and lose strength. The corresponding tower section loses its lateral load-bearing capacity. The Y-directional displacement at the tower top increases, while the X-directional displacement diverges, resulting in the overall collapse of the transmission tower.
4.4. Comparative Analysis of the Wind-Induced Failure Modes of the Transmission Tower
A pushover analysis is one method used to assess the wind resistance capacity of transmission towers. The collapse failure modes of the transmission tower obtained through pushover analysis are shown in Figure 18. The static wind load distribution is determined according to DL/T 5551-2018. At θ = 90°, without considering the lateral loads transmitted to the transmission tower by the transmission lines, the critical state of pushover failure is characterized by the emergence of plastic hinges on both main members of the compressed side beneath the lowest cross-arm. This results in an overall side-inclination instability along the X-direction. The ultimate wind speed is 34.6 m/s. In contrast, under θ = 60°, the critical state of pushover failure is marked by the appearance of a plastic hinge on one of the main members on the compressed side beneath the lowest cross-arm. This leads to an overall side-inclination instability at a certain angle with respect to the X-direction. The ultimate wind speed is 33.4 m/s, which is slightly lower than that at θ = 90°.
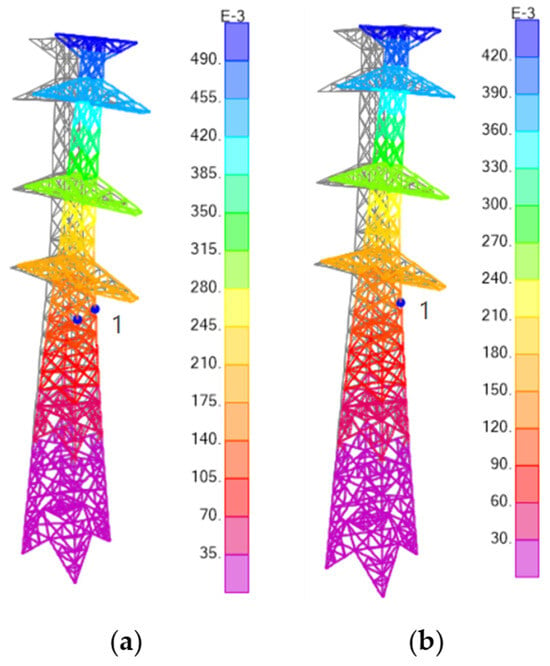
Figure 18.
Pushover failure of the transmission tower. (a) θ = 90°; (b) θ = 60°.
The comparison between the pushover failure and the dynamic collapse failure modes of the transmission tower reveals several similarities and differences. In both cases, the structural weakness is identified as the buckling of the main members on the compressed side beneath the lowest cross-arm. This leads to the loss of lateral resistance, triggering the eventual collapse of the tower. Concerning the tower top displacements, the static pushover analysis yields similar maximum values as the dynamic analysis. Specifically, under θ = 90°, the displacement maximum DX,max of the tower top in the X-direction is approximately 0.507 m, while under θ = 60°, DX,max is approximately 0.428 m and DY,max is approximately 0.088 m. These values align well with the divergence points of the tower top displacements obtained from the dynamic analysis.
However, there are also significant differences due to the differing load patterns, which are mainly due to the ignorance of the contribution of the coupling effect. In particular, under θ = 90°, the equivalent static wind load in the pushover analysis does not account for the transverse wind force effects. This means that the pushover collapse mode cannot fully capture the characteristics of the dynamic collapse failure of the structure. Furthermore, the estimated ultimate wind speed resistance of the tower based on the pushover analysis tends to be lower, resulting in a more conservative estimation of the wind resistance capacity of the tower. While the pushover analysis provides valuable insights into the potential collapse mechanisms and vulnerable regions of the transmission tower, it should be used in conjunction with dynamic analysis to more accurately assess the wind resistance capacity and collapse behavior of the structure.
Upon the aforementioned analysis, it becomes evident that the wind-induced collapse of the tower was directly triggered by the buckling failure of the compressed main members, while the buckling failure of the compressed diagonal members did not directly cause the overall collapse of the structure. The overall failure mode manifested as bidirectional compression-bending instability. Due to the lateral vibration of the transmission tower, particularly under a wind direction of θ = 90°, the tower collapsed in a direction that was not perpendicular to the transmission line. The wind-induced dynamic collapse failure mode of the transmission tower is largely consistent with the actual failure characteristics, as depicted in Figure 1.
Compared with the damage modes of the aeroelastic model of transmission tower-lines observed in [18,20], the similarities can be found in the failure initiation, specifically the buckling of the main members in the compression side of the tower’s mid-to-lower section, which subsequently triggers the overall instability and collapse of the entire structure. This comparison underscores the consistency between the simulation results and experimental observations, despite the inherent differences in experimental setups.
5. Conclusions and Prospects
This paper takes a typical transmission line as the research object. By establishing a finite element model of a typical transmission tower-line system, simulating the fluctuating wind speed in the strong wind field of the transmission line, and modeling the plastic hinge of components, a study on the wind-induced dynamic collapse failure mechanism of the transmission tower-line system was conducted. A comparative analysis was also conducted with pushover analysis and actual wind-induced collapse cases of transmission towers. The following conclusions were obtained:
- (1)
- Compared with transmission towers without wires, the coupling effect of the transmission tower-line system reduces the main vibration mode frequencies of the target transmission tower. This reduction can increase the contribution of the low-frequency energy range of strong winds to the resonant response of structural vibrations to a certain extent.
- (2)
- The wind-induced collapse of the transmission tower is directly triggered by the buckling failure of the main compressive member bars. The primary vulnerable section is situated in the tower body segment beneath the lowest cross-arm. Tower failure is characterized by a bidirectional compression-bending instability failure mode.
- (3)
- The coupling between the tower and lines elicits a potent transverse dynamic effect, resulting in substantial vibrations within the transmission tower laterally, which is ignored in the anti-wind design based on the quasi-static method. The transverse vibration response of the transmission tower significantly affects the wind resistance capacity and evaluation of the failure modes of the transmission tower. In the design phase, it is important to consider the transverse dynamic effect transferred from the transmission line to the transmission tower.
It is worth considering that the transmission tower is a typical lattice steel structure, intricately segmented into primary and secondary components, encompassing main members, diagonal braces, and auxiliary elements. Generally, the failure of secondary structural members does not directly cause the overall collapse of the structure. Rather, a plausible scenario for collapse would entail the secondary members yielding prior to, or in substantial numbers preceding, the primary members. The wind-induced collapse failure modes of the tower studied in this paper deviate from this sequence of member failure. Therefore, in the current separate design approach for transmission towers, considering the transmission line load resulting from the tower-line coupling effect, accurately assessing and optimizing the collapse failure mode of transmission towers would significantly enhance the wind resistance of transmission lines. In the future, ensuring a rationalized wind-induced collapse pattern for transmission towers will stand as a pivotal component in structural optimization research endeavors.
Author Contributions
Conceptualization, S.L. and W.Z.; methodology, W.Z.; software, W.Z.; validation, W.Z., C.L. and L.L.; formal analysis, S.L., W.Z., Q.L., S.Y. and S.Z.; investigation, W.Z.; resources, S.L.; data curation, W.Z.; writing—original draft preparation, W.Z.; writing—review and editing, S.L., W.Z., Q.L., S.Y., S.Z., C.L. and L.L.; supervision, W.Z.; funding acquisition, C.L. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (grant number: 52178491), the Natural Science Foundation of Shenzhen (grant number: JCYJ20210324093809023), the Guangdong Basic and Applied Basic Research Foundation (grant numbers: 2022A1515240062 and 2022A1515240001), the Basic and Applied Basic Guangdong-Dongguan Joint Regional Cultivation Fund of Guangdong Province (grant number: 2022A1515140136), and the Shenzhen Basic Research Program (grant number: GXWD20231130143911001).
Data Availability Statement
The original contributions presented in the study are included in the article.
Acknowledgments
The authors greatly appreciate the support from the National Natural Science Foundation of China, the Natural Science Foundation of Shenzhen, the Guangdong Basic and Applied Basic Research Foundation, the Basic and Applied Basic Guangdong-Dongguan Joint Regional Cultivation Fund of Guangdong Province, and the Shenzhen Basic Research Program. The opinions and statements do not necessarily represent those of the sponsors.
Conflicts of Interest
Authors Shizeng Liu, Qiang Li, Shicheng Yan and Shihong Zhang were employed by the Dali Bureau of EHV Power Transmission Company, China Southern Power Grid International. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- NERC. Hurricane Harvey Event Analysis Report; North American Electric Reliability Corporation: Atlanta, GA, USA, 2018. [Google Scholar]
- Dempsey, D.; White, H.B. Winds wreak havoc on lines. Transm. Distrib. World 1996, 48, 32–42. [Google Scholar]
- Prasad Rao, N.; Samuel Knight, G.M.; Lakshmanan, N.; Iyer, N.R. Investigation of transmission line tower failures. Eng. Fail. Anal. 2010, 17, 1127–1141. [Google Scholar] [CrossRef]
- Prasad Rao, N.; Samuel Knight, G.M.; Mohan, S.J.; Lakshmanan, N. Studies on failure of transmission line towers in testing. Eng. Struct. 2012, 35, 55–70. [Google Scholar] [CrossRef]
- Shukla, V.K.; Selvaraj, M. Assessment of structural behavior of transmission line tower using strain gauging method. Int. J. Steel Struc. 2017, 17, 1529–1536. [Google Scholar] [CrossRef]
- Tian, L.; Guo, L.; Ma, R.; Gai, X.; Wang, W. Full-scale tests and numerical simulations of failure mechanism of power transmission towers. Int. J. Struct. Stab. Dyn. 2018, 18, 1850109. [Google Scholar] [CrossRef]
- Fu, X.; Wang, J.; Li, H.N.; Li, J.X.; Yang, L.D. Full-scale test and its numerical simulation of a transmission tower under extreme wind loads. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 119–133. [Google Scholar] [CrossRef]
- Xie, Q.; Sun, L. Failure mechanism and retrofitting strategy of transmission tower structures under ice load. J. Constr. Steel Res. 2012, 74, 26–36. [Google Scholar] [CrossRef]
- Xie, Q.; Zhan, J. Experimental study on failure modes and retrofitting method of latticed transmission tower. Eng. Struct. 2021, 226, 111365. [Google Scholar] [CrossRef]
- Eslamlou, S.D.; Asgarian, B. Determining critical areas of transmission towers due to sudden removal of members. Case Stud. Eng. Fail. Anal. 2017, 9, 138–147. [Google Scholar] [CrossRef]
- Gao, S.; Wang, S. Progressive collapse analysis of latticed telecommunication towers under wind loads. Adv. Civ. Eng. 2018, 2018, 3293506. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Li, G.; Wang, W.; Tian, L. The numerical analysis of transmission tower-line system wind-induced collapsed performance. Math. Probl. Eng. 2013, 2013, 413275. [Google Scholar] [CrossRef]
- Wang, F.Y.; Xu, Y.L.; Qu, W.L. Multi-scale failure analysis of transmission towers under downburst loading. Int. J. Struct. Stab. Dyn. 2018, 18, 1850029. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Q. Failure analysis of transmission tower subjected to strong wind load. J. Constr. Steel Res. 2019, 160, 271–279. [Google Scholar] [CrossRef]
- Li, J.; Gao, F.; Wang, L.; Ren, Y.; Liu, C.; Yang, A.; Li, C. Collapse mechanism of transmission tower subjected to strong wind load and dynamic response of tower-line system. Energies 2022, 15, 3925. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, Q.; Wang, D.; Huang, G.; Liang, S. Fragility analysis of transmission towers subjected to downburst winds. Appl. Sci. 2023, 13, 9167. [Google Scholar] [CrossRef]
- An, L.; Wu, J.; Zhang, Z.; Zhang, R. Failure analysis of a lattice transmission tower collapse due to the super typhoon Rammasun in July 2014 in Hainan Province, China. J. Wind. Eng. Ind. Aerodyn. 2019, 182, 295–307. [Google Scholar] [CrossRef]
- Liang, S.; Zou, L.; Wang, D.; Cao, H. Investigation on wind tunnel tests of a full aeroelastic model of electrical transmission tower-line system. Eng. Struct. 2015, 85, 63–72. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, G.; Wang, L.; Li, J. Wind-induced coupling vibration effects of high-voltage transmission tower-line systems. Shock. Vib. 2017, 2017, 1205976. [Google Scholar] [CrossRef]
- Chen, B.; Song, X.; Ouyang, Y.; Wu, J. Evaluation on wind-induced damage of transmission tower-line system through aeroelastic model wind tunnel test. In Proceedings of the 15th International Conference on Wind Engineering, Beijing, China, 1–6 September 2019. [Google Scholar]
- GB 50009; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Zhang, W.; Xiao, Y.; Li, C.; Zheng, Q.; Tang, Y. Wind load investigation of self-supported lattice transmission tower based on wind tunnel tests. Eng. Struct. 2022, 252, 113575. [Google Scholar] [CrossRef]
- DL/T5551; Load Code for the Design of Overhead Transmission Line. China Planning Press: Beijing, China, 2018.
- Wilson, E.L. A new method of dynamic analysis for linear and non-linear systems. Finite Elem. Anal. Des. 1985, 1, 21–23. [Google Scholar] [CrossRef]
- Deodatis, G. Simulation of ergodic multivariate stochastic processes. J. Eng. Mech. 1996, 122, 778–787. [Google Scholar] [CrossRef]
- Aboshosha, H.; Elshaer ABitsuamlak, G.; El Damatty, A. Consistent inflow turbulence generator for LES evaluation of wind-induced responses for tall buildings. J. Wind. Eng. Ind. Aerodyn. 2015, 142, 198–216. [Google Scholar] [CrossRef]
- Von Karman, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Shiotani, M. Some notes on the structure of wind in the lowest layer of the atmosphere. J. Meteorol. Soc. Jpn. 1953, 31, 327–335. [Google Scholar] [CrossRef]
- Zhang, W.; Xiao, Y.; Li, C. Strong wind-induced vibration analyses of uncoupled transmission tower-line model. In Proceedings of the 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 7 June 2020; pp. 1898–1902. [Google Scholar]
- GB 50017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- DL/T 5154; Technical Regulation of Design for Tower and Pole Structures of Overhead Transmission Line. China Planning Press: Beijing, China, 2012.
- Loredo-Souza, A.M.; Davenport, A.G. The effects of high winds on transmission line. J. Wind. Eng. Ind. Aerodyn. 1998, s74–s76, 987–994. [Google Scholar] [CrossRef]
- Cluni, F.; Gusella, V.; Bartoli, G. Wind tunnel scale model testing of suspended cables and numerical comparison. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1134–1140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).