Abstract
Oil-filled motors (OFMs) are widely used in deep-sea exploration and oil well extraction. During motor operation, the rotor stirs the oil in the air gap, causing viscous loss. Viscous loss affects the temperature distribution inside the motor. Accurately calculating the viscous loss and temperature rise in OFMs can provide a basis for optimizing the motor’s structural design. Motor structural parameters, including the rotor’s outer diameter, air gap, and slot opening, have a significant impact on viscous loss. The working conditions of OFMs, such as rotor speed and environmental temperature, also affect viscous loss. The viscosity of hydraulic oil is highly influenced by temperature, and changes in viscosity can lead to changes in viscous loss. These changes in viscous loss, in turn, alter the temperature distribution. Therefore, the coupling relationship between viscous loss and temperature must be considered. Additionally, when Taylor vortices occur in the fluid, the surface roughness of the rotor also has a significant influence on viscous loss. Currently, both domestic and international research on viscous loss and thermal analysis struggle to simultaneously consider the coupling of viscous loss and the temperature field, rotor surface roughness, and the effect of motor structure. This paper summarizes the methods used in recent years for studying viscous loss and thermal analysis, and puts forward some suggestions for future research on the coupling of the OFM temperature field and viscous loss.
1. Introduction
With the ongoing development of new trends and application scenarios in the energy sector, OFMs are receiving increasing attention and research. In deep-sea development, conventional motors struggle to operate normally under extreme high-pressure conditions. However, OFMs can balance the pressure difference between the inside and outside of the motor by injecting hydraulic oil into the motor air gap, allowing it to function properly [1,2,3,4]. As a result, OFMs are widely used in autonomous underwater vehicles (AUVs), remotely operated vehicles (ROVs), electric propulsion, and pump drive systems [5,6,7]. In the aerospace sector, with the electrification of hydraulic systems becoming a mainstream trend, Electro-Hydrostatic Actuators (EHAs) are gaining popularity, replacing traditional hydraulic systems for functions such as braking and landing [8,9,10,11]. OFMs, due to their capability for oil cooling, are used as core drive components in EHAs [12]. The structure of an EHA is shown in Figure 1. In the oil well extraction field, modern extraction generally uses submersible motors, as shown in Figure 2, to extract oil to the wellhead for harvesting [13]. Given the high-temperature environment underground, injecting mineral lubricating oil into the motor air gap has become an effective means of ensuring the stable operation of motors. These OFMs play a crucial role in driving submersible electric pumps. In mobile construction machines, OFMs are commonly used as hydraulic pumps in hydrostatic drivetrains (HSTs). A hydrostatic drivetrain can decouple the vehicle speed from the engine speed, allowing for improved engine efficiency [14,15].
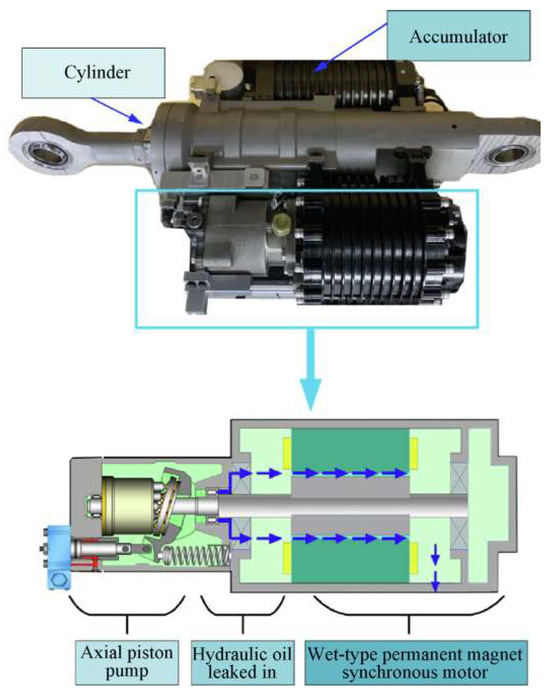
Figure 1.
Integrated EHA (In the blue box at the top of the figure is the EHA) with wet-type permanent magnet synchronous motor (WPMSM). [16].

Figure 2.
Schematic of a submersible motor [14].
During the operation of OFMs, the rotation of the rotor stirs the oil inside the motor air gap. At the outer diameter of the rotor in the motor air gap, the oil flow rate equals the rotor’s linear velocity; near the inner diameter of the stator, the oil flow rate is zero. The air gap height is often only a few millimeters or even less than a millimeter, resulting in a significant velocity gradient in the air gap, which leads to substantial viscous loss [17]. Under high-speed conditions, viscous loss can account for more than 50% of total motor loss [18]. On the other hand, due to the enclosed working environment of OFMs, heat dissipation performance is poor, and excessive temperatures can cause the irreversible demagnetization of permanent magnets [19]. Therefore, research on viscous loss and the temperature field of OFMs is of great significance.
Additionally, viscous loss in OFMs will cause oil temperature rise, and the temperature increase will affect oil viscosity in the air gap. The viscosity of oil decreases while the temperature rises, and viscous loss decreases as oil viscosity decreases. This indicates that the calculation of viscous loss is coupled with the calculation of temperature rise [20]. Hence, studying the coupled relationship between these two aspects is crucial for accurately calculating viscous loss and temperature rise.
In current research, analytical formulas mostly assume that fluid flow is laminar, without considering the effects of turbulence. When the rotational speed increases or viscosity decreases, the Reynolds number (ReG) increases, leading to a higher degree of turbulence in the flow. As a result, the accuracy of these analytical formulas is insufficient, especially in cases of high rotational speed and low viscosity, where the actual viscous losses may reach nearly ten times the calculated results. Some studies that calculate viscous losses using CFD often do not account for the effect of temperature-dependent viscosity in their calculations, thus limiting the calculation to a specific temperature point and preventing an accurate assessment of viscous losses after the motor reaches a thermal steady state. Most research does not include experimental measurements of viscous loss to validate the accuracy of calculations. Furthermore, few studies consider the impact of viscosity, motor structural parameters, and rotor surface roughness on viscous loss, while also coupling temperature with viscous loss calculations.
The purpose of this paper is to review the analysis of the temperature field and viscous loss in OFMs, focusing on the multi-physics coupling analysis of viscous loss. The paper is structured as follows: Section 2 focuses on the calculation methods of viscous loss and the research progress on multi-physics coupling analysis methods; Section 3 briefly introduces the methods and developments for analyzing the temperature field of OFMs; Section 4 provides some suggestions for future related work; and the final section summarizes this review.
2. Advancements in the Study of Viscous Loss
2.1. Methods for Calculating Viscous Loss
Viscous loss is essentially a friction loss of a viscous fluid, and the analysis of the fluid flow state at the air gap is not yet theoretically perfected, making the calculation of viscous loss a challenging task. Currently, the most commonly used methods for calculating viscous loss include simulation methods based on CFD and analytical formulas. Flow-field simulation can accurately reflect the impact of motor structure on the internal flow field, thus providing high calculation accuracy. However, this method involves a complex preprocessing process, and the computational requirements for flow-field calculations are substantial, resulting in long computation times. In contrast, analytical methods can clearly demonstrate the influence of various factors on the loss, requiring relatively less computation and offering faster calculation speeds. Therefore, they are more suitable for the iterative optimization design of motor schemes [21].
Windage loss is a type of viscous loss and can be referenced for the calculation of oil viscous loss. Usually, it is calculated using the equations found in reference [22], and can be expressed as follows:
where ρ is the density of the fluid, in this case air, ω is the angular velocity, l is the length of the cylinder, and r is the radius. Cf, the friction coefficient, depends on the structure of the surface. In this case, the surface is assumed to be smooth. A rough surface gives a higher friction coefficient [23].
In this expression, the only coefficient that needs to be determined for calculating viscous loss, Cf, cannot be measured directly. Table 1 shows the relationship between the friction coefficient Cf, the Reynolds number, and the Taylor number (Ta).

Table 1.
Empirical equations for the estimation of the rotor skin friction coefficient.
Table 1.
Empirical equations for the estimation of the rotor skin friction coefficient.
| Authors | Empirical Equations | Range | |
|---|---|---|---|
| Wendt [24] | (2) | 400 < ReG < 104 | |
| (3) | 104 < ReG < 105 | ||
| Yamada [25] | (4) | ||
| Bilgen and Boulos [26] | (5) | 500 < ReG < 104 | |
| (6) | ReG > 104 | ||
| Nakabayashi [27] | (7) | Ta < 1700 | |
| (8) | 1700 < Ta < 104 | ||
| (9) | Ta > 104 |
For the calculation of viscous loss caused by oil, in 2011, Li Jianjun [28] treated the air gap as a concentric ring and proposed an analytical calculation formula for viscous loss:
where δ is the air gap height (m), μ is the dynamic viscosity of the oil (Pa·s), ω is the motor’s angular velocity (rad/s), r1 is the outer radius of the rotor (m), and r2 is the inner radius of the stator (m). This formula assumes that the oil in the air gap is in a laminar flow state. Laminar flow refers to the flow pattern where all fluid particles move in an orderly manner, with trajectories of smooth curves [29]. In contrast, turbulent flow refers to the flow pattern where some or all fluid particles move in a disordered manner [30]. Therefore, this formula is only applicable when the motor speed is relatively low.
Reference [31] used experimental data to correct the model parameters of viscous loss, ensuring the accuracy of the viscous loss calculation formula at high speeds, while also considering the relationship between viscosity and temperature. This semi-analytical formula, based on experimental data, can describe the viscous loss of this specific motor structure well, but the complex experimental process makes its application unfriendly, and its applicability to other motors cannot be guaranteed. The proportion coefficient f, the fluid dynamic viscosity μ, the motor speed n, and the constant k related to the motor’s structural parameters are used in the following expression:
Existing analytical calculations, based on the general characteristics of motor rotor structures, divide the loss into air-gap friction loss and end-face friction loss, with the total viscous loss being the algebraic sum of these losses. Some studies [32,33,34] suggest that the annular-gap fluid friction loss in the air gap is the primary source of viscous loss in OFMs, assuming the fluid flow in this area is incompressible laminar flow, and establish a laminar flow model for calculation.
However, the drawback of the analytical formulas for viscous loss lies in assuming laminar flow and neglecting the effects of turbulence and the Reynolds stress equation. Most of the fluid inside the motor is turbulent, and centrifugal forces can also generate Taylor vortices. Considering these factors results in a very complex flow field, making it difficult to derive analytical formulas. With the improvement of computer performance, current research often employs CFD-based simulation analysis and semi-empirical formulas corrected by experimental data.
To predict viscous loss, A. B. Nachouane [35] used CFD methods to characterize the flow structure inside the air gap and to predict the friction coefficient Cf, which requires solving the following conservation equations [36]:
- Mass conservation: Continuity equation:
- Momentum conservation: Navier–Stokes equation:
- Energy conservation: Heat equation:
Yamada [25] conducted extensive experimental tests on the viscous loss at the air gap and proposed a highly accurate semi-empirical analytical model. For the motor rotor, apart from the cylindrical surface at the air gap, there are also two end faces. Regarding the loss at these locations, Kreith [37] assumed an infinitely large end space and used the π theorem to nondimensionalize the fluid motion equations, resulting in an analytical model for end-face friction loss. Reference [38] used the Kreith model to calculate the air friction loss at the end face of a 100 kW, 32,000 rpm high-speed permanent magnet motor. However, the model assumes an infinitely large end space. When the motor rotor is close to the wall, the Daily–Nece model, which considers wall spacing, can be used. Reference [39] used this model to calculate the end-face loss of a 33 kW, 55,332 rpm high-speed motor and used it for temperature rise calculations, yielding high accuracy. Hu Yan and Li Longbiao [40] from Shenyang University of Technology used fluent to establish a 3D fluid field model and calculated the viscous loss. Compared to Chen Hao’s model [41], their model showed some progress by establishing a complete motor model that considered slots. Li Liping and Peng Bing [42] established a 3D fluid field model for OFMs and used CFD to calculate viscous loss at fixed viscosities from 500 to 3000 rpm and at fixed speeds from 0 to 100 °C, respectively, studying the impact of temperature and speed on viscous loss. However, they did not conduct simulations on viscous loss at varying speeds and temperatures, and the simulated speed range was small. Wang Y and Kou G [43] calculated the viscous loss of a high-speed oil-cooled motor in an EHA system based on the inlet and outlet temperatures of the oil, the specific heat capacity of the oil, and the flow rate. This method can only be used for calculating viscous loss under actual working conditions and is not helpful for estimating viscous loss during motor design. Cai M and Wu S [44] conducted viscous loss measurement experiments on three oils with different viscosities at 0 or 25 °C and four pressure levels (0, 20, 40, 60). These comprehensive experiments provided a detailed experimental basis for analyzing the viscous loss of OFMs. The experiment-based method adopted by reference [45] can accurately measure the oil viscous loss of the high-speed WPMSM. However, this method lacks universality and has a high cost burden, making it highly dependent on the test prototype.
2.2. Factors Affecting Viscous Loss
From the previous analysis, it is evident that, in OFMs, the rotation of the rotor stirs the oil in the air gap, and the oil velocity varies at different radial distances. As a viscous fluid, oil experiences significant friction loss, known as viscous loss, due to this relative motion. Furthermore, the rate of oil movement, the viscosity coefficient, and the motion cross-section directly impact the frictional resistance. Therefore, it can be inferred that viscous loss is closely related to rotor speed, motor structural parameters associated with the air gap, and temperature, which affects oil viscosity.
- Rotor Speed
Based on the study of the relationship between temperature field distribution and rotor speed [46], Ahmed M. Teamah et al. [47] further investigated the relationship between viscous loss and rotor speed. They used a wattage meter connected to the variable frequency drive (VFD) to estimate the amount of heat from viscous loss. The rotor speed was varied by adjusting the frequency to the VFD from 900 to 3600 rpm. The results indicated that oil viscous loss is proportional to the 2nd–3rd power of the rotational speed. Figure 3 shows the effect of rotor rotational speed on viscous loss at a constant gap size of 1.4 mm, stator inner diameter of 55 mm, rotor length of 0.14 m, and oil volume percentage inside the annular area (OV) of 100%.
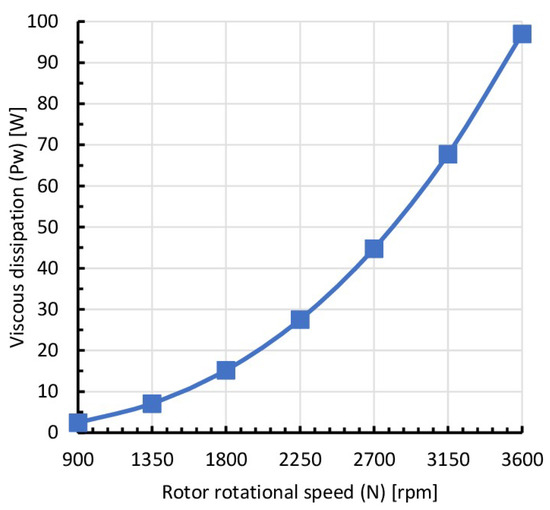
Figure 3.
Effect of rotor rotational speed on viscous loss [47].
Reference [48] used an improved analytical method and a Volume of Fluid (VOF) model to calculate the viscous loss of an oil-immersed cooling in-wheel motor. By comparing the results from Kori’s method with a three-dimensional transient CFD model based on the VOF, as well as actual measurements, as shown in Figure 4, they found that the VOF model was more precise but more time-consuming, and that oil viscous loss is proportional to the 2nd–3rd power of the rotational speed.
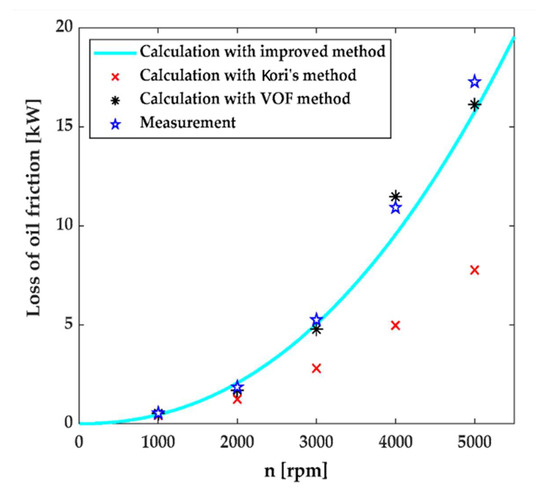
Figure 4.
Relationship between oil viscous loss and rotation speed n [48].
Reference [4] also considered the factor of rotor speed and concluded that viscous loss is proportional to the cube of the rotational speed. They also studied the impact of external pressure on viscous loss. The calculated and experimental results showed a significant increase in viscous drag loss at high pressure. The study of pressure provides insights for future research.
- Motor Structural Parameters
The team led by Ahmed M. Teamah [47] also analyzed the effects of gap size (Gw), stator inner diameter (Dsi), and rotor length (L) on viscous loss in oil-immersed motors. Their experimental results show that viscous loss decreases nonlinearly with increasing gap length. This is related to the increase in ReG due to the increased gap length, which leads to a decrease in Cf, as shown in the following equation:
Meanwhile, with increasing Dsi, the viscous loss increased dramatically. The viscous loss increases as r is raised to the power of 4, according to (1). Additionally, the relationship between L and viscous loss shows a linear proportionality.
Reference [13] analyzed the effects of rotor outer diameter and gap size on viscous loss, considering the impact of turbulence. They used the CFD method to simulate the viscous loss of a WPMSM. To verify the accuracy of their results, they employed a novel experimental method with a test platform, as shown in Figure 5. The high-speed motor system drives the internal cylinder inside the concentric cylinder oil simulator to rotate, emulating the WPMSM operation. Temperature and torque sensors are used to measure the oil temperature and load torque of the concentric cylinder oil simulator, respectively. The results indicate that viscous loss increases with the rotor outer diameter, proportional to the rotor outer diameter to the power of 3.4. Viscous loss decreases with increasing gap size, and is inversely proportional to the gap size to the power of 0.2.

Figure 5.
Oil viscous loss experimental platform.
Wenjuan Qi’s team [18] focused on the impact of slot openings on viscous loss, using CFD simulations to calculate the viscous loss caused by slot openings and verifying the results through experiments under the same environmental conditions to ensure accuracy. Their research results indicate that the size of the slot openings has little effect on viscous loss. However, generally, for motors of the same size, motors with closed slots have slightly lower viscous loss compared to those with open slots.
On the other hand, Jiang Peng et al. [49] have different views. Addressing the issue of large errors in viscous loss calculations for traditional oil-cooled hub motors due to the failure to consider the effects of teeth slots and the cup-shaped structure formed by the recessed rotor yoke in the integrated design of hub motors and reducers, Jiang Peng’s team designed an improved analytical model. They established independent and combined analytical models for the air-gap teeth and slot openings and divided the rotor of the hub motor into different regions to establish analytical models for each region, forming a comprehensive viscous loss analytical model. Finally, by comparing the measured values with the analytical calculation values and CFD simulation values, they found that the calculation accuracy was greatly improved.
- Temperature and Viscosity
Reference [50] calculated the viscous loss of an oil-cooled motor for the aerospace sector using internal hydraulic oil for cooling to improve heat dissipation and output efficiency. Their research shows that the loss power at 40 °C is significantly higher than that at 60 °C, and this change increases rapidly with the increase in speed.
Reference [31] analyzed the relationship between oil viscosity and temperature in detail and used experimental data to correct the parameters of the viscous loss analytical model. In their research, the viscosity of the oil changes negatively exponentially with temperature; the higher the temperature, the lower the oil viscosity and the lower the viscous loss. They further studied the impact of different types of oil on viscous loss and found that when external pressure changes, the impact of different oils on viscous loss varies greatly, as shown in Figure 6. The effect of the type of oil on viscous loss is actually the effect of viscosity. In addition, their research on external pressure and oil type can greatly help optimize motor performance and provide some ideas for future work.
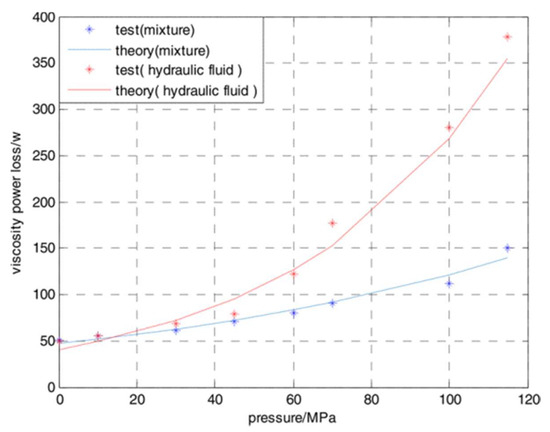
Figure 6.
Viscous power loss of wrist-turning [31].
In reference [51], the authors investigated the effect of rotational speed on viscous loss and focused on the relationship between viscous loss and temperature. In the CFD model, the viscosity of the oil was altered to obtain different viscous losses, and then the relationship between these viscous losses and temperature was fitted using (16). Figure 7 shows the change in viscous loss with temperature.
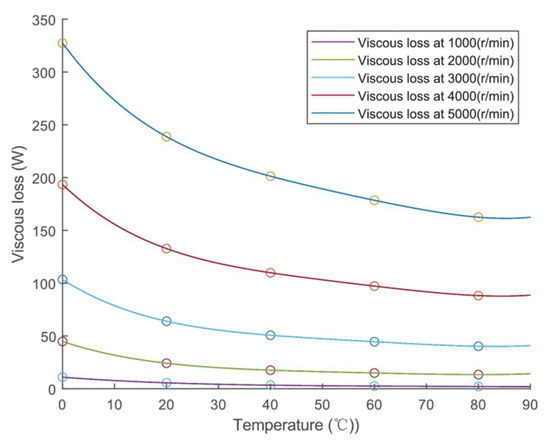
Figure 7.
Viscous loss varies with temperature [51].
Reference [52] measured the viscosity of oil at different temperatures through experiments and obtained the viscous loss at different temperatures through a CFD simulation model. From their research, it can be seen that viscous loss decreases with increasing temperature. This is related to the decrease in oil viscosity with rising temperature, which is consistent with (10).
Through comparing the experimentally measured viscous loss data at different oil viscosities with the simulated relationship curves of viscous loss and rotor speed at different temperatures, the shortcomings of the analytical formula were identified in [53]: it does not consider the change in viscosity nor the impact of turbulence, resulting in the analytical values being much smaller than the actual values. Therefore, it is first necessary to compensate for the theoretical oil wear loss results under low-viscosity and high-speed conditions. Secondly, the effects of viscosity and speed on the theoretical oil wear loss results should be mutually restrictive: at high viscosity, the impact of speed decreases, and the same applies at high speed. Finally, based on the results obtained from CFD simulations, a correction formula is proposed:
where μ0 is the dynamic viscosity of the oil at 0 °C and k is the proportional coefficient, taken as 0.5.
- Rotor Surface Roughness
Currently, there is a lack of research on the impact of rotor surface roughness on viscous loss in OFMs. Existing studies mainly focus on the effect of air-induced viscous losses in the air gap, serving as significant references for understanding oil viscous losses.
According to reference [54], when Taylor–Couette flow appears in the fluid flow, rotor surface roughness has a substantial impact on viscous losses. The study indicates that the surface roughness of the rotor has a significant impact on viscous losses. Specifically, a smoother surface with lower roughness results in smaller viscous losses because the friction between the smooth surface and the air is reduced. Conversely, a rougher surface with higher roughness leads to greater viscous losses due to increased air turbulence and friction. Through experimental measurements and computer simulations, the researchers analyzed the viscous losses of rotors under different roughness conditions. The results show a positive correlation between surface roughness and viscous losses, meaning that the higher the roughness, the greater the viscous losses.
Accurately calculating Cf is key to obtaining an analytical formula for viscous losses. References [24,25,26,27] provides several analytical formulas for Cf, but they generally assume a smooth rotor surface. In contrast, A. B. Nachouane [35] used the CFD method to derive expressions for Cf with and without rotor surface roughness height (Ks). When Ks = 0 mm, it indicates a smooth rotor surface. Additionally, for Ks = 0 mm, the analytical intervals were divided into three regions based on Ta.
- When the rotor surface is smooth (Ks = 0 mm), the friction coefficient Cf is given by the following:
- Zone 1: Linear theory regime (Ta < TaC1):
- Zone 2: Non-linear theory regime (TaC1 < Ta < TaC2):where Cf0 = 2.468η1/2 TaC11/2.
- Zone 3: Fully turbulent regime (Ta > TaC2):
- When the rotor surface is smooth (Ks ≠ 0 mm), the friction coefficient Cf is given by the following expression in the fully turbulent zone:where = (Ri + Ks)/Ri is the roughness ratio.
3. Progress in the Study of the Temperature Field of OFMs
3.1. Methods for Analyzing the Temperature Field
The analysis methods for OFM temperature fields mainly include Lumped-Parameter Thermal Network (LPTN), CFD, and Finite Element Method (FEM) approaches [55]. The advantage of the LPTN lies in its fast computation speed and simple model algorithm, making it widely used in motor design and temperature analysis. Its drawback, however, is that temperature results are highly influenced by thermal parameters, necessitating careful consideration in parameter setting.
Both CFD and FEM approaches are numerical analysis methods that involve building a physical geometric model of the motor for the precise numerical analysis of temperature distributions at various node points. The key difference lies in how the FEM requires setting thermal parameters such as convective heat transfer coefficients empirically, which significantly affects the final temperature field analysis. CFD methods excels in fluid–structure coupling, simulating convective heat transfer phenomena based on fluid movement states, but they demand higher-quality model grids and computational resources.
3.1.1. LPTN
The LPTN utilizes real heat sources and thermal resistances equivalent to certain centralized nodes, modeling heat conduction between nodes using thermal resistance. Thermal resistance for heat conduction between solids is mainly determined by material thermal conductivity and specific dimensions. For convective heat transfer at the interface between fluids and solids, the convective environment of the fluid needs determination and to be coupled with corresponding material properties to compute convective heat transfer coefficients and thereby equivalently calculate heat transfer surfaces to obtain convective heat transfer thermal resistance. Each part’s losses are loaded as heat sources into corresponding nodes, making the temperature field equivalent to an electric field, with heat sources regarded as current sources, thermal resistances as resistors, and temperature as voltage, establishing an equivalent thermal path, and thereby allowing the calculation of the motor’s various parts’ temperature rise. The LPTN can be used to quickly analyze the temperature field of an OFM, but the thermal parameters need to be accurate enough.
In the field of oil-filled aircraft motor system design and analysis, Johansson Björn [56] proposed a thermal network model for aircraft electric–hydraulic actuation systems that includes motors, hydraulic pumps, and power electronics. The motor in the model uses a simplified approach, considering only eddy current losses, copper losses, and windage losses, which may not fully reflect actual motor conditions, especially under different cooling conditions and temperature rises. Reference [57] established an eight-node lumped-parameter thermal model for Brushless DC Motors (BLDCs) with internal oil filling in Electro-Hydrostatic Actuators (EHAs), as shown in the figure. This model enables temperature rise analysis under various operating conditions but does not detail the acquisition of thermal parameters nor validate results with experimental data. The thermal parameters in the thermal network include empirical formulas for heat transfer coefficients, heat capacity, and thermal conductivity. Regarding heat transfer coefficients, P.-O. Gronwald [58] summarized empirical formulas for heat transfer coefficients at various parts of the motor. It was observed that different motor structures exhibit significant differences in their empirical heat transfer formulas, and there is limited research applicable to OFMs, making it challenging to obtain suitable empirical formulas for heat transfer coefficients. C. Sciascera [59] conducted research on heat capacity and thermal conductivity coefficients. In their study, an LPTN was implemented to model heat flow within a permanent magnet synchronous motor (PMSM). Due to the motor’s low rated speed, both mechanical and iron losses were neglected. They proposed a method to calibrate thermal parameters based on experimental data, using Sequential Quadratic Programming (SQP) algorithms to adjust thermal resistance correction coefficients. Reference [51] combined CFD and LPTN methods. The convective and conductive heat transfer coefficients obtained from a CFD-modified model were incorporated into a thermal network model, as shown in Figure 8, to achieve a more accurate temperature field model. In this case, yellow blocks represent thermal resistance including convective thermal resistance and conduction thermal resistance, white blocks represent thermal resistance including conduction thermal resistance, red circles mean nodes with heat source, and white circles mean nodes without heat source.
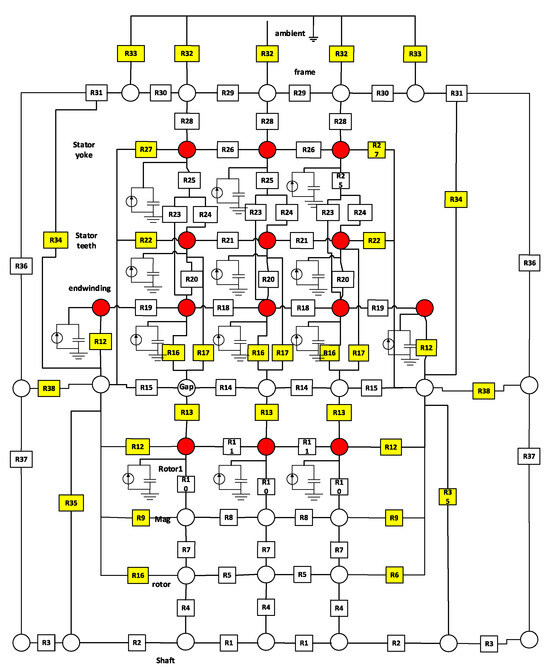
Figure 8.
Lumped-parameter thermal model of total motor [51].
3.1.2. CFD
CFD methods apply fluid–structure coupling and conjugate heat transfer methods to simultaneously analyze the fluid field and temperature field of OFMs, obtaining the surrounding fluid movement conditions and overall temperature field distribution. In addition to solving the overall temperature rise in the motor, CFD can also be used to analyze and optimize the motor’s cooling fan and cooling water channels. Moreover, CFD can be used to better simulate the thermal convection phenomenon inside OFMs, as well as to obtain more accurate thermal convection and thermal conductivity coefficients.
Shafigh Nategh [60] employed a combined CFD and LPTN analysis method to analyze the temperature field of an oil-cooled motor. This method accurately predicted the internal temperature distribution of the motor and compared the effects of traditional cooling methods with direct cooling methods. The study showed that direct cooling methods significantly improved the motor’s heat dissipation efficiency and reduced the operating temperature of key components, allowing the proposal of further optimization methods and suggestions for motor cooling design. La Rocca [61] modeled the complex structure of the end windings of a totally enclosed fan-cooled (TEFC) motor with distributed windings. Using CFD, they solved the fluid state and thermal convection phenomena of the end windings, achieving good results. The thermal convection results are shown in Figure 9.
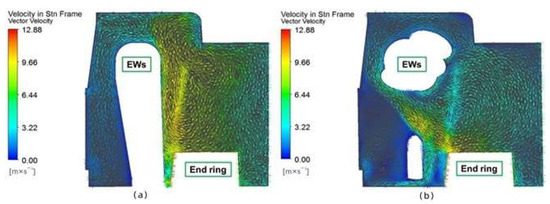
Figure 9.
(a) Model with secondary flow and simplified EWs (end windings); (b) model with secondary flow and new EWs [61].
Guo B [62] combined the thermal network and CFD methods to analyze the temperature field of a conical rotor motor. By using CFD simulations to study the fluid state within the motor, he obtained accurate convective heat transfer coefficients and applied them to the thermal network. Finally, the accuracy of the model was validated through temperature experiments. Fu Min and Yan Hai et al. [63] established a new fluid field model by adding a fluid domain (e.g., air or seawater) outside the motor. Since the convective coefficient of the motor housing was calculated using fluid–structure coupling rather than traditional theoretical formulas, the convective coefficient was no longer a fixed constant but varied with the current fluid and temperature fields. However, during their viscous loss simulation, they used viscosity at a fixed temperature and subsequently incorporated this fixed viscous loss into the temperature field simulation. They did not consider the impact of oil viscosity changes with temperature on viscous loss, resulting in theoretically higher viscous loss and temperature rise values, and did not validate the simulation with experiments.
3.1.3. FEM
The FEM analyzes the actual state of objects using mathematical approximation, discretizing the solution region into multiple elements and connecting these elements to form a mathematical model for temperature calculations. Solving this model yields the temperature rise in each element. The FEM is more accurate than the equivalent thermal network method and has a simple calculation process, but errors in boundary condition calculations can directly affect the accuracy of the temperature field calculations.
Kyuho Sim et al. [64] employed finite element analysis to comprehensively study the thermal behavior of high-speed permanent magnet motors (HSPMMs) with various cooling fluid schemes and gas foil bearings (GFBs). This approach not only helps predict the motor’s temperature distribution, but also provides a scientific basis for designing and optimizing cooling systems. Their analysis combined thermal conduction and fluid dynamics to perform multi-physics coupling, simulating heat flow and heat transfer processes within the motor. This coupled analysis provides more accurate predictions of the motor’s temperature distribution and thermal management effectiveness under real operating conditions.
Zengliang Li et al. [65] used analytically calculated viscous loss as a heat source to build a 3D finite element analysis (FEA) temperature field of an OFM. By establishing a magneto-thermal-fluid coupled finite element model, they conducted an in-depth analysis of the temperature field of the underwater motor. The study indicated that in underwater environments, the temperature field distribution of the motor is significantly affected by electromagnetic losses, cooling methods, and environmental temperatures. External factors such as environmental temperature and pressure also have a significant impact on the motor’s temperature field; high ambient temperatures lead to higher motor temperatures, and changes in pressure affect the flow characteristics of the cooling water, thereby influencing the cooling effect.
The combination of CFD simulation and the LPTN is currently the optimal solution for analyzing the temperature field of oil-filled motors. Due to the oil-filled characteristic between the stator and rotor of such motors, their heat convection coefficient and other parameters differ significantly from those of conventional motors. Through CFD simulations, accurate parameters such as the heat convection coefficient and thermal resistance can be obtained, as has already been experimentally validated in previous studies. By incorporating these parameters into the LPTN, the temperature field distribution of the motor can be quickly and accurately determined. It is hoped that future research will focus more on this method.
3.2. Research on the Temperature Rise in OFMs
The viscosity and flow characteristics of oil are significantly different from those of air, inevitably leading to a distinct internal fluid field distribution in OFMs compared to conventional motors. Additionally, the temperature field distribution and temperature rise in OFMs differ from those in conventional motors.
Firstly, the differences in fluid field distribution and viscosity result in a convective heat transfer coefficient for OFMs that is markedly different from that of conventional motors. Furthermore, the convective heat transfer coefficients derived from oil-related theoretical formulas have not been widely validated through experiments, which can lead to considerable deviations.
Secondly, oil has a much higher thermal conductivity than air, facilitating heat transfer between motor components and resulting in a smaller temperature difference between components within OFMs compared to conventional motors.
Finally, the substantial increase in viscous loss significantly raises the heat generation within the motor, making heat dissipation more challenging. Moreover, viscous loss varies significantly with temperature, complicating the precise calculation of temperature rise.
These factors combined result in a temperature field distribution and temperature rise in OFMs that are significantly different from those in conventional motors. Therefore, accurately calculating the internal fluid field and temperature field distribution in OFMs, as well as summarizing the characteristics of temperature rise, is particularly important. This has significant implications for the design of parameters related to OFMs.
Ahmed M. Teamah et al. [46] developed a finite element model for a self-contained drum motor (SCDM) to study its temperature rise. The study covers a range of rotational speeds from 0 to 150 rpm and oil levels from 0% (i.e., 100% air-filled) to 100%. Figure 10 indicates the effect of rotational speed, N, on the heat transfer inside the system for the case of OV = 100%. This provides a basis for selecting the appropriate oil level at a given rotor speed to achieve optimal temperature field distribution.
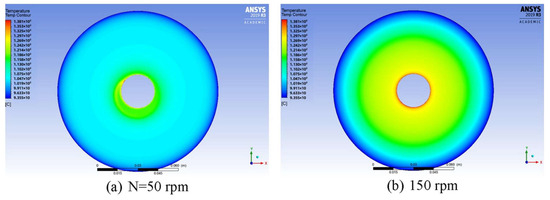
Figure 10.
Effect of rotational speed on temperature distribution within the annular space for OV = 100 case [46].
Feng Wei et al. [66] conducted a temperature rise study on a high-temperature, ultra-slim submersible motor, establishing a three-dimensional finite element model. However, they simply assumed the viscous loss to be 1% of the rated power based on design experience, resulting in precision even less accurate than that given by analytical formulas. They calculated the oil’s convective heat transfer coefficient using theoretical formulas and did not validate the results through experiments.
In reference [67], the temperature rise is calculated by iterative coupling between the fluid field and the temperature field using a 3D CFD model of the motor. The specific steps are as follows:
- Set the initial temperature and, based on the corresponding viscosity of the oil at this initial temperature, perform fluid field simulation to obtain the viscous losses.
- Based on the obtained viscous losses, set the heat source in the temperature field model and calculate the temperature rise.
- Based on the average temperature of the oil calculated from the temperature rise, obtain a new value for the average viscosity of the oil, and then repeat steps 1 and 2.
Reference [68] addresses the important issue of how to calculate viscous losses after the motor reaches steady-state operation by using a User-Defined Function (UDF) to consider the change in viscous losses with temperature in the temperature-rise calculation. Accurate viscous loss calculations under steady-state temperature conditions are crucial for accurate temperature-rise calculations. The study uses the flow velocity distribution results from each iteration step’s fluid field simulation to calculate the convective heat transfer coefficient, addressing the inadequacy in the accuracy of the formula for the convective heat transfer coefficient of the oil. The article presents the functions of parameters such as viscous losses with temperature changes, considering the temperature field simulation results under different conditions, and points out the unique temperature rise characteristics of OFMs.
Considering the impact of rotational speed and temperature on viscous losses, the study in reference [69] first utilized CFD simulations to modify the empirical formula for viscous losses and validated it through experiments. Subsequently, the study implemented a magnetic–thermal coupling heat source allocation method using a UDF and determined the convective heat transfer coefficients for various parts via CFD. Finally, the modified convective heat transfer coefficients and heat sources were incorporated into the constructed LPTN model to achieve coupled calculations of viscous losses and temperature rise, as shown in Figure 11. The temperature-rise results obtained from solving the thermal network were consistent with the experimental results.
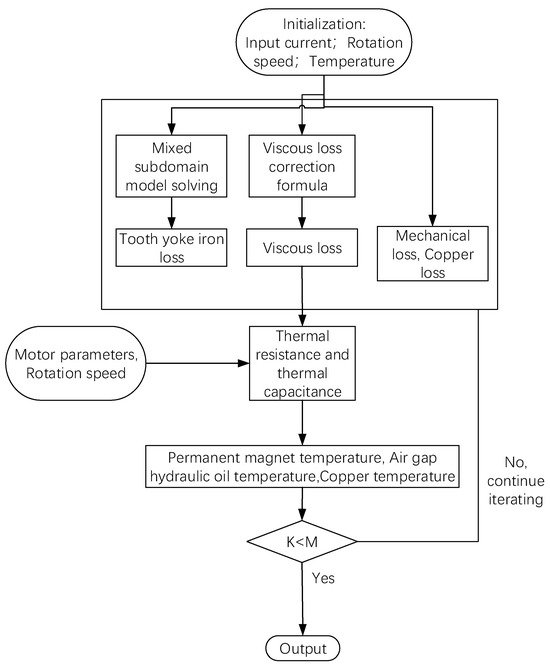
Figure 11.
Transient thermal coupling solution process [67].
The current optimal coupling calculation method involves using CFD simulations to correct the analytical formula for viscous losses, which is then applied to the LPTN to obtain the motor’s temperature rise. The coupling calculation of viscous losses and temperature rise, considering the variation in viscous losses with temperature, addresses the critical issue of calculating viscous losses after the motor reaches steady-state operation. Accurate viscous loss at the steady-state temperature is a key prerequisite for precise temperature-rise calculations. However, there is limited research on the coupling calculation of the temperature field and viscous losses in oil-filled motors. To accurately calculate the temperature rise, many factors must be considered, such as rotor operating conditions, oil type and viscosity, rotor surface roughness, and slot opening shape. These factors can vary even within the same type of motor, making this a challenging issue that requires breakthroughs. As mentioned earlier, even a slight change in factors such as the ReG or rotor surface roughness can lead to differences in the results by orders of magnitude. More attention should be given to the accurate calculation of viscous losses and their coupling with temperature rise.
4. Discussion and Future Challenges
This review mainly focuses on the analysis of the temperature field and viscous losses in OFMs. With the increasing demand for energy and the development of related fields, OFMs will attract more attention. As the main form of loss in OFMs during high-speed operation, viscous losses will also require more in-depth research in the future.
Future research directions may also be highlighted. The complexity of viscous losses in OFMs necessitates a multi-dimensional approach for future research. Detailed suggestions are as follows:
4.1. Coupled Calculation of Viscous Losses and Temperature
Develop comprehensive models that couple temperature, viscosity, and viscous losses. These models should account for the impact of temperature on oil viscosity, the effect of viscosity changes on viscous losses, and the feedback effect of viscous losses on temperature.
Use CFD and thermal analysis tools (e.g., ANSYS Fluent 2024 and CFX 2024) for dynamic simulations to model temperature distribution and changes in viscous losses under various operating conditions.
Set up a test bench to conduct long-term operational tests, collecting temperature and viscous loss data to validate and refine numerical models.
4.2. Impact of Oil Type on Viscous Losses
Systematically study the viscosity–temperature relationship of different oil types (e.g., mineral oils, synthetic oils) and develop corresponding viscosity–temperature models.
Investigate the impact of various additives on oil viscosity and viscous losses, and optimize additive formulations to enhance oil performance.
Conduct accelerated aging tests to study how oil viscosity and viscous losses change over different usage periods, and establish suitable replacement intervals and maintenance strategies.
4.3. Influence of Rotor Surface Roughness
The research findings on the friction coefficient of the rotor surface should be applied to OFMs to adjust the parameters of their analytical models.
Research and optimize rotor surface treatment technologies, exploring the effects of different treatments (e.g., coating, polishing) on surface roughness and oil film formation.
Systematically measure and analyze the impact of different roughness parameters on viscous losses and develop a relationship model between surface roughness and viscous losses.
Integrate experimental data with numerical simulation results to analyze the impact of different surface roughnesses in actual operation and optimize rotor surface design.
4.4. Influence of Motor Structural Parameters
Study the impact of different slot shapes on oil flow and temperature distribution, and optimize slot design to reduce viscous losses.
Consider the coupling effects between motor structural parameters (e.g., air gap, stator tooth shape, slot shape) and oil properties to optimize overall design.
Use multi-physics simulation tools to conduct coupled analyses of the motor’s electromagnetic, thermal, and fluid fields, and study the combined effects of various structural parameters on viscous losses.
Future research should focus on interdisciplinary studies combining experiments, numerical simulations, and intelligent technologies to thoroughly analyze and optimize viscous losses in oil-filled electric motors. By understanding the interactions between viscous losses, temperature, oil type, rotor surface roughness, and structural parameters, optimal design and operational strategies can be developed to enhance overall motor performance and reliability.
5. Conclusions
OFMs are extensively used in deep-sea exploration, EHAs, and oil extraction due to their ability to function under high-pressure conditions by balancing internal and external pressures with hydraulic oil. However, the rotation of the rotor stirs the oil, causing significant viscous loss, which affects temperature distribution within the motor. This review paper focuses on summarizing recent methods for analyzing viscous loss and thermal effects in OFMs, considering factors such as motor structural parameters, rotor speed, and oil viscosity.
This review highlights the importance of accurately calculating viscous loss and temperature rise to optimize motor design. It points out that motor structure, rotor surface roughness, and working conditions significantly influence viscous loss. The viscosity of hydraulic oil, highly affected by temperature, leads to changes in viscous loss, which in turn alters the temperature distribution. The coupling relationship between viscous loss and temperature must be considered for precise analysis.
Current research struggles to simultaneously account for the coupling of viscous loss and the temperature field, rotor surface roughness, and motor structure effects. This paper covers multi-physics coupling methods to analyze these factors comprehensively. It includes the following:
- The use of corrected analytical formulas in CFD simulations or thermal network calculations for iterative solving, achieving fluid and temperature field coupling while enhancing computational efficiency.
- Analytical formulas for viscous loss considering temperature’s impact on oil viscosity.
- The influence of motor structural parameters and rotor surface roughness on viscous loss.
In conclusion, the paper provides insights into the current state of research on viscous loss in and the thermal analysis of OFMs, suggesting future work should focus on improving coupling analysis methods and validating theoretical models with experimental data to enhance the accuracy of motor design and optimization.
Author Contributions
Conceptualization, J.Z. and J.W.; validation, Y.S. and Y.L.; formal analysis, X.H., K.W. and L.C.; data curation, X.H. and Y.F.; writing—original draft preparation, J.Z., Y.S. and X.H.; writing—review and editing, Y.L., K.W. and L.C.; supervision, X.H. and Y.F.; project administration, J.Z. and J.W.; funding acquisition, J.Z. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Key Project of the State Key Laboratory of Fluid Power and Mechatronic Systems SKLoFP_ZZ_2405, the Key Research and Development Program of Zhejiang Province under Grant 2024C01140, the Key R&D Plan Projects in Zhejiang Province 2022C01001 and the National Natural Science Foundation of China under Grant 51977192.
Data Availability Statement
The datasets generated during and/or the analyses undertaken during the current study are not publicly available due to confidentiality but are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| OFM | oil-filled motor |
| AUV | autonomous underwater vehicle |
| ROV | remotely operated vehicle |
| EHA | Electro-Hydrostatic Actuator |
| HST | hydrostatic drivetrain |
| WPMSM | wet-type permanent magnet synchronous motor |
| LPTN | Lumped-Parameter Thermal Network |
| BLDC | Brushless DC Motors |
| PMSM | permanent-magnet synchronous machine |
| SQP | Sequential Quadratic Programming |
| CFD | Computational Fluid Dynamics |
| TEFC | totally enclosed fan-cooled |
| FEM | Finite Element Method |
| HSPMM | high-speed permanent magnet motors |
| GFB | gas foil bearing |
| FEA | finite element analysis |
| EW | end winding |
| SCDM | self-contained drum motor |
| OV | oil volume percentage inside the annular area |
| VFD | variable frequency drive |
| VOF | Volume of Fluid |
| UDF | User-Defined Function |
References
- Zhang, J.; Wang, R.; Fang, Y.; Lin, Y. Insulation Degradation Analysis Due to Thermo-Mechanical Stress in Deep-Sea Oil-Filled Motors. Energies 2022, 15, 3963. [Google Scholar] [CrossRef]
- Li, D.; Guo, F.; Xu, L.; Wang, S.; Yan, Y.; Ma, X.; Liu, Y. Analysis of Efficiency Characteristics of a Deep-Sea Hydraulic Power Source. Lubricants 2023, 11, 485. [Google Scholar] [CrossRef]
- Zou, J.; Qi, W.; Xu, Y.; Xu, F.; Li, Y.; Li, J. Design of Deep Sea Oil-Filled Brushless DC Motors Considering the High Pressure Effect. IEEE Trans. Magn. 2012, 48, 4220–4223. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Q.; Tian, Q.; Yan, S.; Tang, Y.; Zhang, A. Performance and experiment of deep-sea master-slave servo electric manipulator. In Proceedings of the CEANS 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ishak, D.; Manap, N.A.; Ahmad, M.S.; Arshad, M.R. Electrically actuated thrustersfor autonomous underwater vehicle. In Proceedings of the 2010 11th IEEE International Workshop on Advanced Motion Control (AMC), Nagaoka, Japan, 21–24 March 2010; pp. 619–624. [Google Scholar]
- Cho, C.P.; Fussell, B.K.; Hung, J.Y. A novel integrated electricmotor pump for underwater applications. J. Appl. Phys. 1996, 79, 5548–5550. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Liao, H.J. A wide speed range sensorless control technique of brushless DC motors for electric propulsors. J. Mar. Sci. Tech. 2010, 18, 735–745. [Google Scholar] [CrossRef]
- Nagel, N. Actuation Challenges in the More Electric Aircraft: Overcoming Hurdles in the Electrification of Actuation Systems. IEEE Electrification Mag. 2017, 5, 38–45. [Google Scholar] [CrossRef]
- Sayed, E.; Abdalmagid, M.; Pietrini, G.; Sa’adeh, N.M.; Callegaro, A.D.; Goldstein, C.; Emadi, A. Review of electric machines in more-/hybrid-/ turbo-electric aircraft. IEEE Trans. Transp. Electrif. 2021, 7, 2976–3005. [Google Scholar] [CrossRef]
- Jiao, Z.; Li, Z.; Shang, Y.; Wu, S.; Song, Z.; Pan, Q. Active load sensitive electrohydrostatic actuator on more electric aircraft: Concept, design, and control. IEEE Trans. Ind. Electron. 2022, 69, 5030–5040. [Google Scholar] [CrossRef]
- Xu, J.; Du, Y.; Fang, H.; Guo, H.; Chen, Y.-H. A Robust Observer and Nonorthogonal PLL-Based Sensorless Control for Fault-Tolerant Permanent Magnet Motor with Guaranteed Postfault Performance. IEEE Trans. Ind. Electron. 2020, 67, 5959–5970. [Google Scholar] [CrossRef]
- Jiao, Z.; Li, Y.; Yu, T.; Jiang, C.; Huang, L.; Shang, Y. Dynamic thermal coupling modeling and analysis of wet electro-hydrostatic actuator. Chin. J. Aeronaut. 2022, 35, 298–311. [Google Scholar] [CrossRef]
- Yu, S. Design and Loss Analysis of High Speed Submersible Permanent Magnet Motor. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2018. [Google Scholar]
- Xiang, Y.; Tang, T.; Su, T.; Brach, C.; Liu, L.; Mao, S.S.; Geimer, M. Fast CRDNN: Towards on Site Training of Mobile Construction Machines. IEEE Access 2021, 9, 124253–124267. [Google Scholar] [CrossRef]
- Xiang, Y.; Li, R.; Brach, C.; Liu, X.; Geimer, M. A Novel Algorithm for Hydrostatic-Mechanical Mobile Machines with a Dual-Clutch Transmission. Energies 2022, 15, 2095. [Google Scholar] [CrossRef]
- Xu, J.; Jin, W.; Guo, H.; Yu, T.; Fan, W.; Jiao, Z. Modeling and analysis of oil frictional loss in wet-type permanent magnet synchronous motor for aerospace electro-hydrostatic actuator. Chin. J. Aeronaut. 2023, 36, 328–341. [Google Scholar] [CrossRef]
- Ahmed, S.; Toliyat, H.A. Coupled Field Analysis Needs in the Design of Submersible Electric Motors. In Proceedings of the 2007 IEEE Electric Ship Technologies Symposium, Arlington, VA, USA, 21–23 May 2007; pp. 231–237. [Google Scholar]
- Wenjuan, Q.; Jibin, Z.; Jianjun, L. Numerical calculation of viscous drag loss of oil-filled BLDC motor for underwater applica-tions. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 1739–1742. [Google Scholar]
- Jung, J.-W.; Lee, B.-H.; Kim, K.-S.; Kim, S.-I. Interior Permanent Magnet Synchronous Motor Design for Eddy Current Loss Reduction in Permanent Magnets to Prevent Irreversible Demagnetization. Energies 2020, 13, 5082. [Google Scholar] [CrossRef]
- Seeton, C.J. Viscosity–temperature correlation for liquids. Tribol. Lett. 2006, 22, 67–78. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Y.; Cao, L.; Zhuo, L.; Liu, A. Analysis and calculation of friction loss of high-speed permanent magnetic shielding motor. Trans. China Electrotech. 2023, 38, 3122–3129. [Google Scholar]
- Saari, J. Thermal Analysis of High-Speed Induction Machines. Acta Polytechnica Scandinavica Electrical Engineering Series. Ph.D. Thesis, Helsinki University of Technology, Otaniemi, Finland, 1998; 73p. [Google Scholar]
- Aglen, O. Loss calculation and thermal analysis of a high-speed generator. In Proceedings of the IEEE International Electric Machines and Drives Conference, 2003. IEMDC’03, Madison, WI, USA, 1–4 June 2003; pp. 1117–1123. [Google Scholar]
- Wendt, F. Turbulente Strmungen zwischen zwei rotierenden konaxialen Zylinderen. Ing-Arch. 1933, 9, 577–595. [Google Scholar] [CrossRef]
- Yamada, Y. Torque Resistance of a Flow between Rotating Co-Axial Cylinders Having Axial Flow. Bull. JSME 1962, 5, 634–642. [Google Scholar] [CrossRef]
- Bilgen, E.; Boulos, R. Functional Dependence of Torque Coefficient of Coaxial Cylinders on Gap Width and Reynolds Numbers. J. Fluids Eng. 1973, 95, 122–126. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Yamada, Y.; Kishimoto, T. Viscous frictional torque in the flow between two concentric rotating rough cyl-inders. J. Fluid Mech. 1982, 119, 409–422. [Google Scholar] [CrossRef]
- Jianjun, L. Loss and Temperature Field Analysis for Deep-Sea Brushless DC Motor. Ph.D. Thesis, Department of Electrical Engineering, Harbin Institute of Technology, Harbin, China, 2011, unpublished. [Google Scholar]
- Escudier, M.; Oliveira, P.; Pinho, F. Fully developed laminar flow of purely viscous non-Newtonian liquids through annuli, including the effects of eccentricity and inner-cylinder rotation. Int. J. Heat Fluid Flow 2002, 23, 52–73. [Google Scholar] [CrossRef]
- Noui-Mehidi, M.N.; Ohmura, N.; Kataoka, K. Dynamics of the helical flow between rotating conical cylinders. J. Fluids Struct. 2005, 20, 331–344. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Q.; Fan, Y.; Wang, H.; Zhang, A. Research and Experiment on Viscous Friction Power Loss of Deep-Sea Electric Manipulator. In Proceedings of the OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Ji, Z.Q.; Zhu, B.-H.; Lou, Z.-K.; Qian, P.-C. Study of Resistant Torque for “Small Aspect Ratio” Submersible Rotor in Hydraulic Motor Pump. Chin. Hydraul. Pneum. 2018, 2, 20–26. [Google Scholar] [CrossRef]
- Jin, Z.; Zhao, L.; Zhao, X. Research on characteristics of oil immerserd motor for deep water servo application. J. Tianjin Univ. Technollogy 2021, 37, 40. [Google Scholar]
- Yongming, X.; Dawei, M.; Guohui, L. Mechanical loss analysis and calculation of diving oil motor. Electr. Mach. Control. 2004, 8, 370–372. [Google Scholar]
- Nachouane, A.B.; Abdelli, A.; Friedrich, G.; Vivier, S. Estimation of windage losses inside very narrow air gaps of high speed electrical machines without an internal ventilation using CFD methods. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2704–2710. [Google Scholar]
- Nachouane, A.B.; Abdelli, A.; Friedrich, G.; Vivier, S. Numerical approach for thermal analysis of heat transfer into a very narrow air gap of a totally enclosed permanent magnet integrated starter generator. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1749–1756. [Google Scholar]
- Kreith, F. Convection heat transfer in rotating systems. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1969; p. 129. [Google Scholar]
- Han, B.; Liu, X.; Huang, Z.; Zhang, X.; Zhou, Y. Loss Calculation, Thermal Analysis, and Measurement of Magnetically Suspended PM Machine. IEEE Trans. Ind. Electron. 2017, 65, 4514–4523. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss Calculation and Thermal Analysis of Rotors supported by Active Magnetic Bearings for High-speed Permanent Magnet Electrical Machines. IEEE Trans. Ind. Electron. 2015, 63, 2027–2035. [Google Scholar] [CrossRef]
- Hu, Y.; Li, L. Calculating the Oil-Filled Submersible Motor Starting Performance Based on the Fluid-Structure Interaction Meth-od. Small Spec. Electr. Mach. 2013, 41, 38–41. [Google Scholar]
- Chen, H. Research on the Deep-Ocean Pressure-Compensated Oil-Filled Motor. Master’s Thesis, Zhejiang University, Hangzhou, China, 2007. [Google Scholar]
- Li, L.; Peng, B. Analysis and Calculation of Viscous Friction Loss of Rotor of Submersible Motor. In Proceedings of the 14th Shenyang Science Annual Conference (Science, Engineering, Agriculture and Medicine), Shenyang, China, 31 August 2017. [Google Scholar]
- Wang, Y.; Kou, G.; Hu, S. Thermal modeling and analysis of oil-cooled high speed permanent magnet motor in the EHA system. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018. [Google Scholar]
- Cai, M.; Wu, S.; Yang, C. Effect of low temperature and high pressure on deep-sea oil-filled brushless DC motors. Mar. Technol. Soc. J. 2016, 50, 83–93. [Google Scholar] [CrossRef]
- Wrobel, R.; Vainel, G.; Copeland, C.; Duda, T.; Staton, D.; Mellor, P.H. Investigation of Mechanical Loss Components and Heat Transfer in an Axial-Flux PM Machine. IEEE Trans. Ind. Appl. 2015, 51, 3000–3011. [Google Scholar] [CrossRef]
- Teamah, A.M.; Hamed, M.S. Investigation of transient multiphase Taylor-Couette flow. Alex. Eng. J. 2022, 61, 2723–2738. [Google Scholar] [CrossRef]
- Teamah, A.M.; Hamned, M.S. Numerical and Experimental Study of The Viscous Dissipation of Oil inside the Electric Motor’s Gap. J. Fluid Flow, Heat Mass Transf. 2023, 10, 45. [Google Scholar] [CrossRef]
- Yin, Y.; Li, H.; Xiang, X. Oil Friction Loss Evaluation of Oil-Immersed Cooling In-Wheel Motor Based on Improved Analytical Method and VOF Model. World Electr. Veh. J. 2021, 12, 164. [Google Scholar] [CrossRef]
- Peng, J.; Hui, L.I.; Xuewei, X.; Yi, Y.; Bin, Y. Analytical calculation of oil friction loss taking into account action of cup-shaped rotor and teeth-grooves stator. Electr. Mach. Control. 2023, 27, 9–19. [Google Scholar]
- Meng, L.; Bo, Y.; Yuru, Z.; Lei, T. Analysis and research of oil friction loss of oil-cooled motor for aero. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2022), Nanching, China, 17–20 August 2022; pp. 634–637. [Google Scholar]
- Wu, K.; Cai, L.; Zhang, J.; Fang, Y.; Wang, Y. Thermal analysis of deep-sea oil-filled motor using lumped-parameter thermal model and CFD. In Proceedings of the 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 28–31 October 2022; pp. 1–5. [Google Scholar]
- Liu, J.; Yan, L.; He, X.; Zhou, Y.; Yu, Z. Analysis of Oil Viscous Drag Loss of Deep-sea Motor Based on CFD Method. In Proceedings of the 2022 IEEE 17th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 16–19 December 2022; pp. 1289–1293. [Google Scholar]
- Cai, L. Analysis of Viscous Loss and Temperature Field of Oil-Filled Permanent-Magnet Synchronous Motor. Master’s Thesis, Zhejiang University, Hangzhou, China, 2023. [Google Scholar]
- Geng, W.; Zhu, T.; Zhang, Y.; Wu, C.; Wang, Y.; Li, Q.; Zhang, Z. Rotor Air-Friction Loss and Thermal Analysis of IPM Rotors for High Speed Axial-Flux Machine. IEEE Trans. Ind. Appl. 2022, 59, 779–788. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and Modern Approaches for Thermal Analysis of Electrical Machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Björn, J.; Johan, A.; Petter, K. Thermal Modelling of an Electro-hydrostatic Actuation System. In Proceedings of the Recent Advance in Aerospace Actuation System and Components, Toulouse, France, 13–15 June 2001. [Google Scholar]
- Jiang, Y.; Huang, X. Thermal Analysis of BLDC Motors Using Thermal Network Modeling for Aerospace Applications. Mi-cromotors 2013, 46, 19–23. [Google Scholar]
- Gronwald, P.O.; Kern, T.A. Traction Motor Cooling Systems: A Literature Review and Comparative Study. IEEE Trans. Transp. Electrif. 2021, 7, 2892–2913. [Google Scholar] [CrossRef]
- Sciascera, C.; Giangrande, P.; Papini, L.; Gerada, C.; Galea, M. Analytical Thermal Model for Fast Stator Winding Temperature Prediction. IEEE Trans. Ind. Electron. 2017, 64, 6116–6126. [Google Scholar] [CrossRef]
- Nategh, S.; Huang, Z.; Krings, A.; Wallmark, O.; Leksell, M. Thermal Modeling of Directly Cooled Electric Machines Using Lumped Parameter and Limited CFD Analysis. IEEE Trans. Energy Convers. 2013, 28, 979–990. [Google Scholar] [CrossRef]
- La Rocca, S.; Pickering, S.J.; Eastwick, C.N.; Gerada, C.; Rönnberg, K. Fluid flow and heat transfer analysis of TEFC machine end regions using more realistic end-winding geometry. J. Eng. 2019, 2019, 3831–3835. [Google Scholar] [CrossRef]
- Guo, B.; Huang, Y.; Guo, Y.; Zhu, J. Thermal Analysis of the Conical Rotor Motor Using LPTN With Accurate Heat Transfer Co-efficients. IEEE Trans. Appl. Supercond. 2016, 26, 1–7. [Google Scholar]
- Min, F.; Hai, Y.; Zhaoyang, Y.; Wenliang, W.; Chunxu, M. Coupling calculation of 3D whole domain steady flow and temperature field for underwater oil-filled brushless DC motors. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Sim, K.; Lee, Y.-B.; Jang, S.-M.; Kim, T.H. Thermal analysis of high-speed permanent magnet motor with cooling flows supported on gas foil bearings: Part I—coupled thermal and loss modeling. J. Mech. Sci. Technol. 2015, 29, 5469–5476. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Yu, R.; Zhang, L.; Xu, C. Analysis of Influence Factors of Underwater Motor Temperature Field Based on Magne-to-thermal-flux Coupling. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 773–778. [Google Scholar]
- Feng, W.; Yang, S.; Zhang, B. Research on Temperature Rise of High-Temperature Ultra-Slim Long Submersible Permanent Magnet Motor. Electr. Mach. Control. Appl. 2021, 48, 50–56. [Google Scholar]
- Zhang, X. Study on the Temperature Field of the Submersible Permanent Magnet Synchronous Motor; China University of Petroleum (EastChina): Dongying, China, 2017. [Google Scholar]
- Wang, J.; Xu, L.; Cai, L.; Zhang, J.; Tian, J. CFD-based Temperature Field Analysis and Lifetime Prediction of Brushless DC Motor. In Proceedings of the 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 28–31 October 2022; pp. 1–5. [Google Scholar]
- Wu, L.W. Calculation of Viscous Losses and Temperature Field Analysis for Oil-Filled Permanent Magnet Synchronous Motors Based on CFD-LPTN. Master’s Thesis, Zhejiang University, Hangzhou, China, 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).