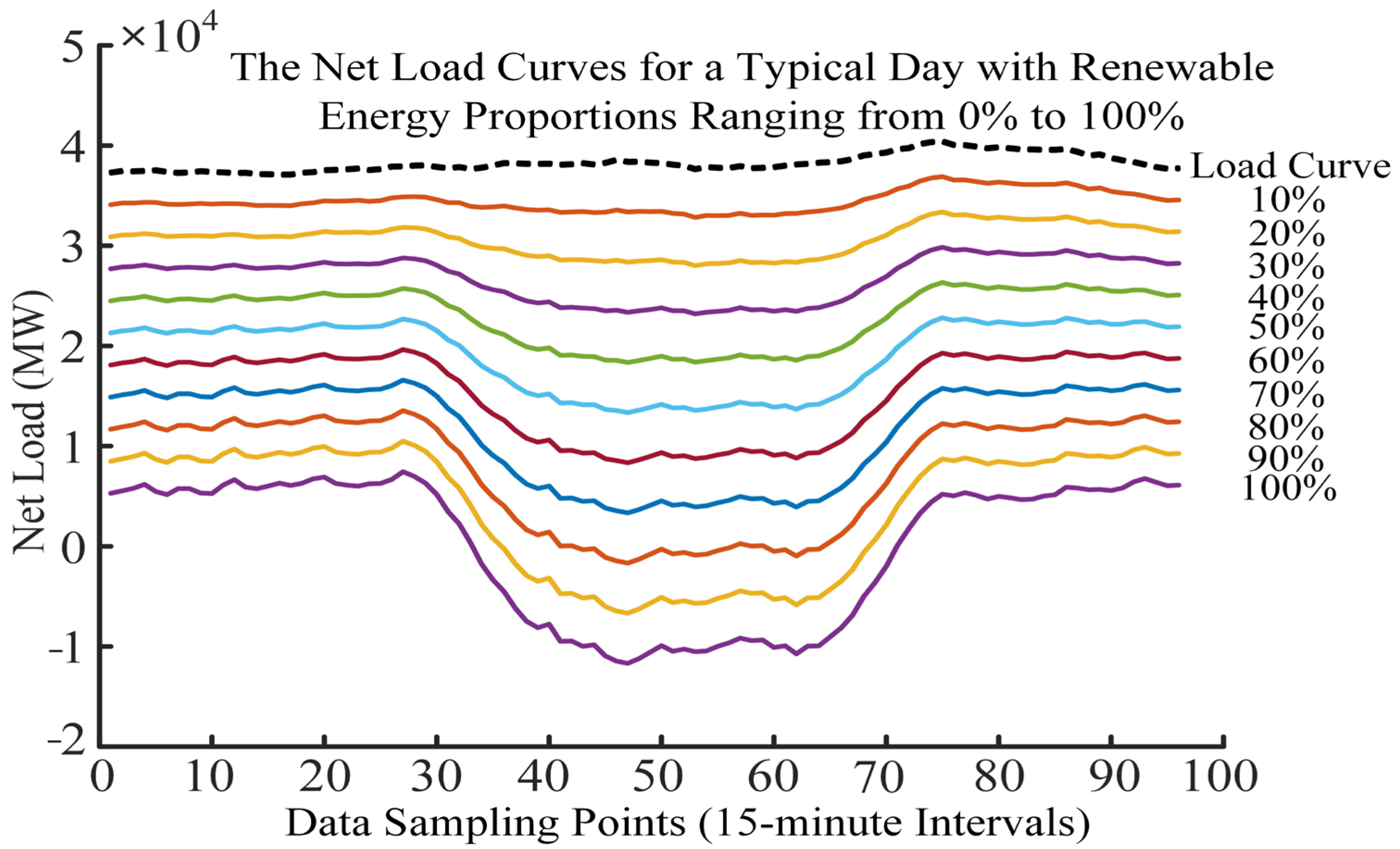
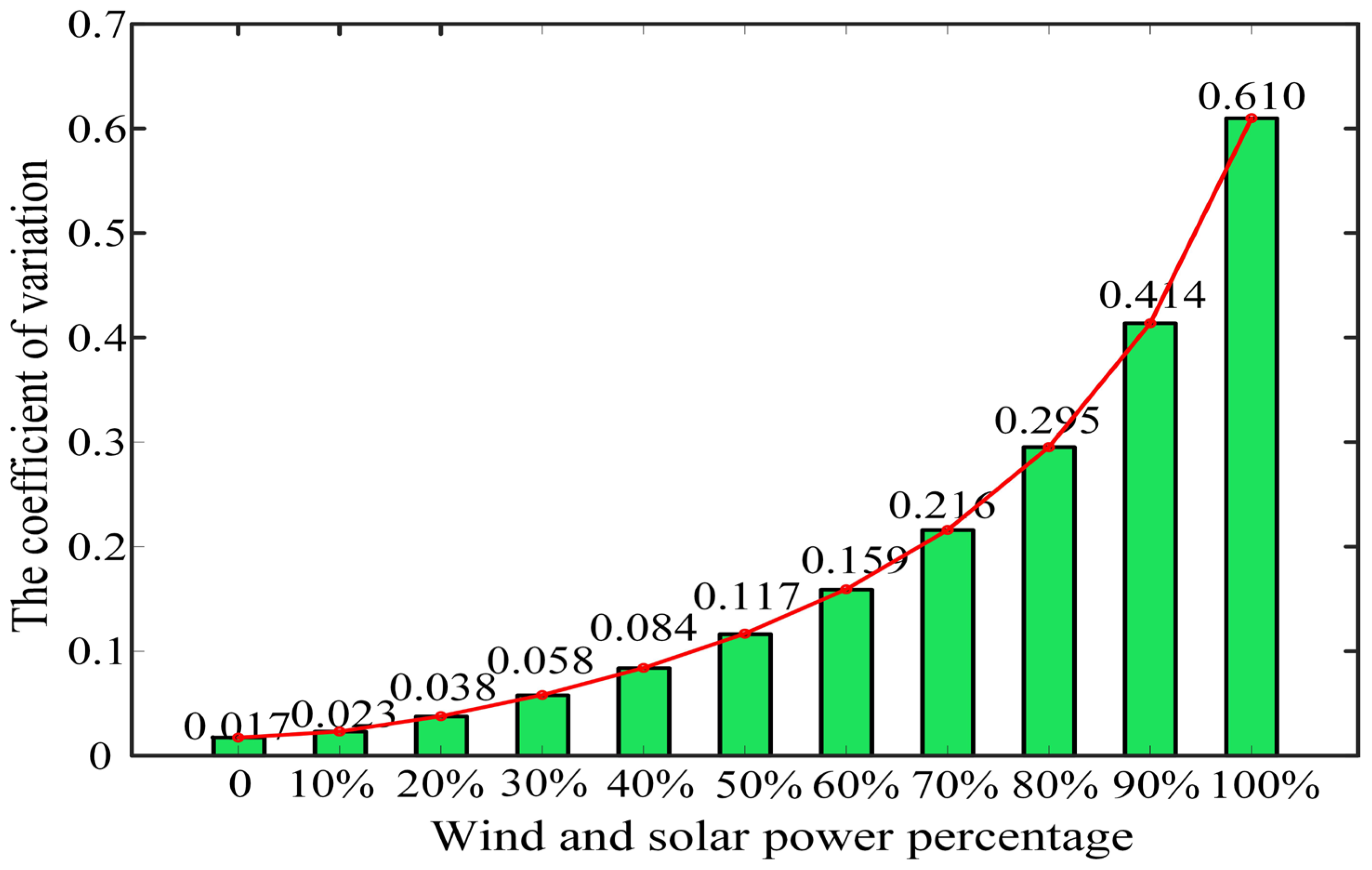
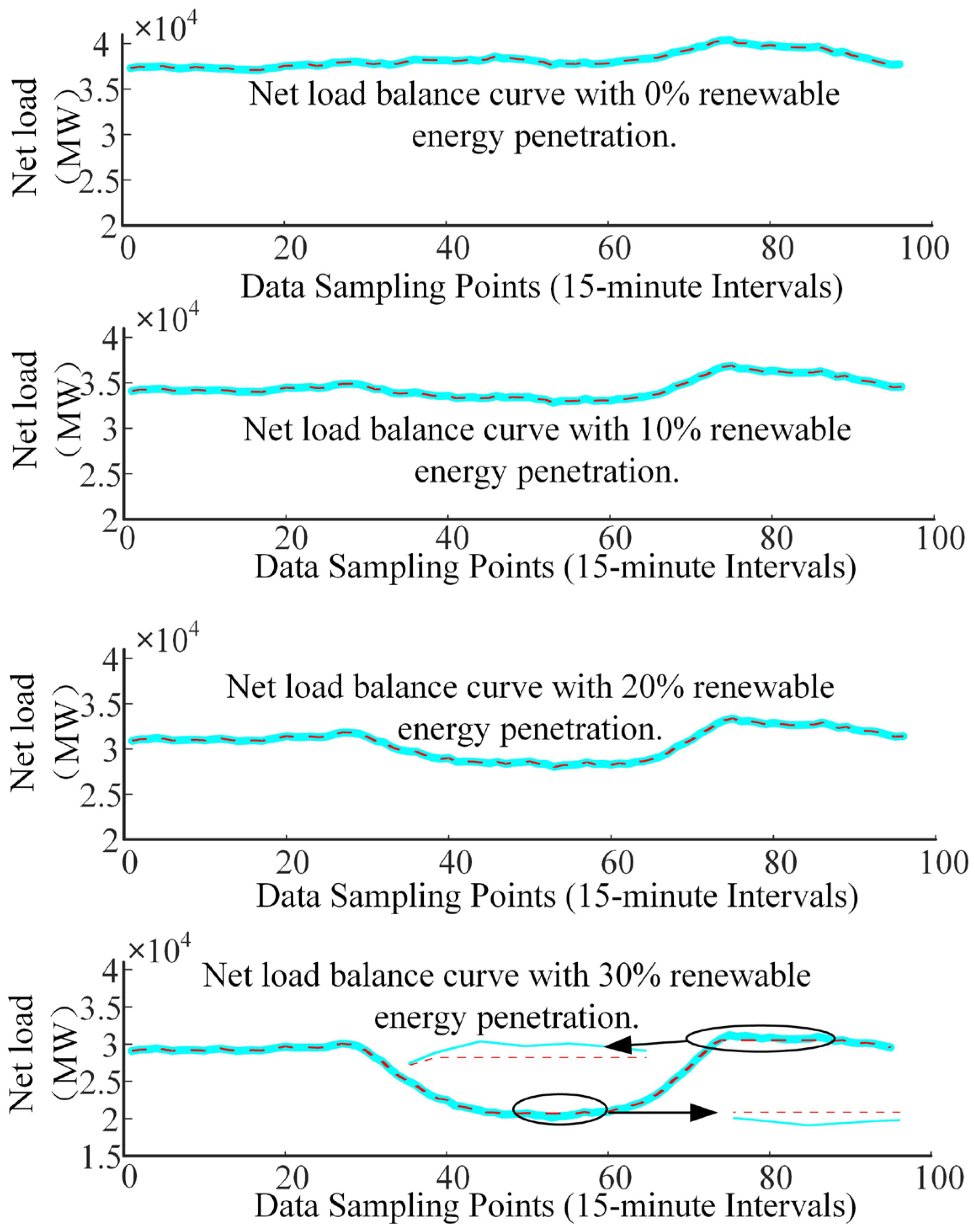
4.1. Impact of Variable Renewable Energy on Power System Balancing Mechanisms
Wind and solar power generation are characterized by high levels of variability due to fluctuating wind and sunlight conditions. As the installed capacity of wind and solar energy increases, this variability directly impacts the stability of the power grid. In traditional power systems, balancing mechanisms rely on conventional generators, such as coal and hydropower, to adjust their output and maintain the balance between supply and demand. However, with the growth of wind and solar energy, these traditional balancing mechanisms are becoming less effective.
Firstly, the output of wind and solar power is highly dependent on weather conditions, making it difficult for conventional power sources to adjust quickly enough to meet the fast-changing demand. Secondly, in systems with a high penetration of renewable energy, the load variability increases significantly, leading to greater uncertainty. With a high proportion of photovoltaic generation, the power system’s balancing mechanism increasingly depends on flexible energy storage systems to manage the frequent fluctuations in the net load curve [
20].
To address these challenges, the power system must enhance its regulation capabilities on multiple levels. First, existing coal and hydropower units can be retrofitted to improve their flexibility. Second, energy storage systems, such as pumped hydro and battery storage, can play a critical role in regulating grid frequency and voltage. Finally, adjustable loads can contribute through demand response mechanisms, storing energy during periods of low demand and releasing it during peak periods, thereby smoothing the net load curve.
4.2. Modeling of Regulation Resources
In the power system, the main regulating resources include traditional thermal power plants, such as coal-fired, oil-fired, and gas-fired plants, along with adjustable hydroelectric stations, pumped storage plants, various new energy storage devices (excluding pumped storage), adjustable loads, and interconnection lines. The models for the participation of these regulating resources in system regulation are as follows.
1. Conventional Thermal Power Plants
Conventional thermal power plants have long been the primary energy source in power systems, providing the foundation for ensuring safe and stable grid operation. They have historically been the cornerstone of traditional power systems. Despite the rapid growth of wind and solar energy, conventional coal-fired plants will continue to play a crucial role in system regulation for some time. The model for thermal power plant participation in system regulation is presented in Equation (8)
where
and
represent the upward and downward regulation capabilities of thermal power plants,
and
represent the maximum and minimum generation output,
represents the current generation output of thermal power plants,
and
represent the upward and downward ramp rates of coal-fired generating units, and
represents the ramping time interval.
2. Adjustable Hydroelectric Stations
Adjustable hydropower stations are also a crucial regulation resource, with their ability to start, stop, and adjust output quickly, making them well suited to system regulation. They play a significant role in maintaining power system stability. The model for hydropower station participation in system regulation is provided in Equation (9).
where
and
represent the upward and downward regulation capabilities of adjustable hydroelectric stations,
and
represent the maximum and minimum generation output of adjustable hydroelectric stations,
represents the current generation output of adjustable hydroelectric stations,
and
represent the upward and downward ramp rates of adjustable hydroelectric stations, and
represents the ramping time interval.
3. Pumped Storage Power Stations
Pumped storage power plants play a critical role in modern power systems, particularly with the integration of high proportions of renewable energy. They balance supply and demand by storing excess electricity during periods of low demand and generating power during peak times. With their ability to respond rapidly to grid fluctuations, pumped storage facilities support the growth of renewable energy and contribute to grid stability. Currently, they are the most economical, mature, and reliable form of energy storage in power systems. The model for their participation in system regulation is shown in Equation (10).
where
and
represent the generation mode and pumping mode of pumped storage power stations,
and
represent the maximum generation power and maximum pumping power of pumped storage power stations, St represents the energy corresponding to the current water storage level, Smax represents the energy corresponding to the maximum water storage level,
represents the energy corresponding to the minimum water storage level,
represents the generation efficiency,
represents the pumping efficiency, and
represents the time interval for generation or pumping.
4. New Energy Storage Devices
With the rapid growth of wind and solar energy, the role of emerging energy storage technologies in power systems has become increasingly prominent. Their fast regulation capabilities offer more flexible solutions for maintaining system stability and facilitating the integration of renewable energy. A model of the participation of emerging energy storage in system regulation is presented in Equation (11).
where
and
represent the discharge and charge modes of the new energy storage device,
and
represent the maximum discharge and maximum charge power of the energy storage device,
represents the current state of charge of the energy storage device,
represents the total energy capacity of the energy storage device,
and
represent the discharge and charge efficiencies, and
is the charging or discharging time interval.
5. Controllable Loads
Controllable loads are a crucial regulation resource in future power systems with a high share of renewable energy. In this context, it is essential to fully leverage the load-side regulation capacity. The model for controllable load participation in system regulation is provided in Equation (12).
where
and
represent the upward and downward regulation capabilities of a controllable load,
and
represent the maximum power change limits for upward and downward adjustments of the controllable load,
and
represent the upward and downward regulation rates of controllable load, and
is the regulation time interval.
6. Interconnection Lines
Interconnection lines between systems enable cross-regional power transmission, facilitating electricity exchange between grids. This helps balance supply and demand differences across regions, enhancing both the stability and flexibility of the power system. A model of the role of system interconnections in grid regulation is provided in Equation (13).
where
and
represent the upward and downward regulation capabilities of interconnection lines,
and
represent the maximum and minimum transmission capacity limits of interconnection lines,
represents the current transmission power of the interconnection lines,
and
represent the upward and downward ramp rates of interconnection line power adjustment, and
is the regulation time interval.
4.3. Turning Point in the Demand for Power System Regulation
As the proportion of renewable energy generation in the power system increases, the demand for system regulation rises, making an ample regulation capacity essential for the safe and stable operation of the system [
15]. In scenarios with no or low renewable energy penetration, both overall and local net load fluctuations are minimal, and the regulation capabilities of traditional sources like thermal and hydroelectric power are sufficient to match the net load curve. However, as the share of renewable energy grows, coordinated efforts from power sources, the grid, loads, and energy storage become necessary to mitigate net load fluctuations. The turning point in regulation demand is closely linked to the level of renewable energy development.
Existing studies often measure renewable energy development using the penetration rate of capacity or energy [
21,
22,
23,
24]. However, relying solely on installed capacity or energy output is insufficient due to variations in load characteristics, resource availability, and grid structures across different power systems. Therefore, this paper categorizes the stages of renewable energy development based on the turning point in regulation demand. This approach allows for a more accurate analysis of system characteristics and serves as an effective supplement in assessing different levels of renewable energy integration.
Low-Proportion Renewable Energy Power System: Net load fluctuations are minimal, and regulation demand is low. Conventional regulation from thermal and hydroelectric sources is sufficient to meet this demand.
Medium-to-High-Proportion Renewable Energy Power System: Net load fluctuations increase, and traditional power sources continue to be the primary means of regulation. However, additional measures, such as enhancing system flexibility [
20], are needed to meet growing regulation demands.
High-Proportion Renewable Energy Power System: As net load fluctuations rise further, loads and grid interconnections must participate in regulation. Pumped storage, new energy storage systems, and other storage facilities are introduced as supplemental resources. Power sources, the grid, loads, and storage collectively participate in system regulation.
Ultra-High-Proportion Renewable Energy Power System: Net load fluctuations are significant, and energy storage shifts from a supplemental to a primary regulatory role. The required scale of energy storage surpasses the combined regulation capacity of other resources.
4.4. Optimal Load Balancing Method Considering the Turning Point of Regulation Demand
The core function of traditional power systems is to maintain a balance between generation and consumption. With the integration of renewable energy, the primary objective shifts to meeting both load demand and incorporating renewable energy. Effective system operation now requires using various regulation resources to track and smooth the net load. By applying the regulation resource models from
Section 4.2 and the concept of a turning point in the regulation demand from
Section 4.3, an optimal net load balancing method is developed. This method prioritizes traditional power sources for regulation, followed by controllable loads and system interconnections. Once the regulation capacity of conventional sources is fully utilized, energy storage systems are employed. The goal is to determine the optimal combination of regulation resources to manage net load fluctuations. Due to the diversity and complexity of these resources, the optimization problem is nonlinear, multi-objective, and presents challenges in terms of the solution space.
Considering the robust parallel search capability of the genetic algorithm (GA), along with its flexibility in adjusting parameters such as population size, iteration count, crossover rate, and mutation rate [
16,
17], GA is used for optimization. Its dynamic adaptability and resistance to local optima make it suitable for solving this complex problem. This paper employs a novel approach by using GA to track the net load curve, incorporating a fitness function designed to optimize the use of multiple regulation resources, thereby revealing the evolution of regulation demand in power systems.
To prioritize achieving a specific proportion of new energy generation without curtailment while ensuring supply reliability, the adaptation function F is designed to maximize the tracking of the target net load by various regulation resources, considering their participation as a priority, as shown in (14).
where
represents the cumulative curtailment of new energy,
represents the cumulative tracking deviation;
Φ is the penalty term set, where
G,
H,
L,
T,
S, and
E, respectively, represent the scale of the participation of thermal power, hydroelectric power, adjustable loads, system interconnection power control, pumped storage power stations, and new energy storage in the regulation;
α,
β,
γ,
φ,
ϵ,
ρ,
δ,
θ are corresponding penalty coefficients used to adjust the influence of each parameter, balancing different performance indicators, according to the overall net load tracking scheme for power optimization.
The specific tracking method is as follows:
First, determine the initial outputs
at time
t = 0 based on the overall adjustment range of the regulating resources:
where
represents the initial value of the net load,
r denotes the type of regulating resource,
R represents the set of regulating resource types,
denotes the minimum adjustment capacity of a certain type of regulating resource, and
represents the maximum adjustment capacity of a certain type of regulating resource.
Next, iterate to calculate the output for each data point. For each time point
t, adjust the output based on the difference between the target net load and the current output:
where
represents the net load at time
t,
is the current output of the regulating resource at time
t, and
is the difference between the target load and the current output of the regulating resource at the current time, used to determine how to adjust the output of the regulating resource to match the target load.
If
> 0, the ramping demand
is:
If
< 0, the ramping demand
is:
The output power of the regulating resource
at time
t is:
The flowchart of the net load balancing method is shown in
Figure 7.