Probabilistic Assessment of the Impact of Electric Vehicle Fast Charging Stations Integration into MV Distribution Networks Considering Annual and Seasonal Time-Series Data
Abstract
1. Introduction
- Method for Generating Synthetic EV Load Profiles: The approach employs various probability distributions for stochastic variables related to EV charging and seasonal variations. A software code was developed to generate EV fast-charging profiles for an FCS. The code realistically models an FCS with selectable charging points according to the implementation requirements. Each charging point randomly selects the number of EVs to charge during the day and their arrival times, considering whether there is a holiday season. During the holiday season, EV charging increases. Charging power for each EV is calculated, considering random battery capacity, the initial/final state of charge, and charging duration. The charging profile of the FCS results from summing individual EV charging profiles throughout the day. This process is repeated for additional days to cover an entire year. The code for generating these profiles is available at the provided URL: https://drive.google.com/drive/folders/1tRKRfQQbBUYsdyXWh5N0iVXT8fdUiVPm?usp=sharing (accessed on 25 June 2024).
- Time Series of Probability Limit Violations: While the study focuses on an accurate feeder in Brazil, it is important to note that the approach applies to any feeder. It assesses monthly probabilities of exceeding permissible limits for network variables (voltage, element overload, and losses). The monthly time series over a year empowers network engineers to make informed decisions, mitigating the negative impact of fast EV charging. This contribution fills a gap in the literature, as existing cases rarely evaluate monthly and yearly probabilities of exceeding network variable limits.
2. Materials and Methods
3. Simulation Procedure and Fast Charging Modeling
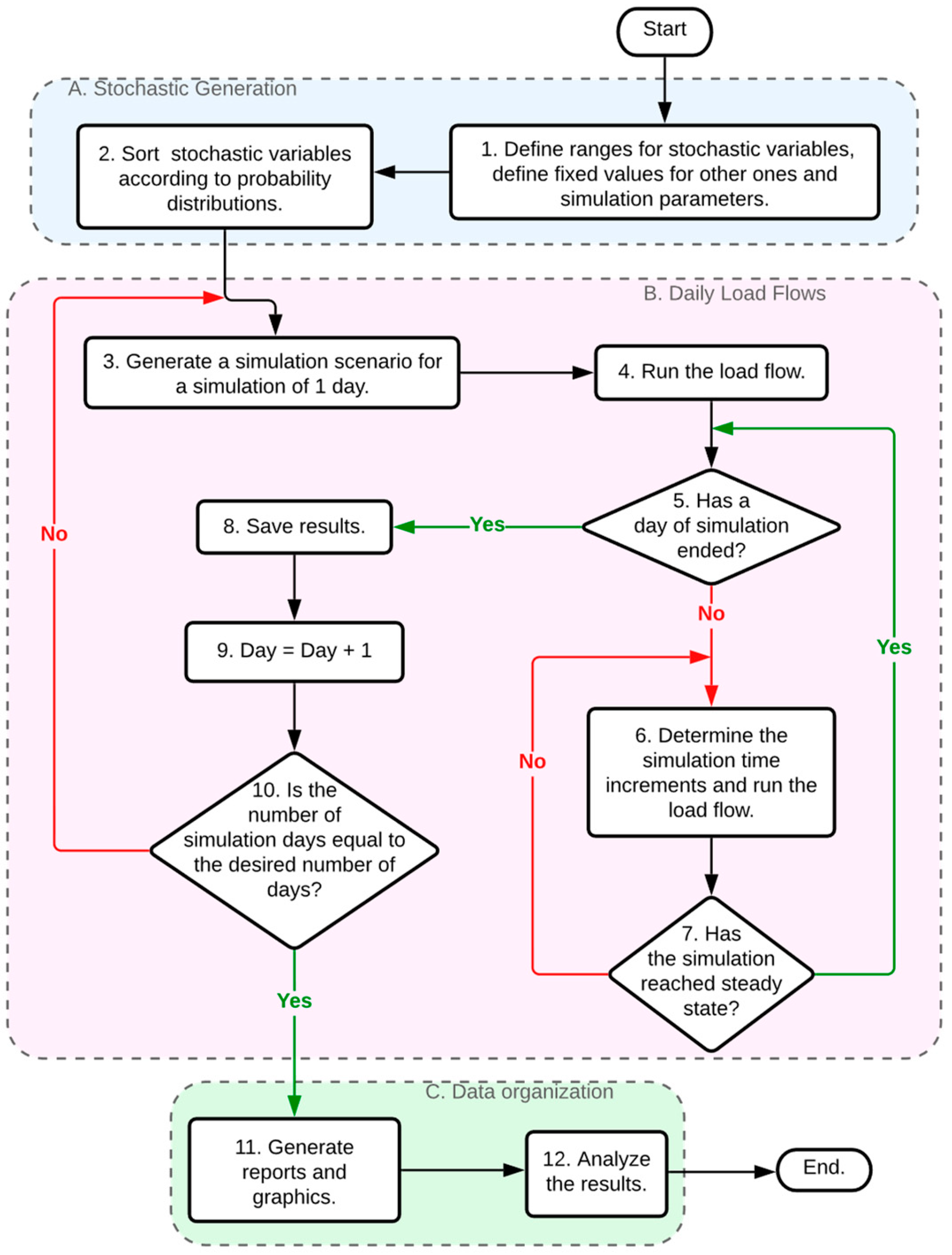
3.1. Simulation Procedure
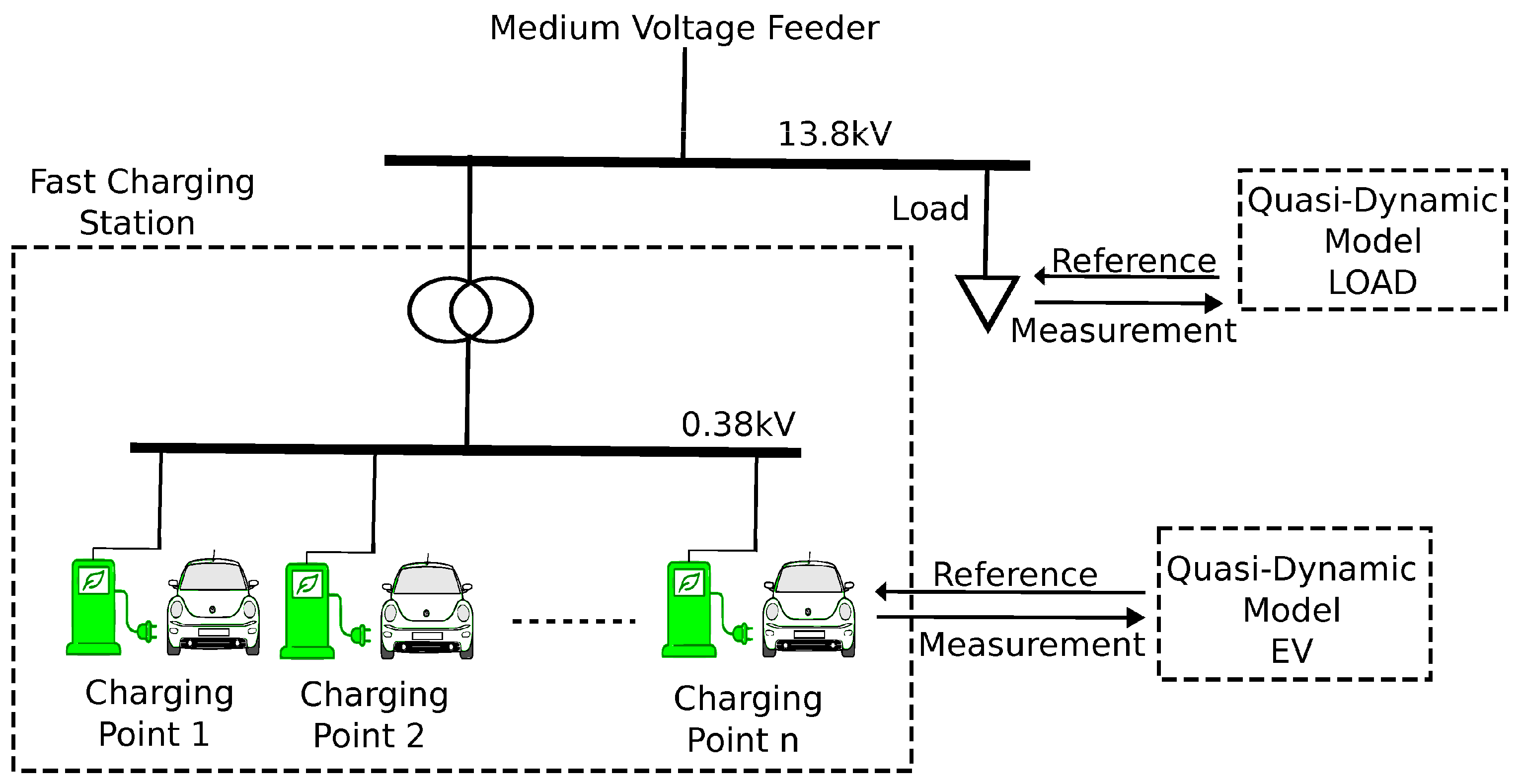
3.2. Quasi-Dynamic Model for a Fast Charging Station
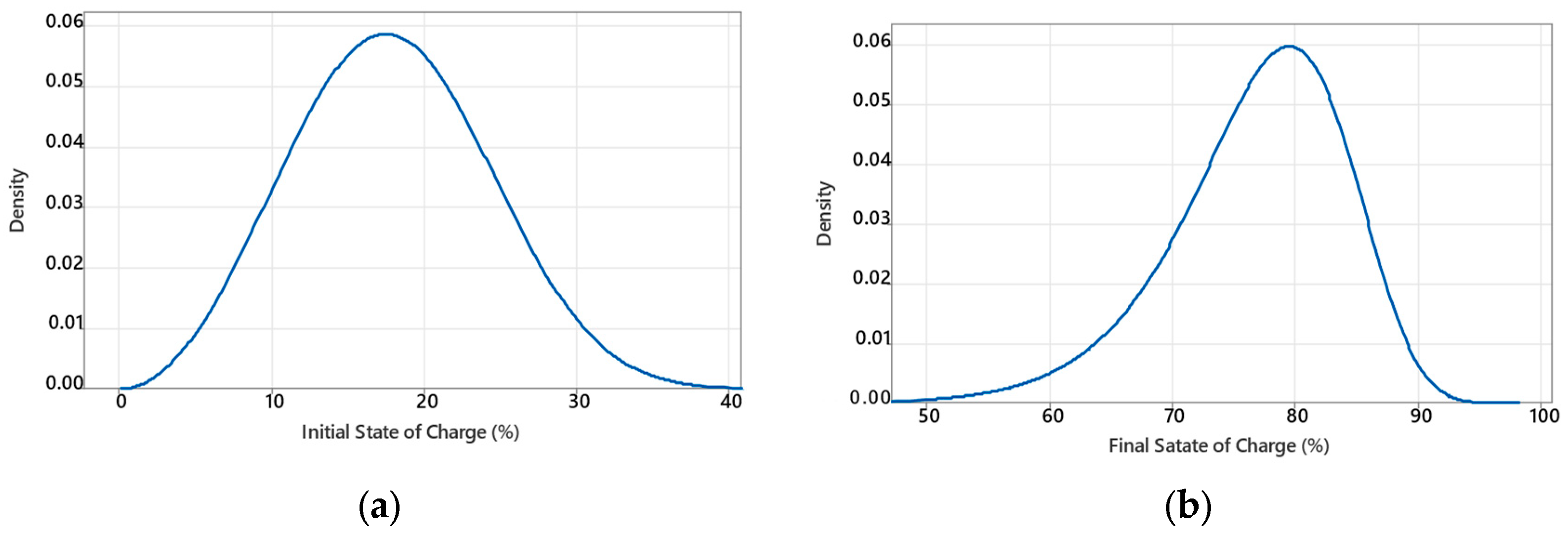
- Battery’s initial state of charge (SOCini): When an EV arrives at a charging station, the battery’s initial state of charge remains undetermined. A Weibull probability distribution characterized by a shape parameter of 3 and a scale parameter of 20 is used to generate this variable. This approach enables the random generation of initial SOC up to 40%, as depicted in Figure 4a.
- Final state of charge (SOCfin): The developed model considers the possibility of a user departing from the charging point without reaching full charge. This scenario is modeled using a Weibull probability distribution with a shape parameter of 13 and a scale parameter of 80. This approach allows for the random generation of final charge states within an approximate SOC range of 50% to 95%, as demonstrated in Figure 4b. This flexibility in modeling user behavior is a key feature of our simulation model.
- Arrival time of the EV at the charging point: The specific time when an EV arrives at a charging station during the day cannot be precisely determined. A normal probability distribution with a mean of 13 h and a standard deviation of 4 h is selected to address this variability. This statistical approach produces a higher frequency of predicted arrival times around midday.
- Battery’s capacity (Cbat): This variable is generated using a uniform distribution, considering the diverse battery capacities of EVs arriving at the charging station. This approach accounts for the commercially available range of battery capacities, which typically spans from 30 to 67 kW/h.
- EV charging time (Tch): This is the required time to charge the EV. It is modeled using a uniform distribution that spans a timeframe of 20 to 40 min for the charging process.
- Number of EVs arriving at an FCS: The EV charging points account for charging between 20 and 40 EVs each. The specific number of EVs to be charged is randomly generated using a uniform distribution.
| Listing 1. Segment of the developed code in MATLAB© environment. |
| % Definition of constants MIN_DIA = 1440; %Minutes in a day DIAS_ANO = 365; %Number of days in the year n_Punt_Rec = 6; %Number of charging points within an FCS MAX_VE = 40; %Maximum number of EV at the charging point MIN_VE = 20; %Minimum number of EV at the charging point T_CAR_MIN = 20; %Minimum charging time in minutes T_CAR_MAX = 40; %Maximum charging time in minutes … for punt=1:n_Punt_Rec*N_Estac for ve=1:N_VE(punt) SOC_INI(ve,punt) = round(wblrnd(20,3),1); %Weibull for SOC ini SOC_FIN(ve,punt) = round(wblrnd(80,13),1); %Weibull for SOC fin T_CAR(ve,punt) = round(unifrnd(T_CAR_MIN,T_CAR_MAX)); if dia_ano == 1 T_ARR(ve,punt) = round(normrnd(MU,SIGMA)); else T_ARR(ve,punt) = round(normrnd(((dia_ano-1)*MIN_DIA+MU),SIGMA)); end AUX = round(unifrnd(1,8)); %Random aux for sort C bat switch AUX case 1 C_BAT(ve,punt) = 30; case 2 C_BAT(ve,punt) = 33; case 3 C_BAT(ve,punt) = 38; case 4 C_BAT(ve,punt) = 40; case 5 C_BAT(ve,punt) = 42; case 6 C_BAT(ve,punt) = 50; case 7 C_BAT(ve,punt) = 52; otherwise C_BAT(ve,punt) = 67; end end end … |
4. Test System and Study Cases
4.1. Network Description
4.2. Study Cases
- Case 1—Base Case: The Base Case does not have FCSs.
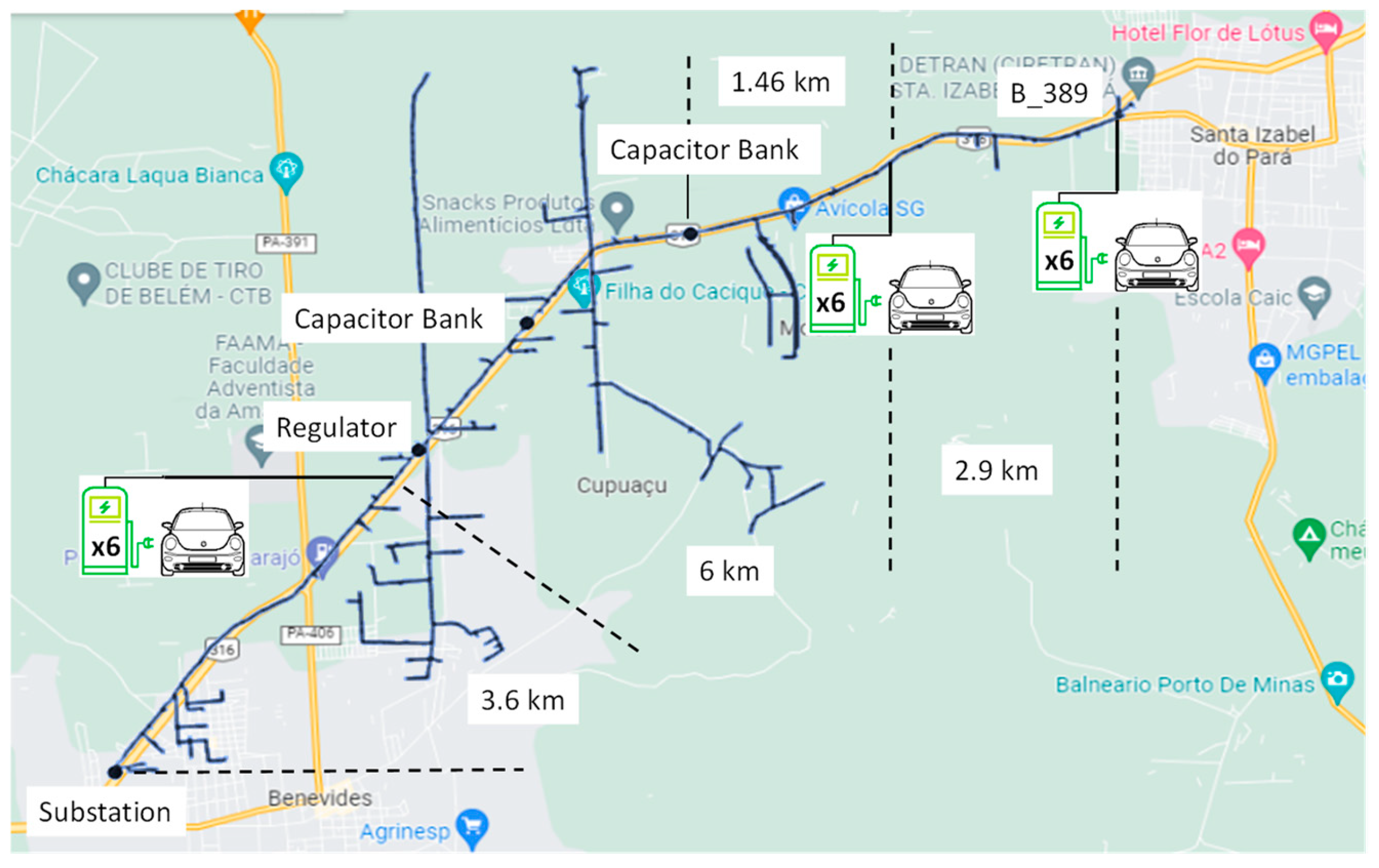
- Case 2—Feeder BENBN-01 with three FCSs located along the feeder: Three FCSs are located at different places in the feeder, as illustrated in Figure 6.
- Case 3—Feeder BENBN-01 with concentrated fast charging points at the end of the feeder: In this case, the B_389 bus has 18 charging points from an FCS. A 13.8/0.38 kV, 2.5 MVA, three-phase transformer feeds the charging points.
5. Results and Discussion
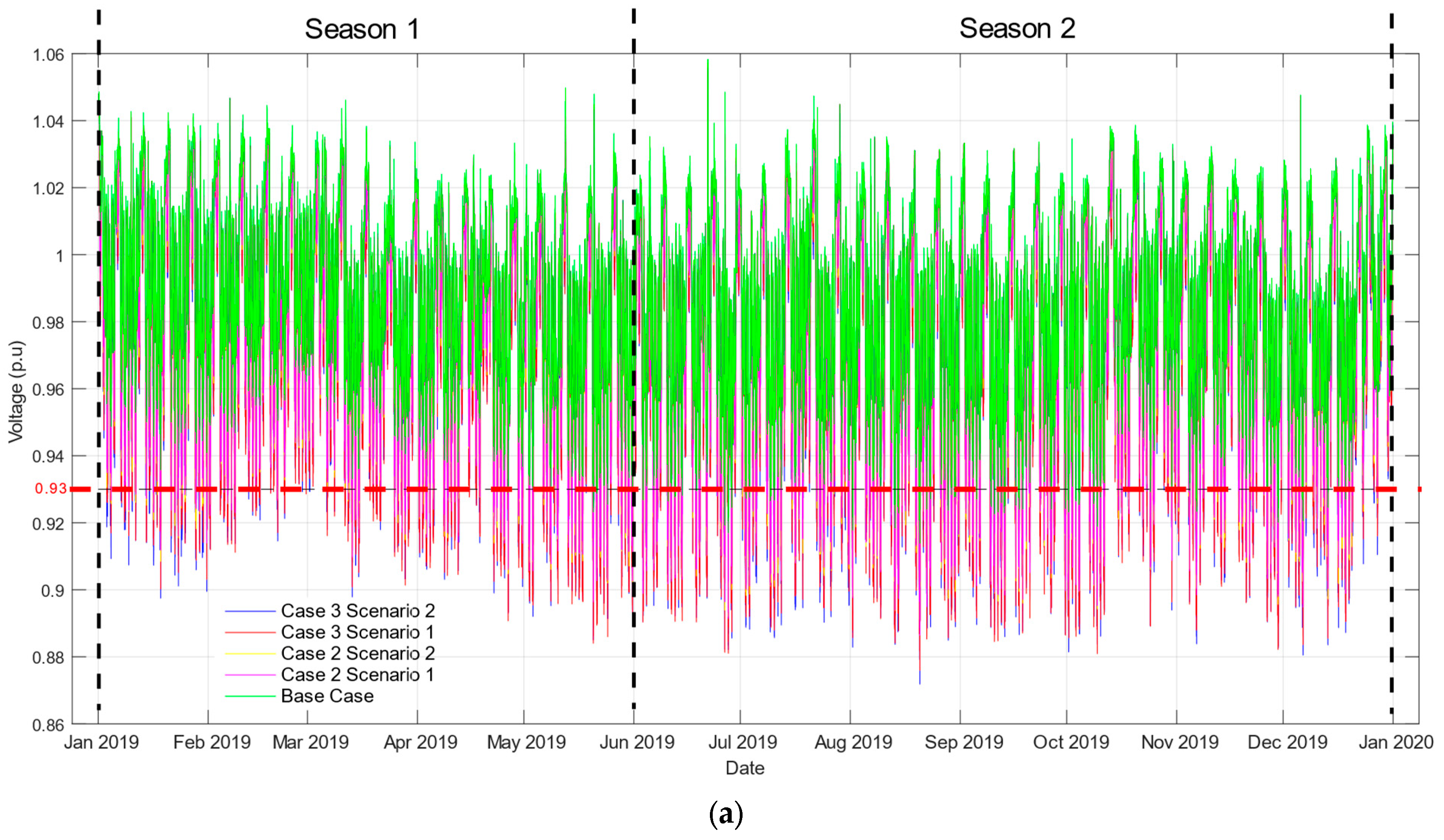
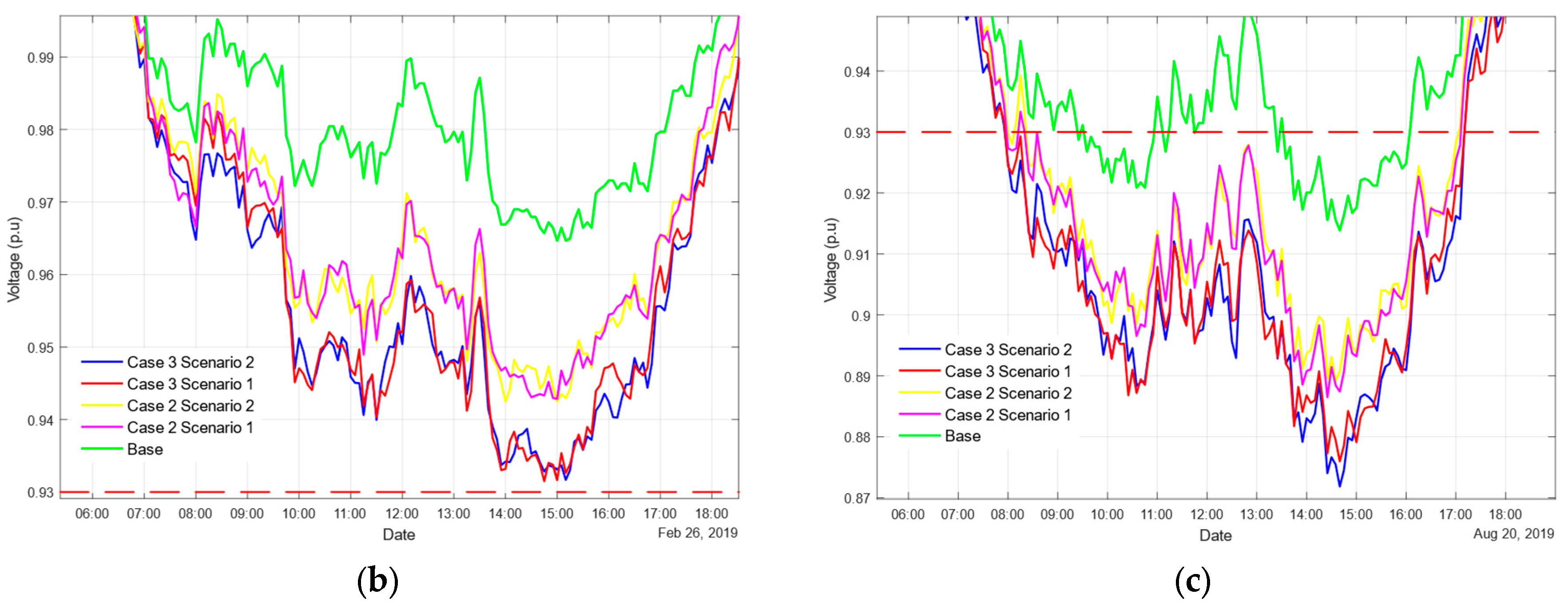
5.1. Assessment of Undervoltage Violations
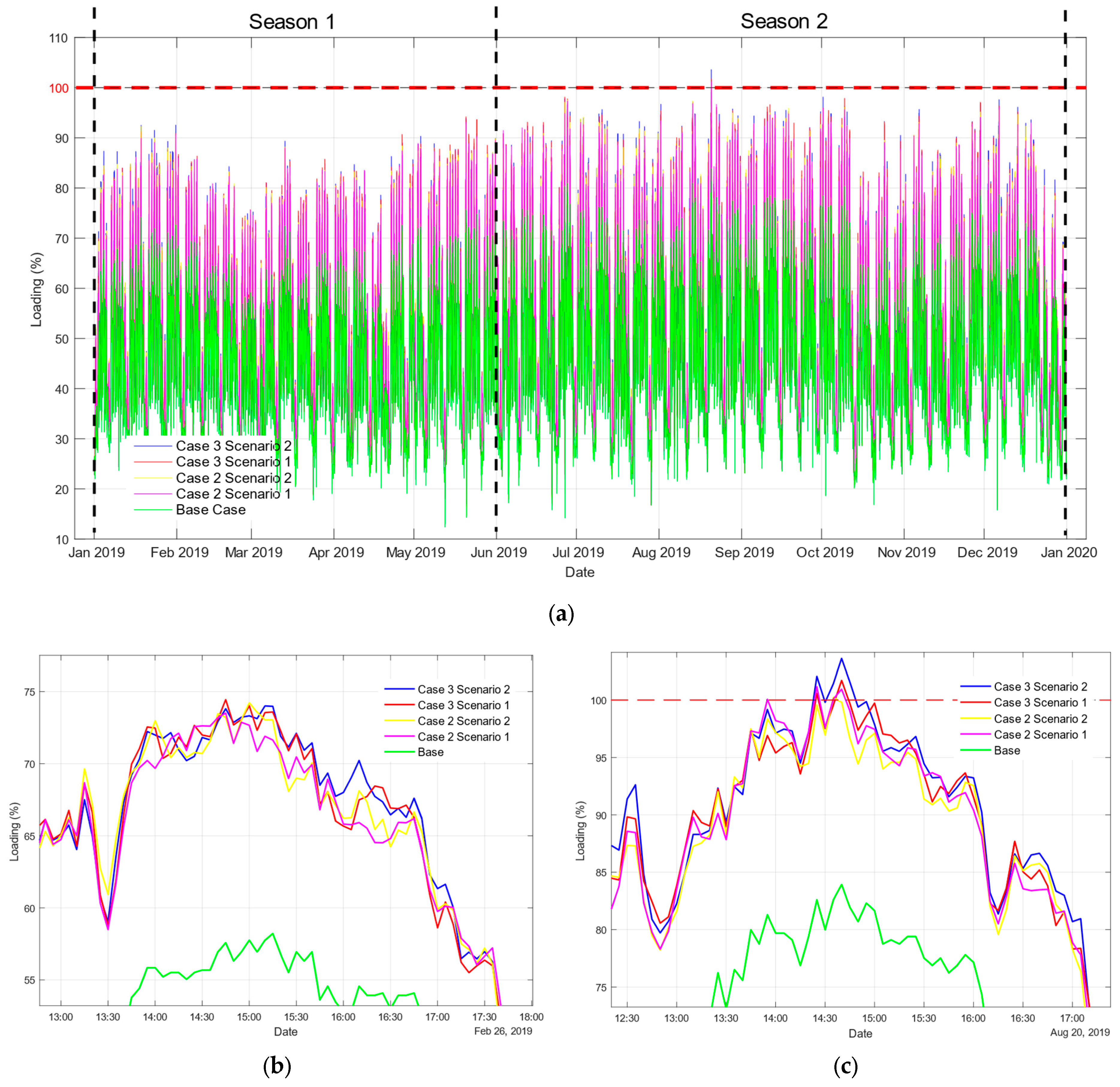
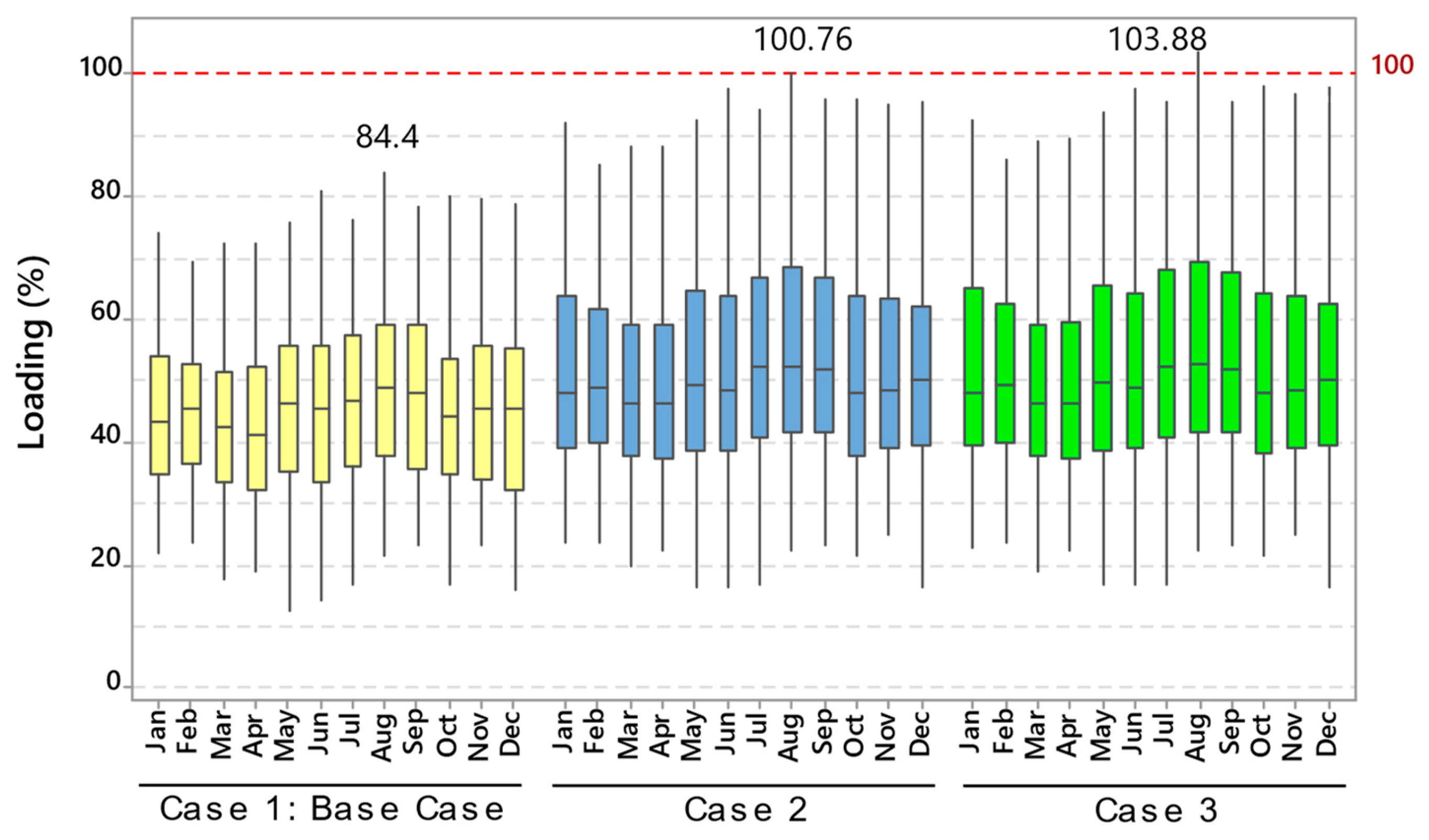
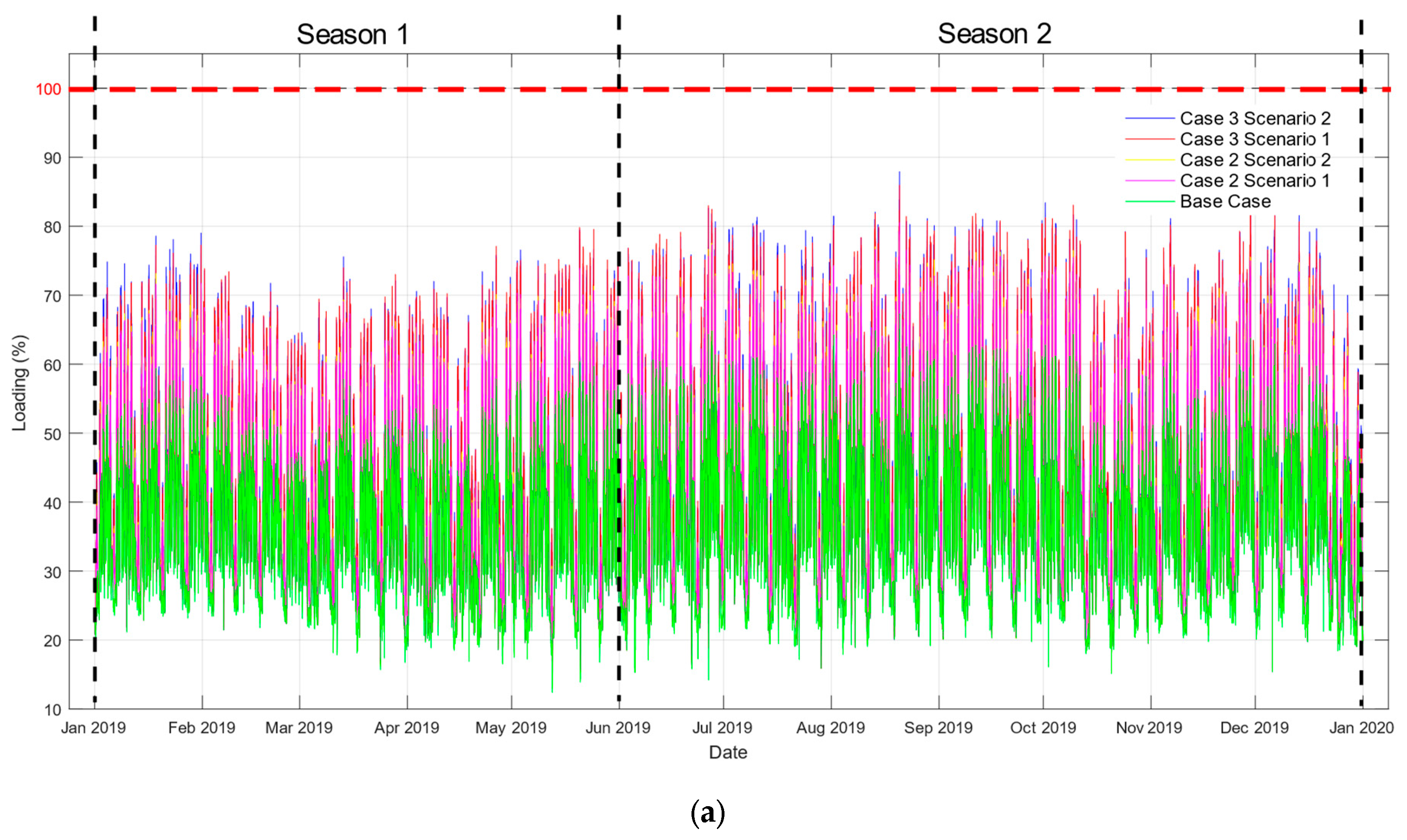
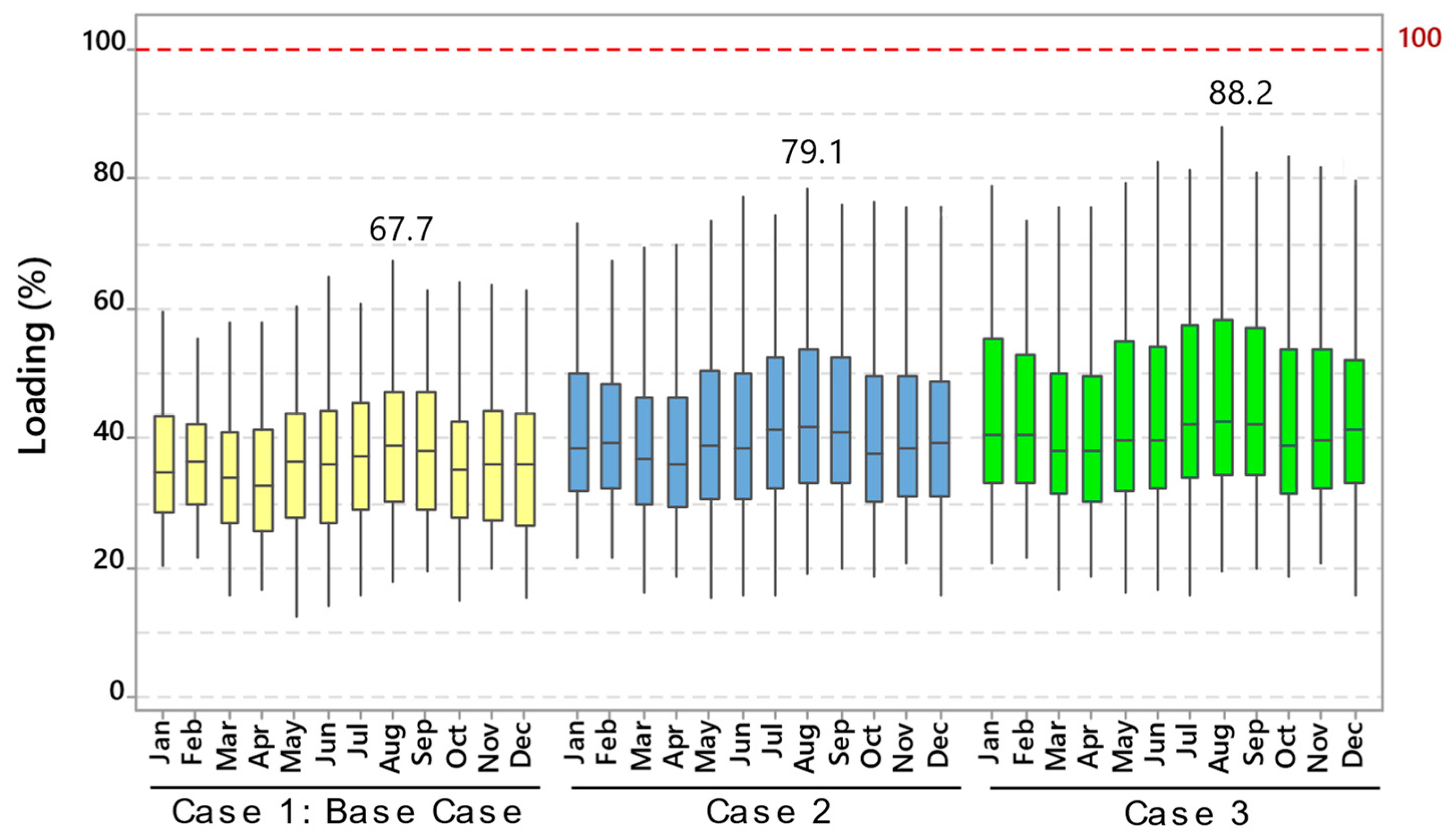
5.2. Assessment of Equipment Overload
5.3. Assessment of Step Voltage Regulator Load Violation
5.4. Assessment of Active Power Losses in the Feeder
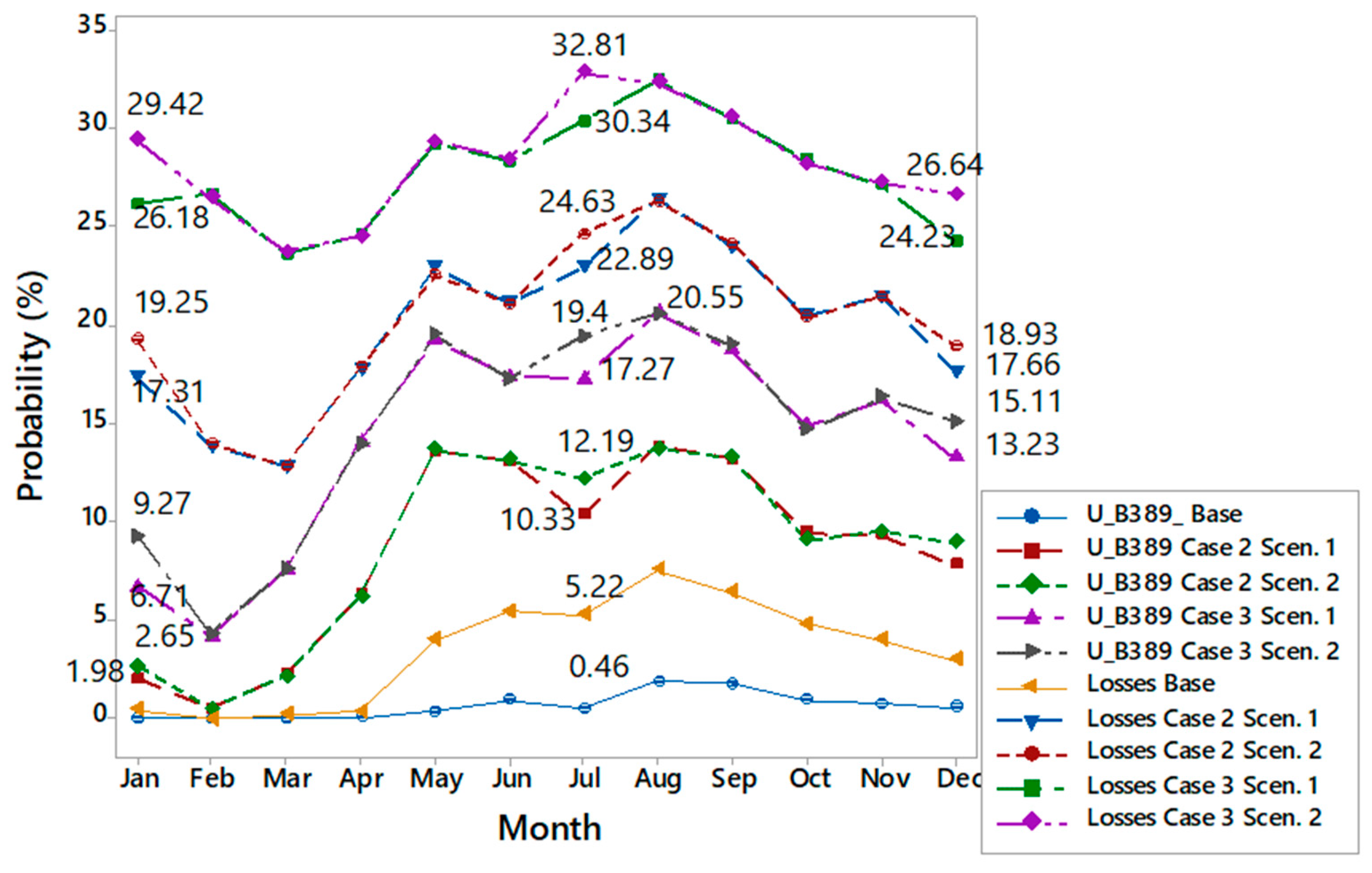
5.5. Probability of Limit Violation of the Investigated Issues
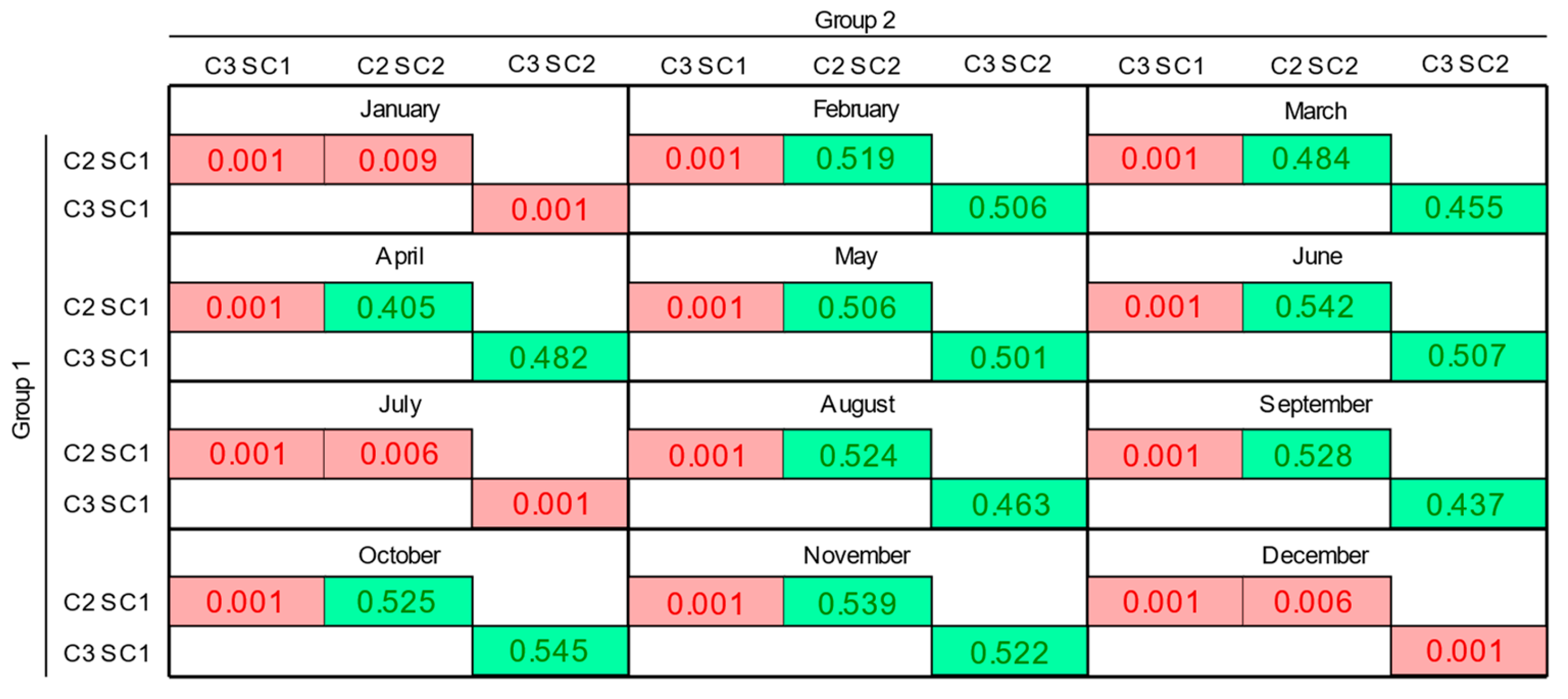
5.6. Relationship between Seasonality and the Analyzed Variables
5.6.1. Relationship between Seasonality and Bus Voltage
5.6.2. Relationship between Seasonality and Feeder Losses
- Energy Demand: With the expected surge in EV adoption, utility engineers must anticipate a substantial increase in electricity demand. Proper planning for capacity and distribution is essential to meet future energy requirements.
- Infrastructure: Engineers must carefully assess feeder reinforcement for charging stations. Ensuring the operational security of distribution networks is crucial to handling the growing load.
- Reactive Power Injection: Engineers should consider utilizing reactive power injection from the FCSs to mitigate undervoltage issues.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Global Electric Vehicle Outlook 2023 Catching Up with Climate Ambitions. Available online: https://www.iea.org/reports/global-ev-outlook-2023 (accessed on 8 April 2024).
- Amer, A.; Azzouz, M.A.; Azab, A.; Awad, A.S.A. Stochastic Planning for Optimal Allocation of Fast Charging Stations and Wind-Based DGs. IEEE Syst. J. 2021, 15, 4589–4599. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef]
- González, L.G.; Siavichay, E.; Espinoza, J.L. Impact of EV Fast Charging Stations on the Power Distribution Network of a Latin American Intermediate City. Renew. Sustain. Energy Rev. 2019, 107, 309–318. [Google Scholar] [CrossRef]
- Paudyal, P.; Ghosh, S.; Veda, S.; Tiwari, D.; Desai, J. EV Hosting Capacity Analysis on Distribution Grids. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Basta, B.; Morsi, W.G. Probabilistic Assessment of the Impact of Integrating Large-Scale High-Power Fast Charging Stations on the Power Quality in the Distribution Systems. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–6. [Google Scholar]
- Alshareef, S. Voltage Sag Assessment, Detection, and Classification in Distribution Systems Embedded with Fast Charging Stations. IEEE Access 2023, 11, 89864–89880. [Google Scholar] [CrossRef]
- Caballero-Peña, J.; Cadena-Zarate, C.; Osma-Pinto, G. Hourly Characterization of the Integration of DER in a Network from Deterministic and Probabilistic Approaches Using Co-Simulation PowerFactory-Python. Alex. Eng. J. 2023, 63, 283–305. [Google Scholar] [CrossRef]
- Kenari, M.T.; Ozdemir, A. Probabilistic Models for the Analysis of Electric Vehicle Fast-Charging Station and Photovoltaic Unit Impacts on the Operation of Active Distribution Grids. In Proceedings of the 2023 International Conference on Power, Energy and Innovations (ICPEI), Phrachuap Khirikhan, Thailand, 18–20 October 2023; pp. 27–30. [Google Scholar]
- Benavides, D.; Arévalo, P.; Villa-Ávila, E.; Aguado, J.A.; Jurado, F. Predictive Power Fluctuation Mitigation in Grid-Connected PV Systems with Rapid Response to EV Charging Stations. J. Energy Storage 2024, 86, 111230. [Google Scholar] [CrossRef]
- Amini, M.H.; Boroojeni, K.G.; Wang, C.J.; Nejadpak, A.; Iyengar, S.S.; Karabasoglu, O. Effect of Electric Vehicle Parking Lots’ Charging Demand as Dispatchable Loads on Power Systems Loss. In Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; pp. 499–503. [Google Scholar]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of Electric Vehicle Charging Station Load on Distribution Network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Fatah Mochamad, R.; Ehsan, A.; Pambudi, B.A. Probabilistic Assessment of Electric Vehicle Impact on Distribution Network of Surabaya, Indonesia. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar]
- Toledo-Orozco, M.; Bravo-Padilla, E.; Álvarez-Bel, C.; Morales-Jadan, D.; Gonzalez-Morales, L. Methodological Evaluation to Integrate Charging Stations for Electric Vehicles in a Tram System Using OpenDSS—A Case Study in Ecuador. Sustainability 2023, 15, 6382. [Google Scholar] [CrossRef]
- Roy, P.; Ilka, R.; He, J.; Liao, Y.; Cramer, A.M.; Mccann, J.; Delay, S.; Coley, S.; Geraghty, M.; Dahal, S. Impact of Electric Vehicle Charging on Power Distribution Systems: A Case Study of the Grid in Western Kentucky. IEEE Access 2023, 11, 49002–49023. [Google Scholar] [CrossRef]
- Bucarelli, M.A.; Geri, A.; Maccioni, M.; Gatta, F.M.; Bragatto, T.; Paulucci, M. Impact of Ultrafast EV Charging Stations on the Electrical Distribution Grid: A Case Study in Terni. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar]
- Rahman, M.M.; Al-Ammar, E.A.; Das, H.S.; Ko, W. Comprehensive Impact Analysis of Electric Vehicle Charging Scheduling on Load-Duration Curve. Comput. Electr. Eng. 2020, 85, 106673. [Google Scholar] [CrossRef]
- Vopava, J.; Koczwara, C.; Traupmann, A.; Kienberger, T. Investigating the Impact of E-Mobility on the Electrical Power Grid Using a Simplified Grid Modelling Approach. Energies 2020, 13, 39. [Google Scholar] [CrossRef]
- Visakh, A.; Selvan, M.P. Seasonal Effects of Electric Vehicle Charging on the Aging of Distribution Transformers. In Proceedings of the 2021 13th IEEE PES Asia Pacific Power & Energy Engineering Conference (APPEEC), Thiruvananthapuram, India, 21–23 November 2021; pp. 1–6. [Google Scholar]
- Agência Nacional de Energia Elétrica. ANEEL Procedimentos de Distribuição de Energia Elétrica No Sistema Elétrico Nacional—PRODIST. Módulo 8—Qualidade da Energia Elétrica. Available online: https://www2.aneel.gov.br/cedoc/aren2021956_2_7.pdf (accessed on 28 March 2024).
- Gnann, T.; Funke, S.; Jakobsson, N.; Plötz, P.; Sprei, F.; Bennehag, A. Fast Charging Infrastructure for Electric Vehicles: Today’s Situation and Future Needs. Transp. Res. D Transp. Environ. 2018, 62, 314–329. [Google Scholar] [CrossRef]
- Xing, Q.; Chen, Z.; Zhang, Z.; Xu, X.; Zhang, T.; Huang, X.; Wang, H. Urban Electric Vehicle Fast-Charging Demand Forecasting Model Based on Data-Driven Approach and Human Decision-Making Behavior. Energies 2020, 13, 1412. [Google Scholar] [CrossRef]






| Article | Year | Seasonality | Impact * | Actual Grid | Article | Year | Seasonality | Impact * | Actual Grid |
|---|---|---|---|---|---|---|---|---|---|
| [4] | 2019 | ✗ | H, LL, V | ✓ | [5] | 2021 | ✗ | TL, V | ✓ |
| [6] | 2020 | ✗ | H, V | ✗ | [7] | 2023 | ✗ | V | ✗ |
| [8] | 2023 | ✗ | PL, V | ✗ | [9] | 2023 | ✗ | V | ✗ |
| [10] | 2024 | ✗ | PQ | ✗ | [11] | 2016 | ✗ | PL | ✓ |
| [12] | 2018 | ✗ | V, PL, R | ✗ | [13] | 2021 | ✗ | PL, V | ✓ |
| [14] | 2023 | ✗ | PP, PL, V | ✓ | [15] | 2023 | ✗ | OL | ✓ |
| [16] | 2023 | ✗ | OL, PC, V | ✓ | [17] | 2020 | One day in Summer | LP, V, F, H, PL | ✓ |
| [18] | 2020 | Annual | LP | ✓ | [19] | 2020 | Summer and Winter | DT | ✗ |
| This Work | 2024 | Annual | V, OL, PL | ✓ |
| Variable | Arrival Time (h) | Battery Capacity (kW/h) | Charging Time (min) | Initial State of Charge (%) | Final State of Charge (%) | Number of EVs |
|---|---|---|---|---|---|---|
| Parameter | μ = 13, σ = 4 | 30–67 | 20–40 | Shape = 3, Scale = 20 | Shape = 13, Scale = 80 | 20–40 |
| Distribution | Normal | Uniform | Uniform | Weibull | Weibull | Uniform |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Gómez, O.M.; Abreu Vieira, J.P. Probabilistic Assessment of the Impact of Electric Vehicle Fast Charging Stations Integration into MV Distribution Networks Considering Annual and Seasonal Time-Series Data. Energies 2024, 17, 4624. https://doi.org/10.3390/en17184624
Hernández-Gómez OM, Abreu Vieira JP. Probabilistic Assessment of the Impact of Electric Vehicle Fast Charging Stations Integration into MV Distribution Networks Considering Annual and Seasonal Time-Series Data. Energies. 2024; 17(18):4624. https://doi.org/10.3390/en17184624
Chicago/Turabian StyleHernández-Gómez, Oscar Mauricio, and João Paulo Abreu Vieira. 2024. "Probabilistic Assessment of the Impact of Electric Vehicle Fast Charging Stations Integration into MV Distribution Networks Considering Annual and Seasonal Time-Series Data" Energies 17, no. 18: 4624. https://doi.org/10.3390/en17184624
APA StyleHernández-Gómez, O. M., & Abreu Vieira, J. P. (2024). Probabilistic Assessment of the Impact of Electric Vehicle Fast Charging Stations Integration into MV Distribution Networks Considering Annual and Seasonal Time-Series Data. Energies, 17(18), 4624. https://doi.org/10.3390/en17184624







