A Literature Review of the Design, Modeling, Optimization, and Control of Electro-Mechanical Inlet Valves for Gas Expanders
Abstract
1. Introduction
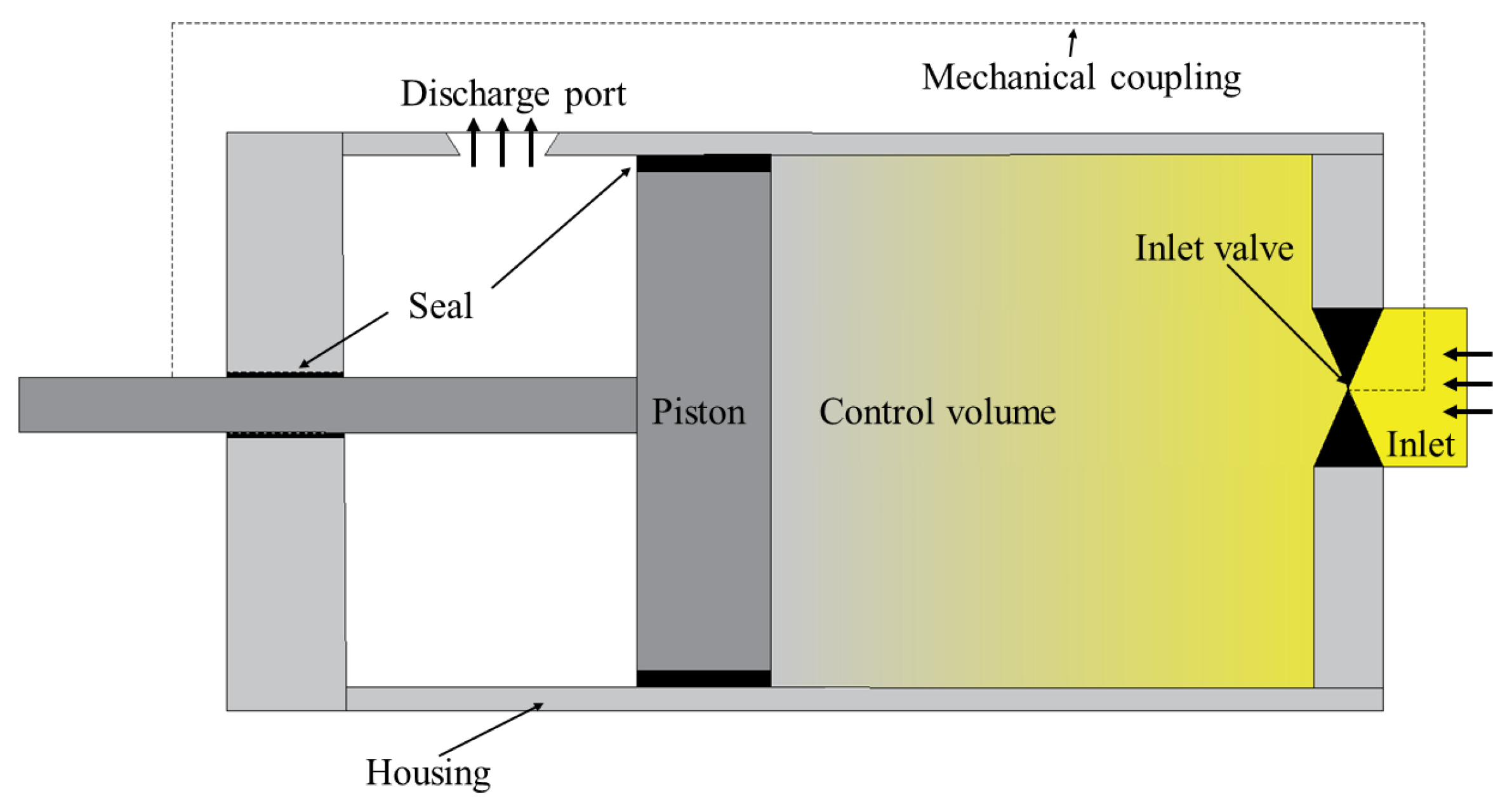
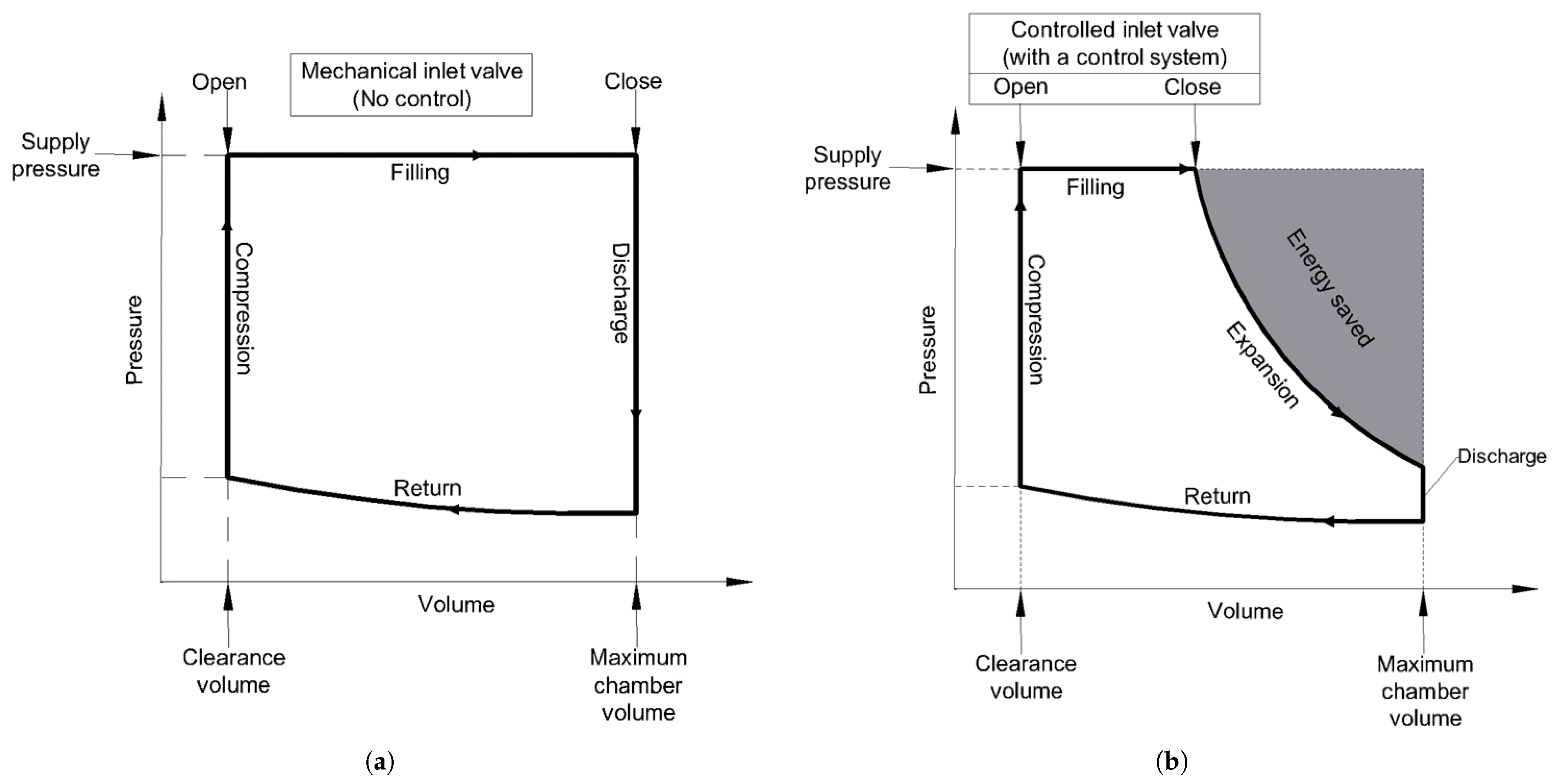
2. Utility of Inlet Control Valve in Gas Expander Operation
3. The Challenge
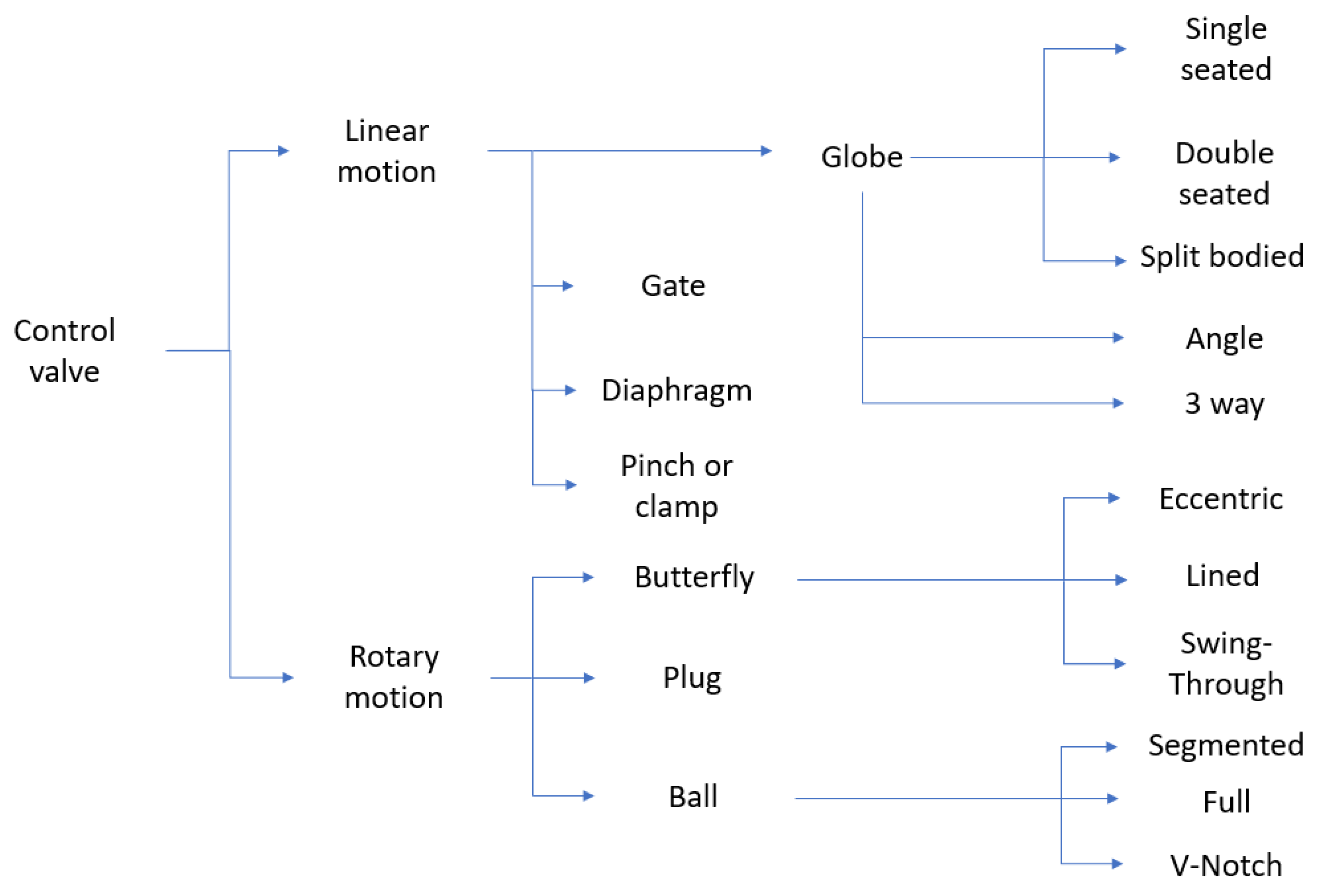
4. Control Valve Designs
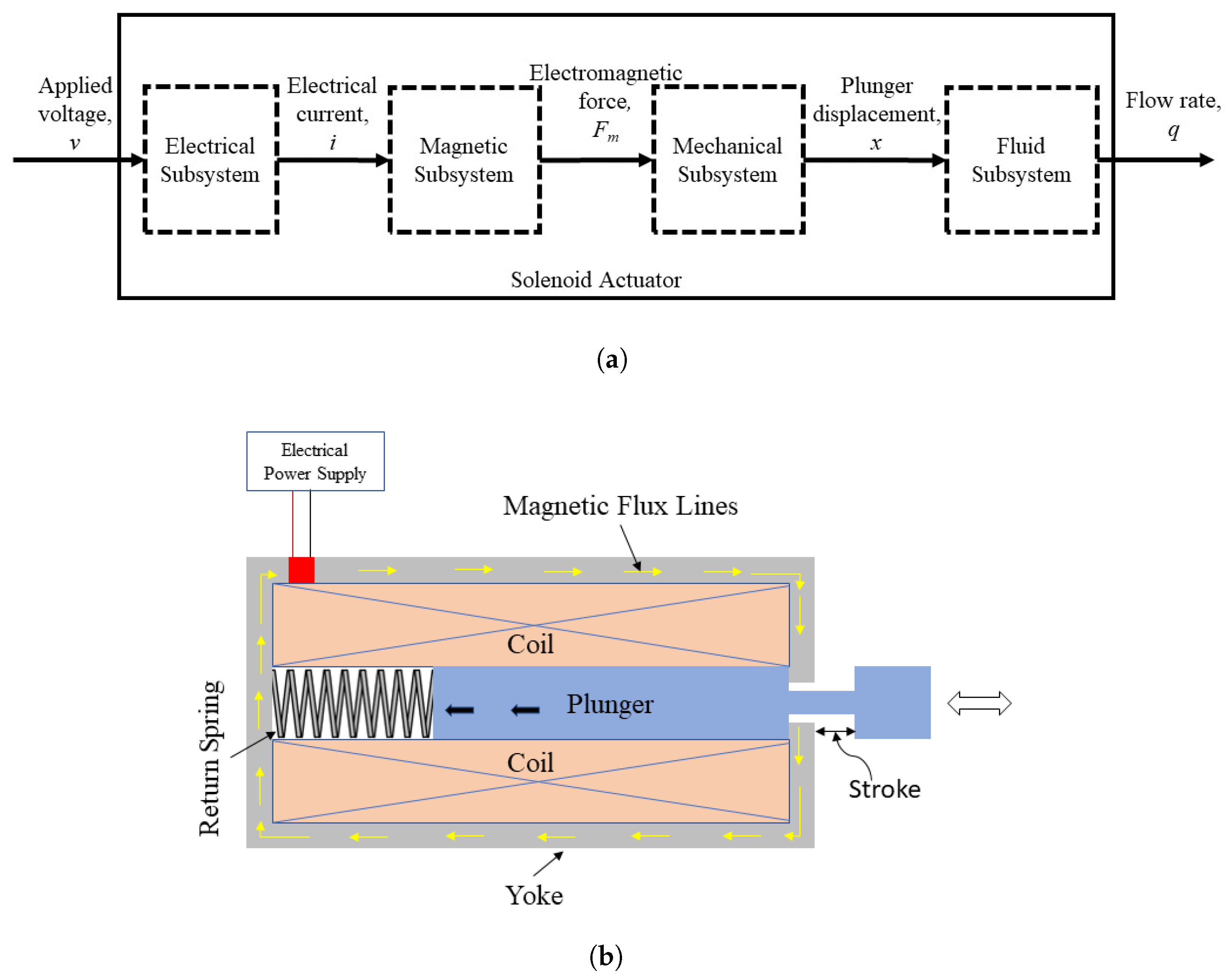
4.1. Solenoid Valve (SV)
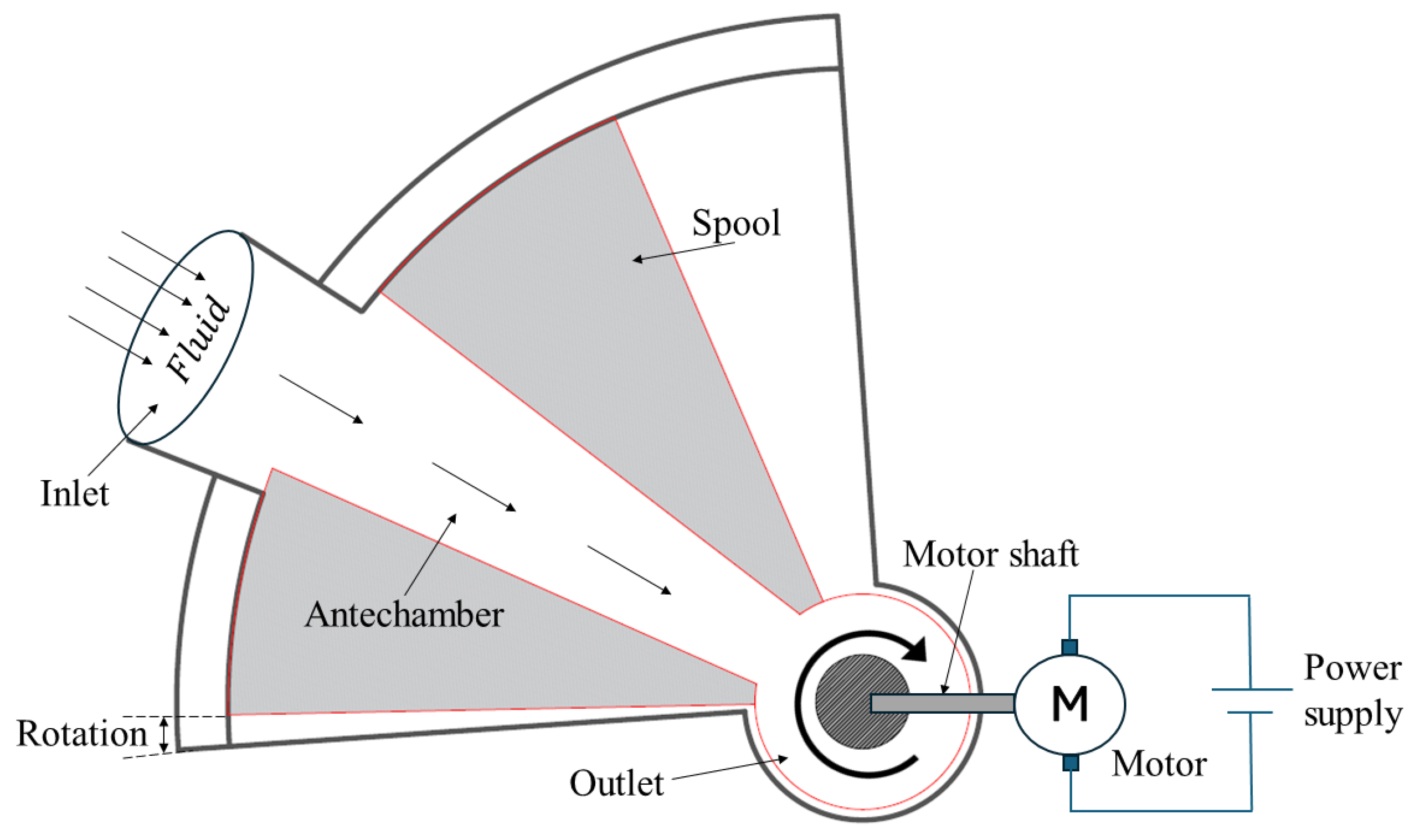
4.2. Motor Operated Valve (MoV)
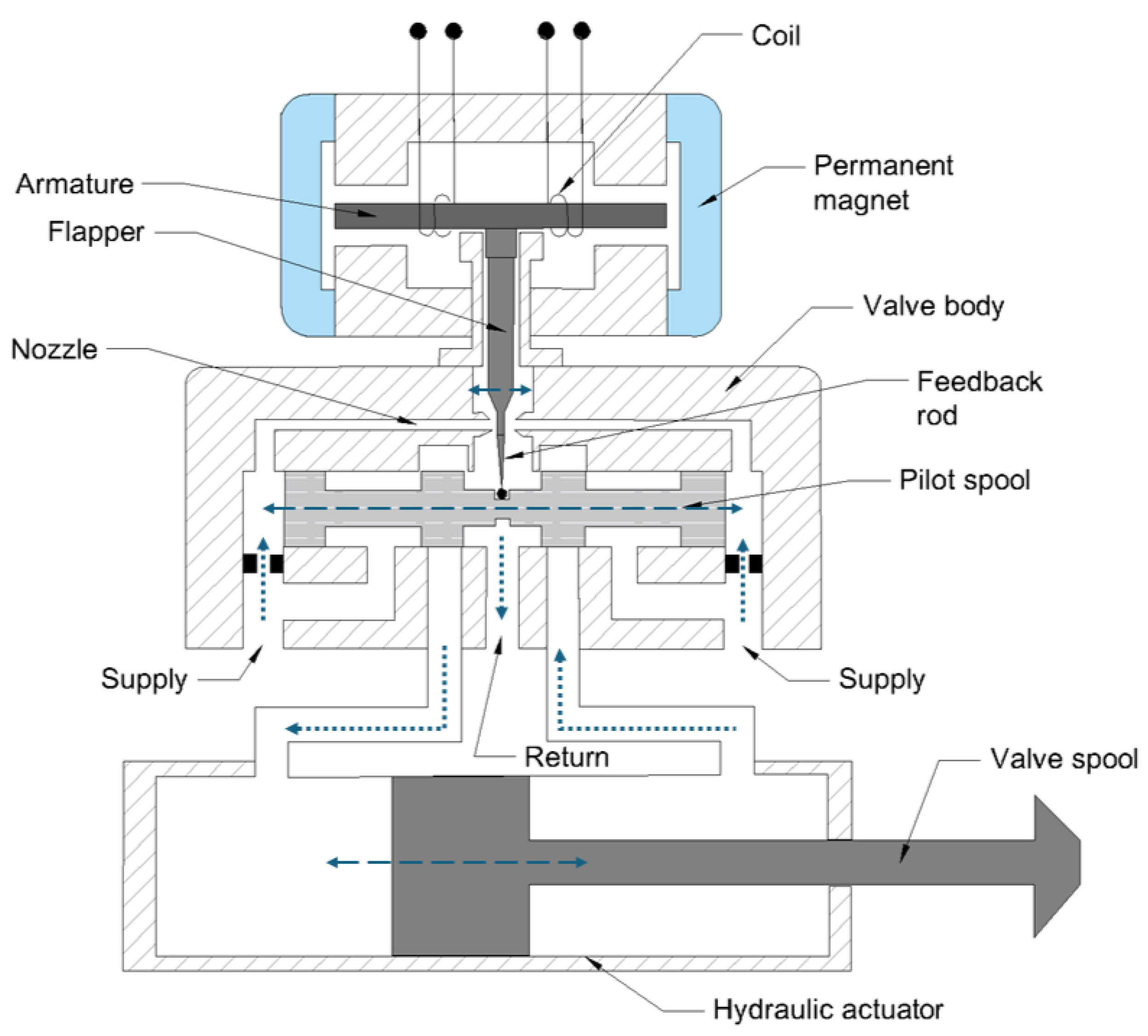
4.3. Electromagnetic Servo Valve (ESV)
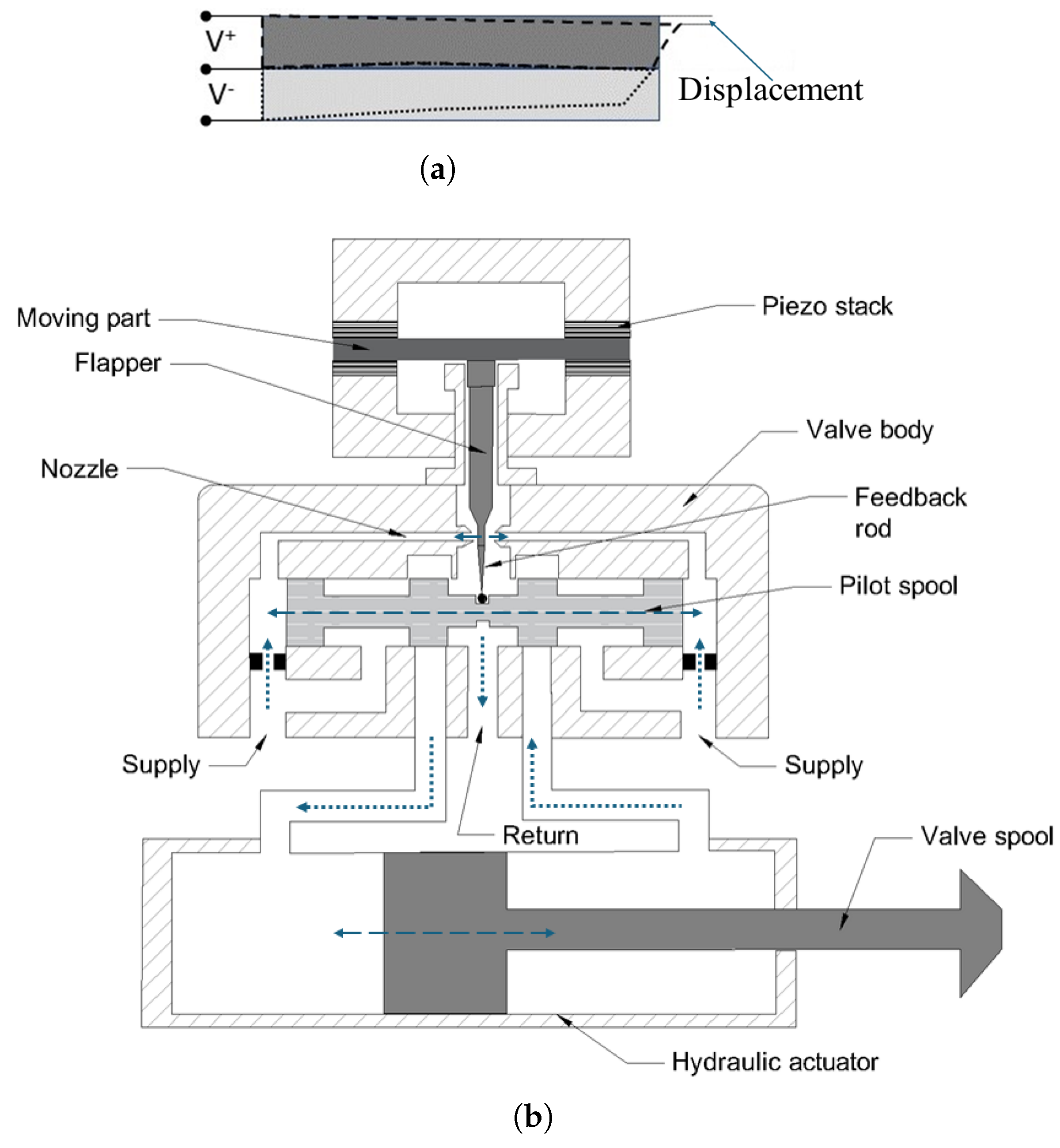
4.4. Piezoelectric Servo Valve (PSV)
5. Control Valve Mathematical Modeling
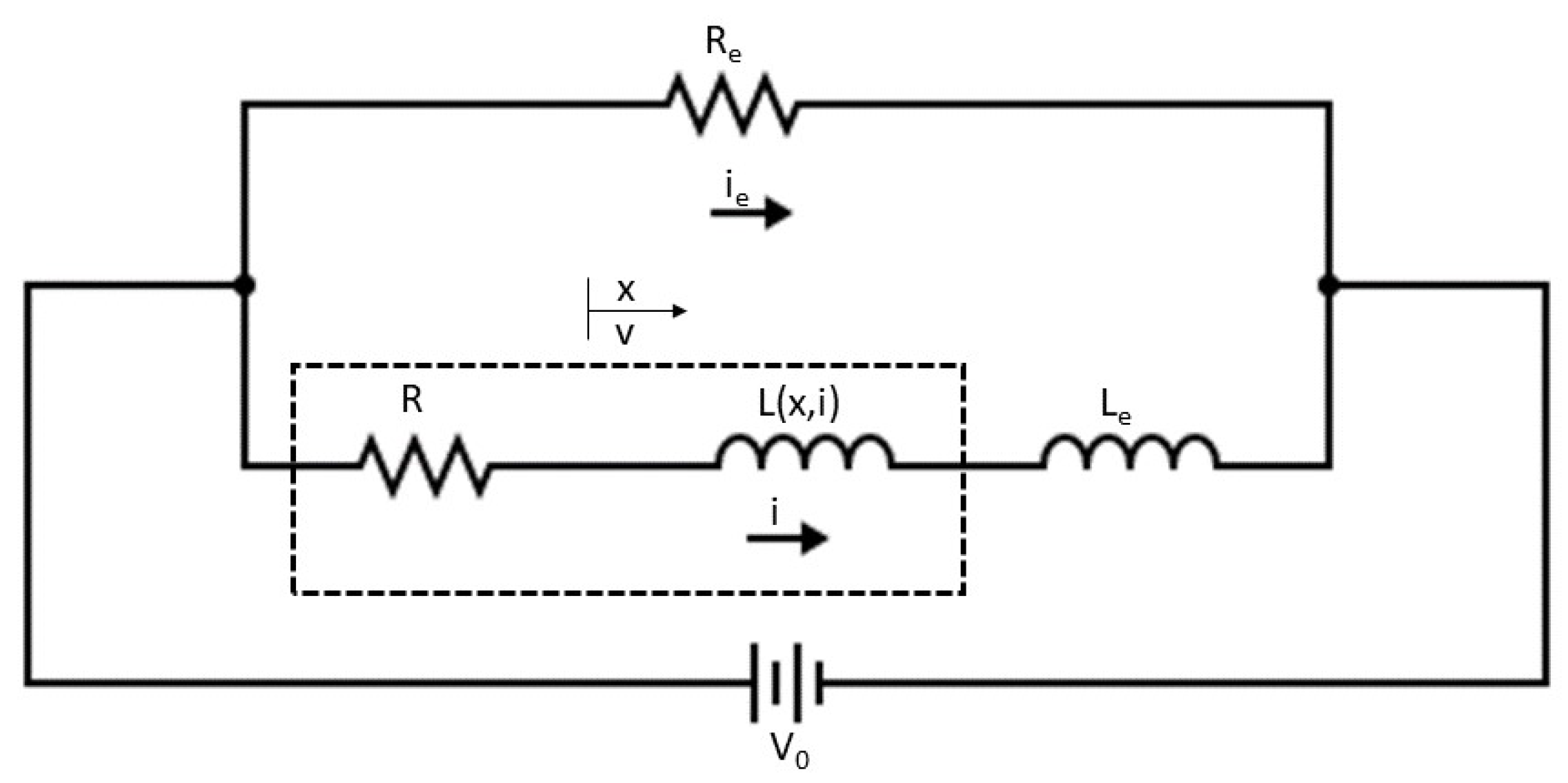
5.1. Solenoid Valve (SV) Modeling
5.2. Motor-Operated Valve (MoV) Modeling
5.3. Electromagnetic Servo Valve (ESV) Modeling
5.4. Piezoelectric Servo Valve (PSV) Modeling
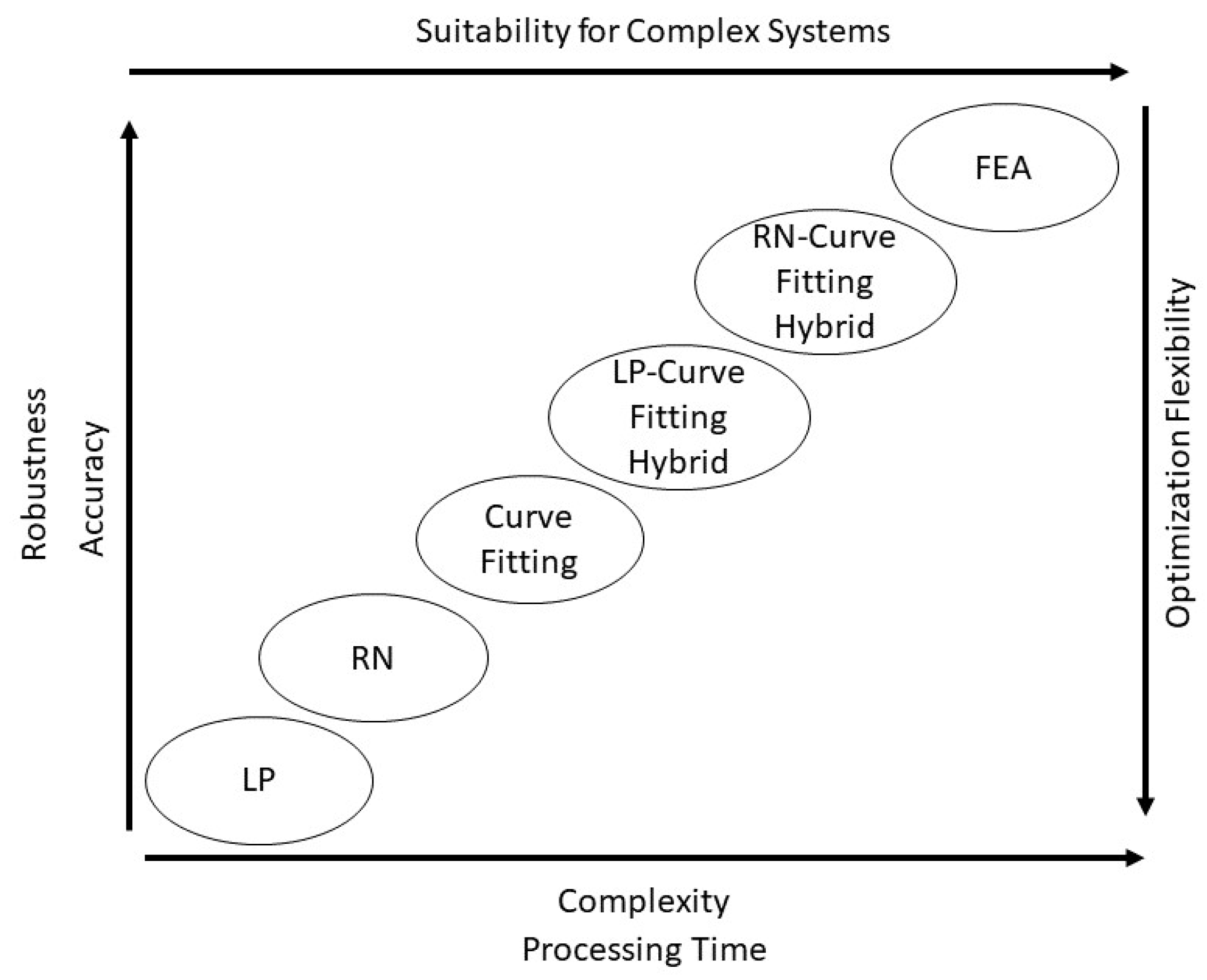
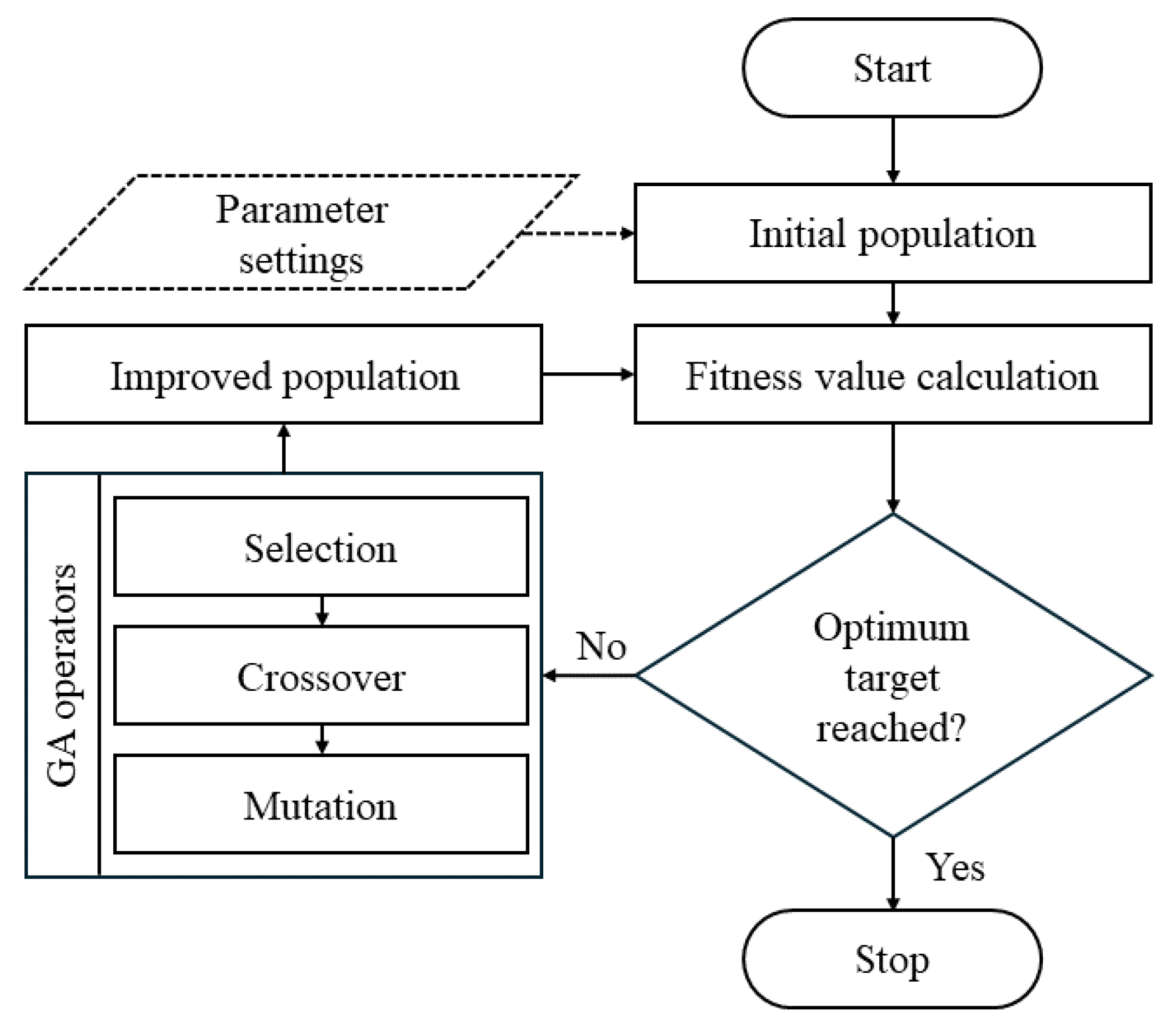
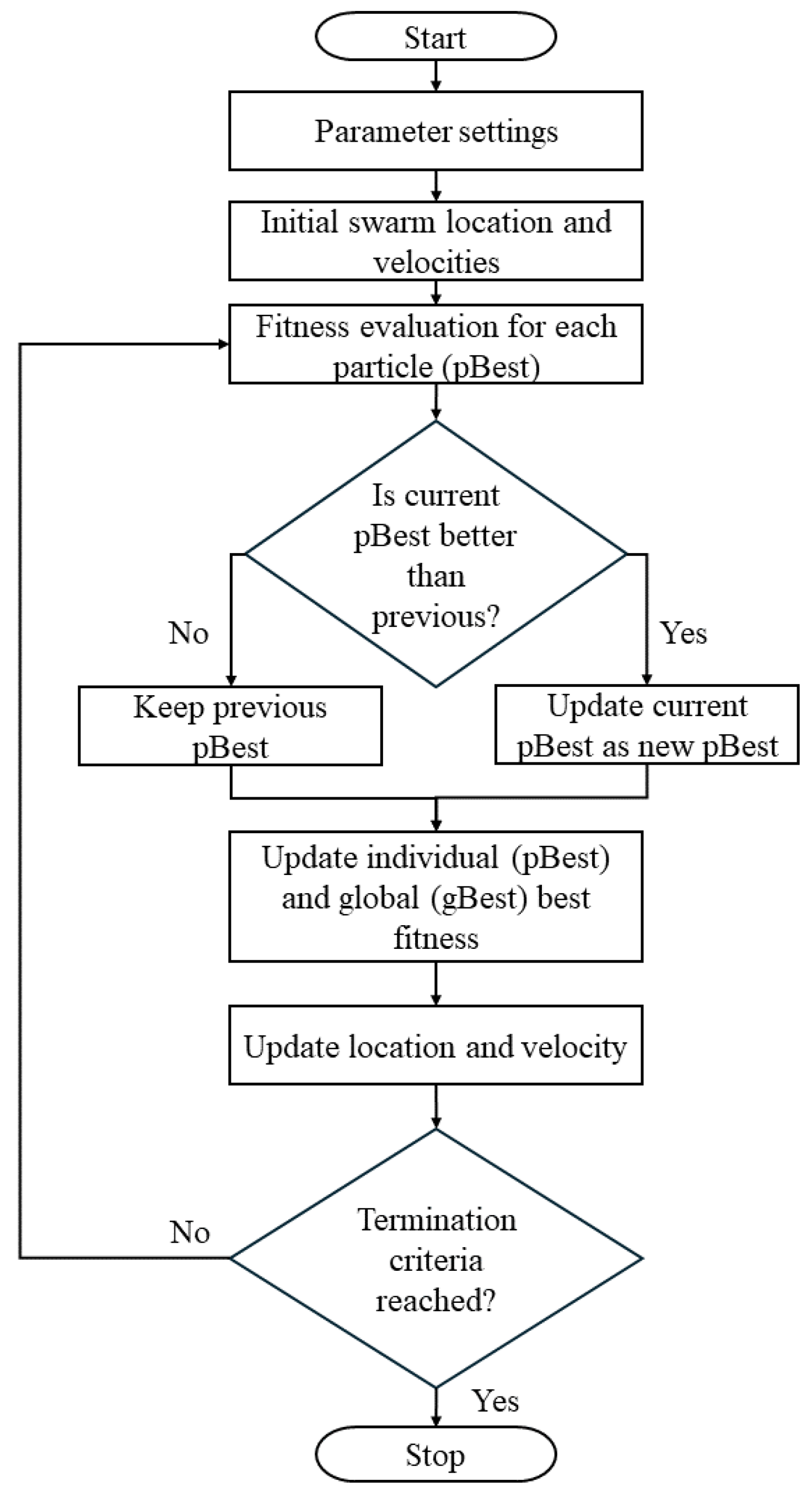
6. Optimization Techniques
7. Control Schemes
8. Challenges and Opportunities for Future Studies
9. Conclusions
Funding
Conflicts of Interest
Abbreviations
| ORC | Organic Rankine cycle |
| PWM | Pulse width modulation |
| PV | Process variable |
| SP | Set point |
| SV | Solenoid valve |
| HSV | High-speed on/off valve |
| MoV | Motor-operated valve |
| ESV | Electromagnetic servo valve |
| PSV | Piezoelectric servo valve |
| NSGA-II | non-dominated sorting genetic algorithm-II |
| LP | Lumped parameter |
| FEA | Finite element analysis |
| RN | Reluctance network |
| DP | Distributed parameter |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| EEFO | Electric eel foraging optimization |
| MOBMA | Multi-objective boxing match algorithm |
| YDSE | Young’s double-slit experiment |
| AOA | Arithmetic optimization algorithm |
| CFD | Computational fluid dynamics |
| BPNN | Back propagation neural network |
| SPSA | Simultaneous perturbation stochastic approximation |
| PID | Proportional-integral-derivative |
| N-M | Nelder–Mead |
| Z-N | Ziegler–Nichols |
| KF | Kalman filter |
| UKF | Unscented Kalman filter |
| EKF | Extended Kalman filter |
| PEM | Polymer electrolyte membrane |
| SMC | Sliding mode controller |
| ARC | Adaptive robust control |
| VSC | Variable structure controller |
| FL | Feedback linearization |
| QFT | Quantitative feedback theory |
| MPC | Model predictive controller |
| ANN | Artificial neural network |
| ML | Machine learning |
References
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Bademlioglu, A.; Canbolat, A.; Yamankaradeniz, N.; Kaynakli, O. Investigation of parameters affecting Organic Rankine Cycle efficiency by using Taguchi and ANOVA methods. Appl. Therm. Eng. 2018, 145, 221–228. [Google Scholar] [CrossRef]
- Ibarra, M.; Rovira, A.; Alarcón-Padilla, D.C.; Blanco, J. Performance of a 5kWe Organic Rankine Cycle at part-load operation. Appl. Energy 2014, 120, 147–158. [Google Scholar] [CrossRef]
- Alshammari, F.; Usman, M.; Pesyridis, A. Expanders for Organic Rankine Cycle Technology. In Organic Rankine Cycle Technology for Heat Recovery; Wang, E., Ed.; IntechOpen: Rijeka, Croatia, 2018; Chapter 3. [Google Scholar] [CrossRef]
- Li, L.; Tao, J.; Wang, Y.; Su, Y.; Xiao, M. Effects of Intake Valve Closing Timing on Gasoline Engine Performance and Emissions. SAE Trans. 2001, 110, 2270–2276. [Google Scholar]
- Sultan, I.A. Optimum design of limaçon gas expanders based on thermodynamic performance. Appl. Therm. Eng. 2012, 39, 188–197. [Google Scholar] [CrossRef]
- Benstead, R.; Redford, S.J.; Henshaw, I.J.; Derby, J.W. A Method and Apparatus for Improving the Operation of Positive Displacement Expanders. U.S. Patent WO2006090175A1, 28 August 2006. [Google Scholar]
- Chotai, N.J.; Patel, V.; Savsani, V.; Karan, M. Performance enhancement of camless air engine by optimising the inlet-valve cut-off position. Int. J. Ambient Energy 2022, 43, 7173–7181. [Google Scholar] [CrossRef]
- Hossain, M.S.; Sultan, I.; Phung, T.; Kumar, A. Performance Improvement of a Limaçon Gas Expander Using an Inlet Control Valve: Two Case Studies. Energies 2024, 17, 2427. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M. Dynamics of Machines and Hydraulic Systems: Mechanical Vibrations and Pressure Pulsations; Springer Nature: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Deptuła, A.; Urbanowicz, K.; Skačkauskas, P.; Deptuła, A.M.; Danilevičius, A.; Šukevičius, Š.; Łapka, M. Research of Vibration Effects on a Hydraulic Valve in the Pressure Pulsation Spectrum Analysis. J. Mar. Sci. Eng. 2023, 11, 301. [Google Scholar] [CrossRef]
- Sultan, I. The Limaçon of Pascal: Mechanical Generation and Utilization For Fluid Processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 813–822. [Google Scholar] [CrossRef]
- Hossain, M.S.; Sultan, I.; Phung, T.; Kumar, A. An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander. Dynamics 2024, 4, 457–474. [Google Scholar] [CrossRef]
- Wang, B.; Liu, H.; Hao, Y.; Quan, L.; Li, Y.; Zhao, B. Design and Analysis of a Flow-Control Valve with Controllable Pressure Compensation Capability for Mobile Machinery. IEEE Access 2021, 9, 98361–98368. [Google Scholar] [CrossRef]
- Yun, S.N.; Lee, Y.L.; Khan, H.A.; Kang, C.N.; Ham, Y.B.; Park, J.H. Proportional Flow Control Valve for Construction Vehicle. In Proceedings of the 2019 23rd International Conference on Mechatronics Technology (ICMT), Salerno, Italy, 23–26 October 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Anusha, M.R.; Veena, M.G. PWM Controlled Solenoid Valves for Automatic Gear Change in Four-Wheelers. In Advances in Communication, Signal Processing, VLSI, and Embedded Systems; Kalya, S., Kulkarni, M., Shivaprakasha, K., Eds.; Springer: Singapore, 2020; pp. 335–344. [Google Scholar]
- Kumar, S.; Tewari, V.K.; Bharti, C.K.; Ranjan, A. Modeling, simulation and experimental validation of flow rate of electro-hydraulic hitch control valve of agricultural tractor. Flow Meas. Instrum. 2021, 82, 102070. [Google Scholar] [CrossRef]
- Agh, S.M.; Pirkandi, J.; Mahmoodi, M.; Jahromi, M. Development of a novel rotary flow control valve with an electronic actuator and a pressure compensator valve for a gas turbine engine fuel control system. Flow Meas. Instrum. 2020, 74, 101759. [Google Scholar] [CrossRef]
- Morselli, S.; Gessi, S.; Marani, P.; Martelli, M.; De Hieronymis, C.M.R. Dynamics of pilot operated pressure relief valves subjected to fast hydraulic transient. AIP Conf. Proc. 2019, 2191, 020116. [Google Scholar] [CrossRef]
- Dasgupta, K.; Karmakar, R. Dynamic analysis of pilot operated pressure relief valve. Simul. Model. Pract. Theory 2002, 10, 35–49. [Google Scholar] [CrossRef]
- Liu, J.; Xie, H.; Yang, H. Static and dynamic performance improvement of a hydraulic feedback valve for load control by introducing force feedback and compensation orifice. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 3837–3848. [Google Scholar] [CrossRef]
- Cană, P.; Ripeanu, R.G.; Pătîrnac, I.; Diniță, A.; Tănase, M. Investigating the Impact of Operating Conditions on Relief Pressure Valve Flow through CFD and Statistical Analysis. Processes 2023, 11, 3396. [Google Scholar] [CrossRef]
- Ren, H.P.; Fan, J.T.; Kaynak, O. Optimal design of a fractional-order proportional-integer-differential controller for a pneumatic position servo system. IEEE Trans. Ind. Electron. 2018, 66, 6220–6229. [Google Scholar] [CrossRef]
- Ma, Z. Enhanced Component Performance Study: Air-Operated Valves 1998–2020; Technical Report; Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2022. [Google Scholar]
- Choi, J.; Ahn, J.H.; Kim, H.Y. Modeling the Dynamic Behavior of a Pilot-Operated Solenoid Valve for an Ultra-High Pressure Vessel. Appl. Sci. 2021, 11, 2329. [Google Scholar] [CrossRef]
- Hossain, M.S.; Phung, T.; Kumar, A.; Sultan, I. A Direct Drive Rotary Valve for Efficient Power Generation in Gas Expander Based Small Scale Power Plants. In Proceedings of the 2023 33rd Australasian Universities Power Engineering Conference (AUPEC), Ballarat, Australia, 25–27 September 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wang, P.; Liu, B.; Wang, G. Monitoring and evaluation of the status of Motor-Operated Valves in nuclear power plants. J. Phys. Conf. Ser. 2024, 2703, 012090. [Google Scholar] [CrossRef]
- Zhang, Z.; An, Q.; Li, J.; Zhang, W. Piezoelectric friction-inertia actuator - A critical review and future perspective. Int. J. Adv. Manuf. Technol. 2012, 62, 669–685. [Google Scholar] [CrossRef]
- Hunstig, M. Piezoelectric Inertia Motors—A Critical Review of History, Concepts, Design, Applications, and Perspectives. Actuators 2017, 6, 7. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, Y.; Tao, Z.; Lian, Z.; Zhao, R. Modeling and Dynamic Characteristics of a Novel High-Pressure and Large-Flow Water Hydraulic Proportional Valve. Machines 2022, 10, 37. [Google Scholar] [CrossRef]
- Zhao, R.; Liao, Y.; Lian, Z.; Li, R.; Guo, Y. Research on the performance of a novel electro-hydraulic proportional directional valve with position-feedback groove. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1930–1944. [Google Scholar] [CrossRef]
- Gui, S.; Zhang, S.; Fu, B.; Ling, M. Fluid-dynamic analysis and multi-objective design optimization of piezoelectric servo valves. Flow Meas. Instrum. 2022, 85, 102157. [Google Scholar] [CrossRef]
- Ling, M.; Wang, J.; Wu, M.; Cao, L.; Fu, B. Design and modeling of an improved bridge-type compliant mechanism with its application for hydraulic piezo-valves. Sens. Actuators A Phys. 2021, 324, 112687. [Google Scholar] [CrossRef]
- Sangiah, D.K.; Plummer, A.R.; Bowen, C.R.; Guerrier, P. A novel piezohydraulic aerospace servo valve. Part 1: Design and modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 371–389. [Google Scholar] [CrossRef]
- Topçu, E.E.; Yüksel, İ.; Kamış, Z. Development of electro-pneumatic fast switching valve and investigation of its characteristics. Mechatronics 2006, 16, 365–378. [Google Scholar] [CrossRef]
- Glück, T.; Büchl, D.; Krämer, C.; Pfeffer, A.; Risle, A.; Hägele, L.; Kugi, A. Modeling and control of a novel pneumatic two-stage piezoelectric-actuated valve. Mechatronics 2021, 75, 102529. [Google Scholar] [CrossRef]
- MacIsaac, B.; Langton, R. Gas Generator Fuel Control Systems. In Gas Turbine Propulsion Systems; Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 37–88. [Google Scholar] [CrossRef]
- Yamane, H.; Takahara, Y.; Oyobe, T. Aspects of aircraft engine control systems R&D. Control Eng. Pract. 1997, 5, 595–602. [Google Scholar] [CrossRef]
- Simic, M.; Herakovic, N. Piezo Actuators for the Use in Hydraulic and Pneumatic Valves. In Proceedings of the International Conference Fluid Power 2017, Linköping, Sweden, 7–9 June 2017; pp. 207–218. [Google Scholar] [CrossRef]
- Fabbrini, A.; Garulli, A.; Mercorelli, P. A Trajectory Generation Algorithm for Optimal Consumption in Electromagnetic Actuators. IEEE Trans. Control Syst. Technol. 2012, 20, 1025–1032. [Google Scholar] [CrossRef]
- Gant, P. Solenoid Valves Evolve with Medical Devices. 2015. Available online: https://www.mddionline.com/components/solenoid-valves-evolve-with-medical-devices (accessed on 1 August 2024).
- Mercorelli, P. An Adaptive and Optimized Switching Observer for Sensorless Control of an Electromagnetic Valve Actuator in Camless Internal Combustion Engines. Asian J. Control 2014, 16, 959–973. [Google Scholar] [CrossRef]
- Nagy, L.; Szabó, T.; Jakab, E. Electro-Dynamical Modeling of a Solenoid Switch of Starter Motors. Procedia Eng. 2012, 48, 445–452. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y. Dynamic Characteristics of Pressure Compensator in Underwater Hydraulic System. IEEE/ASME Trans. Mechatron. 2014, 19, 777–787. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, Y.; Burton, R. Modeling and robust discrete-time sliding-mode control design for a fluid power electrohydraulic actuator (EHA) system. IEEE/ASME Trans. Mechatron. 2013, 18, 1–10. [Google Scholar] [CrossRef]
- Nguyen, T.; Leavitt, J.; Jabbari, F.; Bobrow, J.E. Accurate Sliding-mode control of pneumatic systems using low-cost solenoid valves. IEEE/ASME Trans. Mechatron. 2007, 12, 216–219. [Google Scholar] [CrossRef]
- Hosseini, A.M.; Arzanpour, S.; Golnaraghi, F.; Parameswaran, A.M. Solenoid actuator design and modeling with application in engine vibration isolators. J. Vib. Control 2013, 19, 1015–1023. [Google Scholar] [CrossRef]
- Lee, H.R.; Ahn, J.H.; Kim, H.Y. Design of a Solenoid Actuator for a Cylinder Valve in a Fuel Cell Vehicle. Appl. Sci. 2016, 6, 288. [Google Scholar] [CrossRef]
- Angadi, S.; Jackson, R.; yul Choe, S.; Flowers, G.; Suhling, J.; Chang, Y.K.; Ham, J.K.; il Bae, J. Reliability and life study of hydraulic solenoid valve. Part 2: Experimental study. Eng. Fail. Anal. 2009, 16, 944–963. [Google Scholar] [CrossRef]
- Deepak, S.S.; Kumar, K.S. Investigation of Response Time Analysis of a Pneumatic Valve. Int. J. Eng. Res. Technol. (IJERT) 2016, 5, 342–347. [Google Scholar]
- Li, P.X.; Su, M.; Zhang, D.B. Response characteristic of high-speed on/off valve with double voltage driving circuit. IOP Conf. Ser. Mater. Sci. Eng. 2017, 220, 012028. [Google Scholar] [CrossRef]
- Angadi, S.; Jackson, R.; Choe, S.Y.; Flowers, G.; Suhling, J.; Chang, Y.K.; Ham, J.K. Reliability and life study of hydraulic solenoid valve. Part 1: A multi-physics finite element model. Eng. Fail. Anal. 2009, 16, 874–887. [Google Scholar] [CrossRef]
- Lee, I.Y. Switching Response Improvement of a High Speed On/Off Solenoid Valve by Using a 3 Power Source Type Valve Driving Circuit. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 1823–1828. [Google Scholar] [CrossRef]
- Zhong, Q.; Xie, G.; Wang, X.; LI, Y.; Yang, H.; Zhang, B.; Chen, B. Performance Analysis of High Speed on/off Valve by Multi-voltages Compound Excitation. J. Mech. Eng. 2021, 57, 191. [Google Scholar] [CrossRef]
- Zhong, Q.; Zhang, B.; Yang, H.Y.; Ma, J.E.; Fung, R.F. Performance analysis of a high-speed on/off valve based on an intelligent pulse-width modulation control. Adv. Mech. Eng. 2017, 9, 168781401773324. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, H.; Huang, G.; Zhang, Y.; Chen, C. A Study on the Fast Response Solenoid Valve in the Electronic Control of Diesel Engine. In Proceedings of the Seoul 2000 FISITA World Automotive Congress, Seoul, Republic of Korea, 12–15 June 2000. [Google Scholar]
- Zheng, K.; Chen, M. High-Speed Solenoid. Valve. Patent CN201520372416.6, 3 June 2015. [Google Scholar]
- Li, W.H.; Shao, W.L. Study of Flow Characteristics and Control Circuit on High-Speed Solenoid Valve. Adv. Mater. Res. 2013, 619, 107–110. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, L.; Peng, X.; Xu, Z. Design and Analysis of a Fully Variable Valve Actuation System. Energies 2020, 13, 6391. [Google Scholar] [CrossRef]
- Rybarczyk, D. Concept and modelling of the electrohydraulic valve with DC and stepper motors. MATEC Web Conf. 2019, 252, 06003. [Google Scholar] [CrossRef][Green Version]
- Han, M.; Liu, Y.; Liao, Y.; Wang, S. Investigation on the Modeling and Dynamic Characteristics of a Novel Hydraulic Proportional Valve Driven by a Voice Coil Motor. J. Mech. Eng. Vestn. 2021, 67, 223–234. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, Y.; Hou, J.; Wu, H. Simulation on Linear-Motor-Driven Water Hydraulic Reciprocating Plunger Pump. Adv. Mater. Res. 2013, 842, 530–535. [Google Scholar] [CrossRef]
- Chen, Z.; Ge, S.; Jiang, Y.; Cheng, W.; Zhu, Y. Refined modeling and experimental verification of a torque motor for an electro-hydraulic servo valve. Chin. J. Aeronaut. 2023, 36, 302–317. [Google Scholar] [CrossRef]
- Shahroudi, K.E. Robust Servo Control of a High Friction Industrial Turbine Gas Valve by Indirectly Using the Standard μ-Synthesis Tools. IEEE Trans. Control Syst. Technol. 2006, 14, 1097–1104. [Google Scholar] [CrossRef]
- Li, Z.; Chang, L.; Zhao, J.; Cao, J.; Ruan, J. Development of a Novel Two-Dimensional(2d) Three-Way(3w) Fuel Flow Control Servo Valve with Constant Pressure Difference. Flow Meas. Instrum. 2022, 87, 102210. [Google Scholar] [CrossRef]
- Mojallal Agh, S.; Pirkandi, J.; Mahmoodi, M.; Jahromi, M. Optimum design, simulation and test of a new flow control valve with an electronic actuator for turbine engine fuel control system. Flow Meas. Instrum. 2019, 65, 65–77. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, H.; Yu, L.; Ye, Z. Study of Temperature Effect on Servovalve-Controlled Fuel Metering Unit. J. Eng. Gas Turbines Power 2015, 137, 061503. [Google Scholar] [CrossRef]
- Dólleman, P.; Carneiro, J.F.; Gomes De Almeida, F. Exploring the use of two servo-valves for servo-pneumatic control. Int. J. Adv. Manuf. Technol. 2018, 97, 3963–3980. [Google Scholar] [CrossRef]
- Li, P.Y. Dynamic redesign of a flow control servo valve using a pressure control pilot. J. Dyn. Syst. Meas. Control. Trans. ASME 2002, 124, 428–434. [Google Scholar] [CrossRef][Green Version]
- Meng, B.; Xu, H.; Ruan, J.; Li, S. Theoretical and experimental investigation on novel 2D maglev servo proportional valve. Chin. J. Aeronaut. 2021, 34, 416–431. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, L.; Duan, Z.; Jiao, Z.; Gerada, C.; Chen, I.M. High Torque Density Torque Motor with Hybrid Magnetization Pole Arrays for Jet Pipe Servo Valve. IEEE Trans. Ind. Electron. 2020, 67, 2133–2142. [Google Scholar] [CrossRef]
- Karunanidhi, S.; Singaperumal, M. Design, analysis and simulation of magnetostrictive actuator and its application to high dynamic servo valve. Sens. Actuators A Phys. 2010, 157, 185–197. [Google Scholar] [CrossRef]
- Ikebe, Y.; Nakada, T. On a piezoelectric flapper type servovalve operated i f a pulse-width-modulated-signal. J. Dyn. Syst. Meas. Control. Trans. ASME 1974, 96, 88–94. [Google Scholar] [CrossRef]
- Mercorelli, P.; Werner, N. Integrating a piezoelectric actuator with mechanical and hydraulic devices to control camless engines. Mech. Syst. Signal Process. 2016, 78, 55–70. [Google Scholar] [CrossRef]
- Juuti, J.; Kordás, K.; Lonnakko, R.; Moilanen, V.P.; Leppävuori, S. Mechanically amplified large displacement piezoelectric actuators. Sens. Actuators A Phys. 2005, 120, 225–231. [Google Scholar] [CrossRef]
- Croft, D.; Shed, G.; Devasia, S. Creep, hysteresis, and vibration compensation for piezoactuators: Atomic force microscopy application. J. Dyn. Syst. Meas. Control. Trans. ASME 2001, 123, 35–43. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, S.H.; Kwaka, Y.K. Development of a piezoelectric actuator using a three-dimensional bridge-type hinge mechanism. Rev. Sci. Instrum. 2003, 74, 2918–2924. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Gao, F.; Yang, M.; Sun, L.; Du, Z.; Tang, J.; Zhang, D. Development and analysis of a bridge-lever-type displacement amplifier based on hybrid flexure hinges. Precis. Eng. 2018, 54, 171–181. [Google Scholar] [CrossRef]
- Haus, B.; Aschemann, H.; Mercorelli, P.; Werner, N. Nonlinear modelling and sliding mode control of a piezo-hydraulic valve system. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016. [Google Scholar] [CrossRef]
- Fang, J.; Wang, X.; Wu, J.; Yang, S.; Li, L.; Gao, X.; Tian, Y. Modeling and Control of A High Speed On/Off Valve Actuator. Int. J. Automot. Technol. 2019, 20, 1221–1236. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, H.; Cao, D.; Chen, H. System Modeling, Coupling Analysis, and Experimental Validation of a Proportional Pressure Valve with Pulsewidth Modulation Control. IEEE/ASME Trans. Mechatron. 2016, 21, 1742–1753. [Google Scholar] [CrossRef]
- Chladny, R.R.; Koch, C.R.; Lynch, A.F. Modeling automotive gas-exchange solenoid valve actuators. IEEE Trans. Magn. 2005, 41, 1155–1162. [Google Scholar] [CrossRef]
- Liu, P.; Fan, L.; Zhou, W.; Ma, X.; Song, E. Dynamic performances analysis and optimization of novel high-speed electromagnetic actuator for electronic fuel injection system of diesel engine. J. Mech. Sci. Technol. 2017, 31, 4019–4028. [Google Scholar] [CrossRef]
- Koch, C.R.; Lynch, A.F.; Chladny, R.R. Modeling and Control of Solenoid Valves for Internal Combustion Engines. IFAC Proc. Vol. 2002, 35, 197–202. [Google Scholar] [CrossRef]
- Bayat, F.; Tehrani, A.F.; Danesh, M. Finite element analysis of proportional solenoid characteristics in hydraulic valves. Int. J. Automot. Technol. 2012, 13, 809–816. [Google Scholar] [CrossRef]
- Demarchi, A.; Farçoni, L.; Pinto, A.; Lang, R.; Romero, R.; Silva, I. Modelling a solenoid’s valve movement. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2018; Volume 11175 LNAI, pp. 290–301. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, L.; Liu, P.; Grekhov, L.; Ma, X.; Song, E. Investigation on Electromagnetic Models of High-Speed Solenoid Valve for Common Rail Injector. Math. Probl. Eng. 2017, 2017, 9078598. [Google Scholar] [CrossRef]
- Chillet, C.; Voyant, J.Y. Design-oriented analytical study of a linear electromagnetic actuator by means of a reluctance network. IEEE Trans. Magn. 2001, 37, 3004–3011. [Google Scholar] [CrossRef]
- Grekhov, L.; Zhao, J.; Ma, X. Fast-Response solenoid actuator computational dimulation for engine fuel systems. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2017, St. Petersburg, Russia, 16–19 May 2017. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, X.; Li, C.; Jiao, Z.; Qu, F. Multiobjective Optimization of a Hollow Plunger Type Solenoid for High Speed On/Off Valve. IEEE Trans. Ind. Electron. 2018, 65, 3115–3124. [Google Scholar] [CrossRef]
- Vogel, O.; Ulm, J. Theory of Proportional Solenoids and Magnetic Force Calculation Using COMSOL Multiphysics. In Proceedings of the 2011 COMSOL Conference, Stuttgart, Germany, 26–28 October 2011. [Google Scholar]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Xiang, J.Y. Modeling and control of a Linear Electro-Mechanical Actuator (LEMA) for operating engine valves. In Proceedings of the Conference Record—IAS Annual Meeting (IEEE Industry Applications Society), Pittsburgh, PA, USA, 13–18 October 2002; Volume 3, pp. 1943–1949. [Google Scholar] [CrossRef]
- di Gaeta, A.; Glielmo, L.; Giglio, V.; Police, G. Modeling of an electromechanical engine valve actuator based on a hybrid analytical - FEM approach. IEEE/ASME Trans. Mechatron. 2008, 13, 625–637. [Google Scholar] [CrossRef]
- Li, Y. Steady-state modelling and performance of a rotary direct drive digital valve. Meas. Control 2020, 53, 311–319. [Google Scholar] [CrossRef]
- Shan, J.; Shi, Y.; Ji, H.; Cao, S.; Li, Z.; Zhang, H. Moment-Frequency Characteristics of Limited-Angle Torque Motors for Direct-Drive Servo Rotary Valve. In The 8th International Conference on Advances in Construction Machinery and Vehicle Engineering; Halgamuge, S.K., Zhang, H., Zhao, D., Bian, Y., Eds.; Springer: Singapore, 2024; pp. 719–733. [Google Scholar]
- Meng, B.; Dai, M.; Zhu, C.; Zhang, C.; Ding, C.; Ruan, J. Analytical Modelling and Experiment of Novel Rotary Electro-Mechanical Converter with Negative Feedback Mechanism for 2D Valve. Chin. J. Mech. Eng. 2022, 35, 122. [Google Scholar] [CrossRef]
- Hossain, M.S.; Sultan, I.; Phung, T.; Kumar, A. An Optimized Artificial Neural Network Model of a Limaçon-to-Circular Gas Expander with an Inlet Valve. Thermo 2024, 4, 252–272. [Google Scholar] [CrossRef]
- Loukianov, A.G.; Sanchez, E.; Lizalde, C. Force tracking neural block control for an electro-hydraulic actuator via second-order sliding mode. Int. J. Robust Nonlinear Control 2008, 18, 319–332. [Google Scholar] [CrossRef]
- Rahmat, M.F.; Husain, A.R.; Ishaque, K.; Irhouma, M. Self-Tuning Position Tracking Control of an Electro-Hydraulic Servo System in the Presence of Internal Leakage and Friction. Int. Rev. Autom. Control 2010, 3, 673–683. [Google Scholar]
- Alleyne, A.; Hedrick, J. Nonlinear adaptive control of active suspensions. IEEE Trans. Control Syst. Technol. 1995, 3, 94–101. [Google Scholar] [CrossRef]
- Luo, C.; Shang, Y.; Jiao, Z.; Wang, Z. A new type of electro-hydraulic actuator used for aircraft structural test. IET Conf. Publ. 2012, 2012, 191–194. [Google Scholar] [CrossRef]
- Kaddissi, C.; Kenne, J.p.; Saad, M. Indirect Adaptive Control of an Electro-Hydraulic Servo System Based on Nonlinear Backstepping. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 4, pp. 3147–3153. [Google Scholar] [CrossRef]
- Niksefat, N.; Sepehri, N. A QFT fault-tolerant control for electrohydraulic positioning systems. IEEE Trans. Control Syst. Technol. 2002, 10, 626–632. [Google Scholar] [CrossRef]
- Ling, T.G.; Rahmat, M.F.; Husain, A.R. System identification and control of an Electro-Hydraulic Actuator system. In Proceedings of the 2012 IEEE 8th International Colloquium on Signal Processing and Its Applications, Malacca, Malaysia, 23–25 March 2012; pp. 85–88. [Google Scholar] [CrossRef]
- Bouc, R. Forced vibration of mechanical systems with hysteresis. In Proceedings of the Fourth Conference on Nonlinear Oscillation, Prague, Czech Republic, 5–9 September 1967; p. 315. [Google Scholar]
- Wen, Y.-K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Zhong, Q.; Wang, J.; Xu, E.; Yu, C.; Li, Y. Multi-objective optimization of a high speed on/off valve for dynamic performance improvement and volume minimization. Chin. J. Aeronaut. 2024. [Google Scholar] [CrossRef]
- Qingtong, L.; Fanglong, Y.; Songlin, N.; Ruidong, H.; Hui, J. Multi-objective optimization of high-speed on-off valve based on surrogate model for water hydraulic manipulators. Fusion Eng. Des. 2021, 173, 112949. [Google Scholar] [CrossRef]
- Ren, J.; Zhou, F.; Wang, N.; Hu, G. Multi-Objective Optimization Design and Dynamic Performance Analysis of an Enhanced Radial Magnetorheological Valve with Both Annular and Radial Flow Paths. Actuators 2022, 11, 120. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Abedinifar, M.; Ertugrul, S.; Tayyar, G.T. Design optimization of a solenoid actuator using particle swarm optimization algorithm with multiple objectives. Adv. Mech. Eng. 2022, 14, 16878132221135737. [Google Scholar] [CrossRef]
- Xu, H.; Meng, B.; Zhu, C.; Heng, Y.; Ruan, J. Multi-objective optimization design of two-dimensional proportional valve with magnetic coupling. Adv. Mech. Eng. 2022, 14, 16878132221134986. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Khodadadi, N.; Cao, Q. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Hosein Akbari, A.; Tanhaeean, M.; Moghdani, R.; Gholian-Jouybari, F.; Hajiaghaei-Keshteli, M. Multi-objective boxing match algorithm for multi-objective optimization problems. Expert Syst. Appl. 2024, 239, 122394. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Young’s double-slit experiment optimizer: A novel metaheuristic optimization algorithm for global and constraint optimization problems. Comput. Methods Appl. Mech. Eng. 2023, 403, 115652. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, L.; Zhao, J.; Grekhov, L. Research on Multi-Objective Optimization of High-Speed Solenoid Valve Drive Strategies under the Synergistic Effect of Dynamic Response and Energy Loss. Energies 2024, 17, 300. [Google Scholar] [CrossRef]
- Ren, H.P.; Wang, X.; Fan, J.T.; Kaynak, O. Adaptive Backstepping Control of a Pneumatic System With Unknown Model Parameters and Control Direction. IEEE Access 2019, 7, 64471–64482. [Google Scholar] [CrossRef]
- Yoon, Y.; Yang, M.; Sun, Z. Robust position tracking control of a camless engine valve actuator with time-varying reference frequency. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014. [Google Scholar] [CrossRef]
- Gu, W.; Yao, J.; Yao, Z.; Zheng, J. Robust Adaptive Control of Hydraulic System with Input Saturation and Valve Dead-Zone. IEEE Access 2018, 6, 53521–53532. [Google Scholar] [CrossRef]
- Chung, S.K.; Koch, C.R.; Lynch, A.F. Flatness-Based Feedback Control of an Automotive Solenoid Valve. IEEE Trans. Control Syst. Technol. 2007, 15, 394–401. [Google Scholar] [CrossRef]
- Mercorelli, P.; Werner, N. A cascade controller structure using an internal PID controller for a hybrid piezo-hydraulic actuator in camless internal combustion engines. In Proceedings of the 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013. [Google Scholar] [CrossRef]
- Persson, L.J.; Plummer, A.R.; Bowen, C.R.; Brooks, I. Design and modelling of a novel servovalve actuated by a piezoelectric ring bender. In Proceedings of the ASME/BATH 2015 Symposium on Fluid Power and Motion Control, FPMC 2015, Chicago, IL, USA, 12–14 October 2015. [Google Scholar] [CrossRef]
- Ringwood, J.; dePaor, A. Actuator linearisation for multivariable control applications. In Proceedings of the 2009 3rd International Conference on Signals, Circuits and Systems (SCS), Medenine, Tunisia, 6–8 November 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Tajjudin, M.; Ishak, N.; Ismail, H.; Rahiman, M.H.F.; Adnan, R. Optimized PID control using Nelder-Mead method for electro-hydraulic actuator systems. In Proceedings of the 2011 IEEE Control and System Graduate Research Colloquium, ICSGRC 2011, Shah Alam, Malaysia, 27–28 June 2011; pp. 90–93. [Google Scholar] [CrossRef]
- Ishak, N.; Tajjudin, M.; Ismail, H.; Hezri, M.; Rahiman, F.; Sam, Y.M.; Adnan, R. PID Studies on Position Tracking Control of an Electro-Hydraulic Actuator. Int. J. Control Sci. Eng. 2012, 2012, 120–126. [Google Scholar] [CrossRef]
- Rozali, S.M.; Rahmat, M.F.; Wahab, N.A.; Ghazali, R.; Zulfatman. PID controller design for an industrial hydraulic actuator with servo system. In Proceedings of the 2010 IEEE Student Conference on Research and Development—Engineering: Innovation and Beyond, SCOReD 2010, Kuala Lumpur, Malaysia, 13–14 December 2010; pp. 218–223. [Google Scholar] [CrossRef]
- Vargas, A.N.; Menegaz, H.M.; Ishihara, J.Y.; Acho, L. Unscented Kalman Filters for Estimating the Position of an Automotive Electronic Throttle Valve. IEEE Trans. Veh. Technol. 2016, 65, 4627–4632. [Google Scholar] [CrossRef]
- Wang, M.; Li, P.Y. Event based Kalman filter observer for rotary high speed on/off valve. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 1546–1551. [Google Scholar] [CrossRef]
- Hahnel, C.; Aul, V.; Schultze, M.; Horn, J. State estimation of exhaust valve position by Kalman Filter in PEM fuel cell systems. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications, ICRERA 2015, Palermo, Italy, 22–25 November 2015; pp. 590–595. [Google Scholar] [CrossRef]
- Soufi, Y.; Kahla, S.; Bechouat, M. Particle swarm optimization based sliding mode control of variable speed wind energy conversion system. Int. J. Hydrogen Energy 2016, 41, 20956–20963. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–485. [Google Scholar] [CrossRef]
- Samani, R.; Khodadadi, H. A particle swarm optimization approach for sliding mode control of electromechanical valve actuator in camless internal combustion engines. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017. [Google Scholar] [CrossRef]
- Guan, C.; Pan, S. Nonlinear Adaptive Robust Control of Single-Rod Electro-Hydraulic Actuator with Unknown Nonlinear Parameters. IEEE Trans. Control Syst. Technol. 2008, 16, 434–445. [Google Scholar] [CrossRef]
- Yao, B.; Al-Majed, M.; Tomizuka, M. High-performance robust motion control of machine tools: An adaptive robust control approach and comparative experiments. IEEE/ASME Trans. Mechatron. 1997, 2, 63–76. [Google Scholar] [CrossRef]
- Lu, L.; Chen, Z.; Yao, B.; Wang, Q. Desired Compensation Adaptive Robust Control of a Linear-Motor-Driven Precision Industrial Gantry with Improved Cogging Force Compensation. IEEE/ASME Trans. Mechatron. 2008, 13, 617–624. [Google Scholar] [CrossRef]
- Mohanty, A.; Yao, B. Indirect Adaptive Robust Control of Hydraulic Manipulators with Accurate Parameter Estimates. IEEE Trans. Control Syst. Technol. 2011, 19, 567–575. [Google Scholar] [CrossRef]
- Rybarczyk, D.; Milecki, A. The Use of a Model-Based Controller for Dynamics Improvement of the Hydraulic Drive with Proportional Valve and Synchronous Motor. Energies 2022, 15, 3111. [Google Scholar] [CrossRef]
- Angue Mintsa, H.; Venugopal, R.; Kenne, J.P.; Belleau, C. Feedback Linearization-Based Position Control of an Electrohydraulic Servo System With Supply Pressure Uncertainty. IEEE Trans. Control Syst. Technol. 2012, 20, 1092–1099. [Google Scholar] [CrossRef]
- Seoa, J.; Venugopal, R.; Kennéa, J.P. Feedback linearization based control of a rotational hydraulic drive. IFAC Proc. Vol. (IFAC-Pap.) 2007, 7, 940–945. [Google Scholar] [CrossRef]
- Polton, C.; Boje, E. Quantitative Feedback Theory design of valve position control for co-ordinated superheater control of main steam temperatures of power plant boilers. IFAC-PapersOnLine 2020, 53, 13070–13075. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T. Chapter 1—An introduction to backstepping control. In Backstepping Control of Nonlinear Dynamical Systems; Vaidyanathan, S., Azar, A.T., Eds.; Advances in Nonlinear Dynamics and Chaos (ANDC); Academic Press: Cambridge, MA, USA, 2021; pp. 1–32. [Google Scholar] [CrossRef]
- Enyan, M.; Bing, Z.; Junsen, R.; Amu-Darko, J.; Issaka, E.; Páez, L. Nonlinear Position Control of Electro-Hydraulic Servo System Based on Lyapunov Robust Integral Backstepping Controller. Eng. Res. Express 2023, 5, 045024. [Google Scholar] [CrossRef]
- Yang, G.; Jiang, P.; Lei, L.; Wu, Y.; Du, J.; Li, B. Adaptive Backstepping Control of Vacuum Servo System Using High-Speed on-off Valves. IEEE Access 2020, 8, 129799–129812. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J.; Wang, Y.; Yang, X.; Chen, J. Output feedback backstepping control of hydraulic actuators with valve dynamics compensation. Mech. Syst. Signal Process. 2021, 158, 107769. [Google Scholar] [CrossRef]
- Han, C.; Choi, S.B.; Han, Y.M. A Piezoelectric Actuator-Based Direct-Drive Valve for Fast Motion Control at High Operating Temperatures. Appl. Sci. 2018, 8, 1806. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, T.; Xie, Q.I.; Wei, Q. Intelligent Electro-Pneumatic Position Tracking System Using Improved Mode-Switching Sliding Control with Fuzzy Nonlinear Gain. IEEE Access 2018, 6, 34462–34476. [Google Scholar] [CrossRef]
- Mercorelli, P.; Werner, N.; Becker, U.; Harndorf, H. A robust model predictive control using a feedforward structure for a hybrid hydraulic piezo actuator in camless internal combustion engines. In Proceedings of the International Multi-Conference on Systems, Signals and Devices, SSD 2012—Summary Proceedings, Chemnitz, Germany, 20–23 March 2012. [Google Scholar] [CrossRef]
- Ahn, K.; Truong, D. Online tuning fuzzy PID controller using robust extended Kalman filter. J. Process Control 2009, 19, 1011–1023. [Google Scholar] [CrossRef]
- Dimitrova, Z.; Tari, M.; Lanusse, P.; Aioun, F.; Moreau, X. Robust control for an electromagnetic actuator for a camless engine. Mechatronics 2019, 57, 109–128. [Google Scholar] [CrossRef]
- He, H.; Quan, S.; Wang, Y.X. Hydrogen circulation system model predictive control for polymer electrolyte membrane fuel cell-based electric vehicle application. Int. J. Hydrogen Energy 2020, 45, 20382–20390. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, Z.; Li, K.; Liu, J.; Zhang, Y.; Dan, D.; Wu, C.; Wang, P.; Wang, X. An improved intelligent model predictive controller for cooling system of electric vehicle. Appl. Therm. Eng. 2021, 182, 116084. [Google Scholar] [CrossRef]
- Feng, G.; Lei, S.; Gu, X.; Guo, Y.; Wang, J. Predictive control model for variable air volume terminal valve opening based on backpropagation neural network. Build. Environ. 2021, 188, 107485. [Google Scholar] [CrossRef]
- Ghoniem, M.; Awad, T.; Mokhiamar, O. Control of a new low-cost semi-active vehicle suspension system using artificial neural networks. Alex. Eng. J. 2020, 59, 4013–4025. [Google Scholar] [CrossRef]
- Lou, Z.; Zhu, G. Review of Advancement in Variable Valve Actuation of Internal Combustion Engines. Appl. Sci. 2020, 10, 1216. [Google Scholar] [CrossRef]
| Type | Mechanism | Pros | Cons |
|---|---|---|---|
| Hydraulic | Pilot-operated [19,20,21] | Reliable, precise control, and high flow capacity | Slower response, complex architecture, and costly manufacturing |
| Pressure-assisted [22] | Suitable for high-pressure systems and reliable | Slower response and complex mechanism | |
| Pneumatic | Pilot-operated [23] | High power-to-weight ratio, high flow rates, and reduced energy consumption | Sensitive to contaminants and higher initial cost |
| Air-operated [24] | Simplicity and lower installation cost | Slower actuation and limited pressure handling capacity | |
| Electrical | Solenoid [13,25] | Faster response, simple control, and compact design | Limited pressure and flow capacity, sensitivity to voltage fluctuations, and heating and hysteresis effect |
| Motor [9,26,27] | High precision and torque, simpler control, and suitable for high-pressure systems | Higher energy consumption | |
| Piezoelectric [28,29] | Very fast and precise response with minimal power consumption | Limited force and stroke, requires displacement amplifiers, not suitable for high-pressure systems, and higher cost | |
| Hybrid | Electro-hydraulic [30,31,32,33,34] | High force, large pressure handling, high precision, and versatile architecture | Complex and maintenance-intensive design and higher installation costs |
| Electro-pneumatic [35,36] | Fast response and precise control and energy-efficient | Complex installation and sensitivity to environmental conditions |
| Name of the Algorithm | Pros | Cons |
|---|---|---|
| Electric eel foraging optimization (EEFO) [115] | High searching efficiency, simplicity, scalability, robustness, and ease of implementation | Less effective in discrete optimization problems and unable to achieve a quasi-optimal solution close to the global optimum for certain problems |
| Multi-objective boxing match algorithm (MOBMA) [116] | High convergence rate and effective for complex problems with multiple objectives | Requires incorporation of other learning algorithms for better performance |
| Young’s double-slit experiment (YDSE) optimizer [117] | Suited for multi-objective problems | Several parameters need to be tuned and require incorporation of other stochastic algorithms for faster convergence |
| Arithmetic optimization algorithm (AOA) [118] | Ability to escape local minima | This is an initial framework that should be enhanced according to the specific problems |
| Name of the Algorithm | Pros | Cons |
|---|---|---|
| PID [124] |
|
|
| KF [130,131,132] |
|
|
| SMC [45,79,99,133,135] |
|
|
| Backstepping [145,146,147] |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.S.; Sultan, I.; Phung, T.; Kumar, A. A Literature Review of the Design, Modeling, Optimization, and Control of Electro-Mechanical Inlet Valves for Gas Expanders. Energies 2024, 17, 4569. https://doi.org/10.3390/en17184569
Hossain MS, Sultan I, Phung T, Kumar A. A Literature Review of the Design, Modeling, Optimization, and Control of Electro-Mechanical Inlet Valves for Gas Expanders. Energies. 2024; 17(18):4569. https://doi.org/10.3390/en17184569
Chicago/Turabian StyleHossain, Md Shazzad, Ibrahim Sultan, Truong Phung, and Apurv Kumar. 2024. "A Literature Review of the Design, Modeling, Optimization, and Control of Electro-Mechanical Inlet Valves for Gas Expanders" Energies 17, no. 18: 4569. https://doi.org/10.3390/en17184569
APA StyleHossain, M. S., Sultan, I., Phung, T., & Kumar, A. (2024). A Literature Review of the Design, Modeling, Optimization, and Control of Electro-Mechanical Inlet Valves for Gas Expanders. Energies, 17(18), 4569. https://doi.org/10.3390/en17184569








