LightGBM-, SHAP-, and Correlation-Matrix-Heatmap-Based Approaches for Analyzing Household Energy Data: Towards Electricity Self-Sufficient Houses

Abstract

The rapidly growing global energy demand, environmental concerns, and the urgent need to reduce carbon footprints have made sustainable household energy consumption a critical priority. This study aims to analyze household energy data to predict the electricity self-sufficiency rate of households and extract meaningful insights that can enhance it. For this purpose, we use LightGBM (Light Gradient Boosting Machine)-, SHAP (SHapley Additive exPlanations)-, and correlation-heatmap-based approaches to analyze 12 months of energy and questionnaire survey data collected from over 200 smart houses in Kitakyushu, Japan. First, we use LightGBM to predict the ESSR of households and identify the key features that impact the prediction model. By using LightGBM, we demonstrated that the key features are the housing type, average monthly electricity bill, presence of floor heating system, average monthly gas bill, electricity tariff plan, electrical capacity, number of TVs, cooking equipment used, number of washing and drying machines, and the frequency of viewing home energy management systems (HEMSs). Furthermore, we adopted the LightGBM classifier with ${\ell }^1$ regularization to extract the most significant features and established a statistical correlation between these features and the electricity self-sufficiency rate. This LightGBM-based model can also predict the electricity self-sufficiency rate of households that did not participate in the questionnaire survey. The LightGBM-based model offers a global view of feature importance but lacks detailed explanations for individual predictions. For this purpose, we used SHAP analysis to identify the impact-wise order of key features that influence the electricity self-sufficiency rate (ESSR) and evaluated the contribution of each feature to the model’s predictions. A heatmap is also used to analyze the correlation among household variables and the ESSR. To evaluate the performance of the classification model, we used a confusion matrix showing a good F1 score (Weighted Avg) of 0.90. The findings discussed in this article offer valuable insights for energy policymakers to achieve the objective of developing energy-self-sufficient houses.

1. Introduction

In recent years, population growth, rapid urbanization, economic growth, and advancements in healthcare systems have led to a rise in global electricity demand [1]. According to several articles and reports (like: international energy agency-IEA), the global electricity demand is expected to rise drastically in the next few decades [2]. The residential sector accounts for a substantial portion of global electricity usage and CO₂ emissions and significantly affects global climate change. Coal, oil, and natural gas remain the primary energy sources for electrical power generation worldwide [3]. The use of these fossil fuels in electrical power generation damages the environment by emitting harmful greenhouse gases (GHGs) such as carbon dioxide (CO₂) and methane [4,5]. Coal power generation is the largest contributor to global greenhouse gas (GHG) emissions, as carbon dioxide released from coal combustion alone accounts for a major share of global warming [6,7]. Coal, the most carbon-intensive fossil fuel, has historically been the primary choice for electricity generation due to its widespread availability and relatively low cost. The combustion of coal releases substantial amounts of carbon dioxide (CO₂) and other atmospheric pollutants, contributing significantly to global warming and resulting in adverse effects such as rising temperatures, climate change, altered weather patterns, and the accelerated melting of polar ice caps and glaciers [8,9,10].

Global warming presents a formidable threat to the sustainability of life on Earth, necessitating immediate and concerted efforts to mitigate its effects and transition towards more sustainable energy sources and practices. The escalating concerns over global warming and its profound ramifications for the environment have sparked an urgent call for transformative actions worldwide across various sectors of society [11,12,13]. In the joint statement of the G20 summit held in New Delhi in 2023, member nations also emphasized the importance of adopting carbon-efficient, climate-adaptive, and eco-friendly development pathways. The G20 nations also agreed to the effective implementation of the Paris Agreement (2015) and its objective to keep the rise in global average temperature significantly below 2 °C (3.6 °F) compared to pre-industrial levels [14].

At the forefront of this global challenge lies the imperative to transition towards a low-carbon society. Among the myriad contributors to carbon emissions, household electricity consumption wields significant influence, collectively accounting for a substantial portion of global carbon emissions.

Efforts to mitigate this impact introduced the concept of electricity-self-sufficient houses, representing a significant shift towards sustainable and eco-conscious living. The aim of Electricity self-sufficient houses is to generate sufficient renewable energy for self-sufficiency, eliminating the need for reliance on the grid and achieving autonomy in generating nearly 100% of its clean energy. Achieving the goal of establishing nearly zero-carbon homes requires a systematic approach involving the meticulous management of electricity resources, household electricity consumption patterns, and the widespread integration of renewable technologies.

Governments are formulating energy policies to achieve households’ electricity self-sufficiency targets. These strategies involve installing renewable sources like solar panels or fuel cells at home and using behavioral approaches such as surveys to raise awareness among households about electricity savings.

The residential sector’s electricity usage constitutes a substantial share of global energy consumption [15]. Integrating renewable energy sources such as solar panels and fuel cells into houses enhances electricity self-sufficiency.

Electricity self-sufficiency (ESS) is the ability of a household to generate or produce enough electricity to fulfill its requirements without heavy reliance on external sources. Electricity self-sufficiency rate (ESSR) is a metric used to measure the extent to which a household can meet its electricity needs using locally generated energy, such as from renewable sources like solar panels or inverters, without relying on external power from the grid.

Achieving the target of electricity self-sufficient houses requires strategic planning, substantial investment, and supportive policy frameworks to develop robust, resilient, and eco-friendly electrical energy infrastructures. To achieve these targets, it is essential to develop an efficient predictive model for estimating the electricity self-sufficiency rate (ESSR) of households and understanding the factors that significantly affect model output, as detailed below:

Predicting the electricity self-sufficiency rate of households is crucial for several reasons as given below:

• Electricity Management and Efficiency: Accurate predictions enable better management of energy resources within households. By understanding and anticipating electricity needs, house owners and energy service providers can optimize energy usage, reduce waste, and implement more effective electrical energy-saving measures.
• Cost Savings: Forecasting ESSR aids in planning and budgeting for energy costs. Households can identify patterns in their energy usage and take steps to reduce their consumption during peak periods, potentially lowering their electricity bills.
• Integration of Renewable Energy: For households investing in renewable energy technologies such as solar panels or fuel cells, accurate consumption predictions are essential. By knowing their electricity needs, homeowners can size their renewable energy systems appropriately and ensure that these systems meet their demands effectively.
• Grid Management and Stability: On a larger scale, predicting ESSR aids in managing and stabilizing the electricity grid. Accurate forecasts help utility companies balance supply and demand, preventing outages and ensuring a reliable power supply.
• Environmental Impact: Reducing electricity consumption through accurate predictions can decrease a household’s carbon footprint. Lower energy use translates to reduced greenhouse gas emissions, contributing to broader efforts to combat climate change.

Factors influencing the successful prediction of ESSR include:

• Climate and Weather Conditions: Weather patterns significantly impact household electricity use. For instance, heating needs in winter and cooling demands in summer can cause fluctuations in electricity consumption. Accurate weather data and forecasts are necessary for precise predictions.
• Household Size and Occupancy: The number of residents and their daily activities influence electricity use. Larger households or those with varying occupancy patterns may have different consumption patterns compared to smaller or consistently occupied homes.
• Income and Lifestyle: Household income and lifestyle choices affect energy consumption. Higher-income households might use more energy-intensive appliances, while lifestyle habits, such as energy-efficient practices, can also play a role.
• Appliance Usage: The type, age, and efficiency of appliances and electronics in a household impact electricity consumption. Energy-efficient appliances and smart home technologies can help reduce overall usage, while older or less efficient appliances may lead to higher consumption.
• Behavioral Patterns: Individual behaviors, such as the frequency of using electrical appliances and the times when energy is used, influence overall consumption. Behavioral data, including patterns of use, can improve the accuracy of consumption predictions.
• Building Characteristics: The design and insulation of a home, including factors like the size of the home, insulation quality, and window types, affect heating and cooling needs, which in turn impact electricity consumption.
• Energy Policies and Tariffs: Changes in energy policies and tariffs can influence household electricity use. For instance, time-of-use pricing might encourage households to shift their energy use to off-peak hours.

By considering these factors, predictions of household electricity consumption can be more accurate and useful for managing energy use, optimizing costs, and supporting sustainability efforts. Understanding the correlation among household energy variables and their potential impact on ESSR is also crucial for developing energy policies to reduce household energy consumption. In this article, we present a predictive model for estimating the ESSR (based on household electricity consumption). Additionally, we also address the factors influencing ESSR, correlation among household variables and with ESSR, which supports the goal of achieving zero-carbon housing.

1.1. Related Work

Research in this field is at an early stage, as governments of various countries have only recently acknowledged the threat of global warming and started backing research efforts related to climate change. Research shows that developed countries are implementing energy policies to lower carbon emissions, and their carbon emissions are decreasing. Meanwhile, in developing countries, due to a lack of effective energy policies and economic and population growth, carbon emissions are increasing.

Nejat et al. provide a comprehensive analysis of residential energy use and CO₂ emissions globally, focusing particularly on the top ten CO₂-emitting countries: China, the United States, India, Russia, Japan, Germany, South Korea, Canada, Iran, and the United Kingdom. The study uses datasets from the International Energy Agency (IEA) to analyze energy consumption trends, the impact of urbanization and economic growth, and the effectiveness of energy policies. Subsequently, the study reveals that the residential sector contributes significantly to global energy consumption (27%) and CO₂ emissions (17%), especially in developing countries, where energy use and carbon emissions are rising due to rapid urbanization and economic growth. This study concludes that developed countries are making progress in lowering carbon emissions, but the lack of effective policies in developing countries remains a significant challenge. The reliance on secondary data limits the study’s ability to empirically predict the effectiveness of future policies [16].

In this field, limited articles are available on enhancing household electricity self-sufficiency.

As explained below, a few authors have analyzed household energy data and demonstrated how installing renewable energy sources, such as solar systems and fuel cells, at home can improve electricity self-sufficiency and the factors affecting it.

Camargo et al. enhanced electricity self-sufficiency using PV and battery systems by optimizing the sizes of these components based on technical requirements and weather-dependent scenarios. The authors identified the most efficient combinations of PV and battery sizes through linear optimization modeling to ensure a reliable electricity supply [17].

Li et al. discussed methods like solar tracking panels and energy storage systems to enhance self-sufficiency rates. Their study recommends creating a local grid by connecting rooftops within an area to enhance energy independence [18].

Harke et al. investigated electricity self-sufficiency by estimating PV area and battery capacity requirements for households in Germany. They explored cost optimization strategies and modeled hourly electricity consumption using representative data. This article used the Fourier series and statistical models to model the hourly electricity demand for households [19].

Colmenar et al. discussed mathematical models to evaluate the profitability of photovoltaic systems to boost household electricity self-sufficiency in Spain. By utilizing photovoltaic systems, households can produce their own electricity, supplementing grid power and feeding excess energy back into the grid for remuneration. This approach empowers households to become more self-sufficient in meeting their electricity needs while promoting the use of renewable energy [20].

Bruni et al. increased electricity self-sufficiency in their Matlab/Simulink-based study by introducing a novel definition of energy-efficiency parameters and evaluating the performance of energy conversion components such as PV modules and fuel cells [21].

Ozcan et al. discussed Turkey’s decreasing self-sufficiency in electricity generation due to its reliance on imported fossil fuels and underutilizing renewable energy sources (RESs) [22].

All of the models mentioned above are based on theories, mathematical modeling, statistics, analytical methods, and simulations. They demonstrate that households can enhance their electricity self-sufficiency by utilizing renewable sources such as fuel and solar cells. Furthermore, as explained below, some articles applied machine learning techniques to analyze energy consumption data.

Beckel et al. used supervised machine learning to analyze smart meter data for inferring household characteristics, such as socio-economic status and appliance stock [23]. Edwards et al. discussed using a gate network to determine expert networks for accurate energy consumption prediction using feed-forward neural networks (FFNNs), LS-SVM, etc., ref. [24]. Thakur et al. used the algorithms XGBoost, CatBoost, and LightGBM to analyze energy consumption [25]. Chou et al. provided a detailed analysis of energy consumption forecasting in residential buildings using machine learning techniques such as ANNs and gradient boosting machines (GBMs) [26]. The above articles used traditional machine learning techniques to analyze household energy data but did not examine electricity self-sufficiency or questionnaire surveys.

The articles mentioned below offer significant advancements in optimizing energy management and forecasting in power systems. From improving vehicle-to-grid dispatch with federated learning to leveraging multi-task deep learning for load prediction, these methods demonstrate enhanced accuracy and performance.

Shang et al. introduced the FedPT-V2G framework, which employs federated learning to enhance the vehicle-to-grid (V2G) dispatch by optimizing load management and PV energy self-consumption while ensuring data privacy. By integrating a proximal algorithm with a Transformer model, it effectively addresses challenges posed by non-IID data across various charging stations. The framework achieves an impressive accuracy of 98.93% in dispatch decisions and demonstrates superior performance compared to traditional methods, particularly in handling imbalanced datasets. Overall, it showcases a promising approach for real-time V2G applications. This study acknowledges several limitations, including the reliance on historical data, which may not fully capture future uncertainties in EV behavior and energy generation. Additionally, while the FedPT-V2G framework effectively addresses non-IID data, its performance may still be influenced by extreme data imbalances or variations in local conditions across charging stations [27].

Tan et al. presented a novel multi-task deep learning approach for multi-node load forecasting in power systems, utilizing a soft sharing mechanism and a multi-modal feature extraction module. This method effectively captures spatial–temporal correlations among different nodes, improving prediction accuracy compared to traditional single-task models. The proposed framework demonstrates significant performance enhancements through rigorous testing on real-world New Zealand and Australia datasets. This study acknowledges several limitations, including the reliance on historical load data, which may not fully account for sudden changes in consumption patterns due to external factors such as economic shifts or extreme weather events. Additionally, the model’s performance may vary across different geographical regions and power systems, limiting its generalizability [28].

Zhu et al. presented a novel graph-based model for predicting power generation from renewable power plants (RPPs), demonstrating significant improvements in prediction accuracy compared to existing models. The proposed model achieves reductions in error metrics, highlighting the importance of its designed modules for performance. Future research directions include exploring finer-granularity data and integrating weather features to enhance correlation analysis among RPPs [29].

The work described above has limitations related to its reliance on historical data and real-time adaptability. Shang et al.’s model may not handle future changes or data imbalances effectively. Tan et al.’s approach could struggle with sudden external shifts and lacks regional generalizability. Zhu et al.’s model would improve with finer data and weather integration to better predict renewable power generation.

1.2. Research Gap

As outlined in the literature review, most researchers used mathematical modeling, statistical analyses, and various analytical methods to analyze household energy data and identify key factors influencing household electricity self-sufficiency. Some studies applied traditional machine learning techniques to analyze household energy data but did not provide definitive insights into the electricity self-sufficiency rate. Moreover, the aforementioned studies did not incorporate questionnaire surveys to explore how behavioral approaches could contribute to achieving nearly zero-energy houses.

Despite the promising results shown by the above articles, common challenges remain, such as reliance on historical data and the need to address regional variations and uncertainties.

1.3. Motivation

Global warming presents a critical environmental issue and is responsible for the gradual rise in Earth’s average temperature, primarily due to the accumulation of greenhouse gases in the atmosphere. Incorporating smart household energy management systems, adopting behavioral changes to reduce energy consumption, etc., can further enhance the electrical self-sufficiency of households. These combined efforts can also help in the realization of nearly zero-energy houses. The Jono district in Kitakyushu City, Japan, has several smart houses equipped with solar panels and fuel cells, making it an ideal location to conduct our research aimed at understanding how household energy data analysis and questionnaire survey results can be utilized to achieve the realization of nearly zero-energy houses (nZEHs). Therefore, we collected real data (original data collected by us) from these households. In our study, we utilized SHAP-, heatmap-, and LightGBM-based approaches to uncover nuanced insights and correlations essential to realizing energy-self-sufficient houses.

1.4. Novelty and Contributions

To address the identified research gap, we conducted a comprehensive study involving the collection of original household energy and questionnaire survey data from the Jono district of Kitakyushu, Japan. In this article, we used LightGBM, SHAP, and a correlation-heatmap-based framework to scrutinize household energy and questionnaire survey data.

Initially, we utilized LightGBM-based analysis to extract the importance of features derived from household energy and questionnaire survey data. Subsequently, we implemented a LightGBM with ${\ell }^1$ regularization-based analysis to pinpoint the factors most significantly impacting the electricity self-sufficiency rate, establishing correlations between these factors and the electricity self-sufficiency rate. This LightGBM model can also predict the electricity self-sufficiency of households that did not participate in the questionnaire survey. Further, we used a SHAP summary plot to observe the contribution of each feature to the model’s output, i.e., the ESSR. In the above analysis, we used LightGBM because it is a cutting-edge machine learning framework, recently developed by Microsoft, renowned for its efficiency and performance in predictive modeling tasks [30].

We analyzed the questionnaire data using a correlation-matrix-based heatmap to further explore the interrelationships among household variables and their potential impact on the ESSR. This comprehensive framework provides valuable insights for energy policymakers and researchers, facilitating the development of strategies to achieve the development of net-zero-energy houses.

1.5. Organization of This Article

This work is organized in the following manner:

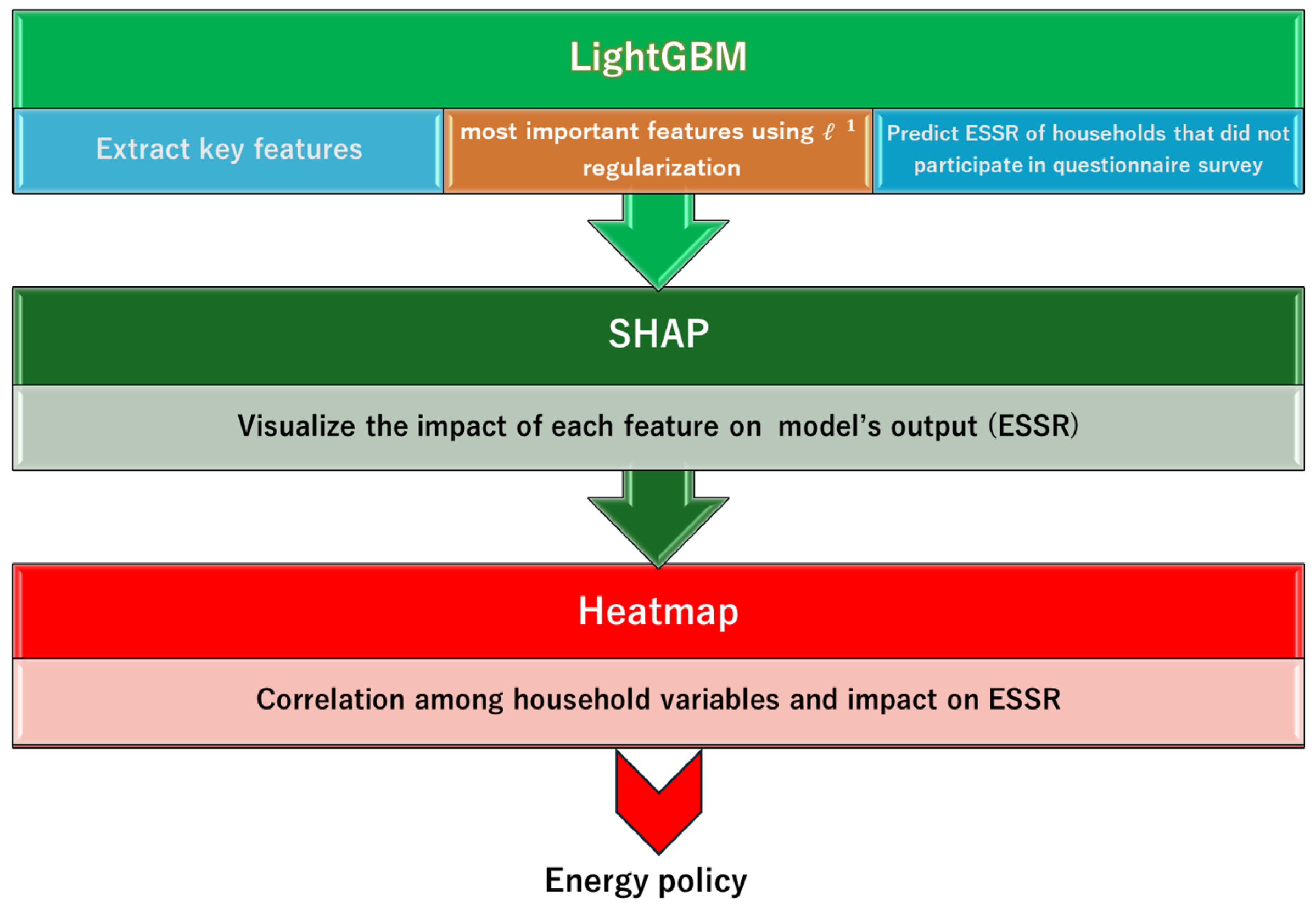
• LightGBM-Based Prediction Model: We use LightGBM to identify key features that affect the electricity self-sufficiency rate of households. We used ${\ell }^1$ regularization to discard the less important features (although these discarded features cannot be completely ignored). Furthermore, this model can forecast the electricity self-sufficiency rate of households omitted from the questionnaire survey while pinpointing the predominant factors influencing electricity self-sufficiency.
• SHAP-based Feature Analysis: This study utilized the LightGBM-based SHAP summary plot to highlight important household features in order of rank of feature importance from top to bottom.
• Understanding the Correlation of Various Household Variables in Questionnaire Survey Data and Their Impact on the ESSR: We analyzed the questionnaire survey data using a correlation-matrix-based heatmap to understand the relationships among different variables and their impact on the ESSR.

As shown in Figure 1, this comprehensive data analysis-based study can be used to guide energy policy.

2. Materials and Methods

2.1. Data Collection and Description

This article scrutinized household electricity data obtained from smart meters and questionnaire survey results. The energy data were recorded at 30-min intervals over one year, from 1 April 2022 to 31 March 2023, across 578 smart homes in Kitakyushu, Japan. Each household was assigned a unique ID number. The household energy data consisted of three types, as shown in

Table 1. Household electrical energy data description.

Variables	Energy Type	Unit
$E_1$	Electrical energy generated from solar panels	Watt-hour
$E_2$	Electrical energy generated from fuel cells	Watt-hour
$E_3$	Total electrical energy consumption	Watt-hour

below.

2.2. Questionnaire Survey

In our analysis, we also incorporated the findings from a 23-question survey concerning household characteristics, such as the number of appliances and housing type, etc. The questionnaire survey used in this article is provided in the Supplementary Materials.

We collected the household energy data in CSV format. For the CSV file-based questionnaire survey, we assigned numeric values ranging from 1 to 5 to each response option, corresponding to the option number for each survey question.

2.3. Data Pre-Processing

The household energy data were collected from an intervention experiment involving 578 households in Kitakyushu City, Japan. Out of these, 151 households had critical inaccuracies in their data, which we excluded from the dataset.

Among the remaining 427 households, 201 answered the survey questions. We use these 201 households to estimate the electricity self-sufficiency rate (ESSR) of households using the LightGBM classifier.

2.4. Electricity Self-Sufficiency Rate

We used 201 households to calculate the electricity self-sufficiency rate (ESSR) of households, which is a metric that indicates the proportion of a household’s total electricity consumption that is met by its own renewable energy sources, such as solar panels and fuel cells. This rate provides insights into how independent a household is from the electricity grid and measures its ability to sustain its energy needs through self-generated power. The electricity self-sufficiency rate can be influenced by various factors, as given below:

• Renewable Energy Sources: The use of solar panels, fuel cells, inverters, or other renewable energy installations that can generate electricity or heat for the household.
• Energy Storage Systems: The presence of batteries or other storage systems that can store energy produced during peak production periods for use during periods when production is low.
• Energy Efficiency Measures: The implementation of energy-saving practices and technologies, such as high-efficiency appliances, LED lighting, proper insulation, and smart thermostats.
• Geographical Location: The availability and effectiveness of renewable energy sources vary by location. For example, solar power is more effective in regions with abundant sunlight.

The electricity self-sufficiency rate (ESSR) of households is calculated using the following formula:

$$\mathrm{ESSR}=\left({\displaystyle \frac{\mathrm{Electricity}\mathrm{generated}\mathrm{from}\mathrm{renewable}\mathrm{energy}\mathrm{sources}(\mathrm{Wh})}{\mathrm{Total}\mathrm{Electricity}\mathrm{Consumption}\mathrm{of}\mathrm{Household}(\mathrm{Wh})}}\right)$$

(1)

where

• Electricity Produced by Household (Wh): The amount of electricity generated by the household’s renewable energy sources, measured in watt-hours (Wh).
• Total Electricity Consumption of Household (Wh): The total amount of electricity consumed by the household from all sources, including both self-generated electricity and any additional electricity drawn from the grid or other external sources, measured in watt-hours (Wh).

By multiplying the ESSR by 100, we can express it as a percentage (%).

For the electricity self-sufficiency rate (ESSR), we used the following equation:

$$ESSR=(E_1+E_2)/E_3,$$

(2)

where ESSR stands for the electricity self-sufficiency rate and $E_1$, $E_2$, and $E_3$ are the variables described in Table 1.

2.5. Data Analysis Techniques

2.5.1. LightGBM ( Light Gradient Boosting Machine)

We used the LightGBM-based model to identify factors that affect the ESSR most significantly and predict households’ electricity self-sufficiency rate.

LightGBM is a gradient-boosting algorithm that grows decision trees using a novel approach, enhancing both performance and efficiency. Unlike traditional gradient-boosting methods that grow trees depth-wise, LightGBM uses a leaf-wise growth strategy. This approach selects the leaf with the maximum loss reduction, leading to faster convergence and reduced memory usage [31].

By leveraging histogram-based algorithms, continuous feature values were placed into discrete bins, which speeds up training without compromising accuracy. This makes LightGBM particularly suited for tasks involving high-dimensional data or millions of instances.

LightGBM also shows advantages such as flexibility and scalability, making it adaptable to various tasks. It can be parallelized across multiple CPU cores or GPUs, making it suitable for both training and deployment in production environments where real-time predictions are required. The framework also includes built-in mechanisms for dealing with missing data and regularization techniques to prevent overfitting, ensuring robust model performance. LightGBM’s features can be summarized as follows:

• Gradient-Based One-Side Sampling (GOSS): LightGBM retains instances with large gradients while randomly sampling instances with smaller gradients. This approach reduces the number of data points processed and accelerates computation without significantly compromising accuracy.
• Exclusive Feature Bundling (EFB): LightGBM combines mutually exclusive features that rarely have non-zero values simultaneously, decreasing the total number of features and enhancing training efficiency.
• Histogram-based Decision Tree Learning: LightGBM employs a histogram-based technique to determine optimal split points by converting continuous feature values into discrete bins. This method simplifies the learning process and accelerates training.
• Leaf-wise Tree Growth: In contrast to traditional level-wise tree growth methods, such as those used by XGBoost, LightGBM adopts a leaf-wise strategy. It selects the leaf with the highest delta loss for expansion, resulting in deeper trees and improved accuracy.

The objective function in LightGBM (light gradient boosting machine) is critical in guiding the model’s training process. It defines how the model’s predictions are evaluated and optimized during the iterative boosting process.

The objective function ($\mathcal{L}$) in LightGBM involves minimizing the loss function concerning the model’s predictions, which can be written mathematically as

$$\mathcal{L}=\sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)+\sum _{k=1}^N\mathrm{\Omega }(f_k)$$

(3)

where

• $l(y_i,{\widehat{y}}_i)$ is the loss function;
• ${\widehat{y}}_i$ is the prediction for instance i;
• $\mathrm{\Omega }(f_k)$ is the regularization term for the k-th tree $f_k$;
• n is the no. of instances;
• N is the no. of trees.

Instead of the traditional level-wise (breadth-first) tree growth used in algorithms like XGBoost, LightGBM uses a leaf-wise growth strategy for decision trees. It selects the leaf with the maximum delta loss to grow, leading to deeper trees and better accuracy as compared to other tree-based machine learning algorithms.

The gain from splitting a node is given by

$$\mathrm{Gain}(S)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{G_L^2}{H_L+\lambda }}+{\displaystyle \frac{G_R^2}{H_R+\lambda }}-{\displaystyle \frac{{(G_L+G_R)}^2}{H_L+H_R+\lambda }}\right)-\gamma$$

(4)

where

• $G_L$ and $G_R$ are the sums of the gradients for the left and right splits, respectively;
• $H_L$ and $H_R$ are the sums of the second-order gradients (Hessians) for the left and right splits, respectively;
• $\lambda$ is the regularization parameter;
• $\gamma$ is the regularization term for the number of leaves.

The objective function in LightGBM guides the training process by balancing the model’s predictive accuracy (through the loss function) with its complexity (through regularization). By optimizing this objective function during training, LightGBM efficiently builds a boosted ensemble of trees that generalize well to unseen data while maintaining computational efficiency and scalability [32].

We used LightGBM to analyze household energy data from 201 households, aiming to pinpoint the key features that predict the electricity self-sufficiency rate.

We used the following input and output variables:

• Input variables—Survey responses (option number 1–5 for each survey question);
• Output variable—Electricity self-sufficiency rate;
• Evaluation function—Mean absolute error (MAE).

We applied ${\ell }^1$ regularization to induce sparsity in the model’s coefficients [33]. This technique modifies the model’s loss function by adding a penalty term, which promotes selecting only the most relevant features for prediction. We validated the performance of the LightGBM-based model using the stratified k-fold cross-validation (cv) method. The mean absolute error, LightGBM’s default for regression, worked as a cost function for this model.

Ultimately, we identified features of importance for predicting the electricity self-sufficiency rate of various households.

2.5.2. Feature Analysis Based on SHAP (SHapley Additive exPlanations)

We used the LightGBM-based SHAP summary plot to identify key factors that influenced the electricity self-sufficiency rate of households. The SHAP summary plot provides a visual representation of feature importance [34]. Each dot represents a Shapley value for a given feature and instance. The color coding shows the feature value, where red denotes a high value and blue signifies a low value. The features can be ranked based on their SHAP values. Features with higher SHAP values are considered more important.

A SHAP summary plot is a combination of feature importance and feature effects, providing a comprehensive overview of how features influence the model’s predictions.

SHAP values provide a unified measure of feature importance, grounded in cooperative game theory. The SHAP value for feature i is

$${\varphi }_i=\sum _{S\subseteq N\setminus \left\{i\right\}}{\displaystyle \frac{\left|S\right|!(|N|-|S|-1)!}{\left|N\right|!}}[k(S\cup \left\{i\right\})-k(S)]$$

(5)

where

• ${\varphi }_i$ is the SHAP value for feature i;
• S is a subset of features excluding i;
• N is the set of all features;
• $k(S)$ is the value function for the subset S;

The value function k is typically the expected value of the model’s output conditioned on the feature subset S.

2.5.3. Correlation-Matrix-Based Heatmap

We also analyzed questionnaire survey data using the correlation heatmap matrix to understand the relationships among household energy variables and their impact on ESSR.

A correlation heatmap is a visual representation of the correlation matrix, where each cell in the matrix shows the correlation between two variables, as explained below:

Correlation Coefficient:

The correlation coefficient r between two variables x and y is calculated as

$$r_{xy}={\displaystyle \frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(x_i-\overline{x})}^2{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}}$$

(6)

where

• $x_i$ and $y_i$ are individual sample points;
• $\overline{x}$ and $\overline{y}$ are the means of x and y, respectively;
• n is the number of data points.

Correlation Matrix:

The correlation matrix $\mathbf{R}$ for n variables is given by

$$\mathbf{R}=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1n}\\ r_{21}& r_{22}& \cdots & r_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{nn}\end{array}\right]$$

(7)

where $r_{ij}$ is the correlation coefficient between variable i and variable j.

Each cell in the matrix represents the correlation coefficient between two variables, with values ranging from −1 (strong negative correlation) to +1 (strong positive correlation). Values close to 0 indicate little to no linear relationship between the variables. The diagonal line of red cells indicates perfect self-correlation. A paraphrased version is given below.

A correlation matrix displays the correlation coefficients between various variables, indicating the strength and direction of their linear relationships. Energy policymakers can use this matrix to pinpoint variables with strong correlations.

2.5.4. Mean Absolute Error (MAE)

We used the mean absolute error (MAE) of household energy data to extract key features using LightGBM. MAE is a metric used to evaluate the performance of a regression model. It measures the average magnitude of errors in a set of predictions, without considering their direction. MAE is the average of the absolute differences between predicted and actual values. It provides a straightforward interpretation of the error magnitude, where smaller MAE values indicate better model performance.

For a given set of predictions, MAE is calculated as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(8)

where

• n denotes the total number of observations;
• $y_i$ represents the actual value for the i-th observation;
• ${\widehat{y}}_i$ denotes the predicted value for the i-th observation;
• $\left|y_i-{\widehat{y}}_i\right|$ indicates the absolute error for the i-th observation.

2.5.5. Confusion Matrix

A confusion matrix is a table used to evaluate the performance of a classification model. It compares the actual target values with those predicted by the model, providing insights into the types of errors the model makes. These matrices are especially useful in binary classification but can be extended to multiclass classification problems.

For a binary classification problem, the confusion matrix is a 2 × 2 table as shown in

Table 2. Confusion matrix for a binary classification problem.

	Predicted Positive	Predicted Negative
Actual Positive	True Positive (TP)	False Negative (FN)
Actual Negative	False Positive (FP)	True Negative (TN)

:

Several important performance metrics can be derived from the confusion matrix:

• Accuracy: The ratio of correctly predicted instances to the total instances. It is given by

  $$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$
• Precision: The ratio of correctly predicted positive observations to the total number of predicted positive observations. It is given by

  $$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$
• Recall (Sensitivity or True Positive Rate): The ratio of correctly predicted positive observations to all observations in the actual positive class. It is given by

  $$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$
• F1 Score: The harmonic mean of precision and recall. It is given by

  $$\mathrm{F}1\mathrm{Score}=2\times {\displaystyle \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

The confusion matrix can be interpreted as follows:

• True Positives (TP): Model correctly predicts the positive class.
• True Negatives (TN): Model correctly predicts the negative class.
• False Positives (FP): Model incorrectly predicts the positive class when it is actual negative. This is also known as a Type I error.
• False Negatives (FN): Model incorrectly predicts the negative class when it is actual positive. This is also known as a Type II error.

The confusion matrix provides a comprehensive overview of how well the model performs, making it easier to identify which errors are most common. By analyzing the confusion matrix, one can better understand the model’s behavior and identify areas for improvement.

3. Results and Discussion

We analyzed household energy data using LightGBM, SHAP summary plots, and correlation heatmaps. Furthermore, we used a confusion matrix to check the reliability of the classification model. Using these analytical tools, we also recommend energy policies to reduce household energy consumption, as explained below in detail.

3.1. Electricity Self-Sufficiency Rate (ESSR)

The electricity self-sufficiency rate measures the extent to which a region, country, or household can meet its electricity demand through its own energy production. It reflects the ability to generate enough electricity locally to fulfill consumption needs without relying on imports from other areas, countries, or external grids.

Figure 2 illustrates the electricity self-sufficiency rate for 201 households that participated in the questionnaire survey. This graph indicates that the electricity self-sufficiency rate for several households is equal to or exceeds one, suggesting that renewable energy sources can significantly improve the electricity self-sufficiency of detached houses.

From Figure 2, we can summarize that incorporating solar panels and fuel cells into detached houses profoundly impacts their electricity self-sufficiency rate. Solar panels harness solar energy to generate electricity, enabling houses to produce power and reduce reliance on the grid. Solar panels decrease electricity costs and contribute to a more sustainable energy ecosystem by reducing dependence on non-renewable sources. Fuel cells complement solar energy by providing a reliable backup power source, particularly useful during low solar generation or grid outages. When integrated into detached houses, these renewable energy technologies enhance self-sufficiency, fostering resilience and environmental sustainability. Moreover, in the context of net-zero-energy houses (nZEHs), which aim to produce as much clean electrical energy as they consume over a given period, adopting solar panels and fuel cells plays a pivotal role in achieving this goal.

3.2. LightGBM (Gradient Boosting Machine)-Based Analysis

LightGBM is a fast, efficient gradient-boosting framework that uses a leaf-wise tree growth strategy to provide improved accuracy and performance, especially on large datasets. It is widely used for both classification and regression tasks due to its scalability and ability to handle high-dimensional data.

As shown in Figure 3, we conducted a LightGBM-based analysis on questionnaire survey data and the electricity self-sufficiency rate.

The explanatory and target variables for the LightGBM-based prediction model are given below:

• Explanatory variables—Questionnaire survey data;
• Target variables—Electricity self-sufficiency rate (ESSR);
• Evaluation method—Mean absolute error (MAE), 0.23.

Based on Figure 3, we can conclude that the significant features influencing electricity self-sufficiency include the following:

• MAE of housing type (Q2);
• Average monthly electricity bill (Q16);
• Type of floor heating (Q10);
• Average monthly gas bill (Q17);
• Electricity tariff plan (Q3);
• Electrical capacity (Q4);
• Number of TVs (Q12)
• Cooking equipment (Q11);
• Number of washing and drying machines (Q12);
• The frequency of viewing HEMSs (home energy management systems) (Q20).

To understand how these key features can help implement policies, please refer to the questionnaire provided in the Supplementary Material and also Section 4 of this article.

In Figure 3, we observe several factors influencing the electricity self-sufficiency rate. When designing energy policies, it is crucial to consider all of the important features identified by LightGBM. However, if there is a need to reduce the number of features, ${\ell }^1$ regularization can be applied to eliminate less significant features and retain only the most crucial ones, as discussed below.

The most significant features extracted after applying ${\ell }^1$ regularization on LightGBM can be seen in Figure 4.

• MAE of housing type (Q2);
• average monthly electricity bill (Q16);
• type of floor heating (Q10).

The LightGBM-based model has a mean absolute error (MAE) of 0.21.

This analysis not only identifies the factors that influence the ESSR but also enables policymakers to formulate effective energy policies to enhance self-sufficiency in households. By leveraging insights derived from this model, policymakers can design intervention strategies focused on reducing carbon emissions from residential areas, a few key factors of which are discussed below.

3.2.1. Housing Type (Q2)

Explanation: Housing type emerged as the most significant factor affecting the ESSR. Different housing types, such as detached houses (one-story, two-story, or three-story) and apartments, present varying capacities and opportunities for implementing energy self-sufficiency measures.

Recommendations for enhancing the ESSR:

• Incentivizing Solar Panel Installation: For detached houses, especially one-story and two-story homes, government subsidies or incentives for installing solar panels should be provided. Solar panels significantly enhance the ESSR by generating renewable energy at home.
• Retrofitting Housing Complexes: Governments should encourage retrofitting existing housing complexes with energy-efficient technologies and renewable energy systems. Collective solar panel installations or centralized battery storage could be explored for large complexes.
• Customized Energy Efficiency Programs: Governments should develop targeted energy efficiency programs based on housing type—for example, insulation and smart energy systems for older detached houses or energy-efficient communal heating for housing complexes.

3.2.2. Average Monthly Electricity Bill (Q16)

Explanation: The average monthly electricity bill is a critical indicator of household energy consumption patterns. Higher bills often reflect higher energy usage, which could reduce the ESSR if the energy consumed is not sustainably sourced.

Recommendations for enhancing the ESSR:

• Tiered Pricing and Rebates: Governments should implement a tiered electricity pricing system where households with lower energy consumption receive rebates or lower rates. This could incentivize energy-saving behavior and improve the ESSR by reducing reliance on non-renewable energy sources.
• Energy Efficiency Audits: Governments should offer free or subsidized energy-efficiency audits to households with high electricity bills. These audits can help to identify inefficiencies in energy usage and suggest improvements, such as better insulation, energy-efficient appliances, or behavioral changes.
• Promotion of Energy-Efficient Appliances: Governments should encourage the adoption of energy-efficient appliances through rebates, discounts, or tax incentives. Households with lower energy consumption will rely more on self-generated renewable energy, thus improving their ESSR.

3.2.3. Floor Heating (Q10)

Explanation: The presence and type of floor heating can impact the energy consumption of a household. Electric floor heating, in particular, may increase energy consumption, thus affecting the ESSR negatively unless paired with renewable energy sources.

Recommendations for enhancing the ESSR:

• Encourage Renewable Energy Pairing: For homes with electric floor heating, governments should promote the pairing of such systems with renewable energy sources, such as solar panels, to ensure that the heating system’s energy demand is met sustainably.
• Subsidies for Efficient Heating Systems: Governments should provide subsidies for switching from electric to more energy-efficient heating systems, such as gas-powered hot-water floor heating or other renewable heating solutions like heat pumps.
• Education on Energy Management: Governments should educate homeowners on managing their heating systems more efficiently, such as using programmable thermostats or zone heating to reduce unnecessary energy consumption.

3.2.4. Formulating Policies to Improve the ESSR (Based on above Mentioned 3 Most Significant Features

• Targeted Incentives Based on Housing Type: Recognizing that the type of housing plays a pivotal role in the ESSR, policies should focus on providing tailored incentives for different housing types. For example, promoting solar panels for detached houses and communal energy solutions for complexes can improve the overall ESSR.
• Energy Consumption Management: By addressing households with higher electricity bills through tiered pricing, energy audits, and the promotion of energy-efficient appliances, we can encourage energy conservation and reduce dependency on non-renewable energy, thus improving the ESSR.
• Heating Systems Optimization: Since floor heating has a significant impact on energy consumption, especially in homes with electric systems, policies should encourage the use of renewable energy and more efficient heating solutions. This will help to mitigate the negative impact on the ESSR and promote sustainable energy use.

Similarly, we can review the rest of the key features. These strategies, informed by the LightGBM model’s feature importance, can guide the development of effective policies to enhance the ESSR.

3.2.5. Statistical Relationship between ESSR and above Mentioned 3 Most Significant Features

We also established a statistical relationship between the ESSR and the most significant features, as shown in the violin plot (which combines aspects of a box plot and a kernel density plot) in Figure 5. In the violin plot, the x-axis represents the option number of the corresponding survey question.

This LightGBM-based prediction model can also be used to predict the electricity self-sufficiency rate of households that did not participate in the questionnaire survey.

This approach represents a step towards fostering sustainability and resilience in the residential energy sector, aligning with broader environmental conservation goals.

Figure 5 illustrates the statistical correlation between the electricity self-sufficiency rate (ESSR) and housing type (Q2), as determined by the survey question related to the type of house. This figure highlights that households selecting options 1 and 2—indicating houses with roofs—exhibit a high electricity self-sufficiency rate. This increased ESSR is largely attributable to the presence of solar panels installed on the roofs of these homes. Based on this correlation, we can infer the electricity self-sufficiency rate of households that did not participate in the survey.

Figure 6 depicts the correlation between the electricity self-sufficiency rate and survey questions related to the type of floor heating (Q10).

The violin plot visualizes the distribution of the electricity self-sufficiency rate (ESSR) across different types of floor heating installations as reported in the questionnaire (Q10). The x-axis represents the four response options for Q10, while the y-axis shows the ESSR values.

Interpretation of the Violin Plot:

• Option 1 (No floor heating): The ESSR distribution is relatively narrow, indicating that most households without floor heating have a lower and more consistent electricity self-sufficiency rate. The median ESSR is low.
• Option 2 (Electric floor heating): The distribution is slightly wider than Option 1, showing some variability in the ESSR, but still with a lower median ESSR. This suggests that electric floor heating, likely due to its higher energy demand, is associated with a lower ESSR.
• Option 3 (Gas hot-water floor heating): The distribution is narrow again with a slightly higher median ESSR compared to Options 1 and 2. This type of heating seems to offer a more efficient use of energy, contributing to a moderate ESSR.
• Option 4 (Other hot-water floor heating): This option shows the widest distribution with a higher median ESSR. This indicates that households with other types of hot-water floor heating (such as OM solar) tend to have a higher self-sufficiency rate, likely because these systems are more efficient or are paired with renewable energy sources.

The violin plot suggests that the type of floor heating installed in a residence significantly impacts the electricity self-sufficiency rate. Specifically, homes with “Other hot-water floor heating” (Option 4) generally achieve a higher ESSR, likely due to the efficiency of these systems and their potential integration with renewable energy sources. In contrast, homes with no or electric floor heating tend to have a lower ESSR. This insight can guide energy policy by promoting more efficient heating systems that improve the ESSR.

Figure 7 illustrates the relationship between the ESSR and the average monthly electricity bill. From this relationship, we can also determine the average monthly electricity bill of households that did not participate in the questionnaire survey.

Similar to Figure 5, Figure 6 and Figure 7, we can also establish relationships between other key features (as shown in Figure 3) and the ESSR based on the questionnaire survey responses, allowing us to draw conclusions regarding the enhancement of the electricity self-sufficiency of households, as described below and also in Section 4 of this article.

These findings collectively provide a robust foundation for policymakers, researchers, and stakeholders to design strategies to foster sustainability, resilience, and reduced carbon emissions in the residential energy sector. Energy policies, such as incentives, subsidies, and regulatory frameworks, further incentivize the adoption of renewable energy technologies in residential properties, accelerating the transition towards sustainable and self-sufficient housing (please refer to the questionnaire survey and all figures provided in this section to understand this). These policies promote innovation, investment, and consumer awareness, facilitating the widespread adoption of solar panels, fuel cells, and other clean energy solutions. In summary, the integration of solar panels and fuel cells not only enhances the electricity self-sufficiency of houses but also contributes to the realization of zero-energy houses and aligns with supportive energy policies aimed at advancing sustainability goals.

3.3. SHAP (SHapley Additive exPlanations)-Based Analysis

LightGBM, as a gradient-boosting framework, generates complex ensemble models that aggregate multiple decision trees, resulting in intricate relationships between features and outputs. This complexity makes it challenging to discern how individual features influence specific predictions or the overall model. Consequently, the insights gained from LightGBM alone may lack clarity, which is particularly critical in analyzing household energy data to improve the ESSR.

To address these issues, we used SHAP (SHapley Additive exPlanations) analysis, which offers a detailed and intuitive breakdown of how each feature contributes to every individual prediction, enhancing the interpretability of the model.

SHAP analysis offers both local explanations for individual predictions and global insights into feature importance across the entire dataset and provides feature-level explanations, enabling the identification of key drivers behind model predictions.

A shape plot is a visual representation of the impact of different features on the model’s output. It illustrates the contribution of each feature to the model’s predictions.

Figure 8 summarizes the SHAP plot for a LightGBM (gradient boosting machine)-based analysis of household energy data. SHAP analysis interprets the model’s predictions by attributing the contribution of each feature to these predictions. SHAP values help in understanding the impact of each feature.

To extract the important features that affect the ESSR significantly, we used LightGBM-based SHAP analysis. The explanatory and target variables are given below.

• Explanatory variables—Questionnaire data;
• Target variable—Electricity self-sufficiency rate (ESSR).

In the SHAP plot, features are listed along the y-axis, and the corresponding SHAP values are represented by horizontal bars. The color of each bar indicates whether a feature has a negative or positive impact on the model’s output. The bar’s length represents the impact’s magnitude—longer bars indicate features with a greater influence on the model’s predictions.

Figure 8 shows the influence of different household characteristics (important features) on the model’s output (electrical self-sufficiency rate). The graph presents a spectrum of factors ranging from `housing type (Q2)’ to that of the `number of cars (Q25)’, along with their corresponding effects on the model’s output, rated on a low to high impact scale. Except for the feature ’housing type (Q2), for all of the features, the SHAP plot utilizes a numerical scale ranging from −0.50 to 0.25 to represent SHAP values, with markers indicating each factor’s position in terms of its impact, from low to high. This visualization provides valuable insights into the complex relationships between household characteristics and their specified impacts accordingly.

As shown in Figure 8, the key features that significantly affect the electricity self-sufficiency rate are listed below.

• Housing type (Q2);
• Average monthly electricity bill (Q16);
• Type of floor heating (Q10);
• Cooking equipment (Q11);
• Electric capacity (Q4);
• Number of washing and drying machines (Q12);
• Average monthly gas bill (Q17);
• Electricity tariff (fee) plan (Q3);
• Number of TVs (Q12);
• The frequency of viewing HEMSs (Home Energy Management Systems) (Q20).

Like in LightGBM, the most significant features are listed as follows:

• Housing type (Q2);
• Average monthly electricity bill (Q16);
• Type of floor heating (Q10).

We can see that the key features and most significant features (order-wise) are the same as in LightGBM, meaning that we can state that our models are good.

The SHAP plot provides valuable insights into how various household characteristics impact the electricity self-sufficiency rate. The color gradient in the plot, ranging from blue to red, represents the values of each feature. The SHAP value on the x-axis indicates whether a feature has a positive or negative impact on the predicted electricity self-sufficiency rate. Below is an explanation of how different features, based on their color in the SHAP plot, can guide policy-making.

• Housing Type (Q2):

  –

  Red points (higher values): Larger or detached houses are associated with a higher electricity self-sufficiency rate. These homes are more likely to accommodate renewable energy installations such as solar panels and fuel cells.

  –

  Blue points (lower values): Smaller or less independent housing types, such as apartments, generally show lower levels of electricity self-sufficiency.

• Average Monthly Electricity Bill (Q16):

  –

  Blue points (lower values): Represent lower electricity bills, indicating reduced energy consumption and a positive contribution to the electricity self-sufficiency rate.

  –

  Red points (higher values): Reflect higher electricity bills, which correspond to increased energy usage that negatively impacts self-sufficiency.

• Floor Heating (Q10):

  –

  Red points (higher values): Indicate the presence of electric floor heating systems, which generally increase electricity consumption and reduce self-sufficiency.

  –

  Blue points (lower values): Suggest the absence of floor heating or the use of non-electric systems, which are less likely to impact electricity consumption significantly and contribute positively to self-sufficiency.

• Cooking Equipment (Q11):

  –

  Blue points (lower values): Represent non-electric cooking systems, such as gas stoves, which consume less electricity and thus enhance self-sufficiency.

  –

  Red points (higher values): Indicate the use of electric cooking equipment, which increases electricity usage and reduces self-sufficiency.

• Electric Capacity (Q4):

  –

  Blue points (lower values): Indicate a lower contracted electric capacity, such as 30A, suggesting reduced potential energy usage and a positive impact on self-sufficiency.

  –

  Red points (higher values): Suggest higher electric capacity, implying greater potential electricity usage which could decrease self-sufficiency.

Based on the SHAP summary plot, several strategies can be developed to guide energy policy-making:

• Identifying Key Factors: The SHAP plot reveals which household characteristics most strongly influence electricity self-sufficiency. This insight can guide policymakers to focus on areas such as promoting renewable energy systems in specific housing types.
• Customizing Interventions: Policies can be tailored to address the significant features identified by the SHAP plot. For instance, households with higher electricity bills could be incentivized to adopt solar panels, or those using electric heating might be encouraged to transition to more energy-efficient systems.
• Educational Programs: The SHAP plot highlights the importance of environmental awareness and education. Policymakers could develop initiatives to increase homeowner knowledge about energy management and the benefits of systems like home energy management systems (HEMSs).
• Infrastructure Development: Factors such as total floor area and the number of electrical appliances suggest a need for infrastructure that supports energy-efficient technologies. This could involve developing resources and systems to facilitate the adoption of such technologies.
• The SHAP plot provides valuable insights into the factors driving electricity self-sufficiency in households. Utilizing these insights allows policymakers to make informed, data-driven decisions aimed at promoting renewable energy adoption and enhancing energy efficiency.

Based on the analyses, the following policies could be developed to enhance electricity self-sufficiency:

• Promote Detached and Independent Housing:

  –

  Governments should encourage the development of larger, independent housing types, such as detached houses, which have shown a positive impact on self-sufficiency. Policies could include incentives for integrating renewable energy systems like solar panels.

• Subsidize Energy-Efficient Appliances and Systems:

  –

  Governments should promote the adoption of energy-efficient or non-electric alternatives, such as gas heating systems or solar water heaters, to counteract the negative impacts of electric floor heating and cooking equipment on self-sufficiency.

  –

  Governments should also encourage households to opt for lower contracted electric capacities to help manage energy consumption and enhance self-sufficiency.

• Energy Consumption Awareness and Reduction:

  –

  Since lower energy bills correlate with higher self-sufficiency, educational campaigns focusing on energy-saving practices and the benefits of energy-efficient appliances could help to reduce household consumption.

• Support for Renewable Energy Installations:

  –

  Governments should incentivize the installation of renewable energy systems, such as solar panels, particularly in housing types with the necessary space and capacity for these installations.

• Tailored Programs for Specific Housing Types:

  –

  Policies should be customized to address the unique needs and potentials of different housing types. For example, governments should offer different incentives for energy upgrades in apartment complexes compared to detached houses.

By considering these factors, policies can be developed to specifically target the elements that influence electricity self-sufficiency, leading to more sustainable energy consumption practices across diverse household types.

From the SHAP analysis, we can conclude that the key feature titled ‘housing type’ (Q2) is very dominant in developing an ESSR-based predictive model, and if we do not consider this feature, the model will not be reliable. Additionally, the features titled ‘average monthly electricity bill’ (Q16) and ‘type of floor heating’ (Q10) also significantly impact the model’s output. In the absence of these three features, we cannot develop a reliable model for enhancing the ESSR.

Policymakers can use this analysis to develop targeted strategies promoting energy efficiency and achieving net-zero-energy homes. For example, creating guidelines and incentives for households with higher energy consumption patterns, encouraging the adoption of energy-efficient appliances, and designing tiered energy-saving programs can effectively reduce energy usage. These focused interventions not only address the immediate factors affecting electricity self-sufficiency but also contribute to broader goals of sustainability and meeting national and global energy efficiency targets.

This comprehensive analysis is a crucial resource for researchers, policymakers, and individuals interested in understanding the interplay between household dynamics and broader societal or environmental outcomes.

3.4. Correlation-Heatmap-Based Analysis

We also analyzed questionnaire survey and energy data using a correlation matrix to visualize the relationships among various household energy-related variables and their potential impact on the electricity self-sufficiency rate (ESSR). Understanding the correlation among household energy variables, as well as the relationship between these variables and the household’s electricity self-sufficiency rate, is crucial for several reasons. First, it helps in identifying how different factors such as appliance usage, insulation, and energy efficiency are interconnected, allowing households to implement comprehensive energy-saving strategies. Additionally, by analyzing how these energy variables impact electricity self-sufficiency, homeowners can better gauge their reliance on external energy sources and make more informed decisions about adopting renewable energy technologies like solar panels. This understanding also enables more accurate predictions of energy needs, optimizing both energy consumption and self-sufficiency efforts. In the broader context, recognizing these correlations supports the development of more effective energy policies and sustainability programs tailored to household energy dynamics

The correlation heatmap can be a powerful tool for guiding energy policies, especially in the context of the electricity self-sufficiency rate. It can be utilized to draw following conclusions:

• Identifying Key Relationships: The correlation matrix allows policymakers to observe the relationships between different variables, such as energy consumption, generation, pricing, and socio-demographic factors. Strong positive or negative correlations can indicate which factors most influence the ESSR.
• Targeting Energy-Efficiency Programs: By understanding which variables are strongly correlated with a high ESSR, policymakers can design targeted interventions to improve energy efficiency. For instance, if the matrix shows a strong correlation between the ESSR and specific types of appliances, energy-efficiency programs could focus on upgrading those appliances.
• Enhancing Energy Self-Sufficiency: The matrix can highlight the factors that contribute to or detract from household electricity self-sufficiency. This insight can guide policies that incentivize the adoption of renewable energy sources like solar panels or home battery storage systems, which are critical for increasing self-sufficiency.
• Policy Evaluation and Adjustment: Over time, as policies are implemented, the correlation matrix can be used to assess the impact of these policies by comparing changes in correlations before and after implementation, helping to refine and improve energy policies continuously.

In summary, the correlation matrix serves as a foundational analytical tool for developing data-driven, targeted, and effective energy policies that can promote sustainability and energy self-sufficiency.

Figure 9 presents the correlation heatmap showing the correlation among different household variables and with the ESSR.

The correlation matrix reveals several significant relationships among household energy variables and the ESSR, and a few of them are explained here.

3.4.1. ESSR Is Negatively Correlated with Housing Type (Q2)

The heatmap shows that the electricity self-sufficiency rate is negatively correlated with housing type (Q2), and we discuss how this can be used to formulate energy policy below.

• Housing Type (Q2): The survey’s housing type question (Q2) categorizes households into different types, such as apartments and detached houses. The type of housing plays a crucial role in various aspects of energy consumption and the ability to achieve self-sufficiency. Factors such as the availability of space for installing solar panels, the quality of insulation, and the overall energy needs of the household are directly influenced by the type of housing.
• Negative Correlation: When two variables are negatively correlated, it means that as one variable increases, the other tends to decrease. In this context, a negative correlation between the electricity self-sufficiency rate and housing type (Q2) implies that certain housing types are associated with lower electricity self-sufficiency.
• Implications of this Negative Correlation—Apartments versus Detached Houses: Apartments or smaller housing units generally have less roof space available for the installation of solar panels, which limits their potential for energy self-sufficiency. In contrast, detached houses usually offer more space, making it easier to install larger or multiple solar panels, thus enhancing the household’s ability to generate its own electricity.
• Energy Demand and self-sufficiency: Different housing types come with varying energy demands and levels of efficiency. For instance, larger homes tend to have higher energy requirements but also offer more opportunities to utilize renewable energy sources. On the other hand, smaller or more densely situated homes may not only have reduced energy demands but also less capacity for generating their own electricity, which can result in lower self-sufficiency rates.
• Policy implication: The observed negative correlation between the electricity self-sufficiency rate and housing type indicates that the type of dwelling significantly influences a household’s ability to achieve energy self-sufficiency. Policymakers should take these differences into account when developing energy policies or programs. Tailored incentives for renewable energy installations could be particularly beneficial in housing types that typically show lower self-sufficiency rates.

3.4.2. ESSR Is Negatively Correlated with Fee Plan (Q3)

The heatmap shows a negative correlation between the electricity self-sufficiency rate (ESSR) and the fee plan (Q3) from the survey data. Below, we break down what this means and its implications.

• Fee Plan (Q3): The fee plan question (Q3) in the survey refers to the type of electricity pricing or payment plan that households are enrolled in. This could include fixed-rate plans, time-of-use pricing, or other types of billing structures. Different fee plans might incentivize or de-incentivize certain behaviors related to energy use and the adoption of renewable energy sources such as solar panels and fuel cells.
• Implications of the Negative Correlation-Fixed-Rate Plans: Households on a fixed-rate plan may have less motivation to manage their electricity usage carefully since their costs do not vary with consumption. This could lead to a lower ESSR if these households are less likely to invest in renewable energy systems that would enhance self-sufficiency.
• Time-of-Use (TOU) Plans: Conversely, TOU plans, which charge different rates at different times of day, might encourage more strategic use of electricity but could also be associated with lower self-sufficiency if households on these plans do not invest in storage solutions or renewable energy systems that align with their usage patterns.
• Incentives for Renewable Energy: Some fee plans may not provide sufficient incentives for households to invest in renewable energy systems (e.g., solar panels) that would improve their self-sufficiency. For example, if a plan offers very low rates, the financial return on investing in self-generation might be less attractive, leading to a lower ESSR.
• Policy Implications: The negative correlation suggests that households on certain fee plans are less likely to achieve high levels of electricity self-sufficiency, possibly due to the structure of the fee plan not encouraging or supporting investments in renewable energy or efficient energy use. The negative correlation between the ESSR and fee plan (Q3) indicates that the type of electricity pricing plan that a household is enrolled on can significantly impact its energy self-sufficiency. Households on plans that do not incentivize or support self-generation and efficient energy use may have a lower ESSR. This insight could be valuable for utility companies and policymakers aiming to design fee structures that better encourage the adoption of renewable energy technologies and improve overall energy self-sufficiency.

3.4.3. ESSR Is Positively Correlated with Floor Heating Type (Q10)

The heatmap provided shows a positive correlation between floor heating (Q10) and the electricity self-sufficiency rate (ESSR). A detailed explanation of this is provided below.

• Floor Heating (Q10): In this survey, Q10 asks respondents whether their household is equipped with a floor heating system or not, and what type of floor system they are using.

The implications of this positive correlation are as follows:

• Integration with Renewable Energy: Most households with floor heating systems use renewable-energy-based floor heating systems, such as solar panels and fuel cells. It is well known to households that floor heating is typically a consistent and significant energy draw, and it makes sense for households to seek self-sufficiency through renewable energy sources to offset the cost, thus increasing their ESSR.
• Potential for Energy Storage: Households that utilize floor heating may also invest in energy storage solutions to balance the load during non-peak production times. During the day, when solar panels produce excess energy, this energy can be stored and later used for heating the home during the evening or at night. This practice can further enhance the ESSR.
• Household Investment in Energy Systems: The presence of floor heating systems may indicate a household’s overall investment in modern, efficient energy systems. Such investments often go hand in hand with a focus on sustainability and self-sufficiency, which contributes to a higher ESSR.
• Energy Use and Behavioral Patterns: The correlation might also reflect the fact that households with floor heating are more conscious of their energy use and are therefore more proactive in adopting technologies that support self-sufficiency, like solar panels and energy storage systems.
• Policy Implications: The positive correlation between floor heating (Q10) and the ESSR indicates that households equipped with floor heating systems tend to have a higher electricity self-sufficiency rate. This is because most of the households use solar power and fuel cell-operated floor heating systems, and the likelihood is that these households are more invested in achieving energy self-sufficiency. This insight can be valuable for policymakers and energy planners when designing programs to enhance household energy efficiency and self-sufficiency, particularly in promoting the integration of efficient heating systems with renewable energy sources.

The correlation heatmap indicates a positive correlation between the electricity self-sufficiency rate (ESSR) and electrical capacity (Q4), which implies that households with greater electrical capacity are better positioned to generate and manage their own electricity, thereby achieving higher levels of self-sufficiency. This finding could inform energy policies and incentives, encouraging households to upgrade their electrical systems and invest in renewable energy technologies to enhance their self-sufficiency rates.

As explained above, policymakers can find correlations between the ESSR and other variables to formulate energy policy decisions.

3.4.4. Correlation among Household Variable

Below, we discuss a few correlations among household variables.

The data show a negative correlation between the frequency of viewing HEMSs and the number of home appliances, indicating that households using HEMSs to monitor and optimize their energy usage tend to have fewer appliances. Similarly, a negative correlation between HEMS viewing frequency and energy awareness suggests that individuals who actively monitor their energy consumption are already knowledgeable about energy usage. Similarly, a negative correlation between the monthly electricity bill and energy awareness suggests that households with higher electricity bills tend to have lower environmental awareness. Conversely, there is a positive correlation between HEMS viewing frequency and participation in environmental activities, highlighting that those who frequently use HEMSs are also more engaged in sustainability efforts. Additionally, energy awareness is positively correlated with participation in environmental activities, suggesting that informed individuals are more likely to be environmentally active.

To enhance the electricity self-sufficiency rate and achieve zero-energy homes, several strategies can be implemented based on these correlations, and policymakers can focus on both positive and negative areas. Integrated energy efficiency programs should address electricity consumption by incentivizing energy-efficient appliances, improving insulation, and promoting smart thermostats and energy management systems. The promotion of solar energy and monitoring systems should include subsidizing solar panel installations and providing training on using HEMSs, encouraging households to monitor their energy usage regularly. Environmental awareness campaigns should target households with high energy consumption and low environmental consciousness by launching educational campaigns and offering workshops on energy conservation and sustainability. Lastly, feedback and incentive systems should encourage frequent interaction with HEMSs and energy-saving behaviors by providing real-time energy consumption data and offering financial incentives or rewards for reducing energy consumption or achieving sustainability milestones. By addressing these correlations, a comprehensive approach can be developed to reduce energy consumption and promote the adoption of zero-energy homes. By addressing both the highly positive and negative correlations, these policies can create a comprehensive approach to reducing energy consumption and promoting the adoption of zero-energy houses.

3.5. Confusion Matrix

We use a confusion matrix to provide a complete picture of the model’s effectiveness in predicting household electricity self-sufficiency rate.

A confusion matrix is a tool used to evaluate the performance of a classification model. It provides a summary of the prediction results based on a classification problem by comparing the actual (true) labels with the predicted labels.

The confusion matrix predicts how well the classification model will perform in differentiating between classes. As shown in Figure 10 shows, the confusion matrix is used to evaluate a classification model to predict the electricity self-sufficiency rate of households based on various input features.

The classification report provides a detailed performance evaluation of a classification model. It includes metrics such as precision, recall, and F1-score for each class, as well as overall metrics like accuracy, macro average, and weighted average.

From

Table 3. Classification report.

	Precision	Recall	F1-Score	Support
0	0.89	0.74	0.81	57
1	0.90	0.97	0.93	144
Accuracy			0.90	201
Macro Avg	0.90	0.85	0.87	201
Weighted Avg	0.90	0.90	0.90	201

, we can see that our model has an accuracy of 90%.

4. Policy Implications

The policy implications drawn from the analysis of household energy data using different machine learning techniques and the insights discussed in this article suggest the need for a comprehensive approach to enhancing energy sustainability. Governments and policymakers should focus on promoting renewable energy, modernizing infrastructure, engaging with the public, ensuring financial inclusivity, and adapting to regional needs, as explained in detail below.

4.1. Promotion of Renewable Energy and Storage Systems

• Incentivization of renewable technologies: Policies should focus on providing financial incentives such as subsidies, tax breaks, and low-interest loans to encourage the installation of renewable energy systems such as solar panels and fuel cells. This can enhance the electricity self-sufficiency of households and reduce the dependency on the grid.
• Energy storage solutions: Policies should promote the development and adoption of energy storage systems, allowing households to store excess energy generated during peak production times and use it during periods of low production.

4.2. Regulatory Framework Adjustments

• Flexible tariffs and net metering: Introducing flexible tariffs that reflect energy demand and supply variations and enhancing net metering policies can encourage households to produce their own electricity and feed excess power back into the grid.
• Support for microgrids: Developing regulatory frameworks that support microgrids can enhance electricity self-sufficiency in localized areas, especially in remote or underserved regions.

4.3. Public Engagement and Education

• Awareness campaigns: Governments should run campaigns to educate the public about the benefits of energy self-sufficiency and renewable energy technologies. This includes information on available technologies, financial benefits, and the environmental impact.
• Community participation: Engaging communities in energy projects can lead to greater acceptance and success of renewable energy initiatives. Local governments should involve communities in co-designing policies and projects that address local needs and capacities.

4.4. Financial Mechanisms

• Green financing options: Providing green financing options, such as low-interest loans and grants for renewable energy systems, can make it easier for households to transition to self-sufficient energy solutions.
• Carbon pricing and financial penalties: Implementing carbon pricing can make renewable energy more competitive compared to fossil fuels, encouraging the adoption of cleaner energy solutions. Financial penalties for excessive carbon emissions can further support this transition.

4.5. Equity and Inclusivity

• Support for vulnerable populations: Policies should address financial barriers faced by low-income households in adopting renewable energy technologies. Targeted subsidies, grants, and educational programs can ensure that all segments of the population benefit from energy self-sufficiency.
• Regional policy adaptation: Policies should be adaptable to regional contexts, considering varying energy needs and resources. For instance, areas with abundant sunlight should focus on solar energy, while those with wind resources might prioritize wind energy.

4.6. Urban Planning and Building Standards

• Energy-efficient building codes: Updating building codes to require higher energy efficiency standards in new constructions can significantly reduce energy demand. Retrofitting existing buildings with energy-efficient technologies should also be encouraged through policy measures.
• Integration of renewable energy in urban planning: Urban planning should incorporate renewable energy considerations, such as the placement of solar panels on rooftops and the inclusion of green spaces that support energy-efficient designs.

4.7. Monitoring and Evaluation

• Data-driven policymaking: Continuous monitoring of energy self-sufficiency rates and the effectiveness of implemented policies is crucial. Policies should be adaptable based on data and feedback to ensure that they remain effective and relevant.

Governments and policymakers need to consider economic, infrastructural, educational, and equity aspects to effectively promote household energy self-sufficiency. By addressing these areas, policies can not only support the adoption of renewable energy technologies but also contribute to broader sustainability goals. The effective implementation of these measures can lead to significant improvements in energy self-sufficiency at both the household and community levels.

5. Conclusions

This article uses LightGBM-, SHAP-, and correlation-heatmap-based approaches to analyze energy and questionnaire data collected from more than 200 households. We use LightGBM-based analysis to determine the key features affecting the electricity self-sufficiency rate. Following the LightGBM-based analysis, we concluded that key features like housing type, average monthly electricity bill, presence of floor heating, average monthly gas bill, electricity tariff plan, electrical capacity, number of TVs, cooking equipment used, number of washing and drying machines, and the frequency of viewing home energy management systems (HEMSs) are crucial in determining the electricity self-sufficiency rate of households. Further, we use the ${\ell }^1$ regularization-based technique to identify the most significant features and discard less important features. Furthermore, we establish a statistical correlation between the most significant features and the ESSR. This LightGBM-based model can also predict the ESSR of households that did not participate in the survey.

We used SHAP summary plots to visualize the impact of individual features on the ESSR. Additionally, we use a correlation matrix heatmap to observe the correlation among various household variables and their potential impact on the ESSR.

To evaluate the performance of the classification model, we used a confusion matrix to predict the ESSR based on feature inputs and achieved 90% accuracy.

The entire procedure outlined in this article can also be applied to household and commercial buildings’ gas and water consumption data to extract meaningful insights.

In this article, we analyze data using diverse approaches to extract valuable insights, enabling the development of tailored energy policies that address both regional and national needs.

The findings discussed in this article are encouraging and can be utilized to develop effective intervention strategies to enhance the ESSR of households and achieve the target of realizing net-zero-energy houses. This article may assist both policymakers in making energy-saving policies and researchers in analyzing household energy data effectively to reduce residential energy consumption.

6. Future Directions and Challenges

Future directions and limitations of this work have been discussed in detail, as given below:

6.1. Future Directions

However, the energy policies discussed in this article are designed to be applicable on a broader scale. Their reliability and acceptability for widespread implementation can be enhanced through careful adaptation and continuous refinement based on regional feedback and evolving conditions. Consequently, this study can be further extended to provide a detailed roadmap for developing effective intervention strategies and energy policies aimed at enhancing household electricity self-sufficiency at the macro level to improve the national energy self-sufficiency rate, as summarized below:

6.1.1. Expansion to Different Geographic Contexts

• Application in diverse regions: Future studies could apply the machine learning-based models and frameworks proposed in this work to energy data collected from various geographic regions, particularly in areas with different levels of access to renewable energy resources. This approach would help us to assess the generalizability of the models and allow for their adaptation to local conditions. The energy policies discussed in this work can also be implemented in these diverse regions. After gathering feedback from data over time, these policies can be adjusted accordingly to better meet regional needs and improve effectiveness.

6.1.2. Policy and Economic Impacts

• Impact of policy changes on adoption rates: Future work could include scenario analysis to predict how changes in government policies (e.g., subsidies, tariffs) might impact the adoption rates of renewable energy technologies and subsequent electricity self-sufficiency rate.
• Economic viability studies: Expanding the analysis to include detailed economic assessments, such as cost–benefit analyses and return on investment calculations for households and governments, would provide a more comprehensive understanding of the financial implications of self-sufficiency initiatives.

6.1.3. Longitudinal Studies

• Long-term impact analysis: Conducting longitudinal studies to track the long-term impact of adopting renewable energy on household self-sufficiency, grid stability, and overall energy costs could provide valuable insights for both policymakers and researchers.
• Behavioral studies: Future research could investigate how consumer behavior changes over time with increased awareness and accessibility to renewable energy technologies and the subsequent effects on energy consumption patterns.

6.2. Challenges

For the generalization of energy policies that could impact a country’s national energy self-sufficiency rate, several challenges persist that require careful consideration during the design and implementation of these policies at a macro level, as discussed below.

6.2.1. Trade-Off between Accuracy and Interpretability

• While more complex models can offer better predictive accuracy, they often do so at the expense of interpretability. This is a limitation for policymakers and stakeholders who need to understand the model’s decision-making process and should focus on developing models that balance these two aspects.

6.2.2. Applicability across Different Contexts

• For the full generalization of energy policies across different geographic or socioeconomic contexts, future research should focus on testing and validating models in diverse settings to ensure their robustness.

6.2.3. Policy Uncertainty Due to Economic Constraints

• The impact of potential changes in government policies, such as subsidy removal or changes in energy pricing, introduces uncertainty in long-term planning. This limitation underscores the need for robust scenario planning in future work.

6.2.4. Economic Barriers

• The economic feasibility of large-scale renewable energy adoption, especially in lower-income regions, remains a significant limitation. Future research should focus on developing cost-effective solutions that are accessible to a broader population.

6.2.5. Energy Storage Constraints

• Current limitations in energy storage technology restrict the full potential of renewable energy to achieve self-sufficiency. This is a significant technological barrier that needs to be addressed by policymakers.

6.2.6. Grid Integration Challenges

• The integration of renewable energy into existing grid infrastructures presents technical challenges, such as managing energy variability and ensuring grid stability. These limitations need to be carefully considered by energy stakeholders and governments at the macro level.

6.2.7. Grid Modernization and Energy Infrastructure

• Development of smart grids: Modernizing the grid to support decentralized energy production is crucial. Implementing smart grids can help in managing energy flows more efficiently, especially with the integration of renewable energy sources that have variable outputs.
• Energy storage solutions: Policies should promote the development and adoption of energy storage systems, allowing households to store excess energy generated during peak production times and use it during periods of low production.