Short-Term Campus Load Forecasting Using CNN-Based Encoder–Decoder Network with Attention
Abstract
1. Introduction
- Autoregressive (AR) Model;
- Moving Average (MA) Model;
- Autoregressive Moving Average (ARMA) Model;
- Autoregressive Integrated Moving Average (ARIMA) Model;
- Seasonal Autoregressive Integrated Moving Average (SARIMA) Model;
- ARIMAX and SARIMAX models;
- Kalman Filtering Algorithm;
- Gray Models;
- Exponential Smoothing (ES).
- Artificial Neural Network Algorithms (ANNs)
- Extreme learning machines (ELMs);
- Support Vector Machines (SVMs);
- Fuzzy Logic;
- Wavelet Neural Networks (WNNs);
- Genetic Algorithms (GAs);
- Expert System.
- A novel deep learning network architecture for short-term electric load forecasting. The architecture uses a hybrid neural network to make use of spatiotemporal patterns in the data for forecasting. It consists of a 1D CNN and a GRU-based encoder–decoder with Bahdanau attention for short-term electric load forecasting. The author has not observed the use of this attention mechanism in the literature for multivariate short-term load forecasting for campuses.
- Input horizon optimization for more accurate forecasting results. This novel neural network decouples the input window length from the number of training parameters. This allows much faster training times for longer input windows.
- A robustness-testing framework for deep neural network algorithms. A robustness-testing framework is developed and utilized to assess the change in model performance in the case of the addition of noise to the data.
- Model performance comparison between the proposed architecture and other popular algorithms for campus electric load forecasting. The data used for this comparison study are taken from Memorial University St. John’s Campus, along with metrological data of the city. A comparison is carried out with other deep learning techniques, which include a GRU-based RNN, an LSTM-based RNN, and a 1D CNN + encoder–decoder model without attention. The model shows a higher R2 score and lower MAPE, MAE, and MSE.
2. Data Description
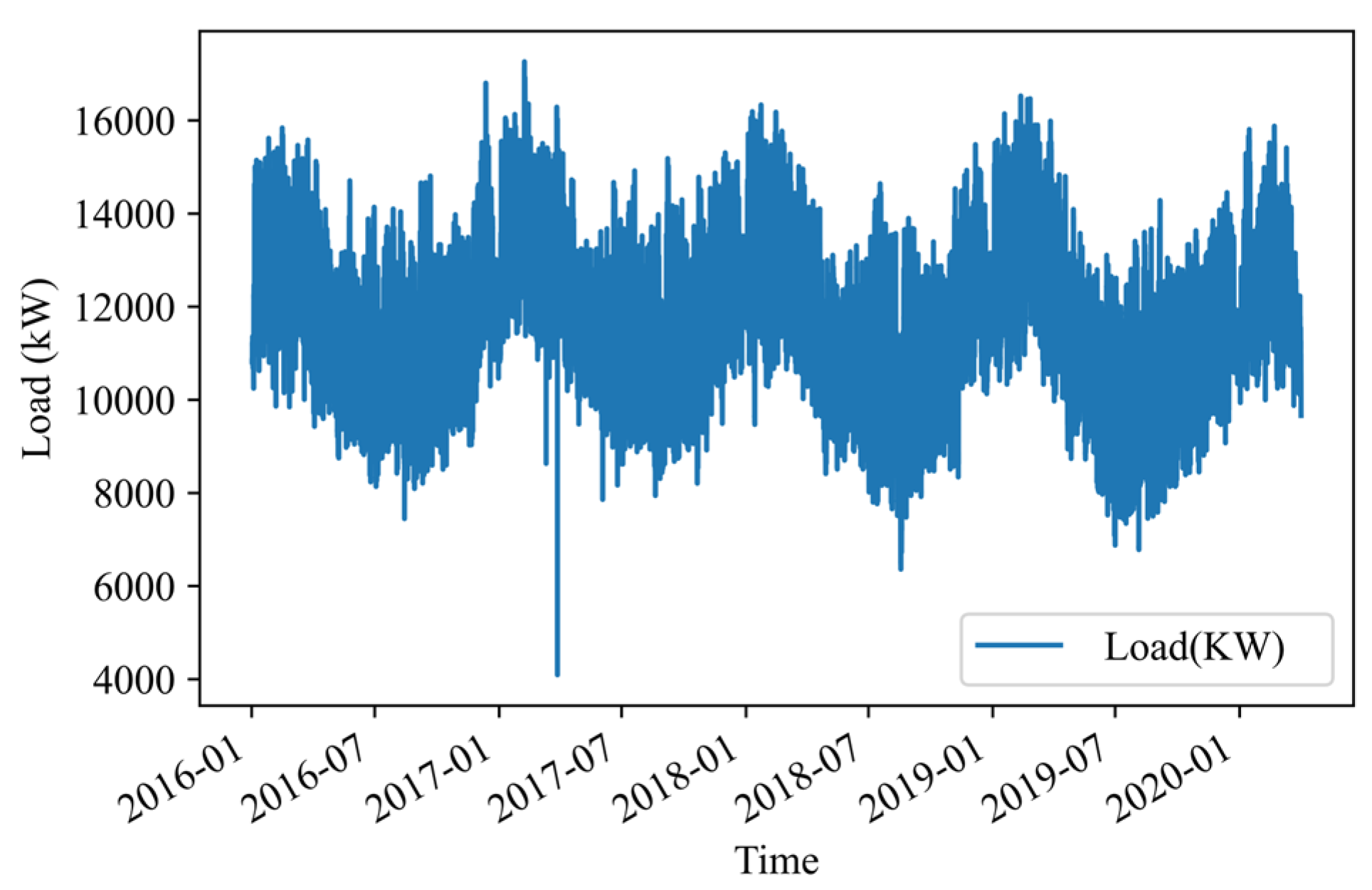
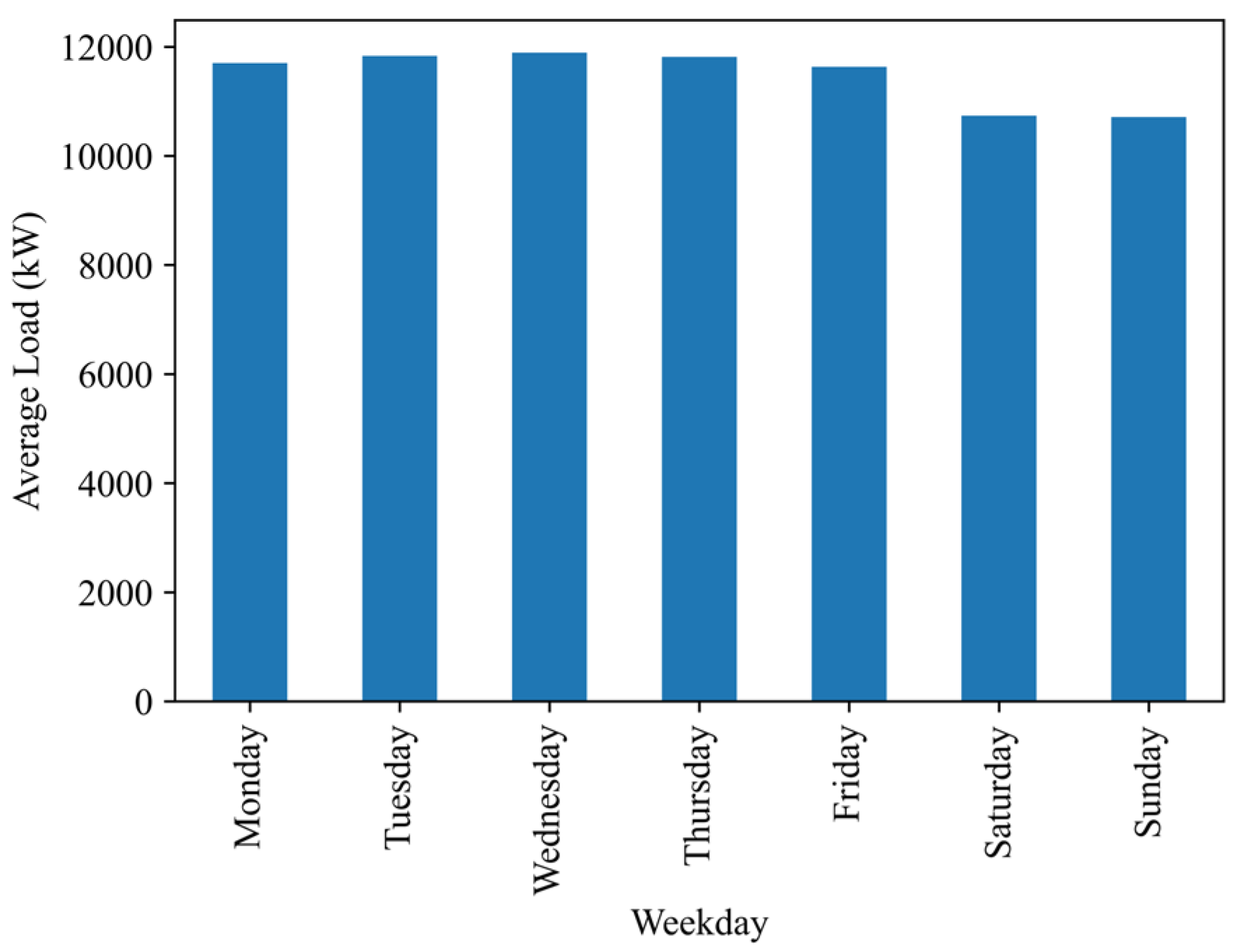
2.1. Campus Load Information
2.2. Metrological Data
- Dry Bulb Temperature: The temperature visible on a thermometer when it is exposed to the air in the absence of moisture and radiation is called the dry bulb temperature. It is proportional to the mean kinetic energy of the air molecules.
- Dew Point: The temperature required at constant pressure to achieve a relative humidity of 100% is called the dew point of the air. It is directly proportional to the moisture in the air.
- Relative Humidity: At any given temperature, the water mass ratio to air mass represents absolute humidity. The relative humidity is obtained by dividing the absolute humidity by the maximum possible humidity at any given temperature.
- Wind Direction: This represents the direction of the blowing wind. A value of 0 denotes that the wind is calm. A value of 9 represents that the wind is blowing from the east, while a value of 36 means that the wind is blowing from the north.
- Wind Speed: This is the speed of the wind. It is measured at a distance of 10 m from the ground. In our data, we use km/h as the measuring unit.
- Visibility: Visibility is the distance at which an object of tangible size can be observed. In our data, we use kilometers as the measuring unit.
- Atmospheric Pressure: The atmospheric pressure is the force exerted per unit area at the height of the measuring station.
3. Algorithms, Evaluation Metrics, and Loss Functions
3.1. Algorithms
3.1.1. Seasonal Autoregressive Integrated Moving Average (SARIMA)
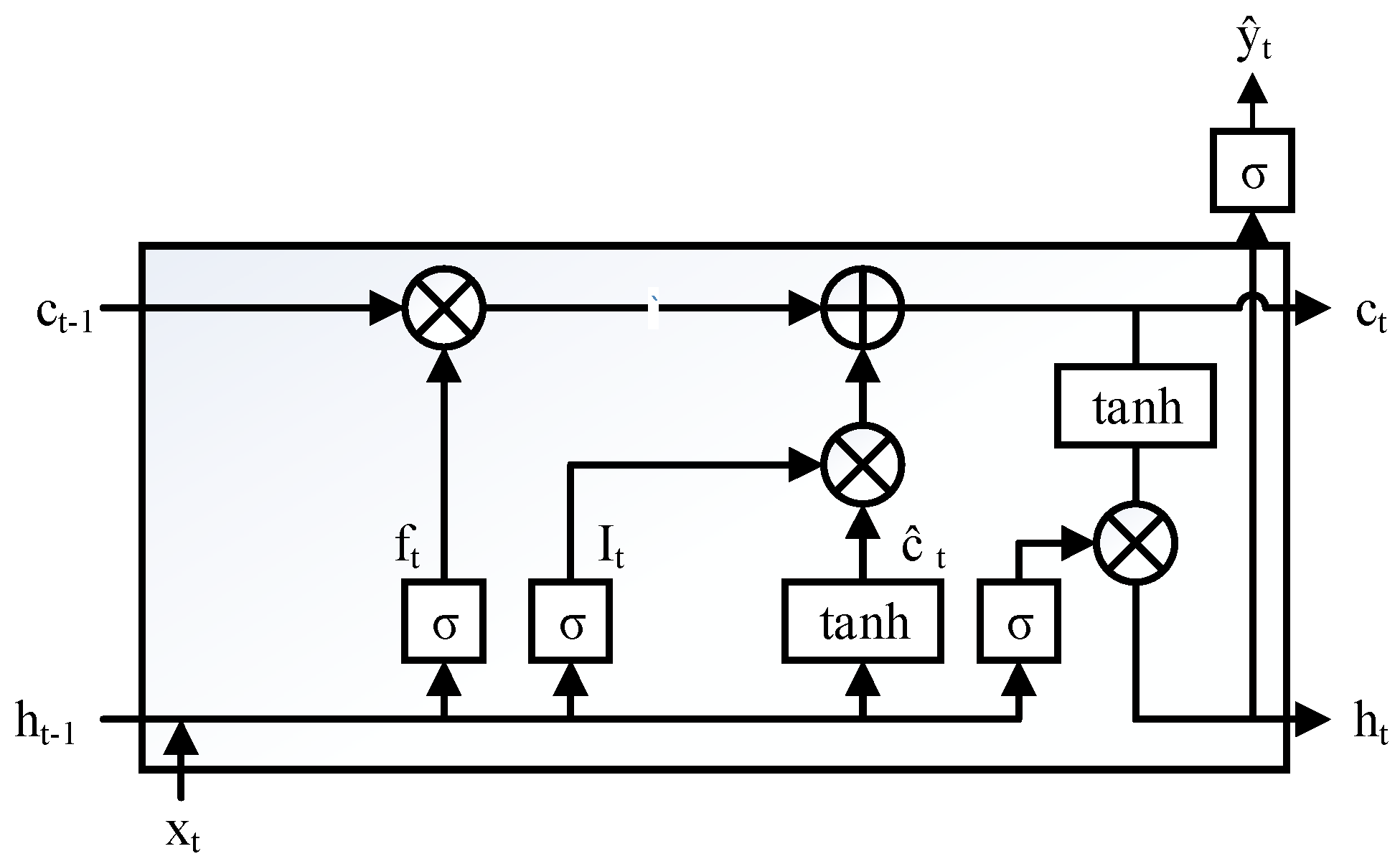
3.1.2. Long Short Term Memory Recurrent Neural Network
3.1.3. Gated Recurrent Unit
3.1.4. Bi-Directional Recurrent Neural Networks
3.1.5. Convolutional Neural Network
3.1.6. Sequence to Sequence (Seq2Seq) Model
3.1.7. Sequence to Sequence (Seq2Seq) Model with Attention
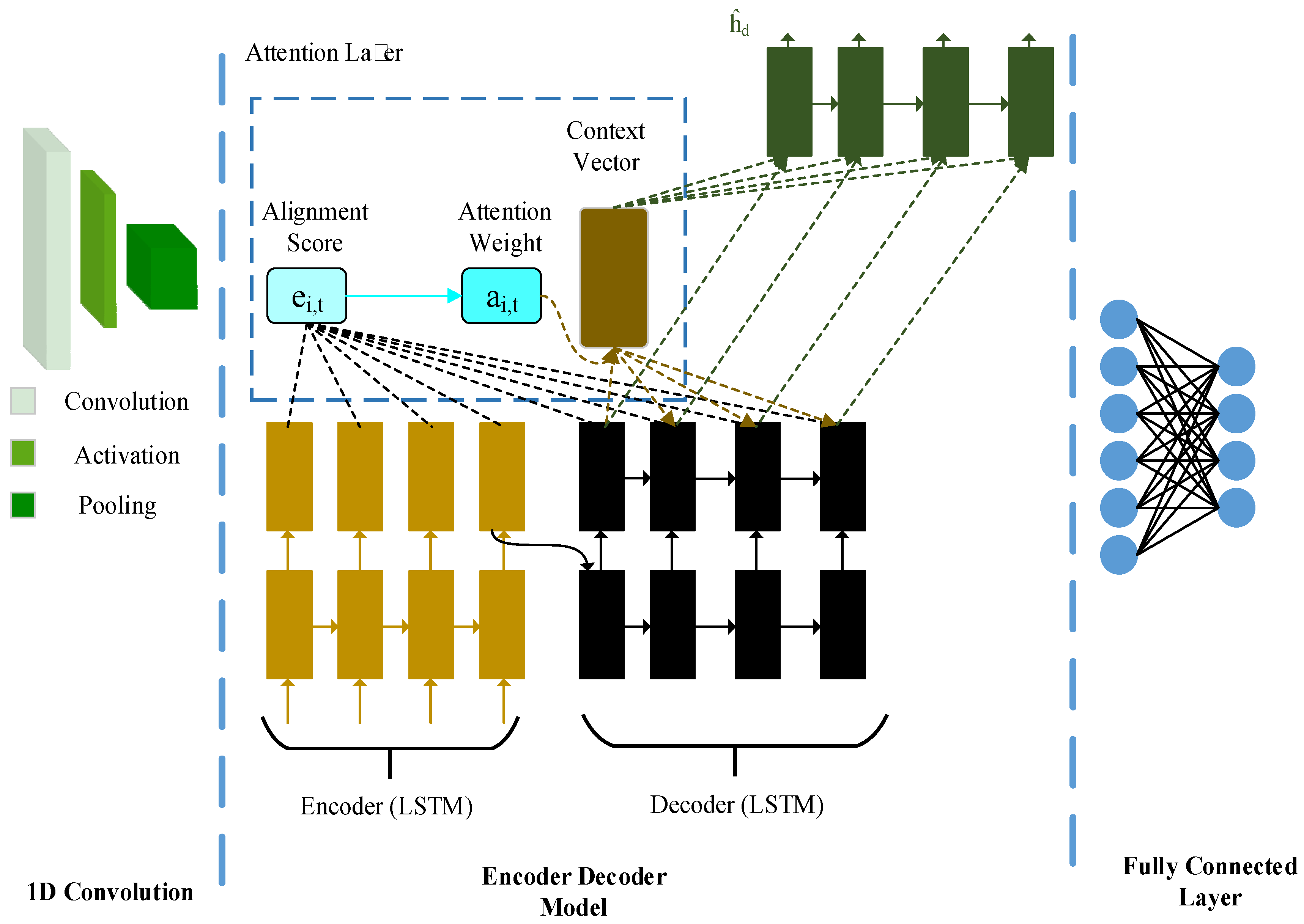
3.1.8. Proposed Custom Architecture
3.2. Evaluation Metrics
3.2.1. Mean Absolute Error (MAE)
3.2.2. Mean Squared Error
3.2.3. R2 Score
3.2.4. Mean Absolute Percentage Error (MAPE)
4. Methodology and Results
4.1. Methodology
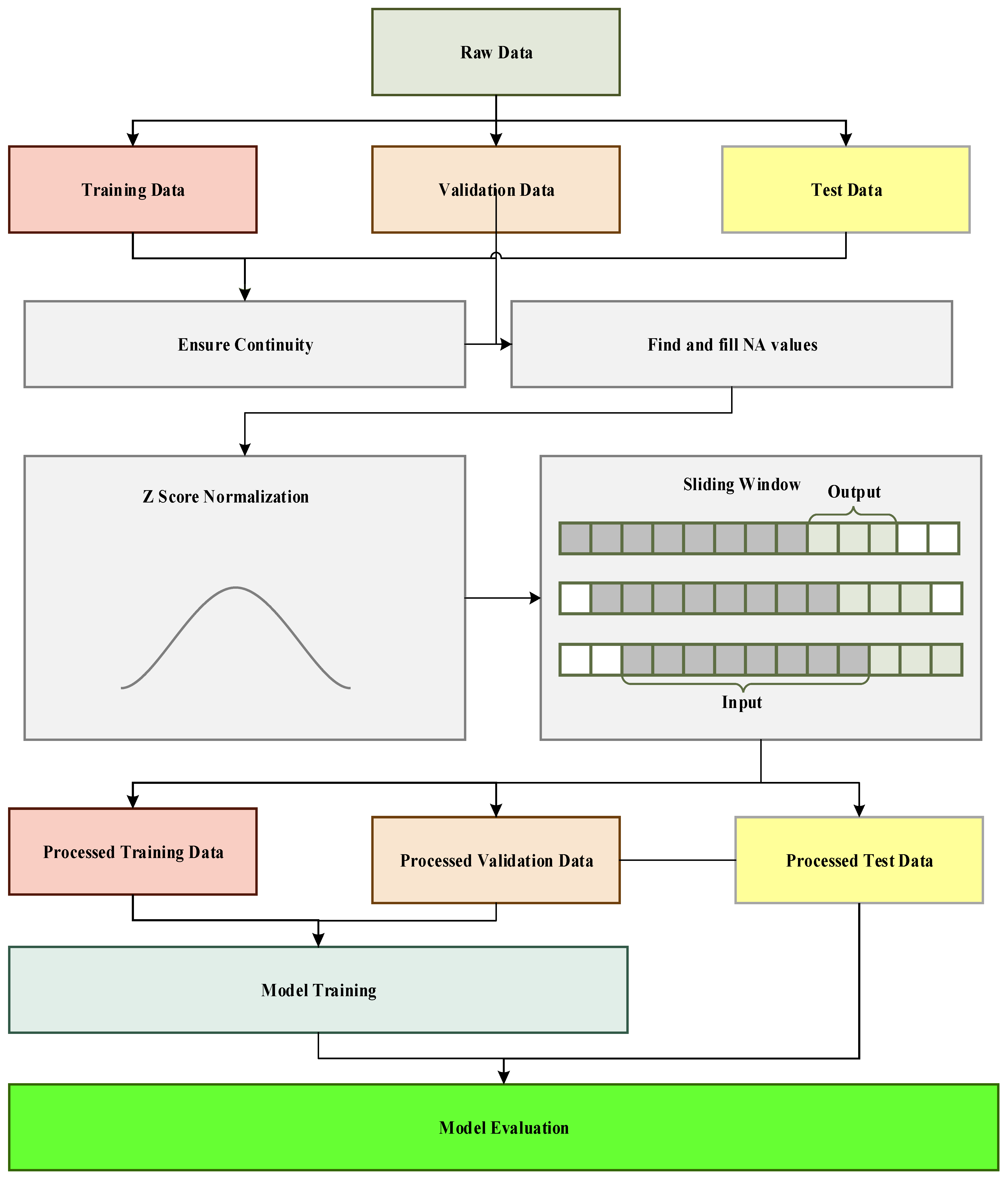
4.1.1. Data Cleaning
4.1.2. Data Preprocessing
4.1.3. Network Architecture
4.1.4. Training
4.2. Results
4.2.1. Model Comparison
4.2.2. Input Horizon Optimization
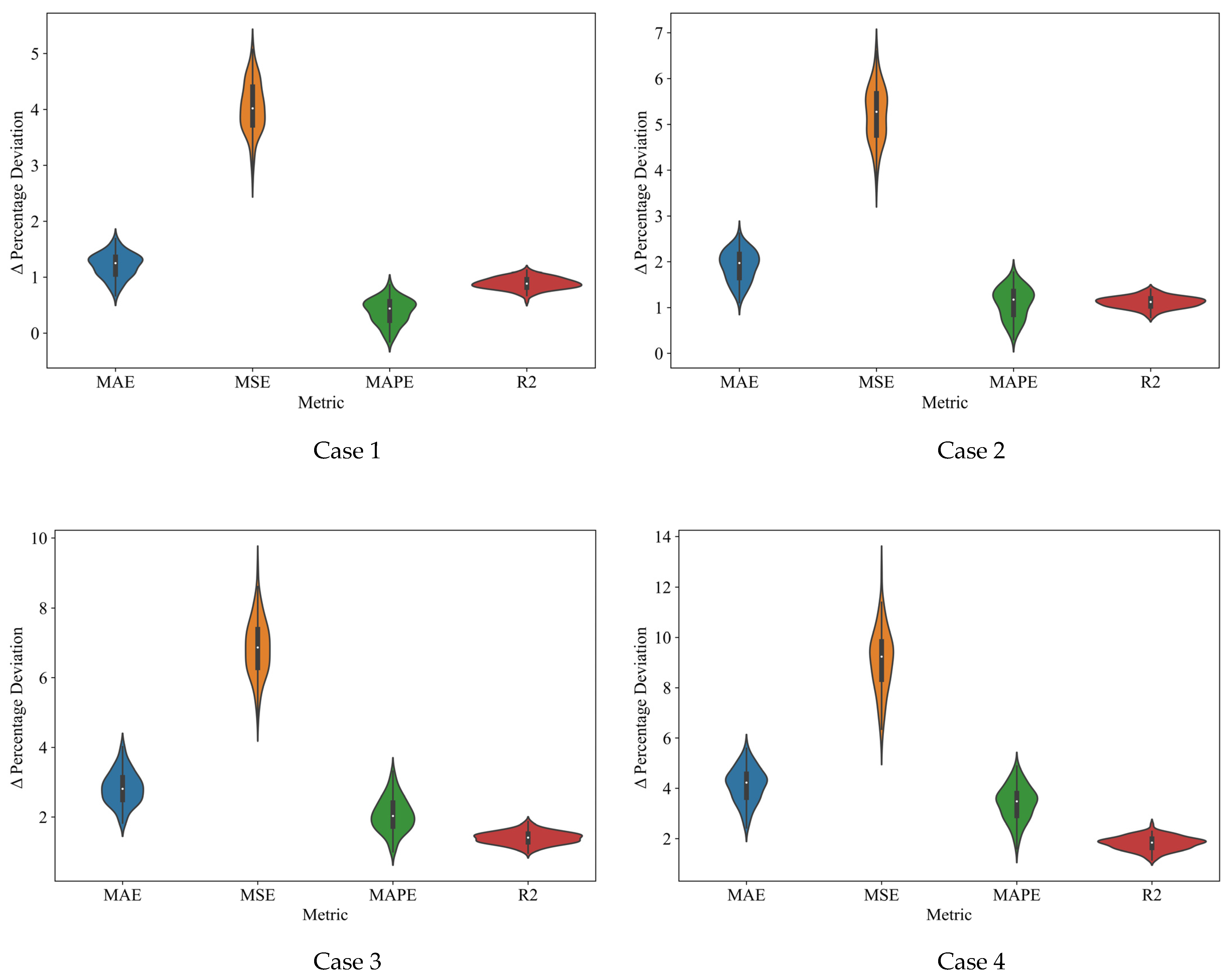
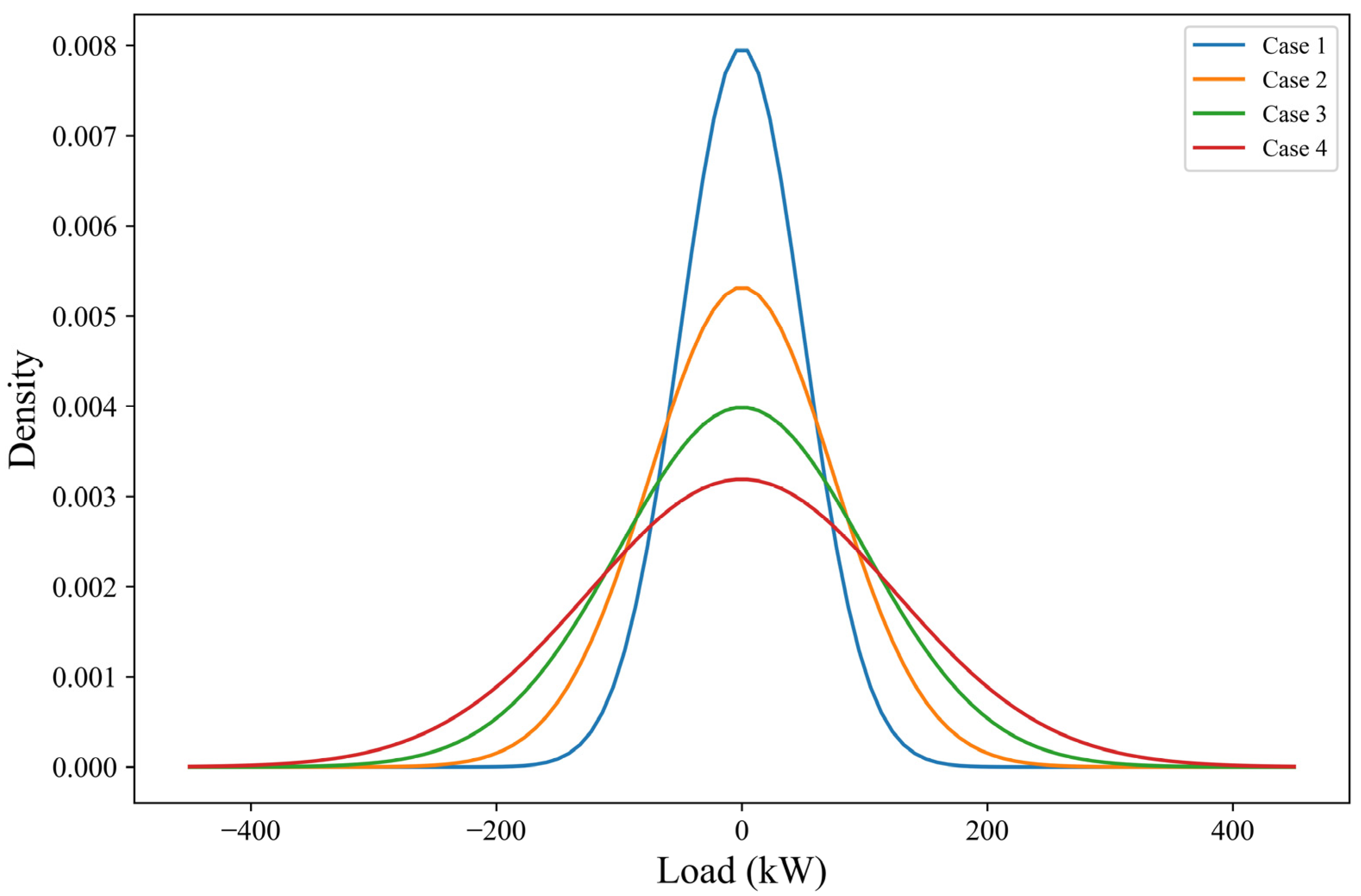
4.2.3. Robustness Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Sunny, M.S.H.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Bashari, M.; Rahimi-Kian, A. Forecasting Electric Load by Aggregating Meteorological and History-Based Deep Learning Modules. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2 August 2020; pp. 1–5. [Google Scholar]
- Zhang, W.; Chen, Q.; Yan, J.; Zhang, S.; Xu, J. A Novel Asynchronous Deep Reinforcement Learning Model with Adaptive Early Forecasting Method and Reward Incentive Mechanism for Short-Term Load Forecasting. Energy 2021, 236, 121492. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Wang, M.; Wang, K.; Huang, Y.; Xu, Z. Power Sharing and Storage-Based Regenerative Braking Energy Utilization for Sectioning Post in Electrified Railways. IEEE Trans. Transp. Electrif. 2024, 10, 2677–2688. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, Z.; Xia, H.; Lin, F. Brake Voltage Following Control of Supercapacitor-Based Energy Storage Systems in Metro Considering Train Operation State. IEEE Trans. Ind. Electron. 2018, 65, 6751–6761. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep Learning for Estimating Building Energy Consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Lin, Y.; Luo, H.; Wang, D.; Guo, H.; Zhu, K. An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting. Energies 2017, 10, 1186. [Google Scholar] [CrossRef]
- Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and Models for Electric Load Forecasting: A Comprehensive Review. Logist. Supply Chain Sustain. Glob. Chall. 2020, 11, 51–76. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. An Overview and Comparative Analysis of Recurrent Neural Networks for Short Term Load Forecasting. arXiv 2017, arXiv:1705.04378. [Google Scholar]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric Load Forecasting in Smart Grids Using Long-Short-Term-Memory Based Recurrent Neural Network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Wang, X.; Tian, W.; Liao, Z. Statistical Comparison between SARIMA and ANN’s Performance for Surface Water Quality Time Series Prediction. Environ. Sci. Pollut. Res. 2021, 28, 33531–33544. [Google Scholar] [CrossRef] [PubMed]
- Muzaffar, S.; Afshari, A. Short-Term Load Forecasts Using LSTM Networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Jain, M.; AlSkaif, T.; Dev, S. Are Deep Learning Models More Effective against Traditional Models for Load Demand Forecasting? In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5 September 2022; pp. 1–6. [Google Scholar]
- Madhukumar, M.; Sebastian, A.; Liang, X.; Jamil, M.; Shabbir, M.N.S.K. Regression Model-Based Short-Term Load Forecasting for University Campus Load. IEEE Access 2022, 10, 8891–8905. [Google Scholar] [CrossRef]
- Yi, L.; Zhu, J.; Liu, J.; Sun, H.; Liu, B. Multi-Level Collaborative Short-Term Load Forecasting. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November 2022; pp. 1–5. [Google Scholar]
- Aouad, M.; Hajj, H.; Shaban, K.; Jabr, R.A.; El-Hajj, W. A CNN-Sequence-to-Sequence Network with Attention for Residential Short-Term Load Forecasting. Electr. Power Syst. Res. 2022, 211, 108152. [Google Scholar] [CrossRef]
- Zuo, C.; Wang, J.; Liu, M.; Deng, S.; Wang, Q. An Ensemble Framework for Short-Term Load Forecasting Based on TimesNet and TCN. Energies 2023, 16, 5330. [Google Scholar] [CrossRef]
- Fan, C.; Nie, S.; Xiao, L.; Yi, L.; Wu, Y.; Li, G. A Multi-Stage Ensemble Model for Power Load Forecasting Based on Decomposition, Error Factors, and Multi-Objective Optimization Algorithm. Int. J. Electr. Power Energy Syst. 2024, 155, 109620. [Google Scholar] [CrossRef]
- Jawad, M.; Nadeem, M.S.A.; Shim, S.-O.; Khan, I.R.; Shaheen, A.; Habib, N.; Hussain, L.; Aziz, W. Machine Learning Based Cost Effective Electricity Load Forecasting Model Using Correlated Meteorological Parameters. IEEE Access 2020, 8, 146847–146864. [Google Scholar] [CrossRef]
- Schaeffer, R.; Szklo, A.S.; Pereira de Lucena, A.F.; Moreira Cesar Borba, B.S.; Pupo Nogueira, L.P.; Fleming, F.P.; Troccoli, A.; Harrison, M.; Boulahya, M.S. Energy Sector Vulnerability to Climate Change: A Review. Energy 2012, 38, 1–12. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yamak, P.T.; Yujian, L.; Gadosey, P.K. A Comparison between ARIMA, LSTM, and GRU for Time Series Forecasting. In Proceedings of the Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 20 December 2019; pp. 49–55. [Google Scholar]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air Pollution Forecasting Using a Deep Learning Model Based on 1D Convnets and Bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.; Hinton, G. Speech Recognition with Deep Recurrent Neural Networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Boureau, Y.-L.; Ponce, J.; LeCun, Y. A Theoretical Analysis of Feature Pooling in Visual Recognition. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Wang, T.; Wu, D.J.; Coates, A.; Ng, A.Y. End-to-End Text Recognition with Convolutional Neural Networks. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 3304–3308. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent Advances in Convolutional Neural Networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Wijnhoven, R.G.J.; de With, P.H.N. Fast Training of Object Detection Using Stochastic Gradient Descent. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 424–427. [Google Scholar]





| Research Article | Spatiotemporal Mapping | Robustness Testing | Input Horizon Optimization |
|---|---|---|---|
| [13] | No | No | No |
| [14] | No | No | No |
| [15] | Yes | No | No |
| [16] | Yes | No | No |
| Parameter | Value |
|---|---|
| Data start date | 2 January 2016 |
| Data end date | 31 March 2020 |
| Data interval | 1 h |
| Total data points | 37,221 |
| Features | 08 |
| Hyperparameters | Values |
|---|---|
| Epochs | 100 |
| Loss Function | Huber Loss |
| Batch Size | 128 |
| Optimizer | Adams Optimizer |
| Early Stopping Patience | 20 |
| Early Stopping Parameter | Validation Loss |
| Input Features | 10 |
| Output Window Width | 24 |
| Input Window Width | 672 |
| Parameter | Value (Seconds) |
|---|---|
| Training time | 257.4 |
| Inference time | 0.21 |
| Algorithm/Metric | MAE (kW) | R2 Score | MSE (kW2) | MAPE (% Age) | Chief Parameters |
|---|---|---|---|---|---|
| LSTM | 442.94 | 0.77 | 340,026.33 | 3.64 | Hidden units = 64 Dropout = 0.1 Number of layers = 1 |
| GRU | 493.72 | 0.739 | 386,019.62 | 4.05 | Hidden units = 32 Dropout = 0.05 Number of layers = 1 |
| 1D CNN + Encoder Decoder | 423.326 | 0.8011 | 294,162.21 | 3.51 | Encoder Hidden units = 32 Decoder Hidden Units = 64 Number of layers = 1 |
| RQ-GPR [14] | 450.21 | 0.71 | 401,264.54 | 4.98 | Length Scale = 1.0 Scale mixture parameter = 5.0 Noise level range = [0.1, 1] |
| Sequence to Sequence + Luong Attention [16] | 410.11 | 0.795 | 298,765.45 | 3.40 | Encoder Hidden Size = 32 Decoder Hidden Size = 64 Attention Layer Hidden Size = 16 |
| Proposed Network Architecture | 407.308 | 0.805 | 287,346.33 | 3.37 | Encoder Hidden Size = 32 Decoder Hidden Size = 32 Attention Layer Hidden Size = 8 |
| Architecture | Train Steps | MSE kW2 | MAE kW | R2 Score | MAPE (×100%) |
|---|---|---|---|---|---|
| GRU | 24 | 536,352.076 | 541.330 | 0.663 | 0.045 |
| 48 | 464,480.438 | 501.336 | 0.708 | 0.043 | |
| . | . | . | . | . | |
| . | . | . | . | . | |
| 168 | 328,631.031 | 435.952 | 0.786 | 0.037 | |
| 192 | 284,889.734 | 408.822 | 0.814 | 0.034 | |
| 216 | 287,705.298 | 412.394 | 0.812 | 0.035 | |
| . | . | . | . | ||
| . | . | . | . | . | |
| . | . | . | . | . | |
| 648 | 364,983.889 | 458.885 | 0.754 | 0.038 | |
| 672 | 385,770.860 | 471.314 | 0.739 | 0.039 | |
| LSTM | 24 | 508,925.840 | 533.137 | 0.680 | 0.045 |
| 48 | 488,299.198 | 532.989 | 0.693 | 0.045 | |
| . | . | . | . | . | |
| . | . | . | . | . | |
| 168 | 344,335.384 | 448.178 | 0.776 | 0.038 | |
| 192 | 356,604.350 | 465.067 | 0.767 | 0.039 | |
| 216 | 345,513.005 | 452.298 | 0.775 | 0.038 | |
| 240 | 302,698.183 | 421.951 | 0.802 | 0.035 | |
| 264 | 400,005.317 | 477.321 | 0.738 | 0.040 | |
| . | . | . | . | . | |
| . | . | . | . | . | |
| 648 | 413,153.544 | 505.153 | 0.721 | 0.042 | |
| 672 | 368,893.385 | 473.734 | 0.751 | 0.039 |
| Case | Study Details | Test Parameters | Evaluation Metrics | |||
|---|---|---|---|---|---|---|
| % ∆MAE | % ∆MSE | % ∆MAPE | % ∆R2 | |||
| 1 | [0, 50] | Average | 1.241453 | 4.06674 | 0.417076 | 0.89951 |
| Maximum | 1.863907 | 5.261097 | 1.003151 | 1.157584 | ||
| Standard Deviation | 0.283457 | 0.509466 | 0.285956 | 0.112588 | ||
| 2 | [0, 75] | Average | 1.85939 | 5.20309 | 1.051538 | 1.111195 |
| Maximum | 2.71684 | 6.87143 | 1.879937 | 1.437032 | ||
| Standard Deviation | 0.393231 | 0.663161 | 0.397011 | 0.13982 | ||
| 3 | [0, 100] | Average | 2.796778 | 6.779848 | 2.024935 | 1.405992 |
| Maximum | 4.115265 | 9.339956 | 3.419123 | 1.944015 | ||
| Standard Deviation | 0.546864 | 0.948765 | 0.559865 | 0.203264 | ||
| 4 | [0, 125] | Average | 4.02232 | 8.966153 | 3.297807 | 1.807394 |
| Maximum | 5.781688 | 12.74125 | 5.005656 | 2.662423 | ||
| Standard Deviation | 0.624861 | 1.205047 | 0.629848 | 0.268467 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, Z.; Jamil, M.; Khan, A.A. Short-Term Campus Load Forecasting Using CNN-Based Encoder–Decoder Network with Attention. Energies 2024, 17, 4457. https://doi.org/10.3390/en17174457
Ahmed Z, Jamil M, Khan AA. Short-Term Campus Load Forecasting Using CNN-Based Encoder–Decoder Network with Attention. Energies. 2024; 17(17):4457. https://doi.org/10.3390/en17174457
Chicago/Turabian StyleAhmed, Zain, Mohsin Jamil, and Ashraf Ali Khan. 2024. "Short-Term Campus Load Forecasting Using CNN-Based Encoder–Decoder Network with Attention" Energies 17, no. 17: 4457. https://doi.org/10.3390/en17174457
APA StyleAhmed, Z., Jamil, M., & Khan, A. A. (2024). Short-Term Campus Load Forecasting Using CNN-Based Encoder–Decoder Network with Attention. Energies, 17(17), 4457. https://doi.org/10.3390/en17174457







