Optimization of Bi-LSTM Photovoltaic Power Prediction Based on Improved Snow Ablation Optimization Algorithm
Abstract
1. Introduction
2. Data Processing and Analysis
2.1. Data Processing
2.2. Pearson Correlation Coefficient Analysis
2.3. K-Means Clustering Analysis
- (1)
- The distinction between rainfall weather and other weather conditions can be made based on the quantity of rainfall at different intervals of each day and the occurrence of rain. Herein, the lower threshold is set at 0.5 mm. If the cumulative daily rainfall exceeds 0.5 mm, the weather of that day is classified as a rainy day.
- (2)
- GHI fluctuation: Sunny days usually have a consistently stable irradiance, resulting in stable and high-power output from photovoltaic modules. Conversely, the movement of clouds in cloudy weather leads to rapid changes in irradiance, thereby causing fluctuations in PV power generation. In this study, the standard deviation of irradiance fluctuation is used as a judgment indicator. If the standard deviation of irradiance exceeds 50 W/m2, it is determined as a cloudy day; otherwise, it is determined as a sunny day. The reason for choosing the standard deviation as the evaluation criterion lies in that the standard deviation can effectively measure the degree of dispersion of irradiance values and reflect the magnitude of irradiance fluctuation.
- (1)
- Specify the number of clusters K: Set the number of clusters K for the samples at three, corresponding respectively to the three weather types, namely sunny, cloudy, and rainy. Select three samples from the sample set as the initial cluster centers.
- (2)
- The Euclidean distance from each data point to the center point of k classes is calculated in turn, and all samples are divided into the nearest class according to the principle of the nearest to the center point of K. The Euclidean distance is:
- (3)
- Determines whether the conditions for terminating clustering are met, and if not, returns to step 2. The condition of termination is to meet the following objective function, that is, if the sum of squares of the deviation of each sample to the center point of the class is less than the specified value, and the clustering terminates.
3. GVSAO-Bi-LSTM Algorithm
3.1. Good Point Strategy
3.2. Vibration Strategy
3.3. Snow Ablation Optimization Algorithm
3.4. Bi-LSTM Neural Network Model
3.5. LSTM Neural Network Model
4. Analysis on the Implementation Process and Test Functions of GVSAO
4.1. The Implementation Procedure of GVSAO
4.2. Analysis of Test Functions
- Unimodal function
- Multimodal function
- Combined function
5. Construction of PV Power Prediction Model Based on GVSAO-Bi-LSTM
5.1. The Process of Model Construction
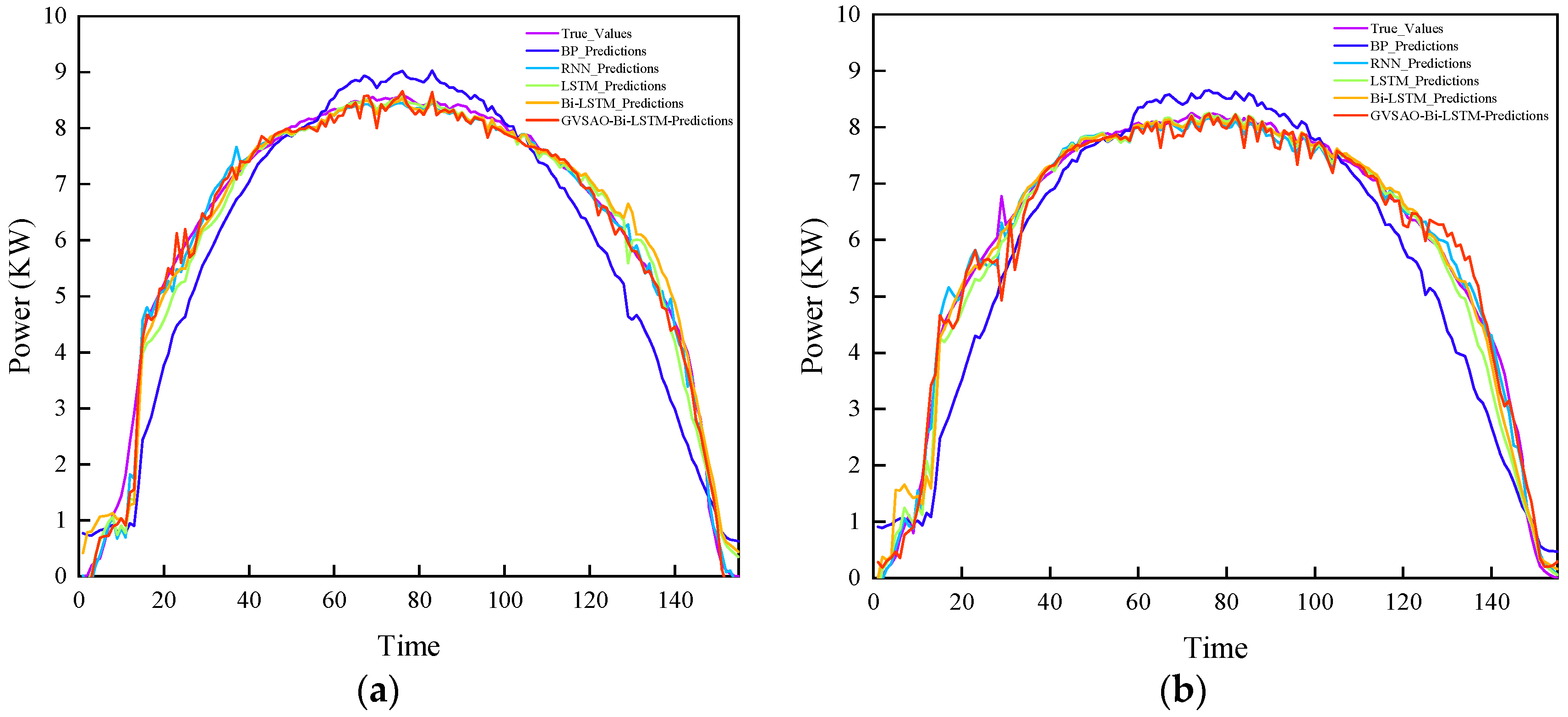
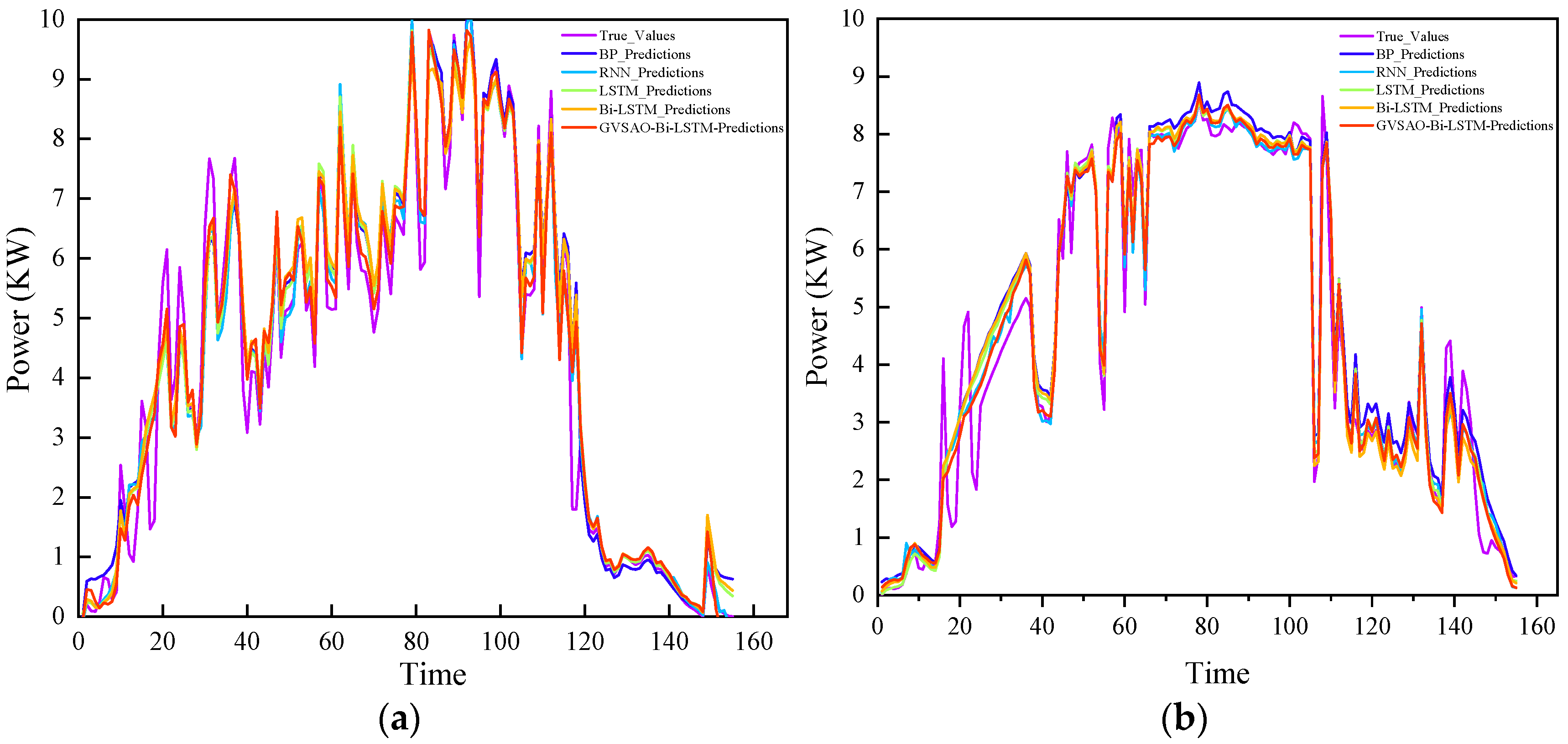
5.2. Case Verification and Analysis
- (1)
- Data normalization and denormalization procedures
- (2)
- Analysis of the prediction outcomes of PV power generation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Deventer, W.Y.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, L.; Lu, Y.; Zhang, M.; Qin, W.; Wang, S.; Wang, L. Potential assessment of photovoltaic power generation in China. Renew. Sustain. Energy Rev. 2022, 154, 111900. [Google Scholar] [CrossRef]
- Hosenuzzaman, M.; Rahim, N.A.; Selvaraj, J.; Hasanuzzaman, M.; Malek, A.B.M.A.; Nahar, A. Global prospects, progress, policies, and environmental impact of solar photovoltaic power generation. Renew. Sustain. Energy Rev. 2015, 41, 284–297. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, C.; Xu, Y.; Zhang, Y.; Sun, H. Statistical Machine Learning for Power Flow Analysis Considering the Influence of Weather Factors on Photovoltaic Power Generation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 109, 38587954. [Google Scholar] [CrossRef]
- Amole, A.O.; Oladipo, S.; Olabode, O.E.; Makinde, K.A.; Gbadega, P. Analysis of grid/solar photovoltaic power generation for improved village energy supply: A case of Ikose in Oyo State Nigeria. Renew. Energy Focus 2023, 44, 186–211. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Sun, X.; Qin, M.; Pan, R.; Yang, Y. The diffusion path of distributed photovoltaic power generation technology driven by individual behavior. Energy Rep. 2024, 11, 651–658. [Google Scholar]
- Al-Duais, F.; Al-Sharpi, R. A unique Markov chain Monte Carlo method for forecasting wind power utilizing time series model. Alex. Eng. J. 2023, 74, 51–63. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, X.; Li, G.; Gu, P.; Huang, J.; Yang, B. Xgboost–sfs and double nested stacking ensemble model for photovoltaic power forecasting under variable weather conditions. Sustainability 2023, 15, 13146. [Google Scholar] [CrossRef]
- Bai, R.; Shi, Y.; Yue, M.; Du, X. Hybrid model based on K-means++ algorithm, optimal similar day approach, and long short-term memory neural network for short-term photovoltaic power prediction. Glob. Energy Interconnect. 2023, 6, 184–196. [Google Scholar] [CrossRef]
- Houran, M.A.; Salman Bukhari, S.M.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
- Guo, W.; Xu, L.; Wang, T.; Zhao, D.; Tang, X. Photovoltaic Power Prediction Based on Hybrid Deep Learning Networks and Meteorological Data. Sensors 2024, 24, 1593. [Google Scholar] [CrossRef]
- Li, C.; Pan, P.; Yang, W. Power Forecasting for Photovoltaic Microgrid Based on MultiScale CNN-LSTM Network Models. Energies 2024, 17, 3877. [Google Scholar] [CrossRef]
- Liu, L.; Liu, D.; Sun, Q.; Li, H.; Wennersten, R. Forecasting power output of photovoltaic system using a BP network method. Energy Procedia 2017, 142, 780–786. [Google Scholar] [CrossRef]
- Castillo-Rojas, W.; Bekios-Calfa, J.; Hernández, C. Daily prediction model of photovoltaic power generation using a hybrid architecture of recurrent neural networks and shallow neural networks. Int. J. Photoenergy 2023, 1, 2592405. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, Z.; Tang, W.; Xu, P. Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation. Energies 2024, 17, 3435. [Google Scholar] [CrossRef]
- Zhang, J.; Hong, L.; Ibrahim, S.; He, Y. Short-term prediction of behind-the-meter PV power based on attention-LSTM and transfer learning. IET Renew. Power Gener. 2024, 18, 321–330. [Google Scholar] [CrossRef]
- Wentz, V.H.; Maciel, J.N.; Ledesma, J.J.G. Solar Irradiance Forecasting to Short-Term PV Power: Accuracy Comparison of ANN and LSTM Models. Energies 2022, 15, 2457. [Google Scholar] [CrossRef]
- Xiao, Z.; Huang, X.; Liu, J.; Li, C.; Tai, Y. A novel method based on time series ensemble model for hourly photovoltaic power prediction. Energy 2023, 276, 127542. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, Y.; Ji, S.; Mae, M.; Imaizumi, T. Improved multistep ahead photovoltaic power prediction model based on LSTM and self-attention with weather forecast data. Appl. Energy 2024, 359, 122709. [Google Scholar] [CrossRef]
- Li, M.; Wang, W.; He, Y.; Wang, Q. Deep learning model for short-term photovoltaic power forecasting based on variational mode decomposition and similar day clustering. Comput. Electr. Eng. 2024, 40, 39–50. [Google Scholar] [CrossRef]
- Lu, X.; Guan, Y.; Liu, J.; Yang, W.; Sun, J.; Dai, J. Research on Real-Time Prediction Method of Photovoltaic Power Time Series Utilizing Improved Grey Wolf Optimization and Long Short-Term Memory Neural Network. Processes 2024, 12, 1578. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Zhao, S. A Novel Photovoltaic Power Prediction Method Based on a Long Short-Term Memory Network Optimized by an Improved Sparrow Search Algorithm. Electronics 2024, 13, 993. [Google Scholar] [CrossRef]
- Liang, L.; Su, T.; Gao, Y.; Qin, F.; Pan, M. FCDT-IWBOA-LSSVR: An innovative hybrid machine learning approach for efficient prediction of short-to-mid-term photovoltaic generation. J. Clean. Prod. 2023, 385, 135716. [Google Scholar] [CrossRef]
- Hua, L.; Wang, Y. Application of Number Theory in Modern Analysis, 1st ed.; China Science Publishing & Media Ltd.: Beijing, China, 1978; pp. 1–99. [Google Scholar]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]














| Function Number | Function | Dimension | Value Range | Minimum Value |
|---|---|---|---|---|
| F1 | 30 | [−100, 100] | 0 | |
| F2 | 30 | [−32, 32] | 0 | |
| F3 | 2 | [−5, 5] | 0.398 |
| Function | Evaluation Index | GVSAO | SAO | GWO | PSO | GA |
|---|---|---|---|---|---|---|
| F1 | avg | 3.28 × 10−92 | 3.12 × 10−80 | 1.31 × 10−27 | 0.51 | 0.0007 |
| F2 | avg | 4.44 × 10−16 | 2.86 × 10−15 | 5.93 × 10−14 | 0.95 | 0.057 |
| F3 | avg | 0.398093 | 0.397968 | 0.397889 | 0.397887 | 0.396761 |
| Weather Type | Model | Error Index | |||
|---|---|---|---|---|---|
| MSE | RMSE | MAE | MAPE | ||
| Clear | BP | 0.4462 | 0.6681 | 0.4813 | 95.81% |
| RNN | 0.3169 | 0.5629 | 0.3677 | 78.01% | |
| LSTM | 0.2868 | 0.5356 | 0.3395 | 61.06% | |
| Bi-LSTM | 0.2322 | 0.4819 | 0.2876 | 36.59% | |
| GVSAO-Bi-LSTM | 0.2048 | 0.4526 | 0.2714 | 4.75% | |
| Cloudy | BP | 0.4529 | 0.6731 | 0.5152 | 335.20% |
| RNN | 0.3384 | 0.5817 | 0.3723 | 147.58% | |
| LSTM | 0.2879 | 0.5366 | 0.3449 | 73.16% | |
| Bi-LSTM | 0.2392 | 0.4891 | 0.3073 | 48.93% | |
| GVSAO-Bi-LSTM | 0.2092 | 0.4574 | 0.2919 | 5.41% | |
| Rainy | BP | 0.5607 | 0.7489 | 0.5658 | 338.24% |
| RNN | 0.3549 | 0.5957 | 0.3774 | 259.27% | |
| LSTM | 0.3517 | 0.5931 | 0.3711 | 141.08% | |
| Bi-LSTM | 0.2898 | 0.5383 | 0.3338 | 73.32% | |
| GVSAO-Bi-LSTM | 0.2714 | 0.5209 | 0.3241 | 14.37% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xiang, C.; Qian, H.; Zhou, P. Optimization of Bi-LSTM Photovoltaic Power Prediction Based on Improved Snow Ablation Optimization Algorithm. Energies 2024, 17, 4434. https://doi.org/10.3390/en17174434
Wu Y, Xiang C, Qian H, Zhou P. Optimization of Bi-LSTM Photovoltaic Power Prediction Based on Improved Snow Ablation Optimization Algorithm. Energies. 2024; 17(17):4434. https://doi.org/10.3390/en17174434
Chicago/Turabian StyleWu, Yuhan, Chun Xiang, Heng Qian, and Peijian Zhou. 2024. "Optimization of Bi-LSTM Photovoltaic Power Prediction Based on Improved Snow Ablation Optimization Algorithm" Energies 17, no. 17: 4434. https://doi.org/10.3390/en17174434
APA StyleWu, Y., Xiang, C., Qian, H., & Zhou, P. (2024). Optimization of Bi-LSTM Photovoltaic Power Prediction Based on Improved Snow Ablation Optimization Algorithm. Energies, 17(17), 4434. https://doi.org/10.3390/en17174434






