A New Approach to Examine the Dynamics of Switched-Mode Step-Up DC–DC Converters—A Switched State-Space Model
Abstract
1. Introduction
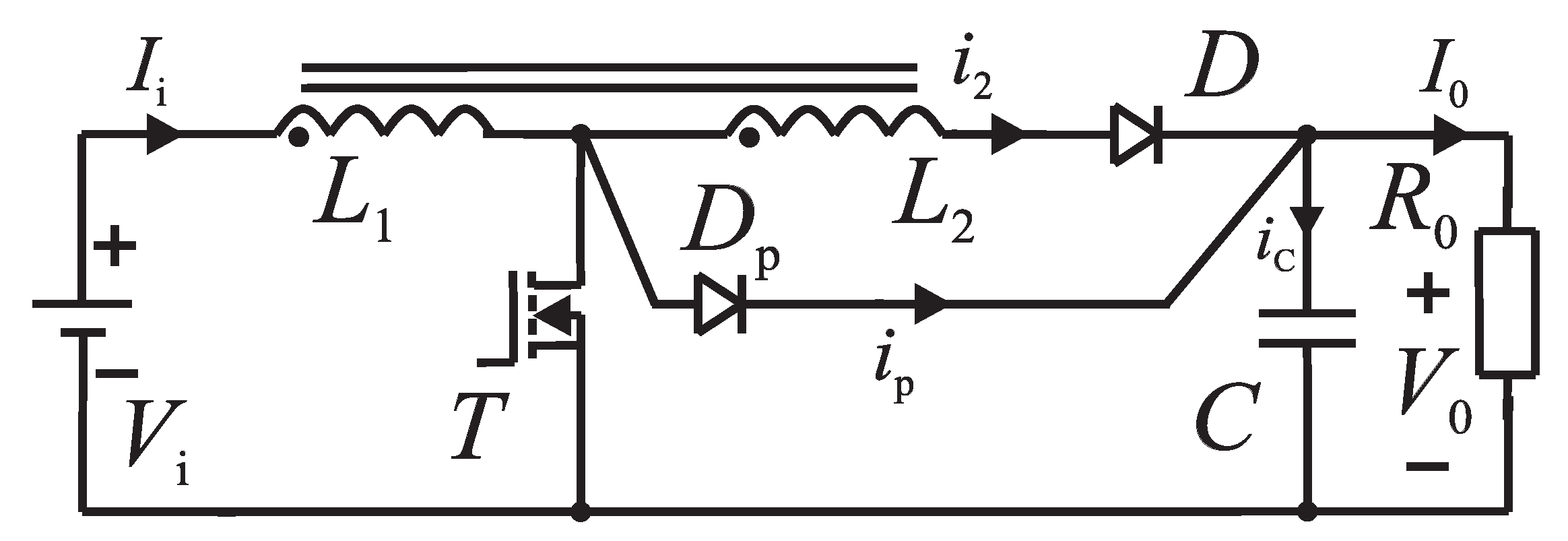
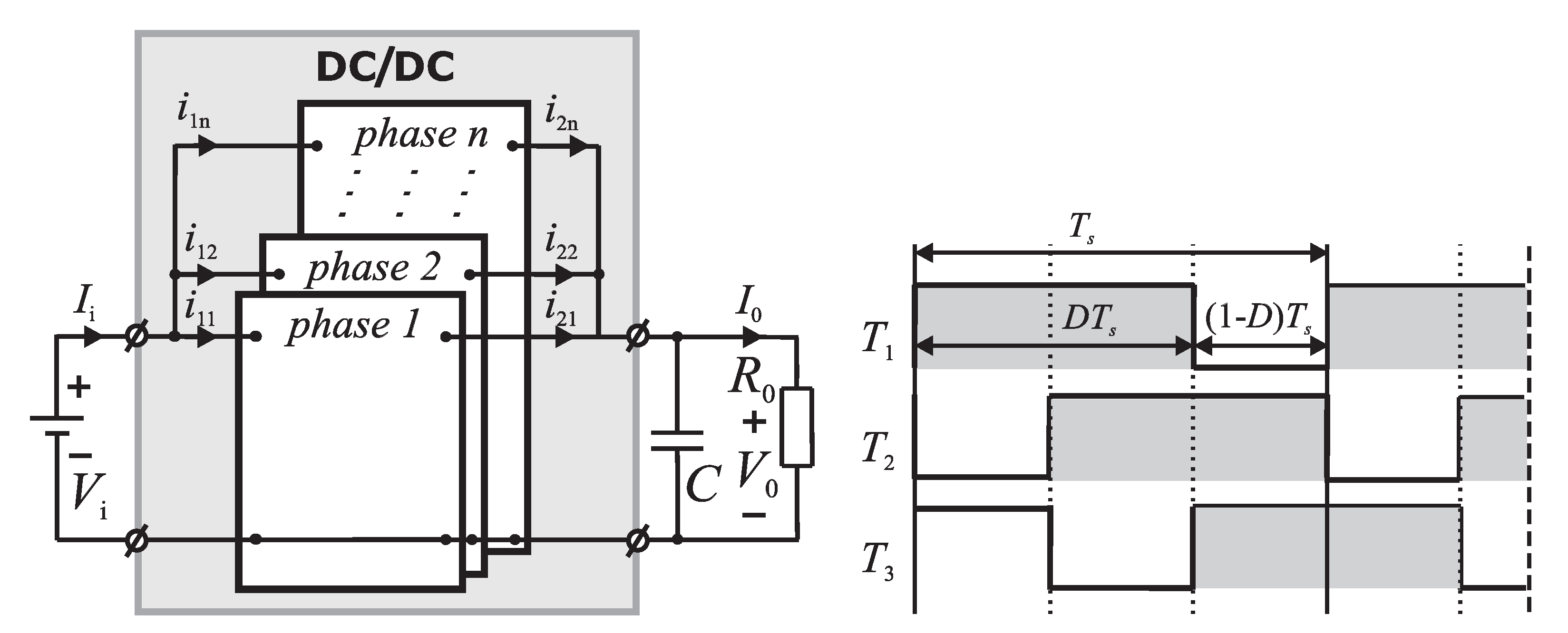
2. Interleaved Step-Up DC–DC Converter
2.1. Topology of the Converter
2.2. Time Domain Analysis of the Converter’s Work
2.3. Active Component Choice
2.4. Assumptions to the Model
- The transistor during the on period is represented by constant drain-to-source resistance ;
- The conducting diode is represented by its series dynamic resistance ;
- Diodes and transistors during the turn-off period are considered infinite resistances;
- The resistances of the inductor windings (i.e., and ) include both DC and AC resistance components [29];
- The inductor operates in the linear part of its curve;
- The converter operates in constant current mode (CCM);
- The rated power of a single phase does not exceed 650 W.
3. Converter Dynamics Analysis
3.1. Small-Signal Averaging Method
3.2. Switched State–Space Model Approach
3.3. PSpice Model
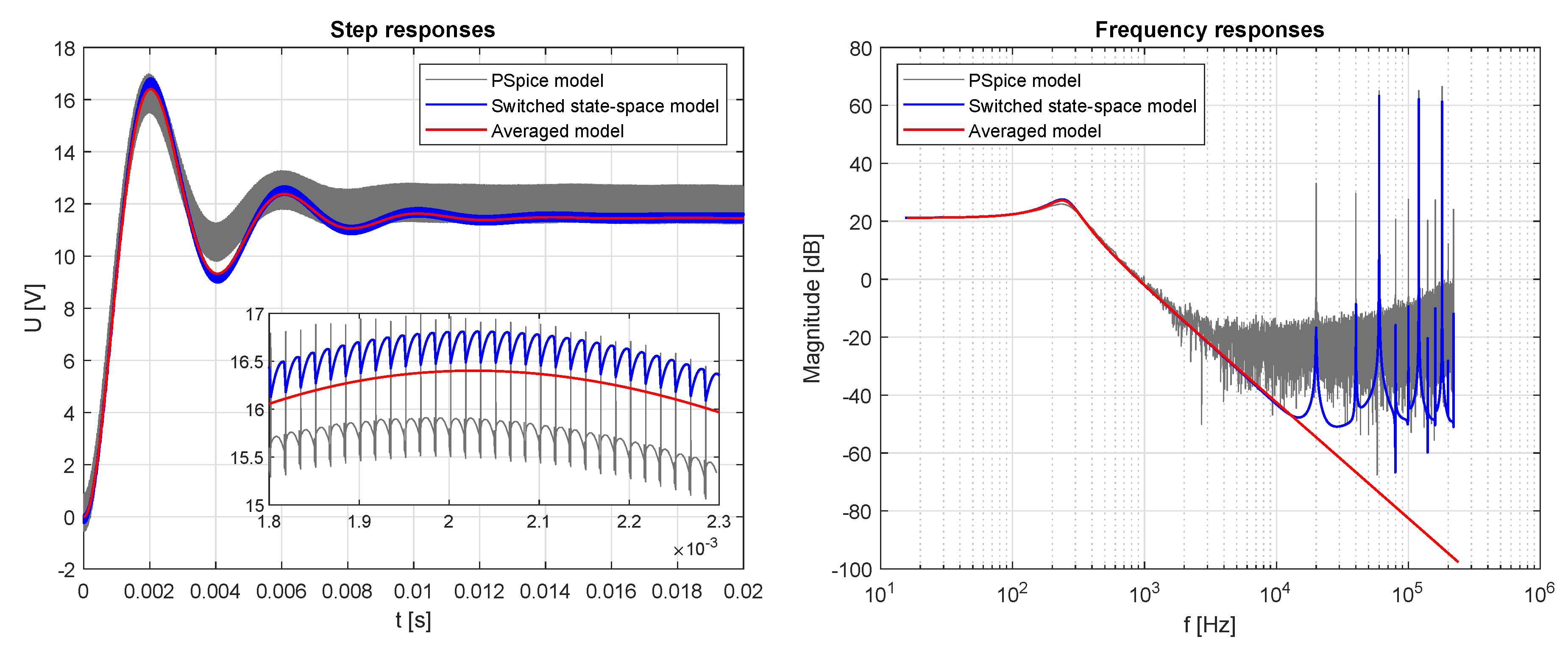
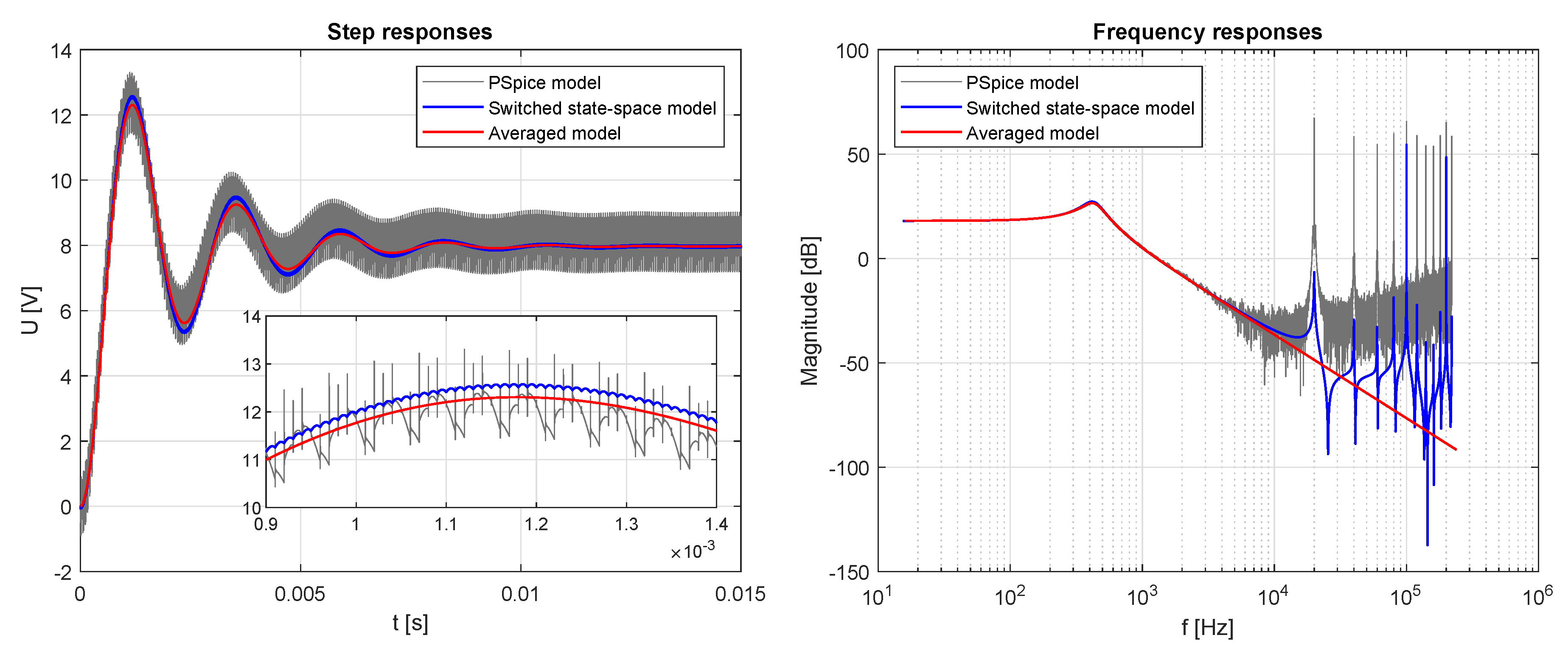
4. Results
- 1.
- , , and (half-rated power);
- 2.
- , , and (full power);
- 3.
- , , and (half-rated power);
- 4.
- , , and (full power).
5. Discussion
- , , and —relative errors of the first and second oscillations’ peak amplitudes and the relative error of the steady state value expressed bywhere values for the PSpice and switched state–space models were computed as average values over one period;
- —maximum time shift between oscillations peak amplitudes over the entire response;
- —difference between rise times, i.e., times taken by signals to change from to .
6. Conclusions
- An interleaved tapped-inductor step-up DC–DC converter model with parasitic parameters of the components has been developed. Based on this proposition, the small-signal averaged model of the converter has been obtained.
- A novel switched state-space model of the analyzed converter has been derived from state–space equations and compared to the small-signal averaged model, showing the advantages of the former one.
- The effectiveness of the presented approach has been demonstrated and discussed in comparison with the PSpice simulation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaabjerg, F.; Guerrero, J.M. Smart grid and renewable energy systems. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–10. [Google Scholar]
- Blaabjerg, F.; Yang, Y.; Ma, K.; Wang., X. Power electronics—The key technology for renewable energy system integration. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1618–1626. [Google Scholar]
- Blaabjerg, F.; Iov, F.; Kerekes, T.; Teodorescu, R. Trends in power electronics and control of renewable energy systems. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, North Macedonia, 6–8 September 2010; pp. K–1–K–19. [Google Scholar]
- Dwari, S.; Parsa, L. A Novel High Efficiency High Power Interleaved Coupled-Inductor Boost DC-DC Converter for Hybrid and Fuel Cell Electric Vehicle. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 399–404. [Google Scholar]
- Li, W.; Xiang, X.; Li, C.; Li, W.; He, X. Interleaved High Step-Up ZVT Converter With Built-In Transformer Voltage Doubler Cell for Distributed PV Generation System. IEEE Trans. Power Electron. 2012, 28, 300–313. [Google Scholar] [CrossRef]
- Gitau, M.N.; Hofsajer, I.W. Analysis of a 4-phase tapped-inductor DC-DC converter for high boost ratio wide input voltage range applications. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 5468–5474. [Google Scholar]
- Tomaszuk, A.; Krupa, A. High efficiency high step-up DC/DC converters—A review. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 59, 475. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics, 3rd ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters, 2nd ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Antsaklis, P.J.; Michel, A.N. Linear Systems; Birkhäuser: Boston, MA, USA, 2005. [Google Scholar]
- Chakraborty, S.S.; Hatua, K.; Bhattacharya, S. A Control Method to Reduce Overshoots in High-Frequency Link Current and Voltages at Load Transients of a Dual-Active-Bridge Series-Resonant Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 4, 525–537. [Google Scholar] [CrossRef]
- Harasimczuk, M.; Kopacz, R.; Tomaszuk, A. Lossless Clamp Circuit With Turn-OFF Voltage and Current Reduction in High Step-Up DC–DC Converter With Coupled Inductor. IEEE Trans. Power Electron. 2024, 39, 1074–1086. [Google Scholar] [CrossRef]
- Zhang, J. Analysis of High Gain DC-DC Converters for DC Microgrid. In Proceedings of the 2023 IEEE 3rd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 29–31 January 2023. [Google Scholar]
- Xu, H.; Zhu, Y.; Lin, Z. Beat Frequency Oscillation Analysis for a DC Microgrid with Multiple Boost Converters. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 866–870. [Google Scholar]
- Yue, X.; Boroyevich, D.; Lee, F.C.; Chen, F.; Burgos, R.; Zhuo, F. Beat Frequency Oscillation Analysis for Power Electronic Converters in DC Nanogrid Based on Crossed Frequency Output Impedance Matrix Model. IEEE Trans. Power Electron. 2018, 33, 3052–3064. [Google Scholar] [CrossRef]
- Yue, X.; Wang, X.; Blaabjerg, F. Review of Small-Signal Modeling Methods Including Frequency-Coupling Dynamics of Power Converters. IEEE Trans. Power Electron. 2018, 34, 3313–3328. [Google Scholar] [CrossRef]
- Xiangpeng, C.; Jinjun, L.; Danhong, X.; Zipeng, L. An Enhanced Multi-frequency Small-signal Model for the Close-loop Design in Buck Converters. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1453–1458. [Google Scholar]
- Xiangpeng, C.; Jinjun, L.; Yiming, T.; Danhong, X. A Comparison of Average Model, Sampled-data Model and Multi-frequency Model Based on DC/DC Converters. In Proceedings of the 2018 International Power Electronics Conference (IPEC—Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2435–2440. [Google Scholar]
- Li, J.; Lee, F.C. New Modeling Approach and Equivalent Circuit Representation for Current-Mode Control. IEEE Trans. Power Electron. 2010, 25, 1218–1230. [Google Scholar]
- Azer, P.; Emadi, A. Generalized State Space Average Model for Multi-Phase Interleaved Buck, Boost and Buck-Boost DC-DC Converters: Transient, Steady-State and Switching Dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control. In Systems and Control: Foundations and Applications; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Becerra, G.J. Control and Observation of Switched Systems. Application to Power Converters. PhD Thesis, INSA de Lyon, Villeurbanne, France, 2019. [Google Scholar]
- Corona, D.; Buisson, J.; De Schutter, B.; Giua, A. Stabilization of switched affine systems: An application to the buck-boost converter. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 6037–6042. [Google Scholar]
- Deaecto, G.S.; Geromel, J.C.; Garcia, F.S.; Pomilio, J.A. Switched affine systems control design with application to DC–DC converters. Iet Control. Theory Appl. 2010, 4, 1201–1210. [Google Scholar] [CrossRef]
- Hashemi, T.; Esfanjani, R.M.; Kaleybar, H.J. Composite Switched Lyapunov Function-Based Control of DC–DC Converters for Renewable Energy Applications. Electronics 2024, 13, 84. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Wang, Q.; Wang, Y. Stable Switching Rule Design for Buck Converter via Affine Switched Systems. Math. Probl. Eng. 2019, 2019, 1–7. [Google Scholar] [CrossRef]
- Ndoye, A.; Delpoux, R.; Trégouët, J.F.; Lin-Shi, X. Switching control design for LTI system with uncertain equilibrium: Application to parallel interconnection of DC/DC converters. Automatica 2022, 145, 110522. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Wu, H.; Xing, Y.; Batarseh, I. Overview of High-Step-Up Coupled-Inductor Boost Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 689–704. [Google Scholar] [CrossRef]
- Kawahara, S.; Umetani, K.; Hiraki, E. Analysis and Prediction of AC Resistance of Litz Wire with Rectangular Cross-Section. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3273–3279. [Google Scholar]





| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Input voltage | 40 | V | |
| Primary winding inductance | 77 | H | |
| Turns ratio | N | - | |
| Coupling coefficient | k | - | |
| Primary winding resistance | 4 | m | |
| Secondary winding resistance | 110 | m | |
| Transistor T (STW88N65M5) on resistance | 30 | m | |
| Dynamic resistance of diode D (CSD10120) | 75 | m | |
| Capacitor shunt resistance | 50 | m | |
| Load capacitance | C | 60 | F |
| Load resistance | 127 (for ) | ||
| 77 (for ) | |||
| Switching frequency | 20 | kHz |
| Parameter | Unit | Averaged Model | Switched Model |
|---|---|---|---|
| , and | |||
| % | |||
| % | |||
| % | |||
| ms | |||
| s | |||
| , and | |||
| % | |||
| % | |||
| % | |||
| ms | |||
| s | |||
| , and | |||
| % | |||
| % | |||
| % | |||
| ms | |||
| s | |||
| , and | |||
| % | |||
| % | |||
| % | |||
| ms | |||
| s | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomaszuk, A.; Borawski, K. A New Approach to Examine the Dynamics of Switched-Mode Step-Up DC–DC Converters—A Switched State-Space Model. Energies 2024, 17, 4413. https://doi.org/10.3390/en17174413
Tomaszuk A, Borawski K. A New Approach to Examine the Dynamics of Switched-Mode Step-Up DC–DC Converters—A Switched State-Space Model. Energies. 2024; 17(17):4413. https://doi.org/10.3390/en17174413
Chicago/Turabian StyleTomaszuk, Adam, and Kamil Borawski. 2024. "A New Approach to Examine the Dynamics of Switched-Mode Step-Up DC–DC Converters—A Switched State-Space Model" Energies 17, no. 17: 4413. https://doi.org/10.3390/en17174413
APA StyleTomaszuk, A., & Borawski, K. (2024). A New Approach to Examine the Dynamics of Switched-Mode Step-Up DC–DC Converters—A Switched State-Space Model. Energies, 17(17), 4413. https://doi.org/10.3390/en17174413






