Overview of Wind and Photovoltaic Data Stream Classification and Data Drift Issues

Abstract

The development in the fields of clean energy, particularly wind and photovoltaic power, generates a large amount of data streams, and how to mine valuable information from these data to improve the efficiency of power generation has become a hot spot of current research. Traditional classification algorithms cannot cope with dynamically changing data streams, so data stream classification techniques are particularly important. The current data stream classification techniques mainly include decision trees, neural networks, Bayesian networks, and other methods, which have been applied to wind power and photovoltaic power data processing in existing research. However, the data drift problem is gradually highlighted due to the dynamic change in data, which significantly impacts the performance of classification algorithms. This paper reviews the latest research on data stream classification technology in wind power and photovoltaic applications. It provides a detailed introduction to the data drift problem in machine learning, which significantly affects algorithm performance. The discussion covers covariate drift, prior probability drift, and concept drift, analyzing their potential impact on the practical deployment of data stream classification methods in wind and photovoltaic power sectors. Finally, by analyzing examples for addressing data drift in energy-system data stream classification, the article highlights the future prospects of data drift research in this field and suggests areas for improvement. Combined with the systematic knowledge of data stream classification techniques and data drift handling presented, it offers valuable insights for future research.

1. Introductions

To address the global warming and climate crisis, humanity has had to reduce the use of fossil fuels and shift towards the development of renewable energy. For instance, considering wind and solar energy, as of 2022, the global installed capacity of wind and solar power has reached 1951.94 GW [1], as shown in the Figure 1. With the development of clean energy power, the amount of data generated in the field of wind and photovoltaic power prediction has shown explosive growth, resulting in massive data streams. How to mine valuable information from the massive data streams is a problem that has received extensive attention [2]. Data streams reflect the real-time information of the data, and compared with traditional classification algorithms, data stream classification has the advantage that the classification model can be continuously adjusted according to the dynamic changes in the data [3]. Classification is an important form of data analysis which predicts the class labels of unknown data from existing data. In traditional classification algorithms, once the classification model is trained, it becomes fixed, and no further adjustments are made. Such a classification model cannot cope with dynamically changing data streams. Data streams are different from traditional static data, which often have the characteristics of unlimited numbers, fast arrival, and concept drift. Therefore, mining knowledge and patterns of interest from data streams requires a brand-new algorithmic framework.

For wind and photovoltaic power generation, to improve the efficiency of power generation, generator sets are often installed in remote suburban areas far from urban centers, resulting in slow detection of generator failures and difficulties in maintaining generator sets. According to statistics, due to manufacturing and installation errors, unit aging, harsh environments, extreme weather, etc., each wind turbine generator set experiences an average downtime of 52 to 237 h per year due to faults, which has a huge impact on the economic and social benefits of wind farms [4]. To ensure the normal operation of wind turbine generators (WTGs) and minimize their downtime, the traditional solution is to create regular inspection plans based on the service life, health condition, and failure probability of WTG components, and then perform regular manual overhauls and maintenance according to these plans. On the one hand, this maintenance method cannot provide timely warnings of turbine failures; on the other hand, it relies heavily on the experience and common sense of the maintenance staff, resulting in an inability to make quick and accurate analyses of turbine failures [5]. A similar problem exists for photovoltaic power generation, seriously hampering its power generation efficiency.

In recent years, the rapid advancement of IoT and big data technologies has enabled the real-time recording and processing of generator operating status indicators through multiple sensors on server clusters. Mining and analyzing massive real-time data to explore the patterns of generator operating status can help to some extent in monitoring the operating status of generators.

In the field of data mining, data stream classification, one of the most important research topics, is crucial for data analysis and pattern recognition, among other purposes. Classification can be applied in various aspects, such as spam filtering, mineral type identification, risk prediction, oil and water layer identification in geology, and so on. Among the many methods used to solve classification problems, each has its advantages and shortcomings. To be precise, no classification algorithm can “perfectly” solve any type of classification problem in all fields. With the development of the big data era, traditional small-sample machine learning methods encountered certain difficulties in dealing with data stream mining tasks. Therefore, algorithms for data stream mining emerged and have been widely used in many fields, including decision trees, neural networks, and Bayesian networks.

With the generation of massive power data, the data drift problem has gained increasing attention in the field of machine learning in recent years and has become one of the main challenges faced by machine learning models in actual production. When the distribution of data changes gradually over time, the distribution of the data to be predicted and the data used for training show obvious shifts, which constitutes the data drift problem. Briefly, data drift can be divided into three categories: covariate drift, prior probability drift, and concept drift. Covariate drift refers to a shift in the data distribution, i.e., the independent variable $P\left(X\right)$ changes and the class distribution does not change, i.e., $P(Y|X)$ remains unchanged; priori probability drift means that the data distribution does not change, i.e., the independent variable $P\left(X\right)$ remains unchanged while the class distribution changes, i.e., $P(Y|X)$ changes; while concept drift means that the relationship between the feature and the target variable is shifted, i.e., the data distribution and the class distribution change at the same time, that is, $P_t\left(X,y\right)\ne P_{t+1}\left(X,y\right),$ and more specific definitions will be noted later.

This paper will introduce the research progress in data stream classification and its application in wind power and photovoltaics in the second part; in the third part, it will introduce the current research status of the data stream drift problem; finally, it will make a summary and provide an outlook on the future development of wind power and photovoltaic data streams.

2. Research on Data Stream Classification Methods and Their Applications

2.1. Data Stream Classification Methods

With the development of the big data era, decision trees, neural networks, and Bayesian networks have become commonly used algorithms for data stream mining tasks.

A decision tree [6,7], used for classification traditionally, forms several branches based on the values of the corresponding attributes of each sample, categorizing similar samples under the same branch. Due to its nonparametric nature, the decision tree is less susceptible to the influence of outliers, capable of managing linearly inseparable data, and offers high performance with relatively low computational requirements. However, it is difficult to process high-dimensional data with it, and it is prone to overfitting. A neural network algorithm [8] simulates the structure of neurons to process information, making it suitable for addressing problems characterized by nonlinear relationships. Conventional algorithms are often constrained by assumptions such as normality, linearity, and variable independence. In contrast, neural networks are more versatile and are capable of capturing a diverse array of relationships. Some of the common neural network algorithms are back-propagation neural networks, probabilistic neural networks, and complementary neural networks. The most commonly used is the first one, but it tends to be slower to train than any of the others and can be problematic in very large networks with large amounts of data. The Bayesian network [9] combines network structure with probabilistic statistics and can be used for uncertainty problems, and it is one of the most classical methods in the field of data mining due to its simplicity, efficiency, and probabilistic expressiveness. However, its structure is complex and less efficient, thus the emergence of the plain Bayesian algorithm [10]. The plain Bayesian algorithm assumes strong independence between child nodes. If this assumption holds, this type of classifier converges faster than discriminative models (e.g., logistic regression) and requires less training time. Unlike neural networks or support vector machines (SVMs), it has no parameters to set, which greatly simplifies the plain Bayesian algorithm. However, in practice, it is often necessary to consider the interactions between attributes, which limits the plain Bayesian network classification algorithm.

Numerous researchers have proposed many more effective improvement algorithms in various directions, such as structure extension, instance weighting, attribute selection, and attribute weighting. The current status of their research is described in detail below.

In terms of structural extensions, the most classical model is the tree-extended plain Bayesian model proposed by Geiger [11] in 1992, which has a more complex structure compared to the plain Bayesian model. Friedman et al. [12] studied the tree-extended plain Bayesian model and then simplified the model based on it to achieve a structural relaxation of the independence assumption. Webb et al. [13] proposed an average one-dependent estimation model, which has the advantage that there is no need to learn the topology between attribute nodes. This model directly treats each attribute node as the parent of the remaining nodes, constructs base classifiers for each attribute, and averages all the base classifiers when calculating the classification accuracy, making the algorithm simpler and more efficient.

In terms of instance weighting, the core of improving classification algorithms for plain Bayesian networks lies in the weighting strategy for the instances [14]. Jiang et al. [15] proposed an instance weighting algorithm known as discriminatively weighted plain Bayes, which improves the plain Bayes algorithm by discriminatively weighting the instances. The algorithm evaluates the weights of the instances using classification accuracy and updates the weights of all instances during each iteration. Cai et al. [16] weighted each training instance based on the similarity between the pattern of the training instances and the rest of the training instances. Classifying the updated set of instances greatly improves the efficiency of the algorithm.

Instance cloning can be considered a special case of instance weighting, where each training instance has a different number of clones. How many clones there are depends on the importance of the instance during classification. Zhang et al. [17] proposed a local plain Bayesian algorithm based on instance cloning. The basis of cloning in the algorithm is the similarity between an instance and the test instances in other neighborhoods, and the classifier is constructed on the set of instances expanded by the clones. The similarity of instances in the algorithm is based on various metric functions and does not change the distribution of classes [18].

In terms of attribute selection, the focus of the improvement of the classification algorithm for plain Bayesian networks is on the methods and metrics for selecting subsets of attributes, i.e., how to find the best subset of attributes over the full set of attributes. One of the most classical is the correlation-based approach to attribute selection (CFS) proposed by Langley and Sage [19]. It uses a forward selection method to select a valid subset of attributes and build a classifier on the subset of attributes. Pazzani [20] used backward elimination methods to aid this so that both efficiency and a better subset of attributes can be obtained. Bidi and Elberrichi [21] used an optimization algorithm based on a genetic algorithm to obtain the optimal subset of attributes; the algorithm was validated on a text dataset and achieved higher accuracy with a smaller-sized subset of attributes selected. Dubey and Saxena [22] proposed a clustering-based filtering algorithm for attribute selection in multiclass high-dimensional datasets. The algorithm uses a K-means clustering algorithm to cluster attributes based on cosine similarity and then applies information gain to the best attributes identified. The algorithm can produce higher classification accuracy with a sufficiently small selection of attributes compared to the original information gain-based filtering method. Chuang et al. [23] proposed a binary particle swarm optimization algorithm improved based on the catfish effect. In this algorithm, when the globally optimal particle cannot be improved within a given number of iterations, 10% of the inferior particles are exchanged with the newly generated particles. Experimental results show that this algorithm performs better than the improved hybrid genetic algorithms (HGAs) based on the genetic algorithm proposed by Oh et al. [24]. Unler et al. [25] proposed a particle swarm algorithm that combines the advantages of filtering and packing methods to achieve better classification results.

In attribute weighting, the core idea of the improvement of plain Bayes is to assign different weights according to the importance of attributes for classification. The focus of the attribute-weighted plain Bayesian network classification algorithm is on the attribute-weighting process. Yan et al. [26] proposed a plain Bayesian model based on attribute bi-weighting, using the Normalized Likelihood Allocation (NLA) algorithm attributes to set weights for attributes automatically; tested the effect of each attribute on different classes of labels; and achieved good classification results in multilabel classification. Wu et al. [27] proposed an attribute weighting algorithm based on a differential evolutionary algorithm. The algorithm takes four parameters, maximum iteration, initial population size, mutation, and crossover probability, as factors to measure the weights and updates the weights continuously until the optimal result is achieved. Jiang et al. [28] introduced deep feature weighting for the plain Bayes algorithm. To some extent, it has weakened the attribute independence assumption of plain Bayes. However, they did not consider the frequency distribution. Taheri et al. [29] proposed a new attribute-weighted plain Bayesian classifier by considering the weights of conditional probabilities. Based on the structure and attribute weights of the plain Bayesian classifier, the objective function is modeled and the optimal weights are determined using a local optimization method.

2.2. Application of Data Stream Classification to Wind and Photovoltaic Power Data

2.2.1. Data Streaming in Wind Power

Through the continuous efforts of researchers in recent years, the data stream diagnostic techniques related to wind turbine faults have become more mature. The state indicators of a wind turbine at work, including physical indicators such as temperature, stress, and torque, and electrical indicators such as current, voltage, and power, can reflect its health to a certain extent. Currently, most of the wind turbine fault monitoring systems that have been put into use were developed based on the vibration signals of wind turbines. Simultaneously, fault diagnosis methods based on electrical indicators such as current and power are also receiving more and more attention because of their good applicability and low transformation costs.

• Fault Diagnosis Based on Electrical Indicators

There are relatively few domestic studies related to wind turbine fault diagnosis based on electrical indicators, while foreign scholars have conducted a large number of exploratory studies in the field of wind and machine fault diagnosis based on electrical indicators. For example, Kia S.H. et al. [30] used model simulation to analyze the correlation characteristics between current signals and gearbox faults of motor drive systems containing gearboxes and verified the results of simulation analysis with experimental data; Stack J.R. et al. [31] achieved a reliable classification of different faults in bearings by detecting prominent changes in current eigenfrequencies or energy changes over a wide frequency range caused by different defective faults; Gong X et al. [32] carried out an effective study on bearing failure on direct-drive wind turbines based on current signals and obtained significant findings.

In recent years, some scholars in China have also begun to use electrical signals to carry out relevant fault diagnosis of electric motors. Lin Tao et al. [33] constructed an optimization neural network fault diagnosis model based on temperature characteristics and used residual analysis of the temperature indexes to obtain the fault state of gearboxes. Liang Tao et al. [34] monitored the working status of wind turbines by calculating the multivariate kurtosis and multivariate skewness indicators of wind turbine power characteristics. Li et al. [35] analyzed the connection between common faults and fault current characteristics of wind turbines and constructed a fault diagnosis model based on current signals.

Wind turbine fault diagnosis based on electrical indicators does not require the installation of additional sensors and can be directly performed on the generator’s current, voltage, and power, making it highly applicable. However, compared to temperature, vibration, and other physical signals, electrical signals contain relatively weak fault information, often obscured by the generator’s inherent electrical fluctuations and environmental noise. Consequently, extracting the electrical signal fault characteristics and other useful information is more difficult. Therefore, how to effectively extract the fault characteristics in electrical signals is also a current research focus.

2.

Fault Diagnosis Based on Vibration Signals

Compared to wind turbine fault diagnosis based on electrical indicators, researchers at home and abroad have focused more on vibration signals as wind turbine status indicators, aimed at realizing early warning and diagnosis of faults by monitoring the vibration state of wind turbines. As the rolling bearings, gearboxes, blades, and other key components of wind turbines rotate smoothly and periodically during operation, periodic, nonsmooth fault impact signals appear when a fault occurs. These signals allow for the extraction of vibration signal features that characterize the operating state of wind turbines.

Foreign researchers have made considerable attempts in fault diagnosis research based on vibration signals. For example, Caesarendra W. et al. [36] proposed a feature extraction method based on the maximum Lyapunov exponent, which effectively monitors the state of low-speed bearings. Tang B. et al. [37] analyzed the vibration signals after noise reduction to construct effective features and used a flow learning algorithm to achieve the diagnosis of early weak faults in wind turbines. Barszcz T. et al. [38] achieved the diagnosis of gearbox fault types by analyzing the spectral cragginess characteristics of faulty impact signals.

Domestic scholars have also conducted a lot of research on the vibration signals of wind turbines in recent years. Liu Qingqing et al. [39] introduced the double-tree complex wavelet transform into the vibration signal analysis of wind turbine gearboxes, and achieved wind turbine fault diagnosis by calculating the cragginess values of the components in each frequency band; Zhang Xizheng et al. [40] used a genetic algorithm to optimize a back-propagation (BP) neural network and a hybrid algorithm to construct a vibration signal-based fault diagnosis model for wind turbine gearboxes; Guo Dongjie et al. [41] used a BP neural network and an improved wavelet transform to extract the feature quantities from some sub-band signals to diagnose and locate the faults of wind turbines, and this method can effectively determine early faults in wind turbines [41].

Based on the current development status of vibration signal-based wind turbine fault diagnosis, more and more scholars at home and abroad have gradually begun to shift from traditional analysis methods to applying machine learning and artificial intelligence technology to fault diagnosis. The corresponding fault features are extracted from the vibration signals; then, machine learning methods are used for feature fusion, dimensionality reduction, classification, and other operations; finally, fault diagnosis is carried out through pattern recognition methods. Although the wind turbine fault diagnosis technology based on vibration signals has become more and more mature, most of the current wind turbine fault diagnosis methods use SAS 9.4, MATLABr2018a, and other analysis software systems to analyze the offline data stored in databases. However, since the working state of wind turbines in the industrial field is dynamic and variable, developing an efficient and stable online monitoring system will be the next research focus to monitor the working state of turbines in a timely and accurate manner.

2.2.2. Data Streaming in Photovoltaics

Over the last decade, the installed capacity of photovoltaic (PV) power generation has continuously broken through new levels, but the information management of PV power stations, especially the construction of station-related data platforms, has been relatively stagnant. As a result, the power generation cost and the operation and maintenance efficiency of PV power stations are also affected, reflecting the imbalance and insufficiency in the development of the photovoltaic industry. Utilizing photovoltaic data resources to research the power generation performance of photovoltaic equipment is an important topic. These tools can comprehensively monitor the equipment’s performance, identify potential issues early on, and prevent ongoing degradation from affecting the power generation quality of the entire branch. At the same time, PV sampling data can be used to study and analyze the characteristics of module power generation performance, as well as the relationship between power generation and environmental parameters, which plays a crucial role in predicting the module power that should be generated, screening the abnormal performance of components, regulating the fluctuation of the power grid, and improving the quality of photovoltaic power, among other topics. By analyzing component monitoring data over a long time scale, we can grasp the performance degradation of the component equipment in the actual-use environment, more accurately assess the health status of the components after different periods of service, and realize early positioning, proactive overhaul, and replacement of the components that have exceeded the normal rate of degradation.

Currently, the fault diagnosis of PV equipment mainly relies on the abnormal alarms of the input and output sides of the inverter and rarely collects data at the component level, with fault judgments based on component-level data being even more scarce. Although collecting data at the component level will increase costs to some extent, it can help to find and specify the cause and location of faults earlier. The alarm rules that come with the inverter are often based on single-point data information, which lack effective horizontal connections between devices and fail to consider vertical trends over time, often leading to false alarms and omissions. By analyzing on-site data from multiple angles to obtain information on the operating status of components, actively collecting equipment data, conducting proactive analysis, and performing active operation and maintenance, the life cycle of the equipment can be extended and the efficiency of PV power plant operation and maintenance can be improved.

Faults in photovoltaic modules are reflected in power data. By identifying abnormal power in sample modules, potential equipment faults can be initially identified. In the study of related methods for module power anomaly detection relying on field sampling data, Shi Xiaobing [42] carried out more work on power anomalies based on module current data. Focusing, on the one hand, on the differentiation of component working conditions, and on the other hand, on abnormal judgment after the subdivision of component data under different working conditions, aiming at the nonlinearity and nonstationarity of the operation process of PV power generation regarding meteorological conditions, we chose to construct a Long Short-Term Memory (LSTM) prediction model to learn and explore the law of change in current measurement point data and realize the prediction of current measurement point data through the law of change. Based on the excellent prediction model, the predicted value is used as a comparison with the actual measurement value of the current measurement point, and the corresponding threshold value is set to realize the early warning of abnormality. However, due to the limitation of the data source, this work did not input environmental parameters to the network and made judgments based only on the component’s current values, which makes the judgments less credible. Iddrisu et al. [43] pointed out that the 3-sigma principle in statistical probability should not be used only as the basis for anomaly judgment and proposed an algorithm for anomalous data recognition based on the probabilistic power curves of copula theory. The method is suitable for the high proportion of PV power anomaly data, and the algorithm can be used to improve the anomaly judgment criteria and the adaptability of power anomaly judgment. Livani et al. [44] proposed an outlier detection method using spectral clustering for anomalous sample detection, providing enlightening insights into the horizontal linkage between device data for anomaly detection in PV module fault diagnosis. Park et al. [45] proposed the use of Generative Adversarial Networks (GANs) to generate virtual samples, thereby improving the strength of the model’s discrimination of anomalous samples. The bearing and train door system were considered to examine the approach’s capabilities. The data acquired for the normal condition are used to train the GAN, the health is monitored over time using the trained GAN indicator, and the anomaly is successfully detected by identifying a decrease at a point in time. It points out another path to improve the accuracy of anomaly detection models. Usually, related research uses existing samples to train a model and tries to expand the richness of the sample set or subdivide the samples and then make the model judgment. Using GAN to form an adversarial approach makes the anomaly detection model no longer rely on a large number of samples, which is a kind of solution to be further studied. Shang Yongjie [46] analyzed the mathematical model of photovoltaic module power generation, compared the prediction effects of multiple methods on module power, and, based on this, carried out outlier detection and corrected the prediction algorithm to further improve the effectiveness of anomaly detection.

In the fault diagnosis of photovoltaic modules, the fault diagnosis method based on power sampling data, which is derived from the relevant methods of photovoltaic power data analysis, is less difficult to realize, the cost of power station renovation is low, and the value of engineering applications is greater. Lina Zhang [47] proposed a novel PV array fault detection and localization method for solar PV arrays, i.e., the global chunk stepwise approximation method. The algorithm is based on matrix processing and deep mining of data to determine whether there is a fault in a PV module by evaluating the voltage fluctuation, which solves the problem of the huge amount of data. The global block step-by-step approximation algorithm is implemented in MATLAB, simulation verification is carried out on large matrix data of 100 × 100, and the simulation results show that the algorithm can effectively detect fault locations. The method is still essentially outlier detection for power anomaly screening of single-point data, and the discriminative power is low. Pataru et al. [48] proposed a PV array fault diagnosis method using the fast oversampling principal component analysis (OS-PCA) algorithm for detecting and identifying component shadow shading, short-circuit, and disconnection faults in PV arrays. By detecting the current signal of each string, the fast OS-PCA algorithm is used to calculate the anomaly degree of each string, to detect the faulty string; the photovoltaic array engineering model is optimized through the error compensation, and the fault type is identified by analyzing the state of the working point of the array at the time of the fault. The method proposed in this study is based on group string data signaling and does not go deeper into component-level device information. Yan Tianyi [49] designed and realized a system platform for online monitoring and fault diagnosis, which details the system construction, photovoltaic data monitoring methods, inter-module communication methods, etc., but does not elaborate on the methods of fault judgment.

With the development of big data algorithms, research on data stream fault diagnosis based on clustering algorithms [50], data expansion algorithms [51], etc., has been continuously proposed by scholars, making increasing contributions to PV fault diagnosis.

3. Functions for Various Drifts in the Data Stream and Their Forms

First and foremost, it is necessary to clarify that, in this paper, the phenomenon of model performance degradation caused by the time-varying nature of data’s statistical properties in data stream classification problems will be uniformly referred to as data drift. The types of data drift include concept drift, covariate drift, and prior probability drift. From a definitional perspective, the latter two can be considered as specialized cases of concept drift. Therefore, this section will first clarify the concept of data drift and then provide a detailed introduction to concept drift, with a focused analysis of concept drift issues in data stream classification research within energy systems.

3.1. Covariate Drift

Covariate drift is also known as virtual concept drift in some studies, and this definition was first proposed by Shimodaira [52] in 2000, which focuses on the variation in the input quantity, $x$. However, there is some confusion in the definition of this concept in some earlier studies, and so combining the combing and summarizing of definitions by Jose [53], the definition of covariate drift in this paper is shown in Figure 2.

Firstly, covariate drift refers specifically to the change from X to Y. Suppose a mapping $\mathit{y}=\mathit{f}\left(\mathit{x}\right)$. When covariate drift occurs, $\mathit{f}$ in the mapping $\mathit{y}=\mathit{f}\left(\mathit{x}\right)$ does not change (see the curve in Figure 2), which suggests that ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}(\mathit{Y}|\mathit{X})={\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}(\mathit{Y}|\mathit{X})$ is invariant. But ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}\left(\mathit{X}\right)\ne {\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{X}\right)$ changed significantly, and, ideally, since the mapping did not change, our model would still make correct predictions; for example, the model in the left-hand side of Figure 2 makes exactly the right classification predictions in the right-hand side of Figure 2, the triangles and circles in the figure means different classification and the white and black color represents the new data after covariate drift.

But the reality is more complex, and this drift can be interpreted as a “difference in emphasis”. In this example, our training input distribution, ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}\left(\mathit{X}\right)$, is relatively broad-spectrum, while the test input distribution is restricted to a specific domain, ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{X}\right)$. When a model trained for a general domain is applied to a specific domain, the test accuracy tends to drop. Alternatively, in some cases, the dataset used for training is relatively limited, so that the algorithm learns incomplete or erroneous decision boundaries, and performance degradation occurs when it is applied to a domain with a wider coverage. Unlike concept drift, however, covariate drift can be addressed by improving the model generalization capabilities.

3.2. Prior Probability Drift

A prior probability drift refers to a change in Y representing the category variable, which in past studies is generally referred to as a change in the class distribution and specifically refers to a change in the category Y concerning the input X, combined with a summary of the definitions of this concept by Quiñonero-Candela [54]. In this paper, the definition of prior probability drift is as follows:

For a mapping, $\mathit{y}=\mathit{f}\left(\mathit{x}\right)$, a causal model of the form $\mathit{P} \left(\mathit{X},\mathit{Y}\right)$ is assumed to be valid, which can be decomposed into $\mathit{P} \left(\mathit{X},\mathit{Y}\right)=\mathit{P} (\mathit{X}|\mathit{Y})\mathit{P}\left(\mathit{Y}\right)$ according to Bayes’ law. When prior probability drift occurs, ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}(\mathit{X}|\mathit{Y})={\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}(\mathit{X}|\mathit{Y})$ is invariant, which means that the dots representing the data distribution in the plot are unchanged but the f in the mapping changes, which is ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}\left(\mathit{Y}\right)\ne {\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$ (the curve in the figure), and changes significantly.

This type of drift can lead to degradation in model performance when it occurs, but it is easier to correct, as it is assumed that ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}(\mathit{X}|\mathit{Y})={\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}(\mathit{X}|\mathit{Y})$ is unchanged, just that ${\mathit{P}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}}\left(\mathit{Y}\right)$ fails, and therefore the model can be corrected for drift by using the known class distribution, ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$, of the test input instead. However, the class distribution of the test input is not known in all cases, and when ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$ is unknown, the solution to prior probability drift is a little more complicated. One can first determine the prior distribution of the valid ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$ and then compute the posterior distribution of ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$ based on the covariates in the given model, $\mathit{P} (\mathit{X}|\mathit{Y})$, and test data. The target of the prediction is then given by calculating the sum of the predictions obtained by weighting each ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$ with the posterior probability of ${\mathit{P}}^{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathit{Y}\right)$.

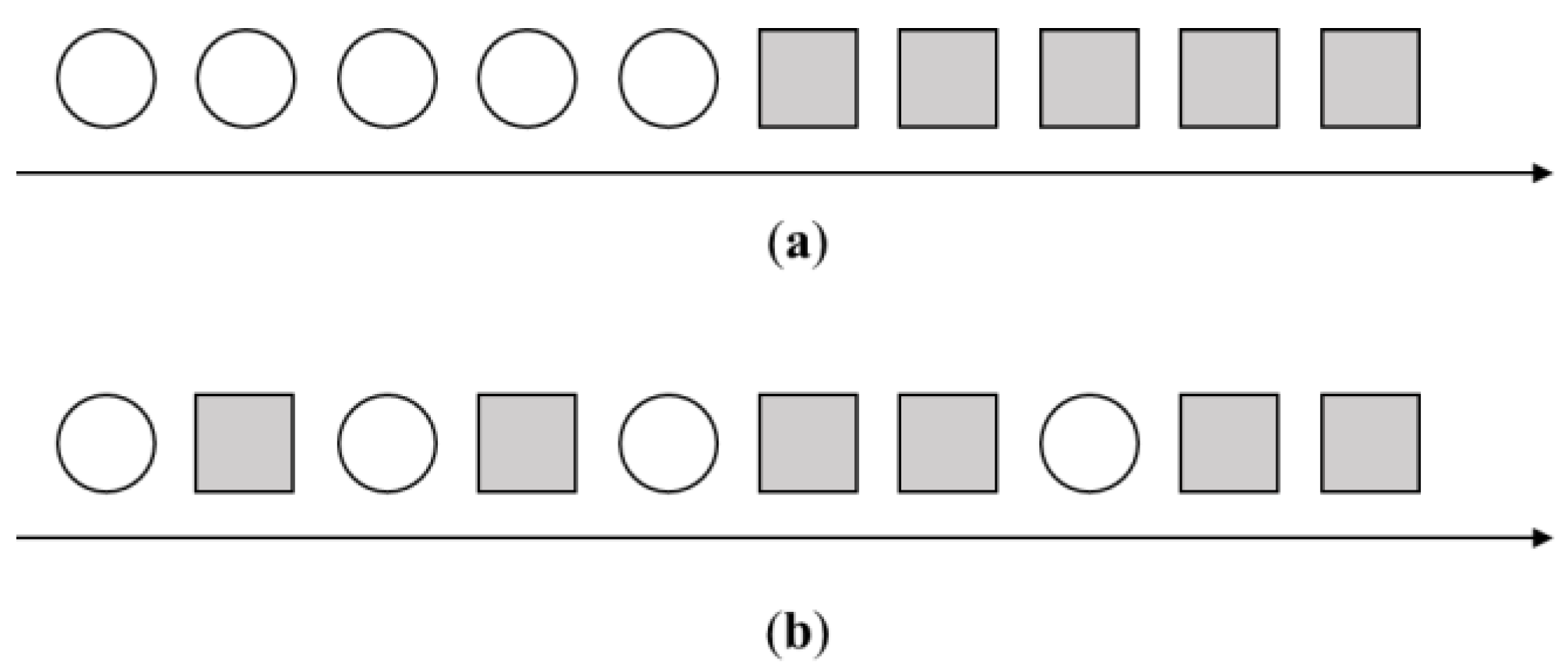
3.3. Concept Drift

Concept drift is a phenomenon of data variation where the statistical properties of the target domain change over time in an arbitrary manner, deviating from the source domain data in a non-negligible way. It was originally proposed by Schlimmer et al. [55] to highlight changes in noisy data over time in incremental learning. Liu [56] has shown that concept drift may be caused by changes in hidden variables that cannot be measured directly. Formally, concept drift is defined as Figure 3:

For a given time period, [0, t], there is a set of samples, denoted as ${\mathit{S}}_{\mathbf{0},\mathit{t}}=\{{\mathit{d}}_{\mathbf{0}},\dots ,{\mathit{d}}_{\mathit{i}},\dots ,{\mathit{d}}_{\mathit{t}}\}$, where ${\mathit{d}}_{\mathit{i}}=\left({\mathit{X}}_{\mathit{i}},{\mathit{y}}_{\mathit{i}}\right)$ is an observation (or an instance of the data), ${\mathit{X}}_{\mathit{i}}$ is the feature vector, $y_i$ is the label, and $S_{0,t}$ follows the determined distribution ${\mathit{F}}_{\mathbf{0},\mathit{t}}\left(\mathit{X},\mathit{y}\right)$. Concept drift occurs at time $\mathit{t}+\mathbf{1}$; then, ${\mathit{F}}_{\mathbf{0},\mathit{t}}\left(\mathit{X},\mathit{y}\right)\ne {\mathit{F}}_{\mathit{t}+\mathbf{1},\mathbf{\infty }}\left(\mathit{X},\mathit{y}\right)$, that is, $\exists \mathit{t}:{\mathit{P}}_{\mathit{t}}\left(\mathit{X},\mathit{y}\right)\ne {\mathit{P}}_{\mathit{t}+\mathbf{1}}\left(\mathit{X},\mathit{y}\right)$.

3.3.1. Different Forms of Concept Drift

Considering the characteristics of power streaming data, this section describes three forms of concept drift: label drift, feature drift, and instance drift.

• Label drift

Considering the consistency of data distribution between the training set and the test set, the labeled data used for defect prediction face a severe class imbalance problem, i.e., ${\displaystyle \frac{{\mathit{y}}_{\mathit{d}\mathit{e}\mathit{f}\mathit{e}\mathit{c}\mathit{t}}}{\left({\mathit{y}}_{\mathit{c}\mathit{l}\mathit{e}\mathit{a}\mathit{n}}+{\mathit{y}}_{\mathit{d}\mathit{e}\mathit{f}\mathit{e}\mathit{c}\mathit{t}}\right)}}\ne {\displaystyle \frac{{\mathit{y}}_{\mathit{c}\mathit{l}\mathit{e}\mathit{a}\mathit{n}}}{\left({\mathit{y}}_{\mathit{c}\mathit{l}\mathit{e}\mathit{a}\mathit{n}}+{\mathit{y}}_{\mathit{d}\mathit{e}\mathit{f}\mathit{e}\mathit{c}\mathit{t}}\right)}}$ [57]. Class-imbalanced labeled data can make the trained defect model gain more knowledge about the majority class while ignoring the minority class. Data instances in the minority class are often the objects of interest for practitioners, such as defect modules in software projects. This may cause the defect model to produce false alarms when judging potential defect modules. Considering the data distribution of the training set and test set for cross-version defect prediction, if their prior probabilities can be obtained by $\mathit{P}\left(\mathit{y}\right){\displaystyle \frac{{\mathit{y}}_{\mathit{d}\mathit{e}\mathit{f}\mathit{e}\mathit{c}\mathit{t}}}{\left({\mathit{y}}_{\mathit{c}\mathit{l}\mathit{e}\mathit{a}\mathit{n}}+{\mathit{y}}_{\mathit{d}\mathit{e}\mathit{f}\mathit{e}\mathit{c}\mathit{t}}\right)}}$, then label drift can be expressed as ${\mathit{P}}_{{\mathit{D}}_{\mathit{i}}}\left(\mathit{y}\right)\ne {\mathit{P}}_{{\mathit{D}}_{\mathit{i}+\mathbf{1}}}\left(\mathit{y}\right)$. Label drift will cause a deviation between the knowledge learned by machine learning in the source domain and the knowledge information of the target domain [58]. In a past study, Zhang et al. [59] calculated label drift as shown in the formula below:

$$\mathit{\varphi }\left({\mathbf{y}}_{\mathbf{i}}+{\mathbf{y}}_{\mathbf{i}+\mathbf{1}}\right)={\displaystyle \frac{{{\displaystyle \sum }}_{\mathbf{k}}\mathbf{m}\mathbf{i}\mathbf{n}\left({\mathbf{n}}_{\mathbf{i}}\left({\mathbf{y}}_{\mathbf{k}}\right),{\mathbf{n}}_{\mathbf{i}+\mathbf{1}}\left({\mathbf{y}}_{\mathbf{k}}\right)\right)}{\mathbf{n}}},{\mathbf{y}}_{\mathbf{k}}\in \left({\mathbf{y}}_{\mathbf{i}}{\displaystyle \cap }{\mathbf{y}}_{\mathbf{i}+\mathbf{1}}\right)$$

where ${\mathbf{n}}_{\mathbf{i}}\left({\mathbf{y}}_{\mathbf{k}}\right)$ denotes the number of instances labeled ${\mathit{y}}_{\mathit{k}}$ in ${\mathit{S}}_{\mathit{i}}$, $\mathit{k}$ denotes the number of categories of ${\mathbf{y}}_{\mathbf{i}}{\displaystyle \cap }{\mathbf{y}}_{\mathbf{i}+\mathbf{1}}$, and $n$ denotes the number of instances in ${\mathit{S}}_{\mathit{i}}$. This method is suitable for label drift detection between two data blocks in streaming data.

2.

Feature Drift

From a feature perspective, feature drift is caused by changes in code attributes, such as the number of lines of code, cyclomatic complexity, and the number of branching paths. These changes alter the correlations between feature variables and response variables, making them hidden and difficult to detect. If a feature variable has a strong correlation with the response variable, it contributes more significantly to defect predictions. Figure 4 provides a visual representation of the change in the importance of feature variables between versions, with the thickness of the stripes indicating their importance. This figure clearly shows the change in the importance of the variables between versions. Tsymbal et al. [60] pointed out that even if concept drift occurs in the entire dataset, some regions of the feature space remain stable longer than others.

Feature-based concept drift detection is a common approach in previous studies. For example, Alippi et al. [61] proposed a real-time adaptive classifier based on feature changes to detect data drift. Yu [62] addressed concept drift in each feature variable using the Kolmogorov–Smirnov (KS) test in the case of relatively few true labels. Zhang et al. [59] calculated feature drift by evaluating the contribution of feature variables to labels to detect whether there is a significant change between historical and new data blocks as shown in the Equation below:

$$\mathit{\varphi }\left(\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}}},\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}+\mathbf{1}}}\right)=\mathit{J}\mathit{a}\mathit{c}\left(\overrightarrow{{\mathit{F}}_{\mathit{i}}},\overrightarrow{{\mathit{F}}_{\mathit{i}+\mathbf{1}}}\right)={\displaystyle \frac{\overrightarrow{{\mathit{F}}_{\mathit{i}}}{\displaystyle \cap }\overrightarrow{{\mathit{F}}_{\mathit{i}+\mathbf{1}}}}{\overrightarrow{{\mathit{F}}_{\mathit{i}}}{\displaystyle \cup }\overrightarrow{{\mathit{F}}_{\mathit{i}+\mathbf{1}}}}}$$

where $\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}}}$ denotes the eigenvector of ${\mathit{X}}_{\mathit{i}}$ and $\overrightarrow{{\mathit{F}}_{\mathit{i}}}$ denotes the eigenvector reconstructed by $\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}}}$ according to specific conditions. When $\mathit{\varphi }\left(\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}}},\overrightarrow{\mathit{I}{\mathit{V}}_{\mathit{i}+\mathbf{1}}}\right)$ is smaller than the set threshold, it can be considered that feature drift occurs because of a significant change in the importance of the feature variables related to the categorization in the two data blocks.

3.

Instance Drift

Figure 4b shows an example of the change in the distribution of defective instances for any two versions of a particular project, with triangles and circles representing different categories of instances. Instance drift is a more granular type of data drift than feature drift. Instance drift is more difficult to detect because individual data instances do not carry enough information to infer the overall distribution.

Data distribution-based drift detection methods can directly quantify the severity of concept drift. Such algorithms use a distance function or metric to quantify the dissimilarity between historical and new data distributions. For example, Dasu et al. [63] designed a drift detection technique using Kullback–Leibler divergence (relative entropy). Lu et al. [64] proposed an empirical distance based on competency to represent the difference between two data samples. Kifer et al. [65] used a relaxation of the total variation distance to measure the difference between two data distributions. In addition, locating concept drift regions facilitates drift adaptation. Lu et al. [64] showed that identifying drift regions helps to identify outdated data that conflict with the current concept. Lu et al. [66] solved the concept drift problem by eliminating conflicting instances. Local Drift Degree-based Density Synchronized Drift Adaptation (LDD-DSDA) [56] utilizes drift regions as an instance selection strategy to construct a training set that continuously tracks new concepts. When concept drift is detected, conflicting instances are removed from the instance pool.

Many previous studies have used online error rates to detect whether a new instance of data is a conflicting instance. Gama et al. [67] proposed the Drift Detection Method (DDM) to identify significant increases in the overall online error rate within a time window. Herbold et al. [68] also used the online error rates of nodes within the decision tree to detect drift data in localized regions of the instance space. Because this approach focuses on the accuracy of the learner, it cannot directly measure the severity of instance drift. However, the degree of learning accuracy degradation can be used as an indirect measure to indicate the severity of concept drift.

To clarify the extent of instance drift between versions, the two principles for detecting redundant instances described above (distance-based and error-rate-based) are used to identify unordered instances in data. When the classifier error rate decreases (i.e., accuracy increases) after the detector removes an instance from the training set, the instance is confirmed to be a conflicting instance. On the contrary, it is not. From this, instance drift ($ID$) is obtained by the following equation.

$$\mathit{I}\mathit{D}={\displaystyle \frac{\mathit{c}\mathit{o}\mathit{n}\mathit{f}\mathit{l}\mathit{i}\mathit{c}\mathit{t} \mathit{i}\mathit{n}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{c}\mathit{e}\mathit{s}}{\mathit{a}\mathit{l}\mathit{l} \mathit{i}\mathit{n}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{c}\mathit{e}\mathit{s}}}\times \mathbf{100}\%$$

where $ID$ indicates the membership of the defect data from the historical version to the new version. For example, there is a historical version containing 200 instances of defects, 12 of which have a membership probability less than the threshold in the new version of the data distribution, so their ID = 12/200 = 6%.

3.3.2. Concept Drift over Different Time Intervals

In data stream classification, due to the large volume of data, the space capacity required to store the data is far beyond the capacity of the memory; to enable the algorithm to be able to deal with massive data, the sliding window mechanism is generally used, that is, each time only one or several blocks of data are input to the system, only the current window of the block of data processing is completed before starting to deal with the next window of the block of data.

Let the data in the sliding window at time t, which has been trained to obtain the target concept, be M. After time $\Delta t$, the sliding window is trained again using the data to obtain the concept N. If M ≠ N, the data stream is said to have undergone concept drift. As shown in Figure 5, concept drift can be categorized into two types according to $\Delta t$: when $\Delta t$ is short, the concept drift that occurs is called abrupt concept drift, and when $\Delta t$ is long, the concept drift that occurs is called gradual concept drift.

After the occurrence of concept drift, the distribution of data within the sliding window is changed; at this time, the performance of the classifier will decline, and if no corresponding measures are taken, the error rate of the classification results will continue to rise. How to more effectively detect concept drift and take certain measures to better cope with concept drift is an urgent problem that needs to be solved in data stream classification.

3.3.3. Concept Drift Detection Methods

Considering the different characteristics of detection algorithms, four different classes of concept drift detection algorithms are presented in this section: error rate-based concept drift detection methods; window-based concept drift detection methods; data distribution-based concept drift detection methods; and multiple hypothesis testing drift detection methods.

• Error Rate-based Concept Drift Detection Method

The error rate-based concept drift detection method is the largest and most widely used of the detection methods, generating a concept drift alarm by detecting the error rate of the recorded online base learner when the obtained change in the error rate is statistically significant. The most famous error rate-based detection method is the concept drift detection method (DDM) proposed by Gama [67]. It is the first algorithm proposed to categorize concept drift alarms into warning levels as well as drift levels. The DDM maintains the error rate of the base classifier and uses the mean and variance of the error rate as statistics for detection. A warning occurs when the value of the quantity is greater than the warning level, and if it continues to increase above the drift level, a concept drift signal is generated. The method works well for abrupt concept drift but is not very sensitive to gradual concept drift, and the DDM has a strong dependence on the performance of the classifier. The Early Concept Drift Detection Method (EDDM) proposed by Baena-Garc et al. [69] is similar to DDM, using warnings as well as a drift level mechanism. The method uses the distance error rate instead of the classifier error rate. The main difference between the two is that EDDM provides good accuracy compared to DDM when both abrupt concept drift, as well as gradual concept drift, occurs. Another method is the Exponentially weighted moving average charts (EWMA) for Concept Drift Detection (ECDD) algorithm proposed by Ross et al. [70] In ECDD, probabilities are computed online and the probability of success or failure is found. The base learner uses training examples to determine the initial classification accuracy, and the estimator detects the expected time between two false-positive samples. ECDD is more suitable for detecting gradual concept drift than sudden concept drift. The Reactive Drift Detection Method (RDDM) proposed by Barros et al. [71] is based on the DDM with some modifications, such as discarding old instances of very long concepts to detect drifts as early as possible. This improves the accuracy of the classifier and increases the sensitivity to detecting progressive concept drifts. A variant of RDDM is the Fuzzy Windowing Drift Detection Method (FW-DDM) [72], which is based on the fuzzy windowing mechanism used for concept drift detection, which identifies examples from different concepts more accurately by sliding the window and including overlapping windows, and detects noise by checking how accurately the instances are represented in both the old concepts and the current concept to detect noise and treating it as noise if the accuracy of both concepts is degraded. Similar error-rate based methods include Heoffding’s inequality-based Drift Detection Method (HDDM) [73], Learning with Local Drift Detection (LLDD) [74], and Dynamic Extreme Learning Machine (DELM) [75], among others.

2.

Window-based Concept Drift Detection Methods

Window-based concept drift detection methods typically maintain two windows of data instances, the first for storing old instances and the second for storing new instances of the data stream. The comparison between these two window instances reacts to changes in the data distribution and signals drift. The window size can be fixed or adaptive; a fixed window means that it has the same size for the entire analysis, while an adaptive window adjusts its size according to drift conditions, shrinking if drift is detected and enlarging if there is no drift condition. The best-known algorithm is the Adaptive Sliding Window Algorithm (ADWIN) proposed by Bifet [76]. It can adaptively adjust the size of the window according to the distribution of the data, and the window size is dynamically increased or decreased based on whether there is no change or a change in the distribution of the data, and a drift alarm occurs when the difference in the average distribution of two consecutive windows is more significant than a predefined threshold. In addition, ADWIN performs well in drift detection because it limits the false-alarm and miss rates. The limitation of ADWIN is that it is only suitable for one-dimensional data, and for multidimensional data it requires window maintenance for each latitude, which requires a lot of time and memory. Bifet et al. [76] proposed a modified version of ADWIN that requires less time and memory. The One-Class Drift Detector (OCDD) proposed by Can et al. [77] is one of the implicit concept drift detectors based on the sliding window mechanism. It approximates the distribution of new concepts, categorizes samples, and estimates whether they belong to the current distribution or are outliers. The percentage of outliers is calculated in real time, and a sliding window uses the percentage of outliers to determine if concept drift has occurred. It can work with any classifier that does not have a drift adaptation mechanism. Another window-based drift detector is Paired Learners (PL), proposed by Bach [78]. It uses two base learners: stable and reactive. The stabilizing learner trains based on previous instances and predicts new instances. The reactive learner learns recent instances and predicts instances in the current window. It uses the difference in accuracy between these two learners to detect concept drift. Other window-based drift detection algorithms are Statistical Test of Equal Proportions Detection (STEPD) [79], the Fast Hoeffding Drift Detection Method (FHDDM) [80], and the Group Drift Detection Method (GDDM) [81], among others.

3.

Concept Drift Detection Method based on Data Distribution

Concept drift detection algorithms based on data distributions achieve concept drift detection by comparing the differences between old or historical data and current data instances. These types of methods are often used in conjunction with window-based methods and analyze statistical significance, where the computation of changes in data distribution yields information about where the drift occurred.

The hybrid forest algorithm proposed by Rad [82] focuses on random forests using Hovdean trees. The method is divided into three phases: in the first phase, a data frame is created to obtain multiple features; in the second phase, a weak learner is generated and learns using some of the features; in the third phase, all the learners are run at the same time. At the end, there is a combining phase to compute the final result, and based on the result of the computation, it is decided whether concept drift has occurred or not. Another typical method is the Information-Theoretic Approach (ITA) proposed by Dasu [63]. The basic idea of the algorithm is to use a k-d tree to partition the old data as well as the new data into a series of boxes. Then, Kullback–Leibler (KL) divergence scattering is used to compute the distinctiveness of the densities in each box, and hypothesis testing on the distinctiveness is finally used to determine whether concept drift has occurred. Similar distribution-based detection algorithms are available Statistical Change Detection (SCD) [83], Competence Model-based drift detection (CM) [66], Equal Density Estimation (EDE), and Local Drift Degree-based Density Synchronized Drift Adaptation (LDD-DSDA) [56].

4.

Multiple Hypothesis Testing Drift Detection Methods

The multiple hypothesis testing detection method uses similar algorithms to the previous three methods. The algorithm is characterized by its use of multiple hypothesis testing to detect concept drift from different paths, i.e., after the algorithm detects data drift, it uses parallel or hierarchical multiple hypothesis testing to repeatedly test the detection results to ensure statistical significance. Compared with the classical detection methods, the multiple hypothesis testing method enhances the reliability and stability of the detection results. Just-In-Time adaptive classifiers (JIT) proposed by Alippi [84] was the first algorithm to apply multiple hypothesis testing methods to detection methods. The algorithm extends the Cumulative Sum (CUSUM) table to detect average changes in the learning system’s features of interest by setting up four parallel constructs of hypothesis tests. A similar strategy is used in Linear Four Rate drift detection (LFR) [85], proposed by Wang. Similarly, a three-tier drift detection algorithm based on Information Value and Jaccard similarity (IV-Jac) [59] was proposed by Zhang. Ensemble of Detectors (e-Detector) [86], the Drift Detection Ensemble (DDE) [87], and the Hierarchical Change-Detection Tests (HCDTs) [88] proposed by Boracch are different from the above algorithms. The innovative use of a strategy employing layered multiple hypothesis testing divides the algorithm into a detection layer and a validation layer, where the detection layer is the existing detection method and the validation layer is an additional hypothesis testing method by which a secondary test for drift is performed. Similarly, the Hierarchical Linear Four Rate (HLFR) [89] proposed by Yu is based on the LFR method proposed above with additional detection layers. In addition, there are Two-Stage Multivariate Shift-Detection based on EWMA [90], Hierarchical Hypothesis Testing with Classification Uncertainty (HHT-CU) [62], and other methods that also use multiple hypothesis testing.

So far, a very large number of concept drift detection methods have appeared at home and abroad as shown in the

Table 1. Summary of drift detection algorithms.

Category	Algorithms
Error rate-based	DDM [67]
	EDDM [69]
	ECDD [70]
	RDDM [71]
	FW-DDM [72]
	HDDM [73]
	LLDD [74]
	DELM [75]
Window-based	ADWIN [76]
	OCDD [77]
	PL [78]
	STEPD [79]
	FHDDM [80]
	GDDM [81]
Data distribution-based	ITA [63]
	SCD [84]
	CM [56]
	EDE [91]
	LDD-DSDA [66]
Multiple hypothesis testing	JIT [84]
	LFR [85]
	IV-Jac [59]
	e-Detector [86]
	DDE [87]
	HCDTs [87]
	HLFR [89]
	HHT-CU [62]

. The concept drift detection algorithm based on the error rate has wider applicability and easily deals with multidimensional data, the complexity of the algorithm is generally lower, and it is easier to meet the real-time requirements of streaming data; the detection approach based on a window is based on recent data and does not rely on a learner, but it is more complex for the processing of high-dimensional data; detection based on the distribution of data algorithms starts from the data, mining the data for statistical information or changes in distribution; detection algorithms for multiple hypothesis testing increase the statistical significance of drift results by improving the hypothesis testing method based on existing algorithms but also increase the complexity of the algorithm.

3.3.4. Model Updating Strategies for Addressing Conceptual Drift

When a detection algorithm detects the occurrence of concept drift and issues an alert, the algorithm needs to update the existing model to accommodate the new concept to ensure the performance and accuracy of the learning model. There are generally three broad strategies for updating models: retraining a new learning model to replace the old one; modifying the old model; and fusing multiple old models to construct a new one.

The typical update strategy of retraining a new model to replace the old one is used in the PL algorithm [78] proposed by Stephe. The method pairs a stabilizing online learner with a reactive online learner, where the stabilizing learner makes predictions based on all of its experience and the reactive learner makes predictions based on its experience in a recent short-term time window. The method works by comparing the accuracy of the two learners in the most recent short-term time window; the reactive learner will perform better when concept drift occurs, and when the difference in accuracy reaches a threshold, the stabilizing learner will be replaced based on the target concepts in the reactive learner, and the new stabilizing learner will make predictions based on all its experience from the time of replacement.

A similar scheme is used in the ADWIN [76], but it is optimized in the selection of the window, which is no longer the fixed-size window determined a priori in the old methods, the window size being determined by adaptive computation based on the observed rate of change in the data in the window, and the window grows automatically when the data are stationary and stable to improve the accuracy and shortens when the data change to discard obsolete data. There are also a series of algorithms such as DELM [75] and JIT [84] that follow this update strategy.

Compared to retraining a new model, adaptively adjusting a model to update relevant parts of the functionality in response to changes in the data distribution is a more effective model update strategy when localized data drift occurs. However, this approach is limited to the algorithm used to learn the model itself, requiring the algorithm itself to be able to examine and adapt to each data subregion individually, and, in general, models based on decision tree algorithms can apply this strategy. The Concept-adapting Very Fast Decision Tree (CVFDT) [92] is based on the Very Fast Decision Tree (VFDT) [93]. It has the ability to learn decision trees in high-speed time-varying data streams: when the drift substance occurs and the performance of the old subtree begins to decline, CVFDT generates a spare subtree; when the accuracy of the new subtree is greater than that of the old subtree, it will replace the subtree, and the original outdated subtree will be pruned, so that the algorithm’s instantaneity can be guaranteed while making full use of the old data. Similar decision tree-based algorithms include the Extremely Fast Decision Tree [94], the concept-adapting evolutionary algorithm for decision trees (CEVDT) [95], and the Uncertainty-handling and Concept-adapting Very Fast Decision Tree (UCVFDT) [96].

The update strategy of reusing and aggregating old models can update a model more cost-effectively and efficiently in response to recurring concept drift. The Dynamic Weighted Majority (DWM) [97] proposed by Jeremy is a collection of base learners, each of which is a learning algorithm and each of which has an associated weight of its own. Given an instance, each base learner gives a prediction, and, combined with their respective weights, DWM gives a global prediction. The weighted majority vote of these base learners is reused for prediction, and base learners are dynamically created and removed based on changes in algorithm performance. When the algorithm’s global prediction is wrong, a new learner is added to the set. When the prediction of a base learner is wrong, the DWM down-weights that learner. If it is wrong multiple times and its weight falls below a set threshold, the base learner is deleted. However, in this algorithm, there is only a setting for down-weighting and no setting for up-weighting. A base learner will not be activated again after it is eliminated, and it lacks the consideration of its usage time and prediction history. The Learn++.NSE method [98] proposed by Ryan determines the weight of each classifier’s vote based on its time-adjusted accuracy in the current versus the past environment. For each new batch of data received, the algorithm creates a new classifier and integrates it into the existing set. It then dynamically adjusts the weights based on the performance of the classifiers on recent and past data. Poorly performing classifiers are given a lower weight and are temporarily deactivated when their weights fall below a set threshold. The algorithm does not discard such classifiers altogether; they still participate in each round of prediction. If the deactivated classifiers become relevant and effective again at some time in the future, their weights are increased and they are reactivated. Such a design allows the algorithm to retain historically learned knowledge, enabling it to adapt more efficiently to concept drifts that may recur or change periodically. Over time, however, the accumulation of the number of classifiers in the ensemble can lead to significant consumption of memory and computational resources.

In addition to this, in a recent study, the online Gaussian Mixture Model with a Noise Filter For Handling Virtual and Real Concept Drifts (OGMMF-VRD) [99] proposed by Gustavo considers the impact of the addition of a noise filter on the adaptation and prediction performance of the model with respect to the decision boundary learned by the classifier over time. OGMMF-VRD takes into account the impact of real and virtual drifts on the adaptation and prediction performance of the decision boundaries learned by the classifiers over time and adds a noise filter to avoid model adaptation to problematic observations, and the algorithm keeps all the old Gaussian Mixture Models in a pool, allowing the system to be invoked to select the optimal classifier. The reference of the pool in this method makes it more efficient to utilize the historically learned knowledge than the traditional nonensemble models, and the robustness to virtual warnings of drift detection caused by noisy samples is greater than that of the ensemble models. However, since it is based on a single classifier, it has limitations in terms of performance.

In general, there are various model updating strategies used to cope with concept drift in existing research: retraining new models is the most universal strategy and can be applied to all models; the adaptive modeling strategy can adapt well to concept drift caused by changes in data distribution, but it can only be applied to models based on specific algorithms that can individually check the adaptation to subregions of the data, such as decision trees; the strategy of reusing and aggregating old models has a higher efficiency in dealing with recurring or periodically changing models.

3.4. The Issue of Concept Drift in Data Stream Classification Research within Energy Systems

In energy systems, the data streams from photovoltaic and wind power generation exhibit significant uncertainty due to time-varying environmental conditions and equipment aging. This uncertainty can lead to frequent changes in data distribution, resulting in the problem of concept drift. This uncertainty can lead to frequent changes in data distribution, affecting the mapping relationship between environmental factors and output results, thereby causing the problem of concept drift. With the rapid development of renewable energy, data stream classification methods have been widely applied in the field of energy systems. However, as shown in Section 2, much of the past research has focused solely on the static optimization of algorithms themselves, often overlooking the issue of algorithm performance degradation caused by concept drift in practical applications. However, some recent studies have begun to address this issue. Severiano et al. [100] proposed a new evolving Multivariate Fuzzy Time Series (e-MVFTS) model, which integrates the evolving mechanism of Typicality and Eccentricity Data Analytics (TEDA) into the fuzzy representation of time series used in the FTS model. This integration allows for dynamic adjustment of the fuzzy set definition and the range of membership functions, effectively addressing spatiotemporal information and uncertainty scenarios. The model adapts to changes in data distribution through online updates, effectively handling multivariate high-dimensional data. It has been validated in forecasting tasks for solar and wind energy, demonstrating improved prediction accuracy in renewable energy systems. However, the model’s performance heavily depends on the parameter settings of the clustering algorithm and fuzzy logic. Additionally, in extreme cases where severe concept drift occurs suddenly, the algorithm may fail to promptly eliminate incorrect sets and rules, lacking the necessary pruning mechanism. Zhang et al. [101] proposed a photovoltaic power forecasting model based on LSTM, which employs the traditional DDM method for drift detection. The model uses an orthogonal weight modification approach for the progressive dynamic adjustment of model weights to adapt to new data distributions. This method ensures model stability while avoiding overfitting to historical data. However, as mentioned earlier, DDM is a relatively rudimentary method that is not sensitive to gradual concept drift, and its performance is highly dependent on parameter settings and the classifier’s performance. Improved methods based on DDM, such as EDDM and RDDM, have shown better performance in drift detection. Li et al. [102] proposed the Drift Detection and Adaptation–Light Gradient Boosting Machine (DDA-LightGBM) model for short-term wind power forecasting. The method mainly consists of three steps: extracting sample-related and sequence-related features from weather data, clustering the data based on the extracted features, and developing a new power forecasting model with automatic drift detection and adaptation capabilities for each cluster. For drift detection and adaptation, the study primarily employs a sliding window detection method to identify drift. In terms of the update strategy, the LightGBM model supports incremental learning, allowing the model to be partially updated based on new data following a drift occurrence. This approach helps to reduce the consumption of computational resources. Although the article concludes by demonstrating through the comparison of prediction results in the test set that this method can address the concept drift problem and effectively improve the model’s forecasting performance, several issues remain. The parameters related to the drift detection algorithm and model update strategy in the model, such as the sliding window size, the maximum cache window size, and the sampling rate, are fixed values that have been specifically optimized for particular clusters. These values offer significant performance advantages only in specific scenarios and lack generalizability. If adaptive methods like ADWIN, OCDD, and PL, which can automatically adjust model parameters, were employed, the generalizability of the model presented in this article could be greatly enhanced. There are many other studies related to the concept drift problem in the classification of data streams in energy systems. For instance, Cabello et al. [103] compared the performance impacts of three different drift detection methods—ADWIN, KSWIN, and others—on a linear regression detection model under various parameter settings. Their work successfully demonstrated the importance of drift detection techniques in the field of wind power forecasting. Wu et al. [104] introduces a replacement learning-based online adaptation framework designed for multivariate multistep time-series forecasting in the energy domain, which tackles concept drift by retraining models from scratch. The approach leverages clustering-based sampling and dimensionality reduction techniques to incorporate historical data, ensuring that the model adapts to changing data distributions over time. Additionally, the paper proposes an incremental learning model that updates the existing model incrementally to address concept drift. Lee et al. [105] innovatively addressed the issue of concept drift in photovoltaic power output forecasting by proposing a model-agnostic online forecasting method—Model-Agnostic Online Forecasting (MAOF). In this approach, the problem of forecasting in a batch learning setting is transformed into a forecasting problem in an online learning setting. The online learning algorithm is then applied to adjust the output of the prediction. This method adjusts the model output in real time through online learning algorithms rather than by retraining the model. This makes the method applicable to any forecasting model, independent of the specific model structure.

From the examples above, it is evident that applying existing solutions from the concept drift domain to the relatively emerging field of energy system data stream classification can effectively improve classification efficiency. This represents a significant trend for the future development of this field.

4. Discussion and Conclusions

In this paper, the current mainstream classification methods for wind power/photovoltaic data streams are meticulously discussed, and the classification methods are reviewed and analyzed from multiple perspectives, including structure extension, instance weighting, attribute selection, and attribute weighting. This study analyzes research on data stream techniques for fault diagnosis in wind and photovoltaic systems and provides a detailed review of the application of these methods.

In addition, the drift problem of the data stream is discussed in detail, and a comprehensive review is made for different forms and different time steps of concept drift. Furthermore, the detection methods and model updating strategies proposed by domestic and foreign scholars to cope with the concept drift problem are also discussed. Through the discussion of drift issues in data stream classification research within the energy system domain, several common problems in existing studies on wind power/photovoltaic data stream classification have been identified: generally, most of the current research only focuses on static optimization of models, lacking dynamic optimization to address the issue of data drift. In a few recent studies that have addressed data drift, most have relied on general methods for managing it. Although these studies have effectively highlighted the importance of tackling data drift in this field, they fall short of providing deeper, more comprehensive research. Using the studies outlined in Section 3 as examples, several prevalent issues emerge: models often have inherent limitations, restricting them to specific scenarios; detection mechanisms tend to be overly simplistic, leading to inefficiencies; and update strategies are often inadequate for managing sudden drifts under extreme conditions. These challenges primarily stem from a lack of systematic understanding among researchers in the energy system data stream classification field regarding effective methods for addressing data drift.

This paper, through a detailed analysis of relevant studies, highlights the substantial potential for applying data drift research in the classification of wind power and photovoltaic data streams and provides valuable information about the wind and photovoltaic power data stream classification problem and the corresponding drift problem, establishing a significant link between clean energy production and data processing. It is expected that the relevant countermeasures for the concept drift of data streams will be applied to the field of wind–photovoltaic data stream classification and fault diagnosis to improve the accuracy and reliability of the results. The paper will contribute to improving the efficiency of clean energy generation and help reduce carbon emissions.